Вычисление площади выпуклого многоугольника по координатам вершин на плоскости
УчебаМатематикаГеометрия
Вычисление площади выпуклого многоугольника по координатам вершин. Выпуклый многоугольник строится по точкам с использованием алгоритма Джарвиса
Калькулятор ниже был написан для решения частной задачи расчета площади выпуклого четырехугольника по координатам его вершин. Он только обобщает эту задачу до задачи расчета площади любого выпуклого многоугольника вообще. Собственно, на сайте уже был подобный калькулятор Площадь многоугольника, но там требовалось вводить длины сторон и диагоналей, а это несколько труднее, чем вводить только координаты вершин.
Принцип работы остается таким же — многоугольник разбивается на непересекающиеся треугольники, подсчитывается площадь всех треугольников (это легко сделать зная длины всех трех сторон — Расчет площади треугольника по формуле Герона), затем площади суммируются. Основная проблема была в том, чтобы сделать его устойчивым к ситуации, когда точки вводят не по порядку.
Предположим, сначала вводят первые четыре точки получая фигуру на рисунке ниже
При добавлении следующей точки, например, так, как на следующем рисунке
должен уже получиться многоугольник ADCBE, а не ABCDE, разбитый на треугольники ADC, ACB и ABE, соответственно.
Чтобы получить правильный многоугольник, фактически требуется получить оболочку введенных точек. Для этого калькулятор использует алгоритм Джарвиса (или алгоритм обхода Джарвиса, или алгоритм заворачивания подарка), который определяет последовательность элементов множества, образующих выпуклую оболочку для этого множества. Метод можно представить как обтягивание верёвкой множества вбитых в доску гвоздей.
Алгоритм работает за время , где n — общее число точек на плоскости, h — число точек в выпуклой оболочке. Для выпуклого многоугольник соответственно будет . Не самый оптимальный алгоритм, зато очень простой, и для этого калькулятора вполне производительный.
Как пользоваться калькулятором: начинаете вводить координаты точек выпуклого многоугольника.
Начиная с трех точек алгоритм Джарвиса будет стоить обтягивающий контур, затем контур будет разбиваться треугольники и подсчитываться общая площадь. Для справки также будут выводиться площади всех треугольников.
Вычисление площади выпуклого многоугольника по координатам вершин на плоскости
Точки многоугольника
| Точка | X | Y | ||
|---|---|---|---|---|
Точки многоугольника
Координата Х
Координата Y
Импортировать данныеОшибка импорта
Данные
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: Lorem ipsum;-50.5;-50.5
Загрузить данные из csv файла
Точность вычисленияЗнаков после запятой: 2
Выпуклый многоугольник
Общая площадь
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Алгоритм Нарайаны
- • Площадь многоугольника
- • Как определить лежит ли точка внутри треугольника или снаружи.
- • Площадь правильного многоугольника
- • Расширенный алгоритм Евклида
- • Раздел: Геометрия ( 97 калькуляторов )
алгоритм алгоритм Джарвиса Геометрия многоугольник треугольник четырехугольник
PLANETCALC, Вычисление площади выпуклого многоугольника по координатам вершин на плоскостиTimur2020-11-03 14:19:34
Поворот точек на произвольный угол онлайн
|
|
|
|||||||||||||||||||||||||||||
Первые полторы тысяч разложений.
Хотелось бы обратить Ваше внимание на то, что не надо высчитывать синус или косинус 70 градусов «в лоб», как иногда захочется сделать.
2679491924311 : 0.26794919243112) 
Угол между ними.
Матрица смежности онлайнФигуры в координатной плоскости
Фигуры на координатной плоскости
В этом уроке мы рассмотрим координатную плоскость и точки построения в
самолет.
Диаграмма, изображенная выше, называется координатной
самолет. Горизонтальная линия с надписью « х »
называется осью x и вертикальной линией
с надписью « y » называется и -ось. Точка, которая нанесена
имеет координаты (1,3), так как точка
1 единица вправо и 3
единиц выше начала координат (точка, где x -оси и y -оси встречаются). Точка
отражается по оси x , если его координата x остается прежней.
то же самое и его координата y умножается на -1.
Графически мы можем представить себе отражение через x — ось при перемещении
к своему зеркальному отображению, где зеркалом является ось x . Точно так же
точка отражается по оси y , если ее y -координата остается прежней, а ее x -координата умножается на
-1.
Графически мы можем думать об отражении
по оси y , перемещая его к своему зеркальному отображению, где зеркало
ось и . Если мы берем точку и перемещаем ее, мы говорим, что мы
переводим суть. Мы также можем подобрать
2-мерный объект и переместите его. Мы говорим, что мы
перевод объекта.
Пример 1
Лицевая сторона кулона показана ниже.
- Если задняя сторона кулона будет нарисована отражением рисунка
по оси x , каковы будут координаты D после отражения?
- Если задняя сторона кулона будет нарисована отражением рисунка
по оси y , каковы будут координаты А после отражения?
Решения
- Поскольку мы отражаем по оси x , координата x остается прежним, а координата y умножается на
-1. Координаты точки Д ар (-4,1),
поэтому координаты D отражаются через
ось x (-4,-1).
Уведомление
что умножение числа на -1 равнозначно
изменение знака числа. Это хорошая идея, чтобы сделать набросок рисунка
области отражения и убедитесь, что координаты совпадают с
координаты точки на отраженной диаграмме. Эскиз
отраженная схема показана ниже. Обратите внимание, что новая точка D имеет координаты
(-4,-1). - Поскольку мы отражаем по оси y , координата y остается прежним, а координата x умножается на
-1. Координаты точки А ар (-3,5),
поэтому координаты A отражаются через
оси и равны (3,5). Эскиз
отраженная схема показана ниже. Обратите внимание, что новая точка У есть координаты
(3,5).
Уведомление
что умножение числа на -1 равнозначно
изменение знака числа. Это хорошая идея, чтобы сделать набросок рисунка
области отражения и убедитесь, что координаты совпадают с
координаты точки на отраженной диаграмме. Эскиз
отраженная схема показана ниже. Обратите внимание, что новая точка D имеет координаты
(-4,-1). Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.
Упражнение 1
Какие координаты изображение B , когда треугольник ABC отражается по оси x ?
Пример 2
Печать на футболке должна быть сделана по приведенной ниже выкройке, включая
второй шаблон, который находится на 5 единиц вправо и
на 3 единицы ниже первого шаблона.
Что будет
новые координаты точки C быть?
Раствор
Перед переводом точка C имеет координаты (-4,1). Поскольку мы перемещаем точка 5 единиц вправо, новая х -координата
х = -4 + 5
= 1
и так как мы перемещаем точку на 3 единицы вниз, новый и -координата
г = 1 — 3
= -2
Итак, новые координаты точки C равны (1,-2).
Эскиз переведенного узора показан ниже. Мы видим, что C имеет координаты (1,-2).
Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.
Упражнение 2
Маргарита хочет нарисовать двух рыбок одинаковой формы. У нее есть
уже нарисованная одна рыба показана ниже. Вторая рыба должна быть нарисована
2 единицы выше и 4
единиц справа от первой рыбы.
Какими будут координаты
новый пункт А ?
CAHSEE часто проверяет, помните ли вы названия общих многоугольники. Напомним, что многоугольник – это замкнутый форма ограничена только прямыми линиями. Вот некоторые из этих определений.
- Треугольник: А
многоугольник с
3 стороны
- Четырехугольник:
Многоугольник с
4 стороны
- Прямоугольник: А
четырехугольник, все углы которого прямые
- Ромб: А
четырехугольник, все стороны которого имеют одинаковую длину
- Параллелограмм:
Четырехугольник, у которого противоположные стороны параллельны. Обратите внимание, что
ромб тоже параллелограмм.
- Трапеция: А
четырехугольник с двумя параллельными сторонами
- Пентагон: А
многоугольник с
5 сторон
- Шестигранник: А
многоугольник с
6 сторон
Пример 3
Точки (2,1), (4,1),
(5,4) и (1,4) являются
вершины многоугольника.
Какой тип многоугольника образован этими точками?
Раствор
Первый набросок точек на xy -плоскость. Затем соедините точки для формирования многоугольника. Эскиз показан ниже.
Так как фигура имеет 4 стороны, это не треугольник, пятиугольник или шестиугольник. Левая и правая стороны не параллельно, значит, это не параллелограмм. Верхняя и нижняя стороны имеют разной длины, так что это не ромб и не квадрат. углы не те прямые углы, значит это не прямоугольник. Обратите внимание, что верхняя и нижняя параллельны, значит это трапеция.
Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.
Упражнение 3
Точки (1,1), (3,1), (4,6) и (2,6) равны вершины многоугольника. Какой тип многоугольника образован этими точками?
А. Треугольник
Б. Трапеция
C. Параллелограмм
Д. Пентагон
Еще одно применение координатной плоскости — определение длин и площадей
заданная геометрическая форма.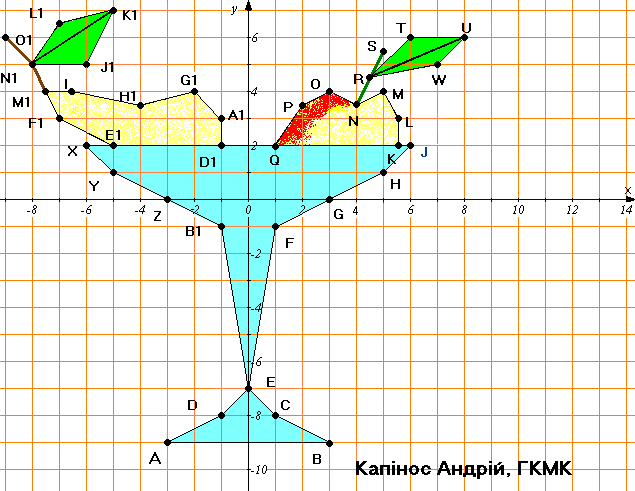
Пример 4
Показан график квадрата ABCD ниже. Какова длина одной из сторон этого квадрата?
Раствор
Поскольку ABCD — квадрат, все стороны равны такой же длины. Найдем расстояние от А к В . Считая, мы видим, что B ровно 3 единиц справа от A . Длина все стороны квадрата равны 3 единицам.
Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.
Упражнение 4
График равностороннего треугольника ABC показано ниже. Какова длина одной из сторон этого равностороннего треугольник?
Пример 5
График прямоугольного треугольника ABC есть показано ниже.
Найдите площадь этого треугольника в квадратных единицах.
Раствор
Используем формулу площади прямоугольного треугольника.
Площадь = 1/2 кв. ч. 90 005
, где b — длина основания треугольника, а h — высота треугольника. Длина основания — это расстояние от до к В . Мы измеряем это как
б = 5 единиц
Высота – это расстояние от A до С . Мы измеряем это как
ч = 3 единицы
Так что
Площадь = (1/2)(5)(3)
= 15/2
= 7,5
Площадь треугольника 7,5 квадратных единиц.
Теперь попробуйте сами. Если хотите увидеть ответ, наведите мышку на желтом прямоугольнике и появится ответ.
Упражнение 5
Показан график прямоугольника ABCD ниже. Какова площадь в квадратных единицах этого прямоугольника?
Как выполнять расчеты с использованием точек на графике (видео и практика)
Здравствуйте и добро пожаловать в это видео о расчетах с использованием точек на координатной плоскости!
Итак, во-первых, давайте вспомним, что одномерная числовая линия — это представление всех действительных чисел, которое бесконечно простирается как в положительном, так и в отрицательном направлении и выглядит примерно так:
Когда две числовые линии пересекаются под прямым углом в их координатах 0, образуется двумерная координатная плоскость, которая обычно выглядит примерно так:
Обычно горизонтальная ось называется осью \(x\), а вертикальная ось называется осью \(y\).
Точка пересечения осей называется началом координат . Построим точку на координатной плоскости.
Местоположение точки А задается как горизонтальная составляющая (\(x\)) и вертикальная составляющая ( y ) и записывается как \((x,y)\). От исходной точки, чтобы добраться до точки А, мы должны отсчитать две единицы вправо и три единицы вверх. Итак, координаты точки А равны \((2,3)\). Точно так же координаты начала координат равны \((0,0)\).
Поскольку координатная плоскость состоит из числовых линий, их можно просматривать «увеличением» или «уменьшением» настолько, насколько это необходимо для передачи данных или истории. Например, ось \(x\) здесь «увеличена»:
Из-за масштаба оси \(x\) точки координат точки B равны \((\frac{1}{2},3)\). 92}\)
Проще говоря, это «квадратный корень из квадрата расстояния по горизонтали плюс квадрат расстояния по вертикали».
В этом случае можно использовать формулу, но поскольку точки A и D лежат на одной горизонтальной линии сетки, все, что нам нужно сделать, это посчитать квадраты (это также работает для двух точек на одной вертикальной линии сетки).
2}\) 92}\)
\(D=\sqrt{1+81}\)
\(D=\sqrt{82}\)
\(D≈9,055\)
В этом случае нам потребуется оценить координаты точки F, потому что она не лежит на пересечении двух линий сетки. Часто бывает так, что нам нужно оценить координаты точки. Предположим, что точка F находится в точке \((-0,4,-350)\). Теперь давайте воспользуемся формулой расстояния, чтобы получить представление о расстоянии между точками C и F: 92}\)
\(D=\sqrt{0,36+422,500}\)
\(D=\sqrt{422 500,36}\)
\(D≈650\)
Используя координаты точек на координатной плоскости, мы также можем вычислить координаты точки, которая находится точно посередине между двумя точками, которая называется средней точкой.
Формула для нахождения координат средней точки выглядит следующим образом:
\(M=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)
На словах это легко запомнить как «среднее значение \(х\), среднее значение \(у\)».
Как мы видели ранее, расстояние между точками A и D равно 6. Половина этого расстояния равна 3. Поскольку точки A и D лежат на одной линии сетки, средняя точка также будет лежать там с координатами \((-1,3)\).
Мы можем проверить это по формуле:
\(M=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)
\(M=(\frac{-4+2}{2},\frac{3+3}{2})\)
\(M=(\frac{-2}{2},\frac{6}{2})\)
\(M=(-1,3)\)
Хотя мы всегда можем вычислить половину расстояния между двумя точками, это не сообщит нам координаты средней точки в этом примере, как это делает формула: 2})\)
\(M=(\frac{2}{2},\frac{-3}{2})\)
\(M=(1,-\frac{3}{2})\)
Чтобы построить график, нам нужно оценить местоположение \(-\frac{3}{2}\).
Ранее мы оценили координаты точки F как \((-0,4,-350)\). Воспользуемся формулой для оценки середины между точками C и F:
\(M=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)
\(M≈(\frac{0,2+(-0,4)}{2},\frac{-350+300}{2) })\)
\(M≈(\frac{-0,2}{2},\frac{-50}{2})\)
\(M≈(-0,1,-25)\)
Чтобы построить график, нам нужно оценить местоположение -25.
Надеюсь, это видео помогло вам понять, как выполнять расчеты с использованием точек на координатной плоскости! Спасибо за просмотр и удачной учебы!
Вопрос №1:
Каково расстояние между точками (2, 7) и (31, 25)?
22,54
34,13
27,92
31,79
Показать ответ Ответ: 900 06 Правильный ответ: 34,13. Формула расстояния: 92}\)\(=\sqrt{841+324}\)
\(=\sqrt{1,165}≈34,13\) Скрыть ответ Вопрос №2:
Какова середина точек (3, 5) и (4, 17)?
(\(\frac{7}{2}\), 11)
(7, 22)
(\(\frac{5}{2}\), 6)
(5, 12)
Показать ответ 90 396 Ответ: Правильный ответ: (\(\frac{7}{2}\), 11). Формула для нахождения средней точки:
\(M=(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\) 92}\)
\(=\sqrt{9+9}\)
\(=\sqrt{18}≈4.24\)
Какова середина точек (-7, 3) и (14, -9)?
(-11, 8)
(7, -6)
(\(-\frac{11}{2}\), 4)
(\(\frac{7}{2}\), -3)
Показать ответ 9 0396 Ответ: Правильный ответ: (\(\frac{7}{2}\), -3).
Ваш комментарий будет первым