Построение графиков тригонометрических функций — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Построение графиков тригонометрических функций
y2
2
3 3
4
5
6
2
7
6
5
4 4
3
3
2
3
4
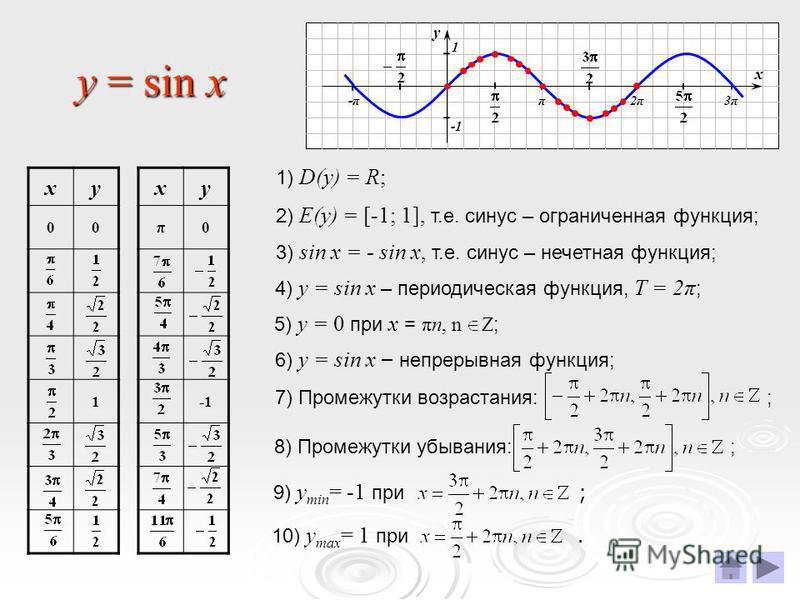
y = sin x
1
6
0
0
11
7 6
5 4
-1
3
6 4 3
2
2 3 5
3 4 6
х
y = sin x
2
3 3
4
5
6
2
7
6
5
4 4
3
3
2
3
4
6
0
11
5 4
3
7 5 4
6 4 3
3
2
5 7 11 2
3 4 6
х
y
3
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
y = sin x
2 5 7
2 3 6
6
3
2
х
y
3
2
y = соs x
— 3
2
1
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
2 5 7
2 3 6
6
3
2
х
y
3
2
y = соs x
— 3
2
1
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
y = sin x
2 5 7
2 3 6
6
3
2
х
№ 16.
27 (а)y = sin x
y = sin(x )
3
y
3
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
№ 16.27 (б)
y = sin x
y = sin(x + )
4
y
3
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
№ 16.28 (а)
y = sin x
y = sin x 2
y
3
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
№ 16.28 (б)
y = sin x
y = sin x + 1
y
3
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
№ 16.29 (а)
y
y = sin x
3
2
y = sin(x – )
4
y = sin(x – ) + 1
4
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
№ 16.
30 (а)y
3
y = sin x
y = – sin x
y = – sin(x + 6 )
2
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
y
3
y = sin x
y = sin 2x
y = sin 0,5x
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
y
3
y = соs x
y = соs 3x
y = соs 3x/2
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
y
3
y = 3sin x
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
y = sinx
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
y
y = tg x
2
2
3
4
6
1
0
2
6
4
3
2
3
4
6
6 4 3
0
-1
-2
2
х
3
y = tg x
y = – tg x
y = – tg(x + 6 )
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
y
3
y = tg 2x
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
2 5 7
2 3 6
6
3
2
х
y
2
0
6
4
3
2 2
3
3
5 4
6
y = сtg x
1
0
-1
-2
6 4 3
2
2 3 5
3 4 6
х
3
y = сtg x
y = – сtg x
2
1
— 3
2
5 2
— 7 — — 6 — 3 — 2 — 3 — 6
6
0
6 3
-1
-2
-3
х
2 5 7
2 3 6
6
3
2
y
y = сtg 2x
3
2
—
— 5
— 3
4
4
4
5 2
— 3
— 7 — — 6 — 3 — 2 — 3 — 6
2
6
1
4
0
6 3
-1
-2
-3
3
5
4
4
2 5 7
2 3 6
6
3
2
х
English Русский Правила
Построение графиков тригонометрических функций средствами табличного процессора Microsoft Excel
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа № 3»
Воскресенского муниципального района Московской области
140200.
Московская область, г.Воскресенск, ул. Зелинского д.5Д
Тел. 8496-44-2-20-60, E-mail: [email protected]
_____________________________________________________________________________
Урок по математике
в 10 классе по теме:
«Построение графиков тригонометрических функций средствами табличного процессора Microsoft Excel»
Учитель математики и информатики
Лоскутова О.Н.
г.
Воскресенск
2017г.
Открытый урок по теме
Построение графиков тригонометрических функций средствами табличного процессора Microsoft Excel
Учитель: | Лоскутова О. Н. |
Образовательное учреждение: | МОУ «Средняя общеобразовательная школа №3» |
Предмет: | Информатика |
Краткая аннотация урока | (интегрированный урок) |
Класс, профиль: | 10 класс, базовый уровень |
Тема: | Построение графиков тригонометрических функций средствами табличного процессора Microsoft Excel |
Тип урока: | комбинированный (изучение нового материала,
закрепление навыков на построение диаграмм). |
Цели: | · научить строить графики элементарных математических функций с помощью табличного процессора Excel; · показать возможности использования программы Excel для решения задач по алгебре; · закрепить навыки работы с Мастером диаграмм |
Задачи: | ознакомление учащихся с основными приемами построения графиков тригонометрических функций в программе Excel |
Технологии обучения: | ИКТ, здоровьесберегающая, групповая технология |
Приобретаемые навыки детей: | умение выполнять построения графиков тригонометрических функций в программе Excel |
Формы организации работы детей: | индивидуальная, разноуровневая |
Формы организации работы учителя: | обобщение материала по средствам электронной таблицы теме Microsoft Excel и изучение нового материала на тему «Построение тригонометрических графиков функций средствами табличного процессора Microsoft Excel» |
Используемое оборудование: | компьютеры, мультимедийный проектор, экран |
Используемые ресурсы из других общедоступных источников: | Интернет-ресурсы, единая цифровая коллекция образовательных ресурсов: http://school-collection. http://uchitelu.net/media/231 http://www.rosinka.vrn.ru/dinex/og_graf.htm http://tvsh3004.narod.ru/alg07.html |
edu.ru/catalog/
Цели:
· научить строить графики элементарных математических функций с помощью табличного процессора Microsoft Excel;
· показать возможности использования программы Microsoft Excel для решения задач по алгебре;
· закрепить навыки работы с Мастером диаграмм.
Задачи
образовательные:
· ознакомление учащихся с основными приемами построения графиков тригонометрических функций в программе Microsoft Excel;
развивающие:
· формирование у учащихся логического и алгоритмического мышления;
· развитие познавательного интереса к предмету;
· развитие умения оперировать ранее полученными знаниями;
·
развитие умения планировать свою
деятельность.
воспитательные:
· воспитание умения самостоятельно мыслить, ответственности за выполняемую работу, аккуратности при выполнении работы.
Тип урока: комбинированный (изучение нового материала, закрепление навыков по теме: «Построение диаграмм»).
Раздаточный материал: разноуровневые карточки с индивидуальными заданиями на построение графиков функций, тест.
Оборудование: экран, мультимедийный проектор, компьютеры, раздаточный материал, справочный материал.
Ход урока
1. Организационный момент (3 мин)
(проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока.)
Слайд 1
На предыдущих уроках мы с вами работали в прикладной
программе Microsoft Excel.
И выяснили, что данная
программа упрощает работу с таблицами, может подсчитать различной сложности
данные, отсортировать их. Что же еще можно сделать с помощью электронной
таблицы? Давайте вернемся к королеве наук – математике.
Учитель: Что это?
cos(x) = tg(x)*cos(x) (написано на листе бумаги)
Учитель: Каким образом можно узнать решение данного уравнения?
Ученики: Алгебраическим и геометрическим способом.
Учитель: Чтобы решить геометрически, что надо для этого сделать?
Ученики: Построить графики, точка пересечения и будет являться решением данного уравнения.
Учитель: Вы наверно догадались, какая тема сегодняшнего урока?
Ученики: Построение графиков.
Учитель: Тема сегодняшнего
урока «Построение графиков функций средствами табличного
процессора Microsoft Excel» и мы научимся строить графики элементарных
математических функций с помощью табличного процессора Microsoft Excel.
2. Проверка Д/з (3 мин)
Учитель:
— Сегодня мы с вами немного посоревнуемся и проверим домашнее задание. Вы разделены на команды, одни сидят по правую сторону от меня – это команда 1, другие по левую – команда 2. Перед тем как мы перейдем к изучению новой темы, давайте выясним, усвоили ли вы предыдущие темы.(команды задают друг — другу по 3 вопроса, за каждый правильный ответ – 1 балл.)
— Для чего предназначена электронная таблица?
(Ответ учащихся: Электронная таблица используется для обработки преимущественно числовых данных, структурированных с помощью таблицы.)
— Что из себя представляет электронная таблица?
(Ответ учащихся: Она представлена в виде совокупности нумерованных строк и поименованных буквами латинского алфавита столбцов.)
— Как задается имя ячейки?
(Ответ
учащихся: Имя ячейки обозначается именем столбца и номером строки, на
пересечении которых она располагается.
)
— Какую ячейку называют активной?
(Ответ учащихся: Ячейку, в которой выполняется ввод данных, называют активной.)
— Перечислите действия пользователя, позволяющие сделать ячейку активной.
(Ответ учащихся: Чтобы сделать ячейку активной на нее необходимо указать курсором, нажать левую клавишу мыши. Правильность выполнения операции будут отражена в выделении ячейки прямоугольной рамки.)
— Как электронная таблица отличает совокупность символов от формулы?
(Ответ учащихся: Признаком формулы является знак «=» стоящий перед совокупностью символов).
3. Объяснение нового материала. (10 минут)
Учитель:
Слайд 2
— Ребята, обратите внимание! На экране написаны высказывания известного человека о математике:
Рано или поздно всякая правильная математическая идея
находит применение в том или ином деле.
(А.
Н. Крылов, русский и советский кораблестроитель, специалист в области
механики, математики)
Эти слова написаны неслучайно. Сегодняшний урок, как я вам уже говорила, связан с математикой и сейчас мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических работах вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Microsoft Excel.
Учитель: Для исследования функции и построения ее графика требуется много времени, приходится выполнять много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.
Рассмотрим построение графиков функций на примере функции у = sin x.
Вид данного графика хорошо известен вам по урокам математики, все помнят как долго строится данный график Слайд 3, попробуем построить график функции у = sin x средствами в Excel.
Программа будет строить график по точкам: точки с известными значениями будут
плавно соединяться линией.
Эти точки нужно указать программе, поэтому, сначала
создается таблица значений функции у = f(х).
Чтобы создать таблицу, нужно определить
· отрезок оси ОХ, на котором будет строиться график.
· шаг переменной х, т.е. через какой промежуток будут вычисляться значения функции.
· попробуем построить график функции у=sin x.
Слайд 4
Задание. Построить график функции у = sin x на отрезке [– 6; 6] с шагом h = 0,5.
В ячейку А1 введем х,
в ячейку В1 у = sin x. Затем в А2 введем -6, а в А3 значение
-5,5. Выделим диапазон A2:A3 и с помощью маркера автозаполнения введем значения
аргумента x до 6.
Выделим ячейку В2, вызовем Мастер функций, в категории
математические выберем функцию SIN, в качестве аргумента функции выберем ячейку
А2. Применим автозаполнение ячеек формулой. Выделим
заполненные ячейки и применим выравнивание по центру и установим черные,
сплошные тонкие внешние границы.
К диапазону ячеек А1:В1 применим форматирование:
выравнивание по центру, шрифт полужирный, наклонный.
Выделим заполненный диапазон, нажмем на кнопку мастера диаграмм на стандартной панели, выберем тип диаграммы Точечная, Вид как на рис. и нажмем кнопку Готово.
4. Физкультминутка. (3 минуты). Здоровье сберегающая технология
Учитель: А для того чтобы мы смогли продолжить работу за компьютером без риска для здоровья давайте выполним зарядку для глаз.
Комплекс упражнений для глаз
Упражнения выполняются сидя в удобной позе, позвоночник прямой, глаза раскрыты, взгляд – прямо, отвернуться от компьютера.
Упражнение 1. Взгляд направить влево — вправо, вправо-влево, вверх — прямо, вниз — прямо без задержки в каждом положении. Повторить 5 раз и 5 раз в противоположном положении.
Упражнение 2. Закройте глаза на счет «раз-два», откройте глаза и посмотрите на кончик
носа на счет «три-четыре».
Упражнение 3. Круговые движения глазами: до 5 кругов влево и вправо.
4. Самостоятельная работа по закреплению у учащихся навыков на построение графиков функций средствами табличного процессора Microsoft Excel (по группам)(10 мин)
1 группа выполняет лабораторную работу на построение графика функции в электоронной таблице Microsoft Excel (задания разноуровневые).
2 группа выполняет тест по теме «Электронные таблицы Excel», состоящий из 16 вопросов с 4 вариантами ответов. По истечении времени группы меняются видами деятельности.
Результаты теста, представленные на Слайде 5, проверяются сразу по его окончании. Ученики сверяют свои ответы с ответами на слайде и выставляют себе оценку. (3 мин)
Лабораторная работа
Задание (1 вариант). Построить график функции у = sin x на отрезке [– 4;4] с шагом h = 0,25.
Задание (2 вариант) Построить график функции у = sin x на отрезке [– 5; 5] с шагом h = 0,5
Тест по теме «Электронные таблицы Excel»
1.
Электронная
таблица — это:
1. прикладная программа, предназначенная для обработки структурированных в виде таблицы данных;
2. прикладная программа для обработки кодовых таблиц;
3. устройство ПК, управляющее его ресурсами в процессе обработки данных в табличной форме;
4. системная программа, управляющая ресурсами ПК при обработке таблиц.
2. Электронная таблица предназначена для:
1. обработки преимущественно числовых данных, структурированных с помощью таблиц;
2. упорядоченного хранения и обработки значительных массивов данных;
3. визуализации структурных связей между данными, представленными в таблицах;
4. редактирования графических представлений больших объемов информации.
3. Электронная таблица представляет собой:
1.
совокупность нумерованных строк и поименованных буквами латинского алфавита
столбцов;
2. совокупность поименованных буквами латинского алфавита строк и нумерованных столбцов;
3. совокупность пронумерованных строк и столбцов;
4. совокупность строк и столбцов, именуемых пользователем произвольным образом.
4. Строки электронной таблицы:
1. именуются пользователями произвольным образом;
2. обозначаются буквами русского алфавита;
3. обозначаются буквами латинского алфавита;
4. нумеруются.
5. В общем случае столбы электронной таблицы:
1. обозначаются буквами латинского алфавита;
2. нумеруются;
3. обозначаются буквами русского алфавита;
4.
именуются
пользователями произвольным образом;
6. Для пользователя ячейка электронной таблицы идентифицируются:
1. путем последовательного указания имени столбца и номера строки, на пересечении которых располагается ячейка;
2. адресом машинного слова оперативной памяти, отведенного под ячейку;
3. специальным кодовым словом;
4. именем, произвольно задаваемым пользователем.
7. Вычислительные формулы в ячейках электронной таблицы записываются:
1. в обычной математической записи;
2. специальным образом с использование встроенных функций и по правилам, принятым для записи выражений в языках программирования;
3. по правилам, принятым исключительно для электронный таблиц;
4. по
правилам, принятым исключительно для баз данных.
8. Выражение 5(A2+C3):3(2B2-3D3) в электронной таблице имеет вид:
1. 5(A2+C3)/3(2B2-3D3) ;
2. 5*(A2+C3)/3*(2*B2-3*D3) ;
3. 5*(A2+C3)/(3*(2*B2-3*D3)) ;
4. 5(A2+C3)/(3(2B2-3D3)) .
9. Выберите верную запись формулы для электронной таблицы:
1. C3+4*D4
2. C3=C1+2*C2
3. A5B5+23
4. =A2*A3-A4
10. При перемещении или копировании в электронной таблице абсолютные ссылки:
1. не изменяются;
2. преобразуются вне зависимости от нового положения формулы;
3. преобразуются в зависимости от нового положения формулы;
4. преобразуются в зависимости от длины формулы;
11.
При
перемещении или копировании в электронной таблице относительные ссылки:
1. преобразуются вне зависимости от нового положения формулы;
2. преобразуются в зависимости от длины формулы;
3. не изменяются;
4. преобразуются в зависимости от нового положения формулы.
12. Диапазон — это:
1. совокупность клеток, образующих в таблице область прямоугольной формы;
2. все ячейки одной строки;
3. все ячейки одного столбца;
4. множество допустимых значений.
13. Активная ячейка — это ячейка:
1. для записи команд;
2. содержащая формулу, включающую в себя имя ячейки, в которой выполняется ввод данных;
3.
формула в
которой содержатся ссылки на содержимое зависимой ячейки;
4. в которой выполняется ввод команд.
14. Какая формула будет получена при копировании в ячейку С3, формулы из ячейки С2:
1. =A1*A2+B2;
2. =$A$1*$A$2+$B$2;
3. =$A$1*A3+B3;
4. =$A$2*A3+B3;
5. =$B$2*A3+B4?
15. Чему будет равно значение ячейки С1, если в нее ввести формулу =А1+B1:
1. 20;
2. 15;
3. 10;
4. 30?
16. Чему будет равно значение ячейки С1, если в нее ввести формулу =СУММ(A1:A7)/2:
1. 280;
2. 140;
3. 40;
4.
35?
Ответы
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
1 | 1 | 1 | 4 | 1 | 1 | 2 | 3 | 4 | 1 | 4 | 1 | 4 | 3 | 4 | 2 |
Критерии оценки
15-16 заданий 12-14 заданий 8-11 заданий Менее 8 заданий | «5» «4» «3» «2» |
Обратная связь «Ученик – учитель» по результатам выполненного диктанта:
— «5» — ……….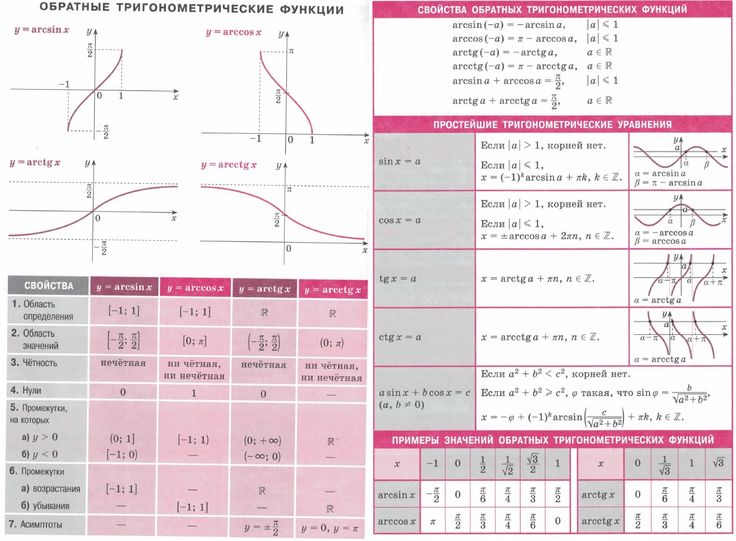
. человек
— «4» — ……….. человек
— «3» — ……….. человек
— «2» — ……….. человек
Учитель: Сегодня мы с вами научились строить графики элементарных математических функций с помощью табличного процессора Excel; показали возможности использования программы Excel для решения задач по математике; закрепили навыки работы с Мастером диаграмм.
5. Подведение итогов урока. Рефлексия (3 мин)
Учитель: Ребята, подведем итоги нашего урока.
— Что повторили сегодня на уроке?
(Ответы детей: как работать с формулами с данными и формулами в Microsoft Excel)
— Что вызвало у вас затруднение?
(Ответы детей: как форматировать графики построенных функций)
— Что вы сегодня научились делать?
(Ответы детей: Решать уравнения графическим способом; отработать алгоритм решения.)
— Как сэкономить время решения уравнений графически?
(Ответы детей: Использовать
компьютерную программу – Master Function.
)
— Какие выводы вы сделали в процессе решения?
(Ответы детей: С помощью компьютера можно рассмотреть случаи решения уравнений на большем промежутке, рассмотреть большое количество разнообразных графиков, их взаимное расположение.)
Учитель: Сегодня на уроке информатики вы пополнили свои знания и по математике и убедились, что многие школьные предметы связаны друг с другом. Я хотела бы вам пожелать:
Учитель: Вы хорошо поработали, спасибо за урок.
Учитель выставляет оценки за математический диктант и самостоятельную работу.
6. Постановка Д/З (1 мин)
Литература:
1.
Алгебра и начала математического анализа.10 класс:
учеб. Для общеобразоват. учреждений: базовый и профил. уровни/ [С.м.
Никольский, М.К. Потапов, Н.Н. решетников, А.В. Шевкин]. – 9-е изд. – М.:
Просвещение, 2010. – 464 с.: ил.- (МГУ – школе).
2. Семакин И. Г. Информатика и ИКТ. Базовый уровень : учебник для 10-11 классов / И. Г. Семакин, Е. К. Хеннер. – 6-е изд. – М. : БИНОМ. Лаборатория знаний, 2010. – 246 с. : ил.
3. Соколова О.Л. Универсальные поурочные разработки по информатике. 10 класс. М.: ВАКО, 2006. – 400 с. – (В помощь школьному учителю).
4. Шелепаева А.Х. Поурочные разработки по информатике: базовый уровень. 10-11 классы. – М.: ВАКО, 2007. – 352 с. – (В помощь школьному учителю).
5. Шелепаева А.Х. Поурочные разработки по информатике: базовый уровень. 10-11 классы. – М.: ВАКО, 2007. – 352 с. – (В помощь школьному учителю).
Интернет-ресурсы:
http://school-collection.edu.ru/catalog/
http://uchitelu.
net/media/231
http://www.rosinka.vrn.ru/dinex/og_graf.htm
http://tvsh3004.narod.ru/alg07.html
Графики тригонометрических функций — изучайте и разбирайтесь онлайн
Наше изучение тригонометрии часто связано с поиском недостающих углов и длин. При этом мы часто сталкиваемся с тригонометрическими значениями , которые нам нужно вычислить, чтобы получить наш результат. Например, мы можем обнаружить, что недостающую длину треугольника можно найти, вычислив 50sin(70). Итак, мы просто берем наш удобный калькулятор, набираем 50sin(70) и Боб становится вашим дядей. Однако вы могли задаваться вопросом, почему значение sin(70) такое, какое оно есть; откуда номер? В этой статье мы рассмотрим графики тригонометрических функций помогут нам ответить на этот вопрос.
Вспомните, когда мы изучали тригонометрические отношения, мы смотрели на функции sin(x),cos(x) и tan(x).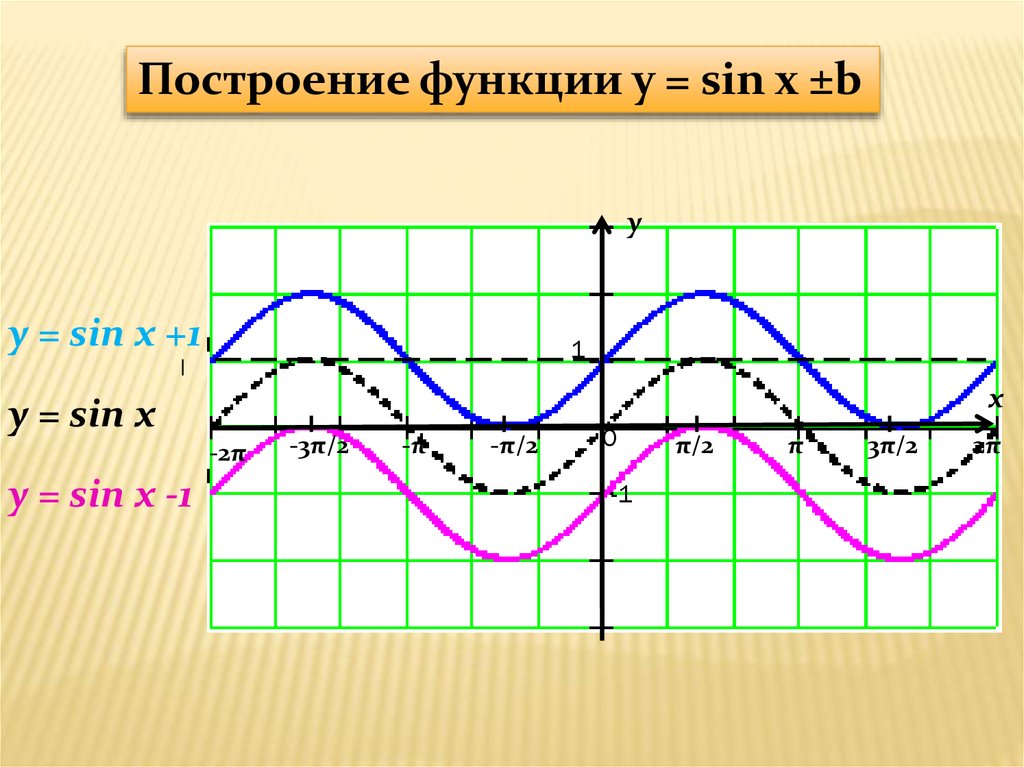
Тригонометрическая функция — это функция, которая связывает размер угла в прямоугольном треугольнике с длинами его сторон.
Свойства тригонометрических графиков
При изучении графиков тригонометрических функций нас интересуют три графика: графики sin(x) , cos (x ) и tan(x) . Для математики GCSE вам нужно запомнить, как выглядят эти графики. Тем не менее, у них есть ключевых свойства , которые делают их довольно простыми в рисовании. Начнем с графика y=sin(x).
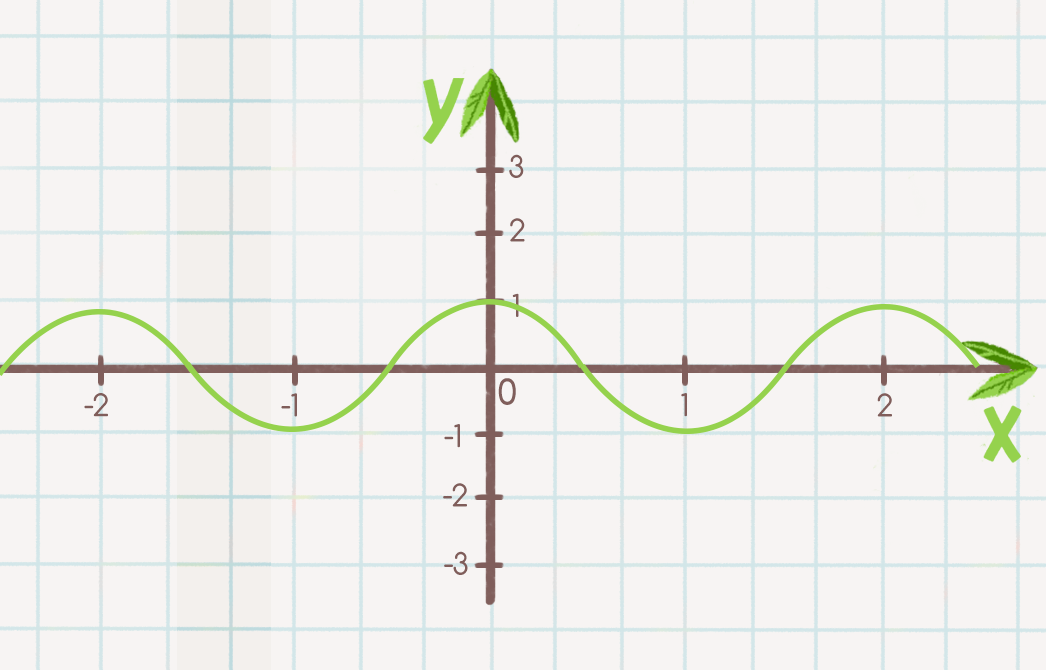
График y=sin(x)
Графики тригонометрической функции — График y=sin(x), Jordan Madge — StudySmarter Originals
Ключевые свойства
Мы видим, что график y=sin(x) имеет максимальное значение 1 и минимальное значение -1. Отсюда мы можем сделать вывод, что значение sin(x) может быть только между 1 и -1.
Таким образом, если у нас есть уравнение, в котором sin(x)=1,4, то оно не имеет решений.Значения x возрастают с интервалами в 90 градусов и периодически повторяют в цикле 360 градусов. Другими словами, через каждые 360 градусов мы замечаем, что график повторяет .
В различных точках граф симметричен . Например, у нас есть симметрия относительно линии x=90°. Это пригодится нам в дальнейшем при поиске множественных решений тригонометрических уравнений.
Таким образом, если у нас есть уравнение, в котором sin(x)=1,4, то оно не имеет решений. Предположим, что sin(x)=1. Глядя на график, мы видим, что sin(x)=1 при x=-270°, x=90° и x=450°. Поскольку график sin(x) будет продолжать колебаться бесконечно, мы могли бы заключить из этого, что уравнение sin(x)=1 имеет бесконечное количество решений. Если тригонометрическое уравнение имеет одно решение, оно будет иметь бесконечное число решений, и позже мы будем использовать свойство симметрии, чтобы попытаться найти такие решения.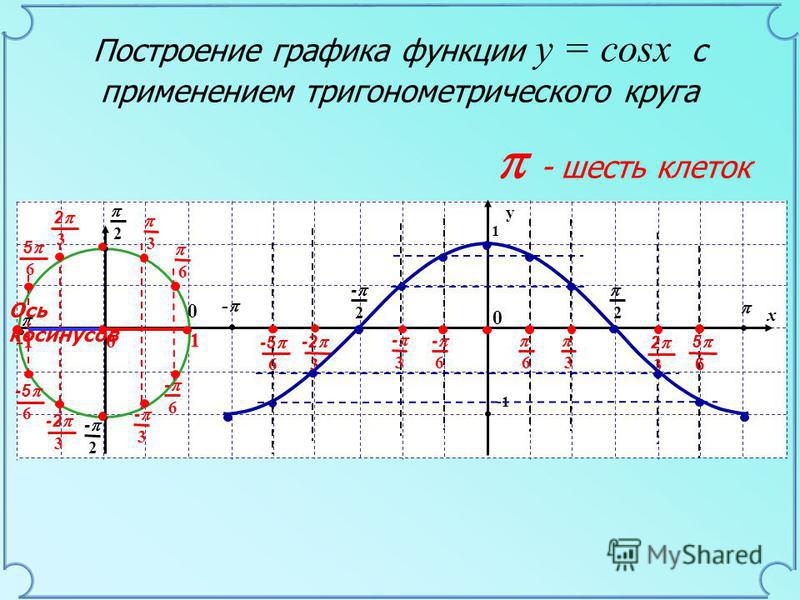
Официальное название графика, имеющего форму синусоиды, — синусоидальная волна . Многие вещи естественным образом принимают форму синусоиды, например, движение планет вокруг Солнца.
График y=cos(x)
Графики тригонометрической функции – график y=cos(x), Jordan Madge – StudySmarter Originals
Ключевые свойства
Если вы не внимательно изучали последний раздел, то можете подумать, что этот график почти такой же, как график sin(x). Однако, если вы вернетесь назад и сыграете в игру нахождения различий, вы заметите, что график cos(x) — это просто график sin(x) , сдвинутый на 90 градусов на влево .
Подобно sin(x), график cos(x) также имеет максимум при 1, минимум при -1, а также свойство симметрии . Мы просто должны помнить, что график cos(x) начинается с 1, тогда как график sin(x) начинается с 0.
График y=tan(x)
y=tan(x), Jordan Madge-StudySmarter Originals
Ключевые свойства
График tan(x) немного отличается от cos(x) и sin(x). Тем не менее, это похоже в том смысле, что это периодический , и мы видим, что он повторяется каждые 180 градусов .
На графике tan(x) есть вещи, называемые асимптотами , которые представляют собой точки, к которым график стремится, но никогда не достигает их. На графике они представлены пунктирными линиями. Мы видим, что первая положительная асимптота появляется при x=90°, а затем они повторяются каждые 180°.
В отличие от cos(x) и sin(x), график tan(x) не имеет максимума или минимума плюс или минус 1; он имеет максимум и минимум плюс-минус бесконечность . Таким образом, можно решить уравнение tan(x)=3,8, чтобы получить бесконечное число действительных значений x.
Графики тригонометрических функций Методы
Нахождение решений тригонометрических уравнений
В предыдущем разделе мы вкратце коснулись того факта, что если тригонометрическое уравнение имеет одно решение, то оно будет иметь бесконечное число решений. В следующем разделе мы разберемся, как найти несколько решений тригонометрических уравнений.
Поскольку тригонометрические уравнения могут иметь бесконечное число решений, нам нужно указать границу при формулировке ответов, чтобы мы не тратили бесконечное количество времени на поиск каждого решения. Эта граница обычно выражается в виде интервала, например, 0°≤x≤360° или -180°≤x≤180°. Обязательно обратите внимание на эту границу, отвечая на вопросы.
Графики тригонометрических функций Примеры
Найдите решение уравнения sin(x)=0,9 для интервала 0°≤x≤360°.
Решение:
Первым шагом является построение графика y=sin(x) и y=0,9 на одной оси для интервала 0°≤x≤360°.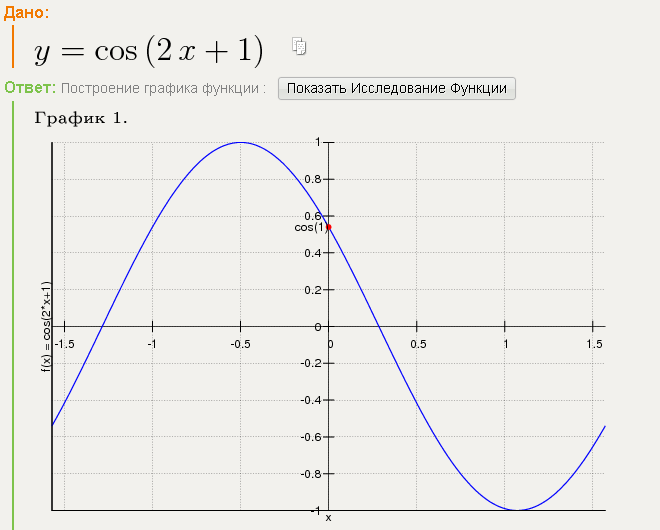
Графики тригонометрических функций — График, показывающий решения sin(x) = 0,9, Jordan Madge — StudySmarter Originals
Точки пересечения отмечены оранжевым цветом как 1 и 2, это решения, которые мы ищем, чтобы найти точное значения.
Второй шаг — найти точное значение начального решения. Это можно сделать, набрав sin-1(0.9) в наш калькулятор. Сделав это, мы получим x=64,2°. Очевидно, это первое решение, отмеченное на диаграмме, поскольку оно находится между 0° и 90°.
Важно отметить, что ваш калькулятор должен быть в режиме градусов при расчете тригонометрических значений, так как мы работаем в градусах. Если ваш калькулятор находится в режиме радиан , ответ может отличаться, и вы можете получить неверный ответ. Вы знаете, что ваш калькулятор находится в режиме градусов, когда в верхней части экрана появляется маленькая буква D. Если вы видите букву R или любую другую букву, это означает, что выбран неправильный режим, и его необходимо изменить.
Следующий шаг — найти другое решение, используя свойство симметрии графика sin(x). Если мы заметим, график симметричен относительно role=»math» x=90°. Таким образом, мы можем найти второе решение, вычислив расстояние между 64,2° и 90°, а затем прибавив это значение к 90°. Это можно проиллюстрировать на диаграмме ниже:
Графики тригонометрических функций — График, показывающий решения sin(x) = 0,9, Jordan Madge — StudySmarter Originals
Поскольку расстояние между 64,2° и 90° — это 25,8°, второе решение — role=»math» 90+25,8=115,8°. Следовательно, двумя решениями уравнения sin(x)=0,9 в интервале 0°≤x≤360° являются role=»math» x=64,2° и role=»math» x=115,8°.
Найдите решение cos(x)=-0,2 для интервала -180°≤x≤180°.
Решение:
Первый шаг — начертить графики y=cos(x) и role=»math» y=-0,2 на одних и тех же осях для интервала -180°≤x≤180°, так что что мы можем видеть решения, которые мы пытаемся найти.
Графики тригонометрических функций. График, показывающий решения cos(x)=-0,2, Jordan Madge- StudySmarter Originals
Следующим шагом является нахождение начального решения путем ввода cos-1(-0,2) в наш калькулятор. Получаем role=»math» x=101,5°. Ясно, что это решение, отмеченное на диаграмме цифрой 2, так как это немного больше, чем role=»math» 90°, но меньше, чем role=»math» 180°.
Теперь нам нужно найти другое решение, изображенное на диаграмме. Поскольку график cos(x) симметричен относительно линии x=0, мы можем видеть, что другое решение должно быть при role=»math» x=-101,5°. Таким образом, двумя решениями для role=»math» cos(x)=-0,2 в интервале -180°≤x≤180° являются role=»math» x=101,5° и role=»math» x=-101,5° .
Найдите решение уравнения tan(x)=2,3 для интервала 0°≤x≤360°.
Решение:
Первым шагом, как обычно, является построение графиков y=tan(x) и role=»math» y=2.3 на тех же осях для интервала 0°≤x≤360° .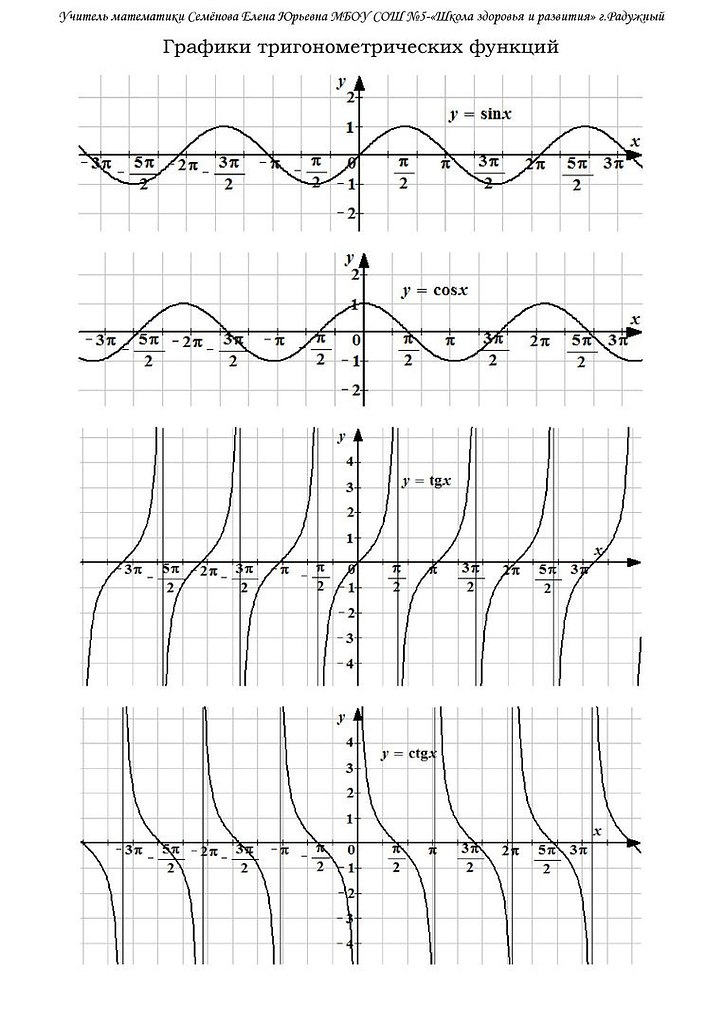
Графики тригонометрических функций — график, показывающий решения tan(x)=2,3, Джордан Мэдж — StudySmarter Originals
Мы видим, что есть две точки пересечения и, следовательно, два решения tan(x)=2,3. Первое решение можно найти, введя в наш калькулятор role=»math» tan-1(2.3). Таким образом, мы получаем role=»math» x=66,5°Это явно первое решение, так как оно находится между 0 и 9.0 градусов.
График tan(x) периодически повторяется после поворота на 180 градусов. Следовательно, мы можем найти следующее решение, прибавив множители 180 к исходному решению. Итак, второе решение находится при role=»math» 180+66,5=246,5°. Следовательно, два решения tan(x)=2,3 в интервале 0°≤x≤360° — это role=»math» x=66,5° и role=»math» x=246,5°.
Решения любых уравнений, содержащих tan(x), можно найти, прибавив к исходному решению число, кратное 180.
Найдите решения уравнения 4tan(x)=3 для интервала -180°≤x≤180°.
Решение:
Мы не можем решить это уравнение в его текущей форме.
Сначала нам нужно разделить обе части на 4, чтобы получить tan(x) сам по себе. Получаем тангенс(х)=34. Теперь мы можем найти первое решение уравнения, взяв обратный тангенс обеих сторон, чтобы получить x=tan-134=36,9°.
Теперь, поскольку он коричневый, мы знаем, что решения можно найти, добавляя или вычитая кратные 180° к исходному решению. Таким образом, следующее решение будет на уровне 36,9.+180=216,9, однако это выходит за пределы допустимого диапазона. Мы можем получить другое решение, вычитая 180° из 36,9°, чтобы получить -143,1°, что находится в диапазоне. Вычитание еще 180° даст решение вне диапазона, поэтому два решения 4tan(x)=3 в интервале -180°≤x≤180° равны x=36,9° и x=-143,1°.
Графики тригонометрических функций — основные выводы
- При изучении графиков тригонометрических функций нас интересуют три графика: графики sin(x), cos(x) и tan(x).
- Графики sin(x) и cos(x) имеют максимальное значение 1 и минимальное значение -1, график tan(x) имеет максимум и минимум плюс или минус бесконечность.
- График cos(x) — это просто график sin(x), сдвинутый влево на 90 градусов.
- Графики sin(x) и cos(x) обладают свойствами симметрии, которые позволяют нам находить несколько решений при решении уравнений.
- Для уравнений, содержащих tan(x), мы можем получить каждое решение, прибавив к каждому решению число, кратное 180.
Графики тригонометрических функций: примеры | StudySmarter
Безусловно, лучший способ понять поведение тригонометрических функций — создать визуальное представление их графиков на координатной плоскости. Это помогает нам определить их ключевые особенности и проанализировать влияние этих функций на внешний вид каждого графика. Однако знаете ли вы, какие шаги нужно выполнить, чтобы построить график тригонометрических функций и их обратных функций? Если ваш ответ отрицательный, не беспокойтесь, мы проведем вас через весь процесс.
В этой статье мы определим, что такое графики тригонометрических функций, обсудим их ключевые особенности и покажем вам, как строить графики тригонометрических функций и их обратных функций на практических примерах.
Графики тригонометрических функций представляют собой графическое представление функций или отношений, определенных на основе сторон и углов прямоугольного треугольника. К ним относятся функции синуса (sin), косинуса (cos), тангенса (tan) и соответствующих им обратных функций косеканса (csc), секанса (sec) и котангенса (cot).
Каковы основные особенности графиков тригонометрических функций?
Прежде чем мы приступим к построению графика тригонометрических функций, нам необходимо определить некоторые ключевые характеристики о них:
Амплитуда
Амплитуда тригонометрических функций относится к коэффициенту вертикального растяжения , который вы можете рассчитать как абсолютное значение половины разницы между его максимальным значением и его минимальным значением.
Амплитуда функций y=sinθ и y=cosθ равна 1-(-1)2=1.
Для функций вида y=asinbθ или y=acosbθ амплитуда равна абсолютному значению a.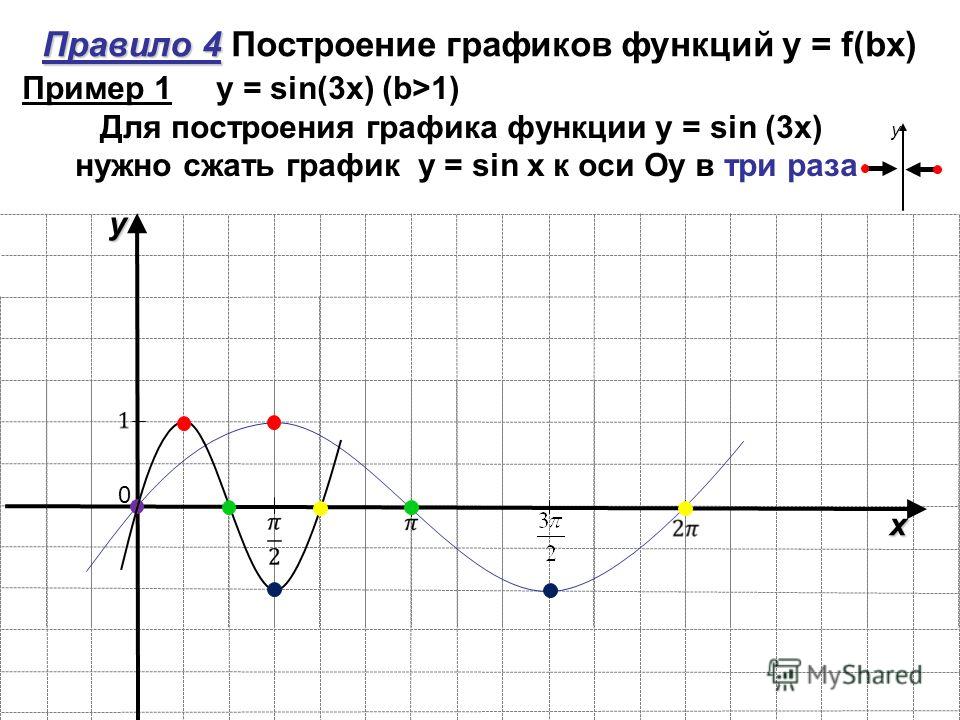
Amplitude=a
Если у вас есть тригонометрическая функция y=2sinθ, то амплитуда функции равна 2. максимальное значение.
Период
Период тригонометрических функций представляет собой расстояние по оси X от начала узора до точки, где он начинается снова.
Период синуса и косинуса равен 2π или 360º.
Для функций вида y=asinbθ или y=acosbθ, b известен как коэффициент горизонтального растяжения , и вы можете рассчитать период следующим образом:
Period=2πbor360°b
Для функций в
Период=πbor180°b
Найдите период следующих тригонометрических функций: 4
- y=tan13θ
Период=πb=π13=π13=3π
Область и диапазон
Область и область значений основных тригонометрических функций следующие: метрическая функция
..Помните, что все тригонометрические функции являются периодическими , потому что их значения повторяются снова и снова через определенный период времени.
Как построить график тригонометрических функций?
Чтобы построить график тригонометрических функций, выполните следующие действия:
Если тригонометрическая функция представлена в виде y=asinbθ, y=acosbθ или y=atanbθ, то определите значения a и b , и определите значения амплитуды и периода, как описано выше.
Создайте таблицу упорядоченных пар для точек, которые вы будете включать в график.
Первое значение в упорядоченных парах будет соответствовать значению угла θ, а значения y будут соответствовать значению тригонометрической функции для угла θ, например, sin θ, поэтому упорядоченная пара будет (θ , sin θ). Значения θ могут быть либо в градусах, либо в радианах.
Первое значение в упорядоченных парах будет соответствовать значению угла θ, а значения y будут соответствовать значению тригонометрической функции для угла θ, например, sin θ, поэтому упорядоченная пара будет (θ , sin θ). Значения θ могут быть либо в градусах, либо в радианах.Единичный круг можно использовать для определения значений синуса и косинуса для наиболее часто используемых углов. Пожалуйста, прочитайте о тригонометрических функциях, если вам нужно вспомнить, как это сделать.
График синусов
Синус — это отношение длины противоположной стороны прямоугольного треугольника к длине гипотенузы.
График функции синуса y=sinθ выглядит следующим образом:
График синуса, Марилу Гарсиа Де Тейлор — StudySmarter Originals график повторяется каждые 2π радиан или 360°.
Минимальное значение синуса равно -1.
Максимальное значение для синуса равно 1.
Это означает, что амплитуда графика равна 1, а его период равен 2π (или 360°).
График пересекает ось x в точке 0 и через каждые π радиан до и после этого.
Функция синуса достигает своего максимального значения при π/2 и каждые 2π до и после этого.
Функция синуса достигает минимального значения при 3π/2 и каждые 2π до и после этого.
График тригонометрической функции y=4sin2θ
- Определите значения a и b
a=4,b=2
Амплитуда=а =4=4Period=2πb=2π2=2π2=π
- Таблица упорядоченных пар:
| θ | y=4sin2θ | 33 | ||||||||||||||||||||
| π4 | 4 | |||||||||||||||||||||
| π2 | 0 | |||||||||||||||||||||
| 3π4 | -4 | |||||||||||||||||||||
| π | 1 0 77
θ | y=2cos12θ | 33 | 0 |
| π | 0 | ||
| 2π | — 2 | ||
| 3π | 0 | ||
| 4π | 2 |
- 6 90 Постройте точки и соедините их плавной кривой: 90
График повторяется через каждые π радиан или 180°.
Нет минимального значения.
Максимальное значение отсутствует.
Это означает, что функция тангенса не имеет амплитуды и ее период равен π (или 180°).
График пересекает ось x в точке 0 и через каждые π радиан до и после этого.
График касательной имеет асимптоты , которые являются значениями, где функция не определена .
Эти асимптоты находятся на π/2 и каждом π до и после этого.
- Определить значения a и b a 87 :
- Вычисление амплитуды и периода:
- Нанесите точки и соедините их:
- Косеканс является обратной величиной по синусу .
- Секанс является обратной величиной косинуса .
- Котангенс является обратной величиной тангенса .
Пример диаграммы косинуса, Марилу Гарсия Де Тейлор — StudySmarter Originals
Диаграмма касательной
Касательная представляет собой отношение длины противоположной стороны прямоугольного треугольника к длине прилежащей стороны.
График функции тангенса y=tanθ, однако, выглядит несколько иначе, чем функции косинуса и синуса. Это не волна, а прерывистая функция с асимптотами:
Диаграмма тангенса, Марилу Гарсия Де Тейлор — StudySmarter Originals
Наблюдая за этим графиком, мы можем определить ключевых характеристики функции тангенса :
Тангенс угла также можно найти по этой формуле:
tanθ=sinθcosθ
Построить график тригонометрической функции y=34tanθ
a=34,b=1
Касательные функции имеют нет амплитуды . Period=πb=π1=π1=π
Пример касательного графика, Марилу Гарсиа Де Тейлор — StudySmarter Originals
Каковы графики обратных тригонометрических функций?
Каждой тригонометрической функции соответствует обратная функция:
Для построения графика обратной тригонометрической функции можно действовать следующим образом:
График косеканса
График функции косеканса y=cscθ можно получить следующим образом: это как ориентир.
График косеканса, Марилу Гарсия Де Тейлор — StudySmarter Originals
График функции косеканса имеет тот же период, что и график синуса, т.е. 2π или 360°, и не имеет амплитуды.
График Взаимная тригонометрическая функция y = 2CSCθ
- A = 2, B = 1
- Без амплитуды
- Период = 2πb = 2π1 = 2π1 = 2π
Cosecant Graph Пример, Marilú Garcí Deaylor — Studylor — Studylor — Studylor — Studylor — Studylor — Studylor — Studylor — Studys. . Чтобы построить график функции секанса y=secθ, вы можете выполнить те же шаги, что и раньше, но используя соответствующую функцию косинуса в качестве ориентира. График секущих выглядит следующим образом: График секущих, Марилу Гарсия Де Тейлор — StudySmarter Originals График функции секущей имеет тот же период, что и график косинуса, который равен 2π или 360°, и также не имеет амплитуды. График обратной тригонометрической функции y=12sec2θ График котангенса очень похож на график тангенса, но вместо того, чтобы быть возрастающей функцией, котангенс является убывающей функцией. График котангенса будет иметь асимптоты во всех точках, где функция тангенса пересекает ось x. График котангенса, Марилу Гарсия Де Тейлор — StudySmarter Originals Период графика котангенса такой же, как и период графика касательной, π радиан или 180°, и он также не имеет амплитуды. График обратной тригонометрической функции y=3cotθ Обратные тригонометрические функции относятся к функциям арксинуса, арккосинуса и арктангенса, которые также могут быть записаны как Sin-1, Cos-1 и Tan-1. Эти функции противоположны функциям синуса, косинуса и тангенса, что означает, что они возвращают угол, когда мы подставляем в них значение sin, cos или tan. Помните, что обратная функция получается путем замены x и y , то есть x становится y и y становится x . Инверсия y=sinx равна x=siny, и вы можете увидеть ее график ниже: График инверсии синуса, Marilu García De Taylor — StudySmarter Originals Однако для того, чтобы обратные тригонометрические функции стали функциями , нам нужно ограничить свой домен . В противном случае обратные функции не являются функциями, поскольку они не проходят тест вертикальной линии.
График секущей
График котангенса
Какие бывают графики обратных тригонометрических функций?
Значения в ограниченных областях тригонометрических функций известны как основные значения , а для обозначения того, что эти функции имеют ограниченную область определения, мы используем заглавные буквы: Тригонометрическая функция Обозначение ограниченной области Основные значения у=синкс -π2≤x≤π2 Косинус y=Cosx 0≤x≤π Тангенс y=Tanx -π2x 920321 327 График арксинуса
Арксинус является обратной функцией синуса. Инверсия y=Sinx определяется как x=Sin-1y или x=Arcsiny. Область функции арксинуса будет состоять из действительных чисел от -1 до 1, а ее диапазон представляет собой набор мер угла от -π2≤y≤π2. График функции арксинуса выглядит следующим образом:
График арксинуса, Марилу Гарсия Де Тейлор — StudySmarter Originals
График арккосинуса
Арккосинус является обратной функцией косинуса.
Инверсия y=Cosx определяется как x=Cos-1y или x=Arccosy. Область функции арккосинуса также будет состоять из всех действительных чисел от -1 до 1, а ее диапазон представляет собой набор угловых мер от 0≤y≤π. График функции арккосинуса показан ниже:
График арккосинуса, Марилу Гарсия Де Тейлор — StudySmarter Originals
График арктангенса
Арктангенс является обратной функцией тангенса. Инверсия y=Tanx определяется как x=Tan-1y или x=Arctany. домен функции арктангенса будет состоять из действительных чисел, а его диапазон представляет собой набор мер угла между -π2 График арктангенса, Марилу Гарсиа Де Тейлор — StudySmarter Originals Если мы начертим все обратные функции вместе, они будут выглядеть следующим образом: Графики арксинуса, арккосинуса и арктангенса вместе, Марилу Гарсиа Де Тейлор — StudySmarter Originals Дополнительные сведения по этой теме см.
в статье «Обратные тригонометрические функции». Графики тригонометрических функций. Ключевые выводы
Ваш комментарий будет первым