Преобразование графиков тригонометрических функций — презентация онлайн
Похожие презентации:
Преобразование графиков тригонометрических функций и их свойства
Преобразование графиков функций
Преобразование графиков тригонометрических функций
Преобразования графиков функций
Преобразование графиков функции
Преобразование графиков функции
Преобразование графиков тригонометрических функций
Творческая работа: «Преобразования графиков функции»
Преобразование графиков тригонометрических функций
Преобразование графиков функций
1. Преобразование графиков тригонометрических функций
Авторы проектаучителя математики
ГБС(К)ОУ школы –
интерната №113
г.о.Самара
Губарева Е.Г.
Пискаева С.В.
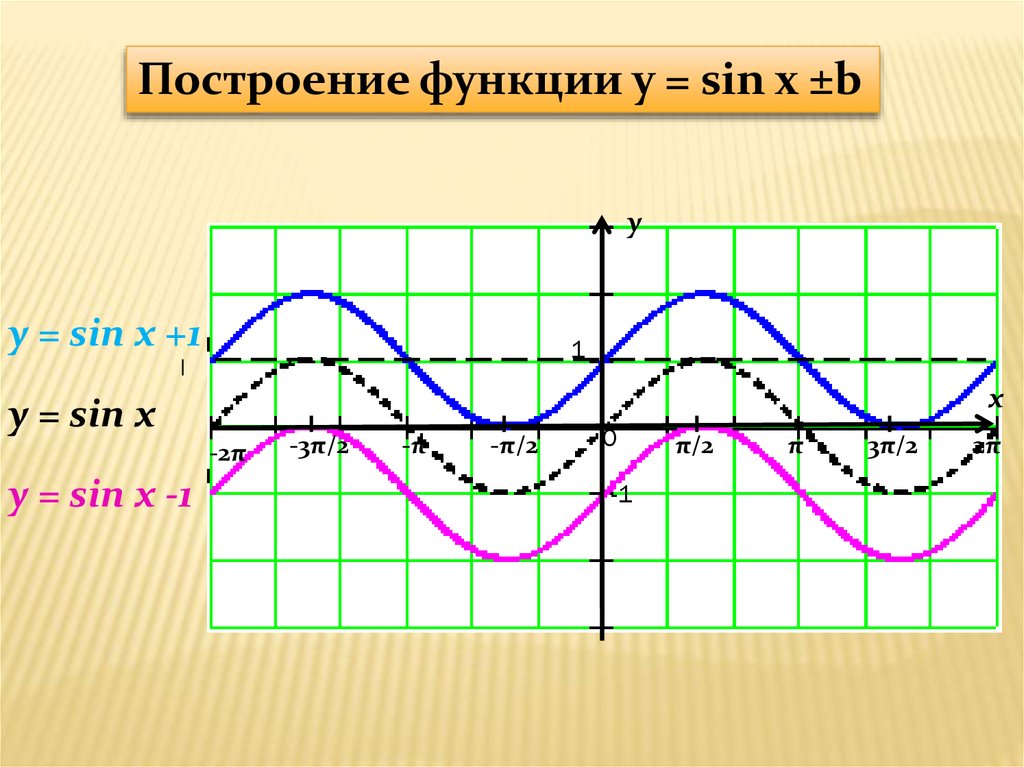
2. Параллельный перенос на вектор (0; b) вдоль оси ординат: График функции f(x)+b получается параллельным переносом графика f(x) в
положительном направлении оси ОУ на ǀbǀ единиц при b>0 и в отрицательномнаправлении этой оси на ǀbǀ единиц при b<0.

3. Параллельный перенос вдоль оси абсцисс на вектор (c; 0). График функции f(x+с) получается параллельным переносом в
отрицательном направлении оси ОХ на ǀсǀ при с>0 и в положительномнаправлении на ǀсǀ при с<0.
4. Растяжение вдоль оси ОX с коэффициентом k, которое задается формулами х₁=kх, у₁=y. График функции f(kx) получается сжатием
графика f(x) в k раз к оси ОУ при k>1 или растяжением в1/k раз от оси ОУ при 0<k<1.
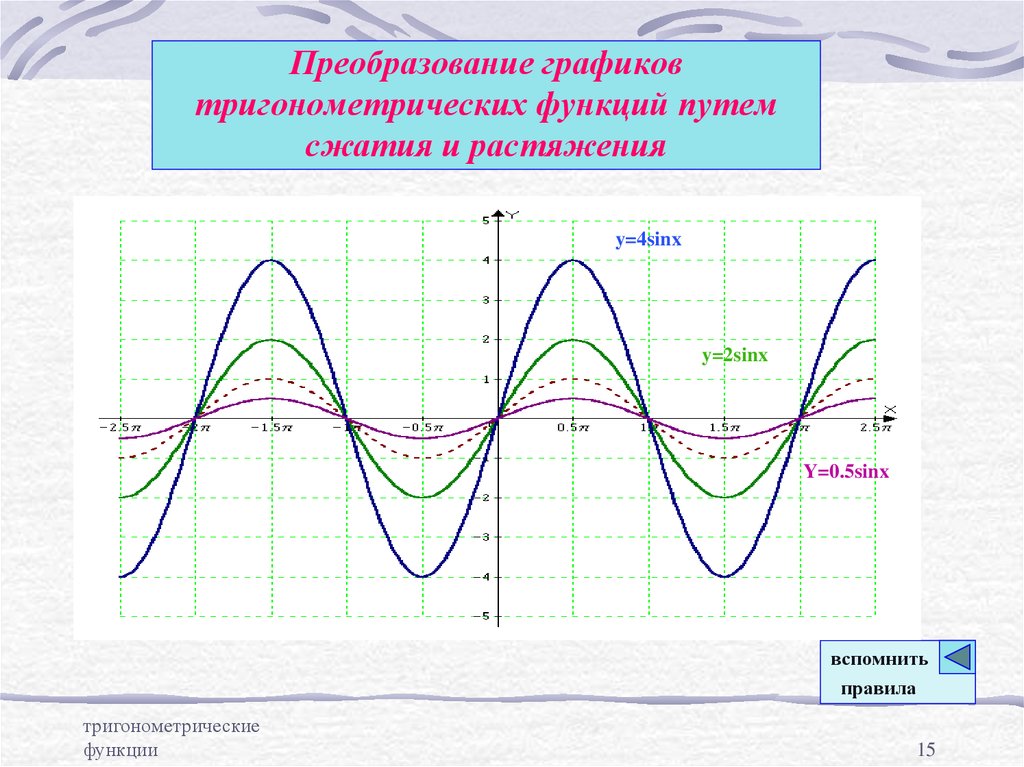
5. Растяжение вдоль оси ОУ с коэффициентом a, которое задается формулами х₁=х, у₁=ay. График функции аf(x) получается растяжением
графика f(x) вдоль оси ОУ в а раз приа > 1 и сжатием вдоль оси ОУ в 1/a раз при 0 < a < 1.
6. График функции y= f(-x) получается симметричным отображением графика f(x) относительно оси ОУ.
7. График функции y= -f(x) получается симметричным отображением графика f(x) относительно оси ОX.
8. График функции │f(x)│ получается из графика f(x) так: часть графика f(x), лежащая над осью ОХ, сохраняется, часть , лежащая под
осью ОХ, отображается симметричноотносительно оси ОХ.
9. График функции f(│x│) получается из графика функции f(x) так: при х ≥ 0 график f(x) сохраняется, а при х < 0 полученная часть
График функции f(│x│)получается из графика функции f(x) так: при х ≥ 0 график f(x) сохраняется, а при
х < 0 полученная часть графика отображается симметрично относительно оси ОУ.
10. Пошаговое построение графика функции у = 2sin(2x-π/3)
1. Построим график функции у = sin x2. Строим график функции y = sin 2x, сжимая
исходный график в 2 раза к оси ОУ
3. Строим график функции у = sin(2x – π/3), сдвигая
параллельным переносом в положительном
направлении на π/3 график
y = sin2x
4. Строим график функции у = 2sin(2x — π/3),
растяжением вдоль оси ОУ в 2 раза графика
у = sin(2x – π/3)
11. Проверь себя:
12. Итоговый график
1213. Список используемых источников
1. Учебник для 10-11 классов общеобразовательных учреждений«Алгебра и начала анализа» под редакцией А.
 Н.Колмогоров
Н.Колмогоров2. www.cleverstudents.ru/function_graph_transformations.html
3. www.distedu.ru/mirror/_fiz/archive.1september.ru/mat/2001/47/no47_01.htm
Построение графиков функций, содержащих знак модуля
t heory.html
Элементарные функции и их графики
5. uztes.ru/abstracts/?idabstract=51
Тригонометрические функции. Синус и косинус
13
English Русский Правила
Свойства и графики тригонометрических функций. Базовый уровень 10 класс онлайн-подготовка на Ростелеком Лицей |
Тригонометрические функции числового аргумента
Основное отличие науки от искусства в том, что результат научного опыта, воспроизведенный разными людьми, будет одинаковым (если соблюдены основные условия проведения такого опыта). Произведение искусства каждый понимает по-своему, и единого правильного мнения о таком произведении быть не может.
Русский язык позволяет нам описать процессы, которые происходят вокруг: птица летит и машет крыльями, дерево согнулось под порывом ветра. Поэт может и более изящно воспользоваться языком: «…летят серебряные птицы, седые птицы – журавли…». Это описание помогает нам воспринимать окружающий мир, вдохновляться ним.
Поэт может и более изящно воспользоваться языком: «…летят серебряные птицы, седые птицы – журавли…». Это описание помогает нам воспринимать окружающий мир, вдохновляться ним.
Но для более практичных вопросов такого описания недостаточно. Почему летит птица? Можем ли мы это использовать и построить аппарат для полетов? При каких условиях дерево сломается? Можно ли это предотвратить? Для ответа на эти вопросы нужен другой язык – математический. Мы строим математическую модель процесса, описываем его на математическом языке. И в дальнейшем эти расчеты позволяют создавать самолеты и строить небоскребы, которые защищены от ураганов и землетрясений.
Множество процессов, которые окружают нас – периодически повторяющиеся. Это и различные колебания, о которых вы знаете из курса физики («Механические колебания», «Механические волны. Звук»), и периодические спады и подъемы в экономике.
Конечно, в реальном мире не существует идеальных периодических процессов. Да, зима наступает каждый год, но мы не можем предсказать заранее, в какой именно день выпадет снег, когда станет холодно и т.
Но, как мы уже знаем, точность решения задачи определяется целью. Поэтому во многих случаях мы можем с достаточной степенью точности использовать модель периодически повторяющегося процесса и решать с помощью этой модели различные задачи.
Чтобы построить математическую модель всех этих повторяющихся событий, нужен определенный инструмент – тригонометрические функции. С этим инструментом мы уже немного знакомы: умеем вычислять значения тригонометрических функций и упрощать выражения, которые их содержат. Но чтобы полноценно использовать тригонометрические функции для построения математической модели периодических процессов, нам еще нужно изучить свойства и графики этих функций, а также научиться решать уравнения и неравенства, которые их содержат.
Об уравнениях речь пойдет позже, а сегодня мы займемся свойствами и графиками тригонометрических функций.
Мы определили тригонометрические функции как функции, которые ставят в соответствие углу поворота координаты (или их отношение) соответствующей точке на окружности (см. рис. 1):
Рис. 1. Единичная окружность
Понятно, что при повороте на полный оборот значения тригонометрических функций начинают повторяться (мы каждый день наблюдаем это на примере часов: прошло 12 часов, и стрелки снова на своих местах). Поэтому тригонометрические функции будут периодическими – их значения после изменения значения аргумента на определенное число будут повторяться. Периодических функций можно ввести много, самых разных. Мы рассмотрим свойства базовых, с помощью комбинаций которых можно выразить остальные. Звуки – это механические колебания, их вокруг нас великое множество. Но при этом все их с той или иной степенью точности можно математически описать с помощью набора базовых тригонометрических функций.
Мы выделили и изучили свойства некоторых видов функций: линейной, квадратичной, функции квадратного корня и других («Свойства функций. Базовые функции»). Воспользуемся готовой схемой изучения свойств функций для тригонометрических функций:
Правда, есть небольшая загвоздка: мы изучали числовые функции – в них числу ставится в соответствие число. В тригонометрических же функциях мы говорили, что углу ставится в соответствие число. Разрешить эту ситуацию просто: будем брать величину угла, выраженную в радианах. Под записью будем понимать, что числу ставится в соответствие число . Причем так, что значение равно синусу радиан. Например,
Аналогично и для косинуса, тангенса и котангенса.
Как исследовать числовые функции, мы уже знаем. Можно построить их графики и рассмотреть различные характеристики:
- область определений и область значений;
- нули функции, промежутки знакопостоянства;
- промежутки монотонности: возрастания и убывания;
- четность;
- периодичность.

Про четность и периодичность тригонометрических функций, на самом деле, мы уже знаем. Вспомним, что функция называется четной, если для всех ее допустимых аргументов выполняется соотношение:
А для нечетных функций выполняется соотношение:
Мы знаем, что , а . Соответственно, функция является четной функцией; – нечетной.
Для тангенса и котангенса выполнены следующие соотношения:
Значит, функции и также являются нечетными.
Теперь про периодичность. Вспомним, что функция называется периодической, если для всех ее аргументов выполняется соотношение:
Величина называется периодом функции. Мы знаем соотношения:
Значит, все тригонометрические функции являются периодическими. Причем синус и косинус имеют период , а тангенс и котангенс – период .
Об остальных свойствах и характеристиках тригонометрических функций, а также об их графиках мы поговорим далее в уроке.
Синус и косинус
Начнем с построения графика функции синуса:
Мы знаем значения синуса для некоторых углов:
|
Градусы |
|||||
|
Радианы |
|||||
По ним мы можем составить таблицу значений для нашей функции.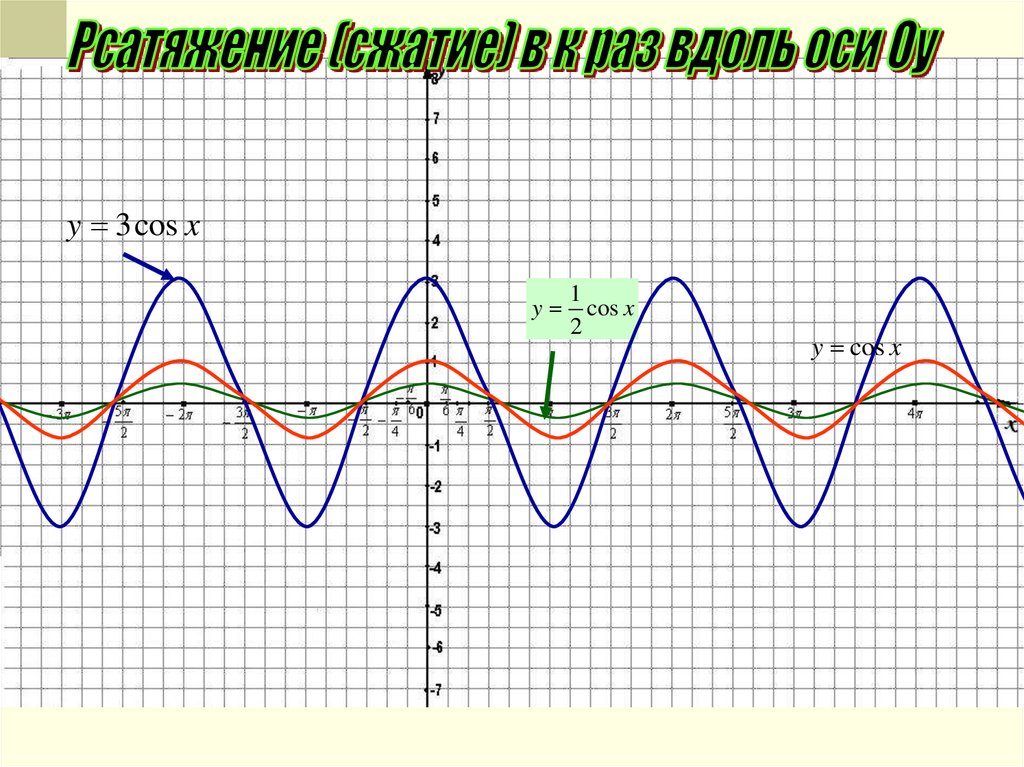 Помним, что числовой аргумент функции – это величина угла в радианах. Поэтому получаем следующую таблицу:
Помним, что числовой аргумент функции – это величина угла в радианах. Поэтому получаем следующую таблицу:
Отметим эти точки на графике и соединим плавной линией (см. рис. 2).
Рис. 2. Соединенные точки
Обратите внимание на масштаб оси . Ранее мы изучали такие функции, в которых аргументом удобно было брать целые значения. Поэтому и цену деления было удобно брать целым числом. У тригонометрических же функций мы знаем значения для аргументов, пропорциональных . Поэтому и выбираем соответствующий масштаб.
Далее воспользуемся соотношением:
Его можно получить из формул приведения:
Это соотношение означает, что для аргументов, лежащих слева и справа от на равном расстоянии, значения синусов будут одинаковы. Получаем следующий график (см. рис. 3).
Рис. 3. Полученный график
Теперь воспользуемся тем, что синус – нечетная функция. Графики нечетных функций симметричны относительно начала координат. Отражаем график. Мы получили график функции на промежутке от (см. рис. 4).
рис. 4).
Рис. 4. График функции на промежутке от
Далее пользуемся периодичностью. Период синуса равен , значит, прибавив к аргументу , мы получим те же значения функции. Прибавляя еще или вычитая , мы будем получать те же значения. Наш кусочек функции будет как бы «копироваться» влево и вправо бесконечное количество раз. Полученная линия и будет являться графиком функции (см. рис. 5). Эту кривую еще называют синусоидой.
Рис. 5. График функции
1. Областью определения являются все действительные числа:
Мы расширили понятие угла так, что его величина может быть любым числом. А величина угла в радианах – и есть аргумент функции.
2. Область значений:
Мы определяли синус как ординату точки на единичной окружности. Соответственно, значения синуса могут лежать только в пределах от до .
3. Нули функции – это решения уравнения . С решениями уравнений подробнее вы познакомитесь на следующем уроке. А пока можем воспользоваться графиком. Нули функции: . В общем виде это можно записать так: , где – целое число.
С решениями уравнений подробнее вы познакомитесь на следующем уроке. А пока можем воспользоваться графиком. Нули функции: . В общем виде это можно записать так: , где – целое число.
4. Промежутки знакопостоянства также отметим по графику. От до функция принимает положительные значения; от до – отрицательные. Это же поведение мы видим и на других участках графика. В общем виде:
5. По графику также можно определить промежутки монотонности. От до функция возрастает; от до – убывает. На других участках графика то же самое. Тогда в общем виде:
Теперь перейдем к косинусу. Его график легко построить, воспользовавшись соотношением, которое мы уже сегодня доказывали:
Т. е. график функции совпадает с графиком функции . А этот график мы можем построить с помощью преобразования . Оно соответствует сдвигу графика на единиц влево. Значит, для построения график функции достаточно сдвинуть график синуса на влево.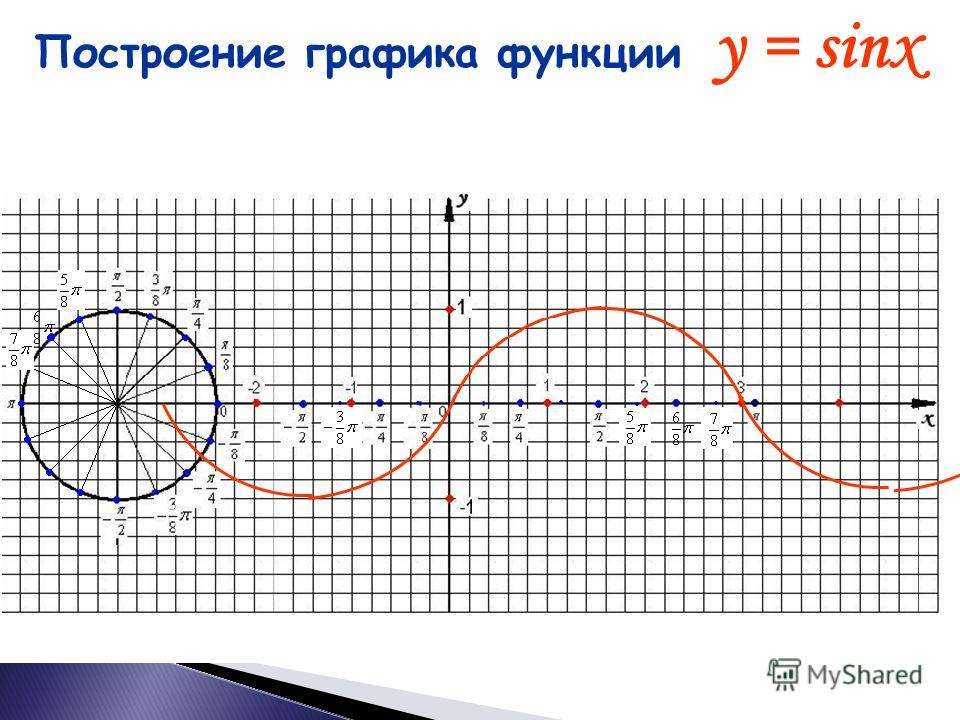 Вот и получили график косинуса (см. рис. 6).
Вот и получили график косинуса (см. рис. 6).
Рис. 6. График функции
Видим, что область определения и область значений у косинуса такие же, как и у синуса:
А вот нули функции, промежутки знакопостоянства и монотонности сдвинутся вместе с графиком на влево. Нули:
Положительные и отрицательные значения:
Функция возрастает и убывает при:
Тангенс и котангенс
Теперь перейдем к тангенсу и котангенсу. Начнем строить график тангенса по точкам.
|
Радианы |
||||
Соответственно, таблица значений:
Тангенс не определен, ведь , а деление на ноль не определено.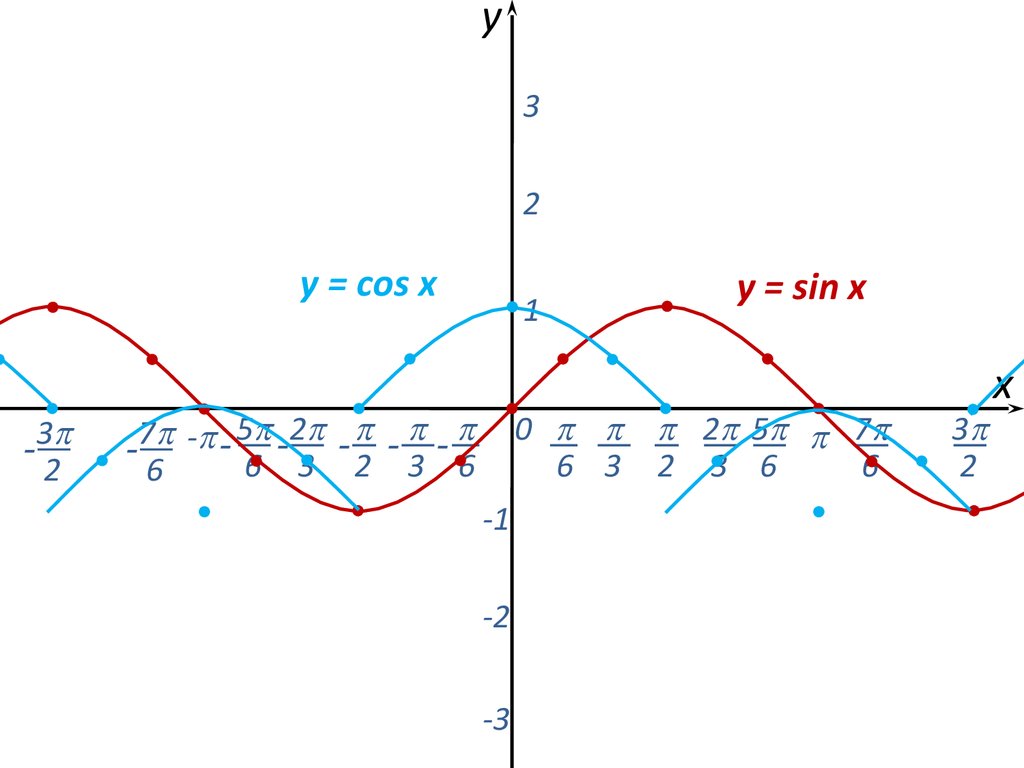 Что же делать? Соединим уже имеющиеся точки и посмотрим, что будет происходить с графиком по мере приближения аргумента к (см. рис. 7).
Что же делать? Соединим уже имеющиеся точки и посмотрим, что будет происходить с графиком по мере приближения аргумента к (см. рис. 7).
Рис. 7. Соединенные точки
будет приближаться к , – приближаться к , а значение дроби будет становиться все больше и больше. Т. е. значение тангенса будет все расти и расти. Но график никогда не пересечет прямую , ведь при этом значении аргумента функция не определена. Подобную ситуацию мы видели на графике функции (см. рис. 8).
Рис. 8. График функции
При приближении аргумента к нулю значение функции неограниченно убывало. При этом график не пересекал прямую . Вспомним, что подобная прямая называется асимптотой графика. Соответственно, асимптотой графика будет прямая .
Мы построили часть графика тангенса. Теперь воспользуемся тем, что эта функция нечетная. Значит, график симметричен относительно начала координат. Далее пользуемся периодичностью функции. Период тангенса равен , значения функции будут повторяться через этот промежуток. Получили график функции (см. рис. 9).
Получили график функции (см. рис. 9).
Рис. 9. График функции
Видим, что этот график имеет множество асимптот, уравнения которых в общем виде можно описать так:
Эти асимптоты разбивают график на отдельные части, которые еще называют ветками тангенса. Ветка, которая проходит через начало координат, называют главной веткой.
По графику определим характеристики функции.
1. Область определения:
2. Область значений:
3. Нули функции: . В общем виде все их можно описать так:
Несложно понять, почему они совпадают с нулями синуса, если вспомнить, что тангенс – отношение синуса и косинуса, а дробь равна только тогда, когда ее числитель равен .
4. В общем виде:
5. На каждой своей ветке функция возрастает:
При этом корректно говорить, что функция возрастает на каждом из этих интервалов. Но нельзя сказать, что она возрастает на всей области определения, ведь при переходе через асимптоту функция меняет значение с положительного на отрицательное. Т. е. значение уменьшается.
Т. е. значение уменьшается.
Теперь, наконец, рассмотрим функцию . Для ее построения удобно воспользоваться формулой приведения:
Т. е. нам достаточно построить график функции . В этом нам помогут преобразования графиков. Сначала строим – график тангенса отражается симметрично относительно оси . Затем сдвигаем его на влево. Получаем график функции , он же будет графиком функции .
Рис. 10. График функции
Отметим характеристики.
1. Область определения:
2. Область значений:
3. Нули функции (совпадают с нулями косинуса, объясните сами, почему):
4. В общем виде:
5. На каждой своей ветке функция убывает:
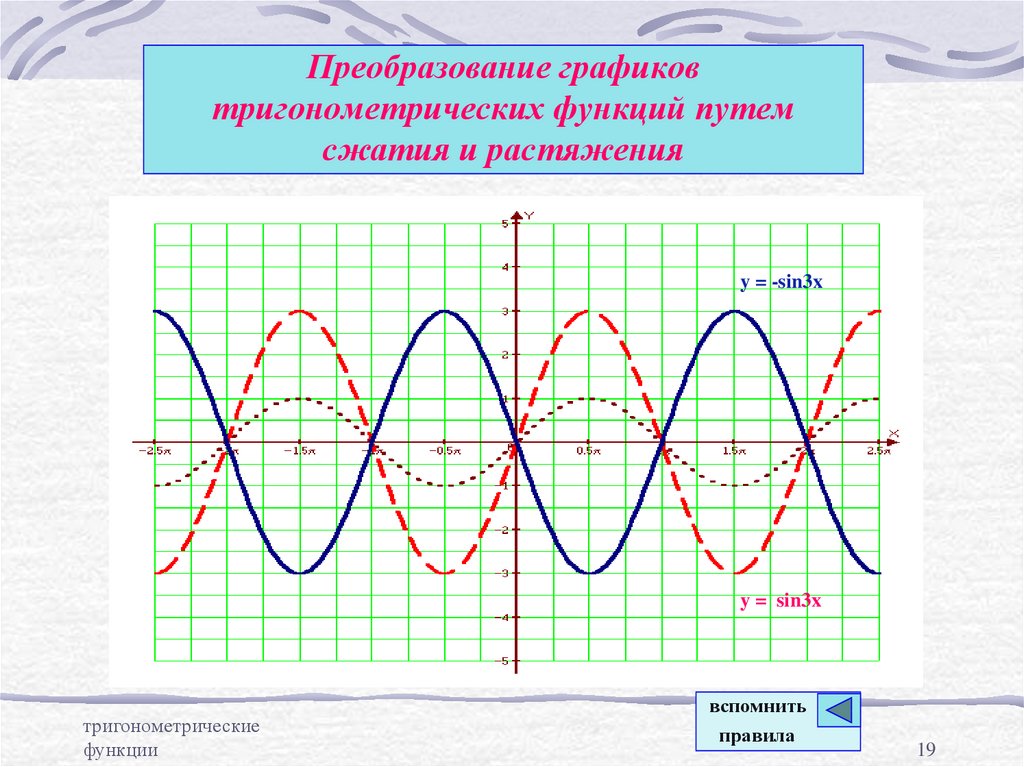
Преобразования графиков тригонометрических функций
Мы рассмотрели характеристики и графики тригонометрических функций , , и . Но при моделировании процессов обычно встречаются более сложные функции, например:
Чтобы исследовать подобные функции, достаточно применить преобразования графиков к уже изученным. Вспомним эти преобразования (можете пересмотреть соответствующие уроки «Повторение и систематизация курса алгебры 7-9 класса. Функции», «Преобразование графиков функций»).
Вспомним эти преобразования (можете пересмотреть соответствующие уроки «Повторение и систематизация курса алгебры 7-9 класса. Функции», «Преобразование графиков функций»).
- Прибавление числа к функции сдвигает график вдоль оси .
- Прибавление числа к аргументу сдвигает график вдоль оси .
- Умножение значения функции на число растягивает или сжимает график вдоль оси . Если , то еще и симметрично отражает график относительно оси .
- Умножение аргумента на число растягивает или сжимает график вдоль оси x. Если , то еще и симметрично отражает график относительно оси .
Соответственно, чтобы построить график функции , необходимо:
1. Построить график функции (см. рис. 11).
Рис. 11. График функции
2. Сжать его вдоль оси в раз, получив график (см. рис. 12).
Рис. 12. График функции
3. Растянуть его вдоль оси (см. рис. 13), а затем симметрично отразить относительно оси . В итоге получим график функции (см. рис. 14).
В итоге получим график функции (см. рис. 14).
Рис. 13. График функции
Рис. 14. График функции
По построенному графику функции можно указать все ее свойства. В частности, стоит обратить внимание, что у данной функции изменилась область значений и период по сравнению с функцией . Область значений данной функции: .
Период был , после сжатия вдоль оси он уменьшился в раз:
В общем случае про изменение области значений и периода функций можно сказать следующее.
- При преобразованиях вида и соответствующим образом изменяется область значений: сдвигается на или расширяется/сужается в раз.
- При преобразовании вида период функций увеличивается или уменьшается в раз.
- При преобразовании вида период функции и ее область значений остается прежней.
Итак, применяя различные преобразования графиков, мы можем исследовать тригонометрические функции вида , где – некоторые числа. Аналогично и для косинусов, тангенсов и котангенсов. Но в математической модели могут встретиться и другие тригонометрические выражения. Например, при колебаниях математического маятника зависимость его скорости от времени выглядит следующим образом:
Но в математической модели могут встретиться и другие тригонометрические выражения. Например, при колебаниях математического маятника зависимость его скорости от времени выглядит следующим образом:
Тогда выражение для кинетической энергии принимает вид:
Константы и деление на можем объединить в одну положительную константу . Получим функцию кинетической энергии от времени: , где – некоторые числа. Как видите, здесь мы столкнулись с квадратом тригонометрической функции. Как же ее исследовать? Здесь нам поможет известный нам математический прием: свести нашу задачу к той, решение которой мы знаем.
Для начала перейдем к более привычным обозначениям:
Теперь используем формулу понижения степени:
Получаем:
А уже эту функцию мы уже знаем, как исследовать. Здесь нам помогут преобразования графиков. Базовая функция (см. рис. 15):
Рис. 15. График функции
Умножаем аргумент на :
При этом график сожмется вдоль оси в раз (см. рис. 16).
рис. 16).
Рис. 16. График функции
Период функции станет в раз меньше:
Далее умножаем функцию на :
График растягивается вдоль оси в раз и отражается симметрично относительно оси (см. рис. 17).
Рис. 17. График функции
При этом область значений расширяется в раз: было , станет:
И наконец, прибавляем :
График поднимается на (см. рис. 18).
Рис. 18. График функции
Область значений также смещается на :
Таким образом, мы смогли исследовать функцию, содержащую квадрат тригонометрической функции. Посмотрели, какой будет ее область значений и ее период.
Список литературы
- Алимов Ш.А., Колягин Ю.М., Ткачева М.В. Математика. Алгебра и начала математического анализа, геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
- Мордкович А.Г., Семенов П.В. Математика. Алгебра и начала математического анализа, геометрия. 10-11класс.
 Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.
Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019. - Никольский С.М., Потапов М.К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – АО «Издательство “Просвещение”»
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru
- Интернет-портал ru.solverbook.com
- Интернет-портал math34.ru
Домашнее задание
- Определить промежутки возрастания (убывания) функции на промежутке .
- Найти множество значений функции , если .
- Построить график функции:
Тригонометрический калькулятор. Простой способ найти sin, cos, tan, cot
Автор: Hanna Pamula, PhD
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 23 декабря 2022 г.
Содержание:- Что такое тригонометрия?
- Тригонометрический калькулятор для определения sin, cos, tan, cot, sec, csc
- Тригонометрический калькулятор как инструмент для решения прямоугольного треугольника
- FAQ
Этот тригонометрический калькулятор поможет вам в двух популярных случаях, когда необходима тригонометрия. Если вы хотите найти значения синуса, косинуса, тангенса и их обратных функций, используйте первую часть калькулятора. Вы ищете недостающую сторону или угол в прямоугольном треугольнике с помощью тригонометрии? Наш инструмент также является беспроигрышным вариантом! Введите 2-3 заданных значения во второй части калькулятора, и вы найдете ответ в мгновение ока. Прокрутите вниз, если хотите узнать о тригонометрии и о том, где ее можно применить.
Если вы хотите найти значения синуса, косинуса, тангенса и их обратных функций, используйте первую часть калькулятора. Вы ищете недостающую сторону или угол в прямоугольном треугольнике с помощью тригонометрии? Наш инструмент также является беспроигрышным вариантом! Введите 2-3 заданных значения во второй части калькулятора, и вы найдете ответ в мгновение ока. Прокрутите вниз, если хотите узнать о тригонометрии и о том, где ее можно применить.
Есть много других полезных инструментов для решения задач тригонометрии. Ознакомьтесь с двумя популярными тригонометрическими законами с калькулятором закона синусов и нашим калькулятором закона косинусов, которые помогут вам решить любой треугольник.
Что такое тригонометрия?
Тригонометрия — раздел математики. Само слово происходит от греческого trigōnon (что означает «треугольник») и метрон («мера»). Как следует из названия, тригонометрия имеет дело в основном с углами и треугольниками ; в частности, он определяет и использует отношения и отношения между углами и сторонами в треугольниках. Таким образом, основным приложением является решение треугольников, именно прямоугольных треугольников и любого другого типа треугольника, который вам нравится.
Таким образом, основным приложением является решение треугольников, именно прямоугольных треугольников и любого другого типа треугольника, который вам нравится.
🔎 Тригонометрические функции (sin, cos, tan) — это соотношения. Таким образом, вы можете найти недостающие члены, используя только наш калькулятор отношений!
Тригонометрия имеет множество применений: от бытовых задач, таких как вычисление высоты или расстояния между объектами, до системы спутниковой навигации, астрономии и географии. Кроме того, функции синуса и косинуса являются основополагающими для описания периодических явлений — благодаря им мы можем описывать колебательные движения (как в нашем простом маятниковом калькуляторе) и волны, такие как звук, вибрация или свет.
Многие области науки и техники используют тригонометрию и тригонометрические функции, а именно: музыка, акустика, электроника, медицина и медицинская визуализация, биология, химия, метеорология, электрика, механика, гражданское строительство и даже экономика. .. Тригонометрические функции на самом деле вокруг нас!
.. Тригонометрические функции на самом деле вокруг нас!
Калькулятор триггеров для нахождения sin, cos, tan, cot, sec, csc
Чтобы найти тригонометрические функции угла, введите выбранный угол в градусах или радианах. Под калькулятором появятся шесть самых популярных триггерных функций — три основные: синус, косинус и тангенс, а также их обратные величины: косеканс, секанс и котангенс. Кроме того, если угол острый, будет отображаться прямоугольный треугольник, который может помочь вам понять, как можно интерпретировать функции.
Тригонометрический калькулятор как инструмент для решения прямоугольного треугольника
Чтобы найти недостающие стороны или углы прямоугольного треугольника, все, что вам нужно сделать, это ввести известные переменные в тригонометрический калькулятор. Вам нужны только два заданных значения в случае:
- одна сторона и один угол
- две стороны
- площадь и одна сторона
Помните, что если вы знаете два угла, этого недостаточно, чтобы найти стороны треугольника. Два треугольника, имеющие одинаковую форму (что означает, что они имеют равные углы), могут иметь разные размеры (не одинаковую длину стороны) — такое отношение называется сходством треугольника . Если стороны имеют одинаковую длину, то треугольники конгруэнтны .
Два треугольника, имеющие одинаковую форму (что означает, что они имеют равные углы), могут иметь разные размеры (не одинаковую длину стороны) — такое отношение называется сходством треугольника . Если стороны имеют одинаковую длину, то треугольники конгруэнтны .
Часто задаваемые вопросы
Что такое тригонометрия?
Тригонометрия — это изучение взаимосвязей внутри треугольника . Для прямоугольных треугольников отношение между любыми двумя сторонами всегда одинаково и выражается в виде тригонометрических отношений cos, sin и tan. Тригонометрия также может помочь найти недостающую треугольную информацию , например, правило синусов.
Как сделать тригонометрию?
- Найдите , какие две из них у вас есть: гипотенуза, прилежащая или противоположная сторона или угол.
- Выясните , какой из оставшихся вариантов вы пытаетесь рассчитать.
- Выберите , какое отношение вам нужно (помните , SOHCATOA ).

- Введите в данные, которые у вас есть в уравнении.
- Переставьте и решите для неизвестного.
- Проверьте свои ответы с помощью нашего калькулятора триггеров.
Тригонометрия сложна?
Поначалу тригонометрия может показаться сложной, но после некоторой практики вы ее освоите! Вот несколько советов по тригонометрии:
- Обозначьте гипотенузу, смежные и противоположные стороны треугольника, чтобы понять, какое тождество использовать.
- Запомни мнемонику SOHCATOA для тригонометрических соотношений!
Для чего используется тригонометрия?
Тригонометрия используется для поиска информации обо всех треугольниках , в частности о прямоугольных треугольниках. Поскольку треугольников повсюду в природе , тригонометрия используется вне математики в таких областях, как строительство, физика, химическая технология и астрономия.
Кто изобрел тригонометрию?
Поскольку тригонометрия представляет собой отношение между углами и сторонами треугольника, его никто не изобретал , он все еще был бы там, даже если бы никто о нем не знал! Первыми, кто открыл часть тригонометрии, были древние египтяне и вавилоняне , но Евклид и Архимид первыми доказали тождества, хотя и сделали это с помощью форм, а не алгебры.
В каком классе преподается тригонометрия?
Тригонометрия обычно преподается подросткам в возрасте 13-15 лет , то есть 8 и 9 классы в США и лет 9 и 10 в Великобритании. Точный возраст, в котором преподается тригонометрия, зависит от страны, школы и способностей учеников.
Как преобразовать десятичную дробь в градусы в тригонометрии?
- Найдите , какое тригонометрическое соотношение вы используете с SOHCATOA.
- Возьмем обратное значение вашей десятичной дроби, например, sin⁻¹(0,5).

- Полученное число равно градусам вашего угла .
- Проверьте свои результаты с помощью нашего тригонометрического калькулятора.
Как найти высоту треугольника с помощью тригонометрии?
- Нарисуйте свой треугольник и отметьте высоту. Вам нужно будет разделить треугольник на два меньших треугольника.
- Решите любой из этих оставшихся треугольников, используя обычную тригонометрию, чтобы найти высоту. Противоположная или соседняя теперь будет гипотенузой меньшего треугольника.
- Проверьте свои ответы с помощью Omni Calculator.
Ханна Памула, доктор философии
Тригонометрические функции: sin, cos, tan…
…или тригонометрия в прямоугольном треугольнике
Угол α
Угол β
Посмотреть 20 похожих калькуляторов тригонометрии Калькулятор Pro Trig 4080
Расчетные отрасли
(пока отзывов нет) Написать обзор
Calculated Industries
Calculated Industries Construction Master Pro Trig Calculator 4080
Рейтинг Обязательно Выберите рейтинг1 звезда (худший)2 звезды3 звезды (средний)4 звезды5 звезд (лучший)
Имя
Тема отзыва Требуется
Комментарии Обязательно
- Артикул:
- КАЛ4080
- MPN:
- 4080
Сейчас: $68,99
Текущий запас:
Количество:
Часто покупают вместе:
- Описание
- Информация о гарантии
- Дополнительная информация
- 0 отзывов
Описание
Усовершенствованный строительно-математический калькулятор с дробями на футы и дюймы с полным набором триггерных функций
Construction Master Pro Trig предоставляет профессионалам-строителям полные триггерные функции, помогающие им быстро и легко решать сложные математические задачи. Это экономит время, снижает затраты и предотвращает повторную работу. Вы можете легко работать и конвертировать между футами, дюймами, дробями и метрическими единицами. Мгновенно рассчитывайте сложные строительные задачи для лестничных площадок, крыш, каркаса и многого другого. Полные триггерные функции с синусом, косинусом, тангенсом, арксинусом, арккосинусом и арктангенсом.
Это экономит время, снижает затраты и предотвращает повторную работу. Вы можете легко работать и конвертировать между футами, дюймами, дробями и метрическими единицами. Мгновенно рассчитывайте сложные строительные задачи для лестничных площадок, крыш, каркаса и многого другого. Полные триггерные функции с синусом, косинусом, тангенсом, арксинусом, арккосинусом и арктангенсом.
Строительные расчеты:
- Работа и преобразование между любыми размерами здания, включая метрические
- Триггерная функция
- Найти вес на объем
- Встроенные угловые решения
- Полные схемы лестниц
- Решения для крыши, стропил и каркаса
- Окружность: дуги, окружность, сегменты и многое другое
- Лестницы — Установите высоту подступенка и решите для проема лестничной клетки
- Шпильки — Найти число по центру для введенной длины
- Составные торцевые скосы
- Равносторонние многоугольники
Для подрядчиков, архитекторов, инженеров, руководителей проектов, сметчиков, чертежников, строителей, монтажников, плотников, торговцев — Дюймовые дроби, десятичные футы, дюймы и метрические единицы, включая площадь и объем
Встроенные функции экономии времени:
- Полные расчеты лестниц для подступенков, проступей, длины косоура и угла наклона
- Установить высоту подступенка и решить для проема лестничной клетки
- Встроенные функции прямого угла
- Функция крыши находит площадь, связки, квадраты и обшивку 4×8 для плоских или скатных крыш
- Функция нестандартных стропил обеспечивает обычные стропила, обычные и нестандартные вальмы, ендовы и домкраты; мгновенные углы резки (щека, уровень и отвес)
- Результаты домкрата для крыш с постоянным и неправильным уклоном.
 Найдите шпильки для наклонных стен с межосевым расстоянием
Найдите шпильки для наклонных стен с межосевым расстоянием - Соединение под углом — Сохраните угол короны и введите угол угла стены, чтобы рассчитать наклон и угол отвала для резки под углом
- Усовершенствованные решения для кругов, арок, колонн, конусов, столбов, окон и отверстий для стоек
- Арочные стены с межцентровым расстоянием
- Шпильки — Расчет количества центральных шпилек для введенной длины
- Равносторонний многоугольник — Расчет угла и биссектрисы, длины стороны, периметра и площади
- Ножки для досок Смета пиломатериалов
Дополнительные функции:
- Пользовательские настройки: Установите пользовательские параметры, такие как дробные параметры от 1/2 до 1/64 дюйма и высоту перемычки лестницы, десятичные градусы и т. д.
- Экспоненциальное представление: Ввод и отображение экспоненциальных значений
- Клавиша Backspace: Облегчает изменение только что введенных значений
- Константный оператор: Упрощает повторяющиеся вычисления
- Цена за единицу: Простое определение себестоимости и ценообразования за единицу
- Накопительная память (M+) плюс три дополнительных ячейки памяти
- «Безбумажная» лента: Позволяет просмотреть последние 20 записей; перепроверьте итоги
- Стандартные вычисления: Работает как математический калькулятор с +, -, +/-, ×, ÷, %, π, 1/x, x 2 и √
- Автоматическое отключение экономит заряд батареи
Включает:
- Прочный корпус Armadillo Gear с защитой от ударов, пыли и влаги
- Карманные справочники на английском и испанском языках
- Две батареи LR44 с длительным сроком службы
- Гарантия на один год
Вспомогательные материалы:
- Руководство пользователя
- Карманный справочник
- Спецификация
- Таблица сравнения продуктов
Просмотреть всеЗакрыть
Информация о гарантии
Включена годовая гарантия от Calculated Industries
Просмотреть всеЗакрыть
Дополнительная информация
3 Размер: | 5,7″ x 3,0″ x 0,65″ (145 мм x 76 мм x 17 мм) |
Вес изделия: | 4,6 унции (130 г) Включает футляр и карманное справочное руководство |
Мощность: | Две батареи 1,5 В LR-44/A76 с длительным сроком службы |
Тип дисплея: 905:30 | 11 цифр (7 обычных, 4 дроби) |
Размеры дисплея: | 0,625″ x 2,5″ (16 мм x 63,5 мм) |
Точность: | 12-разрядная внутренняя точность |
Просмотреть всеЗакрыть
0 Отзывы
Просмотреть всеЗакрыть
- сопутствующие товары
- Клиенты также просмотрели
Сопутствующие товары
В корзину
Быстрый просмотр
Calculated Industries Measure Master Pro Calculator 4020
Расчетные отрасли
Сейчас:
$35. 99
99
Калькулятор метрических и метрических размеров в футах и дюймах Всегда получайте профессиональные результаты с помощью этого удобного и простого в использовании инструмента для проектов, связанных с измерениями. Работайте и конвертируйте между…
CAL4020
В корзину
Быстрый просмотр
Calculated Industries Construction Master Pro Calculator 4065
Расчетные отрасли
Сейчас: 58,99 $
Усовершенствованный строительно-математический калькулятор Construction Master Pro — это отмеченный наградами усовершенствованный строительно-математический калькулятор с долями футов и дюймов с мощными встроенными решениями, идеально подходящими для выполнения…
CAL4065
Быстрый просмотр
Настольный калькулятор Calculated Industries Construction Master Pro 44080
Calculated Industries
Усовершенствованный настольный строительно-математический калькулятор с полным набором триггерных функций
Construction Master Pro Trig — Desktop предоставляет профессионалам в области строительства полный набор функций триггера, чтобы помочь им. ..
..
CAL44080
В корзину
Быстрый просмотр
Calculated Industries Ultra Measure Master Calculator 8025
Расчетные отрасли
Сейчас: 45,99 долларов США
Калькулятор преобразования стандарта США в метрическую систему профессионального уровня Ultra Measure Master — это полный и простой в использовании калькулятор преобразования стандарта США в метрическую систему для инженеров, архитекторов,…
CAL8025
Клиенты также просмотрели
В корзину
Быстрый просмотр
Calculated Industries Construction Master Pro Calculator 4065
Расчетные отрасли
Сейчас: 58,99 $
Усовершенствованный строительно-математический калькулятор
Construction Master Pro — это отмеченный наградами усовершенствованный строительно-математический калькулятор с долями футов и дюймов с мощными встроенными решениями, идеально подходящими для выполнения. ..
..
CAL4065
В корзину
Быстрый просмотр
Calculated Industries Measure Master Pro Calculator 4020
Расчетные отрасли
Сейчас: $35.99
Калькулятор метрических и метрических размеров в футах и дюймах Всегда получайте профессиональные результаты с помощью этого удобного и простого в использовании инструмента для проектов, связанных с измерениями. Работайте и конвертируйте между…
CAL4020
Быстрый просмотр
Настольный калькулятор Calculated Industries Construction Master Pro 44080
Calculated Industries
Усовершенствованный настольный строительно-математический калькулятор с полным набором триггерных функций
Construction Master Pro Trig — Desktop предоставляет профессионалам в области строительства полный набор функций триггера, чтобы помочь им.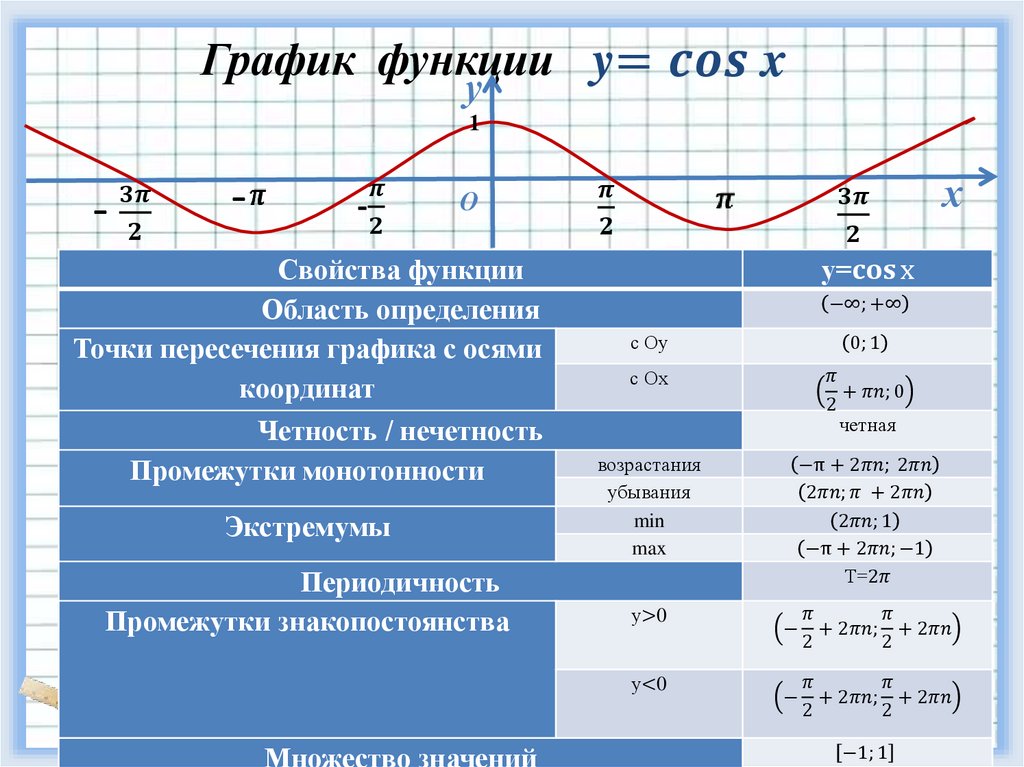

 Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.
Учебник. – ООО «ИОЦ МНЕМОЗИНА», 2019.

 Найдите шпильки для наклонных стен с межосевым расстоянием
Найдите шпильки для наклонных стен с межосевым расстоянием
Ваш комментарий будет первым