Построение точек на координатной плоскости онлайн: Бесплатное он-лайн геометрическое приложение

Содержание

Проекция точки на плоскость онлайн

С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Для нахождения проекции точки M₀ на плоскость α, необходимо:

построить прямую L, проходящую через точку M₀ и ортогональной плоскости α.
найти пересечение данной плоскости α с прямой L(Рис.1).

Общее уравнение плоскости имеет вид:

где n(A,B,C

)− называется нормальным вектором плоскости.

Уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:

Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .

Таким образом, уравнение прямой, проходящей через точку M₀(x₀, y₀, z₀) и ортогональной плоскости (1) имеет следующий вид:

Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее

Выразим переменные x, y, z через рараметр

Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.

A(At+x₀)+B(Bt+y₀)+C(At+z₀)+D=0,

A²t+Ax₀+B²t+By₀+C²t+Cz₀+D=0,

Подставляя значение параметра t в выражения (4), находим проекцию M₁ точки M₀ на плоскость (1).

Пример 1.Найти проекцию M₁ точки M₀(4, -3, 2) на плоскость

Решение.

Нормальный вектор плоскости имеет вид:

n=(5, 1, −8),

т.е. A=5, B=1, C=−8.

Координаты точки M₀: x₀=4, y₀=−3, z₀=2.

Подставляя координаты точки M₀ и нормального вектора плоскости в (5), получим:

Из выражений (7) находим:

Ответ:

Проекцией точки M₀(4, -3, 2) на плоскость (6) является точка:

Координатная плоскость 6 класс онлайн-подготовка на Ростелеком Лицей

Основные сведения о координатной плоскости

Как известно, на каждом доме указаны его номер и название улицы – это адрес дома. На билете в любой зрительный зал написаны номер ряда и номер места – это адрес кресла. Для определения положения точки на глобусе надо знать долготу и широту – это адрес географической точки (географические координаты). Каждый объект имеет свой упорядоченный адрес (координаты). Таким образом, адрес или координаты – это числовое или буквенное обозначение того места, где находится объект.

Математиками была разработана модель, которая, в частности, позволяет описать любой зрительный зал (расположение мест в зале). Такая модель получила название координатная плоскость.

Чтобы из обычной плоскости получить координатную, необходимо начертить две перпендикулярные прямые, отмечая стрелками направления «вправо» и «вверх» (см. Рис. 1). На прямые наносят деления, как на линейку, причем точка пересечения прямых – это нулевая отметка для обеих шкал. Горизонтальную прямую обозначают и называют осью абсцисс, вертикальную прямую обозначают и называют осью ординат.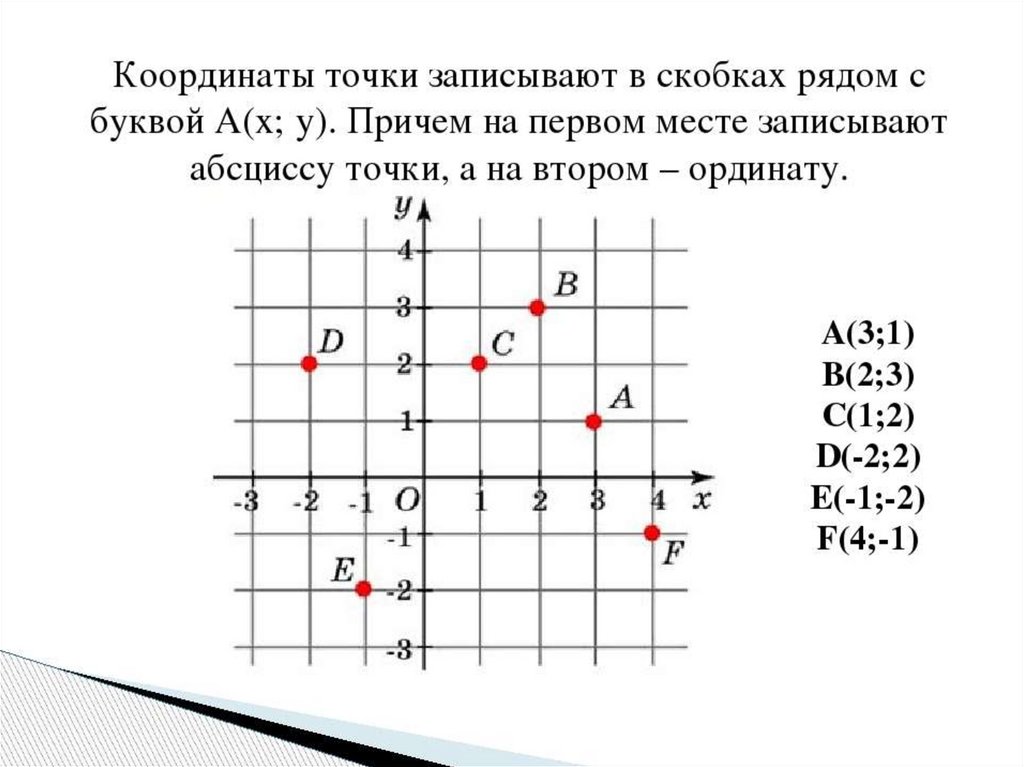

Две перпендикулярные оси и с разметкой называют прямоугольной, или декартовой, системой координат. Название «декартова» происходит от фамилии французского философа и математика Рене Декарта, который ее придумал.

Рис. 1. Координатная плоскость

Координаты точки

Для любой точки на координатной плоскости можно указать два числа (координаты). На рисунке 2 показана точка на координатной плоскости. Для получения координат этой точки необходимо через точку провести две прямые, параллельные координатным осям (обозначены пунктирной линией). Пересечение одной из прямых с осью абсцисс – это координата точки , пересечение другой прямой с осью ординат – это координата точки . Сначала указывают координату , потом . Точка имеет координаты . Аналогично находим координаты точки , она имеет координаты (см. Рис. 2).

Рис. 2. Определение координат точек на координатной плоскости

Можно сделать все и в обратном порядке. То есть изобразить точку на плоскости по известным координатам.

Пример

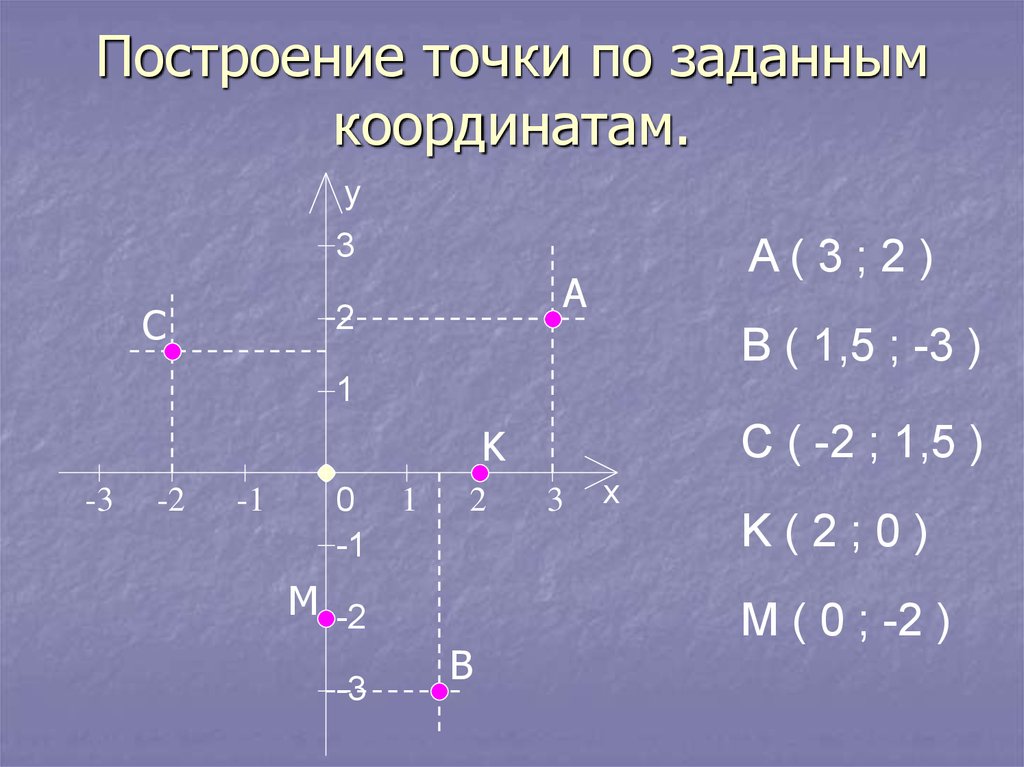
1. Построить точки по заданным координатам ,

Для построения точки необходимо отложить число 2 на оси и провести перпендикулярную прямую; на оси откладываем число 5 и проводим перпендикулярную оси прямую (см. Рис. 3). На пересечении перпендикуляров получим точку с координатами .

Для построения точки необходимо отложить на оси число 3 и провести перпендикулярную оси прямую; на оси откладываем число (–1) и проводим перпендикулярную оси прямую. На пересечении перпендикуляров получим точку с координатами . (см. Рис. 3).

Рис. 3. Построение точек на координатной плоскости по заданным координатам

2. Построить точки по заданным координатам ,

Для построения точки необходимо отложить число 3 на оси . Координата равна нулю, следовательно, точка лежит на оси (см. Рис. 4).

Для построения точки необходимо отложить число 2 на оси . Координата равна нулю, следовательно, точка лежит на оси (см. Рис. 4).

Рис. 4. Построение точек на координатной плоскости по заданным координатам

Таким образом, если нулю равна координата , то точка лежит на оси , а если нулю равна координата , то точка лежит на оси .

Задача

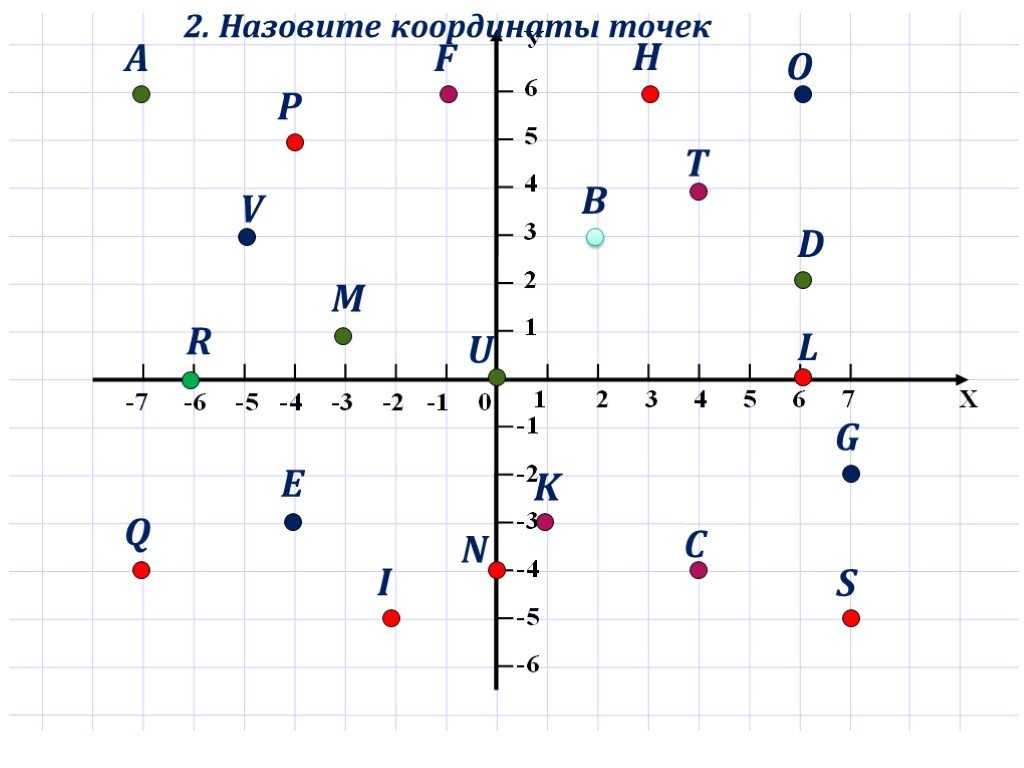
1. Выписать координаты точек , , , (см. Рис. 5).

2. Изобразить точки , , , , .

Рис. 5. Иллюстрация к задаче

Решение

1. Для определения координат точки проведем через нее две прямые, параллельные координатным осям. Пересечение одной из прямых с осью абсцисс – это координата , пересечение другой прямой с осью ординат – это координата . Следовательно, точка имеет координаты (см. Рис. 6).

Для определения координат точки проведем через нее две прямые, параллельные координатным осям. Пересечение одной из прямых с осью абсцисс – это координата , пересечение другой прямой с осью ординат – это координата . Следовательно, точка имеет координаты .

Точка находится на оси , поэтому координата равна нулю. Координата этой точки равна (–2). Следовательно, точка имеет координаты .

Точка находится на оси , поэтому координата равна нулю. Координата этой точки равна –5. Следовательно, точка имеет координаты .

Рис. 6. Иллюстрация к задаче

2. Для построения точки откладываем число (–3) на оси и проводим перпендикулярную прямую; на оси откладываем число (–2) и проводим перпендикулярную оси прямую (см. Рис. 7). На пересечении перпендикуляров получим точку с координатами .

Координата точки равна нулю, поэтому эта точка лежит на оси .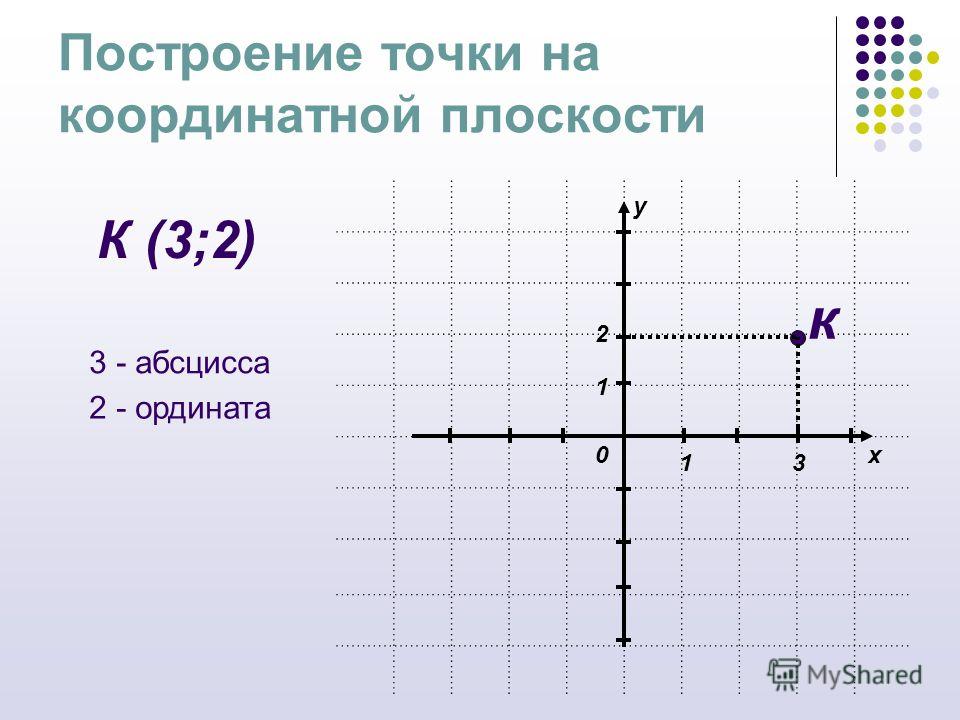 Отложим на оси число 5 и получим точку с координатами .

Для построения точки откладываем число 3 на оси и проводим перпендикулярную оси прямую; на оси откладываем число 4 и проводим перпендикулярную оси прямую. На пересечении перпендикуляров получим точку с координатами .

Координата точки равна нулю, поэтому эта точка лежит на оси . Отложим на оси число (–4) и получим точку с координатами .

Две координаты точки равны нулю, следовательно, эта точка лежит на оси и на оси , то есть является точкой пересечения двух осей (начало координат).

Рис. 7. Иллюстрация к задаче

Координатные четверти

Координатные оси разбивают координатную плоскость на четыре части – четверти. Порядковые номера четвертей принято считать против часовой стрелки (см. Рис. 8).

Рис. 8. Нумерация четвертей координатной плоскости

Если точка имеет положительную координату и положительную координату , то она лежит в первой четверти.

Если точка имеет отрицательную координату и положительную координату , то она лежит во второй четверти.

Если точка имеет отрицательную координату и отрицательную координату , то она лежит в третьей четверти.

Если точка имеет положительную координату и отрицательную координату , то она лежит в четвертой четверти.

Например, у точки координата положительная, а координата отрицательная, следовательно, эта точка находится в четвертой четверти.

Другие системы координат

Чтобы присвоить точке числовой «адрес» (координаты), используются и другие системы координат.

Причины использования различных систем координат:

1. Размерность.

На этом уроке мы рассматривали прямоугольную систему координат на плоскости. Размерность такого пространства равна 2, то есть точка задавалась двумя координатами. Однако пространство может иметь другую размерность, например равную единице, когда точка может менять свое положение только в одном направлении (двигаться вперед-назад или вверх-вниз). В качестве примера можно привести движение автомобиля по ровной дороге или движение лифта. Для указания местоположения точки нужна только одна координата. Эта координата будет означать то расстояние, которое проехал автомобиль (см. Рис. 9), или этаж, на котором находится лифт (см. Рис. 10).

Рис. 9. Координата в данном случае – это расстояние, на которое отъехал автомобиль

Рис. 10. Координата в данном случае – этаж, на котором находится лифт

В математике такая система координат представлена числовой или координатной осью. Чтобы из любой прямой получить координатную ось, необходимо отметить на прямой начало отсчета, масштаб и направление отсчета (см. Рис. 11). По одной координате можно однозначно понять, где находится точка.

Рис. 11. Координатная ось

Размерность пространства может быть равной трем (пространство, в котором мы живем, имеет три измерения). Для указания места положения точки в этом случае нужны три координаты. Например, если в высотном здании на каждом этаже находится кинотеатр, то для указания места в билете должны быть указаны три координаты – этаж, ряд, номер кресла. В математике такая система координат строится точно так же, как на плоскости, только добавляется третья ось (см. Рис. 12).

Рис. 12 Декартова система координат в пространстве

2. Другой метод задания координат точки (использование полярной системы координат на плоскости).

Проводится ось , а для точки указывается расстояние от нуля до нее и угол, который образует отрезок с осью . Эти два числа и будут являться координатами точки (см. Рис. 13).

Рис. 13. Полярная система координат на плоскости

В трехмерном пространстве строятся аналогичные системы, например сферическая или цилиндрическая система координат.

Таким образом, прямоугольная система координат широко применяется в математике, но не является единственной.

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.

2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.

3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.

4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.

5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.

6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт mathematics-repetition.com (Источник)

2. Интернет-сайт youtube.com (Источник)

3. Интернет-сайт exponenta.ru (Источник)

Домашнее задание

1. Вопросы в конце раздела 45 (§9), задание 1393, 1394, 1396, 1398 (стр. 245-246) – Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 (Источник)

2. Выберите точки расположенные выше оси абсцисс: , , , , .

3. В координатной плоскости построить следующие точки, соединяющие их последовательно с предыдущей точкой отрезком (получите определенный рисунок): , , , , , , , , , , , , , , , , , , , , , , , , , , , .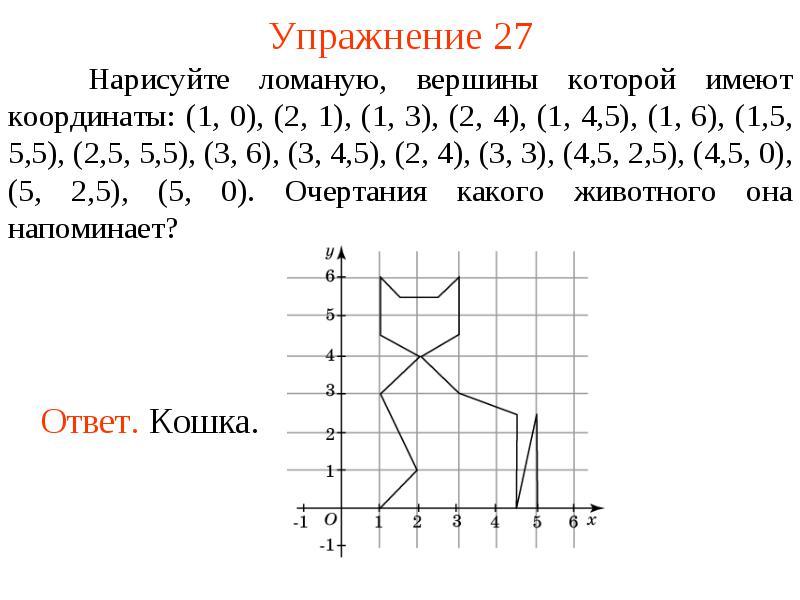

Как мне «нанести точки» на декартовой плоскости?

Декартовы плоскостные квадранты

Purplemath

Когда вы пытались найти свою улицу на этой карте, вы переходили к D, а затем к 12. И это обозначение «D12» было недвусмысленным, потому что было легко определить, какой знак обозначало направление (поскольку буквы были сверху, а цифры — слева).

Содержание продолжается ниже

MathHelp.com

Декартова координатная сетка

Даже если бы обозначение было написано как «12-D», вы все равно знали бы, к какому ящику идти, потому что «D» по-прежнему было бы сверху, а «12» — вдоль сторона. Но в декартовой плоскости обе оси помечены цифрами. Как вы можете сказать, как далеко влево или вправо идти, или как далеко вверх или вниз идти?

Как наносить точки?

Учитывая точку ( a , b ), вы наносите точку на декартовой плоскости, находя число a по горизонтали или x — по оси; затем вы прослеживаете прямо вверх или вниз от этого места, двигаясь параллельно вертикальной или y — оси, пока не достигнете высоты числа b . Это место является местоположением точки ( a , b ).

Что такое координаты?

Координаты — это числа в названии точки. Например, точка (−3, 4) имеет координату x −3 и координату y 4. x -координата первая координата; координата y — это вторая координата.

Например, предположим, что вам сказали найти «(5, 2)» (произносится как «точка пять два» или просто «пять два») на плоскости. Куда бы вы посмотрели? Чтобы понять значение «(5, 2)», вы должны знать следующее правило: координата x (то есть число для оси

x ) всегда идет первым. Первое число (называемое «первой координатой») равно 9.0019 всегда по горизонтальной оси.

Итак, для точки (5, 2) вы должны начать с начала координат (то есть вы должны начать с точки пересечения двух осей):

…затем досчитать до «пяти» на x -ось:

…затем сосчитайте до «два», двигаясь параллельно оси y :

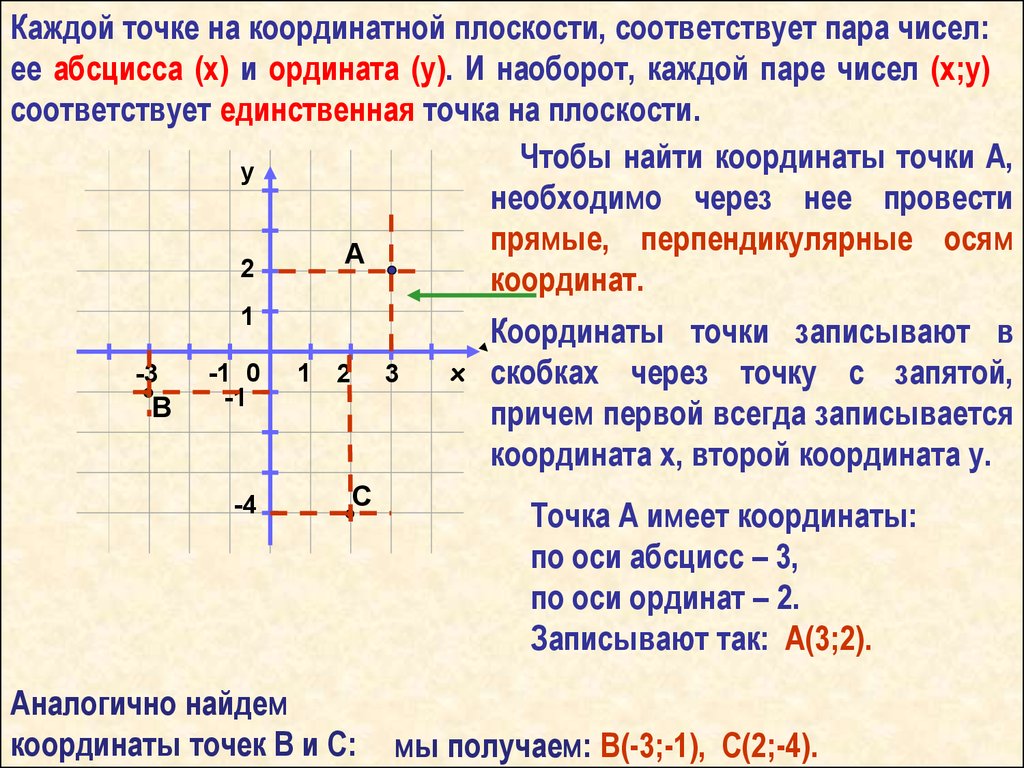. ..и затем нарисуйте точку:

Нахождение местоположения точки (5, 2), а затем рисование его точки называется «построением точки (5, 2)». Рисунок маленькой части x , y -плоскость, оси, и дело в том, чего они ждут от вашего ответа на руки.

(Обозначение точки ее координатами [чего, нет, я не делал выше] никогда не помешает, особенно если у вас один из самых строгих инструкторов.

При построении помните, что первое число соответствует горизонтальная ось, а второе число для вертикальной оси. Вы всегда идете «до сих пор вверх или вниз», а затем «так далеко вверх или вниз»

Нанесите точку (4, −5)

Я начну с исходной точки:

…затем я сосчитаю четыре единицы по горизонтальной оси x :

…затем я отсчитаю вниз по на пять единиц параллельно y -ось:

…и затем я нарисую свою точку:

Как вы можете видеть выше, отрицательная y -координата означает, что вы будете считать вниз по оси y , не вверх; вы будете идти ниже горизонтальной оси, а не выше.

(И на этот раз я пометил точку. Если не указано иное в инструкциях, это не потребуется. Если вы чувствуете потребность в точках домового, это не помешает.)

Сюжет точка (−3, −1).

Я начну с исходной точки:

…затем я посчитаю в обратном направлении три единицы по оси x :

…затем я буду считать вниз на одну единицу параллельно и -ось:

…и затем я нарисую свою точку:

Таким образом, чтобы нанести заданную точку ( a , b ):

Нарисуйте и обозначьте *аккуратную* систему координат (то есть, используйте линейку, чтобы нарисовать и обозначить две перпендикулярные числовые линии).
Найдите исходную точку (то есть начните с точки (0, 0), где пересекаются две оси).
Сдвинуться вправо на a единиц — или, если число a отрицательное, сдвинуться влево | и | единицы измерения.

От этой точки по оси x (то есть от этой точки по горизонтальной числовой строке) переместитесь вверх на b единиц — или вниз на | b |, если b сама по себе отрицательная — всегда движется параллельно оси y (то есть параллельно вертикальной числовой прямой).
Нарисуйте точку в последнем месте; это ваша намеченная точка.

Примечание. Если вы хотите постоянно получать полную оценку за свои графики, убедитесь, что вы используете линейку для рисования линий и маркировки шкал, некоторые из этих отметок с цифрами, чтобы ваш смысл был ясен, и убедитесь, что вы рисуете свою точку там, где она должна быть. Не рисуйте точку в непосредственной близости, а затем рисуйте огромную точку, чтобы «включить» как первую точку, так и место, где эта точка *должна* была появиться в первую очередь.

URL: https://www.purplemath.com/modules/plane2.htm

Page 1Page 3

Координируйте действия в плоскости, чтобы попробовать

Автор Tyne Brack

20 декабря

3 акции

Координатная плоскость — мой личный фаворит. Он практический, укрепляет порядок рациональных чисел и охватывает все среднее образование. Если и есть юнит, которого я больше всего жду, так это этот!

Сегодня я поделюсь некоторыми советами по обучению сложностям этой сетки и несколькими увлекательными занятиями, которые понравятся вам и вашим ученикам.

Три совета по обучению

Наиболее распространенное заблуждение, с которым вы можете столкнуться, состоит в том, что учащиеся перемещаются вверх и вниз по оси Y, прежде чем двигаться вправо или влево по оси X. Существует множество трюков с памятью, таких как «вы должны проползти, прежде чем вы сможете подняться» или «вы должны перейти улицу, прежде чем вы сможете сесть в лифт», чтобы помочь учащимся планировать свои шаги. Поскольку построение графика на координатной плоскости не требует «демонстрации работы», такой как построение пропорции, у меня нет проблем с тем, чтобы попросить учащихся аннотировать координаты. Я буду моделировать и требовать, чтобы учащиеся писали крошечную стрелку вправо или влево над координатой x и крошечную стрелку вверх или вниз над координатой y каждый раз, когда они сталкиваются с набором координат. Я также прошу учащихся обозначить свои графики «осью X» и «осью Y».

Не переоценивайте учеников! Легко думать, что шестиклассники могут построить график во всех 4 квадрантах в первый день. Начните с построения графика только в Квадранте I в первый день. Затем переходите к построению графика по всем 4 квадрантам на второй день. К третьему дню вы будете более успешно рисовать рациональные числа.

Графики на осях могут быть особенно сложными. Когда я видел, как учащиеся путают координаты, это обычно происходило потому, что одна из координат была равна 0. Совет: напомните учащимся, что если для этой координаты есть 0, то она не будет отображаться на этой оси. Например, (0, 4) означает, что он не может оказаться на оси x, потому что у него есть 0 для координаты x. Он должен заканчиваться на оси Y.

Занятия с координатной плоскостью

Координатная плоскость. Этот модуль для 6-го класса отлично подходит для обучения работе со строительными лесами. Кроме того, студенческие раздаточные материалы, домашнее задание, учебное пособие и оценка сделаны для вас!

Демонстрация действий на плоскости координат — Десмос действительно демонстрирует этот навык. Я связал весь объем их практики координатной плоскости, но этот мраморный слайд для мини-гольфа особенно полезен для нанесения точек, включая анализ ошибок. Морские бои — это пьеса о Морском корабле, и я могу представить себе бой!

Координатная плоскость Цифровые упражнения. Вам нужна практика для всех стандартов координатной плоскости CCSS для 6-го класса — знакомство с частями графика, построением графика, отражениями и расстоянием? Эти цифровые задания охватывают все, включают в себя выходной билет с двумя вопросами для каждого навыка и включают в себя 16 заданий.

Онлайн-игра «Запасись на полках». Это онлайн-практика для построения графика целых чисел во всех 4 квадрантах. Мне нравится, что если учащийся ошибается, ему приходится продолжать попытки, прежде чем он сможет перейти к следующей задаче.

Проектирование комнаты в общежитии. Задача производительности. Эта задача производительности координатной плоскости может быть типичным заданием, групповым проектом или расширением. Это требует от учащихся нестандартного мышления, когда они решают реальные и математические задачи, строя графики на координатной плоскости.

Создайте координатную плоскость на своем этаже . Член нашей команды МТМ и нынешний учитель Марисса — большая поклонница этого занятия. Она пододвигает все парты учеников к краю своего класса и использует малярный скотч, чтобы создать гигантскую координатную плоскость. Затем учащихся просят пройти по графику так, как они наносят точки (начать с начала координат, пройти по оси X, а затем двигаться вертикально по оси Y). В этом упражнении она предлагает учащимся практиковаться в отражении над осями, используя партнера для представления своего отражения.

Координатная охота за мусором на самолете

. Учащиеся будут перемещаться по карте города с координатной плоскостью, используя подсказки, предоставленные на каждой станции.