Вычислить объем тела ограниченного поверхностями
Задача.
Вычислить объем тела, ограниченного поверхностями:
Решение.
Указанные уравнения задают соответствующие поверхности, которыми ограничена фигура, объем которой мы будем находить.
Для вычисления объема поверхности используется формула .
Разберемся сначала, что за тело получится при построении всех поверхностей. Для этого выполним чертеж.
Изобразим сначала параллельную ортогональную проекцию тела на координатную плоскость XOY. Поскольку проецирование будет проводиться вдоль оси OZ, то в прежде всего нужно разобраться с теми поверхностями, которые являются параллельными данной оси. Обратим внимание, что такие уравнения не содержат букву z. В условии задачи таких уравнений 3:
1. задаёт плоскость YOZ, проходящую через ось OY;
2. задаёт плоскость XOZ, проходящую через ось OX;
3. задаёт плоскость, которая проходит через прямую параллельно оси OZ.
задаёт плоскость, которая проходит через прямую параллельно оси OZ.
Треугольник будет проекцией в том случае, если его не обрежет какая-нибудь из оставшихся поверхностей.
Проанализируем остальные поверхности.
Выясним, чем тело будет ограничено сверху, снизу и выполним пространственный чертёж.
Вернемся к условию задачи и посмотрим на поверхности, которые остались:
описывает координатную плоскость XOY;
описывает параболический цилиндр, который расположен над плоскостью XOY и проходит через ось ОХ.
Следовательно, проекцией тела действительно будет треугольник.
Обратим внимание, что в условии мы обнаружили избыточность условия, то есть достаточно было меньшее количество уравнений для решения задачи. Например, уравнение плоскости XOZ лишнее, так как поверхность касается оси ОХ и замыкает тело. Но в таком случае проекцию невозможно было бы начертить сразу, а лишь после анализа уравнения поверхности .

Начертим часть параболического цилиндра:
Данный чертеж позволяет определить порядок обхода тела.
Определим порядок обхода проекции. Для этого очень удобно использовать двумерный чертеж. Получаем:
Затем посмотрим на наш трёхмерный чертёж снизу вверх. Сначала мы натыкаемся на плоскость и проходим далее через поверхность . Получаем следующий порядок обхода тела:
Запишем тройной интеграл, от которого перейдём к повторным:
Интегралы будем находить отдельно:
1) Начнем с внутреннего интеграла от переменной z. Согласно формуле Ньютона-Лейбница:
Полученный результат подставим в следующий интеграл от переменной y:
Ответ. куб. ед.
Конечно, решение можно было записать одной строкой, но с пояснениями оно получилось достаточно длинным, но при таком варианте возможность допустить ошибку намного меньше.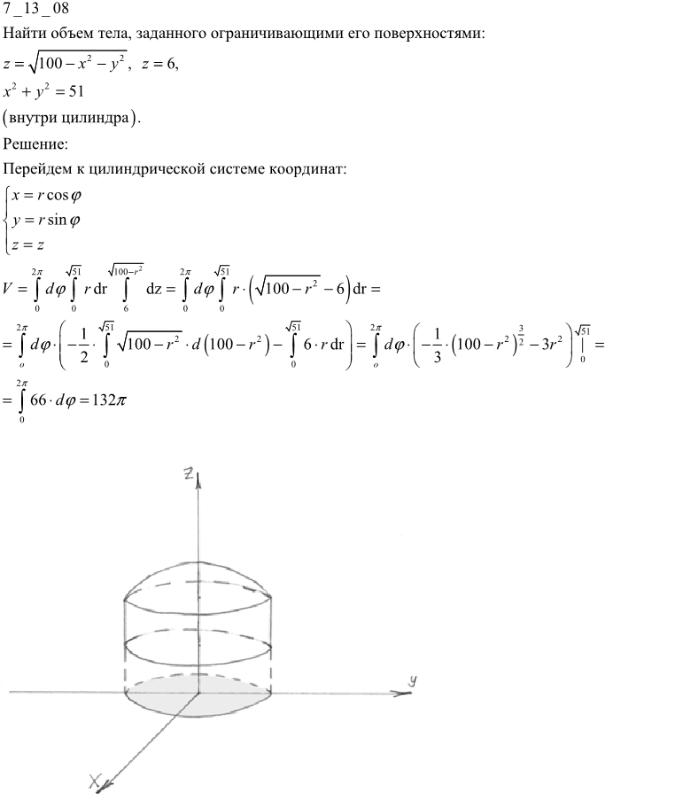
Вычисление потока векторного поля
На предыдущем уроке проанализированы более простые примеры на вычисления потока векторного поля. Здесь задания усложняются поверхностью интегрирования, которая ограничена как одним, так и двумя сечениями.
Как следствие, больше расчетов пределов интегрирования, более сложные двойные интегралы и сами вычисления.
Все важные переходы и приемы хорошо расписаны, а примеры отвечают учебным программам большинства ВУЗов Украины.
ЗАДАНИЕ 8.2 Найти поток векторного поля через замкнутую поверхность S: x2+y2=z2, z=1, z=5 (нормаль внешна).
Решение: Поверхность x2+y2=z2 — описывает часть конуса с вершиной в начале координат, которое вытянуто вдоль оси Oz и ограничена плоскостями z=1, z=5.
В этом и следующих примерах для представления приведенны рисунки поверхности интегрирования и их проекции в декартовую плоскость
В сечении получили два круга с радиусами, соответственно R=1, R=5.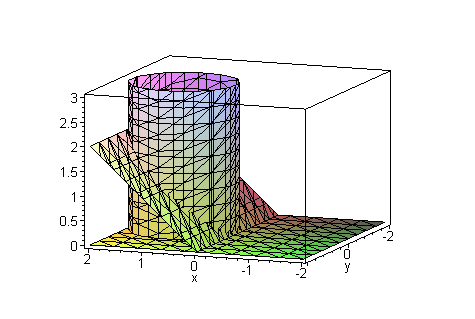
В силу симметрии нет необходимости интегрировать по кругу, достаточно найти пределы четверти круга :
Напоследок результирующий интеграл множим на четверку.
В примерах на интегрирование по поверхностям нужно быстро выполнять построение классических тел вращения.
Также необходимо правильно находить пересечения плоскостями, иначе правильного ответа не получите.
Вы должны уметь удачно учитывать симметричность функций, их четность или нечетность.
Вычислим дивергенцию векторного поля :
где функции являются соответствующими множителями при орте векторного поля
P=P(x;y;z)=e2z+2x, Q=Q(x;y;z)=ex-y, R=R(x;y;z)=2z-e2y.
За формулой Остроградського-Гаусса находим поток векторного поля
Из тройного интеграла видим, что кроме того, что нужно хорошо уметь верно расставлять пределы интегрирования, умение пользоватся методом замены переменных тоже важно.
Без этого Вы остановитесь на середине интеграла и не будете знать, как возвести интеграл к конечному ответу.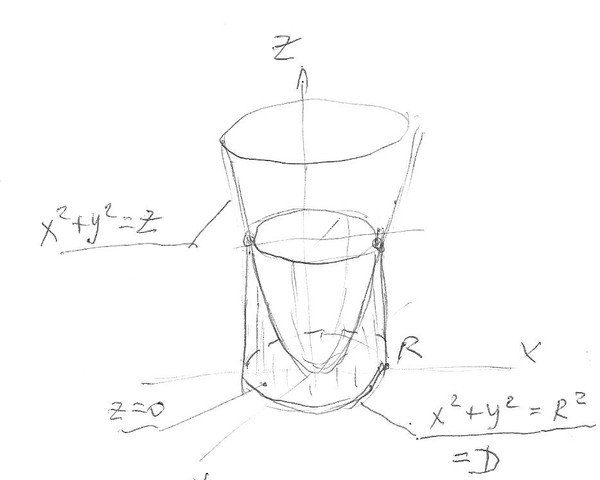
ЗАДАНИЕ 8.4 Вычислить поток векторного поля через замкнутую поверхность S: x2+y2=6z, z=1 (нормаль внешна).
Решение: Поверхность x2+y2=6z — коловий параболоид с вершиной в начале координат, который вытянут вдоль оси Oz и ограничен плоскостью z=1.
В перерезе получили круг с радиусом равным корню из шести
Как знать, что получим в перерезе плоскостью?
Кто хорошо читал теорию, тот делает это автоматически, а в целом в уравнение поверхности x2+y2=6z подставляем плоскость z=1.
В результате получим уравнение круга x2+y2=6.
Справа имеем квадрат радиуса, вот и весь анализ.
И такая схема справедлива для целого класса рассмотренных задач.
Как видим из рисунку четверть области V ограничена пределами:
Как и в предыдущем задании, здесь учитываем четность всех функций.
Это позволяет упростить само интегрирование и не разбивать доминирующий интеграл на несколько с одинаковым конечным значением.
Учитывая это, результат умножим на 4.
Но к нему еще следует дойти, потому сначала вычисляем дивергенцию векторного поля :
где функции P, Q, R принимают значение
P=P(x;y;z)=ez+4x, Q=Q(x;y;z)=2xz-y, R=R(x;y;z)=-2z-x2y.
Вычисляем поток векторного поля по известной формулой:
Для большинства приведенных примеров переход к полярной системе координат под интегралом позволяет упростить дальнейшее их нахождение. Детально останавливаться на этом не будем, в формуле выписаны все этапы интегрирования и замены, поэтому анализируйте самостоятельно.
ЗАДАНИЕ 8.7 Найти поток векторного поля через замкнутую поверхность S:
2(x2+y2)=z2, z=2, z=6 (нормаль внешна).
Решение: Уравнение 2(x2+y2) =z2 описывает конус с вершиной в начале координат (0;0;0) что вытянут вдоль оси Oz и ограничен плоскостями z=2, z=6 по условию.
В сечении получили круги с радиусами, соответственно корень из двух и восемнадцати
В силу симметрии рассматриваем четверть области V, которая ограничена поверхностями:
Результат интегрирования умножим на 4.
Определяем дивергенцию векторного поля :
где функции задаются зависимостями
За формулой Остроградського-Гаусса находим поток поля F:
Формулы не из легких, однако достаточно распространены на практике, потому не спеша хорошо проанализируйте расстановку пределов интегрирования и замену переменных.
Применение перехода к полярной СК позволяет свести корневые функции к показательным.
ЗАДАНИЕ 8.8 Вычислить поток векторного поля через замкнутую поверхность S: x2+y2+z2=4x-2y-4 (нормаль внешна).
Решение: Сведем поверхность x2+y2+z2=4x-2y-4 к каноническому виду
x2-4x+4+y2+2y+1+z2=4+1-4, (x-2)2+(y+1)2+z2=1 — сфера с центром (2;-1;0) и радиусом R=1.
Ее график и проекция на плоскость Oxy приведены ниже
Как можно видеть из рисунку, 1/8 поверхности сферы задается пределами:
Здесь учли четность функций, поэтому интеграл будем множить на 8 (верхняя и нижняя полусферы).
Дивергенцию векторного поля находим по формуле:
где P=P(x;y;z)=sin(2y)+x, Q=Q(x;y;z)=y-sin2(x), R=R(x;y;z)=z-cos(x*y).
Дальше интегрированием вычисляем поток векторного поля: где R=1 — радиус сферы.
Так как здесь подинтегральная функция равна постоянной, то тройной интеграл не что иначе, как объем сферы с радиусом 1, разделенный на 8 (согласно упрощений).
На основе выше рассмотренных задач, попробуйте самостоятельно найти тройной интеграл и убедиться в правильности рассуждений.
ЗАДАНИЕ 8.14 Найти поток векторного поля через замкнутую поверхность S: , (нормаль внешна).
Решение: Поверхность задает конус с вершиной в (0;0;4), что вытянут вдоль оси Oz вниз и ограничен плоскостью z=1.
Графически поверхность интегрирования можно представить из следующих рисунков
В сечении z=1 получим круг с радиусом R=3.
В силу симметрии четверть области V задается следующими пределами:
Не забываем, что при этом нужно интеграл кмножить на 4.
Находим дивергенцию поля :
функции P, Q, R
Поток векторного поля находим по формуле Остроградського-Гаусса :
Тройной интеграл не тяжелый в плане вычислений, и схемы применения замены переменных и возведения к простому виду хорошо расписаны в предыдущих примерах.
Потек равен П=27pi.
ЗАДАНИЕ 8.15 Вычислить поток векторного поля через замкнутую поверхность S: 2y-x+z=2, x=0, y=0, z=0 (нормаль внешна).
Решение: Уравнение 2y-x+z=2, -x/2+y/1+z/2=1- описывает плоскость, которая является одной из граней треугольной пирамиды.
Чтобы лучше это представить рассмотрите следующие рисунки к задаче.
Из построения видим, что область V ограничена поверхностью:
Такой анализ позволяет коректно расставить пределы интегрирования в тройном интеграле.
Вычисляем дивергенцию векторного поля :
где P=P(x;y;z)=x+4yz, Q=Q(x;y;z)=ez+x+y, R=R(x;y;z)=-3z-x2y.
Вычисляем поток векторного поля F:
Интеграл не из легких, поэтому внимательно разберите как расставленные пределы, проанализируйте эффективность замены переменных при упрощении повторного интеграла.
ЗАДАНИЕ 8.25 Вычислить поток векторного поля через замкнутую поверхность S: z=-1 (нормаль внешна).
Решение: Анализ уравнения — конус со смещенной относительно начала координат вершиной (0;0;- 3), который вытянут вдоль оси Oz вверх и ограничен сверху плоскостью z=-1.
В сечении имеем круг с радиусом R=2.
Четверть области V описываем следующими пределами:
Правильно найденные пределы интегрирования играют определяющую роль при интегрировании, поэтому помните что это одна из ответственных частей приведенных расчетов.
Результат интегрирования не забывайте множить на 4.
Дивергенцию поля через частичные производные равны:
здесь учтено P=P(x;y;z)=x/2+ln(1-z), Q=Q(x;y;z)=y, R=R(x;y;z)=x2+z/3.
По формуле вычисляем поток векторного поля F:
Переход от повторного к двойному определенному интегралу лучше делать через приведенную замену переменных, остальное интегрирование сводится к простым табличным формулам и определения значений на пределах.
Будьте внимательные при расчетах, в первую очередь проверяйте правильность расстановки пределов интегрирования.
Хорошо заучите замену переменных, которая здесь приведена и применяйте ее в примерах, что подобные за конструкцией к рассмотренным.
При вычислении интегралов проверяйте себя на каждом шагу, наименьшая ошибка при переходах в начале приведет к неправильному ответу напоследок расчетов.
Insights of SOLIDWORKS Surfacing: советы и рекомендации
Что такое поверхность? Чтобы понять, что такое поверхность, мы должны понять, что такое твердое тело. В твердом теле каждое ребро является границей между двумя гранями , что создает водонепроницаемый замкнутый объем, который может содержать массу. Это означает, что, наоборот, поверхностное тело будет иметь ребра, которые ограничивают только одну грань, оставляя открытую модель с открытым объемом. Ребра тела будут черный , а края поверхности будут синими . В этом блоге мы рассмотрим все, что вам нужно знать о SOLIDWORKS Surfacing.
В этом блоге мы рассмотрим все, что вам нужно знать о SOLIDWORKS Surfacing.
Видео по теме: SOLIDWORKS — Основы работы с поверхностями 02 Рис. 1. Грань поверхности
Параметризация граней поверхности
Все поверхности в SOLIDWORKS определяются сеткой кривых U-V, которую можно увидеть с помощью:
- Кривые граней
- Купол
- Поверхность заполнения
- Граничная поверхность
- Произвольная форма
- Лофт
Рисунок 3: Параметризация U-V
Сетка всегда будет иметь перпендикулярных кривых, однако не все формы четырехсторонние. Программное обеспечение обычно обрезает четырехстороннюю поверхность для создания трехсторонней формы. Кроме того, если одна или несколько сторон имеют нулевую длину, кривые в этом направлении пересекаются в точке, называемой сингулярностью. Это называется дегенерируют поверхность и могут вызвать проблемы на твердом уровне.
Алгебраическая поверхность
U-V кривые на алгебраических поверхностях представляют собой прямые линии, дуги или окружности. Отличными примерами являются пирамиды, кубы, сферы и цилиндры.
Рис. 4: 3-сторонний вырез
Линейчатая
Линейчатая поверхность — это поверхность, каждая точка которой имеет прямую, проходящую через нее и лежащую на поверхности.
Рисунок 5: Линейчатая поверхность
Развертываемая поверхность
Развертываемая поверхность — это часть линейчатой поверхности, которую можно сгладить без растяжения поверхности. Часто плоские, конические и цилиндрические, и это единственный тип поверхности, которую также можно сплющить в листовом металле.
NURBS
(неоднородный рациональный B-сплайн) — это технология наплавки, при которой поверхность интерполируется между параметризованными сплайнами вместо других алгебраических форм.
Технический совет. Алгебраические, линейчатые и развертываемые поверхности иногда называют аналитическими поверхностями . NURBS-поверхности часто называют алгоритмическими поверхностями.
Зачем использовать поверхности в SOLIDWORKS?
Существует три основных причины использования поверхности:
- Некоторые формы нельзя создавать из твердых тел
- Поверхности создают форму, по одной грани за раз
- Поверхности как справочная геометрия
Некоторые формы нельзя создать с помощью твердых тел
В этом видео объясняется, что купол нельзя создать на плоском конце лофта, а заполненная поверхность с непрерывной непрерывностью закроет плоский конец, чтобы сделать его круглым. Большая часть твердотельной геометрии создает плоскую грань, поэтому моделирование поверхностей может помочь нам закрыть плоские концы или создать неплоскую геометрию.
Поверхности строят форму, по одной грани за раз
Поверхности позволяют управлять каждой отдельной гранью объекта вместо одновременного построения нескольких сторон в одном направлении. Это позволяет создавать органические и неалгебраические формы в нескольких направлениях, но его следует использовать только в том случае, если это является целью дизайна.
Как правило, гибридное моделирование предпочтительнее, чем просто поверхностное моделирование, так как многие стороны объекта могут вытекать из одного направления с большей частью геометрии, с определенной гранью или подмножеством граней, которыми можно индивидуально манипулировать в контексте твердого тела. граница. Ниже приведены некоторые примеры того, как SOLIDWORKS использует гибридное моделирование с этими методами:
- Заменить грань
- До поверхности конечное состояние
- Использование поверхности для вырезания или лепки
- Использование поверхности для разделения тела на несколько тел
Поверхности в качестве справочной геометрии
Во многих случаях плоскость, ось или точка не являются достаточной справочной геометрией для управления геометрией по ссылке.
Рис. 6. Поверхность как эталонная геометрия. SOLIDWORKS (часть 1) )
Хорошие методы обработки поверхностей:
Некоторые ключевые методы, которые следует учитывать при моделировании поверхностей:
- Определение функциональных граней и симметрии
- Организация дерева функций
- Использовать объект проверки
- Проверка при восстановлении
- Очистить
Рисунок 7
Идентификация функциональных граней и симметрии
Начало работы со сложными формами без плоских граней может быть затруднено. Постарайтесь максимально использовать симметрию детали, отслеживая изображения эскиза, расположенные вокруг исходной точки. Если передняя или правая плоскость детали делится пополам в центре объекта, ее будет легче совместить в сборке и упростить моделирование. См. приведенный ниже пример для справки. Чтобы создать дверную ручку, я использовал правую плоскость для создания половины модели. Проецируя эскизы правой и верхней плоскости, я могу перейти от эскиза правой плоскости к спроецированной кривой, чтобы упростить создание моей сложной формы. Если вы можете, используйте плоские грани или алгебраические формы для создания эскизов, чтобы использовать изменения и дополнения, как в твердотельной модели.
Постарайтесь максимально использовать симметрию детали, отслеживая изображения эскиза, расположенные вокруг исходной точки. Если передняя или правая плоскость детали делится пополам в центре объекта, ее будет легче совместить в сборке и упростить моделирование. См. приведенный ниже пример для справки. Чтобы создать дверную ручку, я использовал правую плоскость для создания половины модели. Проецируя эскизы правой и верхней плоскости, я могу перейти от эскиза правой плоскости к спроецированной кривой, чтобы упростить создание моей сложной формы. Если вы можете, используйте плоские грани или алгебраические формы для создания эскизов, чтобы использовать изменения и дополнения, как в твердотельной модели.
Рисунок 8: Позиционирование
Организация дерева признаков
Моделирование поверхностей позволяет нам создавать объекты по одной грани за раз, и в результате поверхности часто могут создавать большое дерево признаков. Многие функции, которые вы строите на этой основе, относятся к определенной области модели.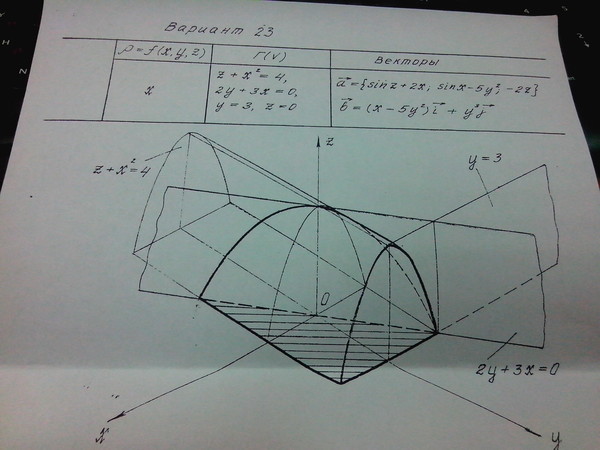 Попробуйте организовать каждую область модели со связанными функциями в папку, чтобы было проще вносить необходимые изменения и сделать дерево функций управляемым. Вы можете просто щелкнуть правой кнопкой мыши объект, чтобы добавить его в папку, и соответствующим образом перетаскивать объекты туда и обратно.
Попробуйте организовать каждую область модели со связанными функциями в папку, чтобы было проще вносить необходимые изменения и сделать дерево функций управляемым. Вы можете просто щелкнуть правой кнопкой мыши объект, чтобы добавить его в папку, и соответствующим образом перетаскивать объекты туда и обратно.
Use Check Entity
Чтобы получить доступ к инструменту Check Entity , выберите Инструменты > Проверить объект или выберите его на вкладке Оценить в диспетчере команд. Этот инструмент позволит пользователю определить проблемы с геометрией, которые могут привести к сбою функции без видимой причины. Инструмент поможет пользователям найти открытые кромки поверхности, которые могут препятствовать соединению поверхности с твердым телом, или короткие кромки и минимальные радиусы, которые могут предотвратить обстрел твердого тела. Хорошей практикой является использование этого инструмента для оценки после создания нескольких элементов поверхности. Поверхностные элементы строятся лицом к лицу и не подвергаются такой же тщательной проверке, как твердотельные элементы.
Рисунок 9: Проверка сущности
Проверка при перестроении
Проверка при перестроении — еще один отличный инструмент, рекомендуемый при создании поверхностей. Его можно найти в разделе Инструменты > Параметры > Производительность > Проверка при перестроении . Отмечайте этот параметр только при работе с поверхностными моделями. Этот инструмент повышает уровень проверки ошибок, выполняя проверку каждого нового или измененного элемента на всех существующих гранях и ребрах, а не только на смежных гранях и ребрах. Объекты с недопустимой геометрией не будут работать, если этот флажок установлен. Почему только с поверхностями? Этот параметр делает моделирование более ресурсоемким для ЦП и может снизить производительность. Он применяется ко всем открытым документам, поскольку он находится в качестве общесистемного параметра. Не забудьте отключить эту опцию, когда закончите всплытие.
Force Rebuild ( CRTL+Q ) = перестраивает все функции в модели
Rebuild ( CRTL+B ) = перестраивает только новые или измененные функции и связанные с ними дочерние функции.
Очистка
Очистка модели необязательна, но может помочь в соблюдении правил «домашнего хозяйства». Используйте Удалить тела , чтобы удалить оставшиеся поверхности или твердые тела. Он преобразует эти тела в элемент дерева, который можно подавить, отредактировать или удалить позже, если к этим элементам потребуется доступ для последующих ревизий.
Рис. 10. Очистка
Надеюсь, этот блог SOLIDWORKS Surfacing был вам полезен. Чтобы узнать больше советов и рекомендаций, ознакомьтесь с нашими последними статьями ниже.
Наши последние советы и рекомендации по SOLIDWORKS
Использование функции перемещения/копирования тела в SOLIDWORKS
Поиск функций в SOLIDWORKS 2021
Как установить шрифты и устранить неполадки со шрифтами в SOLIDWORKS
Виртуальные компоненты: детали это не части
SOLIDWORKS Custom Property Tab Builder: пошаговое руководство
Great Pacific Garbage Patch
Этот ресурс также доступен на испанском языке.
Большое тихоокеанское мусорное пятно – это скопление морского мусора в северной части Тихого океана. Морской мусор — это мусор, который попадает в океаны, моря и другие крупные водоемы.
Большое тихоокеанское мусорное пятно, также известное как Тихоокеанский мусорный вихрь, простирается от западного побережья Северной Америки до Японии. Патч на самом деле состоит из Западного мусорного пятна, расположенного недалеко от Японии, и Восточного мусорного пятна, расположенного между американскими штатами Гавайи и Калифорнией.
Эти области вращающихся обломков связаны друг с другом Северо-Тихоокеанской субтропической зоной конвергенции, расположенной в нескольких сотнях километров к северу от Гавайев. В этой зоне конвергенции теплая вода из южной части Тихого океана встречается с более прохладной водой из Арктики. Зона действует как шоссе, по которому мусор перемещается с одного участка на другой.
Все Большое тихоокеанское мусорное пятно ограничено субтропическим круговоротом северной части Тихого океана. Национальное управление океанических и атмосферных исследований (NOAA) определяет круговорот как большую систему закрученных океанских течений. Однако мусорное пятно все чаще упоминается как вихрь пластиковых отходов и мусора, разбитого на мелкие частицы в океане. Северо-Тихоокеанский субтропический круговорот образован четырьмя течениями, вращающимися по часовой стрелке на площади 20 миллионов квадратных километров (7,7 миллиона квадратных миль): Калифорнийским течением, Северным экваториальным течением, течением Куросио и Северо-Тихоокеанским течением.
Национальное управление океанических и атмосферных исследований (NOAA) определяет круговорот как большую систему закрученных океанских течений. Однако мусорное пятно все чаще упоминается как вихрь пластиковых отходов и мусора, разбитого на мелкие частицы в океане. Северо-Тихоокеанский субтропический круговорот образован четырьмя течениями, вращающимися по часовой стрелке на площади 20 миллионов квадратных километров (7,7 миллиона квадратных миль): Калифорнийским течением, Северным экваториальным течением, течением Куросио и Северо-Тихоокеанским течением.
Область в центре круговорота имеет тенденцию быть очень спокойной и стабильной. Круговое движение круговорота втягивает обломки в этот устойчивый центр, где они и попадают в ловушку. Например, пластиковая бутылка с водой , выброшенная у побережья Калифорнии, ведет Калифорнийское течение на юг, в сторону Мексики. Там он может поймать Северное экваториальное течение, которое пересекает обширный Тихий океан. У побережья Японии бутылка может двигаться на север по мощному течению Куросиро. Наконец, бутылка движется на восток по Северо-Тихоокеанскому течению. Мягко вращающиеся вихри Восточного и Западного мусорных пятен постепенно затягивают бутылку.
Наконец, бутылка движется на восток по Северо-Тихоокеанскому течению. Мягко вращающиеся вихри Восточного и Западного мусорных пятен постепенно затягивают бутылку.
Количество мусора в Большом тихоокеанском мусорном пятне накапливается, потому что большая его часть не поддается биологическому разложению. Многие пластмассы, например, не изнашиваются; они просто разбиваются на все более и более мелкие кусочки.
У многих людей представление о «мусорном пятне» вызывает в воображении образы острова мусора, плавающего в океане. На самом деле эти пластыри почти полностью состоят из крошечных кусочков пластика, называемого микропластиком. Микропластик не всегда можно увидеть невооруженным глазом. Даже на спутниковых снимках не видно гигантского пятна мусора. Микропластик Большого тихоокеанского мусорного пятна может просто сделать воду похожей на мутный суп. Этот суп смешивают с более крупными предметами, такими как рыболовные снасти и обувь.
Морское дно под Большим тихоокеанским мусорным пятном также может быть подводной кучей мусора. Недавно океанографы и экологи обнаружили, что около 70 процентов морского мусора фактически опускается на дно океана.
Недавно океанографы и экологи обнаружили, что около 70 процентов морского мусора фактически опускается на дно океана.
В то время как океанографы и климатологи предсказывали существование Большого тихоокеанского мусорного пятна, на самом деле мусорный вихрь обнаружил капитан гоночной лодки по имени Чарльз Мур. Мур плыл с Гавайев в Калифорнию после участия в гонке на яхтах. Пересекая субтропический круговорот северной части Тихого океана, Мур и его команда заметили миллионы кусков пластика, окружающие его корабль.
Морской мусор
Никто не знает, сколько мусора составляет Большое тихоокеанское мусорное пятно. Северо-тихоокеанский субтропический круговорот слишком велик, чтобы ученые могли его проследить. Кроме того, не весь мусор всплывает на поверхность. Более плотные обломки могут погружаться на сантиметры или даже несколько метров под поверхность, что делает измерение площади вихря практически невозможным.
По оценкам, 80 процентов пластика в океане поступает из наземных источников, а остальные 20 процентов поступают с лодок и других морских источников. Однако эти проценты варьируются в зависимости от региона. Исследование 2018 года показало, что синтетические рыболовные сети составляют почти половину массы Большого тихоокеанского мусорного пятна, в основном из-за динамики океанских течений и увеличения рыболовной активности в Тихом океане.
Однако эти проценты варьируются в зависимости от региона. Исследование 2018 года показало, что синтетические рыболовные сети составляют почти половину массы Большого тихоокеанского мусорного пятна, в основном из-за динамики океанских течений и увеличения рыболовной активности в Тихом океане.
Хотя в океан попадает множество различных видов мусора, пластик составляет большую часть морского мусора по двум причинам. Во-первых, долговечность, низкая стоимость и пластичность пластика означают, что он используется во все большем количестве потребительских и промышленных товаров. Во-вторых, пластмассовые изделия не разлагаются биологическим путем, а вместо этого распадаются на более мелкие кусочки.
В океане солнце разбивает этот пластик на все более и более мелкие кусочки. Этот процесс известен как фоторазложение. Большая часть этого мусора происходит из пластиковых пакетов, крышек от бутылок, пластиковых бутылок с водой и стаканов из пенопласта.
Морской мусор может быть очень вредным для морской жизни в круговороте. Например, головастые морские черепахи часто принимают пластиковые пакеты за желе, свою любимую еду. Альбатросы принимают шарики из пластиковой смолы за икру рыб и скармливают их птенцам, которые умирают от голода или разрывов органов.
Например, головастые морские черепахи часто принимают пластиковые пакеты за желе, свою любимую еду. Альбатросы принимают шарики из пластиковой смолы за икру рыб и скармливают их птенцам, которые умирают от голода или разрывов органов.
Тюлени и другие морские млекопитающие особенно подвержены риску. Они могут запутаться в брошенных пластиковых рыболовных сетях, которые выбрасываются в основном из-за ненастной погоды и незаконного рыболовства. Тюлени и другие млекопитающие часто тонут в этих забытых сетях — явление, известное как «призрачная рыбалка».
Морской мусор также может нарушать морские пищевые сети в субтропическом круговороте северной части Тихого океана. Поскольку микропластик и другой мусор собираются на поверхности океана или рядом с ней, они блокируют доступ солнечного света к планктону и водорослям внизу. Водоросли и планктон являются наиболее распространенными автотрофами или производителями в морской пищевой сети. Автотрофы – это организмы, которые могут производить собственные питательные вещества из углерода и солнечного света.
Если сообщества водорослей и планктона находятся под угрозой, вся пищевая сеть может измениться. Животные, которые питаются водорослями и планктоном, такие как рыбы и черепахи, будут иметь меньше пищи. Если популяция этих животных уменьшится, у высших хищников, таких как тунец, акулы и киты, останется меньше пищи. Со временем морепродукты становятся менее доступными и более дорогими для людей.
Эти опасности усугубляются тем фактом, что пластмассы вымывают и поглощают вредные загрязнители. По мере того как пластмассы разрушаются в результате фотодеградации, они вымывают красители и химические вещества, такие как бисфенол А (BPA), которые связаны с проблемами для окружающей среды и здоровья. И наоборот, пластмассы также могут поглощать загрязняющие вещества, такие как ПХБ, из морской воды. Затем эти химические вещества могут попасть в пищевую цепь при потреблении морскими обитателями.
Исправление патча
Поскольку Большое тихоокеанское мусорное пятно находится так далеко от береговой линии какой-либо страны, ни одна страна не возьмет на себя ответственность и не предоставит финансирование для его очистки.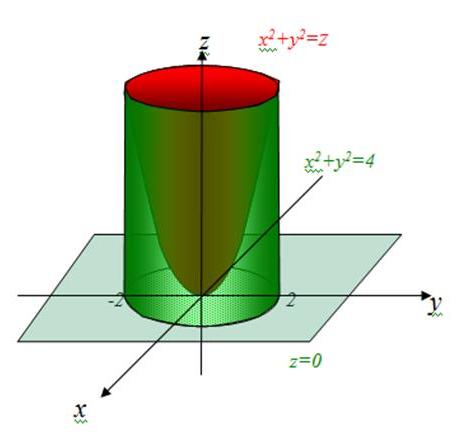 Чарльз Мур, человек, открывший вихрь, говорит, что очистка мусорного пятна «обанкротит любую страну», которая попытается это сделать.
Чарльз Мур, человек, открывший вихрь, говорит, что очистка мусорного пятна «обанкротит любую страну», которая попытается это сделать.
Однако многие частные лица и международные организации стремятся предотвратить рост пятна.
Уборка морского мусора не так проста, как кажется. Многие микропластики имеют такой же размер, как мелкие морские животные, поэтому сети, предназначенные для сбора мусора, могут поймать и этих существ. Даже если бы мы могли разработать сети, которые просто собирали бы мусор, размеры океанов делают эту работу слишком трудоемкой, чтобы ее рассматривать. По оценкам Национального управления океанических и атмосферных исследований, в рамках программы по сбору морского мусора потребуется 67 судов в год, чтобы очистить менее одного процента северной части Тихого океана.
Многие экспедиции прошли через Большое тихоокеанское мусорное пятно. Чарльз Мур, обнаруживший это пятно в 1997 году, продолжает повышать осведомленность о нем через свою собственную экологическую организацию, Фонд морских исследований Альгалита.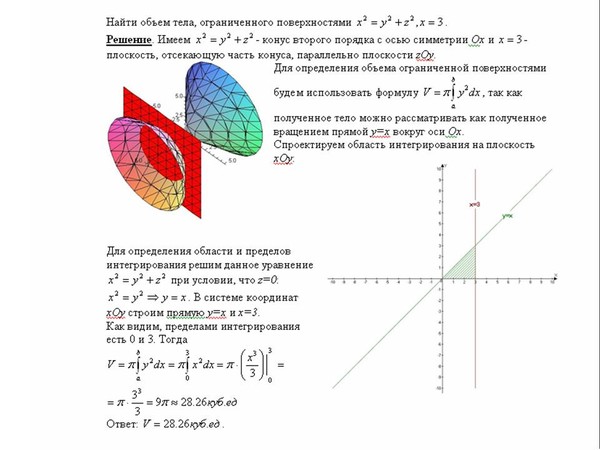 Во время экспедиции 2014 года Мур и его команда использовали воздушные дроны, чтобы сверху оценить размеры мусора внизу. Дроны определили, что пластика по весу в 100 раз больше, чем измерялось ранее. Команда также обнаружила более постоянные пластиковые объекты или острова, некоторые из которых имеют длину более 15 метров (50 футов).
Во время экспедиции 2014 года Мур и его команда использовали воздушные дроны, чтобы сверху оценить размеры мусора внизу. Дроны определили, что пластика по весу в 100 раз больше, чем измерялось ранее. Команда также обнаружила более постоянные пластиковые объекты или острова, некоторые из которых имеют длину более 15 метров (50 футов).
Плавающий пластик Большого тихоокеанского мусорного пятна вдохновил исследователя National Geographic Дэвида де Ротшильда и его команду из Adventure Ecology на создание большого катамарана из пластиковых бутылок: Plastiki . Прочность Plastiki продемонстрировала прочность и долговечность пластмасс, творческие способы их перепрофилирования и угрозу, которую они представляют для окружающей среды, если они не разлагаются. В 2010 году команда успешно провела судно «Пластики» из Сан-Франциско, штат Калифорния, в Сидней, Австралия.
Ученые и исследователи согласны с тем, что ограничение или отказ от использования одноразового пластика и увеличение использования биоразлагаемых ресурсов будет лучшим способом очистить Большое тихоокеанское мусорное пятно. Такие организации, как Коалиция за загрязнение пластиком и Фонд пластиковых океанов, используют социальные сети и кампании прямого действия для поддержки отдельных лиц, производителей и предприятий при переходе от токсичных одноразовых пластиков к биоразлагаемым или многоразовым материалам.
Такие организации, как Коалиция за загрязнение пластиком и Фонд пластиковых океанов, используют социальные сети и кампании прямого действия для поддержки отдельных лиц, производителей и предприятий при переходе от токсичных одноразовых пластиков к биоразлагаемым или многоразовым материалам.
Краткий факт
Капитан
«Итак, на обратном пути в наш порт приписки в Лонг-Бич, штат Калифорния, мы решили срезать путь через круговорот, который редко когда-либо пересекают моряки. Рыбаки избегают его, потому что в нем мало воды.
Краткий факт
Странный груз
Когда корабли попадают в шторм, они часто теряют груз в океане. лишь несколько странных предметов, выброшенных на берег:
Краткий факт
Мусорные пятна по всему миру
Большое тихоокеанское мусорное пятно — не единственный морской мусорный вихрь — он просто самый большой. Мусорные вихри есть и в Атлантическом, и в Индийском океанах.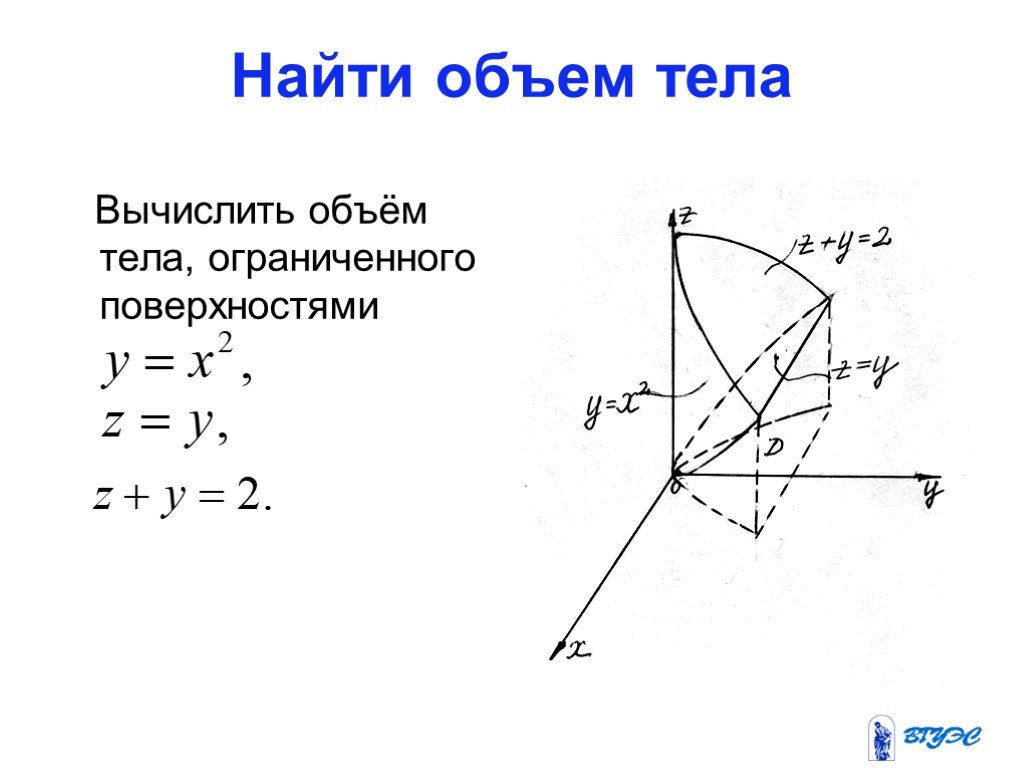
Ваш комментарий будет первым