Построение прямой по уравнению онлайн: Онлайн калькулятор. Уравнение прямой проходящей через две точки

Общее уравнение прямой на плоскости

Уравнение вида называется общим уравнением прямой на плоскости. При различных численных значениях A, B и C, в том числе нулевых, оно может определять всевозможные прямые без исключения.

Одна из фундаментальных задач аналитической геометрии — составление общего уравнения прямой по точке, ей принадлежащей, и вектору нормали.

Вектор нормали — это вектор, перпендикулярный искомой прямой. Вектор нормали чаще всего записывается так: . Координаты точки — и .

Общее уравнение прямой на плоскости по точке и вектору нормали составляется по формуле:

  (1).

Пример 1. Составить общее уравнение прямой на плоскости, если она проходит через точку и вектор нормали к ней .

Решение. Используя формулу (1), получаем:

Из примера 1 видно, что координаты вектора нормали пропорциональны числам A и B из общего уравнения прямой на плоскости. Это не совпадение, а закономерность! Поэтому в общем случае, если известно общее уравнение прямой на плоскости, то вектор нормали к прямой можно записать так: .

Пример 2. Задано общее уравнение прямой на плоскости: . Записать вектор нормали к этой прямой.

Решение. В заданном уравнении , . Поэтому вектор нормали запишется:

.

Если вектор нормали перпендикулярен искомой прямой, то направляющий вектор параллелен ей. Направляющий вектор обычно записывается так: . Имеет место следующая зависимость координат направляющего вектора от чисел

A и B общего уравнения прямой: .

Пример 3. Составить общее уравнение прямой на плоскости, если она проходит через точку и её направляющий вектор .

Решение. Используя формулу (2), имеем:

.

Далее путём преобразований получаем:

На всякий случай сделаем проверку — подставим в полученное общее уравнение прямой координаты точки, которая должна ей принадлежать:

.

Получили верное равенство. А координаты вектора связаны с числами A и B уравнения закономерностью . Значит, задание выполнено корректно.

---

Пример 4. Задано общее уравнение прямой на плоскости: . Записать направляющий вектор к этой прямой.

Решение. В заданном уравнении , . Поэтому направляющий вектор запишется:

.

Решая задачи контрольных работ, особенно, если задач много и к концу контрольной студент стремится наверстать упущенное за время обдумывания заданий, можно запутаться в знаках, записывая вектор нормали и направляющий вектор. Будьте внимательны!

Если заданы две точки и , то уравнение прямой, проходящей через эти точки, можно составить по формуле

.   (3)

Полученное выражение следует преобразовать к виду общего уравнения прямой.

Пример 5. Составить общее уравнение прямой на плоскости, если она проходит через точки и .

Решение. Используя формулу (3), имеем:

.

Далее путём преобразований получаем:

Получили общее уравнение плоскости.

Во многих задачах аналитической геометрии возникает необходимость преобразовать уравнения одного вида к уравнению другого вида. Преобразование уравнения прямой с угловым коэффициентом в общее уравнение прямой делается достаточно просто: в уравнении вида всё переносим в левую часть, а в правой остаётся нуль. Получается уравнение вида .

Пример 7. Дано уравнение прямой с угловым коэффициентом . Записать уравнение этой прямой в общем виде и направляющий вектор этой прямой.

Решение. Всё переносим в левую часть, а в правой оставляем нуль:

.

Получили общее уравнение прямой. В нём . Поэтому направляющий вектор запишется так:

.

Рассмотрим особенности расположения прямой на плоскости в тех случаях, когда те или иные коэффициенты общего уравнения прямой равны нулю.

1. При уравнение определяет прямую, проходящую через начало координат, так как кординаты точки удовлетворяют этому уравнению.

3. При уравнение определяет ось Ox, так как эта прямая одновременно параллельна оси Ox и проходит через начало координат. Аналогично, при уравнение определяет ось Oy.

Всё по теме «Прямая на плоскости

описание, примеры, решение задач, уравнение прямой в отрезках

Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках,  построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.

Уравнение прямой в отрезках – описание и примеры

Пусть на плоскости расположена прямоугольная  система координат Oxy.

Прямая линия на плоскости в декартовой системе координат Oxy задается уравнением вида xa+yb=1, где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях Ox и Oy. Длины отрезков считаются от начала координат.

Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a, 0 и 0, b принадлежат данной прямой линии, так как aa+0b=1⇔1≡1 и 0a+bb=1⇔1≡1. Точки a, 0 и b, 0 расположены на осях координат Ox и Oy и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b. Знак «-» обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.

Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат Oxy на схематическом чертеже. Уравнение прямой в отрезках xa+yb=1 применяется для построения прямой линии в декартовой системе координат Oxy. Для этого нам необходимо отметить на осях точки a, 0 и b, 0, а затем соединить эти точки линией при помощи линейки.

На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.

Рассмотрим пример.

Пример 1

Прямая линия задана уравнением прямой в отрезках вида x3+y-52=1. Необходимо построить эту прямую на плоскости в декартовой системе координат Oxy.

Решение

 Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3, 0, 0, -52. Отметим их и проведем линию.

Приведение общего уравнения прямой к уравнению прямой в отрезках

Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.

Полное общее уравнение прямой линии на плоскости имеет вид Ax+By+C=0, где А, В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на –С. При этом, коэффициенты при x и y мы отправляем в знаменатели:

Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1

Для осуществления последнего перехода мы воспользовались равенством pq=1qp, p≠0, q≠0.

В результате, мы осуществили переход от общего уравнения прямой Ax+By+C=0 к уравнению прямой в отрезках xa+yb=1, где a=-CA, b=-CB.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Разберем следующий пример.

Пример 2

Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x-7y+12=0.

Решение

Переносим одну вторую в правую часть равенства x-7y+12=0⇔x-7y=-12.

Делим обе части равенства на -12: x-7y=-12⇔1-12x-7-12y=1.

Преобразуем полученное равенство к нужному виду: 1-12x-7-12y=1⇔x-12+y114=1.

Мы получили уравнение прямой в отрезках.

Ответ: x-12+y114=1

В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.

Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида xa+yb=1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y.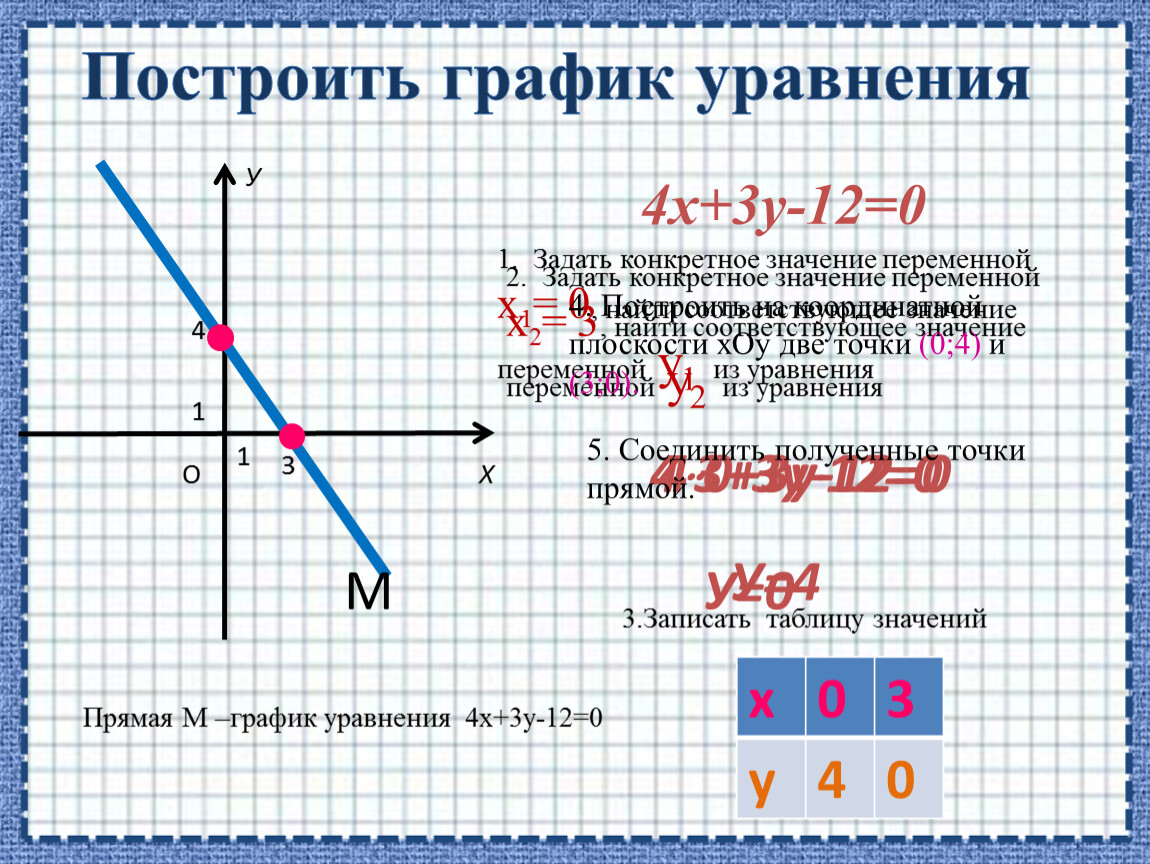

xa+yb=1⇔xa+yb-1=0⇔1a·x+1b·y-1=0

Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».

Пример 3

Уравнение прямой в отрезках имеет вид x23+y-12=1. Необходимо написать общее уравнение прямой на плоскости.

Решение

Действует по заранее описанному алгоритму:

x23+y-12=1⇔123·x+1-12·y-1=0⇔⇔32·x-112·y-1=0

Ответ: 32·x-112·y-1=0

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Прямая в пространстве – виды уравнения прямой в пространстве

Параметрическое и каноническое уравнение прямой в пространстве

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать реферат

Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку параллельно направляющему вектору .

Определение

Пусть, – произвольная точка прямой, тогда векторы и коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:

(1)

это и есть канонические уравнения прямой.

Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:

(2)

Уравнение прямой в пространстве, которая проходит через две заданные точки

Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.

Итак, через две точки и можно не только геометрично провести линию, но и сложить её уравнения.

Определение

За направляющий вектор возьмём , тогда по формуле (1) у нас получается:

(3)

 уравнение прямой в пространстве, которые проходят через две заданные точки.

Общее уравнение прямой – переход к каноническому уравнению

Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.

Определение

Пусть известны их уравнения:

(4)

Тогда система (4) называется общим уравнением прямой.

Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку этой прямой.

Точку  находим, как один из решений системы (4). Например, положив в (4) находим , тогда и точку . Направляющий вектор , который параллелен к каждой из плоскостей и и перпендикулярен к их нормальным векторам и , то есть , . (см. рис. 1). Поэтому вектор можно найти при помощи векторного произведения и

= x =

Найдены координаты и подставим в каноническое уравнение (1).

Например, от общих уравнений прямой:

Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём . Нормальные векторы и . Тогда направляющий вектор

Рис. 1

  x = ,

и канонические уравнения станут:

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Угол между двумя прямыми :

и

равен углу между их направляющими векторами и , поэтому

=

(5)

Условия параллельности и перпендикулярности прямых соответственно запишутся:

и .

(6)

Примеры решения задач

Давайте рассмотрим первый пример, где можно двумя способами построить прямую:

Пример 1

Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:

Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.

Аналитическая геометрия в пространстве. Плоскость и прямая в пространстве

1. Аналитическая геометрия в пространстве

Плоскость и прямая в
пространстве

2. Плоскость

Основные уравнения плоскости
1. Уравнение плоскости, проходящей через заданную
точку M 0 ( x0 ; y0 ; z0 ) перпендикулярно
заданному вектору N A; B; C
N A; B; C
A( x x0 ) B( y y0 ) C ( z z0 ) 0
2. Общее уравнение плоскости
M 0 ( x0 ; y0 ; z0 )
Ax By Cz D 0
N A; B; C
Z
— вектор нормали
c
3. Уравнение плоскости « в отрезках»
x y z
1
a b c
Y
a
X
b

3.

Уравнения плоскости 4. Уравнение плоскости, проходящей через три
заданные точки M 1 ( x1 ; y1 ; z1,) M 2 ( x2 ; y2 ; z2 ) и M 3 ( x3 ; y3 ; z3 )
N A; B; C
M ( x; y; z )
M 2 ( x2 ; y 2 ; z 2 )
M 1 ( x1 ; y1 ; z1 )
M 3 ( x3 ; y3 ; z3 )
Условие компланарности векторов
x x1
y y1
z z1
x2 x1
y2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
M 1M x x1 ; y y1 ; z z1
M 1M 2 x2 x1 ; y2 y1 ; z 2 z1
M1M 3 x3 x1; y3 y1 ; z3 z1
( M 1M M 1M 2 M 1M 3 ) 0

4. Составление уравнений плоскости

1. Составить уравнение плоскости, проходящей через точку
M 0 ( 1;3; 5) перпендикулярно вектору N 3; 2;4
Исходное уравнение:
A( x x0 ) B( y y0 ) C ( z z0 ) 0
Подставляем координаты точки и вектора
3( x 1) 2( y 3) 4( z 5) 0
Раскрываем скобки
3x 3 2 y 6 4 z 20 0
Приводим подобные
3x 2 y 4 z 29 0
Получили общее уравнение плоскости.
2. Составить уравнение плоскости, проходящей через три
заданные точки
M 1 ( 1;3; 5), M 2 (2; 1;0), M 3 (0; 4;7)
В данном случае можно воспользоваться формулой уравнения плоскости,
проходящей через три точки:
x x1
y y1
z z1
x2 x1
y2 y1
z 2 z1 0
x3 x1
y3 y1
z3 z1
Подставляем в это уравнение координаты точек и раскладываем
определитель по элементам первой строки
x 1
y 3
z 5
x 1 y 3 z 5
2 1 1 3 0 5 0
3
4
5
0 1 4 3 7 5
1
7
12
13( x 1) 31( y 3) 17( z 5) 0
13x 31y 17z 5 0
0

6.

Построение плоскостей Построить плоскость:
3x 4 y 6 z 12 0
1. Координаты точек пересечения плоскости с осями координат:
Z
x
0
0
4
y
0
3
0
z
2
0
0
2
3 Y
4
X
2. Привести уравнение плоскости к уравнению «в отрезках»:
3x 4 y 6 z 12
3x 4 y 6 z
1
12 12 12
x y z
1
4 3 2

7. Построение плоскостей

3z 8 0
2. Построить плоскость
В уравнении отсутствуют две переменные x и y. Такая плоскость
проходит параллельно и оси OX , и оси OY, т.е. она проходит
параллельно координатной плоскости XOY через точку z=8/3 на оси OZ.
Z
8/3
Y
X
0
Аналогично строятся плоскости,
в уравнениях которых отсутствуют
две переменные
• Если в уравнении плоскости отсутствует одна
переменная, то плоскость проходит параллельно
той оси координат, переменной которой нет в
уравнении.
• Если в уравнении плоскости отсутствует
свободный коэффициент , то плоскость проходит
через начало координат.
• Если в уравнении плоскости отсутствуют две
переменные, то плоскость проходит параллельно
координатной плоскости, переменных которой
нет в уравнении.
• Уравнения координатных плоскостей
x 0
y 0
z 0
— уравнение плоскости YOZ
— уравнение плоскости XOZ
— уравнение плоскости XOY

9. Взаимное расположение плоскостей

1. Условие параллельности плоскостей
N 1 || N 2
A1 B1 C1
A2 B2 C 2
N1 A1 ; B1 ; C1
N 2 A2 ; B2 ; C2
2. Условие перпендикулярности плоскостей
N1
N2
( N1 N 2 ) 0
A1 A2 B1 B2 C1 C 2 0
N1
N2
3. Косинус угла между плоскостями
Угол между плоскостями – это угол между векторами
нормалей этих плоскостей
cos cos( N1 , N 2 )
A1 A2 B1 B2 C1 C2
A12 B12 C12 A22 B22 C22

10. Расстояние от точки до плоскости

Расстояние от точки M 1 ( x1 ; y1 ; z1 ) до плоскости
Ax By Cz D 0 находится по формуле
d
| Ax1 By1 Cz1 D |
M 1 ( x1 ; y1 ; z1 )
d
A2 B 2 C 2
Расстояние – это длина перпендикуляра, опущенного из точки на плоскость
Найти расстояние от точки
M (5; 3; 2)
до плоскости
3x 4 y z 9 0
Используем формулу расстояния от точки до плоскости
d
d
| Ax1 By1 Cz1 D |
A2 B 2 C 2
3 5 4 3 1 ( 2) 9
32 ( 4) 2 ( 1) 2
| 4 |
4
26
26

12.

Прямая в пространстве. Основные уравнения 1. Уравнение прямой, проходящей через заданную
точку M 0 ( x0 ; y0 ; z0 ) параллельно заданному вектору
s m; n; p
x x0 y y0 z z0
m
n
p
— канонические уравнения
s m; n; p — направляющий вектор
2. Параметрические уравнения
x x0 y y0 z z0
t,
m
n
p
s m; n; p
x mt x0
y nt y
0
z pt z0
M 0 ( x0 ; y0 ; z0 )
3. Уравнение прямой, проходящей через две заданные
точки M 1 ( x1 ; y1 ; z1 ) и M 2 ( x2 ; y2 ; z2 )
x x1
y y1
z z1
x2 x1 y2 y1 z 2 z1
s M 1M 2
M 2 ( x2 ; y 2 ; z 2 )
M 1 ( x1 ; y1 ; z1 )

13. Прямая в пространстве. Основные уравнения

4. Общее уравнение прямой в пространстве
A1 x B1 y C1 z D1 0
A2 x B2 y C2 z D2 0
Направляющий вектор
i
j
k
s N1 N 2 A1 B1 C1
A2 B2 C 2
s m; n; p
N1 A1 ; B1 ; C1
N 2 A2 ; B2 ; C2

14. Взаимное расположение прямых в пространстве

1. Нахождение угла между прямыми.
Прямые в пространстве заданы каноническими уравнениями, поэтому
угол между прямыми – это угол между направляющими векторами
( s1 s2 )
m1m2 n1n2 p1 p2
cos
2
2
s1 s2
m1 n12 p12 m2 n22 p22
s2
s1
2. Проверка условий параллельности и
перпендикулярности прямых
Условие параллельности прямых
s1 || s2
m1 n1 p1
m2 n2 p 2
s2
s1
Условие перпендикулярности прямых
s1
s2
( s1 s2 ) 0
m1m2 n1n2 p1 p2 0
s2
s1

15. Расстояние от точки до прямой в пространстве

Задача о нахождении расстояния от точки M 1 ( x1 ; y1 ; z1 )
до прямой x x0 y y0 z z0
m
n
p
На векторах
M 0 M1 x1 x0 ; y1 y0 ; z1 z0
И s m; n; p строим
M 1 ( x1 ; y1 ; z1 )
d
параллелограмм. Высота этого
параллелограмма
–
искомое
расстояние.
s
M 0 ( x0 ; y0 ; z0 )
Высоту находим как отношение площади параллелограмма к длине
основания. Площадь параллелограмма – это модуль векторного
произведения векторов, а длина основания – это длина вектора
d
M
0
M1 s
s
s
Найти расстояние от точки M ( 1;4; 2)
до прямой x 2 y 4 z
3
5 1
Искомое расстояние – это высота
параллелограмма, построенного на
векторах
M ( 1;4; 2)
d
s 3; 5;1
s 3; 5;1
и
M 0 M 3;8; 2
M 0 (2; 4;0)
Площадь параллелограмма находим, используя векторное произведение
i
S s M 0M 3
3
j
5
8
k
1 2i 3 j 9k
2
s 3; 5;1
s 32 ( 5) 2 12 35
S
94
d
Расстояние от точки до прямой
35
s
Длина основания – это длина вектора
2 2 32 9 2 94

17. Взаимное расположение прямой и плоскости в пространстве

1. Условие параллельности прямой и плоскости
N A; B; C
s m; n; p
s
( N s) 0
N
Am Bn Cp 0
2. Условие перпендикулярности прямой и плоскости
s m; n; p
N A; B; C
N || s
A B C
m n p

18.

Взаимное расположение прямой и плоскости в пространстве 3. Нахождение угла между прямой и плоскостью
s m; n; p
N A; B; C
Углом между прямой и плоскостьюугол между этой прямой
и ее ортогональной проекцией на
эту плоскость
Из уравнений прямой и плоскости
известны направляющий вектор
прямой и вектор нормали плоскости.
Угол между этими векторами —
cos sin
Так как в сумме углы дают 90 градусов, а значит
Поэтому при нахождении угла между прямой и плоскостью находят
не косинус, а синус угла. Так как синус угла между прямой и плоскостью
может быть только положительным, то:
| ( N s) |
| Am Bn Cp |
sin
2 2 2
2
2
2
N s
A B C m n p

19. Решение типовых задач

1. Составить уравнение плоскости, проходящей через точку
параллельно
двум
векторам
и
a 2; 7;5 b 3;0; 4
M 0 ( 1;3; 5)
b
Используем уравнение
N
a
A( x x0 ) B( y y0 ) C ( z z0 ) 0
Координаты точки нам известны. Необходимо найти координаты вектора
нормали. Из рисунка видно, что в качестве вектора нормали можно взять
вектор, являющийся векторным произведением данных в условии задачи
векторов, так как такой вектор перпендикулярен каждому из данных
векторов, а значит перпендикулярен и плоскости.
i
N a b 2
3
j
7
0
k
5 28i 7 j 21k
Итак,
N 28; 7; 21
4
Подставляем все данные в уравнение плоскости
28( x 1) 7( y 3) 21( z 5) 0
4( x 1) ( y 3) 3( z 5) 0
4 x y 3z 8 0
2. Составить уравнение плоскости, проходящей через точку M (2; 1;5)
4 x y 3z 2 0
перпендикулярно двум плоскостям
x 2 y 5z 3 0
N
N1 4; 1;3
N 2 1;2; 5
Основное уравнение:
A( x x0 ) B( y y0 ) C ( z z0 ) 0
M
Для составления уравнения плоскости есть точка M (2; 1;5) .
Вектором нормали может являться вектор, равный векторному
произведению векторов нормалей данных плоскостей.
i
j
N N1 N 2 4 1
1
2
k
3 i 23 j 9k
5
Остается только подставить
все данные в уравнение.
3. Составить уравнение плоскости, проходящей через точку
M (2; 1;3)
перпендикулярно прямой x 1 y 2
z
5
3
4
Основное уравнение плоскости
s
N
M
A( x x0 ) B( y y0 ) C ( z z0 ) 0
Из рисунка видно, что в качестве
вектора нормали плоскости можно
взять направляющий вектор прямой
N s {5;3; 4}
Таким образом, для составления уравнения плоскости есть все данные:
координаты точки и вектора нормали
5( x 2) 3( y 1) 4( z 3) 0
5x 3 y 4 z 5 0
4. Составить уравнение плоскости, проходящей через точку M (4; 2; 1)
и отсекающую на осях координат одинаковые отрезки
Для решение задачи используем уравнение плоскости «в отрезках»
x y z
1
a b c
Отрезки на осях одинаковые, поэтому
x y z
1
a a a
или x y z a
Для нахождения a подставляем в это уравнение координаты
точки M
4 2 1 a
a 1
Итак, уравнение плоскости: x y z 1
5. Составить уравнение прямой, проходящей через точку M ( 3; 1;5)
параллельно оси OY.
В качестве направляющего вектора можно использовать любой вектор,
параллельный оси OY. Самый простой вектор – это единичный вектор оси OY
s j 0;1;0
Канонические уравнения прямой
x 3 y 1 z 5
0
1
0
6. Составить канонические уравнения прямой, проходящей через две
точки M (3; 2;0) и M (0;6; 4)
1
2
В качестве направляющего вектора можно использовать вектор,
соединяющий эти точки.
s M 1M 2 3;8; 4
Уравнения прямой:
x 3 y 2
z
3
8
4
! Использовать можно координаты любой точки
7. Составить уравнение прямой, проходящей через точку M ( 3;5; 2)
перпендикулярно плоскости 4 x y 3z 1 0
Канонические уравнения прямой
s
M
x x0 y y0 z z0
m
n
p
N
Из рисунка видно, что в качестве
направляющего вектора прямой можно
взять вектор нормали плоскости
s N {4; 1;3}
Таким образом, для составления уравнения прямой есть все данные:
координаты точки и направляющего вектора
x 3 y 5 z 2
4
1
3

Мерзляк.

Решебник с пояснениями и теорией

ГДЗ по математике для 5 класса Мерзляк – это онлайн-решебник, который включает в себя комплекс решенных задач по одноименному учебнику математики от авторитетных математиков-методистов России – Мерзляка А.Г., Полонского В.Б., Якира М.С. Ныне он используется в программах многих центральных и региональных школ РФ.

Нужны ли ГДЗ по математике учебника Мерзялка пятиклассникам?

Хотя в 5 классе программа изучения математики относительно проста, многие школьники испытывают сложности с пониманием арифметических примеров и задач. Обусловлено это рассмотрением сложным тем, связанных с дробными числами, системой координат, построением графиков функций.

При таком раскладе ГДЗ по математике для 5 класса Мерзляк становятся важным практическим дополнением, которое демонстрирует школьникам готовые решения и разъясняет алгоритм выполнения расчетов. Решебники играют важную роль и для родителей, помогая им контролировать успеваемость детей и помогать им в постижении предмета.

На сайте ГДЗ Путина можно найти нужный ответ всего за пару секунд: достаточно выбрать нужный решебник и кликнуть номер задания в таблице. Кроме того, ресурс позволяет:

• найти выполненные задачки и примеры с планшета, телефона или компьютера;
• получить несколько вариантов решения одного и того же примера;
• использовать самые свежие и актуальные версии решебников.

Если школьник не сумел разобраться с решением арифметических задач и примеров в классе, то он может самостоятельно или вместе с родителями сделать это дома на основе готовых домашних заданий онлайн.

Решебник по математике за 5 класс Мерзляка – важные вехи в изучении дисциплины

Программа изучения арифметики в 5 классе раскрывает перед школьником спектр значимых тем, которые являются основой дальнейшего изучения алгебры, геометрии, физики и иных точных дисциплин.

В издании учебника Мерзляка А.Г. 2014 года приведены примеры, уравнения и задачи по таким темам:

• ряд натуральных чисел, шкалы и координаты;
• отрезки, прямые, лучи, углы и их свойства;
• сложение и вычитание натуральных чисел, многоугольники и их равенство, треугольники и их виды, ось симметрии фигуры;
• умножение и деление натуральных чисел, степень числа, площадь прямоугольника;
• обыкновенные дроби, действия с ними и смешанные числа;
• десятичные дроби, математические действия с ними;
• среднее арифметическое и проценты.

Представленные выше темы в дальнейшем находят свое продолжение в алгебре и геометрии, что подчеркивает значимость их понимания школьником.

Благодаря онлайн-решебнику по математике для 5 класса Мерзляк родителям не придется отправлять ребенка на дополнительные занятия или приглашать репетитора: со сложными задачами и примерами он разберется сам.

«Решается, какой станет Германия после Меркель». Мировые СМИ о выборах в Бундестаг

Напряженная предвыборная гонка в Германии завершилась таким же драматичным исходом голосования. Основные конкуренты, Социал-демократическая партия (СДПГ) и блок ХДС/ХСС, пришли к финишу почти вровень, заручившись поддержкой около четверти избирателей. На третьем месте с большим отставанием «Зеленые» (14,8%), вслед за ними правые популисты из «Альтернативы для Германии» (10,3%). Что пишут о перспективах формирования нового кабинета министров в ФРГ мировые СМИ — в материале ТАСС.

Германия

Muenchner Merkur: «В конце гениально проведенной избирательной кампании Олаф Шольц все же проиграл: кандидат в канцлеры от Социал-демократической партии Германии (СДПГ), стремясь создать себе оптимальную договорную базу для коалиционных переговоров, никак не хотел исключать вариант формирования «красно-зелено-красной» правительственной коалиции (СДПГ, «Зеленые» и Левая партия — по цветам партий). Однако тем самым он придал «кажущемуся мертвым» блоку ХДС/ХСС импульс в предвыборной кампании.

ХДС и ХСС вместе со своим безликим кандидатом в канцлеры Армином Лашетом спасли кампанию от полного провала в последний момент

Шольц теперь вынужден мириться со стратегически невыгодным положением, заключающимся в том, что избиратели убрали со стола вариант «красно-зелено-красного» альянса, который имел для него высокую политическую цену. Он дорого заплатил за то, чтобы такой вариант оставался возможным, и в конце концов ничего не выиграл. Вместо этого Лашет может возиться с либеральной Свободной демократической партией (СвДП), формируя коалицию «Ямайка» (состоящую из ХДС/ХСС, «Зеленых» и либералов — по цветам, совпадающим с цветами флага Ямайки — прим. ТАСС).

Stuttgarter Nachrichten: «Время народных партий прошло. По крайней мере, это ясный результат нынешних выборов в Бундестаг. Консервативный блок Христианско-демократического и Христианско-социального союзов утратил свой статус последней партии, которая могла набрать по всей стране более 30% голосов. Насколько этот статус в последнее время зависел от личности уходящего канцлера Ангелы Меркель, теперь тоже ясно. Было бы примитивно свалить этот спад в блоке ХДС/ХСС исключительно на его кандидата в канцлеры Армина Лашета.

Конечно, он не будоражил нервы многих избирателей. Но также многие интриганы в его собственных рядах — прежде всего в ХСС — придали большой импульс его спаду. Как и проваленная кампания, которая никогда не использовала сильные стороны Лашета на посту главы правительства Северного Рейна — Вестфалии».

Koelner Stadt-Anzeiger: «Ослабленному премьер-министру земли Северный Рейн — Вестфалия предстоит очередное испытание на прочность внутри партии. В конце концов, если ему не удастся создать правительственный союз, его политическая карьера, вероятно, будет завершена. «Светофор» или «Ямайка»? На долгом пути переговоров стороны должны овладеть искусством уступок, готовности к компромиссам и сохранить свое лицо».

На эту тему

Sueddeutsche Zeitung: «Все кандидаты в Бундестаг от Социал-демократической партии Германии, для которых мандат в течение нескольких месяцев казался иллюзией и которые теперь все же получили его, еще какое-то время будут видеть в лице Шольца своего героя. Разница между «эффектом Шульца» 2017 года (Мартин Шульц — кандидат в канцлеры от СДПГ в 2017 году — прим. ТАСС) и «эффектом Шольца» 2021 года заключается в том, что последний удержался. Но по возможной коалиции в СДПГ будут голосовать рядовые члены, которые менее привержены Шольцу и которые, возможно, внушат себе, что эта прекрасная мечта о канцлерстве не принесет никакой пользы, когда, по правде говоря, (возможный) министр финансов Кристиан Линднер будет определять политический курс. Против них Шольц не может пойти, чтобы добиться создания коалиции «светофор» (состоящей из СДПГ, «Зеленых» и либералов — прим. ТАСС), а в локальных войнах своих лидеров СДПГ всегда была хороша».

Handelsblatt: «Социал-демократическая партия Германии попытается сделать либералам предложение, от которого те не смогут отказаться. Шольц доверительно и обещающе агитирует за необходимость соблюдения договора. Он знает о травме СвДП, которая чувствовала себя обманутой Меркель. Лашет, в свою очередь, должен убедить «Зеленых» в том, что им будет лучше с ним, нежели с социал-демократами. Ему будет сложнее балансировать, чем Шольцу. В конце этого исторического дня происходит следующее: занавес опускается, и все вопросы остаются без ответа».

Badische Zeitung: «Примечательно, что лидер Свободной демократической партии Кристиан Линднер предложил «Зеленым» провести переговоры вечером в день выборов. Что было еще примечательно, так это то, что Анналена Бербок (кандидат в канцлеры от «Зеленых» — прим. ТАСС) сразу же приняла предложение…

Такого рода зондирующие переговоры между более мелкими потенциальными партнерами раньше были бы немыслимы. Кто знает, возможно, здесь уже наметились первые изменения в политической культуре, к которым приводят результаты этих выборов».

На эту тему

Франция

La Tribune: «Итоги голосования определят, какой станет Германия в эпоху после Меркель. В ее правление страна была символом предсказуемости в Европе. Это может измениться по итогам голосования, обещающего дробление голосов и создание нестабильного трехпартийного правительства, которому придется управлять крупнейшей экономической державой Европы.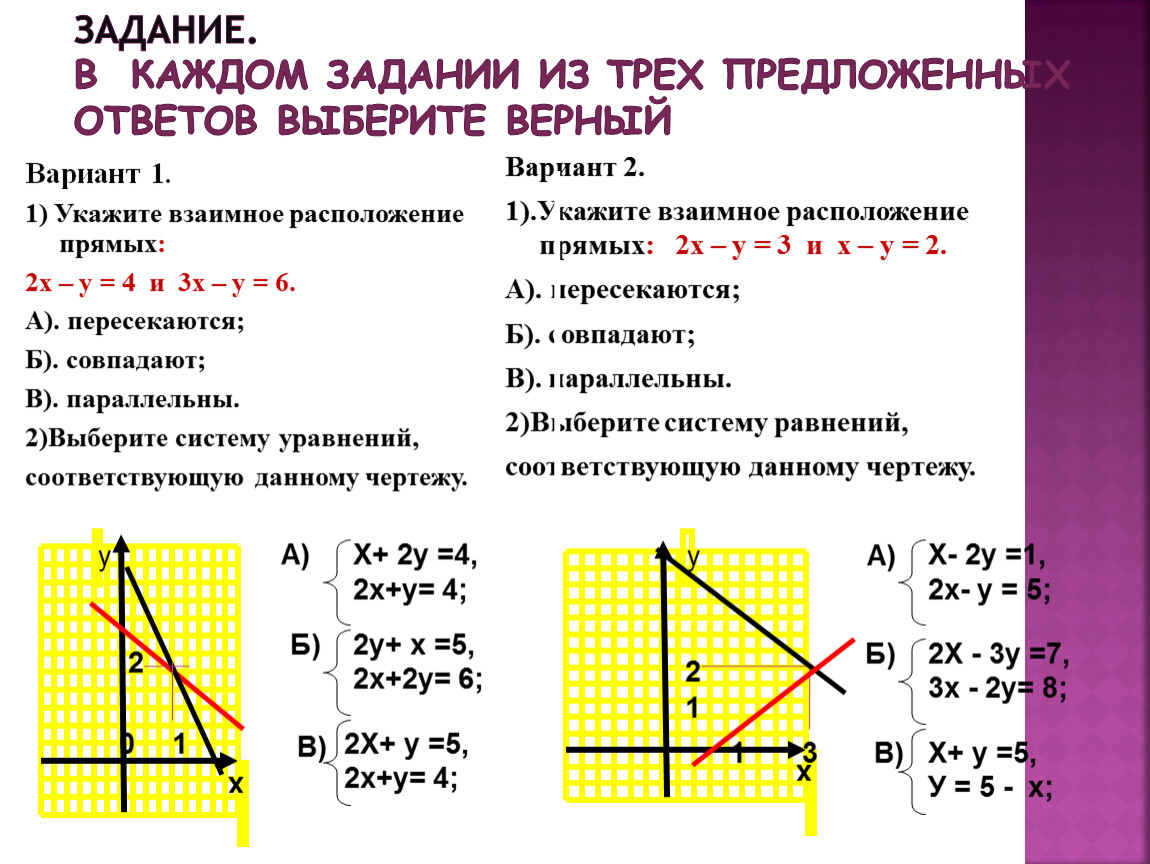  Как «Зеленые», которые претендуют на 16% голосов, так и либералы (СвДП), примерно с 11% голосов, могут оказаться в положении «серого кардинала» в будущем коалиционном правительстве. В парламенте возможны различные партийные комбинации — от чисто левого блока до коалиции с правым уклоном. Все это предвещает упорные переговоры по формированию нового кабинета. Партнеры Германии опасаются длительного периода бездействия в тот момент, когда Европа пытается избежать геополитической маргинализации. Окончательный профиль правительства серьезным образом повлияет на будущую внешнюю политику Германии, даже если три основные партии вели кампанию в центре политического поля.

Страна окажется более склонной к финансовой солидарности в Европе при формировании кабинета под руководством социал-демократов и «Зеленых», нежели в том случае, если у власти окажутся консерваторы и либералы. Последние более позитивно настроены к проведению военных операций за рубежом, чем левые. Германия может пережить период напряженности в отношениях с НАТО, если в состав правительства войдут левые радикалы из Левой партии, которые обещают распустить Североатлантический альянс.

Эволюция франко-германского партнерства, подчас переживавшего неудачи в эпоху Ангелы Меркель, будет также зависеть от финального уравнения. Это тем более вероятно, учитывая, что французам также предстоит явиться на избирательные участки в апреле 2022 года. С приходом нового правительства «можно ожидать, что Германия станет более важным генератором идей на европейском уровне», полагает сотрудник Комитета франко-германских программ Французского института международных исследований (IFRI) Поль Морис».

Les Echos: «Эти первоначальные результаты основаны на данных без учета голосования по почте. Однако они могут составлять более 50% голосов. Поэтому неопределенность особенно велика и обещает держать страну в напряжении. С учетом снижения почти на 18% за четыре года результат ХДС/ХСС обещает быть худшим в истории партии Ангелы Меркель.

Трижды за пять дней канцлер появлялась на публике вместе с кандидатом от христианских демократов Армином Лашетом, что позволило ее партии наверстать отставание от СДПГ, проявившееся на финишной прямой. Угроза поворота влево заметно мобилизовала избирателей ХДС/ХСС. Структура избирателей в Германии консервативна и характеризуется неприятием сильных потрясений. После наблюдавшихся в течение десятилетия климатических изменений немцы в целом приветствуют борьбу с климатическим кризисом, но реформы не должны быть слишком радикальными и не должны слишком сильно мешать их собственному образу жизни».

La Croix: «Для СДПГ даже предварительные результаты — уже победа. Партия смогла набрать на 5 процентных пунктов больше, чем на прошлых выборах в 2017 году… При этом ХДС/ХСС потерпели историческое поражение.

Для экологистов нынешние результаты — это наполовину победа. С одной стороны, они потеряли шансы на продвижение своего кандидата Анналены Бербок на пост канцлера, с другой — получили самый высокий за свою историю результат на федеральном уровне.

Будучи третьей политической силой в стране, «Зеленые» становятся неотъемлемым участником переговоров в предстоящие недели и однозначно будут участвовать в формировании правящей коалиции

Берлин замер в ожидании, чтобы понять, куда движется страна: в сторону коалиции а-ля «светофор» между СДПГ, СвДП и «Зелеными» или «ямайской» между ХДС/ХСС, «Зелеными» и либералами».

Agence France Presse: «Христианские демократы потерпели беспрецедентное поражение, которое вызовет внутренние потрясения и сулит сложный переход власти от Ангелы Меркель. Социал-демократ Олаф Шольц, с небольшим отрывом лидирующий на парламентских выборах, претендует на то, чтобы стать преемником Ангелы Меркель на посту канцлера. Но его консервативный соперник Армин Лашет также говорит, что готов возглавить следующее правительство.

Победу одержит тот, кто сумеет создать коалицию большинства из трех партий после переговоров, которые начнутся в понедельник. Только после того, как ее сменщик будет избран Бундестагом, через несколько недель или месяцев, Ангела Меркель сможет уйти на пенсию. Переговоры в любом случае отсрочат фактический уход 67-летней Меркель, которая более 30 лет посвятила политике».

Le Parisien: «Зарождающаяся конкуренция (между Лашетом и Шольцем) рискует ввергнуть крупнейшую экономику Европы в длительный период политического паралича и межпартийных переговоров. Период после Меркель таит в себе угрозу новой войны между лидерами правых сил страны, среди которых уже выражаются сомнения по поводу будущего Армина Лашета во главе ХДС спустя восемь месяцев после его избрания».

На эту тему

Великобритания

The Independent: «Впервые за поколение, качнувшись влево, Германия избрала в воскресенье новый парламент, который готов выбрать канцлера-левоцентриста на смену уходящей со своего поста нынешней обладательницы этой должности Ангелы Меркель. Ему предстоит стать лидером самой влиятельной и преуспевающей страны континентальной Европы. Социал-демократическая партия Германии (СДПГ), которая давно и гордо хранит традиции рабочего движения в Германии, но в последние восемь лет прозябала на вторых ролях в не отличающейся взаимной любовью коалиции с партией Меркель, твердо решила порвать с консерваторами и попытаться сформировать собственную коалицию с небольшими партиями. Таким образом, в Германии может появиться первая с послевоенного времени трехпартийная коалиция, в которой будет лишним по крайней мере одно из колес, что вызывает опасения по поводу того, как долго она продержится и насколько она будет стабильной.

При этом консервативные христианские демократы (ХДС/ХСС) Меркель потерпели самое тяжелое в своей истории поражение, скатились на второе место и были позорно отлучены от власти впервые за 19 лет, набрав лишь 24% голосов по сравнению с 32,9% четыре года назад. Их кандидат в канцлеры — склонный к оплошностям Армин Лашет, не отличающийся харизмой премьер-министр земли Северный Рейн — Вестфалия, — растерял все преимущество, которое имел по итогам ранних опросов, допуская одну постыдную ошибку за другой, что привлекло существенное внимание к предвыборной кампании, являвшейся в остальном довольно скучной».

The Times: «Исход выборов еще слишком рано предсказывать из-за близости результатов соперников, но он будет лишь первой частью истории о борьбе за власть в Германии. Ангела Меркель будет оставаться действующим канцлером, пока конкурирующие претенденты на трон будут вести затяжную борьбу, пытаясь получить парламентское большинство. Учитывая слабость крупнейших партий и многочисленные расхождения по политическим вопросам, вполне вероятно, что преемник Меркель станет известен лишь в начале 2022 года. Внимание будет приковано к «Зеленым» и Свободной демократической партии (СвДП), которые вместе имеют возможность определить следующего канцлера.

Лидеры «Зеленых», 40-летняя Анналена Бербок и 52-летний Роберт Хабек, отдают предпочтение сделке с СДПГ и СвДП. Их коллега из СвДП, 42-летний Кристиан Линднер, впрочем, заявил, что хотел бы видеть канцлером Лашета, а ХДС — главной силой в правительстве. Заставить две небольшие партии забыть о разногласиях и создать коалицию — ключ к должности канцлера, но вместе с тем и самая сложная задача для переговорщика в современной политической истории Германии».

На эту тему

Financial Times: «Сегодняшние выборы в Бундестаг были первыми в послевоенной истории Германии, когда действующий канцлер не добивается переизбрания, и это обстоятельство сделало предвыборную гонку одной из самых переменчивых и непредсказуемых на памяти последних нескольких поколений. С начала года рейтинги СДПГ, ХДС/ХСС и «Зеленых» колебались из стороны в сторону на 10 пунктов.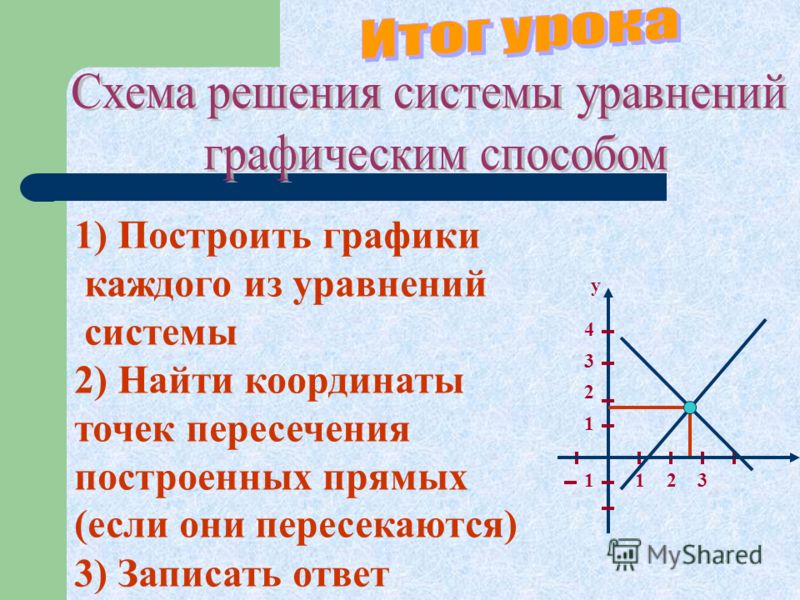 Уход Меркель означает, что миллионы избирателей, которые на предыдущих выборах голосовали именно за нее, не являясь преданными сторонниками ХДС/ХСС, имели возможность поменять свои политические предпочтения. Это объясняет сильное снижение уровня поддержки партии, которая, набрав в 2017 году 32,9% голосов, теперь получает лишь около 25%».

The Economist: «Опросы показывают, что в Германии будет парламентская неразбериха, когда не только одна партия, но даже союз двух не может сформировать правительство. Вместо этого вырисовывается нестройная идеологически коалиция трех партий, в которой настроенным много тратить «Зеленым» и выступающим в поддержку бизнеса либералам будет сложно договориться о чем-либо серьезном. Это еще один симптом безмятежной эпохи Меркель. Довольные жизнью и осторожные немцы, кажется, не заинтересованы в том, чтобы серьезно обсуждать будущее. Разрешение кризисных ситуаций подменило собой инициативу. У кандидатов нет мотивации выдвигать на передний план очевидные проблемы своей страны. Миру следует ждать, что переговоры о формировании коалиции займут месяцы, парализовав на это время европейскую политику. В конце концов у руля в Германии может оказаться неспособное чего-либо достичь правительство. Это — тот беспорядок, который оставляет после себя Меркель».

Италия

Corriere della sera: «Выборы в Германии оказались больше чем голосованием. Они обернулись революцией. Германия оставила позади эпоху Ангелы Меркель с наиболее непредсказуемым, необычным и проблематичным результатом за всю демократическую историю страны. Результат выборов отражает политическую картину, в которой превалирует раздробленность, что обещает долгий и мучительный процесс образования правительства. Но как бы ни пошел этот процесс, в этих выборах есть один победитель и один проигравший: первый — Олаф Шольц, второй — Армин Лашет. Кандидат от социал-демократов воскресил Социал-демократическую партию Германии (СДПГ), он принес ей первое место, сделав ставку на прерывание преемственности Меркель с программой, нацеленной на перемены. На фланге консерваторов блок Христианско-демократического и Христианско-социального союзов (ХДС/ХСС) получил худший результат в своей истории».

La Stampa: «Немцы решили не решать, кто займет место Ангелы Меркель. Исход дуэли Олафа Шольца и Армина Лашета определят не голоса, а переговоры с другими партиями, в которых нуждаются оба политика для достижения парламентского большинства. От выборов политический процесс переходит к базару. В стабильной Германии это демократическое упражнение. У него будет два этапа: первый — выбор, с кем вступать в альянсы, второй — программа правительства, которая станет самым настоящим контрактом, тщательно подготовленным и выполненным до конца. Для Европы это может означать семь месяцев паралича, который вынудит заморозить все основные досье: реформа пакта о стабильности и соглашения о предоставлении убежища, а также «Зеленое соглашение», новые правила для цифровых гигантов, открытые вопросы с Венгрией и Польшей о соблюдении прав человека, европейская оборона. Без правительства в Берлине невозможно двигаться по этому пути реформ. Проблема в том, что зазор между голосованием в Германии и выборами во Франции слишком большой. Когда Германия наконец получит нового канцлера и новую коалицию, Франция уже погрузится в избирательную кампанию».

La Repubblica:

Согласно результатам голосования, без Ангелы Меркель Германия оказалась не с одним, а с двумя кандидатами в канцлеры

Сейчас начинается длинная и сложная гонка, исход которой даст понять, кто первым сумеет сформировать правительство. И дело не в близости результатов двух кандидатов, это случается не в первый раз. Впервые надо будет вести переговоры не с одной, а двумя разными партиями, возможными союзниками обоих конкурентов».

Польша

Rzeczpospolita: «Германия была стабильной, хаос после выборов с ней не ассоциировался. Только старшее поколение помнит о партийной разобщенности, правлении в группе больше двух. На протяжении многих лет существовали две крупные партии — правоцентристская ХДС/ХСС и социал-демократическая СДПГ, захватившие подавляющее большинство электората. Сейчас царит хаос и неопределенность. Неопределенность царила перед выборами, которые заранее считались историческими, потому что после них начинается эпоха без Ангелы Меркель. Неопределенность все еще сохраняется…

У Германии есть традиция долго формировать коалицию, возможно месяцами. А ситуация требует быстрых действий, как в Германии и в Европейском союзе, так и на всем Западе. Идет пандемия, есть столкновение между Америкой и Китаем, есть афганцы, которые могут массово постучать в ворота Европы».

На эту тему

Gazeta Wyborcza: «В истории Германии текущие выборы — это конец эпохи, и не только потому, что Ангела Меркель, правившая 16 лет, уходит на политическую пенсию. Христианские демократы и социал-демократы, когда-то большие народные партии, доминировавшие на политической арене, значительно ослабли. Это результат разочарования избирателей в их совместной власти в составе последовательных крупных коалиций, созданных под руководством Меркель. Широкие альянсы привели партии к стагнации, притупили их идеологические платформы и в конечном итоге довели до потери доверия избирателей, как это видно по опросам. Сегодня и социал-демократы, и христианские демократы нуждаются для получения власти не в одном, а в двух партнерах по коалиции. Построение такого правительства будет нелегкой задачей. В Берлине уверены, что канцлер Ангела Меркель выступит с новогодним обращением к нации, потому что ее преемник еще не будет приведен к присяге».

Испания

El Pais: «Германию, похоже, ждут очень долгие переговоры. Четыре года назад Меркель потребовалось почти полгода, чтобы сформировать третью большую коалицию за 16 лет ее правления. Паралич самой густонаселенной страны (около 83 млн жителей), имеющей самый большой экономический вес в Евросоюзе, грозит оставить европейский клуб без лидера на несколько месяцев, когда на горизонте вырисовываются серьезные вызовы. ЕС должен решить важные вопросы: когда восстановить налоговые правила, чтобы не воспрепятствовать выходу из кризиса, или какой ответ нужно дать на новый международный сценарий в связи с кризисом в Афганистане и проблемами администрации Байдена с Францией из-за военного альянса, который Вашингтон создал с Великобританией и Австралией».

El Mundo: «Наследие Ангелы Меркель находится в подвешенном состоянии. Стабильность, которую канцлер обеспечивала в течение 16 лет правления в своей стране и тем самым в Евросоюзе, будет зависеть от правительственной коалиции, которая появится в результате длительного процесса переговоров, который сейчас должен начаться. Разделение голосов поровну между СДПГ и ХДС/ХСС станет дополнительной трудностью. Обе политические силы чувствуют себя так или иначе легитимными для формирования правительства».

Швейцария

Le Temps: «Анализируя итоги воскресных выборов, трудно представить, что необходимой легитимностью для создания коалиции со Свободной демократической партией и «Зелеными» обладает Армин Лашет, чья партия получила наихудший результат в ее истории. Кандидат ХДС, премьер-министр земли Северный Рейн — Вестфалия, сумел минимизировать потери благодаря участию в последнюю минуту канцлера в предвыборной кампании, однако результат остается посредственным. Он сам заявил в воскресенье вечером, что потеря столь большого числа голосов в пользу СДПГ — «это нехорошо». Вместе с тем он настаивает, что вопрос о коалиции, которая будет управлять первой экономической державой Европы и четвертой экономической державой мира, не должен решаться путем простых арифметических подсчетов. Он должен отражать приоритеты, которые обеспечат стабильность и процветание Германии…

На эту тему

То, что социал-демократы пришли в форму, не гарантирует Олафу Шольцу пост канцлера, но позволяет к нему приблизиться. Он уверен в своей способности сформировать коалицию до Рождества. В пользу СДПГ явно сыграли отсутствие социальной безопасности ввиду пандемии COVID-19, а также личность ее кандидата, который, как и Меркель, вселяет уверенность манерой всегда двигаться к сути проблемы. Отсутствие у него харизмы является скорее гарантией серьезности. Для него итоги воскресных выборов — это ясный выбор в пользу его партии. Это в любом случае результат, который делает его победителем голосования.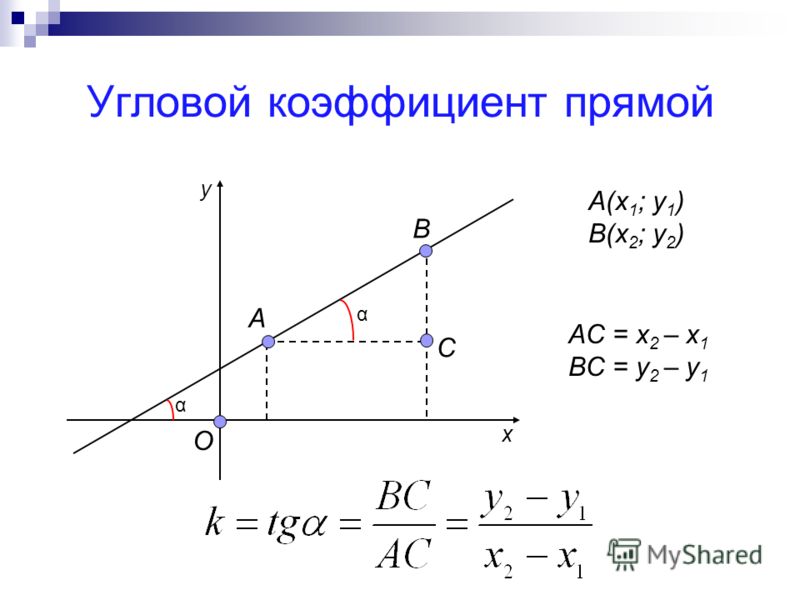 Большая трудность, с которой столкнется Олаф Шольц, — это поиск пространства для согласия с партнерами по коалиции, в частности с СвДП…

По итогам выборов в Германии представляется примечательной констатация того, что на политической сцене доминируют прежде всего центристские партии. В отличие от других европейских демократий Германия, несомненно, вновь будет управляться центристами. Потребуются, возможно, месяцы переговоров, однако априори будет обеспечена преемственность в плане стабильности».

Tribune de Geneve: «Кто бы ни стал (канцлером Германии) — Олаф Шольц от левых или Армин Лашет от правых, — Германию не ожидает революция. Они являются не кандидатами перемен, а поборниками преемственности. Прежде всего это относится к стилю управления, хотя их характеры очень разные: слева — аскетичный, справа — веселый. Оба фаворита гонки за пост канцлера хотят быть такими, как Ангела Меркель, то есть проводить стабильную и обнадеживающую политику. Они оба претендовали на «наследство» Меркель во время предвыборной кампании. Олаф Шольц, будучи из другой партии, сумел представить себя как естественный преемник нынешнего канцлера, хотя именно Лашет стремился принять эстафетную палочку…  и Лашету пришлось догонять, позвав на помощь «мамочку». Канцлер, которая не планировала вмешиваться в кампанию, согласилась показаться рядом с ним на последних митингах. Она была в субботу вечером вместе с ним в его родном городе Ахене. Цель состояла в том, чтобы в последнюю минуту нарисовать картину гармонии, укрепив мысль о том, что Армин Лашет действительно является естественным преемником Меркель.

Хотя два кандидата официально являются противниками, они имеют схожие подходы по принципиальным вопросам. Оба выступают за возвращение к бюджетной дисциплине и следование курсом по сдерживанию роста задолженности…

В международной политике сохранится статус-кво. Даже после фиаско в Афганистане, где немцы потеряли 59 солдат, новый канцлер по-прежнему будет равняться на Вашингтон.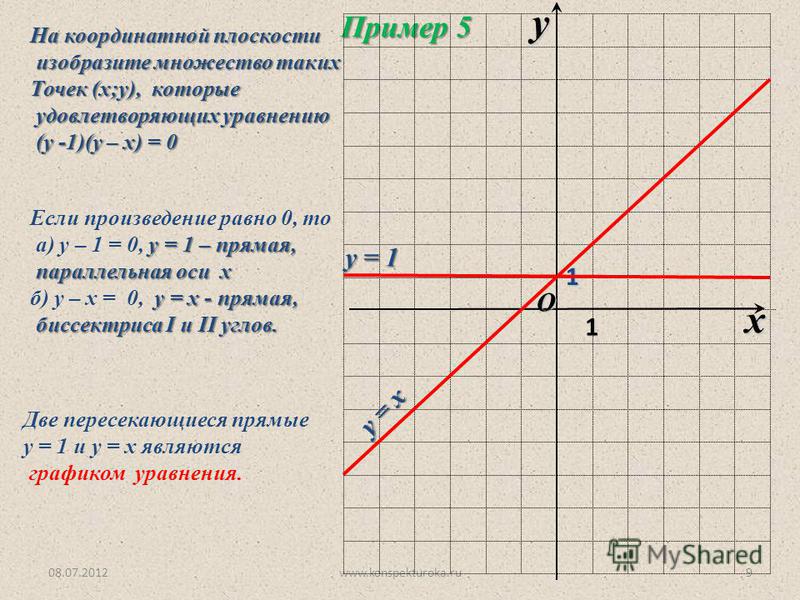 Речь не идет о выходе из НАТО! Как и Меркель, Шольц и Лашет постараются сохранить экономические интересы Германии в Китае (где «Фольксваген» сбывает более трети своей продукции), осуждая одновременно (как вопрос принципа) нарушения прав человека».

Чехия

Denik N: «Немцам уже, совершенно очевидно, не хватает Ангелы Меркель, которая стоит во главе ФРГ в течение последних 16 лет. Об этом свидетельствуют итоги парламентских выборов, в которых партия канцлера ХДС/ХСС получила наименьшее число голосов в истории именно потому, что кандидат консерваторов не был и не хотел быть прохожим на Ангелу Меркель. Наоборот, их конкуренты, социал-демократы, смогли подняться с политического дна прежде всего потому, что их лидер сознательно представлял себя ее клоном.

Пустота, возникающая с уходом Ангелы Меркель из германской политики, стала ключевым фактором, который повлиял на парламентские выборы

Не только ее партия ХДС/ХСС не знала, как заменить ее в качестве своего председателя. Избиратели тоже не могли решить, кто должен сменить ее в кресле канцлера».

Cesky rozhlas: «Избиратели четко не определили, кого хотят видеть канцлером после Ангелы Меркель, остающейся до определения своего преемника на этом посту. Почти во всех федеральных землях ФРГ у власти находятся коалиции, состоящие из совершенно разных партий. Пестрые политические порядки в них указывают на раскрывающийся веер возможностей формирования правительственной коалиции. Этот веер также можно назвать веером неопределенности, который раскрыли германские избиратели, не отдав явного предпочтения кому-либо в ходе выборов в Бундестаг».

Hospodarske noviny: «Когда Олаф Шольц в декабре 2019 года проиграл битву за пост председателя социал-демократов, казалось, что его время в большой политике истекло. Тогда победу над Шольцом одержали практически неведомые общественности кандидаты. Для вице-канцлера и министра финансов это был настоящий разгром, но не прошло и двух лет, как Шольц вновь оказался на пути к посту германского канцлера. Он, однако, должен убедить другие партии в необходимости войти в коалицию с его СДПГ. Шансы управлять ФРГ до сих пор остаются и у консервативного блока ХДС/ХСС — партии уходящей в отставку канцлера Ангелы Меркель».

Reflex: «Новое германское правительство будет политически хрупким и очень «зеленоватым»… Германия будет и далее плыть на большой зеленой волне, будет колебаться в центре политического спектра…

От нового правительства в Берлине мы не ожидаем никаких экстравагантных шагов и революций. Немцы любят покой. Для большинства избирателей принципиальным вопросом является поддержание в стране высокого жизненного уровня. Они не хотят потрясений. Поэтому и в воскресенье голоса распределись равномерно между крупнейшими партиями. Не будет согласия со всем, что каким-либо образом угрожало устоявшимся порядкам. Уже в 1957 году под лозунгом «Никаких экспериментов» на выборах победил славный германский политик Конрад Аденауэр. Этот лозунг остается актуальным.

Однако возникает несколько серьезных вопросов по поводу функционирования Германии. Сможет ли она сохранить лидирующее положение в Евросоюзе? И это потому, что немцы, кроме политики, определяют направление в областях климата, новых технологий и торговли. С новым канцлером после ухода Меркель, пусть им будет кто угодно, положение Германии в Евросоюзе будет значительно более сложным».

США

The Washington Post: «От результатов выборов зависит будущее политики не только в Берлине, но и по всей Европе, где опытной руки Меркель больше не будет. Экзитполы свидетельствуют о том, что предстоят длительные переговоры по формированию нового правительства и ни для одной из ведущих партий — ни для христианских демократов, ни для социал-демократов — не будет легкого пути при создании правящей коалиции в парламенте. Все это происходит на фоне сложной ситуации в Евросоюзе, которому предстоит урегулировать проблемы с финансами, вызванные пандемией коронавируса, а также скоординировать позицию стран континента по отношению к России и Китаю».

The Wall Street Journal: «Германии предстоят недели, а возможно, и месяцы неопределенности, после того как прошедшие в воскресенье федеральные выборы оставили под вопросом форму и повестку будущего правительства и не прояснили вопрос о том, кто будет наследником Ангелы Меркель. По крайней мере, в первое время четвертая экономика мира и ведущая страна Евросоюза окажется без уверенного лидерства, а затем, на протяжении следующих четырех лет, с ослабленным правительством…

Перспектива переговоров о создании коалиции, на которые уйдет несколько недель, по всей видимости, приведет к смятению в остальной Европе. Союзники Германии ждут позиции Берлина по таким важным проектам, как пакет мер по борьбе с изменением климата и поправки к правилам о размерах задолженности ЕС и дефициту. Если переговоры о коалиции продлятся до 17 декабря, то Меркель установит рекорд по длительности пребывания на посту канцлера, опередив Гельмута Коля».

На эту тему

The New York Times: «После 16 лет пребывания Меркель у власти немцы щедро раскидали голоса по всему политическому спектру на прошедших выборах. Такой дробный результат предсказывает более сумбурную эру в политике Германии и ослабление ведущей роли Германии в Европе. Предварительные результаты показывали небольшое лидерство занимающих более левые позиции социал-демократов, однако разница столь небольшая, что никто не мог сказать, кто будет следующим канцлером и как будет выглядеть следующее правительство. Ясно лишь одно: потребуются недели, если не месяцы, торгов, чтобы сформировать коалицию. Это оставит крупнейшую демократию Европы в подвешенном состоянии в тот критический момент, когда континент пытается восстановиться после пандемии, а Франции, которая наряду с Германией составляет ядро Европы, следующей весной предстоят свои собственные сложные выборы».

Axios: «Решение Меркель покинуть политическую арену после 16 лет на посту канцлера (первый раз в истории федеративной республики действующий канцлер не идет на выборы) оставило вакуум в сердце германской политики, которая в течение долгого времени была известна своей умеренностью и стабильностью. Все три кандидата, которые могут занять пост канцлера, достаточно непопулярны…

Сложная система пропорционального представительства, с помощью которой граждане избирают членов Бундестага, означает, что крупные партии должны рассчитывать на поддержку более мелких партий, чтобы сформировать правительство большинства. Переговоры о формировании коалиции могут длиться многие месяцы. Наиболее вероятный сценарий — либо СДПГ, либо ХДС/ХСС объединятся с «Зелеными» или со Свободной демократической партией Германии (СвДП), которая представляет интересы бизнеса».

CBS: «Результаты, судя по всему, свидетельствуют о том, что крупнейшую экономику Европы ждет длительный торг по поводу формирования нового правительства, а Меркель останется на посту канцлера на временной основе до тех пор, пока к присяге не приведут ее преемника. Формирование трехпартийной правящей коалиции, в которой будут две оппозиционные партии, традиционно находившиеся во враждующих идеологических лагерях — «Зеленые» и СвДП, — станет самым надежным способом прийти к власти для двух ведущих кандидатов…

Не так просто будет тому, кто займет пост канцлера после Меркель, которая заслужила любовь граждан, успешно проведя страну сквозь несколько крупных кризисов. Ее преемнику придется заняться восстановлением страны после пандемии коронавируса… Внешняя политика особо не фигурировала в предвыборной кампании, хотя «Зеленые» занимают жесткую позицию в отношении Китая и России».

Bloomberg: «В ситуации, когда выборы в Германии не выявили явного победителя, две основные партии — социал-демократы министра финансов Олафа Шольца и консервативный блок Христианско-демократического и Христианско-социального союзов (ХДС/ХСС) Армина Лашета — обдумывают свои следующие шаги, чтобы добиться поста канцлера. Расколотый политический ландшафт означает, что им потребуются «Зеленые» и выступающая от имени бизнеса Свободная демократическая партия, чтобы сформировать большинство. В этом-то и будет вся сложность… Будут срывы, скрытые угрозы и заседания ночи напролет. В конце концов коалиционное соглашение окажется размером с книгу, и в нем будет изложено все, что планирует делать правительство. Подписать его должны все партии. Социал-демократы ранее ставили такие серьезные решения на внутрипартийное голосование, что может еще сильнее задержать процесс…

Если сформировать правительство не получится, будет необходимо провести новые выборы. Но немецкие власти ценят политическую стабильность, так что такое развитие событий было бы крайне необычным. Вероятнее всего, президент Штайнмайер призовет партии прийти к соглашению ради блага всей страны — как это было в 2017 году. Когда Меркель сообщила Штайнмайеру, что ее первая попытка сформировать коалицию провалилась, давление со стороны президента сыграло ключевую роль в том, чтобы вернуть колеблющихся социал-демократов за стол переговоров».

Япония

NHK: «Потенциальный преемник Меркель — кандидат от Социал-демократической партии Германии (СДПГ) Олаф Шольц — менее харизматичен. Однако его отличает спокойствие, твердость и богатый политический опыт. Вместе с тем в 2017 году, когда он был мэром Гамбурга, там проходил саммит G20, и во время него в городе вспыхнули массовые беспорядки и погромы. В связи с этим внимание будет приковано к тому, улучшил ли Шольц навыки управления в кризисных ситуациях».

Nikkei shimbun: «Что касается переговоров о коалиции, то Социал-демократическая партия Германии близка в своей политике к партии «Зеленых». С другой стороны, политика блока Христианско-демократического и Христианско-социального союзов (ХДС/ХСС) близка к Свободной демократической партии (СвДП). Однако по итогам нынешних выборов в зависимости от окончательного результата голосования будет сложно получить большинство при заключении двухпартийной коалиции. В результате может сложиться ситуация, при которой придется формировать трехпартийную коалицию, и одна из трех партий будет отличаться от других членов коалиции по своим политическим взглядам».

Китай

Global Times: «Несомненно, следующий германский лидер продолжит проводить прагматичную политику в отношении Китая так, как это делала Ангела Меркель… Эксперты считают, что китайско-германским отношениям предстоит короткий период колебаний после того, как пост главы государства в ФРГ займет новый политик… По их мнению, при Олафе Шольце Германия не станет предпринимать непродуманные действия в отношении других стран. Лидер Социал-демократической партии Германии говорил очень мало о Китае.

Китай не был в центре внимания в ходе выборов в ФРГ — это означает, что германские партии не имеют больших расхождений во взглядах на внешнюю политику страны, в том числе по отношению к КНР. Поэтому можно ожидать, что Берлин продолжит придерживаться своей традиционной стратегии в отношении Пекина».

China Daily: «Меркель удостоилась громких оваций, поскольку под ее руководством Германия несколько раз успешно преодолевала кризисные ситуации. Новый канцлер должен будет стремиться к восстановлению (национальной экономики) от пандемии. ФРГ преодолела ее довольно хорошо благодаря масштабной программе по оказанию поддержки населению… По мнению аналитиков, передача власти в Германии повлияет не только на внутреннюю политику, но и отразится на европейском курсе ФРГ и скажется на позиции Берлина в отношении всего мира».

Xinhua: «Германии нужно больше взаимодействовать с Китаем в эпоху, которая начинается с уходом Меркель… Поскольку ситуация в мире все более нестабильна, Китай и ФРГ должны выполнять возложенные на них важные обязательства и вопросы двустороннего сотрудничества, должны выходить за обычные рамки выстраивания отношений между двумя странами. Устойчивое стратегическое взаимодействие между КНР и Германией, а также между ФРГ и Евросоюзом не только выгодно китайскому народу и населению Европы, оно будет способствовать укреплению доверия и обеспечивать стабильность в мире».

Израиль

The Jerusalem Рost: «Теперь внимание будет переключено на неформальные коалиционные дискуссии, за которыми последуют уже более формальные переговоры о коалиции. Ее формирование может занять несколько месяцев, на протяжении которых Меркель будет оставаться у власти».

Саудовская Аравия

Ashark al-Awsat: «Канцлер Германии Ангела Меркель, которую когда-то называли лидером свободного мира во время подъема популизма в Европе и Соединенных Штатах, оставила после себя неоднозначное политическое наследие, пробыв у власти 16 лет и вырастив целое поколение, которое не знало другого руководителя страны. Длительное правление, покрывшее 67-летнюю Меркель мантией «вечного канцлера», тем не менее не отразилось на ее популярности, которая, вне сомнений, позволила бы ей выиграть рекордный пятый срок, если бы она решилась этого добиваться…

Сторонники Меркель до сих пор видят в ней объединяющую фигуру, которая обеспечивала стабильное и прагматичное руководство перед лицом бесчисленных глобальных кризисов. Однако критики считают, что, взяв курс на адаптацию мигрантов и стремясь получить наибольшую базу консенсуса, Меркель уже не хватало смелого видения, чтобы подготовить Европу и ее крупнейшую экономику в лице Германии к предстоящим десятилетиям».

Найти уравнение прямой проходящей через точки онлайн. Различные уравнения прямой

Прямая, проходящая через точку K(x 0 ; y 0) и параллельная прямой y = kx + a находится по формуле:

y — y 0 = k(x — x 0) (1)

Где k — угловой коэффициент прямой.

Альтернативная формула:
Прямая, проходящая через точку M 1 (x 1 ; y 1) и параллельная прямой Ax+By+C=0 , представляется уравнением

A(x-x 1)+B(y-y 1)=0 . (2)

Пример №1 . Составить уравнение прямой, проходящей через точку M 0 (-2,1) и при этом:
а) параллельно прямой 2x+3y -7 = 0;
б) перпендикулярно прямой 2x+3y -7 = 0.
Решение . Представим уравнение с угловым коэффициентом в виде y = kx + a . Для этого перенесем все значения кроме y в правую часть: 3y = -2x + 7 . Затем разделим правую часть на коэффициент 3 . Получим: y = -2/3x + 7/3
Найдем уравнение NK, проходящее через точку K(-2;1), параллельно прямой y = -2 / 3 x + 7 / 3
Подставляя x 0 = -2, k = -2 / 3 , y 0 = 1 получим:
y-1 = -2 / 3 (x-(-2))
или
y = -2 / 3 x — 1 / 3 или 3y + 2x +1 = 0

Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение . Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: . Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .

Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 / 7 x – 4 / 7 (здесь a = 5 / 7). Уравнение искомой прямой есть y – 5 = 5 / 7 (x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .

Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.

Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).

Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.

Yandex.RTB R-A-339285-1

Пусть на плоскости задана прямоугольная система координат O x y .

Теорема 1

Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А, В, С.

Доказательство

указанная теорема состоит из двух пунктов, докажем каждый из них.

1. Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.

Пусть существует некоторая точка М 0 (x 0 , y 0) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A (x — x 0) + B (y — y 0) = 0 . Оно эквивалентно A x + B y + C = 0 .

Полученное уравнение A (x — x 0) + B (y — y 0) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = (A , B) и M 0 M → = (x — x 0 , y — y 0) . Таким образом, множество точек M (x , y) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = (A , B) . Можем предположить, что это не так, но тогда бы векторы n → = (A , B) и M 0 M → = (x — x 0 , y — y 0) не являлись бы перпендикулярными, и равенство A (x — x 0) + B (y — y 0) = 0 не было бы верным.

Следовательно, уравнение A (x — x 0) + B (y — y 0) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.

1. Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .

Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 (x 0 , y 0) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = (A , B) .

Пусть также существует некоторая точка M (x , y) – плавающая точка прямой. В таком случае, векторы n → = (A , B) и M 0 M → = (x — x 0 , y — y 0) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:

n → , M 0 M → = A (x — x 0) + B (y — y 0) = 0

Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C: C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .

Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.

Определение 1

Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .

Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.

Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .

Рассмотрим конкретный пример общего уравнения прямой.

Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = (2 , 3) . Изобразим заданную прямую линию на чертеже.

Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.

Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.

Определение 2

Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А, В, С отличны от нуля. В ином случае уравнение является неполным .

Разберем все вариации неполного общего уравнения прямой.

1. Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек (x , y) , координаты которых равны одному и тому же числу — C B .
2. Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
3. Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
4. Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
5. Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел (0 , 0) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .

Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.

Пример 1

Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.

Решение

Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:

A · 2 7 + C = 0

Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0

Ответ: 7 x — 2 = 0

Пример 2

На чертеже изображена прямая, необходимо записать ее уравнение.

Решение

Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку (0 , 3) .

Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки (0 , 3) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С: С = — 3 . Используем известные значения В и С, получаем требуемое уравнение прямой: y — 3 = 0 .

Ответ: y — 3 = 0 .

Общее уравнение прямой, проходящей через заданную точку плоскости

Пусть заданная прямая проходит через точку М 0 (x 0 , y 0) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A (x — x 0) + B (y — y 0) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 (x 0 , y 0) и имеет нормальный вектор n → = (A , B) .

Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.

Пример 3

Даны точка М 0 (- 3 , 4) , через которую проходит прямая, и нормальный вектор этой прямой n → = (1 , — 2) . Необходимо записать уравнение заданной прямой.

Решение

Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:

A (x — x 0) + B (y — y 0) = 0 ⇔ 1 · (x — (- 3)) — 2 · y (y — 4) = 0 ⇔ ⇔ x — 2 y + 22 = 0

Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:

A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0

Теперь найдем значение С, используя заданную условием задачи точку М 0 (- 3 , 4) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .

Ответ: x — 2 · y + 11 = 0 .

Пример 4

Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.

Решение

Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:

2 3 x 0 — y 0 — 1 2 = 0

Определяем y 0: 2 3 · (- 3) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2

Ответ: — 5 2

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно

Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.

Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .

Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .

Это равенство возможно записать как пропорцию: x + C A — B = y A .

В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .

Перепишем равенство в виде пропорции: x — B = y + C B A .

Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.

Пример 5

Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.

Решение

Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .

Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.

Ответ: x — 3 = y — 4 3 0 .

Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.

Пример 6

Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.

Решение

Осуществим переход от общего уравнения к каноническому:

2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2

Теперь примем обе части полученного канонического уравнения равными λ , тогда:

x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R

Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .

Пример 7

Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.

Решение

Произведем нужные действия по алгоритму:

2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x

Ответ: y = — 2 7 x .

Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y:

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Пример 8

Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.

Решение

Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Ответ: x — 1 2 + y 1 14 = 1 .

В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.

Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:

x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0

Каноническое уравнение преобразуется к общему по следующей схеме:

x — x 1 a x = y — y 1 a y ⇔ a y · (x — x 1) = a x (y — y 1) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0

Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0

Пример 9

Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.

Решение

Осуществим переход от параметрических уравнений к каноническому:

x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0

Перейдем от канонического к общему:

x + 1 2 = y — 4 0 ⇔ 0 · (x + 1) = 2 (y — 4) ⇔ y — 4 = 0

Ответ: y — 4 = 0

Пример 10

Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.

Решение:

Просто перепишем уравнение в необходимом виде:

x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0

Ответ: 1 3 x + 2 y — 1 = 0 .

Составление общего уравнения прямой

Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A (x — x 0) + B (y — y 0) = 0 . Там же мы разобрали соответствующий пример.

Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.

Пример 11

Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 (4 , 1) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.

Решение

Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = (2 , — 3) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:

A (x — x 0) + B (y — y 0) = 0 ⇔ 2 (x — 4) — 3 (y — 1) = 0 ⇔ 2 x — 3 y — 5 = 0

Ответ: 2 x — 3 y — 5 = 0 .

Пример 12

Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.

Решение

Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .

Тогда n → = (3 , 5) . Прямая проходит через начало координат, т.е. через точку О (0 , 0) . Составим общее уравнение заданной прямой:

A (x — x 0) + B (y — y 0) = 0 ⇔ 3 (x — 0) + 5 (y — 0) = 0 ⇔ 3 x + 5 y = 0

Ответ : 3 x + 5 y = 0 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Прямая линия на плоскости – это одна из простейших геометрических фигур, знакомая вам ещё с младших классов, и сегодня мы узнаем, как с ней справляться методами аналитической геометрии. Для освоения материала необходимо уметь строить прямую; знать, каким уравнением задаётся прямая, в частности, прямая, проходящая через начало координат и прямые, параллельные координатным осям. Данную информацию можно найти в методичке Графики и свойства элементарных функций , я её создавал для матана, но раздел про линейную функцию получился очень удачным и подробным. Поэтому, уважаемые чайники, сначала разогрейтесь там. Кроме того, нужно обладать базовыми знаниями о векторах , иначе понимание материала будет неполным.

На данном уроке мы рассмотрим способы, с помощью которых можно составить уравнение прямой на плоскости. Рекомендую не пренебрегать практическими примерами (даже если кажется очень просто), так как я буду снабжать их элементарными и важными фактами, техническими приёмами, которые потребуются в дальнейшем, в том числе и в других разделах высшей математики.

• Как составить уравнение прямой с угловым коэффициентом?
• Как ?
• Как найти направляющий вектор по общему уравнению прямой?
• Как составить уравнение прямой по точке и вектору нормали?

и мы начинаем:

Уравнение прямой с угловым коэффициентом

Всем известный «школьный» вид уравнения прямой называется уравнением прямой с угловым коэффициентом . Например, если прямая задана уравнением , то её угловой коэффициент: . Рассмотрим геометрический смысл данного коэффициента и то, как его значение влияет на расположение прямой:

В курсе геометрии доказывается, что угловой коэффициент прямой равен тангенсу угла между положительным направлением оси и данной прямой : , причём угол «откручивается» против часовой стрелки.

Чтобы не загромождать чертёж, я нарисовал углы только для двух прямых. Рассмотрим «красную» прямую и её угловой коэффициент . Согласно вышесказанному: (угол «альфа» обозначен зелёной дугой). Для «синей» прямой с угловым коэффициентом справедливо равенство (угол «бета» обозначен коричневой дугой). А если известен тангенс угла, то при необходимости легко найти и сам угол с помощью обратной функции – арктангенса. Как говорится, тригонометрическая таблица или микрокалькулятор в руки. Таким образом, угловой коэффициент характеризует степень наклона прямой к оси абсцисс .

При этом возможны следующие случаи:

1) Если угловой коэффициент отрицателен: , то линия, грубо говоря, идёт сверху вниз. Примеры – «синяя» и «малиновая» прямые на чертеже.

2) Если угловой коэффициент положителен: , то линия идёт снизу вверх. Примеры – «чёрная» и «красная» прямые на чертеже.

3) Если угловой коэффициент равен нулю: , то уравнение принимает вид , и соответствующая прямая параллельна оси . Пример – «жёлтая» прямая.

4) Для семейства прямых , параллельных оси (на чертеже нет примера, кроме самой оси ), углового коэффициента не существует (тангенс 90 градусов не определён) .

Чем больше угловой коэффициент по модулю, тем круче идёт график прямой .

Например, рассмотрим две прямые . Здесь , поэтому прямая имеет более крутой наклон. Напоминаю, что модуль позволяет не учитывать знак, нас интересуют только абсолютные значения угловых коэффициентов.

В свою очередь, прямая более крутА, чем прямые .

Обратно: чем меньше угловой коэффициент по модулю, тем прямая является более пологой .

Для прямых справедливо неравенство , таким образом, прямая более полога. Детская горка, чтобы не насадить себе синяков и шишек.

Зачем это нужно?

Продлить ваши мучения Знания вышеперечисленных фактов позволяет немедленно увидеть свои ошибки, в частности, ошибки при построении графиков – если на чертеже получилось «явно что-то не то». Желательно, чтобы вам сразу было понятно, что, например, прямая весьма крутА и идёт снизу вверх, а прямая – очень полога, близко прижата к оси и идёт сверху вниз.

В геометрических задачах часто фигурируют несколько прямых, поэтому их удобно как-нибудь обозначать.

Обозначения : прямые обозначаются маленькими латинскими буквами: . Популярный вариант – обозначение одной и той же буквой с натуральными подстрочными индексами. Например, те пять прямых, которые мы только что рассмотрели, можно обозначить через .

Поскольку любая прямая однозначно определяется двумя точками, то её можно обозначать данными точками: и т.д. Обозначение совершенно очевидно подразумевает, что точки принадлежат прямой .

Пора немного размяться:

Как составить уравнение прямой с угловым коэффициентом?

Если известна точка , принадлежащая некоторой прямой, и угловой коэффициент этой прямой, то уравнение данной прямой выражается формулой :

Пример 1

Составить уравнение прямой с угловым коэффициентом , если известно, что точка принадлежит данной прямой.

Решение : Уравнение прямой составим по формуле . В данном случае:

Ответ :

Проверка выполняется элементарно. Во-первых, смотрим на полученное уравнение и убеждаемся, что наш угловой коэффициент на своём месте. Во-вторых, координаты точки должны удовлетворять данному уравнению. Подставим их в уравнение:

Получено верное равенство, значит, точка удовлетворяет полученному уравнению.

Вывод : уравнение найдено правильно.

Более хитрый пример для самостоятельного решения:

Пример 2

Составить уравнение прямой, если известно, что её угол наклона к положительному направлению оси составляет , и точка принадлежит данной прямой.

Если возникли затруднения, перечитайте теоретический материал. Точнее больше практический, многие доказательства я пропускаю.

Прозвенел последний звонок, отгремел выпускной бал, и за воротами родной школы нас поджидает, собственно, аналитическая геометрия. Шутки закончились…. А может быть только начинаются =)

Ностальгически машем ручкой привычному и знакомимся с общим уравнением прямой. Поскольку в аналитической геометрии в ходу именно оно:

Общее уравнение прямой имеет вид : , где – некоторые числа. При этом коэффициенты одновременно не равны нулю, так как уравнение теряет смысл.

Оденем в костюм и галстук уравнение с угловым коэффициентом . Сначала перенесём все слагаемые в левую часть:

Слагаемое с «иксом» нужно поставить на первое место:

В принципе, уравнение уже имеет вид , но по правилам математического этикета коэффициент первого слагаемого (в данном случае ) должен быть положительным. Меняем знаки:

Запомните эту техническую особенность! Первый коэффициент (чаще всего ) делаем положительным!

В аналитической геометрии уравнение прямой почти всегда будет задано в общей форме. Ну, а при необходимости его легко привести к «школьному» виду с угловым коэффициентом (за исключением прямых, параллельных оси ординат).

Зададимся вопросом, что достаточно знать, чтобы построить прямую? Две точки. Но об этом детском случае позже, сейчас властвуют палочки со стрелочками. У каждой прямой есть вполне определённый наклон, к которому легко «приспособить» вектор .

Вектор, который параллелен прямой, называется направляющим вектором данной прямой . Очевидно, что у любой прямой бесконечно много направляющих векторов, причём все они будут коллинеарны (сонаправлены или нет – не важно).

Направляющий вектор я буду обозначать следующим образом: .

Но одного вектора недостаточно для построения прямой, вектор является свободным и не привязан к какой-либо точке плоскости. Поэтому дополнительно необходимо знать некоторую точку , которая принадлежит прямой.

Как составить уравнение прямой по точке и направляющему вектору?

Если известна некоторая точка , принадлежащая прямой, и направляющий вектор этой прямой, то уравнение данной прямой можно составить по формуле :

Иногда его называют каноническим уравнением прямой .

Что делать, когда одна из координат равна нулю, мы разберёмся в практических примерах ниже. Кстати, заметьте – сразу обе координаты не могут равняться нулю, так как нулевой вектор не задаёт конкретного направления.

Пример 3

Составить уравнение прямой по точке и направляющему вектору

Решение : Уравнение прямой составим по формуле . В данном случае:

С помощью свойств пропорции избавляемся от дробей:

И приводим уравнение к общему виду:

Ответ :

Чертежа в таких примерах, как правило, делать не нужно, но понимания ради:

На чертеже мы видим исходную точку , исходный направляющий вектор (его можно отложить от любой точки плоскости) и построенную прямую . Кстати, во многих случаях построение прямой удобнее всего осуществлять как раз с помощью уравнения с угловым коэффициентом. Наше уравнение легко преобразовать к виду и без проблем подобрать ещё одну точку для построения прямой.

Как отмечалось в начале параграфа, у прямой бесконечно много направляющих векторов, и все они коллинеарны. Для примера я нарисовал три таких вектора: . Какой бы направляющий вектор мы не выбрали, в результате всегда получится одно и то же уравнение прямой .

Составим уравнение прямой по точке и направляющему вектору :

Разруливаем пропорцию:

Делим обе части на –2 и получаем знакомое уравнение:

Желающие могут аналогичным образом протестировать векторы или любой другой коллинеарный вектор.

Теперь решим обратную задачу:

Как найти направляющий вектор по общему уравнению прямой?

Очень просто:

Если прямая задана общим уравнением в прямоугольной системе координат, то вектор является направляющим вектором данной прямой.

Примеры нахождения направляющих векторов прямых:

Утверждение позволяет найти лишь один направляющий вектор из бесчисленного множества, но нам больше и не нужно. Хотя в ряде случаев координаты направляющих векторов целесообразно сократить:

Так, уравнение задаёт прямую, которая параллельна оси и координаты полученного направляющего вектора удобно разделить на –2, получая в точности базисный вектор в качестве направляющего вектора. Логично.

Аналогично, уравнение задаёт прямую, параллельную оси , и, разделив координаты вектора на 5, получаем в качестве направляющего вектора орт .

Теперь выполним проверку Примера 3 . Пример уехал вверх, поэтому напоминаю, что в нём мы составили уравнение прямой по точке и направляющему вектору

Во-первых , по уравнению прямой восстанавливаем её направляющий вектор: – всё нормально, получили исходный вектор (в ряде случаев может получиться коллинеарный исходному вектор, и это обычно несложно заметить по пропорциональности соответствующих координат).

Во-вторых , координаты точки должны удовлетворять уравнению . Подставляем их в уравнение:

Получено верное равенство, чему мы очень рады.

Вывод : задание выполнено правильно.

Пример 4

Составить уравнение прямой по точке и направляющему вектору

Это пример для самостоятельного решения. Решение и ответ в конце урока. Крайне желательно сделать проверку по только что рассмотренному алгоритму. Старайтесь всегда (если это возможно) выполнять проверку на черновике. Глупо допускать ошибки там, где их 100%-но можно избежать.

В том случае, если одна из координат направляющего вектора нулевая, поступают очень просто:

Пример 5

Решение : Формула не годится, так как знаменатель правой части равен нулю. Выход есть! Используя свойства пропорции, перепишем формулу в виде , и дальнейшее покатилось по глубокой колее:

Ответ :

Проверка :

1) Восстановим направляющий вектор прямой :
– полученный вектор коллинеарен исходному направляющему вектору.

2) Подставим координаты точки в уравнение :

Получено верное равенство

Вывод : задание выполнено правильно

Возникает вопрос, зачем маяться с формулой , если существует универсальная версия , которая сработает в любом случае? Причин две. Во-первых, формула в виде дроби гораздо лучше запоминается . А во-вторых, недостаток универсальной формулы состоит в том, что заметно повышается риск запутаться при подстановке координат.

Пример 6

Составить уравнение прямой по точке и направляющему вектору .

Это пример для самостоятельного решения.

Вернёмся к вездесущим двум точкам:

Как составить уравнение прямой по двум точкам?

Если известны две точки , то уравнение прямой, проходящей через данные точки, можно составить по формуле:

На самом деле это разновидность формулы и вот почему: если известны две точки , то вектор будет направляющим вектором данной прямой. На уроке Векторы для чайников мы рассматривали простейшую задачу – как найти координаты вектора по двум точкам. Согласно данной задаче, координаты направляющего вектора:

Примечание : точки можно «поменять ролями» и использовать формулу . Такое решение будет равноценным.

Пример 7

Составить уравнение прямой по двум точкам .

Решение : Используем формулу:

Причёсываем знаменатели:

И перетасовываем колоду:

Именно сейчас удобно избавиться от дробных чисел. В данном случае нужно умножить обе части на 6:

Раскрываем скобки и доводим уравнение до ума:

Ответ :

Проверка очевидна – координаты исходных точек должны удовлетворять полученному уравнению:

1) Подставим координаты точки :

Верное равенство.

2) Подставим координаты точки :

Верное равенство.

Вывод : уравнение прямой составлено правильно.

Если хотя бы одна из точек не удовлетворяет уравнению, ищите ошибку.

Стоит отметить, что графическая проверка в данном случае затруднительна, поскольку построить прямую и посмотреть, принадлежат ли ей точки , не так-то просто.

Отмечу ещё пару технических моментов решения. Возможно, в данной задаче выгоднее воспользоваться зеркальной формулой и, по тем же точкам составить уравнение:

Таки дробей поменьше. Если хотите, можете довести решение до конца, в результате должно получиться то же самое уравнение.

Второй момент состоит в том, чтобы посмотреть на итоговый ответ и прикинуть, нельзя ли его ещё упростить? Например, если получилось уравнение , то здесь целесообразно сократить на двойку: – уравнение будет задавать ту же самую прямую. Впрочем, это уже тема разговора о взаимном расположении прямых .

Получив ответ в Примере 7, я на всякий случай, проверил, не делятся ли ВСЕ коэффициенты уравнения на 2, 3 или 7. Хотя, чаще всего подобные сокращения осуществляются ещё по ходу решения.

Пример 8

Составить уравнение прямой, проходящей через точки .

Это пример для самостоятельного решения, который как раз позволит лучше понять и отработать технику вычислений.

Аналогично предыдущему параграфу: если в формуле один из знаменателей (координата направляющего вектора) обращается в ноль, то переписываем её в виде . И снова заметьте, как неуклюже и запутанно она стала выглядеть. Не вижу особого смысла приводить практические примеры, поскольку такую задачу мы уже фактически прорешали (см. № 5, 6).

Вектор нормали прямой (нормальный вектор)

Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), причём все векторы нормали прямой будут коллинеарными (сонаправленными или нет – без разницы).

Разборки с ними будут даже проще, чем с направляющими векторами:

Если прямая задана общим уравнением в прямоугольной системе координат, то вектор является вектором нормали данной прямой.

Если координаты направляющего вектора приходится аккуратно «вытаскивать» из уравнения, то координаты вектора нормали достаточно просто «снять».

Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения :

Приведу примеры с теми же уравнениями, что и для направляющего вектора:

Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Если известен вектор нормали, то однозначно определено и направление самой прямой – это «жёсткая конструкция» с углом в 90 градусов.

Как составить уравнение прямой по точке и вектору нормали?

Если известна некоторая точка , принадлежащая прямой, и вектор нормали этой прямой, то уравнение данной прямой выражается формулой :

Тут всё обошлось без дробей и прочих нежданчиков. Такой вот у нас нормальный вектор. Любите его. И уважайте =)

Пример 9

Составить уравнение прямой по точке и вектору нормали . Найти направляющий вектор прямой.

Решение : Используем формулу:

Общее уравнение прямой получено, выполним проверку:

1) «Снимаем» координаты вектора нормали с уравнения : – да, действительно, получен исходный вектор из условия (либо должен получиться коллинеарный исходному вектор).

2) Проверим, удовлетворяет ли точка уравнению :

Верное равенство.

После того, как мы убедились в том, что уравнение составлено правильно, выполним вторую, более лёгкую часть задания. Вытаскиваем направляющий вектор прямой:

Ответ :

На чертеже ситуация выглядит следующим образом:

В целях тренировки аналогичная задача для самостоятельного решения:

Пример 10

Составить уравнение прямой по точке и нормальному вектору . Найти направляющий вектор прямой.

Заключительный раздел урока будет посвящен менее распространённым, но тоже важным видам уравнений прямой на плоскости

Уравнение прямой в отрезках.
Уравнение прямой в параметрической форме

Уравнение прямой в отрезках имеет вид , где – ненулевые константы. Некоторые типы уравнений нельзя представить в таком виде, например, прямую пропорциональность (так как свободный член равен нулю и единицу в правой части никак не получить).

Это, образно говоря, «технический» тип уравнения. Обыденная задача состоит в том, чтобы общее уравнение прямой представить в виде уравнения прямой в отрезках . Чем оно удобно? Уравнение прямой в отрезках позволяет быстронайти точки пересечения прямой с координатными осями, что бывает очень важным в некоторых задачах высшей математики.

Найдём точку пересечения прямой с осью . Обнуляем «игрек», и уравнение принимает вид . Нужная точка получается автоматически: .

Аналогично с осью – точка, в которой прямая пересекает ось ординат.

Каноническими уравнениями прямой в пространстве называются уравнения, определяющие прямую, проходящую через заданную точку коллинеарно направляющему вектору.

Пусть дана точка и направляющий вектор . Произвольная точка лежит на прямой l только в том случае, если векторы и коллинеарны, т. е. для них выполняется условие:

.

Приведённые выше уравнения и есть канонические уравнения прямой.

Числа m , n и p являются проекциями направляющего вектора на координатные оси. Так как вектор ненулевой, то все числа m , n и p не могут одновременно равняться нулю. Но одно или два из них могут оказаться равными нулю. В аналитической геометрии допускается, например, такая запись:

,

которая означает, что проекции вектора на оси Oy и Oz равны нулю. Поэтому и вектор , и прямая, заданная каноническими уравнениями, перпендикулярны осям Oy и Oz , т. е. плоскости yOz .

Пример 1. Составить уравнения прямой в пространстве, перпендикулярной плоскости и проходящей через точку пересечения этой плоскости с осью Oz .

Решение. Найдём точку пересечения данной плоскости с осью Oz . Так как любая точка, лежащая на оси Oz , имеет координаты , то, полагая в заданном уравнении плоскости x = y = 0 , получим 4z — 8 = 0 или z = 2 . Следовательно, точка пересечения данной плоскости с осью Oz имеет координаты (0; 0; 2) . Поскольку искомая прямая перпендикулярна плоскости, она параллельна вектору её нормали . Поэтому направляющим вектором прямой может служить вектор нормали заданной плоскости.

Теперь запишем искомые уравнения прямой, проходящей через точку A = (0; 0; 2) в направлении вектора :

Уравнения прямой, проходящей через две данные точки

Прямая может быть задана двумя лежащими на ней точками и В этом случае направляющим вектором прямой может служить вектор . Тогда канонические уравнения прямой примут вид

.

Приведённые выше уравнения и определяют прямую, проходящую через две заданные точки.

Пример 2. Составить уравнение прямой в пространстве, проходящей через точки и .

Решение. Запишем искомые уравнения прямой в виде, приведённом выше в теоретической справке:

.

Так как , то искомая прямая перпендикулярна оси Oy .

Прямая как линия пересечения плоскостей

Прямая в пространстве может быть определена как линия пересечения двух непараллельных плоскостей и , т. е. как множество точек, удовлетворяющих системе двух линейных уравнений

Уравнения системы называются также общими уравнениями прямой в пространстве.

Пример 3. Составить канонические уравнения прямой в пространстве, заданной общими уравнениями

Решение. Чтобы написать канонические уравнения прямой или, что то же самое, уравнения прямой, проходящей через две данные точки, нужно найти координаты каких-либо двух точек прямой. Ими могут служить точки пересечения прямой с какими-нибудь двумя координатными плоскостями, например yOz и xOz .

Точка пересечения прямой с плоскостью yOz имеет абсциссу x = 0 . Поэтому, полагая в данной системе уравнений x = 0 , получим систему с двумя переменными:

Её решение y = 2 , z = 6 вместе с x = 0 определяет точку A (0; 2; 6) искомой прямой. Полагая затем в заданной системе уравнений y = 0 , получим систему

Её решение x = -2 , z = 0 вместе с y = 0 определяет точку B (-2; 0; 0) пересечения прямой с плоскостью xOz .

Теперь запишем уравнения прямой, проходящей через точки A (0; 2; 6) и B (-2; 0; 0) :

,

или после деления знаменателей на -2:

,

В данной статье мы рассмотрим общее уравнение прямой на плоскости. Приведем примеры построения общего уравнения прямой, если известны две точки этой прямой или если известна одна точка и нормальный вектор этой прямой. Представим методы преобразования уравнения в общем виде в канонический и параметрический виды.

Пусть задана произвольная декартова прямоугольная система координат Oxy . Рассмотрим уравнение первой степени или линейное уравнение:

где A, B, C − некоторые постоянные, причем хотя бы один из элементов A и B отлично от нуля.

Мы покажем, что линейное уравнение на плоскости определяет прямую. Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат на плоскости каждая прямая линия может быть задана линейным уравнением. Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат на плоскости определяет прямую линию.

Доказательство. Достаточно доказать, что прямая L определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть на плоскости задана прямая L . Выберем систему координат так, чтобы ось Ox совпадал с прямой L , а ось Oy был перпендикулярной к ней. Тогда уравнение прямой L примет следующий вид:

Все точки на прямой L будут удовлетворять линейному уравнению (2), а все точки вне этой прямой, не будут удовлетворять уравнению (2). Первая часть теоремы доказана.

Пусть задана декартова прямоугольная система координат и пусть задана линейное уравнение (1), где хотя бы один из элементов A и B отличен от нуля. Найдем геометрическое место точек, координаты которых удовлетворяют уравнению (1). Так как хотя бы один из коэффициентов A и B отличен от нуля, то уравнение (1) имеет хотя бы одно решение M (x 0 ,y 0). (Например, при A ≠0, точка M 0 (−C/A , 0) принадлежит данному геометрическому месту точек). Подставляя эти координаты в (1) получим тождество

Вычтем из (1) тождество (3):

A (x −x 0)+B (y −y 0)=0.

(4)

Очевидно, что уравнение (4) эквивалентно уравнению (1). Поэтому достаточно доказать, что (4) определяет некоторую прямую.

Поскольку мы рассматриваем декартову прямоугольную систему координат, то из равенства (4) следует, что вектор с компонентами {x−x 0 , y−y 0 } ортогонален вектору n с координатами {A,B }.

Рассмотрим некоторую прямую L , проходящую через точку M 0 (x 0 , y 0) и перпендикулярной вектору n (Рис.1). Пусть точка M (x ,y) принадлежит прямой L . Тогда вектор с координатами x−x 0 , y−y 0 перпендикулярен n и уравнение (4) удовлетворено (скалярное произведение векторов n и равно нулю). Обратно, если точка M (x ,y) не лежит на прямой L , то вектор с координатами x−x 0 , y−y 0 не ортогонален вектору n и уравнение (4) не удовлетворено. Теорема доказана.

Доказательство. Так как прямые (5) и (6) определяют одну и ту же прямую, то нормальные векторы n 1 ={A 1 ,B 1 } и n 2 ={A 2 ,B 2 } коллинеарны. Так как векторы n 1 ≠0, n 2 ≠0, то существует такое число λ , что n 2 =n 1 λ . Отсюда имеем: A 2 =A 1 λ , B 2 =B 1 λ . Докажем, что C 2 =C 1 λ . Очевидно, что совпадающие прямые имеют общую точку M 0 (x 0 , y 0). Умножая уравнение (5) на λ и вычитая из него уравнение (6) получим:

Так как выполнены первые два равенства из выражений (7), то C 1 λ −C 2 =0. Т.е. C 2 =C 1 λ . Замечание доказано.

Заметим, что уравнение (4) определяет уравнение прямой, проходящей через точку M 0 (x 0 , y 0) и имеющий нормальный вектор n ={A,B }. Поэтому, если известен нормальный вектор прямой и точка, принадлежащая этой прямой, то можно построить общее уравнение прямой с помощью уравнения (4).

Пример 1. Прямая проходит через точку M =(4,−1) и имеет нормальный вектор n ={3, 5}. Построить общее уравнение прямой.

Решение. Имеем: x 0 =4, y 0 =−1, A =3, B =5. Для построения общего уравнения прямой, подставим эти значения в уравнение (4):

Ответ:

Вектор параллелен прямой L и, следовательно, перпердикулярен нормальному вектору прямой L . Построим нормальный вектор прямой L , учитывая, что скалярное произведение векторов n и равно нулю. Можем записать, например, n ={1,−3}.

Для построения общего уравнения прямой воспользуемся формулой (4). Подставим в (4) координаты точки M 1 (можем взять также координаты точки M 2) и нормального вектора n :

Подставляя координаты точек M 1 и M 2 в (9) можем убедится, что прямая заданная уравнением (9) проходит через эти точки.

Ответ:

Вычтем (10) из (1):

Мы получили каноническое уравнение прямой. Вектор q ={−B , A } является направляющим вектором прямой (12).

Обратное преобразование смотрите .

Пример 3. Прямая на плоскости представлена следующим общим уравнением:

Переместим на право вторую слагаемую и разделим обе части уравнения на 2·5.

Уравнение прямой | Геометрия | Решенные примеры

Решенные примеры

Карлос начнет посещать занятия в шестом классе со следующей недели.

Он вдруг понял, что у него нет ни блокнота, ни ручки.

Он идет в магазин, чтобы купить их, и понимает, что тетрадь стоит вдвое больше, чем 5 долларов за ручку.

Представьте эту информацию, используя уравнение прямой линии.

Решение

Предположим следующее.

Стоимость ручки = $ \ (x \)

Стоимость блокнота =

$ \ (y \)

Согласно предоставленной информации,

\ (\ следовательно \) Уравнение прямой: \ (y = 2x +5 \).

Посмотрите на график численности населения и года.

Можете ли вы определить численность населения в 2010 году, используя наклон прямой AB?

Решение

Линия AB проходит через \ (A (1985, 92) \) и \ (B (1995, 97) \).

Пусть \ (x_1 = 1985, y_1 = 92, x_2 = 1995 \) и \ (y_2 = 97 \).

Используя уравнение наклона, мы можем вычислить наклон линии AB.

\ [\ begin {align} \ text {Наклон AB} & = \ dfrac {y_2-y_1} {x_2-x_1} \\ & = \ dfrac {1995-1985} {97-92} \\ & = \ dfrac {1} {2} \ end {align} \]

Пусть население в 2010 году будет \ (z \).

Тогда прямая AB должна проходить через \ (C (2010, z) \).

\ [\ begin {align} \ text {Уклон AB} & = \ text {Уклон BC} \\\ dfrac {1} {2} & = \ dfrac {z-97} {2010-1995} \\ \ dfrac {15} {2} & = z-97 \\ z & = 104.5 \ end {align} \]

\ (\ следовательно \) Население в 2010 году составляет 104,5 миллиона человек.

Учитель Джолли попросил ее найти уравнение прямой, проходящей через две точки, как показано на доске.

Можете ли вы ей помочь?

Решение

Получены два балла:

\ [\ begin {выравнивается} (x_1, y_1) & = (1,3) \\ [0,2 см] (x_2, y_2) & = (- 2, 4) \ end {выравнивается} \]

Чтобы использовать форму «точка-наклон», нам сначала нужно найти наклон линии.

Наклон прямой определяется с помощью уравнения наклона.

\ [\ begin {align} m & = \ dfrac {y_2-y_1} {x_2-x_1} \\ [0,2 см] & = \ dfrac {4-3} {- 2-1} \\ [0,2 см] & = \ dfrac {1} {- 3} \\ [0,2 см] & = — \ dfrac {1} {3} \ end {align} \] Уравнение линии находится с использованием формы точечного уклона. \ [\ begin {align} y-y_1 & = m (x-x_1) \\ [0,2 см] y-3 & = — \ dfrac {1} {3} (x-1) \\ [0,2 см] y-3 & = — \ dfrac {1} {3} x + \ dfrac {1} {3} \\ [0,2 см] \ text {Добавление 3} & \ text {с обеих сторон}, \\ [0,2 см] y & = — \ dfrac {1} {3} x + \ dfrac {10} {3} \ end {align} \]

Чтобы выразить это в стандартной форме, сначала умножим обе части на \ (3 \)

\ [3y = -x + 10 \]

Добавление \ (x \) с обеих сторон,

\ [x + 3y = 10 \]

\ (\ следовательно \) Уравнение данной строки в стандартной форме имеет вид \ (x + 3y = 10 \).

Определите уравнение прямой, параллельной оси \ (x \) и проходящей через точку (1, 3).

Решение

Прямая, параллельная оси \ (x \), имеет наклон 0.

Итак, \ (m = 0 \).

Пусть \ (x_1 = 1 \) и \ (y_1 = 3 \).

По форме точечного уклона уравнение прямой имеет вид \ ({y-y_1 = m (x-x_1)} \)

\ [\ begin {align} y-3 & = 0 \ times (x-1) \\ y-3 & = 0 \\ y & = 3 \ end {align} \]

\ (\ следовательно \) Уравнение линии \ (y = 3 \).

Аналитический центр

1. Какой из следующих графиков может представлять уравнение \ ({y + 2 = -2 (x-1)} \)?

Интерактивные вопросы

Вот несколько занятий для вас.

Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

---

Подведем итоги

Мы надеемся, что вам понравилось изучать уравнение прямой с примерами и практическими вопросами.Теперь вы легко сможете решать задачи на концентрических кругах.

О компании Cuemath

В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы, в Cuemath, верим.

---

Часто задаваемые вопросы по уравнению прямой

1. Что такое прямая линия в математике?

Прямая линия — это фигура, образованная, когда две точки \ (A (x_1, y_1) \) и \ (B (x_2, y_2) \) соединены с минимальным расстоянием между ними, а оба конца вытянуты в бесконечность.

2. Кто придумал уравнение прямой?

Рене Декарт изобрел уравнение прямой.

3. Какая формула уравнения прямой?

Обычно мы представляем прямую линию по формуле: \ (ax + by = c \), где \ (x \) и \ (y \) — переменные.

4. Что такое формула пересечения оси Y?

Если прямая пересекает ось \ (y \) в точке \ ((0, c) \), то \ (c \) является точкой пересечения \ (y \).

5. Как найти наклон и точку пересечения по оси Y уравнения?

Наклон \ (m \) линии, соединяющей две точки \ ((x_1, y_1) \) и \ ((x_2, y_2) \), определяется как \ (m = \ dfrac {y_2-y_1} {x_2- x_1} \).

Пересечение \ (y \) прямой \ (ax + by = c \) находится путем замены \ (x \) на 0.

6.Как вы изобразите уравнение угла наклона?

Форма пересечения наклона задается как \ (y = mx + c \). Он нанесен на график путем соединения двух точек, удовлетворяющих уравнению.

7. Что такое пересечение оси y в y = -2x?

Перехватчик \ (y \) в \ (y = -2x \) равен 0.

8. Как написать уравнение для вертикальной и горизонтальной линии?

Уравнение горизонтальной прямой, проходящей через \ ((a, b) \), имеет вид \ (y = b \).

Уравнение вертикальной прямой, проходящей через \ ((a, b) \), имеет вид \ (x = a \).

9. Как найти уравнение прямой, когда даны две точки?

Уравнение прямой, соединяющей две точки \ ((x_1, y_1) \) и \ ((x_2, y_2) \), задается формулой \ ((y-y_1) = \ dfrac {y_2-y_1} {x_2- х_1} (х-х_1) \).

10. Как найти уравнение прямой из пары прямых?

Пара прямых дает нам два уравнения прямых.

Найдите уравнение прямой, зная две точки, через которые она проходит

Быстро! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombinations, Find allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, MassConversion анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные числа, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители с GCF Полиномы, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, РазделениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Методы Правые треугольники, Ветер, рисунок

Графические прямые линии: обзор

Purplemath

В этом обзоре мы начнем с построения прямых линий, а затем перейдем к другим графикам.Единственное существенное различие, на самом деле, заключается в том, сколько точек вам нужно построить, чтобы построить хороший график. Но это увеличенное количество точек будет зависеть от «интересных» проблем, связанных с различными типами графиков.

Прежде чем мы начнем, позвольте мне сказать следующее: вы должны сделать аккуратных графика , что означает, что вы должны использовать линейку. Если у вас нет линейки, возьмите ее. Сейчас. Дешевая пластиковая шестидюймовая машина очень поможет, и вы можете получить от своего инструктора большие «баллы», используя ее.

MathHelp.com

И нет, использование миллиметровой бумаги , а не не освобождает вас от использования линейки.

---

Построение прямых графиков

Предположим, нам дано уравнение y = 3 x + 2 для построения графика. Поскольку переменные в этом уравнении имеют простую форму — просто x , в отличие, скажем, от x ² или | x | — это уравнение отображается в виде простой прямой линии. Чтобы начать построение этого уравнения, нам нужно нарисовать так называемую «Т-диаграмму».

Т-диаграмма выглядит так:

Затем мы выберем значения для x , подставим их в уравнение и решим это уравнение для соответствующих значений y .

Мы должны быть осторожны, чтобы не забыть выбрать хотя бы одно или два отрицательных значения для x ; использование только положительных чисел может впоследствии ввести в заблуждение, поэтому лучше не создавать эту дурную привычку сейчас. Также мы должны попытаться нанести минимум три точки. Так намного безопаснее: если мы ошибемся в одном пункте, мы узнаем, потому что эта точка не будет совпадать с другими.

Вот как выглядит T-диаграмма с некоторыми подключенными значениями:

Некоторым людям нравится добавлять третий столбец, в котором они записывают фактические точки сюжета, который выглядит следующим образом:

(Если вы используете графический калькулятор, вы, вероятно, можете попросить калькулятор заполнить Т-образную диаграмму за вас.Найдите в своем руководстве утилиту «ТАБЛИЦА» или просто прочтите главу о построении графиков. Как только вы научитесь использовать эту утилиту, вы можете просто скопировать свою Т-диаграмму с экрана калькулятора.)

Теперь, когда у нас есть точки на графике, мы рисуем НАСТОЯЩИЙ аккуратный набор осей, используя нашу линейку. Это означает рисование ЧЕТНОЙ, СОГЛАСОВАННОЙ шкалы на осях (то есть рисование равномерно распределенных отметок для чисел на осях) и, возможно, даже маркировку осей их переменными. Мы рисуем стрелки на концах осей, где числа становятся больше (это то, что обозначают стрелки, вы знаете!), И рисуем стрелки НИГДЕ ЕЩЕ.

Для сравнения:

Это хороший график:

Это плохой график:

(Кстати, вы заметили, что мои отметки 5 и 10 на моих осях выше длиннее, чем у других? Это не то, что мы «должны» делать, но из опыта я узнал, что это может быть очень полезно, когда Я рассчитываю, чтобы изложить свои соображения.)

Теперь наносим наши точки:

Точки совпадают правильно, поэтому мы знаем, что мы правильно выполнили вычисления и построили график. Теперь мы можем поставить линейку напротив точек и провести линию:

График представляет собой красивую прямую линию, идущую вверх (чего и следовало ожидать, поскольку уравнение имеет положительное значение наклона м = 3) и пересекает ось y на значении пересечения y б = 2.

И помните: на концах графических линий нет стрелок. Да, я знаю, что многие американские учебники для средних и старших классов рисуют вещи именно так. Остальной мир (и остальная математика) рисует свои линии, как показано выше. Независимо от вашего нынешнего возраста, вы можете рисовать «взрослые» графики уже сейчас.

---

Партнер

---

Иногда они дают нам уравнение типа 2 y — 4 x = 3.Первое, что я всегда хочу сделать, это решить уравнение для « y =». (Среди прочего, форма « y =» — единственный способ, которым мой графический калькулятор может принять уравнение.) Процесс решения работает следующим образом:

2 y -4 x = 3

2 y = 4 x + 3

y = 2 x + 1,5

Тогда мы можем построить график как обычно.

Кстати, часто неплохо использовать значения x , которые немного разбросаны. Если нанесенные точки расположены слишком близко друг к другу, мы можем оказаться не совсем уверены в угле линии, которую строим. Для строки выше я, вероятно, выбрал бы такие точки, как x = –4, x = –2, x = 0 и x = 2.

---

Иногда мы хотим уточнить значения, которые мы выбираем для x .Например, предположим, что нам нужно построить график y = (2/3) x + 4. Мы можем значительно облегчить нашу жизнь, выбрав значения x , кратные 3. Поступая таким образом, мы будем иметь возможность вычеркнуть 3 в знаменателе и, таким образом, избежать дробей в точках нашего графика. Я имею в виду, что выбор x = 5 сам по себе не является неправильным, но выбор x = 3 даст нам гораздо более приятное значение y для точки, нанесенной на график для этого уравнения. Если бы знаменатель дроби был, скажем, 7, тогда было бы полезно выбрать значения x , кратные 7.И так далее.

(Если вы хотите более подробно изучить построение линейных уравнений в виде графиков, см. «Построение графиков линейных уравнений».)

---

URL: https://www.purplemath.com/modules/graphing.htm

Постройте прямую линию (y = mx + c) в Python / Matplotlib

Уравнение наклона $ y = mx + c $ в том виде, в каком мы его знаем сегодня, приписывают Рене Декарту (1596–1650 гг. Н. Э.), Отцу аналитической геометрии.

Портрет Рене Декарта (1596-1650) работы Франса Хальса. Общественное достояние

Уравнение $ y = mx + c $ графически представляет прямую линию, где $ m $ — ее наклон / градиент, а $ c $ — ее точка пересечения. В этом руководстве вы узнаете, как построить график $ y = mx + b $ в Python с помощью Matplotlib.

Рассмотрим прямую $ y = 2x + 1 $, уклон / уклон которой составляет $ 2 $, а пересечение — $ 1 $. Прежде чем строить график, нам нужно импортировать NumPy и использовать его функцию linspace () для создания равномерно распределенных точек в заданном интервале.В приведенном ниже примере linspace (-5,5,100) возвращает 100 равномерно распределенных точек в интервале [-5,5], и этот массив точек используется как первый аргумент функции plot () , за которым следует сама функция, за которой следует сокращенный стиль линий (который здесь '-' ) и цвет ( 'r' , что означает красный). Последний аргумент — это метка легенды.

импортировать matplotlib.pyplot как plt
импортировать numpy как np
х = нп.linspace (-5,5,100)
у = 2 * х + 1
plt.plot (x, y, '-r', label = 'y = 2x + 1')
plt.title ('График y = 2x + 1')
plt.xlabel ('x', цвет = '# 1C2833')
plt.ylabel ('y', color = '# 1C2833')
plt.legend (loc = 'верхний левый')
plt.grid ()
plt.show ()

Помимо - , в Matplotlib доступно множество других стилей линий.

То же самое и с цветом. Ниже вы можете ознакомиться с оставшимися основными встроенными цветами.

• b : синий
• г : зеленый
• r : красный
• c : голубой
• м : пурпурный
• и : желтый
• к : черный
• w : белый

Когда мы строим линию с наклоном и пересечением, мы обычно / традиционно располагаем оси в середине графика.В приведенном ниже коде мы перемещаем левый и нижний шипы в центр графика, применяя set_position ('center') , в то время как правый и верхний шипы скрыты, установив для них значение none с помощью set_color ('none') . Функция set_ticks_position () устанавливает положение градаций вдоль применяемой оси.

импортировать matplotlib.pyplot как plt
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
топор.шипы ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
ax.spines ['правильно']. set_color ('нет')
ax.spines ['вверху']. set_color ('none')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
plt.plot ()
plt.show ()

Теперь мы рисуем несколько линий на одном графике, располагая оси в центре.

импортировать matplotlib.pyplot как plt
импортировать numpy как np
fig = plt.фигура()
ax = fig.add_subplot (1, 1, 1)
x = np.linspace (-5,5,100)
ax.spines ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
ax.spines ['правильно']. set_color ('нет')
ax.spines ['вверху']. set_color ('none')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
plt.plot (x, 2 * x + 1, '-r', label = 'y = 2x + 1')
plt.plot (x, 2 * x-1, '-. g', label = 'y = 2x-1')
plt.plot (x, 2 * x + 3, ': b', label = 'y = 2x + 3')
plt.plot (x, 2 * x-3, '- m', label = 'y = 2x-3')
plt.легенда (loc = 'верхний левый')
plt.show ()

Калькулятор уклона

По определению, наклон или уклон линии описывает ее крутизну, уклон или уклон. Где м — уклон θ — угол наклона

Если известны 2 точки

Если известны 1 точка и наклон

Уклон, иногда называемый в математике градиентом, — это число, которое измеряет крутизну и направление линии или участка линии, соединяющей две точки, и обычно обозначается м .Как правило, крутизна линии измеряется абсолютным значением ее уклона, м . Чем больше значение, тем круче линия. Учитывая м , можно определить направление линии, которую описывает м , на основе ее знака и значения:

• Линия увеличивается и идет вверх слева направо, когда m> 0
• Линия убывает и идет вниз слева направо, когда m <0
• Линия имеет постоянный наклон и является горизонтальной при m = 0
• Вертикальная линия имеет неопределенный наклон, так как это приведет к дроби с 0 в знаменателе.См. Приведенное ниже уравнение.

Наклон — это, по сути, изменение высоты при изменении горизонтального расстояния, и его часто называют «подъем через пробег». Он находит применение в градиентах в географии, а также в гражданском строительстве, например, в строительстве дорог. В случае дороги «подъем» — это изменение высоты, а «пробег» — это разница в расстоянии между двумя фиксированными точками, если расстояние для измерения недостаточно велико, чтобы кривизна земли была рассматривается как фактор.Математически наклон представлен как:

В приведенном выше уравнении y ₂ — y ₁ = Δy или вертикальное изменение, а x ₂ — x ₁ = Δx или горизонтальное изменение, как показано на представленном графике. Также видно, что Δx и Δy — это отрезки прямых, которые образуют прямоугольный треугольник с гипотенузой d , причем d — это расстояние между точками (x ₁ , y ₁ ) и (x ₂ , y ₂ ) .Поскольку Δx и Δy образуют прямоугольный треугольник, можно вычислить d , используя теорему Пифагора. Обратитесь к калькулятору треугольника для получения более подробной информации о теореме Пифагора, а также о том, как рассчитать угол наклона θ , указанный в калькуляторе выше. Кратко:

d = √ (x ₂ — x ₁ ) ² + (y ₂ — y ₁ ) ²

Приведенное выше уравнение является теоремой Пифагора в своем корне, где гипотенуза d уже решена, а две другие стороны треугольника определяются вычитанием двух значений x и y , заданных двумя точками. .Учитывая две точки, можно найти θ , используя следующее уравнение:

м = тангенс угла (θ)

По точкам (3,4) и (6,8) найдите наклон линии, расстояние между двумя точками и угол наклона:

d = √ (6-3) ² + (8-4) ² = 5

Хотя это выходит за рамки данного калькулятора, помимо его основного линейного использования, концепция наклона важна в дифференциальном исчислении. Для нелинейных функций скорость изменения кривой меняется, а производная функции в данной точке — это скорость изменения функции, представленная наклоном линии, касательной к кривой в этой точке.

1: Использование Excel для графического анализа данных (эксперимент)

Часть 1: Простой линейный график

Сценарий: Определенный эксперимент предназначен для измерения объема 1 моля газообразного гелия при различных температурах, поддерживая постоянное давление газа на уровне 758 торр:

Температура (К)	Объем гелия (л)
203	14.3
243	17,2
283	23,1
323	25,9
363	31,5

1. Запустите программу Microsoft Excel ^© (версия 2016 года, есть на всех компьютерах во всех компьютерных центрах на территории кампуса). Нажмите кнопку «Пуск» (в левом нижнем углу экрана), затем нажмите «Программы», а затем — Microsoft Excel ^© .
2. Введите указанные выше данные в первые два столбца электронной таблицы.

• Зарезервируйте первую строку для меток столбцов.
• Значения x необходимо вводить слева от значений y в электронной таблице. Помните, что независимая переменная (та, которую вы, как экспериментатор, контролируете) перемещается по оси x, а зависимая переменная (измеренные данные) перемещается по оси y.

3. Выделите набор данных (не метки столбцов), которые вы хотите построить (рис. 1).

• Нажмите Вставить> Рекомендуемые диаграммы , а затем Scatter (Рисунок 2).

• Выберите диаграмму разброса, на которой показаны только точки данных без соединительных линий — вариант, обозначенный как Точечная диаграмма с только маркерами (рис. 3).

• Теперь вы должны увидеть диаграмму рассеяния на экране Excel, которая обеспечивает предварительный просмотр вашего графика (рисунок 4).

4. Если все в порядке, пора добавить заголовки и пометить оси вашего графика (рис. 5).

• Сначала щелкните внутри диаграммы.
• Перейдите на вкладку Design и нажмите Добавить Элемент диаграммы> Заголовок диаграммы> Над диаграммой
• Графику следует дать понятный пояснительный заголовок, который начинается со слов «Y против X», за которым следует описание вашей системы.
• Щелкните заголовок оси (выберите заголовок основной горизонтальной оси и заголовок основной вертикальной оси ), чтобы добавить метки к осям x и y.Обратите внимание, что важно маркировать оси как используемыми измерениями, так и используемыми единицами.

• Чтобы изменить заголовки, щелкните текстовое поле для каждого заголовка, выделите текст и введите новый заголовок (рис. 6).

5. Следующим шагом будет добавление линии тренда к нанесенным на график точкам данных. Линия тренда представляет наилучшее линейное соответствие вашим данным. Для этого вам сначала нужно «активировать» график. Сделайте это, щелкнув любую из точек данных.Когда вы это сделаете, все точки данных будут выделены.

• Нажмите кнопку Элементы диаграммы рядом с правым верхним углом диаграммы.
• Отметьте поле Trendline .
• Щелкните Дополнительные параметры . Откроется опция, показанная на Рисунке 7.
• Обратите внимание, что кнопка Linear уже выбрана. Теперь выберите поле Display Equation on Chart и Display R-squared value on Chart .Затем нажмите кнопку Закрыть .

6. Уравнение, которое теперь отображается на вашем графике, является уравнением подогнанной линии тренда. Значение R ² дает меру того, насколько хорошо данные соответствуют уравнению. Чем ближе значение R ² к 1, тем лучше подходит. Как правило, подходят значения R ² 0,95 или выше. Обратите внимание, что программа всегда подгоняет линию тренда к данным, независимо от того, насколько хороши или ужасны данные.Вы должны оценить качество соответствия и соответствие этого типа вашему набору данных.
7. Распечатайте полноразмерную копию подготовленного графика и приложите ее к отчету. Затем запишите в свой отчет следующую информацию:

• уравнение линии тренда, наиболее подходящей для ваших данных
• наклон линии тренда
• пересечение линии тренда по оси y
• , является ли соответствие линии данным хорошим или плохим и почему.

8. Графически отображая пять измеренных значений, устанавливается связь между объемом газа и температурой. График содержит визуальное представление взаимосвязи (график) и математическое выражение взаимосвязи (уравнение). Теперь с его помощью можно делать определенные прогнозы.

Например, предположим, что образец газообразного гелия объемом 1 моль охлаждается до тех пор, пока его объем не составит 10,5 л. Вас попросят определить температуру газа. Обратите внимание, что значение 10.5 L выходит за рамки нанесенных на график данных. Как узнать температуру, если она не находится между известными точками? Есть два способа сделать это.

Метод (1): Экстраполируйте линию тренда и оцените, где находится точка на линии.

• Щелкните вкладку Layout в верхнем меню, затем Trendline > More Trendline Options .
• В разделе с меткой Прогноз введите число в поле с меткой Назад , поскольку мы хотим удлинить линию тренда в обратном направлении по оси x.Чтобы решить, какое число ввести, посмотрите на свой график, чтобы увидеть, как далеко назад по оси x вам нужно пройти, чтобы охватить область, где объем = 10,5 л. После ввода числа нажмите Закрыть и линию на вашем графике теперь должен быть расширен в обратном направлении.
• Теперь используйте свой график, чтобы оценить значение x, представив прямую линию вниз от y = 10,5 L до оси x. Запишите это значение в свой отчет.

Метод (2): Подставьте это значение объема в уравнение линии тренда и решите для неизвестной температуры.Сделайте это и запишите свой ответ в своем отчете. Обратите внимание, что этот метод, как правило, более точен, чем экстраполяция и просмотр графика.

Часть 2: Два набора данных с наложением

Сценарий: В одном эксперименте спектрофотометр используется для измерения светопоглощения нескольких растворов, содержащих разные количества красного красителя. Два набора собранных данных представлены в таблице ниже:

Вы хотели бы увидеть, как эти два набора данных связаны друг с другом.Для этого вам нужно будет разместить оба набора данных как независимые отношения на одном графике. Обратите внимание, что этот процесс работает только при одинаковых значениях осей и величинах.

1. Введите эти новые данные на новой странице (Лист 2) в Excel. Обязательно пометьте столбцы данных A и B. И снова не забудьте ввести значения x слева от значений y.
2. Во-первых, постройте данные A только как график разброса по XY (так же, как вы это делали с данными в Части 1). Подгоните линию тренда к этим данным, используя линейную регрессию, и получите уравнение этой линии.
3. Теперь вам нужно добавить данные B к этому графику.

• Активируйте график, щелкнув одну из точек на графике.
• Щелкните диаграмму правой кнопкой мыши и выберите Выбрать данные . На листе появится поле Select Data Source с исходными данными диаграммы.
• Щелкните вкладку Добавить и введите «Данные B» в поле «Имя серии».
• Щелкните маленький значок под Значения серии X , затем выделите значения оси X данных B.
• Нажмите ввод, затем повторите эту процедуру для значений Y серии , выделив значения оси Y данных B. Для каждого из этих шагов вы должны увидеть дисплей, аналогичный показанному на рисунке 8. Обратите внимание на небольшие отличия. может появиться из-за версии Microsoft Excel ^© , установленной на вашем компьютере.

• Дважды нажмите OK , чтобы вернуться в главное окно Excel.
• На этом этапе вы должны увидеть новые точки данных (помеченные как Series 2), как показано на рисунке 9.Теперь вы можете независимо проанализировать этот набор данных, вставив линию тренда, как раньше.

4. Распечатайте полноразмерную копию подготовленного графика и приложите ее к отчету. Затем запишите в свой отчет следующую информацию:

• уравнение наиболее подходящей линии тренда для данных A,
• уравнение наиболее подходящей линии тренда для данных B,
• Если бы эти линии тренда были экстраполированы, они бы пересеклись. Определите значения x и y для точки пересечения, используя систему уравнений.

Часть 3: Статистический анализ и простые точечные диаграммы

Когда выполняется много независимых измерений для одной переменной, в данных неизбежно присутствует некоторый разброс (шум). Обычно это результат случайных ошибок, над которыми экспериментатор не может повлиять.

Сценарий: Десять разных студентов из двух разных колледжей каждый измеряют концентрацию сульфат-иона в образце водопроводной воды:

Колледж № 1, набор данных	35.9 страниц в минуту	43,2 частей на миллион	33,5 частей на миллион	35,1 частей на миллион	32,8 частей на миллион	37,6 частей на миллион	31,9 частей на миллион	36,6 частей на миллион	35,0 частей на миллион	32,0 частей на миллион
Колледж № 2, набор данных	45,1 частей на миллион	34,2 частей на миллион	36,8 частей на миллион	31.0 частей на миллион	40,7 частей на миллион	29,6 частей на миллион	35,4 частей на миллион	32,5 частей на миллион	43,5 частей на миллион	38,8 частей на миллион

Простой статистический анализ этих наборов данных может включать вычисления средней и медианной концентрации, а также стандартного отклонения. Среднее значение (\ (\ bar {x} \)) — это просто среднее значение, определяемое как сумма (\ (\ Sigma \)) каждого из измерений (\ (x_ {i} \)) в наборе данных. разделенное на количество измерений (\ (N \)):

\ [\ bar {x} = \ frac {\ sum x_ {i}} {N} \ label {6} \]

Медиана (\ (M \)) — это среднее значение численно упорядоченного набора данных, где половина измерений выше медианы, а половина — ниже.Среднее положение измерений \ (N \) можно найти с помощью:

\ [M = \ frac {N + 1} {2} \ label {7} \]

Когда \ (N \) — нечетное число, формула возвращает целое число, которое представляет значение, соответствующее среднему положению в упорядоченном распределении измерений. {2}} {N-1}} \ label {8} \]

Итак, чтобы найти \ (s \), вычтите каждое измерение из среднего, возведите этот результат в квадрат, добавьте его к результатам квадратов разницы друг друга, разделите эту сумму на количество измерений минус один, затем извлеките квадратный корень из этого результат.Чем больше это значение, тем больше разброс данных и ниже точность измерений.

Хотя среднее значение, медиана и стандартное отклонение можно рассчитать вручную, для определения этих значений часто удобнее использовать калькулятор или компьютер. Microsoft Excel ^© особенно хорошо подходит для такого статистического анализа, особенно для больших наборов данных.

1. Введите данные, полученные студентами Колледжа № 1 (только), в один столбец ячеек на новой странице (Лист 4) в Excel.Затем в любой пустой ячейке (обычно рядом с ячейками данных) дайте команду программе выполнить необходимые функции с данными. Например, чтобы вычислить среднее или среднее значение данных, введенных в ячейки от a1 до a10, необходимо:

• щелкните мышью в пустой ячейке
• тип «= средний (a1: a10)»
• и нажмите возврат

Для получения медианы введите «= median (a1: a10)». Чтобы получить стандартное отклонение, введите «= stdev (a1: a10)».

2. Запись в отчете:

• Среднее значение, медиана и стандартное отклонение, рассчитанные в Excel для набора данных College # 1.
• В качестве дополнительного упражнения вычислите вручную стандартное отклонение этого набора данных и сравните его со значением, полученным из программы.

Отклонение выбросов

Все ли измерения в наборе данных Колледжа № 1 одинаково хороши для вас, или есть какие-то значения, которые не соответствуют другим? Если да, то можете ли вы отклонить эти измерения?

Выбросы — это точки данных, которые лежат далеко за пределами диапазона, определенного остальными измерениями, и могут в значительной степени исказить ваши результаты.Если вы определили, что выброс возник из-за очевидной экспериментальной ошибки (например, вы неправильно считали показания прибора или подготовили решение), вы можете без колебаний отклонить точку. Если, однако, ни одна из этих ошибок не очевидна, вы должны проявлять осторожность при принятии решения о сохранении или отклонении точки. Одним из грубых критериев отклонения точки данных является то, находится ли она на больше двух стандартных отклонений от среднего или среднего значения.

3. Используя вышеуказанные критерии, определите, есть ли какие-либо выбросы в наборе данных College # 1.

• Запишите эти выбросы (если есть) в свой отчет.
• Затем, исключая выбросы, повторно вычислите среднее значение, медианное значение и стандартное отклонение этого набора данных (используйте Excel).

Невозможно отклонить точки данных только потому, что вы хотите, чтобы ваши результаты выглядели лучше. Если вы решите отклонить выброс по какой-либо причине, вы всегда должны включать в свой лабораторный отчет документацию, в которой четко указано:

• , что вы отклонили точку
• какой пункт вы отклонили
• почему вы его отклонили

Неспособность раскрыть это может представлять собой научное мошенничество.

Построение точечной диаграммы

В отличие от линейных графиков, созданных до сих пор, график рассеяния просто показывает изменение в измерениях одной переменной в данном наборе данных, то есть обеспечивает визуальное представление «шума» в данных. Данные представлены в виде столбца, и здесь нет зависимости x-y (рисунок 10). Обратите внимание, что наборы данных с большей степенью разброса будут иметь более высокое стандартное отклонение и будут состоять из менее точных измерений, чем наборы данных с небольшой степенью разброса.

Чтобы получить такой график в Excel, все значения x для каждого набора данных должны быть идентичными. Таким образом, пусть данным Колледжа № 1 присвоено x = 1, и пусть x = 2 для всех данных Колледжа № 2:

Измерения студентов колледжа № 1		Измерения студентов колледжа № 2
Колледж 1	[\ (\ ce {SO4 ^ {- 2}} \)] (частей на миллион)	Колледж 2	[\ (\ ce {SO4 ^ {- 2}} \)] (частей на миллион)
1	35.9	2	45,1
1	43,2	2	34,2
1	33.5	2	36,8
1	35,1	2	31,0
1	32.8	2	40,7
1	37,6	2	29,6
1	31.9	2	35,4
1	36,6	2	32,5
1	35.0	2	43,5
1	32,0	2	38,8

4. Введите данные, как показано выше, в первые четыре столбца вашей электронной таблицы.

• Постройте набор данных College # 1 как диаграмму рассеяния XY.
• Теперь добавьте набор данных College # 2 к этому графику, применив те же шаги, которые вы использовали для создания предыдущего графика в разделе «Два набора данных с наложением» (Часть 2).
• Добавьте соответствующие метки оси и заголовок. Вы также можете настроить масштабы оси X и оси Y, чтобы улучшить окончательный вид вашего графика.

5. Распечатайте полноразмерную копию подготовленного графика и прикрепите ее к отчету.Затем запишите в свой отчет следующую информацию:

• Какой набор данных (колледж №1 или колледж №2) показывает наименьший разброс? Чем больше стандартное отклонение? Чем точнее измерения?

Построение линии наилучшего соответствия

Лучшие линии
также можно называть: Линейная регрессия
Линии тренда

Вопросы, которые просят вас нарисовать наиболее подходящую линию или тенденцию в данных, обычно не требуют, чтобы вы «соединяли точки».Вместо этого вопрос просит вас подумать о том, как два набора данных ведут себя по отношению друг к другу. Как правило, мы подгоняем линии к данным, когда хотим использовать их для целей прогнозирования или для определения общей тенденции данных.

Большинство ученых используют компьютерную программу для построения линии, наиболее подходящей для набора данных, но построение ее для себя — хороший способ узнать, как это делается. Поскольку компьютер этого не делает, вы можете обнаружить, что ваша линейка «наиболее подходящих» немного отличается от ваших партнеров по лаборатории.В большинстве случаев это нормально, если вы имитировали тенденцию данных.

Почему (и когда) мне следует использовать наиболее подходящую леску?

Во вводном курсе наук о Земле большинство упражнений, в которых вам предлагается построить наиболее подходящую линию, связаны с желанием уметь распознавать взаимосвязи между переменными на Земле или предсказывать поведение системы (в данном случае системы Земли). Мы хотим знать, существует ли взаимосвязь между количеством азота в воде и интенсивностью цветения водорослей, или мы хотим знать взаимосвязь одного химического компонента породы с другим.В целях прогнозирования мы могли бы предпочесть знать, как часто может произойти землетрясение по конкретному разлому или вероятность очень большого наводнения на данной реке. Все эти приложения используют наиболее подходящие линии на диаграммах рассеяния (графики x-y только с точками данных, без линий).

Если вы столкнулись с вопросом, в котором вас просят провести линию тренда, линейную регрессию или наиболее подходящую линию, вас наверняка попросят провести линию через точки данных на диаграмме рассеяния. Вас также могут попросить приблизить тренд или нарисовать линию, имитирующую данные.Эта страница создана, чтобы помочь вам ответить на любой из этих типов вопросов. Если вы не знаете, как отвечать на вопросы о тенденциях и наиболее подходящих линиях, рассмотрите его и примеры проблем.

Как построить линию наилучшего соответствия?

Линия наилучшего соответствия предназначена для имитации тенденции данных. Во многих случаях линия может не проходить через очень многие точки на графике. Вместо этого идея состоит в том, чтобы получить линию с равным количеством точек с обеих сторон. Большинство людей начинают с анализа данных.

1. Взгляните на данные и сами ответьте на эти вопросы
   • Данные выглядят как линия? или большая капля? Постарайтесь мысленно представить общий тренд данных (даже если это просто капля)
   • Тенденция точек выглядит положительно коррелированной (как будто они поднимаются вправо; щелкните изображение справа) или отрицательно коррелированной (как будто они начинаются высоко около оси x и опускаются по мере приближения к оси y; см. изображение слева)? Ваша линия тренда (когда вы закончите со следующими шагами) должна имитировать эти корреляции.
   • Если вы затуманите глаза, сможете ли вы увидеть толстую линию, которая тянется в том или ином направлении? Это еще один способ визуализировать тенденцию изменения данных.
2. Теперь, когда у вас есть представление об общей тенденции данных, есть два возможных способа построить на глаз наиболее подходящую линию. Вы можете использовать любой из них; оба являются правильными и относительно простыми способами получить довольно точное представление о наиболее подходящей линии. Выберите тот, который вам больше всего подходит. Первый метод заключается в заключении данных в область:
   1. Начните с нанесения всех ваших данных.В этом примере мы будем использовать некоторые геохимические данные с пика Лассен, вулкана в Северной Калифорнии, который последний раз извергался в 1915 году (данные были собраны студентом-исследователем Университета Висконсина Ошкош!). Вот график зависимости оксида натрия (Na2O) от кремнезема (SiO2) в результате извержения пика Лассена в 1915 году. Вы можете загрузить и распечатать этот график (Acrobat (PDF) 171 КБ, 27 августа 2008 г.) для использования в этом упражнении.

      Геохимические данные по дацитам, прорвавшимся с пика Лассен в 1915 году. Данные собраны Рашель Кернен, студентки Висконсинского университета в Ошкоше и представлены на осеннем заседании AGU в 2007 году.

   
   
   2. Нарисуйте фигуру, охватывающую все данные (постарайтесь сделать ее гладкой и относительно ровной).
   3. Нарисуйте линию, разделяющую область, в которой заключены данные, на две области одинакового размера. Другими словами, разделите область пополам линией, идущей от одного края участка к другому.
   4. Поздравляем! Вы только что построили наиболее подходящую линию по данным! Обратите внимание, что линия не обязательно должна проходить через ЛЮБУЮ из точек на графике, важно только, чтобы ваша линия делила пополам (разрезала пополам) область, которая охватывает точки данных.Теперь вы можете использовать линию для прогнозирования поведения. Или вы можете изучить другой метод и попробовать его.
   Обратите внимание, что чем более плотно кластеризованы данные, тем меньше будет область. Мы можем сделать то же самое с данными Al ₂ O ₃ с пика Лассена и увидеть разницу.
   1. Начнем с построения графика зависимости данных Al ₂ O ₃ от SiO ₂ . Вы можете загрузить и распечатать этот график (Acrobat (PDF) 164 КБ, 27 августа 2008 г.), чтобы использовать его при выполнении этого упражнения.

      Геохимические данные по дацитам, прорвавшимся с пика Лассен в 1915 году. Данные собраны Рашель Кернен, студентки Висконсинского университета в Ошкоше и представлены на осеннем собрании AGU в 2007 году.

   
   
   2. Нарисуйте фигуру, охватывающую все данные. Обратите внимание, что площадь меньше, чем на графике Na выше, потому что в этих данных меньше разброс.
   3. Нарисуйте линию, разделяющую область, в которой заключены данные, на две области одинакового размера.Другими словами, разделите область пополам линией, идущей от одного края участка к другому.
   Второй метод включает разделение данных на две равные группы, аппроксимацию центра каждой группы и построение линии между двумя центрами.
   1. Начните с построения всех ваших данных. Для этого упражнения мы будем использовать данные Na2O, указанные выше.

      Геохимические данные по дацитам, прорвавшимся с пика Лассен в 1915 году. Данные собраны Рэйчел Кернен, студенткой Висконсинского университета Ошкош и представлены на осеннем собрании AGU в 2007 году.

   
   
   2. Нарисуйте пунктирную линию, разделяющую данные на две части (четное количество точек по обе стороны от линии)
      В данном случае на графике 21 точка, поэтому, насколько вы можете, начертите линию с примерно 10,5 точками по обе стороны от нее. Есть три точки, которые действительно близки к линии, так что постарайтесь.
   3. Поместите x (или +, или точку) в вашу интерпретацию центра данных по обе стороны от линии.
      Ваши метки x могут быть не в том же месте, что и мои — это нормально, мы все видим вещи немного по-другому. Однако они не должны быть слишком далеко.
   4. Соедините метки x линией, доходящей до краев графика.
   5. Поздравляем! Вы только что построили наиболее подходящую линию по данным! Обратите внимание, что линия не обязательно должна проходить через ЛЮБУЮ из точек на графике, важно только, чтобы ваши метки x находились в центре нанесенных на график данных, а ваша линия соединяла эти метки x.Теперь вы можете использовать линию для прогнозирования поведения. Или вы можете изучить другой метод и попробовать его.
3. Оцените наиболее подходящую вам стропу. Вернитесь к вопросам под номером 1. Ваша линия выглядит так, как вы думали?
   • Вы видите, что на каждой стороне линии примерно одинаковое количество точек данных?
   • И равномерно ли они распределены (то есть убедитесь, что графики с различными значениями x находятся наверху (и внизу) линии, а не сверху на нижнем конце и наиболее низко на верхнем)?
   • Минимизирует ли ваша линия среднее расстояние от нее до каждой точки данных?
   Обратите внимание, что в некоторых случаях наиболее подходящие линии не проходят через и точки на графиках.При построении наиболее подходящей линии нет необходимости соединять какие-либо точки.

Вы также можете загрузить и распечатать отдельный лист для построения наиболее подходящей линии с помощью метода площадей (Acrobat (PDF) 33 КБ, 10 сентября 08) или метода разделения (Acrobat (PDF) 34 КБ, 10 сентября 2008 г.).

Где это используется в науках о Земле?

В науках о Земле есть много примеров, когда ученые используют наиболее подходящую линию. Во вводной части наук о Земле мы используем их для:

• Кривые частоты наводнений
• прогноз землетрясений
• Прогноз падения метеорита
Частота землетрясений
• vs.величина
• изменение климата

Следующие шаги — Некоторые практические задачи

Готова к ПРАКТИКЕ! Если вы думаете, что умеете построить наиболее подходящую линию, нажмите на эту полосу, чтобы попробовать несколько практических задач с отработанными ответами!

Если вы хотите узнать больше о наиболее подходящих линиях, вы можете использовать ссылки ниже, чтобы узнать о них больше

Ссылки и ресурсы

.