Построение плоскости по уравнению онлайн: Онлайн калькулятор. Уравнение плоскости

Уравнение плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Очистить все ячейки?

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

 

Уравнение плоскости, проходящей через три точки

Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы и не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M₁, M₂, M₃ тогда и тольно тогда, когда векторы M₁M₂, M₁M₃ и компланарны. Но векторы M₁M₂, M₁M₃, M₁M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов

M₁M₂, M₁M₃, M₁M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:

Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M₁, M₂, M₃:

Ax+By+Cz+D=0.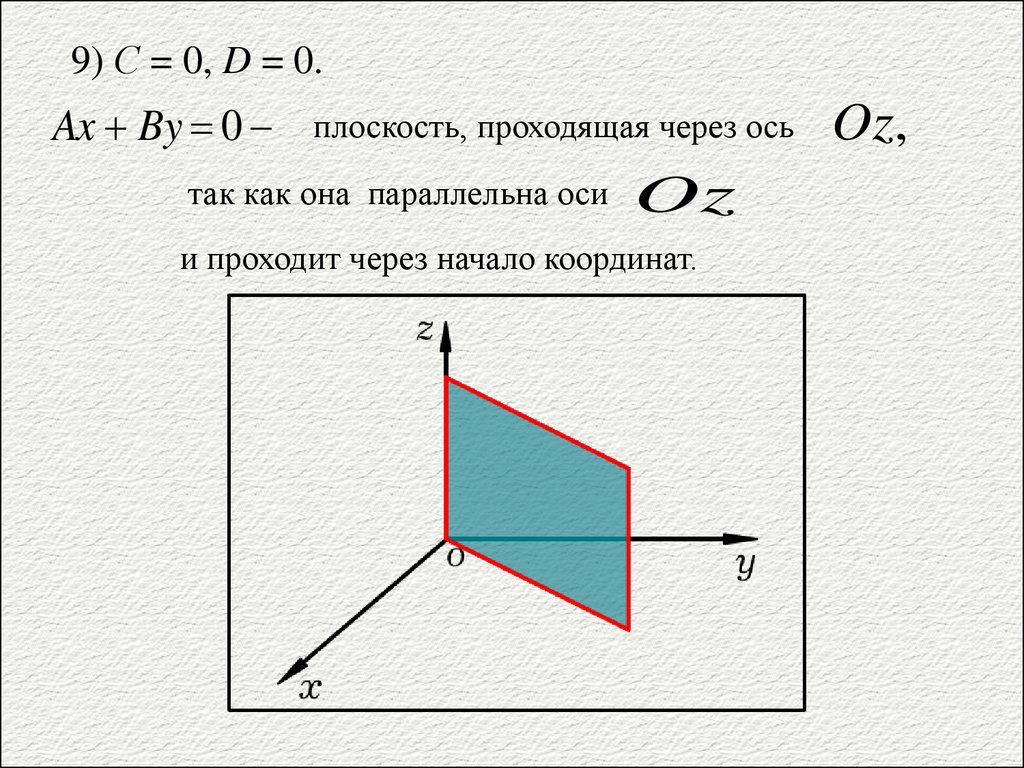

Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).

Решение.

Уравнение плоскости, проходящей через точки A(x₁, y

₁, z₁), B(x₂, y₂, z₂) и C(x₃, y₃, z₃) имеет следующий вид:

Подставляя координаты точек A, B, C в (1), получим:

Упростим:

Разложим определитель по первому столбцу:

Упростим выражение:

или

Ответ:

Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:

Уравнение плоскости, проходящей через одну точку и имеющий нормаль 

n

Пример 2. Построить плоскость, проходящую через точку M₀(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).

Решение.

Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) и имеющей нормаль n(A, B, C) имеет следующий вид:

Подставляя координаты векторов M₀ и n в (2), получим:

или

Уравнение плоскости по координатам трех точек

Любая плоскость может быть проведена через три точки, не принадлежащие одной прямой. Автоматический сервис находит уравнение плоскости, которая проходит через эти три точки.

x-xay-yaz-zaxb-xayb-yazb-zaxc-xayc-yazc-za=0.

Чтобы решить уравнение плоскости по трем точкам онлайн, выполните простые действия:

• впишите значения точек A, B, C в соответствующие пустые поля;
• для получения решения воспользуйтесь кнопкой «Рассчитать».

Zaochnik предоставляет пошаговые вычисления и точный ответ бесплатно.

Как найти уравнение плоскости по координатам трех принадлежащих ей точек с помощью онлайн-калькулятора

Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Пусть нужно найти уравнение плоскости, проходящей через три известные точки. Для этого в онлайн-калькуляторе просто зададим эти точки:

Важно: точки не должны принадлежать одной прямой!

Зададим точки произвольно и нажмем «Рассчитать»:

После этого калькулятор выдаст ответ с подробными выкладками решения:

Материалы, которые помогут вам лучше разобраться в теме:

• Уравнение плоскости, виды уравнения плоскости
• Общее уравнение плоскости : описание, примеры, решение задач
• Нормальное уравнение плоскости: описание, примеры, решение задач
• Уравнение плоскости в отрезках: описание, примеры, решение задач
• Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой
• Прямоугольная система координат на плоскости и в пространстве

Ответ:

Решение

Ответ:

• list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

• Длина отрезка. Расстояние между точками
• Середина отрезка
• Каноническое уравнение прямой проходящей через две точки
• Параметрическое Уравнение прямой проходящей через две точки
• Расстояние от точки до прямой на плоскости
• Уравнение плоскости (координаты вектора нормали и точки)
• Точка пересечения прямых (с угловыми коэффициентами)
• Расстояние от точки до прямой в пространстве
• Расстояние от точки до плоскости
• Расстояние между плоскостями
• Угол между плоскостями
• Угол между прямой и плоскостью

Уравнение плоскости онлайн по 3 точкам

Построить плоскость по уравнению онлайн понадобится:

• студентам университетов при выполнении заданий по математическим дисциплинам;
• школьникам, которые готовятся к поступлению в технические ВУЗы и участникам олимпиад;
• преподавателям, проверяющим работы учащихся и составляющим задачи;
• инженерам для облегчения процесса расчетов.

Цель сервиса – помощь в самостоятельных вычислениях учащимся. Автоматическая формула ускоряет получение ответа на задачу, позволяет избежать ошибок и не требует многократной перепроверки одних и тех же действий. Онлайн-калькулятор позволяет осуществлять подготовку к занятиям с усвоением непонятого ранее материала, запоминать и применять готовые алгоритмы решений.

Если возникла необходимость заказать услуги опытных преподавателей по решению уравнений или заданий на другие темы, обратитесь к консультанту. Мы гарантируем оперативный ответ и выгодное предложение.

Понравился калькулятор? Поделись с друзьями!

Нормальный вектор к плоскости спросил

5 лет, 5 месяцев назад

Изменено 12 месяцев назад

Просмотрено 59 тысяч раз

$\begingroup$

Предположим, у нас есть самолет с уравнением $3x-7z=12$. Как найти его вектор нормали?

Плоскость с уравнением $Ax+By+Cz+D=0$ имеет вектор нормали $\mathbb{n}=(A,B,C)$. Используя это, мы получаем, что плоскость выше имеет вектор нормали $(3,0,-7)$, верно?

Применим другой метод. Возьмем три точки, лежащие на плоскости, а именно $A=(4,0,0), \ B=(0,0,-\frac{12}{7}), \ C=(1,0,\frac {-9}{7})$, затем вектор $AB=(-4,0,-\frac{12}{7})$ и $AC=(-3,0,-\frac{9}{7} )$. Взяв их векторное произведение, мы получим нулевой вектор. Что не так в моей идее?

• векторов

$\endgroup$

5

$\begingroup$

В ответ на первую часть:

Предположим, что две точки $P(x,y,z)$ и $P_0(x_0, y_0, z_0)$ лежат на плоскости с вектором нормали $\mathbf{ п}$. Кроме того, пусть $\mathbf{r}$ обозначает вектор положения $P$, а $\mathbf{r_0}$ обозначает вектор положения $P_0$. 3$, ортогональный к исходным векторам. Теперь у вас есть фиксированные точки $A=(4,0,0),\:B=(0,0,-\frac{12}{7}),\:C=(1,0,\frac{9{7})$ в самолете. Мы можем построить векторы, лежащие в плоскости, определив $\vec{AB}= (B-A), \vec{AC}=(C-A).$

Вычисление компонент за компонентом дает

$$\vec{AB}= (0-4,0-0,-\frac{12}{7}-0)=(-4,0,-\frac{12}{7})$$ $$ \vec{AC}=(1-4,0-0,\frac{9}{7}-0)=(-3,0,\frac{9}{7}).$$ Вычисление перекрестного произведения этих векторов дает результирующий вектор, ортогональный плоскости. Ваша ошибка в том, что вы допустили ошибку при вычитании и получили векторы $v=(-4,0,-\frac{12}{7}), w=(-3,0,-\frac{9{7})$. Обратите внимание, что $\frac{4}{3}w=v$. Итак, поскольку эти векторы коллинеарны, их векторное произведение вырождено и возвращает вектор $0$.

$\endgroup$

2

$\begingroup$

вектор $$\vec{AC}$$ задается как $$\vec{AC}=\left(-3;0;\frac{9}{7}\right)$$ $$A(4;0;0),C\left(1;0;\frac{9}{7}\right)$$, затем $$\vec{AC}=\left(1-4;0- 0;\frac{9}{7}-0\right)$$

$\endgroup$

1

$\begingroup$

К сожалению, два выбранных вами вектора параллельны (все три точки лежат на прямой на плоскости), поэтому их векторное произведение обязательно будет равно нулю; если вы выберете одну из ваших трех точек, чтобы она не лежала на одной линии в плоскости, тогда векторное произведение будет параллельно вашему извлеченному вектору нормали.

$\endgroup$

Дифференциальные уравнения — Фазовая плоскость

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т.е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 5.6: Фазовая плоскость

Прежде чем приступить к непосредственному решению систем дифференциальных уравнений, нам нужно рассмотреть одну тему. Это тема, которая не всегда преподается в классе дифференциальных уравнений, но если вы учитесь на курсе, где она преподается, мы должны осветить ее, чтобы вы были к ней готовы.

Начнем с общей однородной системы,

\[\begin{уравнение}\vec x’ = A\vec x\label{eq:eq1}\end{уравнение}\]

Обратите внимание, что

\[\vec х = \vec 0\]

является решением системы дифференциальных уравнений. Мы хотели бы спросить, приближаются ли другие решения системы к этому решению по мере увеличения \(t\) или они удаляются от этого решения? Мы сделали что-то подобное, когда классифицировали равновесные решения в предыдущем разделе. На самом деле то, что мы здесь делаем, — просто распространение этой идеи на системы дифференциальных уравнений.

Решение \(\vec x = \vec 0\) называется равновесным решением для системы. Как и в случае с одним дифференциальным уравнением, равновесными решениями являются такие решения, для которых

\[A\vec х = \vec 0\]

Предположим, что \(A\) является невырожденной матрицей и, следовательно, имеет только одно решение,

\[\vec х = \vec 0\]

и поэтому у нас будет только одно равновесное решение.

Вернувшись к случаю с одним дифференциальным уравнением, вспомним, что мы начали с выбора значений \(y\) и подстановки их в функцию \(f(y)\) для определения значений \(y’\). Затем мы использовали эти значения для наброска касательных к решению при этом конкретном значении \(y\). Исходя из этого, мы могли бы набросать некоторые решения и использовать эту информацию для классификации равновесных решений.

Здесь мы собираемся сделать что-то подобное, но тоже немного по-другому. Во-первых, мы собираемся ограничиться случаем \(2 \times 2\). Итак, мы будем рассматривать системы вида

\[\begin{array}{*{20}{c}}\begin{align*}{{x’}_1} & = a{x_1} + b{x_2}\\ {{x’}_2} & = c {x_1} + d {x_2} \ end {align *} & {\ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ vec x ‘ = \ left ( {\ begin { array}{*{20}{c}}a&b\\c&d\end{массив}} \right)\vec x}\end{массив}\]

Решения для этой системы будут иметь вид

\[\vec x = \left( {\begin{array}{*{20}{c}}{{x_1}\left(t\right)}\\{{x_2}\left(t\right)} \конец{массив}} \справа)\]

и наше единственное равновесное решение будет

\[\vec x = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\]

В случае одного дифференциального уравнения мы смогли нарисовать решение \(y(t)\) в плоскости y-t и увидеть фактические решения. Однако в данном случае это было бы несколько сложно, поскольку наши решения на самом деле являются векторами. Здесь мы собираемся представить решения системы как точки на плоскости \({x_1}\,{x_2}\) и нанести эти точки на график. Наше равновесное решение будет соответствовать началу координат \({x_1}\,{x_2}\). плоскость, а плоскость \({x_1}\,{x_2}\) называется фазовая плоскость .

Чтобы набросать решение на фазовой плоскости, мы можем выбрать значения \(t\) и подставить их в решение. Это дает нам точку на \({x_1}\,{x_2}\) или фазовой плоскости, которую мы можем построить. Выполнение этого для многих значений \(t\) даст нам набросок того, что решение будет делать на фазовой плоскости. Эскиз частного решения на фазовой плоскости называется траекторией решения. Когда у нас есть набросок траектории решения, мы можем задаться вопросом, будет ли решение приближаться к равновесному решению по мере увеличения \(t\).

Мы хотели бы иметь возможность набрасывать траектории, не имея готовых решений. Есть несколько способов сделать это. Мы рассмотрим один из них здесь, а другой — в следующих нескольких разделах.

Один из способов получить набросок траекторий — сделать что-то похожее на то, что мы делали в первый раз, когда рассматривали равновесные решения. Мы можем выбрать значения \(\vec x\) (обратите внимание, что это будут точки на фазовой плоскости) и вычислить \(A\vec x\). Это даст вектор, который представляет \(\vec x’\) в этом конкретном решении. Как и в случае с одним дифференциальным уравнением, этот вектор будет касаться траектории в этой точке. Мы можем набросать несколько касательных векторов, а затем начертить траектории.

Это довольно трудоемкий способ сделать это, и в целом это не так. Однако это способ получить траектории без выполнения какой-либо работы по решению. Все, что нам нужно, это система дифференциальных уравнений. Давайте быстро рассмотрим пример.

Пример 1 Нарисуйте несколько траекторий системы. \[\begin{array}{*{20}{c}}\begin{align*}{{x’}_1} & = {x_1} + 2{x_2}\\ {{x’}_2} & = 3 {x_1} + 2 {x_2} \ end {align *} & {\ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ vec x ‘ = \ left ( {\ begin {array} {* {20} {c}}1&2\\3&2\end{массив}} \right)\vec x}\end{массив}\]

Показать решение

Итак, нам нужно выбрать несколько точек на фазовой плоскости, подключить их к правой стороне системы. Мы сделаем это для пары точек.

\[\begin{align*}\vec x & = \left( {\begin{array}{*{20}{c}}{ — 1}\\1\end{array}} \right) & \Rightarrow \hspace{0,25 дюйма}\vec x’& = \left( {\begin{array}{*{20}{c}}1&2\\3&2\end{массив}} \right)\left({\begin{ array}{*{20}{c}}{ — 1}\\1\end{массив}} \right) = \left( {\begin{array}{*{20}{c}}1\\{ — 1}\end{массив}} \right)\\ \vec x & = \left( {\begin{array}{*{20}{c}}2\\0\end{array}} \right) & \Rightarrow \hspace{0. 25in}\vec x’ & = \ left ( {\ begin {array} {* {20} {c}} 1 & 2 \\ 3 & 2 \ end {array}} \ right) \ left ( {\ begin {array} {* {20} {c}} 2\\0\end{массив}} \right) = \left( {\begin{array}{*{20}{c}}2\\6\end{массив}} \right)\hspace{0,25 дюйма }\\ \vec x & = \left( {\begin{array}{*{20}{c}}{ — 3}\\{ — 2}\end{array}} \right) & \Rightarrow \hspace{0,25 дюйма }\vec x’ & = \left( {\begin{array}{*{20}{c}}1&2\\3&2\end{array}} \right)\left( {\begin{array}{*{ 20}{c}}{- 3}\\{- 2}\end{массив}} \right) = \left( {\begin{array}{*{20}{c}}{- 7}\\ {- 13}\конец{массив}} \right)\hspace{0,25 дюйма}\end{выравнивание*}\]

Итак, что это нам говорит? Ну в точке \(\left( { — 1,1} \right)\) на фазовой плоскости будет вектор, указывающий в направлении \(\left\langle {1, — 1} \right\rangle \ ). В точке \(\left( {2,0} \right)\) будет вектор, указывающий в направлении \(\left\langle {2,6} \right\rangle \). В точке \(\left( { — 3, — 2} \right)\) будет вектор, указывающий в направлении \(\left\langle { — 7, — 13} \right\rangle \).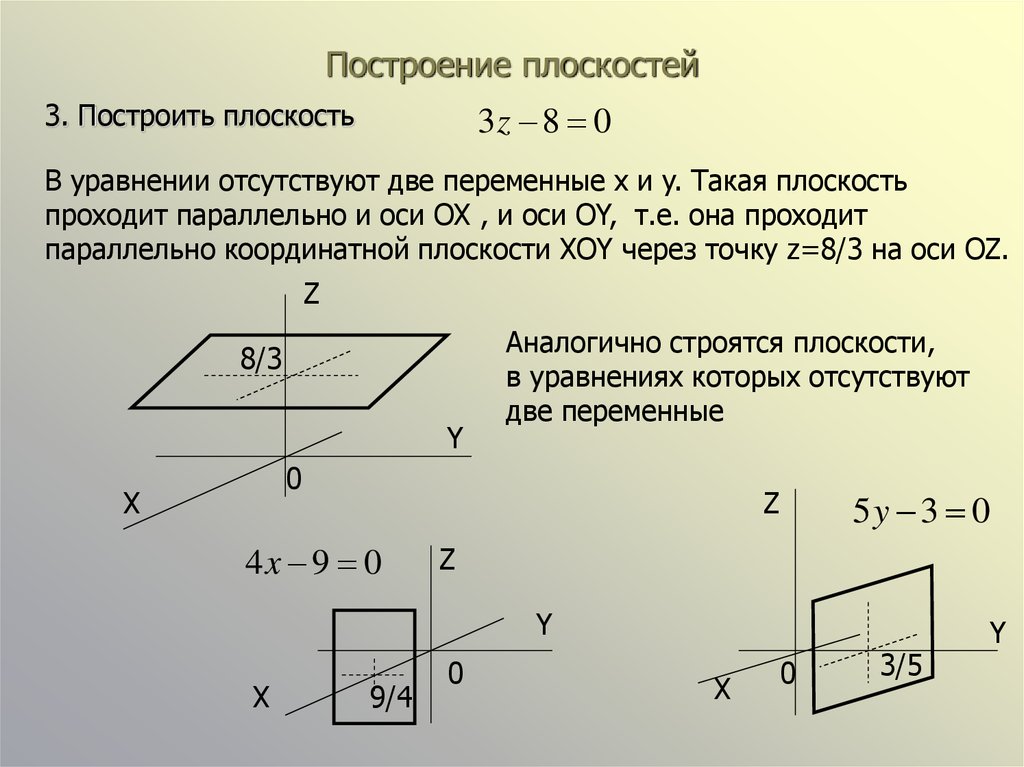

Выполнение этого для большого количества точек на фазовой плоскости даст следующий набросок векторов.

Теперь все, что нам нужно сделать, это набросать несколько траекторий. Для этого все, что нам нужно сделать, это помнить, что векторы на эскизе выше касаются траекторий. Кроме того, направление векторов задает направление траектории по мере увеличения \(t\), поэтому мы можем показать зависимость решения от времени, добавив стрелки к траекториям.

Это дает следующий эскиз.

Этот эскиз называется фазовым портретом . Обычно фазовые портреты включают только траектории решений, а не какие-либо векторы. Все наши фазовые портреты, формирующие эту точку, будут включать только траектории.

В этом случае похоже, что большинство решений сначала будут отклоняться от равновесного решения, затем, когда \(t\) начнет увеличиваться, они будут приближаться к равновесному решению, а затем, в конце концов, снова начнут отдаляться от равновесного решения.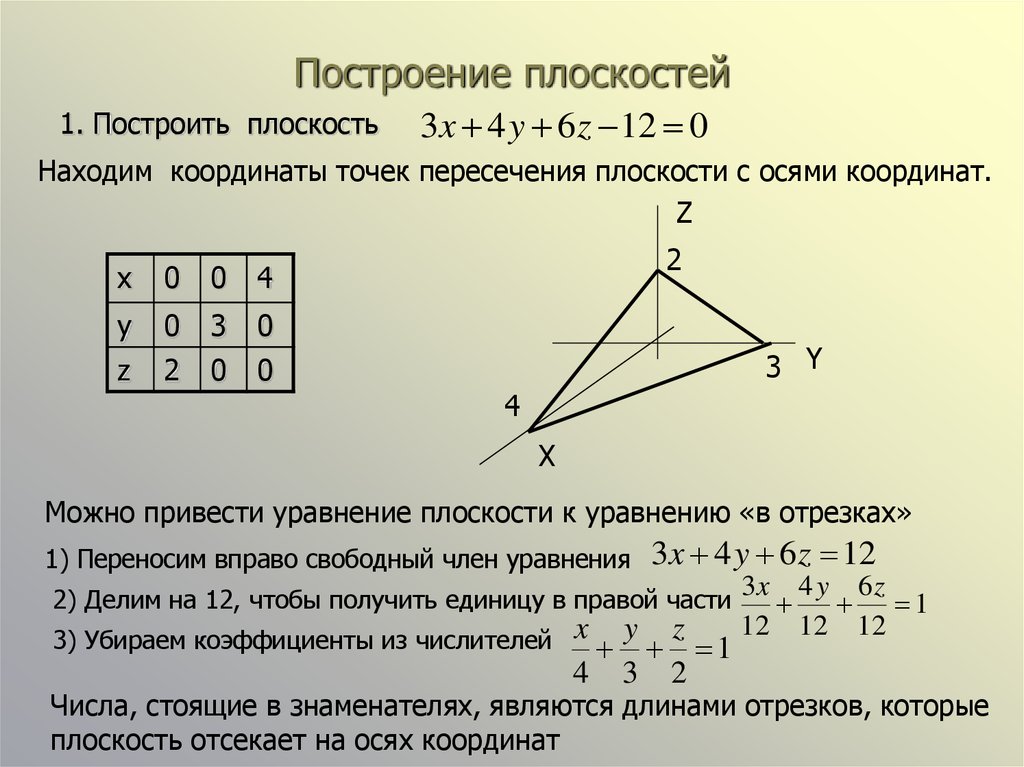

Кажется, есть четыре решения, которые немного отличаются друг от друга. Похоже, что два решения начинаются с (или, по крайней мере, рядом) равновесного решения, а затем сразу же удаляются от него, в то время как два других решения начинаются с равновесного решения, а затем движутся прямо к равновесному решению.

В таких случаях мы называем точку равновесия седловой точкой и называем точку равновесия в этом случае неустойчивой , поскольку все решения, кроме двух, удаляются от нее по мере увеличения \(t\).

Как мы уже отмечали ранее, это обычно не тот способ, которым мы рисуем траектории. Все, что нам действительно нужно для получения траекторий, — это собственные значения и собственные векторы матрицы \(A\). Мы увидим, как это сделать, в следующих парах разделов, когда будем решать системы.

Вот еще несколько фазовых портретов, чтобы вы могли увидеть еще несколько возможных примеров. На самом деле мы создадим несколько из них в течение следующих нескольких разделов.