Построение парабол онлайн: Построение графика функции онлайн

Содержание

Построение графика квадратичной функции — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

ТЕМА
Построение графика
квадратичной
функции
Хасанова Анфиса Абубакировна
учитель математики
МБОУ МО г.Нягань
«СОШ № 4»
Повторим?
Назовите координаты вершин парабол, ось симметрии.
Установите соответствие между графиком функции
формулой и координатами вершины параболы:
9
У
У
9
9
4
4
1
-1

У
4
1
-1
1 2 3
1
1 2 3
Х
-1
1 2 3
Х
1
y ( x 2 )2
2
2 ;0
y 2 ( x 3 )2
0 ; 2
y x2 2
3 ;0
Х
Установите соответствие между графиком функции,
формулой и координатами вершины параболы:
9
У
У
9
9
4
4
1
-1
4
1
-1
1 2 3
1
1 2 3
y ( x 3) 3
2
3 ;1
У
-1
Х
1 2 3
5 ;2
y 2 ( x 3 )2 1
Х
1
2
y ( x 5) 2
2
3 ; 3
Х
Опираясь на ранее изученный материал определить, по
какому признаку можно объединить следующие
рисунки

6.

Падение баскетбольного мяча

7. Параболический фонтан

8. Библиотека с крышей в форме параболы в Норвегии

9. Лучи прожектора

10. Параболическая солнечная электростанция в Калифорнии (США)

11. Вращающийся сосуд с жидкостью

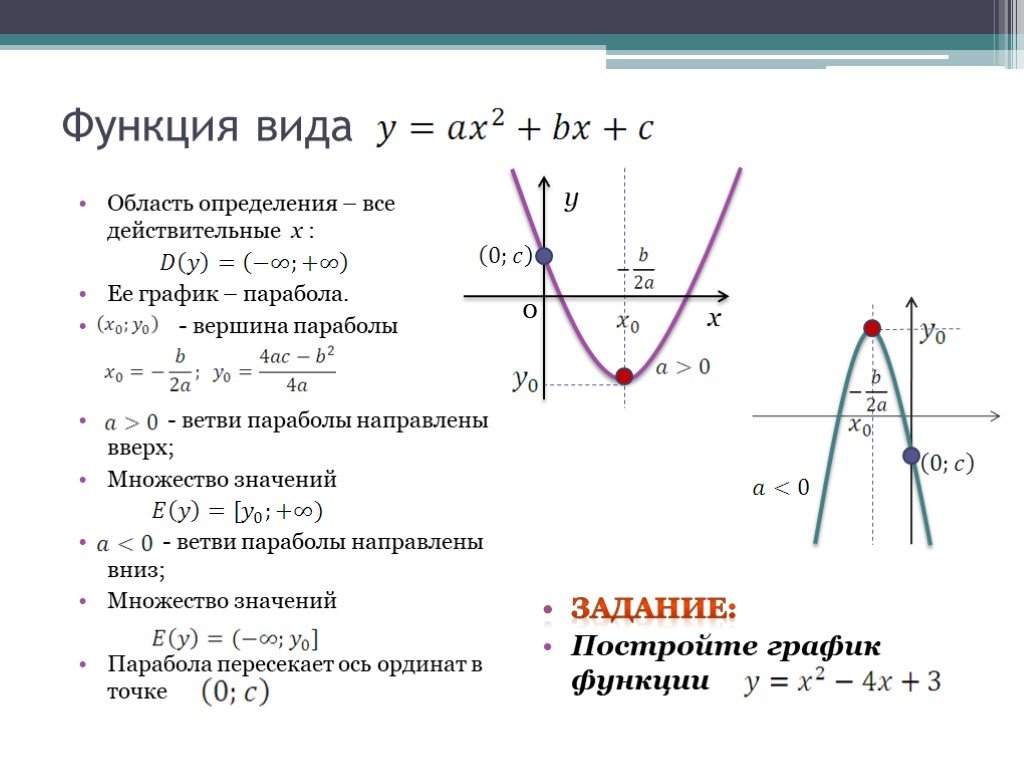
Цели урока:
Сформулировать алгоритм построения
графика квадратичной функции, т. е.
функции вида y = ax2+bx+c.
Выработать умение строить график
квадратичной функции по алгоритму.

13. Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c, где x- независимая переменная, a, b и

с некоторые числа (причём а≠0).
Например:
•у = 5х²+6х+3,
•у = -7х²+8х-2,
•у = 0,8х²+5,
•у = ¾ х²-8х,
•у = -12х²

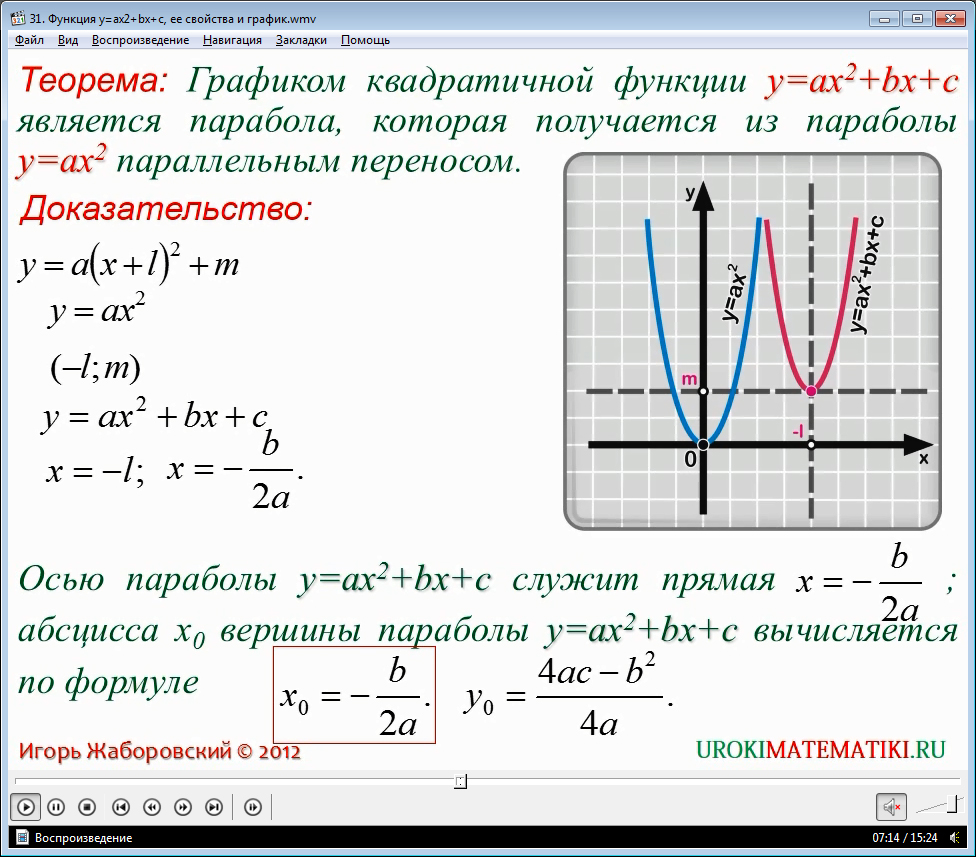
14. Графиком квадратичной функции является парабола, ветви которой направлены вверх (если а>0) или вниз (если а<0).

Графиком квадратичной функции является
парабола, ветви которой направлены
вверх (если а>0) или вниз (если а<0).

Например:
О
х
у
О
х
• у=2х²+4х-1 – графиком
является парабола, ветви
которой направлены вверх
(т.к. а=2, а>0).
• у= -7х²-х+3 – графиком
является парабола, ветви
которой направлены вниз
(т.к. а=-7, а<0).

15. Чтобы построить график функции надо

1. Описать функцию:
•что является
графиком функции
•куда направлены
ветви параболы
Пример: у = х²-2х-3
• графиком является
парабола,
• ветви которой
направлены вверх
(т.к. а=1, а>0)

16. Чтобы построить график функции надо

2. Найти координаты вершины Пример: y=x2 -2x-3
параболы А(m;n) по формулам: (a=1, b=-2, c=-3)

English Русский Правила

§ Квадратичная функция. Как построить параболу

Квадратичная функция. Как построить параболу Как решать задачи на квадратичную функцию

Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют функцией в математике.

Если вы прочно закрепите общие знания о функции (способы задания, понятие графика) дальнейшее изучение других видов функций будет даваться значительно легче.

Запомните!

Квадратичная функция — это функция вида

y = ax² + bx + c,

где a, b и с — заданные числа.

Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень, в которой стоит «x» — это «2», то перед нами квадратичная функция.

Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a», «b» и «с».

Квадратичная функция	Коэффициенты
y = 2x² − 7x + 9	a = 2 b = −7 с = 9
y = 3x² − 1	a = 3 b = 0 с = −1
y = −3x² + 2x	a = −3 b = 2 с = 0

Как построить график квадратичной функции

Запомните!

График квадратичной функции называют параболой.

Парабола выглядит следующим образом.

Также парабола может быть перевернутой.

Существует четкий алгоритм действий при построении графика квадратичной функции. Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.

Чтобы было проще понять этот алгоритм, сразу разберем его на примере.

Построим график квадратичной функции «y = x² −7x + 10».

Направление ветвей параболы Запомните!
Если «a > 0», то ветви направлены вверх.
Если «a
В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.
Координаты вершины параболы Запомните!
Чтобы найти «x₀» (координата вершины по оси «Ox») нужно использовать формулу:
x₀ =
Найдем «x₀» для нашей функции «y = x² −7x + 10».
x₀ =
− (−7)
2 · 1
= = 3,5
Теперь нам нужно найти «y₀» (координату вершины по оси «Oy»). Для этого нужно подставить найденное значение «x
0» в исходную функцию. Вспомнить, как найти значение функции можно в уроке «Как решать задачи на функцию» в подразделе «Как получить значение функции».
y₀(3,5) = (3,5)² − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 = −12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат. Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график относительно оси «Oy».
Нули функции
Для начала давайте разберемся, что называют нулями функции.
Запомните!
Нули функции — это точки пересечения графика функции с осью «Ox» (осью абсцисс).

Наглядно нули функции на графике выглядят так:
Свое название нули функции получили из-за того, что у этих точек координата по оси «Oy» равна нулю.
Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!
Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо «y = 0».
Подставим в заданную функцию «y = x² −7x + 10» вместо «y = 0» и решим полученное квадратное уравнение относительно «x» .
0 = x² −7x + 10
x² −7x + 10 = 0
x_1;2 =
7 ± √49 − 4 · 1 · 10
2 · 1

x_1;2 =

7 ± √9
2

x_1;2 =
7 ± 3
2

x₁ = x₂ =
7 − 3
2
x₁ = x₂ =
x₁ = 5 x₂ = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения с осью «Ox». Назовем эти точки и выпишем их координаты.
- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.

Дополнительные точки для построения графика

Возьмем четыре произвольные числовые значения для «x». Целесообразно брать целые числовые значения на оси «Ox», которые наиболее близки к оси симметрии. Числа запишем в таблицу в порядке возрастания.

x	1	3	4	6
y

Для каждого выбранного значения «x» рассчитаем «y».

y(1) = 1² − 7 · 1 + 10 = 1 − 7 + 10 = 4
y(3) = 3² − 7 · 3 + 10 = 9 − 21 + 10 = −2
y(4) = 4² − 7 · 4 + 10 = 16 − 28 + 10 = −2
y(6) = 6² − 7 · 6 + 10 = 36 − 42 + 10 = 4

Запишем полученные результаты в таблицу.

x	1	3	4	6
y	4	−2	−2	4

Отметим полученные точки графика на системе координат (зеленые точки).

Теперь мы готовы построить график. На забудьте после построения подписать график функции.

Краткий пример построения параболы

Рассмотрим другой пример построения графика квадратичной функции. Только теперь запишем алгоритм построения коротко без подробностей.

Пусть требуется построить график функции «y = −3x² − 6x − 4».

Направление ветвей параболы
Координаты вершины параболы x₀ =
x₀ =
−(−6)
2 · (−3)
=
= −1
y₀(−1) = (−3) · (−1)² − 6 · (−1) − 4 = −3 · 1 + 6 − 4 = −1
(·) A (−1; −1) — вершина параболы.
Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x² − 6x − 4
−3x² − 6x − 4 = 0 |·(−1)
3x² + 6x + 4 = 0
x_1;2 =
−6 ± √6² − 4 · 3 · 4
2 · 1
x_1;2 =
−6 ± √36 − 48
2
x_1;2 =
−6 ± √−12
2
Ответ: нет действительных корней.
Так как корней нет, значит, график функции не пересекает ось «Ox».
Вспомогательные точки для: «x = −3»; «x = −2»; «x = 0»; «x = 1». Подставим в исходную функцию «y = −3x² − 6x − 4».
- y(−3) = −3 · (−3)² − 6 · (−3) − 4 = −3 · 9 + 18 − 4 = −27 + 14 = −13
- y(−2) = −3 · (−2)² − 6 · (−2) − 4 = −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4
- y(0) = −3 · 0² − 6 · 0 − 4 = −4
- y(1) = −3 · 1² − 6 · 1 − 4 = −3 −6 − 4 = −13
x −3 −2 0 1
y −13 −4 −4 −13

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые не выходят за масштаб нашей системы координат, то есть точки «(−2; −4)» и «(0; −4)». Построим и подпишем график функции.

Квадратичная функция. Как построить параболу Как решать задачи на квадратичную функцию

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:


Отправить

Парабола

Когда вы пинаете футбольный мяч (или пускаете стрелу, выпускаете ракету или бросаете камень), он взмывает в воздух дугой и снова падает…

… по траектории параболы!

(За исключением влияния воздуха. )

Попробуйте ударить по мячу:

изображений/parabola-ball.js?mode=ball

Определение

Парабола – это кривая, в которой любая точка находится на равном расстоянии от:

фиксированная точка (точка фокус ) и
фиксированная прямая линия ( Директриса )

На бумаге

Возьмите лист бумаги, нарисуйте на нем прямую линию, затем сделайте большую точку для фокуса (не на линии!).

Теперь поэкспериментируйте с некоторыми измерениями, пока не получите еще одну точку, которая находится на точно таком же расстоянии от фокуса и прямой линии.

Продолжайте, пока у вас не будет много маленьких точек, затем соедините маленькие точки, и вы получите параболу!

Так же, как в этом интерактиве (попробуйте переместить точку P):

. ./sets/images/geom-locus.js?mode=parabola

Имена

Вот важные имена:

Директриса и фокус (объяснено выше)
ось симметрии (проходит через фокус, под прямым углом к директрисе)
вершина (где парабола делает самый крутой поворот) находится на полпути между фокусом и директрисой.

Отражатель

А парабола обладает этим удивительным свойством:

Любой луч, параллельный оси симметрии, отражается от поверхности прямо и попадает в фокус .

И это объясняет, почему эта точка называется фокусом …

… потому что там собираются все лучи!

Таким образом, парабола может быть использована для:

спутниковые антенны,
радарные тарелки,
концентрация солнечных лучей в горячей точке,
рефлектор на прожекторы и фонари,
и т. д.

Мы также получаем параболу, когда разрезаем конус (срез должен быть параллелен стороне конуса).

Итак, парабола является коническим сечением (сечением конуса).

Уравнения

Простейшее уравнение для параболы: y = x ²

Если перевернуть на бок, получится у ² = х

(или y = √x только для верхней половины)

Немного шире:

г ² = 4 оси

, где a — расстояние от начала координат до фокуса (а также от начала координат до директрисы)

Пример: Найдите фокус уравнения y

² = 5x

Преобразовывая y ² = 5x в y ² = 4ax , получаем y ² = 4 (5/4) x ,

так что a = 5/4 , а фокус y ² =5x равен:

F = (a, 0) = (5/4, 0)

Уравнения парабол в различных ориентациях выглядят следующим образом:

y ² = 4ax

y ² = −4ax

x ² = 4ay

90 179 х ² = −4ay

Размеры параболической тарелки

Если вы хотите построить параболическую тарелку, фокус которой находится на высоте 200 мм над поверхностью, какие размеры вам потребуются?

Чтобы упростить построение, давайте направим его вверх, и поэтому мы выберем уравнение x ² = 4ay.

И мы хотим, чтобы «а» равнялось 200, поэтому уравнение принимает следующий вид:

x ² = 4ay = 4 × 200 × y = 800y

Перестановка, чтобы мы могли вычислить высоту:

у = х ² /800

И вот несколько замеров роста во время бега:

	Расстояние вдоль («x»)	Высота («у»)
	0 мм	0,0 мм
	100 мм	12,5 мм
	200 мм	50,0 мм
	300 мм	112,5 мм
	400 мм	200,0 мм
	500 мм	312,5 мм
	600 мм	450,0 мм

Попробуйте собрать его сами, это может быть весело! Только будьте осторожны, отражающая поверхность может концентрировать много тепла в фокусе.

567 568 833 834, 2088, 2089, 2086, 2087, 3334, 3335

Что такое параболы, их уравнения, их правила?

Получение информации из уравнений Получение уравнений из задач и калькуляторов InfoWord

Purplemath

Что такое парабола?

Парабола — это особый тип геометрической кривой, которая алгебраически соответствует квадратному уравнению. Геометрически парабола соответствует краю среза перевернутого конуса; этот срез и есть то, что называется коническим «сечением».

Содержание продолжается ниже. с этой палкой, и потянув эту палку вокруг первой палки. Эллипс формируется путем помещения двух палочек в песок, наматывания веревки вокруг них обеих (эта петля должна быть достаточно длинной, чтобы свободно обхватывать палочки), помещения третьей палки в петлю, вытягивания провисания и вытягивания этой палки. вокруг двух палок в земле.

Как строится парабола?

Параболу можно построить с помощью таврового угольника и рельса. Положите Т-образный угольник на рейку. Поместите булавку на доску над рельсом. Вставьте еще одну булавку в верхнюю часть Т-образного квадрата. Натяните нить вдоль вертикального края Т-образного квадрата. Сдвиньте Т-образный квадрат из стороны в сторону, удерживая маркер и нить напротив вертикального края. Полученная кривая представляет собой параболу.

(Эти физические чертежи, называемые конструкциями из булавок и струн, может быть трудно представить себе в голове. Если вы хотите увидеть эти конструкции, посмотрите это видео. Парабола начинается прямо на минутной отметке.)

В алгебре работа с параболами обычно означает построение графика квадратичных уравнений или нахождение максимальных/минимальных точек (то есть вершин) парабол для решения квадратных задач. Однако в контексте коников есть некоторые дополнительные соображения.

Каковы ключевые слова для парабол?

Ключевые слова для парабол: вершина, фокус, директриса и ось симметрии. Чтобы сформировать параболу в соответствии с древнегреческими определениями, вы должны начать с прямой линии и точки в одну сторону; линия называется директрисой; точка называется фокусом. Парабола — это кривая, образованная всеми точками ( x , y ), которые равноудалены от директрисы и фокуса.

Линия, перпендикулярная директрисе и проходящая через фокус (т. е. линия, разделяющая параболу посередине), называется осью симметрии. Точка на этой оси, которая находится точно посередине между фокусом и направляющей, является вершиной; вершина — это точка, в которой парабола меняет направление.

Рассмотрим эту «правильную» (то есть прямую или перевернутую, но не боковую) параболу:

На картинке выше сама парабола нарисована синим цветом. Фокус (отмечен зеленым) находится внутри параболы, вершина (отмечена оранжевым) находится в точке поворота графика, директриса (отмечена фиолетовым) — прямая по другую сторону вершины от фокуса, а ось симметрии (отмечена красным) проходит вертикально через фокус и перпендикулярна директрисе.

Вы почти всегда будете иметь дело с вертикальными параболами, как показано выше. Но вы могли бы также (но только в разделе о кониках) иметь дело с горизонтальными, как это:

Это боковая или горизонтальная парабола (синий). На этом графике вы можете видеть фокус (отмеченный зеленым цветом) внутри параболы, вершину (отмеченную оранжевым цветом) на графике, директрису (отмеченную фиолетовым цветом) по другую сторону от вершины от фокуса и ось симметрии (отмечено красным), проходящей через фокус и перпендикулярной директрисе. Фокус параболы всегда находится внутри параболы; вершина всегда находится на параболе; директриса всегда находится вне параболы.

Откуда произошло слово парабола?

Название «парабола» происходит от нового латинского термина, означающего что-то похожее на сравнение или уравновешивание, и относится к тому факту, что расстояние от параболы до фокуса всегда равно (то есть всегда находится в равновесии) расстояние от параболы до директрисы. С практической точки зрения вам, вероятно, нужно будет только знать, что вершина находится ровно посередине между директрисой и фокусом.

Какое основное физическое свойство парабол?

Основным свойством параболы в реальной жизни является то, что любой свет, спутниковый сигнал, звуковая волна и т.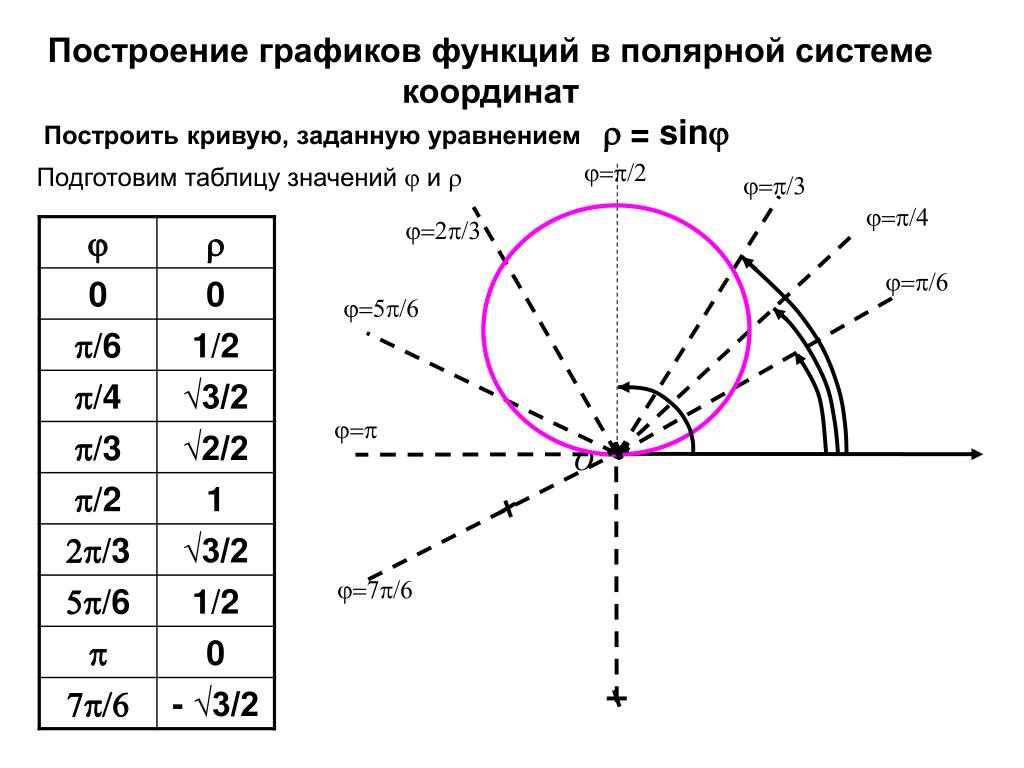 д., которые входят в параболу параллельно оси симметрии и достигают внутренней поверхности параболической чаши (например, спутниковой антенны), будут отражается обратно в фокус. Параболические антенны, такие как бионические уши и радиотелескопы, используют это свойство для концентрации сигнала на приемнике.

Какова общая форма уравнения параболы?

Общая форма уравнения параболы — это квадратное уравнение, к которому вы привыкли:

y = ax ² + bx + c

— если квадратное число не является боковым, в этом случае уравнение будет выглядеть примерно так:

х = ² + на + c

Важным отличием двух уравнений является то, в какой переменной возводится в квадрат: для правильных (то есть вертикальных) парабол часть x возводится в квадрат; для боковых (то есть для горизонтальных) парабол и часть в квадрате.

Что такое вершинная форма уравнения параболы?

Форма вершины параболы — с вершиной в точке ( h , k ) — равна:

обычная: y = a ( x 9033 9 − ч ) ² + к
сбоку: x = a ( y − k ) ² + h

Форма вершины также может быть выражена как:

обычный: y − k = a ( x − h ) ²
сбоку: x − ч = a ( у — к ) ²

Что такое коническая форма уравнения параболы?

Коническая форма уравнения параболы (которую вы найдете в продвинутых или старых текстах):

обычная: 4 p ( y − k ) = ( x − h ) ²
сбоку: 4 p ( x − h ) = ( y − k ) ²

Почему мы используем буквы

h , k и p в уравнениях параболы?
Почему ( h , k ) для вершины и p вместо a в старинной формуле для коник? Не знаю. И даже неправда, что «все» используют эти буквы. (Обсуждение Math StackExchange со ссылкой на архивную статью AskDrMath) Так что ваше предположение так же хорошо, как и мое (хотя, если вы столкнетесь с источником, который кажется авторитетным, пожалуйста, напишите мне).
Какая связь между вершинной и геометрической формами уравнения параболы?
Важно отметить, работаете ли вы с вершинной формой или геометрической формой (т. k всегда остается с частью y , и что p всегда находится на неквадратной переменной части .
Фактически связь между вершинной формой уравнения и конической формой уравнения есть не что иное, как перестановка:

y = a ( x − h ) ² + к
y − k = a ( x − h ) ²
(1/ a )( 9033 8 г — к ) = ( x — ч ) ²
4 p ( y − k ) = ( x − h ) ²

Другими словами, значение 4 9033 8 p на самом деле совпадает со значением 1/ и ; это просто два способа сказать одно и то же. Но эта новая переменная p — это та переменная, с которой вам нужно иметь возможность работать, когда вы рисуете параболы в контексте коник: она представляет расстояние между вершиной и фокусом, а также то же самое, что и (что также равно) расстоянию между вершиной и направляющей; так 2 p — это расстояние между фокусом и директрисой.

Какая связь между вершиной и общими формами уравнения параболы?

Вершинная форма уравнения параболы преобразуется в общую форму путем умножения всего и выделения неквадратичной переменной с одной стороны знака «равно» с квадратным выражением с другой стороны. Общая форма уравнения параболы преобразуется в форму вершины путем завершения квадрата или с помощью следующей формулы, чтобы получить значение h , являющееся x -координатой вершины:

h = − b /(2 a )

Затем подключите значение х дюймов для х дюймов общую форму параболы и упростите, чтобы получить значение y = k .

Каковы правила парабол?

Правила для парабол:

Вершина всегда находится в точке ( h , k ; это точка, в которой кривая на графике разворачивается и начинает двигаться в обратном направлении.
Независимо от того, работаете ли вы со старшим коэффициентом a или геометрическим коэффициентом p (где p = 1/ a ):
- если коэффициент положительный, то кривая разворачивается вверх (или, если вбок, вправо).
- , если коэффициент отрицательный, то кривая разворачивается вниз (или, если вбок, влево).
Ось симметрии — это линия, которая делит параболу на две равные половины.
- Если парабола вертикальна, то ось симметрии проходит через вершину и представляет собой вертикальную линию x = h .
- Если парабола направлена боком, то ось симметрии проходит через вершину и является горизонтальной линией y = k .
Фокус будет в точке p единиц от вершины и будет находиться внутри параболы на оси симметрии
Направляющей будет линия p единиц от вершины, и она будет вне параболы и перпендикулярна оси симметрии.

Как вы помните правила построения парабол?

По моему опыту, лучший способ выучить и запомнить правила построения парабол — и особенно отношения между общей, вершинной и геометрической формами — это практиковаться, практиковаться и еще раз практиковаться. Ваш мозг достаточно устанет (или достаточно разочаруется) от необходимости снова и снова искать один и тот же материал, и начнет вспоминать отношения из чистой лени. По крайней мере, так работает *мой* мозг.

URL: https://www.purplemath.com/modules/parabola.htm

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске вершины. Попробуйте введенное упражнение или введите свое собственное упражнение.

x	−3	−2	0	1
y	−13	−4	−4	−13