Аналитическая геометрия на плоскости — презентация онлайн
1. ЛЕКЦИЯ №5
ТЕМА ЛЕКЦИИ:«АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ НА
ПЛОСКОСТИ»
Раздел «Аналитическая геометрия на
плоскости» курса «Высшая математика»
включает две основные темы:
1.
2.
Прямая на плоскости
Кривые 2-го порядка
3. Прямая на плоскости
Основные уравнения прямой на плоскости1. Уравнение прямой, проходящей через заданную
точку M 0 ( x0 ; y0 ) перпендикулярно
N A; B
заданному вектору N A; B
A( x x0 ) B( y y0 ) 0
M 0 ( x0 ; y0 )
2. Общее уравнение прямой
N A; B
Ax By C 0
— вектор нормали
3. Уравнение прямой « в отрезках»
x y
1
a b
Y
b
X
a
4. Прямая на плоскости. Основные уравнения
4. Уравнение прямой, проходящей через заданнуюточку M 0 ( x0 ; y0 ) параллельно заданному вектору s m; n
x x0 y y 0
m
n
— каноническое уравнение
s m; n — направляющий вектор
s m; n
5.
 Параметрические уравнения
Параметрические уравненияx mt x0
y nt y 0
M 0 ( x0 ; y0 )
6. Уравнение прямой, проходящей через две
заданные точки M 1 ( x1 ; y1 ) и M 2 ( x2 ; y2 )
x x1
y y1
x2 x1 y2 y1
s M 1M 2
M 2 ( x2 ; y 2 )
M 1 ( x1 ; y1 )
5. Прямая на плоскости. Основные уравнения
7. Уравнение прямой, проходящей через заданнуюточку M 0 ( x0 ; y0 ) с заданным угловым коэффициентом
y y0 k ( x x0 )
k tg
Y
y
y0
X
O
x0
x
Угловой коэффициент k — это тангенс угла наклона прямой.
Угол отсчитывается от положительного направления оси OX
8. Уравнение прямой с угловым
коэффициентом
y kx b
Y
b
O
X
6. Задачи на составление уравнений прямой , определение параметров уравнений
1. Составить уравнение прямой, проходящей через точку M 0 (2;4)параллельно прямой
5x 3 y 15 0 . Построить прямую.
Решение. Нам задано уравнение прямой общего вида
Ax By C 0
N A; B
-вектор нормали
Сравнивая с заданным уравнением, получаем координаты
вектора нормали N 5; 3 Так как все параллельные прямые
можно охарактеризовать одним вектором нормали, то можно составить
уравнение параллельной прямой, проходящей через данную
в условии точку.
 За основу берем уравнение A( x x0 ) B( y y0 ) 0
За основу берем уравнение A( x x0 ) B( y y0 ) 05( x 2) 3( y 4) 0
5x 10 3 y 12 0
5x 3 y 2 0
Y
Найдем угловой коэффициент
5x 2 3 y
5
2
y x
3
3
N 5; 3
s 3;5 -направляющий вектор
k
5
3
2
3
2
5
O
X
2. Составить уравнение прямой, проходящей через данную точку
M 0 ( 3;4) параллельно прямой x 1 y 3
2
5
Из канонического уравнения заданной прямой можно определить
ее направляющий вектор s 2; 5
Поскольку для всех параллельных прямых можно взять один и тот
же направляющий вектор, то берем за основу каноническое
уравнение x x0 y y 0 и подставляем в него координаты точки
m
n
и направляющего вектора
x 3 y 4
2
5
Это уравнение можно преобразовать к уравнению
общего вида и к уравнению с угловым коэффициентом
x
0
y
7
2
7
5
0
Y
5x 15 2 y 8
5( x 3) 2( y 4)
7
5x 2 y 7 0
7
5
5
( y 4) ( x 3)
2
2
5
k
N 5;2 — вектор нормали
угловой коэффициент
2
X
3.
 Составить уравнение прямой, проходящей через точку A( 5;2)
Составить уравнение прямой, проходящей через точку A( 5;2)параллельно прямой y 3x 5 .
В данном случае прямая задана уравнением с известным
угловым коэффициентом y=kx+b.
K=3
Все параллельные прямые имеют один угловой коэффициент.
Y
Т.о. нам известна точка на прямой и угловой коэффициент.
Y
Берем уравнение y y0 k ( x x0 )
Y
y 2 3( x 5)
17
y 2 3x 15
y 3x 17
Записав уравнение в виде
X
17 / 3
3x y 17 0 , определим вектор нормали
N 3; 1 и направляющий вектор
s 1;3
Для построения прямой используем таблицу
x
y
0
-17/3
17
0
4. Составить уравнение прямой, проходящей через точку M 0 (2;4)
перпендикулярно прямой 5x 3 y 15 0
N 5; 3
M 0 (2;4)
5x 3 y 15 0
Из рисунка видно, что вектор
нормали известной прямой
является направляющим для
искомой прямой, поэтому
используем каноническое уравнение
x x0 y y 0
m
n
3( x 2) 5( y 4)
x 2 y 4
5
3
3x 6 5 y 20
3x 5 y 26 0
Таким образом, получили общее уравнение прямой, из которого
определяем вектор нормали N 3;5
Из канонического уравнения можно перейти к уравнению
с угловым коэффициентом
x 2 y 4
5
3
3
x y 4
5
3
y x 4
5
k 3 / 5
5.
 Составить уравнение прямой, проходящей через точку M 0 (4; 1)
Составить уравнение прямой, проходящей через точку M 0 (4; 1)перпендикулярно прямой
x 3t 1
y 2t 5
M 0 (4; 1)
s 3; 2
A( x x0 ) B( y y0 ) 0
3( x 4) 2( y 1) 0
Прямая задана параметрическими
уравнениями, из которых найдем
направляющий вектор s 3; 2
Из рисунка видно, что
направляющий вектор известной
прямой является вектором нормали
для искомой прямой, поэтому
используем уравнение прямой с
известной точкой и вектором
нормали
3x 12 2 y 2 0
3x 2 y 14 0
Получили общее уравнение прямой, из которого N 3; 2 ,
Записав уравнение в виде
3
( y 1) ( x 4) ,
2
3
найдем угловой коэффициент k
2
s 2;3
6. Составить уравнение прямой, проходящей через точку
перпендикулярно прямой y 1 x 3
5
M 0 (3;2)
Из уравнения заданной прямой можно взять угловой коэффициент
k
1
5
Из условия перпендикулярности прямых
можно найти угловой коэффициент
перпендикулярной прямой
k2
k1 k 2 1
1
1
5
k1
( 1 / 5)
Теперь берем уравнение прямой с угловым коэффициентом и
подставляем координаты точки и значение углового коэффициента
y y0 k ( x x0 )
y 5x 13
y 2 5( x 3) y 2 5x 15
Или 5x y 13 0 — общее уравнение N 5; 1 ,
s 1;5
12.
 Взаимное расположение прямых на плоскостиЗадачи на взаимное расположение прямых включают слежующие
Взаимное расположение прямых на плоскостиЗадачи на взаимное расположение прямых включают слежующиевопросы:
1.
Нахождение точки пересечения.
2.
Нахождение угла между прямыми
3.
Проверка условий параллельности и перпендикулярности
прямых
Для нахождения точки пересечения нужно решить систему,
составленную из уравнений этих прямых, например
2 x 5 y 4 0
3x 2 y 1 0
2 5
3
y
2
4 ( 15) 19
2 4
3
1
Систему можно решить методом Крамера
2 ( 12) 14
x
4 5
x
1
2
8 ( 5) 3
x 3
19
Точка пересечения
y
y
3 14
M ;
19 19
14
19
13. Нахождение угла между прямыми
.1 Если прямые заданы общими уравнениями, то угол между
прямыми – это угол между векторами нормалей и используется
формула косинуса угла между векторами
cos
( N1 N 2 )
N1 N 2
A1 A2 B1 B2
A1 B12 A2 B22
2
2
2. Если прямые заданы каноническими уравнениями, то угол между
прямыми – это угол между направляющими векторами
( s1 s2 )
m1m2 n1n2
cos
2
2
s1 s2
m1 n12 m2 n22
3.
 Если прямые заданы угловыми коэффициентами, то находят
Если прямые заданы угловыми коэффициентами, то находяттангенс угла
k k
tg 2 1
1 k1 k 2
14. Проверка условий параллельности и перпендикулярности прямых
1. Условия параллельности прямыхA1 B1
A2 B2
m1 n1
m2 n2
k1 k 2
2. Условия перпендикулярности прямых
1 k1 k 2 0
A1 A2 B1 B2 0
m1m2 n1n2 0
1
k2
k1
Расстояние от точки M 1 ( x1 ; y1 ) до прямой Ax By C 0
d
Ax1 By1 C
A2 B 2
Для нахождения расстояния от точки до прямой нужно координаты точки
Подставить в левую часть уравнения прямой, разделить на длину
вектора нормали и полученное значение взять по абсолютной величине.
Уравнение прямой должно быть приведены к общему виду
x 4 y 9
1. Найти угол между прямыми 2 x y 3 0 и
5
4
Из уравнения первой прямой определяем вектор нормали N1 2; 1
Из уравнения второй прямой находим направляющий вектор s 5;4
Тогда вектор нормали этой прямой N 2 4; 5
Используем формулу cos ( N1 N 2 )
N1 N 2
cos
A1 A2 B1 B2
A1 B12 A2 B22
2
2
2 4 ( 1) ( 5)
13
4 1 16 25
5 41
2.
 Найти расстояние от точки M 0 ( 1; 4) до прямой
Найти расстояние от точки M 0 ( 1; 4) до прямойПриведем сначала уравнение прямой к общему виду
x y
1
5 7
7 x 5 y 35
или 7 x 5 y 35 0 . Теперь можно использовать формулу
Ax By C 7( 1) 5( 4) 35 62
62
d 1 2 1 2
74
74
A B
7 2 52
16. Кривые 2-го порядка
Общее уравнение прямой на плоскости – есть уравнениелинейное относительно переменных x и y
Ax By C 0
Уравнение кривой 2-го порядка
Ax 2 2 Bxy Cy 2 Dx Ey F 0
Ax 2 2 Bxy Cy 2 квадратичная часть
линейная часть
Dx Ey F 0
В дальнейшем
будем рассматривать уравнения кривых,
.
в которых отсутствует произведениеxy
Ax2 Cy 2 Dx Ey F 0
К кривым 2-го порядка относятся :
окружность, эллипс, гипербола и парабола.
Основная задача состоит в умении по уравнению определить
тип кривой, привести само уравнение к каноническому
виду и построить кривую в системе координат.
17. 1. Окружность
Определение. Окружностью называется множество точекплоскости, равноудаленных от одной точки, называемой центром
Уравнение окружности с центром в начале координат
x2 y2 R2
Уравнение окружности со смещенным центромO ‘ ( x0 ; y0 )
( x x0 ) 2 ( y y 0 ) 2 R 2
!
В уравнение окружности входят квадраты переменных,
причем коэффициенты при квадратах и знаки
при них одинаковые.

Y
Y
y0
O
O’
X
O
x0
X
18. Построение окружностей
1. Построить окружность2. Построить окружность
x2 y2 9
3
( x 1) 2 ( y 2) 2 9
Y
O
Y
R 3
3 X
2
O’
1
3. Построить окружность
y 1 x2
Y
y 2 ( 1 x 2 ) 2
y2 1 x2
y2 x2 1
O
y 0
1
1 X
O
X
2
2
Построить окружность x 6 x y 4 y 12
( x x0 ) 2 ( y y 0 ) 2 R 2
Каноническое уравнение
Формула квадрата суммы и разности двух чисел
( a b) 2 a 2 2 a b b 2
1. ( x 6 x) ( y 4 y ) 12
2
2
2
2
2
2
2. ( x 2 x 3 3 3 ) ( y 2 y 2 2 2 ) 12
2
2
Y
3. [( x 3) 9] [( y 2) 4] 12
2
4.
2
( x 3) 2 ( y 2) 2 9 4 12
2
2
(
x
3
)
(
y
2
)
25
5.
2
2
2
(
x
3
)
(
y
2
)
5
6.
O ( 3;2) центр окружности,
‘
R 5 радиус окружности
O’
3
2
O
X
20.
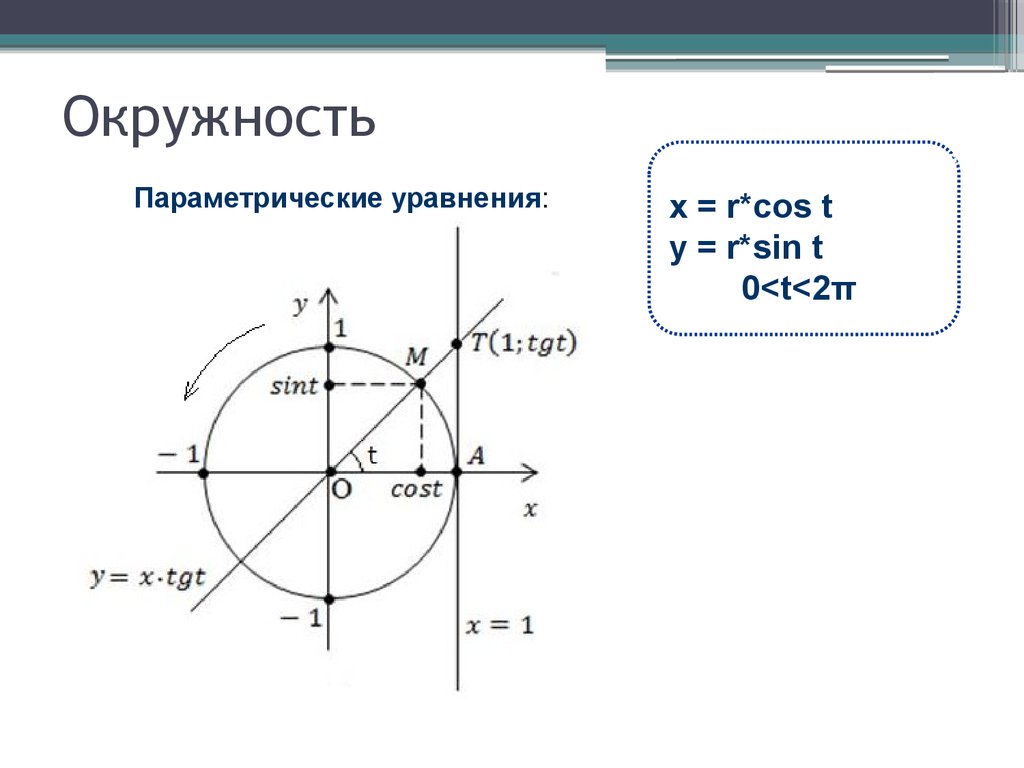 2. ЭллипсОпределение. Эллипсом называется множество точек
2. ЭллипсОпределение. Эллипсом называется множество точекплоскости, сумма расстояний которых до двух данных точек,
называемых фокусами , есть величина постоянная, равная
длине большой оси 2a .
Каноническое уравнение эллипса
Y
b B1 M ( x; y)
x2 y2
2 1, причем
2
A2 F2
a
b
F1 A1
c
O
a c
a
X
B2
a 2 b2 c 2
b
A1 (a;0) A2 ( a;0)
F1 (c;0)
F2 ( c;0)
вершины эллипса
B1 (0; b) B2 (0; b)
фокусы эллипса
A1 A2 2a
большая ось эллипса
F1 F2 2c фокусное расстояние
B1 B2 2b
малая ось эллипса
В уравнение эллипса входят квадраты переменных,
причем знаки при квадратах одинаковые, а коэффициенты
при квадратах разные.
!
21. Разновидности эллипса
Уравнение эллипса со смещенным центромY
( x x0 ) 2 ( y y0 ) 2
1
2
2
a
b
O ‘ ( x0 ; y 0 ) — центр эллипса
b
a
x0
X
y0
a
O’
b
Если в уравнении эллипса b a , то большой осью будет ось
B1 B2 2b , фокусы эллипса будут
B1 b
.
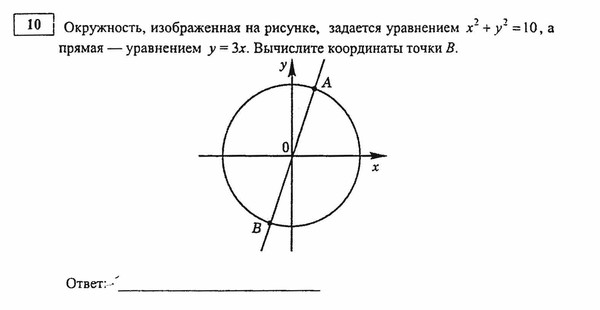
лежать на этой оси и связь
между параметрами эллипса
будет такой:
b2 a 2 c 2
F1 c
a
O
.
F2 c
B2 b
a
22. Построение эллипса
1. Построить эллипсx2 y2
1
4
2
Для построения эллипса нужно знать координаты центра и
размеры полуосей a и b
Y
Центр эллипса O(0;0)
2
Полуоси a 4 a 2,
b2 2 b 2
2
.
Расстояние между фокусами
2 2
c 2 a 2 b 2 4 2 2,
c 2 , т.е. 2c 2 2
O
.
2
X
2
2
Можно найти площадь фигуры, ограниченной эллипсом по формуле
S a b
Для данного примера получим
S 2 2 2 2
2. Построить эллипс
9 x 2 5 y 2 45
Для получения канонического уравнения делаем некоторые
преобразования:
1) Делим все члены уравнения на 45, так чтобы получит единицу
в правой части уравнения
9×2 5 y 2
1
45
45
2) Убираем в знаменатель коэффициенты из числителей
x2
y2
1
45 / 9 45 / 5
x2 y2
1
5
9
Получили уравнение эллипса, из которого определяем положение
Y
центра и размеры полуосей
3
O(0;0) — центр эллипса
a 2 5 a 5,
— полуоси
b2 9 b 3
b a
3) Строим эллипс
5
O
5
3
X
3.
 Построить кривую
Построить кривуюx 1 9 4 y 2
Y
2
2
1. ( x 1) 4 y 9
2. x 1
9 4 y2
3. ( x 1) 9 4 y
2
b
a
2
O’
1
O
X
2
2
(
x
1
)
4
y
9
4.
( x 1) 2 4 y 2
1
5.
9
9
( x 1) 2
y2
1
9
9/4
Таким образом, центр эллипса имеет координаты
Полуоси эллипса
O ‘ ( 1;0)
a 2 9 a 3,
b 2 9 / 4 b 3 / 2 , т.е. a b
При построении необходимо учесть, что уравнение определяет
Только правую половинку эллипса, так как по условию имеем x
1
3x 2 6 x 2 y 2 2 y 0
4. Построить кривую
Данное уравнение определяет эллипс, так как есть квадраты
переменных, знаки при которых одинаковые, а коэффициенты
различные. Кроме того, наличие линейной части уравнения
означает, что центр эллипса смещен от начала координат.
Приводим уравнение к каноническому виду
( x x0 ) 2 ( y y0 ) 2
1
2
2
a
b
Используем прием выделения полного квадрата согласно формуле
( a b) 2 a 2 2 a b b 2
2
2
1.
 3( x 2 x) 2( y y ) 0
3( x 2 x) 2( y y ) 02. 3( x 2 x 1 1 1 ) 2( y 2 y 1/ 2 (1/ 2) (1/ 2) ) 0
3. 3[( x 1) 2 1] 2[( y 1 / 2) 2 1 / 4] 0
2
2
2
2
2
4. 3( x 1) 2( y 1 / 2) 3 1 / 2 0
5. 3( x 1) 2 2( y 1 / 2) 2 7 / 2
2
2
( x 1) 2 ( y 1 / 2) 2
6. 3( x 1) 2( y 1 / 2) 1
1
7/2
7/2
7/6
7/4
7
O ‘ ( 1;1/ 2) центр , a 7 / 6 , b
полуоси
2
2
2
Y
2
O’
1/ 2
1
O
X
26. 3. Гипербола
Определение. Гиперболой называется множество точекплоскости, разность расстояний которых до двух данных точек,
называемых фокусами ,по абсолютной есть величина
постоянная, равная длине действительной оси 2a .
Каноническое уравнение гиперболы с центром в начале координат
x2 y2
2 1
2
a b
В этом случае
a действительная полуось
b мнимая полуось
Фокусы гиперболы всегда лежат на действительной оси.
Связь между параметрами гиперболы определяется соотношением
c 2 a 2 b2
!
В уравнение гиперболы входят квадраты
переменных, причем знаки при квадратах разные.

Асимптоты гиперболы – это прямые к которым гипербола
неограниченно приближается на бесконечности.
27. Построение гиперболы
x2 y22 1
2
a b
Построение гиперболы
Для построения гиперболы удобно пользоваться
вспомогательными построениями.
1. В системе координат строим прямоугольник с размерами 2a 2b
на осях OX и OY соответственно.
2. Проводим диагонали этого прямоугольника.
Уравнения диагоналей – это уравнения асимптот гиперболы
b
y x
a
3. На действительной оси отмечаем вершины гиперболы и от них
ведем ветви гиперболы к асимптотам.
Y
Y
Y
b
a
a
b
b
b
X
a
a
b
X
c a
a c
b
X
28. Виды гипербол
YРассмотрим другие виды гипербол
Сопряженная гипербола
2
c
2
x
y
1
2
2
a b
b
a X
b действительная полуось
a мнимая полуось
c
Равнобочная гипербола
2
2
x
y
x 2 y 2 a 2 или 2 2 1
a
a
Y
b
Гипербола со смещенным центром O ( x0 ; y0 )
‘
( x x0 ) ( y y0 )
1
2
2
a
b
Гипербола, приведенная к своим асимптотам
2
xy a
2
или
a
y
x
X
a
O’
Y
X
Рассмотрим примеры построения гипербол
1.
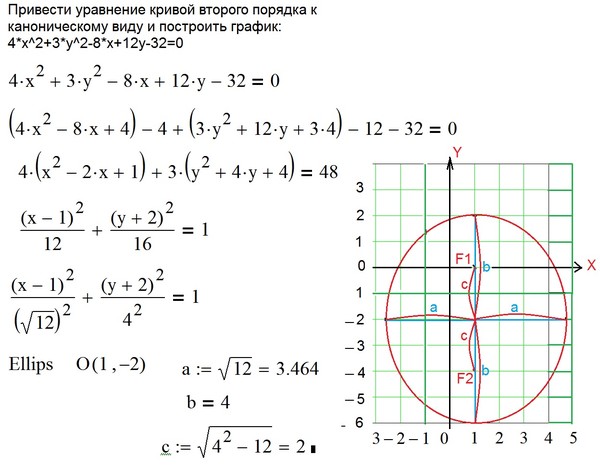 Построить гиперболу 4 x 2 3 y 2 12
Построить гиперболу 4 x 2 3 y 2 122
Y
2
4x 3y
1
12
12
2
x2
y2
1
12 / 4 12 / 3
X
3
x2 y2
1
3
4
2
O(0;0) центр гиперболы
a2 3
3
a 3 действительная полуось
b2 4 b 2
мнимая полуось
c 2 a 2 b 2 3 4 7,
c 7
2c 2 7
расстояние между фокусами
.
2 Построить кривую
y x2 4
Возведем в квадрат обе части уравнения
y2 x2 4
Собираем квадраты переменных в левую часть уравнения
x2 y2 4
Данное уравнение определяет гиперболу, так как знаки при квадратах
переменных разные. Кроме того, данная гипербола
является сопряженной и равнобочной
x2 y2
Можно записать уравнение в виде
1
Y
4
4
a 2 4 a 2 мнимая полуось
2
b 2 4 b 2 действительная
X
полуось
2
2
Оставляем только нижнюю ветвь
2
гиперболы, так как по условию
y 0
3. Построить кривую
4 x 2 3 y 2 12 8 x 12 y
Данное уравнение определяет гиперболу (знаки при квадратах
переменных различные) со смещенным центром (есть линейная часть)
Приведем уравнение к каноническому виду
( x x0 ) 2 ( y y 0 ) 2
1
a2
b2
4( x 2 2 x) 3( y 2 4 y) 12
4 x 2 8 x 3 y 2 12 y 12
Y
4( x 2 2 x 1 12 12 ) 3( y 2 2 y 2 2 2 2 2 ) 12
4[( x 1) 2 1] 3[( y 2) 2 4] 12
4( x 1) 2 4 3( y 2) 2 12 12
1
4( x 1) 2 3( y 2) 2 4
4( x 1) 2 3( y 2) 2
1
4
4
X
2
O’
( x 1) 2 ( y 2) 2
1
1
4/3
O ‘ ( 1; 2) центр гиперболы
4
2
b
мнимая полуось
a 1 действительная полуось
3
3
32.
 4. ПараболаОпределение. Параболой называется множество точек
4. ПараболаОпределение. Параболой называется множество точекплоскости, равноудаленных от одной точки, называемой
фокусом, и от данной прямой, называемой директрисой.
Виды парабол
Парабола с осью симметрии OX
x 2 2 py
y 2 px
2
Y
Y
y 2 px
2
Парабола c осью симметрии OY
y 2 2 px
X
x 2 2 py
X
x 2 2 py
Парабола со смещенной вершиной O’ ( x0 ; y0 )
Парабола с осью симметрии OX
Парабола c осью симметрии OY
( x x0 ) 2 2 p( y y0 )
( y y0 ) 2 2 p( x x0 )
Y
y0
Y
O’
x0
x0
!
X
y0
Отличительные признаки уравнения параболы:
отсутствует квадрат одной переменной.
O’
X
34. Построение парабол
Для построения параболы нужно знать:O’ ( x0 ; y0 ) .
Координаты вершины
Ось симметрии параболы (определяется по той переменно,
квадрат которой отсутствует в уравнении)
Направление ветвей (определяется по знаку : если в правой
части канонического уравнения знак плюс, то ветви параболы
идут в положительном направлении оси симметрии, если знак
минус, то в отрицательном )
Параметр параболы p определяется по коэффициенту при
переменной, стоящей в каноническом уравнении в первой
степени, и определяет «ширину» параболы.
 Знание параметра
Знание параметрапомогает более качественно получить начальный участок
параболы.
2
(
y
2
)
4( x 1)
1. Построить параболу
Данное уравнение является каноническим уравнением параболы,
так как отсутствует квадрат переменной x . Поэтому осью
симметрии параболы будет ось OX.
Вершина параболы в точке O’ (1;2)
Ветви параболы направлены в положительном направлении оси OX,
так как в правой части уравнения знак “плюс”.
2 p 4 ширина параболы
p 2 параметр параболы
p
1
2
Y
p
2
O’ p p
2
1
X
2. Построить кривую
y 3 2 1 x
Y
y 3 2 1 x
( y 3) 2 4(1 x)
( y 3) 2 4( x 1)
y 3
3
O’
X
O
1
O’ (1;3) вершина параболы
Ось симметрии параболы OX, так как отсутствует квадрат
переменной x
Ветви параболы направлены влево, так как в правой части уравнения
получился знак “минус”
p 2 параметр параболы
Так как по условию y 3 , то уравнение определяет только
верхнюю ветвь параболы
3.
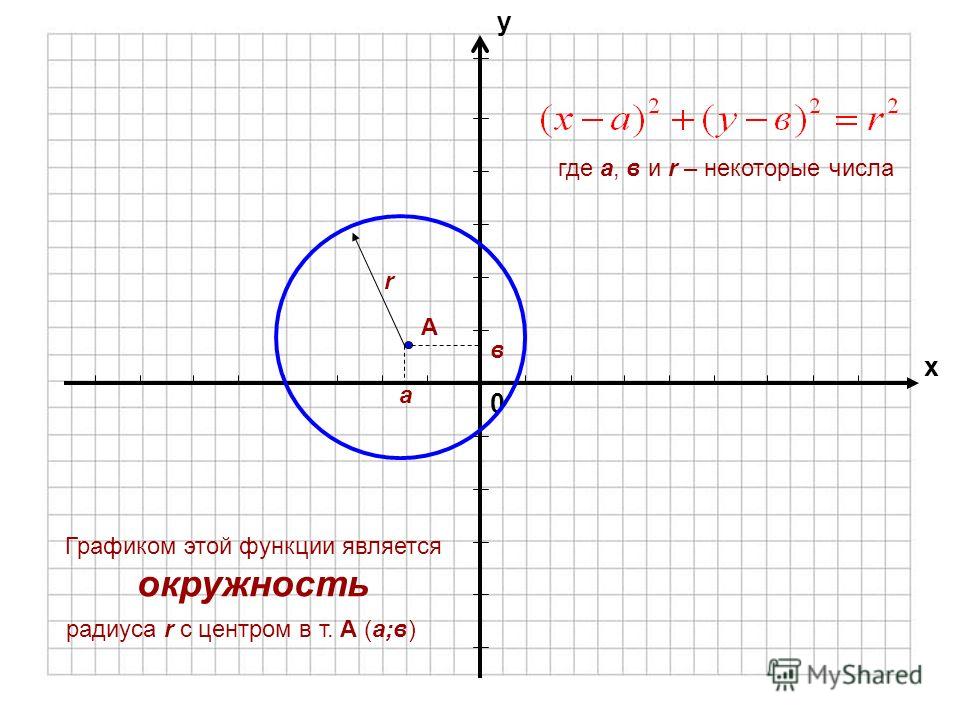 Построить кривую
Построить кривуюy 2 x2
Преобразуем уравнение
x2 2 y
x 2 ( y 2)
Уравнение определяет параболу. Сравнивая с уравнением
( x x0 ) 2 2 p ( y y0 ) , определяем координаты вершины
O’ (0;2) . Ось симметрии OY. Ветви направлены вниз.
1 параметр параболы
p
2
Y
O’ 2
p
1
2
1 1
O
X
4. Построить параболу
4×2 6x 3 y 2 0
В уравнении отсутствует квадрат переменной y, поэтому оно
определяет параболу с осью симметрии OY.
Проведем преобразования уравнения, чтобы привести его к
каноническому виду ( x x0 ) 2 2 p ( y y0 )
6
4 x 2 x 3 y 2 0
4
3
2
4 x 2 x (3 / 4) 2 (3 / 4) 2 3 y 2 0
4
2
3 9
3
9
4 x 3 y 2 0
4 x 3 y 2 0
4 4
4 16
Y
2
3
1
O ‘ y0
4 x 3 y
4
4
X
x0 O
2
3
1
4 x 3 y или
4
12
2
3
3
1
x y
4
4
12
3
3 1
O ‘ ; вершина параболы p параметр параболы
8
4 12
Ветви параболы направлены вниз
2
Уравнение окружности
Прежде всего,
давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что
уравнение с двумя переменными x и y
называется уравнением линии l, если этому уравнению
удовлетворяют координаты любой точки линии l и не
удовлетворяют координаты никакой точки, не лежащей на этой линии.
Сегодня на уроке мы попробуем по геометрическим свойствам линии найти ее уравнение.
В качестве линии рассмотрим окружность радиуса с центром в точке .
Пусть центр окружности имеет координаты . Возьмем на окружности произвольную точку . Запишем формулу расстояния между точками C и M. Мы знаем, что длина отрезка, который соединяет любую точку на окружности с центром окружности – это радиус. Поэтому можно записать, что MC равно r. Возведем MC в квадрат и получим уравнение MC2 = r2
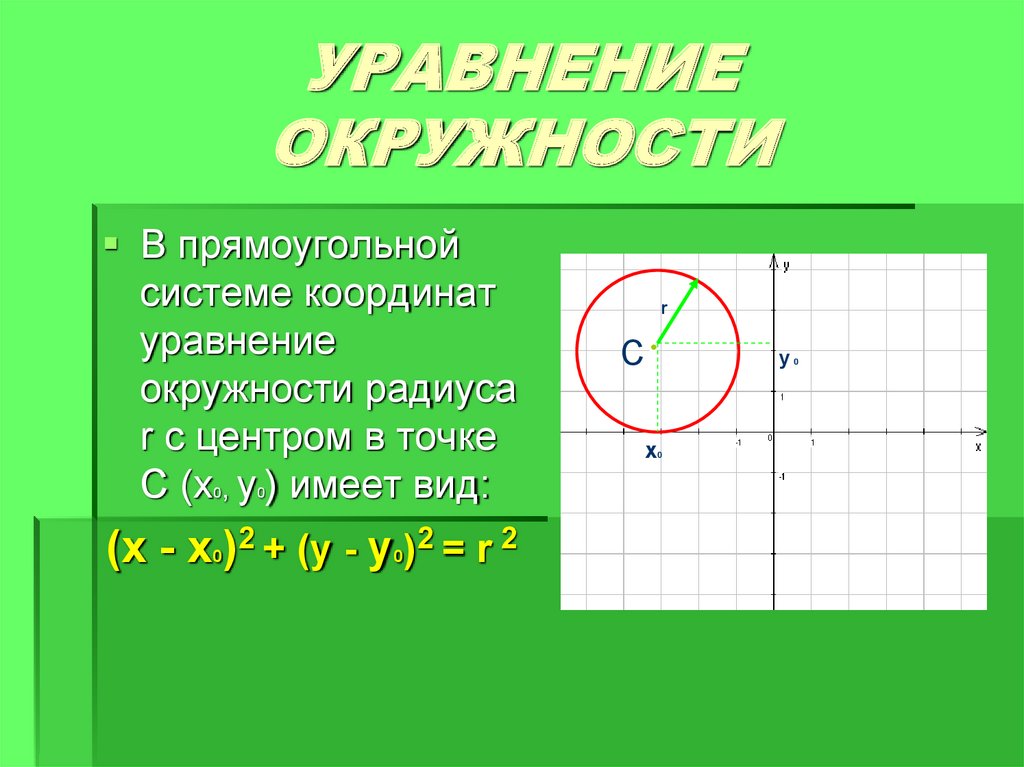
Задача. Записать уравнение окружности с радиусом и центром в начале координат.
Решение.
Начало координат имеет координаты (0;0). Подставим их в уравнение окружности и получим, что уравнение окружности с радиусом r и центром в начале координат имеет вид
.
Задача. Начертить окружность, заданную уравнением .
Решение.
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего, определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь давайте определим величину радиуса окружности.
Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 4. Получим 2.
Значит наша формула задает окружность с центром в точке с координатами пять три и радиусом равным двум.
Задача. Начертить
окружность, заданную уравнением .
Решение.
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего определимся с координатами центра окружности.
Это будут числа -4 и 2. Теперь давайте определим величину радиуса окружности.
Задача. Начертить окружность, заданную уравнением .
Решение. Уравнениями такого типа описываются окружности с центром в начале координат. Теперь давайте определим величину радиуса окружности. Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 9.
Значит наша формула задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.
Теперь давайте попробуем решить задачу обратную данным.
Задача. Составить уравнение окружности, которая показана на рисунке.
Как и в предыдущих
задачах мы начнем с определения координат центра окружности. Сделать это
нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр
окружности имеет координаты (0;0).
Сделать это
нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр
окружности имеет координаты (0;0).
Нетрудно заметить, что радиус окружности равен 4.
Запишем уравнение окружности и подставим найденные значения.
Ответ: .
Решим еще одну задачу.
Задача. Составить уравнение окружности, которая показана на рисунке.
Решение.
– центр окружности
– радиус окружности
Ответ:.
Задача. Составить уравнение окружности, которая показана на рисунке.
Решение.
– центр окружности
– радиус окружности
Ответ:.
Решая задачи, мы с вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот порядок.
Для того, что бы составить уравнение окружности и построить ее надо:
1.
2. Найти длину радиуса этой окружности.
3. Записать уравнение окружности.
4. Подставить полученные значения в уравнение окружности.
5. Построить окружность, если это требуется для решения задачи.
Рассмотрим еще одну задачу.
Написать уравнение окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм имеет координаты шесть три.
Задача. Написать уравнение окружности с диаметром , если , .
Решение.
Найдем координаты центра окружности. Центр окружности является серединой диаметра. Воспользуемся формулами для нахождения координат середины отрезка.
Получим, что центр окружности имеет координаты .
Теперь определим радиус окружности. Для этого найдем расстояние от центра окружности до концов диаметра.
Запишем общее
уравнение окружности и подставим в него найденные значения.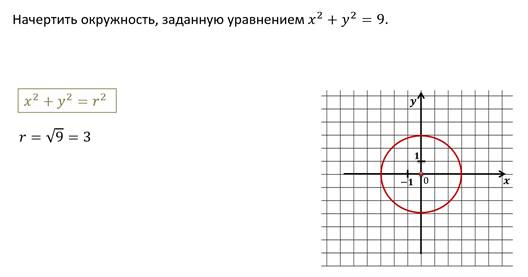 Тогда получим, что
уравнение данной окружности имеет вид:
Тогда получим, что
уравнение данной окружности имеет вид:
Ответ: .
Подведем итоги урока.
На сегодняшнем уроке мы познакомились с формулой, которая задает окружность с центром в точке С (x0; y0) и радиусом r.
Также мы познакомились с формулой, которая задает окружность с центром в начале координат и радиусом r.
Мы рассмотрели задачи на составление уравнения окружности по рисунку и на построение окружности по заданному уравнению.
Общая форма уравнения окружности Калькулятор
Создано Rijk de Wet
Отредактировано Стивеном Вудингом
Последнее обновление: 11 октября 2022 г.
Содержание:- Что такое уравнение окружности в общем виде?
- Как привести общее уравнение окружности к стандартной форме?
- Как преобразовать общее уравнение окружности в параметрическую форму?
- Как использовать общую форму уравнения окружности калькулятора?
- Связанные калькуляторы
- Часто задаваемые вопросы
Добро пожаловать в общую форму калькулятора уравнения окружности , который может помочь вам преобразовать ваше уравнение окружности из общей формы в стандартную и параметрическую форму или наоборот. Здесь мы узнаем:
Здесь мы узнаем:
- Как выглядит уравнение окружности в общем виде ;
- Как написать уравнение окружности в общем виде ; и
- Как преобразовать общую форму уравнения окружности в другие формы .
Что такое уравнение окружности в общем виде?
Общая форма уравнения окружности задается как x² + y² + Dx + Ey + F = 0 с параметрами D, E и F , определяющими свойства окружности, такие как радиус и центр.
Как привести общее уравнение окружности к стандартной форме?
Стандартная форма уравнения окружности (x−A)² + (y−B)² = C . Мы можем записать общую форму уравнения окружности в стандартную форму, вычислив неизвестные A, B и C из параметров общего уравнения D, E и F .
К счастью, эта математика проста!
- А = -D/2;
- В = -Е/2; и
- С = А² + В² — F.

Как преобразовать общее уравнение окружности в параметрическую форму?
Параметрическая форма уравнения окружности x = A + r cos(α) и y = B + r sin(α) . Чтобы записать общую форму уравнения окружности в параметрическое уравнение, мы вычисляем неизвестные A, B и r :
- A = −D/2;
- В = -Е/2; и
- г = √(А² + В² — F).
Как использовать общую форму уравнения окружности калькулятора?
Общая форма уравнения окружности калькулятор проста в использовании! Вот как:
- Введите уравнение вашего круга
- Найдите свой круг, переписанный в стандартной и параметрической формах ниже.
- Также найдите свойства круга , такие как центр, радиус и площадь в самом низу.
В маловероятном случае, если общая форма калькулятора уравнения окружности не соответствует вашим потребностям, рассмотрите один из наших других калькуляторов окружности :
- Калькулятор уравнения окружности;
- Вычислитель центра окружности;
- Калькулятор стандартного уравнения окружности;
- Калькулятор уравнения окружности с диаметрами концов;
- Общая к стандартной форме кругового калькулятора; и
- Стандартная форма к общей форме кругового калькулятора.

Часто задаваемые вопросы
Какова общая форма уравнения (x−3)² + (y+2)² = 25?
Общий вид: x² + y² — 6x + 4y — 12 = 0
. Преобразование из стандартной формы (x − A)² + (y − B)² = C (с параметрами A = 3, B = −2 и C = 25) до x² + y² + Dx + Ey + F = 0 , мы рассчитать:- D = −2A = −6;
- Е = -2В = 4; и
- F = А² + В² — С = -12.
Каково общее уравнение окружности с (x−6)² + (y−6)² = 49?
Общая форма этого круга: x² + y² − 12x − 12y + 23 = 0 . У нас есть A = 6, B = 6 и C = 49 в стандартной форме (x−A)² + (y−B)² = C . Итак, чтобы преобразовать в x² + y² + Dx + Ey + F = 0 , вычисляем:
- D = −2A = −12;
- Е = -2В = -12; и
- F = А² + В² — С = 23.
Какова общая форма уравнения окружности с (x+3)² + (y−5)² = 49?
Общий вид: x² + y² + 6x — 10y — 15 = 0 . Преобразование из стандартной формы (x−A)² + (y−B)² = C (с параметрами A = −3, B = 5 и C = 49) в x² + y² + Dx + Ey + F = 0
Преобразование из стандартной формы (x−A)² + (y−B)² = C (с параметрами A = −3, B = 5 и C = 49) в x² + y² + Dx + Ey + F = 0
- Д = -2А = 6;
- Е = -2В = -10; и
- F = А² + В² — С = -15.
Rijk de Wet
Введите общее уравнение вашего круга ниже, и мы покажем вам стандартный и параметрический эквиваленты и центр круга и его свойства ниже.
Общее уравнение: x² + y² + Dx + Ey + F = 0
Стандартное уравнение: (x − A)² + (y − B)² = C
Параметрическое уравнение: x = A + r cos(α) , y = B + r sin(α)
Центральные координаты
X-координата
Y-координата
Свойства круга
Радиус
Диаметр
Окружение
Проверьте 8 аналогичных калькуляторов круга ⭕
Длина дуги. Длина дуги. a, r… еще 5
Уравнение окружности Калькулятор
Создано Богной Шик и Ханной Памула, кандидатом наук
Отзыв от Jack Bowater
Последнее обновление: 28 июля 2022 г. 0003 Содержание:
0003 Содержание:
- Что такое стандартное уравнение окружности?
- Параметрическое уравнение окружности
- Стандартное уравнение к параметрическому уравнению окружности
- Как найти уравнение окружности?
- Другая форма уравнения окружности
- Как использовать это уравнение калькулятора окружности?
Неважно, насколько хорошо вы разбираетесь в геометрии круга, от уравнения круга у вас может закружиться голова. Если это так, не волнуйтесь! Это стандартное уравнение калькулятора окружности поможет вам определить радиус окружности и координаты центра в мгновение ока. Если вам интересно, как найти уравнение окружности, прокрутите вниз, и вы найдете объяснение формулы.
Если геометрическая фигура, которую вы пытаетесь проанализировать, выглядит немного сплющенной, вероятно, это эллипс. В таком случае отправляйтесь прямо к нашему калькулятору эллипса!
🔎 Если вы новичок в кругах, вам могут быть полезны другие, более простые инструменты, такие как окружность и площадь круга , окружность до диаметра или квадратных метра круга и круг калькуляторы длины.
Что такое стандартное уравнение окружности?
Стандартное уравнение окружности — это способ описать все точки, лежащие на окружности, с помощью всего одной формулы: 92r2 — это радиус круга, возведенный в степень двойки, поэтому, чтобы найти радиус, возьмите квадратный корень из этого значения.
Наш калькулятор уравнения круга находит не только эти значения, но также диаметр, длину окружности и площадь круга — все для экономии вашего времени!
Параметрическое уравнение окружности
Уравнение окружности можно определить по-разному; не только в стандартной форме, показанной выше. Окружность также может быть описана как геометрическое место всех точек, удовлетворяющих уравнениям:
х=rcos(α)y=rsin(α)\маленький \начать{выравнивать*} х &= г \cos(\alpha)\\[.5em] у &= г \ грех (\ альфа) \end{align*}xy=rcos(α)=rsin(α)
где:
(x,y)(x,y)(x,y) — Координаты любой точки на окружности, как и раньше;
rrr – Радиус окружности; и
α\alphaα – Угол, образуемый точкой в центре окружности.

Если сместить центр круга на (A, B) координат, вы просто добавите их к координатам x и y, чтобы получить общее параметрическое уравнение окружности:
x=A+rcos(α)y=B+rsin(α)\small \начать{выравнивать*} x &= A + r \cos(\alpha)\\[.5em] y &= B + r \sin(\alpha) \end{align*}xy=A+rcos(α)=B+rsin(α)
Как и выше, вы должны быть осторожны со знаками центральной точки.
Стандартное уравнение в параметрическое уравнение окружности
Чтобы продемонстрировать, что эти две формы формулы окружности эквивалентны, давайте сделаем преобразование между ними. 92 = 1 x2+y2=1
Вот и мы! Это стандартное уравнение окружности.
Как найти уравнение окружности?
Итак, вы узнали о различных уравнениях окружности. Но откуда они? Давай выясним!
- Выберите центр круга, O=(A,B)O = (A, B)O=(A,B). Не выбирайте его в качестве начала системы координат.
- Нарисовать окружность выбранного радиуса rrr.
- Выберите любую точку на окружности.
 Предположим, что координаты этой точки равны P=(x,y)P = (x,y)P=(x,y). 92 (x−A)2+(y−B)2=r2
Предположим, что координаты этой точки равны P=(x,y)P = (x,y)P=(x,y). 92 (x−A)2+(y−B)2=r2- Использовать тригонометрию :
Выразить стороны треугольника POC с помощью функций синуса и косинуса:
cos(α)=OC/r ⟹ OC=rcos(α)sin(α)=CP/r ⟹ CP=rsin(α)\small\quad\ \ \начать{выравнивать*} \cos(\alpha) &= OC / r \подразумевает \\[.5em]OC &= r\cos(\alpha)\\[1em] \sin(\alpha) &= CP / r \подразумевает \\[.5em]CP &= r\sin(\alpha) \end{align*} cos(α)OCsin(α)CP=OC/r⟹=rcos(α)=CP/r⟹=rsin(α)
Координаты точки P могут быть выражены как:
x=A+OC & y=B+CP⇓x=A+rcos(α)y=B+rsin(α)\small\quad\ \ \начать{выравнивать*} x = A + OC\ \ &\&\ \ y = B + CP\\[.5em] &\Стрелка вниз\\[.5em] х = А &+ г \ соз (\ альфа) \\ y = B &+ r\sin(\alpha) \end{align*} x=A+OC x=Ay=B& y=B+CP⇓+rcos(α)+rsin(α)
Два последних уравнения представляют собой параметрические уравнения окружности.
Теперь, когда вы знаете, как найти уравнение окружности, попробуйте этот калькулятор!
Другая форма уравнения окружности 92 = 5 (x+2)2+(y−3)2=5
Готово — это стандартная форма круга с центром в точке (−2,3)(-2, 3)( −2,3) и радиусом, равным 5\sqrt55.

Естественно, вам не нужно проходить весь этот процесс самостоятельно. Вместо этого используйте это уравнение калькулятора окружности!
Как пользоваться калькулятором уравнения окружности?
Если вы все еще не знаете, как использовать наш инструмент, взгляните на этот простой пример ниже.
Предположим, вы хотите использовать стандартное уравнение окружности . Итак, это первая часть калькулятора.
Введите данные . Допустим, параметры вашего уравнения окружности равны A = 7, B = -2 и C = 9.
Тадаа! Калькулятор уравнения окружности сделал свое дело! Инструмент покажет вам, какие параметры есть в других формах уравнения, объяснив, каковы значения A и B (координаты центра окружности), и дополнительно рассчитает другие значения, такие как:
- Радиус – что равно 3 для нашего круга;
- Диаметр – в нашем случае 6;
- Площадь для нашего примера равна 28,3; и
- Длина окружности равна 18,85.

- Использовать тригонометрию :
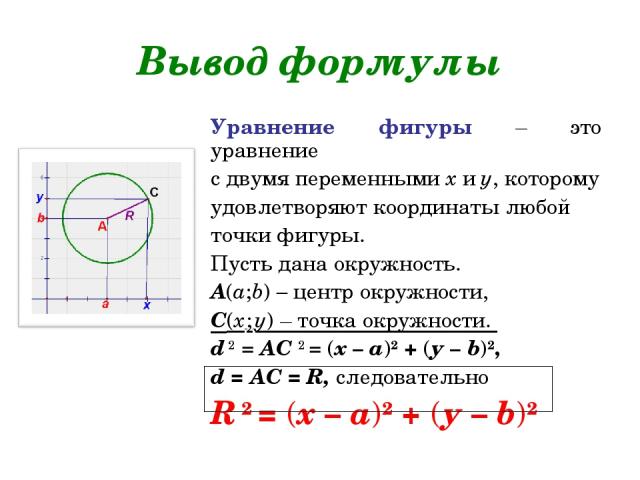


 Предположим, что координаты этой точки равны P=(x,y)P = (x,y)P=(x,y). 92 (x−A)2+(y−B)2=r2
Предположим, что координаты этой точки равны P=(x,y)P = (x,y)P=(x,y). 92 (x−A)2+(y−B)2=r2

Ваш комментарий будет первым