Построение окружности по уравнению онлайн: Каноническое уравнение окружности

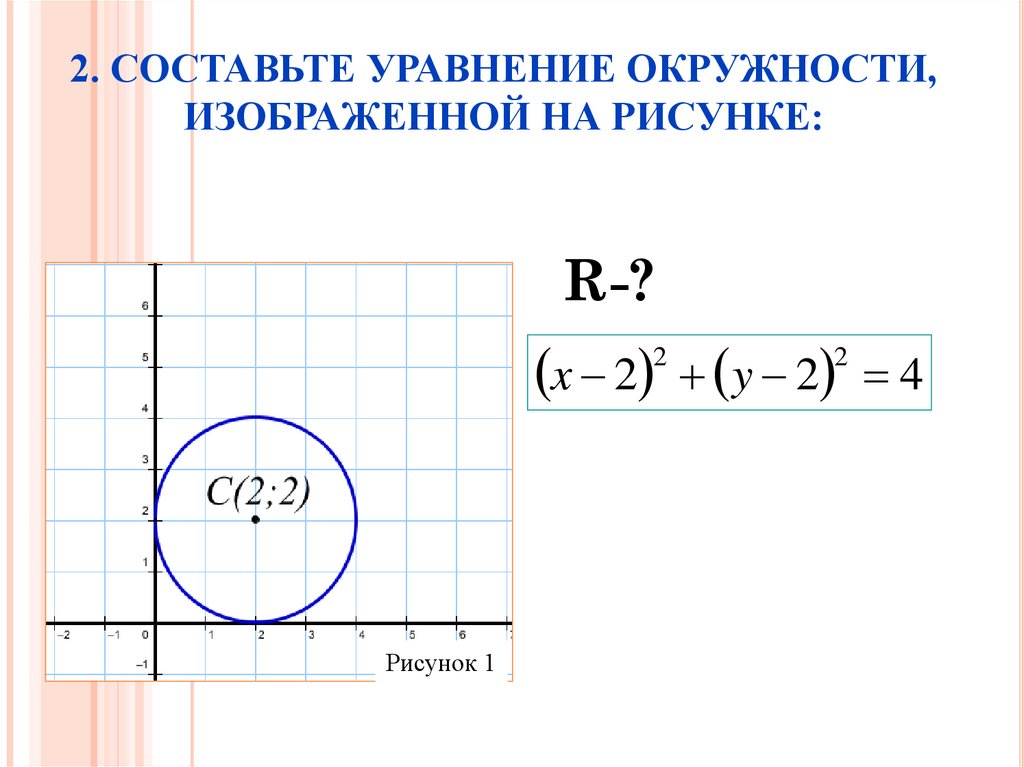
Уравнение Окружности Калькулятор — Mathcracker.Com

Инструкции: Используйте данный калькулятор для расчета формулы окружности, заданной радиусом и координатами x и y ее центра. Введите необходимую информацию в поля ниже.

Подробнее об этом уравнении окружности калькулятор

Данный калькулятор позволит вам получить уравнение окружности в стандартной форме и в общая форма , где показаны все шаги. Вам необходимо указать правильный радиус окружности (правильное положительное числовое выражение), а также координаты x и y ее центра.

Числовые выражения, которые вы предоставите, могут быть чем-то вроде ‘1/2’ или составным выражением вроде ‘1/3+1/4’. Обратите внимание, что радиус должен быть положительным.

После того, как вы предоставите необходимую информацию с правильными данными, вам нужно будет нажать на кнопку «Рассчитать», и все этапы расчетов будут показаны вам.

Самый простой способ действовать в этом случае — сначала получить стандартная форма окружности с предоставленными данными, а затем просто расширить это выражение, чтобы получить общая форма уравнения окружности .

2\), где все, что вам нужно знать, это радиус r

Обратите внимание, что вышеописанный процесс заключается в нахождении уравнения окружности с заданными центром и радиусом. Другой способ получить уравнение окружности — начать с общего уравнения окружности, а затем сгруппировать и обработать выражение так, чтобы найти радиус и центр.

Уравнение окружности с пояснениями

У уравнения окружности есть два пути, обратных и в плане формулировки, и в плане интерпретации. С одной стороны, если вы знаете радиус r окружности и ее центр \((x_0, y_0)\), можно сказать, что вы уже знаете все, что вам нужно знать об окружности, по крайней мере, геометрически.

То есть, зная радиус и центр, вы можете нарисовать окружность. 2 \]

В таком случае вы знаете, что r — это радиус, а \((x_0, y_0)\) — его центр. Почему? Ну, это следует непосредственно из Теорема Пифагора .

Общее уравнение окружности калькулятор

Если уравнение дано в стандартной форме, вы будете знать все, что нужно знать об окружности, потому что вам напрямую известны радиус и центр. Но что если вам дано общее уравнение?

• Шаг 1: Определите заданное общее уравнение. Это должно быть уравнение, квадратичное по x и y, иначе вы не сможете продолжить
• Шаг 2: Получив общее уравнение, убедитесь, что коэффициенты умножения x^2 и y^2 одинаковы, иначе вы не сможете продолжить
• Шаг 3: После того, как у вас есть действительное общее уравнение, вы выполняете процедуру Заполните квадраты процедура для x и y
• Шаг 4: Получив стандартное уравнение путем заполнения квадратов и перестановки членов, вы определяете центр и радиус напрямую

Процедура заполнения квадрата может быть утомительной, но она является систематической, и ее проведение не должно быть слишком сложным. 2 = 1\). Все остальные окружности могут быть получены на основе единичной окружности путем преобразований и расширений или сужений.

Однако центром всех кругов является единичный круг, который прочно укоренился в алгебре и тригонометрии.

Пример: вычисление уравнения окружности

Вычислите следующее: Уравнение окружности с радиусом r = 3 и центром (3, -4).

Решение:

Нам нужно найти стандартную форму окружности, где заданный радиус равен \(r = \displaystyle 3\), а заданный центр — \(\left(\displaystyle 3, -4 \right)\). 2-6x+8y+16 = 0\).

Пример: подробнее о нахождении уравнения окружности

Вычислите следующее: \(\frac{1}{3} + \frac{5}{4} — \frac{5}{6}\)

Решение:

чем завершается расчет.

Пример: вычисления уравнения окружности

Рассчитайте \( \left(\frac{2}{3} \times \frac{6}{5} \right)+ \frac{2}{5} \).

Решение:

чем завершается расчет.

Другие полезные калькуляторы окружностей

Окружности и их свойства играют важнейшую роль в математике. Что можно сделать с помощью формула окружности ? Много! Например, вы можете использовать формула для площади круга или также использовать его формула окружности чтобы получить площадь и периметр, соответственно.

В кругах есть то, что неотъемлемо присуще математике. Его совершенная симметрия и тесная связь с \(\pi\) превратили их в увлекательный объект изучения для математиков всех времен.

Прямая на плоскости. Кривые второго порядка

Раздел «Аналитическая геометрия на
плоскости» курса «Высшая математика»
включает две основные темы:
1.
2.
Прямая на плоскости
Кривые 2-го порядка

2. Прямая на плоскости

Основные уравнения прямой на плоскости
1. Уравнение прямой, проходящей через заданную
точку M 0 ( x0 ; y0 ) перпендикулярно
N A; B
заданному вектору N A; B
A( x x0 ) B( y y0 ) 0
M 0 ( x0 ; y0 )
2. Общее уравнение прямой
N A; B
Ax By C 0
— вектор нормали
3. Уравнение прямой « в отрезках»
x y
1
a b
Y
b
X
a

3. Прямая на плоскости. Основные уравнения

4. Уравнение прямой, проходящей через заданную
точку M 0 ( x0 ; y0 ) параллельно заданному вектору s m; n
x x0 y y 0
m
n
— каноническое уравнение
s m; n — направляющий вектор
s m; n
5. Параметрические уравнения
x mt x0
y nt y 0
M 0 ( x0 ; y0 )
6. Уравнение прямой, проходящей через две
заданные точки M 1 ( x1 ; y1 ) и M 2 ( x2 ; y2 )
x x1
y y1
x2 x1 y2 y1
s M 1M 2
M 2 ( x2 ; y 2 )
M 1 ( x1 ; y1 )

4. Прямая на плоскости. Основные уравнения

7. Уравнение прямой, проходящей через заданную
точку M 0 ( x0 ; y0 ) с заданным угловым коэффициентом
y y0 k ( x x0 )
k tg
Y
y
y0
X
O
x0
x
Угловой коэффициент k — это тангенс угла наклона прямой.
Угол отсчитывается от положительного направления оси OX
8. Уравнение прямой с угловым
коэффициентом
y kx b
Y
b
O
X

5. Задачи на составление уравнений прямой , определение параметров уравнений

1. Составить уравнение прямой, проходящей через точку M 0 (2;4)
параллельно прямой
5x 3 y 15 0 . Построить прямую.
Решение. Нам задано уравнение прямой общего вида
Ax By C 0
N A; B
-вектор нормали
Сравнивая с заданным уравнением, получаем координаты
вектора нормали N 5; 3 Так как все параллельные прямые
можно охарактеризовать одним вектором нормали, то можно составить
уравнение параллельной прямой, проходящей через данную
в условии точку. За основу берем уравнение A( x x0 ) B( y y0 ) 0
5( x 2) 3( y 4) 0
5x 10 3 y 12 0
5x 3 y 2 0
Y
Найдем угловой коэффициент
5x 2 3 y
5
2
y x
3
3
N 5; 3
s 3;5 -направляющий вектор
k
5
3
2
3
2
5
O
X
2. Составить уравнение прямой, проходящей через данную точку
M 0 ( 3;4) параллельно прямой x 1 y 3
2
5
Из канонического уравнения заданной прямой можно определить
ее направляющий вектор s 2; 5
Поскольку для всех параллельных прямых можно взять один и тот
же направляющий вектор, то берем за основу каноническое
уравнение x x0 y y 0 и подставляем в него координаты точки
m
n
и направляющего вектора
x 3 y 4
2
5
Это уравнение можно преобразовать к уравнению
общего вида и к уравнению с угловым коэффициентом
x
0
y
7
2
7
5
0
Y
5x 15 2 y 8
5( x 3) 2( y 4)
7
5x 2 y 7 0
7
5
5
( y 4) ( x 3)
2
2
5
k
N 5;2 — вектор нормали
угловой коэффициент
2
X
3. Составить уравнение прямой, проходящей через точку A( 5;2)
параллельно прямой y 3x 5 .
В данном случае прямая задана уравнением с известным
угловым коэффициентом y=kx+b.
K=3
Все параллельные прямые имеют один угловой коэффициент.
Y
Т.о. нам известна точка на прямой и угловой коэффициент.
Y
Берем уравнение y y0 k ( x x0 )
Y
y 2 3( x 5)
17
y 2 3x 15
y 3x 17
Записав уравнение в виде
X
17 / 3
3x y 17 0 , определим вектор нормали
N 3; 1 и направляющий вектор
s 1;3
Для построения прямой используем таблицу
x
y
0
-17/3
17
0
4. Составить уравнение прямой, проходящей через точку M 0 (2;4)
перпендикулярно прямой 5x 3 y 15 0
N 5; 3
M 0 (2;4)
5x 3 y 15 0
Из рисунка видно, что вектор
нормали известной прямой
является направляющим для
искомой прямой, поэтому
используем каноническое уравнение
x x0 y y 0
m
n
3( x 2) 5( y 4)
x 2 y 4
5
3
3x 6 5 y 20
3x 5 y 26 0
Таким образом, получили общее уравнение прямой, из которого
определяем вектор нормали N 3;5
Из канонического уравнения можно перейти к уравнению
с угловым коэффициентом
x 2 y 4
5
3
3
x y 4
5
3
y x 4
5
k 3 / 5
5. 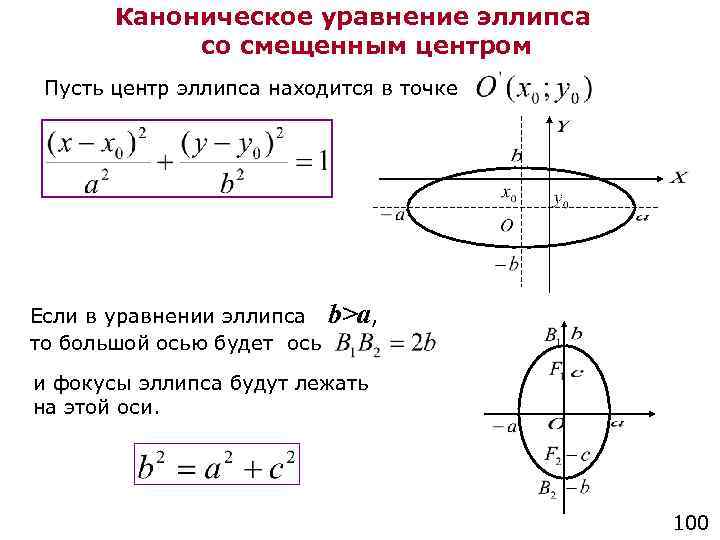Составить уравнение прямой, проходящей через точку M 0 (4; 1)
перпендикулярно прямой
x 3t 1
y 2t 5
M 0 (4; 1)
s 3; 2
A( x x0 ) B( y y0 ) 0
3( x 4) 2( y 1) 0
Прямая задана параметрическими
уравнениями, из которых найдем
направляющий вектор s 3; 2
Из рисунка видно, что
направляющий вектор известной
прямой является вектором нормали
для искомой прямой, поэтому
используем уравнение прямой с
известной точкой и вектором
нормали
3x 12 2 y 2 0
3x 2 y 14 0
Получили общее уравнение прямой, из которого N 3; 2 ,
Записав уравнение в виде
3
( y 1) ( x 4) ,
2
3
найдем угловой коэффициент k
2
s 2;3
6. Составить уравнение прямой, проходящей через точку
перпендикулярно прямой y 1 x 3
5
M 0 (3;2)
Из уравнения заданной прямой можно взять угловой коэффициент
k
1
5
Из условия перпендикулярности прямых
можно найти угловой коэффициент
перпендикулярной прямой
k2
k1 k 2 1
1
1
5
k1
( 1 / 5)
Теперь берем уравнение прямой с угловым коэффициентом и
подставляем координаты точки и значение углового коэффициента
y y0 k ( x x0 )
y 5x 13
y 2 5( x 3) y 2 5x 15
Или 5x y 13 0 — общее уравнение N 5; 1 ,
s 1;5

11.

Взаимное расположение прямых на плоскостиЗадачи на взаимное расположение прямых включают слежующие
вопросы:
1.
Нахождение точки пересечения.
2.
Нахождение угла между прямыми
3.
Проверка условий параллельности и перпендикулярности
прямых
Для нахождения точки пересечения нужно решить систему,
составленную из уравнений этих прямых, например
2 x 5 y 4 0
3x 2 y 1 0
2 5
3
y
2
4 ( 15) 19
2 4
3
1
Систему можно решить методом Крамера
2 ( 12) 14
x
4 5
x
1
2
8 ( 5) 3
x 3
19
Точка пересечения
y
y
3 14
M ;
19 19
14
19

12. Нахождение угла между прямыми

.
1 Если прямые заданы общими уравнениями, то угол между
прямыми – это угол между векторами нормалей и используется
формула косинуса угла между векторами
cos
( N1 N 2 )
N1 N 2
A1 A2 B1 B2
A1 B12 A2 B22
2
2
2. Если прямые заданы каноническими уравнениями, то угол между
прямыми – это угол между направляющими векторами
( s1 s2 )
m1m2 n1n2
cos
2
2
s1 s2
m1 n12 m2 n22
3. Если прямые заданы угловыми коэффициентами, то находят
тангенс угла
k k
tg 2 1
1 k1 k 2

13. Проверка условий параллельности и перпендикулярности прямых

1. Условия параллельности прямых
A1 B1
A2 B2
m1 n1
m2 n2
k1 k 2
2. Условия перпендикулярности прямых
1 k1 k 2 0
A1 A2 B1 B2 0
m1m2 n1n2 0
1
k2
k1
Расстояние от точки M 1 ( x1 ; y1 ) до прямой Ax By C 0
d
Ax1 By1 C
A2 B 2
Для нахождения расстояния от точки до прямой нужно координаты точки
Подставить в левую часть уравнения прямой, разделить на длину
вектора нормали и полученное значение взять по абсолютной величине.
Уравнение прямой должно быть приведены к общему виду
x 4 y 9
1. Найти угол между прямыми 2 x y 3 0 и
5
4
Из уравнения первой прямой определяем вектор нормали N1 2; 1
Из уравнения второй прямой находим направляющий вектор s 5;4
Тогда вектор нормали этой прямой N 2 4; 5
Используем формулу cos ( N1 N 2 )
N1 N 2
cos
A1 A2 B1 B2
A1 B12 A2 B22
2
2
2 4 ( 1) ( 5)
13
4 1 16 25
5 41
2. Найти расстояние от точки M 0 ( 1; 4) до прямой
Приведем сначала уравнение прямой к общему виду
x y
1
5 7
7 x 5 y 35
или 7 x 5 y 35 0 . Теперь можно использовать формулу
Ax By C 7( 1) 5( 4) 35 62
62
d 1 2 1 2
74
74
A B
7 2 52

15. Кривые 2-го порядка

Общее уравнение прямой на плоскости – есть уравнение
линейное относительно переменных x и y
Ax By C 0
Уравнение кривой 2-го порядка
Ax 2 2 Bxy Cy 2 Dx Ey F 0
Ax 2 2 Bxy Cy 2 квадратичная часть
линейная часть
Dx Ey F 0
В дальнейшем
будем рассматривать уравнения кривых,
.
в которых отсутствует произведениеxy
Ax2 Cy 2 Dx Ey F 0
К кривым 2-го порядка относятся :
окружность, эллипс, гипербола и парабола.
Основная задача состоит в умении по уравнению определить
тип кривой, привести само уравнение к каноническому
виду и построить кривую в системе координат.

16. 1. Окружность

Определение. Окружностью называется множество точек
плоскости, равноудаленных от одной точки, называемой центром
Уравнение окружности с центром в начале координат
x2 y2 R2
Уравнение окружности со смещенным центромO ‘ ( x0 ; y0 )
( x x0 ) 2 ( y y 0 ) 2 R 2
!
В уравнение окружности входят квадраты переменных,
причем коэффициенты при квадратах и знаки
при них одинаковые.
Y
Y
y0
O
O’
X
O
x0
X

17. Построение окружностей

1. Построить окружность
2. Построить окружность
x2 y2 9
3
( x 1) 2 ( y 2) 2 9
Y
O
Y
R 3
3 X
2
O’
1
3. Построить окружность
y 1 x2
Y
y 2 ( 1 x 2 ) 2
y2 1 x2
y2 x2 1
O
y 0
1
1 X
O
X
2
2
Построить окружность x 6 x y 4 y 12
( x x0 ) 2 ( y y 0 ) 2 R 2
Каноническое уравнение
Формула квадрата суммы и разности двух чисел
( a b) 2 a 2 2 a b b 2
1. ( x 6 x) ( y 4 y ) 12
2
2
2
2
2
2
2. ( x 2 x 3 3 3 ) ( y 2 y 2 2 2 ) 12
2
2
Y
3. [( x 3) 9] [( y 2) 4] 12
2
4.
2
( x 3) 2 ( y 2) 2 9 4 12
2
2
(
x
3
)
(
y
2
)
25
5.
2
2
2
(
x
3
)
(
y
2
)
5
6.
O ( 3;2) центр окружности,
‘
R 5 радиус окружности
O’
3
2
O
X

19.

2. ЭллипсОпределение. Эллипсом называется множество точек
плоскости, сумма расстояний которых до двух данных точек,
называемых фокусами , есть величина постоянная, равная
длине большой оси 2a .
Каноническое уравнение эллипса
Y
b B1 M ( x; y)
x2 y2
2 1, причем
2
A2 F2
a
b
F1 A1
c
O
a c
a
X
B2
a 2 b2 c 2
b
A1 (a;0) A2 ( a;0)
F1 (c;0)
F2 ( c;0)
вершины эллипса
B1 (0; b) B2 (0; b)
фокусы эллипса
A1 A2 2a
большая ось эллипса
F1 F2 2c фокусное расстояние
B1 B2 2b
малая ось эллипса
В уравнение эллипса входят квадраты переменных,
причем знаки при квадратах одинаковые, а коэффициенты
при квадратах разные.
!

20. Разновидности эллипса

Уравнение эллипса со смещенным центром
Y
( x x0 ) 2 ( y y0 ) 2
1
2
2
a
b
O ‘ ( x0 ; y 0 ) — центр эллипса
b
a
x0
X
y0
a
O’
b
Если в уравнении эллипса b a , то большой осью будет ось
B1 B2 2b , фокусы эллипса будут
B1 b
.
лежать на этой оси и связь
между параметрами эллипса
будет такой:
b2 a 2 c 2
F1 c
a
O
.
F2 c
B2 b
a

21. Построение эллипса

1. Построить эллипс
x2 y2
1
4
2
Для построения эллипса нужно знать координаты центра и
размеры полуосей a и b
Y
Центр эллипса O(0;0)
2
Полуоси a 4 a 2,
b2 2 b 2
2
.
Расстояние между фокусами
2 2
c 2 a 2 b 2 4 2 2,
c 2 , т.е. 2c 2 2
O
.
2
X
2
2
Можно найти площадь фигуры, ограниченной эллипсом по формуле
S a b
Для данного примера получим
S 2 2 2 2
2. Построить эллипс
9 x 2 5 y 2 45
Для получения канонического уравнения делаем некоторые
преобразования:
1) Делим все члены уравнения на 45, так чтобы получит единицу
в правой части уравнения
9×2 5 y 2
1
45
45
2) Убираем в знаменатель коэффициенты из числителей
x2
y2
1
45 / 9 45 / 5
x2 y2
1
5
9
Получили уравнение эллипса, из которого определяем положение
Y
центра и размеры полуосей
3
O(0;0) — центр эллипса
a 2 5 a 5,
— полуоси
b2 9 b 3
b a
3) Строим эллипс
5
O
5
3
X
3. Построить кривую
x 1 9 4 y 2
Y
2
2
1. ( x 1) 4 y 9
2. x 1
9 4 y2
3. ( x 1) 9 4 y
2
b
a
2
O’
1
O
X
2
2
(
x
1
)
4
y
9
4.
( x 1) 2 4 y 2
1
5.
9
9
( x 1) 2
y2
1
9
9/4
Таким образом, центр эллипса имеет координаты
Полуоси эллипса
O ‘ ( 1;0)
a 2 9 a 3,
b 2 9 / 4 b 3 / 2 , т.е. a b
При построении необходимо учесть, что уравнение определяет
Только правую половинку эллипса, так как по условию имеем x
1
3x 2 6 x 2 y 2 2 y 0
4. Построить кривую
Данное уравнение определяет эллипс, так как есть квадраты
переменных, знаки при которых одинаковые, а коэффициенты
различные. Кроме того, наличие линейной части уравнения
означает, что центр эллипса смещен от начала координат.
Приводим уравнение к каноническому виду
( x x0 ) 2 ( y y0 ) 2
1
2
2
a
b
Используем прием выделения полного квадрата согласно формуле
( a b) 2 a 2 2 a b b 2
2
2
1. 3( x 2 x) 2( y y ) 0
2. 3( x 2 x 1 1 1 ) 2( y 2 y 1/ 2 (1/ 2) (1/ 2) ) 0
3. 3[( x 1) 2 1] 2[( y 1 / 2) 2 1 / 4] 0
2
2
2
2
2
4. 3( x 1) 2( y 1 / 2) 3 1 / 2 0
5. 3( x 1) 2 2( y 1 / 2) 2 7 / 2
2
2
( x 1) 2 ( y 1 / 2) 2
6. 3( x 1) 2( y 1 / 2) 1
1
7/2
7/2
7/6
7/4
7
O ‘ ( 1;1/ 2) центр , a 7 / 6 , b
полуоси
2
2
2
Y
2
O’
1/ 2
1
O
X

25. 3. Гипербола

Определение. Гиперболой называется множество точек
плоскости, разность расстояний которых до двух данных точек,
называемых фокусами ,по абсолютной есть величина
постоянная, равная длине действительной оси 2a .
Каноническое уравнение гиперболы с центром в начале координат
x2 y2
2 1
2
a b
В этом случае
a действительная полуось
b мнимая полуось
Фокусы гиперболы всегда лежат на действительной оси.
Связь между параметрами гиперболы определяется соотношением
c 2 a 2 b2
!
В уравнение гиперболы входят квадраты
переменных, причем знаки при квадратах разные.
Асимптоты гиперболы – это прямые к которым гипербола
неограниченно приближается на бесконечности.

26. Построение гиперболы

x2 y2
2 1
2
a b
Построение гиперболы
Для построения гиперболы удобно пользоваться
вспомогательными построениями.
1. В системе координат строим прямоугольник с размерами 2a 2b
на осях OX и OY соответственно.
2. Проводим диагонали этого прямоугольника.
Уравнения диагоналей – это уравнения асимптот гиперболы
b
y x
a
3. На действительной оси отмечаем вершины гиперболы и от них
ведем ветви гиперболы к асимптотам.
Y
Y
Y
b
a
a
b
b
b
X
a
a
b
X
c a
a c
b
X

27. Виды гипербол

Y
Рассмотрим другие виды гипербол
Сопряженная гипербола
2
c
2
x
y
1
2
2
a b
b
a X
b действительная полуось
a мнимая полуось
c
Равнобочная гипербола
2
2
x
y
x 2 y 2 a 2 или 2 2 1
a
a
Y
b
Гипербола со смещенным центром O ( x0 ; y0 )
‘
( x x0 ) ( y y0 )
1
2
2
a
b
Гипербола, приведенная к своим асимптотам
2
xy a
2
или
a
y
x
X
a
O’
Y
X
Рассмотрим примеры построения гипербол
1. Построить гиперболу 4 x 2 3 y 2 12
2
Y
2
4x 3y
1
12
12
2
x2
y2
1
12 / 4 12 / 3
X
3
x2 y2
1
3
4
2
O(0;0) центр гиперболы
a2 3
3
a 3 действительная полуось
b2 4 b 2
мнимая полуось
c 2 a 2 b 2 3 4 7,
c 7
2c 2 7
расстояние между фокусами
.
2 Построить кривую
y x2 4
Возведем в квадрат обе части уравнения
y2 x2 4
Собираем квадраты переменных в левую часть уравнения
x2 y2 4
Данное уравнение определяет гиперболу, так как знаки при квадратах
переменных разные. Кроме того, данная гипербола
является сопряженной и равнобочной
x2 y2
Можно записать уравнение в виде
1
Y
4
4
a 2 4 a 2 мнимая полуось
2
b 2 4 b 2 действительная
X
полуось
2
2
Оставляем только нижнюю ветвь
2
гиперболы, так как по условию
y 0
3. Построить кривую
4 x 2 3 y 2 12 8 x 12 y
Данное уравнение определяет гиперболу (знаки при квадратах
переменных различные) со смещенным центром (есть линейная часть)
Приведем уравнение к каноническому виду
( x x0 ) 2 ( y y 0 ) 2
1
a2
b2
4( x 2 2 x) 3( y 2 4 y) 12
4 x 2 8 x 3 y 2 12 y 12
Y
4( x 2 2 x 1 12 12 ) 3( y 2 2 y 2 2 2 2 2 ) 12
4[( x 1) 2 1] 3[( y 2) 2 4] 12
4( x 1) 2 4 3( y 2) 2 12 12
1
4( x 1) 2 3( y 2) 2 4
4( x 1) 2 3( y 2) 2
1
4
4
X
2
O’
( x 1) 2 ( y 2) 2
1
1
4/3
O ‘ ( 1; 2) центр гиперболы
4
2
b
мнимая полуось
a 1 действительная полуось
3
3

31.

4. ПараболаОпределение. Параболой называется множество точек
плоскости, равноудаленных от одной точки, называемой
фокусом, и от данной прямой, называемой директрисой.
Виды парабол
Парабола с осью симметрии OX
x 2 2 py
y 2 px
2
Y
Y
y 2 px
2
Парабола c осью симметрии OY
y 2 2 px
X
x 2 2 py
X
x 2 2 py
Парабола со смещенной вершиной O’ ( x0 ; y0 )
Парабола с осью симметрии OX
Парабола c осью симметрии OY
( x x0 ) 2 2 p( y y0 )
( y y0 ) 2 2 p( x x0 )
Y
y0
Y
O’
x0
x0
!
X
y0
Отличительные признаки уравнения параболы:
отсутствует квадрат одной переменной.
O’
X

33. Построение парабол

Для построения параболы нужно знать:
O’ ( x0 ; y0 ) .
Координаты вершины
Ось симметрии параболы (определяется по той переменно,
квадрат которой отсутствует в уравнении)
Направление ветвей (определяется по знаку : если в правой
части канонического уравнения знак плюс, то ветви параболы
идут в положительном направлении оси симметрии, если знак
минус, то в отрицательном )
Параметр параболы p определяется по коэффициенту при
переменной, стоящей в каноническом уравнении в первой
степени, и определяет «ширину» параболы. Знание параметра
помогает более качественно получить начальный участок
параболы.
2
(
y
2
)
4( x 1)
1. Построить параболу
Данное уравнение является каноническим уравнением параболы,
так как отсутствует квадрат переменной x . Поэтому осью
симметрии параболы будет ось OX.
Вершина параболы в точке O’ (1;2)
Ветви параболы направлены в положительном направлении оси OX,
так как в правой части уравнения знак “плюс”.
2 p 4 ширина параболы
p 2 параметр параболы
p
1
2
Y
p
2
O’ p p
2
1
X
2. Построить кривую
y 3 2 1 x
Y
y 3 2 1 x
( y 3) 2 4(1 x)
( y 3) 2 4( x 1)
y 3
3
O’
X
O
1
O’ (1;3) вершина параболы
Ось симметрии параболы OX, так как отсутствует квадрат
переменной x
Ветви параболы направлены влево, так как в правой части уравнения
получился знак “минус”
p 2 параметр параболы
Так как по условию y 3 , то уравнение определяет только
верхнюю ветвь параболы
3. Построить кривую
y 2 x2
Преобразуем уравнение
x2 2 y
x 2 ( y 2)
Уравнение определяет параболу. Сравнивая с уравнением
( x x0 ) 2 2 p ( y y0 ) , определяем координаты вершины
O’ (0;2) . Ось симметрии OY. Ветви направлены вниз.
1 параметр параболы
p
2
Y
O’ 2
p
1
2
1 1
O
X
4. Построить параболу
4×2 6x 3 y 2 0
В уравнении отсутствует квадрат переменной y, поэтому оно
определяет параболу с осью симметрии OY.
Проведем преобразования уравнения, чтобы привести его к
каноническому виду ( x x0 ) 2 2 p ( y y0 )
6
4 x 2 x 3 y 2 0
4
3
2
4 x 2 x (3 / 4) 2 (3 / 4) 2 3 y 2 0
4
2
3 9
3
9
4 x 3 y 2 0
4 x 3 y 2 0
4 4
4 16
Y
2
3
1
O ‘ y0
4 x 3 y
4
4
X
x0 O
2
3
1
4 x 3 y или
4
12
2
3
3
1
x y
4
4
12
3
3 1
O ‘ ; вершина параболы p параметр параболы
8
4 12
Ветви параболы направлены вниз
2

Общая форма уравнения окружности Калькулятор

Создано Rijk de Wet

Отредактировано Стивеном Вудингом

Последнее обновление: 19 января 2023 г.

Содержание:

• Что такое уравнение окружности в общем виде?
• Как привести общее уравнение окружности к стандартной форме?
• Как преобразовать общее уравнение окружности в параметрическую форму?
• Как использовать общую форму уравнения окружности калькулятора?
• Связанные калькуляторы
• Часто задаваемые вопросы

Добро пожаловать в общую форму калькулятора уравнения окружности , который может помочь вам преобразовать ваше уравнение окружности из общей формы в стандартную и параметрическую форму или наоборот. Здесь мы узнаем:

• Как выглядит уравнение окружности в общем виде ;
• Как написать уравнение окружности в общем виде ; и
• Как преобразовать общую форму уравнения окружности в другие формы .

Что такое уравнение окружности в общем виде?

Общая форма уравнения окружности задается как x² + y² + Dx + Ey + F = 0 с параметрами D, E и F , определяющими свойства окружности, такие как радиус и центр.

Как привести общее уравнение окружности к стандартной форме?

Стандартная форма уравнения окружности (x−A)² + (y−B)² = C

. Мы можем записать общую форму уравнения окружности в стандартную форму, вычислив неизвестные A, B и C из параметров общего уравнения D, E и F .

К счастью, эта математика проста!

1. А = -D/2;
2. В = -Е/2; и
3. С = А² + В² — F.

Как преобразовать общее уравнение окружности в параметрическую форму?

Параметрическая форма уравнения окружности x = A + r cos(α) и y = B + r sin(α) . Чтобы записать общую форму уравнения окружности в параметрическое уравнение, мы вычисляем неизвестные A, B и r :

1. A = −D/2;
2. В = -Е/2; и
3. г = √(А² + В² — F).

Как использовать общую форму уравнения окружности калькулятора?

Общая форма уравнения окружности калькулятор проста в использовании! Вот как:

1. Введите уравнение вашего круга в общем виде вверху калькулятора.
2. Найдите свой круг, переписанный в стандартной и параметрической формах ниже.
3. Также найдите свойства круга , такие как центр, радиус и площадь в самом низу.

В маловероятном случае, если общая форма калькулятора уравнения окружности не соответствует вашим потребностям, рассмотрите один из наших других калькуляторов окружности :

• Калькулятор уравнения окружности;
• Вычислитель центра окружности;
• Калькулятор стандартного уравнения окружности;
• Общая к стандартной форме кругового калькулятора; и
• Стандартная форма к общей форме кругового калькулятора.

Часто задаваемые вопросы

Какова общая форма уравнения (x−3)² + (y+2)² = 25?

Общий вид: x² + y² — 6x + 4y — 12 = 0 . Преобразование из стандартной формы (x — A)² + (y — B)² = C (с параметрами A = 3, B = -2 и C = 25) в x² + y² + Dx + Ey + F = 0 , вычисляем:

1. D = −2A = −6;
2. Е = -2В = 4; и
3. F = А² + В² — С = -12.

Каково общее уравнение окружности с (x−6)² + (y−6)² = 49?

Общая форма этого круга: x² + y² — 12x — 12y + 23 = 0 . У нас есть A = 6, B = 6 и C = 49 в стандартной форме (x−A)² + (y−B)² = C . Итак, чтобы перевести в x² + y² + Dx + Ey + F = 0 , мы вычисляем:

1. Д = -2А = -12;
2. Е = -2В = -12; и
3. F = А² + В² — С = 23.

Какова общая форма уравнения окружности с (x+3)² + (y−5)² = 49?

Общий вид: x² + y² + 6x — 10y — 15 = 0 . Преобразование из стандартной формы (x−A)² + (y−B)² = C (с параметрами A = −3, B = 5 и C = 49) в x² + y² + Dx + Ey + F = 0 , вычисляем:

1. D = −2A = 6;
2. Е = -2В = -10; и
3. F = А² + В² — С = -15.

Rijk de Wet

Введите общее уравнение

вашего круга ниже, и мы покажем вам стандартные и параметрические эквиваленты и центр круга и его свойства ниже.

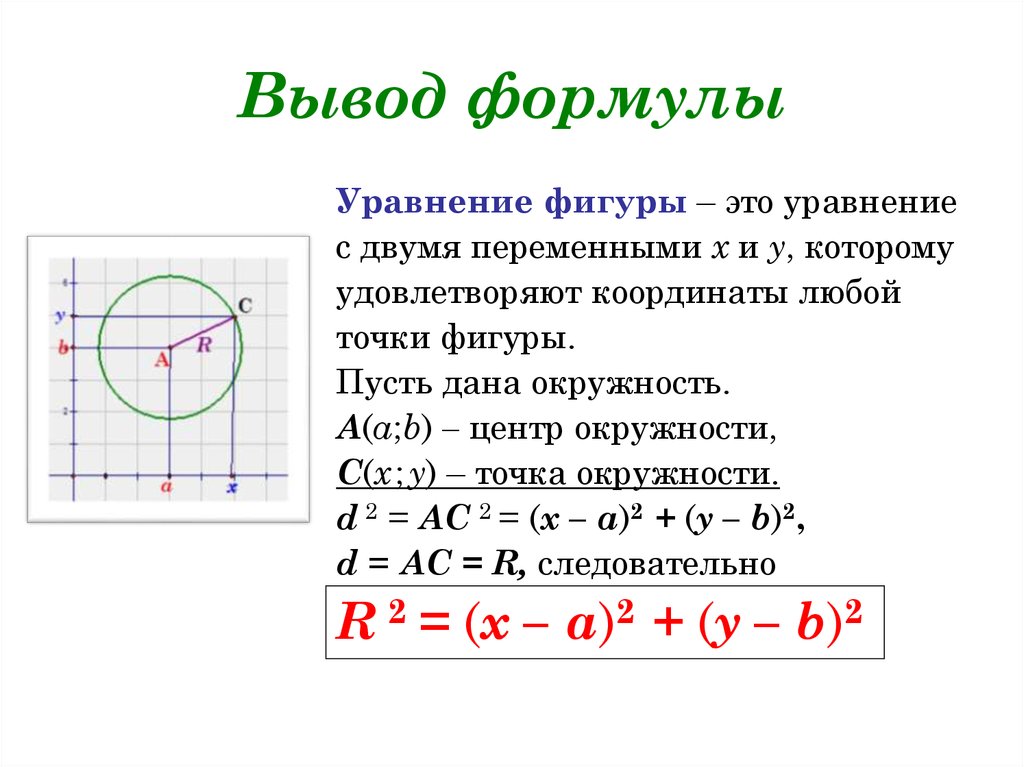
Общее уравнение: x² + y² + Dx + Ey + F = 0

Стандартное уравнение: (x − A)² + (y − B)² = C

Параметрическое уравнение: x = A + r cos(α) , y = B + r sin(α)

Координаты центра

координата x

координата y

свойства окружности

радиус

диаметр

длина окружности

проверить 9 подобных калькуляторов окружности подробнее

Уравнение окружности (примеры вопросов)

Окружность – это множество всех точек на плоскости, равноудаленных от центральной точки. Радиус окружности — это отрезок, концы которого находятся в центре и в любой точке на окружности окружности. 92\).

x	y	x² + y²
4	3	4² + 3² = 25
0	5	0² + 5² = 25
5	0	5² + 0² = 25
-4	3	(-4) ² + 3 3	(-4) ² + 3	(-4). Published in Разное Ваш комментарий будет первым Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий Имя* Email* Веб-сайт Scroll to the top