Решение интеграла онлайн. Неопределенный интеграл.
Что делать, если решение не появляется (пустой экран)?Данный калькулятор по решению интегралов онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
Решение интеграла онлайн
Неопределенный интеграл
Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции.
Решить неопределенный интеграл
Онлайн сервис на matematikam.ru позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте. Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт matematikam.ru поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте matematikam.ru, вы всегда получите точный ответ.
Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн без каких-либо усилий. Для практических задач по нахождению интеграла функции онлайн этот сервер очень полезен. Необходимо ввести заданную функцию, получить онлайн решение неопределенного интеграла
Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн без каких-либо усилий. Для практических задач по нахождению интеграла функции онлайн этот сервер очень полезен. Необходимо ввести заданную функцию, получить онлайн решение неопределенного интеграла
Похожие сервисы:
Решение неопределенного интегралаCalculate indefinite integral online
Решение дифференциальных уравнений онлайн
| Введите дифференциальное уравнение: |
|
Пример: y»+9y=7sin(x)+10cos(3x) |
| Введите задачу Коши (необязательное поле): |
|
Пример: y(0)=7,y'(6)=-1 |
| x | y | π | e | 1 | 2 | 3 | ÷ | триг.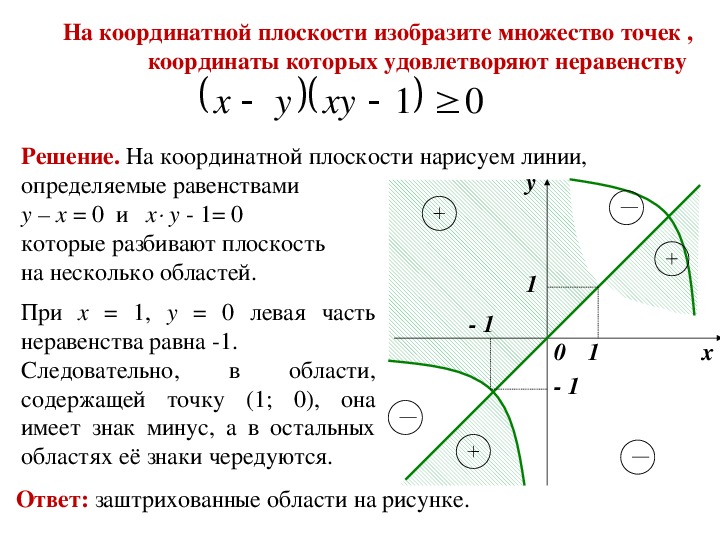 «>ab «>ab | ab | exp | 4 | 5 | 6 | × | стереть |
||||
| ( | ) | |a| | ln | 7 | 8 | 9 | — | ↑ | ↓ | ||||||||||
| √ | 3√ | C | loga | 0 | . | ↵ | + | ← | → | ||||||||||
| TRIG: | sin | cos | tan | csc | sec | назад | ||||
| INVERSE: | arcsin | arccos | arctan | acot | acsc | asec | стереть |
|||
| HYPERB: | sinh | cosh | tanh | coth | x | π | ↑ | ↓ | ||
| OTHER: | ‘ | , | y | = | < | > | ← | → | ||
Данный калькулятор по решению диф.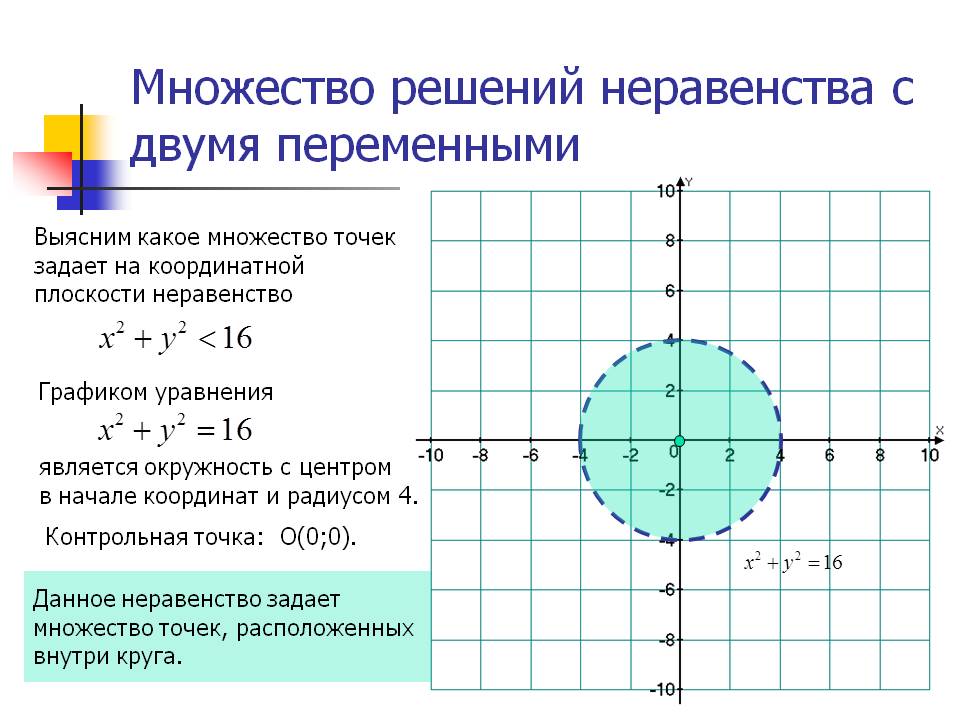 уравнений онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
уравнений онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
Полезные ссылки:
Типы дифференциальных уравнений и методы их решения
Решить дифференциальное уравнение
Дифференциальное уравнение
Дифференциальное уравнение — это уравнение, в котором свзяны между собой переменные, постоянные коэффициенты, искомая функция и производные от функции любого порядка. При этом максимальный порядок производной функции, который присутствует в уравнении, определяет порядок всего дифференциального уравнения. Решить диф уравнение — это определить искомую функцию, как зависимость от переменной.
Современные компьютеры позволяют решать сложнейшие диф уравнения численно. Нахождение же аналитического решения является сложной задачей. Существует множество типов уравнений и для каждого теория предлагает свои методы решения. На сайте matematikam.ru 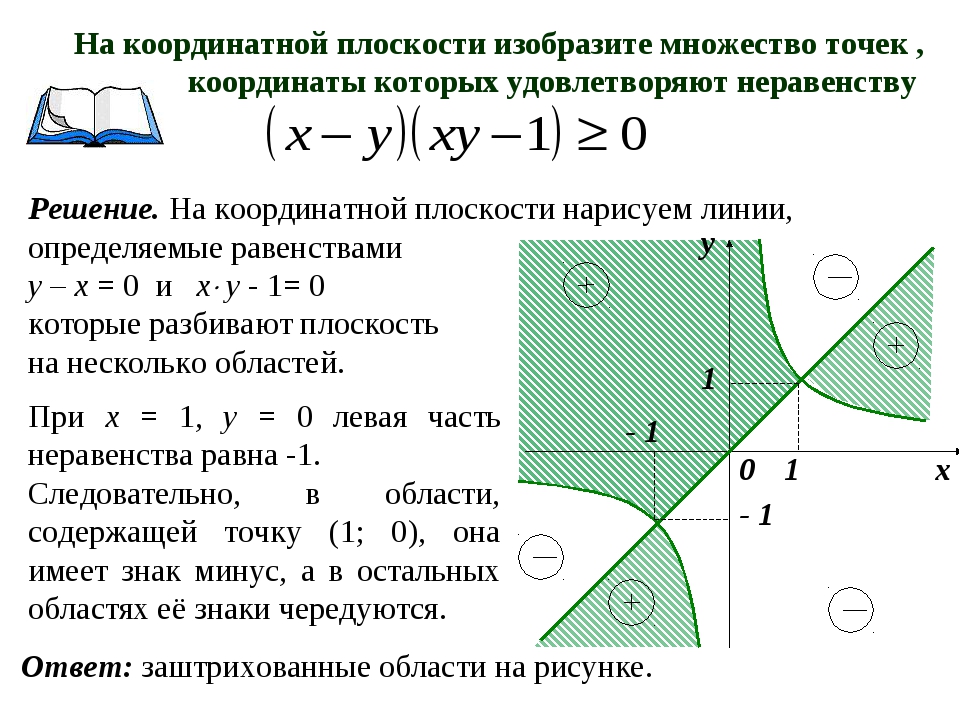 д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям. Мы предлагаем для решения заполнить два поля: само собственно уравнение и при необходимости — начальные условия (задачу Коши) — то есть информацию о граничных условиях искомой функции. Ведь как известно, диф уравнения имеют бесконечное количество решений, поскольку в ответе присутствуют константы, которые могут принимать произвольное значение. Задав задачу Коши, мы из всего множества решений выбираем частные.
д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям. Мы предлагаем для решения заполнить два поля: само собственно уравнение и при необходимости — начальные условия (задачу Коши) — то есть информацию о граничных условиях искомой функции. Ведь как известно, диф уравнения имеют бесконечное количество решений, поскольку в ответе присутствуют константы, которые могут принимать произвольное значение. Задав задачу Коши, мы из всего множества решений выбираем частные.
Данный онлайн калькулятор разработан компанией WolframAlpha и позволяет решать как стандартные дифференциальные уравнения, так и уравнения, не имеющие стандартного подхода для решения.
Похожие сервисы:
Solve differential equation online
Уравнение плоскости по трём точкам
В математике, плоскость — это плоская, двумерная поверхность, которая простирается бесконечно далеко
Общее уравнение плоскости выглядит так:
Плоскость может быть проведена через три не коллинеарные точки ( точки не лежат на одной прямой). И калькулятор ниже может это сделать. Вы вводите координаты трех точек, и калькулятор вычисляет уравнение плоскости, проходящей через эти три точки. Как всегда, объяснения и теорию вы можете найти ниже под калькулятором.
И калькулятор ниже может это сделать. Вы вводите координаты трех точек, и калькулятор вычисляет уравнение плоскости, проходящей через эти три точки. Как всегда, объяснения и теорию вы можете найти ниже под калькулятором.
Уравнение плоскости по трем точкам
Точность вычисленияУравнение плоскости
Вектор коэффициентов
content_copy Ссылка save Сохранить extension Виджет
Плоскость, проходящая через три точки
Зная три точки плоскости, мы знаем, что они удовлетворяют уравнению плоскости. Мы можем выразить это математически:
Точки нам даны, и коэффициенты a, b, c, d нужно найти. Это значит, что мы составляем систему из трех линейных уравнений с четырьмя переменными a, b, c, d:
Или в матричной форме это будет выглядеть так:
Хоть мы и имеем только три уравнения для трех неизвестных, это означает, что система уравнений имеет бесконечное множество решений; тем не менее мы все еще можем использовать этот калькулятор — Решение системы линейных алгебраических уравнений методом Гаусса для получения решения в стандартной форме с неизвестными переменнами ( это значит, что переменные могу принимать любое значение).
В нашем случае, мы имеет только одну независимую переменную. Если все координаты — целые числа, то калькулятор выбирает значение неизвестной переменной так, чтобы оно было наименьшим общим кратным (НОК) из всех знаменателей с другими коэффициентами, чтобы избавиться от фракций в ответе. Если координаты — не целые числа, значение независимой переменной нужно принять за 1.
Построение графика функции онлайн | umath.ru
- Обязательно писать все знаки умножения
- Десятичные дроби нужно разделять точкой
- Список функций и констант смотрите ниже
Как пользоваться программой:
- Можно строить графики сразу нескольких функций. Для этого просто разделяйте функции точкой с запятой (;).
- Масштаб изменяется с помощью кнопок «+» и «−». Кнопка «100%» меняет масштаб на стандартный.
- Положение экрана можно менять, перетаскивая его мышью, а можно стрелками на панели слева.
- Кнопка «·» в центре джойстика переносит начало координат в центр экрана.

- Кнопка «↺» изменяет масштаб на стандартный и переносит начало координат в центр.
- В форме под графиком можно выбрать точку, которую нужно расположить в центре экрана.
Режимы
Обычный. В этом режиме можно строить графики функций, заданных уравнением
Параметрический. Этот режим предназначен для построения графиков кривых, заданных параметрически, то есть в виде
Полярные координаты. Режим позволяет построить график кривой, заданной в полярной системе координат, то есть уравнением где — радиальная координата, а — полярная координата.
Список констант
| Константа | Описание |
|---|---|
pi | Число =3,14159... |
e | Число Эйлера =2,71828... |
Список функций
| Функция | Описание |
|---|---|
+ − * / | Сложение, вычитание, умножение, деление |
( ) | Группирующие скобки |
abs() или | | | Модуль числа. 3 дают 3 дают x в третьей
степени |
sqrt() | Квадратный корень |
sin() | Синус |
cos() | Косинус |
tg() | Тангенс |
ctg() | Котангенс |
arcsin() | Арксинус |
arccos() | Арккосинус |
arctg() | Арктангенс |
arcctg() | Арккотангенс |
ln() | Натуральный логарифм числа |
lg() | Десятичный логарифм числа |
log(a, b) | Логарифм числа b по основанию a |
exp() | Степень числа e |
sh() | Гиперболический синус |
ch() | Гиперболический косинус |
th() | Гиперболический тангенс |
cth() | Гиперболический котангенс |
График функции
Графиком функции называется множество точек плоскости таких, что абсциссы и ординаты
этих точек удовлетворяют уравнению .
Программа создана для школьников и студентов и позволяет строить графики функций онлайн. Во многих браузерах (например, Google Chrome) картинку с графиком функции можно сохранить на компьютер.
Пожалуйста, все предложения и замечания по работе программы пишите в комментариях.
Кроме того мы планируем создать библиотеку функций с интересными и забавными графиками. Если вы открыли функцию с таким графиком, то обязательно напишите об этом в комментариях! Ваше открытие будет опубликовано и станет носить ваше имя ;).
Построение графика по точкам онлайн. График функции
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x) .
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 у = х 2 — 2х принимает при х = 1 .
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) .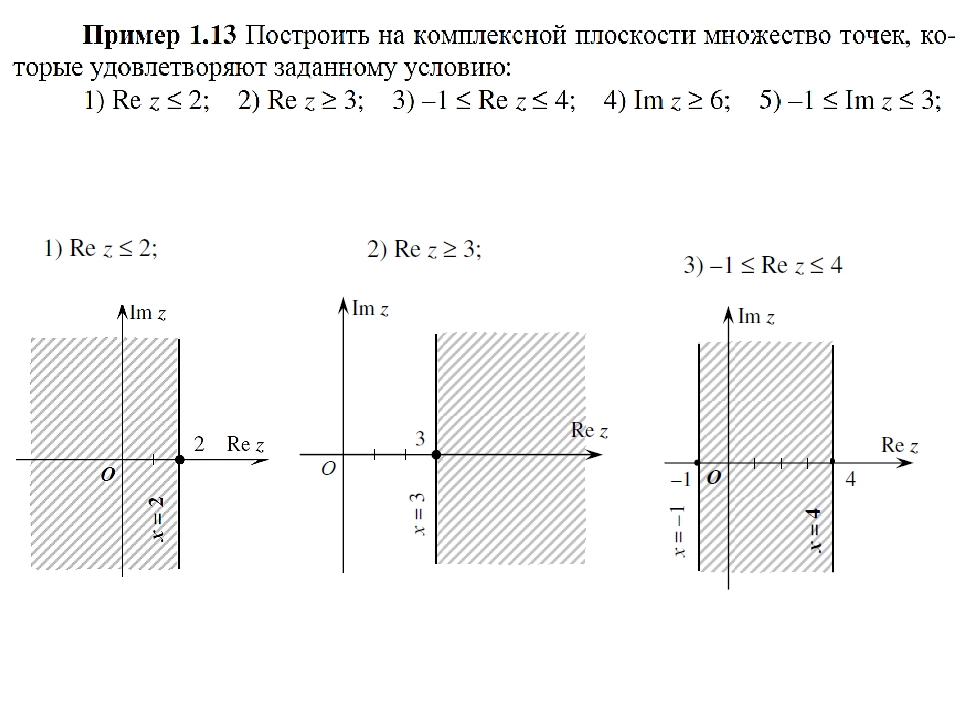 Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
Соответствующие пять точек показаны на рис. 48.
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция.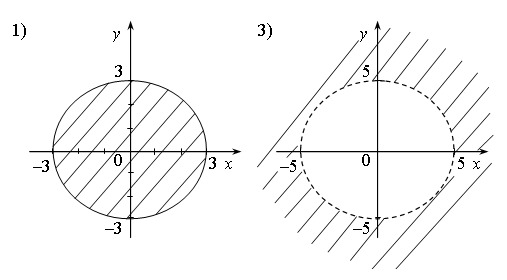 Напомним, как это делается. По определению абсолютной величины числа можно написать
Напомним, как это делается. По определению абсолютной величины числа можно написать
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).
Пример 2. Построить график функции у = |х|.
Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3 . Построить график функции y = |x 2 — 2x|.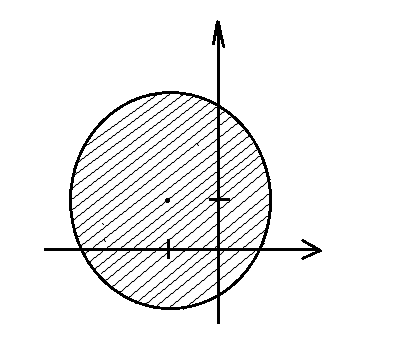
Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x
График функции y = f(x) + g(x)
Рассмотрим задачу построения графика функции y = f(x) + g(x). если заданы графики функций y = f(x) и y = g(x) .
Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).
Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т.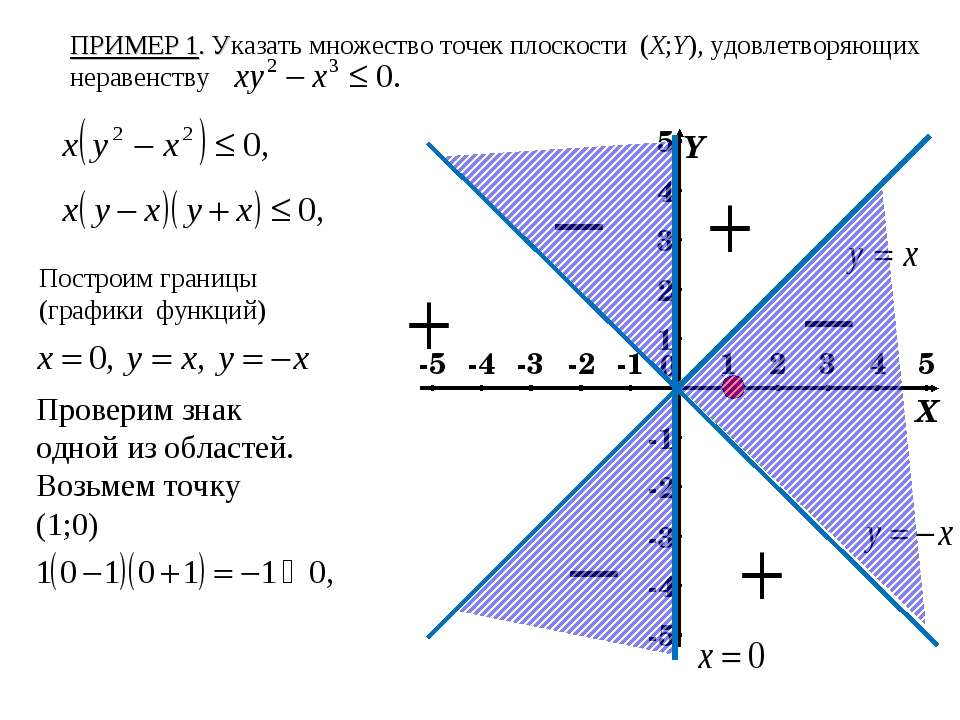 е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
е. y 1 = f(x 0), y 2 = g(х 0). Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .
Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)
Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .
При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.
В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.
Что такое график функций
Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .
Сервисы для построения графиков функций онлайн
Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.
Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.
Инструкция:
- Введите ваше уравнение в поле после знака «=».
- Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.
В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.
Инструкция:
- Выберите необходимый способ задания графика.
- Введите уравнение.
- Задайте интервал.
- Нажмите кнопку «Построить» .
Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.
Инструкция:
- Найдите в списке необходимую вам функцию.
- Щелкните на нее левой кнопкой мыши
- При необходимости введите коэффициенты в поле «Функция:» .

- Нажмите кнопку «Построить» .
В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.
Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).
Инструкция:
- В левом столбце кликните правой кнопкой мыши по свободной строке.
- В нижнем левом углу нажмите на значок клавиатуры.
- На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
- График строится в реальном времени.
Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.
Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos. com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Задание фигур на координатной плоскости уравнениями и неравенствами
Пусть задано уравнение с двумя переменными F(x; y). Вы уже познакомились со способами решения таких уравнений аналитически. Множество решений таких уравнений можно представить и в виде графика.
Вы уже познакомились со способами решения таких уравнений аналитически. Множество решений таких уравнений можно представить и в виде графика.
Графиком уравнения F(x; y) называют множество точек координатной плоскости xOy, координаты которых удовлетворяют уравнению.
Для построения графика уравнения с двумя переменными сначала выражают в уравнении переменную y через переменную x.
Наверняка вы уже умеете строить разнообразные графики уравнений с двумя переменными: ax + b = c – прямая, yx = k – гипербола, (x – a)2 + (y – b)2 = R2 – окружность, радиус которой равен R, а центр находится в точке O(a; b).
Пример 1.
Построить график уравнения x2 – 9y2 = 0.
Решение.
Разложим на множители левую часть уравнения.
(x – 3y)(x+ 3y) = 0, то есть y = x/3 или y = -x/3.
Ответ: рисунок 1.
Особое место занимает задание фигур на плоскости уравнениями, содержащими знак абсолютной величины, на которых мы подробно остановимся.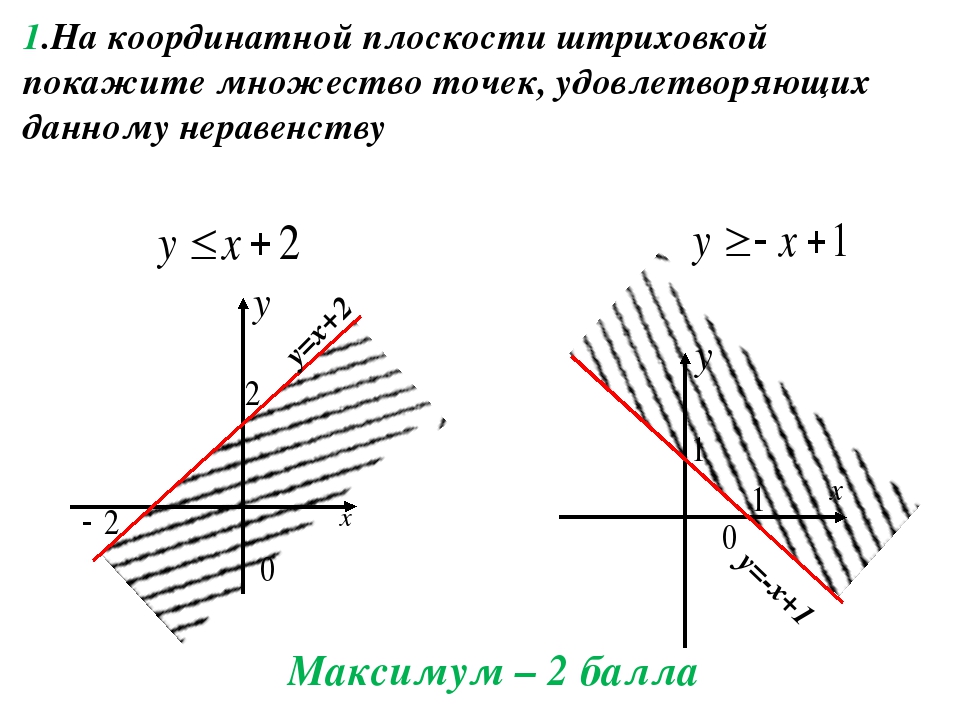 Рассмотрим этапы построения графиков уравнений вида |y| = f(x) и |y| = |f(x)|.
Рассмотрим этапы построения графиков уравнений вида |y| = f(x) и |y| = |f(x)|.
Первое уравнение равносильно системе
{f(x) ≥ 0,
{y = f(x) или y = -f(x).
То есть его график состоит из графиков двух функций: y = f(x) и y = -f(x), где f(x) ≥ 0.
Для построения графика второго уравнения строят графики двух функций: y = f(x) и y = -f(x).
Пример 2.
Построить график уравнения |y| = 2 + x.
Решение.
Заданное уравнение равносильно системе
{x + 2 ≥ 0,
{y = x + 2 или y = -x – 2.
Строим множество точек.
Ответ: рисунок 2.
Пример 3.
Построить график уравнения |y – x| = 1.
Решение.
Если y ≥ x, то y = x + 1, если y ≤ x, то y = x – 1.
Ответ: рисунок 3.
При построении графиков уравнений, содержащих переменную под знаком модуля, удобно и рационально использовать метод областей, основанный на разбиении координатной плоскости на части, в которых каждое подмодульное выражение сохраняет свой знак.
Пример 4.
Построить график уравнения x + |x| + y + |y| = 2.
Решение.
В данном примере знак каждого подмодульного выражения зависит от координатной четверти.
1) В первой координатной четверти x ≥ 0 и y ≥ 0. После раскрытия модуля заданное уравнение будет иметь вид:
2x + 2y = 2, а после упрощения x + y = 1.
2) Во второй четверти, где x < 0, а y ≥ 0, уравнение будет иметь вид: 0 + 2y = 2 или y = 1.
3) В третьей четверти x < 0, y < 0 будем иметь: x – x + y – y = 2. Перепишем этот результат в виде уравнения 0 · x + 0 · y = 2.
4) В четвертой четверти, при x ≥ 0, а y < 0 получим, что x = 1.
График данного уравнения будем строить по четвертям.
Ответ: рисунок 4.
Пример 5.
Изобразить множество точек, у которых координаты удовлетворяют равенству |x – 1| + |y – 1| = 1.
Решение.
Нули подмодульных выражений x = 1 и y = 1 разбивают координатную плоскость на четыре области. Раскроем модули по областям. Оформим это в виде таблицы.
| Область | Знак подмодульного выражения | Полученное уравнение после раскрытия модуля |
| I | x ≥ 1 и y ≥ 1 | x + y = 3 |
| II | x < 1 и y ≥ 1 | -x + y = 1 |
| III | x < 1 и y < 1 | x + y = 1 |
| IV | x ≥ 1 и y < 1 | x – y = 1 |
Ответ: рисунок 5.
На координатной плоскости фигуры могут задаваться и неравенствами.
Графиком неравенства с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого неравенства.
Рассмотрим алгоритм построения модели решений неравенства с двумя переменными:
- Записать уравнение, соответствующее неравенству.

- Построить график уравнения из пункта 1.
- Выбрать произвольную точку в одной из полуплоскостей. Проверить, удовлетворяют ли координаты выбранной точки данному неравенству.
- Изобразить графически множество всех решений неравенства.
Рассмотрим, прежде всего, неравенство ax + bx + c > 0. Уравнение ax + bx + c = 0 задает прямую, разбивающую плоскость на две полуплоскости. В каждой из них функция f(x) = ax + bx + c сохраняет знак. Для определения этого знака достаточно взять любую точку, принадлежащую полуплоскости, и вычислить значение функции в этой точке. Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.
Рассмотрим примеры графического решения наиболее часто встречающихся неравенств с двумя переменными.
1) ax + bx + c ≥ 0. Рисунок 6.
2) |x| ≤ a, a > 0. Рисунок 7.
3) x2 + y2 ≤ a, a > 0. Рисунок 8.
Рисунок 8.
4) y ≥ x2. Рисунок 9.
5) xy ≤ 1. Рисунок 10.
Если у вас появились вопросы или вы хотите попрактиковаться изображать на плоскости модели множества всех решений неравенств с двумя переменными с помощью математического моделирования, вы можете провести бесплатное 25-минутное занятие с онлайн репетитором после того, как зарегистрируетесь. Для дальнейшей работы с преподавателем у вас будет возможность выбрать подходящий для вас тарифный план.
Остались вопросы? Не знаете, как изобразить фигуру на координатной плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Векторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия.
Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину. Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».
Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину. Работе с векторами можно провести аналогию с целыми числами, — как только появляются отрицательные числа на числовой оси, приходится не только считать значение примера, но и все время обращать внимание на знаки. Так и с векторами, во всех действиях – будь то сложение, вычитание, умножение скалярное или векторное и другие действия, приходится не только учитывать реальные масштабы вектора – координаты, длина или угол, но и принимать в расчет его направление. К слову, направления векторов также находят отражение в знаках – обратный изначальному вектор всегда будет со знаком «минус».
В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.
Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.
индивидуальных (x, y) точек графика — WebMath
Быстро! Мне нужна помощь с: Выберите элемент справки по математике … Исчисление, Производные вычисления, Интеграционное вычисление, Частное правило, Монеты, Подсчет комбинаций, Поиск всех комплексных чисел, Сложение комплексных чисел, Вычисление с комплексными числами, Умножение комплексных чисел, Степени комплексных чисел, Преобразование вычитания, Преобразование площади, Преобразование скорости, Преобразование длины , VolumeData Analysis, Find the AverageData Analysis, Find the Standard DeviationData Analysis, HistogramsDecimals, Convert to a дробь, Электричество, Стоимость разложения, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DécimalFractions, Convert to a decimalFractions ВычитаниеФракции, Что это такое: Геометрия, Коробки, Геометрия, Круги, Геометрия, Цилиндры, Геометрия, Прямоугольники, Геометрия, Правые треугольники, Геометрия, Сферы, Геометрия, Квадраты, Графики, Линии, Графики, Любая функция hing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, Equation from point and slopeLines, The Equation from slopeLinesLines Theotation, The Equation from slopeLines Theotation и Y-intation , Нахождение шансов, Математика, Практика многочленов, Математика, Практика основ Квадратные многочлены, Деление многочленов, Факторизация разности квадратов многочленов, Факторизация триномов многочленов, Факторинг с GCF Полиномы, Умножение многочленов, Возведение в степеньПрактика, Математические задачиПропорции, Квадратные уравнения ormulaQuadratic Equations, Solve by FactoringRadicals, Other RootsRadicals, Square RootsRatios, Что они представляют собой Устранение, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, УмножениеФормы, ПрямоугольникиУпрощение, Упрощение, Упрощение продуктов, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение, Упрощение продуктов , Правые треугольники, Ветер, Рисунок
Плоттер наточек — (Line / Dot Connect)
Поиск инструмента
Плоттер точек
Инструмент / Плоттер для рисования точек (точечной диаграммы или кривой) на графике или 2D-плоскости (и при необходимости соединения точек) в соответствии с их координатами.
Результаты
Плоттер точек — dCode
Тег (ы): Функции, теория графов
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Построить точки с их координатами (x, y)
Ответы на вопросы (FAQ)
Как построить точки (x, y)?
Используйте график с двумерной системой координат, например: горизонтальная ось $ x $ и вертикальная ось $ y $.
Найдите положение каждой координаты точек на каждой оси, разместив значение абсциссы на оси $ x $ и значение ординаты на оси $ y $.
Положение точки находится на пересечении вертикальной линии, проходящей через абсциссу, и горизонтальной линии, проходящей через ординату.
Пример: Поместите точку с координатами $ (x, y) = (1,2) $, точка находится в горизонтальном положении $ x = 1 $ и вертикальном положении $ y = 2 $
Для представления значений функции (аффинной, полиномиальной, экспоненциальной и т. Д.), используйте изображение на специальной странице функции в dCode.
Д.), используйте изображение на специальной странице функции в dCode.
Как соединить точки?
Проведите линию между каждой найденной точкой и следующей так, чтобы образовать кривую по частям.
Полученный путь может представлять рисунок, если порядок точек сохраняется.
Как найти функции, соответствующие точкам?
Как нарисовать 2 графика на одном графике?
Используйте вторую таблицу данных, чтобы указать координаты. Укажите разные легенды, чтобы различать две кривые.
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Плоттер точек». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент «Point Plotter» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой «Point Plotter» ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Плоттера точек» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Плоттера точек» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
график, график, точка, координата, абсцисса, ордината
Ссылки
Источник: https: // www.dcode.fr/points-plotter
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокешинга / CTF.точек на графике или плоскости XY
В этом уроке я подготовил восемь (8) разработанных примеров того, как построить точку на декартовой плоскости (названной в честь французского математика Рене Декарта).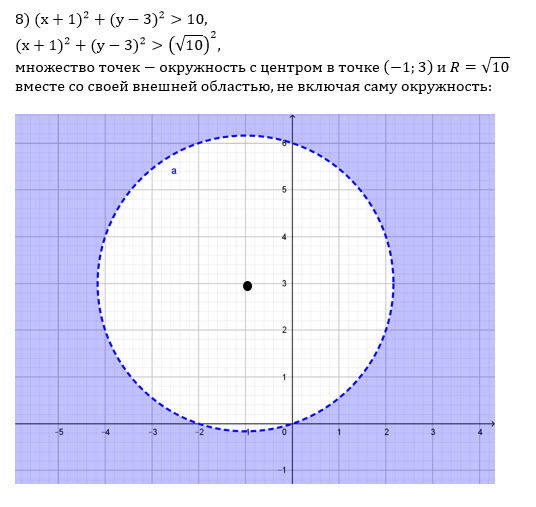 Чтобы построить точку, нам нужны две вещи: точка и координатная плоскость .
Чтобы построить точку, нам нужны две вещи: точка и координатная плоскость .
Давайте кратко поговорим о каждом.
A точка
Точка на плоскости состоит из двух компонентов, в которых порядок имеет значение! Он имеет форму (x, y), где x идет первым, а y — вторым.
- Значение x указывает, как точка перемещается вправо или влево вдоль оси x . Эта ось является главной горизонтальной линия прямоугольной оси или декартовой плоскости.
- Значение y указывает, как точка перемещается вверх или вниз по оси y.Эта ось является главной вертикальной линией прямоугольной оси или декартовой плоскости.
КООРДИНАТНАЯ ПЛОСКОСТЬ (декартова плоскость)
Координатная плоскость состоит из двух линий, пересекающихся под углом под углом 90 градусов (что делает их перпендикулярными линиями) в точке (0,0) , известной как начало координат .
- Компонент x точки (x, y) перемещает точку вдоль горизонтальной линии. Если значение x положительное, точка перемещается на «единицы x» вправо.С другой стороны, если значение x отрицательное, точка перемещается на «единицы x» влево.
- Компонент Y точки (x, y) перемещает точку вдоль вертикальной линии. Если значение y положительное, точка перемещается на «единицы y» вверх. Однако, если значение y отрицательное, точка перемещается на «единицы y» вниз.
Квадранты декартовой плоскости
Пересечение оси x и оси y приводит к созданию четырех (4) секций или делений декартовой плоскости.
- Первый квадрант расположен в верхней правой части плоскости.
- Второй квадрант расположен в верхней левой части плоскости.
- Третий квадрант расположен в нижней левой части плоскости.
- Четвертый квадрант расположен в нижней правой части плоскости.

Примеры нанесения точек на график и определения его квадранта
Пример 1 : Постройте точку (4,2) и определите, в каком квадранте или оси она расположена.
Я начну с размещения точки в начале координат, которая является пересечением осей x и y. Думайте о происхождении как о «доме», откуда берутся все точки.
Затем я перемещу точку от начала координат на 4 единицы вправо, поскольку x = 4 (положительное значение по оси x означает перемещение вправо). Помните, что значение x — это первое число в упорядоченной паре (4,2).
С того места, где я остановился, мне нужно переместить 2 единицы вверх, параллельно главной вертикальной оси, поскольку y = 2 (положительное значение по оси y означает движение вверх).Значение y — это второе число в упорядоченной паре (4,2).
Окончательный ответ должен выглядеть так…
Точка (4,2) расположена в квадранте I .
Пример 2 : Постройте точку (–5, 4) и определите, в каком квадранте или оси она расположена.
Начните с размещения точки в начале координат, известном как центр декартовой координатной оси.
Из начала координат, поскольку x = −5 , переместитесь на 5 единиц влево.
… с последующим перемещением точки на 4 единицы вверх, потому что y = 4 .
Это окончательный ответ. Поскольку нанесенная точка находится в верхнем левом углу оси xy, она должна находиться в квадранте II.
Пример 3 : Постройте точку (5, –3) и определите, в каком квадранте или оси она расположена.
Начать из центра декартовой плоскости.
Переместите 5 единиц вправо, так как x = 5 .
Далее следует перемещение на 3 единицы вниз, так как y = −3 .
Последняя нанесенная точка показана ниже. Находясь в правом нижнем углу декартовой плоскости, это означает, что он находится в квадранте IV.
Пример 4 : Постройте точку (–2, –5) и определите, в каком квадранте или оси она расположена.
Поместите точку в начало координат (центр оси xy). Поскольку x = −2 , переместите точку на 2 единицы влево по оси x.Наконец, спуститесь на 5 единиц параллельно оси y, потому что y = −5 .
См. Анимированное решение ниже.
Точка на графике расположена в нижней левой части декартовой плоскости. Таким образом, он находится в Квадранте III.
Пример 5 : Постройте точку (0,3) и определите, в каком квадранте или оси она расположена.
Я начинаю с анализа данной упорядоченной пары. Поскольку x = 0 , это означает, что нет движения по оси x .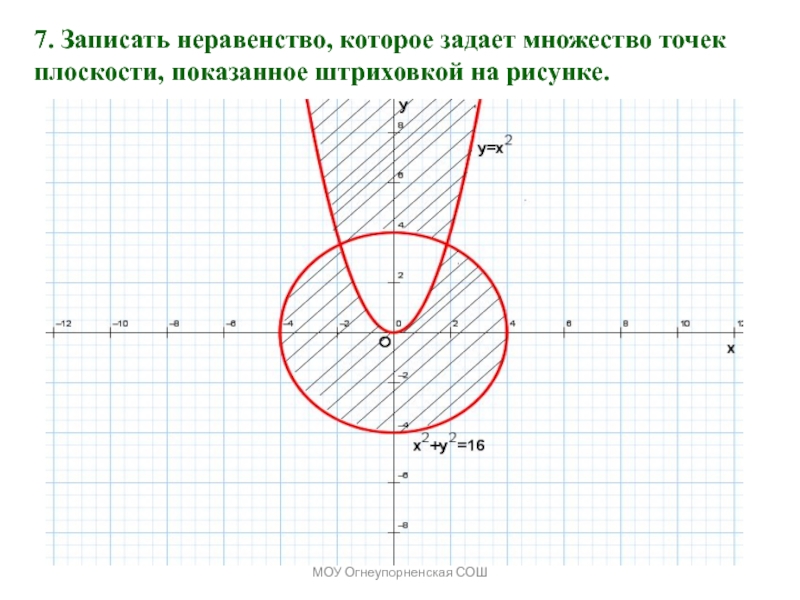 Однако y = 3 означает, что мне нужно переместить его на на 3 единицы вверх на .
Однако y = 3 означает, что мне нужно переместить его на на 3 единицы вверх на .
Точка на графике — , ни ни в Квадранте I, ни в Квадранте II. Чтобы описать его местоположение, мы говорим, что он находится вдоль положительной оси ординат.
Пример 6 : Постройте точку (0, –4) и определите, в каком квадранте или оси она расположена.
Это очень похоже на пример 5. Не будет движения по оси x, так как x = 0 .С другой стороны, y = — 4 говорит мне, что мне нужно переместить точку от начала координат на 4 единицы вниз.
Конечная точка не находится ни на , ни на в квадранте III и не в квадранте IV. Я могу утверждать, что он находится вдоль отрицательной оси ординат.
Пример 7 : Постройте точку (–3,0) и определите, в каком квадранте или оси она расположена.
Из начала координат я сдвину его на 3 единицы влево по оси x, так как x = −3. Если y = 0, это означает, что движения по оси y не последует.
Точка не находится ни на , ни на в квадранте II и не в квадранте III. Он находится вдоль отрицательной оси абсцисс.
Пример 8 : Постройте точку (2,0) и определите, в каком квадранте или оси она расположена.
При x = 2 мне нужно переместить его на 2 единицы вправо. Если y = 0 , это означает, что движения по оси Y не произойдет.
Точка на графике не находится ни на , ни на в Квадранте I или Квадранте IV.Он находится вместе с положительной осью абсцисс.
Практика с рабочими листами
Онлайн-калькулятор для построения графиков точек в прямоугольной системе координат. Определение прямоугольной системы координатСистема координат прямоугольника или декартова плоскость — это набор из двух пересекающихся и перпендикулярных осей, образующих плоскость xy.Горизонтальные оси обычно обозначаются как ось x, а вертикальные оси обычно обозначаются как ось y. Две оси делят плоскость на четыре части, называемые квадрантами. Любая точка на плоскости соответствует упорядоченной паре (x, y) действительных чисел x и y. x называется координатой x, а y называется координатой y. Ниже представлен апплет, который можно использовать для интерактивного исследования точек в прямоугольной системе координат.Построить точки в прямоугольной системе координатвведите координату x и координату y и нажмите «Построить точку». Урок 1 — Квадранты в прямоугольной системе координатДля каждой точки или упорядоченной пары введите x и y и постройте соответствующую точку. Определите квадрант или ось, где расположена каждая точка.(2, 3), (-2, -1), (0, -2), (2, -1), (0, 0), (-2, 3), (2, 0) (-2, 2), (0, 3), (1, -2), (2, 1), (-3, 0), (-2, -3), (2, -2) Вопрос Часть 1 — (см. Ответы ниже)Используйте результаты из приведенного выше руководства и, возможно, некоторые другие моменты, чтобы ответить на следующие вопросы.1 — Для каких значений x и y точка (x, y) находится в квадранте I? 2 — Для каких значений x и y точка (x, y) находится во втором квадранте? 3 — При каких значениях x и y точка (x, y) находится в квадранте III? 4 — Для каких значений x и y точка (x, y) находится в квадранте IV? 5 — Для каких значений x и y точка (x, y) на оси x? 6 — Для каких значений x и y точка (x, y) находится на оси y? Вопрос Часть 2Для каждой ситуации укажите координаты точки и используйте апплет, чтобы проверить свой ответ.(Примечание: на эти вопросы есть бесконечное количество возможных ответов). 1 — точка (x, y) находится во II квадранте. 2 — точка (x, y) находится в квадранте IV. 3 — точка (x, y) находится на оси x. 4 — точка (x, y) находится в квадранте III. 5 — точка (x, y) находится в квадранте I. 6 — точка (x, y) находится на оси y. Ответы на вышеперечисленные вопросы в части 11 — Точка (x, y) такая, что x> 0 и y> 0 расположена в квадранте I. 2 — Точка (x, y) такая, что x <0 и y> 0, расположена в квадранте II. 3 — Точка (x, y) такая, что x <0 и y <0, расположена в квадранте III. 4 — Точка (x, y) такая, что x> 0 и y <0, расположена в квадранте IV. 5 — Точка (x, y) такая, что y = 0, расположена на оси x? 6 — Точка (x, y) такая, что x = 0 расположена на оси y? Дополнительные ссылки и ссылкиГрафические калькуляторы. |
Рекомендуемое (бесплатное) программное обеспечение для построения точек в 3D
Рекомендуемое (бесплатное) программное обеспечение для построения точек в 3D — Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 106k раз
$ \ begingroup $Ищу (желательно бесплатное) программное обеспечение для:
1) построить 3D-точки, считанные из файла.Диаграмма рассеяния подойдет.
2) При желании раскрашиваем точки по свойству — также читаем из файла
Было бы замечательно, если бы эта программа могла также вычислять и отображать наиболее подходящую плоскость через эти точки.
задан 23 мая ’11 в 5: 242011-05-23 05:24
Эндрю С. Эндрю С.47311 золотой знак77 серебряных знаков1111 бронзовых знаков
$ \ endgroup $ 2 $ \ begingroup $Существует множество бесплатных программ, которые это делают.
- Gnuplot, с очень интересными не так часто задаваемыми здесь вопросами (архивная версия) , подходит легко получается. Хорошие выходы в PDF и LaTeX
- Matplotlib: требуется Python, поэтому, вероятно, это не лучший вариант, если вам нужно быстро создавать графики, но если вы думаете о долгосрочном решении, я бы выбрал это,
- R, обычно для статистических вычислений, но неплохие возможности построения графиков. Кроме того, это программное обеспечение, предназначенное для чтения данных в файлах, поэтому оно имеет очень мощные и простые в использовании функции для импорта файлов CSV и т.п.,
- Octave не большой поклонник.Однако не знаю нового основного выпуска. Предыдущие выпуски были основаны на Gnuplot для графической части,
- Scilab непрерывно рос на протяжении многих лет, так что теперь он превратился в монстра. Тоже не большой поклонник.
Надеюсь, вы найдете здесь лучший выбор !!! Удачи, Себастьян
Создан 23 мая ’11 в 6: 142011-05-23 16:14
СебастьянСебастьен58144 серебряных знака1010 бронзовых знаков
$ \ endgroup $ 5 $ \ begingroup $Я проверил все вышеперечисленные опции, и если вы хотите построить что-то в 3D в ближайшие десять минут, а не через десять дней, попробуйте Graphing Calculator 3D.
Создан 28 янв.
Билл ДжемперБилл Джемпер7911 серебряный знак11 бронзовый знак
$ \ endgroup $ $ \ begingroup $Асимптотический язык векторной графики.Ознакомьтесь с галереей графиков / графиков / эскизов. Вот очень красивые примеры / кодовая страница из Франции.
Создан 04 авг.
Джон АлексиуДжон Алексиу9,977 11 золотой знак2525 серебряных знаков5555 бронзовых знаков
$ \ endgroup $ $ \ begingroup $Другой — Plotly, который полностью основан на сети и бесплатен для публичного использования.
Отказ от ответственности: я помогаю разрабатывать Plotly
Создан 06 янв.
$ \ endgroup $ 1 $ \ begingroup $ Математическая программаDataMelt для числовых и статистических вычислений хорошо подходит для построения графиков функций, данных и гистограмм в 3D, а также для сохранения результатов в форматах векторной графики.Он бесплатный и написан на Java (поэтому работает на любом компьютере). Кроме того, он портативный, поэтому с установкой проблем не возникнет.
Вот один пример функции и гистограммы:
Создан 02 апр.
жениться2111 бронзовый знак
$ \ endgroup $ $ \ begingroup $Есть еще MayaVi2:
http: // mayavi.sourceforge.net/
Но я не уверен, как он сравнивается с другими библиотеками визуализации … хотел бы услышать больше комментариев по этому поводу.
Создан 03 июн.
Ян Царь ИньЯнь Царь Инь99344 серебряных знака1515 бронзовых знаков
$ \ endgroup $ 1 $ \ begingroup $Лично я предпочитаю использовать GeoGebra, в нем есть простые функции построения графиков, а также красивые трехмерные графики.Чтобы ввести точку, все, что вам нужно, это упорядоченная тройка, и она построит ее для вас. Он также может отображать сферы и тому подобное.
Надеюсь, это поможет.
Создан 26 авг.
$ \ endgroup $ 1 $ \ begingroup $Посмотри максимы отрисовки втк.
Один из критериев, который я применяю к трехмерным графикам, заключается в том, что они иметь правильную перспективу. Под этим я подразумеваю, что строки и объекты кажутся меньше по мере удаления от зрителя они есть.
Также скрытая линия и поверхность. Трехмерное вращение; масштабирование.
Обновление в реальном времени.
Наконец, возможно, трассировка лучей.
Создан 17 янв.
$ \ endgroup $ $ \ begingroup $Я опаздываю на эту тему, но геогебра: https: // www.geogebra.org/ — отличный простой инструмент. Он может работать в веб-браузере и очень прост в использовании.
Создан 27 янв.
$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Координатная плоскость
Координатная плоскость — это двумерная плоскость, образованная пересечением оси x и оси y.Его можно использовать для поиска точек на плоскости. На рисунке ниже показана координатная плоскость, определяющая пять точек: A, B, C, D и E.
Координатная плоскость также может называться декартовой координатной плоскостью, поскольку она используется как часть декартовой системы координат.
Свойства координатной плоскости
Координатная плоскость характеризуется несколькими свойствами.
ось x и ось y
Координатная плоскость образована пересечением горизонтальной числовой линии, называемой осью x, и вертикальной числовой линии, называемой осью y.Две оси (множественное число для оси) пересекаются по вертикали в точке, называемой началом координатной плоскости.
Сетка часто рисуется на координатной плоскости, чтобы упростить поиск точки. Сетка — это набор равномерно расположенных горизонтальных и вертикальных линий. Сетка на координатной плоскости выше показана светло-серыми отрезками линий.
Квадранты и упорядоченные пары
Местоположение точки задается упорядоченной парой чисел (x 1 , y 1 ).Первое число в паре называется координатой x. Он представляет положение точки на оси x. Точно так же второе число представляет положение точки на оси y и соответственно называется координатой y.
Оси также делят координатную плоскость на четыре области, называемые квадрантами, как показано на координатной плоскости выше.
Определение точки на координатной плоскости
Начать с начала координат при нахождении точки на координатной плоскости.Считайте в положительном (вправо) или отрицательном (влево) направлении по оси x, чтобы определить горизонтальное положение точки. Считайте в положительном (вверх) или отрицательном (вниз) направлении по оси Y, чтобы определить вертикальное положение точки, как показано на рисунке ниже.
Две точки, одна в квадранте I и одна в квадранте III, показаны на рисунке выше.
Пример:
Запишите упорядоченные пары для точек A, B и C, показанных на координатной плоскости ниже.
Начиная с происхождения:
Для точки A переместитесь на 2 единицы влево, чтобы получить x-координату -2.Поскольку вертикального расстояния для перемещения нет, координата y равна 0. Упорядоченная пара для точки A равна (-2, 0).
Для точки B переместитесь на 4 единицы вправо, чтобы получить координату x, равную 4, затем переместитесь на 3 единицы, чтобы получить координату y, равную -3. Упорядоченная пара для точки B — (4, -3).
Для точки C переместитесь на 3 единицы вправо, чтобы получить координату x, равную 3, затем переместитесь на 5 единиц, чтобы получить координату y, равную 5. Упорядоченная пара для точки C для (3, 5).
Построение набора решений в координатной плоскости
График уравнения, записанного в терминах x и y в координатной плоскости, представляет собой набор точек (x, y), который представляет набор решений уравнения.
Например, три решения (их бесконечно много) для y = 2x-1 показаны ниже.
| x | y = 2x — 1 | (x, y) |
|---|---|---|
| -2 | y = 2 (-2) — 1 = -5 | (-2, -5) |
| 0 | y = 2 (0) — 1 = -1 | (0, -1) |
| 2 | y = 2 (2) — 1 = 3 | (2, 3) |
График набора решений показан в координатной плоскости ниже.
График содержит три точки, определенные выше. Любая точка на графике линии является частью решения, установленного для y = 2x — 1. Например, (3, 5) — это еще одна точка на линии, и ее включение дает:
5 = 2 (3) — 1
5 = 5 — истинное утверждение, поэтому (3, 5) — решение для y = 2x — 1.
Знаете ли вы?
Сегодня используется много других систем координат. Одна из них — Глобальная система позиционирования (GPS), система, которая позволяет вам определять ваше местоположение в любой точке Земли в любое время, независимо от погоды.
Декартова плоскость
Декартова плоскостьСодержание: Эта страница соответствует § P.5 (с. 49) текста.
Предлагаемые проблемы из текста:
Стр. 55 # 1, 3, 5, 7, 11, 25, 37, 38, 39, 41, 47, 51, 53, 59.
Координаты на плоскости
Формула расстояния
Формула средней точки
Точечные диаграммы
Координаты на плоскости
Декартова плоскость, названная в честь математика Рене Декарта (1596 — 1650), представляет собой плоскость с прямоугольным система координат, которая связывает каждую точку на плоскости с парой чисел.Основные определения и терминология рассматриваются в разделе P.5 (с.49) текста.
Местоположение точки P определяется упорядоченной парой чисел (a, b).
Приведенный ниже Java-апплет (программа) показывает координатную плоскость и точку (-2, 1). Когда вы перетаскиваете точку, координаты указаны в текстовом поле под графиком. (Когда мы говорим «перетащить точку», мы имеем в виду щелкнуть кнопкой мыши на точку, затем переместите мышь, удерживая нажатой кнопку.) Если щелкнуть и перетащить в точку от указанного точки видимая часть графика изменится. Вы также можете изменить координаты в текстовом поле, а затем нажать введите, чтобы показать положение точки. Учтите, что координаты нужно вводить как число, число. (Некоторые браузеры возвращает ошибку, если перед запятой или после нее стоит пробел.)
Упражнение 1 :
(a) Нарисуйте набор осей координат и нанесите точки (-2,3), (4,5), (3, -4) и (-1, -3).Используйте программу-справочник Плоттер для проверки вашей работы.
(b) Если точка находится на 3 единицы слева от оси y и на 4 единицы выше оси x, то каковы ее координаты?
Вернуться к содержанию
Формула расстояния
Расстояние от точки (x 1 , y 1 ) до точки (x 2 , y 2 ) определяется как
Если A и B — точки, то d (A, B) обозначает расстояние от A до B.
Примечание по технике :
Формула расстояния, приведенная выше, на самом деле является файлом изображения (изображением), отображаемым на этой странице. В настоящее время, это наиболее практичный способ поместить математические формулы на веб-страницы, и он довольно громоздкий. Если здесь есть много формул для отображения, тогда ваш браузер должен загрузить много файлов изображений, и это значительно увеличивает время, которое вам нужно подождать, чтобы увидеть результаты.2).
Это те же символы, которые используются в калькуляторе Java, которые могут быть вызывается с этих страниц курса. Для этого в верхней части всех страниц с содержанием будет ссылка на Калькулятор. курс.
При нажатии на ссылку Java Calculator открывается новое окно браузера, достаточно большое, чтобы вместить калькулятор, чтобы текущая страница все еще была видна. Если щелкнуть текущую страницу при открытом калькуляторе, тогда окно калькулятора переместится за текущее окно, но его можно будет восстановить, щелкнув Калькулятор на панели задач в среде Windows.2).
Расчеты, подобные этому, выполняются в поле в верхней части калькулятора. После ввода формулы нажмите клавишу ввода. (В большинстве случаев после того, как вы нажмете клавишу ввода, отобразится результат, и курсор переместится на следующая строка. Затем вы готовы провести еще один расчет. В некоторых версиях Internet Explorer курсор остается где это было при нажатии Enter. В этом случае вам нужно переместить курсор на новую строку после результата. чтобы сделать следующий расчет.2, результат 169 будет отображаться, потому что после первого вычисления a было установлено равным 13. Значение a можно проверить. набрав и введите.
(b) Убедитесь, что расстояние от (4,3) до (-1, -2) составляет (приблизительно) 7,071.
Вернуться к содержанию
Формула средней точки
Средняя точка отрезка, соединяющего точку (x 1 , y 1 ) с точкой (x 2 , y 2 ) равно
Средняя точка = ((x 1 + x 2 ) / 2, (y 1 + y 2 ) / 2).
Например, средняя точка отрезка, соединяющего (-1,2) и (3,9), равна ((-1 + 3) / 2, (2 + 9) / 2) = (1, 5.5).
Упражнение 3:
(a) M = (1, -2) — средняя точка отрезка от A = (-2, -3) до B = (4, -1). В результате d (A, M) = d (M, Б). Убедитесь, что два расстояния d (A, M) и d (M, B) равны.
(b) Найдите середину отрезка от (-5,3) до (2, -1).
(c) Пусть A = (3,2) и M = (0,4). Если M — середина отрезка от A до точки B, то каковы координаты? из B? Подсказка: возможно, поможет нанесение точек.
Вернуться к содержанию
Точечные диаграммы
Наиболее важной причиной нанесения точек на график является изучение взаимосвязей между переменными. Рассмотрим, например, история сбора средств небольшой общественной радиостанции. В течение первого года работы вклад слушателей составила 70 000 долларов.В таблице ниже указаны суммы взносов за несколько лет.
год | 1 | 3 | 5 | 8 | 11 | 14 |
публикации | 70 000 долл. США | 145 000 долл. США | 190 000 долл. США | 230 000 долл. США | 270 000 долл. США | 290 000 долл. США |
Чтобы получить полезный график этих данных, нам нужно иметь разные масштабы на двух осях.Первое координатой каждой из шести точек будет год, и мы будем измерять взносы с шагом 10 000 долларов США, поэтому первая точка будет (1,7), вторая (3,14,5) и т. д.
Точечная диаграмма данных вклада
Из диаграммы разброса легко увидеть, что, хотя взносы растут, они увеличиваются быстрее в ранние годы. Это визуальное представление данных делает тенденции и закономерности более очевидными, чем они Таблица данных.
Упражнение 4:
Создайте диаграмму рассеяния данных в следующей таблице.
3
7
9
11
8
4
12
2
6
1
10
14
12
7
13
12
4
7
14
3
Существует инструмент Java под названием Scatter Plot, который можно использовать для сюжеты.Чтобы ввести точку, введите ее координаты в текстовое поле с надписью Координаты и нажмите клавишу ввода .


 д.
д.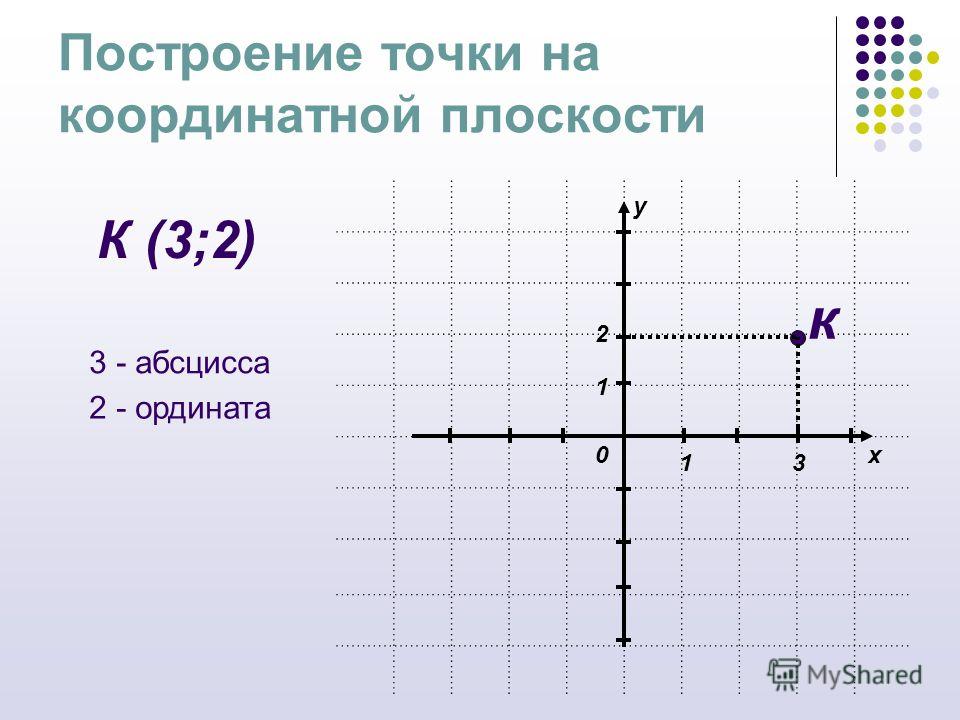 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.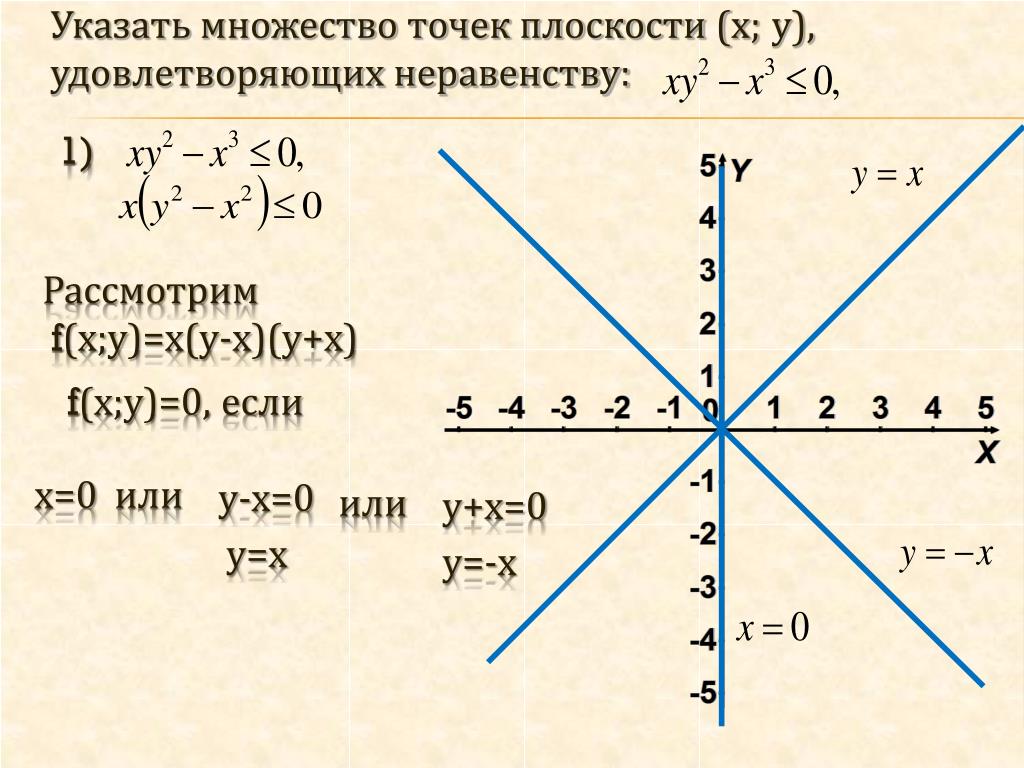

 С помощью этих руководств вы сможете изучить свойства точек и квадрантов в прямоугольных системах координат. При необходимости доступна бесплатная миллиметровка.
С помощью этих руководств вы сможете изучить свойства точек и квадрантов в прямоугольных системах координат. При необходимости доступна бесплатная миллиметровка.
Ваш комментарий будет первым