Линейный График — Mathcracker.Com
Линейный График — Mathcracker.ComРешатели Алгебра
Инструкции: Используйте этот калькулятор, чтобы найти график линейной функции на основе предоставленной вами информации с указанием всех шагов. Для этого вам необходимо предоставить некоторую информацию о линейной функции, которую вы хотите вычислить.
Существуют различные параметры, которые можно использовать для задания линейной функции.
(1) как наклон, так и y-интерцепт,
(2) вы можете ввести любое линейное уравнение (например: \(x + 3y = 2 + \frac{4}{3}x\)),
(3) можно указать наклон и точку, через которую проходит линия, или
(4) можно указать две точки, через которые проходит линия.
▹ Select one of the options:
Provide the slope and y-interceptProvide an equationProvide the slope and one point the line passess throughProvide two points the line passess throughВведите наклон \(m\) линии (числовое выражение. Пример: 2, 1/3 и т. д.) =
Введите точку пересечения оси y \(n\) строки (числовое выражение. Пример: 2, 1/3 и т. д.) =
Линейные графики
p>This linear graph calculator will allow you generate the graph of a линейная функция by providing sufficient information to determine the function.
Варианты определения линейной функции следующие: (1) дать линейное уравнение в x и y, которое можно решить для y; (2) дать непосредственно наклон m и y-интерцепт n; (3) дать наклон линии и точку, через которую она проходит, или (4) дать две точки, через которые проходит линия.
После того, как один из вариантов определения линии будет успешно предоставлен, вы можете нажать кнопку «Graph it», и вам будут предоставлены все шаги для создания графика.
Процедура построения графика функции очень проста, если вы знаете наклон и y-интерцепт, поэтому обычно самое сложное — получить их, когда они не даны напрямую. Имея наклон и y-интерцепт, вы можете получить простейшую форму линии, а именно форма пересечения наклона .
Как получить линейный график?
Как мы уже упоминали в предыдущем параграфе, построение графика линейной функции является тривиальным, если у вас есть линейная функция в виде
\[f(x) = a + bx \]Каковы этапы получения линейного графика?
- Шаг 1: Определите представленную информацию и выполните указанные действия здесь
- Шаг 2: Независимо от того, как вы изначально определили линейную функцию, вы хотите прийти к ее форме с наклоном и перехватом f(x) = a + b x
- Шаг 3: Узнав наклон b и y-пересечение a, вы узнаете, что линия пересекает ось y в точке (0, a), а ее наклон равен b, что означает, что при увеличении оси x на 1 единицу значение y увеличивается на b единиц (если b отрицательно, то y уменьшается)
Вычитание дробей — это просто производная от суммы дробей: Чтобы вычесть две дроби, нужно просто умножить вторую на -1, а затем прибавить ее к первой .
Как работает построитель линейных графиков?
Основная идея заключается в том, чтобы прибыть в форма пересечения наклона независимо от типа предоставляемой информации. При этом мы можем получить наклон и y-интерцепт, элементы с четкой геометрической интерпретацией, что позволяет нам однозначно идентифицировать функцию.
Как сделать нелинейный график?
Конечно, есть примечательные случаи нелинейных функций, которые имеют специальные структуры, которые можно анализировать отдельно, например, случай экспоненциальный график а также Логарифмический график .
Объяснение линейных графиков
Существует несколько различных способов определения линейного графика, но наиболее практичный из них заключается в том, чтобы дать
наклон
а также
Y-перехват
.
Y-интерцепт определяет точку, через которую проходит функция, но этого недостаточно, нам нужно знать ее «направление», которое задается наклоном.
Пример: линейный график
Постройте график следующим образом: \(\frac{2}{3}x + \frac{5}{4}y = \frac{7}{6}\)
Отвечать: Нам было предложено следующее уравнение:
\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=\frac{7}{6}\]которая имеет общий вид. Первое, что мы можем сделать, это упростить константы:
\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=\frac{7}{6}\]Помещая \(y\) в левую часть и \(x\) и константу в правую часть, мы получаем
\[\displaystyle \frac{5}{4}y = -\frac{2}{3}x +\frac{7}{6}\]Теперь, находя \(y\) путем деления обеих частей уравнения на \(\frac{5}{4}\), получается следующее
\[\displaystyle y=-\frac{\frac{2}{3}}{\frac{5}{4}}x+\frac{\frac{7}{6}}{\frac{5}{4}}\] Заключение: Таким образом, работа, показанная выше, показывает, что уравнение имеет вид \(\displaystyle f(x)=-\frac{8}{15}x+\frac{14}{15}\), что соответствует линии с наклоном \(\displaystyle b = -\frac{8}{15}\) и y-пересечением \(\displaystyle a = \frac{14}{15}\).
Исходя из этой информации, график является:
Пример: более линейные графы
Интерпретируйте геометрически график линейной функции: \(f(x) = \frac{1}{3} + \frac{5}{4}x\)
Отвечать: В этом случае заданная функция \(f(x) = \frac{1}{3} + \frac{5}{4}x\) задана в форме наклона-пересечения, то есть \(y = a + bx\).
В данном контексте наклон равен \(b = \frac{5}{4}\), что указывает на то, что при увеличении на одну единицу в x, линия увеличивается на \(\frac{5}{4}\) единиц в y.
Кроме того, y-пересечение равно \(a = \frac{1}{3}\), что указывает на то, что линия пересекает y-пересечение в точке \( (0, \frac{1}{3})\).
чем завершается расчет.
Пример: еще один пример линейного графика
Является ли график x = 4 линейным графиком?
Отвечать:
Да, в том смысле, что график является линией. Но в данном случае это линия с x = 4 для всех значений y, так что тогда это вертикальная линия.
Но в данном случае это линия с x = 4 для всех значений y, так что тогда это вертикальная линия.
чем завершается расчет.
Другие полезные линейные калькуляторы
Линейные функции настолько важны, что с ними можно сделать очень многое. Во-первых, вы можете найти Перпендикулярные линии и вы можете решать системы уравнений когда у вас есть более одной линейной функции.
Применение линейные функции а также Линейные уравнения бесконечны во всех областях математики.
Сброс пароля
зарегистрироваться
Линейная функция. Построение графика линейной функции.
- Понятие функции
- Линейная функция
- Построение графика линейной функции
Сегодняшняя статья посвящена понятию «функция». Линейная функция и координатная плоскость. Изучение правил построения графика линейной функции.
Линейная функция и координатная плоскость. Изучение правил построения графика линейной функции.
Понятие функции
Рассмотрим следующую конструкцию: y = f(x).
В школе так обозначают функцию. Многих учеников пугает данная запись, но, если заменить слово функция на слово зависимость, вся эта конструкция прочитается уже немножко по-другому. Если вместо F поставить слово «зависит», то мы прочитаем «Y зависит от X». F — это некоторые правила или формула, зная которые при помощи подстановки вместо X каких-то чисел мы можем найти Y. Правила эти задаются совершенно разными формулами. Например, самый простой пример: y = 2x +1
2x+1 – это и есть правило, которое в уравнении функции обозначается буквой F. Если мы вместо X поставим 1, мы всегда можем посчитать Y.
Правило может быть любым, например: x2+x-1
Значение Y полностью зависит от значения X. X — это независимая переменная, Y — зависимая переменная. Буква X в этом уравнении функции y=f(x) называется аргументом. Y называется значением функции или просто функцией.
Y называется значением функции или просто функцией.
Линейная функция
Возьмём уравнение функции, которое мы уже рассматривали
y = 2x +1
Составим следующую табличку, как показано на рисунке. Вместо X мы будем подставлять любые числа, какие захотим. После того, как мы выбрали значения Х, нужно найти соответствующие им значения Y и записать их в таблицу.
Что же за числа у нас получились. Это те самые значения аргумента и значения нашей функции. А теперь давайте представим, что пары чисел X и Y – это координаты точек на координатной плоскости. Обозначив и соединив эти точки, мы получим графическое изображение функции, это самой зависимости. Если взять абсолютно любую точку на получившейся прямой, найти ее координаты и подставить уравнение функции, то это уравнение превратится в верное равенство. Олимпиада по математике на 20% состоит из заданий на различного рода функции, и знать самую основную из них — это очень важно.
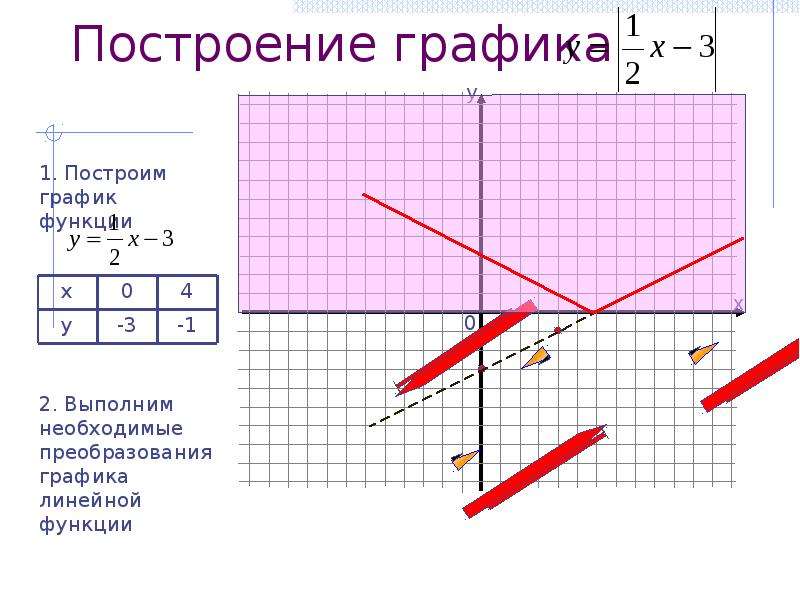
Построение графика линейной функции
График функции — это множество точек, соединенных между собой линией, а точки эти получены при подставлении вместо X каких-то чисел и подсчете Y.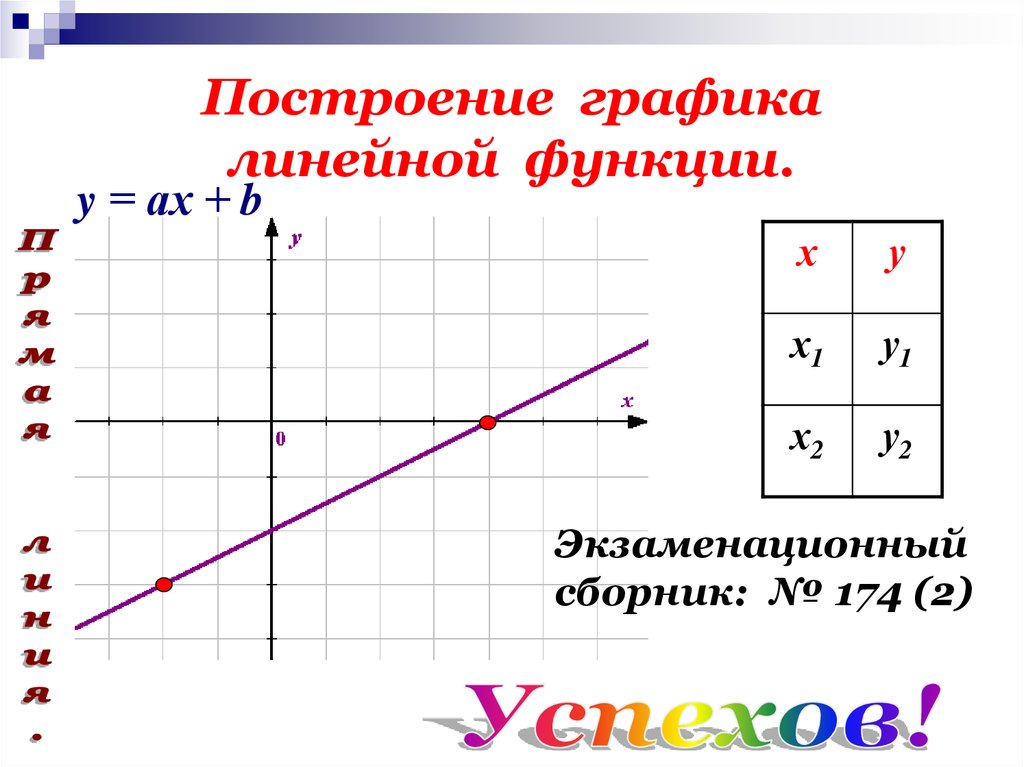
Линейная функция — одна из самых основных, самая простая функция, графиком которой является простая прямая линия.
y = kx + b, где x — независимая переменная, k и b — любые числа. Если K положительное, то график функции идет вверх, то есть возрастает. Если он отрицателен, то график функции идет вниз, то есть убывает. Если функция возрастает, то угол между этой прямой и осью Х острый, если функция убывает, то угол между этой прямой и осью Х всегда тупой. Именно поэтому этот самый коэффициент назвали угловым коэффициентом этой прямой. Если угловой коэффициент равен нулю, то прямая параллельна оси X. Число B – это координата Y точки пересечения графика функции с осью Y.
Преподавание линейных уравнений в математике
Назад к формеМатематика
Фигурный посох
Чтение через 10 мин
Для многих учащихся 8-х классов и старше числа и фигуры, которые они узнали, действительно начинают складываться воедино, когда они составляют и решают линейные уравнения. Эта тема объединяет идеи об алгебре, геометрии и функциях, и многим детям — и взрослым! — может быть трудно усвоить ее. В этой статье объясняется, что такое линейное уравнение, и рассматриваются различные примеры. Затем он предлагает уроки для введения и развития концепции линейных уравнений с одной переменной для ваших студентов.
Что такое линейное уравнение?
Как и любое другое уравнение, линейное уравнение состоит из двух выражений, равных друг другу. Есть некоторые ключевые особенности, общие для всех линейных уравнений:
- Линейное уравнение имеет только одну или две переменные.
- Ни одна переменная в линейном уравнении не возводится в степень больше 1 и не используется в качестве знаменателя дроби.
- Когда вы находите пары значений, которые делают линейное уравнение верным, и наносите эти пары на координатную сетку, все точки лежат на одной линии.
 График линейного уравнения представляет собой прямую линию.
График линейного уравнения представляет собой прямую линию.
Линейное уравнение с двумя переменными может быть описано как линейная зависимость между х и y , то есть двумя переменными, в которых значение одной из них (обычно y ) зависит от значение другого (обычно x ). В этом случае х является независимой переменной, а х зависит от нее, поэтому х называется зависимой переменной.
Независимо от того, помечено ли это значение x , независимая переменная обычно откладывается по горизонтальной оси. Большинство линейных уравнений являются функциями. Другими словами, каждому значению x соответствует только одно значение y . Когда вы присваиваете значение независимой переменной x , вы можете вычислить значение зависимой переменной y . Затем вы можете нанести точки, названные каждой парой ( x , y ) на координатной сетке.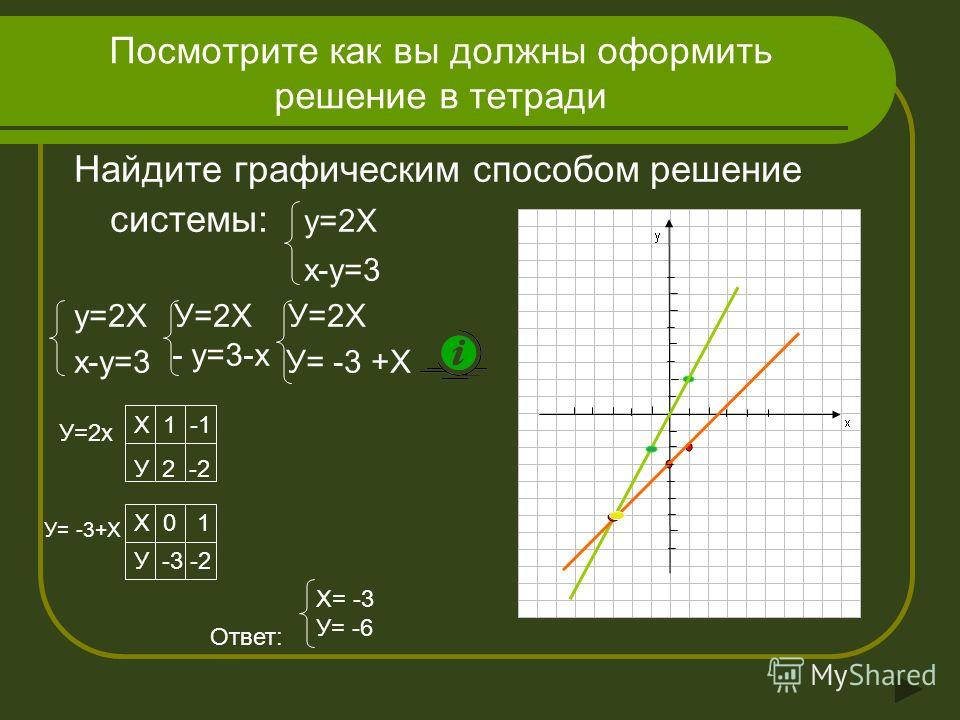
Описание линейных отношений
Учащиеся уже должны знать, что любые две точки определяют линию. Таким образом, для построения графика линейного уравнения на самом деле требуется только найти две пары значений и провести линию через точки, которые они описывают. Все остальные точки на линии дадут значения x и y , которые удовлетворяют уравнению.
Графики линейных уравнений всегда являются линиями. Однако важно помнить, что не каждая точка на линии, описываемой уравнением, обязательно будет решением задачи, описываемой уравнением. Например, задача может не иметь смысла для отрицательных чисел (скажем, если независимой переменной является время) или очень больших чисел (скажем, для чисел больше 100, если зависимой переменной является оценка в классе).
Как выглядит линейное уравнение?
Пример 1: расстояние = скорость × время В этом уравнении для любой постоянной скорости зависимость между расстоянием и временем будет линейной. Однако расстояние обычно выражается положительным числом, поэтому на большинстве графиков этого отношения точки отображаются только в первом квадранте. Обратите внимание, что направление линии на графике ниже — снизу слева направо вверх. Линии, стремящиеся в этом направлении, имеют положительные уклон . Положительный наклон указывает, что значения по обеим осям увеличиваются слева направо.
Однако расстояние обычно выражается положительным числом, поэтому на большинстве графиков этого отношения точки отображаются только в первом квадранте. Обратите внимание, что направление линии на графике ниже — снизу слева направо вверх. Линии, стремящиеся в этом направлении, имеют положительные уклон . Положительный наклон указывает, что значения по обеим осям увеличиваются слева направо.
Опять же, на этом графике мы связываем значения, которые имеют смысл только в том случае, если они положительны, поэтому мы показываем точки только в первом квадранте. Более того, в этом случае, поскольку ни один многоугольник не имеет менее 3 сторон или углов, а количество сторон или углов многоугольника должно быть целым числом, мы показываем график, начинающийся с (3,3), и указываем пунктирной линией, что точки между нанесенными на график не имеют отношения к задаче.
Более того, в этом случае, поскольку ни один многоугольник не имеет менее 3 сторон или углов, а количество сторон или углов многоугольника должно быть целым числом, мы показываем график, начинающийся с (3,3), и указываем пунктирной линией, что точки между нанесенными на график не имеют отношения к задаче.
Поскольку совершенно разумно иметь как положительные, так и отрицательные температуры, мы наносим точки на этом графике на полной координатной сетке. (Хотя это и не видно на графике, самая низкая возможная физическая температура составляет около –460° по Фаренгейту, поэтому не каждое решение на графике полезно!) линия относится к y- ось и наклон линии вверх или вниз, если смотреть на нее слева направо. С технической точки зрения, наклон показывает скорость, с которой зависимая переменная изменяется по отношению к изменению независимой переменной.
Расчет уклона
Выберите любые две точки на линии. Чтобы найти скорость изменения y , вычтите значение y первой точки из значения y второй точки: ( y 2 – y 1 ). Чтобы найти скорость изменения x , вычтите значение x первой точки из значения x второй точки: ( x 2 – x 1 ). Чтобы найти скорость, с которой y изменяется по отношению к изменению x , рассчитайте отношение: ( y 2 – y 1 )/( 902 9029 x 0 х 1 ).
Чтобы найти скорость изменения y , вычтите значение y первой точки из значения y второй точки: ( y 2 – y 1 ). Чтобы найти скорость изменения x , вычтите значение x первой точки из значения x второй точки: ( x 2 – x 1 ). Чтобы найти скорость, с которой y изменяется по отношению к изменению x , рассчитайте отношение: ( y 2 – y 1 )/( 902 9029 x 0 х 1 ).
Если мы обозначим точку A в качестве первой точки и Point B в качестве второй точки, наклон линии равен (–2 – 4)/(–1 – 2) = –6/–3 или 2. Не имеет значения. какие точки на линии вы обозначили как A и B , при условии, что мы согласны с тем, какая точка является «первой» ( x 1 , y 1 ), а какая «второй» ( х 2 , у 2 ). Если мы обозначим точку B как первую точку, а точку A в качестве второй точки, значение наклона такое же: (4 – -2)/(2 – -1) = 6/3 или 2. Это также то же значение, которое вы получите, если выберете любую другую пару точек на линии для вычисления уклона.
Если мы обозначим точку B как первую точку, а точку A в качестве второй точки, значение наклона такое же: (4 – -2)/(2 – -1) = 6/3 или 2. Это также то же значение, которое вы получите, если выберете любую другую пару точек на линии для вычисления уклона.
Уравнение прямой можно записать в форме, которая делает наклон очевидным и позволяет рисовать линию без каких-либо вычислений. Если учащимся удобно решать простое линейное уравнение, состоящее из двух шагов, они могут написать линейные уравнения в форме пересечения наклона. Форма линейного уравнения с пересечением наклона: y = м x + b . В уравнении x и y являются переменными. Числа м и b дают наклон линии ( м ) и значение y , когда x равно 0 ( b ). Значение y , когда x равно 0, называется y -перехватом , потому что (0, y ) — точка, в которой линия пересекает ось y .
Вы можете нарисовать линию для уравнения, соответствующего этой линейной формуле, построив график (0, b ), а затем используя м , чтобы найти другую точку. Например, если м равно 1/2, вы можете интерпретировать это как разницу в 1 среди y координат для каждой разницы в 2 среди x координат (то есть ( y 2 – y 1 )/( х 2 – x 1 ) = 1/2). Отсчитайте +2 по оси x-, затем +1 по оси y-, чтобы добраться до другой точки: (2, b + 1).
Уравнение для этой прямой: y + 3 = 2 x . В форме пересечения уклона уравнение имеет вид y = 2 x – 3. В этой форме вы можете легко увидеть, что уклон м = 2. Глядя на график, уклон действительно равен 2, так как для каждого + 2 изменения в y , есть +1 изменение в х . Теперь посмотрите на b в уравнении: –3 должно быть там, где линия пересекает ось y , и это так.
Когда линия наклоняется вверх слева направо, она имеет положительный наклон. Это означает, что положительное изменение х связано с положительным изменением х . Чем круче наклон, тем больше скорость изменения х по отношению к изменению х . Уклон 6 круче, чем уклон 1, который, в свою очередь, круче, чем уклон 1/6. Когда линия представляет точки реальных данных, нанесенные на координатную плоскость, положительный наклон указывает на положительную корреляцию, и чем круче наклон, тем сильнее положительная корреляция.
Рассмотрим линейное уравнение, в котором независимая переменная g — это количество использованного газа в галлонах, а зависимая переменная d — пройденное расстояние в милях. Если вы водите большую старую машину, у вас будет плохой расход бензина. Количество пройденных миль мало по сравнению с количеством израсходованного газа, поэтому значение м является малым числом. Наклон линии достаточно плавный. Если вместо этого вы едете на легком экономичном автомобиле, вы увеличиваете расход бензина. Вы проезжаете больше миль относительно того же количества потребляемого газа, поэтому значение м больше и линия круче. Обе ставки положительны, потому что вы по-прежнему проезжаете положительное количество миль на каждый галлон бензина, который вы потребляете.
Наклон линии достаточно плавный. Если вместо этого вы едете на легком экономичном автомобиле, вы увеличиваете расход бензина. Вы проезжаете больше миль относительно того же количества потребляемого газа, поэтому значение м больше и линия круче. Обе ставки положительны, потому что вы по-прежнему проезжаете положительное количество миль на каждый галлон бензина, который вы потребляете.
Когда линия наклонена вниз слева направо, она имеет отрицательный наклон. Это означает, что отрицательное изменение х связано с положительным изменением х . Когда линия представляет точки реальных данных, нанесенные на координатную плоскость, отрицательный наклон указывает на отрицательную корреляцию, и чем круче наклон, тем сильнее отрицательная корреляция.
Рассмотрим строку, представляющую количество перцев, оставшихся для посадки после нескольких минут, проведенных в саду. Если в саду может поместиться 18 растений перца, а вы сажаете 1 растение перца в минуту, то скорость, с которой садовая квартира опустеет, довольно высока, поэтому абсолютное значение м — большее число, а линия круче. Если вместо этого вы сажаете только 1 растение перца каждые 2 минуты, вы все равно опустошите садовую квартиру, но скорость, с которой вы это делаете, будет ниже. Абсолютное значение м ниже (1/2 вместо 1), и линия не такая крутая.
Если вместо этого вы сажаете только 1 растение перца каждые 2 минуты, вы все равно опустошите садовую квартиру, но скорость, с которой вы это делаете, будет ниже. Абсолютное значение м ниже (1/2 вместо 1), и линия не такая крутая.
Когда y не изменяется при изменении x , график линии горизонтален. Горизонтальная линия имеет нулевой наклон.
Неопределенный наклонКогда x не изменяются при изменении y , график линии является вертикальным. Вы не можете вычислить наклон этой линии, потому что вам нужно разделить на 0. Обратите внимание, что вы можете думать об этих линиях как о «бесконечно крутых», либо положительно или отрицательно. Наклон вертикальной линии не определяется.
Линии с одинаковым уклоном Две линии с одинаковым уклоном имеют одинаковую крутизну. Это означает одно из двух: либо линии параллельны, либо они являются одной и той же линией.
Во всех этих трех строках каждое изменение на 1 единицу в y связано с изменением на 1 единицу в x . Все три имеют наклон 1.
Решение двухшаговых линейных уравнений с рациональными числамиКогда линейное уравнение имеет две переменные (как это обычно бывает), оно имеет бесконечное число решений. Каждое решение представляет собой пару чисел ( x , y ), которые делают уравнение верным. Решение линейного уравнения обычно означает нахождение значения y для заданного значения x .
Когда уравнение уже имеет форму пересечения наклона
Если уравнение уже имеет форму y = m x + b , с переменными x и y и m и b рациональными числами, решение для конкретных значений является простым. Выберите значение для x, и вычислите соответствующее значение для y . Вы заметите, что для x легко выбрать значение 0, потому что в этом случае y = b . Студентам может быть предложено составить таблицы значений для линейных уравнений. Это просто Т-таблицы со списками значений для x с соответствующими значениями для y .
Студентам может быть предложено составить таблицы значений для линейных уравнений. Это просто Т-таблицы со списками значений для x с соответствующими значениями для y .
Двухшаговые уравнения включают поиск значений для выражений, которые имеют более одного члена . Терм может быть числом, переменной или числами и переменными, перемноженными вместе. Члены выражения разделяются символами сложения или вычитания. 2 x — это выражение с одним членом. 2 x + 6 имеет два члена. Чтобы найти значение y по заданному значению x , подставьте x -значение в выражение.
Рассмотрим уравнение y = 2 x + 6. Найдите значение для y , когда x = 5:
| Подставьте значение для в уравнение. | y = 2(5) + 6 |
| Умножить. | у = 10 + 6 |
Доп. | y = 16 |
Когда уравнение не в форме пересечения наклона
Если линейное уравнение не представлено в форме пересечения наклона (то есть не записано как y = m x + b ), учащиеся могут составить таблицу значений, чтобы найти решения уравнения, но может быть проще сначала представить уравнение в форме пересечения наклона. Это требует зеркального отображения операций с каждой стороны уравнения до тех пор, пока y не окажется в одной части уравнения, равным линейному выражению, включающему x . Вы можете манипулировать уравнением таким образом из-за свойств равенства:
- Если a = b , то a + c = b + c.
- Если a = b , то a – c = b – c.
- Если a = b , то ac = до н.э.
- Если a = b , то a ÷ c = b ÷ c (пока c ≠ 0).

Рассмотрим 2 x + y – 6 = 0. Это уравнение не в форме пересечения наклона, но вы можете использовать свойства равенства, чтобы получить y на одной стороне уравнения.
- Вы можете вычесть y из обеих частей уравнения, чтобы получить 2 x – 6 = – y . Затем умножьте обе части уравнения на –1, чтобы получить –2 x + 6 = лет.
- В качестве альтернативы можно вычесть 2 x и прибавить 6 к обеим частям уравнения, чтобы получить y = –2 x + 6.
Два уравнения: –2 x + 6 = y и y 6 –0030 2 x эквивалентны. Вы можете превратить одно в другое, используя коммутативное свойство сложения, которое утверждает, что a + b = b + a , и симметричное свойство равенства, которое утверждает, что если a = б , затем б = а .
| Переместительное свойство сложения | –2x + 6 = y эквивалентно 6 – 2 x = y . |
| Симметричное свойство равенства | 6 – 2 x = y эквивалентно y = 6 – 2 x . |
Линейные уравнения: знакомство с концепцией
Материалы: Координатная сетка, которую могут видеть все учащиеся (сетка должна идти как минимум от –10 до +10 по обеим осям), инструмент для разметки сетки точками и строки
Подготовка: Поскольку учащиеся будут считывать точки с графиков и строить линии из списков точек, они (и вы) должны быть готовы использовать линейку для создания точных прямых линий. При онлайн-обучении используйте цифровой инструмент, способный генерировать точки и линии.
Необходимые навыки и понятия: Учащиеся должны уметь наносить точки на координатную плоскость и должны быть знакомы с различными способами обозначения умножения и деления в уравнении. Они также должны быть знакомы с порядком операций и свойствами равенства.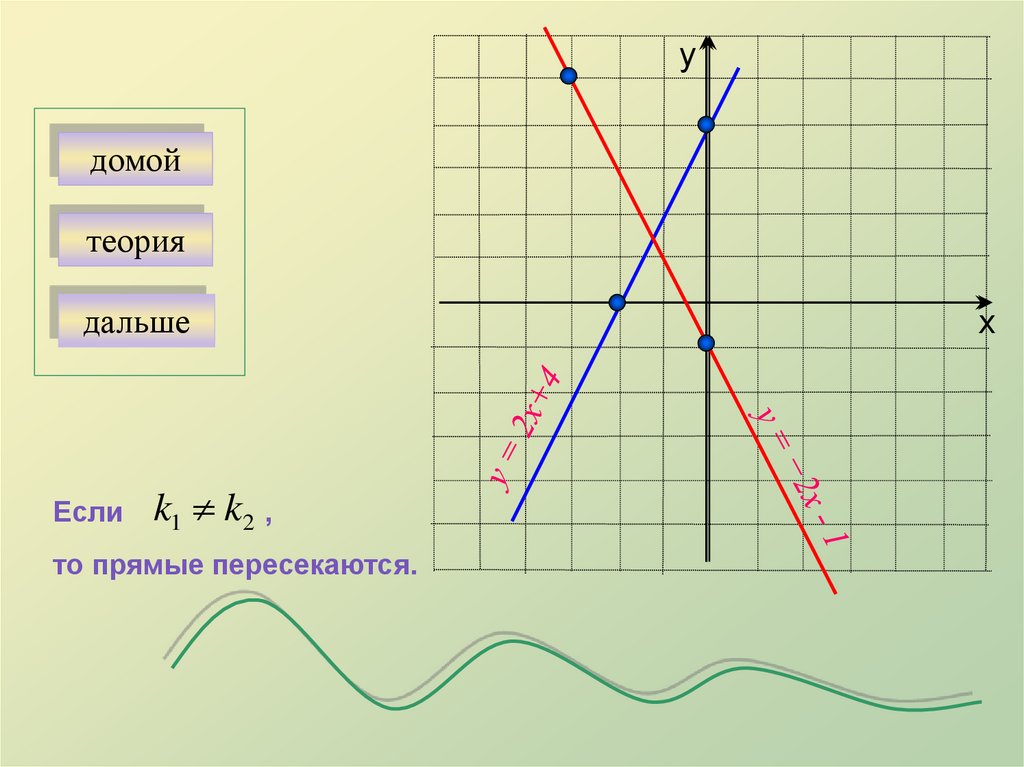
- Аккуратно проведите линию через (0,0) и (2,2) на сетке. Не забудьте расширить его в обоих направлениях, чтобы на нем было много точек, которые легко назвать.
- Скажем: Назовите несколько точек на этой прямой. Учащиеся должны составить список точек с целочисленными координатами. Если нет, потратьте некоторое время на присвоение имен точкам на сетке, прежде чем продолжить этот урок. Если учащиеся называют нецелые точки, например (1,5, 1,5), уделите время объяснению, почему они тоже находятся на прямой.
- Спросите: Можете ли вы дать мне правило, как найти y, когда мы знаем x в этой строке? Обсудите, как связаны координаты, затем попросите учащихся записать правило в виде уравнения. Уравнение для этой линии: y = x .
- Скажем: Это была линия для уравнения y = x. H Как бы вы нарисовали линию для уравнения y = x + 3? Предложите учащимся самостоятельно провести линию.
 Если это возможно, попросите их объединиться в пары и сравнить их линии. Организуйте обсуждение различных линий, нарисованных учащимися, выделяя сходства и различия. Затем покажите один из способов рисования линии: подставьте несколько значений вместо 9.0029 x в уравнение, найдите соответствующие значения для y , а затем постройте эти пары координат. Две точки дают вам достаточно информации для проведения линии, но поскольку возможны ошибки, а человеческий рисунок не идеален, безопаснее создать по крайней мере три точки. Отобразите T-таблицу со связанными значениями x и y и нарисуйте график линии.
Если это возможно, попросите их объединиться в пары и сравнить их линии. Организуйте обсуждение различных линий, нарисованных учащимися, выделяя сходства и различия. Затем покажите один из способов рисования линии: подставьте несколько значений вместо 9.0029 x в уравнение, найдите соответствующие значения для y , а затем постройте эти пары координат. Две точки дают вам достаточно информации для проведения линии, но поскольку возможны ошибки, а человеческий рисунок не идеален, безопаснее создать по крайней мере три точки. Отобразите T-таблицу со связанными значениями x и y и нарисуйте график линии. - Скажем: Теперь, как бы вы нарисовали линию для уравнения у = 2 х + 3? Учащиеся, скорее всего, будут использовать стратегию составления Т-таблицы и вычисления баллов. Если они забудут умножить свои значения x на 2 перед добавлением 3, напомните им о порядке операций (умножение или деление слева направо, затем сложение или вычитание слева направо).
 Попросите разных учащихся сформулировать разные точки зрения, обсуждая их рассуждения по ходу дела.
Попросите разных учащихся сформулировать разные точки зрения, обсуждая их рассуждения по ходу дела. - Спросите: Кто-нибудь может дать мне число от –5 до 5? А как насчет числа от –10 до 10? Используйте эти числа для создания линейных уравнений. Первое число будет коэффициентом х , а второе будет добавлено к терму х . Создавайте уравнения, находите точки, затем рисуйте линии. Вы можете сделать это упражнение более похожим на игру, попросив учащихся бросать кубики с реальными или виртуальными числами. Если вы работали с наклоном, эти задачи также дадут вам возможность укрепить эту концепцию. (Спросите: как вы думаете, будет ли наклон этой линии положительным или отрицательным? Как вы думаете, он будет очень крутым или не таким крутым? Пройдет ли эта линия через начало координат?)
Линейные уравнения: развитие концепции
Материалы: Координатная сетка, которую могут видеть все учащиеся (сетка должна идти как минимум от –10 до +10 по обеим осям), инструмент для разметки сетки точками и линиями
- Скажем Когда мы создавали точки для линий на прошлом уроке, наши уравнения всегда выглядели одинаково.
 Другими словами, они всегда были в одной и той же форме. Сегодня мы рассмотрим, как они могут выглядеть по-разному.
Другими словами, они всегда были в одной и той же форме. Сегодня мы рассмотрим, как они могут выглядеть по-разному. - Скажем, Может кто-нибудь описать, как найти некоторые пары координат для линейного уравнения, 2 x + y = 15? Это двухшаговое уравнение. Решения включают присвоение значения x , затем умножение этого значения на 2, прежде чем пытаться выяснить, какое значение y удовлетворяет уравнению. Учащиеся могут использовать метод проб и ошибок или преобразовать уравнение, используя свойства равенства:
Напишите уравнение. 2 x + y = 15 Присвойте значение x . 2(3) + y = 15 Умножить. 6 + y = 15 Вычтите 6 с каждой стороны. 6 – 6 + y = 15 – 6 Вычесть. 
y = 9 Это решение дает нам точку (3,9). Продолжайте находить решения или согласовывать пары для этого уравнения до тех пор, пока вы не будете удовлетворены тем, что учащиеся довольны процессом. Затем нанесите точки на сетку и нарисуйте линию.
Скажем, Может кто-нибудь описать, как найти некоторые точки на линии, описываемой уравнением y + x/3 = 5?
Это решение дает нам точку (3,4).Напишите уравнение. y + x /3 = 5 Присвойте значение x . у + 3/3 = 5 Разделить. y + 1 = 5 Вычтите по 1 с каждой стороны. y + 1 – 1 = 5 – 1 Вычесть. y = 4  Студенты могут заметить, что это не похоже на предыдущие линейные уравнения. Объясните, что, поскольку x /3 — это то же самое, что (1/3) x , x /3 по-прежнему является обычным термином. Продолжайте находить решения или согласовывать пары для этого уравнения до тех пор, пока вы не будете удовлетворены тем, что учащиеся довольны процессом. Затем нанесите точки на сетку и нарисуйте линию.
Студенты могут заметить, что это не похоже на предыдущие линейные уравнения. Объясните, что, поскольку x /3 — это то же самое, что (1/3) x , x /3 по-прежнему является обычным термином. Продолжайте находить решения или согласовывать пары для этого уравнения до тех пор, пока вы не будете удовлетворены тем, что учащиеся довольны процессом. Затем нанесите точки на сетку и нарисуйте линию.- Скажем, Кто-нибудь может описать, как найти некоторые точки на прямой, описываемой уравнением y – 6 = 2x?
Напишите уравнение. y – 6 = 2 x Присвойте значение x . y – 6 = 2(3)
Умножить. y – 6 = 6 Добавьте по 6 с каждой стороны. у – 6 + 6 = 6 + 6 Доп. 
y = 12 Это решение дает нам точку (3,12).
- К настоящему времени учащиеся должны были заметить, что простая замена x равна 0. Эта замена даст вам точку, в которой линия пересекает ось y . Предложите учащимся прийти к этому пониманию, если они не делают этого самостоятельно.
Когда учащиеся решают многошаговые уравнения, обратите особое внимание на то, соблюдают ли они порядок операций. Это важное алгебраическое понятие.
Кроме того, следите за тем, действительно ли учащиеся понимают, что свойства равенства говорят о том, что если вы делаете что-то с одной частью уравнения, вы ДОЛЖНЫ сделать то же самое с другой частью уравнения. То, что вы делаете, определяется действием, указанным уравнением. Если число вычитается из и , и вы хотите y , чтобы быть само по себе, добавьте это число к каждой части уравнения, и его противоположное число «переместится» на другую часть уравнения. Точно так же, если y умножить на число, деление поможет вам получить y само по себе.
Точно так же, если y умножить на число, деление поможет вам получить y само по себе.
***
Ищете решение для учащихся 5-х классов и старше, которое поможет разблокировать изучение уравнений и формул линейных отношений и не только? Исследуйте Math 180 , революционный подход к математическому вмешательству.
Получить нашу бесплатную электронную книгу Math Intervention сегодня.
Скачать
Математика Мероприятия и уроки 6-8 классы 9-12 классы Вмешательство
Связанные материалыРичард Бланкман
Фасонный РедакторАли Хабаши
Фасонный РедакторДженнифер Корухо
Фасонный Редактор
Математика Мероприятия и уроки 6-8 классы 9 класс-12 Intervention
Электронная книга Math Intervention
Получить
наш бесплатный путеводитель, полный исследовательской информации.
Скачать
Учебное пособие. Первый этап создания графической машины
Это задание и последующее домашнее задание предназначены для того, чтобы помочь учащимся на начальных этапах разработки графической утилиты с помощью App Inventor. Целью этого будет дать учащимся другой способ взглянуть и понять уравнения, функции и их графики, а также дать представление о программировании других графических утилит, таких как графический калькулятор. Студенты могут использовать его в течение года, добавляя функции по мере необходимости. Разминка : Построение графика зависимости расстояния от времени. Это задание предназначено для того, чтобы напомнить учащимся о некоторых проблемах, связанных с графическим представлением данных. Студенты должны будут подумать о единицах измерения, о том, как измерять, как фиксировать данные относительно начала координат и набора осей.
Материалы : Секундомер (не обязательно, так как учащиеся могут быть неточным или игнорировать фактическое время здесь), наклейки, скотч, мешки с фасолью, бумага и карандаш для записи данных и нанесения точек через каждые две секунды. Можно также использовать систему CBL/CBR.
Процедура : Это может быть как научный эксперимент, так и
хочет учитель. Можно либо генерировать данные, буквально идя/двигаясь по
путь в течение заданного периода времени или просто выбор каждой парой некоторых значений y, которые
соответствуют некоторым заданным значениям x. С минимальными начальными инструкциями
учащиеся будут работать в парах над построением графика зависимости расстояния от времени. Для сбора данных они должны идти с места
и они должны вычислить расстояние.
Учащиеся будут вычислять расстояния в дискретные моменты времени, бросая боб.
пакет/наклейка маленькой наклейки на пол и т. д. каждые две секунды в течение 20 секунд.
Возможные проблемы: контрольная точка (начало), набор осей для расстояние (пифагорейское), Как заставить калькулятор просто построить ряд точек по формуле или уравнению. Студенты должны думать не только о том, как заставить компьютер делать это должным образом, но они должны думать о что указывает на график, как создать или смоделировать непрерывность, проблемы масштабирования в соответствии с требованиями к экрану конкретного устройства.
Основной вопрос: Как калькулятор строит график?
Занятия в классе и последующие задания ведут к построению плоттера для построения линейного графика. Через
год, когда учащиеся будут использовать этот шаблон для построения функций, позволяющих
их для построения различных функций в течение года. Конструкция каждого
функциональный плоттер дал бы им представление о том, как должен работать калькулятор, чтобы быть
умеет составлять уравнения. Это также дает им практический опыт использования
функции и процедуры в программировании.
Создание нашего приложения:
Давайте начнем новый проект под названием functionGrapher. Ваш пользователь интерфейс позволит вам добавить горизонтальное расположение с четырьмя текстовыми полями и три метки, холст и кнопка ниже, как показано здесь. Текстовые поля и метки должны быть расположены, как указано выше, с текстовые поля имеют ширину 30 пикселей, а метки — 20 пикселей. Также, установите флажки только для чисел во всех четырех текстовых полях.
Как вы могли видеть или не видеть в своей первоначальной деятельности,
нам нужна система отсчета, чтобы нарисовать наш график, т.
Начнем с простой линейной функции. Мы можем либо установить все текстовые поля на 1, или инициализируйте их на единицу, или установите их на единицу в пользовательский интерфейс.
Опять же, я собираюсь использовать процедуру, которая будет называться при нажатии кнопки functionGraphButton. Предоставление учащимся вышеуказанного надеюсь, некоторые из них возразят, что вы все, возможно, думаю прямо сейчас, но пока подыграйте мне, и мы посмотрим, как это выглядит. Итак, теперь пришло время настроить нашу functionGraphButton. Когда кнопка functionGraphButton нажата, нам нужно несколько вещи, чтобы случиться. Нам нужно, чтобы холст был четким, нам нужно вызвать оси, чтобы тогда нарисуйся.
Мы создали переменные для коэффициента x,
yкоэффициент, xpower и ypower так, чтобы было куда добавить добавленные значения
в эти ящики для хранения. Это то, что вы предсказывали?
Здесь представлена первоначальная проблема, с которой вы, вероятно, столкнулись.
уже задумался. Наше первое преобразование должно быть сосредоточено на нашем графике.
и использовать значения координат, которые будут отображаться на наших осях. Это может быть трудно
изначально закодировано, но в конечном итоге мы можем использовать функцию, которая вводит значения x
и позволяет корректно выводить значения y на холст, чтобы
функция выглядит так, как если бы она была на оси x-y. Вы должны использовать существующий код для линейной функции и добавить квадратичную функцию. Если вам не удалось правильно преобразовать сегодня в классе, посмотрите на код выше. Если возможно, используйте этот же коэффициент преобразования при написании кода для этого задания. Вам не разрешено использовать функцию экспоненты, содержащуюся в математических командах, но вы должны использовать фундаментальную идею того, как работают степени, чтобы написать свой код. Вам не нужно добавлять ни отдельную кнопку, ни какие-либо другие переменные. Убедитесь, что ваш графограф может отображать как линейные, так и квадратичные уравнения, а не только одно или другое. Ваша первоначальная попытка может выглядеть примерно так.
После преобразования квадратичного уравнения в график, пожалуйста, оцените свои результаты. Чем вы довольны? Что бы вы хотели улучшить? Приходите на занятия, готовые представить идеи по улучшению ваших графиков. 1) реагировать на нажатие кнопки «Нажмите здесь» без значений в текстовых полях «степень х» или «коэффициент х». 2) Создайте отвлечение, чтобы занять пользователя, или сообщение, которое информирует пользователя, пока приложение выполняет данную команду. Упражнения на расширение: это базовое упражнение может быть расширено настолько, насколько вы пожелаете. Учащиеся могут комбинировать функцию определения местоположения с построением графиков, чтобы учащиеся могли создавать графики своих позиций за заданный период времени. Они могли бы определить это для отношений времени/расстояния или посмотреть на разницу между общим пройденным расстоянием и расстоянием от начала. |
 График линейного уравнения представляет собой прямую линию.
График линейного уравнения представляет собой прямую линию. 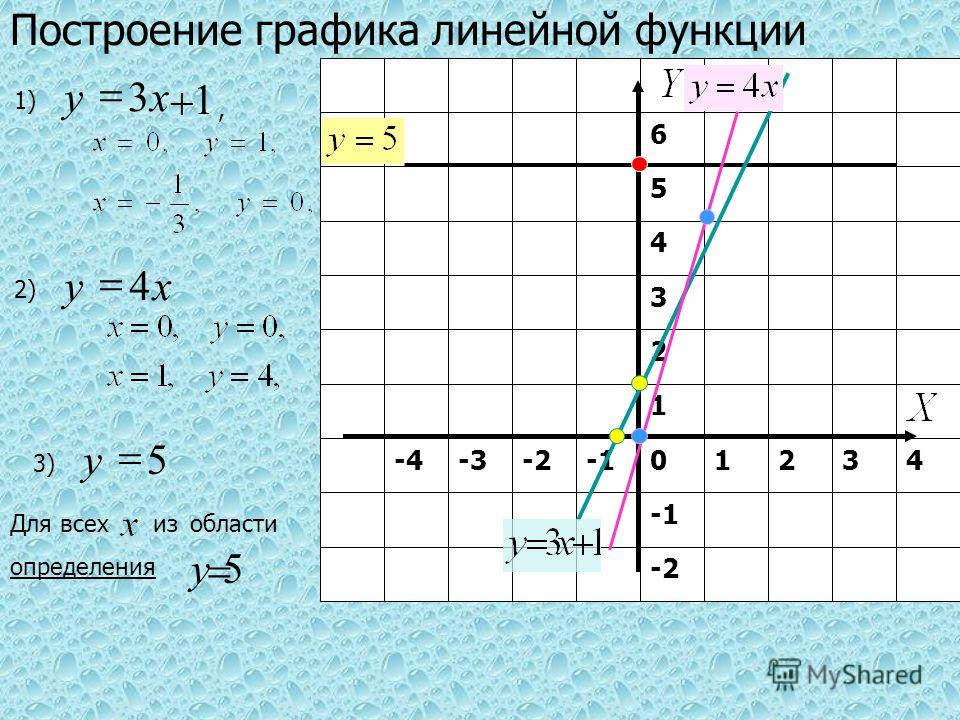
 Если это возможно, попросите их объединиться в пары и сравнить их линии. Организуйте обсуждение различных линий, нарисованных учащимися, выделяя сходства и различия. Затем покажите один из способов рисования линии: подставьте несколько значений вместо 9.0029 x в уравнение, найдите соответствующие значения для y , а затем постройте эти пары координат. Две точки дают вам достаточно информации для проведения линии, но поскольку возможны ошибки, а человеческий рисунок не идеален, безопаснее создать по крайней мере три точки. Отобразите T-таблицу со связанными значениями x и y и нарисуйте график линии.
Если это возможно, попросите их объединиться в пары и сравнить их линии. Организуйте обсуждение различных линий, нарисованных учащимися, выделяя сходства и различия. Затем покажите один из способов рисования линии: подставьте несколько значений вместо 9.0029 x в уравнение, найдите соответствующие значения для y , а затем постройте эти пары координат. Две точки дают вам достаточно информации для проведения линии, но поскольку возможны ошибки, а человеческий рисунок не идеален, безопаснее создать по крайней мере три точки. Отобразите T-таблицу со связанными значениями x и y и нарисуйте график линии. Попросите разных учащихся сформулировать разные точки зрения, обсуждая их рассуждения по ходу дела.
Попросите разных учащихся сформулировать разные точки зрения, обсуждая их рассуждения по ходу дела. Другими словами, они всегда были в одной и той же форме. Сегодня мы рассмотрим, как они могут выглядеть по-разному.
Другими словами, они всегда были в одной и той же форме. Сегодня мы рассмотрим, как они могут выглядеть по-разному. 
 Студенты могут заметить, что это не похоже на предыдущие линейные уравнения. Объясните, что, поскольку x /3 — это то же самое, что (1/3) x , x /3 по-прежнему является обычным термином. Продолжайте находить решения или согласовывать пары для этого уравнения до тех пор, пока вы не будете удовлетворены тем, что учащиеся довольны процессом. Затем нанесите точки на сетку и нарисуйте линию.
Студенты могут заметить, что это не похоже на предыдущие линейные уравнения. Объясните, что, поскольку x /3 — это то же самое, что (1/3) x , x /3 по-прежнему является обычным термином. Продолжайте находить решения или согласовывать пары для этого уравнения до тех пор, пока вы не будете удовлетворены тем, что учащиеся довольны процессом. Затем нанесите точки на сетку и нарисуйте линию.
 Это поднимет вопросы масштаба и, возможно, другие идеи.
Это поднимет вопросы масштаба и, возможно, другие идеи.
 В этом есть потенциальная выгода
учащиеся получают дополнительное понимание того, как функция принимает ввод
значение и должна возвращать значение, в то время как процедура принимает запрос и выполняет
какая-то операция, которая может возвращать или не возвращать значение. Предполагается, что учащийся имеет начальный уровень опыта работы с App Inventor и знаком с процедурами, функциями и базовой настройкой.
В этом есть потенциальная выгода
учащиеся получают дополнительное понимание того, как функция принимает ввод
значение и должна возвращать значение, в то время как процедура принимает запрос и выполняет
какая-то операция, которая может возвращать или не возвращать значение. Предполагается, что учащийся имеет начальный уровень опыта работы с App Inventor и знаком с процедурами, функциями и базовой настройкой. е. набор осей. Я собираюсь
используйте процедуру, и я использовал высоту и ширину холста для управления
высота и ширина осей, но они, безусловно, могут быть жестко закодированы.
е. набор осей. Я собираюсь
используйте процедуру, и я использовал высоту и ширину холста для управления
высота и ширина осей, но они, безусловно, могут быть жестко закодированы. По мере того, как программа расширяется и становится более сложной, нам потребуются разные значения для этих переменных. Первый раз по программе со студентами
эти значения могут быть предварительно заданы либо в пользовательском интерфейсе, либо в приведенном выше
вкладки. Мы также можем игнорировать if-else для
прямо сейчас и просто используйте диапазон for с линейным вызовом draw. Можете ли вы предсказать, как это будет выглядеть?
По мере того, как программа расширяется и становится более сложной, нам потребуются разные значения для этих переменных. Первый раз по программе со студентами
эти значения могут быть предварительно заданы либо в пользовательском интерфейсе, либо в приведенном выше
вкладки. Мы также можем игнорировать if-else для
прямо сейчас и просто используйте диапазон for с линейным вызовом draw. Можете ли вы предсказать, как это будет выглядеть? 2.
2. 2. Приложение должно соответствующим образом реагировать на значения, указанные в текстовых полях коэффициента и мощности. 10% присуждается за вдумчивый и интересный анализ программы (это значит хорошие вопросы и наблюдения!). Последние 10% будут присуждены за продуманные, творческие идеи, которые помогут улучшить программу. Дополнительные баллы будут начисляться за программу, которая может:
2. Приложение должно соответствующим образом реагировать на значения, указанные в текстовых полях коэффициента и мощности. 10% присуждается за вдумчивый и интересный анализ программы (это значит хорошие вопросы и наблюдения!). Последние 10% будут присуждены за продуманные, творческие идеи, которые помогут улучшить программу. Дополнительные баллы будут начисляться за программу, которая может: Первый пример потенциально создает функцию «один к одному», а другой (потенциально) создает функцию «многие к одному». Класс может смотреть на обратные функции. Они могли бы проанализировать эту идею в своем программировании, когда они строят свои функции, либо переключая координаты, либо отменяя исходную функцию с помощью операций. Возможно, было бы проще всего даже создать какое-то отражение над линией y = x. Учащиеся могут посмотреть на отношения, которые не являются функциями, установив для степени y значение >1. Можно добавить тест вертикальной линии, чтобы дать визуальную проверку того, является ли данное уравнение функцией. Студенты также должны подумать, что может означать отрицательное значение x в контексте графика и их проблемы. Что произойдет, если мы также изменим высоту, например, что, если кто-то заберется на стол? Что происходит с расстоянием в самолете? Что происходит с общим расстоянием? Есть много потенциальных вопросов, которые могут возникнуть в связи с обдумыванием и реализацией этого проекта.
Первый пример потенциально создает функцию «один к одному», а другой (потенциально) создает функцию «многие к одному». Класс может смотреть на обратные функции. Они могли бы проанализировать эту идею в своем программировании, когда они строят свои функции, либо переключая координаты, либо отменяя исходную функцию с помощью операций. Возможно, было бы проще всего даже создать какое-то отражение над линией y = x. Учащиеся могут посмотреть на отношения, которые не являются функциями, установив для степени y значение >1. Можно добавить тест вертикальной линии, чтобы дать визуальную проверку того, является ли данное уравнение функцией. Студенты также должны подумать, что может означать отрицательное значение x в контексте графика и их проблемы. Что произойдет, если мы также изменим высоту, например, что, если кто-то заберется на стол? Что происходит с расстоянием в самолете? Что происходит с общим расстоянием? Есть много потенциальных вопросов, которые могут возникнуть в связи с обдумыванием и реализацией этого проекта.
Ваш комментарий будет первым