Исследовательская работа «Полярные координаты»
Муниципальное автономное образовательное учреждение
«Средняя общеобразовательная школа №47»
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
на тему:
«ПОЛЯРНЫЕ КООРДИНАТЫ »
Выполнили:
ученики 10 класса
Чугаев Егор Андреевич
Полканов Владислав Алексеевич
Руководитель:
учитель математики
Карнишина Валентина Ивановна
Пермь 2019
Оглавление
Введение. ………………………………………………………………………………………………………3
………………………………………………………………………………………………………3
Полярная система координат 4
Графическое представление……………………………. 4
История создания…………………………………………………………………………………………..5
Прямоугольная система координат на плоскости…………………………………………….6
Связь между декартовыми и полярными координатами 7
Уравнения кривых в полярных координатах7
Решение задач………………………………………………………………………….8
Заключение.10
Использованная литература…………………………………………………………………………..11
Приложения………………………………………………………………………………………………….12
Введение
Точке на плоскости соответствуют ее координаты.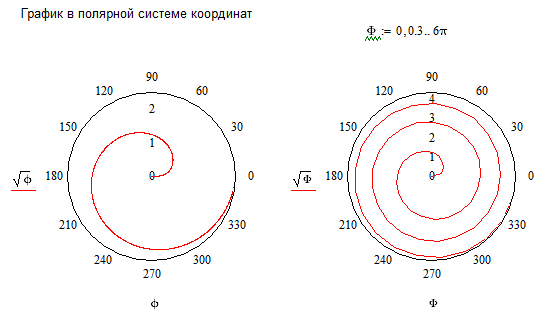 Не
всегда удобно и рационально использовать привычную нам прямоугольную декартовую
систему координат. Существуют и другие системы. Например, полярная. Правильный
выбор системы координат может значительно упростить решение той или иной
задачи, получить желаемую наглядность результата.
Не
всегда удобно и рационально использовать привычную нам прямоугольную декартовую
систему координат. Существуют и другие системы. Например, полярная. Правильный
выбор системы координат может значительно упростить решение той или иной
задачи, получить желаемую наглядность результата.
Именно полярная система координат будет объектом исследования в данной работе. Данная тема актуальна, т.к. не изучается в школьной программе, несмотря на то, что не все графики удобно строить в декартовой системе. Различные кривые, построенные в такой системе, имеют большое применение на практике.
Цель работы: изучение полярной системы координат; ознакомление с некоторыми кривыми, построенными в этой системе; приобретение навыков решения простейших задач в полярной системе координат.
Задачи:
· изучить основную теорию полярной системы координат;
· сравнить полярную систему координат с декартовой;
· рассмотреть основные кривые и их применение в жизни;
·
научиться решать
простейшие задачи в полярной системе координат.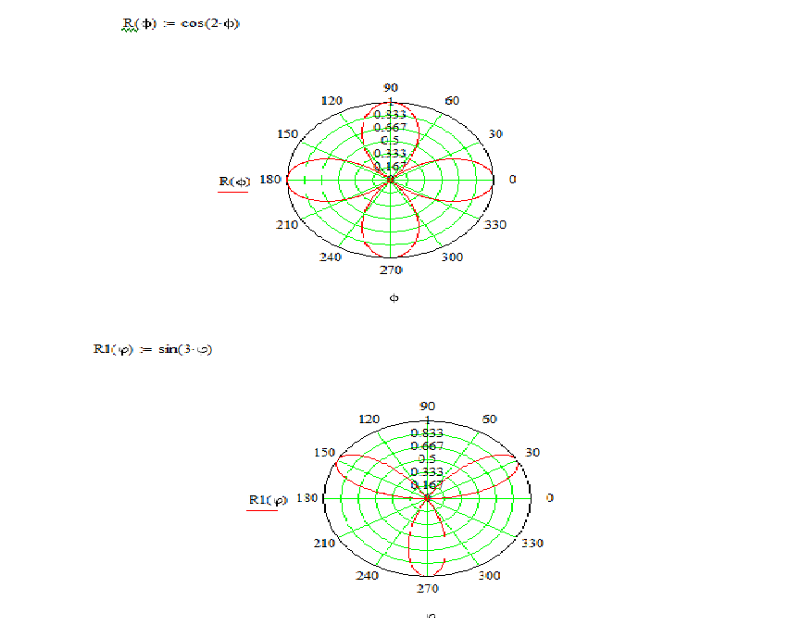
Полярная система координат (рис. 1,2) – двухмерная
система координат, в которой каждая точка на плоскости однозначно определяется
двумя числами – полярным углом и полярным радиусом. Полярная система координат
особенно полезна в случаях, когда отношения между точками проще изобразить в
виде радиусов и углов; в более распространённой декартовой, или прямоугольной,
системе координат, такие отношения можно установить только путём применения
тригонометрических уравнений.
Графическое представление
Каждая точка в полярной системе координат
может быть определена двумя полярными координатами, что обычно называются r и φ. Координата r соответствует расстоянию от точки до центра, или полюса
системы координат, а координата равна углу, отсчитываемого в направлении против
часовой стрелки от луча через 0°.
Координата r соответствует расстоянию от точки до центра, или полюса
системы координат, а координата равна углу, отсчитываемого в направлении против
часовой стрелки от луча через 0°.
Полярный угол измеряется в радианах и отсчитывается от полярной оси:
в положительном направлении (против направления движения часовой стрелки), если значение угла положительное; в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное. Одной из важных особенностей полярной системы координат является то, что одна и та же точка может быть представлена бесконечным количеством способов. Это происходит потому, что для определения азимута точки нужно повернуть полярную ось так, чтобы она указывала на точку. Но направление на точку не изменится, если осуществить произвольное число дополнительных полных оборотов. Углы в полярных координатах задаются либо в градусах, либо в радианах, при этом 2π =360°.
История создания
Существуют разные версии о
введении полярных координат в качестве формальной системы координат. Полная
история возникновения и исследования описана в работе профессора из Гарварда
Джулиан Лоувел Кулидж «Происхождение полярных координат». Грегуар де Сен-Венсан
и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в
середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625
году, напечатав свои труды в 1647; а Кавальери напечатал свои труды в 1635
году, и исправленную версию в 1653 году. Кавальери применял полярные координаты
для вычисления площади, ограниченной спиралью Архимеда. Блез Паскаль
впоследствии использовал полярные координаты для вычисления длин параболических
дуг.
Полная
история возникновения и исследования описана в работе профессора из Гарварда
Джулиан Лоувел Кулидж «Происхождение полярных координат». Грегуар де Сен-Венсан
и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в
середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625
году, напечатав свои труды в 1647; а Кавальери напечатал свои труды в 1635
году, и исправленную версию в 1653 году. Кавальери применял полярные координаты
для вычисления площади, ограниченной спиралью Архимеда. Блез Паскаль
впоследствии использовал полярные координаты для вычисления длин параболических
дуг.
В книге «Метод флюксий» (англ.
Method of Fluxions, написана в 1671 году, напечатана в 1736 году) сэр Исаак
Ньютон исследовал преобразование между полярными координатами, которые он
обозначал как «Седьмой способ; Для спиралей» («англ. Seventh Manner; For
Spirals»), и девятью другими системами координат. В статье, опубликованной в
1691 году в журнале Acta eruditorum, Якоб Бернулли использовал систему с точкой
на прямой, которые он назвал полюсом и полярной осью соответственно. Координаты
задавались как расстояние от полюса и угол от полярной оси. Работа Бернулли
была посвящена проблеме нахождения радиуса кривизны кривых, определённых в этой
системе координат.
Координаты
задавались как расстояние от полюса и угол от полярной оси. Работа Бернулли
была посвящена проблеме нахождения радиуса кривизны кривых, определённых в этой
системе координат.
Введение термина «полярные координаты» приписывают Грегорио Фонтана. В XVIII веке он входил в лексикон итальянских авторов.
Прямоугольная система координат на плоскости (рис. 3, 4)
Прямоугольная система координат – прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует её широкому применению.
Прямоугольная система координат на
плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y.
Положение точки A на плоскости определяется двумя координатами x и y.
Координата x
равна длине отрезка OB, координата y – длине отрезка OC в
выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X
соответственно. При этом координате x
приписывается знак минус, если точка B лежит
на луче OX’ (а не на луче OX, как на рисунке). Координате y приписывается знак минус, если точка C лежит на луче OY’.
Таким образом, OX’ и OY’
являются отрицательными направлениями осей координат (каждая ось координат
рассматривается как числовая ось). Ось x
называется осью абсцисс, а ось y – осью ординат. Координата x называется абсциссой точки A,
координата y – ординатой точки A. Символически это записывают так: A(x,y)
или A = (x,y) В правосторонней системе координат положительное
направление осей выбирают так, чтобы при направлении оси Y’Y вверх, ось X’X смотрела направо.
Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y называются координатными углами, четвертями или квадрантами плоскости.
Точки внутри координатного угла I имеют положительные абсциссы и ординаты.
Точки внутри координатного угла II имеют отрицательные абсциссы и положительные ординаты.
Точки внутри координатного угла III имеют отрицательные абсциссы и ординаты
Точки внутри координатного угла IV имеют положительные абсциссы и отрицательные ординаты.
Связь между декартовыми и полярными координатами
Полярные координаты r и φ можно перевести в декартовы координаты x и y путем применения тригонометрических функций синуса и косинуса (при этом предполагается, что нулевой луч полярной системы координат совпадает с осью x декартовой системы):
r² = y² + x²,
φ = arctg y/x; x ≠ 0;
в то время как декартовы координаты x и y могут быть переведены в полярные координаты r и φ следующим образом:
x = r cos φ,
y = r sin φ.
Уравнения кривых в полярных координатах
Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат было бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль.
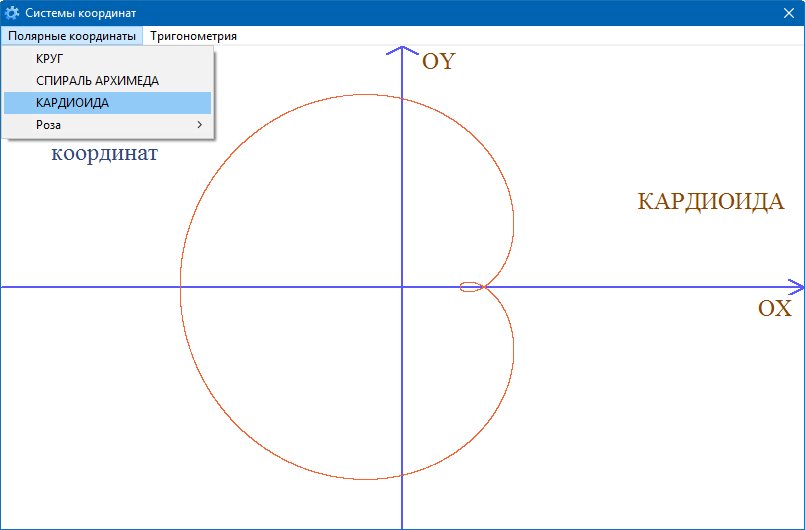
1. Окружность в полярной системе (рис. 5).
Общее уравнение окружности с центром в (r0, θ) и радиусом a имеет вид:
r2 – 2rr0 cos(φ — θ) + r02 = a2.
Это уравнение может быть упрощено для частных случаев, например: r(φ) = a является уравнением, определяющим окружность с центром в полюсе и радиусом a.
2. Полярная роза (рис. 6).
Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:
r(φ) = a cos(kφ + θ)
для произвольной постоянной θ (включая 0). Если k –
целое число, то это уравнение будет определять розу с k лепестками для нечётных k, либо с 2k лепестками для чётных k. Если k – рациональное, но не целое,
график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут
перекрываться.
Если k –
целое число, то это уравнение будет определять розу с k лепестками для нечётных k, либо с 2k лепестками для чётных k. Если k – рациональное, но не целое,
график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут
перекрываться.
Практическое применение розы.
В различных областях науки и техники
Применяется в измерительных лабораториях и цехах предприятий точного приборостроения, машиностроения, микроэлектроники, в инструментальном производстве, а также в лабораториях НИИ (рис. 9).
В математическом дизайне и архитектуре малых форм.
С помощью выращенных цветов, различных кривых в полярных координатах и графических редакторов можно сделать например различные рисунки, рамки-орнаменты, или украсить ими различные предметы (рис. 10).
В военном деле.
Координаты цели могут выдаваться в полярной системе координат (азимут, дальность), прямоугольной (X, Y) (рис. 8).
3. Спираль Архимеда (рис. 7).
Архимедова спираль названа в честь
её изобретателя, древнегреческого математика Архимеда.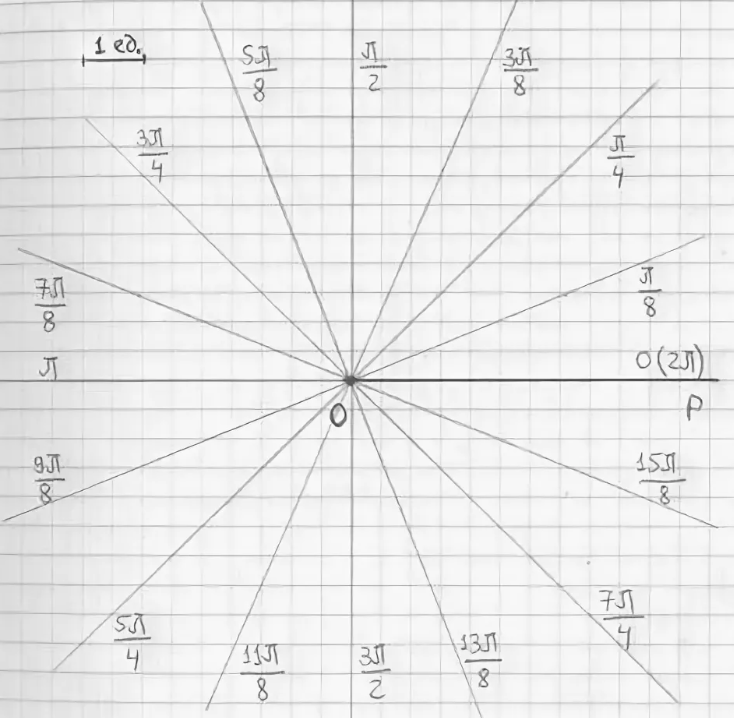 Эту спираль можно
определить с помощью простого полярного уравнения:
Эту спираль можно
определить с помощью простого полярного уравнения:
r(φ) = a + bφ.
Изменения параметра a приводят к повороту спирали, а параметра b – расстояния между витками, которое является константой для конкретной спирали.
Практическое применение спирали
В III веке да нашей эры Архимед на основе своей спирали изобрёл винт, который успешно применяли для передачи воды в оросительные каналы из водоёмов (рис. 11).
В автомобильной технике архимедовы винты могут применяться вместо колес. Принцип движения шнекороторного вездехода прост. При вращении они отталкиваются от кашеобразной или жидкой субстанции, по которой движется вездеход, и продвигают его вперед (рис. 11).
Решение задач
1. Задача на перевод координат из полярной в декартову систему и наоборот.
Возьмём точку в декартовой системе координат A(4;3).
Воспользуемся формулами по переводу в полярную систему координат:
r² = y² + x²,
φ = arctg y/x; x ≠ 0;
И получаем, что r2 = 32 + 42, r=5.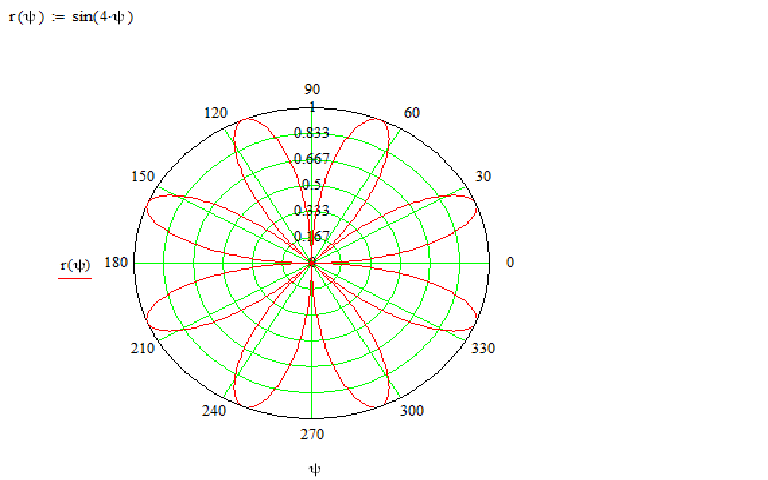
φ = arctg ¾, φ = 0.64 rad
A(5;0.64 )
Теперь переведем из полярной системы в декартову
Возьмем точку M(5; 5/6 π)
x = r cos φ,
y = r sin φ.
С помощью этих формул найдем абсциссу и ординату точки:
x = 5 cos(5/6 π), x ≈ -4,3,
y = 5 sin(5/6 π), y = 2,5.
2. Построение лемнискаты Бернулли
Рассмотрим уравнение кривой в декартовой системе координат:
(x2 + y2)2 = 2c2 (x2 – y2).
Переведем в полярную систему с помощью формул
x = r cos φ,
y = r sin φ.
(r2 cos2 φ + r2 sin2 φ)2 = 2c2 (r2 cos2 φ – r2 sin2 φ).
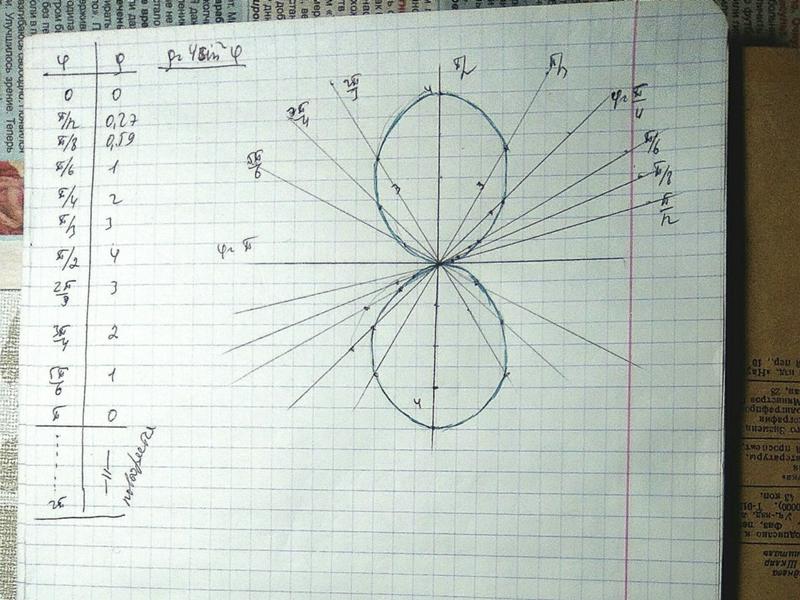
Получим: r2 = 2c2 cos2φ.
Построим эту кривую.
φ | 0 | π/12 | π/8 | π/6 | π/4 | 3π/4 | 5π/6 | 7π/8 | 11π/12 | π |
r | ≈1,4 | ≈1,3 | ≈1,1 | 1 | 0 | 0 | 1 | ≈1,1 | ≈1,3 | ≈1,4 |
Дальше точки симметричные.
Как мы можем заметить, в уравнении полярной системы происходят более легкие подсчеты, чем в декартовой.
Это уравнение лемнискаты Бернулли. Плоская алгебраическая кривая. По форме напоминает восьмёрку или символ бесконечности (рис. 12).
Заключение
В данной работе мы исследовали полярную систему координат на плоскости.
Рассмотрели связь между декартовыми и полярными координатами, а так же уравнения линий в полярных координатах
Научились: переводить координаты одной системы в другую и наоборот, решать задачи на построение сложных кривых и узнали, как они используются в жизни.
Узнали, что в полярной системе координат, в отличие от прямоугольной, некоторые кривые могут быть достаточно просто описаны полярным уравнением.
Использованная литература
1. https://ru.wikipedia.org/wiki/Лемниската_Бернулли
https://ru.wikipedia.org/wiki/Лемниската_Бернулли
2. http://mathprofi.ru/poljarnye_koordinaty.html
3. https://ru.wikipedia.org/wiki/Полярная_система_координат
4. https://infourok.ru/proekt-na-temu-zamechatelnie-krivie-3010763.html
5. https://ru.wikipedia.org/wiki/Прямоугольная_система_координат
6. https://www.matburo.ru/ex_ag.php?p1=agpsk
Приложения
рис. 1
1
рис. 2 рис. 3
рис. 4 рис. 5 рис. 6
рис. 7
рис. 8 рис. 9
7
рис. 8 рис. 9
рис. 10 рис. 11
рис. 12
5.2. Построение графиков в полярной системе координат при помощи MathCad
Для того чтобы построить график в полярной системе координат при помощи MathCAD, необходимо:
Определить как дискретную переменную (в пределах области определения).
Задать функцию () .
Щелкнуть мышью в свободном месте.
 Выбрать из
меню «Графика» PolarPlot (Полярный график).
Выбрать из
меню «Графика» PolarPlot (Полярный график).В появившемся шаблоне напечатать в нижнем поле, напечатать () в левом поле.
Щелкнуть мышью вне графика.
Пример 2. Построим график функции (спираль Архимеда) при помощиMathCAD.
Решение.
График в полярных координатах можно форматировать.
Чтобы открыть окно форматирования графика поступают также как при форматировании декартово графика. Аналогично декартовому графику, для полярного графика можно задать стиль оформления осей (в частности, для наглядности удобно отразить вспомогательные угловые линии), изменить параметры кривой, создать надписи.
5.3. Задания для самостоятельного решения
1. Построить (в тетради) в полярной системе координат линию по точкам, придавая значения от 0 до с шагом (для вычисления значений можно использовать возможности MathCAD):
1. | ,, | 11. | , , |
2. | , , | 12. | , , |
3. | , , | 13. | , , |
4. | , , | 14. | , , |
5. | , , | 15. | ,, |
6. | , , | 16. | , , |
7. | , , | 17. | , , |
8. | , , | 18. | , , |
9. | , , | 19. | , , |
10. | , , | 20. | , , |
2. При помощи MathCAD построить кривые в полярной системе координат, придавая различные значения параметру а:
1. | 11. | ||
2. | 12. | ||
3. | 13. | ||
4. | 14. | ||
5. | 15. | ||
6. | 16. | ||
7. | 17. | ||
8. | 18. | ||
9. | 19. | ||
10. | 20. |
Лабораторная работа № 6 Тема: Символьные вычисления
Цель работы: Научиться производить символьные вычисления: преобразовывать выражения, вычислять пределы.
MathCAD позволяет получить значение некоторого выражения в численном виде (при помощи обычного знака равенства) или в символьном виде (при помощи знака символьного равенства, о котором будет рассказано ниже). В первом случае после знака равенства появляется одно или несколько чисел. Во втором случае результатом вычислений является некоторое выражение.
Прежде, чем производить символьные вычисления, необходимо убедиться, что символьный процессор включен в работу: в меню «Math» должны быть отмечены команды «Live Symbolics» («Использовать символику») и «Automatic Mode» («Автоматический режим»).
Знак
символьного равенства
представляет собой стрелку вправо ()
и набирается сочетанием клавиш [Ctrl]
и [. ],
либо с палитры «Преобразования».
],
либо с палитры «Преобразования».
Чтобы произвести символьные вычисления, необходимо:
Ввести выражение, которое надо вычислить или преобразовать.
Выделить выражение синей выделительной рамкой и набрать знак символьного равенства.
Щелкнуть мышью вне выражения.
Проиллюстрируем разницу между численным и символьным результатом на простом примере. Вычислим двумя способами:
Следует отметить, что для одних выражений можно произвести как численные, так и символьные вычисления, для других – только численные, для третьих – только символьные.
При помощи символьных вычислений можно вычислять пределы, решать неопределенные системы уравнений (т.е. системы, которые имеют множество решений), преобразовывать выражения, находить производные и т.д.
Function Grapher
Добро пожаловать в самый передовой в мире Function Grapher . Этот уникальный интерактивный онлайн-график функций способен графически отображать в неперпендикулярных декартовых системах координат по вращающимся осям , а также способен анимировать полярных графических процессов 9 0004 .
Этот уникальный интерактивный онлайн-график функций способен графически отображать в неперпендикулярных декартовых системах координат по вращающимся осям , а также способен анимировать полярных графических процессов 9 0004 .
Использование самых сложных декартовых и полярных систем координат , этот графический инструмент является единственным графическим редактором функций , который позволяет вам вращать любую из осей координат и, таким образом, отображать функции в неортогональных декартовых системах координат . Это также единственный графограф полярных функций , способный анимировать процесс построения полярных графиков для визуализации того, как полярные кривые построены .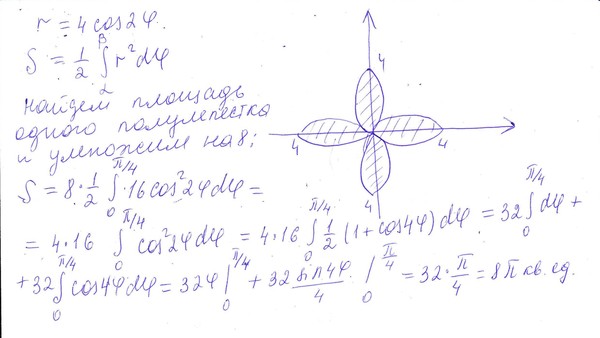
Советы: по мере ввода:
- ..t заменяется на θ . ( Вы также можете использовать x или t. Они внутренне заменены на θ ).
- пи заменяется на π .
- inf ( бесконечность ) заменяется на ∞ .
Для построения графика кусочно определенных функций введите каждую часть с соответствующим подынтервалом как одиночную функцию .
Самый быстрый способ ввести dom=(0, 2π) или dom=(-∞, ∞) — это полностью удалить домен, включая dom= .
МышьМатикс! Вы можете использовать мышь, чтобы Повернуть оси , Переместить и Изменить масштаб
В дополнение к вводу данных — сначала нажав кнопку шестеренки — вы можете использовать мышь для выполнения некоторых функций, уникальных для этого интерактивный функциональный граф , как описано ниже.
- Щелкните по оси (или рядом с ней) и переместите мышь. Это будет вращать ось . графики перерисовываются в неперпендикулярной декартовой системе координат или обобщенной полярной системе координат . Нажмите еще раз, чтобы освободить ось.
- Перетащите мышь на , переместите систему координат вместе с графиками.
- Дважды щелкните на холсте, чтобы переместить начало координат туда, где был сделан щелчок.
- Удерживая клавишу Alt, щелкните по оси, чтобы изменить масштаб (увеличение в одном направлении) ; в точка, по которой был сделан щелчок, будет помечена как «1» (или «-1») и станет новой единицей измерения для этой оси.
Анимация вращения оси: Икс у ► ⬛
сообщение
f(x) =
?
f( ) =
⌨
4 Десятичные разряды
FinenessGraph FinenessBest (медленно)+2+1Normal-1-2Fast (низко)
Label Axes ось x: ось y: Повернуть оси Ось x°: Ось Y°: 92-4)Прочие графики
√(4sin(2x)) √(4cos(2x))
Функции — Полярный
Линии
2csc(θ) 2сек(θ) 1/(sin(θ) — cos(θ))
Круги
1 2 6sin(θ) 8cos(θ)
Спирали
θ θ/5 дом=(0, 10π) √(θ) дом=(0, 10π) 1/θ дом=(0, 10π)
Розы
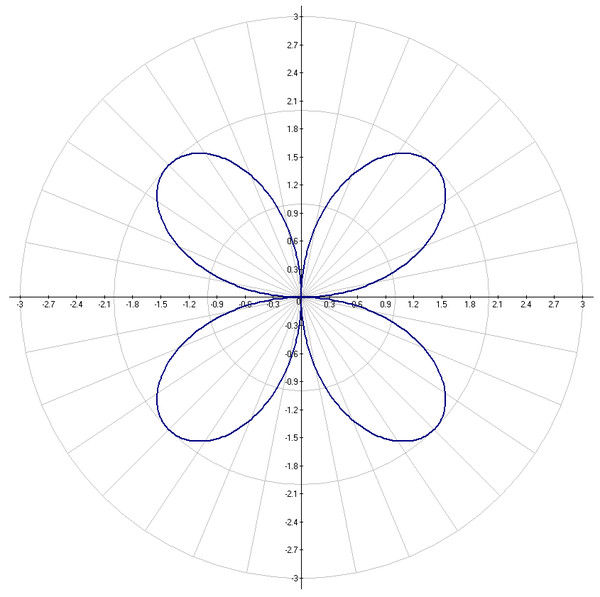
4sin(3θ) 4sin(2θ) 4sin(5θ) 4sin(4θ)
Эллипсы
1/(1-. 8cos(θ))
1/(1-0,8sin(θ))
1/(1+.8cos(θ))
1/(1+.8sin(θ))
8cos(θ))
1/(1-0,8sin(θ))
1/(1+.8cos(θ))
1/(1+.8sin(θ))
Параболы
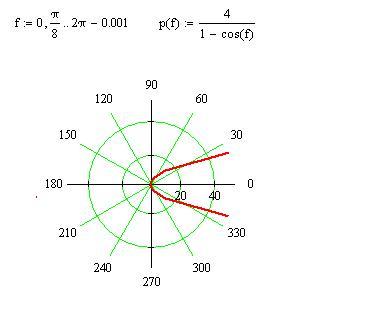
1/(1-sin(θ)) 1/(1+cos(θ)) 1/(1+sin(θ)) 1/(1-cos(θ))
Гипербола
1/(1+2cos(θ)) 4/(1+2sin(θ)) 1/(1-2cos(θ)) 4/(1-2sin(θ)) 95 дом = (0, 12π)
РАД Полярный
🔍+ 1 🔍−
время построения графика (с)
Калькулятор загружается.
Пожалуйста, подождите….
Сделайте это прозрачным
Толщина графика Угловой режим РАД градус ГРД График по мере ввода (взаимодействие) Скрыть оси Скрыть сетки Показать интерфейс анимации осей…
Медленный Быстрый
Показать угловые оси Сделанный
подпись Отключить программную клавиатуру
Чтобы скопировать или сохранить графики, щелкните правой кнопкой мыши изображение сохраненного графика ниже и выберите «Копировать изображение» или «Сохранить изображение» во всплывающем меню.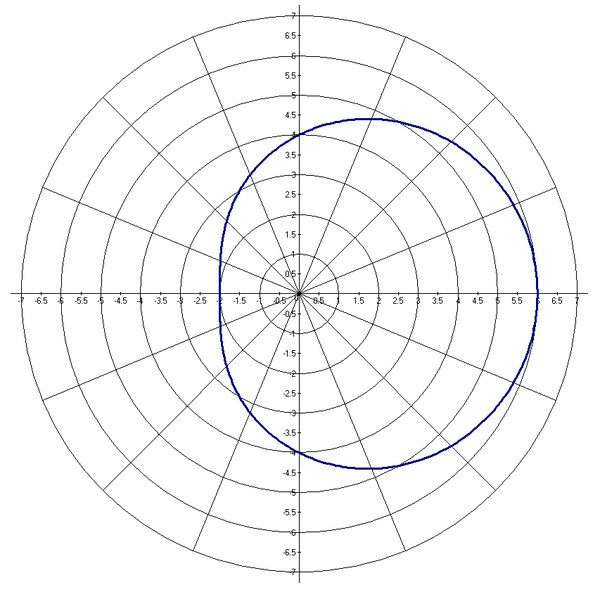
Темы
Декартова и полярная системы координат Функции и графики
Легко использовать функциональный граф ; введите функцию в любое поле выражения . function grapherr выводит на график при вводе (по умолчанию) заданное функциональное выражение в выбранной системе координат , декартовой или полярной системе координат .
- К график две или более функции в одной и той же системе координат нажмите » для отображения мультиграфической панели . Панель с несколькими графиками состоит из панелей выражений , которые можно добавить или удалить по желанию, нажав + или × .
на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.

- Для удобства функция графического редактора добавляет подходящий интервал dom к выражениям функций и графикам в указанном домене. При желании можно изменить конечные точки .
- Для построения полярных графиков заданных функций установите флажок Полярный . Вы можете Анимировать полярные кривые , чтобы увидеть, как они построены.
- Вы можете использовать эту чрезвычайно полезную функцию, нажав ► в нижней части графического редактора функций (если он скрыт, сначала нажмите кнопку Animate ).
- Запускает анимацию процесса построения полярных графиков функции в фокусе . График рисуется последовательно от начального значения до конечного значения θ.
- Затем вы можете нажать || до пауза анимация или нажмите Готово до остановить это.
 Это также закрывает интерфейс анимации. Чтобы отобразить его снова, нажмите Кнопка Animate в верхней части полярного графа.
Это также закрывает интерфейс анимации. Чтобы отобразить его снова, нажмите Кнопка Animate в верхней части полярного графа. - Вы также можете изменить скорость анимации полярной графики с помощью ползунка , предоставленного
- Этот бесплатный онлайн-график полярных функций также рисует полярные графики с повернутой полярной осью .
- Вы можете установить тонкость кривых, выбрав нужный вариант из Раскрывающийся список Graph Fineness . В целом, чем выше точность, тем больше времени требуется -графику полярных функций для построения графиков функций.
- Чтобы скопировать или сохранить графики, сначала нажмите кнопку Копировать/Сохранить график . Изображение графиков появится под графиком функций . Затем вы можете использовать возможности вашего браузера, чтобы сохранить его или скопировать его в ваши документы.

- Чтобы вычислить функцию , введите число или числовое (постоянное) выражение в соответствующем поле; Графический редактор функций отображает рассчитанные значения функций с количеством десятичных разрядов, которое можно указать с помощью предоставленного ползунка.
Интересные кривые : Нарисуйте график любого функционального выражения в разделе Интересные графики , щелкнув по нему. Для достижения наилучших результатов вам может потребоваться выбрать Точность графика как «+1» или выше.
Чтобы эффективно использовать этот онлайн-график функций , используйте последние версии браузеров Chrome , Microsoft Edge , Firefox , Opera или Safari . В противном случае некоторые компоненты графического редактора функций могут не отображаться или работать.
Вставка 1 St производная Вставка 2 и производная
Как рисовать полярные кривые — Криста Кинг Математика
Определение различных форм полярных кривых
Мы нарисуем полярные кривые, нанеся значения для ???r??? при известных значениях ???\theta???.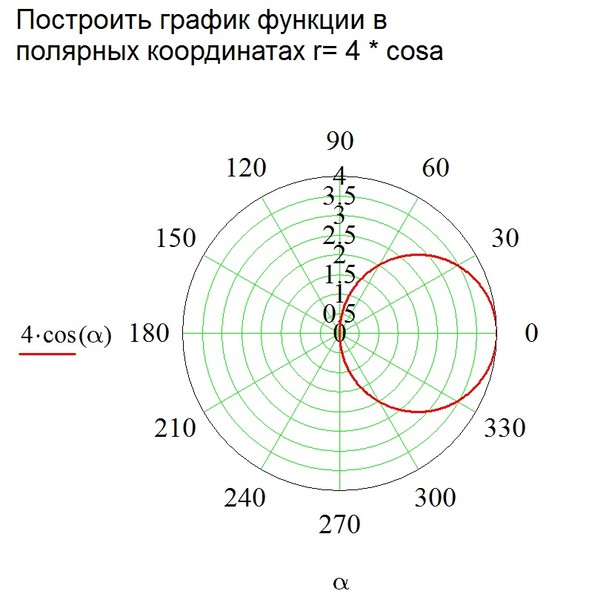 Мы также можем использовать приведенную ниже таблицу для быстрого построения полярных кривых, представленных в этих стандартных формах.
Мы также можем использовать приведенную ниже таблицу для быстрого построения полярных кривых, представленных в этих стандартных формах.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Если мы не можем использовать приведенную выше таблицу, чтобы найти стандартную форму для заданной нами полярной кривой, то мы всегда можем создать таблицу координат точек ???(r,\theta)???. Для этого мы возьмем значение внутри тригонометрической функции, включающее ???\тета???, установим его равным ???\пи/2???, а затем найдем ???\тета ???. Например, учитывая полярную кривую ???r=6\sin{3\theta}???,
???3\theta=\frac{\pi}{2}???
???\theta=\frac{\pi}{6}???
Тогда мы найдем ???r??? для приращений ???\pi/6??? на интервале ???0\leq\theta\leq 2\pi???.
Отложив эти точки на полярных осях, получим
Пошаговый пример построения полярной кривой
Пройти курс
Хотите узнать больше об исчислении 2? У меня есть пошаговый курс для этого.
 🙂
🙂Узнать больше
График линий в полярных координатах
Пример
График полярных кривых на тех же осях.
???\theta=\frac{\pi}{3}???
???r\cos{\theta}=3???
???r\sin{\theta}=-2???
Используя таблицу стандартных кривых, мы можем построить их все на одних и тех же осях.
???\тета=\пи/3??? похоже на ???\theta=\beta???, так что это прямая линия, проходящая через начало координат под углом ???\pi/3???.
???r\cos{\theta}=3??? похож на ???r\cos{\theta}=a???, так что это вертикальная линия, проходящая через ???x=3???.
???r\sin{\theta}=-2??? похож на ???r\sin{\theta}=b???, так что это горизонтальная линия, проходящая через ???y=-2???.
Давайте попробуем несколько примеров с окружностями, заданными в полярных координатах.
Чтобы построить полярную кривую, найдите точки с шагом тета, а затем нанесите их на полярные оси.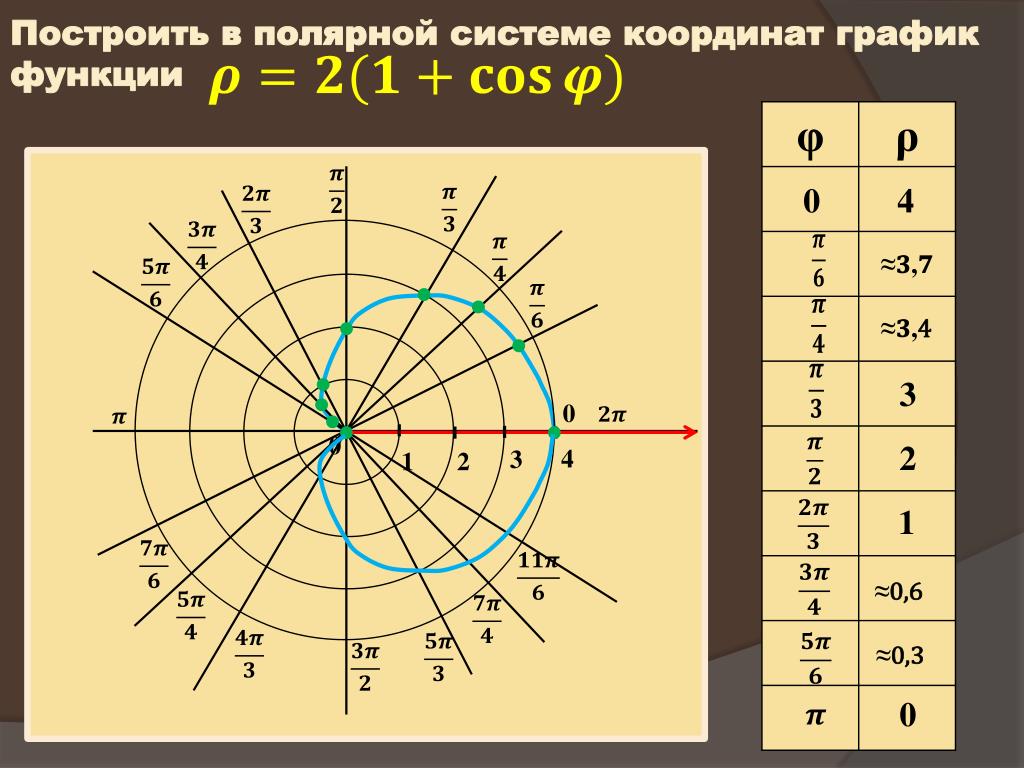 2}=\sqrt{10}???.
2}=\sqrt{10}???.
График кардиоид, лимаконов и роз
Пример
График полярных кривых.
???r=3+3\sin{\theta}???
???r=2+4\cos{\theta}???
???r=7+6\cos{\theta}???
???r=6\sin{2\theta}???
Для ???r=3+3\sin{\theta}???:
???r=3+3\sin{\theta}??? похоже на ???r=a\pm{a}\sin{\theta}???, так что это кардиоида в начале координат. Мы создадим таблицу значений на интервале ???0\le\theta\le2\pi???.
Имея эти точки и зная форму нашей полярной кривой, мы можем нарисовать график.
Для ???r=2+4\cos{\theta}???:
???r=2+4\cos{\theta}??? похоже на ???r=a\pm{b}\cos{\theta}??? с ???a Имея эти точки и зная форму нашей полярной кривой, мы можем нарисовать график. Для ???r=7+6\cos{\theta}???: ???r=7+6\cos{\theta}??? похоже на ???r=a\pm{b}\cos{\theta}??? с ???a>b???, так что это лимасон без внутренней петли. Мы создадим таблицу значений на интервале ???0\le\theta\le2\pi???. Имея эти точки и зная форму нашей полярной кривой, мы можем нарисовать график. Для ???r=6\sin{2\theta}???: ???r=6\sin{2\theta}??? не соответствует ни одной из стандартных форм в нашей таблице. В этом случае мы установим значение внутри нашей тригонометрической функции равным ???\pi/2??? а затем найти ???\тета???. ???2\theta=\frac{\pi}{2}??? ???\theta=\frac{\pi}{4}??? Тогда мы найдем ???r??? для приращений ???\pi/4??? на интервале ???0\leq\theta\leq 2\pi???. Отложив эти точки на полярных осях, получим
Получить доступ к полному курсу Calculus 2
Начать
Изучение математикиКриста Кинг
 Выбрать из
меню «Графика» PolarPlot (Полярный график).
Выбрать из
меню «Графика» PolarPlot (Полярный график).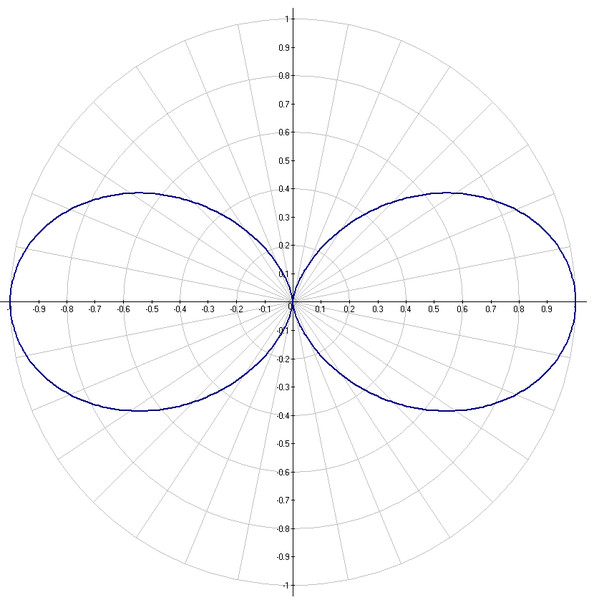


 Это также закрывает интерфейс анимации. Чтобы отобразить его снова, нажмите Кнопка Animate в верхней части полярного графа.
Это также закрывает интерфейс анимации. Чтобы отобразить его снова, нажмите Кнопка Animate в верхней части полярного графа.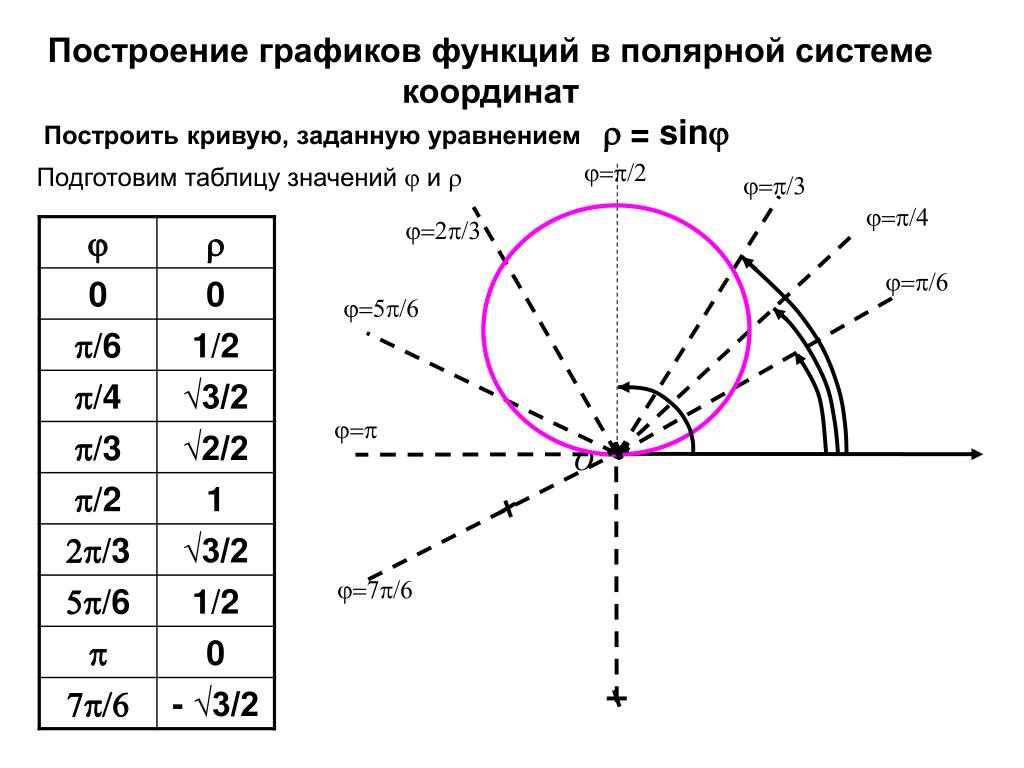
Ваш комментарий будет первым