Построение графиков в c: Программа на си для рисования графиков функций

Построение графиков тригонометрических функций с помощью преобразований

Учебник: Алгебра и начала анализа: учеб. для 10-11 кл. общеобразоват. учреждений /А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницын и др.; под ред. А.Н.Колмогорова.

Цели урока:

• повторить построение графиков функций , на примере построения графиков тригонометрических функций;
• рассмотреть преобразование при построении графиков тригонометрических функций;
• прививать интерес к математике;
• воспитывать графическую культуру, умение видеть красоту математики.

План урока:

1. Построение графиков с помощью преобразования y = f(x) +a.
2. Построение графиков с помощью преобразования y = kf(x).
3. Построение графиков с помощью преобразования y = kf(x).
4. Построение графиков с помощью преобразования y = f(kx).
5. Построение графиков с помощью преобразований.
6. Практическая работа.

Каждый этап урока предусматривает построение графиков сначала фронтально, затем индивидуально с последующей проверкой. Практическая работа, в зависимости от уровня подготовленности класса, может выполняться на оценку, а может с последующей фронтальной проверкой. Если практическая работа будет проверяться фронтально, то усвоение материала урока можно проверить в виде домашней самостоятельной или практической работы.

Ход урока

1.1. Повторить построение графиков с помощью преобразований . (Презентация, слайд 5).

Для построения графика функции , где a — постоянное число, надо перенести график y=f(x) на вектор (0;а) вдоль оси ординат. Если >0, то график переносим параллельно самому себе вверх, если a < 0, то – вниз.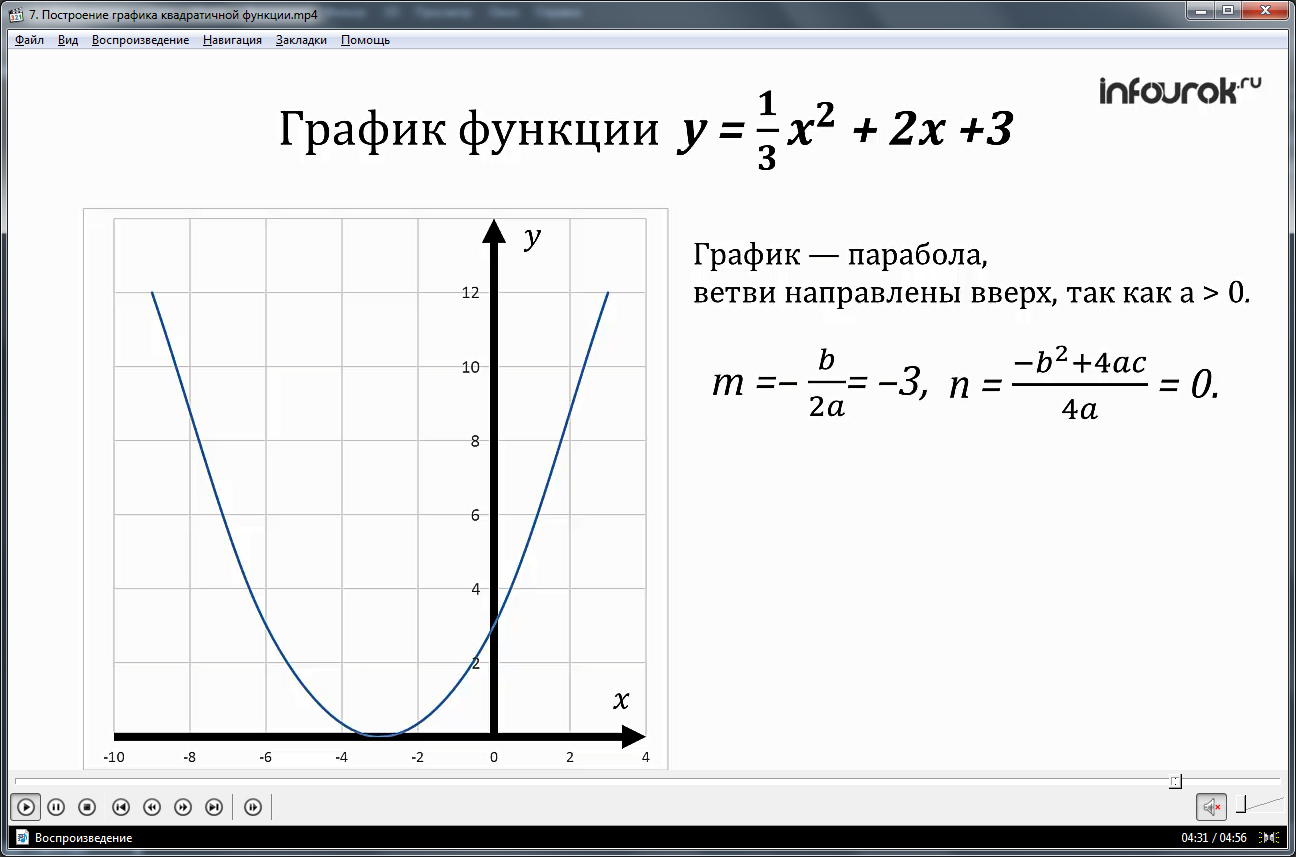

1.2. Обсудить построение и построить . (Презентация, слайд 6).

График функцииполучается из графика функции путем параллельного переноса на 3 единицы вниз. (Презентация, слайд 7).

1.3. Обсудить и построить . (Презентация, слайд 7).

График функции получается из графика функции путем параллельного переноса на 1 единицу вверх.

1.4. Построить самостоятельно и проверить. (Презентация, слайд 8).

2.1. Повторить построение графиков с помощью преобразований (Презентация, слайд 10).

Для построения графика функции надо растянуть график функции

y=f(x) в k раз вдоль оси ординат. Если , то происходит растяжение графика вдоль оси Oy, если 0<|k|<1, то – сжатие.

2. 2. Обсудить построение и построить . (Презентация, слайд 11).

График функции получается из графика функции , каждая ордината которого изменяется в -2 раза. Для этого график сначала отображаем симметрично относительно оси Ox, а затем растягиваем в 2 раза вдоль оси Oy.

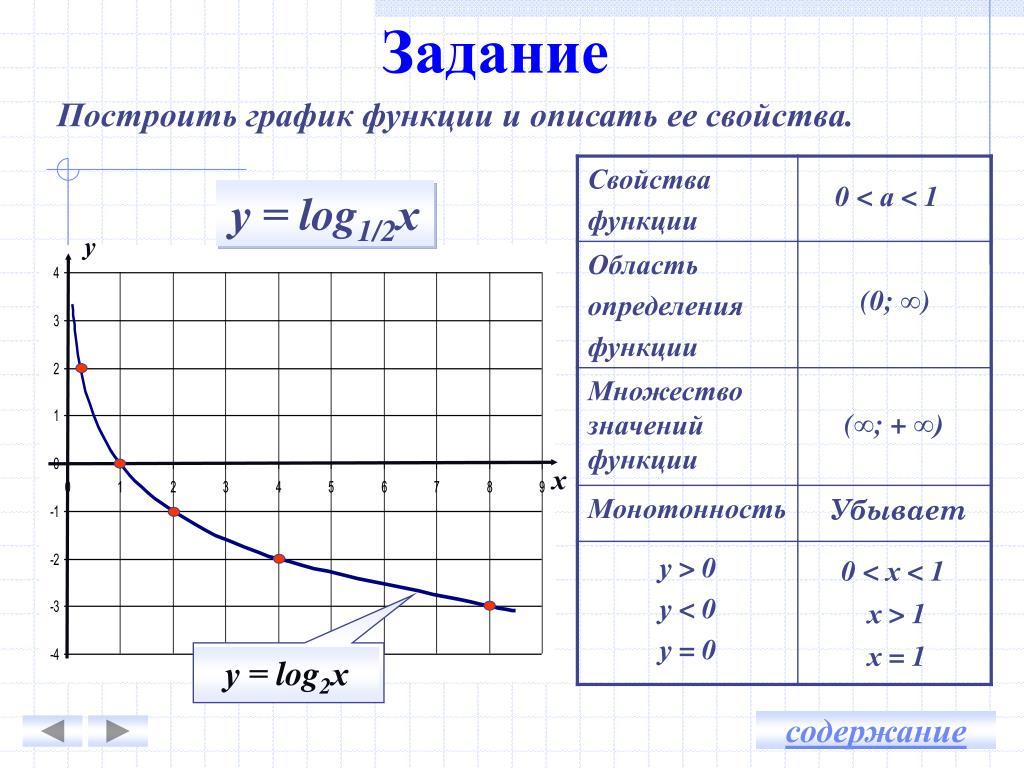
2.3. Обсудить построение и построить . (Презентация, слайд 12).

График функции получается из графика функции путем растяжения его в 3 раза вдоль оси Oy.

2.4. Построить самостоятельно и проверить. (Презентация, слайд 13).

3.1. Повторить построение графиков с помощью преобразований . (Презентация, слайд 15).

График функции получается из графика y=f(x) путем параллельного переноса вдоль оси абсцисс на вектор . Если , то график перемещается влево, если , то – вправо.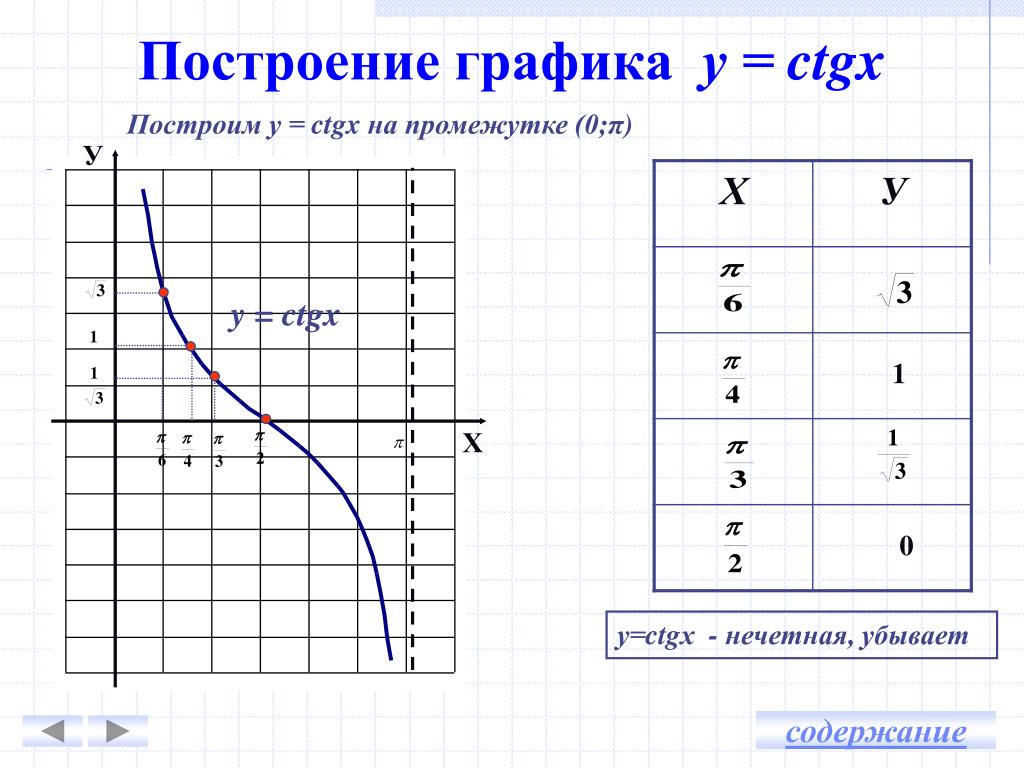

3.2. Обсудить построение и построить (Презентация, слайд 16).

График функции получается из графика функции параллельным переносом вдоль оси Ox на влево.

3.3. Обсудить построение и построить . (Презентация, слайд 17).

График функции получается из графика функции путем параллельного переноса вдоль оси Ox на вправо.

3.4. Построить самостоятельно и проверить. (Презентация, слайд 18)

4.1. Рассмотреть построение графиков с помощью преобразований y = f(kx) (Презентация, слайд 20).

Для построения графика функции надо подвергнуть график y=f(x) растяжению с коэффициентом k вдоль оси абсцисс. Если , то происходит сжатие графика вдоль оси Ox, если 0<|k|<1 , то – растяжение.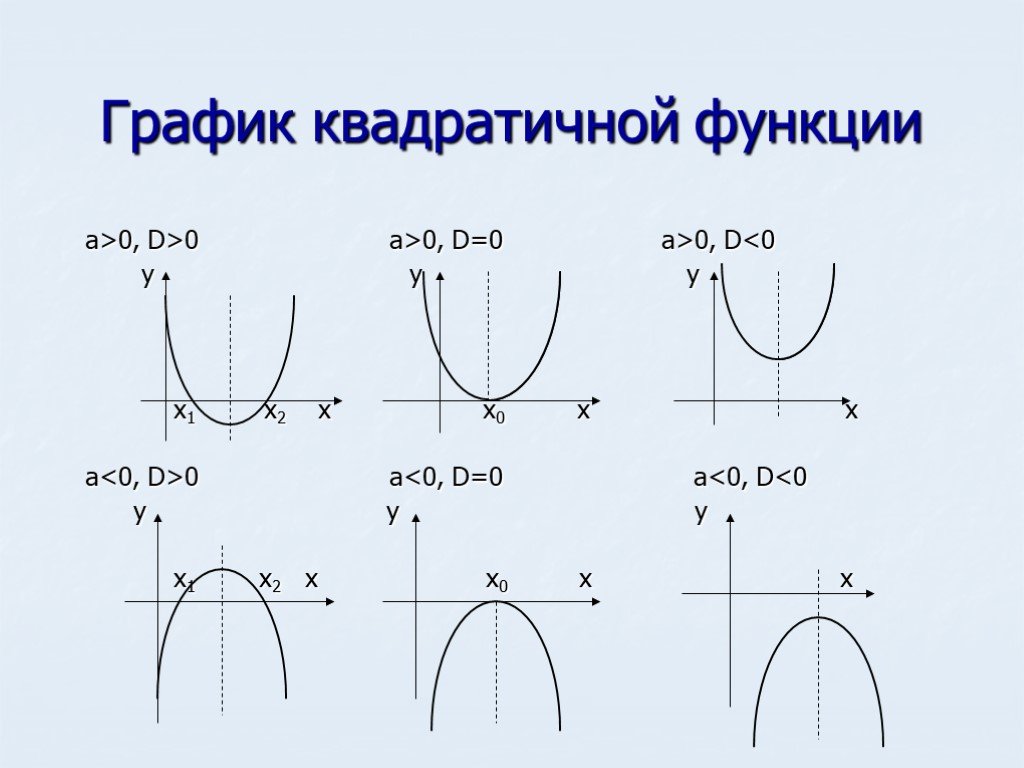

4.2. Обсудить построение и построить . (Презентация, слайд 21).

График функции получается из графика путем растяжения вдоль оси Ox в 2 раза.

4.3. Обсудить построение и построить (Презентация, слайд 22).

График функции получается из графика путем сжатия вдоль оси Ox в 2 раза.

4.4. Построить самостоятельно и проверить. (Презентация, слайд 23).

5.1. . (Презентация, слайд 25).

График функции получается из графика путем последовательного выполнения следующих преобразований:

а) сжатие в 2 раза вдоль оси Ox;

б) симметричное отображение относительно оси Ox;

в) параллельный перенос на 3 единицы вверх вдоль оси Oy.

5. 2. Обсудить построение и построить . (Презентация, слайд 26).

График функции получается из графика путем последовательного выполнения следующих преобразований:

а) растяжение в 3 раза вдоль оси Ox;

б) параллельный перенос на 2 единицы вниз вдоль оси

Oy.

6. Построить самостоятельно (Презентация, слайд 27):

• (Презентация, слайд 28)
• (Презентация, слайд 29)
• (Презентация, слайд 30)
• (Презентация, слайд 31)

7. Итог урока: повторить построение графиков функций с помощью преобразований, проговорить построение графиков в самостоятельной работе, в зависимости от уровня подготовки класса самопроверка (взаимопроверка) самостоятельной работы или собрать работы, а затем проверить (презентация).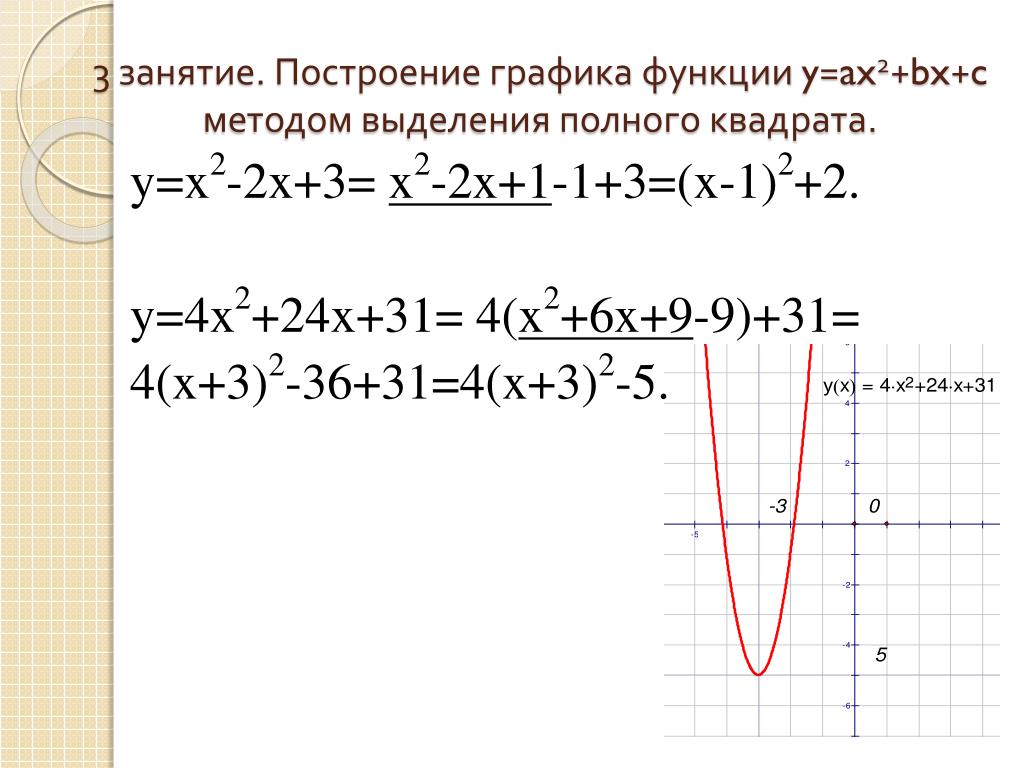

8. Домашнее задание индивидуально, в зависимости от того, как выполнена самостоятельная работа.

Функции построения графиков в Gnuplot — GeeksforGeeks

Gnuplot — это портативная, бесплатная, управляемая командами, интерактивная программа для построения графиков данных и функций для Linux, OS/2, MS Windows, OSX, VMS и многих других платформ. Несмотря на защиту авторских прав, исходный код находится в свободном доступе. Первоначально он был разработан, чтобы позволить исследователям и студентам интерактивно визуализировать математические функции и данные, но с тех пор он расширился, чтобы охватить широкий спектр неинтерактивных целей, включая веб-скрипты. Сторонние программы, такие как Octave, также используют его в качестве механизма построения графиков. Многочисленные типы графиков поддерживаются Gnuplot как в 2D, так и в 3D. Он может рисовать с использованием различного связанного текста, а также линий, точек, прямоугольников, контуров, векторных полей и поверхностей.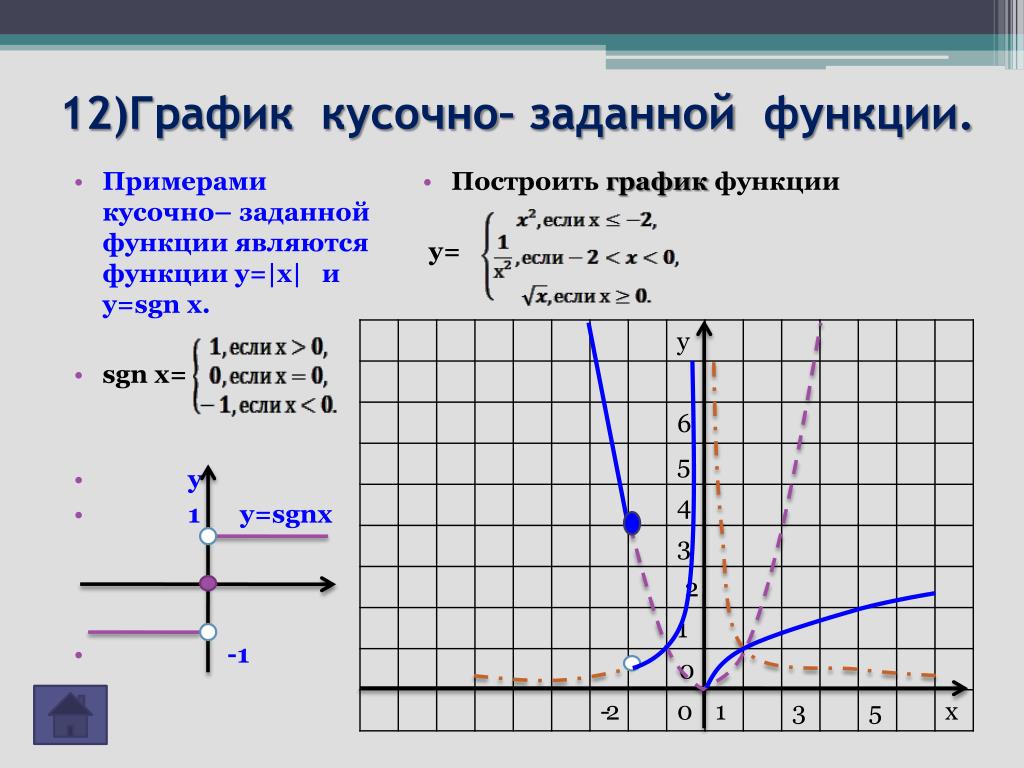 используется **, поэтому для построения простой функции, такой как  94 / 4)

В Gnuplot функция выглядит следующим образом:

f(x) = exp(-x**4/4)

Введите следующую команду:

plot exp(-x** 4 / 4)

 

Вывод:

 

минимум:максимум] перед функцией. Можно также оставить yrange или оба. Ниже приведена исправленная версия приведенного выше примера:

plot [-4:4] exp(-x**4 / 4)

Вывод:

 

Построение более одной функции

Чтобы построить более одной функции, перечислите все функции разделены через запятую. Ниже приведен пример реализации концепции:

plot [-4:4] exp(-x**2 / 2), x**2 / 16

Вывод:

 

Определение функции

Можно определить функцию один раз, чтобы не было необходимости вводить ее каждый раз заново.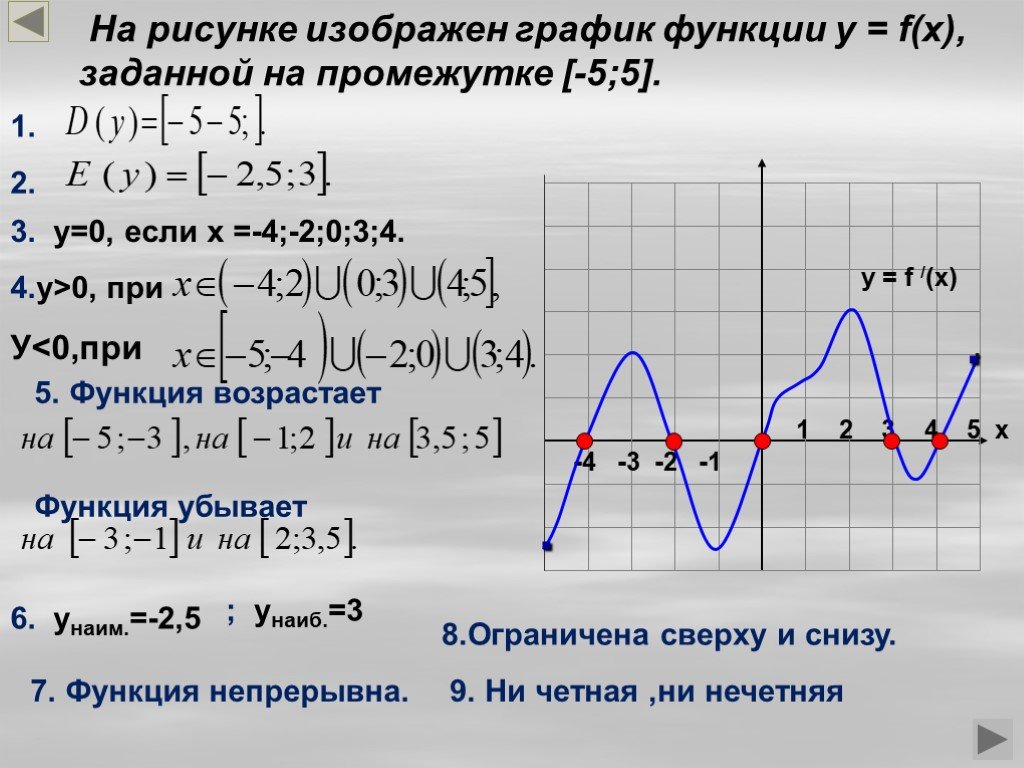 Ниже приведен пример реализации концепции:

f(x) = exp(-x**4 / 4)

график [t=-4:4] f(t), t**2 / 16

 

Построение тригонометрической функции

Ниже приведен пример построения функции синуса и косинуса:

a = 0,9
f(x) = a * sin(x)
g(x) = a * cos(x)
# Plot
plot f(x) title ‘sin(x)’ с линиями linestyle 1, \
    g(x) notitle с линиями linestyle 2

Здесь
f(x) и g(x) — это функция.
Операторы, начинающиеся с #, являются комментариями.

 

Вывод:

 

R Графика — Построение

❮ Предыдущая Далее ❯

---

График

Функция plot() используется для рисования точек (маркеров) на диаграмме.

Функция принимает параметры для указания точек на диаграмме.

Параметр 1 указывает точки на оси x .

Параметр 2 указывает точки на ось Y .

В самом простом случае вы можете использовать функцию plot() для построения двух чисел относительно друг друга:

Пример

Нарисуйте одну точку на диаграмме в позиции (1) и позиции (3):

plot (1, 3)

Результат:

Попробуйте сами »

Чтобы нарисовать больше точек, используйте векторы:

Пример

Нарисуйте две точки на диаграмме, одну в позиции (1, 3) и одну в позиции ( 8, 10):

сюжет(с(1, 8), с(3, 10))

Результат:

Попробуйте сами »

---

---

Несколько точек

Вы можете построить любое количество точек, просто убедитесь, что у вас одинаковое количество точек на обеих осях:

Пример

plot( с (1, 2, 3, 4, 5), c(3, 7, 8, 9, 12))

Результат:

Попробуйте сами »

Для лучшей организации, когда у вас много значений, лучше использовать переменные:

Пример

х <- с(1, 2, 3, 4, 5)
у <- с(3, 7, 8, 9, 12)

plot(x, y)

Результат:

Попробуйте сами »

---

Последовательности точек

Если вы хотите рисовать точки последовательно, на обеих оси x 900 06 и ось Y , используйте : оператор:

Пример

plot(1:10)

Результат:

Попробуйте сами »

---

Нарисуйте линию

Функция plot() также принимает параметр типа со значением l провести линию, соединяющую все точки в диаграмма:

Пример

plot(1:10, type=»l»)

Результат:

Попробуйте сами »

---

Метки графика

Функция plot() также принять другие параметры, например, основной , xlab и ylab если вы хотите настроить график с основным заголовком и различными метками для оси X и Y:

Пример

plot(1:10, main=»Мой график», xlab=»Ось X», ylab=»Ось Y»)

Результат:

Попробуйте сами »

---

Внешний вид графика

Существует множество других параметров, которые можно использовать для изменения внешнего вида точек.

Цвета

Используйте col=" color " , чтобы добавить цвет к баллы:

Пример

plot(1:10, col=»red»)

Результат:

Попробуйте сами »

Размер

Использование cex= номер 9 0130 для изменения размера точек ( 1 используется по умолчанию, а 0,5 означает уменьшение на 50 % и 2 означает увеличение на 100 %):

Пример

plot(1:10, cex=2)

Результат:

Попробуйте сами »

Форма точки

Использование 90 129 пк со значением от 0 до 25 Чтобы изменить формат формы точки:

Пример

График (1:10, PCH = 25, CEX = 2)

Результат:

Попробуйте это самостоятельно »

до 25, что означает, что мы можем выбрать до 26 различных типов точечные формы:

❮ Предыдущий Далее ❯

ВЫБОР ЦВЕТА

---

---

---

Лучшие учебники

Учебник по HTML
Учебник по CSS
Учебник по JavaScript
Учебник How To
Учебник по SQL
Учебник по Python
Учебник по W3.