Построение графиков системы уравнений онлайн: Построение графика функции онлайн

Графер Линейных Уравнений — Mathcracker.Com

Инструкции: Используйте этот Linear Equation Grapher для построения графика любого линейного уравнения, которое вы предоставите, с отображением всех этапов. Вам нужно указать линейное уравнение, график которого вы хотите построить, в поле формы ниже.

Подробнее об этом графере линейных уравнений

Построение графиков линий является фундаментальным умением, и этот калькулятор поможет вам в этом. Для начала вам необходимо предоставить линейное уравнение вы хотите построить график.

Вы можете привести любое линейное уравнение в явном виде, например, x + 3y = 2 , или то, которое не полностью упрощено, например, x + 3y = 2/3 x.

Графические линии имеет так много применений, что это становится очень практичным навыком. Геометрически линии имеют очень простую интуицию, что облегчает построение графиков, поскольку для их задания нам не требуется много информации.

Как построить график линейных уравнений?

Вы можете использовать это графический калькулятор для построения графиков линий.

Если вы решите сделать это вручную, вам нужно знать, что данный подход требует преамбулы, которая будет зависеть от типа предоставляемой информации.

Каковы этапы построения графика линии?

• Шаг 1: Определите тип предоставленной информации. Представлено ли уравнение, есть ли две точки, точка и наклон, наклон и y-интерцепт? Четко оцените, что
• Шаг 2: Независимо от полученной информации, используйте ее для нахождения двух точек, через которые проходит прямая. Для заданного уравнения решите y, например, для x = 0 и x = 1. Для наклонной и y-пересечения постройте уравнение y = a + bx и найдите две точки. Если у вас есть одна точка и наклон, определите y = y1 + b(x-x1) и вставьте его в точку x = 0
• Шаг 3: Получив две точки, через которые проходит линия, с помощью линейки проведите через них линию

Линии рисовать очень легко, просто нужно быть методичным и знать, какой информацией вы располагаете.

Даже если вы делаете это вручную, всегда приятно иметь под рукой линейку графический калькулятор онлайн чтобы проверить свои результаты.

Графические линии

Графические линии имеют очень много применений. Например, вы можете решить систему уравнений построив график соответствующих линий и посмотрев, где они пересекаются.

При использовании этого метода, когда прямые параллельны и не пересекаются, решений не будет.

Подобно тому, как это произошло со сложением и вычитанием, деление дробей просто вытекает из умножения дробей: Чтобы разделить две дроби, нужно просто умножить первую на обратная дробь второй (обратная дробь получается путем замены числителя на знаменатель в дроби).

Другие применения линейных графов

Линии или Линейные графики действительно присутствуют везде. линейные функции постоянно появляются в приложениях, в расчетах и оптимизации, поэтому они действительно полезны.

Пример: пример графера линейных уравнений

Постройте график следующих уравнений: \(\frac{1}{2}x + \frac{7}{4}y = 0\)

Отвечать: Мы должны работать со следующим уравнением:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Сначала работаем с константами:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Результат получается, если поставить (y) в левую часть, а (x) и константу — в правую:

\[\displaystyle \frac{7}{4}y = -\frac{1}{2}x \]

Затем процесс продолжается путем решения для \(y\), а затем путем деления обеих сторон уравнения на \(\frac{7}{4}\).

Получаем:

\[\displaystyle y=-\frac{\frac{1}{2}}{\frac{7}{4}}x\]

и после упрощения результат будет следующим.

\[\displaystyle y=-\frac{2}{7}x\]

Вывод : На основании имеющихся данных мы приходим к выводу, что уравнение линии в форме наклон-пересечение имеет вид \(\displaystyle y=-\frac{2}{7}x\) с наклоном \(\displaystyle b = -\frac{2}{7}\) и y-пересечением \(\displaystyle n = 0\).

Следовательно, график представленной линии имеет вид

Пример: пример графера линейных уравнений

Получите строку, которая представляет: \(\frac{2}{3}x + \frac{5}{4}y = — \frac{5}{6}x + 2\)

Отвечать: Нам было предложено следующее уравнение:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Работа с константами:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Теперь, положив \(y\) в левой части, \(x\) и константу в правой части, получим

\[\displaystyle \frac{5}{4}y = \left(\frac{-5}{6}-\frac{2}{3}\right)x +2\]

Теперь член, умножающий \(y\), равен \( \frac{5}{4} — 0 = \frac{5}{4}\), а так как \( -\frac{5}{6} — \frac{2}{3} = -\frac{3}{2}\), то получается следующее

\[\displaystyle \frac{5}{4}y=-\frac{3}{2}x+2\]

Теперь, находя \(y\) путем деления обеих частей уравнения на \(\frac{5}{4}\), получается следующее

\[\displaystyle y=-\frac{\frac{3}{2}}{\frac{5}{4}}x+\frac{2}{\frac{5}{4}}\]

и упрощая окончательно получаем следующее

\[\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\]

Вывод : На основании предоставленных данных мы заключаем, что уравнение линии в форме наклона-отрезка имеет вид \(\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\), с наклоном \(\displaystyle b = -\frac{6}{5}\) и точкой пересечения по оси y \(\displaystyle n = \frac{8}{5}\).

Линейный график

Другие линейные калькуляторы

Линии настолько важны, что заслуживают собственного раздела в книге по математике. Вы можете вычислить Линейные уравнения в различных формах, в зависимости от конкретных потребностей.

Определение линий, которые в конечном итоге понадобятся две точки, через которые проходит линия , который может быть предоставлен прямо или косвенно.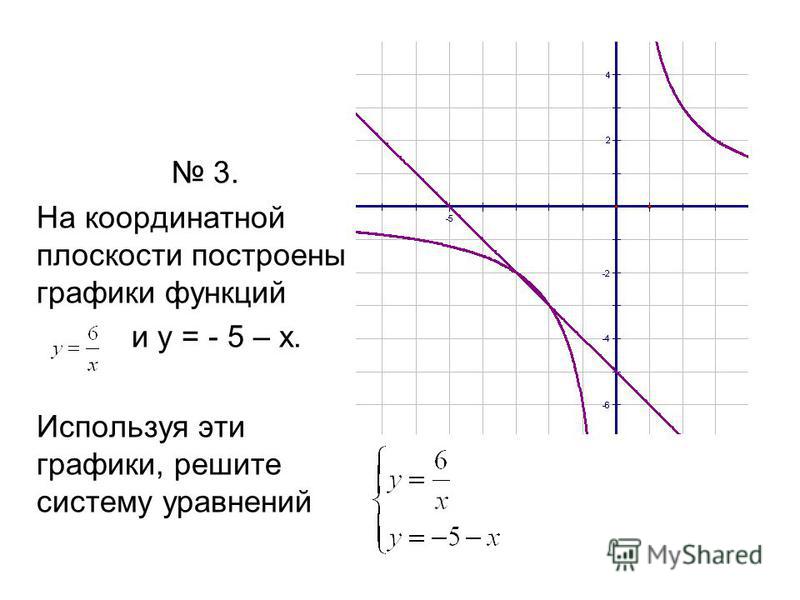

Господин Экзамен

Данный сайт позволяет решать некоторые математические задачи онлайн с подробными пошаговыми действиями.

Дифференциальные уравнения по шагам

Для однородных и неоднородных линейных дифференциальных уравнений первого и второго порядков, дифф. ур-ний с разделяющимися переменными, с заменой и др. с подробным пошаговым решением.

Обычные уравнения по шагам

Калькулятор обычных уравнений умеет решать уравнения со степенями, в том числе квадратные и кубические, некоторые четвёртой степени, уравнения с модулем, простые линейные, показательные уравнения, простые тригонометрические и некоторые др. Любые другие уравнения с ответом. Есть возможность решать уравнения численно.

Упрощение выражений

Введите упрощаемое выражение и калькулятор найдёт все возможные виды упрощений алгебраического выражения или сложного числа.

Системы уравнений по шагам

Для линейных систем уравнений Вы получите несколько подробных решений, в том числе решение «в лоб», методом Крамера и методом Гаусса.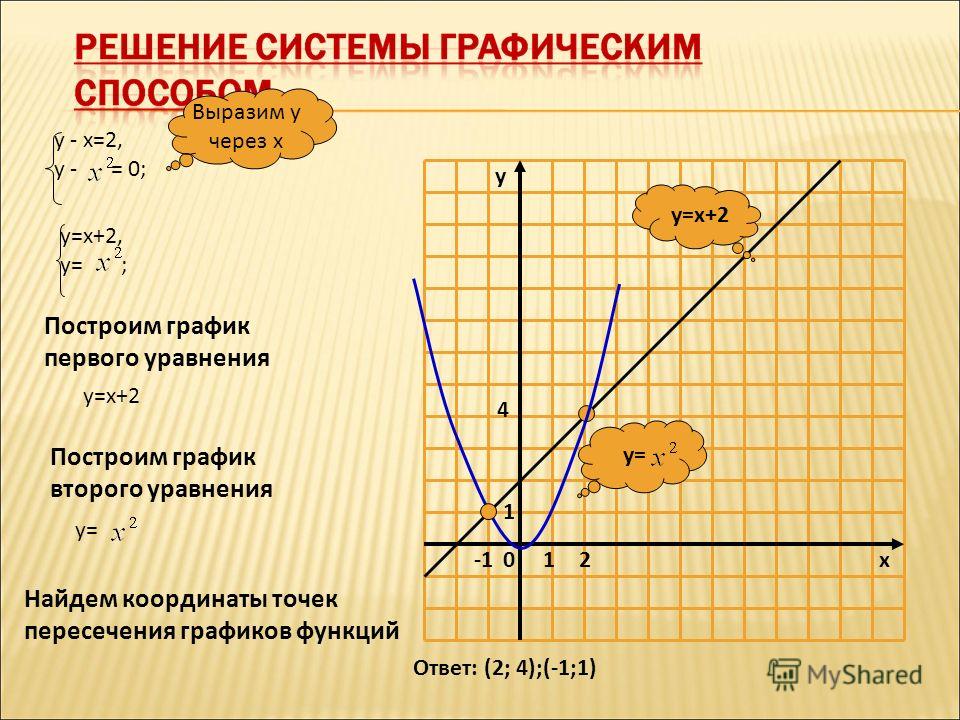 Для любых других систем уравнений будет дан быстрый ответ.

Неравенства по шагам

Кроме аналитического решения неравенства вы увидите решение неравенства на графике.

Системы неравенств по шагам

Иногда, неравенства представлены системой нескольких неравенств с одной или двумя переменными.

Построение графика функции по шагам

Калькулятор строит график функции в декартовых координатах, возможно задать промежуток построения графика, на этом графике отображаются точки пересечения, если функций задано несколько, а также производится исследование соответствующей функции.

Исследование графика функции по шагам

Калькулятор генерирует подробное исследование графика функции: экстремумы функций, горизонтальные и вертикальные асимптоты, наклонные асимптоты, чётность и нечётность функции, точки перегибов, точки пересечения графика с осью X и Y, область определения функции, а также построение графика соответствующей функции.

График параметрической функции

Вы можете построить график функциии, заданной параметрами

Построение поверхности

Вы вводите функцию поверхности или же поверхность, заданную уравнением

Построение поверхности, заданной параметрически

Вы вводите несколько функций, которые задают поверхность параметрически

Построение кривой в пространстве

Вы вводите несколько функций, которые параметрически задают кривую в пространстве

График неявной функции

Вы можете построить график неявной функциии, заданной уравнением

График полярной функции

Вы вводите функцию, заданную в полярных координатах

Производная по шагам

С помощью калькулятора производных можно вычислить производную функции с одной переменной с подробным решением, частные производные от функции двух и трёх переменных, а также производную от неявной функции, заданной уравнением.

Производная функции, заданной параметрически

Вы указываете функцию, заданную двумя параметрами, а калькулятор вам подсчитает производную данной функции

Производная неявной функции

Укажите функцию, заданную неявно и калькулятор найдёт её производную

Ряд Тейлора по шагам

Есть возможность с помощью этого калькулятора разложить функцию в ряд Тейлора до заданного показателя степени ряда.

Ряд Фурье по шагам

Этот калькулятор позволяет разложить функцию в ряд Фурье на заданном отрезке на оси X.

Сумма ряда по шагам

Даёт аналитический и численный ответ суммы ряда, а также график скорости сходимости суммы ряда.

Произведение ряда

Арифметическая прогрессия

Геометрическая прогрессия

Интеграл по шагам

Этот калькулятор интегралов предоставляет возможность решать определённые, неопределённые, несобственные интегралы с решением по шагам.

Несобственный интеграл по шагам

Позволяет вычислить несобственный интеграл, можно задать пределы интегрирования равные плюс или минус бесконечности.

Двойной интеграл

Тройной интеграл

Канонический вид

Приводит вид уравнений для линий на плоскости и в пространстве 2-го порядка и поверхностей 2-го порядка к каноническому виду.

Комлексные числа по шагам

Проводятся операции над комплексными числами: деление, умножение и другое упрощение, нахождение комплексно-сопряжённого числа, алгебраическая, тригонометрическая и экспоненциальная формы комплексного числа.

Также вы найдёте модуль комплексного числа.

Матрицы

В этом разделе Вы можете выполнить как стандартные операции с матрицами, такие как умножение, сложение, детерминант, обратная, ранг, так и экзотические операции с матрицами: комлексно-сопряжённая, собственные вектора и собственные значения, QR и LU.

Математическая логика

Калькулятор умеет расставлять скобки, упрощать логические выражения, строить таблицу истинности, находит нормальную форму выражения.

Пределы по шагам

Калькулятор пределов позволяет найти предел функции в конечной точке или на бесконечности с пошаговым решением, а также с применением метода Лопиталя.

Калькулятор градусов

Калькулятор градусов позволяет делать различные преобразования с углами.

Кусочно-заданная функция

Укажите кусочно-заданную функцию и перейдите к нужному вам сервису, например, к одному из: нахождению интеграла, производной, исследованию и построение графика и др.

Коэффициент Стьюдента

Факториал числа

Как пользоваться сервисами

Информация для покупателей

О сайте

Решение линейных уравнений высшего порядка с помощью программы «Пошаговое решение математических задач».

уравнения. Один из способов получить такую ​​упорядоченную пару — построить график двух уравнений на той же системе осей и определения координат точки, где они пересекаются.

Пример 1

Графические уравнения

x + y = 5

x — y = 1

на том же наборе осей и определить упорядоченную пару, являющуюся решением для каждой уравнение.

Решение

Используя метод построения графика, мы находим, что две упорядоченные пары, которые решения x + y = 5 равны

(0, 5) и (5, 0)

. Две упорядоченные пары, являющиеся решениями

x — y = 1, равны

(0,-1) и (1,0)

. Графики уравнений показаны.

Точка пересечения (3, 2). Таким образом, (3, 2) должны удовлетворять каждому уравнению.

На самом деле, 3 + 2 = 5 и 3 — 2 = 1

В общем, графические решения являются приблизительными. Мы разработаем методы для точных решений в последующих разделах.

Линейные уравнения, рассматриваемые вместе таким образом, образуют систему уравнения. Как и в приведенном выше примере, решение системы линейных уравнений может быть одной упорядоченной парой. Компоненты этой упорядоченной пары удовлетворяют каждому из два уравнения.

Некоторые системы не имеют решений, а другие имеют бесконечное число решений. ции. Если графики уравнений системы не пересекаются, т. е. если прямые параллельны (см. рис. 8.1а) — говорят, что уравнения равны не соответствует , а там нет упорядоченной пары, удовлетворяющей обоим уравнениям. Если графики уравнений той же прямой (см. рис. 8.1b), уравнения называются зависимыми , и каждое упорядоченная пара, удовлетворяющая одному уравнению, будет удовлетворять обоим уравнениям. Заметить, что когда система несовместима, наклоны линий одинаковы, но y-перехваты разные. Когда система зависима, наклоны и y-пересечения одинаковы.

В нашей работе нас в первую очередь будут интересовать системы, имеющие один и только один решения, которые называются непротиворечивыми и независимыми.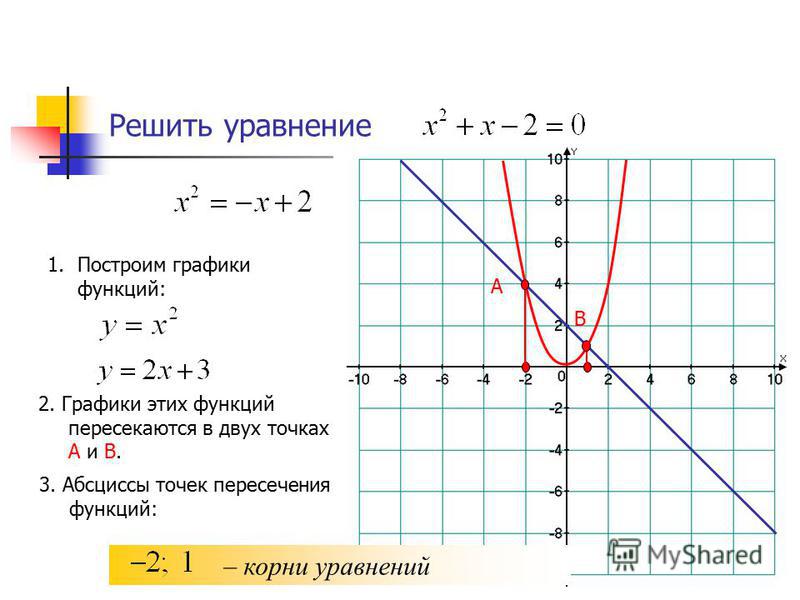 График такой система показана в решении примера 1.

РЕШЕНИЕ СИСТЕМ С ПОМОЩЬЮ ДОПОЛНЕНИЯ I

Мы можем решать системы уравнений алгебраически. Более того, решения, которые мы полученные алгебраическими методами, являются точными.

Система в следующем примере — это система, которую мы рассматривали в разделе 8.1. на стр. 335.

Пример 1

Решить

x + y = 5 (1)

x — y = 1 (2)

Решение
Мы можем получить уравнение с одной переменной, добавив E уравнения (1) и (2)

Решение полученного уравнения относительно x дает

2x = 6, x = 3

Теперь мы можем заменить x на 3 в уравнении (1) или уравнении (2), чтобы получить соответствующее значение у. В этом случае мы выбрали уравнение (1) и получили

(3) + y = 5

y = 2

Таким образом, решение x = 3, y = 2; или (3, 2).

Обратите внимание, что мы просто применяем свойство сложения равенства, чтобы мы могли получить уравнение, содержащее одну переменную. Уравнение с одной переменной, вместе с любым из исходных уравнений, затем образует эквивалентную систему решение которой легко получить.

В приведенном выше примере мы смогли получить уравнение с одной переменной с помощью добавление уравнений (1) и (2), потому что члены +y и -y являются отрицательными значениями каждого другой. Иногда необходимо умножить каждый член одного из уравнений на -1, так что члены одной и той же переменной будут иметь разные знаки. Пример 2 , чтобы получить

2a + b = 4 (3)

-a — b = — 3 (4′)

, где +b и -b отрицательные значения друг друга.

Символ ‘, называемый «штрихом», указывает на эквивалентное уравнение; то есть уравнение, имеющее те же решения, что и исходное уравнение. Таким образом, уравнение (4′) эквивалентно уравнению (4). Теперь сложив уравнения (3) и (4’), мы получим

. Подставив 1 вместо a в уравнение (3) или уравнение (4) [скажем, уравнение (4)], мы получим

1 + b = 3

b = 2

и наше решение: a = 1, b = 2 или (1, 2). Когда переменными являются a и b, упорядоченная пара задается в виде (a, b).

РЕШЕНИЕ СИСТЕМ СЛОЖЕНИЕМ II

Как мы видели в разделе 8.2, решение системы уравнений методом сложения зависит от одна из переменных в обоих уравнениях с коэффициентами, отрицательными друг друга. Если это не так, мы можем найти эквивалентные уравнения, которые действительно имеют переменные с такими коэффициентами.

Пример 1

Решите систему

-5x + 3y = -11

-7x — 2y = -3

Решение

Если мы умножим каждый член уравнения (1) на 2 и каждый член уравнения (2) на 3 получаем эквивалентную систему

(2) (-5х) + (2)(3у) = (2)(-11)

(3) (-7х) — (3)(2у) = (3)(-3)

или

-10х + 6у = -22 ( 1′)

-21x — 6y = -9 (2′)

Теперь, складывая уравнения (1′) и (2′), мы получаем

-31x = -31

х = 1

Замена x на 1 в уравнении (1) дает

-5(1) + 3г = -11

3г = -6

у = -2

Решение x = 1, y = -2 или (1, -2).

Обратите внимание, что в уравнениях (1) и (2) члены, включающие переменные, находятся в левый член, а постоянный член находится в правом члене. Мы будем ссылаться к таким договоренностям как к стандартной форме для систем. Удобно организовать системы в стандартной форме, прежде чем приступить к их решению. Например, если мы хочу решить систему

3у = 5х — 11

-7x = 2y — 3

сначала мы запишем систему в стандартной форме, добавив -5x к каждому элементу уравнения (3) и путем добавления -2y к каждому члену уравнения (4). Таким образом, мы получаем

-5x + 3y = -11

-lx — 2y = -3

, и теперь мы можем действовать, как показано выше.

РЕШЕНИЕ СИСТЕМ ПОДСТАВКОЙ

В разделах 8.2 и 8.3 мы решали системы уравнений первой степени в двух вариантах: можно методом сложения. Другой метод, называемый методом замещения, также могут быть использованы для решения таких систем.

Пример 1

Решить систему

-2x + y = 1 (1)

x + 2y = 17 (2)

Решение

Решив уравнение (1) относительно y через x, получим

у = 2х + 1 (1′)

Теперь мы можем заменить 2x + 1 на y в уравнении (2), чтобы получить

х + 2 (2х + 1) = 17

х + 4х + 2 = 17

5x = 15

х = 3 (продолжение)

Подставив 3 вместо x в уравнение (1′), мы получим

y = 2(3) + 1 = 7

Таким образом, решение системы есть: x = 3, y = 7; или (3, 7).

В приведенном выше примере было легко выразить y явно через x, используя Уравнение (1). Но мы также могли бы использовать уравнение (2), чтобы явно записать x в терминах г

х = -2у + 17 (2′)

Теперь подставив — 2y + 17 вместо x в уравнении (1), мы получим

Подставив 7 вместо y в уравнение (2′), мы получим

. х = -2(7) + 17 = 3

Решение системы снова (3, 7).

Обратите внимание, что метод подстановки полезен, если мы можем легко выразить одну переменную с точки зрения другой переменной.

ПРИЛОЖЕНИЯ, ИСПОЛЬЗУЮЩИЕ ДВЕ ПЕРЕМЕННЫЕ

Если две переменные связаны одним уравнением первой степени, существует бесконечное число множество упорядоченных пар, являющихся решениями уравнения. Но если две переменные связанных двумя независимыми уравнениями первой степени, может быть только одно упорядоченное пара, являющаяся решением обоих уравнений. Поэтому для решения задач с помощью двух переменных, мы должны представить две независимые зависимости с помощью двух уравнений . Мы часто можем легче решать проблемы, используя систему уравнений, чем используя одно уравнение с одной переменной. Мы будем следовать шести шагам, описанным на стр. 115, с небольшими изменениями, как показано в следующем примере.

Пример 1

Сумма двух чисел равна 26. Большее число в 2 раза больше, чем в три раза. меньшее число. Найдите числа.

Решение

Шаги 1-2
Мы представляем то, что мы хотим найти, как фразы из двух слов. Тогда мы представить словосочетания в терминах двух переменных.
Меньшее число: x
Большое число: y

Шаг 3 Эскиз неприменим.

Шаг 4 Теперь мы должны написать два уравнения, представляющие указанные условия.

Сумма двух чисел равна 26.

Шаг 5. Чтобы найти числа, решаем систему

x + y = 26 (1)

y = 2 + 3x (2)

Поскольку уравнение (2) показывает y явно через x, мы будем решать систему следующим образом: метод замещения. Подставляя 2 + 3x вместо y в уравнении (1), мы получаем

х + (2 + 3х) = 26

4x = 24

х = 6

Подставив x в уравнение (2) на 6, мы получим

y = 2 + 3(6) = 20

Шаг 6 Меньшее число равно 6, а большее число равно 20. система уравнений . Решение как правило, одна упорядоченная пара. Если графики уравнений представляют собой 90 232 параллельных прямых 90 233 , то уравнения, как говорят, несоответствие ; если графики представляют собой одну и ту же линию , уравнения говорят, что они зависимы от .

Мы можем решить систему уравнений методом сложения , если сначала запишем система в стандартной форме , в которой термины, включающие переменные, находятся в левый член, а постоянный член находится в правом члене.

Мы можем решить систему уравнений методом подстановки , если одна переменная в хотя бы одно уравнение в системе сначала явно выражается через другое переменная.

Мы можем решать текстовые задачи, используя две переменные, представляя два независимых связи двумя уравнениями.

Калькулятор линейных уравнений | Бесплатные онлайн-инструменты для решения системы уравнений

Интересно, как понять базовый уровень понятий линейных уравнений за считанные секунды. Это не проблема, поскольку мы создали концептуальные калькуляторы линейных уравнений. Эти калькуляторы для решения линейных уравнений бесплатны и удобны. Это помогает детям, а также учителям найти точный результат предоставленных линейных уравнений в течение нескольких секунд. Перейдите на эту страницу и воспользуйтесь возможностью использовать бесплатные онлайн-инструменты для расчета линейных уравнений.

Быстрый подход к решению вычислений линейных уравнений, таких как линейные уравнения с одной переменной, линейные уравнения с двумя переменными, графическое построение линейных уравнений и т. д., заключается в использовании калькуляторов линейных уравнений. Список бесплатных онлайн-калькуляторов по линейным уравнениям представлен здесь по быстрым ссылкам. Перейдите по этим доступным ссылкам калькулятора и с легкостью решите вычисления линейных уравнений.

Калькуляторы для решения линейных уравнений

• Калькулятор решения линейных уравнений
• Линейные уравнения в калькуляторе с одной переменной
• Калькулятор линейных уравнений с двумя переменными
• Калькулятор линейных уравнений с тремя переменными
• Графический калькулятор линейных уравнений
• Решение линейного уравнения с использованием правила Крамерса (3 переменные)
• Решение линейных уравнений с использованием обратной матрицы (2 переменные)
• Решение линейных уравнений с помощью обратной матрицы (4 переменные)
• Решение линейных уравнений с использованием операций со строками (2 переменные)
• Решение линейных уравнений с использованием расширенной матрицы (2 переменные)

• Калькулятор нелинейных уравнений
• Линейные уравнения с помощью калькулятора подстановок
• Линейные уравнения с калькулятором дробей
• Калькулятор линейных уравнений и неравенств
• Решение линейного уравнения с использованием правила Крамерса (4 переменные)
• Решение линейного уравнения с использованием правила Крамерса (2 переменные)
• Решение линейных уравнений с использованием обратной матрицы (3 переменные)
• Решение линейных уравнений методом подстановки (2 переменные)
• Решение линейных уравнений с использованием операций со строками (3 переменные)
• Решение линейных уравнений с использованием расширенной матрицы (3 переменные)

 

Наши решения класса 6 в Раджастхане Вопросы и ответы

Наши решения класса 6 в Раджастхане Вопросы и ответы

• Глава 1 Раджастхан. Введение
• Глава 2 История Раджастхана
• Глава 3 Источники истории
• Глава 4 Места древней цивилизации в Раджастхане
• Глава 5 Форма правления до обретения независимости
• Глава 6 Физическое формирование Раджастхана
• Глава 7 Водные ресурсы и сохранение
• Глава 8 Основные средства к существованию
• Глава 9Основные услуги в Раджастхане
• Глава 10 Народная культура и искусство

Решения класса 7 в Раджастхане Вопросы и ответы

Решения класса 7 в Раджастхане Вопросы и ответы

• Глава 1 Леса, дикая природа и ее охрана
• Глава 2 Минералы и энергетические ресурсы
• Глава 3 Сельское хозяйство и ирригация
• Глава 4 Сельскохозяйственный маркетинг в Раджастане
• Глава 5 Торговля в Раджастане
• Глава 6. Выдающиеся правители Раджастхана
• Глава 7 Движение за независимость и Раджастхан
• Глава 8 Социальные и образовательные реформы в Раджастане до обретения независимости
• Глава 9 Вклад Раджастхана в создание Конституции

Решения класса 8 в Раджастхане Вопросы и ответы

Решения класса 8 в Раджастхане Вопросы и ответы

• Глава 1 Леса, дикая природа и ее охрана
• Глава 2 Минералы и энергетические ресурсы
• Глава 3 Сельское хозяйство и ирригация
• Глава 4 Сельскохозяйственный маркетинг в Раджастане
• Глава 5 Торговля в Раджастане
• Глава 6. Выдающиеся правители Раджастхана
• Глава 7 Движение за независимость и Раджастхан
• Глава 8 Социальные и образовательные реформы в Раджастане до обретения независимости
• Глава 9 Вклад Раджастхана в создание Конституции

Калькулятор дробей

• Сложение дробей
• Вычитание дроби
• Умножение дробей
• Дробный отдел
• Упрощение дробей
• Эквивалент дроби
• Десятичная дробь
• Проценты в доли
• Доля до десятичной дроби
• Доля в процентах

Калькулятор решения линейных уравнений

Решение линейных уравнений вида Ax+By=C представляет собой слияние двух переменных и константы. Здесь x и y — переменные, а A, B и C — константы. Этот бесплатный онлайн-калькулятор точно вычисляет значения переменных.

Например, 2x+6y=4 и 5x+1y=2 являются линейными уравнениями.

Калькулятор линейных уравнений с одной переменной

Уравнение, имеющее одну переменную со степенью, равной единице, называется линейным уравнением с одной переменной. Стандартное уравнение линейного уравнения с одной переменной записывается в виде ax+b=0, где x — переменная, а a, b — константы. Он дает решение для одной переменной.

Например, 3x-5=10 — это линейные уравнения с одной переменной. Следовательно, х=5.

Калькулятор линейных уравнений с двумя переменными

Линейное уравнение с двумя переменными — это решение переменных Стандартная форма уравнения, т. е. ax+by+c=0, называется линейным уравнением с двумя переменными x и y, где мы получаем решение для двух переменных. Если a,b,c — действительные числа и они равны 0, то линейное уравнение с двумя переменными имеет вид ax+by=c.

Например, x + 2y = 10, 2x + y = 20 — линейное уравнение с двумя переменными, а значит, x = -3 и y = 26 — решения данного линейного уравнения с двумя переменными.

Калькулятор построения графиков линейных уравнений

A Графики линейных уравнений представляют собой графическое представление линейных уравнений. Для решения системы линейных уравнений мы используем различные методы, одним из которых является построение линейных уравнений в виде графика, в результате которого получается прямая линия.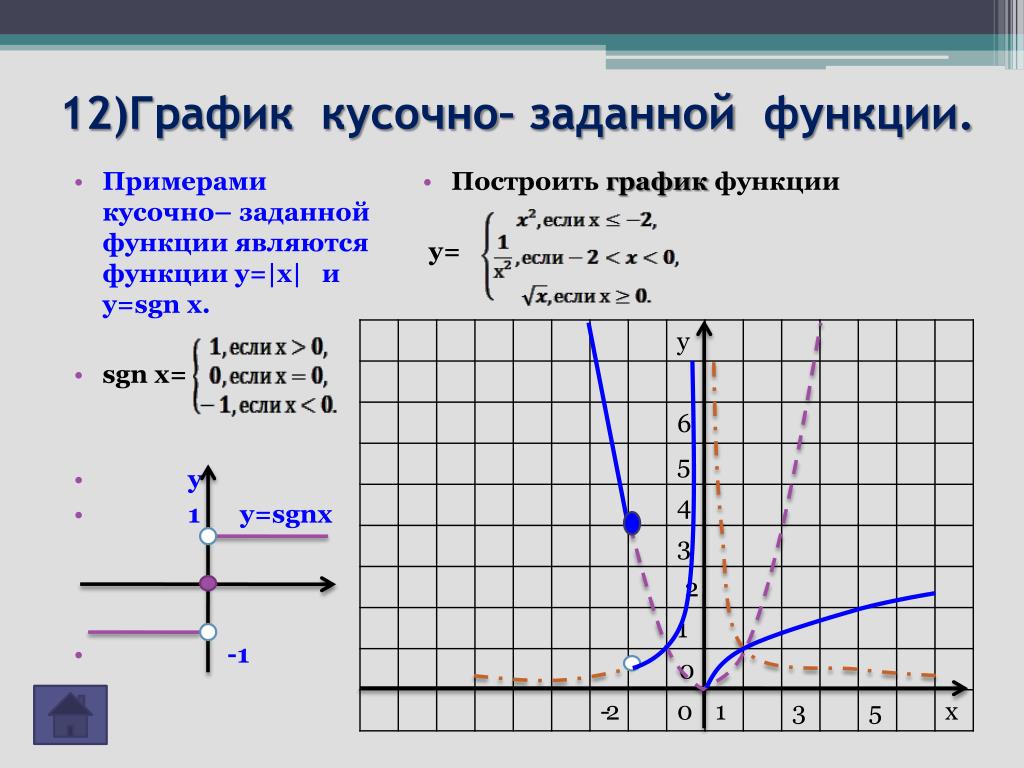

Например, y=mx+b является графическим примером линейных уравнений.

Калькулятор нелинейных уравнений

Нелинейное уравнение — это уравнение, в котором переменная имеет степень 2 или более двух. Стандартная форма нелинейного уравнения: ax² + by² = c, где a, b, c — константы, а x и y — переменные. Нелинейное уравнение на графике представляет собой кривую и имеет переменное значение наклона.

Например, 2x² — 4y² = 1 и 3x² + 2x + 1 = 0 являются двумя экземплярами системы нелинейных уравнений.

Калькулятор линейных уравнений методом подстановки

Решение системы уравнений методом подстановки — самый простой способ решения расчетов линейных уравнений. Калькулятор линейных уравнений с помощью подстановки находит значения переменных для заданной пары уравнений.

Например, решая линейные уравнения x-3y=4, x+2y=1 с помощью подстановки, получаем x=11/5, y=-3/5.

Калькулятор линейных уравнений с дробями

Дробное линейное уравнение — это уравнение, содержащее дробные члены в числителе/знаменателе.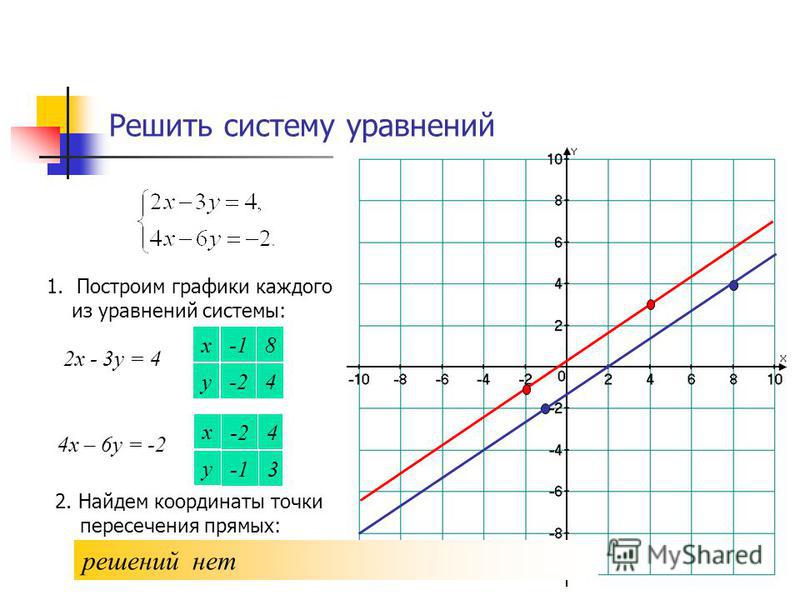 Онлайн-калькулятор линейных уравнений с дробями сначала решает выражение, исключая знаменатели, а затем продолжает тот же процесс решения линейных уравнений.

Например: (2x+2y)/(x-y) — это линейное уравнение с дробями, и его решение равно 2(x+y)/(x-y).

Калькулятор линейных уравнений и неравенств

Линейные функции, включенные в неравенства, такие как меньше (<), больше (>), меньше или равно (≤), больше или равно (≥) символов, легко вычисляются с помощью линейных уравнений с помощью калькулятора неравенств.

Например, 2x-5/3 > 3x+3/4 является примером функции линейного неравенства. следовательно, решение уравнения x < -29.

Различные формы линейных уравнений с примерами

Линейное уравнение	Общая форма	Пример
Форма пересечения уклона	у = мх + б	у + 2х = 3
Точечно-наклонная форма	у – у1 = м(х – х1)	у – 3 = 6(х – 2)
Общая форма	Топор + В + С = 0	2х + 3у – 6 = 0
Форма перехвата	х/а + у/б = 1	х/2 + у/3 = 1

Методы решения линейных уравнений с двумя переменными

Для решения линейных уравнений с двумя переменными существуют различные методы, и они следующие:

• Метод подстановки
• Метод перекрестного умножения
• Метод устранения
• Графический метод

Стандартная форма формулы линейного уравнения?

Стандартная форма формулы линейного уравнения состоит из переменной и константы.