Разработка урока по теме «График линейного уравнения с двумя переменными»
Отдел образования
муниципального образования «Городской округ Ногликский»
муниципальное бюджетное образовательное учреждение
средняя общеобразовательная школа №1
План урока алгебры
в 7 классе по теме
«График линейного уравнения
с двумя переменными»
Автор работы:
Агиенко Татьяна Ивановна,
учитель математики.
2013г
Авторы учебника Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов.
Тема урока: «График линейного уравнения с двумя переменными» (2 часа)
Урок №2.
Цели урока:
-создать условия для повторения определения линейной функции, линейного уравнения с двумя переменными, их графиков в зависимости от значений коэффициентов, формул сокращенного умножения;
-создать условия для проверки умений построения графиков линейных уравнений с двумя переменными, нахождения ординаты и абсциссы точки, нахождения соответствия между заданными графиками и уравнениями;
-создать условия для развития логического мышления, внимания, памяти, математически грамотной речи, самостоятельности;
-создать условия для развития познавательного интереса к математике, настойчивости, целеустремленности в учебе, дисциплинированности, воспитанности.
Тип урока: комплексное применение знаний, умений и навыков.
Оборудование: доска, мел, линейки, таблицы, компьютер, проектор, экран, карточки с
заданиями и листы с клетками для самостоятельной работы.
Оформление доски:
таблицы:
1)Взаимное расположение графиков линейных функций в зависимости от k и b.
2)Расположение графиков линейных уравнений с двумя переменными в зависимости от коэффициентов а, b и с.
3)Алгоритм (правило) построения графика линейного уравнения с двумя переменными.
( Приложения №1 — №7)
Ход урока.
1.Организационный этап
а) Проверка готовности учащихся к уроку.
Для того, чтобы хорошо работать на уроке, нужен настрой. А настроиться на работу нам помогут следующие уравнения.
(Приложение №8. Из презентации слайд №1)
«Развитие и образование ни одному человеку
не могут быть даны или сообщены.
Всякий, кто желает к ним приобщиться,
должен достигнуть этого собственной
деятельностью, собственными силами,
собственным напряжением.
Извне он может получить только
возбуждение.
А. Дистервег.
(Немецкий физик и математик)
(1790 – 1866г.г)
Пусть эти слова будут эпиграфом к сегодняшнему уроку.
(Справка: Эпиграф — изречение, краткая цитата, предпосланная произведению или его части и характеризующая их основную идею.)
Ребята! Как вы думаете, о чем говорят нам эти слова?
Так давайте проявим самостоятельность, трудолюбие, смекалку и терпение при изучении материала сегодняшнего урока. Предлагаю улыбнуться друг другу, чтобы наше настроение на уроке было отличным.
б) Сообщение темы и формулирование цели урока вместе с учащимися.
Проблемная ситуация:
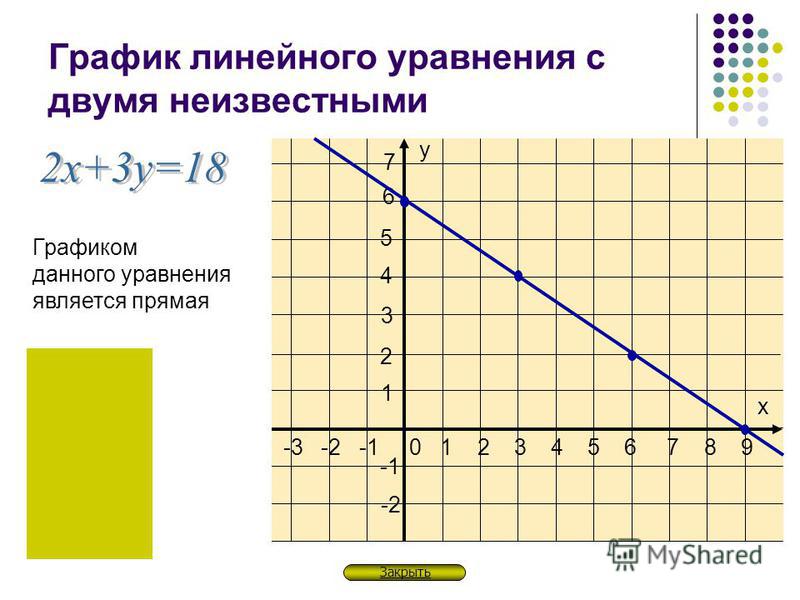
1) Что из себя представляет график линейного уравнения вида
ах + ву = с?
2) А можно ли сразу сказать, какой фигурой являются графики уравнений
2(х – у) + 3у = 4 и 2(0,5х — 1,2у) – (0,6у + х) = 6?
Значит, кроме закрепления навыков и умений построения графиков уравнений вида
ах + ву = с, над чем еще нам сегодня необходимо поработать?
Верно:
— выяснить, что из себя представляют графики уравнений
2(х – у) + 3у = 4 и 2(0,5х — 1,2у) – (0,6у + х) = 6;
— научиться строить графики уравнений, заданных в подобном виде.
2.Проверка домашнего задания.
Проверим ваши знания и умения, которые вы применяли при выполнении домашнего задания и которые вам понадобятся сегодня на уроке.
На доске 3 учащихся выполняют номера домашнего задания.
№1049
а) Построить график уравнения х + у = 5.
Построение.
х + у = 5.
Линейное уравнение.
График — прямая линия.
у = 5 — х
0
3
у
5
2
№1050
б) Построить график уравнения 3х = у + 4.
Построение.
3х = у + 4
Линейное уравнение. График – прямая линия.
у = 3х — 4
0
1
у
-4
-1
№1.Построить график уравнения с двумя переменными:
-2х + 3у = 9.
Построение.
-2х + 3у = 9
Линейное уравнение. График – прямая линия.
0
3
у
3
5
№1052
Известно, что ордината некоторой точки прямой, являющейся графиком уравнения
12х – 5у = 132, равна 0. Найдите абсциссу этой точки.
Решение.
Точка (х;0) принадлежит графику уравнения 12х -5у=132, значит
Ответ: абсцисса точки равна 11.
3.Актуализация опорных знаний и способов деятельности.
Остальные учащиеся:
а) Выполняют словарную работу в рабочей тетради, записывая под диктовку учителя следующие понятия:
Линейная функция, график линейной функции, линейное уравнение с двумя переменными, решение уравнения, график линейного уравнения, алгоритм.
б) Устно формулируют определения понятий, использованных в словарной работе и выполняют задания, представленные им в презентации:
1.Решить уравнения с одной переменной.
2.Определение линейной функции.
3.Определение графика линейной функции.
4.Расположение графиков линейных функций в зависимости от коэффициентов k и b.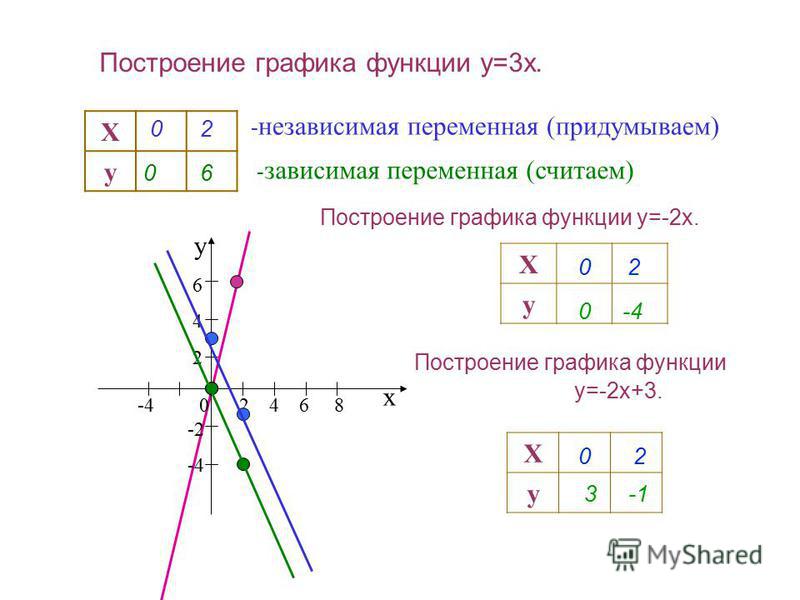
5.Подготовка к ГИА. (Задания на применение определения линейной функции и ее графика).
6.Определение линейного уравнения с двумя переменными.
7.Определение решения линейного уравнения с двумя переменными.
8.Выбрать пару значений переменных, являющуюся решением линейного уравнения с двумя переменными.
9.Определение графика линейного уравнения с двумя переменными.
10.Алгоритм (правило) построения графика линейного уравнения с двумя переменными.
11.Расположение графиков линейных уравнений с двумя переменными в зависимости от коэффициентов а, в и с.
12.Формулы сокращенного умножения.
(Приложение №.8, слайды №2 — №18).
4.Применение знаний, умений и навыков.
«Да, путь познания не гладок.
Но знаем мы уж много лет,
Загадок больше, чем разгадок
И поискам предела нет!»
А теперь давайте выясним, что из себя представляют графики уравнений, данных в №1.
№1.Построить графики уравнений с двумя переменными:
а) 3(х – у) + 4у = 4;
б) 2(0,5х — 1,2у) – (0,6у + х) = 6.
У доски работают 3 учащихся, остальные – в тетрадях.
№1
а) 3(х – у) + 4у = 4;
Раскроем скобки и приведем подобные слагаемые:
3х – 3у + 4у = 4
3х+ у = 4.
Получили линейное уравнение. Значит его графиком является прямая линия.
Выразим переменную у через х, получим у = 4 – 3х.
Начертим таблицу и найдем координаты двух точек этой прямой.
0
2
у
4
-2
Построим график.
Аналочично выясним, что из себя представляет график уравнения
2(0,5х — 1,2у) – (0,6у + х) = 6.
№1.
б) 2(0,5х — 1,2у) – (0,6у + х) = 6
х – 2,4у – 0,6у – х = 6
-3у = 6
у = 6:(-3)
у = -2
Также получили линейное уравнение.
График – прямая линия, параллельная оси х и проходящая через точку (0;-2)
.
Молодцы! Верно говорится в пословице: «Ум без догадки гроша не стоит»
5.Устная работа.
Кроме выполнения построения графиков уравнений необходимо уметь устанавливать соответствие между заданными уравнениями и графиками.
(Приложение №8, слайды №19 и № 20)
6.Повторение.
Любой новый материал невозможно изучить и понять без материала, изученного ранее. Чтобы не забывать прошлый материал, его необходимо периодически повторять. Об этом нам говорит пословица:
Повторение – мать учения!
Гимн формуле.
Формулы всюду – в космосе, в небе,
К Северу, в Африку с ними плыви.
Даже в кино есть такое названье,
Как в алгебре, помните?
«Формула любви».
В физике, химии – формулы,
Нам их не сосчитать.
Алгебра нам поможет
Формулы изучать.
Надо уметь составить!
Надо уметь доказать!
Надо ее использовать,
Ну а короче, — знать!
Л. Финкельштейн.
(Советский журналист и писатель)
Давайте повторим формулы сокращенного умножения и убедимся в очередной раз, как они помогают сократить объем вычислений при нахождении значений выражений с переменными.
(В приложении №8, слайд №21)
№1055.
Найдите значение выражения:
Решение.
6.Подведение итогов работы.
Итак, повторим еще раз:
1)Алгоритм построения графика линейного уравнения с двумя переменными.
2)Как найти ординату (абсциссу) точки прямой, являющейся графиком линейного уравнения с двумя переменными, если известна абсцисса (ордината), не выполняя построения графика.
3)А теперь ребята, я предлагаю вам сделать анализ своей работы на уроке. Для этого ответьте на вопросы:
Какую цель мы ставили для себя в начале урока?
Достигли ли вы этой цели?
Какие трудности возникали на уроке?
Оцените работу друг друга и свою.
4)Выставление оценок учащимся за работу на уроке.
7.Домашнее задание.
Любые знания и умения, для их прочности, необходимо обязательно закреплять!
Поэтому, запишите домашнее задание:
Параграф 15, пункты 40; 41. №1050(г), 1055(б), №1151(в).
Решения заданий домашней работы аналогичны решениям заданий классной работы.
8.Проверочная самостоятельная работа.
А теперь выполните самостоятельную работу, чтобы узнать, насколько прочно вы усвоили материал и над чем вам еще необходимо поработать.
Учащимся выдаются карточки с заданиями.
(Приложение №9)
Приложение №1.
Алгоритм (правило) построения графика линейной функции.
1)Выразить переменную у через х.
2) Начертить таблицу и вычислить координаты двух точек, принадлежащих графику уравнения.
3)Построить точки на координатной плоскости.
4)Через отмеченные точки провести прямую линию.
Приложение №2
Линейная функция у=kх+b при
Приложение №3.
Линейная функция
у=kх+b при
Приложение №4.
Линейное уравнение с двумя переменными.
ах + bу = с
График –прямая линия.
Приложение №5.
Линейное уравнение с двумя переменными.
При а = 0 0х + bу = с
у = с / b у = m
Приложение №6.
Линейное уравнение с двумя переменными.
При b = 0 ах +оу = с
х = с / a х = n
Приложение №7.
Линейное уравнение с двумя переменными.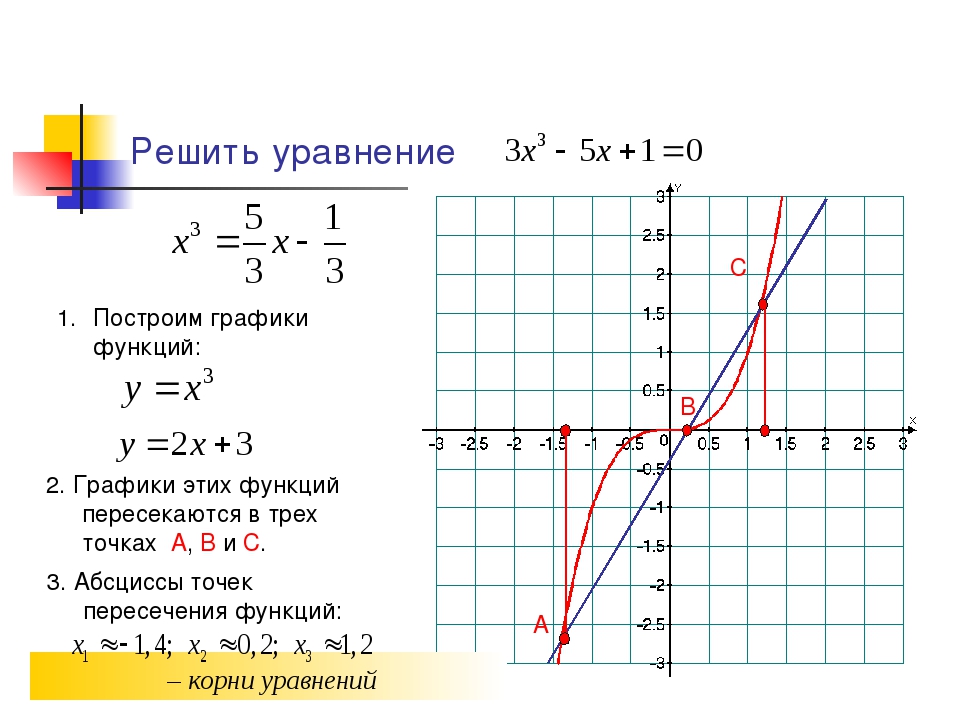
При а = 0, b = 0, с≠0
0х+ 0у = с
Нет решений.
Нет графика.
При а = 0, b = 0, с = 0
0х + 0у = 0
График – вся координатная плоскость.
Приложение №8.
Слайд №1.
——————————————————————————————————————
Слайд №2.
—————————————————————————————————————
Слайд №3.
——————————————————————————————————————-
Слайд №4.
——————————————————————————————————————
Слайд №5.
——————————————————————————————————
Слайд №6.
Слайд №7.
——————————————————————————————————
Слайд №8.
Слайд №9.
Слайд №10.
Слайд №11.
—————————————————————————————————-
Слайд №12.
Слайд №13.
————————————————————————————————————
Слайд №14.
Слайд №15.
———————————————————————————————————
Слайд №16. {2}}-4\cdot \left( -8 \right)}{4}=-\frac{4+32}{4}=-9\)
{2}}-4\cdot \left( -8 \right)}{4}=-\frac{4+32}{4}=-9\)
Точно такой же ответ? Молодец!
И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, \( \displaystyle 3\).
Ты знаешь, что парабола симметрична относительно своей вершины, например:
Алгебра: уроки, тесты, задания.
Алгебра: уроки, тесты, задания.-
Информация о разделе
-
-
Числовые выражения. Алгебраические выражения
-
Математический язык
-
Математические модели реальных ситуаций
-
Линейное уравнение с одной переменной. Алгоритм решения
-
Координатная прямая.
 Числовые промежутки
Числовые промежутки
-
-
-
Координатная плоскость. Координаты точки
-
Линейное уравнение ax + by + c = 0. График линейного уравнения
-
Линейная функция y = kx + m. График линейной функции
-
Линейная функция y = kx, её свойства
-
Взаимное расположение графиков линейных функций
-
-
-
Понятие системы линейных уравнений с двумя переменными
-
Решение систем линейных уравнений.
 Метод подстановки
Метод подстановки
-
Решение систем линейных уравнений. Метод сложения
-
Система линейных уравнений как математическая модель
-
-
-
Понятие степени с натуральным показателем
-
Часто используемые степени
-
Базовые свойства степеней с натуральным показателем
-
Умножение и деление степеней с одинаковыми натуральными показателями
-
Понятие степени с нулевым показателем
-
-
-
Понятие одночлена.
 Приведение одночлена к стандартному виду
Приведение одночлена к стандартному виду
-
Сложение и вычитание подобных одночленов
-
Произведение одночленов и возведение одночлена в степень
-
Деление одночленов
-
-
-
Понятие многочлена. Приведение многочлена к стандартному виду
-
Как складывать и вычитать многочлены
-
Как умножать многочлен на одночлен
-
Как умножать многочлен на многочлен
-
Применение формул сокращённого умножения
-
Как делить многочлен на одночлен
-
-
-
Понятие разложения многочленов на множители
-
Разложение на множители.
 Вынесение общего множителя за скобки
Вынесение общего множителя за скобки
-
Разложение на множители. Способ группировки
-
Разложение на множители. Использование формул сокращённого умножения
-
Разложение на множители. Сочетание различных приёмов
-
Применение разложения на множители для сокращения алгебраических дробей
-
Понятие тождества
-
-
-
Квадратичная функция y = x² и её график
-
Решение уравнений графическим методом
-
Запись функции в виде у = f(x)
-
-
-
Понятие алгебраической дроби
-
Применение основного свойства алгебраической дроби
-
Как складывать и вычитать алгебраические дроби с равными знаменателями
-
Как складывать и вычитать алгебраические дроби с разными знаменателями
-
Как умножать, делить и возводить в степень алгебраические дроби
-
Упрощение рациональных выражений
-
Решение рациональных уравнений
-
-
-
Квадратичная функция y = kx² и её свойства.
 Парабола
Парабола
-
Функция y = k/x и её свойства. Гипербола
-
Как построить график функции у = f(x + l)
-
Как построить график функции у = f(x) + m
-
Как построить график функции y = f(x + l) + m
-
Квадратичная функция y = ax² + bx + c
-
Решение квадратных уравнений с помощью графиков функций
-
-
-
Понятие квадратного корня
-
Функция квадратного корня y = √x, её свойства и график
-
Множество рациональных чисел
-
Базовые свойства квадратных корней
-
Преобразование иррациональных выражений
-
-
-
Какие бывают квадратные уравнения
-
Способы решения квадратных уравнений
-
Решение рационального уравнения, сводящегося к квадратному
-
Использование рациональных уравнений для решения задач
-
Упрощённая формула для решения квадратного уравнения
-
Применение теоремы Виета
-
Решение иррационального уравнения, сводящегося к квадратному
-
-
-
Множества натуральных чисел, целых чисел, рациональных чисел
-
Понятие иррационального числа
-
Множество действительных чисел и её геометрическая модель
-
Модуль действительного числа и его геометрический смысл
-
Приближённые значения по недостатку (по избытку)
-
Понятие степени с отрицательным целым показателем
-
Стандартный вид положительного числа
-
-
-
Понятие числовых промежутков
-
Свойства числовых неравенств.
 Свойства неравенств одинакового смысла
Свойства неравенств одинакового смысла
-
Как решать линейное неравенство
-
Методы решения квадратных неравенств
-
Понятие монотонности функции. Исследование функций на монотонность
-
-
Международная оценка образовательных достижений учащихся (PISA)
-
-
Повторим способы решения линейных и квадратных неравенств
-
Решение рациональных неравенств методом интервалов
-
Множества и подмножества.
 Объединение и пересечение множеств
Объединение и пересечение множеств
-
Системы рациональных неравенств
-
-
-
Понятие системы рациональных уравнений
-
Методы решения систем рациональных уравнений
-
Использование систем рациональных уравнений для решения задач
-
-
-
Определение числовой функции и способы её задания
-
Свойства основных функций
-
Чётные и нечётные функции.
 Определение чётности и нечётности
Определение чётности и нечётности
-
Степенная функция с натуральным показателем
-
Степенная функция с отрицательным целым показателем
-
Функция кубического корня
-
-
-
Понятие числовой последовательности. Способы задания последовательностей
-
Арифметическая прогрессия. Свойства арифметической прогрессии
-
Геометрическая прогрессия. Свойства геометрической прогрессии
-
-
-
Злементы комбинаторики.
 Комбинаторные задачи
Комбинаторные задачи
-
Элементы статистики. Методы обработки информации
-
Элементы теории вероятности. Нахождение вероятности
-
Относительная частота и статистическая вероятность события
-
-
-
Натуральные числа. Повторение
-
Рациональные числа. Повторение
-
Иррациональные числа. Повторение
-
-
-
Обратимая и обратная функции
-
Понятие периодической функции (профильный)
-
-
-
Числовая окружность на координатной плоскости
-
Нахождение значений синуса и косинуса, тангенса и котангенса
-
Числовой аргумент тригонометрических функций
-
Угловой аргумент тригонометрических функций
-
Свойства функции y = sin x и её график
-
Свойства функции y = cos x и её график
-
Периодичность тригонометрических функций, чётность, нечётность
-
Гармонические колебания (профильный)
-
Свойства функций y = tg x, y = ctg x и их графики
-
Функции y = arcsin a, y = arccos a, y = arctg a, y = arcctg a (профильный)
-
-
-
Арккосинус и решение уравнения cos х = a
-
Арксинус и решение уравнения sin x = a
-
Арктангенс и арккотангенс.
 Решение уравнений tg x = a, ctg x = a
Решение уравнений tg x = a, ctg x = a
-
Методы, используемые для решения тригонометрических уравнений
-
-
-
Формулы синуса суммы и разности, косинуса суммы и разности
-
Тангенс суммы и разности
-
Формулы приведения. Общее правило
-
Формулы синуса, косинуса, тангенса двойного угла
-
Формулы понижения степени, или формулы половинного угла (профильный)
-
Формулы сумм тригонометрических функций
-
Формулы произведений тригонометрических функций
-
Метод введения вспомогательного угла (профильный)
-
-
-
Числовые последовательности и их свойства
-
Понятие предела числовой последовательности
-
Как найти сумму бесконечной геометрической прогрессии
-
Предел функции в точке.
 Предел функции на бесконечности
Предел функции на бесконечности
-
Определение производной. Геометрический и физический смысл производной
-
Вычисление производных. Правила дифференцирования
-
Как получить уравнение касательной к графику функции
-
Исследование функций на монотонность и экстремумы
-
Исследование выпуклости и перегиба, построение графиков функции
-
Применение производной для отыскания наибольших и наименьших величин
-
-
-
Понятие корня n-й степени из действительного числа
-
Функция корня n-й степени
-
Свойства корня n-й степени.
 Преобразование иррациональных выражений
Преобразование иррациональных выражений
-
Способы упрощения выражений, содержащих радикалы
-
Понятие степени с рациональным показателем, свойства степеней
-
Свойства степенных функций и их графики
-
-
-
Свойства показательной функции и её график
-
Методы решения показательных уравнений
-
Методы решения показательных неравенств
-
Понятие логарифма.
 Основное логарифмическое тождество
Основное логарифмическое тождество
-
Свойства логарифмической функции и её график
-
Базовые свойства логарифмов
-
Методы решения логарифмических уравнений
-
Методы решения логарифмических неравенств
-
Переход к новому основанию логарифма
-
Системы показательных и логарифмических уравнений
-
Системы логарифмических и показательных неравенств
-
Производная показательной и логарифмической функции
-
-
-
Понятие первообразной
-
Неопределённые и определённые интегралы.
 Методы интегрирования
Методы интегрирования
-
Вычисление площадей с помощью интегралов
-
-
-
Правило суммы
-
Правило произведения
-
Перестановки. Перестановки без повторений
-
Размещения. Размещения с повторениями
-
Сочетания и их свойства
-
Треугольник Паскаля.
 Бином Ньютона
Бином Ньютона
-
-
-
Какие бывают случайные события
-
Комбинации событий. Противоположные события
-
Вероятность события
-
Сложение вероятностей
-
Независимые события. Умножение вероятностей
-
Статистическая вероятность
-
-
-
Случайные величины
-
Центральные тенденции
-
Меры разброса
-
Закон распределения вероятностей.
 Закон больших чисел
Закон больших чисел
-
-
-
Равносильность уравнений. Теоремы о равносильности уравнений
-
Общие методы решения уравнений
-
Равносильность неравенств. Системы и совокупности неравенств
-
Уравнения и неравенства с двумя переменными
-
Общие методы решения систем уравнений
-
Уравнения и неравенства с параметром
-
-
Коллекция интерактивных моделей
Построение графиков в пакете Maple
Министерство образования Ставропольского края
Государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ставропольский государственный педагогический институт»
Кафедра математики и информатики
Методические указания
к проведению практических занятий
Ставрополь 2013
Построение графиков в пакете Maple
/Сост. : А.А.Оленев, К.М. Сагдеев: СГПИ.
–Ставрополь, 2013. — __ с.
: А.А.Оленев, К.М. Сагдеев: СГПИ.
–Ставрополь, 2013. — __ с.
В работе рассмотрены приемы и методы построения различных графиков в пакете компьютерной математики Maple. Основное внимание уделено построению графиков, которые требуется строить при решении задач дисциплины «Математика». Методическая разработка будет полезна студентам всех специальностей дневного и заочного обучения СГПИ, применяющих при решении задач по математике систему компьютерной алгебры Maple.
Содержание
Введение …………………………………………………………………………………………………4
1. Графики на плоскости и в пространстве ……………………………………………….5
2. Функция plot построения графиков на плоскости ………………………………5
2.1. График явно заданной функции ………………………………………………………5
2.2. Построение графика функции, заданной процедурой ………………………6
2.3. График параметрически заданной функции …………………………………….7
2.4. График функции, заданной параметрически процедурами ………………8
2.5. График, построенный по точкам, заданным декартовыми
координатами ……………………………………………………………………………………….9
2.6. Опции функции plot …………………………………………………………………..10
1) опция настройки осей координат ………………………………………………….10
2) опция задания цвета кривой графика …………………………………………….12
3) опция выбора системы координат
. ………………………………………………..12
………………………………………………..12
4) опция, учитывающая разрывы кривой графика ……………………………..12
5) опция, заполнения цветом области между кривой и осью абсцисс. ..14
6) опция, определяющая стиль построения линии графика ………………..14
7) опция, определяющая число точек, по которым строится график ….15
8) опция, определяющая соотношение равного масштаба на осях ……..15
9) опция, определяющая толщину линии …………………………………………..15
10) опция, определяющая размеры окна построения графика ……………15
3. Функция plot3d построения графиков в пространстве ……………………..15
3.1. График функции двух переменных ……………………………………………….16
3.1. График поверхности, заданной параметрически ……………………………17
4. Пакет построения графиков plots ……………………………………………………19
4.1. График неявно заданной функции одной переменной ……………………20
4.2. Текстовые графики на плоскости ………………………………………………….21
4.3. Комбинированные графики …………………………………………………………..22
5. Графические построения при решении задач дисциплины «Математика»
……………………………………………………………………………………………………………..23
5.1. Исследование функций и построение их графиков ………………………..24
5.2. Построение графиков областей на плоскости, ограниченных
заданными кривыми
. …………………………………………………………………………..28
…………………………………………………………………………..28
5.3. Построение областей в пространстве, ограниченных заданными
поверхностями ……………………………………………………………………………………31
5.4. Построение графиков частичных сумм степенного ряда ………………..33
5.5. Построение графиков периодических функций и графиков
частичных сумм ряда Фурье ………………………………………………………………..34
6. Построение графика корреляционной таблицы …………………………………..37
Библиографический список …………………………………………………………………40
Введение
Необходимость построения графиков функций, чертежей геометрических фигур в тетради или на листах ватмана, возникает при решении задач по алгебре и геометрии в школе, при изучении различных разделов дисциплины «Математика» в вузе. Кроме того, потребность в таких построениях возникает при научных исследованиях и на производстве.
До появления компьютерной графики, построение графиков функций и чертежи фигур приходилось делать вручную, используя самые различные инструменты и приспособления, такие как линейки, циркули, кульманы и другие. При этом, нередко, для выполнения построений приходилось выполнять значительное количество предварительных расчетов и, если в этих расчетах появлялись ошибки, то всю работу приходилось переделывать заново.
Появление компьютеров и программ
компьютерной графики избавило от многих
рутинных расчетов и ручной работы,
которую надо было выполнить, чтобы
сделать графические построения. Теперь
любой человек, владеющий навыками
работы с компьютером и установленными
на нем программами компьютерной
графики, может построить самые сложные
графики и фигуры на экране компьютера
и затем, если нужно, распечатать их с
помощью принтера или плоттера.
Среди программ компьютерной графики существуют как простые графические программы, позволяющие строить простые фигуры и графики, так и мощные профессиональные программы технической графики среди которых можно отметить, например, программу AutoCad. К одной из лучших графических программ относится также программа Visio, входящая в настоящее время, в расширенный пакет семейства офисных программ Microsoft Office.
Возможности графических построений имеют также и многие программы, не являющиеся, по сути, графическими программами. Рисунки, например, можно выполнить прямо в текстовом редакторе Word, а строить различные графики можно в электронных таблицах Exel. Мощными графическими возможностями обладают также пакеты компьютерной математики Maple, Mathematica, MathCad,MatLab. При этом эти возможности сочетаются с возможностями математических вычислений и расчетов, чтобы наглядно представить эти расчеты в виде фигур и графиков.
В данной работе рассматриваются возможности графических построений, которые можно выполнить в системе компьютерной математики Maple. Из огромного арсенала возможностей графических построений, которые можно сделать в этой программе, упор сделан на построение графиков и фигур, которые требуется выполнить при решении различных математических задач, встречающихся при изучении дисциплины «Математика».
Как построить график с двумя осями Y и другие хитрости построения графиков в Excel
Некоторое время назад с удивлением обнаружил, что довольно много посетителей с поисковых систем попадают сюда с запросами типа «построить график с двумя осями y excel». А там речь идет про R 🙂Поэтому специально решил написать про то, как все же построить такой график именно в Excel, и заодно поделиться другими тонкостями, которые накопились за 10 лет работы с этой программой.
1. Как построить график с двумя осями Y в Excel?
По всей видимости, корни недоразумений кроются в том, что в разных версиях Excel это может происходить по разному. Поэтому пользователи, которые все еще переходят с Excel 2003 могут столкнуться с тем, что в новых версиях (2007 и позднее), известная методика не работает. На самом деле все просто — нужно сначала построить необходимый график с одной осью Y. А потом уже задать вторую ось, она называется «вспомогательная».
Поэтому пользователи, которые все еще переходят с Excel 2003 могут столкнуться с тем, что в новых версиях (2007 и позднее), известная методика не работает. На самом деле все просто — нужно сначала построить необходимый график с одной осью Y. А потом уже задать вторую ось, она называется «вспомогательная».К примеру, имеется такой набор данных (это объемы экспорта нефти из России):
| Год | Объем экспорта сырой нефти, млн т | Средняя экспортная цена, $/баррель |
| 2000 | 144.4 | 23.9 |
| 2001 | 164.5 | 20.8 |
| 2002 | 189.5 | 21.0 |
| 2003 | 228.0 | 23.8 |
| 2004 | 260.3 | 31.0 |
| 2005 | 252.5 | 45.2 |
| 2006 | 248.4 | 56.3 |
| 2007 | 258.6 | 64.3 |
| 2008 | 243.1 | 90.7 |
| 2009 | 247.5 | 55.6 |
| 2010 | 250.7 | 74.1 |
| 2011 | 244.5 | 101.7 |
| 2012 | 240.0 | 103.1 |
Сначала строим просто график с линиями: Щелкаем мышкой на нижний ряд. Появляется окно «Формат ряда данных». Во вкладке параметры ряда выбираем «По вспомогательной оси» и получаем итоговый результат (с некоторыми дополнительными манипуляциями, о которых речь пойдет ниже).
2. Используйте собственные шаблоны графиков в Excel
Нет ничего страшнее экселевских графиков, которые создаются «по умолчанию». Никогда их не используйте, если хотите, чтобы ваши результаты воспринимались серьезно. Честно. Вот, как к примеру, выглядит график по умолчанию с другим набором данных (это цены на нефть разных сортов).
Для рабочего использования — посмотреть на данные подойдет, но для использования в отчетах/презентациях — нет. В Excel есть отличный инструмент отказаться от стандартных настроек построения графиков — собственные шаблоны. Пользоваться ими очень просто. Создайте типовой график — выставьте необходимые шрифты, цвета линий и заполнения, оформите оси и прочие параметры. Обратите внимание, что эти параметры не должны являться уникальными для этого конкретного графика, а подходить ко всему классу графиков подобного вида. Еще обратите внимание, что можно выставить типовые размеры для графика (к примеру 8 х 6 см). Потом идете в меню Конструктор — Сохранить как шаблон. Появляется новое окно «Сохранение шаблона диаграмма».
И сохраняете свой шаблон в формате .crtx Как видно по рисунку, у меня сохранено около 10 шаблонов — на разные варианты оформления, тип графиков и используемую цветовую палитру.
Теперь, чтобы создать график на новых данных с тем же оформлением необходимо сделать лишь одно дополнительное движение: Вставка — маленькая стрелка в нижем правом углу меню диалогового меню «Диаграммы». Появляется окно «Вставка диаграммы», которое выглядит вот так:
Самая верхняя вкладка — «Шаблоны» — показывает как раз сохраненные вами шаблоны. Выбираете нужный и строите график. Обратите внимание на нижнюю кнопку «Управлением шаблонами». Если нажать на нее откроется новое окно Проводника с папкой, содержащей сохраненные шаблоны в виде отдельных файлов. Вы можете их скопировать, чтобы потом вставить в аналогичную папку на другом компьютере (к примеру, ноутбук/домашний компьютер или поделиться с коллегами с тем, чтобы вы использовали идентичные шаблоны). Тогда на всех ваших компьютерах будут предлагаться одинаковые к использованию шаблоны графиков. Вуаля!
3. Используйте нестандартные палитры цветов.
Стандартная палитра цветов, которая используется в Excel по умолчанию всем хорошо известна и порядком надоела. Создайте свою палитру (или несколько палитр — для разных типов данных) или позаимствуйте. Если в вашей компании существует корпоративная палитра цветов, вы можете внести ее коды RGB и удобно использовать ее для построения графиков. Вам не придется каждый раз менять цвета для каждого отдельного графика.
Если в вашей компании существует корпоративная палитра цветов, вы можете внести ее коды RGB и удобно использовать ее для построения графиков. Вам не придется каждый раз менять цвета для каждого отдельного графика.Заходим в раздел «Другие цвета» — вкладки «Цвет линии» (или другой аналогичной вкладки), забиваем свои коды по RGB или HSL, сохраняем как шаблон.
Вот еще один полезный бесплатный ресурс, с помощью которого можно «позаимствовать» палитры цветов. Изначально эти палитры создавались для карт, но ничто не мешает их использовать и для обычных графиков. Еще один рецепт — если вы увидели понравившуюся вам палитру цветов в Сети, вы легко можете посмотреть точные коды цветов, которые в ней используются. Для этого подойдет специальная надстройка для браузера. Я пользуюсь Eye Dropper для Chrome.
4. Обязательно убирайте лишние знаки после запятой
При создании графика Excel часто оставляет лишние знаки после запятой (к примеру, повторяющиеся нули). Эти знаки не несут никакой смысловой нагрузки и только «засоряют» пространство графика лишней информацией.Поэтому в обязательном порядке убирайте лишние знаки после запятой. Делается это очень просто. Заходите в «Формат оси» — вкладка «Число». Выбираете нужный числовой формат и правильно число десятичных знаков (в данном случае это 0). Это относится и к единицам измерениям — переводите тонны в миллионы тонн, если у вас шестизначные цифры. В той же вкладке «Формат оси» — «Параметры оси», если удобная опция «Цена деления». Можно изменить размерность единицы измерения, не меняя исходные данные на рабочем листе.
5. Корректируйте максимальное/минимальное значение по оси при необходимости
Excel пытается по умолчанию автоматически определить оптимальное максимальное и минимальное значение по оси. Часто у него получается вполне нормально, но иногда он ошибается. Если такое произошло, скорректируйте эти значения вручную.
К примеру, для графика с ценами на нефть имеет смысл увеличить минимальное значение. Excel всегда начинает его от 0 в подобных случаях. В данном случае из-за этого появляется пустое пространство и изменения цен становятся мало различимыми.
Excel всегда начинает его от 0 в подобных случаях. В данном случае из-за этого появляется пустое пространство и изменения цен становятся мало различимыми.
Изменения стали более выраженными. Хотя верхние три линии все равно сильно сливаются, возможно, надо уменьшить толщину линий или убрать одну из них.
6. Не засоряйте ось X на временных рядах
В экономике и финансах один из наиболее часто встречающихся типов графиков — временные ряды. По оси Х — время, по оси Y — какое-то значение. Можно по разному представлять ось времени, выбирайте то представление, которое наилучшим образом отражает ваши цели.К примеру, можно нарисовать вот вот так:
или так (для подобной двойной оси, нужно выбрать две строки/столбца в качестве подписи по горизонтальной оси).
7. Вставляйте графики Excel в векторном виде в Word/Powerpoint
Зачастую графики Excel создаются для того, чтобы использовать их в других программах — документах Word, либо презентациях PowerPoint. В большинстве случаев наиболее оптимальный вариант вставки — векторный формат emf или wmf.
По умолчанию графики вставляются как объекты Office (первая строка в окне наверху). Это приводит к тому, что их можно бы потом редактировать в Word или Powerpoint. Но в результате, увеличиваются размеры файлов (при больших файлах Excel), а также то, что весь ваш рабочий лист становится виден читателям Word/Powerpoint (возможно, это не тот результат, который вы желаете получить). Если использовать вставку в растровом формате (gif/png/jpeg), сильно ухудшается качество графики. Это особенно заметно при печати на бумаге — графики становятся «смазанными». Поэтому удобным является формат EMF/WMF. Он векторный, поэтому качество графики не уменьшается при изменении масштабов, а файлы занимают не очень много места. Единственная проблема в том, что его поддерживают в основном только программное обеспечение Microsoft.
 К сожалению, даже новейший MS Office 2013 не поддерживает альтернативные векторные форматы — тот же SVG.
К сожалению, даже новейший MS Office 2013 не поддерживает альтернативные векторные форматы — тот же SVG.8. Подгоняйте правильные размеры графиков в Excel
Удобство иногда идет не на пользу. После вставки в Word размеры графиков можно поменять с помощью мыши. Вроде бы удобно, но в результате могут получиться вот такие вот графики:Смотрятся они некрасиво. Поэтому лучше выставить «правильные» размеры графиков непосредственно в Excel. К примеру, в Word вы можете точно оценить необходимую ширину графика (с учетом всех отступов) и задать эту ширину сразу в Excel. При вставке в Word график будет точно подогнан по ширине.
Вот и все, что я вспомнил. В Excel можно делать очень многое, в том числе и с точки зрения графических возможностей. Ограничения стандартных представлений можно расширить с помощью собственных макросов VBA или отдельных хаков. К примеру, вот хак как строить waterfall charts в Excel.
Но имейте в виду следующее. Если вы уже достигли хорошего уровня в Excel — не имеет смысл на нем зацикливаться. Есть и другие пути. Графические возможности того же R на порядок выше того, что может дать Excel, и, как правило, требуют меньше мороки.
Синусоида — онлайн построение графика
Следующий калькулятор служит для построения параметрической синусоиды в диапазоне от 0 до 2П.
при чем коэффициент k может задать сам пользователь.
Есть 3-и возможности введения коэффициентов: в радианах, градусах, пи радианах. По дефолту k = 1, а = 0, при этом функция графика выглядит так:
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
Линейная интерполяция Онлайн
можно использовать:
дроби
дробные числа
квадратный корень
тригонометрия
возведение в степень
арифметические операции
Сервис интерполяции и экстраполяции онлайн (линейная интерполяция/экстраполяция) поможет вам вычислить значение линейной функции, имея в распоряжении f(x) в двух различных точках, а также рассчитает уравнение прямой. Данный сервис автоматически определит нужный способ расчета — вам лишь надо ввести значения в двух произвольных точках, и указать необходимую точку, в которой нужно рассчитать значение.
Если установить «галку» внутри кнопки «Рассчитать», калькулятор будет рассчитывать значение автоматически при любом изменении входных данных. Пример расчета интерполяции
Данный сервис автоматически определит нужный способ расчета — вам лишь надо ввести значения в двух произвольных точках, и указать необходимую точку, в которой нужно рассчитать значение.
Если установить «галку» внутри кнопки «Рассчитать», калькулятор будет рассчитывать значение автоматически при любом изменении входных данных. Пример расчета интерполяции
Интерполяция — (от латинского interpolatio изменение, переделка), в математике и статике это способ вычислить промежуточное значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x), известны результаты значения f(x) в точке x0 и точке x2, интерполяця помогает найти значение f(x1) при условии что x1 принадлежит интервалу от x0 до x2. Если x1 лежит вне интервала (x0, x2), интерполяция не поможет, для этого нужно использовать «экстраполяцию». Этот метод часто называют «линейная интерполяция«, он дает 100% верный результат для уравнения прямой. Для вычесления резултата функций с двумя переменными существует «Билинейная интерполяция (Двойная интерполяция)». Также для рассчета интерполяции можно воспользоваться сервисом Интерполяция — полином Ньютона и Интерполяция — полином Лагранжа
Экстраполяция — в математике и статике это способ вычислить значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x),
известны результаты значения f(x) в точке x1 и точке x2, экстраполяция помогает найти
значение f(x0) либо f(x3) при условии что x0 либо x3 меньше либо
больше интервала x1 до x2. Если xn лежит в
интервале (x1, x2), экстраполяция не поможет, для того вам нужно
использовать «интерполяцию» — для функций с одной переменной, и «двойная интерполяция» — для функций с двумя переменными.
Этот метод часто называют «линейная экстраполяция«, он дает 100% верный результат для уравнения прямой.
Как для интерполяции так и для экстраполяции в основе их рассчета лежит пропорция (y1 — y0)/(y2 — y0) = (x1 — x0)/(x2 — x0), прирощение значения в первой точке к прирощению значения во второй точке относится также как прирощение переменной в первой точке к прирощению переменной во второй точке (все относительно нулевой точки отсчета), из этой пропорции легко получить формулу рассчета любого значения
Графические неравенства с программой «Пошаговое решение математических задач»
В предыдущих главах мы решали уравнения с одной неизвестной или переменной. Теперь мы изучим методы решения систем уравнений, состоящих из двух уравнений и двух переменных.
ТОЧКИ НА САМОЛЕТЕ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Представьте декартову систему координат и определите начало координат и оси.
- Для упорядоченной пары найдите эту точку в декартовой системе координат.
- Для данной точки в декартовой системе координат укажите связанную с ней упорядоченную пару.
Мы уже использовали числовую прямую, на которой мы представили числа в виде точек на прямой.
Обратите внимание, что это понятие содержит элементы из двух областей математики, строки из геометрии и чисел из алгебры. Рене Декарт (1596-1650) разработал метод соотношения точек на плоскости с алгебраическими числами. Эта схема называется декартовой системой координат (от Декарта) и иногда упоминается как прямоугольная система координат.
Эта система состоит из двух числовых линий, перпендикулярных в своих нулевых точках.
| Перпендикуляр означает, что две прямые расположены под прямым углом друг к другу. |
Внимательно изучите диаграмму, отмечая каждый из следующих фактов.
Числовые линии называются осями . Горизонтальная линия — это ось x , а вертикальная — ось y . Нулевая точка, в которой они перпендикулярны, называется исходной точкой .
| Оси множественного числа. Ось особенная. |
Положительный — справа и вверх ; отрицательный — к слева и вниз .
| Стрелки указывают, что числовые линии продолжаются бесконечно. Таким образом, плоскость бесконечно простирается во всех направлениях. |
Самолет разделен на четыре части, называемые квадрантами . Они пронумерованы в направлении против часовой стрелки, начиная с верхнего правого угла.
Точки на плоскости обозначаются упорядоченными парами чисел, записанными в скобках с запятой между ними, например (5,7). Это называется упорядоченной парой, потому что важен порядок, в котором написаны числа. Заказанная пара (5,7) — это , а не , как заказанная пара (7,5). Точки расположены на плоскости следующим образом.
Сначала начните с начала координат и посчитайте слева или справа количество пробелов, обозначенных первым числом в упорядоченной паре.Во-вторых, от точки на оси x, заданной первым числом, отсчитайте вверх или вниз количество пробелов, обозначенных вторым числом упорядоченной пары. Упорядоченные пары всегда сначала пишутся с x, а затем y, (x, y). Числа, представленные x и y, называются координатами и точки (x, y).
| Это важно. Первое число упорядоченной пары всегда относится к горизонтальному направлению, а второе число всегда относится к вертикальному направлению. |
Пример 1 В следующей декартовой системе координат точки A (3,4), B (0,5), C (-2,7), D (-4,1), E (-3 , -4), F (4, -2), G (0, -5) и H (-6,0) обозначены.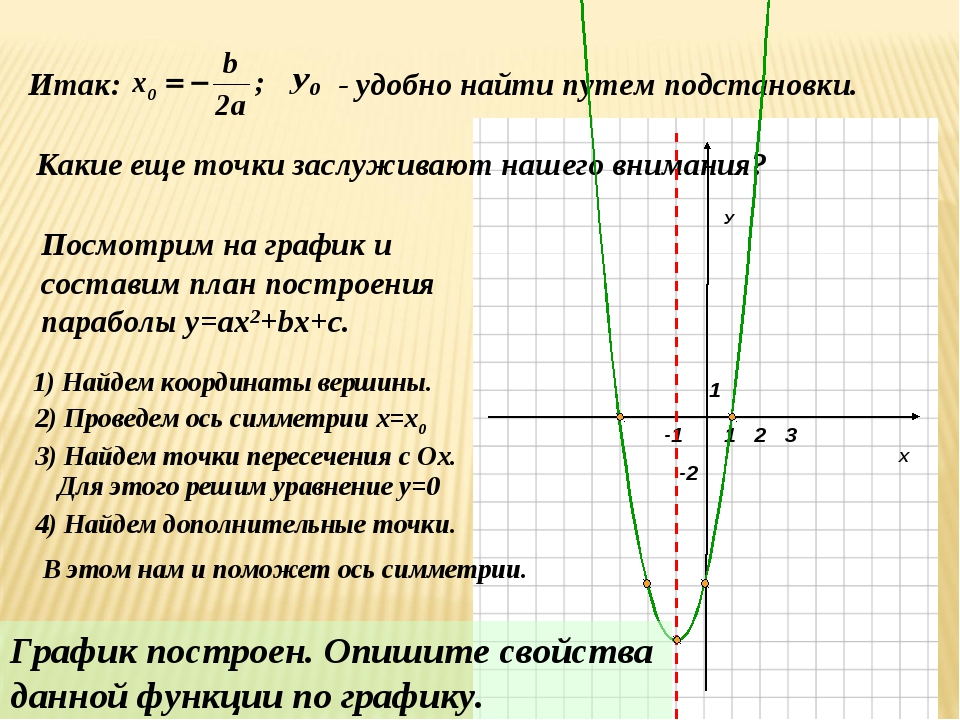 Проверьте каждый, чтобы определить, как они расположены.
Проверьте каждый, чтобы определить, как они расположены.
| Каковы координаты начала координат? |
ГРАФИЧЕСКИЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Найдите несколько упорядоченных пар, которые делают данное линейное уравнение истинным.
- Найдите эти точки в декартовой системе координат.
- Проведите прямую линию через те точки, которые представляют график этого уравнения.
График — это графическое изображение пронумерованных фактов. Есть много типов диаграмм, таких как гистограммы, круговые диаграммы, линейные диаграммы и так далее. Примеры таких графиков обычно можно найти в финансовом разделе газеты. Графики используются, потому что изображение обычно упрощает понимание числовых фактов.
В этом разделе мы обсудим метод построения графика уравнения с двумя переменными. Другими словами, мы нарисуем картину уравнения с двумя переменными.
Рассмотрим уравнение x + y — 7 и заметим, что мы легко можем найти множество решений. Например, если x = 5, то y — 2, поскольку 5 + 2 = 7. Кроме того, если x = 3, то y = 4, поскольку 3 + 4 = 7. Если мы представим эти ответы в виде упорядоченных пар (x, y) , то у нас есть (5,2) и (3,4) как две точки на плоскости, которые представляют ответы на уравнение x + y = 7.
Все возможные ответы на это уравнение, расположенные в виде точек на плоскости, дадут нам график (или картинку) уравнения.
Конечно, мы никогда не сможем найти все числа x и y такие, что x + y = 7, поэтому мы должны довольствоваться наброском графика. Эскиз можно охарактеризовать как «кривую наилучшего соответствия». Другими словами, необходимо найти достаточно точек, чтобы получить достаточно точную картину уравнения.
Помните, существует бесконечно много упорядоченных пар, которые удовлетворяли бы уравнению. |
Пример 1 Нарисуйте график 2x + y = 3.
Решение Мы хотим найти несколько пар чисел, которые сделают это уравнение истинным. Мы добьемся этого, выбрав число для x, а затем найдя соответствующее значение для y. Таблица значений используется для записи данных.
В верхней строке (x) мы разместим числа, которые мы выбрали для x. Затем в нижней строке (y) мы поместим соответствующее значение y, полученное из уравнения.
| Конечно, мы могли бы также начать с выбора значений для y, а затем найти соответствующие значения для x. |
В этом примере мы позволим x принимать значения -3, -2, -1,0, 1,2,3.
| Эти значения произвольны. Мы могли выбирать любые значения. |
| Обратите внимание, что после того, как мы выбрали значение для x, значение для y определяется с помощью уравнения. |
| Эти значения x дают целые числа для значений y.Таким образом, это хороший выбор. Предположим, мы выбрали |
Эти факты дают нам следующую таблицу значений:
Теперь мы находим упорядоченные пары (-3,9), (-2,7), (-1,5), (0,3), (1,1), (2, -1), (3, -3) на координатной плоскости и соедините их линией.
Теперь у нас есть график 2x + y = 3.
| Линия указывает, что все точки на линии удовлетворяют уравнению, а также точки из таблицы.Стрелки указывают, что линия продолжается бесконечно. |
Графики всех уравнений первой степени с двумя переменными будут прямыми линиями. Этот факт будет использован здесь, хотя в математике будет гораздо позже, прежде чем вы сможете доказать это утверждение. Такие уравнения первой степени называются линейными уравнениями .
Такие уравнения первой степени называются линейными уравнениями .
| Таким образом, любое уравнение вида ax + by — c, где a, b и c — действительные числа, является линейным уравнением. |
Уравнения с двумя неизвестными более высокой степени дают графики, которые представляют собой кривые разных типов.Вы изучите их на будущих курсах алгебры.
Поскольку график уравнения первой степени с двумя переменными представляет собой прямую линию, необходимо иметь только две точки. Однако ваша работа будет более точной, если вы найдете хотя бы три точки. Ошибки можно найти и исправить, если найденные точки не лежат на одной линии. Таким образом, мы называем третью точку «контрольной точкой».
| Это важно. Не пытайтесь сократить свою работу, найдя только два момента.Вы будете удивлены, как часто вы обнаружите ошибку, обнаружив все три точки. |
Пример 2 Нарисуйте график 3x — 2y — 7.
Решение Сначала составьте таблицу значений и выберите три числа, которые будут заменять x. Попробуем 0, 1,2.
| Опять же, вы также могли начать с произвольными значениями y. |
Ответ не так легко найти на графике, как целое число.Похоже, что x = 0 был не очень удачным выбором. Иногда можно заглянуть вперед и сделать лучший выбор для x.
| Поскольку и x, и y являются целыми числами, x = 1 был хорошим выбором. |
Точку (1, -2) будет легче найти. Если x = 2, у нас будет другая дробь.
Точку (3,1) легко найти.
| x = 3 был еще одним хорошим выбором. |
Скорректируем таблицу значений и будем использовать точки, дававшие целые числа. Это не всегда возможно, но попытка получить целые значения даст более точный набросок. Теперь у нас есть таблица для 3x — 2y = 7.
Это не всегда возможно, но попытка получить целые значения даст более точный набросок. Теперь у нас есть таблица для 3x — 2y = 7.
| Мы можем это сделать, поскольку выбор x был произвольным. |
Расположение точек (1, -2), (3,1), (- 1, -5) дает график 3x — 2y = 7.
| Сколько упорядоченных пар удовлетворяют этому уравнению? |
НАКЛОН ЛИНИИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Свяжите уклон линии с ее крутизной.
- Запишите уравнение прямой в форме пересечения наклона.
- Постройте прямую линию, используя ее наклон и точку пересечения по оси Y.
Теперь мы хотим обсудить важную концепцию, называемую наклоном линии. Интуитивно мы можем думать об уклоне как о крутизне линии по отношению к горизонтали.
Ниже приведены графики из нескольких линий. Внимательно изучите их и мысленно ответьте на следующие вопросы.
Какая линия круче?
Как выглядит связь между коэффициентом при x и крутизной Какой график будет круче: линии, когда уравнение имеет вид y = mx?
| Какой график будет круче: y = 3x или y = 7x? |
Теперь изучите следующие графики.
Какая линия круче?
Как отрицательное значение m влияет на график?
| Какой график будет круче: y = 3x или y = 7x? |
Для графика y = mx необходимо было сделать следующие наблюдения.
- Если m> 0, то
- по мере увеличения значения m крутизна линии увеличивается и
- линия поднимается вправо и опускается влево.
- Если м
- по мере увеличения значения m крутизна линии уменьшается и
- линия поднимается влево и опускается вправо
Помните, m> 0 означает, что «m больше нуля. « « |
Другими словами, в уравнении вида y — mx, m управляет крутизной линии. В математике мы используем слово наклон для обозначения крутизны и формируем следующее определение:
В уравнении вида y = mx, m — это наклон графика уравнения.
Пример 1 Нарисуйте график y = 6x и укажите наклон линии.
Решение Сначала мы составим таблицу, показывающую три набора упорядоченных пар, которые удовлетворяют уравнению.
| Помните, нам нужны только две точки для определения линии, но мы используем третью точку в качестве проверки. |
Затем мы делаем набросок графика.
Значение m равно 6, следовательно, наклон равен 6. Мы можем просто написать m — 6.
Пример 2 Нарисуйте график и укажите наклон
.Решение Выбирая значения x, которые делятся на 3, получаем таблицу
| Зачем использовать значения, которые делятся на 3? |
Тогда график
Склон
Теперь мы хотим сравнить графики двух уравнений, чтобы установить другую концепцию.
Пример 3 Нарисуйте графики y 3x и y — 3x + 2 на одном и том же наборе координатных осей.
| Сравните коэффициенты при x в этих двух уравнениях. |
Решение
В примере 3 посмотрите на таблицы значений и обратите внимание, что для данного значения x, значение y в уравнении y = 3x + 2 на два больше, чем соответствующее значение y в уравнении y = 3x.
Теперь посмотрите на графики двух уравнений и обратите внимание, что график y = 3x + 2, кажется, имеет тот же наклон, что и y = 3x.Также обратите внимание, что если весь график y = 3x перемещается вверх на две единицы, он будет идентичен графику y = 3x + 2. График y = 3x пересекает ось y в точке (0,0). , а график y = 3x + 2 пересекает ось y в точке (0,2).
График y = 3x пересекает ось y в точке (0,0). , а график y = 3x + 2 пересекает ось y в точке (0,2).
| Снова сравните коэффициенты при x в двух уравнениях. |
Сравните эти таблицы и графики, как в примере 3.
| Обратите внимание: когда две линии имеют одинаковый наклон, они параллельны. |
Наклон от одной точки на линии к другой определяется отношением изменения y к изменению x. То есть
| Если вы хотите произвести впечатление на своих друзей, вы можете написать , где греческая буква (дельта) означает «изменение». |
Обратите внимание, что изменение x равно 3, а изменение y равно 2.
Изменение x равно -4, изменение y равно 1.
| Можно также сказать, что изменение x равно 4, а изменение y равно -1.Это приведет к той же строке. |
Пример 7 На графике y = 3x — 2 наклон равен 3.
Изменение x равно 1, а изменение y равно 3.
y = mx + b называется формой с пересечением наклона уравнения прямой линии. Если уравнение имеет такую форму, m — это наклон линии, а (0, b) — точка, в которой график пересекает (пересекает) ось y.
| Точка (0, b) называется точкой пересечения по оси y. |
Если уравнение прямой имеет форму пересечения наклона, можно нарисовать его график, не составляя таблицу значений. Используйте точку пересечения оси Y и наклон, чтобы нарисовать график, как показано в примере 8.
Обратите внимание, что это уравнение имеет вид y = mx + b. |
Сначала найдите точку (0, -2). Это одна из точек на линии. Наклон показывает, что изменение x равно 4, поэтому из точки (0, -2) мы перемещаем четыре единицы в положительном направлении параллельно оси x.Поскольку изменение y равно 3, мы перемещаем три единицы в положительном направлении параллельно оси y. Получившаяся точка тоже находится на линии. Поскольку две точки определяют прямую линию, мы рисуем график.
| Всегда начинайте с точки пересечения оси Y. Распространенная ошибка, которую допускают многие студенты, — это путать точку пересечения оси y с точкой пересечения оси x (точка, в которой линия пересекает ось x). |
Пример 9 Задайте наклон и точку пересечения по оси Y и нарисуйте график y = 3x + 4.
Решение m = -3, точка пересечения по оси y = (0,4).
Чтобы выразить наклон в виде отношения, мы можем написать -3 как или. Если мы запишем наклон как, то из точки (0,4) мы перемещаем одну единицу в положительном направлении параллельно оси x, а затем перемещаем три единицы в отрицательном направлении параллельно оси y. Затем мы проводим линию через эту точку и (0,4).
Предположим, уравнение не имеет формы y = mx + b. Сможем ли мы найти наклон и точку пересечения по оси Y? Ответ на этот вопрос — да.Однако для этого мы должны изменить форму данного уравнения, применив методы, использованные в разделе 4-2.
| Раздел 4-2 посвящен решению буквальных уравнений. Вы можете просмотреть этот раздел. |
Пример 10 Найдите наклон и точку пересечения оси Y для 3x + 4y = 12.
Решение Во-первых, мы понимаем, что уравнение не находится в форме пересечения наклона, необходимой для ответа на заданные вопросы. Чтобы получить эту форму, решите данное уравнение относительно y.
| Нарисуйте здесь диаграмму. |
Пример 11 Найдите наклон и точку пересечения оси y для 2x — y = 7.
Решение Поместив уравнение в форму пересечения наклона, получим
| Нарисуйте график линии на сетке ниже. |
ГРАФИК ЛИНЕЙНЫХ НЕРАВЕНСТВ
ЗАДАЧИ
По завершении этого раздела вы сможете построить график линейных неравенств.
В главе 4 мы построили линейные графики неравенств, например
Это были неравенства с участием только одной переменной. Мы обнаружили, что во всех таких случаях график представлял собой часть числовой прямой. Поскольку уравнение с двумя переменными дает график на плоскости, кажется разумным предположить, что неравенство с двумя переменными будет отображаться как некоторая часть или область плоскости. На самом деле это так. Решение неравенства x + y
Пример 1 Каждая из следующих пар чисел в наборе решений x + y
Решение
| Набор решений состоит из всех упорядоченных пар, которые делают утверждение верным. |
| Подводя итог, следующие упорядоченные пары дают верное утверждение. (2,1), (3, -4), (0,0), (- 1,4) |
| Следующие упорядоченные пары дают ложное утверждение. (5,6), (3,2), (- 2,8) |
Ниже приведен график прямой x + y = 5. Точки из примера 1 указаны на графике с ответами на вопрос «Является ли x + y
Обратите внимание, что все точки, удовлетворяющие уравнению, находятся слева и ниже линии, а все точки, которые не соответствуют, находятся сверху и справа.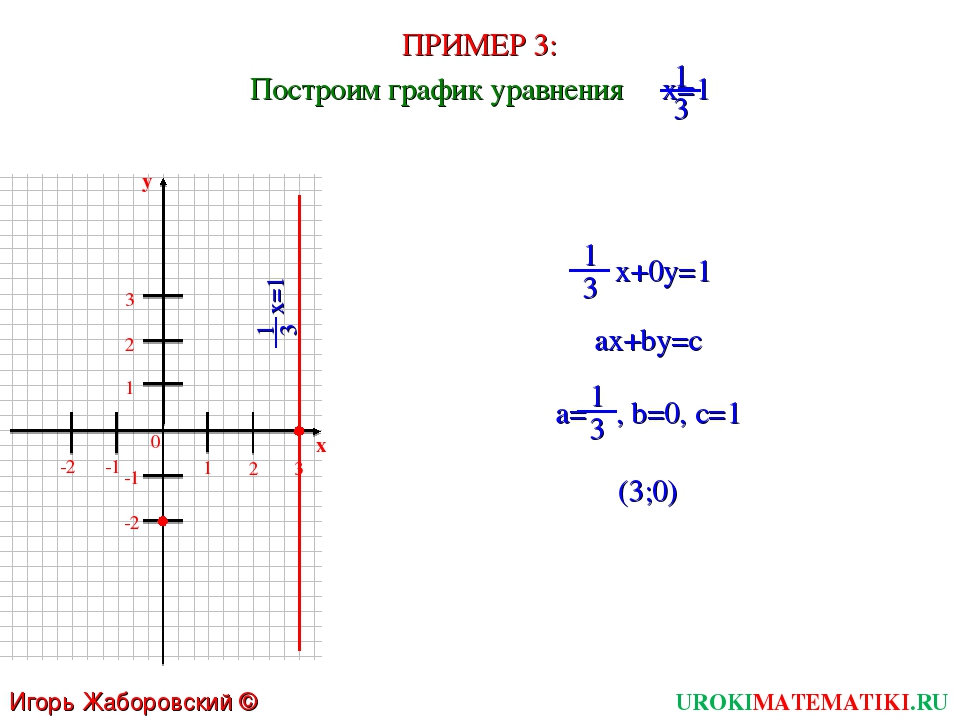 |
Обратите внимание, что все ответы «да» лежат на одной стороне линии x + y = 5, а все ответы «нет» лежат на другой стороне линии или на самой строке.
График прямой x + y = 5 делит плоскость на три части: саму линию и две стороны линий (называемые полуплоскостями).
х + у х + у
Если одна точка полуплоскости находится в наборе решений линейного неравенства, то все точки в этой полуплоскости входят в набор решений.Это дает нам удобный метод построения графиков линейных неравенств.
Построение графика линейного неравенства
1. Замените символ неравенства знаком равенства и нанесите на график полученную линию.
2. Отметьте одну точку, которая, очевидно, находится в определенной полуплоскости этой прямой, чтобы увидеть, входит ли она в набор решений неравенства.
3. Если выбранная точка находится в наборе решений, то вся эта полуплоскость является набором решений. Если выбранная точка не входит в набор решений, тогда другая полуплоскость является набором решений.
| Почему нужно проверять только одну точку? |
Пример 2 Нарисуйте график 2x 4- 3y> 7.
Решение Шаг 1. Сначала нарисуйте график линии 2x + 3y = 7, используя таблицу значений или форму пересечения наклона.
Шаг 2: Затем выберите точку, которая не находится на прямой 2x + 3y = 7. [Если линия не проходит через начало координат, то точка (0,0) всегда является хорошим выбором.] Теперь обратимся к неравенство 2x + 3y>> 7, чтобы увидеть, находится ли выбранная точка в наборе решений.
Шаг 3: Точка (0,0) не входит в набор решений, поэтому полуплоскость, содержащая (0,0), не является набором решений. Следовательно, другая полуплоскость, определяемая линией 2x + 3y = 7, является множеством решений.
Поскольку сама линия не является частью решения, она показана пунктирной линией, а полуплоскость заштрихована, чтобы показать набор решений.
| Набор решений — это полуплоскость сверху и справа от линии. |
Пример 3 Изобразите график решения линейного неравенства 2x — y ≥ 4.
Решение Шаг 1. Первый график 2x — y = 4. Поскольку линейный график для 2x — y = 4 не проходит через начало координат (0,0), проверьте эту точку в линейном неравенстве.
Шаг 2:
Шаг 3: Поскольку точка (0,0) не входит в набор решений, полуплоскость, содержащая (0,0), отсутствует в наборе. Следовательно, решение — другая полуплоскость. Обратите внимание, однако, что строка 2x — y = 4 включена в набор решений. Поэтому нарисуйте сплошную линию, чтобы показать, что это часть графика.
| Набор решений — это линия и полуплоскость ниже и справа от линии. |
Пример 4 График x
Решение Первый график x = y. Затем проверьте точку не на линии. Обратите внимание, что график линии содержит точку (0,0), поэтому мы не можем использовать ее в качестве контрольной точки. Чтобы определить, какая полуплоскость является набором решений, используйте любую точку, которая явно не находится на прямой x = y. Точка (- 2,3) является такой точкой.
Используя эту информацию, построить график x
| Когда график линии проходит через начало координат, любая другая точка на оси x или y также будет хорошим выбором. |
ГРАФИЧЕСКОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Нарисуйте графики двух линейных уравнений в одной и той же системе координат.
- Найдите общее решение двух графиков.
Пример 1 Пара уравнений называется системой линейных уравнений.
Мы заметили, что каждое из этих уравнений имеет бесконечно много решений, и каждое из них будет образовывать прямую линию, когда мы построим его в декартовой системе координат.
Теперь мы хотим найти решения для системы. Другими словами, нам нужны все точки (x, y), которые будут на графике обоих уравнений.
Решение Мы рассуждаем следующим образом: если все решения 2x — y = 2 лежат на одной прямой, а все решения x + 2y = 11 лежат на другой прямой, то решение обоих уравнений будет их точками пересечение (если две прямые пересекаются).
| В этой таблице мы позволяем x принимать значения 0, 1 и 2. Затем мы находим значения для y, используя уравнение. Сделайте это перед тем, как продолжить. В этой таблице мы позволяем y принимать значения 2, 3 и 6. Затем мы находим x, используя уравнение. Также проверьте эти значения. |
| Две прямые пересекаются в точке (3,4). |
Обратите внимание, что точка пересечения выглядит как (3,4). Теперь мы должны проверить точку (3,4) в обоих уравнениях, чтобы убедиться, что это решение системы.
| В качестве проверки мы подставляем упорядоченную пару (3,4) в каждое уравнение, чтобы увидеть, получим ли мы истинное утверждение. Существуют ли другие точки, которые удовлетворяли бы обоим уравнениям? Почему? |
Следовательно, (3,4) является решением системы.
Не все пары уравнений дают единственное решение, как в этом примере. На самом деле существует три возможности, и вы должны знать о них.
Поскольку мы имеем дело с уравнениями, которые представляют собой прямые линии, мы можем исследовать эти возможности, наблюдая за графиками.
1. Независимые уравнения Две прямые пересекаются в одной точке. В этом случае есть единственное решение.
| Приведенный выше пример представляет собой систему независимых уравнений. |
2. Несогласованные уравнения Две линии параллельны. В этом случае решения нет.
| Независимо от того, как далеко протянуты эти линии, они никогда не пересекутся. |
3. Зависимые уравнения Два уравнения дают одну и ту же линию. В этом случае любое решение одного уравнения является решением другого.
| В этом случае общих решений будет бесконечно много. |
На более поздних курсах алгебры будут изучены методы распознавания несовместных и зависимых уравнений. Однако на этом уровне мы будем иметь дело только с независимыми уравнениями. Тогда вы можете ожидать, что для всех проблем, приведенных в этой главе, будут найдены уникальные решения.
| Это означает, что графики всех систем в этой главе будут пересекаться в одной точке. |
Чтобы решить систему двух линейных уравнений с помощью построения графиков
1. Составьте таблицу значений и нарисуйте график каждого уравнения в той же системе координат.
2. Найдите значения (x, y), которые называют точку пересечения линий.
3. Отметьте эту точку (x, y) в обоих уравнениях.
| Опять же, в этой таблице wc произвольно выбрал значения x равными — 2, 0 и 5. Здесь мы выбрали для x значения 2, 4 и 6. Вы можете выбрать любые значения, которые захотите. Мы говорим «кажущийся», потому что мы еще не проверили упорядоченную пару в обоих уравнениях. Как только он проверит, это определенно решение. |
Поскольку (3,2) проверяет оба уравнения, это решение системы.
ГРАФИЧЕСКОЕ РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ НЕРАВЕНСТВ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Постройте два или более линейных неравенства на одном и том же наборе осей координат.
- Определите область плоскости, которая является решением системы.
Более поздние занятия по математике будут включать тему линейного программирования. Несмотря на то, что сама тема выходит за рамки этого текста, одна техника, используемая в линейном программировании, вполне доступна вам — построение графиков систем линейных неравенств — и мы обсудим это здесь.
В предыдущем разделе вы обнаружили, что решение системы линейных уравнений — это пересечение решений каждого из уравнений.Таким же образом решение системы линейных неравенств представляет собой пересечение полуплоскостей (и, возможно, прямых), которые являются решениями каждого отдельного линейного неравенства.
Другими словами, x + y> 5 имеет множество решений и 2x — y
имеет в качестве своего решения область плоскости, которая находится в наборе решений обоих неравенств.
Для построения графика решения этой системы мы наносим на график каждое линейное неравенство на одном и том же наборе координатных осей и указываем пересечение двух наборов решений.
| Обратите внимание, что решением системы линейных неравенств будет набор точек. |
| Опять же, используйте либо таблицу значений, либо форму уравнения с пересечением наклона для построения графика линий. |
Проверка точки (0,0) в неравенстве x + y> 5 показывает, что точка (0,0) не входит в набор ее решений. Мы указываем набор решений x + y> 5 экраном справа от пунктирной линии.
| Эта область находится справа и выше линии x + y = 5. |
Проверка точки (0,0) в неравенстве 2x — y
| Эта область находится слева и выше линии 2x — y = 4. |
Пересечение двух наборов решений — это та область плоскости, в которой пересекаются два экрана. Этот регион показан на графике.
| Еще раз обратите внимание, что решение не включает строки.Если, например, нас попросили построить график решения системы , который указывает, что решение включает точки на линии x + y = 5. |
Результаты показывают, что все точки в заштрихованной части графика будут в наборах решений x + y> 5 и 2x — y.
РЕШЕНИЕ СИСТЕМЫ ПУТЕМ ЗАМЕНЫ
ЗАДАЧИ
По завершении этого раздела вы должны уметь решать систему двух линейных уравнений методом подстановки.
В разделе 6-5 мы решили систему двух уравнений с двумя неизвестными с помощью построения графиков. Графический метод очень полезен, но он был бы непрактичным, если бы решения были дробными. Фактическую точку пересечения может быть очень сложно определить.
Существуют алгебраические методы решения систем. В этом разделе мы обсудим метод подстановки.
Пример 1 Решить методом подстановки:
Решение
Шаг 1 Мы должны решить одну неизвестную в одном уравнении.Мы можем выбрать x или y либо в первом, либо во втором уравнении. Наш выбор может быть основан на получении простейшего выражения. В этом случае мы решим относительно x во втором уравнении, получив x = 4 + 2y, потому что любой другой выбор привел бы к дроби.
| Посмотрите на оба уравнения и посмотрите, есть ли в одном из них переменная с коэффициентом, равным единице. |
Шаг 2 Подставьте значение x в другое уравнение.В этом случае уравнение
2х + 3у = 1.
Подставляя (4 + 2y) вместо x, мы получаем 2 (4 + 2y) + 3y = 1, уравнение только с одной неизвестной.
| Причина этого в том, что если x = 4 + 2y в одном из уравнений, то x должен быть равен 4 + 2y в другом уравнении. |
Шаг 3 Решите неизвестное.
| Помните, сначала удалите скобки. |
Шаг 4 Подставьте y = — 1 в любое уравнение, чтобы найти соответствующее значение для x.Поскольку мы уже решили второе уравнение относительно x через y, мы можем его использовать.
| Мы можем подставить y = — 1 в любое уравнение, поскольку y имеет одинаковое значение в обоих. |
Таким образом, у нас есть решение (2, -1).
| Помните, что x записывается первым в упорядоченной паре. |
Шаг 5 Проверьте решение в обоих уравнениях. Помните, что решение системы должно быть верным для каждого уравнения в системе.С
решение (2, -1) действительно проверяет.
| Это проверяет: 2x + 3y = 1 и x — 2y = 4. |
| Проверьте эту упорядоченную пару в обоих уравнениях. Ни в одном из этих уравнений не было переменной с коэффициентом, равным единице. В этом случае решение заменой — не лучший метод, но мы сделаем это так, чтобы показать, что это возможно. В следующем разделе будет предложен более простой метод. |
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ ДОПОЛНЕНИЕМ
ЗАДАЧИ
По завершении этого раздела вы должны уметь решать систему двух линейных уравнений методом сложения.
Метод сложения для решения системы линейных уравнений основан на двух фактах, которые мы использовали ранее.
Во-первых, мы знаем, что решения уравнения не меняются, если каждый член этого уравнения умножается на ненулевое число. Во-вторых, мы знаем, что если мы добавим одинаковые или равные количества к обеим сторонам уравнения, результаты все равно будут одинаковыми.
Пример 1 Решить сложением:
| Обратите внимание, что мы можем решить эту систему методом подстановки, решив первое уравнение относительно y.Решите эту систему методом подстановки и сравните свое решение с решением, полученным в этом разделе. |
Решение
Шаг 1 Наша цель — сложить два уравнения и исключить одно из неизвестных, чтобы мы могли решить полученное уравнение с одним неизвестным. Если мы сложим уравнения как есть, мы не удалим неизвестное. Это означает, что мы должны сначала умножить каждую сторону одного или обоих уравнений на число или числа, что приведет к исключению одного из неизвестных при сложении уравнений.
Внимательно изучив проблему, мы замечаем, что проще всего устранить неизвестное y. Это делается путем умножения каждой стороны первого уравнения на -2.
| Обратите внимание, что каждый член необходимо умножить на (- 2). |
Шаг 2 Добавьте уравнения.
Шаг 3 Решите полученное уравнение.
| В этом случае мы просто умножаем каждую сторону на (-1). |
Шаг 4 Найдите значение другой неизвестной, подставив это значение в одно из исходных уравнений.Используя первое уравнение,
| Подставьте x = 4 во второе уравнение и посмотрите, получите ли вы такое же значение для y. |
Шаг 5 Если мы проверим упорядоченную пару (4, -3) в обоих уравнениях, мы увидим, что это решение системы.
Пример 2 Решить сложением:
| Обратите внимание, что в этой системе ни одна переменная не имеет коэффициента, равного единице. Поэтому лучший метод решения — метод сложения. |
Решение
Шаг 1 Необходимо изменить оба уравнения, чтобы исключить одно из неизвестных. Ни одно из неизвестных не будет проще другого, поэтому удалите либо x, либо y.
Чтобы исключить x, умножьте каждую сторону первого уравнения на 3 и каждую сторону второго уравнения на -2.
| Если вы решили исключить y, умножьте первое уравнение на — 2, а второе уравнение на 3. Сделайте это и решите систему.Сравните ваше решение с полученным в примере. |
Шаг 2 Сложив уравнения, мы получаем
Шаг 3 Решение для урожайности
Шаг 4 Использование первого уравнения в исходной системе для нахождения значения другой неизвестной дает
Шаг 5 Убедитесь, что упорядоченная пара (- 1,3) является решением системы.
| Чек остается на ваше усмотрение. |
СТАНДАРТНАЯ ФОРМА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Напишите линейное уравнение в стандартной форме.
- Решите систему двух линейных уравнений, если они заданы в нестандартной форме.
Уравнения в предыдущих разделах не содержали дробей, как неизвестные в левой части уравнения, так и неизвестные в том же порядке.
Такие уравнения называются стандартными. То есть они имеют вид ax + by = c, где a, b и c — целые числа. Перед решением методом сложения уравнения необходимо привести к стандартному виду.
Пример 1 Измените 3x = 5 + 4y на стандартную форму.
Решение 3x = 5 + 4y не в стандартной форме, потому что одно неизвестное находится справа. Если мы прибавим -4y к обеим сторонам, мы получим 3x — 4y = 5, что в стандартной форме.
| Будьте осторожны здесь. Многие студенты забывают умножить правую часть уравнения на 24. |
| Опять же, убедитесь, что каждый член умножен на 12. |
Теперь прибавьте — 24x к обеим сторонам, получив — 24x + 9y = -10, что в стандартной форме.Обычно уравнения пишутся так, что первый член положительный. Таким образом, мы умножаем каждый член этого уравнения на (- 1).
| Вместо того чтобы говорить «первый член положительный», мы иногда говорим «ведущий коэффициент положительный». |
ПРОБЛЕМЫ СО СЛОВОМ С ДВУМЯ НЕИЗВЕСТНЫМИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите, когда проблема со словом может быть решена с использованием двух неизвестных.
- Составьте уравнения и решите словесную задачу.
Многие проблемы со словами можно обрисовать и решить, используя два неизвестных.
Пример 1 Сумма двух чисел равна 5. Трижды первое число, умноженное на пять, второе число равно 9. Найдите числа.
Решение Пусть x = первое число
y = второе число
Первое утверждение дает нам уравнение
x + y = 5.
Второе утверждение дает нам уравнение
3x + 5 y = 9.
Теперь у нас есть система
, которую мы можем решить любым из известных нам методов, давая
x = 8 и y = — 3.
| Решите систему с помощью подстановки. |
Пример 2 Два работника получают в общей сложности 136 долларов за 8-часовую работу. Если одному работнику платят на 1 доллар в час больше, чем другому, найдите почасовую ставку для каждого.
Решение Пусть x = почасовая ставка одного работника
y = почасовая ставка другого работника.
| Обратите внимание, что очень важно сказать, что представляют x и y. |
Первое утверждение дает нам уравнение
8x + 8y = 136.
Второе утверждение дает уравнение
х = у + 1.
Теперь у нас есть система (в стандартном виде)
Решение дает x = 9 и y = 8. Ставка одного рабочего составляет 9 долларов в час, а другого — 8 долларов в час.
| Решите эту систему методом сложения. |
РЕЗЮМЕ
Ключевые слова
- Декартова система координат — это метод наименования точек на плоскости.
- Упорядоченные пары чисел используются для обозначения точек на плоскости.
- Линейное уравнение представляет собой прямую линию.
- Наклон от одной точки на линии до другой — это отношение.
- Угол наклона-пересечения уравнения прямой имеет вид y = mx + b.
- Линейное неравенство отображается как часть плоскости.
- Система двух линейных уравнений состоит из линейных уравнений, для которых мы хотим найти одновременное решение.
- Независимые уравнения имеют уникальные решения.
- Противоречивые уравнения не имеют решения.
- Зависимые уравнения имеют бесконечно много решений.
- Система двух линейных неравенств состоит из линейных неравенств, для которых мы хотим найти одновременное решение.
- Стандартная форма линейного уравнения — это ax + by = c, где a, b и c — действительные числа.
Процедуры
- Чтобы нарисовать график линейного уравнения, найдите упорядоченные пары чисел, которые являются решениями этого уравнения.Найдите эти точки в декартовой системе координат и соедините их линией.
- Чтобы нарисовать график линии, используя ее наклон:
Шаг 1 Запишите уравнение прямой в форме y — mx + b.
Шаг 2 Найдите точку пересечения j (0, b).
Шаг 3 Начиная с (0, b), используйте наклон m, чтобы найти вторую точку.
Шаг 4 Соедините две точки прямой линией. - Чтобы построить график линейного неравенства:
Шаг 1 Замените символ неравенства знаком равенства и нанесите на график полученную линию.
Шаг 2 Проверьте одну точку, которая явно находится в определенной полуплоскости этой прямой, чтобы увидеть, входит ли она в набор решений неравенства.
Шаг 3 Если выбранная точка находится в наборе решений, то вся эта полуплоскость является набором решений. Если выбранная точка не входит в набор решений, тогда другая полуплоскость является набором решений. - Чтобы решить систему двух линейных уравнений с помощью построения графиков, тщательно изобразите уравнения в одной и той же системе координат.Их точка пересечения и будет решением системы.
- Чтобы решить систему двух линейных неравенств с помощью построения графиков, определите область плоскости, которая удовлетворяет обоим утверждениям неравенства.
- Чтобы решить систему двух уравнений с двумя неизвестными путем подстановки, решите одну неизвестную одного уравнения через другую неизвестную и подставьте эту величину в другое уравнение. Затем подставьте полученное таким образом числовое значение в любое уравнение, чтобы найти значение другого неизвестного.Наконец, проверьте решение в обоих уравнениях.
- Чтобы решить систему двух уравнений с двумя неизвестными путем сложения, умножьте одно или оба уравнения на необходимые числа так, чтобы при сложении уравнений одно из неизвестных было удалено. Решите оставшиеся неизвестные и подставьте это значение в одно из уравнений, чтобы найти другое неизвестное. Проверьте оба уравнения.
- Чтобы решить словесную задачу с двумя неизвестными, найдите два уравнения, которые показывают связь между неизвестными.Затем решите систему. Всегда проверяйте решение указанной проблемы.
Система 2-х линейных уравнений с 2-мя переменными Калькулятор
- Цель использования
- Учебное пособие
- Комментарий / запрос
- Очень полезно для быстрых ответов на 2 уравнения.
[1] 2021.01.28 10:36 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Очень /
- Цель использования
- , чтобы научиться пользоваться.
[2] 2021.01.20 20:31 Женский / 20-летний уровень / Средняя школа / Университет / аспирант / Полезно /
- Цель использования
- Для проекта строительства моста
- Комментарий / Запрос
- полезно для инженеры
[3] 2020/12/01 19:17 Мужчина / 60 лет и старше / Инженер / Полезно /
- Цель использования
- Статистические решения
- Комментарий / запрос
- Довольно хорошо
[4] 2020/07/23 14:40 Мужчина / До 20 лет / Старшая школа / Университет / аспирант / Очень /
- Комментарий / запрос
- Невозможно вычислить с корневыми значениями
[5] 2020/06/23 12:09 Женщина / Моложе 20 лет / Начальная школа / Младшая ученица средней школы / Немного /
- Цель использования
- Математическое представление / застрял на двух линейных уравнениях
[6] 2020/03/21 05:46 Женский / До 20 лет / Начальная школа / Младший школьник / Полезно /
- Цель использования
- Не терять время.
[7] 2019/11/23 21:00 Мужчины / До 20 лет ars old / Школа / Вуз / Высшее образование / Очень /
- Цель использования
- не хочу решать
- Комментарий / запрос
- просто оставьте его в дробях НЕ НУЖНО РЕШИТЬ в десятичных дробях
[8] 2019/10/15 20:25 Женский / Моложе 20 лет / Старшая школа / Университет / аспирант / Не совсем /
- Назначение используйте
- домашнее задание
- Комментарий / запрос
- нет необходимости в графике, просто скажите
[9] 26.05.2019 04:43 Женщина / До 20 лет / Инженер / Немного /
- Цель использования
- ЧТОБЫ ПРОВЕРИТЬ МОЙ ОТВЕТ
- Комментарий / запрос
- ЭТО ТОЛЬКО ДОЛЖНО БЫТЬ НЕКОТОРЫМ СЛУЧАЙНЫМ №ОТВЕТ НЕ СООТВЕТСТВУЕТ МОИМ РАСЧЕТАМ ИЛИ ОТВЕТАМ В МОЕМ ТЕКСТЕ … Я ХОТЕЛ ПРОВЕРИТЬ, ЧТО ДЕВУШКА ОТЧАЛЯЕТСЯ ОТ ЛЮБВИ … ДАЙТЕ МНЕ УЗНАТЬ НА ЭТОМ САЙТЕ
[10] 2018/12/01 18:21 Мужчина / Моложе 20 лет / Средняя школа / Университет / аспирант / A little /
Графики двух переменных функций
Графики Две переменные функцииМногие типы экономических проблем требуют рассмотрения двух переменных в в то же время. Типичный пример — соотношение между ценой товара и спрос или предложение на этот товар. Отношение можно описать алгебраически функцией или уравнением с двумя переменными.Но часто бывает полезно представить отношение в двумерном графе. Такой график называется разбросом. диаграмма. Это полезное устройство, потому что если есть простая связь между две переменные, это легко наблюдать, как только данные нанесены на график. Как пословица гласит: «Картинка стоит тысячи слов».
Для графического представления функции мы используем две перпендикулярные линии, называемые осями. Их точка пересечения называется началом координат. Этот способ представления называется декартовой системой координат или плоскостью.Числовое значение одного переменная измеряется по нижней или горизонтальной оси. Горизонтальная ось называется осью x. Числовое значение другой переменной измеряется. по боковой или вертикальной оси. Вертикальная ось называется осью y. В четыре участка, на которые разбивается граф, называются квадрантами. Единицы длины указаны по двум осям.
Обратите внимание, что есть четыре квадранта. Если x положительный, мы перемещаемся вправо. Если x отрицателен, мы перемещаемся влево.Если y положительно, мы движемся вверх. Если y отрицательно мы спускаемся.
Координаты
Координаты позволяют нам увидеть взаимосвязь между парами чисел и точки в плоскости. Координаты определяют положение точки P относительно к происхождению.
У нас есть координата x и координата y.
Пусть (x, y) представляет точку, координатами которой являются числа x и y. Обратите внимание, что координата x идет первой.Две координаты говорят нам, как далеко мы должны пройти сначала по оси x, а затем по оси y до точки достигается.
Построение координат: некоторые примеры
Пример 1
Найдите следующие точки
балла а
(2, 4)
балл b (4, -6)
балл c (-2, -6)
балл d (-6,
2)
Пример 2
p = цена ящика с овощами за доллар
f (p) = предложение в тысячах ящиков
У менеджера магазина есть следующие данные, которые относятся к цене ящика овощей в поставку:
| цена | 4 | 6 | 8 | 10 | 14 |
| снабжение | 2 | 14 | 23 | 27 | 29 |
О чем нам говорят данные? График показывает, что, как и следовало ожидать, увеличение в цене связано с увеличением предложения.
[индекс]
Как построить график линейных уравнений с двумя переменными
Обновлено 3 ноября 2020 г.
Кевин Бек
Графики являются одними из самых полезных инструментов в математике для осмысленной передачи информации. Даже те, кто не склонен к математике или испытывает явное отвращение к числам и вычислениям, могут найти утешение в базовой элегантности двухмерного графа, представляющего отношения между парой переменных.
Линейные уравнения с двумя переменными могут иметь вид
Ax + By = C
, и результирующий график всегда представляет собой прямую линию. Чаще уравнение принимает вид
y = mx + b
, где m — наклон линии соответствующего графика, а b — его интервал y , точка, в которой линия пересекает ось y .
Например, 4 x + 2 y = 8 является линейным уравнением, поскольку оно соответствует требуемой структуре.Но для построения графиков и большинства других целей математики записывают это как:
2y = -4x + 8
y = -2x + 4
Переменные в этом уравнении равны x и y. , а наклон и пересечение y — это константы .
Шаг 1. Определите точку пересечения оси y
. Для этого решите интересующее уравнение для y , если необходимо, и определите b .В приведенном выше примере интервал y равен 4.
Шаг 2: Обозначьте оси
Используйте масштаб, удобный для вашего уравнения. Вы можете столкнуться с уравнениями с необычно высокими или низкими значениями интервала y , такими как -37 или 89. В этих случаях каждый квадрат вашей миллиметровой бумаги может представлять десять единиц, а не одну, поэтому оба Это должно обозначать ось x и ось y .
Шаг 3. Постройте пересечение оси y
Нарисуйте точку на оси y в соответствующей точке.Между прочим, пересечение по оси Y — это просто точка, в которой x = 0.
Шаг 4: Определите наклон
Посмотрите на уравнение. Коэффициент перед x — это наклон, который может быть положительным, отрицательным или нулевым (последнее в случаях, когда уравнение имеет вид y = b , горизонтальная линия). Наклон часто называют «нарастанием за пробегом» и представляет собой количество изменений единицы в y для каждого отдельного изменения единицы в x.В приведенном выше примере наклон равен -2.
Шаг 5: Проведите линию через точку пересечения оси y с правильным наклоном
В приведенном выше примере, начиная с точки (0, 4), переместите две единицы в отрицательном направлении y -Направлении и один в положительном направлении x , так как наклон равен -2. Это приводит к точке (1, 2). Проведите линию через эти точки и продолжайте в обоих направлениях, насколько хотите.
Шаг 6: Проверьте график
Выберите точку на графике, удаленную от начала координат, и проверьте, удовлетворяет ли она уравнению.В этом примере точка (6, −8) лежит на графике. Подставляя эти значения в уравнение
y = -2x + 4
\ begin {align} -8 & = (-2) × 6 + 4 \\ -8 & = -12 + 4 \\ -8 & = — 8 \ end {align}
Таким образом, график правильный.
Выбор наилучшего типа графика
>
Адаптировано из книги Фрэнка Харрелла-младшего: на графике: http://biostat.mc.vanderbilt.edu/twiki/pub/Main/StatGraphCourse/graphscourse.pdf
|
Гистограммы, полосы ошибок и точечные диаграммы
Как отмечалось ранее, гистограммы могут быть проблематичными.Вот еще один, представляющий средства и планки погрешностей, но планки погрешностей вводят в заблуждение, потому что они простираются только в одном направлении. Лучшей альтернативой было бы использование полных планок погрешностей с диаграммой рассеяния, как показано ранее (справа).
Источник: Hummer BT, Li XL, Hassel BA (2001) Роль p53 в гене индукция двухцепочечной РНК. J Virol 75: 7774-7777, фиг. 4 |
Рассмотрим четыре графика ниже, показывающих заболеваемость раком по типу.На верхнем левом графике используются ненужные полосы, на которые требуется много чернил. Этот макет также приводит к тому, что шрифты для типов рака становятся слишком маленькими. Мелкий шрифт также является проблемой для точечной диаграммы в правом верхнем углу, и у этого также есть ненужные линии сетки по всей ширине.
График в левом нижнем углу имеет более читаемые метки и использует простой точечный график, но порядок ранжирования трудно определить.
График в правом нижнем углу, несомненно, лучше всех, так как метки читабельны, масштабы заболеваемости четко показаны точечными графиками, а раковые заболевания отсортированы по частоте.
************************* + | |
Одинарная непрерывная числовая переменная
В этой ситуации кумулятивная функция распределения передает больше всего информации и не требует группировки переменной. Ящичковая диаграмма будет эффективно отображать выбранные квантили, а ящичковая диаграмма особенно полезна при стратификации по нескольким категориям другой переменной.
Гистограммы также возможны. Рассмотрим примеры ниже.
График плотности | Гистограмма | Участок |
Две переменные
Адаптировано из книги Фрэнка Э.Харрелл-младший по графике: http://biostat.mc.vanderbiltedu/twiki/pub/Main/StatGraphCourse/graphscourse.pdf Две категориальные переменные
Две непрерывные переменные
|
Два графика ниже суммируют измерения ИМТ (индекса массы тела) по четырем категориям, т.е.е., более молодые и пожилые мужчины и женщины. На графике слева показаны средние значения и 95% доверительный интервал для среднего значения в каждой из четырех групп. Это легко интерпретировать, но зритель не видит, что данные на самом деле сильно искажены. На графике справа показана та же информация, что и в виде прямоугольной диаграммы. С помощью этого метода представления можно лучше понять неравномерное распределение и сравнение групп.
Следующий пример — это диаграмма рассеяния с наложенной сглаженной линией прогноза.Заштрихованная область, охватывающая синюю линию, представляет собой 95% доверительный интервал для предполагаемого прогноза. Это было создано с помощью «ggplot» на языке программирования R.
Источник: Фрэнк Э. Харрелл-младший на графике: http://biostat.mc.vanderbilt.edu/twiki/pub/Main/StatGraphCourse/graphscourse.pdf (стр. 121)
Многомерные данные
|
Пример ниже показывает использование нескольких панелей.
Источник: Кливленд С. Элементы графических данных. Hobart Press, Summit, NJ, 1994.
вернуться наверх | предыдущая страница | следующая страница
10.5 Построение графических квадратичных уравнений с двумя переменными — элементарная алгебра 2e
Задачи обучения
К концу этого раздела вы сможете:
- Распознать график квадратного уравнения с двумя переменными
- Найдите ось симметрии и вершину параболы
- Найдите точки пересечения параболы
- График квадратных уравнений с двумя переменными
- Решите максимальные и минимальные приложения
Будьте готовы 10.13
Прежде чем начать, пройдите тест на готовность.
Постройте уравнение y = 3x − 5y = 3x − 5, нанеся точки.
Если вы пропустили эту проблему, просмотрите Пример 4.11.
Будьте готовы 10.14
Вычислить 2×2 + 4x − 12×2 + 4x − 1, когда x = −3x = −3.
Если вы пропустили эту проблему, просмотрите Пример 1.57.
Будьте готовы 10,15
Вычислить −b2a − b2a, когда a = 13a = 13 и b = 56b = 56.
Если вы пропустили эту проблему, просмотрите Пример 1.89.
Распознать график квадратного уравнения с двумя переменными
У нас есть графические уравнения вида Ax + By = CAx + By = C.Мы назвали уравнения такими линейными уравнениями, потому что их графики представляют собой прямые линии.
Теперь изобразим уравнения вида y = ax2 + bx + cy = ax2 + bx + c. Мы называем этот вид уравнения квадратным уравнением от двух переменных.
Квадратное уравнение с двумя переменными
Квадратное уравнение с двумя переменными, где a, b, andca, b иc — действительные числа, а a ≠ 0a ≠ 0, представляет собой уравнение вида
Точно так же, как мы начали рисовать линейные уравнения с помощью точек, мы сделаем то же самое для квадратных уравнений.
Давайте сначала посмотрим на график квадратного уравнения y = x2y = x2. Мы выберем целые значения xx между −2−2 и 2 и найдем их значения yy. См. Таблицу 10.1.
| y = x2y = x2 | |
| хх | г.г |
| 0 | 0 |
| 1 | 1 |
| -1-1 | 1 |
| 2 | 4 |
| −2−2 | 4 |
Таблица 10.1
Обратите внимание, когда мы полагаем x = 1x = 1 и x = −1x = −1, мы получаем то же значение для yy.
y = x2y = x2y = 12y = (- 1) 2y = 1y = 1y = x2y = x2y = 12y = (- 1) 2y = 1y = 1То же самое произошло, когда мы положили x = 2x = 2 и x = −2x = −2.
Теперь мы построим точки, чтобы показать график y = x2y = x2. См. Рисунок 10.2.
Рисунок 10.2
График — это не линия. Эта фигура называется параболой. Каждое квадратное уравнение имеет график, который выглядит следующим образом.
В примере 10.43 вы попрактикуетесь в построении параболы путем нанесения нескольких точек.
Пример 10.43
Решение
Мы изобразим уравнение, нанося точки.
| Выберите целые числа для x , подставьте их в уравнение и решите относительно y . | ||
| Запишите значения упорядоченных пар в диаграмму. | ||
| Постройте точки и соедините их плавной кривой. Результатом будет график уравнения y = x2−1y = x2−1. | ||
Чем отличаются уравнения y = x2y = x2 и y = x2−1y = x2−1? В чем разница между их графиками? Как их графики совпадают?
Все параболы вида y = ax2 + bx + cy = ax2 + bx + c открываются вверх или вниз. См. Рисунок 10.3.
Рисунок 10.3
Обратите внимание, что единственная разница в двух уравнениях — это отрицательный знак перед x2x2 в уравнении второго графика на рисунке 10.3. Когда член x2x2 положителен, парабола открывается вверх, а когда член x2x2 отрицателен, парабола открывается вниз.
Ориентация параболы
Для квадратного уравнения y = ax2 + bx + cy = ax2 + bx + c, если:
Пример 10.44
Определите, открывается ли каждая парабола вверх или вниз:
ⓐ y = −3×2 + 2x − 4y = −3×2 + 2x − 4 ⓑ y = 6×2 + 7x − 9y = 6×2 + 7x − 9
Решение
| ⓐ Найдите значение « a ». | Поскольку буква «а» отрицательна, парабола откроется вниз. | |
| ⓑ Найдите значение « a ». | Поскольку буква «а» положительна, парабола откроется вверх. | |
Попробовать 10,87
Определите, открывается ли каждая парабола вверх или вниз:
ⓐ y = 2×2 + 5x − 2y = 2×2 + 5x − 2 ⓑ y = −3×2−4x + 7y = −3×2−4x + 7
Попробовать 10,88
Определите, открывается ли каждая парабола вверх или вниз:
ⓐ y = −2×2−2x − 3y = −2×2−2x − 3 ⓑ y = 5×2−2x − 1y = 5×2−2x − 1
Найдите ось симметрии и вершину параболы
Посмотрите еще раз на рисунок 10.3. Видите ли вы, что мы можем сложить каждую параболу пополам и что одна сторона будет лежать поверх другой? «Линия сгиба» — это линия симметрии. Мы называем это осью симметрии параболы.
Мы снова показываем те же два графика с осью симметрии красным цветом. См. Рисунок 10.4.
Рисунок 10.4
Уравнение оси симметрии может быть получено с помощью квадратичной формулы. Мы опустим вывод здесь и перейдем непосредственно к использованию результата. Уравнение оси симметрии графика y = ax2 + bx + cy = ax2 + bx + c имеет вид x = −b2a.х = −b2a.
Итак, чтобы найти уравнение симметрии каждой из парабол, которые мы построили на графике выше, мы подставим в формулу x = −b2ax = −b2a.
Вернитесь к рис. 10.4. Это уравнения, изображенные пунктирными красными линиями?
Точка параболы, которая находится на оси симметрии, является самой низкой или самой высокой точкой параболы, в зависимости от того, открывается парабола вверх или вниз. Эта точка называется вершиной параболы.
Мы можем легко найти координаты вершины, потому что знаем, что она находится на оси симметрии.Это означает, что его координата x равна −b2a − b2a. Чтобы найти координату y вершины, мы подставляем значение координаты x в квадратное уравнение.
Ось симметрии и вершина параболы
Для параболы с уравнением y = ax2 + bx + cy = ax2 + bx + c:
- Осью симметрии параболы является прямая x = −b2ax = −b2a.
- Вершина находится на оси симметрии, поэтому ее координата x равна −b2a − b2a.
Чтобы найти координату y вершины, подставим x = −b2ax = −b2a в квадратное уравнение.
Пример 10.45
Для параболы y = 3×2−6x + 2y = 3×2−6x + 2 найти: ⓐ ось симметрии и ⓑ вершину.
Попробуйте 10,89
Для параболы y = 2×2−8x + 1y = 2×2−8x + 1 найти: ⓐ ось симметрии и ⓑ вершину.
Попробовать 10.90
Для параболы y = 2×2−4x − 3y = 2×2−4x − 3 найти: ⓐ ось симметрии и ⓑ вершину.
Найдите точки пересечения параболы
Когда мы рисовали линейные уравнения, мы часто использовали точки пересечения x и y , чтобы построить графики линий. Определение координат точек пересечения также поможет нам построить график парабол.
Помните, что в точке пересечения y значение xx равно нулю. Итак, чтобы найти точку перехвата y , мы подставляем x = 0x = 0 в уравнение.
Давайте найдем точки пересечения и двух парабол, показанных на рисунке ниже.
Рисунок 10.5
При перехвате x значение yy равно нулю. Чтобы найти точку перехвата x , мы подставляем y = 0y = 0 в уравнение. Другими словами, нам нужно будет решить уравнение 0 = ax2 + bx + c0 = ax2 + bx + c относительно xx.
y = ax2 + bx + c0 = ax2 + bx + cy = ax2 + bx + c0 = ax2 + bx + cНо решение таких квадратных уравнений — это именно то, что мы делали ранее в этой главе.
Теперь мы можем найти точки пересечения x двух парабол, показанных на рисунке 10.5.
Сначала мы найдем точки пересечения параболы x с уравнением y = x2 + 4x + 3y = x2 + 4x + 3.
Теперь мы найдем точки пересечения параболы x с уравнением y = −x2 + 4x + 3y = −x2 + 4x + 3.
Мы будем использовать десятичные аппроксимации пересечений по оси x, чтобы мы могли найти эти точки на графике.
(2 + 7,0) ≈ (4.6,0) (2−7,0) ≈ (−0.6,0) (2 + 7,0) ≈ (4.6,0) (2−7,0) ≈ (- 0,6,0)Соответствуют ли эти результаты нашим графикам? См. Рисунок 10.6.
Рисунок 10.6
How To
Найдите точки пересечения параболы.
Чтобы найти точки пересечения параболы с уравнением y = ax2 + bx + cy = ax2 + bx + c:
y-interceptx-intercepts Letx = 0 и решает для y. Lety = 0 и решает для x. y-interceptx-intercepts Letx = 0 и решает для y. Let = 0 и решает для x.Пример 10.46
Найдите точки пересечения параболы y = x2−2x − 8y = x2−2x − 8.
Решение
Когда y = 0y = 0, то x = 4orx = −2x = 4orx = −2. Перехваты x — это точки (4,0) (4,0) и (−2,0) (- 2,0).
Попробуйте 10.91
Найдите точки пересечения параболы y = x2 + 2x − 8.y = x2 + 2x − 8.
Попробуйте 10.92
Найдите точки пересечения параболы y = x2−4x − 12.y = x2−4x − 12.
В этой главе мы решали квадратные уравнения вида ax2 + bx + c = 0ax2 + bx + c = 0. Мы решили для xx, и результаты были решениями уравнения.
Теперь мы рассматриваем квадратные уравнения с двумя переменными вида y = ax2 + bx + cy = ax2 + bx + c. Графики этих уравнений представляют собой параболы. x -перехваты парабол происходят там, где y = 0y = 0.
Например:
Квадратное уравнение Квадратное уравнение с двумя переменными y = x2−2x − 15×2−2x − 15 = 0 (x − 5) (x + 3) = 0lety = 00 = x2−2x − 150 = (x − 5) (x + 3) x −5 = 0x + 3 = 0x = 5x = −3x − 5 = 0x + 3 = 0x = 5x = −3 (5,0) и (−3,0) пересечение по оси x Квадратное уравнение Квадратное уравнение с двумя переменными y = x2−2x −15×2−2x − 15 = 0 (x − 5) (x + 3) = 0lety = 00 = x2−2x − 150 = (x − 5) (x + 3) x − 5 = 0x + 3 = 0x = 5x = −3x − 5 = 0x + 3 = 0x = 5x = −3 (5,0) и (−3,0) пересечения по оси xРешениями квадратного уравнения являются значения xx интерцептов x .
Ранее мы видели, что квадратные уравнения имеют 2, 1 или 0 решений. На графиках ниже показаны примеры парабол для этих трех случаев. Поскольку решения уравнений дают x -перехвата графиков, количество x -перехватывания равно количеству решений.
Ранее мы использовали дискриминант для определения числа решений квадратного уравнения вида ax2 + bx + c = 0ax2 + bx + c = 0. Теперь мы можем использовать дискриминант, чтобы узнать, сколько точек пересечения x имеется на графике.
Перед тем, как вы начнете решать квадратное уравнение, чтобы найти значения перехватов x , вы можете оценить дискриминант, чтобы знать, сколько решений ожидать.
Пример 10.47
Найдите точки пересечения параболы y = 5×2 + x + 4y = 5×2 + x + 4.
Попробуйте 10.93
Найдите точки пересечения параболы y = 3×2 + 4x + 4.y = 3×2 + 4x + 4.
Попробуйте 10.94
Найдите точки пересечения параболы y = x2−4x − 5.у = х2−4х − 5.
Пример 10.48
Найдите точки пересечения параболы y = 4×2−12x + 9y = 4×2−12x + 9.
Попробуйте 10.95
Найдите точки пересечения параболы y = −x2−12x − 36.y = −x2−12x − 36.
Попробуйте 10.96
Найдите точки пересечения параболы y = 9×2 + 12x + 4.y = 9×2 + 12x + 4.
Графические квадратные уравнения с двумя переменными
Теперь у нас есть все, что нужно для построения графика квадратного уравнения с двумя переменными.Нам просто нужно собрать их вместе. В следующем примере мы увидим, как это сделать.
Пример 10.49
Как построить квадратное уравнение с двумя переменными
График y = x2−6x + 8y = x2−6x + 8.
Попробуйте 10.97
Постройте параболу y = x2 + 2x − 8.y = x2 + 2x − 8.
Попробовать 10.98
Постройте параболу y = x2−8x + 12.y = x2−8x + 12.
How To
Постройте квадратное уравнение с двумя переменными.
- Шаг 1.Напишите квадратное уравнение с yy на одной стороне.
- Шаг 2. Определите, открывается ли парабола вверх или вниз.
- Шаг 3. Найдите ось симметрии.
- Шаг 4. Найдите вершину.
- Шаг 5. Найдите точку пересечения и . Найдите точку, симметричную пересечению y поперек оси симметрии.
- Шаг 6. Найдите перехватчики x .
- Шаг 7. Постройте параболу.
Нам удалось найти перехваты x в последнем примере с помощью факторинга.Мы также находим перехваты x в следующем примере с помощью факторинга.
Пример 10,50
График y = −x2 + 6x − 9y = −x2 + 6x − 9.
Решение
| Уравнение и имеет одну сторону. | ||
| Так как равно −1−1, парабола открывается вниз. Чтобы найти ось симметрии, найдите x = −b2ax = −b2a. | Ось симметрии x = 3.х = 3. Вершина находится на прямой x = 3.x = 3. | |
| Найдите y , когда x = 3.x = 3. | Вершина равна (3,0). (3,0). | |
| Перехват y происходит, когда x = 0.x = 0. Заменить x = 0.x = 0. Упростить. Точка (0, −9) (0, −9) находится на три единицы левее линии симметрии. Точка на три единицы правее линии симметрии равна (6, −9). (6, −9). Точка, симметричная точке пересечения y- , равна (6, −9) (6, −9) | Перехват y равен (0, −9).(0, -9). | |
| Перехват x происходит, когда y = 0.y = 0. | ||
| Заменить y = 0. y = 0. | ||
| Разложите на множители GCF. | ||
| Разложите на множители трехчлен. | ||
| Решите относительно x . | ||
| Соедините точки, чтобы построить параболу. | ||
Попробовать 10,99
Постройте параболу y = −3×2 + 12x − 12.у = −3×2 + 12x − 12.
Попробуйте 10.100
Изобразите параболу y = 25×2 + 10x + 1.y = 25×2 + 10x + 1.
Для графика y = −x2 + 6x − 9y = −x2 + 6x − 9 вершина и пересечение x были одной и той же точкой. Помните, как дискриминант определяет количество решений квадратного уравнения? Дискриминант уравнения 0 = −x2 + 6x − 90 = −x2 + 6x − 9 равен 0, поэтому существует только одно решение. Это означает, что есть только одно пересечение x , и это вершина параболы.
Сколько x -перехватов вы ожидаете увидеть на графике y = x2 + 4x + 5y = x2 + 4x + 5?
Пример 10.51
График y = x2 + 4x + 5y = x2 + 4x + 5.
Решение
| Уравнение имеет y с одной стороны. | ||
| Поскольку a равно 1, парабола открывается вверх. | ||
| Чтобы найти ось симметрии, найдите x = −b2a.x = −b2a. | Ось симметрии x = −2.х = -2. | |
| Вершина находится на прямой x = −2.x = −2. | ||
| Найдите y , когда x = −2.x = −2. | Вершина равна (−2,1). (- 2,1). | |
| Перехват y происходит, когда x = 0.x = 0. Заменить x = 0.x = 0. Упростить. Точка (0,5) (0,5) находится на две единицы правее линии симметрии. Точка на две единицы левее линии симметрии равна (−4,5).(-4,5). | Перехват и равен (0,5). (0,5). Точка, симметричная точке пересечения y- , равна (−4,5) (- 4,5). | |
| Перехват x — происходит, когда y = 0.y = 0. | ||
| Заменить y = 0. y = 0. Проверить дискриминант. | | |
| b2−4acb2−4ac 42−4⋅1542−4⋅15 16−2016−20 −4−4 | ||
| Поскольку значение дискриминанта отрицательное, решения нет и, следовательно, нет точки пересечения x-. Соедините точки, чтобы построить параболу. Вы можете выбрать еще две точки для большей точности. | ||
Попробуйте 10.101
Постройте параболу y = 2×2−6x + 5.y = 2×2−6x + 5.
Попробуйте 10.102
Постройте параболу y = −2×2−1.y = −2×2−1.
Найти перехват y , подставив x = 0x = 0 в уравнение, легко, не так ли? Но нам нужно было использовать квадратичную формулу, чтобы найти точки пересечения x в примере 10.51. В следующем примере мы снова будем использовать квадратичную формулу.
Пример 10.52
График y = 2×2−4x − 3y = 2×2−4x − 3.
Решение
| Уравнение и имеет одну сторону. Так как равно 2, парабола открывается вверх. | ||
| Чтобы найти ось симметрии, найдите x = −b2ax = −b2a. | Ось симметрии x = 1x = 1. | |
| Вершина на прямой x = 1.x = 1. | ||
| Найдите y , когда x = 1x = 1. | Вершина равна (1, −5) (1, −5). | |
| Перехват y происходит, когда x = 0.x = 0. | ||
| Заменить x = 0.x = 0. | ||
| Упростить. | Перехватчик y- равен (0, −3) (0, −3). | |
| Точка (0, −3) (0, −3) находится на одну единицу левее линии симметрии. Точка на одну единицу правее линии симметрии равна (2, −3) (2, −3) | Точка, симметричная точке пересечения y- , равна (2, −3). (2, −3). | |
| Перехват x происходит, когда y = 0y = 0. | ||
| Заменить y = 0y = 0. | ||
| Используйте квадратичную формулу. | ||
| Заменить значениями a, b, c. | ||
| Упростить. | ||
| Упростить внутри радикала. | ||
| Упростим радикал. | ||
| Разложите на множители GCF. | ||
| Удалите общие множители. | ||
| Запишите в виде двух уравнений. | ||
| Приблизительные значения. | ||
| Приблизительные значения точек пересечения x- равны (2.5,0) (2,5,0) и (-0,6,0) (- 0,6,0). | ||
| Постройте параболу, используя найденные точки. | ||
Попробуйте 10.103
Изобразите параболу y = 5×2 + 10x + 3.y = 5×2 + 10x + 3.
Попробуйте 10.104
Постройте параболу y = −3×2−6x + 5.y = −3×2−6x + 5.
Решение максимальных и минимальных приложений
Знание того, что вершина параболы является самой низкой или самой высокой точкой параболы, дает нам простой способ определить минимальное или максимальное значение квадратного уравнения.Координата y вершины является минимальным значением y параболы, которая открывается вверх. Это максимальное значение y параболы, которая открывается вниз. См. Рисунок 10.7.
Рисунок 10.7
Минимальные или максимальные значения квадратного уравнения
Координата y вершины графика квадратного уравнения равна
- минимальное значение квадратного уравнения, если парабола открывается вверх.
- максимальное значение квадратного уравнения, если парабола открывается вниз.
Пример 10.53
Найдите минимальное значение квадратного уравнения y = x2 + 2x − 8y = x2 + 2x − 8.
Попробуйте 10.105
Найдите максимальное или минимальное значение квадратного уравнения y = x2−8x + 12y = x2−8x + 12.
Попробуйте 10.106
Найдите максимальное или минимальное значение квадратного уравнения y = −4×2 + 16x − 11y = −4×2 + 16x − 11.
Мы использовали формулу
h = −16t2 + v0t + h0h = −16t2 + v0t + h0для расчета высоты в футах, hh, объекта, взлетающего в воздух с начальной скоростью v0v0 через tt секунд.
Эта формула представляет собой квадратное уравнение относительно переменной tt, поэтому ее график представляет собой параболу. Решая координаты вершины, мы можем определить, сколько времени потребуется объекту, чтобы достичь максимальной высоты. Затем мы можем рассчитать максимальную высоту.
Пример 10,54
Квадратное уравнение h = −16t2 + v0t + h0h = −16t2 + v0t + h0 моделирует высоту удара волейбольного мяча прямо вверх со скоростью 176 футов в секунду с высоты 4 фута.
- ⓐ За сколько секунд волейбольный мяч достигнет максимальной высоты?
- ⓑ Найдите максимальную высоту волейбольного мяча.
Решение
h = −16t2 + 176t + 4h = −16t2 + 176t + 4
Поскольку a отрицательно, парабола открывается вниз.
Квадратное уравнение имеет максимум.
- ⓐ
Найти ось симметрии. T = −b2at = −1762 (−16) t = 5,5 Ось симметрии ist = 5,5. Вершина находится на прямой = 5,5. Максимум достигается при = 5,5 секунд. Найти ось симметрии. t = −b2at = −1762 (−16) t = 5.5 Ось симметрии ist = 5.5. вершина находится на линии = 5.5. Максимум происходит при nt = 5.5 секунд. - ⓑ
Найдите h , когда t = 5,5t = 5,5. Воспользуйтесь калькулятором для упрощения. Вершина равна (5.5 488) (5.5 488). Поскольку парабола имеет максимум, координата h- вершины является максимальным значением y квадратного уравнения. Максимальное значение квадратичной функции составляет 488 футов, и она возникает при t = 5.5t = 5,5 секунды.
Попробуйте 10.107
Квадратное уравнение h = −16t2 + 128t + 32h = −16t2 + 128t + 32 используется для определения высоты камня, брошенного вверх с высоты 32 фута со скоростью 128 футов / сек. Сколько времени потребуется, чтобы камень достиг максимальной высоты? Какая максимальная высота? Округлите ответы до ближайшей десятой.
Попробуйте 10.108
Игрушечная ракета, взорвавшаяся от земли со скоростью 208 фут / сек, имеет квадратное уравнение h = −16t2 + 208th = −16t2 + 208t.Когда ракета достигнет максимальной высоты? Какая будет максимальная высота? Округлите ответы до ближайшей десятой.
Раздел 10.5 Упражнения
Практика ведет к совершенству
Распознать график квадратного уравнения с двумя переменными
В следующих упражнениях график:
В следующих упражнениях определите, раскрывается ли парабола вверх или вниз.
165.y = −2×2−6x − 7y = −2×2−6x − 7
168.y = −9×2−24x − 16y = −9×2−24x − 16
Найдите ось симметрии и вершину параболы
В следующих упражнениях найдите ⓐ ось симметрии и ⓑ вершину.
172.y = −2×2−8x − 3y = −2×2−8x − 3
Найдите точки пересечения параболы
В следующих упражнениях найдите точки перехвата x и y .
174.y = x2 + 10x − 11y = x2 + 10x − 11
175.y = −x2 + 8x − 19y = −x2 + 8x − 19
177.y = 4×2−20x + 25y = 4×2−20x + 25
178.y = −x2−14x − 49y = −x2−14x − 49
Графические квадратные уравнения с двумя переменными
В следующих упражнениях построите график с помощью точек пересечения, вершины и оси симметрии.
184.y = −x2 + 8x − 16y = −x2 + 8x − 16
185.y = −x2 + 2x − 7y = −x2 + 2x − 7
188.y = 3×2−6x − 1y = 3×2−6x − 1
190.y = −4×2−6x − 2y = −4×2−6x − 2
191.y = −x2−4x + 2y = −x2−4x + 2
193.y = 5×2−10x + 8y = 5×2−10x + 8
194.y = −16×2 + 24x − 9y = −16×2 + 24x − 9
196.y = −2×2 + 8x − 10y = −2×2 + 8x − 10
Решение максимальных и минимальных приложений
В следующих упражнениях найдите максимальное или минимальное значение.
198.y = −4×2 + 12x − 5y = −4×2 + 12x − 5
200.y = −x2 + 4x − 5y = −x2 + 4x − 5
В следующих упражнениях решите. Округлите ответы до ближайшей десятой.
203.Стрела выпущена вертикально вверх с платформы высотой 45 футов со скоростью 168 футов / сек. Используйте квадратное уравнение h = −16t2 + 168t + 45h = −16t2 + 168t + 45, чтобы найти, сколько времени потребуется стрелке, чтобы достичь максимальной высоты, а затем найдите максимальную высоту.
204.Камень бросается вертикально вверх с платформы высотой 20 футов со скоростью 160 футов / сек.Используйте квадратное уравнение h = −16t2 + 160t + 20h = −16t2 + 160t + 20, чтобы найти, сколько времени потребуется камню, чтобы достичь максимальной высоты, а затем найдите максимальную высоту.
205.Владелец компьютерного магазина подсчитал, что, взимая xx долларов за каждый компьютер, он может продавать 40 − x40 − x компьютеров каждую неделю. Квадратное уравнение R = −x2 + 40xR = −x2 + 40x используется для нахождения дохода RR, полученного, когда продажная цена компьютера равна xx. Найдите цену продажи, которая принесет ему максимальный доход, а затем найдите сумму максимального дохода.
206.Розничный торговец, продающий рюкзаки, оценивает, что, продав их по xx долларов за штуку, он сможет продавать 100 x 100 x рюкзаков в месяц. Квадратное уравнение R = −x2 + 100xR = −x2 + 100x используется для нахождения RR, полученного, когда цена продажи рюкзака равна xx. Найдите цену продажи, которая принесет ему максимальный доход, а затем найдите сумму максимального дохода.
207.Владелец ранчо собирается оградить загон с трех сторон у реки. Ему нужно максимально увеличить площадь загона, используя 240 футов ограждения.Квадратное уравнение A = x (240−2x) A = x (240−2x) дает площадь загона AA для длины x, x загона вдоль реки. Найдите длину загона вдоль реки, которая даст максимальную площадь, а затем найдите максимальную площадь загона.
208.Ветеринар огораживает прямоугольную площадку для бега на открытом воздухе напротив своего здания для собак, о которых он заботится. Ему нужно максимально увеличить площадь, используя 100 футов ограждения. Квадратное уравнение A = x (100−2x) A = x (100−2x) дает площадь AA выгула собаки для длины xx здания, которое будет граничить с выгулом собаки.Найдите длину здания, которое должно ограничивать собачий бег, чтобы обеспечить максимальную площадь, а затем найдите максимальную площадь для собачьего бега.
Повседневная математика
209. В предыдущем наборе упражнений вы работали с квадратным уравнением R = −x2 + 40xR = −x2 + 40x, которое моделировало доход, полученный от продажи компьютеров по цене xx долларов. Вы нашли продажную цену, которая дала бы максимальный доход, и рассчитали максимальный доход. Теперь вы ознакомитесь с дополнительными характеристиками этой модели.
ⓐ Изобразите уравнение R = −x2 + 40xR = −x2 + 40x. Ⓑ Найдите значения интерцептов x .
В предыдущем наборе упражнений вы работали с квадратным уравнением R = −x2 + 100xR = −x2 + 100x, которое моделировало доход, полученный от продажи рюкзаков по цене xx долларов. Вы нашли продажную цену, которая дала бы максимальный доход, и рассчитали максимальный доход. Теперь вы ознакомитесь с дополнительными характеристиками этой модели.
ⓐ Изобразите уравнение R = −x2 + 100xR = −x2 + 100x.Ⓑ Найдите значения интерцептов x .
Письменные упражнения
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
14.1: Функции нескольких переменных
Нашим первым шагом является объяснение того, что такое функция нескольких переменных, начиная с функций двух независимых переменных.Этот шаг включает в себя определение области и диапазона таких функций и обучение их построению в виде графиков. Мы также исследуем способы связать графики функций в трех измерениях с графиками более знакомых плоских функций.
Функции двух переменных
Определение функции двух переменных очень похоже на определение функции одной переменной. Основное отличие состоит в том, что вместо отображения значений одной переменной в значения другой переменной мы сопоставляем упорядоченные пары переменных с другой переменной.2 \) на уникальное действительное число z . Множество \ (D \) называется областью определения функции. Диапазон \ (f \) — это набор всех действительных чисел z , который имеет хотя бы одну упорядоченную пару \ ((x, y) ∈D \) такую, что \ (f (x, y) = z \) как показано на рисунке \ (\ PageIndex {1} \).
Рисунок \ (\ PageIndex {1} \): Область определения функции двух переменных состоит из упорядоченных пар \ ((x, y) \).Определение области определения функции двух переменных включает в себя учет любых ограничений области, которые могут существовать.2 \). Чтобы определить диапазон, сначала выберите значение z . Нам нужно найти решение уравнения \ (f (x, y) = z, \) или \ (3x − 5y + 2 = z. \). Одно такое решение можно получить, сначала положив \ (y = 0 \ ), что дает уравнение \ (3x + 2 = z \). Решением этого уравнения является \ (x = \ dfrac {z − 2} {3} \), что дает упорядоченную пару \ (\ left (\ dfrac {z − 2} {3}, 0 \ right) \) как решение уравнения \ (f (x, y) = z \) для любого значения \ (z \). Следовательно, диапазон функции — это все действительные числа или \ (R \).
г.2≤4 \), граница которого имеет окружность радиуса \ (2 \). Диапазон равен \ ([0,6]. \)
.Графические функции двух переменных
Предположим, мы хотим построить график функции \ (z = (x, y). \) Эта функция имеет две независимые переменные (\ (x \) и \ (y \)) и одну зависимую переменную \ ((z) \) . При построении графика функции \ (y = f (x) \) одной переменной мы используем декартову плоскость. Мы можем построить график любой упорядоченной пары \ ((x, y) \) на плоскости, и каждая точка на плоскости имеет связанную с ней упорядоченную пару \ ((x, y) \).С функцией двух переменных каждая упорядоченная пара \ ((x, y) \) в области определения функции отображается в действительное число \ (z \). Следовательно, график функции \ (f \) состоит из упорядоченных троек \ ((x, y, z) \). График функции \ (z = (x, y) \) двух переменных называется поверхностью.
Чтобы более полно понять концепцию построения набора упорядоченных троек для получения поверхности в трехмерном пространстве, представьте плоскую систему координат \ ((x, y) \). Тогда каждая точка в области определения функции f имеет уникальное значение z , связанное с ней.2, \ nonumber \]
, где \ (x \) — количество гаек, проданных в месяц (в тысячах), а \ (y \) — количество болтов, проданных за месяц (в тысячах). Прибыль измеряется тысячами долларов. Нарисуйте график этой функции.
Решение
Эта функция является полиномиальной функцией от двух переменных. 2 = 16 -Z.\ end {align *} \]
Поскольку \ (z <16, \), мы знаем, что \ (16 − z> 0, \), поэтому предыдущее уравнение описывает круг с радиусом \ (\ sqrt {16 − z} \) с центром в точке \ (( 3,2) \). Следовательно. диапазон \ (f (x, y) \) равен \ (\ {z∈ \ mathbb {R} | z≤16 \}. \) График \ (f (x, y) \) также является параболоид, и этот параболоид указывает вниз, как показано.
Рисунок \ (\ PageIndex {5} \): График данной функции двух переменных также является параболоидом.Кривые уровня
Если туристы идут по пересеченным тропам, они могут использовать топографическую карту, показывающую, насколько круто меняются маршруты.Топографическая карта содержит изогнутые линии, называемые контурными линиями. Каждая горизонтальная линия соответствует точкам на карте, имеющим одинаковую высоту (Рисунок \ (\ PageIndex {6} \)). Линия уровня функции двух переменных \ (f (x, y) \) полностью аналогична контурной линии на топографической карте.
Рисунок \ (\ PageIndex {6} \): (а) Топографическая карта Башни Дьявола, Вайоминг. Линии, расположенные близко друг к другу, указывают на очень крутой рельеф. (б) Перспективное фото Башни Дьявола показывает, насколько круты ее стены.2 = 5. \]Это уравнение описывает круг с центром в начале координат и радиусом \ (\ sqrt {5} \). Использование значений c между \ (0 \) и \ (3 \) дает другие круги, также с центром в начале координат. Если \ (c = 3 \), то круг имеет радиус \ (0 \), поэтому он состоит исключительно из начала координат. На рисунке \ (\ PageIndex {7} \) показан график линий уровня этой функции, соответствующих \ (c = 0,1,2, \) и \ (3 \). Обратите внимание, что в предыдущем выводе возможно, что мы ввели дополнительные решения, возведя обе части в квадрат.2 = 25, \), который представляет собой окружность радиуса \ (5 \) с центром в точке \ ((3, −1). \)
Еще один полезный инструмент для понимания графика функции двух переменных называется вертикальной кривой. 2 \).Вертикальный след функции может быть либо набором точек, который решает уравнение \ (f (a, y) = z \) для данной константы \ (x = a \), либо \ (f (x, b ) = z \) для данной константы \ (y = b. \)
Пример \ (\ PageIndex {5} \): поиск вертикальных следов
Найдите вертикальные следы для функции \ (f (x, y) = \ sin x \ cos y \), соответствующей \ (x = — \ dfrac {π} {4}, 0, \) и \ (\ dfrac { π} {4} \) и \ (y = — \ dfrac {π} {4}, 0 \) и \ (\ dfrac {π} {4} \).
Решение
Сначала задайте \ (x = — \ dfrac {π} {4} \) в уравнении \ (z = \ sin x \ cos y: \)
\ (z = \ sin (- \ dfrac {π} {4}) \ cos y = — \ dfrac {\ sqrt {2} \ cos y} {2} ≈ −0.7071 \ cos y. \)
Это описывает косинусный граф на плоскости \ (x = — \ dfrac {π} {4} \). Остальные значения z показаны в следующей таблице.
| \ (с \) | Вертикальный след для \ (x = c \) |
|---|---|
| \ (- \ dfrac {π} {4} \) | \ (z = — \ dfrac {\ sqrt {2} \ cos y} {2} \) |
| 0 | \ (г = 0 \) |
| \ (\ dfrac {π} {4} \) | \ (z = \ dfrac {\ sqrt {2} \ cos y} {2} \) |
Аналогичным образом мы можем подставить \ (y-значения \) в уравнение \ (f (x, y) \), чтобы получить следы в \ (yz-plane, \), как указано в следующая таблица.
| \ (д \) | Вертикальный след для \ (y = d \) |
|---|---|
| \ (\ dfrac {π} {4} \) | \ (z = \ dfrac {\ sqrt {2} \ sin x} {2} \) |
| 0 | \ (г = \ грех х \) |
| \ (- \ dfrac {π} {4} \) | \ (z = \ dfrac {\ sqrt {2} \ sin x} {2} \) |
Три следа в \ (xz-плоскости \) являются косинусоидальными функциями; три следа в \ (yz-плоскости \) являются синусоидальными функциями.2 \). Эта функция описывает параболу, раскрывающуюся вниз в плоскости \ (y = 3 \).
Функции двух переменных могут создавать поразительные поверхности. На рисунке \ (\ PageIndex {11} \) показаны два примера.
Рисунок \ (\ PageIndex {11} \): Примеры поверхностей, представляющих функции двух переменных: (а) комбинация степенной функции и синусоидальной функции и (б) комбинация тригонометрических, экспоненциальных и логарифмических функций.Функции более двух переменных
До сих пор мы рассматривали только функции двух переменных.2) \ sin t− (3x + 5y) \ cos t. \]
В первой функции \ ((x, y, z) \) представляет точку в пространстве, а функция \ (f \) сопоставляет каждую точку в пространстве с четвертой величиной, такой как температура или скорость ветра. Во второй функции \ ((x, y) \) может представлять точку на плоскости, а \ (t \) может представлять время. Функция может сопоставлять точку на плоскости с третьей величиной (например, давлением) в данный момент времени \ (t \). Метод поиска области определения функции более двух переменных аналогичен методу для функций одной или двух переменных.2−4 \} \ nonumber \]
Функции двух переменных имеют кривые уровня, которые показаны как кривые на \ (xy-плоскости. \). Однако, когда функция имеет три переменных, кривые становятся поверхностями, поэтому мы можем определить поверхности уровня для функций трех переменных.
Определение: ровная поверхность функции трех переменных
Для функции \ (f (x, y, z) \) и числа \ (c \) в диапазоне \ (f \) поверхность уровня функции трех переменных определяется как множество точек, удовлетворяющих уравнению \ (f (x, y, z) = c.2 = 16 \) описывает сферу радиуса \ (4 \) с центром в точке \ ((1, −2,3). \)
. Числовые промежутки
Числовые промежутки
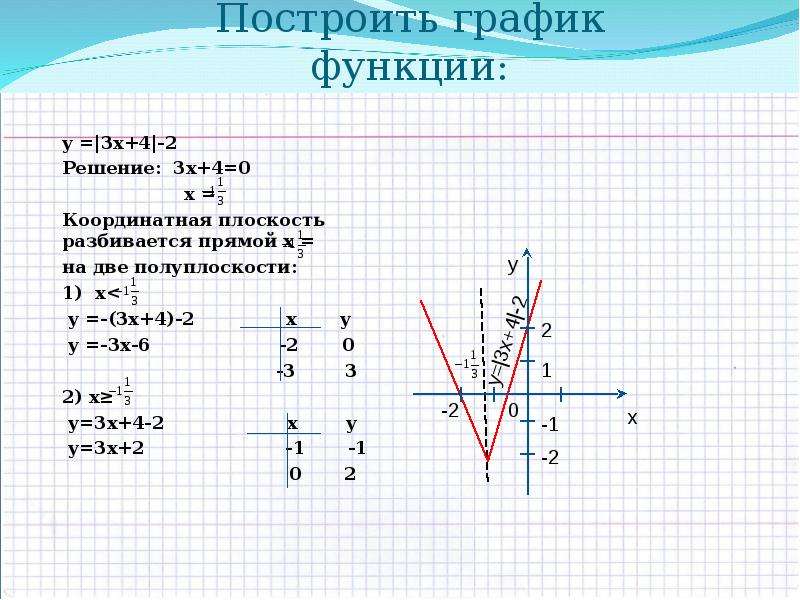 Метод подстановки
Метод подстановки
 Приведение одночлена к стандартному виду
Приведение одночлена к стандартному виду
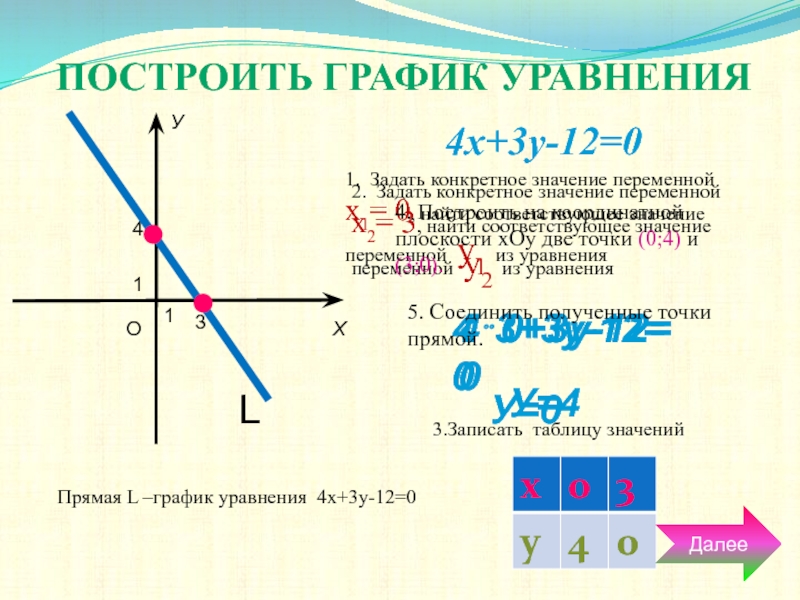 Вынесение общего множителя за скобки
Вынесение общего множителя за скобки
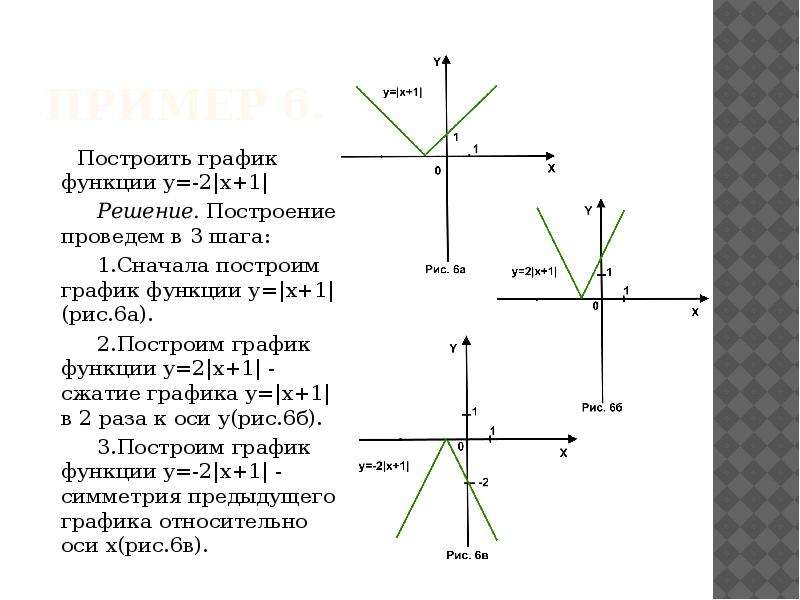 Парабола
Парабола
 Свойства неравенств одинакового смысла
Свойства неравенств одинакового смысла
 Объединение и пересечение множеств
Объединение и пересечение множеств
 Определение чётности и нечётности
Определение чётности и нечётности
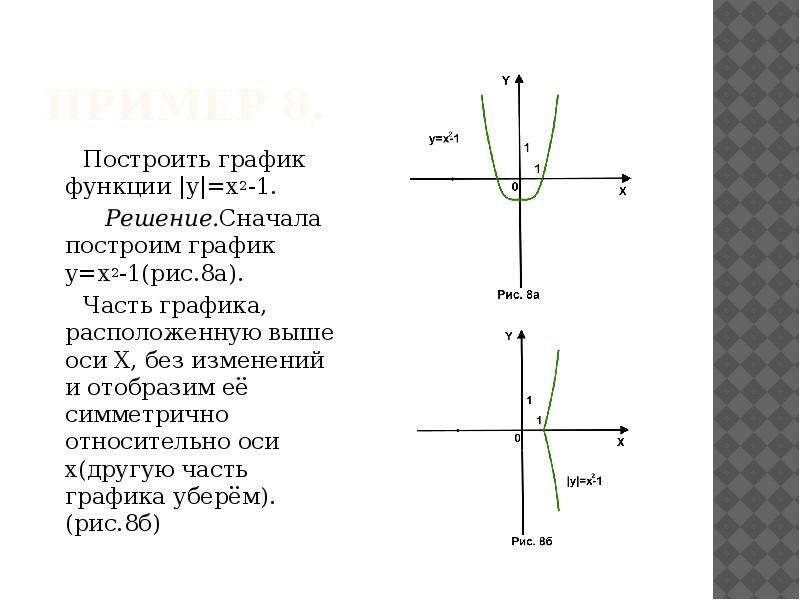 Комбинаторные задачи
Комбинаторные задачи
 Решение уравнений tg x = a, ctg x = a
Решение уравнений tg x = a, ctg x = a
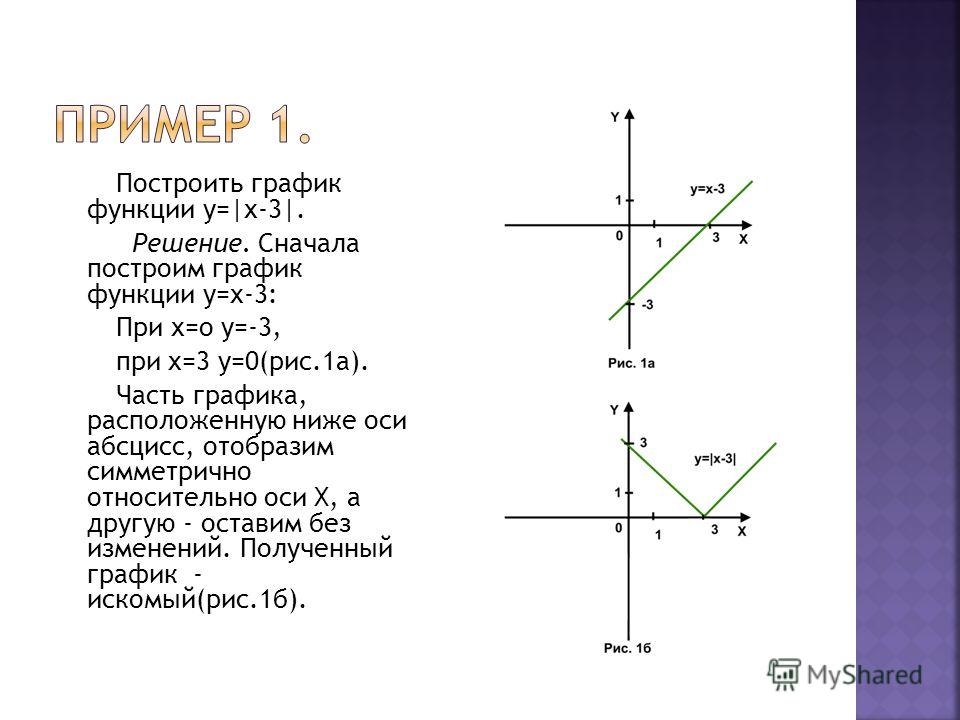 Предел функции на бесконечности
Предел функции на бесконечности
 Преобразование иррациональных выражений
Преобразование иррациональных выражений
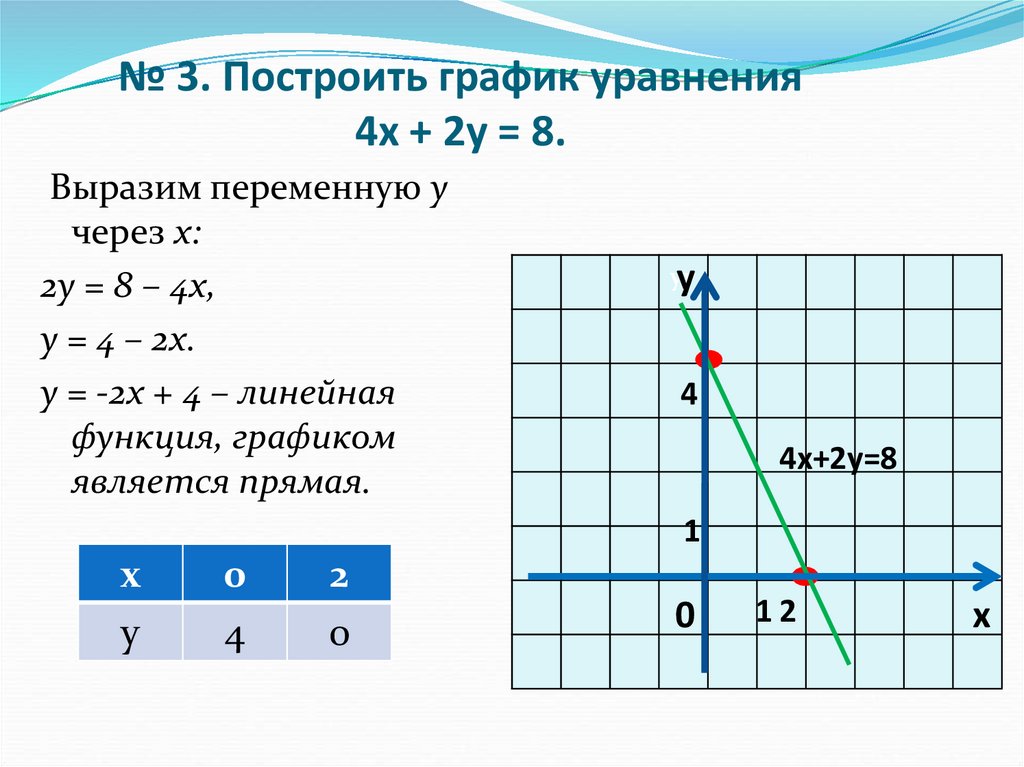 Основное логарифмическое тождество
Основное логарифмическое тождество
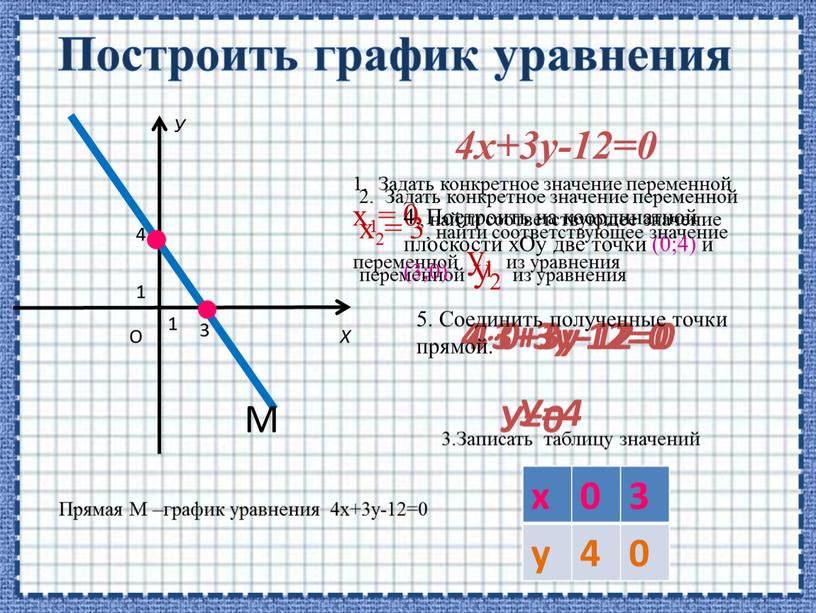 Методы интегрирования
Методы интегрирования
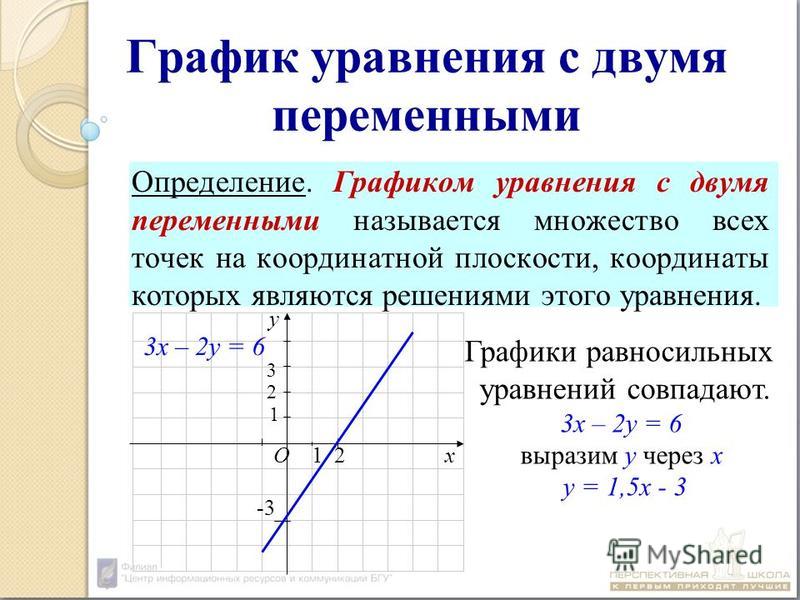 Бином Ньютона
Бином Ньютона
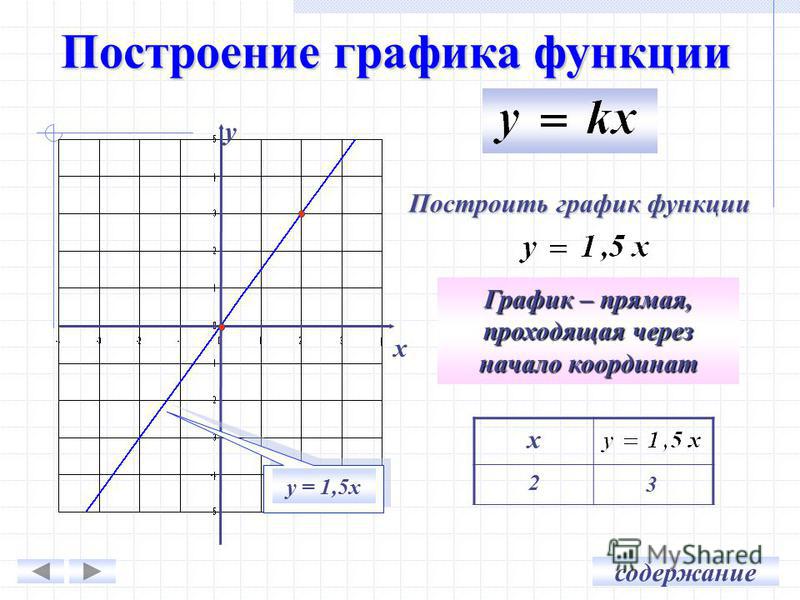 Закон больших чисел
Закон больших чисел
Ваш комментарий будет первым