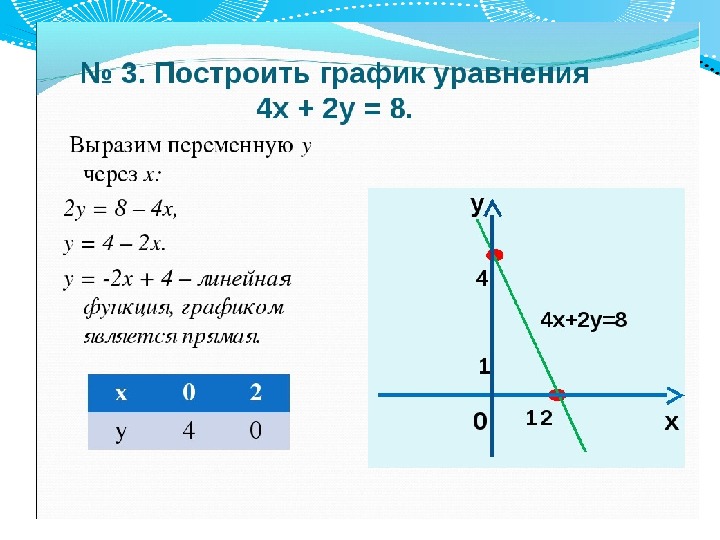
Построение графиков по уравнению: Построение графика функции онлайн

Содержание

Параграф 6

§ 6. ГРАФИКИ УРАВНЕНИЙ И НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ

Таблица 12

1. Построение графиков функции вида y = f (x) + g (x)

Если нам известны графики функций y = f (x) и y = g (x), то эскиз графика функции y = f (x) + g (x) можно построить так: изобразить в одной системе координат графики функций f (x) и g (x), а потом построить искомый график по точкам, выполняя для каждого значения х (из области определения функции f (x) + g (x)) необходимые операции с отрезками, изображающими соответствующие ординаты f (x) и g (x).

Аналогично можно построить и схематические графики функций

y = f (x)-g (x) и y = -1-.

f (x)

86 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА

Продолж. табл. 12

Пример

Комментарий

Постройте график функции

2 1

у = х2 + -.

Построим в одной системе коор-динат графики функций-слагаемых: у = х2 и у = — (на рисунке они

показаны штриховыми линиями).

Для каждого значения х (кроме х = 0, которое не принадлежит области определения заданной функции) справа от оси Оу прибавляем соответствующие отрезки — значения функций f (х) и g (х) (обе функции имеют одинаковые знаки), слева от оси Оу — вычитаем (функции имеют противоположные знаки). На рисунке синей линией изобра-

2 —

жен график функции у = х +—.

2. Графики уравнений и неравенств с двумя переменными

Определение. Графиком уравнения (неравенства) с двумя переменными х и у называется множество всех точек координатной плоскости с координатами (х; у), где пара чисел (х; у) является решением соответствующего уравнения (неравенства).

Графики некоторых уравнений и неравенств

У1 y>f(x) К&/ л/ y<f(x) У1 3 II * х>а У’ х<а в II н

0 X 0 а X 0 а х

у’ х2 + у2 > R2 \

\ о ; х t t *

-Д.’

х2 + у2 < R2

§ 6. Графики уравнений и неравенств с двумя переменными 87

Продолж. — на с. 92 (в последнем случае

f (x)

удобно строить графики функций y = f (x) и у = не в одной системе

f (x)

координат, а в разных, расположенных так, чтобы их оси ординат находились на одной прямой).

Заметим, что такой способ построения графика функции не всегда дает возможность определить все характерные особенности поведения графика (часто это можно сделать только в результате специального исследования функции, которое будет рассмотрено в учебнике для 11 класса), но во многих случаях приведенный способ позволяет получить определенное представление о виде графика заданной функции.

2. Графики уравнений и неравенств с двумя переменными. С понятием графика уравнения с двумя переменными вы ознакомились в курсе алгебры. Аналогично вводится и понятие графика неравенства с двумя переменными. Поэтому можно дать общее определение этих графиков:

Графиком уравнения (неравенства) с двумя переменными х и у называется множество всех точек координатной плоскости с координатами (х; у), где пара чисел (х; у) является решением соответствующего уравнения (неравенства).

9 Для построения графика неравенства y > f (x) (или y < f (x)) достаточно иметь график функции y = f (x). Действительно, по определению график функции y = f (x) состоит из всех точек M координатной плоскости с координатами (x; y) = (x; f (x)). Тогда для каждого значения x точки, координаты которых удовлетворяют неравенству y > f (x), будут находиться выше точки M (рис. 42, а), а точки, координаты которых удовлетворяют неравенству y < f (x), будут находиться ниже точки M (рис. 42, б). Таким образом,

график неравенства y > f (x) состоит из всех точек координатной плоскости, находящихся выше графика функции y = f (я), а график неравенства y < f (я) состоит из всех точек координатной плоскости, находящихся ниже графика функции y = f (я). О

Например, на рисунке 43 изображен график неравенства y > x2, а на рисунке 44 — график неравенства y < x2. Поскольку точки графика y = x2 не принадлежат графику неравенства y > x2, то на первом графике парабола y = x2 изображена штриховой линией; а так как точки графика y = x2 принадлежат графику неравенства y < x2, то на втором графике парабола y = x2 изображена сплошной линией.

Аналогично, если на координатной плоскости есть прямая x = а, то графиком неравенства x > а будут все точки координатной плоскости, находящиеся справа от этой прямой, а графиком неравенства x < а будут все точки координатной плоскости, находящиеся слева от этой прямой.

§ 6. Графики уравнений и неравенств с двумя переменными 89

у\ 1

/(*)

* V>f(x) , А?’

1 0 х х

У f(x) У $ М%» y<f{x)

# 0 X

У1

V \

\ У > х21 1 1 1 1 1 1 1 / i / /

0 ж

Рис. 42

Рис. 43

Рис. 45

Например, на рисунке 45 изображен график неравенства x> 2, а на рисунке 46 — график неравенства x < —1.

Отметим, что в том случае, когда на координатной плоскости есть изо-бражение окружности x2 + y2 = R2, то

графиком неравенства x2 + y2 < R2 будут все точки координатной плоскости, находящиеся внутри окружности, а графиком неравенства x2 + y2 > R2 будут все точки координатной плоскости, находящиеся вне окружности.

0 Действительно, если на координатной плоскости рассмотреть точку M (x, y), то OM2 = x2 + y2 (O — начало координат). Если x2 + y2 = R2 (где R > 0), то OM2 = R2, таким образом, OM = R — точка M лежит на окружности радиуса R с центром в начале координат (рис. 47, а).

Если x2 + y2 < R2, то OM2 < R2, таким образом, OM< R. То есть неравенству x2 + y2 < R2 удовлетворяют координаты всех точек (и только этих точек), которые находятся внутри круга, ограниченного окружностью радиуса R с центром в начале координат (рис. 47, б).

Если x2 + y2 > R2, то OM2 >R2, таким образом, OM> R. То есть неравенству x2 + y2 > R2 удовлетворяют координаты всех точек (и только этих точек), которые находятся вне круга, ограниченного окружностью радиуса R (рис. 47, в).

Аналогично, если на плоскости есть изображение окружности (x — а)2 + + (y — b)2 = R2, то графиком неравенства (x — а)2 + (y — b)2 < R2 будут все точ

90 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА

ки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства (х — а)2 + (у — b)2 > R2 будут все точки координатной плоскости, находящиеся вне окружности. !Я 1 t * / ✓ и

Рис. 47

У’ * * / / / 1 1 х2 + у2>9 ч ч ч \ \ 1 1

ч о з: х t / / / г *

Рис. 48

3. Геометрические преобразования графика уравнения F (я; у) = 0.

О По определению график уравнения

F (х; у) = 0 (1)

состоит из всех точек М (х0; у0) координатной плоскости, координаты (х0; у0) которых являются решениями этого уравнения. Это означает, что при подстановке пары чисел (х0; у0) в данное уравнение оно обращается в верное числовое равенство, таким образом, F (х0; у0) = 0 — верное равенство.

Рассмотрим точку М1 (х0 + а; у0 + b). Если координаты этой точки подставить в уравнение

F (х — а; у — b) = 0, (2)

то получим верное равенство F (х0; у0) = 0. Поэтому координаты точки М1 являются решениями уравнения (2), значит, точка M1 принадлежит графику уравнения F (х — а; у — b) = 0.

Точку М1 (х0 + а; у0 + b) можно получить из точки М (х0; у0) параллельным переносом ее на вектор n (a; b). Поскольку каждая точка М1 графика

уравнения F (х — а; у — b) = 0 получается из точки М графика уравнения F (х; у) = 0 параллельным переносом ее на вектор n (a; b) (рис. 50), то и весь

график уравнения F (я — a; у — b) = 0 можно получить из графика уравнения F (х; у) = 0 параллельным переносом его на вектор

n (a; b). О

• Для обоснования связи между графиками F (х; у) = 0 и F (| х |; у) = 0 до-статочно заметить, что при х 1 0 уравнение F (| х |; у) = 0 совпадает с урав-нением F (х; у) = 0, таким образом, совпадают и их графики справа от оси Оу и на самой оси. Пусть точка M (х0; у0) (где х0 1 0) — одна из общих точек этих графиков. Тогда F (х0; у0) = 0 — верное равенство.

Рассмотрим точку М1 (-х0; у0 ). Если координаты этой точки подставить в уравнение F (| х |; у) = 0 и учесть, что х0 1 0, то получим равенство F (х0; у0) = 0. Поэтому координаты точки М1 являются решениями уравнения F (| х |; у) = 0, значит, точка M1 принадлежит графику этого уравнения. Учитывая, что точки М и М1 симметричны относительно оси Оу (рис. 51) , получаем:

график уравнения F (| х |; у) = 0 можно получить из графика урав-нения F (х; у) = 0 следующим образом: часть графика уравнения F (х; у) = 0 справа от оси Оу (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси Оу. О

Аналогично обосновывается, что

для построения графика уравнения F (х; | у |) = 0 часть графика уравнения F (х; у) = 0 выше оси Ох (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси Ох.

В таблице 12 приведены простейшие примеры использования геометрических преобразований графиков уравнений. Указанные соотношения приходится применять в заданиях типа: построить график уравнения или неравенства или изобразить на координатной плоскости множество точек, координаты которых удовлетворяют заданному уравнению (неравенству).

92 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА

Задача 1*

Примеры решения задач

—

Постройте график функции у =

х — 9

Решение

► х2 — 9 = 0 при х = ±3. = ~2——. Поэтому

проведем через эти точки вертикаль- ные прямые, которые не пересекают

—

график функции у =

f (х)

Затем для

каждого значения х разделим 1 на соответствующее значение ординаты f (х) (используя то, что ординаты f (х) отмечены на верхнем графике). На рисунке синей линией изображен результат — график функции

у = ~2——. (Для построения этого гра-

х2 — 9

фика масштаб по осям Ох и Оу выбран разный.)

Задача 2

Покажите штриховкой на координатной плоскости множество

х2 + у m о, х — у < 2.

Комментарий

точек, координаты которых удовлетворяют системе

Решение ► Заданная система равносильна си-

\у m -х2,

стеме

у > х — 2.

Перепишем заданную систему так, чтобы было удобно изображать графики данных неравенств (то есть запишем неравенства в виде у > f (х)

§ 6. Графики уравнений и неравенств с двумя переменными 93

Изобразим штриховкой графики неравенств системы (первого — вер-тикальной штриховкой, второго — горизонтальной):

наты которых удовлетворяют системе, будет таким:

Задача 3*

или у < f (х)).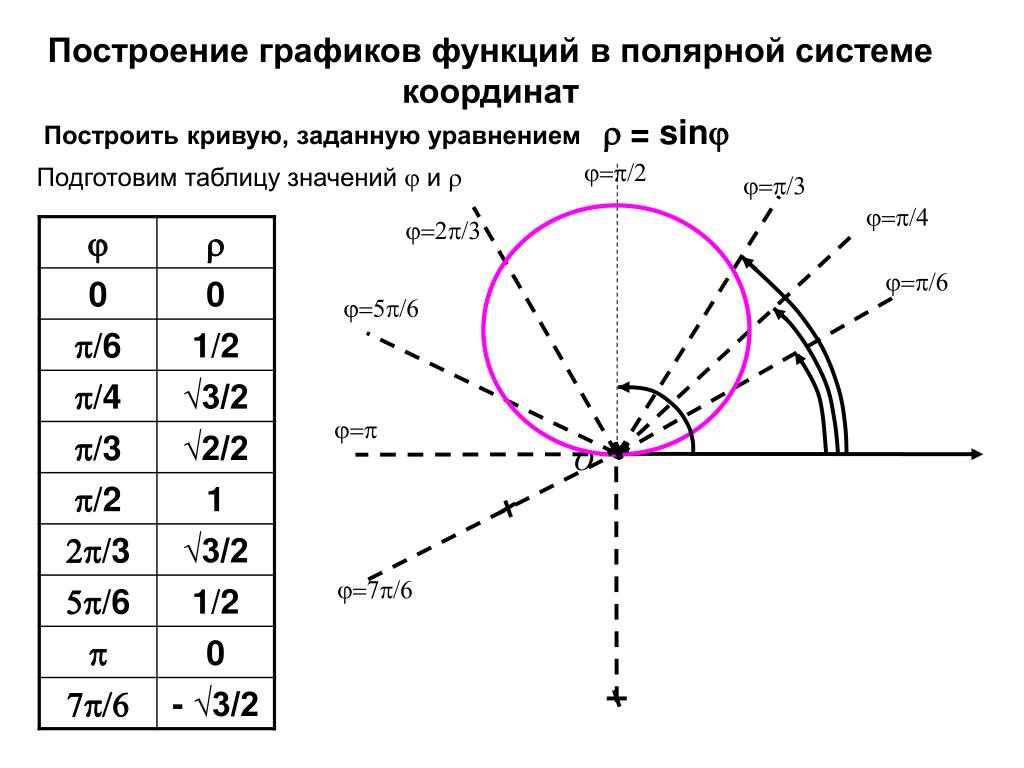 Множество точек, ко-ординаты которых удовлетворяют неравенству у < -х2, является объ-единением точек параболы у = -х2 и точек координатной плоскости, находящихся ниже параболы (на ри-сунке это множество обозначено вер-тикальной штриховкой). Множество точек, координаты которых удовлет-воряют неравенству у > х — 2, состоит из точек координатной плоскости, находящихся выше прямой у = х — 2 (на рисунке это множество обозначено горизонтальной штриховкой).

Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, заданных каждым из неравенств данной системы (на рисунке пересечению множеств соответствует та область, где штриховки наложились друг на друга).

Заметим, что в подобных заданиях можно не выполнять промежуточных рисунков, а сразу штриховать искомое множество точек координатной плоскости (выше прямой у = х — 2 и ниже параболы у = -х2 вместе с той частью параболы, которая лежит выше прямой).

Постройте график уравнения | х — у | + 2 | х+у | = х + 6. Ориентир

Для упрощения выражения с несколькими модулями с двумя переменными можно найти нули подмодульных выражений (то есть приравнять их к нулю) и разбить область определения рассматриваемого выражения на несколько частей, в каждой из которых знак каждого модуля раскрывается однозначно.

Используя этот ориентир, получаем план решения примера.

Приравняем к нулю подмодульные выражения х — у = 0 (отсюда у = х) и х + у = 0 (отсюда у = -х). Прямые у = х и у = -х разбивают координатную плоскость на четыре области. В каждой из этих областей знак каж

94 Раздел 1. ФУНКЦИИ, УРАВНЕНИЯ, НЕРАВЕНСТВА

дого модуля раскрывается однозначно, после преобразования полученного равенства строим соответствующую часть графика заданного уравнения.

Решение

► 1. Область определения: х — любое действительное число, у — любое действительное число.

2. х — у = 0 при у = х; х + у = 0 при у = -х.

3. Прямые у = х и у = -х разбивают координатную плоскость на четыре части, в каждой из которых обозначены знаки первого и второго под- модульных выражений (рис.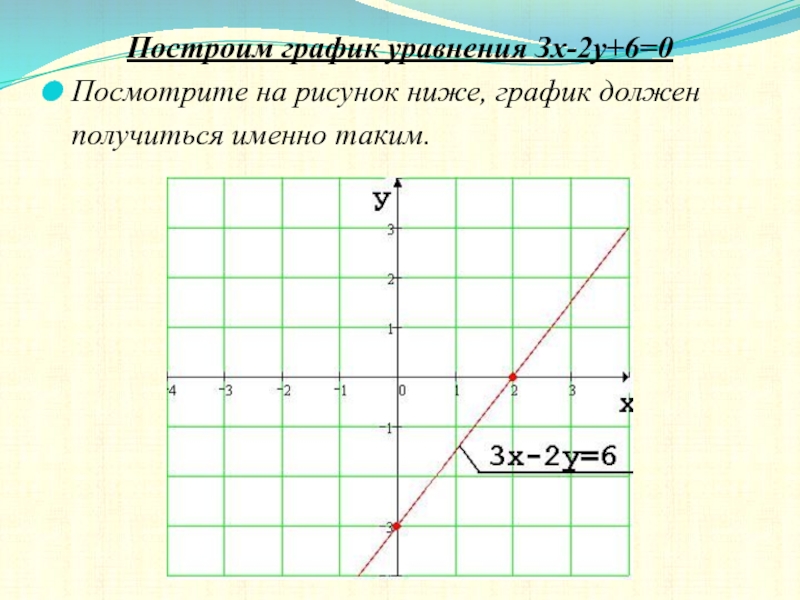

Вопросы для контроля

1. Объясните на примерах, как можно, имея графики функций y = f (х) и y = g (х), построить эскиз графика функции y = f (х) + g (х) и функции

_ 1 у _ f (х).

2. Что называется графиком уравнения с двумя переменными? Что называ-ется графиком неравенства с двумя переменными? Приведите примеры.

3. Как, зная график функции y = f (х), построить график неравенства y > f (х) и неравенства y < f (х)? Приведите примеры.

4. Как, зная график уравнения F (х; y) = 0, можно построить график урав-нения F (х — a; y — b) = 0 и уравнений F (| х| ; y) = 0 и F (х; | y |) = 0? При-ведите примеры.

5*. Обоснуйте правила геометрических преобразований графика уравнения F (х; y) = 0 для получения графиков уравнений F (х — a; y — b) = 0, F (| х |; y) = 0, F (х; | y |) = 0.

6. Объясните на примере, как можно найти на координатной плоскости мно-жество точек, координаты которых удовлетворяют системе неравенств с двумя переменными.

Упражнения

1. Постройте эскиз графика функции:

1) у _ х + —; 2) у _ х — —; 3*) у _ х3 + —; 4*) у _ х2 — —.

х х х х

2. Постройте график уравнения:

1) | y | = х — 2; 2) | y | = х2- х; 3) | х | = -y2;

4) | х | +| y | = 2; 5) | х | — | y | = 2.

3. Постройте график неравенства:

1) y > х2 — 3; 2) у < —; 3) х2 + y2 m 25;

4) (х — 2)2 + (y + 3 )2 > 4.

4. Покажите штриховкой на координатной плоскости множество точек, ко-ординаты которых удовлетворяют системе:

у m 5 — х,

у 1 х,

у m 2х + 4.

5*. Постройте график уравнения:

1) | х — у | — | х + у | = y + 3; 2) | х — 2у | + | 2х — у | = 2 — y;

3) | 3х + у | + | х — у | = 4.

Как построить график в Excel по уравнению правильно

Опубликовано: 03.02.2020Автор: Дмитрий Просветов

Как предоставить информацию, чтобы она лучше воспринималась. Используйте графики. Это особенно актуально в аналитике. Рассмотрим, как построить график в Excel по уравнению.

Содержание

Что это такое
А нужно ли это
Как построить график уравнения регрессии в Excel
Подготовительные работы
Как пользоваться
Анализ
Как построить график квадратного уравнения в Excel
Как построить график линейного уравнения
Вывод

Что это такое

График показывает, как одни величины зависят от других. Информация легче воспринимается. Посмотрите визуально, как отображается динамика изменения данных.

А нужно ли это

Графический способ отображения информации востребован в учебных или научных работах, исследованиях, при создании деловых планов, отчетов, презентаций, формул. Разработчики для построения графиков добавили способы визуального представления: диаграммы, пиктограммы.

Как построить график уравнения регрессии в Excel

Регрессионный анализ — статистический метод исследования. Устанавливает, как независимые величины влияют на зависимую переменную. Редактор предлагает инструменты для такого анализа.

Подготовительные работы

Перед использованием функции активируйте Пакет анализа. Перейдите:
Выберите раздел:
Далее:
Прокрутите окно вниз, выберите:
Отметьте пункт:
Открыв раздел «Данные», появится кнопка «Анализ».

Как пользоваться

Рассмотрим на примере. В таблице указана температура воздуха и число покупателей. Данные выводятся за рабочий день. Как температура влияет на посещаемость. Перейдите:
Выберите:
Отобразится окно настроек, где входной интервал:

Y. Ячейки с данными влияние факторов на которые нужно установить. Это число покупателей. Адрес пропишите вручную или выделите соответствующий столбец;
Х. Данные, влияние на которые нужно установить. В примере, нужно узнать, как температура влияет на количество покупателей. Поэтому выделяем ячейки в столбце «Температура».

Анализ

Нажав кнопку «ОК», отобразится результат.
Основной показатель — R-квадрат. Обозначает качество. Он равен 0,825 (82,5%). Что это означает? Зависимости, где показатель меньше 0,5 считается плохим. Поэтому в примере это хороший показатель. Y-пересечение. Число покупателей, если другие показатели равны нулю. 62,02 высокий показатель.

Как построить график квадратного уравнения в Excel

График функции имеет вид: y=ax2+bx+c. Рассмотрим диапазон значений: [-4:4].

Составьте таблицу как на скриншоте;
В третьей строке указываем коэффициенты и их значения;
Пятая — диапазон значений;
В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3;

Копируем её на весь диапазон значений аргумента вправо.
При вычислении формулы прописывается знак «$». Используется чтобы ссылка была постоянной. Подробнее смотрите в статье: «Как зафиксировать ячейку».
Выделите диапазон значений по ним будем строить график. Перейдите:
Поместите график в свободное место на листе.

Как построить график линейного уравнения

Функция имеет вид: y=kx+b. Построим в интервале [-4;4].

В таблицу прописываем значение постоянных величин. Строка три;
Строка 5. Вводим диапазон значений;
Ячейка В6. Прописываем формулу.

Выделите диапазон ячеек A5:J6. Далее:
График — прямая линия.

Вывод

Мы рассмотрели, как построить график в Экселе (Excel) по уравнению. Главное — правильно выбрать параметры и диаграмму. Тогда график точно отобразит данные.

Графики линейных уравнений — Примеры, Графики линейных уравнений с двумя переменными

30-DAY PROMIS | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЕГ*

*T&C Apply

LearnPracticeDownload

Графики линейных уравнений — это процесс представления линейных уравнений с одной или двумя переменными на графике. Линейное уравнение — это уравнение первой степени, т. е. наивысшее значение степени или показателя степени переменной может быть только 1, но не больше 1 ни в одном из случаев. Решение линейного уравнения заключается в нахождении значений содержащихся в нем переменных, а графический метод является одним из методов решения линейных уравнений, линейных уравнений с одной или двумя переменными.

1.	Что такое графическое отображение линейных уравнений?
2.	Графики линейных уравнений
3.	Графики линейных уравнений с двумя переменными
4.	Часто задаваемые вопросы о графических линейных уравнениях

Что такое графическое отображение линейных уравнений?

Линейные уравнения — это алгебраические уравнения, в которых каждый член имеет вещественную константу, а уравнение содержит 2 переменные старшей степени 1. Мы представляем линейное уравнение в форме y=mx+b, также известной как форма точки пересечения y. Представление линейного уравнения на графике называется графическим отображением линейных уравнений в виде прямой линии с одной или двумя переменными. Давайте посмотрим на пример построения графика линейного уравнения с одной переменной. Мы должны представить уравнение x+2y=7 в виде графика.

Здесь уравнение x+2y=7 образует на графике прямую линию. Точно так же все линейные уравнения создают на графике прямую линию как с одной, так и с двумя переменными. График линейного уравнения с одной переменной x образует вертикальную линию, параллельную оси y, и наоборот, тогда как график линейного уравнения с двумя переменными x и y образует прямую линию. Графики линейных уравнений помогают решить многие реальные задачи линейного программирования.

Примечание:

Точка, в которой любая линия пересекает ось X на графике — точка пересечения с X
Точка, в которой любая линия пересекает ось Y на графике — Y-Intercept

Графики линейных уравнений

График линейного уравнения заключается в решении линейных уравнений и представлении решения в координатной плоскости. При построении уравнения на графике достаточно двух пар (x, y). Однако мы не можем выяснить, есть ли ошибки в получении этих значений, поскольку две точки всегда можно соединить и представить в виде линии. Следовательно, рекомендуется нанести еще одну точку, чтобы убедиться, что решения, полученные для данного линейного уравнения, верны. Для построения линейного уравнения с одной переменной необходимо предпринять следующие шаги:

Убедитесь, что линейное уравнение представлено в виде точки пересечения с точкой y, то есть y = mx + b.
Примените метод проб и ошибок и найдите значения (x, y) до трех пар, которые удовлетворяют линейному уравнению.
Найдите точки пересечения x и y уравнения. Для точки пересечения по оси y подставьте в уравнение значение x = 0. Это приводит к x = a, для x-пересечения подставьте значение y = 0 в уравнение. Это приводит к y = c.
Таким образом, это точки (a, 0) и (0, c). Составьте табличную форму и введите значения x и y соответственно.
Нанесите все точки на миллиметровую бумагу.
Соедините все точки, отмеченные на графике, и вы получите прямую линию, представляющую данное линейное уравнение графически.

Пример: Нарисуйте график линейного уравнения x+2y=7.

Решение: Мы выполним следующие шаги:

Шаг 1: Проверьте, имеет ли данное линейное уравнение x+2y=7 форму y = mx + b. [При преобразовании получаем: у = — (1/2) х + 7/2]
Шаг 2: Найдите точку пересечения x и y соответственно. Для этого в уравнении положим y = 0: x = 7-2(0), x=7. Теперь подставьте x=0 в уравнении. 2y=7-(0), y=7/2 = 3,5
Шаг 3: Примените метод проб и ошибок и найдите 3 пары значений (x, y), которые удовлетворяют заданному линейному уравнению x=7-2y. (см. таблицу ниже)
Шаг 4: Нанесите точки (7,0), (5,1) и (3,2) на график.
Шаг 5: Соедините все точки, отмеченные на миллиметровке, и получите прямую линию, графически представляющую заданное линейное уравнение.

См. значения x и y в следующей таблице:

x	7	5	3
г	0	1	2

Графики линейных уравнений с двумя переменными

Графики линейных уравнений с двумя переменными выполняются так же, как и с одной переменной. Линии, нанесенные на график, могут либо пересекаться друг с другом в одной точке, либо быть параллельными друг другу, что не дает решения. Иногда линии могут совпадать друг с другом, оставляя каждую точку на этой линии в качестве решения, в результате чего данная система имеет бесконечное количество решений. Если система имеет решение, то говорят, что она непротиворечива; в противном случае говорят, что он несовместим. Ниже приведены шаги для построения графика линейных уравнений с двумя переменными:

Шаг 1: Чтобы построить линейное уравнение с двумя переменными, мы рисуем оба уравнения.
Шаг 2. Чтобы построить уравнение вручную, сначала преобразуйте его в форму y=mx+b, решив уравнение относительно y.
Шаг 3: Начните задавать значения x как 0, 1, 2 и т. д. и найдите соответствующие значения y или наоборот.
Шаг 4: Определите точку, где пересекаются обе линии.
Шаг 5: Точка пересечения — это решение.

Пример: Найдите решение следующей системы уравнений графически.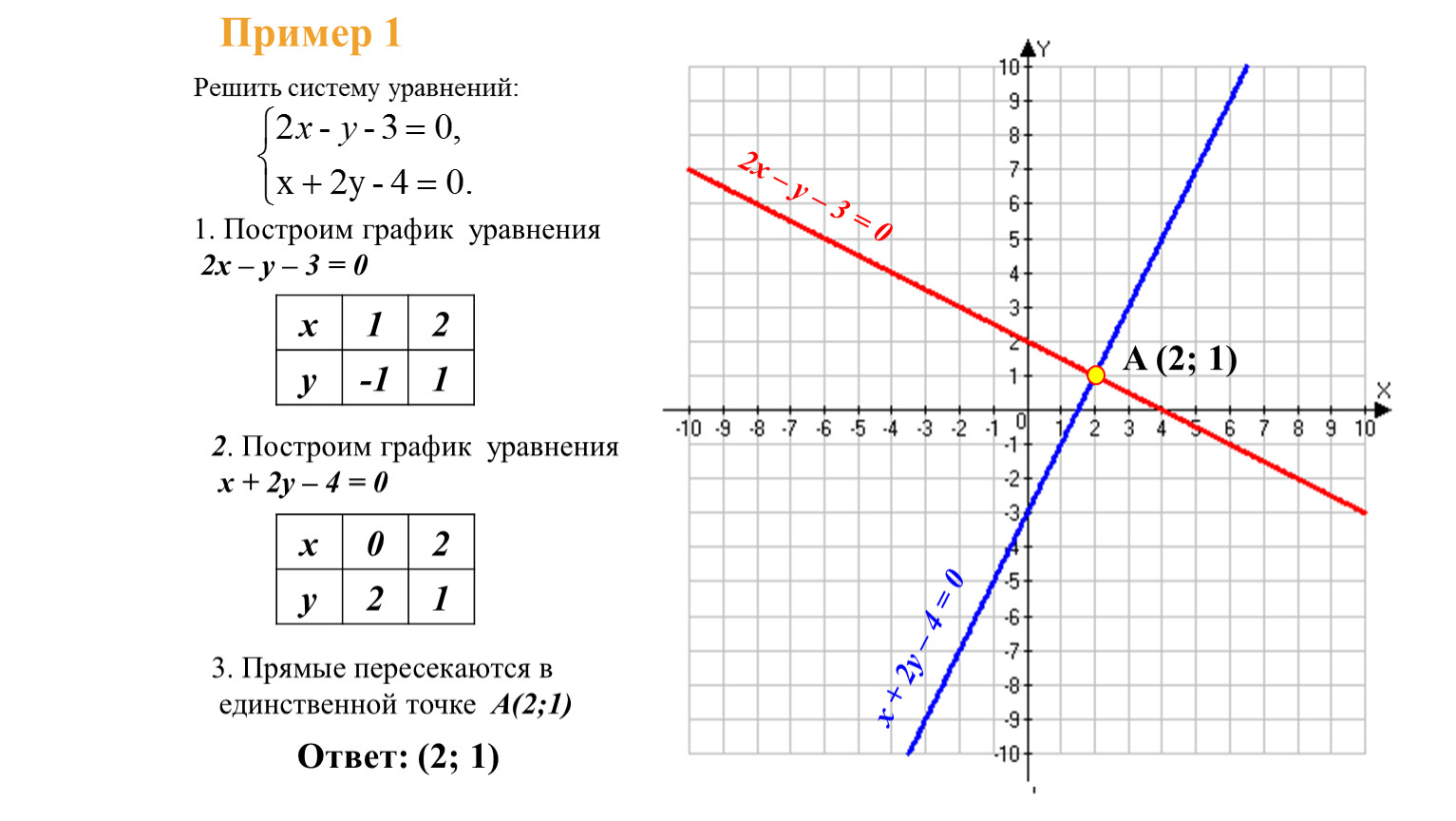

-x+2y-3 =0

3x+4y-11=0

Решение: Используя шаги, упомянутые выше, мы изобразим их на графике и посмотрим, пересекаются ли они в точке. Как вы можете видеть ниже, обе линии встречаются в (1, 2). Таким образом, решение данной системы линейных уравнений есть x=1 и y=2.

Важные моменты

Линейное уравнение с двумя переменными имеет бесконечно много решений.
График линейного уравнения всегда представляет собой прямую линию.
Уравнение y = mx всегда проходит через начало координат (0, 0).

Загадочные вопросы

Сумма цифр двузначного числа равна 8. При перестановке цифр число увеличивается на 18. Найдите число.
В копилке Джейка 11 монет (только четвертак или десятицентовик) номиналом 1,85 доллара. Сколько десятицентовиков и четвертаков в копилке?

Темы по теме

Линейные уравнения
Линейные уравнения с одной переменной
Линейные уравнения с двумя переменными
Калькулятор решения линейных уравнений
Формула линейного уравнения
Перечислите методы, используемые для решения линейных уравнений
Какое решение системы линейных уравнений?

Примеры построения графиков линейных уравнений

Пример 1: Изабелла имеет линейное уравнение x — 2y = 2. Помогите ей нарисовать линейное уравнение на графике.
Решение:
Данное линейное уравнение имеет вид x-2y=2. Преобразуйте уравнение в виде y = mx + b⇒ y = x/2 — 1. Нам нужно найти точки пересечения x и y соответственно. Для этого в уравнении подставьте y=0⇒ x=2(0)+2, x=2. Теперь подставьте x=0 в уравнении. 2у=(0) — 2, у=1. Теперь мы применим метод проб и ошибок и найдем 3 пары значений (x, y), которые удовлетворяют заданному линейному уравнению y=x/2-1. См. значения x и y в следующей таблице:
х 2 4 0
г 0 1 -1
Нанесите точки (2,0),(4,1),(0,-1) на график. Соедините все точки, отмеченные на миллиметровке, и получите прямую линию, графически изображающую заданное линейное уравнение.
Пример 2: Уильям хочет построить график -1/2x+1/3y=1. Помогите ему построить график для линейных уравнений.
Решение:
Данное линейное уравнение имеет вид -1/2x+1/3y=1. Преобразуйте уравнение в виде y = mx + b⇒ 6 + 6x/2. Нам нужно найти точки пересечения x и y соответственно. Для этого мы можем применить метод проб и ошибок, поставив в уравнении y=6⇒ x=3. Теперь подставьте x=2 в уравнении. у=3. См. значения x и y в следующей таблице:
х 2 0
у 6 3
Решения (2,6) (0,3)

х	2	4	0
г	0	1	-1

х	2	0
у	6	3
Решения	(2,6)	(0,3)

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по построению графиков линейных уравнений

перейти к слайдуперейти к слайдуперейти к слайду

Часто задаваемые вопросы о графических линейных уравнениях

Как построить линейное уравнение?

Основные методы построения графика линейного уравнения:

Первый метод заключается в нанесении всех точек на график и последующем проведении линии через эти точки.
Второй способ заключается в использовании точки пересечения оси Y и наклона уравнения.

Какие 3 способа построить линейное уравнение?

3 способа построения графика линейного уравнения:

Использование двух точек для построения графика линейного уравнения.
Используйте наклон и точку пересечения с координатой Y линейного уравнения.
Использование точек пересечения x и y линейного уравнения.

Как построить график линейного уравнения с двумя точками?

Графическое линейное уравнение с двумя точками:

Найдите точку пересечения оси Y из линейного уравнения и постройте точку.
Из точки пересечения оси Y линейного уравнения используйте наклон, чтобы найти вторую точку и нанести ее на график.
Соедините две точки на графике прямой линией.

Какая формула линейного уравнения?

Формула линейного уравнения: y = mx + b.

Как построить линейное уравнение с помощью точек пересечения?

Чтобы найти точки пересечения алгебраически, мы используем тот факт, что все точки пересечения по оси x имеют y=0 и все точки пересечения по оси y имеют x=0.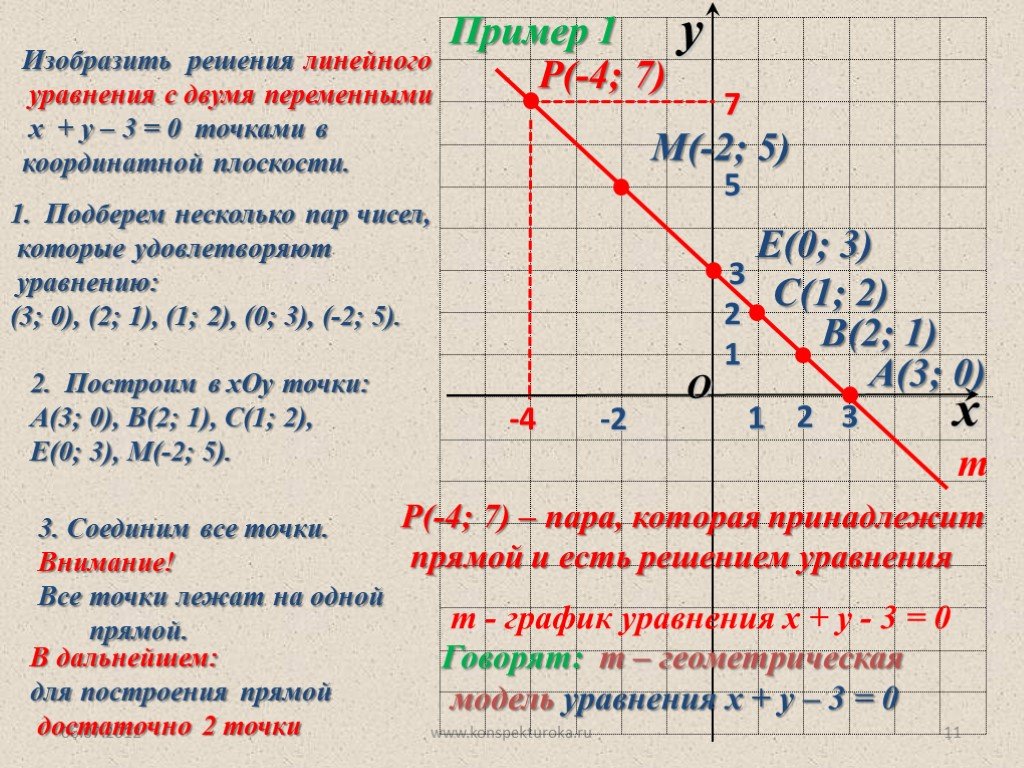

Определите соответствующие значения x и y, подставив значения точек пересечения x и y соответственно.

Какое минимальное количество точек необходимо для построения графика линейного уравнения?

Две точки — это минимальное количество точек, необходимое для построения графика линейного уравнения.

Как найти точку пересечения Y на графике?

Точка пересечения графика по оси Y — это точка, в которой график пересекает ось Y, а в точке Y координата X равна нулю.

Как найти точки пересечения графика?

Прежде всего, уравнение должно удовлетворять условию ax+by=c. Затем вы просто устанавливаете x = 0, чтобы найти точку пересечения с осью y, и устанавливаете y = 0, чтобы найти точку пересечения с x. Затем найдите соответствующие значения.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочий лист линейного уравнения

Рабочие листы по математике и визуальный учебный план

1.1: График линейного уравнения

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 37805

Рупиндер Секон и Роберта Блум
Колледж Де Анза

Цели обучения

В этом разделе вы научитесь:

Рисовать линию, зная ее уравнение
Нарисуйте линию, если вам дано ее уравнение в параметрической форме
Начертите и найдите уравнения вертикальных и горизонтальных линий

Построение линии из уравнения

Уравнения, графики которых представляют собой прямые линии, называются линейными уравнениями. Ниже приведены некоторые примеры линейных уравнений:

$2 x-3 y=6, \quad 3 x=4 y-7, \quad y=2 x-5, \quad 2 y=3, \quad \text { и } \quad x-2=0$

Линия полностью определяется двумя точками. Следовательно, чтобы построить линейное уравнение, нам нужно найти координаты двух точек. Этого можно добиться, выбрав произвольное значение x или y, а затем найдя другую переменную.

Пример $\PageIndex{1}$

Нарисуйте прямую: $y = 3x + 2$

Решение

Нам нужно найти координаты хотя бы двух точек. Мы произвольно выбираем x = — 1, x = 0 и x = 1.

Если x = -1, то y = 3(-1) + 2 или -1. Следовательно, (-1, -1) — точка на этой прямой.
Если x = 0, то y = 3(0) + 2 или y = 2. Отсюда точка (0, 2).
Если x = 1, то y = 5, и мы получаем точку (1, 5).

Ниже результаты суммированы, а линия построена на графике.

х	-1	0	1
у	-1	2	5

Пример $\PageIndex{2}$

Нарисуйте линию: $2x + y = 4$

Решение

Опять же, нам нужно найти координату s не менее двух точек .

Мы произвольно выбираем x = -1, x = 0 и y = 2.

Если x = -1, то 2(-1) + y = 4, что дает y = 6. Следовательно, (-1 , 6) — точка на этой прямой.
Если x = 0, то 2(0) + y = 4, что дает y = 4. Отсюда точка (0, 4).
Если y = 2, то 2x + 2 = 4, что дает x = 1 и дает точку (1, 2).

В таблице ниже показаны точки, а линия построена на графике.

х	-1	0	1
у	6	4	2

Точки пересечения

Точки, в которых линия пересекает оси координат, называются точками пересечения .
При построении линии путем нанесения двух точек часто предпочтительнее использовать точки пересечения, поскольку их легко найти.

Чтобы найти значение абсциссы, положим y = 0
Чтобы найти значение точки пересечения с осью y, мы принимаем x = 0.

Пример $\PageIndex{3}$

Найдите точки пересечения линии: $2x — 3y = 6$ и постройте график.

Решение

Чтобы найти точку пересечения по оси x, пусть y = 0 в уравнении и найдите x.

\[\begin{align*} 2x — 3(0) &= 6 \\[4pt] 2x — 0 &= 6 \\[4pt] 2x &= 6 \\[4pt] x &= 3 \end {align*} \nonumber \]

Таким образом, точка пересечения с x является точкой (3,0).

Чтобы найти точку пересечения с осью y, пусть x = 0 в уравнении и найдите y.

\[\begin{align*} 2(0) — 3y &= 6 \\[4pt] 0 — 3y &= 6 \\[4pt] -3y &= 6 \\[4pt] y &= -2 \end{align*} \nonumber \]

Следовательно, точкой пересечения с осью y является точка (0, -2).

Чтобы построить линию, нанесите точки пересечения по осям x (3,0) и y (0, -2) и используйте их для построения линии.

Построение линии из уравнения в параметрической форме

В высшей математике уравнения прямых иногда записывают в параметрической форме. Например, $x = 3 + 2t$, $y = 1 + t$. Буква $t$ называется параметром или фиктивной переменной.

Параметрические линии можно изобразить в виде графика, найдя значения x и y, заменив t числовыми значениями. Постройте точки, используя их координаты (x, y), и используйте точки, чтобы нарисовать линию.

Пример $\PageIndex{4}$

Нарисуйте линию, заданную параметрическими уравнениями: $x = 3 + 2t$, $y = 1 + t$

Решение

Пусть t = 0, 1 и 2; для каждого значения t найти соответствующие значения для x и y.

Результаты приведены в таблице ниже.

т	х	г	Точка на линии
0	3	1	(3, 1)
1	5	2	(5, 2)
2	7	3	(7, 3)

Горизонтальные и вертикальные линии

Когда уравнение линии имеет только одну переменную, результирующий график представляет собой горизонтальную или вертикальную линию.

График прямой $x = a$, где $a$ — константа, представляет собой вертикальную линию, проходящую через точку $(a, 0)$. Каждая точка на этой линии имеет координату x, равную a, независимо от координаты y.
График прямой $y = b$, где $b$ — константа, представляет собой горизонтальную прямую, проходящую через точку $(0, b)$. Каждая точка на этой прямой имеет координату y, равную b, независимо от координаты x.

Пример $\PageIndex{5}$

Нарисуйте линии: x = -2 и y = 3.

Решение

График линии x = -2 представляет собой вертикальную линию, имеющую координата x -2 независимо от координаты y. График представляет собой вертикальную линию, проходящую через точку (-2, 0).

График линии y = 3 представляет собой горизонтальную линию с координатой y, равной 3, независимо от координаты x. Следовательно, график представляет собой горизонтальную линию, проходящую через точку (0, 3).

Примечание.

Параграф 6

Как построить график в Excel по уравнению правильно

Что это такое

А нужно ли это

Как построить график уравнения регрессии в Excel

Подготовительные работы

Как пользоваться

Анализ

Как построить график квадратного уравнения в Excel

Как построить график линейного уравнения

Вывод

Графики линейных уравнений — Примеры, Графики линейных уравнений с двумя переменными

Что такое графическое отображение линейных уравнений?

Графики линейных уравнений

Графики линейных уравнений с двумя переменными

Примеры построения графиков линейных уравнений

Практические вопросы по построению графиков линейных уравнений

Часто задаваемые вопросы о графических линейных уравнениях

Как построить линейное уравнение?

Какие 3 способа построить линейное уравнение?

Как построить график линейного уравнения с двумя точками?

Какая формула линейного уравнения?

Как построить линейное уравнение с помощью точек пересечения?

Какое минимальное количество точек необходимо для построения графика линейного уравнения?

Как найти точку пересечения Y на графике?

Как найти точки пересечения графика?

1.1: График линейного уравнения

Цели обучения

Построение линии из уравнения

Пример \(\PageIndex{1}\)

Пример \(\PageIndex{2}\)

Точки пересечения

Пример \(\PageIndex{3}\)

Построение линии из уравнения в параметрической форме

Пример \(\PageIndex{4}\)

Горизонтальные и вертикальные линии

Пример \(\PageIndex{5}\)

Ваш комментарий будет первым

Добавить комментарий Отменить ответ