|
№ 1 Воробей
(15; -2), (8; 1), (-1; 7), (-3; 10), (-6; 10), (-7; 8), (-9; 7), (-7; 6), (-6; 5), (-5; 2), (-1; -1) (-2; -6), (-4; -7), (-2; -7), (0; -1), (2; -1), (1; -6)(-1; -7), (1; -7), (3; -1), (4; -1), (6; 0), (13; -4)(15; -2) глаз (-5; 8) |
|
№ 2 Заяц
(1; 7), (0; 10), (-1; 11), (-2; 10), (0; 7), (-2; 5), (-7; 3), (-8; 0), (-9; 1), (-9; 0), (-7; -2), (-2; -2), (-3; -1), (-4; -1), (-1; 3), (0; -2), (1; -2), (0; 0), (0; 3), (1; 4), (2; 4), (3; 5), (2; 6), (1; 9), (0; 10) |
|
№ 3 Волк
(7; -3), (8; -2), (7; 2), (5; 3), (2; 2), (-1; 3)(-3; 4), (-5; 6), (-5; 7), (-6; 6), (-7; 6), (-7,5; 5,5), (-10; 5,5), (-9,5; 4,5), (-7; 4), (-5; 2), (-5; 0), (-4; -2), (-4; -5,5), (-5; -6,5) (-4; -6,5), (-3; -5,5), (-3; -3), (-2; -2), (-2; -1)(1; -1), (3,5; -0,5), (5; -2), (6; -5,5), (5; -6,5), (6; -6,5), (7; -5,5), (6,5; -2,5), (7; -1), (7; 0) и (-2; -2), (-1,5; -5,5), (-2,5; -6,5), (-3,5; -6,5)(-2,5; -5,5), (-3; -3) и (5; -2), (5; -5), (4; -6), (5,5; -6) глаз (-7; 5) |
|
№ 4 Слон
(2; -9), (2; -11), (0; -15), (-2; -13), 9-1; -11), (-1; -10), (-2; -10), (-2; -15), (-5; -15), (-5; -9), (-10; -9), (-9; -13), (-10; -13), (-10; -14), (-13; -14), (-12; -10), (-13; -7), (-16; -9), (-14; -7), (-13; -4), (-10; -2), (-6; -1), (-2; 2), (0; 1), ((4; 1), (6;, 2), (8; 0), (8; -4), (5; -6),(4; -4), (4; -8), (3; -9), (0; -9), (0; -8), (2; -8), (3; -7), (1; -5), (0; -5), (-1; -4), (-2; -6), (-5; -4), (-6; -1) глаза (0; -2) и (4; -2) |
|
№ 5 Кот
(-4; -11), (-11; -11), (-15; -6), (-15; -2), (-12; -1), (-10; -1), (-10; 1), (-6; 3), (2; 3), (3; 4), (5; 4), (6; 5), (6; 4), (7; 5), (7; 4), (8; 2) (8; 1), (5; -1), (5; -2), (7; -2), (7; -3), (5; -3), (5; -4), (1; -4), (1; -5), (-7; -5), (-8; -3), (-10; -3), (-11; -4), (-11; -5), (-6; -7), (-4; -9) (-4; -11) глаз (6; 2) |
|
№ 6 Мышка
(9; 4), (8; 9), (8; 11), (9; 12), (9; 14), (8; 15)(7; 15), (5; 13), (5; 12), (4; 11), (2; 10), (4; 9), (5; 9), (5; 7), (4; 7), (4; 5), (5; 6), (5; 3), (4; 3) (4; 1), (3; 1), (3; 0), (5; 0), 95; 2), (7; 2), (7; 1) (9; 1), (9; 0), (10; 0), (10; 2), (8; 2), (9; 3), (9; 4), (11; 4), (11; 9) |
|
№ 7 Суслик
(-7; -12), (-6; -15), (-2; -19), (3; -21), (5; -22) (7; -21), (8; -20), (8; -21), (9; -21), (10; -19), (9; -17), (9; -15), (9,5; -17), (10,5; -16), (10; -12), (11; -16), (12; -14), (11; -10), (11; -8), (10; -5), (11; -3), (11; -1), (10; 0), (9; -1), (7; -1), (6; 0), (5; -1), (5; -3), (6; -5), (6; -9), (4; -11), (2; -15), (3; -19), (0; -18),(-7; -12) глаза и нос (7; -3) и (9; -3) и (8; -4) |
|
№ 8 Морской котик
(11; 2), (10; 3), (9; 3), (8; 2), (8; 3), (7; 4), (6; 4), (7; 3), (7; 2), (5; 1), (3; 1), (2; 2), (3; 2), (4;3), (2; 3), (1; 2), (0;, 4), (-1; 5), (-2; 5), (-4,5; 4,5), (-2; 3), (-1; 0), (-2; -1), (-3; -1),
(11; 2) глаз (-2; 4) |
|
№ 9 Лось
(3; -1), (2; -3), (2; -5), (3; -5), (3; -4), (5; 0), (6; -1), (6; -6), (8; -6), (7; -3), (7; 1), (5; 3), (6; 5), (6; 7), (4; 8), (-2; 8), (-4; 10), (-6; 9), (-7; 9), (-6; 11), (-7; 11), (-11; 9), (-13; 7), (-13; 6), (-12; 7), (-12; 6), (-10; 6), (-10; 7), (-8; 5), (-7; 5), (-5; 3), (-6; 0), (-6; -4), (-5; -5) (-4; -5), (-5; -4), (-5; -2), (-4; 1), (-3; -1), (-3; -3), (-2; -4), (-3; -5), (-1; -6), (-1; -4), (-3; 3), (-1; 2), (2; 3), (3; 1), (3; -1) Глаз (-9,5; 8,5) |
|
№ 10 Заяц
(-1; -9), (0; -8), (-2; -8), (-1; -9), (-5; -9), (-4; -8), (-6; -5), (-5; -3), (-4; -3), (-4; 0), (-2; 5), (0; 5), (2; 10), (4; 11), (4; 9), (1; 5), (2; 3), (1; 1), (2; 0), (2; -3), ( 3; -3), (4; -5), (2; -8), (3; -9), (-1; -9) и (-2; 2), (-1; 1), (0; 2), (-1; 1), (-1; 2) и (-3; -2), (-2; -2),
(-1; -3), (-1; -5), (-2; -5), (-3; -4), (-4; -4) и (1; -2), (0; -2), (-1; -3), (-1; -5), (0; -5), (1; -4), (2; -4). |
|
№ 11 Верблюд
(-10; -2), (-11; -3), (-10,5; -5), (-11; -7), (-12; -10), (-11; -13), (-13; -13), (-13,5; -7,5), (-13; -7), (-12,5; -5), (-13; -3), (-14; -1), (-14; -4), (-15; -6), (-15; -3), (-14; 2), (-11; 4), (-10; 8), (-8; 9), (-6; 8), (-5; 5), (-3; 8), (-1; 9), (0; 8), (0,5; 6), (0,5; 4), (3; 2,5), (4; 3), (5; 4), (6; 6), (8; 7), (9,5; 7), (10; 6), (11,5; 5,5), (12; 5), (12; 4,5), (11; 5), (12; 4), (11; 4), (10; 3,5), (10,5; 1,5), (10; 0), (6; -3), (2; -5), (1; -7), (1,5; -11), (2; -12), (1; -13), (0; -5), (-0,5; -11), (0; -13), (-1,5; -13), (-1,5; -7), (-2; -5), (-3; -4), (-5; -4,5), (-7; -4,5), (-9; -5), (-10; -6), (-9; -12), (-8,5; -13), (-10; -13), (-10,5; -10), (-10,5; -9,5), (-11; -7) Глаз (8,5; 5,5) |
|
№ 12 Кенгуру
(1,5;. (2; 16), (2,5; 17,5), (2; 18), (1; 16,5), (0,5; 18), (0; 16), (-0,5; 15,5), (-2; 14,5), (-1,5; 14), (-1; 14,5), (-1; 14), (0; 14), (0,5; 13,5), (1,5; 10,5), (0,5; 8), (1; 7), (1; 6), (1,5; 6), (1,5; 7,5), (2,5; 10,5), (2; 7,5), (2,5; 6,5), (3; 6,5), (2,5; 8), (3; 8,5), (3,5; 6,5), (3; 6), (4; 4,5), (4; 3), (0; 3), (0,5; 2), (5,5; 2), (5,5; 4) (6,5; 4), (6,5; 1), (1,5; 0,5) глаз (0; 15,5)
|
|
№ 13 Ёж
(-1; -3), (-3; -3), (-4; -2), (-7; -1), (-6; -1), (-7; 0), (-6; 0), (-7; 1), (-6; 1), (-7; 2), (-6; 2), (-5; 2), (-5; 4), (-4; 3), (-4; 5), (-3; 4), (-2; 6), ( -1; 4), (0; 6), (1; 4), (2; 6), (3; 4), (4; 5), (4; 3), ( 5; 4), (5; 2), (6; 3), (6; 1), (7; 2), (7; 0) (9; -1), (4; -2), (5; -3), (3; -3), (2; -2), (-2; -2), (-1; -3), глаз (5; 0) |
Как построить параболу | Алгебра
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
График квадратичной функции y=x²+bx+c — парабола, ветви которой направлены вверх. Для построения графика достаточно найти координаты вершины параболы. Абсцисса вершины параболы находится по формуле
для нахождения ординаты можно подставить в формулу y=x²+bx+c вместо каждого x найденное значение хₒ: yₒ=xₒ²+bxₒ+c. От вершины (хₒ; yₒ ) строим параболу y=x².
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
y=x²+2x-3
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
y= -x²+2x+8
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Примеры.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем точки пересечения графика с осями координат. В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
y=x²+5x+4
Построить график функции y= -x²-3x.
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
y= -x²-3x
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Matplotlib. Урок 5. Построение 3D графиков. Работа с mplot3d Toolkit
До этого момента все графики, которые мы строили были двумерные, Matplotlib позволяет строить 3D графики. Этой теме посвящен данный урок.
Импортируем необходимые модули для работы с 3D:
import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D
В библиотеке доступны инструменты для построения различных типов графиков. Рассмотрим некоторые из них более подробно.
Линейный графикДля построения линейного графика используется функция plot().
Axes3D.plot(self, xs, ys, *args, zdir=’z’, **kwargs)
- xs: 1D массив
- ys: 1D массив
- zs: скалярное значение или 1D массив
- z координаты.
 Если передан скаляр, то он будет присвоен всем точкам графика.
Если передан скаляр, то он будет присвоен всем точкам графика.
- z координаты.
- zdir: {‘x’, ‘y’, ‘z’}
- Определяет ось, которая будет принята за z направление, значение по умолчанию: ‘z’.
- **kwargs
- Дополнительные аргументы, аналогичные тем, что используются в функции plot() для построения двумерных графиков.
x = np.linspace(-np.pi, np.pi, 50) y = x z = np.cos(x) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot(x, y, z, label='parametric curve')Точечный график
Для построения точечного графика используется функция scatter().
Axes3D.scatter(self, xs, ys, zs=0, zdir=’z’, s=20, c=None, depthshade=True, *args, **kwargs)
- xs, ys: массив
- Координаты точек по осям x и y.
- zs: float или массив, optional
- Координаты точек по оси z.
 Если передан скаляр, то он будет присвоен всем точкам графика. Значение по умолчанию: 0.
Если передан скаляр, то он будет присвоен всем точкам графика. Значение по умолчанию: 0.
- Координаты точек по оси z.
- zdir: {‘x’, ‘y’, ‘z’, ‘-x’, ‘-y’, ‘-z’}, optional
- Определяет ось, которая будет принята за z направление, значение по умолчанию: ‘z’
- s: скаляр или массив, optional
- Размер маркера. Значение по умолчанию: 20.
- c: color, массив, массив значений цвета, optional
- Цвет маркера. Возможные значения:
- Строковое значение цвета для всех маркеров.
- Массив строковых значений цвета.
- Массив чисел, которые могут быть отображены в цвета через функции cmap и norm.
- 2D массив, элементами которого являются RGB или RGBA.
- Цвет маркера. Возможные значения:
- depthshade: bool, optional
- Затенение маркеров для придания эффекта глубины.
- **kwargs
- Дополнительные аргументы, аналогичные тем, что используются в функции scatter() для построения двумерных графиков.

- Дополнительные аргументы, аналогичные тем, что используются в функции scatter() для построения двумерных графиков.
np.random.seed(123) x = np.random.randint(-5, 5, 40) y = np.random.randint(0, 10, 40) z = np.random.randint(-5, 5, 40) s = np.random.randint(10, 100, 20) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.scatter(x, y, z, s=s)Каркасная поверхность
Для построения каркасной поверхности используется функция plot_wireframe().
plot_wireframe(self, X, Y, Z, *args, **kwargs)
- X, Y, Z: 2D массивы
- Данные для построения поверхности.
- rcount, ccount: int
- Максимальное количество элементов каркаса, которое будет использовано в каждом из направлений. Значение по умолчанию: 50.
- rstride, cstride: int
- Параметры определяют величину шага, с которым будут браться элементы строки / столбца из переданных массивов. Параметры rstride, cstride и rcount, ccount являются взаимоисключающими.

- Параметры определяют величину шага, с которым будут браться элементы строки / столбца из переданных массивов. Параметры rstride, cstride и rcount, ccount являются взаимоисключающими.
- **kwargs
- Дополнительные аргументы, определяемые Line3DCollection.
u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j] x = np.cos(u)*np.sin(v) y = np.sin(u)*np.sin(v) z = np.cos(v) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot_wireframe(x, y, z) ax.legend()Поверхность
Для построения поверхности используйте функцию plot_surface().
plot_surface(self, X, Y, Z, *args, norm=None, vmin=None, vmax=None, lightsource=None, **kwargs)
- X, Y, Z : 2D массивы
- Данные для построения поверхности.
- rcount, ccount : int
- rstride, cstride : int
- color: color
- Цвет для элементов поверхности.
- cmap: Colormap
- Colormap для элементов поверхности.
- facecolors: массив элементов color
- Индивидуальный цвет для каждого элемента поверхности.

- Индивидуальный цвет для каждого элемента поверхности.
- norm: Normalize
- Нормализация для colormap.
- vmin, vmax: float
- Границы нормализации.
- shade: bool
- Использование тени для facecolors. Значение по умолчанию: True.
- lightsource: LightSource
- Объект класса LightSource – определяет источник света, используется, только если shade = True.
- **kwargs
- Дополнительные аргументы, определяемые Poly3DCollection.
u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j] x = np.cos(u)*np.sin(v) y = np.sin(u)*np.sin(v) z = np.cos(v) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') ax.plot_surface(x, y, z, cmap='inferno') ax.legend()P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Алгоритм построения графика по точкам
1. Распределите функции по группам.
у=3х-2у= 2х2
у= -4х+5
у= ½ х-5
у=│х│-2
у=-3х+2
у=3х
у=х2-3
у=-3х+7
у=4х-2
2
2
у=
(х+2)
у= -2х
у= -4х+1 у= -4х
у= ½ х-5
у= ½ х
2
у=
(х-3)
у= -½х2
у=-3х+2
у=-3
у=│х│
у=3х-1
у=│х+2│
у=-х2
у=│х-3│
2. Возможный вариант классификации
Линейные (прямая)у=-3х+2
у= ½ х-5
у= -4х
у=-3х+7
у=3х-1
у=-3
у= ½ х
у= -4х+1
у=4х-2
у=3х
у= -4х+5
у=│х+2│
у=│х│
у=│х│-2
у=│х-3│
Квадратичные
(парабола)
у= (х-3)2
у= (х+2)2
у=-х2
у= -½х2
у= -2х2
у=х2-2
3.
 Построить график функции у=-3х+2
Построить график функции у=-3х+2у= -½х2
4. Возможный вариант классификации
Могупостроить
у=-3х+2
у=│х│
у= (х-3)2
у= ½ х-5
у= -4х
у= х2+1
у=-3х+7
у=-х2
у=3х-1
у=-3
у=-3
у= -½х2
у= ½ х
у= -4х+1
у= -2х2
у=4х-2
у=х2-3
у=3х
у=-3х+2
Не могу
построить
у=│х+2│
у= (х-3)2
у=
(х+2)2
у=х2-2
у=│х│-2
у=│х-3│
5. Алгоритм построения графика по точкам:
Составить таблицу с шагом 1 (чеммельче шаг – тем точнее график; чем
больше точек – тем точнее график)
Отметить точки на координатной
плоскости.
Соединить точки линией (какой –
внимание!)
6. Групповая работа. (5минут)
у=│х-3│,где -4≤ х ≤4у=│х│ -2 ,где -4≤ х ≤4
у=х2-2 ,где -4≤ х ≤4
у= (х+2)2 ,где -4≤ х ≤4
у= (х-3)2 ,где -4≤ х ≤4
у=│х+2│ ,где -4≤ х ≤4
7. Групповая работа. (5минут)
у=│х-3│у=│х│ -2
у=х2-2
у= (х+2)2
у= (х-3)2
у=│х+2│
8.
 Алгоритм построения графика с помощью движений. Построить график функции у=f(x)
Алгоритм построения графика с помощью движений. Построить график функции у=f(x)у=f(x)+а – вверх на а
у=f(x)-а – вниз на а
у=f(x-а) – вправо на а
у=f(x+а) – влево на а
9. Построение графика с помощью движений.
Удалось ли увидеть закономерность исовершить открытие? (если не
получилось, то почему)
Как работала группа? (слаженно или
нет, были ли конфликты, кто в группе
самый ценный игрок)
Сможете ли применить свои знания на
практике? (если нет, то почему)
Какую оценку можно поставить группе за
работу?
Оцените работу каждого игрока,
поставьте отметку.
10. Домашнее задание.
Подумать…Построить у=│х+2│+3 и у= (х+2)2 -4
10 ошибок в использовании средств графиков и диаграмм
«Существуют три вида лжи: ложь, наглая ложь и статистика» — Бенджамин Дизраэли.
Перефразируя эту знаменитую фразу, можно сказать, что графики и диаграммы тоже могут лгать. Мало того, что визуализации базируются на цифрах (происхождение которых зачастую вызывает сомнение), так они ещё могут сыграть с нашим восприятием злую шутку, намеренно или ненамеренно исказив информацию, сбив с толку аудиторию, или в лучшем случае сделав эту информацию малопонятной.
Сейчас данных стало так много, что воспринимать их при помощи таблиц уже нереально. В то же время диаграммы позволяют нам быстро и эффективно анализировать большие наборы данных, выделять взаимосвязи и паттерны, концентрировать внимание на важном, и в конце концов – это просто красиво!
Конечно же, не все экономисты и финансисты являются экспертами по визуализации данных, в результате чего мы постоянно сталкиваемся с непонятными графиками и диаграммами. Эта статья описывает 10 наиболее часто встречающихся ошибок в использовании визуализаций и полезные советы по их устранению:
1. Вертикальная ось Y начинается не с 0
Гистограммы (столбчатые диаграммы) в основном используются для визуализации относительных размеров. Соответственно если пользователь информации видит, что один столбик на графике в два раза больше другого, он подсознательно делает вывод о двукратной разнице в количественном значении. Но это сравнение будет ошибочным, если ось не будет начинаться с нулевой отметки.
Легче продемонстрировать этот эффект на примере. На графике слева показана маржинальная прибыль по продуктам компании. Сразу же бросается в глаза, что бананы приносят в 3 раза больше прибыли, чем апельсины. Но если посмотреть на график справа, который отображает ровно ту же информацию – разница будет не настолько драматичная.
Данная ошибка, приводящая к существенному искажению пропорций, является наиболее распространённой. И всё потому, что Excel по умолчанию услужливо подбирает самый красивый способ визуализации, автоматически определяя диапазон значений оси. Поэтому приходится быть всегда начеку, чтобы не допустить игры с нашим восприятием и максимально адекватно отражать данные.
Нужно отметить, что у этого правила есть одно ограничение – на гистограммах плохо различаются незначительные изменения. При необходимости изменить стартовую отметку оси для демонстрации малых колебаний – предпочтительнее использовать линейный график, как на примере ниже.
2.
 Временная ось неправильно отражает целостность периода
Временная ось неправильно отражает целостность периодаДавайте представим ситуацию, когда за первое полугодие на предприятии были продажи только в январе, феврале, апреле и июне. А за март и май продаж не было. На диаграмме слева мы просто не видим этих «провалов».
Это происходит потому, что Excel интерпретирует месяца в данном случае как категорию, а не как непрерывное измерение, и делает равные засечки для неодинаковых интервалов. Другими словами, для Excel ряд значений «январь, февраль, апрель, июнь» является аналогичным ряду «яблоко, апельсин, банан, персик». В таком случае в источнике данных необходимо явно указывать, что в марте и мае продажи равнялись нулю.
3. Выбор неправильного типа графика
График позволяет выразить идею, которую несут данные, наиболее полно и точно, поэтому очень важно выбрать подходящий тип диаграммы. Гистограммы (столбчатые диаграммы) лучше воспринимаются при сравнении категорий, линейные графики — при демонстрации изменения категории во времени, а круговые диаграммы – для визуализации структуры.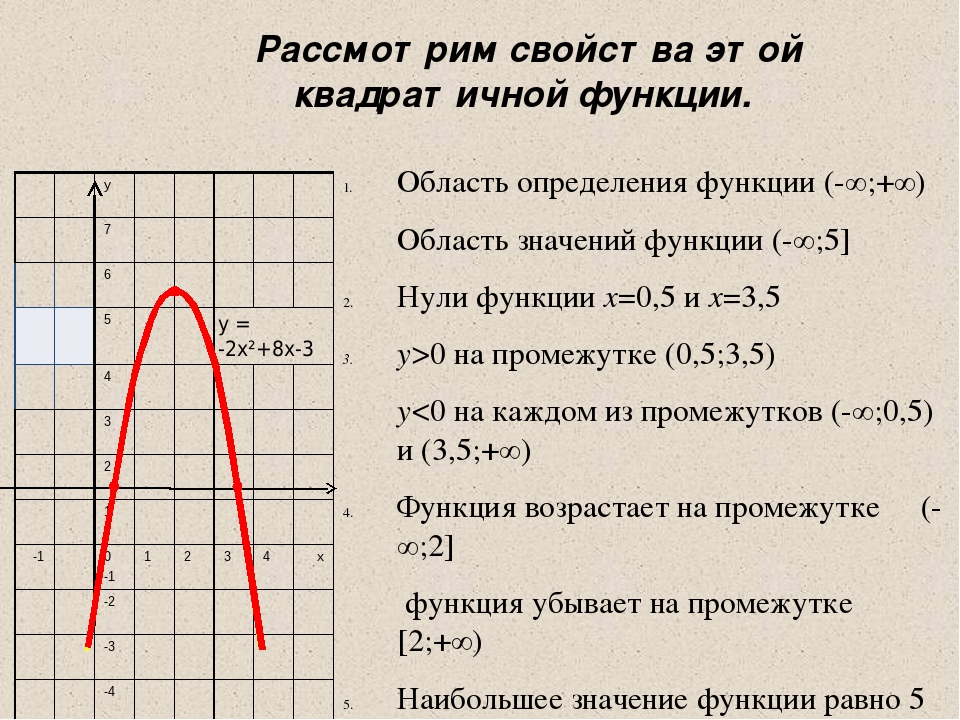 Графики рассеивания (scatter charts) лучше не применять для беседы с нетехническими специалистами, они больше подходят для анализа сырых первичных данных.
Графики рассеивания (scatter charts) лучше не применять для беседы с нетехническими специалистами, они больше подходят для анализа сырых первичных данных.
Первый пример показывает разницу восприятия линейной и столбчатой диаграмм при сравнении категорий (источник данных один и тот же):
А на этом примере сразу видно, какой из типов графиков понятнее и эффективнее передаёт временную динамику показателей:
4. Использование 3D-эффектов
Красота в графике не всегда является синонимом понятности. За счёт добавления дополнительного третьего измерения в диаграммы происходит сильное искажение пропорций по принципу близкий/далёкий объект. Эффект от этого можно увидеть на примере ниже. Как Вы думаете, какую диаграмму легче прочитать?
По этой причине, большинство 3D-визуализаций как минимум не делают информацию понятнее. На 3D круговой диаграмме ниже, какой сектор больше: зелёный или синий, красный или сиреневый? Визуально груш предприятие продало гораздо больше, чем яблок. На самом же деле зелёный и синий сектора абсолютно равны, так же как равны и красный с сиреневым. Это чётко видно на двумерном варианте данной диаграммы справа.
На самом же деле зелёный и синий сектора абсолютно равны, так же как равны и красный с сиреневым. Это чётко видно на двумерном варианте данной диаграммы справа.
Поэтому если у Вас нет действительно очень, очень веской причины использовать 3D диаграммы – лучше просто забыть об их существовании.
5. Плохое или избыточное оформление
Конечно же, на вкус и цвет все фломастеры разные – но всё-таки хорошим тоном в визуализациях считается минимализм, стремление убрать всё лишнее, всё то, что может отвлекать от сути информации. Ниже приведён пример не слишком удачного стиля оформления визуализации (точка безубыточности какого-то производства).
Можно выделить следующие моменты, которые точно не способствуют лучшему восприятию:
- отсутствие заголовка;
- отсутствие подписей осей;
- шрифт с засечками;
- изобилие чёрных вспомогательных линий;
- вертикальные или диагональные надписи – они гораздо хуже читаются;
- отдельная легенда (само собой с чёрной линией границы), при наличии возможности подписать данные на самой диаграмме.

А теперь посмотрим на ту же информацию, только в несколько другом виде. Комментарии тут, я думаю, излишни.
6. Слишком много категорий
Дробление круговой диаграммы (или даже обычной гистограммы) на большое количество секторов делает невозможным быстрое сравнение категорий, особенно маленьких. Зачастую получается просто информационный мусор.
Лучшие практики визуализации советуют делить структуру максимум на 4-5 частей. В крайнем случае, всегда можно применить группировку категорий или разделить информацию на несколько диаграмм. Наглядность это ошибки продемонстрирована на примере ниже.
7. Отсутствие акцента
Любая визуализация – это способ представления информации, способ донести до аудитории какую-то мысль, идею. Вы же собираетесь что-то сказать своим графиком – так сделайте это! Если же на диаграмме нет никакого акцента, взгляд ни за что не цепляется – вы рискуете получить несфокусированное внимание потребителя информации. Ниже пример графиков с явным акцентом.
Ниже пример графиков с явным акцентом.
Это особенно важно при подготовке визуализаций для презентаций. Часто приходится выделять элементы на графиках чуть ли не вручную, чтобы целенаправленно управлять вниманием, показывать куда смотреть. Выделение цветом на контрасте – лучший способ. Также можно делать аннотации – текстовые вставки, объясняющие поведение/изменение графика в заданных точках.
Ещё один совет — в презентациях на слайдах следует показывать минимум информации, только самое необходимое для подкрепления центральной линии повествования. Детальные расшифровки всегда можно сделать в раздаточном материале (который в свою очередь лучше раздавать уже в самом конце, иначе люди будут просто отвлекаться).
8. Искажение при группировке в категорию «Другие»
Категорию «Другие» лучше делать только когда в неё группируется лишь малая часть данных. Иначе можно легко исказить восприятие информации. Для примера посмотрите на эти два графика:
На первом графике категория «Другие» скрыта, что может привести к мысли о том, что эти топ-10 фильмов собрали основную часть совокупных кассовых сборов. Второй график показывает уже немного другую картину.
Второй график показывает уже немного другую картину.
9. Некорректное использование усреднённых данных
Для наглядной демонстрации данной ошибки посмотрите на небольшую визуализацию слева. Что по ней можно сказать? Мы видим позитивную динамику продаж, у предприятия всё хорошо. Но если развернуть эту же информацию по категориям проданных товаров, то ситуация предстаёт совсем в другом свете. Оказывается, по всем категориям, кроме мандаринов, наблюдается спад продаж. И только за счёт мандаринов предприятие в целом смогло продать в 2016 г. больше, чем в 2015 г. С этой точки зрения явно есть над чем задуматься.
Первый график показывает абсолютно правильную информацию. Но на нём мы видим только часть правды, в то время как второй график демонстрирует всю правду, расшифровывая усреднённые цифры. Средние значения или общие суммы могут быть отличным способом быстро оценить бизнес по некоторым ключевым показателям, но нужно правильно их воспринимать и всегда помнить, что они могут скрывать много интересной информации.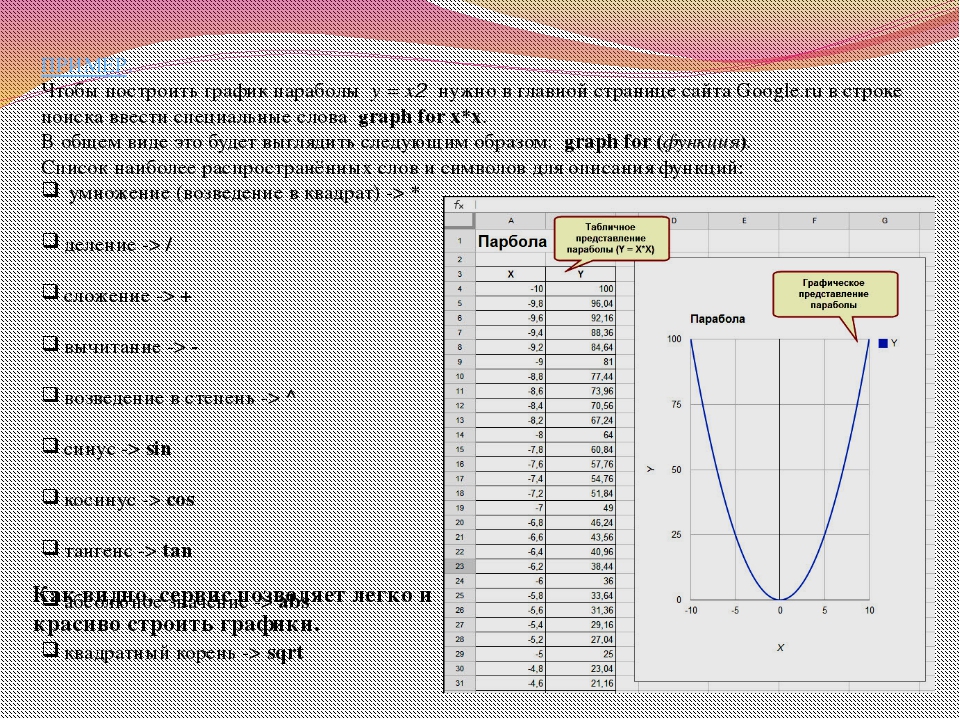
10. Круговые диаграммы не отображают целое (100%)
Иногда круговые диаграммы ошибочно используют не только для демонстрации структуры единого целого, а просто для сравнения категорий – например, средних зарплат по отделам (левая визуализация). В результате получается информация ни о чём. Ведь сумма средних зарплат по отделам не равна средней зарплате по предприятию. Вместо этого корректнее использовать агрегирование по количеству сотрудников, или сумме общего фонда оплаты труда (как на диаграмме справа).
В качестве эпилога
Графики и диаграммы помогают осмысливать данные и превращать информацию в знания. Очень важно правильно использовать этот мощный инструмент. Ведь некорректно реализованная визуализация может не только замедлить восприятие данных, но и исказить их, подталкивая к неверным решениям. Понимание типовых графических ошибок поможет избежать их и реализовать весь потенциал визуализаций, делать понятные, сбалансированные, честные графики и диаграммы.
Автор: Виктор Рыжов
Глава 5 Работа со вставками Mathcad 11
Глава 1 Основы работы с системой Mathcad 11Глава 2 Работа с файлами Mathcad 11
Глава 3 Редактирование документов Mathcad 11
Глава 4 Управление обзором (View) Mathcad 11
Глава 5 Работа со вставками Mathcad 11
Глава 6 Установки форматов объектов системы Mathcad 11
Глава 7 Управление вычислительными процессами Mathcad 11
Глава 8 Работа с символьным процессором Mathcad 11
Глава 9 Работа с окнами Mathcad 11
Глава 10 Работа с информационными ресурсами Mathcad 11
5. 1. Подменю позиции Insert (Вставка) главного меню
Установка любого объекта в окно редактирования называется вставкой MathCAD
реализует различные механизмы вставки — от просто вывода шаблона объекта до
вставки объекта, созданного в другом приложении, через буфер обмена. В версии
MathCAD все виды вставок включены в новую позицию главного меню Insert (Вставка).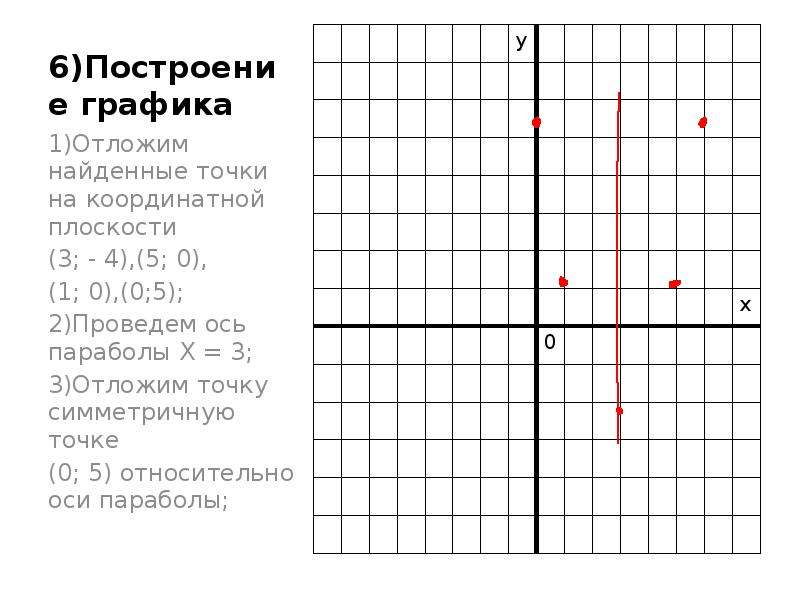
При активизации этой позиции появляется подменю со следующими операциями:
Graph (Графика) — вставка шаблонов графики, Matrix… [Ctrl+ M] (Матрица) — вставка шаблонов матриц и векторов, Function… [Ctrl+ F] (Функция) — вставка шаблонов встроенных функций, Unit… [Ctrl+ U] (Единицы) — вставка единиц измерений размерных величин;
Picture [Ctrl+ T] (Рисунок) — вставка шаблона импортируемого рисунка;
Math Region — вставка в текстовую область (Математическая область) шаблона математической области;
Text Region (Текстовая область) — вставка текстовой области;
Page Break (Разрыв страницы) — вставка линии разрыва страницы;
Hyperlink (Гиперссылка) — вставка гиперссылки;
Reference… (Ссылка) — вставка обращения к заданному файлу активизацией кнопки,
Component… (Компонент) — вставка других компонентов системы, Object… (Объект)
— вставка объекта с установлением динамической связи с порождающим его приложением.
Вид подменю позиции Insert главного меню показан на рис. 5. 1. Для создания графиков в системе MathCAD имеется программный графический процессор. Основное внимание при его разработке было уделено обеспечению простоты задания графиков и их модификации с помощью соответствующих опций. Процессор позволяет строить самые разные графики, например в декартовой и полярной системах координат, трехмерные поверхности, графики уровней и т д
Для построения графиков используются шаблоны Их перечень содержит подменю Graph (Графика) в позиции Insert (Включение) главного меню Большинство параметров графического процессора, необходимых для построения графиков, по умолчанию задается автоматически Поэтому для начального построения графика того или иного вида достаточно задать тип графика В подменю Graph содержится список из семи основных типов графиков. Они позволяют выполнить следующие действия X-Y Plot® (Декартов — создать шаблон двумерного графика график) в декартовой системе координат,
Рис.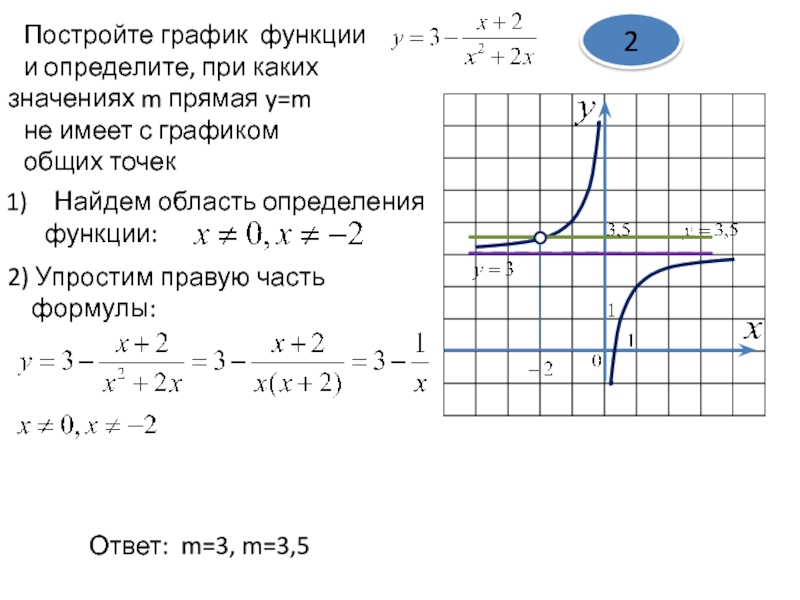 5. 1 Экран системы с открытым подменю Insert
5. 1 Экран системы с открытым подменю Insert
Polar Plot [Ctrl+ 7] — создать шаблон графика в полярной системе (Полярный график) координат, Surface Plot [Ctrl+ 2] — создать шаблон для построения трехмерного (График поверхности) графика, Contour Plot [Ctrl+ 5] — создать шаблон для контурного графика (Карта линий уровня) трехмерной поверхности, 3D Scatter Plot создать шаблон для графика в виде точек (Точечный график) (фигур) в трехмерном пространстве, 3D Bar Chart (Трехмерная создать шаблон для изображения в виде гистограмма) совокупности столбиков в трехмерном про странстве, Vector Field Plot — создать шаблон для графика векторного (Векторное поле) поля на плоскости
Вид окна системы с подменю Insert Graph показан на рис 5. 1. В этом подменю видны команды создания шаблонов указанных выше типов графиков В окне редактирования показаны также два одинаковых графика, но в разных местах и разного размера
5. 2. Установка шаблона двумерных графиков (X-Y Plot @)
2. Установка шаблона двумерных графиков (X-Y Plot @)
Графики в системе MathCAD могут иметь различные размеры и перемещаться в окне редактирования документа. Для наиболее распространенных графиков в декартовой и в полярной системах координат в MathCAD предусмотрен упрощенный и очень удобный способ построения графиков без предварительного задания функции и ранжирования независимой переменной.
Именно так построены графики на рис 5 1 Для упрощенного построения двумерных графиков некоторой функции f (x) надо вывести их шаблон, по вертикали указать эту функцию, а по горизонтали — независимую переменную х. Таким образом можно строить на одном рисунке и графики многих функций, просто опишите их у вертикальной оси, используя запятые для разделения описаний функций. Графики будут построены линиями разного типа и цвета.
Можно вначале записать функцию, а затем вывести шаблон графика;
функция окажется записанной у вертикальной оси, и останется только указать
независимую переменную у горизонтальной оси. Такой простой способ наверняка
порадует начинающих пользователей, плохо сознающих (на первых порах), что графики
в MathCAD всегда строятся по векторам и матрицам их отдельных точек. При указанном
упрощенном способе построения графиков они строятся при изменении независимой
переменной от -10 до+ 10. В дальнейшем операцией форматирования этот диапазон
и все иные данные графиков можно изменить (это называют изменением формата).
Такой простой способ наверняка
порадует начинающих пользователей, плохо сознающих (на первых порах), что графики
в MathCAD всегда строятся по векторам и матрицам их отдельных точек. При указанном
упрощенном способе построения графиков они строятся при изменении независимой
переменной от -10 до+ 10. В дальнейшем операцией форматирования этот диапазон
и все иные данные графиков можно изменить (это называют изменением формата).
Для вывода шаблона двумерной графики в декартовой системе координат служит операция X-Y Plot® (декартов график). Она выводит в текущее положение курсора шаблон графиков 2D-rana или графиков в декартовых координатах. Напоминаем, что это обычный график на плоскости с воображаемыми (или действительно нарисованными) осями Х (горизонтальная) и Y (вертикальная), расположенными под прямым углом друг к другу.
Каждая точка декартова графика характеризуется своими координатами х и у=f(х),
где х — абсцисса точки, а у — ее ордината. Точки соединяются друг с другом разнообразными
линиями (сплошной, пунктирной и т. д.). Могут быть показаны и исходные (узловые)
точки графика в виде жирных точек, квадратиков, кружков и т. д.; возможно и
построение на одном рисунке графиков нескольких функций.
Точки соединяются друг с другом разнообразными
линиями (сплошной, пунктирной и т. д.). Могут быть показаны и исходные (узловые)
точки графика в виде жирных точек, квадратиков, кружков и т. д.; возможно и
построение на одном рисунке графиков нескольких функций.
Перед применением этой команды необходимо определить функции, графики которых должны строиться, и изменение их аргумента (например, х) в заданном интервале. Впрочем, простые функции, если они в дальнейшем не используются, можно указать в шаблоне самого графика. Далее надо приблизительно наметить место левого верхнего угла графика и установить на него графический курсор. Затем следует ввести команду (используя соответствующую позицию меню или нажав клавиши, задающие символ @).
Рис. 5. 2 показывает задание трех функций и вывод шаблона графика (внизу).
Незаполненный шаблон графика представляет собою большой пустой прямоугольник
с шаблонами данных в виде темных маленьких прямоугольников, расположенных около
осей абсцисс и ординат будущего графика. В средние шаблоны данных надо поместить
имя переменной (х у оси абсцисс) и задать формулы для функций (у у оси ординат).
Если строятся графики нескольких функций в одном шаблоне, то для их разделения
следует использовать запятые. Чтобы перемещать по шаблонам метку их выбора и
выделения, следует использовать клавиши перемещения курсора. Можно выбрать шаблон
данных и прямо с помощью мыши, указав нужный шаблон ее курсором и нажав левую
клавишу мыши.
В средние шаблоны данных надо поместить
имя переменной (х у оси абсцисс) и задать формулы для функций (у у оси ординат).
Если строятся графики нескольких функций в одном шаблоне, то для их разделения
следует использовать запятые. Чтобы перемещать по шаблонам метку их выбора и
выделения, следует использовать клавиши перемещения курсора. Можно выбрать шаблон
данных и прямо с помощью мыши, указав нужный шаблон ее курсором и нажав левую
клавишу мыши.
Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будут устанавливаться автоматически. Недостаток тут в том, что масштабы, скорее всего, окажутся
не вполне удобными (например, будут представлены неокругленными десятичными
цифрами), для представления целиком всего графика в максимальном размере. Рекомендуется
всегда вначале использовать автоматическое масштабирование и лишь затем изменять
масштабы на более подходящие.
Чтобы произошло построение графика в автоматическом режиме вычислений, достаточно вывести курсор за пределы графического объекта. В ручном режиме вычислений для этого нужно еще нажать клавишу F9. При построении область графика во время вычислений ординат функций покрывается зеленой штриховкой, затем графики функций появляются в шаблоне (см. рис. 5. 3).
Если что-либо в построенном графике не вполне удовлетворяет пользователя, можно применить описанные ниже операции изменения его формата.
Рис. 5. 3 Пример построения двух графиков трех функций
Эти операции позволяют изменять заданные по умолчанию параметры графиков. Заметим, что окно задания форматов графиков появляется, если выделить график и, установив в его области курсор мыши, дважды быстро щелкнуть ее левой клавишей.
Графики можно перемещать по полю окна документа и изменять их размеры Для этого
надо выделить график (он обводится сплошной линией) Проще всего это можно сделать
так. поместить курсор мыши в область графика и щелкнуть один раз левой клавишей
В правой части рис 5 3 показан тот же график после увеличения его размеров и
завершения редактирования формата
поместить курсор мыши в область графика и щелкнуть один раз левой клавишей
В правой части рис 5 3 показан тот же график после увеличения его размеров и
завершения редактирования формата
Можно поступить и по-иному — поместить курсор мыши вблизи графика и, нажав ее левую клавишу, перемещать мышь в направлении графика наискосок Курсор начнет вычерчивать область выделения в виде прямоугольника из черных пунктирных линий Как только эта область захватит график и он тоже окажется обведен пунктирным прямоугольником, надо отпустить клавишу мыши График будет выделен
Стоит поместить графический курсор вблизи линий рамки, выделяющей область графика,
при этом изображение курсора изменится: вмесго маленького красного крестика
оно приобретет вид ладони. Если теперь нажать левую клавишу мыши и начать ее
перемещать, то весь шаблон графика будет перемещаться по окну Установите его
в нужное место и отпустите левую клавишу мыши. Рисунок окажется на новом месте.
Рисунок окажется на новом месте.
Для изменения размеров рисунка нужно точно подвести графический курсор к специальным шаблонам на рамке, выделяющей рисунок Эти шаблоны имеют вид маленьких черных прямоугольников. Изображение курсора при этом заменяется на двустороннюю стрелку, указывающую, в каких направлениях можно растягивать рисунок. Нажав левую клавишу мыши, можно захватить соответствующую сторону или угол шаблона рисунка и, не отпуская клавишу, начать растягивать или сжимать шаблон. После того как клавиша будет отпущена, рисунок перестроится в новых размерах. Сжимать и растягивать графики можно в вертикальном, горизонтальном и диагональном направлениях
При любом виде выделения рисунка нажатие клавиши F3 стирает рисунок в окне и переносит его в буфер обмена. Переместив курсор, установленный на месте левого верхнего окна бывшего графика, в новое место и нажав клавишу F4, можно перенести рисунок на это место
Особо следует отметить возможность помещения текстовых комментариев в область
графиков. Для этого вначале надо подготовить их в стороне от графика и выделить
пунктирной линией Затем поместив курсор мыши в область текста, надо нажать ее
левую клавишу и перенести текстовый блок в область рисунка. Установив текст
в нужном месте, отпустите клавишу мыши Если при этих операциях или снятии выделений
нанесенные на рисунок надписи исчезают, воспользуйтесь командой восстановления
изображения на экране — Ctrl+ R
Для этого вначале надо подготовить их в стороне от графика и выделить
пунктирной линией Затем поместив курсор мыши в область текста, надо нажать ее
левую клавишу и перенести текстовый блок в область рисунка. Установив текст
в нужном месте, отпустите клавишу мыши Если при этих операциях или снятии выделений
нанесенные на рисунок надписи исчезают, воспользуйтесь командой восстановления
изображения на экране — Ctrl+ R
Этим методом не стоит злоупотреблять, так как надписи сверху, снизу и сбоку графиков (в пределах области их определения) можно создавать с по мощью соответствующих средств задания формата графиков Они будут описаны несколько позже Такие надписи никогда не исчезают Чтобы надписи были на русском языке, следует использовать соответствующие наборы шрифтов. Поскольку шрифт в процессе ввода текста менять нельзя, есть определенные трудности с созданием таких надписей на русском языке
5. 3. Установка шаблона графиков в полярной системе координат (Polar
Plot)
3. Установка шаблона графиков в полярной системе координат (Polar
Plot)
В полярной системе координат каждая точка задается углом W, радиусом и длиной радиус-вектора R (W). График функции обычно строится при изменении угла W в определенных пределах, чаще всего от 0 до 2р. Опция Polar Plot (Полярный график) выводит шаблон таких графиков, показанный на рис. 5. 4. Этот шаблон имеет форму окружности и содержит шаблоны данных.
Рис. 5. 4 Шаблон графиков типа Polar Plot
Перед построением таких графиков надо задать изменение ранжированной переменной W (или с другим именем) в заданных пределах. После вывода шаблона следует ввести W в шаблон снизу и функцию R (W) в шаблон справа, а также указать нижний предел изменения длины радиус-вектора R (W) — Rmin и шаблоне справа внизу и верхний предел — Rmax в шаблоне справа и сверху.
На рис. 5. 5 показано построение графиков в полярной системе координат:
слева — по описанному шаблону, справа — с помощью шаблона обычной двумерной
графики X-Y Plot. Сейчас R (W) =i, так что в обоих случаях строится окружность
(если дисплей имеет различные масштабы по вертикали и горизонтали, окружность
превратится в эллипс).
Сейчас R (W) =i, так что в обоих случаях строится окружность
(если дисплей имеет различные масштабы по вертикали и горизонтали, окружность
превратится в эллипс).
При построении графика в полярной системе координат с использованием шаблона обычного 1рафика в прямоугольной системе координат надо по оси Х установить R (W) -cos (W), а по оси Y — R (W) -sin (W). Построение графиков в полярной системе координат с помощью шаблона обычной графики X-Y Plot в ряде случаев даже более предпочтительно, поскольку в математической литературе графики параметрически заданных функций чаще всего строятся именно таким образом. При задании даже простых функций R (W) графики в полярной системе координат могут иметь весьма причудливый вид.
Надо также отметить новую возможность прямого построения графиков функций в
полярной системе координат, без определения диапазона изменения независимой
переменной W. Пример такого построения дан на рис. 5. 6.
5. 6.
Рис. 5. 5 Графики функций в полярной системе координат
Рис. 5. 6 Пример прямого построения графика параметрически заданной функции
При прямом построении графика достаточно просто заполнить ее шаблон. Саму функцию надо описать ее уравнениями, которые вписываются на места шаблонов по осям Х и Y. Стоит вывести графический курсор мыши из области графика, как последний будет построен.
5. 4. Установка шаблона трехмерных графиков (Surface Plot)
Эта операция служит для построения трехмерной поверхности Z (X, Y), предварительно
представленной матрицей М ординат Z. При этом выводится шаблон графика, левый
верхний угол которого помещается в место расположения курсора. Шаблон, в свою
очередь, содержит единственный шаблон данных — темный прямоугольник у левого
нижнего угла основного шаблона. В него надо занести имя матрицы со значениями
ординат ЗD-поверхности. Разумеется, прежде чем строить график ЗD-поверхности,
нужно ее определить математически.
Разумеется, прежде чем строить график ЗD-поверхности,
нужно ее определить математически.
Наглядность представления трехмерных поверхностей зависит от множества факторов: масштаба построений, углов поворота фигуры относительно осей, применения алгоритма удаления невидимых линий или отказа от него, использования функциональной закраски и т. д. Для изменения этих параметров следует использовать операцию установки формата графика (см. далее). На рис. 5. 8 показано то же построение, что и описанное выше, но с применением алгоритма удаления невидимых линий.
Нетрудно заметить, что применение алгоритма удаления невидимых линий делает
рисунок трехмерной поверхности намного более наглядным. Дальнейшее повышение
наглядности восприятия 3D-поверхностей обеспечивается применением функциональной
закраски. По существу, она дает дополнительную информацию о третьем измерении;
в нашем случае, чем ниже расположена поверхность фигуры, тем она темнее (см. рис. 5. 9).
рис. 5. 9).
Рис. 5. 9 Задание и построение трехмерной поверхности с функциональной закраской
С помощью описываемых ниже команд изменения формата можно получить множество разновидностей 3D-графики. В частности, возможен вывод координатных осей. «параллелепипеда», обрамляющего фигуру, и иных деталей подобных графиков, например титульных надписей.
Поскольку график строится на основе матрицы, содержащей только координаты высот фигуры, то истинные масштабы по осям Х и Y не известны и на рисунках не проставляются. Могут, впрочем, выводиться просто порядковые номера элементов матриц в заданном направлении (по Х и по Y). Надо также следить за тем, как сформировать векторы Х и Y, с тем чтобы фигура выглядела естественно и занимала нужное место в пространстве. Все это несколько затрудняет быстрое создание графиков трехмерных поверхностей нужного вида.
Большие возможности дает несколько иной способ задания трехмерных поверхностей
— в параметрическом виде.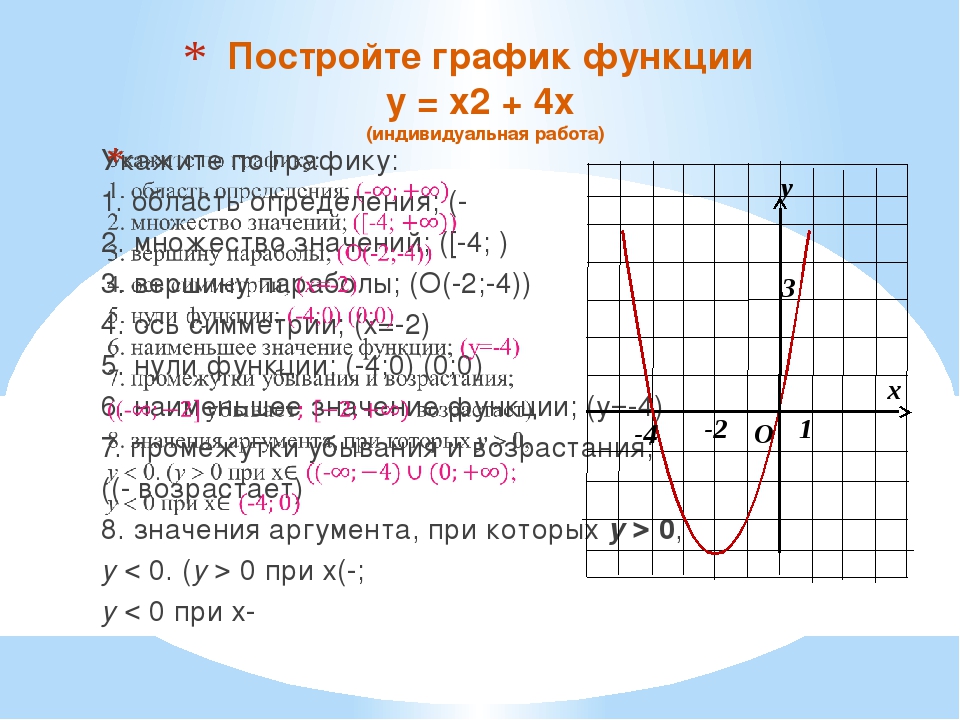 При этом приходится формировать три матрицы — X, Y
и Z — и указывать их в шаблоне в виде X, Y, Z. В Главе 14 (в разделе 14. 1)
дан ряд примеров такого задания трехмерных поверхностей.
При этом приходится формировать три матрицы — X, Y
и Z — и указывать их в шаблоне в виде X, Y, Z. В Главе 14 (в разделе 14. 1)
дан ряд примеров такого задания трехмерных поверхностей.
5. 5. Установка шаблона контурных ЗD-графиков (Contour Plot)
Еще один широко распространенный тип графиков для представления трехмерных поверхностей — график из линий равного уровня. Такие графики широко применяются, например, в картографии. Операция Contour Plot (Карта линий уровня) служит для построения шаблона таких графиков. Он подобен шаблону, описанному в предыдущем разделе (кстати, как и предшествующие выводу шаблона действия по созданию матрицы М).
На рис. 5. 10 показано построение контурного графика в виде линий равного уровня. Численные значения уровней для разных кривых графика представлены рядом цифр.
Рис. 5. 10 Контурный график 3D-поверхности
Такое представление графика удобно для количественных оценок.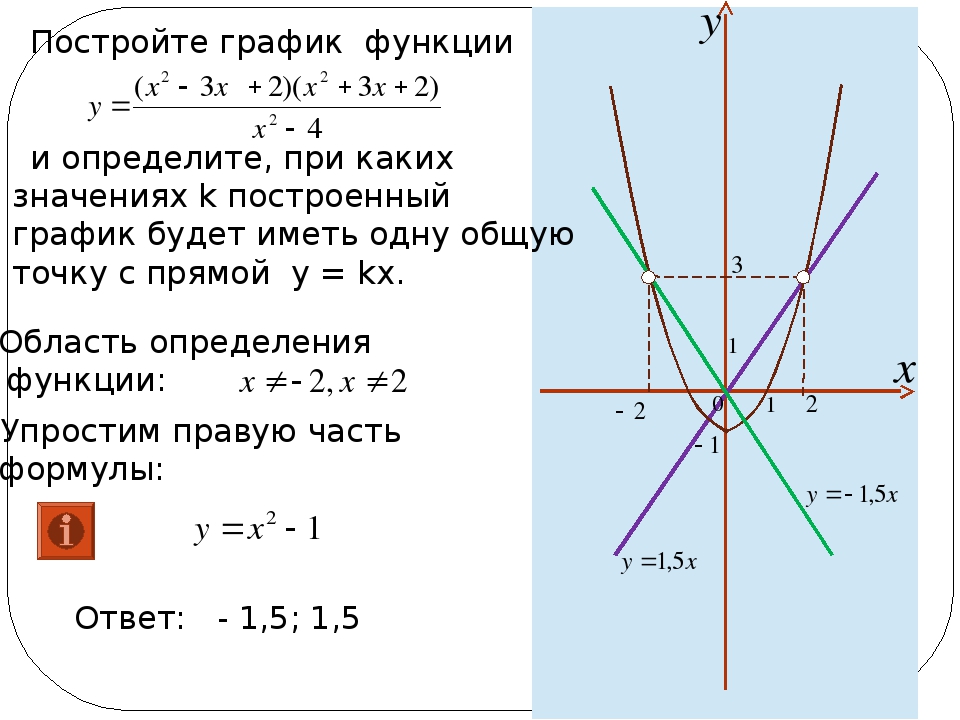 Однако в большинстве
случаев указание количественных значений уровней загромождает график. Возможно
задание высот 3D-поверхности с помощью функциональной окраски. Тогда можно выполнить
построение этой поверхности в виде распределения плотности окраски (см. рис.
5. 11).
Однако в большинстве
случаев указание количественных значений уровней загромождает график. Возможно
задание высот 3D-поверхности с помощью функциональной окраски. Тогда можно выполнить
построение этой поверхности в виде распределения плотности окраски (см. рис.
5. 11).
При использовании цветной функциональной окраски описанные выше типы графиков выглядят весьма впечатляюще. Но неплохие результаты получаются и при задании монохромных графиков. В этом случае гамма цветов заменяется просто разной плотностью серого цвета, от ярко-белого до черного.
Иногда контурные графики получаются даже более информативными, чем просто трехмерные
поверхности. У последних нередко одни части поверхности закрывают другие. Например,
пик на переднем плане может закрыть меньшие пики или впадины на заднем плане.
У контурных графиков такого эффекта нет, и на них легко обнаруживаются все пики
и впадины, правда, при достаточно большом числе линий равного уровня и малом
расстоянии между ними.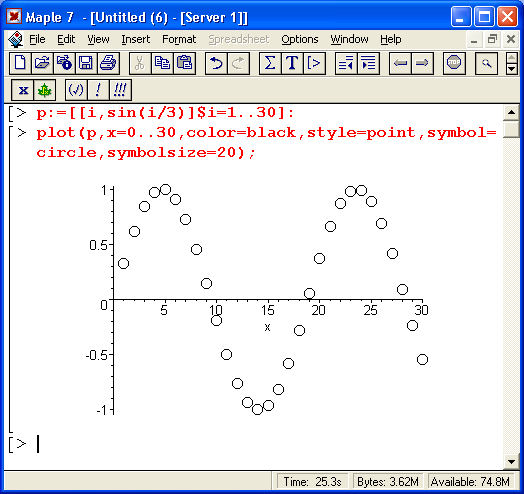
Рис. 5. 11 График распределения плотности ЗD-поверхности
5. 6. Установка шаблона точечного ЗD-графика (3D Scatter Plot)
Нередко трехмерные поверхности представляют в виде находящихся в этом пространстве точек, кружочков или иных фигур. Каждая из этих фигур несет информацию о геометрическом положении ее центра в трехмерном пространстве. Такой график создается операцией 3D Scatter Plot (Точечный график) — см. рис. 5. 12.
Размеры точек, их вид и окраску можно изменять с помощью команды изменения формата ЗD-графика. Обычно достаточно наглядными являются графики с малыми фигурами, расположенными внутри параллелепипеда Однако в целом наглядность таких графиков не очень высока. Их стоит использовать не для показа трехмерных поверхностей, а лишь для демонстрации расположения на них небольшого числа объектов. Объекты могут быть не только в виде точек, но и иных фигур, крестиков, окружностей, квадратов и др
Рис. 5. 12 График ЗD-поверхности в виде разбросанных в пространстве точек
5. 12 График ЗD-поверхности в виде разбросанных в пространстве точек
5. 7. Установка шаблона SD-графиков в виде гистограммы (3D Bar Chart)
Весьма pacпpocтраненной формой представления ЗD-поверхностей является также представление ее рядом трехмерных столбиков, высота которых определяется значением координаты z (x, у) Для этого используется операция 3D Bar Chart (Трехмерная гистограмма) — см рис 513
Рис. 5. 13 Представление ЗD-поверхности трехмерными столбиками
Подобные графики широко применяются при анализе сложных статистических данных, например представленных тремя независимыми переменными Обычно их построение считается высшим пилотажем, но MathCAD превращает этот процесс в обыденную операцию При этом, как видно из рис. 513, достаточно наглядным является представление столбиками и сложных трехмерных поверхностей
5. 8. Установка шаблона ЗD-графиков с векторным представлением (Vector Field Plot)
Еще один вид представления ЗD-поверхности векторное представление Оно задается построением коротких стрелочек векторов Стрелка обращена острием в сторону нарастания высоты поверхности, а плотность расположения стрелок зависит от скорости этого нарастания На рис 514 показан пример подобного графика Для его построения используется команда Field Plot (Векторное поле)
Рис. 5. 14 Представление 3D-поверхности векторами
5. 14 Представление 3D-поверхности векторами
Эти графики применяются редко из-за трудностей построения множества стрелок, для каждой из которых надо рассчитывать градиент поля Но MathCAD дает удобную возможность широкого применения этого вида графиков Он особенно подходит для представления электромагнитных, тепловых, гравитационных и иных полей
5. 9. Установка шаблона матриц и векторов (Matrix…)
Операция Matrix… (Матрицы) обеспечивает задание векторов или матриц Как известно, матрица является заданным своим именем объектом в виде массива данных MathCAD использует одномерные массивы — векторы и двумерные — собственно матрицы
Матрица характеризуется числом строк (Rows) и числом столбцов (Columns). Таким образом, число элементов матрицы или ее размерность равны Rows x Columns Элементами матриц могут быть числа, константы, пере менные и даже математические выражения Соответственно матрицы могут быть численными и символьными
Если использовать операцию Matrix.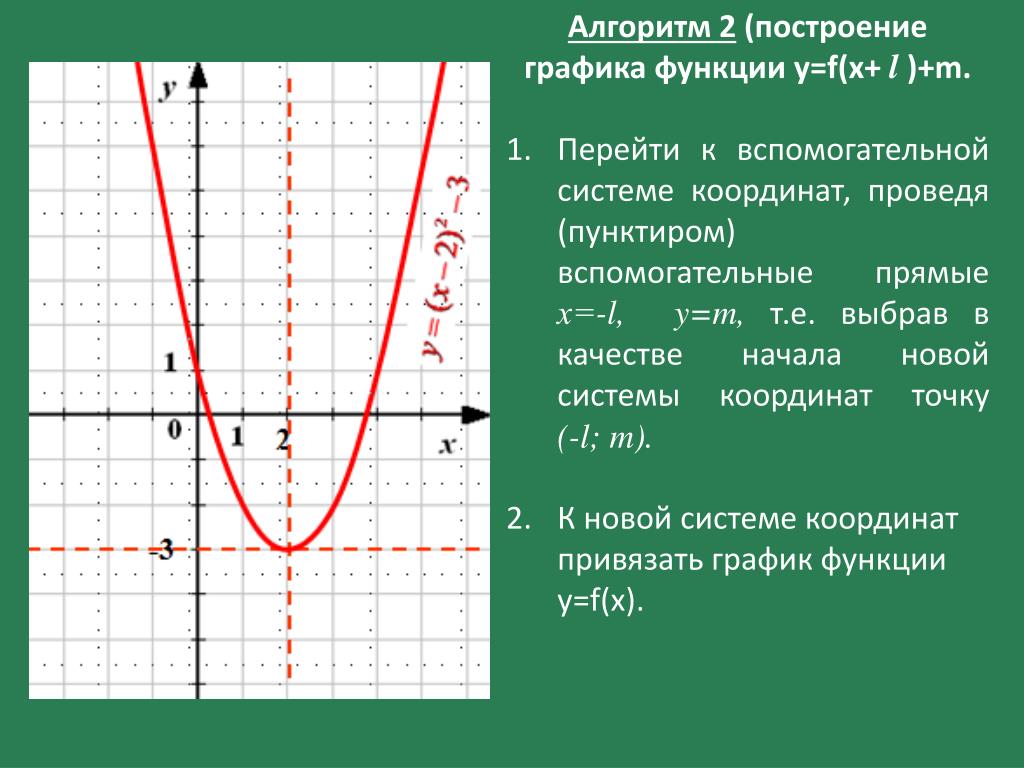 .., то в текущем окне появится не большое
окошко, позволяющее задать размерность вектора или матрицы (см рис 515 справа)
Для этого нужно указать число строк Rows и число сголбцов Columns Нажав клавишу
Enter или указав курсором мыши на изображение клавиши Insert (Вставить) в окошке,
можно вывести шаблон матрицы или вектора (вектор имеет один из параметров размерности,
равный 1)
.., то в текущем окне появится не большое
окошко, позволяющее задать размерность вектора или матрицы (см рис 515 справа)
Для этого нужно указать число строк Rows и число сголбцов Columns Нажав клавишу
Enter или указав курсором мыши на изображение клавиши Insert (Вставить) в окошке,
можно вывести шаблон матрицы или вектора (вектор имеет один из параметров размерности,
равный 1)
Шаблон содержит обрамляющие скобки и темные маленькие прямоугольники, обозначающие места ввода значений (числовых или символьных) для элементов вектора или матрицы. Один из прямоугольников можно сделать активным (отметив его курсором мыши). При этом он заключается в уголок. Это указывает на то, что в него будут вводиться значения соответствующего элемента. С помощью клавиш перемещения курсора можно по горизонтали пробежаться по всем прямоугольникам и ввести все элементы вектора или матрицы.
Рис. 5. 15 Вывод шаблонов вектора и матрицы и их заполнение
5. 15 Вывод шаблонов вектора и матрицы и их заполнение
Пока идет ввод элементов векторов или матриц, пустые шаблоны отображаются без каких-либо комментариев. Однако, если закончить ввод до полного заполнения шаблонов, система выведет сообщение об ошибке — незаполненный шаблон приобретет красный цвет. Вывод несуществующей матрицы или ошибочное указание ее индексов также отображается красным цветом.
Если использовать операцию Insert (Включение) при уже выведенном шаблоне матрицы, то матрица расширяется и ее размер увеличивается. Кнопка Delete (Стирание) позволяет убрать расширение матрицы, вычеркнув из нее строку или столбец.
Каждый элемент матрицы характеризуется индексированной переменной, и его положение
в матрице обозначается двумя индексами: один указывает номер строки, другой
— номер столбца. Для набора индексированной переменной прежде надо ввести имя
переменной, а затем перейти к набору индексов нажатием клавиши, вводящей символ].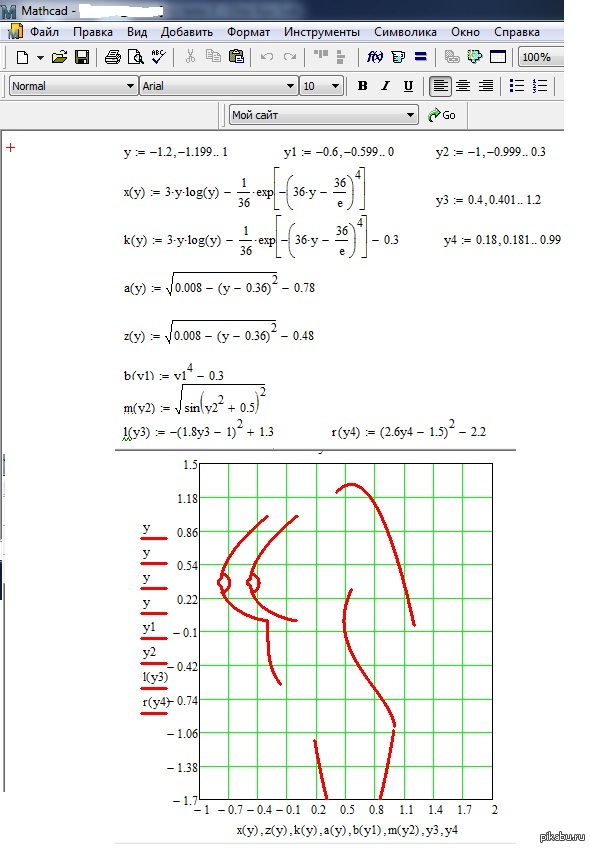 Прежде указывается индекс строки, а затем через запятую индекс столбца. Примеры
вывода индексированных переменных (элементов матрицы М) также даны на рис. 5.
14.
Прежде указывается индекс строки, а затем через запятую индекс столбца. Примеры
вывода индексированных переменных (элементов матрицы М) также даны на рис. 5.
14.
Вырожденная в одну строку или в один столбец матрица является вектором. Его элементы — индексированные переменные с одним индексом. Нижняя граница индексов задается значением системной переменной ORIGIN. Обычно ее значение задают равным 0 или 1.
5. 10. Вывод функций (Choose function…)
Как правило, при подготовке документов имена функций пользователь вводи г самостоятельно. Поскольку функций, встроенных в систему, очень много (около 250), запомнить их все довольно сложно. Это и не нужно, ведь в MathCAD есть средство для ввода имен функций из их общего списка (каталога).
Операция Choose function… (Вставить функцию) выполняет следующие действия:
• выводит полный перечень встроенных в ядро системы функций;
• кратко поясняет назначение каждой функции;
• позволяет корректно ввести шаблон с именем функции в место расположения курсора,
установленного в математическом выражении.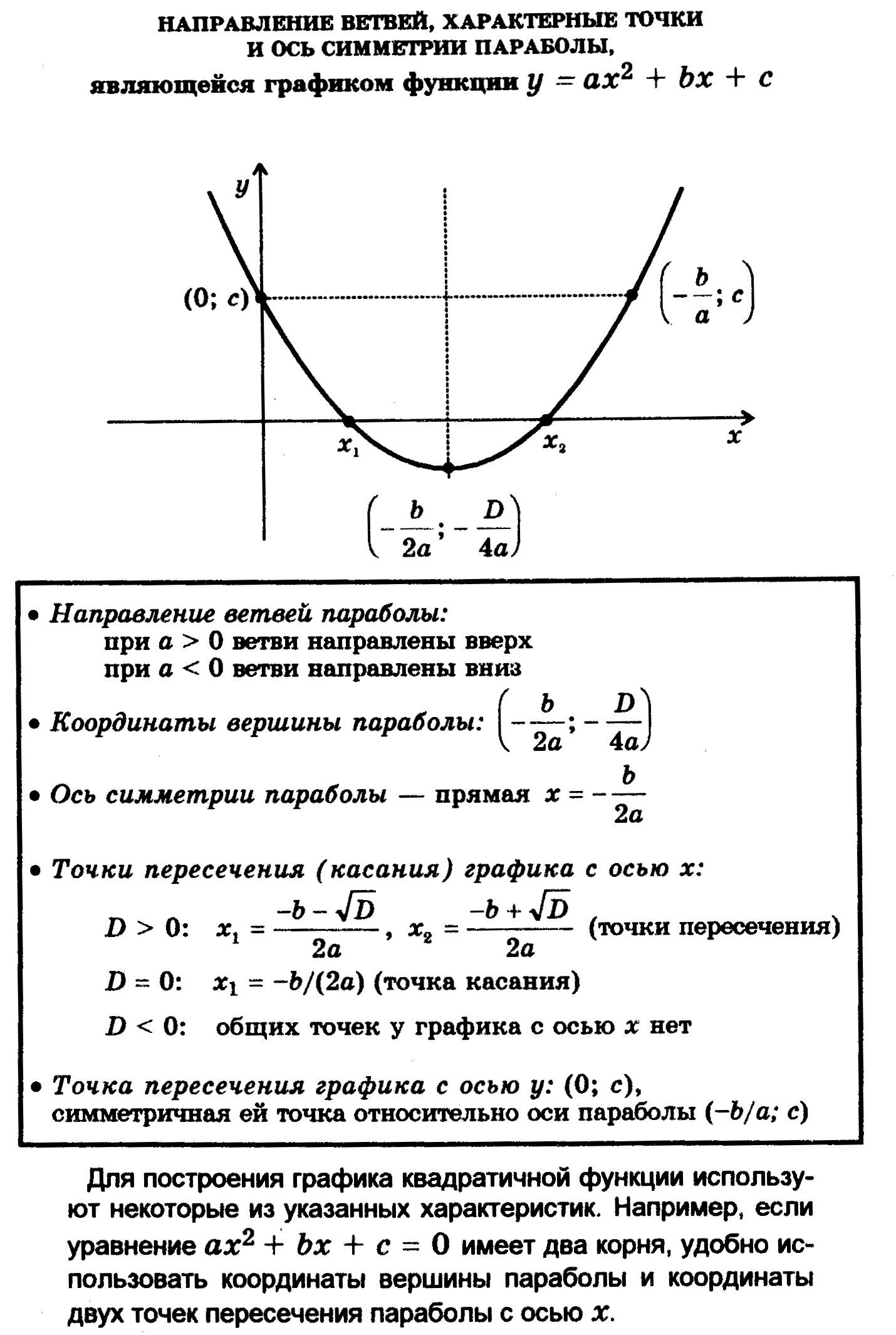
Для реализации этих возможностей команда выводит диалоговое окно, показанное на рис. 5. 16.
Рис. 5. 16 Диалоговое окно встроенных функций
Обратите внимание на то, что запись каждой функции дается в полной синтаксической форме. Это исключает довольно частые ошибки в формулах, вызванные неточностями записи функций. На месте параметров в выведенной функции имеются шаблоны данных для их ввода. Приведенное окно дает полный список встроенных в систему MathCAD функций и является хорошим средством для ознакомления с ними.
5. 11. Установка единиц измерения размерных величин (Units…)
Операция Units… (Единицы) служит для установки единиц измерения размерных величин в заданной системе. Размерные величины широко используются в физических и в научно-технических расчетах.
При использовании операции Units… появляется окно, имеющее список размерных
величин Dimension и относящихся к ним единиц измерения Unit. В окне есть также
указание на то, какая система единиц System используется. Вид окна показан на
рис. 5. 17. По умолчанию используется система единиц SI.
В окне есть также
указание на то, какая система единиц System используется. Вид окна показан на
рис. 5. 17. По умолчанию используется система единиц SI.
Рис. 5. 17 Диалоговое окно вставки единиц измерения размерных величин
Операция Options… в подменю Math главного меню служит для смены используемой системы единиц
Окно вставки единиц измерения размерных величин имеет три кнопки Insert — вставляет выбранную единицу измерения с сохранением окна, OK — вставляет выбранную единицу измерения и закрывает окно, Cancel — отменяет операцию вставки размерных величин
При работе с размерными величинами MathCAD производит необходимые преобразования и выводит числовые значения величин вместе с единицами их измерения
5. 12. Установка шаблона импортируемого рисунка (Picture)
Ценной возможностью систем MathCAD является импорт графических файлов, создаваемых другими графическими системами, например графическими редакторами класса PaintBrush, системами AutoCAD, PCAD и др Это позво ляет включать в документы MathCAD высококачественные графические иллюстрации, что крайне необходимо при создании электронных книг
Перед импортом файла надо подготовить его в соответствующем прило жении и записать
в виде файла в текущий каталог работы Файл может иметь расширение. bmp (BitMap)
Воспринимаются и файлы с расширением msc из прежних версий системы MathCAD
bmp (BitMap)
Воспринимаются и файлы с расширением msc из прежних версий системы MathCAD
Для импорта файла с рисунком достаточно выполнить операцию Picture (Рисунок) — появится шаблон рисунка с единственным маленьким шабло ном в левом нижнем углу В нем надо записать имя файла и, отведя курсор мыши в сторону от рисунка, щелкнуть ее левой клавишей.
Импортируемый рисунок можно, как и любой другой, перемещать с помощью мыши по экрану, растягивать его, выделять и помещать в буфер обмена и т. д. Заглядывая вперед, отметим, что можно перенести в текст документов и множество рисунков из электронного справочника системы. Это заметно облегчает подготовку в среде MathCAD хорошо иллюстрированных учебных программ.
Помимо импорта рисунков из файлов система MathCAD допускает копирование рисунков
из буфера обмена системы Windows. Для этого надо ввести рисунок в этот буфер
(например, используя графический редактор Windows Paint Brush или операции Copy
либо Cut прикладных Windows-программ).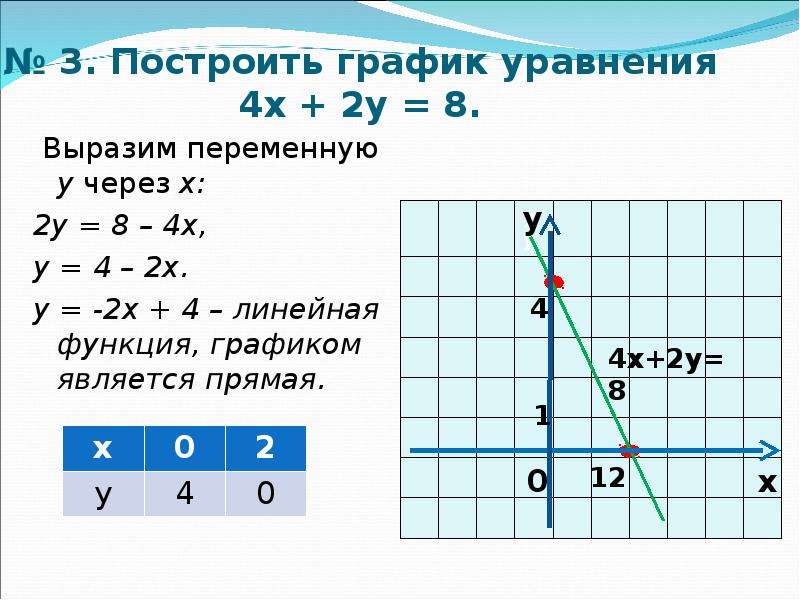 Затем, перейдя к работе с системой MathCAD,
нужно установить курсор на место верхнего левого угла будущего рисунка и выполнить
операцию Paste в позиции Edit главного меню (или нажать клавишу F4).
Затем, перейдя к работе с системой MathCAD,
нужно установить курсор на место верхнего левого угла будущего рисунка и выполнить
операцию Paste в позиции Edit главного меню (или нажать клавишу F4).
5. 13. Вставка текстовой области (Text Region…)
Текстовые области вставляются в документы MathCAD для создания текстовых комментариев. В MathCAD 7. 0 PRO оставлена операция вставки расширяемой текстовой области — Text Region… (Текстовая область). Перед ее применением нужно установить курсор мыши (красный крест) в то место окна редактирования, откуда должен начинаться текст — это левый верхний угол будущей текстовой области. После этого исполняется данная операция и на месте курсора появляется прямоугольник (шаблон текстовой области) с текстовым маркером внутри него.
Перед вводом русскоязычного текста рекомендуется выбрать подходящий шрифт. У многих русскоязычных (кириллических) шрифтов в названии имеется слово «Суг». Если в начале ввода выяснилось, что введена буква не русского алфавита, то при попытке ее стирания шаблон текстовой области исчезает и его придется выводить снова.
5. 14. Вставка в текстовую область математических формул (Math Region…)
В текстовые области нередко надо вставлять математические формулы. Такие объекты не должны быть исполняемыми в отличие от формул в формульных блоках. Эти формулы в ряде случаев (например, при символьных операциях) могут модифицироваться.
Для вставки в текстовые блоки математических формул надо выполнить операцию Math Region… (Математическая область). Кстати, эта операция доступна только в том случае, когда текстовый маркер установлен в нужное место текстовой области. Тогда выполнение операции Math Region… приведет к появлению в текстовой области шаблона в виде маленького черного квадрата. В этом квадрате можно задавать математические формулы, в том числе используя наборные панели с математическими символами.
5. 15. Вставка линии разрыва страницы (Page Break)
Большие документы нередко занимают много страниц. Бывает крайне нежелательно, когда при печати таких документов какой-нибудь график или таблица обрываются линией раздела страниц. Недопустимы и ситуации, когда заголовок раздела оказывается на одной странице, а непосредственно сам раздел начинается на другой.
Для предотвращения таких ситуаций желательно прервать страницу в заданном месте. Для этого служит операция Page Break (Разрыв страницы), вставляющая в документ горизонтальную линию разрыва страницы. На рис. 5. 19 эта линия показана внизу окна редактирования.
5. 16. Вставка гиперссылки (Hyperlink)
Гиперссылки — важный элемент создания сложных документов, обучающих программ и справочных систем. Напомним, что гиперссылка в системе MathCAD представляется подчеркнутым словом, при активизации которого вызывается связанный с ней документ (файл).
Для создания гиперссылки должен быть создан текстовый блок, в котором нужно выделить некоторый фрагмент текста, чаще всего какое-либо слово. Начало создания гиперссылки показано на рис. 5. 20.
После этого надо выполнить операцию Hyperlink (Гиперссылка) с опцией New (Новая) для вывода диалогового окна задания гиперссылки Оно также показано на рис 5. 20 под текстовым блоком В этом окне следует указать в верхнем свободном поле полное имя файла, который будет вызываться данной гиперссылкой В другом поле можно ввести текст сообщения, которое будет появляться в строке состояния (внизу экрана системы) при установке курсора мыши на гиперссылку.
Обычно точное имя файла (с полным путем доступа к нему) запомнить трудно Поэтому, активизируя клавишу Browse (Обзор) окна задания гиперссылки, можно вызвать окно поиска файла — см. рис. 5.21.
После нахождения файла его полное имя появляется в верхнем поле окна гиперссылки, теперь в нижнее поле можно ввести текст сообщения.
Рис. 5. 20 Подготовка к заданию гиперссылки
Для завершения создания гиперссылки достаточно нажать кнопку ОК окна создания гиперссылки. При отказе от ее создания надо нажать кнопку Cancel.
Если установить курсор мыши на гиперссылку, то в строке состояния (внизу экрана системы) появится сообщение, которое было задано ранее. Такие сообщения очень полезны при большом числе ги-перссылок, поскольку позволяют судить об их назначении.
Для осуществления гиперссылки достаточно установить курсор мыши на подчеркнутое слово, гиперссылку, и быстро дважды щелкнуть левой клавишей мыши. Текстовое сообщение, в котором имеется гиперссылка, станет выделенным, и на экране появится вызываемый гиперссылкой докумен.
После ознакомления с вызываемым документом его можно закрыть. До этого возможно редактирование документа. Объектами гиперссылок Могут быть не только документы. Можно, к примеру, дать гиперссылку на рисунок, создаваемый графическим редактором, на электронную таблицу и т. д. Все это позволяет готовить вполне современные и удобные в применении документы не только расчетного, но и информационно-справочного и учебного характера.
Гиперссылку можно убрать с помощью опции Erase (Уничтожить), а также отредактировать, используя опцию Edit… (Редактировать), выводящую окно редактирования гиперссылки.
5. 17. Вставка обращения к заданному файлу активизацией кнопки (Reference…)
Есть еще один удобный способ обращения к заданным файлам путем создания ассоциированного с ними графического объекта — использование кнопок Для этого существует операция Reference… (Ссылка) Она выводит окно задания такой ссылки, показанное на рис 5 25
В этом окне надо либо явно указать полное имя файла (на рис 5 25 это относится к файлу Demo1 mcd), пибо найти его, воспользовавшись кнопкой вызова окна просмотра Browse Нажав далее кнопку ОК, можно вывести по
Рис. 5. 25 Задание гиперссылки в виде кнопки, ассоциированной с файлом
месту расположения курсора мыши кнопку гиперссылки с указанным после нее именем
вызываемого ею файла (вид этой кнопки показан на рис. 5. 25 под окном задания
гиперссылки). Активизация кнопки ОК ведет к появлению окна с вызываемым документом.
Два вида гиперссылок, реализованных в системе MathCAD, расширяют возможности подготовки сложных документов, а возможности использования гиперссылок делают более разнообразными.
5. 18. Связь с другими компонентами системы (Component…)
Одной из главных отличительных особенностей системы MathCAD 7. 0 PRO является возможность подк
Построение графика у — (х)
Иногда бывает полезно разбить члены уравнения /(х) = 0 на две группы, оставив в левой части один или несколько членов и перенеся остальные в правую часть. Тогда уравнение примет вид/1(х) =/з ( ). после чего следует вычертить два графика у = /1 (х) и у =/2 (х) и найти точки пересечения построенных графиков. Абсциссы этих точек являются искомыми корнями уравнения /М=0. [c.237]Рекуррентное соотношение (4.3.13) может быть представлено графически путем одновременного построения графиков у = у(х) и у = х. Пусть Р — I — точка (х У(х 1)) на плоскости (х, у). Чтобы найти точку проведем горизонтальную прямую через точку 1 до пересечения с линией у = X в точке. Затем проведем вертикальную прямую через точку [c.59]
Построение графика показывает, что опытные точки достаточно близко располагаю -ся около прямой линии, поэтому формулу задаем в виде у=аа- -а[Х. [c.94]
Для построения графика функции, являющейся производной от функции у = у(х), которая задана своим графиком, проводим в точке А1 кривой касательную i к этой кривой (рис. 96). Эта касательная образует с осью х угол а. Откладываем по оси абсцисс влево от начала координат отрезок Ор = Н, называемый полюсным расстоянием. Затем проводим из полюса р прямую pd, параллельную касательной 1. к заданной кривой N в точке М. Умножив и разделив выражение (4.18) на величину [c.64]
Вместо построения графика F(x) как функции х (см. фиг. 2.1) иногда целесообразно построение графика х как функции F х), т. е. G [f(A )], которая обозначена через у. Из формулы (2.34) следует, что зависимость между х и у линейная. Название вероятностной бумаги связано с методом масштабирования оси у, закон распределения [c.63]
Для построения графика функции > = f(x) необходимо задать совокупность точек х и у. Для аргумента х это выполняется оператором цикла, для — надлежащим программированием выражения для функции, т.е. необходимо применять знаки арифметических операций над массивами [c.250]
В основном она используется совместно с функциями построения графиков трехмерных поверхностей. Функция преобразует область, заданную векторами х у, в массивы X и Y, которые могут быть использованы для вычисления функции двух переменных и построения трехмерных графиков. Строки выходного массива X являются копиями вектора х, а столбцы У — копиями вектора у. [c.252]
Пример построения графика трехмерной поверхности z = х + у [c.253]
Для построения графика работы берем оси координат Ох и Оу, причем на оси х откладываем малые отрезки S, а на оси у— проекции силы на направление скорости или пути, т. е. Р os о.. [c.107]
Отрицательное натяжение означает, что при отсутствии измеряемой силы струна провисает (зона нестабильности). Если при построении графика принимать характерный размер Ь в ( юрмуле (Х.4), то ордината обобщенной характеристики идеального преобразователя равна единице, если же использовать выражение (Х.5), то ордината в области автомодельности по л равна У/2/Из графика видно, что область использования струн ограничена с одной стороны [c.310]
Для построения графика функции (6.61) рассмотрим геометрический сТу Ысл параметров и 0. Из формулы (6.61) видно, что кривая у = (р(х) достигает максимума при х = гпх, причем г/ ах = = 1/а]/ 2-. С ростом а максимальное значение уменьшается, а так как площадь, ограниченная всей кривой и осью абсцисс равна единице, то с ростом о кривая растягивается вдоль всей оси [c.145]
Преимущество изложенного способа в том, что для построения графика функции в этом случае нет необходимости вычислять значения функции у с определенной ступенью А достаточно иметь таблицу значений у в зависимости от изменяющихся со ступенью Дх значений аргумента х. [c.14]
Линии регрессии, как показано на рис. 26, пересекаются в точке О х, у), соответствующей средним арифметическим значениям корреляционно связанных друг с другом признаков У и X. При построении графиков регрессии по оси абсцисс от- [c.256]
Аналитический способ построения наглядных изображений с позиций машинной графики сводится к вычислению координат и, V проекции некоторой точки оригинала по ее известным координатам х, у, г [c.193]
Для ускорения приближенных расчетов можно использовать графики зависимости у — /(х) (рис. 3.2.2), построенные на основе формулы (3.2.2). При проведении таких расчетов параметр х может оказаться отрицательным (например, при повороте горизонтальных консолей летательного аппарата, движущегося под нулевым углом атаки). В этом случае следует вначале определить из графиков на рис. 3.2.2 условные координаты Ув) >о и (Ун)Г>о для положительного [c.257]
На рис. XII.2 приведены графики зависимостей Р = Р(у) для тре.х значений ф, построенные на основании решения задачи о продольном изгибе достаточно длинного упругого консольного стержня. Это решение получено путем интегрирования точного дифференциального уравнения упругой линии стержня (У.47) [c.352]
Построение -по графику функции у = = / (х) графика ее производной у = =/ (л ) называется графическим дифференцированием и выполняется следующим образом. [c.143]
Количества тепла, получаемые за год от основных и пиковых подогревателей, могут быть определены по годовому графику расхода тепла фиг. 4-14, на котором линия ху разделяет указанные количества тепла. Точки х и у находят построением, ясным фиг. 4-14. Промежуточные точки линии ху находят аналогично определению точек. V и у. [c.341]
Рассматривая одну из исследуемых величин у как функцию второй величины х, наносят результаты опытов, т. е. соответственные значения х и г/ на график в виде точек, которые и служат основой построения кривой. При графическом изображении данных рекомендуется учитывать следующие замечания. [c.15]
На практике часто встречается тот случай, когда задан (или построен по точкам) график (/ , 5) (рис, 77) касательной составляющей силы в зависимости от дуговой координаты 5 точки на кривой введем еще оси Оху и пусть 5 = ХзХ, Гг = х/у, где X, у — отрезки чертежа в сантиметрах, а (Л8, if — масштабные коэффициенты для длин и сил. Мы имеем [c.191]
Типичная зависимость коэффициента х от полного угла закрученности Р показана на рис. 49 (график построен для стержня, у которого отношение главных жесткостей равно 0,2). При углах Р, возрастающих от нуля до значения 2я, коэффициент х постепенно увеличивается, но при больших значениях он остается практически постоянным. [c.53]
Кроме поля рассеяния размеров точность обработки характеризует также закон распределения размеров (кривая распределения). Для построения кривых распределения производят измерения данного размера на определенном количестве деталей (от 50 до 250 деталей). Совокупность измерений деталей разбивают на ряд групп размеров с одинаковыми интервалами, например, О—0,02 0,02— 0,04 мм и т.д. По полученным данным строят график (рис. 193), в котором по оси абсцисс х откладывают размеры групп деталей, а по оси ординат у — число деталей т с размерами в пределах соответствующих групп (частота повторения размеров). [c.276]
Построитель ДРП-ЗМ предназначен для построения графика функции Р (г, у) = О на плоскости в прямоугольной системе координат X, У. Величины X и у в свою очередь являются функциями времени х = = f и), У = I (Й и представляют собой мгновенные значения напря- [c.192]
Очевидно, этот множитель велик, если точки сгруппированы в области значений х, узкой по сравнению с минимальным значением х . Обычно так и бывает при построении графика Дингла, так как диапазон полей, в пределах которого наблюдаются осцилляции, весьма ограничен. Некоторое представление о порядке величины множителя у можно получить, рассмотрев особый случай равномерного распределения значений х. с интервалом с1, т. е. [c.636]
Случай 1 в положении равновесия функция У[рс) имеет минимум. В ма лой окрестности положения равновесия х = х. график У х) имеет в представленный на рис. 2.34,д. Построение фазового портрета в этой ок рестности легко проводится графическим способом на основе формулы [c.80]
Потенциальная энергия равна У(х) = ( //)( 1 — С05Х). График У(х) и построенный по нему фазовый портрет см. на рис. П.35. [c.356]
На рис. 4.1.20 приведена построенная по данным табл. Б векторная диаграмма коэффициеета деления, а на рис. 4.1.2I- 4.1.24 — графики функций р= (х) р=12 у), Р= 4(У — При построении этих диаграмм и графику с помощью интерполяции были найдены положения критической точки С, где рс=ро=1, и точек, для которых р=0 (одна из таких то чек совпала с точкой А передней кромки), а также значение коэффициента давления рв в точке В задней кромки (см. рис. 4,1.20 4.1,24). [c.172]
Трехмерные поверхности описываются функцией двух переменных Z = f x,y). Построение трехмерных графиков требует определения для х ж у двумерных массивов — матриц. Для создания таких массивов служит функция meshgrid, которая записывается следуюш,им образом [c.252]
Шкалы отсчета допусков являются одним из графических способов выражения функциональной зависимости допуска от определяющих его параметров и параметрических комплексов. Они представляются в виде совокупности линейно расположенных отметок, которые изображают параметрический ряд последовательных чисел, соответствующих значениям выбираемых параметров и отсчитываемых допусков. Шкалы отсчета допусков соответствуют уравнению или графику функции у = ах и имеют два вида с равными по величине делениями для допусков и неравными возрастающими по величине делениями — интервалами для параметров. Разбивкой диапазона размеров на интервалы при построении параметрического ряда формируют размерную шкалу, на которой каждый интервал рассматривают как определение отклонения эквивалентности в множестве значений размеров на всем диапазоне (рис. 2.3). Неравенства (х, —Ах)классов эквивалентности) в ь ожестве возможных значений размеров х на всем диапазоне, где Ах равно половине расстояния от среднего до крайнего размера интервала. Для определения допусков и отклонений в системе ИСО принимают среднее геометрическое В крайних размеров каждого интервала, т.е. В = у/в В . [c.61]
Кривые анизотропии пределов прочности при одноосном растяжении или сжатии. Графики изменения относительной величины предела прочности Ов/Оо в зависимости от угла наклона волокон а, построенные А. Н. Флак-серманом по экспериментальным данным, представлены пунктирными линиями на рис. 3.1 и 3.2. Величины Од определялись по диаграммам испытаний. Рис. 3.1 соответствует радиальной, а рис. 3.2 — тангенциальной плоскости, в которых расположены оси всех образцов древесины. Различный вид диаграмм испытания и полиморфизм разрушения образцов привели А. Н. Флаксермана к предположению о связи пределов прочности оГд с величинами напряжений Од., Оу и х у, действующих в сжатом образце по площадкам, параллельным волокнам (рис. 3.3). [c.135]
| Рис. 4.174. Графики зависимости деформация — время, построенные по результатам опытов Хартмана с образцами из 70-30а-латуни, выполненных при помощи двух дифракционных решеток. Я добавил вычисленные значения продолжительности прохождения волны (от ударяемого торца до сечения, отстоящего от него на расстоянии х) и теоретические значения наибольших деформаций при У=0 (сплошная линия), при У= 14 ООО фунт/дюйм (экспериментально найденный квазнстатический предел упругости) и при У = 27 700 фунт/дюйм (динамический предел упругости, найденный по экспериментальному значению Еу)- I — теоретическое значение полученное с использованием параболической зависимости а—е Белла при |
Количества тепла, получаемые за год от основных и пиковых подогревателей, разделяются на годовом графике расхода тепла (фиг. 6-16) линией х—у, точки которой находят построением, ясным из фиг. 6-1би6-17. [c.387]
Технический анализ
(Часть 5): Точечные диаграммы
На прошлой неделе в Части 4 мы рассмотрели графики свечей. На этой неделе мы рассмотрим один из старейших методов построения графиков, популяризированных на Западе: графики Point and Figure. Кому-то диаграммы «Пунктир-н-рисунок» выглядят как прославленная игра в крестики-нолики! Для других они просто бессмысленны или бесполезны. К сожалению, интерес к диаграммам «Point and Figure» ослабевает, и это досадно, потому что, если вы копнете немного глубже, они могут быть очень эффективным подходом к построению графиков, который вы могли бы использовать для своей торговли и инвестирования.Они могут предложить гибкость и другой взгляд на ценовое действие.
История точек и фигур
Этот стиль построения диаграмм существует с 1880-х годов и предшествует гистограммам. Все началось с системы тиковых графиков, разработанной из практической необходимости фиксировать рыночные цены на ходу. Трейдеры разработали эффективную систему регистрации цен, отказавшись от прежних очень утомительных методов регистрации. Его начало было в системе, которая строила ценовые точки между установленным диапазоном, и когда ценовые точки достигли диапазона, число было проиллюстрировано.Отсюда и название этого метода построения графиков.
Основы «Point and Figure»:
- Это исследование чистого движения цены, т.е. оно не принимает во внимание «время» при построении своих графиков (хотя большинство графических пакетов оставляют «время» на Ось X).?
- Регистрируются только изменения цен. Если изменений нет, диаграмма остается нетронутой.
- Point and Figure игнорирует номера томов — фактически объем представлен по-другому i.е. через активность изменения цены на графике. Чем тяжелее активность, тем больше изменений фиксируется.
- Чувствительность графиков можно варьировать, чтобы отображать краткосрочные / среднесрочные / долгосрочные графики, основанные на одних и тех же данных.
- Точечные и графические диаграммы очень хороши для поиска поддержки и сопротивления.
- Запись движения цены на точечных и графических диаграммах — это совсем другой процесс, чем на гистограммах. Он использует столбцы X и O. Опять же: X = движение вверх / рост цен, O’s = движение вниз / падение цены.?
- Диаграмма имеет два основных параметра: значение бокса и критерии разворота. Вы бы изменили их, чтобы увеличить / уменьшить чувствительность графика и количество торговых сигналов, которые вы получаете.?
- Увеличение размера коробки предлагает…
Правила и интерпретация контрольных карт
Март 2016
Контрольные диаграммы — ценный инструмент для мониторинга производительности процесса.Однако вы должны уметь интерпретировать контрольную диаграмму, чтобы она представляла для вас какую-либо ценность. Общение важно в твоей жизни? Конечно, и на работе, и дома. Вот ключ к эффективному использованию контрольных диаграмм — контрольная диаграмма — это способ взаимодействия процесса с вами. Через контрольную диаграмму процесс сообщит вам, все ли находится «под контролем» или существует проблема. Потенциальные проблемы включают большие или маленькие сдвиги, тенденции к росту или снижению, точки, чередующиеся вверх и вниз с течением времени, и наличие смесей.
В публикации этого месяца рассматриваются 8 правил, которые вы можете использовать, чтобы помочь вам интерпретировать то, что вам сообщает контрольная диаграмма. Эти правила помогут вам определить, когда изменение на вашей контрольной диаграмме больше не является случайным, а образует шаблон, который описывается одним или несколькими из этих восьми правил. Эти шаблоны дают вам представление о том, что может быть причиной «особых причин» — проблемы в вашем процессе.
В этом выпуске:
Вы можете скачать эту публикацию в формате pdf по этой ссылке.Вы также можете оставить комментарий в конце публикации.
Обзор вариации
Мы рассмотрели вариации в 11 публикациях за эти годы. Вот выдержка из одного:
«Я время от времени проливал стакан молока, когда был маленьким. Наш стол был наклонен к тому месту, где сидела моя мать. Так что молоко всегда направлялось в ее сторону. И она обычно произносила какие-то избранные слова, когда это происходило. Конечно, я был виноват. Мне нужно было быть более осторожным. Или это действительно так? Если вы поймете вариации, вы поймете, что большинство проблем, с которыми вы сталкиваетесь, возникают не из-за отдельных людей, а из-за процесса — как он был разработан и как управляется изо дня в день.
Вариация происходит из двух источников: общих и особых причин. Подумайте, сколько времени у вас уходит на работу утром. Может быть, на это у вас уходит в среднем 30 минут. В некоторые дни это может занять немного больше времени, в некоторые — короче. Но пока вы находитесь в определенном диапазоне, вас это не беспокоит. Диапазон может составлять от 25 до 35 минут. Эта вариация представляет собой вариацию по общей причине — это вариация, которая всегда присутствует в процессе. И этот тип вариаций является последовательным и предсказуемым.Вы не знаете, сколько времени потребуется, чтобы добраться до работы завтра, но вы знаете, что это займет от 25 до 35 минут, если процесс останется прежним.
Теперь предположим, что у вас спустило колесо, когда вы едете на работу. Как долго ты добираешься до работы? Определенно дольше, чем 25–35 минут в вашем «обычном» варианте. Может, это займет у вас на час больше. Это особая причина вариаций. Что-то другое. Произошло то, чего не должно было случиться. Это не часть обычного процесса.Особые причины непредсказуемы и носят спорадический характер.
Почему важно знать, какие вариации присутствуют в вашем процессе? Потому что действия, которые вы предпринимаете для улучшения вашего процесса, зависят от типа имеющихся вариаций. Если присутствуют особые причины, вы должны найти причину проблемы и, если возможно, устранить ее от повторного появления. Обычно это ответственность человека, наиболее близкого к процессу. Если присутствуют только общие причины, вы должны ФУНДАМЕНТАЛЬНО изменить процесс.Ключевое слово — фундаментально — требуется серьезное изменение процесса, чтобы уменьшить общие причины отклонений. И руководство несет ответственность за изменение процесса.
Было подсчитано, что 94% проблем, с которыми сталкивается компания, вызваны общими причинами. Только 6% вызваны особыми причинами (которые могут быть связаны или не связаны с людьми). Итак, если вы всегда обвиняете в проблемах людей, вы будете ошибаться, по крайней мере, в 85% случаев. В большинстве случаев необходимо изменить процесс. Руководство должно настроить систему, чтобы разрешить изменение процессов.«
Обзор контрольной картыЕдинственный эффективный способ отделить общие причины от особых причин отклонений — использовать контрольные карты. Контрольная диаграмма отслеживает переменную процесса с течением времени — например, время до работы. Среднее значение рассчитывается после того, как у вас будет достаточно данных. Рассчитываются контрольные пределы — верхний контрольный предел (UCL) и нижний контрольный предел (LCL). UCL — это наибольшая ценность, которую вы ожидаете от процесса с присутствующими только общими причинами отклонений.LCL — это наименьшее значение, которое можно ожидать при наличии только общей причины отклонений. Пока все точки находятся в пределах и нет шаблонов, присутствуют только общие причины отклонений. Говорят, что процесс находится «под контролем».
На рис. 1 показан пример контрольной диаграммы с использованием примера движения на работу. Каждый день измеряется время, чтобы добраться до работы. Затем данные наносятся на контрольную диаграмму. Рассчитывается среднее значение. Среднее значение составляет 26,2, что означает, что в среднем каждый день требуется 26.2 минуты до работы. Затем рассчитываются контрольные пределы. UCL составляет 41,9 минуты. Это максимальное время, которое потребуется, чтобы приступить к работе, когда присутствуют только общие причины. LCL составляет 10,6 минут. Это минимальное время, которое потребуется, чтобы приступить к работе, когда присутствуют только общие причины. Пока все точки находятся в контрольных пределах и нет закономерностей, процесс находится в статистическом контроле.
Рисунок 1: Пример контрольной диаграммы
На рисунке 1 есть одна точка за пределами UCL.Это первый паттерн, который указывает на неконтролируемую точку — особую причину вариаций. Одна из возможных причин — спущенное колесо. Есть много других возможных причин — поломка машины, плохая погода и т. Д.
Особые причины отклонений обнаруживаются на контрольных диаграммах по определенным типам паттернов, которые появляются на контрольной диаграмме. Точка за пределами контроля — одна из таких закономерностей. Вы можете увидеть паттерн из 7 последовательных пунктов выше среднего. Этот шаблон указывает на то, что что-то произошло, что привело к увеличению среднего значения вашего процесса — налицо особая причина.Распознавание закономерностей — и того, что они означают в вашем процессе — является одним из ключей к поиску причин особых причин. Все правила контрольной диаграммы — это паттерны, которые формируются на контрольной диаграмме, чтобы указать на наличие особых причин отклонений.
Некоторые из этих моделей зависят от «зон» на контрольной диаграмме. Чтобы увидеть, выходят ли эти паттерны, контрольный график разделен на три равные зоны выше и ниже среднего. Это показано на рисунке 2.
Рисунок 2: Контрольная карта, разделенная на зоны
Зона C — зона, наиболее близкая к средней.Он представляет собой площадь от среднего до одной сигмы выше среднего. Соответствующая зона C ниже среднего. Зона B — это зона от одной до двух сигм выше среднего. Опять же, есть соответствующая зона B ниже среднего. Зона A — это зона от двух до трех сигм выше среднего, а также ниже среднего.
8 правил контрольных карт
Если процесс находится в статистическом контроле, большинство точек будут близки к среднему, некоторые — ближе к контрольным пределам, и никакие точки не будут выходить за контрольные пределы.8 правил контрольной диаграммы, перечисленные в таблице 1, указывают на наличие особых причин отклонений. Опять же, они представляют собой шаблоны.
Таблица 1: Правила контрольной диаграммы
Правило | Название правила | Образец |
1 | Вне пределов | Одна или несколько точек за пределами контроля |
2 | Зона A | 2 из 3 последовательных точек в зоне А или за ее пределами |
3 | Зона B | 4 из 5 последовательных точек в зоне B или за ее пределами |
4 | Зона C | 7 или более последовательных точек по одну сторону от среднего (в зоне C или за ее пределами) |
5 | Тренд | 7 последовательных точек с восходящей или нисходящей тенденцией |
6 | Смесь | 8 последовательных точек без точек в зоне C |
7 | Стратификация | 15 последовательных точек в зоне C |
8 | Чрезмерный контроль | 14 последовательных точек, чередующихся вверх и вниз |
Следует отметить, что цифры могут отличаться в зависимости от источника.Например, некоторые источники будут использовать 8 последовательных точек на одной стороне среднего (тест зоны C) вместо 7, показанных в таблице выше. Но все они очень похожи. Рисунки с 3 по 5 иллюстрируют шаблоны. На рисунке 3 показаны шаблоны для правил с 1 по 4.
Рисунок 3: Тесты зон (правила с 1 по 4)
Правила 1 (точки за контрольными пределами) и 2 (тест зоны А) представляют собой внезапные большие отклонения от среднего значения. Они часто бывают мимолетными — разовое происшествие по особой причине — например, спущенное колесо при движении на работу.
Правила 3 (зона B) и 4 (зона C) представляют меньшие смены, которые поддерживаются с течением времени. Изменение сырья может вызвать эти меньшие сдвиги. Ключевым моментом является то, что сдвиги поддерживаются во времени — по крайней мере, в течение более длительного периода времени, чем правила 1 и 2.
На рисунке 4 показаны правила 5 и 6. Правило 5 (тенденция вверх или тенденция вниз) представляет процесс, который имеет тенденцию в одном направлении. Например, износ инструмента может вызвать такую тенденцию. Правило 6 (смесь) возникает, когда у вас присутствует более одного процесса и вы производите выборку для каждого процесса отдельно.Отсюда и термин «смесь». Например, вы можете получать данные из четырех разных смен. Смены 1 и 2 работают с другим средним значением, чем смены 3 и 4. На контрольной диаграмме могут быть смещения 1 и 2 в зоне B или выше среднего значения, а смещения 3 и 4 в зоне B ниже среднего — и ничего в зоне C.
Рисунок 4: Правила 5 и 6
На рисунке 5 показаны правила 7 и 8. Правило 7 (стратификация) также возникает, когда у вас есть несколько процессов, но вы включаете все процессы в подгруппу.Это может привести к тому, что данные «охватывают» среднее значение — все точки в зоне C без точек за пределами зоны C. Правило 8 (чрезмерный контроль) часто связано с чрезмерной настройкой. Это часто называют «вмешательством» в процесс. Регулировка процесса, находящегося под статистическим контролем, на самом деле увеличивает вариацию процесса. Например, оператор пытается достичь определенного значения. Если результат выше этого значения, оператор выполняет корректировку, чтобы уменьшить значение. Если результат ниже этого значения, оператор вносит коррективы, чтобы увеличить значение.В результате получается зубчатый рисунок.
Рисунок 5: Правила 7 и 8
Правила 6 и 7, в частности, часто применяются из-за способа разделения данных на подгруппы. Рациональное разделение на подгруппы — важная часть создания эффективной контрольной карты. Предыдущая публикация демонстрирует, как может происходить смешение и стратификация на основе выбранной подгруппы.
Эти правила представляют разные ситуации — шаблоны = на контрольном графике. Следует отметить, что не все правила применимы ко всем типам контрольных диаграмм.В таблице 2 приведены сводные правила по типам узоров.
Таблица 2: Правила по типу шаблона
Образец Описание | Правила |
Большие отклонения от среднего | 1, 2 |
Небольшие отклонения от среднего | 3, 4 |
Тенденции | 5 |
Смеси | 6 |
Стратификации | 7 |
Чрезмерный контроль | 8 |
Возможные причины по шаблону
Трудно перечислить возможные причины для каждого шаблона, потому что особые причины (как и общие причины) очень зависят от типа процесса.Производственные процессы имеют другие проблемы, чем процессы обслуживания. Различные типы контрольных диаграмм рассматривают разные источники отклонений. Тем не менее, полезно указать некоторые возможные причины с помощью описания паттернов. В таблице 3 делается попытка сделать это в зависимости от типа шаблона.
Таблица 3: Возможные причины по образцу
Образец Описание | Правила | Возможные причины |
Большие отклонения от среднего | 1, 2 | Новый человек выполняет работу Неправильная установка Ошибка измерения Шаг процесса пропущен Этап процесса не завершен Сбой питания Поломка оборудования |
Небольшие отклонения от среднего | 3, 4 | Замена сырья Изменение рабочей инструкции Другой измерительный прибор / калибровка Другая смена Человек приобретает больше навыков при выполнении работы Изменение в программе ТО Изменение процедуры настройки |
Тенденции | 5 | Износ инструмента Температурные эффекты (охлаждение, нагрев) |
Смеси | 6 | Присутствует более одного процесса (e.грамм. смены, машины, сырье.) |
Стратификации | 7 | Наличие более одного процесса (например, смены, машины, сырье) |
Чрезмерный контроль | 8 | Взлом оператора Альтернативное сырье |
Таблица 3 дает некоторые рекомендации о том, о чем следует думать, пытаясь найти причины особых причин.Например, если нарушается Правило 1 или Правило 2, вы должны спросить: «Что в этом процессе может вызвать большое отклонение от среднего значения?». Или, если возникает правило 6, вы должны спросить: «Что в этом процессе может привести к тому, что будет присутствовать более одного процесса?» Вопросы такого типа могут помочь в ходе мозгового штурма найти причины особой причины отклонений. Тип паттерна может помочь вам в анализе неконтролируемой точки.
Сводка
В этой публикации были рассмотрены 8 правил контрольной диаграммы для определения наличия особой причины отклонений.Правила описывают определенные закономерности вариации, которые помогут вам понять, где искать особую причину вариации. Ни одна таблица не может дать вам причины выхода из-под контроля точек в вашем процессе. Вы должны использовать свои собственные знания (и знания тех, кто ближе всего к процессу), чтобы обнаружить причину.
Видео: расшифровка контрольных диаграмм
Основные типы диаграмм для визуализации данных
Диаграммы являются неотъемлемой частью работы с данными, поскольку они позволяют объединить большие объемы данных в простой для понимания формат.Визуализация данных может помочь в понимании того, кто смотрит на данные впервые, а также передать результаты другим людям, которые не видят необработанные данные. Существует бесчисленное множество типов диаграмм, каждый из которых имеет разные варианты использования. Часто самая сложная часть создания визуализации данных — это выяснить, какой тип диаграммы лучше всего подходит для поставленной задачи.
Ваш выбор типа диаграммы будет зависеть от множества факторов. Какие типы показателей, функций или других переменных вы планируете отобразить? Какую аудиторию вы планируете представить — это всего лишь начальное исследование для вас самих или вы представляете более широкую аудиторию? Какой вывод вы хотите, чтобы читатель сделал?
В этой статье мы дадим обзор основных типов диаграмм, которые чаще всего предлагаются инструментами визуализации.С этими диаграммами у вас будет широкий набор инструментов для удовлетворения ваших потребностей в визуализации данных. Рекомендации по выбору каждого из них в зависимости от варианта использования описаны в следующей статье.
Основополагающая четверка
В своей книге «Покажи мне числа» Стивен Фью предлагает четыре основных кодировки для числовых значений, указывая позиционное значение с помощью полос, линий, точек и прямоугольников. Итак, мы начнем с четырех основных типов диаграмм, по одному для каждого из этих способов кодирования значений.
Гистограмма
На гистограмме значения обозначаются длиной столбцов, каждая из которых соответствует измеряемой группе.Гистограммы могут быть ориентированы вертикально или горизонтально; вертикальные гистограммы иногда называют столбчатыми диаграммами. Горизонтальные гистограммы — хороший вариант, когда у вас есть много столбцов для построения или надписи на них требуют дополнительного места, чтобы их можно было разобрать.
График
Линейные диаграммы показывают изменения значений при непрерывных измерениях, например, сделанных с течением времени. Движение линии вверх или вниз помогает выявить положительные и отрицательные изменения соответственно. Он также может выявить общие тенденции, чтобы помочь читателю делать прогнозы или прогнозы относительно будущих результатов.Множественные линейные диаграммы также могут привести к появлению других связанных диаграмм, таких как спарклайновый или линейный график.
Диаграмма рассеяния
Диаграмма рассеяния отображает значения двух числовых переменных с использованием точек, расположенных на двух осях: по одной для каждой переменной. Диаграммы разброса — это универсальная демонстрация взаимосвязи между нанесенными на график переменными — независимо от того, является ли эта корреляция сильной или слабой, положительной или отрицательной, линейной или нелинейной. Диаграммы разброса также отлично подходят для определения точек выбросов и возможных пробелов в данных.
Коробчатая делянка
Коробчатая диаграмма использует прямоугольники и усы для суммирования распределения значений в измеренных группах. Положение концов прямоугольника и усов показывает области, в которых находится большая часть данных. Чаще всего мы видим коробчатые диаграммы, когда у нас есть несколько групп для сравнения друг с другом; другие диаграммы с более подробной информацией предпочтительнее, когда у нас есть только одна группа для построения.
Таблицы и отдельные значения
Прежде чем переходить к другим типам диаграмм, стоит уделить время тому, чтобы оценить возможность отображения только необработанных чисел.В частности, когда у вас есть только одно число, простое отображение значения является разумным подходом к отображению данных. Когда точные значения представляют интерес для анализа, вы можете включить их в сопроводительную таблицу или с помощью аннотаций в графической визуализации.
Общие вариации
Дополнительные типы диаграмм могут появиться в результате изменения способов использования кодировок или включения дополнительных кодировок. Вторичные кодировки, такие как площадь, форма и цвет, могут быть полезны для добавления дополнительных переменных в более простые типы диаграмм.
Гистограмма
Если группы, изображенные на гистограмме, на самом деле представляют собой непрерывные числовые диапазоны, мы можем сдвинуть столбцы вместе, чтобы создать гистограмму. Длины полос на гистограммах обычно соответствуют количеству точек данных, а их шаблоны демонстрируют распределение переменных в ваших данных. Другой тип диаграммы, такой как линейная диаграмма, как правило, используется, когда значение по вертикали не является счетчиком частоты.
Гистограмма с накоплением
Одной из модификаций стандартной столбчатой диаграммы является разделение каждого столбца на несколько столбцов меньшего размера на основе значений второй группирующей переменной, называемой столбчатой диаграммой с накоплением.Это позволяет не только сравнивать значения основных групп, как на обычной гистограмме, но и проиллюстрировать относительную разбивку каждой группы в целом на составные части.
Сгруппированная линейчатая диаграмма
Если, с другой стороны, суббары размещать бок о бок в кластеры, а не хранить их стопками, мы получим сгруппированную гистограмму. Сгруппированная столбчатая диаграмма не позволяет сравнивать итоги основной группы, но гораздо лучше позволяет сравнивать подгруппы.
Точечная диаграмма
Точечная диаграмма похожа на гистограмму тем, что показывает значения для различных категориальных группировок, но кодирует значения на основе положения точки, а не длины столбца. Точечные диаграммы полезны, когда вам нужно сравнить по категориям, но нулевой базовый уровень не является информативным или полезным. Вы также можете думать о точечном графике как о линейном графике с удаленной линией, чтобы его можно было использовать с переменными с неупорядоченными категориями, а не просто с непрерывными или упорядоченными переменными.
Диаграмма с областями
Диаграмма с областями начинается с того же основания, что и линейная диаграмма — точки значений, соединенных линейными сегментами, — но добавляет концепцию гистограммы с затенением между линией и базовой линией. Эту диаграмму чаще всего можно увидеть в сочетании с концепцией суммирования, чтобы показать, как общая сумма менялась с течением времени, а также как менялись вклады ее компонентов.
Диаграмма с двумя осями
Двухосные диаграммы накладываются на две разные диаграммы с общей горизонтальной осью, но могут иметь разные масштабы вертикальной оси (по одной для каждой диаграммы компонентов).Это может быть полезно, чтобы показать прямое сравнение между двумя наборами вертикальных значений, а также включить контекст переменной горизонтальной оси. Обычно используются разные типы базовых диаграмм, такие как комбинация столбцов и линий, чтобы избежать путаницы с разными масштабами осей для каждой диаграммы компонентов.
Пузырьковая диаграмма
Другой способ показать взаимосвязь между тремя переменными — это модификация диаграммы рассеяния. Когда третья переменная является категориальной, точки могут использовать разные формы или цвета для обозначения членства в группе.Если точки данных упорядочены каким-либо образом, точки также можно соединить отрезками линии, чтобы показать последовательность значений. Когда третья переменная является числовой по своей природе, именно здесь появляется пузырьковая диаграмма. Пузырьковая диаграмма строится на основе базовой диаграммы рассеяния, поскольку значение третьей переменной определяет размер каждой точки.
Кривая плотности
Кривая плотности или оценка плотности ядра — это альтернативный способ отображения распределения данных вместо гистограммы.Вместо того, чтобы собирать точки данных в интервалы частот, каждая точка данных вносит небольшой объем данных, совокупность которых становится кривой плотности. Хотя кривые плотности могут означать некоторые значения данных, которых не существует, они могут быть хорошим способом сгладить шум в данных, чтобы получить представление о сигнале распределения.
Сюжет для скрипки
Альтернативой подходу коробчатой диаграммы к сравнению распределения ценностей между группами является сценарий скрипки. В сюжете скрипки каждый набор ящиков и усов заменяется кривой плотности, построенной вокруг центральной базовой линии.Это может обеспечить лучшее сравнение форм данных между группами, хотя и проигрывает при сравнении точных статистических значений. Частым вариантом для скрипичных сюжетов является добавление пометок в виде прямоугольников поверх скрипичного сюжета, чтобы получить лучшее из обоих миров.
Тепловая карта
Тепловая карта представляет собой сетку значений на основе двух интересующих переменных. Переменные оси могут быть числовыми или категориальными; сетка создается путем разделения каждой переменной на диапазоны или уровни, такие как гистограмма или гистограмма.Ячейки сетки окрашиваются в зависимости от значения, часто более темными цветами, соответствующими более высоким значениям. Тепловая карта может быть интересной альтернативой диаграмме рассеяния, когда нужно построить много точек данных, но плотность точек затрудняет определение истинной взаимосвязи между переменными.
Карты специалистов
Существует множество дополнительных диаграмм, которые кодируют данные другими способами для конкретных случаев использования. Xenographics включает в себя набор некоторых причудливых диаграмм, которые преследовали очень конкретные цели.Тем не менее, некоторые из этих диаграмм имеют достаточно распространенные варианты использования, которые можно считать необходимыми.
Круговая диаграмма
Вы можете быть удивлены, увидев здесь, в разделе «специалистов», круговые диаграммы, учитывая, насколько часто они используются. Однако круговые диаграммы используют необычную кодировку, отображающую значения как области, вырезанные из круглой формы. Поскольку круговая диаграмма обычно не имеет маркировки значений по периметру, обычно трудно получить хорошее представление о точных размерах срезов.Тем не менее, круговая диаграмма и ее двоюродный брат — бублик-график — превосходно говорят читателю, что сравнение частей и целых должно быть основным выводом из визуализации.
Воронкообразная диаграмма
Воронкообразная диаграмма часто встречается в бизнес-контексте, где посетителей или пользователей необходимо отслеживать в конвейерном потоке. Диаграмма показывает, сколько пользователей попадает на каждый этап отслеживаемого процесса, исходя из ширины воронки на каждом этапе деления. Сужение воронки помогает реализовать аналогию, но может сбить с толку истинные коэффициенты конверсии.Гистограмма часто может выполнять те же функции, что и воронкообразная диаграмма, но с более четким представлением данных.
Маркерная таблица
Маркированная диаграмма дополняет одну полосу дополнительными отметками, позволяющими контекстуализировать значение этой полосы. Обычно это означает перпендикулярную линию, показывающую целевое значение, но также и затенение фона для дополнительных тестов производительности. Маркированные диаграммы обычно используются для нескольких показателей и более компактны для рендеринга, чем другие типы более причудливых датчиков.
Земельные участки на карте
Существует несколько семейств специализированных графиков, сгруппированных по использованию, но мы закроем эту статью, коснувшись одного из них: картографических или геопространственных графиков. Когда значения в наборе данных соответствуют фактическим географическим местоположениям, может быть полезно нанести их на карту с помощью какой-либо карты. Типичным примером этого типа карты является хороплет, подобный показанной выше. При этом используется подход тепловой карты для отображения значения с помощью цвета, но вместо значений, отображаемых в сетке, они заполняются областями на карте.
Для получения удобного справочного руководства по дополнительным типам диаграмм и о том, когда их следует использовать, ознакомьтесь с нашей бесплатной электронной книгой «Как выбрать правильную визуализацию данных».
Процедуры прибытия
ПРИМЕР —
- Только боковой / проходной зазор.
«Подтверждено прибытие Тайлера Один».
ПРИМЕЧАНИЕ.
В примере 1 пилотам разрешено летать по боковой траектории схемы.Требуется соблюдение всех опубликованных ограничений скорости. Спуск не разрешен.
- Маршрут с заданной высотой.
«Разрешено прибытие Тайлер Один, снижение и поддержание эшелона полета два четыре ноль».
«Прилет Тайлер-1 разрешен, снижение по усмотрению пилота, поддержание эшелона полета два четыре ноль».
ПРИМЕЧАНИЕ —
В примере 2 первое разрешение требует, чтобы пилот снизился до эшелона полета 240 в соответствии с указаниями, соблюдал все опубликованные ограничения скорости и сохранял эшелон полета 240 до получения разрешения на дальнейшую вертикальную навигацию с вновь назначенной высотой. или разрешение «спуск через».
Второе разрешение разрешает пилоту снижаться до эшелона полета 240 по своему усмотрению, чтобы соблюдать все опубликованные ограничения скорости, а затем поддерживать эшелон полета 240 до получения дальнейших инструкций.
- Боковое / маршрутное и вертикальное навигационное разрешение.
«Спуститесь через прибытие Орловой Пятерки».
«Спуститесь через прибытие Орлиной Пятерки, за исключением того, что пересечете Внном на отметке не менее одной двух тысяч».
ПРИМЕЧАНИЕ.
В примере 3 первое разрешение разрешило воздушному судну снизиться по усмотрению пилота при прибытии Eagul Five; пилот должен снизиться с соблюдением всех опубликованных ограничений по высоте и скорости.
Второе разрешение дает то же самое, но требует от пилота снижения, чтобы пересечь Vnnom на уровне 12000 или выше.
- Боковое / маршрутное и вертикальное навигационное разрешение при назначении высоты, не указанной в схеме.
«Спуститесь через прибытие Eagul Five, за исключением Geeno, поддерживайте одну ноль тысячу».
«Спуститесь через прибытие Eagul Five, кроме пересечения Geeno на отметке одна тысяча, а затем поддерживайте семь тысяч».
ПРИМЕЧАНИЕ —
В примере 4 первое разрешение разрешило воздушному судну следовать в боковом направлении на Eagul Five Arrival и снижаться по усмотрению пилота, чтобы соблюдать все ограничения по высоте и скорости до достижения Geeno, а затем сохранять 10 000.По достижении 10 000 воздушные суда должны поддерживать 10 000 до тех пор, пока диспетчер УВД не разрешит продолжать снижение.
Для второго разрешения требуется то же самое, за исключением того, что самолет должен пересечь Джино на отметке 11000, а затем получить разрешение на снижение до 7000.
- Прямая маршрутизация для перехвата STAR и вертикальное навигационное разрешение.
«Двигайтесь прямо по Leoni, спускайтесь по прибытию Leoni One».
«Двигайтесь прямо, Денис, пересекайте Дениса на эшелоне полета два ноль ноль или выше, затем снижайтесь по прилету Mmell One.”
ПРИМЕЧАНИЕ.
В примере 5 в первом разрешении указывается высота в Леони; самолет следует к Леони, пересекает Леони на заявленной высоте и затем снижается по прибытии. Если в Леони будут опубликованы ограничения скорости, самолет замедлится, чтобы соответствовать опубликованной скорости.
Во втором разрешении высота у Дениса не указана; самолет должен пересечь Дениса на эшелоне FL200 или выше, а затем снизиться через точку прибытия.
Как выбрать лучшие типы диаграмм для ваших данных
Лучшая инфографика объединяет данные с текстом и изображениями, чтобы рассказать убедительную историю.
К сожалению, вы не можете просто вставить некоторые цифры в свою инфографику и ожидать, что ваши читатели извлекут из этого хоть какую-то пользу. Вы должны немного подумать о представлении данных, чтобы внести ясность и улучшить понимание.
Но я гарантирую вам, что немного дополнительных усилий, которые вы приложите для выбора наилучшей диаграммы для ваших данных, того стоят! При правильном использовании диаграммы могут:
Не дизайнер? Без проблем.Создавайте лучшие диаграммы за считанные минуты с помощью Venngage’s Chart Maker.
СДЕЛАТЬ КАРТУ С МЕСТОРОЖДЕНИЕМ
Нажмите, чтобы прыгнуть вперед:
WATCH: как выбрать правильные типы диаграмм для ваших данных
Итак, как вы выбираете лучшие шаблоны диаграмм для своей инфографики?
ПОЛУЧИТЬ ИНФОРМАЦИЮ
Вернуться к содержанию
Добавление данных в диаграммы с помощью импорта CSVПосле того, как вы выбрали диаграмму, вам нужно загрузить данные.В Venngage все просто.
В редакторе дважды щелкните диаграмму, чтобы открыть виджет. На вкладке ДАННЫЕ нажмите зеленую кнопку с надписью ИМПОРТ и выберите файл CSV. На диаграмме сразу же отобразятся ваши данные после импорта.
Вернуться к содержанию
Наиболее распространенные типы диаграмм:
- Гистограммы
- Графики
- Круговая диаграмма
- Пузырьковые диаграммы
- Гистограммы с накоплением
- Карты деревьев
- Облака слов
- Пончиковые диаграммы
- Пиктограммы
- Диаграмма с областями
- Точечные диаграммы
- Многосерийные диаграммы
Вернуться к содержанию
Используйте метод ICCOR, чтобы выбрать лучшую диаграмму для вашей инфографикиВ Venngage мы разработали метод ICCOR, который поможет вам выбрать лучшие диаграммы для вашей инфографики. Чтобы заставить метод ICCOR работать на вас, нужно сделать два шага:
- Определите цель визуализации
- Выберите лучшую диаграмму для достижения этой цели
Если вы попытаетесь погрузиться в визуализацию данных без каких-либо четких целей, вы никогда не получите ничего полезного.
Мусор на входе, мусор на выходе, верно?
Вместо этого начните с определения единственной цели визуализации для вашей диаграммы.Эта цель должна соответствовать одной из наших категорий ICCOR либо к:
- Inform : передать одно важное сообщение или точку данных, не требующую особого контекста для понимания
- Сравнить : показать сходства или различия между значениями или частями целого
- Показать Изменение: визуализировать тенденции во времени или пространстве
- Организовать: показать группы, шаблоны, ранг или порядок
- Выявить взаимосвязи: показать взаимосвязи между переменными или значениями
СДЕЛАТЬ КАРТУ С МЕСТОРОЖДЕНИЕМ
Не уверены, какой должна быть ваша цель? Потратьте некоторое время на изучение ваших данных.Ищите закономерности, группировки, тенденции, выбросы и ключевые точки данных. То, что выделяется для вас, — это то же самое, что вы должны подчеркивать своим читателям.
Вернуться к содержанию
Шаг 2. Выберите наиболее подходящие типы диаграмм для достижения этой целиПомня о своей цели, пора выбрать диаграмму!
Есть несколько диаграмм, которые могут работать для каждой цели ICCOR.
Давайте рассмотрим каждый из них с некоторыми передовыми методами создания диаграмм для каждого.
Лучшие виды графиков для информированияИтак, у вас есть одна точка данных или ключевое сообщение, которым вы хотите поразить своих читателей по голове.
Самый простой способ сделать это в инфографике — просто использовать крупный жирный (красочный) текст.
ПОЛУЧИТЬ ШАБЛОН
В этой стратегии хорошо то, что она переходит прямо к делу — нет места неверному толкованию. Недостаток?
Иногда одно число без какого-либо контекста может показаться не очень важным.Эта проблема легко решается.
Используйте простые символы или значки, чтобы добавить немного контекста — например, стрелку или фон разного размера, чтобы подчеркнуть рост или упадок:
ПОЛУЧИТЬ ШАБЛОН
Или диаграмму значков (значок с двумя цветами заливки, где соотношение представлено высотой основного цвета), чтобы сделать пропорции более ощутимыми.
ПОЛУЧИТЬ ШАБЛОН
Более точный способ представления пропорции — это прямое написание ее в пиктограмме, матрице значков, в которой один значок представляет единицу или группу единиц.
При создании пиктограмм старайтесь использовать красивые круглые числа, такие как 10 или 100, которые легко понять:
ПОЛУЧИТЬ ШАБЛОН
Вернуться к содержанию
Лучшие типы графиков для сравненияЕсли вы хотите показать сходство или различие между ценностями или частями целого, у вас есть много вариантов.
Используйте столбчатую или столбчатую диаграмму для сравнения независимых значенийМы, как читатели, особенно хорошо умеем сравнивать длину столбцов на столбчатой диаграмме (в отличие, например, от сегментов круговой диаграммы), делая столбчатые и столбчатые диаграммы лучшими диаграммами для сравнения.
По большей части гистограммы и столбчатые диаграммы могут использоваться как взаимозаменяемые. Однако, если вы хотите сравнить изменение некоторых показателей с течением времени , лучше придерживаться столбчатой диаграммы, чтобы время отображалось слева направо.
ПОЛУЧИТЬ ШАБЛОН
Если у вас есть длинные метки для каждой точки данных (например, при нанесении на диаграмму результатов опроса), лучше выбрать горизонтальную гистограмму. Это дает дополнительное пространство для каждой метки, чтобы избежать трудностей для чтения вертикального или наклонного текста:
ПОЛУЧИТЬ ШАБЛОН
Обратите внимание на порядок столбцов здесь — поскольку набор данных не имеет внутреннего порядка, сортировка столбцов от наибольшего к наименьшему добавляет дополнительное измерение информации.Также обратите внимание на отношение ширины полосы к расстоянию между полосами. Расстояние между полосами должно составлять примерно половину ширины полосы для оптимальной читаемости.
Вернуться к содержанию
Создайте свою собственную гистограмму в Интернете с помощью бесплатного конструктора гистограмм Venngage.Хотя гистограммы и столбчатые диаграммы являются лучшим выбором с точки зрения удобочитаемости данных, инфографика иногда требует чего-то более уникального и интересного.
Enter: пузырьковая диаграмма.
Используйте пузырьковую диаграмму для сравнения независимых значений с явными выбросамиНа пузырьковой диаграмме значения представлены кружком , площадью вместо длины столбца . Поскольку мы не особенно хорошо умеем делать точные оценки площади круга, рекомендуется использовать пузырьковые диаграммы только при явных выбросах или больших промежутках между каждым значением. Я также рекомендую явно обозначать каждый пузырек его значением.
ПОЛУЧИТЬ ШАБЛОН Используйте круговую диаграмму для сравнения частей целого (композиции)
Самый простой способ визуализировать простые отношения «часть-целое» — это круговая диаграмма.Сделайте круговые диаграммы удобными для чтения:
- Сегменты для заказа от наибольшего до наименьшего
- Начало первого сегмента в 12:00 и продолжение по часовой стрелке
- Ограничение диаграммы до 7 сегментов
ПОЛУЧИТЬ ШАБЛОН
Хотя круговые диаграммы широко распространены и легко понимаются, у них есть свои ограничения (например, при сравнении состава нескольких значений).
Создайте свою собственную круговую диаграмму бесплатно с помощью Venngage Pie Chart Maker.
Используйте гистограмму с накоплением или столбчатую диаграмму с накоплением для сравнения составов нескольких значенийПОЛУЧИТЬ ШАБЛОН
Однако использование даже составных столбчатых диаграмм довольно ограничено. Они действительно работают только тогда, когда у вас очень мало столбцов и очень мало сегментов или когда разница между столбцами очень велика.
Если у вас много данных или различия в ваших данных незначительны, лучшим выбором будет серия гистограмм.
Источник
В основном гистограммы — самый надежный метод визуализации сравнений.
Вернуться к содержанию
Лучшие типы графиков для отображения измененийКогда дело доходит до визуализации тенденций во времени или пространстве, появляется немного больше возможностей.
Используйте линейную диаграмму или диаграмму с областями, чтобы показать непрерывные во времени изменения.Линейные диаграммы являются наиболее эффективными диаграммами для отображения данных временных рядов.Они могут обрабатывать тонны точек данных и несколько рядов данных, и каждый знает, как их читать. Просто убедитесь, что ваши очки упорядочены таким образом, что время идет слева направо, и используйте одинаковые временные интервалы.
ПОЛУЧИТЬ БЕСПЛАТНЫЙ ШАБЛОН
ПОЛУЧИТЬ ШАБЛОН
Создайте свою собственную линейную диаграмму бесплатно с помощью Venngage Line Graph Maker.
Диаграммы с областями могут быть более эстетичными, но требуют большей утонченности.Их можно использовать только с менее чем четырьмя рядами данных, и неплохо было бы добавить некоторую прозрачность, чтобы убедиться, что каждая область видна.
ПОЛУЧИТЬ ДАННУЮ КАРТУ
Но данные временных рядов не всегда являются чисто числовыми!
Используйте инфографику временной шкалы для визуализации событий во времениПОЛУЧИТЬ ДАННУЮ КАРТУ
Вернуться к содержанию
Используйте картографическую карту для отображения данных о местоположении.Хлороплетная карта — это карта, пересеченная с тепловой картой. Обычно они затенены пропорционально значению некоторой переменной и могут использоваться для отображения шаблонов на основе местоположения:
ПОЛУЧИТЬ ДАННУЮ КАРТУ Использование серии карт для отображения изменений данных о местоположении с течением времени
ПОЛУЧИТЬ ШАБЛОН
Создайте свою собственную карту бесплатно с помощью Venngage’s Map Maker.
Лучшие типы диаграмм для организацииДиаграммы для организации данных или информации в инфографике могут принимать разные формы, в зависимости от того, хотите ли вы отобразить группы, шаблоны, ранжирование или порядок.Я коснусь лишь нескольких важных моментов.
Самая простая форма организации инфографики — это список.
Вернуться к содержанию
Используйте нумерованный список для отображения ранга или порядка, если вы хотите предоставить текстовую информацию о каждом элементе (например, при описании линейного процесса)ПОЛУЧИТЬ ШАБЛОН
Вы также можете использовать пирамидальные диаграммы для отображения иерархии или ранжирования информации, особенно той, для которой не требуется столько текста:
ПОЛУЧИТЬ ШАБЛОН Используйте таблицу для упорядочивания, когда вы хотите, чтобы читатели могли искать определенные значения Таблицы
лучше всего подходят, когда требуются точные значения, когда зрителям нужен доступ к отдельным числам или когда набор данных содержит несколько различных единиц (что было бы сложно визуализировать на одном графике).
ПОЛУЧИТЬ ШАБЛОН
Чтобы выделить наиболее важные данные в таблицах, примените несколько уникальных дизайнерских штрихов.
При работе с таблицами в редакторе у вас есть несколько вариантов настройки внешнего вида таблицы. На вкладке данных вы увидите параметры для выбора шрифтов и цветов фона.
Здесь вы можете выбрать разные шрифты, размеры шрифтов, стили и цвета. Вы также можете выбрать определенные ячейки и применить уникальный цвет фона, чтобы ваша информация стала заметной.
Если вам нужно выровнять текст, перейдите на вкладку настроек. В разделе «Параметры тела» вы можете выбрать горизонтальное и вертикальное выравнивание текста в ячейке. Эти простые функции помогают эффективно организовать вашу информацию.
Хотя таблицы могут содержать много деталей, они не дают вам представления о форме данных, поэтому часто рекомендуется включать таблицы в качестве дополнения к более наглядной диаграмме.
Вернуться к содержанию
Используйте простые прямоугольники, границы, стрелки и линии для визуальной организации групп (как показано на диаграммах Венна, интеллектуальных картах и блок-схемах ).Большинство других методов организации информации основываются на двух основных принципах:
- Использование фигур и границ для создания групп
- Использование линий и стрелок указывает отношения между группами (т. Е. Соединить группы)
Некоторые популярные инфографические диаграммы, в которых используются эти принципы, — это диаграмма Венна:
ПОЛУЧИТЬ ШАБЛОН
И интеллектуальная карта:
ПОЛУЧИТЬ ШАБЛОН
С новыми интеллектуальными диаграммами Venngage вы можете легко настраивать интеллект-карты для различных нужд.Добавляйте или удаляйте ветки или круги одним нажатием кнопки.
Поменяйте местами текст, значки, изображения, и интеллектуальная карта автоматически изменяет размер в соответствии с изменяющимися элементами. Используйте функцию Tidy, чтобы автоматически выровнять все формы на вашей интеллект-карте.
Хотите изменить стиль ваших фигур? Используйте кнопку форматирования в меню, чтобы быстро скопировать и вставить форматирование в одну или все фигуры.
Чтобы найти оптимальную организационную схему для своей инфографики, подумайте о структуре своей информации и найдите диаграмму, которая отражает эту структуру.
Наш конструктор блок-схем упростит для вас процесс проектирования. Или создайте диаграмму Венна.
Вернуться к содержанию
Лучшие типы диаграмм для выявления отношенийДва ключевых типа отношений, которые вы можете захотеть выявить в наборе данных, — это корреляция и распределение.
Используйте диаграмму рассеяния, чтобы выявить корреляцию и распределение набора данных с двумя переменными Диаграммы разброса— это самый простой способ изучить потенциальную корреляцию между двумя переменными, а также выявить распределение, кластеризацию и выбросы набора данных.
ПОЛУЧИТЬ ШАБЛОН Диаграммы разброса
удобны, поскольку не требуют агрегирования или предварительной обработки данных для выявления распределения набора данных.
Создайте свою собственную диаграмму рассеяния бесплатно с помощью Venngage’s Scatter Plot Maker.
Если вы хотите провести предварительную обработку или у вас уже есть хорошо агрегированные данные:
Используйте гистограмму, чтобы выявить распределение одной переменнойГистограммы являются стандартным способом отображения демографических данных о возрасте и отлично подходят для всех видов распределений.
ПОЛУЧИТЬ ШАБЛОН
НОВИНКА! Запуск: авторитетное руководство по созданию инфографики
С помощью этого подробного и доступного руководства любой желающий может создать профессиональную инфографику. Он наполнен идеями, передовыми методами, примерами, контрольными списками и многим другим — всем, что вам нужно, чтобы сделать инфографику, которая выделялась бы над сокращением.
Узнайте, как создавать профессиональную инфографику, которая поможет вам в достижении ваших коммуникационных и деловых целей.Книгу можно посмотреть здесь:
ПОЛУЧИТЬ КОПИЮ
Вернуться к содержанию
Советы по созданию инфографических диаграммТеперь, когда мы рассмотрели, как выбрать лучшую диаграмму для каждой цели ICCOR, пора поговорить о стиле диаграммы.
В лучшем случае правильно оформленные диаграммы могут сделать вашу инфографику более ясной и убедительной.
В худшем случае плохо составленные диаграммы могут ввести в заблуждение, создать путаницу, подорвать доверие к автору.Если вам интересно, посмотрите, как плохой дизайн диаграмм использовался в СМИ для искажения данных во время выборов в США в 2016 году.
Чтобы убедиться, что вы создаете четкие, доступные и на 100% понятные диаграммы, давайте рассмотрим некоторые передовые методы разработки диаграмм.
Начните оси диаграммы с нуля и используйте последовательные интервалы для деленийОдной из самых больших ошибок визуализации данных является усечение оси. Начало оси гистограммы или линейной диаграммы на некотором значении, отличном от нуля, — верный способ исказить ваши данные.
В большинстве случаев лучше начинать оси с нуля. Если вы решите не делать этого, убедитесь, что у вас есть для этого веская причина. Точно так же убедитесь, что масштаб вашей диаграммы очевиден, пометив ваши оси равномерно расположенными делениями с логическими интервалами (например, каждые 5, 10 или 100 единиц).
Уменьшить количество чернил без данныхВаши данные всегда должны быть в центре внимания.
Гуру визуализации данных Эдвард Тафте ввел термин «соотношение данных и чернил», чтобы подчеркнуть важность минимализма в дизайне диаграмм.Общая идея: большая часть чернил, необходимая для печати графика, должна непосредственно представлять данные-информацию.
По сути, такие вещи, как границы, линии сетки, цвета фона и другие дополнительные украшения, должны отойти на второй план по сравнению с точками, полосами или линиями, которые фактически представляют данные.
Сделайте все возможное, чтобы сделать надписи и линии сетки светлее, уменьшить цвета, удалить фон, избежать границ и контуров и, прежде всего… избавьтесь от любых 3D или других «специальных» эффектов.
Источник GIF
Не забывайте ярлыки, легенды и аннотацииЯрлыки — ваши друзья.
Надписи, заголовки и аннотации диаграмм следует использовать для явного указания того, что читатели должны вынести из диаграммы, чтобы исключить возможность неправильного толкования.
Не бойтесь быть лишними. Можно повторять ключевые моменты как в подзаголовке, так и в аннотации.
ПОЛУЧИТЬ БЕСПЛАТНЫЙ ШАБЛОН
При маркировке линий, полос или точек старайтесь не полагаться на отдельные легенды. Размещайте метки как можно ближе к соответствующим точкам данных, чтобы вашему читателю не приходилось искать, чтобы сопоставить метки с точками данных.
Да, и не забудьте указать свои источники данных. Ссылка на источник данных в нижней части инфографики мелким шрифтом (размером менее 10 пт). Совет от профессионала: используйте сокращение ссылок, чтобы упростить доступ к вашей ссылке.
Вернуться к содержанию
Используйте цвет для функции, а не для украшенияИспользование цвета играет важную роль в том, насколько «загруженной» будет ваша инфографика.
Чтобы ничего не запуталось, не используйте более шести цветов в любой таблице.Если в инфографике несколько диаграмм, используйте эти цвета последовательно для всех диаграмм.
ПОЛУЧИТЬ ШАБЛОН
Для более сложных диаграмм выберите один ключевой цвет, чтобы отличать более важные значения от менее важных значений (и используйте серый цвет, чтобы ослабить данные, которые вы хотите сделать менее важными).
ПОЛУЧИТЬ ШАБЛОН
Напротив, не полагается на цвет, чтобы сделать вашу диаграмму удобочитаемой — ваша диаграмма должна быть такой же значимой в черно-белом, как и в цвете.
Данные для заказа логическиПредставьте свои данные в том порядке, в каком их ожидает ваш читатель.
Есть временной ряд? Закажите его так, чтобы самая ранняя точка данных находилась слева, а последняя точка данных — справа.
Есть круговая диаграмма? Начиная с двенадцати часов, отсортируйте сегменты по часовой стрелке от наибольшего к наименьшему.
ПОЛУЧИТЬ ШАБЛОН
Представляете категории без естественного порядка? Рассмотрите возможность ранжирования их от наибольшего к наименьшему.
ПОЛУЧИТЬ ШАБЛОН
Вернуться к содержанию
Будьте проще!Наконец, при визуализации данных в инфографике я призываю вас проявлять сдержанность. Не перегружайте графики слишком большим количеством данных.
Инфографические данные должны быть понятными с первого взгляда. Если на диаграмме происходит слишком много всего, ваш читатель, скорее всего, сдастся и двинется дальше.
Некоторые практические правила:
- Использовать менее 6 линий в линейном графике
- Использовать менее 10 столбцов на гистограмме
- Используйте менее 7 сегментов в круговой диаграмме
Если это означает манипулирование данными (путем удаления точек, группировки точек или просмотра более коротких промежутков времени), найдите время, чтобы подумать о компромиссе между удобочитаемостью и точностью данных.Постарайтесь сократить набор данных до самых важных частей, не допуская неточности или искажения данных.
Если вы не можете обойтись без большого количества данных, это еще не конец света. Сравнение одного яркого цвета с приглушенным серым может помочь вашим читателям разобраться даже в сотнях точек данных:
Источник
Хороший способ убедиться, что ваша диаграмма достаточно проста? Попросите друга просмотреть это и не поддавайтесь желанию объяснить ему это.Если ваш друг не может понять вашу диаграмму без каких-либо словесных объяснений, это слишком сложно для инфографики.
Или сделайте тест на косоглазие. Прищуривайте глаза до тех пор, пока не перестанете читать текст — вы все еще что-то понимаете в таблице? Если нет, то еще немного упростите свои диаграммы.
Источник
Итак, подведем итог:
- Будьте внимательны со своими топорами
- Используйте цвет с умом
- минимизировать количество чернил без данных
- не забываем о ярлыках и аннотациях
- цитируйте ваши источники
- логически упорядочить данные
- не перегружайте диаграмму слишком большим количеством данных
К счастью для вас, стиль по умолчанию виджетов диаграмм Venngage позаботится обо всем этом за вас.Просто нажмите на диаграмму, которую хотите использовать, введите свои данные, и все готово!
СДЕЛАТЬ КАРТУ С МЕСТОРОЖДЕНИЕМ Заключение
Не следует недооценивать силу хорошо представленных данных, и правильная диаграмма может иметь решающее значение. Используйте метод ICCOR, чтобы выбрать лучшие диаграммы для ваших инфографических данных.
7 правил правильной интерпретации контрольных карт
Марк Дуривадж, ООО «Система контроля качества»
Контрольные диаграммы строятся на основе периодических проверок, отображая выходные данные процесса и отслеживая его на предмет изменений или тенденций по особым причинам.Контрольные карты — это инструменты для принятия решений, которые предоставляют информацию для своевременных решений относительно недавно произведенных продуктов.
Контрольные карты могут использоваться для определения источников отклонений, как общих, так и особых. Вариации по общей причине — это вариации, присущие процессу. Вариация по общей причине также известна как шум процесса. Процесс с вариациями только по общей причине очень предсказуем. Процесс, которому присущи существенные вариации по общей причине, может быть не в состоянии производить продукты, соответствующие заданным спецификациям.Считается, что отклонения по общей причине составляют 80% отклонений в любом процессе и считаются обязанностью руководства.
Изменения по особой причине — это отклонения, не связанные с процессом. Процесс с изменением по особой причине очень непредсказуем. Считается, что отклонение по особой причине составляет 20% отклонения в любом процессе и считается обязанностью работника.
Контрольные диаграммысодержат центральную линию — обычно это математическое среднее для нанесенных на график выборок — и верхние и нижние статистические контрольные пределы, которые определяют ограничения вариаций по общей причине, а также данные о производительности, нанесенные на график с течением времени.
Есть две общие классификации контрольных диаграмм: диаграммы переменных и диаграммы атрибутов. Переменные — это вещи, которые можно измерить. Атрибуты — это вещи, которые можно подсчитать. Тип данных (переменная или атрибут) будет определять соответствующий тип контрольной диаграммы, необходимой для мониторинга процесса. Таблицу 1 можно использовать для выбора контрольной диаграммы.
Таблица 1: Руководство по выбору контрольной диаграммы
Выбор правильного типа контрольной диаграммы важен для обеспечения того, чтобы основные статистические концепции соответствовали измеряемому объекту или атрибуту.
Процесс считается контролируемым, если контрольная диаграмма не указывает на неконтролируемое состояние и содержит только общие причины отклонений. Если отклонение по общей причине невелико, то для отслеживания процесса можно использовать контрольную диаграмму. Если вариация по общей причине слишком велика, необходимо изменить или улучшить процесс, чтобы уменьшить количество присущих вариаций до приемлемого уровня.
Когда контрольная диаграмма указывает на неконтролируемое состояние (точка за пределами контрольных пределов или соответствие одному или нескольким критериям в приведенных ниже правилах), назначаемые причины отклонений должны быть идентифицированы и устранены.
Следующие правила могут использоваться для правильной интерпретации контрольных диаграмм:
- Правило 1 — Одна точка за контрольным пределом 3 σ
- Правило 2 — Восемь или более точек по одну сторону от средней линии без пересечения
- Правило 3 — Четыре из пяти баллов в зоне B или за ее пределами
- Правило 4 — Шесть или более очков подряд, постоянно увеличивающихся или уменьшающихся
- Правило 5 — Две из трех точек в зоне А
- Правило 6 — 14 очков подряд, чередуя вверх и вниз
- Правило 7 — Любая заметная / предсказуемая модель, цикл или тренд
Анализ контрольной диаграммы на предмет изменения особых причин можно облегчить, если использовать категории, используемые в причинно-следственной диаграмме.Текущие категории, которые я предпочитаю использовать:
- Оборудование, машины и оснастка
- Окружающая среда
- Процесс
- Инспекция
- Материалы
- Оператор
Правило 1 — Одна точка за контрольным пределом 3 σ
Правило 1, на одну точку за контрольными пределами 3 σ, направлено на выявление точек, которые являются случайными или выпадающими, как показано здесь красным.При выявлении случайных или резко отклоняющихся точек следует учитывать следующие возможные особые причины:
- Оборудование, машины и инструменты
- неправильный запуск
- неправильная установка
- внезапный отказ вспомогательной системы (охлаждение, нагрев, сжатый воздух, вакуум, пар и т. Д.)
- отказ / поломка инструмента
- отказ оборудования или машины
- ненадлежащее обслуживание оборудования, станков и инструментов
- Отключение электросети
- Окружающая среда
- температура внезапно слишком низкая / высокая
- влажность внезапно слишком низкая / высокая
- Процесс
- оборудование не стабилизировалось (прогрето)
- ненадлежащие рабочие инструкции
- пропущен этап процесса
- новый процесс
- Инспекция
- Контрольно-измерительное и испытательное оборудование не откалибровано должным образом
- Повреждено контрольно-измерительное и испытательное оборудование
- Материалы
- изменение сырья
- замена комплектующих
- повреждения при перегрузке
- материалы с истекшим сроком годности
- Оператор
- новых операторов
- недостаточная подготовка
- оператор прервал или отвлекся
- Оператор чрезмерно компенсирует корректировку процесса
Правило 2 — Восемь или более точек с одной стороны от средней линии без пересечения
Правило 2, восемь или более точек на одной стороне центральной линии без пересечения считается заметным сдвигом (сдвиг может происходить по обе стороны от центральной линии).Точки, обведенные красным, считаются заметным сдвигом. При выявлении заметного сдвига следует учитывать следующие возможные особые причины:
- Оборудование, машины и инструменты
- неправильная установка
- ненадлежащее обслуживание оборудования, станков и инструментов
- инструмент поврежден
- износ инструмента
- Окружающая среда
- Смещение температуры слишком низкое / высокое
- Влажность сместилась слишком низко / высоко
- Процесс
- новые параметры процесса
- неверные параметры процесса
- процесс улучшился
- процесс ухудшился
- Инспекция
- Контрольно-измерительное и испытательное оборудование не откалибровано должным образом
- Повреждено контрольно-измерительное и испытательное оборудование
- Материалы
- изменение сырья
- замена комплектующих
- материалы с истекшим сроком годности
- Оператор
- новых операторов
- недостаточная подготовка
- оператор прервал или отвлекся
- смена смены
Правило 3 — Четыре из пяти точек в зоне B или за ее пределами
Правило 3, четыре из пяти точек в зоне B или за ее пределами, считается небольшим сдвигом (сдвиг может происходить по обе стороны от центральной линии).Точки, обведенные красным, считаются небольшими сдвигами. При обнаружении небольшого сдвига следует учитывать следующие возможные особые причины:
- Оборудование, машины и инструменты
- неправильная установка
- Периодический отказ системы поддержки (охлаждение, нагрев, сжатый воздух, вакуум, пар и т. Д.)
- ненадлежащее обслуживание оборудования, станков и инструментов
- Окружающая среда
- температура внезапно слишком низкая / высокая
- влажность внезапно слишком низкая / высокая
- Процесс
- новые параметры процесса
- неверные параметры процесса
- процесс улучшился
- процесс ухудшился
- Инспекция
- Контрольно-измерительное и испытательное оборудование не откалибровано должным образом
- контрольно-измерительное и испытательное оборудование, не подходящее для использования по назначению
- Повреждено контрольно-измерительное и испытательное оборудование
- Материалы
- смешанное сырье
- смешанные компоненты
- Оператор
- новых операторов
- недостаточная подготовка
- оператор прервал или отвлекся
- смена смены
Правило 4 — Шесть или более очков подряд, постоянно увеличивающихся или уменьшающихся
Правило 4, шесть или более точек подряд, устойчиво увеличивающихся или уменьшающихся, считается трендом (тренд может быть восходящим или нисходящим).Точки, обведенные красным, считаются трендом. При выявлении тенденции следует учитывать следующие возможные особые причины:
- Оборудование, машины и инструменты
- постепенный отказ системы поддержки (охлаждение, нагрев, сжатый воздух, вакуум, пар и т. Д.)
- износ инструмента
- Окружающая среда
- Температура постепенно дрейфует от слишком низкой / высокой
- Влажность постепенно снижается до слишком низкой / высокой
- Процесс
- процесс медленно деградирует
- Инспекция
- контрольно-измерительное и испытательное оборудование, не подходящее для использования по назначению
- Повреждено контрольно-измерительное и испытательное оборудование
- Материалы
- вариации в сырье
- вариации в компонентах
- Оператор
Правило 5 — Две из трех точек в зоне A
Правило 5, два из трех пунктов в зоне А, считается большим сдвигом.(смещение может быть по обе стороны от средней линии). Точки, обведенные красным, считаются большими сдвигами. При обнаружении большого сдвига следует учитывать следующие возможные особые причины:
- Оборудование, машины и инструменты
- неправильная установка
- отказ системы поддержки (охлаждение, нагрев, сжатый воздух, вакуум, пар и т. Д.)
- ненадлежащее обслуживание оборудования, станков и инструментов
- Окружающая среда
- температура внезапно слишком низкая / высокая
- влажность внезапно слишком низкая / высокая
- Процесс
- новые параметры процесса
- неверные параметры процесса
- процесс ухудшился
- Инспекция
- Контрольно-измерительное и испытательное оборудование не откалибровано должным образом
- контрольно-измерительное и испытательное оборудование, не подходящее для использования по назначению
- Повреждено контрольно-измерительное и испытательное оборудование
- Материалы
- смешанное сырье
- смешанные компоненты
- Оператор
- новых операторов
- недостаточная подготовка
- оператор прервал или отвлекся
- смена смены
Правило 6 — 14 точек подряд, чередуя вверх и вниз
Правило 6, 14 очков подряд, чередующихся вверх и вниз, обычно считается чрезмерным контролем.Очки, заключенные в красный цвет, считаются неконтролируемыми. При выявлении этой ситуации следует учитывать следующие возможные особые причины:
- Оборудование, машины и инструменты
- неправильная установка
- Периодический отказ системы поддержки (охлаждение, нагрев, сжатый воздух, вакуум, пар и т. Д.)
- ненадлежащее обслуживание оборудования, станков и инструментов
- Окружающая среда
- Температура периодически слишком низкая / высокая
- влажность периодически слишком низкая / высокая
- Процесс
- оборудование не стабилизировалось (прогрето)
- новые параметры процесса
- неверные параметры процесса
- ненадлежащие рабочие инструкции
- пропущен этап процесса
- новый процесс
- Инспекция
- контрольно-измерительное и испытательное оборудование, не подходящее для использования по назначению
- Повреждено контрольно-измерительное и испытательное оборудование
- Материалы
- смешанное сырье
- смешанные компоненты
- Оператор
- новых операторов
- недостаточная подготовка
- Оператор чрезмерно компенсирует корректировку процесса
- Оператор, не дожидаясь стабилизации процесса, прежде чем вносить изменения в процесс
Обратите внимание: даже если оператор чрезмерно регулирует процесс, могут быть другие особые причины.
Правило 7 — Любая заметная / предсказуемая модель, цикл или тренд
Правило 7 — это любой заметный / предсказуемый паттерн, цикл или тренд. Точки, обведенные красным, считаются неконтролируемыми. При выявлении таких ситуаций следует учитывать следующие возможные особые причины:
- Оборудование, машины и инструменты
- неправильная установка
- Периодический отказ системы поддержки (охлаждение, нагрев, сжатый воздух, вакуум, пар и т. Д.))
- Постепенный отказ системы поддержки (охлаждение, нагрев, сжатый воздух, вакуум, пар и т. Д.)
- ненадлежащее обслуживание оборудования, станков и инструментов
- износ инструмента
- Окружающая среда
- Температура постепенно дрейфует от слишком низкой / высокой
- Влажность постепенно снижается до слишком низкой / высокой
- температура сместилась слишком низко / высоко
- Влажность сместилась слишком низко / высоко
- Температура периодически слишком низкая / высокая
- влажность периодически слишком низкая / высокая
- Процесс
- оборудование не стабилизировалось (прогрето)
- новые параметры процесса
- неверные параметры процесса
- ненадлежащие рабочие инструкции
- пропущен этап процесса
- новый процесс
- два или более процессов
- Инспекция
- Контрольно-измерительное и испытательное оборудование не откалибровано должным образом
- контрольно-измерительное и испытательное оборудование, не подходящее для использования по назначению
- Повреждено контрольно-измерительное и испытательное оборудование
- Материалы
- изменение сырья
- замена комплектующих
- смешанное сырье
- смешанные компоненты
- вариации в сырье
- вариации в компонентах
- Оператор
- новых операторов
- недостаточная подготовка
- оператор прервал или отвлекся
- несколько смен
Стратификация
Когда выявляется расслоение, это обычно происходит по одной из двух причин.Операторы целенаправленно сокращают измерения, или процесс значительно улучшился, что потребует пересчета пределов статистического контроля.
Заключение
Пришло время рассмотреть возможность дополнения ваших утвержденных процессов производства фармацевтических препаратов, медицинских устройств и салфеток, включая обработку, упаковку и маркировку, непрерывным мониторингом процесса с использованием контрольных диаграмм для обеспечения постоянного соответствия установленным спецификациям и требованиям.
При внедрении контрольных диаграмм в рамках непрерывного мониторинга процессов убедитесь, что люди, ответственные за заполнение диаграмм, были должным образом обучены и понимают семь правил, представленных в этой статье.
Я не могу переоценить важность установления документированных процедур для управления используемыми инструментами и методами. Передовой опыт включает в себя обоснование использования вашей организацией контрольных диаграмм для непрерывного мониторинга процессов.Методы и инструменты, представленные в этой статье, могут и должны использоваться на основе отраслевой практики, руководящих документов и нормативных требований.
Каталожные номера:
- Durivage, M.A., 2014, Статистика практического проектирования, процессов и надежности, Милуоки, ASQ Quality Press
- Durivage, M.A., and Mehta, B., 2016, Practical Process Validation, Milwaukee, ASQ Quality Press
- Durivage, M.A., 2020, https: //www.pharmaceuticalonline.com / doc / как-реализовать-непрерывный-мониторинг-процессов-проверенных-процессов-0001
Об авторе:
Марк Аллен Дуривадж работал практиком, педагогом, консультантом и автором. Он является управляющим главным консультантом в Quality Systems Compliance LLC, членом ASQ и научным сотрудником SRE. Durivage в основном работает с компаниями в отраслях, регулируемых FDA (медицинские устройства, ткани человека, ткани животных и фармацевтика), уделяя особое внимание внедрению, интеграции, обновлению и обучению систем управления качеством.Кроме того, он помогает компаниям, обеспечивая поддержку внутреннего и внешнего аудита, а также FDA 483 и услуги по реагированию на письма с предупреждениями и исправлениям. Он получил степень бакалавра искусств в области компьютерной обработки в Университете Сиены-Хайтс и степень магистра управления качеством в Университете Восточного Мичигана. Он имеет несколько сертификатов, включая CRE, CQE, CQA, CSSBB, RAC (Global) и CTBS. Он написал несколько книг, доступных через ASQ Quality Press, опубликовал статьи в Quality Progress и часто участвует в Life Science Connect.Вы можете связаться с ним по адресу [email protected] и связаться с ним в LinkedIn.
Вот 7 основных графических паттернов, используемых техническими аналитиками для покупки акций.
Брендан МакДермид / Reuters- Технические аналитики считают, что цены на акции часто изменяются по паттернам, поскольку движущими силами движения акций являются люди, а люди — экспонаты. те же эмоции, когда дело касается их денег: страх и жадность.
- Эти две предсказуемые эмоции помогают создавать предсказуемые торговые модели, на которых технические аналитики пытаются извлечь выгоду.
- Вот семь основных бычьих паттернов, которые технические аналитики используют для покупки акций.
- Посетите домашнюю страницу Business Insider, чтобы узнать больше.
Одним из главных факторов роста цен на акции являются человеческие эмоции, особенно страх и жадность.
Инвесторы обычно проявляют предсказуемые эмоции, когда цена акции движется вверх и вниз, и эти эмоции могут привести к торговой активности, которая создает предсказуемые графические модели.
Технические аналитики пытаются избавиться от эмоций при инвестировании, полагаясь исключительно на модели, обнаруженные на графиках, при торговле акциями, потенциально давая им преимущество перед инвесторами, которые склонны к принятию торговых решений, движимых страхом и жадностью.
Хотя эти закономерности можно предсказать, они не являются пуленепробиваемыми. Подделки головы, ловушки для быков и неудачные срывы происходят часто и, как правило, выбивают трейдеров из своих позиций прямо перед большим движением.
Вот почему дисциплина так важна в техническом анализе.
Наличие плана перед входом в позицию может помочь трейдерам выдержать резкие колебания цен, увеличивая их шансы на движение при восходящем тренде и избежание нисходящего тренда.
План перед входом в сделку включает определение уровня «стоп-лосс», при котором, если акция падает до определенной ценовой точки, вы автоматически продаете, получаете небольшой убыток и переходите к следующей торговой возможности.
План также будет включать ценовую цель, при которой трейдер будет стремиться выгрузить часть, если не всю позицию, чтобы зафиксировать прибыль.
Вот семь основных бычьих графических паттернов, которые технические аналитики используют для покупки акций.
Подробнее: Bank of America говорит, что на фондовом рынке может формироваться новый пузырь, и разделяет дешевую стратегию защиты, которая «значительно» более прибыльна, чем за последние 10 лет
1. Двойное дно
Freestockcharts.netДвойное дно — это модель бычьего разворота, которая описывает падение, затем отскок, затем падение и затем второй отскок акции.
Успешный паттерн «двойное дно» выглядит как W.
Паттерн обычно отмечает конец нисходящего и начало восходящего тренда.
Принято считать, что первое и второе дно должны находиться в пределах пары процентов друг от друга, если не на одном уровне.
На формирование двойного дна обычно уходит два-три месяца, и чем дальше друг от друга находятся два дна, тем больше вероятность, что модель будет успешной.
2.Восходящий треугольник
Freestockcharts.comВосходящий треугольник — это модель бычьего продолжения и одна из трех моделей треугольника, используемых в техническом анализе.
Торговая установка обычно находится в восходящем тренде, который формируется, когда акция достигает более высоких минимумов и встречает сопротивление на том же ценовом уровне.
Восходящая поддержка и горизонтальное сопротивление в конечном итоге сходятся на уровне прорыва.
Этот паттерн создает четко определенную установку для трейдеров. Если акция пробивает горизонтальное сопротивление, трейдеры покупают акцию и устанавливают стоп-лосс, как правило, чуть ниже предыдущего уровня сопротивления.
Но если акция прорывается ниже растущего уровня поддержки, будет сгенерирован сигнал о короткой торговле.
Восходящий треугольник — это сетап с высокой вероятностью, если прорыв происходит на большом объеме, и он более надежен, чем паттерн симметричный треугольник.
3. Чашка и ручка
Freestockcharts.comЧашка и ручка — это бычий паттерн, напоминающий чашку, образованный базовым паттерном, который обычно выглядит как буква «U», за которой следует ручка, образованная короткой буквой. термин нисходящий тренд.
Как только акция вырывается выше ручки, технический аналитик покупает эту акцию.
Трейдер может сгенерировать измеренную целевую цену движения, измерив глубину чашки в цене, и добавить эту сумму к крышке чашки.
Этот паттерн обычно расширяет уже существующий восходящий тренд.
П-образная чашка с большей вероятностью устанавливается, чем V-образная чашка, но оба могут работать.
4. Bull Flag
Freestockcharts.netПаттерн бычьего флага возникает, когда акция находится в сильном восходящем тренде, и напоминает флаг с двумя основными компонентами: полюсом и флагом.
Этот паттерн — бычий паттерн продолжения. Обычно трейдеры покупают акции после того, как они пробиваются выше краткосрочного нисходящего тренда или флага.
Целевая цена с измеренным ходом может быть получена путем измерения расстояния до полюса и добавления его к верхнему правому углу флажка.
Бычьи флаги — это краткосрочные модели, которые в идеале длятся от одной до четырех недель, обычно не дольше восьми недель и обычно следуют за резким восходящим трендом.
5. Бычий вымпел
Freestockcharts.comПодобно бычьему флагу, бычий вымпел представляет собой модель продолжения, состоящую из полюса и симметричного треугольника, обычно следующего за восходящим трендом цены.
Вместо периода боковой консолидации в форме прямоугольника, цена консолидируется в форме симметричного треугольника, образуя серию более высоких минимумов и более низких максимумов.
Восходящий тренд ценных бумаг, скорее всего, продолжится, если акция вырвется выше вымпела.
В приведенном выше примере графика показан пример неудачного пробоя или медвежьей ловушки.
Сначала ценная бумага пробивается ниже вымпела, сигнализируя о пробое и потенциально снижении цен в будущем.
Но затем он быстро восстанавливается, пробивается выше вымпела, и восходящий тренд продолжается.
Измеренную подвижную цель можно получить, измерив расстояние до шеста и прибавив его к вершине вымпела треугольника.
6.Бычья свеча поглощения
Freestockcharts.comСвеча — это стиль графика, который показывает цену открытия, цену закрытия, внутридневной максимум и внутридневной минимум.
«Тело» представлено ценой открытия и закрытия акции, а «хвосты» представлены внутридневным максимумом и минимумом.
Свеча бычьего поглощения возникает, когда тело одной торговой сессии полностью поглощает предыдущую сессию.
Это происходит, когда открытие дня ниже, чем в предыдущий день, а его закрытие выше, чем в предыдущий день.
Когда тело свечи «поглощает» предыдущие торговые сессии, это сигнализирует о том, что быки начинают брать контроль над медведями и возможен разворот тренда.
Чем больше торговых сессий охватывает одна свеча, тем сильнее сигнал.
На графике выше, бычья свеча поглощения охватывает предыдущие пять торговых сессий, указывая на вероятность того, что акции движутся вверх.
7.Обратная голова и плечи
Freestockcharts.comОбратная голова и плечи — это модель дна, которая часто сигнализирует о развороте акции после медвежьего тренда.
Перевернутая голова и плечи связана с медвежьей моделью «голова и плечи», которая является фигурой вершины.
Паттерн представляет собой серию из трех оснований, причем второе основание является самым глубоким.
 0,5), (3; 0), (3,5; 0), (8; 0,5), (7,5; 4,5), (9; 3), (12; 1,5), (18; 1,5), (12,5; 3), (11; 3,5), (9,5; 7), (8; 10), (6; 11), (4; 12,5), (3; 14),
0,5), (3; 0), (3,5; 0), (8; 0,5), (7,5; 4,5), (9; 3), (12; 1,5), (18; 1,5), (12,5; 3), (11; 3,5), (9,5; 7), (8; 10), (6; 11), (4; 12,5), (3; 14),
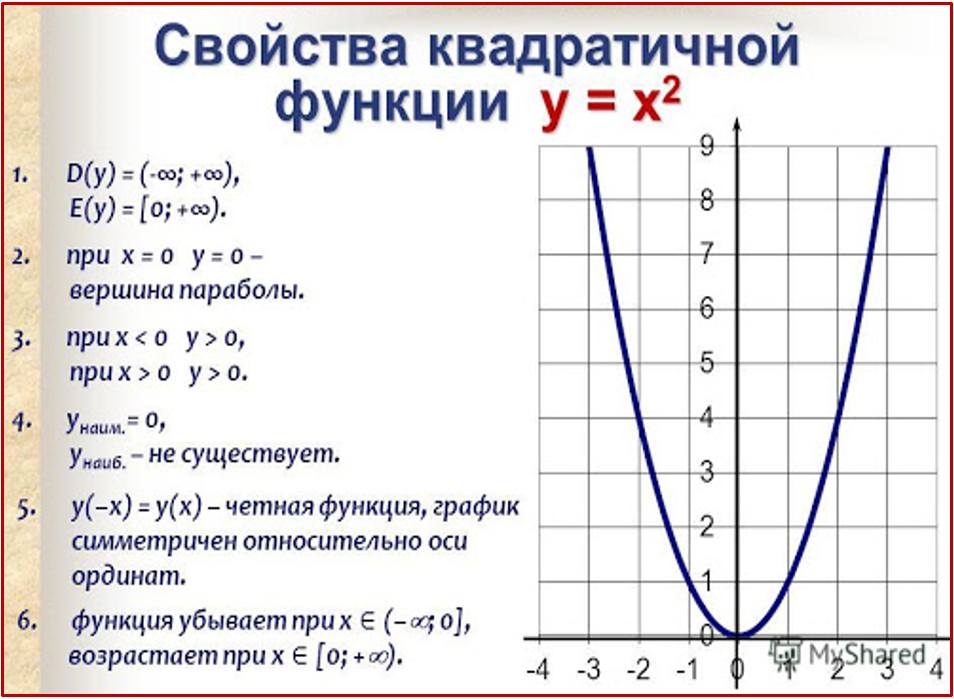 Если передан скаляр, то он будет присвоен всем точкам графика.
Если передан скаляр, то он будет присвоен всем точкам графика.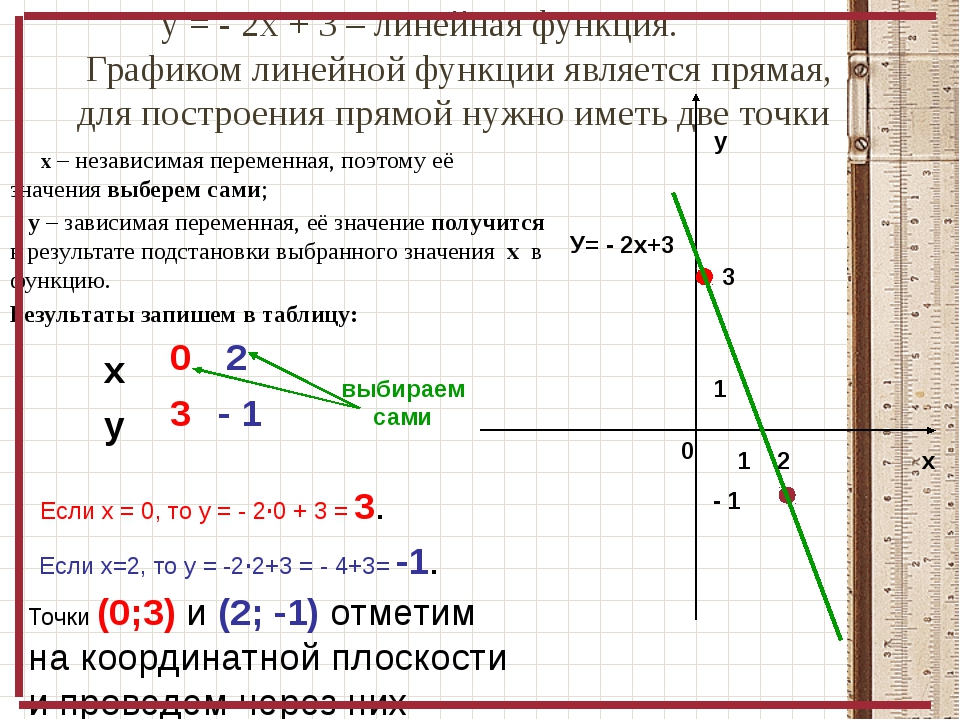 Если передан скаляр, то он будет присвоен всем точкам графика. Значение по умолчанию: 0.
Если передан скаляр, то он будет присвоен всем точкам графика. Значение по умолчанию: 0.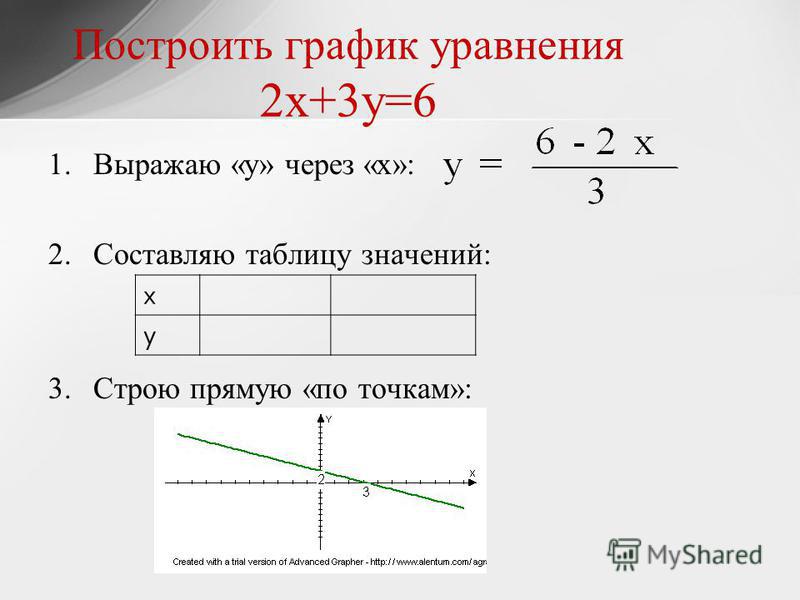


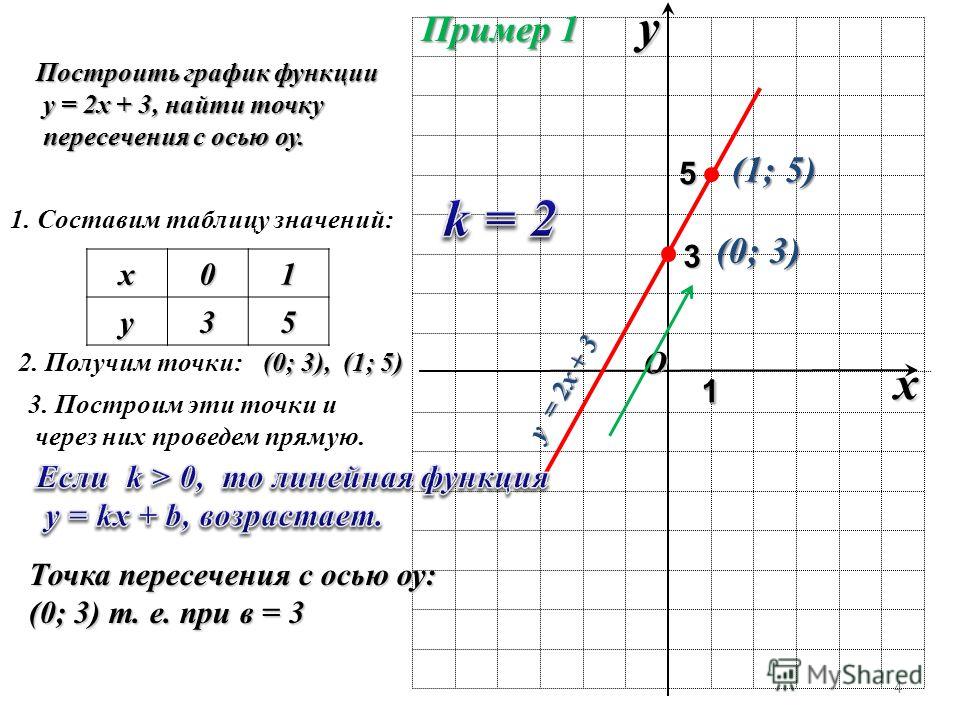
Ваш комментарий будет первым