Поверхностная диаграмма в Excel и пример ее построения
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y]2. Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
все уроки
🐍📈 Как «оживлять» графики и впечатлять всех красивыми анимациями с помощью Python
Если статических графиков недостаточно – нарисуем постоянно меняющиеся анимации!
Каждый Data Scientist знает, что важно не только получить данные, решающие некоторую задачу, но и представить эти данные в виде, удобном для восприятия людей, которые будут принимать решения на их основе.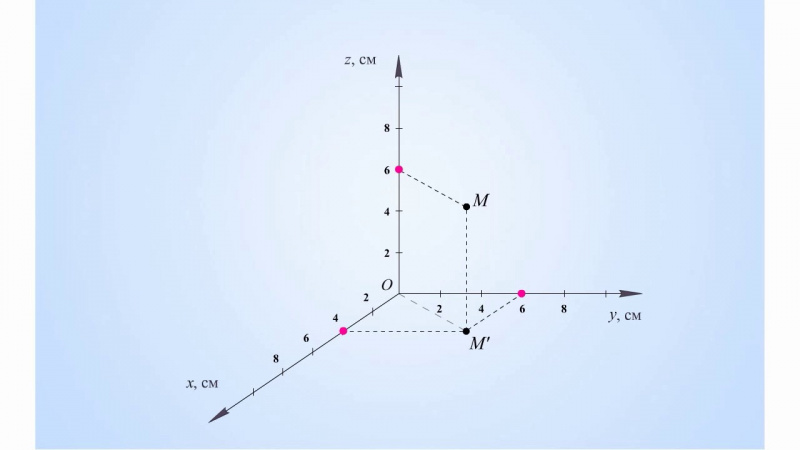
Для этого используются диаграммы, гистограммы, графики и многое другое. Но если вы хотите создать презентацию, по-настоящему привлекающую внимание – статических картинок может оказаться недостаточно. Вам потребуются динамические анимации.
Когда вы прочитаете эту статью, вы сможете воссоздать график, показанный выше, и использовать полученные знания для создания собственных красивых анимаций.
Будем считать, что у вас есть опыт общения с Python’ом, и вы знаете, как выполнять базовые операции манипуляции данными и рисовать графики. Предлагаемый ниже метод анимации – не единственный, и если вы знаете какой-нибудь другой, вам будет интересно сравнить их друг с другом. Мы будем использовать трехмерные линии и точки для создания траекторий, но эти же методы можно распространить на другие визуализации – например, двухмерные линии, столбчатые и секторные диаграммы, контуры и т. д.
Импортируем пакеты
В Python’е есть куча библиотек для анализа данных и мы воспользуемся парой из них.
# Импортируем пакеты
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import animation
- NumPy используется для создания числовых массивов и вызова тригонометрических функций (сокращается до
npдля удобства). - Pyplot из пакета Matplotlib используется для рисования графиков (сокращается до
pltдля удобства). - Axes3D используется создания трехмерной системы координат в наших графиках.
animationиз пакета Matplotlib используется для создания анимаций путем периодического вызова функции, которую мы определим позднее.
Больше полезных материалов вы найдете на нашем телеграм-канале «Библиотека питониста»
Интересно, перейти к каналу
Создадим набор данных
Для этого я создал кое-какие позиционные данные, полученные с помощью функции синуса и временного массива, содержащего значения от 0 до 20 (я обозначил их как секунды анимации).# Временной массив
t = np.linspace(0, 20, 100)
# Позиционные массивы
x = np.sin(np.pi/5 * t)
y = np.sin(np.pi/3 * t)
z = np.linspace(0, 100, 100)
# Задаем набор данных для анимации
dataSet = np.array([x, y, z]) # Комбинируем наши позиционные координаты
numDataPoints = len(t)
Этот код легко понять даже без объяснений. Вы можете поиграть с временным и позиционным массивами для задания собственных траекторий. Переменные dataSet и numDataPoints будут использованы в нашей функции анимации, которую мы сейчас определим.
Функция анимации
Для анимации нашей картинки мы используем функцию FuncAnimation из импортированного класса animation.
Документацию по обоим можно найти здесь. FuncAnimation требует, чтобы мы создали собственную функцию, обновляющую линии, точки и пр., которую мы назовем animate_func.
def animate_func(num):
ax.clear() # Очищаем фигуру для обновления линии, точки,
# заголовка и осей # Обновляем линию траектории (num+1 из-за индексации Python)
ax.plot3D(dataSet[0, :num+1], dataSet[1, :num+1],
dataSet[2, :num+1], c='blue') # Обновляем локацию точки
ax.scatter(dataSet[0, num], dataSet[1, num], dataSet[2, num],
c='blue', marker='o') # Добавляем постоянную начальную точку
ax.plot3D(dataSet[0, 0], dataSet[1, 0], dataSet[2, 0],
c='black', marker='o') # Задаем пределы для осей
ax.set_xlim3d([-1, 1])
ax.set_ylim3d([-1, 1])
ax.set_zlim3d([0, 100])
# Добавляем метки
ax.set_title('Trajectory \nTime = ' + str(np.round(t[num], decimals=2)) + ' sec')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.
set_zlabel('z')
Прежде всего обратим внимание на переменную num, передаваемую в animate_func. Это индекс текущего шага анимации. Когда мы передаем animate_func в FuncAnimation, последняя будет накручивать нашу переменную num. Мы можем использовать эту переменную для итерации по нашему dataSet’у, созданному ранее.
Первое, что делает эта функция – очищает фигуру. Очистка уничтожает линии, точки, оси с метками и заголовок. Затем функция добавляет обновленную линию траектории (от 0 до num) и локацию точки (на шаге num). В этой фигуре начальная точка остается неизменной, так что вы заметите, что num не показывается, поскольку мы не меняем начальную точку. Затем функция определяет наши неизменные пределы по осям. Вы можете убрать эти пределы, если хотите, чтобы оси изменялись по мере продвижения (то есть, ваши оси станут динамическими).
Наконец, наша функция задает заголовок и метки наших осей. Метки очевидны: это x, y, z, обозначающие декартовы координаты. В качестве небольшой дополнительной функциональности у нас есть динамический заголовок, показывающий текущий номер итерации в повременном массиве,
Рисуем нашу анимацию
Последний шаг – это собственно вывод нашей анимации с помощью FuncAnimation. Начнем с создания объекта фигуры с трехмерными осями. Затем вызываем FuncAnimation, принимающую фигуру, нашу функцию анимации, которую мы только что создали, а также значения interval и frames. Interval – это время задержки между фреймами в миллисекундах, а frames – это просто количество фреймов, которые нужно показать.
Два последних аргумента не обязательны, но мне нравится включать их, если я хочу иметь возможность настраивать вид анимация.
# Рисуем анимацию
fig = plt.figure()
ax = plt.axes(projection='3d')
line_ani = animation.FuncAnimation(fig, animate_func, interval=100,
frames=numDataPoints)
plt.show()
Вы можете запустить этот код, и если все сделано правильно, ваш график должен выглядеть примерно так (скорость движения точки может быть разной):
Сохранение нашей анимации (опционально)
Если вы хотите сохранить свою анимацию в файл .gif, можно использовать следующий код, делающий именно это:
# Сохраняем анимацию
f = r"c://Users/(Insert User)/Desktop/animate_func.gif"
writergif = animation.PillowWriter(fps=numDataPoints/6)
line_ani.save(f, writer=writergif)
Нужно выбрать имя файла для сохранения анимации и сохранить его в переменной f.
fps, передаваемое в PillowWriter. Я разделил переменную numDataPoints, которая определяет количество фреймов в FuncAnimation, на 6, чтобы анимация занимала 6 секунд времени.Мы познакомились с пакетами mplot3d и animation, а также научились рисовать анимации графиков и сохранять эти анимации в файлы .gif. Спасибо за прочтение!
***
Материалы по теме
- Анимация графиков в Python за 4 шага
- 🎨 Как нарисовать смайлик и квадрат в онлайн-редакторе графики Paint с помощью Selenium
- 🎞️ Как с помощью Python делать красивые математические анимации
3D-векторный плоттер | Academo.org
Интерактивный график 3D-векторов. Посмотрите, как два вектора связаны с их результирующей, разностью и перекрестным произведением.
Математика Геометрия График сюжет вектор
В приведенной выше демонстрации вы можете ввести до трех векторов в форме (x, y, z). Нажатие кнопки рисования отобразит векторы на диаграмме (масштаб диаграммы будет автоматически подстраиваться под величину векторов). Вы можете перетаскивать диаграмму и увеличивать или уменьшать масштаб, прокручивая мышью. Нажатие на конец вектора также покажет его отдельные компоненты.
Демонстрация также имеет возможность построить 3 других вектора, которые могут быть вычислены из первых двух входных векторов. Первый из них является равнодействующим, и он получается, когда компоненты каждого вектора складываются вместе. Если результат равен \(\textbf{c} \), то
\[ \textbf{c} = \textbf{a} + \textbf{b} \] \[ \left( \begin{массив}{c} с_х \\ с_у \\ c_z \end{массив} \right) = \левый( \начать{массив}{с} а_х \\ а_у \\ а_я \конец{массив} \справа) + \левый( \начать{массив}{с} б_х\\ к \\ б_з \конец{массив} \верно) «=» \левый( \начать{массив}{с} а_х + б_х \\ а_у+б_у\ а_з + б_з \конец{массив} \верно) \]
Аналогичным образом, разница заключается в том, что получается при вычитании одного вектора из другого, в данном случае \(\textbf{d} \),
\[ \textbf{d} = \textbf{a} — \textbf{b} \] \[ \left( \begin{массив}{c} д_х\\ д_у \\ d_z \end{массив} \right) = \левый( \начать{массив}{с} а_х \\ а_у \\ а_я \конец{массив} \справа) — \левый( \начать{массив}{с} б_х\\ к \\ б_з \конец{массив} \верно) «=» \левый( \начать{массив}{с} а_х — б_х\ а_у — б_у\ а_з — б_з \конец{массив} \верно) \]
Наконец, векторное произведение (также известное как векторное произведение) определяется как
\[ \textbf{e} = \textbf{a} \times \textbf{b} = \lvert a \rvert\ \lvert b \rvert\ \sin(\theta)\hat{n} \] \[ \left( \begin{массив}{c} бывший \\ е_у \\ e_z \end{массив} \right) = \левый( \начать{массив}{с} а_х \\ а_у \\ а_я \конец{массив} \справа) \ раз \левый( \начать{массив}{с} б_х\\ к \\ б_з \конец{массив} \верно) «=» \левый( \начать{массив}{с} а_yb_z — а_zb_y\ a_zb_x — a_xb_z\\ а_xb_y — а_yb_x \конец{массив} \верно) \]
С геометрической точки зрения длина перекрестного произведения равна произведению величин \( \textbf{a} \) и \( \textbf{b} \), умноженных на синус угла между ними.
Он указывает в направлении \( \hat{n} \), который представляет собой вектор, указывающий прямо из плоскости, в которой лежат \( \textbf{a} \) и \( \textbf{b} \). означает, что если два вектора указывают в одном (или прямо противоположном) направлении, то их векторное произведение будет равно нулю. Попробуйте выше!
Credits
- Спасибо пользователю https://github.com/harshaxnim за создание возможности добавления дополнительных векторов, а также за реализацию других улучшений кода этой демонстрации
Включите JavaScript для просмотра комментариев с помощью Disqus.
Построение трехмерных точек — Криста Кинг Математика
Как рисовать точки в трех измерениях
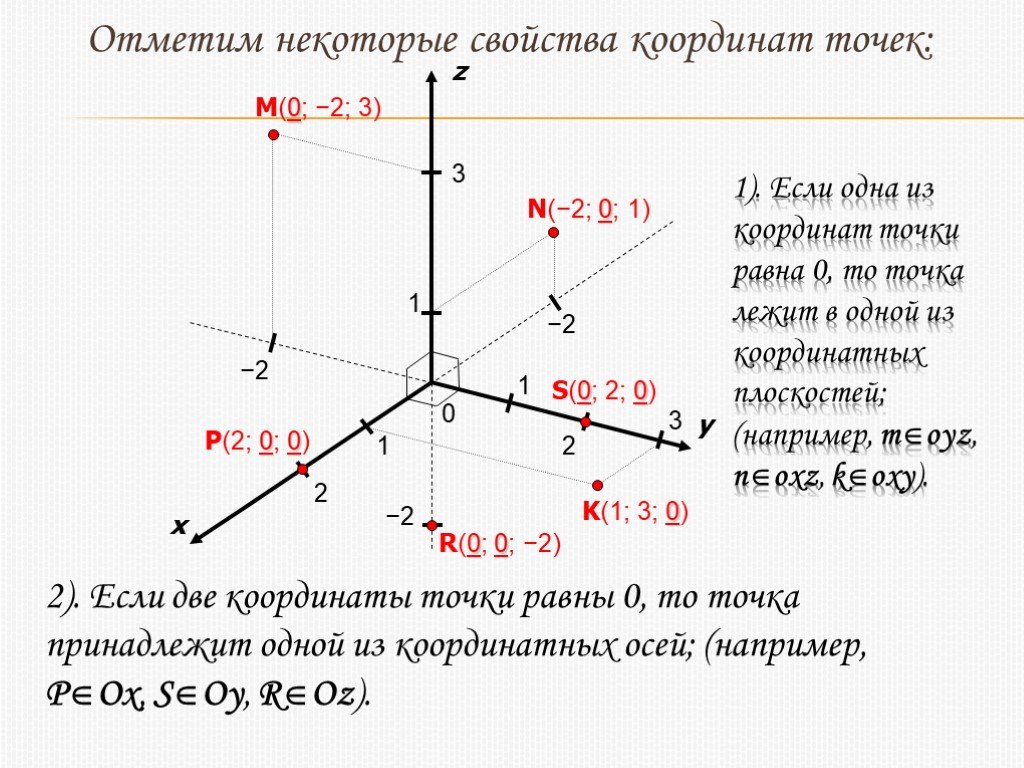
Для построения точек в трехмерном пространстве координат мы начнем с трехмерной системы координат, где ось ???x???- идет к нам слева, ось ???y??? движется вправо, а ось ???z??? является совершенно вертикальной.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Если нам нужно рассмотреть отрицательные значения ???x???, ???y??? или ???z???, то мы должны знать, что отрицательное направление ???x?? ?-ось следует прямой положительной оси ???x???-от нас, что отрицательное направление оси ???y???-оси смещается влево, а отрицательное направление ???z???-ось совершенно вертикальна, простираясь ниже положительного направления ???z???-оси.
Таким же образом, как мы наносим точки в двумерном координатном пространстве, перемещаясь по оси ???x???-к нашему ???x??? значения, а затем двигаясь параллельно оси ???y???, пока не найдем нашу точку, в трехмерном пространстве мы будем двигаться вдоль оси ???x???, затем параллельно оси ?? ?y???-оси, затем параллельно ???z???-оси, пока мы не достигнем нашей координатной точки.
Пошаговое видео о построении четырех разных точек в трехмерном пространстве
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого.
🙂Узнать больше
Еще один пример построения точки в трех измерениях
Пример
Нанесение точки в трехмерной системе координат.
???(4,2,3)???
Мы начнем с рисования наших осей, затем будем двигаться от начала координат вдоль оси ???x???, пока не дойдем до ???x=4???.
Чтобы добраться до ???(4,2)??? в плоскости ???xy??? мы начнем с того места, где остановились на оси ???x???, и будем двигаться параллельно оси ???y???, пока не дойдем до ???у=2???.
Чтобы добраться до ???(4,2,3)??? в трехмерном пространстве мы начнем с того места, где остановились в координатной плоскости ???xy???, и будем двигаться параллельно оси ???z???, пока не доберемся до ???z= 3???.
в трехмерном пространстве мы будем двигаться вдоль оси x, затем параллельно оси y, затем параллельно оси z, пока не достигнем нашей координатной точки.
Ваш комментарий будет первым