Построение графиков с использованием интервальной переменной
Х отя при построении графиков в Mathcad задание аргумента необязательно, иногда оно бывает просто необходимо. Для этого в Mathcad используют интервальную переменную. Например, нам необходимо задать промежуток от -5 до 5 с шагом 0,5. Для этого сначала пишется имя переменной, затем используется знак присваивания значения. Далее указывается начальное значение промежутка, через запятую второе значение. После чего на панели инструментов Matrix (Матрицы), выбирается инструмент интервальной переменной m..n и указывается конечное значение промежутка.
После этого задается формула для графика функции, где в качестве аргумента указывается имя интервальной переменой. Все остальное делается, как уже было описано выше. Например, построим график функции на промежутке от 0 до 2 с шагом 0,01 (см. рис. 7).
Построение графиков в полярной системе координат
Полярная
система координат определяется заданием
некоторой точки, называемой полюсом,
исходящего из этой точки луча ОА,
называемого полярной осью и масштаба
для измерения длин.
К роме того, при задании полярной системы координат должно быть сказано, какие повороты вокруг точки О считаются положительными. Мы с вами будем считать положительными повороты против часовой стрелки. Полярными координатами произвольной точки М (относительно заданной системы) называются числа
=ОМ; =, причем угол измеряют в радианах. (Рис.9).
Символ М(; ) обозначает, что точка М имеет полярные координаты r и j.
Обратите внимание, что так как r — расстояние от начала координат до точки, то оно не может быть отрицательным.
Полярный угол имеет бесконечно много значений, отличающихся друг от друга на величину 2n. Значение полярного угла удовлетворяющего неравенствам , называется главным.
Построим окружность радиусом 5 с центром в начале координат.
В
декартовой системе координат уравнение
окружности c
с центром в начале координат выглядит
как: x2+y2=R2. полярной
же системе это уравнение согласно
определению запишется как =const (расстояние
от центра постоянная заданная величина). Вы видите
насколько проще уравнение окружности
в полярной системе координат. Поэтому
для построения графика остается записать
это уравнение и выбрать мастер построения
графика в полярных координатах (см. рис.
10). Чтобы всю окружность стало видно
измените максимальное значение оси.
полярной
же системе это уравнение согласно
определению запишется как =const (расстояние
от центра постоянная заданная величина). Вы видите
насколько проще уравнение окружности
в полярной системе координат. Поэтому
для построения графика остается записать
это уравнение и выбрать мастер построения
графика в полярных координатах (см. рис.
10). Чтобы всю окружность стало видно
измените максимальное значение оси.
Э то интересно. Естественно между полярными и декартовыми координатами существует определенная взаимосвязь. Для того, чтобы обнаружить эту связь наложим друг на друга полярную и декартовую системы координат так, чтобы их центры совместились, а полярная ось легла на ось абсцисс (Рис.11)
Вспомнив основные тригонометрические соотношения в прямоугольном треугольнике, выразим координаты М(х0,у0), через r и j. А затем используя определение тангенса и теорему Пифагора выразим
М(r
, j)
через х0 и у0.
х0=r cos(j)
у0=r sin(j)
Задание для самостоятельной работы
Построить графики следующих функций с помощью интервальной переменной на указанных промежутках:
А)
В)
Построить графики функций в полярной системе координат:
А)
В)
С)
D)
Трехмерные,
или 3D-графики,
отображают функции двух переменных
вида Z(X, Y). При построении
трехмерных графиков в ранних версиях
MathCAD поверхность нужно
было определить математически (Рисунок
2, способ 2). Теперь применяют функцию
MathCAD CreateMesh.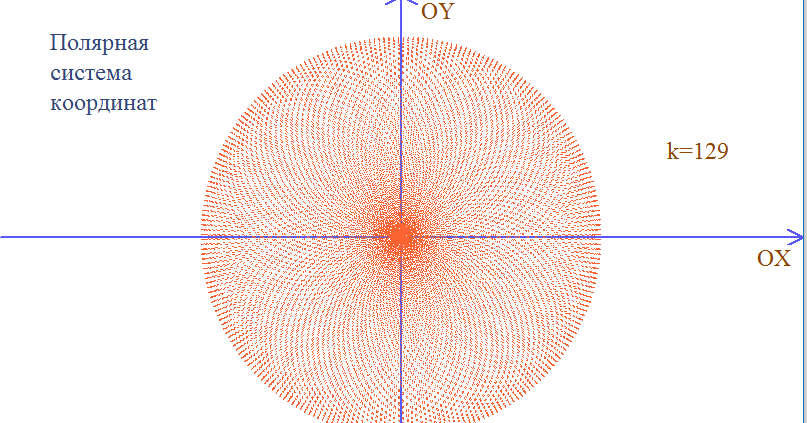
CreateMesh(F (или G, или f
Создает сетку на поверхности, определенной функцией F. x0, x1, y0, y1 – диапазон изменения переменных, xgrid, ygrid – размеры сетки переменных, fmap – функция отображения. Все параметры, за исключением F, — факультативные. Функция CreateMesh по умолчанию создает сетку на поверхности с диапазоном изменения переменных от –5 до 5 и с сеткой 2020 точек.
Пример использования
функции CreateMesh для построения 3D-графиков
приведен на Рисунке 2, способ 1.
Рисунок 1. Пример построения на одном рисунке двух 3D-графиков разного типа
Нередко поверхности и пространственные кривые представляют в виде точек, кружочков или иных фигур. Такой график создается операцией Вставка График 3D Точечный, причем поверхность задается параметрически – с помощью трех матриц (X, Y, Z) (см. Рисунок 3, способ 2), а не одной как в примере на Рисунке 2. Для определения исходных данных для такого вида графиков используется функция CreateSpace (см. Рисунок 3, способ 1).
Рисунок 2. Построение 3D Точечных графиков
CreateSpace (F , t0, t1, tgrid, fmap)
Возвращает вложенный
массив трех векторов, представляющих х-, у-, и z‑координаты
пространственной кривой, определенной
функцией F. t0
и t1 – диапазон
изменения переменной, tgrid – размер сетки переменной, fmap – функция отображения. Все параметры,
за исключением F, —
факультативные.
t0
и t1 – диапазон
изменения переменной, tgrid – размер сетки переменной, fmap – функция отображения. Все параметры,
за исключением F, —
факультативные.
Yotx / Построение графиков функций онлайн
| Robot | Path | Permission |
| GoogleBot | / | ✔ |
| BingBot | / | ✔ |
| BaiduSpider | / | ✔ |
| YandexBot | / | ✔ |
| Title | Построение графиков функций онлайн |
| Description | Сервис построения графиков функций онлайн с автоматическим выбором значений по оси У, с возможностью сохранения графика, печатью, расшаривания в социальных сетях и пр. |
| Keywords | график функции, заданная параметрически функция, функция в полярных координатах, график по точкам, построение, онлайн |
| WebSite | www.yotx.ru |
| Host IP | 81.176.226.80 |
| Location | Russia |
| Site | Rank |
| matematikam.ru | #238,140 |
| reshish.ru | #905,767 |
| umath.ru | #146,806 |
grafikus.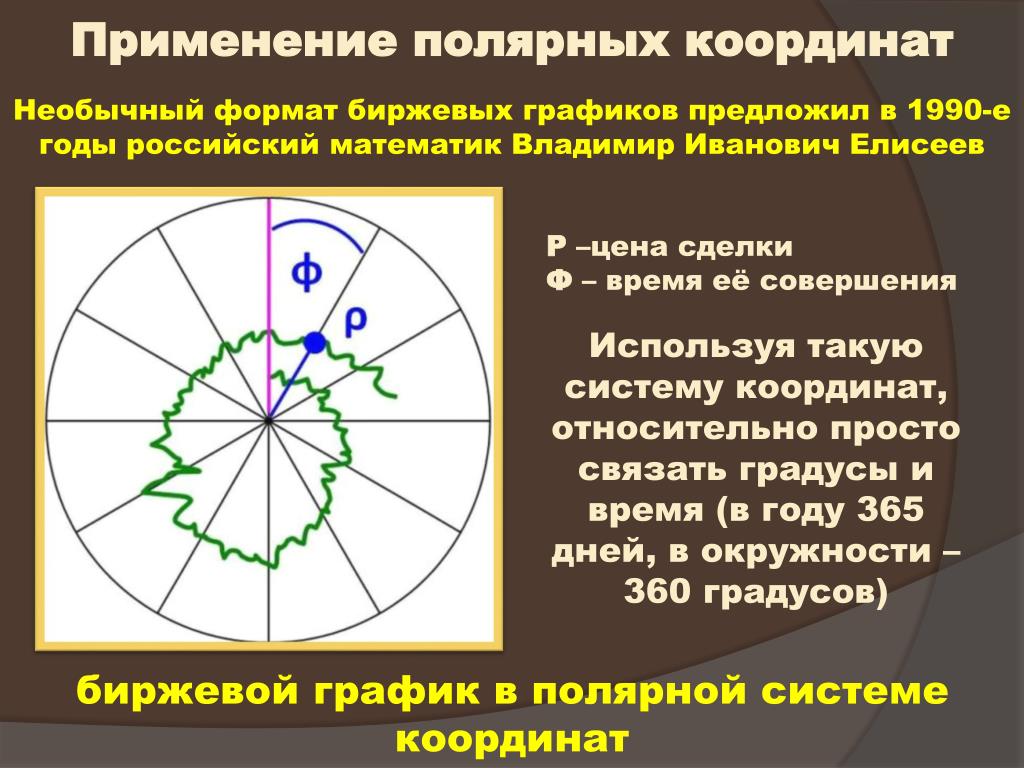 ru ru | #1,806,783 |
| kontrolnaya-rabota.ru | #50,909 |
| yourmomhatesthis.com |
| yspu.org |
| yume.vn |
| yves-rocher.ua |
| ywhmcs.com |
| zamandayolculuk.com |
| zentut.com |
| zeri.info |
| zeroqode.com |
| znaytovar.ru |
| thompsonscandle.com |
tosseduk. com com |
US$73,690 Last updated: Nov 17, 2019 Yotx.ru has global traffic rank of 282,089 and ranks the 8,939th in Russia. Its global rank has gone down by 32,716 positions since 3 months ago. Yotx.ru has an estimated worth of US$ 73,690, based on its estimated Ads revenue. Yotx.ru receives approximately 11,216 unique visitors each day. Its web server is located in Russia, with IP address 81.176.226.80. According to SiteAdvisor, yotx.ru is safe to visit. |
| Purchase/Sale Value | US$73,690 |
| Daily Ads Revenue | US$40 |
| Monthly Ads Revenue | US$1,211 |
| Yearly Ads Revenue | US$14,738 |
| Daily Unique Visitors | 11,216 |
Note: All traffic and earnings values are estimates. | |
| Global Rank | 282,089 |
| Delta (90 Days) | ⬇️ 32,716 |
| Most Popular In Country | Russia |
| Country Rank | 8,939 |
| Host | Type | TTL | Data |
| yotx.ru | A | 3599 | IP: 81.176.226.80 |
| yotx.ru | MX | 3599 | Priority: 8 Target: mail-s7. 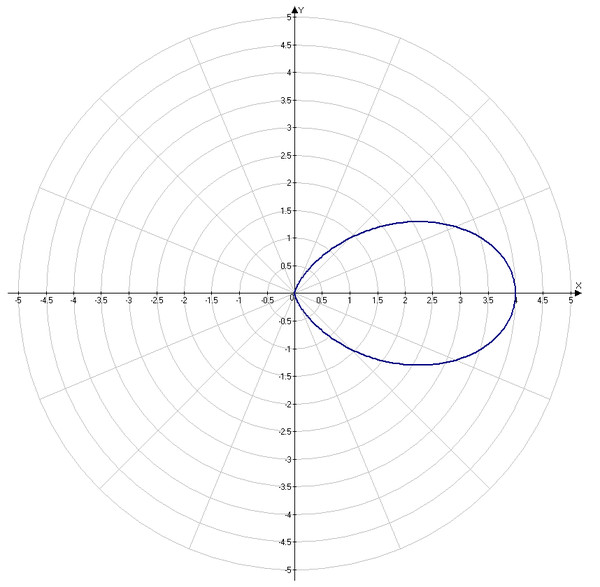 1gb.ru. 1gb.ru. |
| yotx.ru | NS | 3599 | Target: ns2.1gb.ru. |
| yotx.ru | NS | 3599 | Target: ns1.1gb.ru. |
| yotx.ru | SOA | 3599 | MNAME: ns1.1gb.ru. RNAME: noc.1gb.ru. Serial: 63 Refresh: 900 Retry: 600 Expire: 86400 Minimum TTL: 3600 |
HTTP/1.1 200 OK Cache-Control: private Content-Type: text/html; charset=utf-8 Server: Microsoft-IIS/7. |
domain: YOTX.RU nserver: ns1.1gb.ru. nserver: ns2.1gb.ru. nserver: ns3.1gb-ru.com. state: REGISTERED, DELEGATED, VERIFIED person: Private Person registrar: RU-CENTER-RU admin-contact: https://www.nic.ru/whois created: 2009-03-02T21:00:00Z paid-till: 2020-03-02T21:00:00Z free-date: 2020-04-03 source: TCI Last updated on 2019-11-17T18:01:32Z |
Cartesian & Polar Function Grapher
Самый продвинутый в мире Cartesian и полярный функция Grapher для рисования графика функций, способный оживлять полярный график процесса самым правильным образом.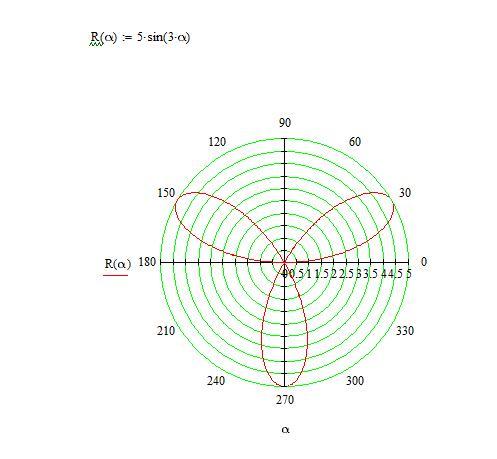 Он показывает, как полярный график функции строится постепенно в своей области определения. Вы также можете графически заданную функцию в Декартова система координат на сняв флажок Полярная .
Он показывает, как полярный график функции строится постепенно в своей области определения. Вы также можете графически заданную функцию в Декартова система координат на сняв флажок Полярная .
Полярный график функций представляет собой калькулятор графических функций , который рисует график функции в заданной области в полярной системе координат. Такой график называется полярным графиком или полярной кривой данной функции.
Процесс построения графика в полярной системе координат и отображение его с помощью графического калькулятора функций принципиально отличается от построения графика в декартовой системе координат . Это связано с тем, что полярный граф необходимо рисовать постепенно, чтобы можно было визуализировать, как полярный граф представляет собой построенный в своей области.
Графический редактор функций , использующий самые сложные декартовы и полярные системы координат , является единственным известным графическим инструментом, который может отображать неперпендикулярную декартову систему координат , а также правильно помогает визуализировать полярную кривую прогрессивно построенную посредством анимации полярного графика . Таким образом, вы можете наблюдать, как шаг за шагом рисуются все ваши крутых полярных графика .
Вы можете использовать эту чрезвычайно полезную функцию, нажав ► в нижней части графического калькулятора функций (если он скрыт, сначала нажмите кнопку Animate ).
Запускает анимацию процесса построения полярных графиков функции в фокусе . График рисуется постепенно от начального значения θ₁ до конечного значения θ₂ радиальной оси . Анимированный полярный график показывает вращения угловых осей ( радиальных осей ) и радиальных расстояний .
Анимированный полярный график показывает вращения угловых осей ( радиальных осей ) и радиальных расстояний .
Затем вы можете нажать ‖ до приостановить анимацию или нажать Готово до остановить ее. Это также закрывает интерфейс анимации. Чтобы отобразить его снова, нажмите кнопку Animate в верхней части полярного графа.
Вы также можете изменить скорость анимации полярной графики с помощью ползунка из комплекта
Этот бесплатный онлайн-калькулятор полярной функции графика также рисует полярных графика с повернутой полярной осью .
Советы: по мере ввода:
- ..t заменяется на θ . ( Вы также можете использовать x или t.
 Они внутренне заменены на θ ).
Они внутренне заменены на θ ). - пи заменяется на π .
- inf ( бесконечность ) заменяется на ∞ .
Для построения графика кусочно определенных функций введите каждую часть с соответствующим подынтервалом как одиночную функцию .
Самый быстрый способ ввести dom=(0, 2π) или dom=(-∞, ∞) — это полностью удалить домен, включая dom= .
МышьМатикс! Вы можете использовать мышь, чтобы Вращать оси , Перемещать и Изменить масштаб
Кроме ввода данных — сначала нажав 9Кнопка шестеренки 0017 — вы можете использовать мышь для выполнения некоторых функций, уникальных для этого интерактивного графического редактора функций , как описано ниже.
- Щелкните по оси (или рядом с ней) и переместите мышь.
 Это будет вращать ось .
графики перерисовываются в неперпендикулярной декартовой системе координат или обобщенной полярной системе координат . Нажмите еще раз, чтобы освободить ось.
Это будет вращать ось .
графики перерисовываются в неперпендикулярной декартовой системе координат или обобщенной полярной системе координат . Нажмите еще раз, чтобы освободить ось. - Перетащите мышь на , переместите систему координат вместе с графиками.
- Дважды щелкните на холсте, чтобы переместить исходную точку туда, где был сделан щелчок.
- Удерживая клавишу Alt, щелкните по оси, чтобы изменить масштаб (увеличение в одном направлении) ; в точка, по которой был сделан щелчок, будет помечена как «1» (или «-1») и станет новой единицей измерения для этой оси.
Анимация вращения оси: Икс у ► ⬛
сообщение
f(x) =
?
f( ) =
⌨
4 Десятичные разряды
Graph FinenessBest (медленно)+2+1Normal-1-2Fast (низко)
Label Axes ось x: ось y: Повернуть оси Ось x°: Ось Y°: 92-4)Другие графики
√(4sin(2x)) √(4cos(2x))
Функции — Полярный
Линии
2csc(θ) 2сек(θ) 1/(sin(θ) — cos(θ))
Круги
1 2 6sin(θ) 8cos(θ)
Спирали
θ θ/5 дом=(0, 10π) √(θ) дом=(0, 10π) 1/θ дом=(0, 10π)
Розы
4sin(3θ) 4sin(2θ) 4sin(5θ) 4sin(4θ)
Эллипсы
1/(1-. 8cos(θ))
1/(1-0,8sin(θ))
1/(1+.8cos(θ))
1/(1+.8sin(θ))
8cos(θ))
1/(1-0,8sin(θ))
1/(1+.8cos(θ))
1/(1+.8sin(θ))
Параболы
1/(1-sin(θ)) 1/(1+cos(θ)) 1/(1+sin(θ)) 1/(1-cos(θ))
Гипербола
1/(1+2cos(θ)) 4/(1+2sin(θ)) 1/(1-2cos(θ)) 4/(1-2sin(θ)) 95 дом = (0, 12π)
РАД Полярный
🔍+ 1 🔍−
время построения графика (с)
Калькулятор загружается.
Пожалуйста, подождите….
Сделайте это прозрачным
Толщина графика Угловой режим РАД градус ГРД График по мере ввода (взаимодействие) Скрыть оси Скрыть сетки Показать интерфейс анимации осейзаголовок
…
Медленный Быстрый
Показать угловые оси Сделанный
Отключить программную клавиатуру
Чтобы скопировать или сохранить графики, щелкните правой кнопкой мыши изображение сохраненного графика ниже и выберите «Копировать изображение» или «Сохранить изображение» во всплывающем меню.
Этот интерактивный полярный график функции был разработан для построения графиков и, в частности, для демонстрации с помощью анимации того, как график функции создается в полярной системе координат . Полярные кривые могут быть очень сложными и могут иметь много петель. Все остальные полярные графы
(до этого графического калькулятора полярных функций — недавно некоторые другие графографы в партнерстве с Google и Microsoft начали следовать этому правилу) отображают полярный график функции, не показывая, где начинается или заканчивается кривая, а также прослеживаются ли петли, если таковые имеются, и как. Этот уникальный калькулятор построения графиков полярных функций представляет правильный способ построения графиков функций в полярных системах координат . А именно, он начинает строить график с начального значения угловой координаты θ₁ и постепенно показывает процесс построения графика до конечного значения θ₂, показывая, повторяются ли петли или какая-либо часть кривой.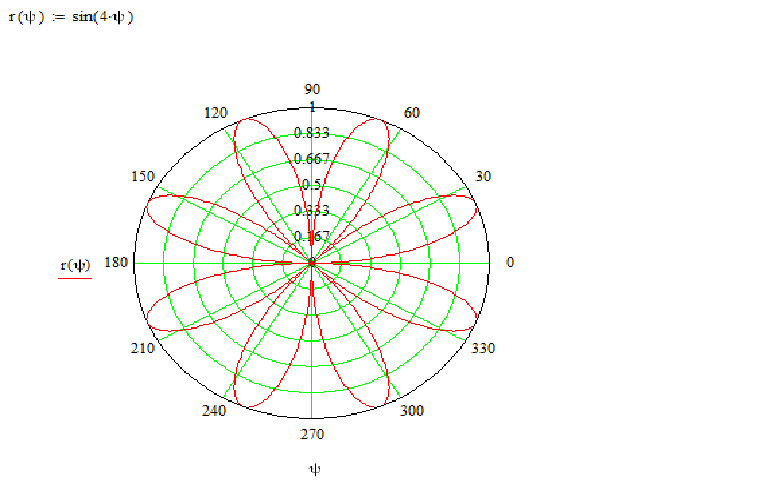 Более того, этот графограф полярных функций позволяет изменять скорость процесса построения полярных графиков.
Более того, этот графограф полярных функций позволяет изменять скорость процесса построения полярных графиков.
Легко использовать декартовых или полярных графических функций ; введите функцию в любое поле выражения , например, f(x) или r(θ) . График функций отображает графики по мере ввода (по умолчанию) в выбранной системе координат . (Не беспокойтесь о том, какую переменную вы используете, функция Grapher автоматически изменяет переменные в соответствии с выбранным система координат.)
- В график две или более функции на одной и той же декартовой или полярной системе координат нажмите » для отображения мультиграфической панели 25 90. Панель с несколькими графиками состоит из панелей выражений , которые можно добавить или удалить по желанию, нажав + или × .
 на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.
на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график. - Для удобства графопостроитель полярных функций или графопостроитель декартовых функций добавляет подходящий интервал, dom = (0, 2π) или dom = (-∞, ∞), соответственно, к функциональным выражениям и графикам на указанных домен. При желании можно изменить конечные точки . Конечные точки должны быть конечными для построения полярного графика. Устройство графического отображения полярных функций автоматически изменяет бесконечности, если таковые имеются, на конечные значения.
- Полярные графики или декартовы графики отображаются сразу же после ввода. Вы можете Анимировать процесс построения полярного графика, как описано выше.
- Можно установить тонкость декартовой или полярной кривых , выбрав нужный вариант из раскрывающегося списка Graph Fineness .
 В целом, чем выше точность, тем больше времени требуется -графику функций для построения графиков функций.
В целом, чем выше точность, тем больше времени требуется -графику функций для построения графиков функций. - Чтобы скопировать или сохранить графики, сначала нажмите кнопку Копировать/Сохранить график . Изображение графиков появится под графиком функций . Затем вы можете использовать возможности вашего браузера, чтобы сохранить его или скопировать его в ваши документы.
- Чтобы оценить функцию , введите число или числовое (постоянное) выражение в соответствующем поле; функциональный граф отображает рассчитанные значения функции с количеством знаков после запятой, которое можно указать с помощью предоставленного ползунка.
Интересные кривые : Нарисуйте любое из выражений в разделе Интересные графики , а также отобразите несколько классных полярных графиков , выбрав его. Для достижения наилучших результатов вам может потребоваться выбрать Graph Fineness как «+1» или выше.
Для достижения наилучших результатов вам может потребоваться выбрать Graph Fineness как «+1» или выше.
Вы можете установить следующие параметры, нажав кнопку ⚙ (шестеренка) в правом верхнем углу графического холста.
- Измените толщину графиков с помощью предоставленного ползунка.
- Выберите режим угла ( радиана – по умолчанию , градуса или градуса ).
- Если вы отмените выбор График при вводе параметра , вам придется нажать График выбранных выражений , который затем появится в нижней части калькулятора, чтобы обновлять графики всякий раз, когда вы вносите какие-либо изменения в выражения или координаты. плоскость (т. е. переместить начало координат, повернуть оси и т. д.).
- При необходимости отобразите элементы управления в верхней части графического редактора функций , которые позволяют запускать/приостанавливать и останавливать вращение любой или всех осей.

- Графический редактор функций запоминает функциональные выражения , которые вы вводите, и извлекает их между посещениями. Вы можете очистить их, нажав кнопку Reset Calculator .
Для эффективного использования этого онлайн-калькулятора функций используйте последние версии браузеров Chrome , Microsoft Edge , Firefox , Opera или Safari . В противном случае некоторые компоненты графического редактора функций могут не отображаться или работать.
Вставка 1 St производная Вставка 2 и производная от
полярных графиков | Математика для школьников
Notes (см. Notes на странице для получения дополнительной информации о различных коллекциях Notes).
- Только математика – полярные кривые
- Математический центр
Полярные координаты — это просто способ определения положения точки в двух измерениях.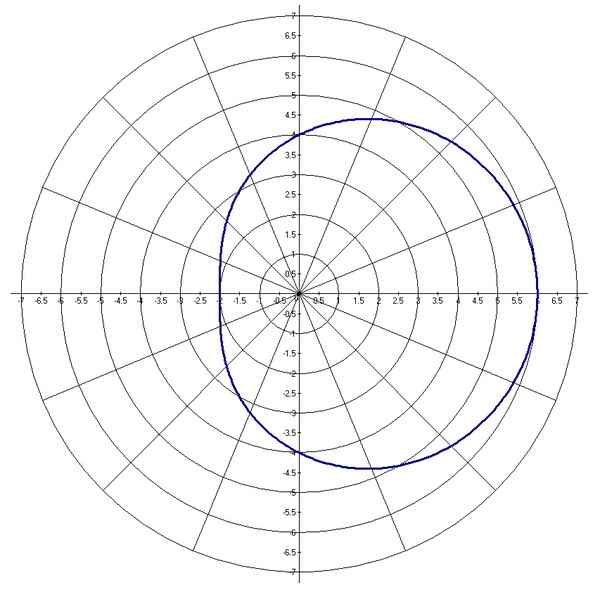 Расстояние от начала координат (r) и угол, образуемый с осью x (измеряется против часовой стрелки), определяют положение точки. Точка на приведенной выше диаграмме находится на расстоянии 3 от начала координат, а угол, образуемый с осью x, составляет 30 °.
Расстояние от начала координат (r) и угол, образуемый с осью x (измеряется против часовой стрелки), определяют положение точки. Точка на приведенной выше диаграмме находится на расстоянии 3 от начала координат, а угол, образуемый с осью x, составляет 30 °.
Попробуйте эту страницу на Desmos поэкспериментировать с точками построения.
Попробуйте соединить точки в упражнении ! Полярные кривые Соедините точки
Для получения отличных ресурсов по полярным кривым см. , эти , из mathcentre, , а для некоторых полярных диаграмм прокрутите страницу вниз на Mathsbits.
Вы можете легко экспериментировать с семействами полярных кривых, используя превосходный графический калькулятор Desmos. Нажмите на изображение ниже и поэкспериментируйте с ползунками.
- Полярная кривая Desmos, нажмите на изображение, чтобы поэкспериментировать
Можно увидеть, как трассируются полярные кривые, используя ползунок в домене графического калькулятора Desmos. Попробуйте выбрать изображение, чтобы увидеть r=acoskθ.
Попробуйте выбрать изображение, чтобы увидеть r=acoskθ.
Другие примеры: r=acos 2 θ , r=a(1-cosθ) r=ae -kθ r 9 = 2 03 2 cos2 θ
Кардиоиды a+bsinθ и a + bcosθ
Когда у вас появляется ямочка?
Когда возникает внутренний цикл?
В качестве альтернативы попробуйте этот Polar Grapher ; используйте ползунок, чтобы изменить угол, и вы увидите, как прослеживается кривая. Обратите внимание, что отображается значение R, чтобы вы могли легко увидеть, положительное оно или отрицательное.
Для действительно четкого плоттера, показывающего связь между декартовым графиком r=f(θ) и графиком в полярных координатах, попробуйте этот Апплет полярных кривых и декартовых графиков . Внимательно следите за дисплеем при перемещении ползунка; вы можете легко увидеть, например, когда r отрицательно.
 0
X-AspNetMvc-Version: 4.0
X-AspNet-Version: 4.0.30319
X-Powered-By: ASP.NET
Date: Sun, 17 Nov 2019 18:02:47 GMT
Content-Length: 28936
0
X-AspNetMvc-Version: 4.0
X-AspNet-Version: 4.0.30319
X-Powered-By: ASP.NET
Date: Sun, 17 Nov 2019 18:02:47 GMT
Content-Length: 28936
 Они внутренне заменены на θ ).
Они внутренне заменены на θ ). Это будет вращать ось .
графики перерисовываются в неперпендикулярной декартовой системе координат или обобщенной полярной системе координат . Нажмите еще раз, чтобы освободить ось.
Это будет вращать ось .
графики перерисовываются в неперпендикулярной декартовой системе координат или обобщенной полярной системе координат . Нажмите еще раз, чтобы освободить ось. на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график.
на каждой панели соответственно. Установка или снятие флажка для любого выражения отображает или скрывает соответствующий график. В целом, чем выше точность, тем больше времени требуется -графику функций для построения графиков функций.
В целом, чем выше точность, тем больше времени требуется -графику функций для построения графиков функций.
Ваш комментарий будет первым