Применение производной к построению графиков функции
Репетиторы ❯ Математика ❯ Применение производной к построению графиков функции
Автор: Валентин В., онлайн репетитор по математике
●
14.11.2011
●
Раздел: Математика
Если на некотором промежутке график функции представляет собой непрерывную линию, иными словами, такую линию, которую можно провести без карандаша от листа бумаги, то такая функция называется непрерывной на этом промежутке. Существуют также функции, которые непрерывными не являются.
х = с разрывна и поэтому на всем отрезке [a; b] не является непрерывной. Все функции, изучаемые нами в школьном курсе математики, – это функции непрерывные на каждом промежутке, на котором они определены.
Отметим, что если на некотором промежутке функция имеет производную, то на этом промежутке она непрерывна.
Обратное утверждение является неверным. Функция, которая непрерывна на промежутке, может не иметь производной в некоторых точках этого промежутка. Например, функция
у = |log 2 x| непрерывна на промежутке х > 0, но в точке х = 1 не имеет производной, в силу того что в этой точке график функции касательной не имеет.
Рассмотрим построение графиков с помощью производной.
Задача 1.
Построить график функции f(x) = x3 – 2x2 + x.
Решение.
1) Эта функция определена при всех х € R.
2) Найдем промежутки монотонности рассматриваемой функции и ее точки экстремума с помощью производной.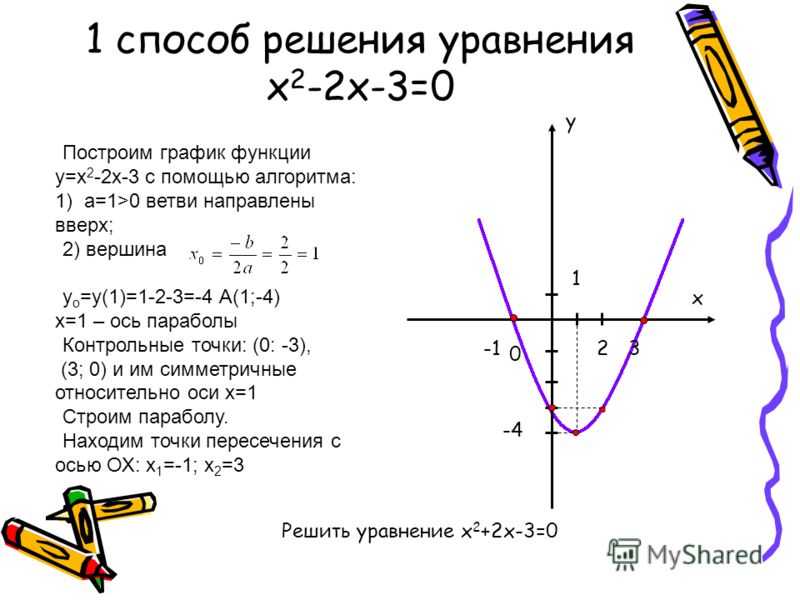 Производная равна f ‘(x) = 3x2 – 4x + 1. Найдем стационарные точки:
Производная равна f ‘(x) = 3x2 – 4x + 1. Найдем стационарные точки:
3x2 – 4x + 1 = 0, откуда х1 = 1/3, х2 = 1.
Для определения знака производной разложим квадратные трехчлен 3x2 – 4x + 1 на множители:
f ‘(x) = 3(х – 1/3)(х – 1). Следовательно, на промежутках х < 1/3 и х > 1 производная положительна; значит, функция возрастает на этих промежутках.
Производная отрицательна при 1/3 < х < 1; следовательно, функция убывает на этом интервале.
Точка х1 = 1/3 является точкой максимума, так как справа от этой точки функция убывает, а слева – возрастает. В этой точке значение функции равно f (1/3) = (1/3)3 – 2(1/3)2 + 1/3 = 4/27.
Точкой минимума является точка х
3) При построение графика обычно находят точки пересечения графика с осями координат.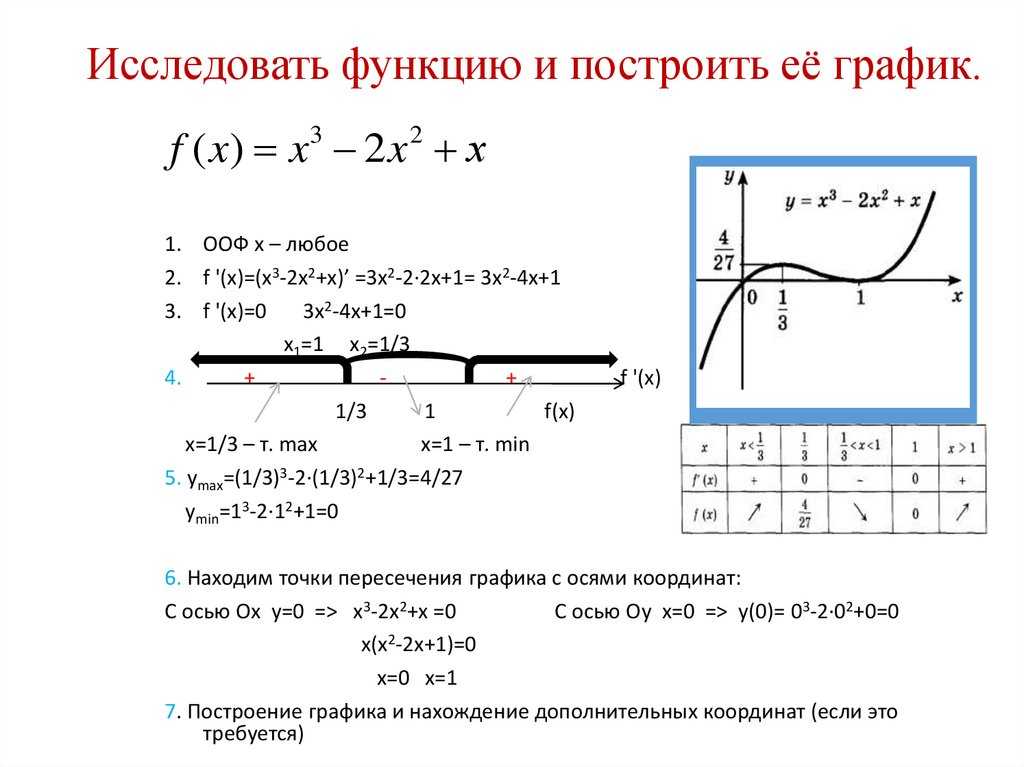 Так как f(0) = 0, то график проходит через начало координат. Решая уравнение f(0) = 0, находим точки пересечения графика с осью абсцисс:
Так как f(0) = 0, то график проходит через начало координат. Решая уравнение f(0) = 0, находим точки пересечения графика с осью абсцисс:
x3 – 2x2 + x = 0, х(x2 – 2х + 1) = 0, х(х – 1) 2 = 0, откуда х = 0, х = 1.
4) Для более точного построение графика найдем значения функции еще в двух точках: f(-1/2) = -9/8, f(2) = 2.
5) Используя результаты исследования (пункты 1 – 4), строим график функции у = x3 – 2x2 + x.
Для построения графика функции обычно сначала исследуют свойства этой функции с помощью ее производной по схеме, аналогичной схеме при решении задачи 1.
Таким образом, при исследовании свойств функции необходимо найти:
1) область ее определения;
2) производную;
3) стационарные точки;
4) промежутки возрастания и убывания;
5) точки экстремума и значения функции в этих точках.
Результаты исследования удобно записывать в виде таблицы. Затем, используя таблицу, строят график функции. Для более точного построения графика обычно находят точки его пересечения с осями координат и – при необходимости – еще несколько точек графика.
Для более точного построения графика обычно находят точки его пересечения с осями координат и – при необходимости – еще несколько точек графика.
Если же мы сталкиваемся с четной или нечетной функцией, то для построения ее графика достаточно исследовать свойства и построить ее график при х > 0, а затем отразить его симметрично относительно оси ординат (начала координат). Например, анализируя функцию f(x) = х + 4/х, мы приходим к выводу о том, что данная функция нечетная: f(-x) = -х + 4/(-х) = -(х + 4/х) = -f(x). Выполнив все пункты плана, строим график функции при х > 0, а график этой функции при х < 0 получаем посредством симметричного отражения графика при х > 0 относительно начала координат.
Для краткости решения задач на построение графиков функции большую часть рассуждений проводят устно.
Также отметим, что при решении некоторых задач мы можем столкнуться с необходимостью исследования функции не на всей области определения, а только на некотором промежутке, например, если нужно построить график, скажем, функции f(x) = 1 + 2x2 – x4 на отрезке [-1; 2].
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос
Математика
Курсы по математике 10 класс
Математика
Курсы по математике 9 класс
Математика
Математика 11 класс
Математика
Курсы по геометрии 7 класс
Математика
Курсы по алгебре 7 класс
Математика
Алгебра 8 класс
Математика
Курсы по геометрии 8 класс
Французский язык
Курсы французского языка для начинающих
5 инструментов для создания удивительных онлайн графиков
Скорее! Вы должны сделать большую презентацию за менее, чем 24 часа, включающую в себя несколько таблиц с данными и электронных таблиц. Эти данные хороши, но там почти не на что смотреть. Вы хотите представить нечто более динамичное , чем просто изображения, но кодировать решение с нуля для вас не вариант.
Эти данные хороши, но там почти не на что смотреть. Вы хотите представить нечто более динамичное , чем просто изображения, но кодировать решение с нуля для вас не вариант.
К счастью, есть некоторые онлайн-решения, которые могут принести привлекательные и динамичные результаты без программирования.
Сегодня мы будем давать вам краткое изложение пяти возможных путей решения, которые могут помочь вам построить больше, чем простое программирование.
Давайте начнем!
Plot.ly
Первое впечатление: Plotly удобен для пользователя, это первое, что можно заметить. После создания учетной записи можно перемещаться по сайту буквально через 5 секунд. В правом верхнем углу, рядом с именем учётной записи вы можете создать свой первый проект.
Здесь вы можете выбрать, что строить – график или сетку. Исходя из этого вы ориентируетесь на импортируемы данные. Если вы просто хотите устроить для Plotly тест-драйв, можете проверить 12 примеров предварительного построения данных. Эти примеры дадут вам представление о том, что Plotly может сделать для вас и, честно говоря, материал впечатляет.
Эти примеры дадут вам представление о том, что Plotly может сделать для вас и, честно говоря, материал впечатляет.
Создание графика является лишь вопросом загрузки вашей информации и настройки следов, макета, осей, заметок и легенды. Одноразовые графики и типы графиков выглядят очень профессионально, так что это идеальное решение для бизнеса и аналитических презентаций.
Это не значит, что те, кто предоставляет случайную информацию, не могут использовать его. Plotly существует для всех, даже если он просто находится в режиме тестирования.
Особенности:
- Plotly бесплатен
- Вы можете создать до 50 личных файлов
- Вы можете сотрудничать с графиками не полагаясь на адрес электронной почты
- Интерактивные графики и разнообразие данных визуализированы для выбора
- Графики могут быть экспортированы в различные форматы, включая EPS, SVG и PDF
Примечание: Plotly ещё относительно нов, но они сообщают о своих последних обновлениях через блог Plotly и так же показывают, что вы можете сделать с программой.
Hohli: Создатель онлайн-графиков
Первое впечатление: Создатель онлайн-графиков Hohli является идеальным для тех, кто ищет графики выше среднего, но без наворотов.
С самого начала пути варианты типов ваших графиков ясны. В общей сложности существует 6 основных типов графиков, три из них могут варьироваться.
Построение нового графика является довольно простым линейным процессом. Это хороший подход, потому что вы никогда не не будете перегружены множеством вариантов, составляя данные.
Существует также возможность настроить размер диаграммы и ориентацию, так что если вам нужен вертикальный график вместо горизонтального, то вам повезло. Есть окно предварительного просмотра в правой части экрана, которое позволяет вам увидеть, что вы делаете и исправить ошибки.
Обосенности:
- Hohli является полностью бесплатным.
- Не требует регистрации
- Индивидуальная настройка графики проста, как несколько щелчков.
 Возможность выбора цвета и ввода ваших данных
Возможность выбора цвета и ввода ваших данных - Вы можете изменить тип вашего графика не начиная все заново
- Возможность загрузки из Google Charts
ChartBlocks
Первое впечатление: создатели ChartBlocks довольно много думали о привлекательности, когда они пришли к подготовке построения этого создателя графиков. После создания аккаунта вы автоматически переходите на создание своего графика.
Также как и Plot.ly, ChartBlocks проведёт вас через ваше творение. Здесь вам даётся три варианта: копировать/вставить вручную или вручную ввести данные, используя те, что вы уже импортировали в ChartBlocks (применимо, только если вы создали диаграмму выше) или же загрузить электронную таблицу с компьютера.
Исходя из этого процесс протекает гладко. На выбор есть 5 типов диаграмм и, к сожалению, если вы используете бесплатный аккаунт, то у вас есть всего несколько шаблонов, предлагающих несколько цветов, а значит есть предел способности персонализировать свой тип диаграммы.
Помимо этого, у вас есть доступ к настраиваемым параметрам, чтобы визуально соответствовать вашей презентации.
Особенности:
- ChartBlocks является freemium моделью – 5 типов графиков
- Три метода ввода данных доступны для вас
- Настраиваемые активы помогут выделиться вашим графикам
- Скачивайте ваши графики в различных форматах, в том числе и PS, SVG и PNG
- Ваши графики могут быть доступны посредством социальных сетей и даже встроены в ваши сайты и презентации.
Online Chart Tool
Первое впечатление: Online Chart Tool напоминает улучшенную версию инструмента Hohli, с намного большим количеством диаграмм и типов графиков.
В целом, существует 10 типов диаграмм на выбор, каждый с уникальным внешним видом. Как в другом создателе графиков “OCT”, стоит подбирать приятный линейный рабочий процесс, если дело доходит до проектировия данных. Однако каждый тип графика поставляется с различным набором вариантов и переменных.
Например, если вы выбираете область диаграммы и вам нужно принять решение о вариантах типов и стилей, Meter Chat потребует от вас только определить свой стиль. Вы можете добавить свои данные вручную или загрузив файл CSV.
Если вам не хватает настраиваемых параметров с выбором стиля вашего графика, вы можете решить как именно ярлки и шрифты появятся на готовом графике. Если вы считаете, что все готово, можете просмотреть график, и если он понравился, завершить его и поделиться им или скачать.
Особенности:
- Online Chart Tool является бесплатной онлайн-программой
- Регистрация не требуется, но вы можете создать свой аккаунт
- Доступно разнообразие графиков и настроек
- Есть 17 типов шрифтов на выборр, если пришло время создания лейбла
- Вы можете сохранить данные графика, чтобы разделить или вернуться к нему позже
- Есть 4 загружаемых варианта для вас на выбор между PDF и CSV
- Сайт предлагает 6 языков, делая его доступней для не англоговорящих людей
RAW
Первое впечатление: RAW отличается от любой другой графической программы. Если вам нравится профессионализм и разнообразие графиков, таких как в Plotly, то вам, вероятно, понравятся графики от RAW.
Если вам нравится профессионализм и разнообразие графиков, таких как в Plotly, то вам, вероятно, понравятся графики от RAW.
Вместо стандартного выбора бар/круговых диаграмм, вы получаете 16 графиков на выбор. Не считая того, что есть возможность создать свой собственный график, если вы того пожелаете.
RAW очень прост в использовании, и нет нужды в кнопке “next”, нажимая которую, вы переходите дальше. Вам даже не нужно регистрироваться, чтобы его использовать.
С другой стороны RAW не предлагает возможность загружать электронную таблицу, но вы просто можете скопировать и вставить свои данные, получая возможность выбора типа диаграммы. Возможно, вы не слышали о многих из типов графиков, но слева удачно появляется разъяснение каждого типа.
Вы можете “наметить расположение” или, другими словами, спланировать, где будет находитьсчя фаша информация. Это делается в свободном стиле перетаскивания, который сильно отличается от других приложений. Перемещение и организация результатов в режиме реального времени изменяет график, так что вы можете проверить, что работает лучше.
Как только вы закончили с этим этапом отображения, вы буквально сделали все, так как нет настройки опций, когда дело доходит до цвета и типа.
Особенности:
- RAW бесплатен для любого пользователя
- Регистрация не обязательна
- Лёгкое создание графика
- Перетаскивание и отображение инструмента, позволяющего изменить информацию без случайных удалений данных
- 16 профессиональных графиков на выбор
- 3 загружаемых варианта наряду с генерацией кода
- Ваши данные в безопасности благодаря не серверным операциям
Примечание: RAW можно свободно скачать и изменить, так как это открытый и настраиваемый проект.
Завершение
Все упомянутые программы являются отличным инструментом для построения и отображения диаграмм без кодирования. Для внимания есть более красочные и профессиональные дизайны, каждому есть, что выбрать.
Если вы ищите удивления от своей презентации, используете Plotly и RAW. Для бесплатных программ эти два дают впечатляющие результаты. Hohli, ChartBlocks и Online Chart Tool предлагают уникальные услуги и являются прекрасными претендентами для тех, кто ищет визуализацию данных.
Для бесплатных программ эти два дают впечатляющие результаты. Hohli, ChartBlocks и Online Chart Tool предлагают уникальные услуги и являются прекрасными претендентами для тех, кто ищет визуализацию данных.
Источник фото – Fotolia.ru
01-04-2016
Калькулятор графического метода — линейное программирование 🥇
Часто ли вас смущают задачи линейного программирования, которые вы не можете решить? Может быть, пришло время получить некоторую помощь. Что ж… Вам повезло! Решать оптимизационные задачи графическим методом будет проще с нашим калькулятором графического метода для задач линейного программирования.
Калькулятор графических методов — линейное программирование
Контент только для зарегистрированных пользователейУ вас уже есть членство?
Получить членство
Вышеупомянутое приложение является упрощенной версией нашего калькулятора графического метода, доступного для студентов, которые имеют членство с нами; тем не менее, он обладает всеми базовыми функциями, необходимыми для построения графиков большинства упражнений по линейному программированию в вашей школе.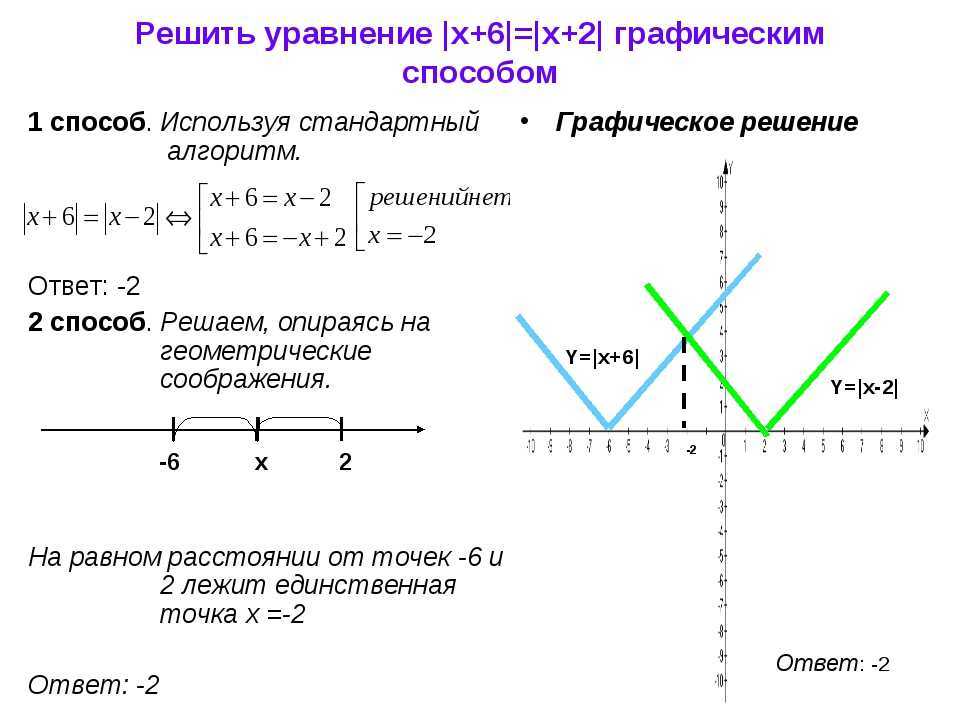
Эта бесплатная версия, как и другие доступные бесплатные калькуляторы линейного программирования, показывает только конечный результат (оптимальное решение и график) задачи. Так как многие студенты не могут адекватно понять, как формировались графики, мы разработали версию с подробными пошаговыми пояснениями решения задачи.
Расширенные функции калькулятора графического метода линейного программирования
Целью нашего членства является помочь вам улучшить свои навыки решения задач и повысить свою успеваемость в школе. Вот почему мы включили ряд онлайн-ресурсов, где линейное программирование является обязательным. В этом приложении вы найдете следующее:
- Расчет пересечений с осями для построения графика каждого ограничения.
- Объяснение заштрихованной области в зависимости от типа неравенства.
- Определение допустимой области.
- Расположение целевой функции на графике, если применимо.
- Определение особых случаев, таких как неограниченные, неограниченные или недопустимые решения.

- Решите упражнения с неравенствами или уравнениями.
- Вы можете ввести не более 10 ограничений и 2 переменных.
Полные примеры работы приложения можно найти по этой ссылке.
Как использовать онлайн-калькулятор графических методов
Использование нашего калькулятора очень простое и интуитивно понятное, однако мы объясним его использование шаг за шагом:
- Прежде чем начать, вы должны сделать подход модели, которую нужно оптимизировать. Помните, что для графического метода мы обычно работаем с двумя переменными решения.
- Необходимо ввести коэффициенты целевой функции и ограничения. Вы можете вводить целые значения, дроби и десятичные дроби. Точно так же вы должны также выбрать знак неравенств.
- Для ввода коэффициентов целевой функции и ограничений можно использовать целые числа, а также дроби и десятичные дроби. Также необходимо выбрать знак неравенств.
- Нажмите «Решить / График» .

- Если вы находитесь в бесплатной версии, вы сразу получите окончательный график и результаты. В полной версии вы сможете увидеть шаг за шагом от создания графиков до конечного результата.
Далее мы увидим несколько изображений работы калькулятора:
Форма для ввода коэффициентов переменных Пример пояснения построения графика Генерация допустимой области показана шаг за шагом Оценка вершин допустимой области Оптимальное решение и граф задачи линейного программированияЭтот калькулятор облегчает изучение графического метода и хорошо сочетается с нашим приложением симплекс-метода (два этапа) и нашим калькулятором метода Big M.
Final Reflection
Мы знаем, что лучший способ чему-то научиться — это иметь для этого правильные инструменты. В PM Calculators мы работаем над тем, чтобы предоставить вам лучшие инструменты, собранные в одном месте. Если у вас есть рекомендации по улучшению нашего калькулятора, напишите нам в контактную форму.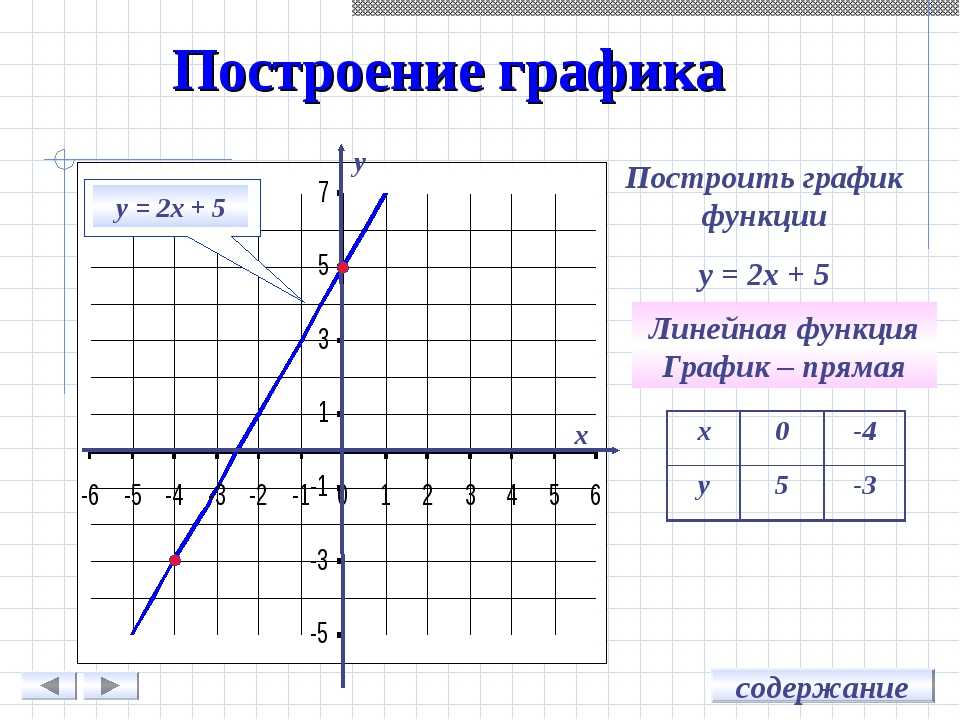
Интегральный калькулятор • С шагами!
Поддержка
Пожертвование
Помог ли вам этот калькулятор? Тогда я был бы очень признателен за вашу поддержку. Вы можете сделать пожертвование через PayPal.
Выше введите функцию для интеграции. Переменная интегрирования , границы интегрирования и многое другое можно изменить в » Опции «. Щелкните « Go! «, чтобы начать вычисление интеграла/первообразной. Результат будет показан далее.
Как работает интегральный калькулятор
Для тех, кто имеет техническое образование, в следующем разделе объясняется, как работает интегральный калькулятор.
Сначала синтаксический анализатор анализирует математическую функцию. Он преобразует его в форму, более понятную компьютеру, а именно в дерево (см. рисунок ниже). При этом интегральный калькулятор должен соблюдать порядок операций. Особенностью математических выражений является то, что знак умножения иногда можно опустить, например, мы пишем «5x» вместо «5*x». Интегральный калькулятор должен обнаруживать эти случаи и вставлять знак умножения.
Интегральный калькулятор должен обнаруживать эти случаи и вставлять знак умножения.
Парсер реализован на JavaScript, основан на алгоритме Shunting-yard и может работать прямо в браузере. Это позволяет быстро получать обратную связь при наборе текста путем преобразования дерева в код LaTeX. MathJax позаботится об отображении его в браузере.
Когда «Вперед!» После нажатия кнопки Калькулятор интегралов отправляет математическую функцию и настройки (переменную интегрирования и границы интегрирования) на сервер, где она снова анализируется. На этот раз функция преобразуется в форму, понятную системе компьютерной алгебры Maxima.
Maxima фактически вычисляет интеграл математической функции. Вывод Maxima снова преобразуется в LaTeX и затем предоставляется пользователю. Первообразная вычисляется с использованием алгоритма Риша, который трудно понять людям. Вот почему показать этапы вычисления интегралов очень сложно.
Чтобы показать шаги, калькулятор применяет те же методы интеграции, что и человек. Программа, которая это делает, разрабатывалась в течение нескольких лет и написана на собственном языке программирования Maxima. Он состоит из более чем 17000 строк кода. Когда подынтегральное выражение соответствует известной форме, оно применяет фиксированные правила для решения интеграла (например, разложение на частичные дроби для рациональных функций, тригонометрическая замена подынтегральных выражений, включающих квадратные корни квадратного многочлена, или интегрирование по частям для произведений определенных функций). . В противном случае он пробует различные подстановки и преобразования до тех пор, пока либо интеграл не будет решен, либо не истечет время, либо не останется ничего, что можно было бы попробовать. Калькулятору не хватает математической интуиции, которая очень полезна для нахождения первообразной, но, с другой стороны, он может перепробовать большое количество возможностей за короткое время. Пошаговые первообразные часто намного короче и элегантнее, чем найденные Максимой.
Программа, которая это делает, разрабатывалась в течение нескольких лет и написана на собственном языке программирования Maxima. Он состоит из более чем 17000 строк кода. Когда подынтегральное выражение соответствует известной форме, оно применяет фиксированные правила для решения интеграла (например, разложение на частичные дроби для рациональных функций, тригонометрическая замена подынтегральных выражений, включающих квадратные корни квадратного многочлена, или интегрирование по частям для произведений определенных функций). . В противном случае он пробует различные подстановки и преобразования до тех пор, пока либо интеграл не будет решен, либо не истечет время, либо не останется ничего, что можно было бы попробовать. Калькулятору не хватает математической интуиции, которая очень полезна для нахождения первообразной, но, с другой стороны, он может перепробовать большое количество возможностей за короткое время. Пошаговые первообразные часто намного короче и элегантнее, чем найденные Максимой.
Функция «Проверить ответ» должна решить сложную задачу определения эквивалентности двух математических выражений. Их разница рассчитывается и максимально упрощается с помощью Maxima. Например, это включает в себя запись тригонометрических/гиперболических функций в их экспоненциальной форме. Если можно показать, что разность упрощается до нуля, то задача решена. В противном случае применяется вероятностный алгоритм, который оценивает и сравнивает обе функции в случайно выбранных местах. В случае первообразных вся процедура повторяется для каждой производной функции, поскольку первообразные могут отличаться на константу.
Графики интерактивных функций рассчитываются в браузере и отображаются в элементе холста (HTML5). Для каждой отображаемой функции калькулятор создает функцию JavaScript, которая затем вычисляется небольшими шагами, чтобы построить график. При построении графика особенности (например, полюса) обнаруживаются и обрабатываются особым образом. Управление жестами реализовано с помощью Hammer.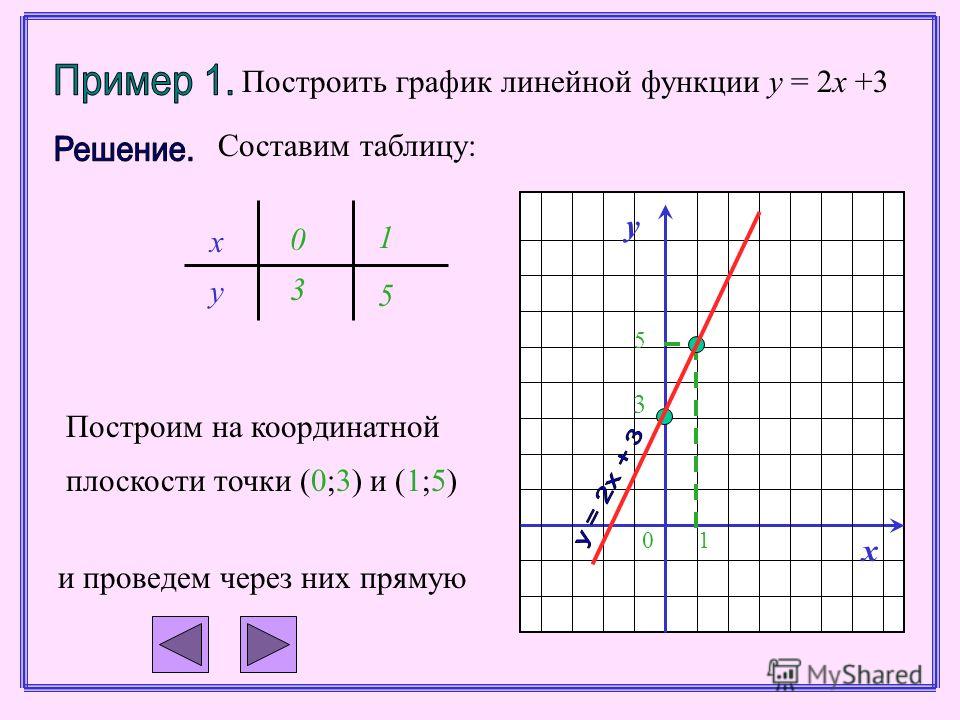
 Возможность выбора цвета и ввода ваших данных
Возможность выбора цвета и ввода ваших данных
Ваш комментарий будет первым