Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций. Практика
На этом практическом занятии мы рассмотрим примеры, демонстрирующие методы построения графиков основных типов простейших функций, решим задания на исследование функции по изображенному графику и задачи на преобразования графиков функций.
Данный урок поможет Вам подготовиться к одному из типов заданий С5.
Подготовка к ЕГЭ по математике
Эксперимент
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций
Практика
Конспект урока
Сначала разберем примеры на построение графиков основных функций.
Задача №1. Построить графики функций: а) 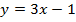
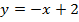 ; в)
; в) 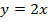 ; г)
; г) 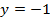 .
.Решение. Воспользуемся методом построения линейных функций «по точкам».
а) 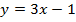
|
|
|
|
0 |
-1 |
|
1 |
2 |

Как видим, 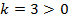 и угол наклона к оси
и угол наклона к оси 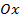 острый,
острый, 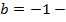 смещение по оси
смещение по оси 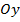
б) 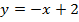
|
|
|
|
0 |
2 |
|
1 |
1 |
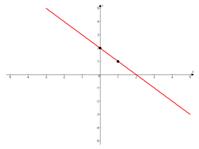
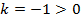
 можно сделать аналогичные выводы, как и в первом пункте.
можно сделать аналогичные выводы, как и в первом пункте.в) 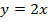
|
|
|
|
0 |
0 |
|
1 |
|
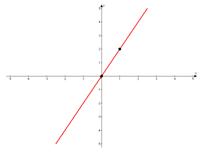
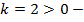 угол наклона к оси
угол наклона к оси острый,
острый,  график проходит через начало координат.
график проходит через начало координат.
г) 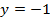
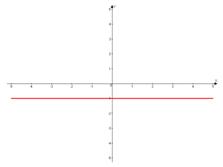
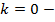
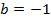 и параллельно оси
и параллельно оси 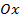 .
.Задача №2. Построить графики функций: а) 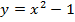 ; б)
; б) 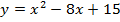 ; в)
; в) 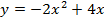 .
.
Решение. Воспользуемся методом построения квадратичных функций «по вершине».
а) 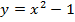
 ветки параболы направлены вверх,
ветки параболы направлены вверх, 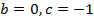 .
.

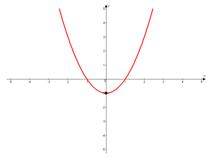
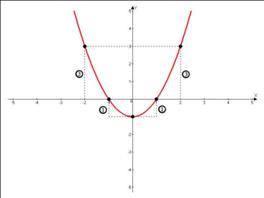
Если возникает вопрос, как точно строится парабола, т.е. с какой именно скоростью растут и убывают ее ветки, то можно запомнить следующий факт: если старший коэффициент 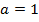
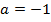 , как это часто бывает, то при смещении от иксовой координаты вершины на единицу влево или вправо значение функции сначала изменяется на 1, потом на 3, затем на 5 и т.д., т.е. на нечетные числа.
, как это часто бывает, то при смещении от иксовой координаты вершины на единицу влево или вправо значение функции сначала изменяется на 1, потом на 3, затем на 5 и т.д., т.е. на нечетные числа.Например, в нашем графике:
Для функций, у которых старший коэффициент  , значения изменений функции умножаются на это «
, значения изменений функции умножаются на это «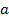 ». Например, построение функции
». Например, построение функции 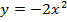
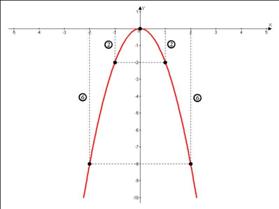
Но, как правило такая точность построения не важна, а нужен только эскиз графика, поэтому в дальнейшем мы не будем это учитывать.
б) 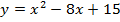
 ветки параболы направлены вверх,
ветки параболы направлены вверх, 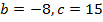 .
.
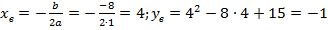
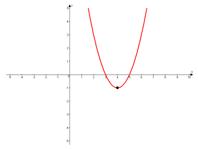
в) 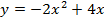
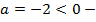 ветки параболы направлены вниз,
ветки параболы направлены вниз, 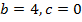 .
.

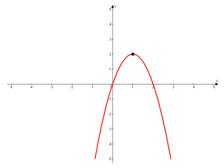
Кстати, график проходит через ноль, что легко проверить подстановкой в функцию точки 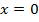
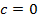 .
.Задача №3. Построить графики функций: а) 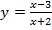 ; б)
; б) 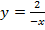 ; в)
; в) 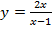 .
.
Решение. Воспользуемся нашим методом построения дробно-рациональных функций «по асимптотам».
а) 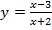
Вертикальная асимптота определяется решением уравнения, которое показывает, что знаменатель дроби равен нулю: 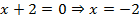 .
.
Горизонтальную асимптоту определим по тому быстрому способу, который мы указали в лекции. Она определяется отношением коэффициентов при иксах в числителе и знаменателе: 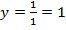 .
.
Для определения расположения веток гиперболы подставим в функцию любую точку из области определения, т.е. кроме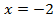 , например,
, например, 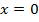 :
: 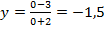 , т.е. координаты этой точки
, т.е. координаты этой точки  через нее и проведем одну ветку гиперболы, вторая будет располагаться наискось.
через нее и проведем одну ветку гиперболы, вторая будет располагаться наискось.
Теперь строим гиперболу, прижимая ее к асимптотам:

Остальные пункты строим аналогично.
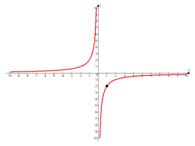
б) 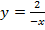
Вертикальная асимптота: 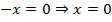 .
.
Горизонтальная асимптота:  , т.е. асимптотами являются оси координат.
, т.е. асимптотами являются оси координат.
Проверочная точка:  .
.
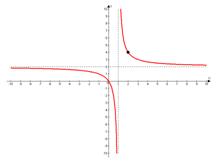
в) 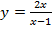
Вертикальная асимптота:  .
.
Горизонтальная асимптота:  .
.
Проверочная точка: 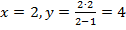 .
.
Задача №4. Построить графики функций: а) 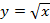 , б)
, б) 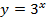 , в)
, в) 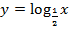 .
.
Решение. По сути дела, указаны функции, которые не имеют особых методов построения их графиков. Поэтому если необходимо изобразить их эскиз, то просто вспоминаем теорию, а если необходимо построить графики более точно, то следует подставить несколько контрольных точек, так и поступим.
а) 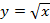
Подставим полные квадраты, чтобы вычислить из них целые значения корня.
|
|
|
|
0 |
0 |
|
1 |
1 |
|
4 |
2 |
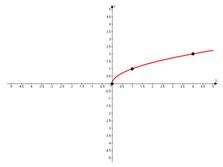
б) 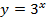
Подставим несколько значений и учтем общий вид графика.
|
|
interneturok.ru
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций. Теория
Подготовка к ЕГЭ по математике
Эксперимент
Урок 13. Построение и преобразование графиков функций. Обзор графиков основных функций
Теория
Конспект урока
Начнем с построения графиков основных функций.
1) Линейная функция. Ее графиком является прямая.
Общий вид линейной функции:
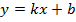
где под 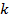 и
и  понимают следующие параметры:
понимают следующие параметры:
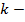 угловой коэффициент;
угловой коэффициент;
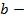 свободный член или смещение по оси ординат.
свободный член или смещение по оси ординат.
Рассмотрим основные формы таких графиков в зависимости от значений параметров и поймем их названия.
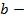 показывает координату пересечения прямой с осью ординат;
показывает координату пересечения прямой с осью ординат;

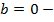 прямая проходит через начало координат;
прямая проходит через начало координат;
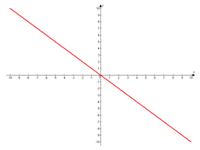
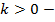 угол наклона прямой к положительному направлению оси абсцисс острый;
угол наклона прямой к положительному направлению оси абсцисс острый;

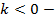 угол наклона прямой к положительному направлению оси абсцисс тупой;
угол наклона прямой к положительному направлению оси абсцисс тупой;
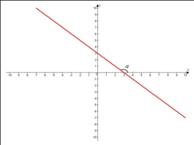
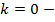 прямая параллельна оси абсцисс.
прямая параллельна оси абсцисс.
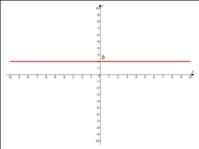
Как видим, параметр «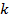 » определяет наклон прямой к оси абсцисс.
» определяет наклон прямой к оси абсцисс.
Метод построения графика линейной функции самый стандартный, и называется «построение по точкам». Поскольку любая прямая может быть однозначно восстановлена по двум точкам, то нам будет достаточно определить координаты двух точек, удовлетворяющих функции, и затем провести через них прямую линию, которая и будет необходимым графиком.
Обычно для этого используется небольшая табличка, в которую записывают произвольно выбранные координаты точек по оси абсцисс, а затем для них вычисляют координаты точек по оси ординат.
Пример. Проделаем эти действия для функции 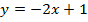 .
.
Решение.
Для вычисления необходимых игреков подставляем значения иксов в формулу, которая задает функцию. При этом удобно выбирать минимальные по модулю целые значения иксов для простоты расчетов:
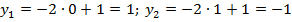
После этого точки наносятся на координатную плоскость, и через них проводится прямая линия, которая и будет графиком.
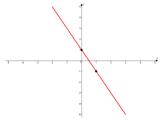
Обратите внимание, что форма графика соответствует знакам коэффициентов функции.
2) Теперь рассмотрим квадратичную функцию и ее график, который принято называть параболой.
Общий вид квадратичной функции:

Где под параметрами  понимают:
понимают:
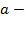 старший коэффициент;
старший коэффициент;
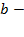 второй коэффициент;
второй коэффициент;
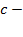 свободный член.
свободный член.
От знаков этих параметров зависит расположение параболы:
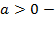 ветки параболы направлены вверх;
ветки параболы направлены вверх;
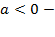 ветки параболы направлены вниз;
ветки параболы направлены вниз;
Знаки коэффициента  явно и наглядно ничего не определяют;
явно и наглядно ничего не определяют;
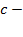 показывает координату пересечения параболы с осью ординат.
показывает координату пересечения параболы с осью ординат.
Уже можно было обратить внимание, что в графиках функций, которые представлены в виде многочленов, свободный коэффициент показывает точку пересечения с осью ординат. А в общем случае такой точкой является значение функции при подстановке аргумента, равного нулю.
Для ознакомления с изображением параболы построение следует начать с простейшего частного случая рассматриваемой функции 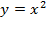 .
.

Для построения параболы по общему виду функции есть несколько стандартных приемов, укажем один наиболее простой и удобный из них.
Метод построения «по вершине».
В этом способе сначала находят координаты вершины, а затем в зависимости от знака старшего коэффициента строят эскиз графика.
Координаты вершины находят по следующим формулам:

Как видим, для вычисления значения игрековой координаты вершины выполняется подстановка в функцию найденного значения иксовой координаты вершины.
После этого вершина обозначается в системе координат и с учетом известного нам направления веток параболы в зависимости от знака старшего коэффициента функции изображается эскиз графика.
Пример. Построить график функции  .
.
Решение. Воспользуемся указанными формулами для 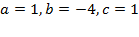 .
.
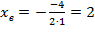 ,
,  .
.
Учтем, что 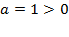 , т.е. ветки параболы направлены вверх. Для точности нанесем точку пересечения с осью
, т.е. ветки параболы направлены вверх. Для точности нанесем точку пересечения с осью  :
: 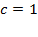 .
.
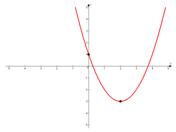
Чтобы увеличить точность построения графика, можно найти и точки его пересечения с осью 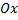 . Решим для этого уравнение
. Решим для этого уравнение 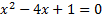 , как мы уже знаем, приравняв функцию к нулю. Но мы не будем делать этого в примере, если вам интересно, то можете проделать это действие самостоятельно и решить квадратное уравнение.
, как мы уже знаем, приравняв функцию к нулю. Но мы не будем делать этого в примере, если вам интересно, то можете проделать это действие самостоятельно и решить квадратное уравнение.
3) Перейдем к простейшему виду дробно-рациональной функции, графиком которой является гипербола.
Общий вид такой функции  , т.е. в числителе и знаменателе дроби находятся линейные двучлены.
, т.е. в числителе и знаменателе дроби находятся линейные двучлены.
У указанных параметров нет общепринятых названий.
Начнем знакомство с графиком, который называют гиперболой, с изображения простейшего частного случая дробно-рациональной функции, когда 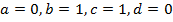 , т.е.
, т.е. 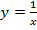 . Он имеет вид:
. Он имеет вид:
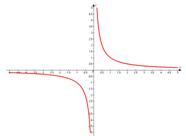
Как видим, у графика есть вспомогательные элементы, которые называются «асимптоты». Их две: горизонтальная и вертикальная.
Вспомним, что вертикальная асимптота строится в координате по оси абсцисс, при которой знаменатель дроби превращается в ноль.
Горизонтальная асимптота проводится в том значении координаты по оси ординат, к которому стремится функция при аргументе, стремящемся к бесконечности. Для функций указанного типа горизонтальную асимптоту можно найти и проще, значением ее игрековой координаты будет отношение коэффициента при иксе в числителе и в знаменателе. Разобраться почему так вы можете изучив тему «Предел функции».
Пример. Построим график дробно-рациональной функции общего положения  .
.
Способ построения мы назовем «по асимптотам» и он будет состоять из трех шагов:
1. Находим уравнение вертикальной асимптоты: 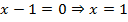 ;
;
2. Находим уравнение горизонтальной асимптоты: 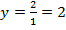 . Можно так же воспользоваться способом приведения числителя к константе, который мы показали в предыдущем уроке.
. Можно так же воспользоваться способом приведения числителя к константе, который мы показали в предыдущем уроке.
3. Расположение веток гиперболы неоднозначно: или справа вверху и слева внизу, например, в простейшем случае
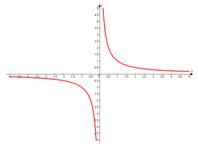
или слева вверху и справа внизу, например,
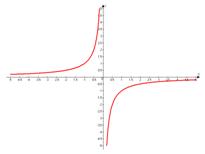
Поэтому необходимо точно определить, как они будут изображаться. Для этого просто подставим любое целое значение икса в функцию из области определения и найдем одну точку, которая принадлежит графику.
Подставим, например, 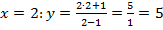 и построим ее в системе координат с найденными асимптотами.
и построим ее в системе координат с найденными асимптотами.
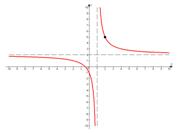
Ветки гиперболы должны прижиматься к асимптотам и по расположению построенной точки мы определяем положение одной из веток гиперболы, а соответственно и другой, т.к. ветки всегда лежат наискось относительно друг друга, если к графику не применялись специальные преобразования.
interneturok.ru
Основные правила преобразования графиков функций. Видеоурок. Алгебра 9 Класс
Если вы знаете, как выглядят графики элементарных функций, или умеете быстро строить их по характерным точкам, то сумеете быстро построить на их основе графики более сложных функций того же класса. Для этого существуют правила преобразования графиков функций, которые мы рассмотрим на этом уроке.
Наверняка многие из вас могут быстро и правильно построить графики некоторых функций, не прибегая к вычислениям значений точек. Всем известно, что график функции  – это прямая, а график функции
– это прямая, а график функции 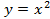 – это парабола. Но как построить, например, график функции
– это парабола. Но как построить, например, график функции 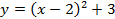 , не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
, не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
Предположим, что у нас есть функция 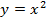 (график этой функции – это парабола) и необходимо построить график функции
(график этой функции – это парабола) и необходимо построить график функции 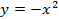 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола (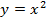 ) зеркально отобразится относительно оси
) зеркально отобразится относительно оси 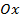 (см. Рис. 1).
(см. Рис. 1).
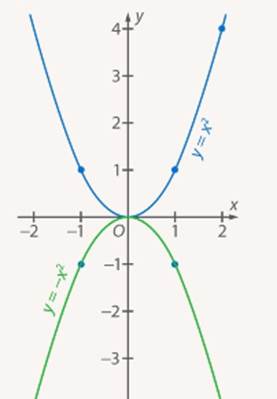
Рис. 1. Графики функций 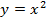 и
и 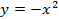
Таким образом, если у нас есть произвольный график 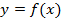 , то для построения графика
, то для построения графика 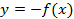 необходимо график
необходимо график 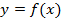 симметрично отразить относительно оси
симметрично отразить относительно оси 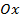 (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси
(см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси 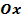 .
.
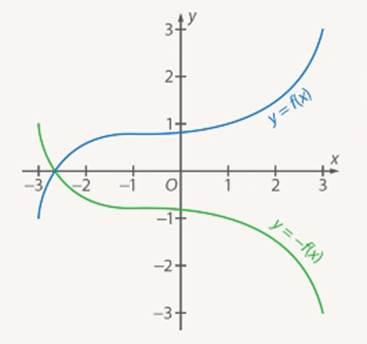
Рис. 2. Преобразование симметрии относительно оси 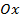
Преобразование симметрии – зеркальное отражение относительно прямой. График  получается из графика функции
получается из графика функции  преобразованием симметрии относительно оси
преобразованием симметрии относительно оси 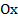 .
.
На рисунке 3 показаны примеры симметрии относительно оси 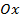 .
.
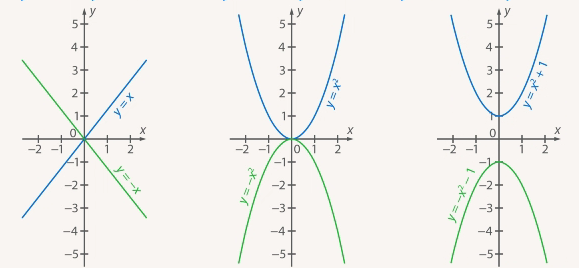
Рис. 3. Симметрия относительно оси Ox
Предположим, что у нас есть функция 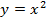 (график этой функции – это парабола) и необходимо построить график функции
(график этой функции – это парабола) и необходимо построить график функции 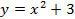 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 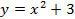 больше на 3 единицы. Графически это означает, что график функции
больше на 3 единицы. Графически это означает, что график функции 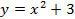 находится на 3 единицы выше, чем график функции
находится на 3 единицы выше, чем график функции 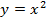 (см. Рис. 4).
(см. Рис. 4).
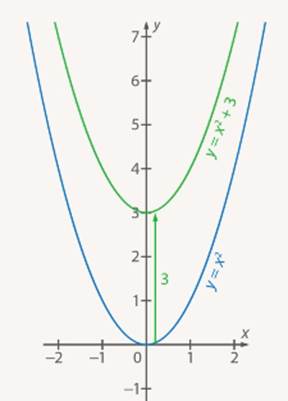
Рис. 4. Графики функций 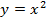 и
и 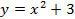
График  получается из графика функции
получается из графика функции параллельным переносом последнего вдоль оси ординат на
параллельным переносом последнего вдоль оси ординат на 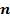 единиц вверх, если
единиц вверх, если 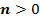 , и на
, и на  единиц вниз, если
единиц вниз, если 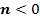 (см. Рис. 5, 6).
(см. Рис. 5, 6).
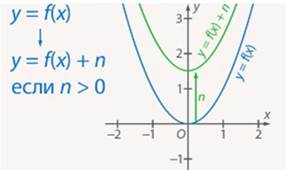
Рис. 5. Параллельный перенос вдоль оси 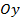 (при
(при 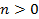 )
)
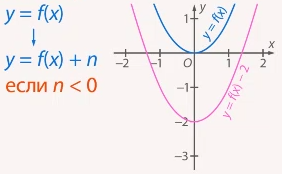
Рис. 6. Параллельный перенос вдоль оси 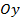 (при
(при  )
)
Предположим, что у нас есть функция 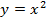 (график этой функции – это парабола) и необходимо построить график функции
(график этой функции – это парабола) и необходимо построить график функции 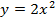 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 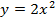 больше в 2 раза. Графически это означает, что график функции
больше в 2 раза. Графически это означает, что график функции 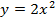 сужается по сравнению с графиком функции
сужается по сравнению с графиком функции 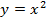 (см. Рис. 7).
(см. Рис. 7).
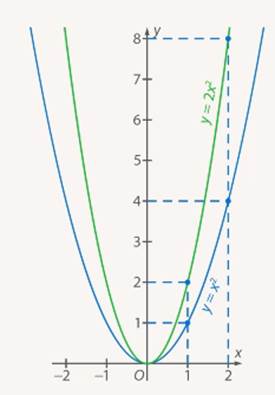
Рис. 7. Графики функций 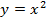 и
и 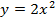
Если необходимо построить график функций 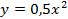 , то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика
, то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 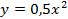 меньше в 2 раза, чем у
меньше в 2 раза, чем у 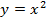 . Графически это означает, что график функции
. Графически это означает, что график функции 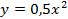 расширяется по сравнению с графиком функции
расширяется по сравнению с графиком функции 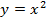 (см. Рис. 8).
(см. Рис. 8).


Рис. 8. Графики функций 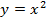 и
и 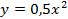
Чтобы построить график функции  , где
, где 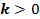 и
и  , нужно ординаты точек заданного графика умножить на
, нужно ординаты точек заданного графика умножить на 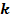 . Такое преобразование называется растяжением от оси
. Такое преобразование называется растяжением от оси 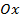 с коэффициентом
с коэффициентом 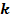 , если
, если 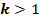 , и сжатием к оси
, и сжатием к оси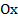 , если
, если  (см. Рис. 9, 10).
(см. Рис. 9, 10).

Рис. 9. Растяжение от оси 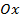

Рис. 10. Сжатие к оси 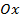
Предположим, что у нас есть функция 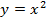 , необходимо построить график функции
, необходимо построить график функции 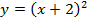 . Вычислим значения некоторых точек для графиков этих функций.
. Вычислим значения некоторых точек для графиков этих функций.

Из таблиц видно, что одинаковым значениям функции соответствуют значения аргумента, отличающиеся на 2 единицы. Это означает, что график данной функции переместился на 2 единицы относительно оси орд
interneturok.ru
Построение графиков функций
Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.
Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».
Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».
Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».
Темы для повторения:
Понятие функции
Типы элементарных функций
Преобразования графиков функций
Производная функции
1. Построим график функции
Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.
Упростим формулу функции:
при
График функции — прямая с выколотой точкой

2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.
3. Построим график функции
Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали

4. Построим график функции
Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:
Действуем по порядку:
1) График функции y=sinx сдвинем на влево;
2) сожмем в 2 раза по горизонтали,
3) растянем в 3 раза по вертикали,
4) сдвинем на 1 вверх

Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».
5. Построим график функции
Область определения функции:
Нули функции: и
Промежутки знакопостоянства функции определим с помощью метода интервалов.

Прямая x = 0 (ось Y) — вертикальная асимптота функции. Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)
Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.
Раскроем скобки в формуле функции:
Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.

6. Построим график функции
Это дробно-рациональная функция.
Область определения функции
Нули функции: точки — 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты:
Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.
Вот эскиз графика:

Еще один интересный прием — сложение графиков.
7. Построим график функции
Если x стремится к бесконечности, то и график функции будет бесконечно близко подходить к наклонной асимптоте
Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:

Вот мы и построили график суммы функций. Теперь график произведения!
8. Построим график функции
Область определения этой функции — положительные числа, поскольку только для положительных x определен
Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при
При , значение {cos x} равно единице. Значение функции в этих точках будет равно

9. Построим график функции
Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.
Нули функции — в точках, где то есть при
Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное ?
Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».

А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.
10. Построим график функции
Область определения функции — все действительные числа, поскольку
Функция нечетна. Ее график симметричен относительно начала координат.
При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.
Если x стремится к бесконечности, то стремится к нулю.
Найдем производную функции
По формуле производной частного,
если или
В точке производная меняет знак с «минуса» на «плюс», — точка минимума функции.
В точке производная меняет знак с «плюса» на «минус», — точка максимума функции.
Найдем значения функции при x=2 и при x=-2.

Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?
Общая схема построения графика функции:
1. Область определения функции
2. Область значений функции
3. Четность — нечетность (если есть)
4. Периодичность (если есть)
5. Нули функции (точки, в которых график пересекает оси координат)
6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).
7. Асимптоты (если есть).
8. Поведение функции в бесконечности
9. Производная функции
10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
20 Построение графиков функций
20 Построение графиков функций
Задача № 1

Ответ:

Решение:

Ответ:

Задача № 2

Ответ:

Решение:

Ответ:

Задача № 3

Ответ:

Решение:

Ответ:

Задача № 4

Ответ:

Решение:

Ответ:

Задача № 5

Ответ:

Решение:

Ответ:

Задача № 6

Ответ:

Решение:

Ответ:

Задача № 7

Ответ:

Решение:

Ответ:

Задача № 8

Ответ:

Решение:

Ответ:

Задача № 9

Ответ:

Решение:

Ответ:

Задача № 10

Ответ:

Решение:

Ответ:

Задача № 11

Ответ:

Решение:

Ответ:

Задача № 12

Ответ:

Решение:

Ответ:

Задача № 13

Ответ:

Решение:

Ответ:

Задача № 14

Ответ:

Решение:

Ответ:

Задача № 15

Ответ:

Решение:

Ответ:

Задача № 16

Ответ:

Решение:

Ответ:

Задача № 17

Ответ:

Решение:

Ответ:

Задача № 18

Ответ:

Решение:

Ответ:

Задача № 20

Ответ:

Решение:

Ответ:

Задача № 21

Ответ:

Решение:

Ответ:

© 2017-2019 Математушка
matematushka.ru

Ваш комментарий будет первым