Построение графиков функций онлайн с решением: Построение графиков функций онлайн

Содержание

§ Построить график функции онлайн

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Математика 5 класс

Математика 6 класс

Алгебра 7 класс

Геометрия 7 класс

Алгебра 8 класс

Алгебра 9 класс

Алгебра 10 класс

Алгебра 11 класс

Ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математическое доказательство. Леонардо да Винчи

на главную Найти репетитора Поддержать сайт ←Вернуться в «Калькуляторы онлайн»

Здесь будет анализ функции…

Инструкции

построить график функции онлайн

укажите функцию в поле выше в виде «y = x² — 3»;
нажмите кнопку «Построить график функции»;
ожидайте результат анализа функции (точки пересечения с осями координат) и график функции под полем задания функции.

При необходимости вы можете построить одновременно графики двух функций онлайн. Для этого нажмите кнопку «Добавить функцию».

В случае построения двух графиков функции будут показаны их точки пересечения.

Таблица обозначений для задания функций

Онлайн калькулятор: График функции

Данный онлайн калькулятор строит графики функций одной переменной. Функция задается при помощи формулы, в которой могут участвовать математические операции, константы и математические функции. Синтаксис описания формулы см. ниже.

Построитель графиков функций одной переменной

Отображать таблицуТочность вычисления

Знаков после запятой: 2

График функции

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить

close

content_copy Ссылка save Сохранить extension Виджет

В формуле допускается использование одной переменной (обозначается как x), числа пи ( pi), следующих математических операторов:

+ — сложение
— — вычитание
* — умножение
/ — деление
^ — возведение в степень

и следующих функций:

sqrt — квадратный корень
rootp — корень степени p, например root3(x) — кубический корень
exp — e в указанной степени
lb — логарифм по основанию 2
lg — логарифм по основанию 10
ln — натуральный логарифм (по основанию e)
logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
cosec — косеканс
arcsin — арксинус
arccos — арккосинус
arctg — арктангенс
arcctg — арккотангенс
arcsec — арксеканс
arccosec — арккосеканс
versin — версинус
vercos — коверсинус
haversin — гаверсинус
exsec — экссеканс
excsc — экскосеканс
sh — гиперболический синус
ch — гиперболический косинус
th — гиперболический тангенс
cth — гиперболический котангенс
sech — гиперболический секанс
csch — гиперболический косеканс
abs — абсолютное значение (модуль)
sgn — сигнум (знак)

Построение графиков функций

Функции и их графики — одна из самых увлекательных тем в школьной математике. Жаль только, что проходит она… мимо уроков и мимо учеников. На нее вечно не хватает времени в старших классах. А те функции, которые проходят в 7-м классе, — линейная функция и парабола — слишком просты и незамысловаты, чтобы показать все разнообразие интересных задач.

Умение строить графики функций необходимо для решения задач с параметрами на ЕГЭ по математике. Это одна из первых тем курса математического анализа в вузе. Это настолько важная тема, что мы в ЕГЭ-Студии проводим по ней специальные интенсивы для старшеклассников и учителей, в Москве и онлайн. И часто участники говорят: «Жаль, что мы не знали этого раньше».

Но это не все. Именно с понятия функции и начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции — это все-таки арифметика. Преобразования выражений — это алгебра. А математика — наука не только о числах, но и о взаимосвязях величин. Язык функций и графиков понятен и физику, и биологу, и экономисту. И, как сказал Галилео Галилей, «Книга природы написана на языке математики».

Точнее, Галилео Галилей сказал так:«Математика есть алфавит, посредством которого Господь начертал Вселенную».

Темы для повторения:

Понятие функции

Типы элементарных функций

Преобразования графиков функций

Производная функции

1. Построим график функции

Знакомая задача! Такие встречались в вариантах ОГЭ по математике. Там они считались сложными. Но сложного ничего здесь нет.

Упростим формулу функции:

при

График функции — прямая с выколотой точкой

2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, применяемый в решении неравенств, построении графиков и оценке целых величин в задачах на числа и их свойства. Он встретится вам также на первом курсе, когда придется брать интегралы.

3. Построим график функции

Он получается из графика функции растяжением в 2 раза, отражением по вертикали и сдвигом на 1 вверх по вертикали

4. Построим график функции

Главное — правильная последовательность действий. Запишем формулу функции в более удобном виде:

Действуем по порядку:

1) График функции y=sinx сдвинем на влево;

2) сожмем в 2 раза по горизонтали,

3) растянем в 3 раза по вертикали,

4) сдвинем на 1 вверх

Сейчас мы построим несколько графиков дробно-рациональных функций. Чтобы лучше понять, как мы это делаем, читайте статью «Поведение функции в бесконечности. Асимптоты».

5. Построим график функции

Область определения функции:

Нули функции: и

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Прямая x = 0 (ось Y) — вертикальная асимптота функции.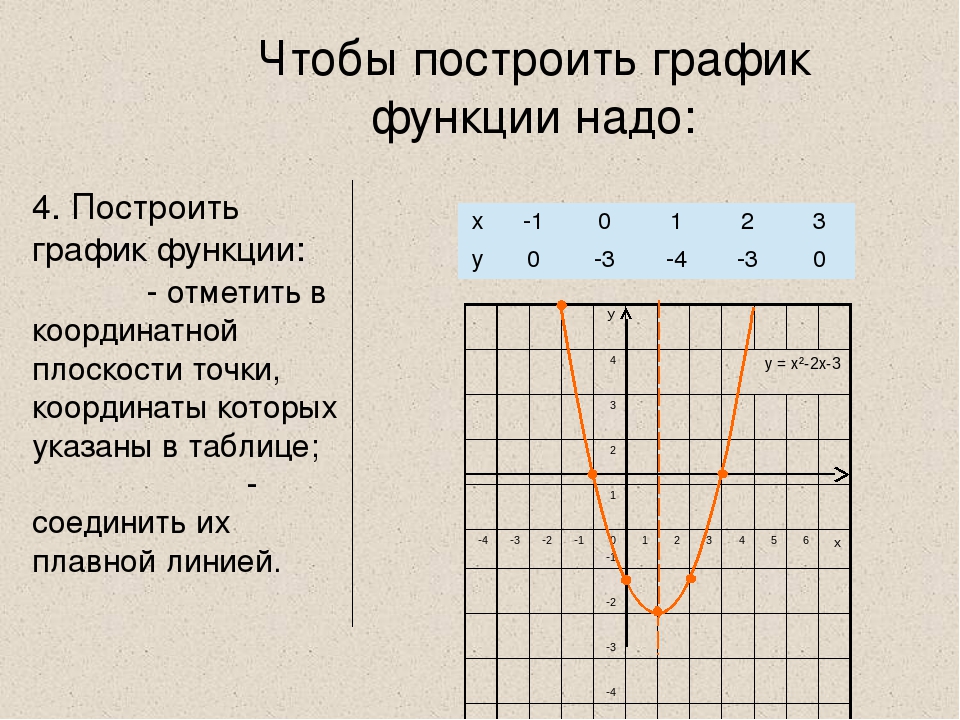 Асимптота — прямая, к которой бесконечно близко подходит график функции, но не пересекает ее и не сливается с ней (смотри тему «Поведение функции в бесконечности. Асимптоты»)

Есть ли другие асимптоты у нашей функции? Чтобы выяснить это, посмотрим, как ведет себя функция, когда x стремится к бесконечности.

Раскроем скобки в формуле функции:

Если x стремится к бесконечности, то стремится к нулю. Прямая является наклонной асимптотой к графику функции.

6. Построим график функции

Это дробно-рациональная функция.

Область определения функции

Нули функции: точки — 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты:

Если x стремится к бесконечности, то у стремится к 1. Значит, — горизонтальная асимптота.

Вот эскиз графика:

Еще один интересный прием — сложение графиков.

7. Построим график функции

Если x стремится к бесконечности, то и график функции будет бесконечно близко подходить к наклонной асимптоте

Если x стремится к нулю, то функция ведет себя как Это мы и видим на графике:

Вот мы и построили график суммы функций. Теперь график произведения!

8. Построим график функции

Область определения этой функции — положительные числа, поскольку только для положительных x определен

Значения функции равны нулю при (когда логарифм равен нулю), а также в точках, где то есть при

При значение cos x равно единице. Значение функции в этих точках будет равно при

9. Построим график функции

Функция определена при Она четная, поскольку является произведением двух нечетных функций и График симметричен относительно оси ординат.

Нули функции — в точках, где то есть при при

Если x стремится к бесконечности, стремится к нулю. Но что же будет, если x стремится к нулю? Ведь и x, и sin x будут становиться меньше и меньше. Как же будет вести себя частное ?

Оказывается, что если x стремится к нулю, то стремится к единице. В математике это утверждение носит название «Первого замечательного предела».

А как же производная? Да, наконец-то мы до нее добрались. Производная помогает более точно строить графики функций. Находить точки максимума и минимума, а также значения функции в этих точках.

10. Построим график функции

Область определения функции — все действительные числа, поскольку

Функция нечетна. Ее график симметричен относительно начала координат.

При x=0 значение функции равно нулю. При значения функции положительны, при отрицательны.

Если x стремится к бесконечности, то стремится к нулю.

Найдем производную функции
По формуле производной частного,

если или

В точке производная меняет знак с «минуса» на «плюс», — точка минимума функции.

В точке производная меняет знак с «плюса» на «минус», — точка максимума функции.

Найдем значения функции при x=2 и при x=-2.

Графики функций удобно строить по определенному алгоритму, или схеме. Помните, вы изучали ее в школе?

Общая схема построения графика функции:

1. Область определения функции

2. Область значений функции

3. Четность — нечетность (если есть)

4. Периодичность (если есть)

5. Нули функции (точки, в которых график пересекает оси координат)

6. Промежутки знакопостоянства функции (то есть промежутки, на которых она строго положительна или строго отрицательна).

7. Асимптоты (если есть).

8. Поведение функции в бесконечности

9. Производная функции

10. Промежутки возрастания и убывания. Точки максимума и минимума и значения в этих точках.

matematikam ru построение графиков — Все о Windows 10

На чтение 3 мин. Просмотров 66 Опубликовано 15.12.2019

Построение графиков онлайн с помощью нашего сервиса является простой задачей. Возможность построения одновременно сразу нескольких функций, помеченных разными цветами.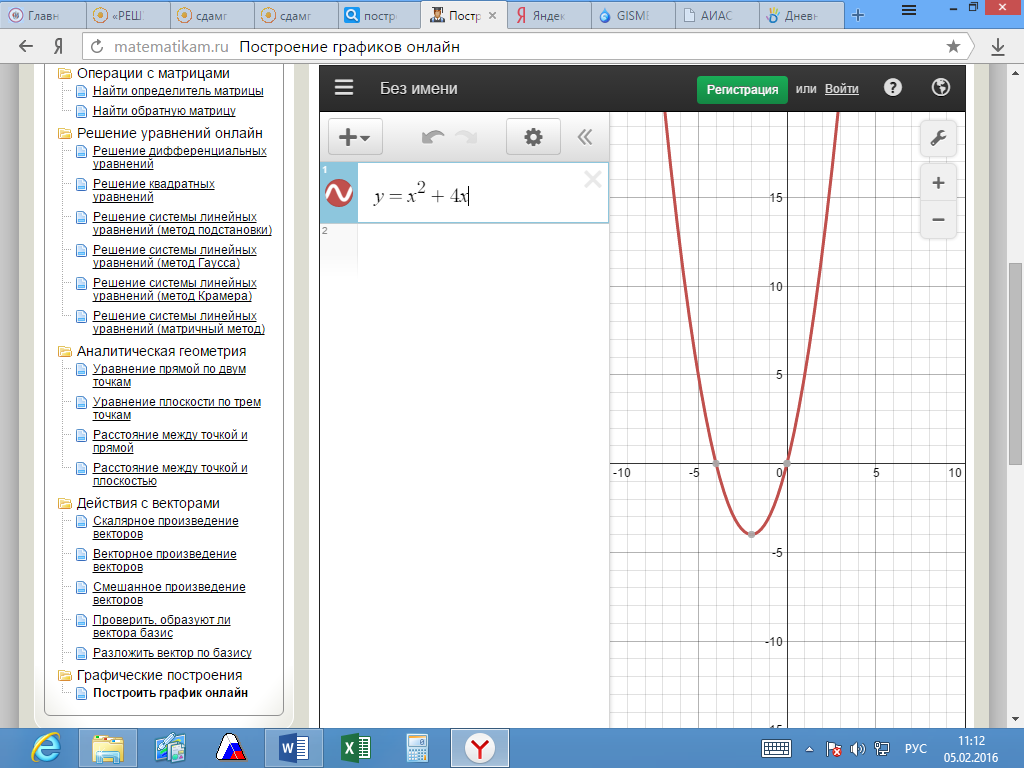 2/16=1)

Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете

Управление масштабом, цветом линий

Возможность построения графиков по точкам, использование констант

Построение одновременно нескольких графиков функций

Построение графиков в полярной системе координат (используйте r и θ( heta) )

С нами легко в режиме онлайн строить графики различной сложности. Построение производится мгновенно. Сервис востребован для нахождения точек пересечения функций, для изображения графиков для дальнейшего их перемещения в Word документ в качестве иллюстраций при решении задач, для анализа поведенческих особенностей графиков функций. Оптимальным браузером для работы с графиками на данной странице сайта является Google Chrome. При использовании других браузеров корректность работы не гарантируется.

Для задания области (например, 1≤x≤7 ) используйте пределы или >= .

Трехмерные графики функции

Чтобы создать трехмерный график достаточно, чтобы в выражении была переменная y (например, y^2-x/3 ). 2-x/3 ).

Чтобы построить трехмерный график в Excel , необходимо указать функцию f(x,y) , пределы по x и y и шаг сетки h .

Принципы и способы построения графика функции

Прикладное применение графика функции

Построить пирамиду ABCD по координатам можно здесь.

Введите график функции

Построим (исследуем) график функции y=f(x), для этого задайте функцию f(x)

Важно: a должно быть меньше b, иначе график не сможет построиться. Cледите за масштабом — если графика на рисунке нету, значит стоит поварьировать значения a и b

Примеры

С применением степени
(квадрат и куб) и дроби

С применением синуса и косинуса

Гиберболические синус и косинус

Гиберболические тангенс и котангенс

Гиберболические арксинус и арккосинус

Гиберболические арктангенс и арккотангенс

Исследование графика функции

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
Умеет определять точки пересечения графика функции с осями координат: Да
Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
Горизонтальные асимптоты графика функции: Да
Наклонные асимптоты графика функции: Да
Четность и нечетность функции: Да

Правила ввода выражений и функций

Построение графика квадратичной функций: алгоритм и примеры

Квадратичной функцией называется функция вида:
y=a*(x^2)+b*x+c,
где а – коэффициент при старшей степени неизвестной х,
b – коэффициент при неизвестной х,
а с — свободный член. 2 + 4*(1)-1= 4.
9. Соединяем полученные точки и подписываем график.

В результате получится такой график.

Нужна помощь в учебе?

Предыдущая тема: Графики функции: от чего зависит вид графика функции
Следующая тема:&nbsp&nbsp&nbspРешение неравенств второй степени с одной переменной: приводим примеры

Построение графиков функций — урок. Алгебра, 10 класс.

построить график функции y=x2+4×2−4.

Решение 1. Обозначим: f(x)=x2+4×2−4. Область определения этой функции: D(f)=(−∞;−2)∪(−2;2)∪(2;+∞), так как x≠2,x≠−2.

2. Проведём исследование функции на чётность/нечётность:

f(−x)=−x2+4−x2−4=x2+4×2−4=f(x).

Функция чётная. Следовательно, можно построить ветви графика функции для x≥0 и отобразить их симметрично относительно оси ординат.

3. Определим асимптоты. Вертикальная асимптота: прямая $x=1$, т. к. при $x=1$ знаменатель дроби равен нулю, а числитель при этом не равен нулю. Для определения горизонтальной асимптоты вычисляем limx→∞f(x):

limx→∞x2+4×2−4=limx→∞x2x2+4x2x2x2−4×2=limx→∞1+4×21−4×2=1.

Следовательно, $y=1$ — горизонтальная асимптота.

4. Определим стационарные и критические точки, точки экстремума и промежутки монотонности функции:

y′=x2+4×2−4′=(x2+4)′⋅(x2−4)−(x2+4)⋅(x2−4)′x2−42=2x⋅(x2−4)−(x2+4)⋅2xx2−42=2×3−8x−2×3−8xx2−42==−16xx2−42.

Производная существует на всей области определения функции, следовательно, критических точек у функции нет.

Стационарные точки определим из уравнения y′=0. Получаем: $-16x=0$ — откуда получаем, что $x=0$. При $x<0$ имеем: y′>0; при $x>0$ имеем: y′<0. Таким образом, в точке $x=0$ функция имеет максимум, причём ymax=f(0)=02+402−4=−1.

При $x>0$ имеем: y′<0. Учитывая точку разрыва $x=2$, делаем вывод: функция убывает на промежутках 0;2) и (2;+∞).

5. Найдём несколько точек, принадлежащих графику функции f(x)=x2+4×2−4 при x≥0:

$x$	$0$	$0.5$	$1$	$3$	$4$
$y$	$-1$	−1715	−53	135	53

6. Сначала нарисуем часть графика при x≥0, потом — часть, симметричную ей относительно оси $y$. Полученный график имеет точку максимума $(0;-2)$, горизонтальную асимптоту $y=1$ и вертикальную асимптоту $x=2$.

График sin 2x. Построение графиков онлайн. Построение графика функции синус х, y=sin(x)

«Построение графика функции с модулем» — Y = lnx. Закрепили знания на ранее изученных функциях. Построение графиков функций. Вопрос классу. Y = x2 – 2x – 3. Проектная деятельность. Урок обобщения и систематизации знаний. График функции. Актуализация знаний о графиках функций. Обобщение. Попробуйте самостоятельно построить графики. Y = f(x).

««Графики функций» 9 класс» — Цели урока. Большему значению аргумента соответствует большее значение функции. Нули функции. Определение. Заполните пропуски. Установите соответствие между функцией и вершиной. Тренажер. Выберите уравнение, с помощью которого задана линейная функция. Установите соответствие. Выберите уравнение. Обратная пропорциональность.

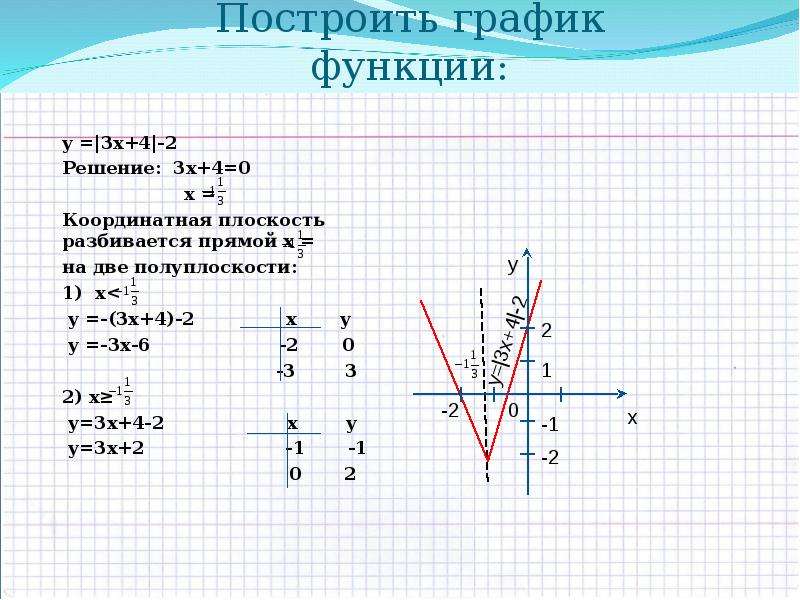
«Графики функций с модулями» — Найдём вершину функции. Кубическая функция. Отрицательная сторона. Графики функций. Квадратичная функция. Сложная функция. Функция с модулем. Графики функций надо обязательно уметь строить. Подготовка к ЕГЭ. Графики функций с модулями. Парабола. График функции.

«Уравнение касательной к графику функции» — Производная в точке. Правила дифференцирования. График функции. Алгоритм нахождения уравнения. Ответьте на вопросы. Геометрический смысл производной. Номера из учебника. Уравнение касательной к графику функции. Определение. Касательная к графику функции. Основные формулы дифференцирования. Провести касательную.

«Построение графиков функций» — Построение графика функции y = sinx. Линия тангенсов. Алгебра. Тема: Построение графиков функций. График функции y = sinx. Выполнила: Филиппова Наталья Васильевна учитель математики Белоярская средняя общеобразовательная школа №1. Построить график функции y=sin(x) +cos(x).

«График обратной пропорциональности» — Применение гиперболы. Гипербола. Монотонность функции. Чётность, нечётность. Функция «Обратная пропорциональность». График. Построение графика обратной пропорциональности. Гипербола и космические спутники. Однополостной гиперболоид. Асимптота. Применение гиперболоидов. Определение обратной пропорциональности.

Всего в теме 25 презентаций

Построить функцию

Мы предлагаем вашему вниманию сервис по потроению графиков функций онлайн, все права на который принадлежат компании Desmos . 2/16=1)

Возможность сохранять графики и получать на них ссылку, которая становится доступной для всех в интернете

Управление масштабом, цветом линий

Возможность построения графиков по точкам, использование констант

Построение одновременно нескольких графиков функций

Построение графиков в полярной системе координат (используйте r и θ(\theta))

Урок и презентация на тему: «Функция y=sin(x). Определения и свойства»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»

Что будем изучать:

Свойства функции Y=sin(X).
График функции.
Как строить график и его масштаб.
Примеры.

Свойства синуса. Y=sin(X)

Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?

Давайте познакомимся поближе с функцией Y=sin(X)

Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π].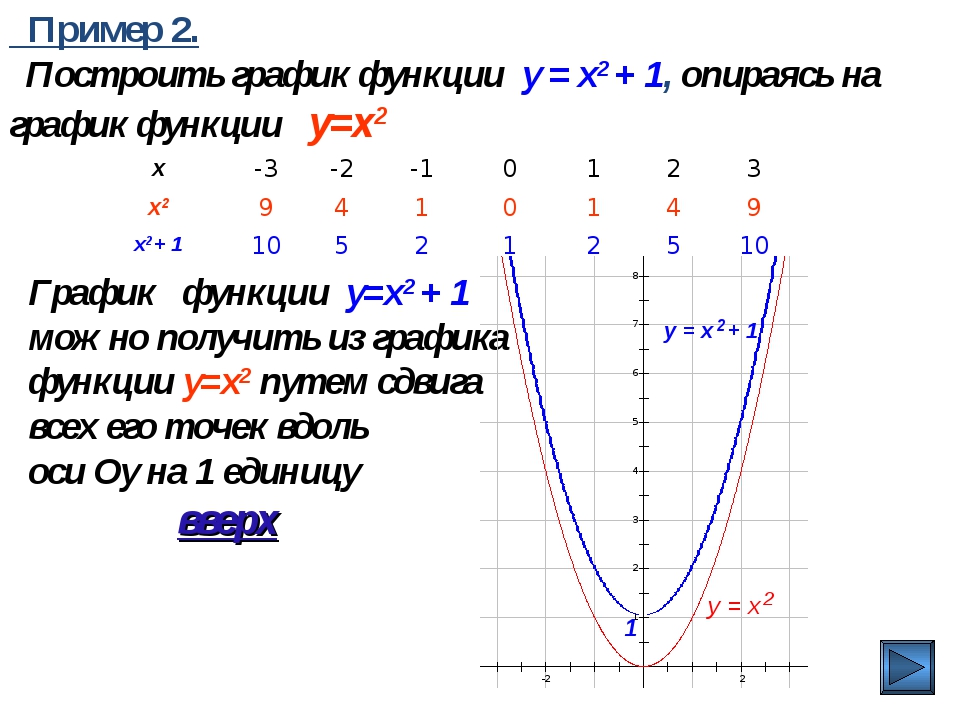 Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.

4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).

Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .

Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).

Построение графика функции синус х, y=sin(x)

Посчитаем значения функции на нашем отрезке:

Построим график по нашим точкам, с учетом третьего свойства.

Таблица преобразований для формул привидения

Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:

Мы знаем, что sin(x+ 2π) = sin(x).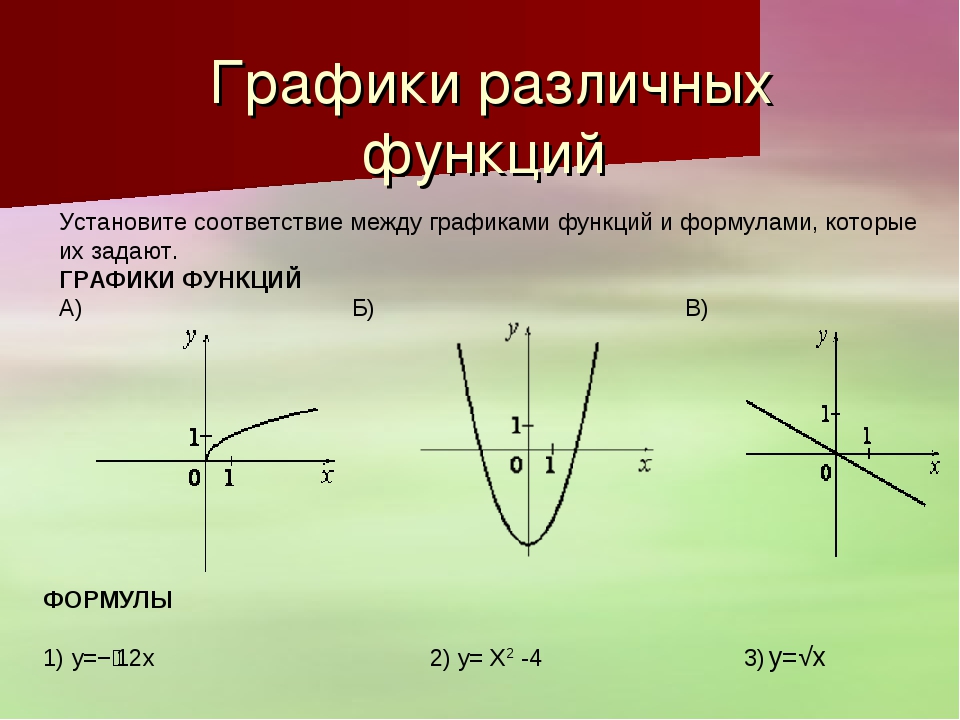 Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.

График функции Y=sin(X) называют — синусоидой.

Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.

Примеры задач с синусом

1. Решить уравнение sin(x)= x-π

Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π

2. Построить график функции y=sin(π/6+x)-1

Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.

Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.

Задачи на синус для самостоятельного решения

Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
Построить график функции y=sin(π/3+x)-2
Построить график функции y=sin(-2π/3+x)+1
Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]

Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .

Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.

Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.

На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.

При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.

Составим таблицу значений синуса на промежутке :

Полученные точки отметим на координатной плоскости:

Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:

Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.

Построение линейного уравнения с помощью таблицы значений

Как построить линейное уравнение

Линейное уравнение — это уравнение с двумя переменными, которое на графике дает нам прямую линию. Вы, наверное, знаете, как читать график линейного уравнения, но как нам нарисовать линейное уравнение на координатной плоскости? Оказывается, на самом деле это не так уж и сложно! Первый шаг — научиться составлять таблицу значений.

Что такое таблица значений

Когда нам нужно построить линейное уравнение, вы начнете с создания таблицы значений.Таблица значений, как следует из названия, представляет собой графический способ определения значений, которые будут использоваться для создания вашего графика. Это место, где вы можете записать ответы, которые вы получите, когда найдете значения x и y. Вам нужно будет использовать как минимум 2 набора точек для построения линейного уравнения, но обычно вы делаете больше в таблице значений.

Таблица значений состоит из двух столбцов. В одном столбце перечислены значения x, а в одном столбце — соответствующие значения y. Давайте перейдем к выяснению того, как эту таблицу можно использовать для построения графиков линейных уравнений.

Построение линейных уравнений с помощью таблицы значений

Когда у вас есть пустая таблица значений и линейное уравнение, которое вы хотите отобразить на графике, вы можете взять любое значение x на оси x по вашему выбору, чтобы начать с таблицы. Допустим, вы берете число 3. Подставьте его в линейное уравнение, чтобы увидеть, что вы получите, когда решите относительно y по оси y. Представим, что у вас -5. Запишите оба этих числа в свою таблицу: 3 в столбце со значениями x и -5 в столбце для значений y.

Выберите другое значение x, с которым вы хотите работать, и снова решите относительно y. Повторите столько раз, сколько хотите, чтобы выработать наборы значений для включения в вашу таблицу. Когда у вас есть сумма, которая вас устраивает или которую требует ваш вопрос, вы можете затем взять эти значения x и y и нанести их в виде координат на график, чтобы отобразить точки на линейном уравнении!

Примеры задач

Вопрос 1:

График следующей функции с использованием таблицы значений

г = 3х — 1

Решение:

Сначала создайте таблицу значений для уравнения. Используйте x, чтобы найти y. Вы можете использовать разные значения, но ваш график будет одним и тем же независимо от того, какие значения вы используете.

Таблица значений x

Для x = -2

у = 3 (-2) — 1

г = -6 — 1

г = -7

Для x = -1

у = 3 (-1) — 1

г = -3 — 1

г = -4

Для x = 0

у = 3 (0) — 1

г = 0 — 1

г = -1

Для x = 1

у = 3 (1) — 1

г = 3 — 1

г = 2

Для x = 2

у = 3 (2) — 1

г = 6 — 1

г = 5

Теперь у нас есть полная таблица значений

Заполненная таблица значений x и y

Теперь мы можем нанести упорядоченные пары на сетку

Построение данных

Затем соедините точки прямой линией, и готово!

Связывание данных по прямой

Вопрос 2:

Изобразите следующую функцию, используя таблицу значений:

2x + 4y = 8

Решение:

Во-первых, мы хотим упростить уравнение

2x + 4y = 8

х + 2у = 4

2у = -x + 4

y = −12 \ frac {-1} {2} 2−1 x + 2

Теперь у нас есть уравнение в форме пересечения наклона.

Затем создайте таблицу значений для уравнения. Используйте x, чтобы найти y.

Таблица x решает относительно y

Для x = -2

y = −12 \ frac {-1} {2} 2−1 (-2) + 2

г = 1 + 2

г = 3

Для x = -1

y = −12 \ frac {-1} {2} 2−1 (-1) + 2

г = 0,5 + 2

г = 2,5

Для x = 0

y = −12 \ frac {-1} {2} 2−1 (0) + 2

у = 0 + 2

г = 2

Для x = 1

y = −12 \ frac {-1} {2} 2−1 (1) + 2

у = -0.5 + 2

г = 1,5

Для x = 2

y = −12 \ frac {-1} {2} 2−1 (2) + 2

г = -1 + 2

г = 1

Теперь у нас есть полная таблица значений

Таблица заполненных данных

Мы можем нанести упорядоченные пары на сетку.

Координаты, построенные с использованием таблицы данных

Затем соедините точки прямой линией, и готово!

Свяжите данные вместе прямой линией

Хотите проверить свой ответ, чтобы увидеть, насколько точен ваш график? Вот онлайн-калькулятор для справки.

Далее, узнайте больше о таблице значений, как построить график линейных неравенств с двумя переменными и как построить график систем линейных неравенств. Вы также можете начать изучение вводных сведений о функциях и о том, как их идентифицировать.

Мягкий вопрос — Какой ваш любимый онлайн-инструмент для построения графиков?

мягкий вопрос — Какой ваш любимый онлайн-инструмент для построения графиков? — Обмен математическими стеками

Сеть обмена стеков

Сеть Stack Exchange состоит из 178 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

0
+0
Авторизоваться Подписаться

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 11 лет, 1 месяц назад

Просмотрено 7к раз

$ \ begingroup $

Мне нужен хороший, быстрый онлайн-инструмент для построения графиков. Также будет удобна возможность ссылаться на вывод или встраивать его.

$ \ endgroup $ 0 $ \ begingroup $ $ \ endgroup $ 1 $ \ begingroup $

desmos.com Это, безусловно, лучшее.

$ \ endgroup $ 2 $ \ begingroup $

Ну, я не уверен, куда вы хотите встраивать графики, но Wolfram Alpha очень удобен для построения графиков.Он обладает большинством функций Mathematica, может обрабатывать 3D-функции, а также причудливое масштабирование и тому подобное. Я очень рекомендую это.

$ \ endgroup $ 1 $ \ begingroup $

Мне очень нравится Geogebra как веб-инструмент для построения графиков (требуется Java).

$ \ endgroup $ 4 $ \ begingroup $

Я искал хорошие интерактивные диаграммы без flash (простой HTML + Javascript) и обнаружил, что http: // DIYcharts.com — самый удобный и простой в использовании, как и Google Charts.

$ \ endgroup $ $ \ begingroup $

Вот онлайн-инструменты, которые я использую ежедневно для построения графиков, а также для построения графиков геометрии:

Desmos (отличное удобство использования, потрясающие функции)
Plotlux (мощный плоттер, на основе fooplot)
График.tk (быстрый и простой плоттер)
JSXGraph (мощный инструмент для графиков и геометрии, однако вам необходимо знать javascript)
Geodrafter (построение простых геометрических фигур)
Геосервант 3D (построение простых 3D объектов)
Geogebra (мощный, всеобъемлющий, но не может использоваться в коммерческих целях)
Эскизы (геометрические объекты, интересное юзабилити)

Как только я открываю для себя новые инструменты, я обновляю свой пост.

$ \ endgroup $ 1 $ \ begingroup $

Я поступил в бакалавриат по специальности математика. Я нашел Desmos чрезвычайно полезным для четкого отображения графиков с лицом пользователя, которое было достаточно простым для работы всех моих учеников. Сочетание этого дисплея с планами уроков и раздаточными материалами Windows Snipping Tool стало проще.

Переключившись на специальность / выпускник со степенью математики и работая над магистром математики с концентрацией статистики, мне очень нравится использовать R.RStudio имеет красивый вывод; на сайте DataCamp есть несколько открытых курсов по созданию диаграмм и графиков на R. Это довольно удобно.

$ \ endgroup $ $ \ begingroup $

Я использую Трансум. Это помогает мне быстро показать график любого правильного уравнения

$ \ endgroup $ Очень активный вопрос .

Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов. Mathematics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.

Принимать все файлы cookie Настроить параметры

Solumaths — Программное обеспечение для Интернета — Математические решения онлайн.

Solumaths — это математический сайт , который предлагает несколько бесплатных приложений по математике онлайн , он особенно подходит для студентов, студентов колледжей, старшеклассников, и учителя.

Доступно несколько типов математических приложений :

Калькулятор: программа символьного и числового расчета онлайн.

Программа онлайн-калькулятор позволяет численные вычисления и компьютерная алгебра. Это мощный калькулятор алгебры.

Это математическое онлайн-программное обеспечение позволяет расчет фракции с калькулятор дробей, буквальное исчисление, числовое вычисление, вычисление по радикалам, вычисление комплексных чисел с его калькулятор комплексных чисел, он имеет мощные функции, позволяющие решать уравнения, решатель уравнений позволяет включать решить уравнение, решить квадратное уравнение, задав решение в точной форме. Решатель также может решить неравенство, является ли это неравенством первой степени или неравенство второй степени, снова решение рассчитывается с его точным видом. Калькулятор умеет вычислять производные функции с помощью калькулятора производных. и вычислить первообразную с первообразным калькулятором. Для некоторых функций можно получить другой шаг вычислений.Этот пошаговый метод облегчает понимание.

Калькулятор позволяет решать математические упражнения онлайн и решение математических задач в Интернете.

Графический калькулятор: онлайн-программа для рисования кривых.

Бесплатные математические игры

Solumaths предлагает разные вычислительные игры на основе арифметических операций , эти онлайн-игр по математике позволяют тренировать в уме и помочь развитию размышлений и стратегии.

На сайте представлены лучшие математические игры. чисел , эти обучающие бесплатные математические игры позволяют практиковать элементарные арифметические операции например, , добавление , вычитание , умножение и Евклидово деление . Эти простые расчетные игры позволяют практиковаться в счете и вычислении, эти игры с числами позволяют практиковать быстрый расчет и мысленный расчет .

На сайте представлен большой выбор расчетных онлайн-игр: количество игр , быстрых вычислений игр , арифметических игр , мысленных арифметических игр , операций игры , математических тестов .

Математическое онлайн-программное обеспечение регулярно обновляется

Solumaths активно развивается, новые функции добавляются регулярно.Не стесняйтесь часто возвращаться, чтобы обнаружить их.

Поделиться Solumaths в социальных сетях

Можно делиться страницами сайта в основных социальных сетях, благодаря использованию панели общего доступа, которая появляется на соответствующих страницах.

Просто щелкните значок социальной сети, из которой вы хотите поделиться страницей. Чтобы показать ссылку для обмена и в других социальных сетях нажмите «поделиться +».

Хорошие расчеты, хорошая графика и хорошие математические игры ;-), на поисковиков .

функций по SAT Math: линейные, квадратичные и алгебраические

Функции SAT имеют сомнительную честь быть одной из самых сложных тем в разделе SAT математики. К счастью, это не потому, что функциональные задачи по своей природе более трудны для решения, чем любые другие математические задачи, а потому, что большинство студентов просто не имеют дела с функциями в той мере, в какой они изучают другие математические темы SAT.

Это означает, что разница между пропущенными пунктами по этой, казалось бы, сложной теме и их выполнением — это просто вопрос практики и ознакомления.А учитывая, что функциональные проблемы обычно возникают в среднем от трех до четырех раз за тест, вы сможете набрать еще несколько математических баллов SAT, если узнаете правила и работу функций.

Это будет ваше полное руководство по функциям SAT. Мы подробно расскажем, что означают функции, как ими пользоваться, манипулировать и идентифицировать, а также какие именно проблемы с функциями вы увидите на тесте SAT.

Что такое функции и как они работают?

Функции — это способ описания взаимосвязи между входами и выходами в форме графика или уравнения. 2 + 2x — 4 $

Функции всегда можно изобразить в виде графиков, а различные виды функций будут создавать графики разного вида. На стандартном координатном графике с осями $ x $ и $ y $ входом графика будет значение $ x $, а выходом — значение $ y $.

Каждый вход (значение $ x $) может давать только один выход, но один выход может иметь несколько входов. Другими словами, несколько входов могут давать один и тот же результат.

Один из способов запомнить это — то, что вы можете иметь «многие к одному» (много входов на один выход), но НЕ «один ко многим» (один вход для многих выходов).

Это означает, что граф функции может иметь потенциально много $ x $ -перехватов, но только один $ y $ -перехватывание. (Почему? Потому что, когда вход $ x = 0 $, может быть только один выход или значение $ y $.)

Функция с несколькими перехватами $ x $ .

Вы всегда можете проверить, является ли график функциональным графиком, используя это понимание входов и выходов. Если вы используете «тест вертикальной линии», вы можете увидеть, является ли график функцией или нет, поскольку график функции НЕ попадет более чем в одну точку на любой вертикальной линии.

Независимо от того, где мы рисуем вертикальную линию на нашей функции, она будет пересекаться с графиком только один раз.

Тест вертикальной линии применяется ко всем типам функций, независимо от того, насколько они выглядят «странно».

Даже «странно выглядящие» функции всегда проходят проверку вертикальной линии.

Но любой график, который не проходит проверку вертикальной линии (пересекаясь с вертикальной линией более одного раза), автоматически НЕ является функцией.

Этот график НЕ является функцией, так как он не проходит проверку вертикальной линии.

Слишком много препятствий на пути восхождения работает как для функций, так и для реальной жизни (то есть: совсем не хорошо).

Термины и определения функций

Теперь, когда мы увидели, что делают функции, давайте поговорим о частях функции.

Функции представлены уравнениями, таблицами или графиками (называемыми «графиком функции»).2 + 5 $

$ f $ — это имя функции

(Примечание: мы можем вызывать нашу функцию другими именами, кроме $ f $. Эта функция называется $ f $, но вы можете видеть функции, записанные как $ h (x) $, $ g (x) $, $ r ( x) $ или что-то еще.)

$ (x) $ — вход

(Примечание: в этом случае наш ввод называется $ x $, но мы можем назвать его как угодно. $ F (q) $ или $ f (\ клубника) $ — обе функции с входами $ q $ и клубники, соответственно.2 + 5 $

$ f (3) = 9 + 5 $

$ f (3) = 14 $

Итак, наша заказанная пара $ (3, 14) $.

Упорядоченные пары также действуют как координаты , поэтому мы можем использовать их для построения графика нашей функции.

Теперь, когда мы понимаем ингредиенты нашей функции, давайте посмотрим, как мы можем соединить их вместе.

Различные типы функций

Ранее мы видели, что функции могут иметь самые разные уравнения для вывода.2 $ равно 9, что означает, что график не может быть прямой линией.

Примеры линейных функций:

$ f (x) = x — 12 $

$ f (x) = 4 $

$ f (x) = 6x + 40 $

Квадратичные функции

Квадратичная функция строит график параболы, что означает, что это график, который изгибается, открываясь вверх или вниз. Это также означает, что наша выходная переменная всегда будет возведена в квадрат .

Причина, по которой наша переменная должна быть возведена в квадрат (не в кубе, не в степени 1 и т. Д.2 $ оба равны 9. Таким образом, у нас есть два входных значения — положительное и отрицательное — которые дают нам одно и то же выходное значение. 2 + bx + c $

Значение $ \ bi a $ сообщает нам, как формируется парабола и в каком направлении она открывается.

положительное значение $ \ bi a $ дает нам параболу, которая открывается вверх.

отрицательный $ \ bi a $ дает нам параболу, которая открывается вниз.

A large $ \ bi a $ значение дает нам тонкую параболу.

A small $ \ bi a $ значение дает нам широкую параболу.

Значение $ \ bi b $ сообщает нам, где находится вершина параболы, слева или справа от начала координат.

положительное значение $ \ bi b $ помещает вершину параболы слева от начала координат.

отрицательное значение $ \ bi b $ помещает вершину параболы вправо от начала координат.

Значение $ \ bi c $ дает нам $ y $ -перехват параболы. Это место, где график достигает оси $ y $ (и всегда будет только одна точка).

(Примечание: когда $ b = 0 $, $ y $ -перехват также будет местоположением вершины параболы.)

Не волнуйтесь, если сейчас кажется, что это много для запоминания — с практикой понимание функциональных проблем и их компонентов станет вашей второй натурой.

Готовы выйти за рамки простого чтения о SAT? Тогда вам понравится бесплатная пятидневная пробная версия для нашей программы SAT Complete Prep . Разработанная и написанная экспертами PrepScholar SAT , наша программа SAT настраивается в соответствии с вашим уровнем навыков по более чем 40 вспомогательным навыкам, чтобы вы могли сосредоточить свое обучение на том, что принесет вам наибольший набор баллов.

Нажмите кнопку ниже, чтобы попробовать!

Типичные функциональные проблемы

Функциональные проблемы

всегда проверят вас, правильно ли вы понимаете взаимосвязь между входами и выходами. Эти вопросы обычно делятся на четыре типа:

# 1 : Функции с заданными уравнениями

# 2 : Функции с графиками

# 3 : Функции с таблицами

# 4 : вложенные функции

Эти три категории могут частично совпадать, но это основные темы, на которых вы будете тестировать, когда дело доходит до функций.Давайте посмотрим на несколько реальных математических примеров SAT каждого типа.

Функциональные уравнения

Задача с уравнением функции даст вам функцию в форме уравнения, а затем попросит вас использовать один или несколько входных данных для поиска выходных данных (или элементов выходных данных).

Чтобы найти конкретный выход, мы должны вставить данный вход для $ x $ в наше уравнение (выход).

Итак, если мы хотим найти $ f (2) $ для уравнения $ f (x) = x + 3 $, мы подставим 2 вместо $ x $.2 + 24 $

$ г (-4) = -16 + 24 $

$ г (-4) = 8 $

Наш окончательный ответ — A, 8.

Графики функций

Вопрос о графике функций предоставит вам уже построенную функцию и задаст вам любое количество вопросов по ней.

Эти вопросы обычно просят вас идентифицировать определенные элементы графика или найти уравнение функции на графике.

До тех пор, пока вы понимаете, что $ x $ — это ваш ввод, а ваше уравнение — это ваш результат, $ y $, тогда вопросы такого типа не будут такими сложными, как кажется.

Минимальное значение функции соответствует $ y $ -координате точки на графике, где оно наименьшее на оси $ y $.

Глядя на график, мы видим, что самая низкая точка функции на оси $ y $ находится в точке $ (- 3, -2) $.

Поскольку мы ищем значение $ x $, когда функция находится на минимальном уровне, нам нужна координата x, которая равна -3.

Итак, наш окончательный ответ — B, -3.

Таблицы функций

Третий способ увидеть функцию — это ее таблица.

Вам будет предоставлена таблица значений для входа и выхода, а затем вам будет предложено найти уравнение функции или график функции.

Часто лучшая стратегия для таких вопросов — это вставить ответы, чтобы упростить нашу жизнь. Таким образом, нам не нужно на самом деле находить уравнение самостоятельно — мы можем просто проверить, какие варианты ответов соответствуют входным и выходным данным, указанным в нашей таблице.

Давайте протестируем вторую упорядоченную пару, $ (3,13) $ с каждым вариантом ответа.Для правильного ответа, когда мы подставляем значение $ x $ (3) в уравнение, мы получим правильное значение $ y $ (13).

A) $ f (x) = 2 (3) +3 = 9 $. Это уравнение неверно, так как 9 не равно 13.

Б) $ f (x) = 3 (3) +2 = 1 $. Это уравнение также неверно.

C) $ f (x) = 4 (3) + 1 = 13 $. Это матч! Это уравнение пока верно.

D) $ f (x) = 5 (3) = 15 $. Это уравнение также неверно.

Похоже, C — правильный ответ, но давайте подключим первую и третью упорядоченные пары, чтобы убедиться.

За первую заказанную пару $ (1,5) $:

$ f (x) = 4 (1) + 1 = 5 $ Верно!

За третью заказанную пару (5,21) $

$ f (x) = 4 (5) + 1 = 21 $ Тоже правильно!

Наш окончательный ответ: C , $ f (x) = 4x + 1 $

Вложенные функции

Последний тип функциональной проблемы, с которой вы можете столкнуться на SAT, называется «вложенной» функцией. По сути, это уравнение внутри уравнения.

Чтобы решить эти типы вопросов, подумайте о них с точки зрения вашего порядка действий.2 — 12x — 2 $

Так как $ g (x) $ вложен наиболее глубоко, мы должны найти его вывод, прежде чем сможем найти $ f (g (x − 2)) $.

Вместо числа для $ x $ дано другое уравнение. Хотя это может отличаться от предыдущих задач, принцип тот же — замените все входные данные для переменной в выходном уравнении.

$ г (x) = 3x + 4 $

$ г (x − 2) = 3 (x − 2) + 4 $

$ г (x − 2) = 3x — 6 + 4 $

$ г (x − 2) = 3x — 2 $

Итак, наш выход $ g (x − 2) $ равен $ 3x − 2 $.2 — 12x — 2 $.

Функции внутри функций, сны внутри снов. Постарайтесь не потеряться по пути.

Стратегии решения функциональных проблем

Теперь, когда вы увидели все различные виды функциональных проблем в действии, давайте рассмотрим несколько советов и стратегий для решения функциональных проблем различных типов.

Для ясности мы разделили эти стратегии на несколько разделов — советы по всем функциональным проблемам и советы по функциональным проблемам по типам.Итак, давайте рассмотрим каждую стратегию.

Стратегии для всех функциональных проблем:

# 1: Тщательно отслеживайте все свои части и записывайте все

Хотя это может показаться очевидным, в пылу сию минуту может быть слишком легко перепутать отрицательные и положительные стороны или неправильно указать, какая часть вашей функции (графика или таблицы) является вашим вводом, а какая — выводом. Круглые скобки имеют решающее значение.

Создатели SAT знают, как легко запутать и перемешать части ваших функциональных уравнений (особенно когда ваш ввод также является уравнением), поэтому внимательно следите за всеми своими движущимися частями и не пытайтесь делать функциональные проблемы в вашей голове.

# 2: При необходимости используйте PIA и PIN-код

Как мы видели в нашей задаче с таблицей функций выше, можно сэкономить много усилий и энергии, если использовать стратегию вставки ответов. Вы также можете использовать технику вставки собственных чисел для проверки точек на графиках функций, работы с любым уравнением функции переменной или работы с вложенными функциями с переменными.

Например, давайте посмотрим на нашу более раннюю проблему вложенных функций с использованием PIN-кода.2 — 12x — 2 $

Если мы вспомним, как работают вложенные функции (что мы всегда работаем наизнанку), то мы можем вставить наш собственный номер для $ x $ в функцию $ g (x − 2) $. Таким образом, нам не придется работать с переменными и вместо этого можно будет использовать действительные числа.

Итак, допустим, что $ x $ — это функция $ g (x − 2) $, равная 5. (Почему 5? Почему нет!)

Теперь $ x − 2 $ будет $ 5−3 $, или 3. Это означает, что $ g (x − 2) $ будет $ g (3) $.

$ г (x − 2) = 3x + 4 $

$ г (3) = 3 (3) + 4 $

$ г (3) = 9 + 4 $

$ г (3) = 13 $

Теперь давайте подставим это число в качестве значения для нашей функции $ g (x − 2) $ во вложенную функцию $ f (g (x − 2)) $.2–12 (5) + 4 $

$ 9 (25) — 60 + 4 $

225–60 долл. США + 4

долл. США

$ 165 + 4 $

169

Это значение все еще слишком велико, но мы видим, что оно ужасно близко к окончательному ответу, который мы хотим. Просто просмотрев наши варианты ответов, мы можем увидеть, что вариант ответа E — это в точности то же выражение, что и вариант ответа D, за исключением последнего целочисленного значения. Если бы мы вычли 2 из 165 вместо добавления 4 (как мы это сделали с вариантом ответа D), мы получили бы наш окончательный ответ 163.2 — 12x — 2 $.

# 3: Практика, практика, практика

Наконец, единственный способ по-настоящему освоиться с любой математической темой — это практиковать как можно больше различных типов вопросов по этой теме. Если функции являются для вас слабым местом, обязательно задавайте дополнительные практические вопросы.

Для функциональных графиков и таблиц:

# 1: Начните с поиска $ \ bi y $ -перехвата

Как правило, проще всего начать работу с графиками и таблицами функций с поиска точки пересечения по оси y.Отсюда вы часто можете исключить несколько различных вариантов ответов, которые не соответствуют нашему графику или нашему уравнению (как мы это делали в наших предыдущих примерах).

Угол пересечения оси Y почти всегда легче всего найти, так что это всегда хорошее место для начала.

# 2: Проверьте свое уравнение на нескольких упорядоченных парах

Всегда полезно найти две или более точек (упорядоченные пары) ваших функций и проверить их на соответствие уравнению потенциальной функции.Иногда одна упорядоченная пара работает для вашего графика, а вторая — нет.

Вы должны сопоставить уравнение с графиком (или уравнение с таблицей), которое работает для для каждой пары координат / упорядоченная пара, а не только для одной или двух.

Для функциональных уравнений и вложенных уравнений:

# 1: Всегда работайте наизнанку

Вложенные функции могут выглядеть ужасно и сложно, но они выполняются по частям. Составьте уравнение в центре, а затем медленно расширяйте его, чтобы не перепутать какие-либо переменные или уравнения.

# 2: Не забудьте FOIL

Очень часто SAT заставляет вас возвести уравнение в квадрат. Это связано с тем, что многие студенты неправильно задают вопросы такого типа и распределяют свои показатели вместо того, чтобы возводить в квадрат все выражение.

Если вы не используете ФОЛЬГ должным образом, вы получите неверный ответ. По возможности старайтесь не терять очки из-за таких неосторожных ошибок.

Например, предположим, что вы должны возвести выражение в квадрат.2 + 9 $ но это неверно . Не попадитесь в такую ловушку!)

Вы все повысились — пора сразиться с большим боссом и применить знания на практике!

Проверьте свои знания

Теперь давайте проверим ваши знания функций на реальных математических задачах SAT.

1. Пусть функция $ f $ определена следующим образом: $ f (x) = 5x-2a $, где $ a $ — константа. Если $ f (10) + f (5) = 55 $, каково значение $ a $?

А) -5

В) 0

С) 5

Г) 10

2. Для функции $ f $ выполняется равенство $ f (2) = 3 $ и $ f (3) = 5 $. Для функции $ g $ выполняется равенство $ g (3) = 2 $ и $ g (5) = 6 $. Какое значение имеет $ f (g (3)) $?

А) 2

В) 3

С) 5

Г) 6

Ответы: C, B, A, D

Объяснение ответа:

1. Как вы можете видеть здесь, нам дано наше уравнение, а также два входа и их объединенный выход.Мы должны использовать эти знания, чтобы найти элемент нашего вывода (в данном случае значение $ a $.)

Итак, давайте найдем наши выходы для каждого заданного нам входа.

$ f (x) = 5x — 2a

$ f (10) = 5 (10) — 2a $

$ f (10) = 50 — 2a

$ f (x) = 5x — 2a

$ f (5) = 5 (5) — 2a

$ f (5) = 25 — 2a

Теперь давайте установим сумму наших двух выходов равной 55 (как было указано в вопросе).

$ 50 — 2a + 25 — 2a = 55 $

75 $ — 4a = 55 $

$ −4a = −20 $

$ a = 5 $

Наш окончательный ответ — C , $ a = 5 $.

2. В вопросе нам сказано, что $ g (3) = 2 $.

Чтобы найти значение $ f (g (3)) $, нам нужно заменить 2 на $ g (3) $. Мы будем использовать это значение в уравнении $ f (x) $.

Замена 2 на $ g (3) $ дает нам $ f (g (3)) $ = $ f (2) $.

Нам также говорят, что $ f (2) = 3 $, это означает, что 3 — правильный ответ.

Наш окончательный ответ — B, 3.

3. Согласно нашим стратегиям, мы начнем с поиска $ y $ -перехвата.2−4x + 4 $

Что даст нам график с $ y $ -перехватом в +4 и вершиной, расположенной справа от оси $ y $.

В процессе исключения остается вариант ответа A. Но, чтобы перепроверить, давайте проверим координатную точку на графике по формуле.

Мы уже знаем, что наше уравнение соответствует координатным точкам $ (0, 2) $, поскольку это наш $ y $ -перехват, но есть еще несколько мест на графике, которые попадают в четные координаты.2 + 2 $

4. Вместо того, чтобы использовать $ x $ для ввода, эта проблема заставляет нас использовать $ t. $ Если вы очень привыкли использовать $ f (x) $, это может показаться дезориентирующим, поэтому вы всегда можете переписать проблему используя $ x $ вместо $ t $.

В этом случае мы продолжим использовать $ t $, чтобы мы могли упорядочить проблему на странице.

Сначала найдем $ y $ -перехват.

$ y $ -перехват — это точка, в которой $ x = 0 $, поэтому мы можем видеть, что это уже дано нам с первым набором чисел в таблице.Когда $ t = 0 $, $ f (t) = −1 $

Следовательно, наш $ y $ -перехват равен -1, что означает, что мы можем автоматически исключить варианты ответов B, C и E.

Теперь давайте снова воспользуемся нашей стратегией вставки чисел.

Наши варианты ответа — от A до D, поэтому давайте сначала проверим A со второй упорядоченной парой.

Наше потенциальное уравнение:

$ f (t) = t — 1 $

И наша заказанная пара:

$ (1, 1)

Итак, давайте объединим их.

$ f (t) = t — 1 $

$ f (1) = 1–1

$ f (1) = 0 $

Это неверно, так как это означало бы, что наш вывод равен 0, когда наш ввод равен 1, и все же упорядоченная пара говорит, что наш вывод будет 1, когда наш ввод равен 1.

Вариант ответа A неверен.

В процессе исключения попробуем вариант ответа D.

Наше потенциальное уравнение:

$ f (t) = 2т — 1 $

И снова наша заказанная пара:

$ (1, 1)

Итак, давайте объединим их.

$ f (1) = 2 (1) — 1 $

$ f (1) = 2 — 1 $

$ f (1) = 1 $

Это соответствует входу и выходу, которые мы даны в нашей упорядоченной паре. Вариант ответа D правильный.

Наш окончательный ответ: D , $ f (t) = 2t — 1 $

Вы сделали это! Дай пять всем вокруг.

На вынос

Многие студенты плохо разбираются в функциях, но не позволяйте таким вопросам пугать или сбивать вас с толку, когда вы видите их на SAT.Принципы, лежащие в основе функций, заключаются в простом вводе, выводе и вставке значений. Тест будет пытаться замутить воду, когда сможет, но всегда помните, что эти вопросы будут казаться более сложными, чем они есть на самом деле.

Хотя можно легко допустить ошибку с вашими знаками или переменными, настоящие проблемы просты по своей сути. Так что будьте внимательны, перепроверьте свою работу, и вскоре вы сможете без проблем справляться с проблемами с функциями.

Что дальше?

Говоря о квадратичных функциях, как вы догадались до завершения квадрата? Узнайте, как и когда завершить квадрат с помощью этого руководства.

Уф! Знание своих функций означает знание значительной части раздела по математике SAT (аплодисменты вам!), Но есть еще очень много тем, которые нужно охватить. Взгляните на все темы, по которым вы будете тестироваться в математическом разделе SAT, а затем перейдите к нашим руководствам по математике, чтобы просмотреть любую тему, в которой вы чувствуете себя неуверенно. Не уверены в своих правилах экспоненты? Как насчет вашего понимания полигонов? Хотите проверить свои склоны? Какая бы ни была тема, мы вам поможем!

Ищете помощь по основам математики? Освежите память о свойствах распределения, точных квадратах и о том, как найти здесь среднее значение набора чисел.

Думаете, вам нужен репетитор по математике? Ознакомьтесь с нашими руководствами о том, как найти репетитора, который наилучшим образом соответствует вашим потребностям (и вашему бюджету).

Не хватает времени на сдачу экзамена по математике? Не волнуйтесь! У нас есть инструменты и стратегии, которые помогут вам опередить время и максимально увеличить количество очков.

Пытаетесь набрать наивысший балл? Узнайте, как увеличить свой результат до максимума, с помощью нашего руководства по получению 800 баллов за SAT, написанного отличным бомбардиром.

Хотите улучшить свой результат SAT на 160 баллов?

Ознакомьтесь с нашей лучшей в своем классе онлайн-программой подготовки к SAT. Мы гарантируем возврат ваших денег , если вы не улучшите свой результат SAT на 160 или более баллов.

Наша программа полностью интерактивна, и она адаптирует то, что вы изучаете, к вашим сильным и слабым сторонам. Если вам понравилось это руководство по математической стратегии, вам понравится наша программа. Наряду с более подробными уроками вы получите тысячи практических задач, организованных по индивидуальным навыкам, чтобы вы учились наиболее эффективно.Мы также дадим вам пошаговую программу, которой нужно следовать, чтобы вы никогда не запутались, что изучать дальше.

Воспользуйтесь нашей 5-дневной бесплатной пробной версией:

Как решать мои математические задачи

Когда студентов спрашивают о том, какой предмет они больше всего ненавидят, большинство из них ответят по математике. В вычислении чисел, нахождении неизвестных и составлении графиков уравнений есть что-то, что учащиеся находят почти невозможным для понимания.Независимо от того, насколько они слушают учителя, учебные пособия, в которых объясняются пошаговые решения, изучают математические концепции и практикуются вне класса, кажется, что некоторые математические уравнения и неравенства просто невозможно решить.

Но, конечно, всегда есть решение, если знать, где искать. А в наши дни вы сделаете себе одолжение, уклоняясь от устаревших методов и обращаясь к онлайн-службам помощи по математике, чтобы сделать вашу математику более увлекательной, получив шаги и подробные инструкции. Хотя вам, возможно, не так весело решать математические задачи, как при изучении других предметов, по крайней мере, вам не придется бояться каждый раз, когда ваш учитель математики дает вам домашнее задание, и вы научитесь решать математические задачи.

Как решать математические задачи

Один из лучших способов начать работу — это познакомиться с некоторыми из самых полезных математических калькуляторов. В цифровую эпоху эти веб-калькуляторы постепенно заменяют свои портативные аналоги. Теперь у вас есть возможность решать сложные уравнения всего за несколько кликов. И что самое приятное, вам будет предоставлено пошаговое объяснение того, как решается проблема, так что вы будете знать, что делать во время экзамена.

Вот краткое изложение лучших приложений-калькуляторов, которые должны быть в вашем арсенале:

1) Калькулятор пределов

Иногда бывает трудно понять математические концепции, если вы не понимаете определения наиболее распространенных используемых терминов.Например, слово «предел» определяется как граница, за которую не может выйти количество, идея или вещь. Во время движения ваша скорость не должна превышать установленную. В математике понятие предела практически такое же. Но если быть более точным, термин «предел» в математических терминах говорит о том, что происходит, когда вы приближаетесь к условию или границе. Минимальные и максимальные значения здесь не главное. Фактически, эти значения могут быть абстрактными в математической концепции предела.

Калькулятор пределов — полезный инструмент для вычисления предела заданной функции в заданной точке.Лучше всего использовать калькулятор, который поддерживает как односторонние, так и двусторонние ограничения. Просто подключив функцию ввода и ограничение, вы получите решение своей проблемы в кратчайшие сроки.

Калькуляторы лимитов можно найти по адресу:

2) Калькулятор производных

В математике термин производная означает скорость изменения функции по отношению к переменной. Производные играют важную роль в решении задач исчисления и дифференциальных уравнений, включая поиск локальных экстремумов, решение задач оптимизации, поиск точек перегиба и описание движения объектов.Геометрически вы можете интерпретировать производную функции в точке как наклон касательной к этому графику функции в этой точке, это также предел отношения изменения y к изменению x как изменение x стремится к нулю.

Все это может быстро запутать, но вы можете сделать вещи более управляемыми, используя калькулятор производных. Он позволяет вычислять производную функции по переменной, используя пошаговые решения. Если вам нужно вычислить производную многочлена, общие производные, производные сумм, производные разностей, производные продуктов или цепочку производных правил, калькулятор производных окажется удобным инструментом.

Производные калькуляторы можно найти по адресу:

3) Графический калькулятор

Если у вас когда-либо было задание по математике, требующее построения графиков для сложных уравнений, то вы знаете, насколько это сложно. К счастью, вы можете использовать графический калькулятор, чтобы ускорить процесс. Это устройство более мощное, чем базовый калькулятор, позволяя обрабатывать несколько уравнений, выполнять более сложные вычисления и отображать результаты на графике, такие как параболы.

Графические калькуляторы впервые появились в 1980-х годах.Сегодня вы можете пользоваться теми же функциями и возможностями, просто используя онлайн-программу для решения математических задач. Многие графические калькуляторы на базе Интернета позволяют учащимся составлять графики сложных уравнений одним щелчком мыши. Что еще более впечатляюще, вы можете получить учебное пособие, которое расскажет вам точные шаги, чтобы прийти к правильному решению. Большинство графических калькуляторов теперь предоставляют учебные пособия для различных типов алгебраических задач, включая квадратные уравнения, линейные уравнения, линейные неравенства и одновременные уравнения.

Графические калькуляторы можно найти по адресу:

4) Калькулятор алгебры

Для многих студентов первым серьезным препятствием на пути к математике является алгебра. Это знаменует собой то время, когда вам нужно думать не только об основных операциях, но и изучать способы решения основных уравнений. Но даже самые простые уравнения могут оказаться непростыми. Хорошей новостью является то, что вы можете использовать калькулятор алгебры, чтобы быстро решать уравнения и понимать все шаги, поэтому вы знаете, как прийти к решению самостоятельно.

Независимо от того, какая у вас задача по алгебре, этот калькулятор даст ответ, который вы ищете. Просто введите проблему в текстовое поле, нажмите «Рассчитать» и просмотрите руководство по расчетам. Прежде чем вы это узнаете, у вас будет рабочее понимание того, как решать даже сложные уравнения.

Вы всегда можете обратиться к калькулятору алгебры , чтобы быстро проверить свое домашнее задание по математике по адресу:

5) Фотоматематический калькулятор

Photomath — это самое популярное приложение для решения математических задач со словами — и не зря! Это приложение использует дополненную реальность, позволяя вам просто навести камеру мобильного устройства на лист бумаги с любой арифметической задачей, и оно немедленно найдет решение.На данный момент приложение работает только с печатными задачами, а это означает, что вам нужно сначала распечатать математическое задание, прежде чем вы сможете успешно использовать приложение. Это небольшая плата за все преимущества калькулятора Photomath.

Помимо решения проблемы, приложение показывает решения на вашем устройстве. Щелчок по «Шагам» дает подробное объяснение того, как решается проблема. Существует также журнал истории, в котором хранятся все решенные уравнения, что позволяет вам просматривать их в любое время.

Несомненно, Photomath незаменим для любого студента, который хочет получить более высокие оценки по математике. Он бесплатный для Android и iOS, поэтому нет причин не попробовать его.

6) Калькуляторы, встроенные в операционные системы

В Windows 7, 8, 10 калькулятор имеет стандартный, научный, программный, статистический режимы. И выход, безусловно, есть для пользователей Mac .

7) Другие калькуляторы

Существуют калькуляторы для конкретных расчетов.

Калькуляторы комплексных чисел

Статистические калькуляторы

Интегральные вычислители

Калькулятор треугольников

Финансовые калькуляторы

Обыкновенные дифференциальные уравнения

Калькуляторы линейной алгебры

Калькуляторы линейного программирования

Калькуляторы для численных методов

Логические калькуляторы

Какие услуги могут помочь мне в решении математических задач

Теперь, когда вы знаете самые полезные приложения-калькуляторы, вы, вероятно, меньше беспокоитесь о выполнении своих математических заданий.Но что бы вы делали в то время, когда у вас практически нет времени уделять домашнее задание? Практически все студенты в тот или иной момент окажутся в этой ситуации, поэтому стоит подготовиться заранее.

Лучше всего нанять настоящих экспертов по математике, которые сделают за вас домашнее задание. Это дает те же преимущества, что и упомянутые математические калькуляторы, но не поднимая пальца самостоятельно. Каким бы ни было ваше домашнее задание по математике, вы можете отдыхать спокойно, зная, что есть эксперт, который может сделать ваше домашнее задание и выполнить его вовремя.

Помимо очевидного преимущества скорости и удобства, вы также можете узнать об уроках математики прямо от профессионалов. Вам будет предоставлено подробное руководство, в котором вы сможете шаг за шагом изучить решения. Это гарантирует, что вы не останетесь в неведении, помогая решать математические задачи, если вы столкнетесь с ними на экзаменах.

Единственное, что осталось сделать, это обратиться к Эксперту по назначениям за лучшей службой помощи по математике . Убедитесь сами, как им за эти годы удалось получить 98% удовлетворенности от своих клиентов.AssignmentExpert.com — это веб-сайт, который решает любые математические задачи, и здесь, , вы даже можете бесплатно получить ответы на домашние задания по математике.

Пошаговый калькулятор функционального состава | Почти развлечение

Калькулятор композиции функций

Входы и выходы функций

Когда вы видите что-то вроде f (g (x)) или (f∘g) x, у вас есть композиция функций.

Прежде всего, подумайте о таких функциях, как поиск и замена.

Когда у нас есть такая функция, как f (x) = 4×2 + 6x + 5, подключение входа для x означает поиск и замену каждого x входным значением.Например, если наш ввод равен 3, мы находим и заменяем, чтобы получить:

f (x) = 4 (x) 2 + 6 (x) +5

⬇️

f (3) = 4 (3) 2 + 6 ( 3) +5

И вы должны убедиться, что вы заменили каждый x. Это похоже на то, как они должны были заменить каждого жуткого Соника новым милым Соником, иначе жуткость все равно была бы там ☠️.

Если вам нужна дополнительная помощь по функциям, ознакомьтесь с нашим уроком по функциям и калькулятором здесь!

Что такое композиция функций?

Идея композиции функций состоит в том, что вместо числа в качестве входных данных выступает другая функция.

Итак, допустим, у нас есть эти две функции:

f (x) g (x) = 4×2 + 6x + 5 = 2x + 1

Если нас спросят f (g (x)), тогда наш ввод — это g (x), и нам нужно заменить каждый x в f (x) на g (x):

f (x) = 4 (x) 2 + 6 (x) +5

⬇️

f (g (x)) = 4 (g (x)) 2 + 6 (g (x)) + 5

И поскольку мы знаем, что g (x) = 2x + 1, мы можем упростить f (g (x)) следующим образом: используя 2x + 1 вместо g (x) справа:

f (g (x)) = 4 (2x + 1) 2 + 6 (2x + 1) +5

И вот как мы получаем f ( g (x))!

Вставка значения

Теперь, если нас просят ввести f (g (3)) вместо f (g (x)), тогда нам нужно выполнить еще один поиск и замену, чтобы заменить каждый x в нашем новом f (g (x)) уравнение с нашим входным значением 3:

f (g (x)) = 4 (2x + 1) 2 + 6 (2x + 1) +5

⬇️

f (g ( 3)) = 4 (2 (3) +1) 2 + 6 (2 (3) +1) +5

Тогда у нас есть все числа в правой части уравнения, и мы можем просто вычислить, чтобы найти окончательный результат. ответ f (g (3)) = 243.

Составление графиков функций

Вы можете получить функции в виде графиков, например:

В этом случае мы используем наши графики, чтобы найти композицию функций. Допустим, нас спрашивают f (g (1)).

Это означает, что сначала нам нужно найти, что такое g (1). Давайте посмотрим на наш график для g (x), где наш x = 1:

Глядя на точку на линии, где x = 1, мы видим, что значение y равно 2. Это означает, что g (1) = 2.

Теперь, если мы вернемся к нашей исходной композиции f (g (1)), мы можем заменить g (1) на 2, чтобы получить f (g (1)) = f (2).

Теперь мы просто смотрим на наш график f (x) в точке, где x = 2:

Глядя на точку на линии, где x = 2, мы видим, что значение y равно 4. Это означает, что f (2) = 4.

Итак, чтобы рассмотреть, чтобы решить для f (g (1)), нам сначала нужно было найти значение g (1). Как только мы обнаружили, что g (1) = 2, мы заменили g (1) на 2, чтобы получить:

f (g (1)) = f (2)

Глядя на график для f (x), мы находим:

f (g (1)) = f (2) = 4

Составление функций с помощью графиков

Допустим, мы ищем f (g (3)).

Шаг 1. Найдите внутреннее значение.

Сначала мы используем график для g (x), чтобы найти значение g (3).

Шаг 2: Вставьте внутреннее значение.

Затем мы вставляем найденное значение в композицию. Допустим, мы обнаружили, что наше значение было 2. Мы вставляем это в нашу композицию, чтобы заменить g (3), чтобы получить f (g (3)) = f (2).

Шаг 3: Найдите окончательное значение.

Наконец, мы используем график для f (x), чтобы найти значение f (2). Как только мы это сделаем, все готово!

8 Функции преподавания и обучения | Как студенты учатся: история, математика и естественные науки в классе

ПРИМЕЧАНИЯ

1.	Изучение функций, как мы определяем его здесь, в значительной степени пересекается с темой «алгебры», традиционно преподаваемой в Соединенных Штатах в девятом классе, хотя национальные стандарты и стандарты многих штатов теперь рекомендуют изучать аспекты алгебры в более ранних классах (поскольку делается в большинстве других стран). Хотя функции являются важной частью алгебры, другие аспекты алгебры, такие как решение уравнений, в этой главе не рассматриваются.
2.	Томас, 1972, стр. 17.
3.	Гольденберг, 1995; Leinhardt et al., 1990; Romberg et al., 1993. .
4.	Натан и Кёдингер, 2000.
5.	Кёдингер и Натан, 2004.
6.	Кёдингер и Натан, 2004.
7.	Koedinger et al., 1997.
8.	Кальчман, 2001.
9.	Schoenfeld et al., 1993.
10.	Schoenfeld et al., 1987.
11.	Schoenfeld et al., 1998, стр. 81.
12.	Chi et al., 1981.
13.	Chi et al., 1981; Schoenfeld et al., 1993.
14.	Кальчман, 2001.

ССЫЛКИ

Chi, M.T.H., Feltovich, P.J., and Glaser, R. (1981). Категоризация и представление физических задач специалистами и новичками. Когнитивная наука , 5 , 121-152.

Гольденберг, Э. (1995). Множественные представления: средство понимания.У Д. Перкинса, Дж. Шварца, М. Уэста и М. Виске (редакторы), Программное обеспечение идет в школу: обучение пониманию с помощью новых технологий (стр. 155-171). Нью-Йорк: Издательство Оксфордского университета.

Кальчман М. (2001). Использование неопиажеской основы для изучения и обучения математическим функциям . Докторская диссертация, Торонто, Онтарио, Университет Торонто.

Кёдингер, К.Р., и Натан, М.Дж. (2004). Реальная история проблем истории: влияние представлений на количественные рассуждения. Журнал обучающих наук , 13 (2).

Кёдингер, К.Р., Андерсон, Дж. Р., Хэдли, У. Х., и Марк, М. А. (1997). Интеллектуальное обучение идет в школу в большом городе. Международный журнал искусственного интеллекта в образовании , 8 , 30-43.

Лейнхардт Г., Заславский О. и Штейн М. (1990). Функции, графики и графики: задачи, обучение и обучение. Обзор исследований в области образования , 60 (1), 1-64.

Натан, М.Дж., и Кёдингер, К.Р. (2000). Убеждения учителей и исследователей о раннем развитии алгебры. Журнал исследований в области математического образования , 31 (2), 168-190.

Ромберг, Т., Феннема, Э., и Карпентер, Т. (1993). Интегрирующие исследования графического представления функций .

\(x\)	\(0\)	\(0.5\)	\(1\)	\(3\)	\(4\)
\(y\)	\(-1\)	−1715	−53	135	53