Построение графиков с модулями методом интервалов — ЗФТШ, МФТИ
Если нужно построить график функции вида y=f(|x−a1|,y = f(|x − a_1|,|x−a2|,…,|x−an|)|x − a_2|,…,|x − a_n|), где a1,a_1,a2,…,ana_2,…,a_n – некоторые фиксированные числа, то в общем случае нет иного подхода, помимо раскрытия всех модулей. Ясно, что для всякого k=1,2,3,…,nk = 1, 2, 3,…, n
|x-ak|=|x — a_k| =x-ak=x-ak, если x ≥ak;ak-x, если x<ak.\left|x-a_k\right|=\left\{\begin{array}{l}x-a_k,\;\mathrm{если}\;x\;\geq a_k;\\a_k-x,\;\mathrm{если}\;x<a_k.\end{array}\right.
Однако, например, в случае a1<a2a_1 < a_2 невозможно выполнение одновременно двух условий: x<a1x < a_1 и x>a2x > a_2. Поэтому простое раскрытие модулей приведет к лишним действиям. Чтобы этого избежать, применяют так называемый метод интервалов. Суть его состоит в следующем. Числа a1a_1, a2,…,ana_2,…, a_n упорядочивают по неубыванию и наносят на числовую ось (рис. 35). Если для определённости положить a1<a2<⋯<ana_1 < a_2 < ⋯ < a_n, то это будет выглядеть так:
Получаем, что числовая ось разбивается на n+1n + 1 интервалов. Если xx лежит в любом из них, то мы однозначно можем определить знаки всех выражений под модулями и раскрыть модули. В каждом из получившихся интервалов график функции выстраивается отдельно. Граничную точку (a1,a2,…,an)(a_1, a_2,…, a_n) можно включать в любой из промежутков, концом которого она является. Проиллюстрируем этот алгоритм на примере.
Если xx лежит в любом из них, то мы однозначно можем определить знаки всех выражений под модулями и раскрыть модули. В каждом из получившихся интервалов график функции выстраивается отдельно. Граничную точку (a1,a2,…,an)(a_1, a_2,…, a_n) можно включать в любой из промежутков, концом которого она является. Проиллюстрируем этот алгоритм на примере.
Перед тем как перейти к нахождению наименьшего значения, сделаем небольшое теоретическое отступление.
С помощью графиков удобно исследовать функции на возрастание и убывание. Функцию y=f(x)y = f(x) называют строго возрастающей, если f(x1)<f(x2)f(x_1) < f(x_2) при x1<x2x_1 < x_2. Строго убывающие функции определяются неравенством f(x1)>f(x2)f(x_1) > f(x_2) при x1<x2x_1 < x_2. Если при x1<x2x_1 < x_2 верно f(x1)≤f(x2)f(x_1) ≤ f(x_2), то функцию y=f(x)y = f(x) называют возрастающей, а если f(x2)≤f(x1)f(x_2) ≤ f(x_1), то – убывающей. Для линейных функций признаком возрастания и убывания является знак коэффициента при хх. Если этот коэффициент отрицателен, то такая функция строго убывает на данном интервале. В случае положительности коэффициента функция строго возрастает. Таким образом, можно сделать такой вывод.
Если этот коэффициент отрицателен, то такая функция строго убывает на данном интервале. В случае положительности коэффициента функция строго возрастает. Таким образом, можно сделать такой вывод.
Характер возрастания (возрастание или убывание) функции вида
f(x)=c1|x−a1|+c2|x−a2|+ …+cn|x−an|f(x) = c_1|x − a_1| + c_2|x − a_2| + … + c_n|x − a_n|,
может меняться только в точках x=a1,a2,…,anx = a_1, a_2,…, a_n (здесь a1≤a2≤…≤ana_1 ≤ a_2 ≤ … ≤ a_n, а c1c_1, c2,…,cnc_2,…, c_n – некоторые числа). Поэтому для нахождения наибольшего или наименьшего значения функции такого вида стoит обратить внимание на то, возрастает или убывает такая функция при x<a1x < a_1 и x>anx > a_n, а также сравнить значения функции ff в точках x=a1,a2,…,anx = a_1, a_2,…, a_n.
Возвращаемся к нашей задаче.
Похожую схему рассуждений можно применить и в задачах следующего типа.
Графики: исследование, построение, алгоритм OTUS
Если нужно построить график некой заданной функции, не обойтись без предварительного исследования этой функции, причем полного.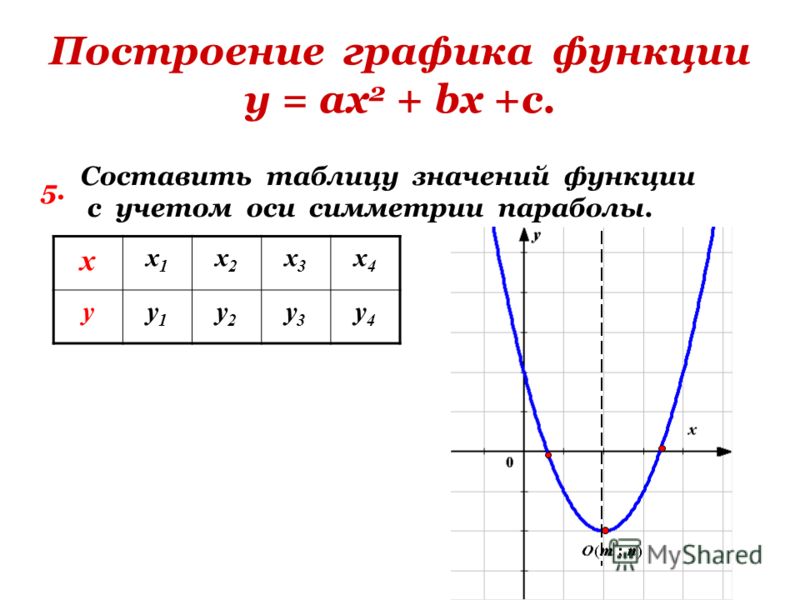 И только потом, применяя полученные данные, можно построить правильный график. На практике построение бывает как отдельной задачей, так и задачей, связанной с графикой (вспомогательной задачей), то есть в последнем случае речь идет о решении уравнений графическим методом. Именно поэтому надо понимать, как происходит исследование и построение.
И только потом, применяя полученные данные, можно построить правильный график. На практике построение бывает как отдельной задачей, так и задачей, связанной с графикой (вспомогательной задачей), то есть в последнем случае речь идет о решении уравнений графическим методом. Именно поэтому надо понимать, как происходит исследование и построение.
Вся работа по исследованию функции и построению выполняется поэтапно, то есть существует алгоритм построения графика функции. Если следовать этому алгоритму, вероятность ошибки будет сведена к минимуму.
Для исследования возьмем функцию y = f(x). Пошаговая реализация алгоритма выглядит следующим образом:
- Нахождение области определения функции D(f). Речь идет об определении интервалов, на которых эта function существует.
- Определение четности или нечетности. Когда область определения симметрична относительно нуля (для любого значения x из D(f) значение -x тоже принадлежит области определения), надо выполнить проверку на четность.
 К примеру, когда f(-x) является равной f(x), функция четная (классическая функция вида y = x 2 является четной). Важное значение имеет факт того, что график четной функции является симметричным относительно оси OY. А вот если f(-x) равняется -f(x), следует говорит о нечетности (для примера нечетности можно вспомнить y = x3). В этом случае график симметричен относительно начала координат. Когда функцию считают четной либо нечетной, есть возможность построить часть ее графика для x ⩾ 0, а потом отразить ее соответствующим образом.
К примеру, когда f(-x) является равной f(x), функция четная (классическая функция вида y = x 2 является четной). Важное значение имеет факт того, что график четной функции является симметричным относительно оси OY. А вот если f(-x) равняется -f(x), следует говорит о нечетности (для примера нечетности можно вспомнить y = x3). В этом случае график симметричен относительно начала координат. Когда функцию считают четной либо нечетной, есть возможность построить часть ее графика для x ⩾ 0, а потом отразить ее соответствующим образом. - Нахождение точек пересечения с осями координат. Речь идет о точках пересечения графика функции y = f(x) с OX — осью абсцисс. Чтобы это сделать, надо решить уравнение f(x) = 0. Корни данного уравнения будут абсциссами точек пересечения графика с осью ОХ. Чтобы найти точку пересечения графика с OY (осью ординат) надо найти значение функции при x = 0.

- Нахождение промежутков знакопостоянства. Следующий важный шаг. Здесь надо найти промежутки, на которых наша ф-я сохраняет знак. Это потребуется в дальнейшем в целях контроля правильности построения нашего графика. Для обнаружения промежутков знакопостоянства надо решить такие неравенства, как f(x) > 0 и f(x) < 0.
- Поиск асимптот. Асимптота — прямая, к которой приближается график функции, делая это бесконечно близко. Бывают горизонтальные асимптоты, вертикальные асимптоты, наклонные асимптоты. Подробнее на эту тему читайте здесь.
- Нахождение периода функции (утверждение справедливо для периодических функций). Также стоит добавить, что если ф-я тригонометрическая, то надо сначала определить, является ли она периодической либо нет.
- Исследование с помощью производной. Исследование заключается в поиске промежутков убывания и возрастания и поиске точек экстремума (точек минимума и максимума).
 Это делается следующим образом:
Это делается следующим образом:
а) ищем производную функции f(x);
б) второй этап — приравнивание производной к нулю с нахождением корней уравнения f(x) = 0 — в данном случае это стационарные точки;
в) третий шаг — найти промежутки знакопостоянства производной.
Промежутки, где производная является положительной, — это промежутки возрастания, где она отрицательна — убывания.
Точки, где производная меняет знак с «+» на «-» — точки максимума, если же с минуса на плюс — это точки минимума.
8. Последний шаг алгоритма — поиск точек перегиба и промежутков вогнутости и выпуклости. Эта тема неплохо рассмотрена вот в этой статье.
Надеемся, что материал был полезен, и у вас не возникнет проблем с построением графиков. И не забывайте, что математика может быть очень полезна в IT-сфере, особенно в Data Science. Если же вы чувствуете, что нужно повторить свои знания по математике, обратите внимание на соответствующий курс в OTUS:
Если же вы чувствуете, что нужно повторить свои знания по математике, обратите внимание на соответствующий курс в OTUS:
Источники:
- https://ege-ok.ru/2013/11/12/issledovanie-funktsii-i-postroenie-grafika;
- https://www.matburo.ru/ex_ma.php?p1=maissl;
- http://matecos.ru/mat/matematika/issledovanie-funktsii-i-postroenie-grafika-funktsii.html.
R Несколько графиков с использованием функции par()
В этой статье вы научитесь использовать функцию par() для размещения нескольких графиков на одном графике путем передачи графических параметров mfrow и mfcol.
Иногда нам нужно разместить два или более графиков на одном графике.
Функция Чт пар()
Мы можем разместить несколько графиков на одном графике, установив некоторые графические параметры с помощью функции par() . Программирование на R имеет множество графических параметров, которые управляют отображением наших графиков.
Функция par() помогает нам в установке или запросе этих параметров. Например, вы можете посмотреть все параметры и их значения, вызвав функцию без каких-либо аргументов.
>пар() $xlog [1] ЛОЖЬ ... $yaxt [1] "с" $ylbias [1] 0,2
Вы увидите длинный список параметров, и чтобы узнать, что каждый из них делает, вы можете проверить раздел справки
Графический параметр mfrow можно использовать для указания количества необходимых нам подзаголовков.
Он принимает вектор формы c(m, n) , который делит данный график на массив m*n подграфиков. Например, если нам нужно построить два графика рядом, у нас будет m=1 и n=2 . Следующий пример иллюстрирует это.
>max.temp # вектор, используемый для построения графика вс пн вт вр чт пт сб 22 27 26 24 23 26 28 par(mfrow=c(1,2)) # установить область построения в виде массива 1*2 барплот (max.temp, main="барплот") круговая диаграмма (max.temp, main="Piechart", radius=1)
Этого же явления можно добиться с помощью графического параметра mfcol .
Единственная разница между ними заключается в том, что mfrow заполняет область подграфика по строкам, а mfcol заполняет ее по столбцам.
Температура <- качество воздуха$Temp Озон <- качество воздуха$Озон номинал (mfrow = c (2,2)) история (температура) boxplot (температура, по горизонтали = ИСТИНА) история (озон) коробчатая диаграмма (озон, по горизонтали = ИСТИНА)
Тот же участок с изменением par(mfcol = c(2, 2)) будет выглядеть следующим образом. Обратите внимание, что отличается только порядок подзаговора.
Более точное управление
Графический параметр рис позволяет точно контролировать положение фигуры на графике.
Нам нужно предоставить координаты в нормализованной форме как c(x1, x2, y1, y2) . Например, вся площадь графика будет равна
Например, вся площадь графика будет равна c(0, 1, 0, 1)
(x1, y1) = (0, 0) будет левым нижним углом, а (x2, y2) = (1, 1) — правый верхний угол. Примечание: мы использовали параметры cex для уменьшения размера меток и mai для определения полей.
# сделать метки и поля меньше номинал (cex = 0,7, mai = c (0,1, 0,1, 0,2, 0,1)) Температура <- качество воздуха$Temp # определить область для гистограммы пар(рис=с(0,1,0,7,0,3,0,9)) история (температура) # определить область для boxplot пар(рис=с(0.8,1,0,1), новый=ИСТИНА) блочная диаграмма (температура) # определяем область для ленточной диаграммы пар(рис=с(0,1,0,67,0,1,0,25), новый=ИСТИНА) полосовая диаграмма (температура, метод = "дрожание")
Числа, присвоенные fig , были получены методом проб и ошибок, чтобы добиться наилучшего вида графика.
- ПРЕДЫДУЩАЯ
Ч Функция графика - СЛЕДУЮЩИЙ
Сохранение участка в R
Домашняя страница PLplot — основная
Введение
PLplot — это кроссплатформенный программный пакет для создания научных графиков, графические символы и текст которого (UTF-8) на практике ограничены только тем, какие системные шрифты с поддержкой Unicode установлены на компьютере. компьютер пользователя. Программное обеспечение PLplot, которое в основном распространяется под лицензией LGPL, имеет чистую архитектуру, которая организована как основная библиотека C, отдельные языковые привязки для этой библиотеки и отдельные драйверы устройств, которые динамически загружаются основной библиотекой и управляют графиками. представлены в неинтерактивных и интерактивных графических контекстах.
компьютер пользователя. Программное обеспечение PLplot, которое в основном распространяется под лицензией LGPL, имеет чистую архитектуру, которая организована как основная библиотека C, отдельные языковые привязки для этой библиотеки и отдельные драйверы устройств, которые динамически загружаются основной библиотекой и управляют графиками. представлены в неинтерактивных и интерактивных графических контекстах.
Основную библиотеку PLplot можно использовать для создания стандартных графиков x-y, полулогарифмических графиков, графиков логарифмического формата, контурных графиков, трехмерных графиков поверхности, сетчатых графиков, гистограмм и круговых диаграмм. Несколько графиков (одинаковых или разных размеров) могут быть размещены на одной странице, и разрешено несколько страниц для тех форматов устройств, которые их поддерживают.
В базовой библиотеке PLplot поддерживаются графические символы и текст, указанные
пользователь в кодировке UTF-8 Unicode. Это означает для многих наших
Устройства с поддержкой Unicode, отображающие символы и текст, ограничены только
коллекция глифов, обычно доступных через установленную систему
шрифты. Кроме того, большое количество наших устройств, поддерживающих Unicode, также
поддержка сложных языков разметки текста (CTL), таких как арабский, иврит,
а также индийские и производные от них CTL-сценарии, такие как деванагари, тайский, лаосский,
и тибетский. Таким образом, для этих устройств PLplot практически любой язык
который поддерживается Unicode, и установленные системные шрифты могут использоваться для
участки с метками.
Кроме того, большое количество наших устройств, поддерживающих Unicode, также
поддержка сложных языков разметки текста (CTL), таких как арабский, иврит,
а также индийские и производные от них CTL-сценарии, такие как деванагари, тайский, лаосский,
и тибетский. Таким образом, для этих устройств PLplot практически любой язык
который поддерживается Unicode, и установленные системные шрифты могут использоваться для
участки с метками.
Обзор функций
Кроссплатформенность
В настоящее время известно, что PLplot работает на следующих платформах:
- Linux, Mac OS X и другие Unices
- MSVC IDE в версии Microsoft Windows (Windows 2000 и более поздние версии)
- Cygwin в версии Microsoft Windows
- MinGW-w64/MSYS2 в версии Microsoft Windows
Для каждой из вышеперечисленных платформ PLplot можно собрать из исходного кода, а для платформ Linux и Mac OS X доступны сторонние бинарные пакеты для PLplot.
Языковые привязки
В настоящее время языковые привязки библиотеки C PLplot следующие:
- Ада
- С++
- Д
- Фортран
- Ява
- Лисп
- Луа
- OCaml
- Октава
- Перл/PDL
- Питон
- Ткл/Тк
Форматы выходных файлов
Драйверы устройств PLplot поддерживают несколько форматов файлов печати.
 К примеру, когда f(-x) является равной f(x), функция четная (классическая функция вида y = x 2 является четной). Важное значение имеет факт того, что график четной функции является симметричным относительно оси OY. А вот если f(-x) равняется -f(x), следует говорит о нечетности (для примера нечетности можно вспомнить y = x3). В этом случае график симметричен относительно начала координат. Когда функцию считают четной либо нечетной, есть возможность построить часть ее графика для x ⩾ 0, а потом отразить ее соответствующим образом.
К примеру, когда f(-x) является равной f(x), функция четная (классическая функция вида y = x 2 является четной). Важное значение имеет факт того, что график четной функции является симметричным относительно оси OY. А вот если f(-x) равняется -f(x), следует говорит о нечетности (для примера нечетности можно вспомнить y = x3). В этом случае график симметричен относительно начала координат. Когда функцию считают четной либо нечетной, есть возможность построить часть ее графика для x ⩾ 0, а потом отразить ее соответствующим образом.
 Это делается следующим образом:
Это делается следующим образом: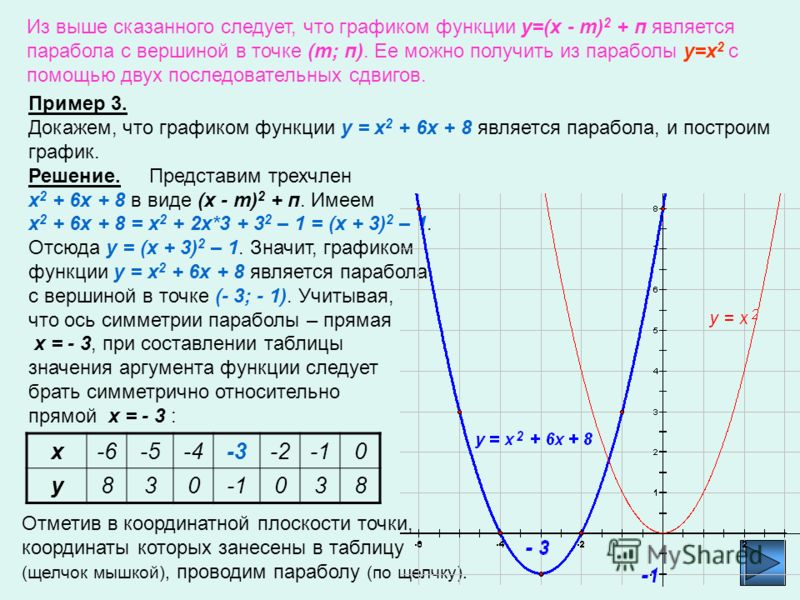 temp, main="барплот")
круговая диаграмма (max.temp, main="Piechart", radius=1)
temp, main="барплот")
круговая диаграмма (max.temp, main="Piechart", radius=1)
Ваш комментарий будет первым