Построение графика квадратного уравнения с двумя переменными. Как построить график уравнения. Преимущества построения графиков онлайн
На этом уроке мы подробно рассмотрим построение графиков уравнений. Вначале вспомним, что такое рациональное уравнение и множество его решений, образующее график уравнения. Подробно рассмотрим график линейного уравнения и свойства линейной функции, научимся читать графики. Далее рассмотрим график квадратного уравнения и свойства квадратичной функции. Рассмотрим гиперболическую функцию и ее график и график уравнения окружности. Далее перейдем к построению и изучению совокупности графиков.
Тема: Системы уравнений
Урок: Графики уравнений
Мы рассматриваем рациональное уравнение вида и системы рациональных уравнений вида
Мы говорили, что каждое уравнение в этой системе имеет свой график, если конечно имеются решения уравнений. Мы рассмотрели несколько графиков различных уравнений.
Сейчас мы систематически рассмотрим каждое из известных нам уравнений, т.е. выполним обзор по графикам уравнений
1. Линейное уравнение с двумя переменными
x, y — в первой степени; a,b,c — конкретные числа.
Пример:
Графиком этого уравнения является прямая линия.
Мы действовали равносильными преобразованиями — y оставили на месте, всё остальное перенесли в другую сторону с противоположными знаками. Исходное и полученное уравнения равносильны, т.е. имеют одно и то же множество решений. График этого уравнения мы умеем строить, и методика его построения такова: находим точки пересечения с координатными осями и по ним строим прямую.
В данном случае
Зная график уравнения, мы можем многое сказать о решениях исходного уравнения, а именно: если сли
Эта функция возрастает, т.е. с увеличением x увеличивается y. Мы получили два частных решения, а как записать множество всех решений?
Если точка имеет абсциссу x, то ордината этой точки
Значит, чисел
У нас было уравнение, мы построили график, нашли решения.
Это рациональное уравнение,
Найдем y, равносильными преобразованиями получаем
Положим и получаем квадратичную функцию, ее график нам известен.
Пример: Построить график рационального уравнения.
Графиком является парабола, ветви направлены вверх.
Найдем корни уравнения:
Схематически изобразим график (Рис. 2).
С помощью графика мы получаем всевозможные сведения и о функции, и о решениях рационального уравнения. Мы определили промежутки знакопостоянства, теперь найдем координаты вершины параболы.
У уравнения бесчисленное множество решений, т.е. бесчисленное множество пар , удовлетворяющих уравнению, но все А каким может быть x? Любым!
Если мы зададим любое x, то получим точку
Решением исходного уравнения является множество пар
3. Построить график уравнения
Необходимо выразить y. Рассмотрим два варианта.
Графиком функции является гипербола, функция не определена при
Функция убывающая.
Если мы возьмем точку с абсциссой , то ее ордината будет равна
Решением исходного уравнения является множество пар
Построенную гиперболу можно сдвигать относительно осей координат.
Например, график функции — тоже гипербола — будет сдвинут на единицу вверх по оси ординат.
4. Уравнение окружности
Это рациональное уравнение с двумя переменными. Множеством решений являются точки окружности. Центр в точке радиус равен R (Рис. 4).
Рассмотрим конкретные примеры.
a.
Приведем уравнение к стандартному виду уравнения окружности, для этого выделим полный квадрат суммы:
— получили уравнение окружности с центром в .
Построим график уравнения (Рис. 5).
b. Построить график уравнения
Вспомним, что произведение равно нулю тогда и только тогда, когда один из сомножителей равен нулю, а второй существует.
График заданного уравнения состоит из совокупности графиков первого и второго уравнений, т.е. двух прямых.
Построим его (Рис. 6).
Построим график функции Прямая будет проходить через точку (0; -1). Но как она пройдет — будет возрастать или убывать? Определить это нам поможет угловой коэффициент, коэффициент при x, он отрицательный, значит функция убывает. Найдем точку пересечения с осью ox, это точка (-1; 0).
Аналогично строим график второго уравнения. Прямая проходит через точку (0; 1), но возрастает, т.к. угловой коэффициент положителен.
Координаты всех точек двух построенных прямых и являются решением уравнения.
Итак, мы проанализировали графики важнейших рациональных уравнений, они будут использоваться и в графическом методе и в иллюстрации других методов решения систем уравнений.
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. — М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
1. Раздел College.ru по математике ().
2. Интернет-проект «Задачи» ().
3. Образовательный портал «РЕШУ ЕГЭ» ().
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 95-102.
Пусть задано уравнение с двумя переменными F(x; y) . Вы уже познакомились со способами решения таких уравнений аналитически. Множество решений таких уравнений можно представить и в виде графика.
Графиком уравнения F(x; y) называют множество точек координатной плоскости xOy, координаты которых удовлетворяют уравнению.
Для построения графика уравнения с двумя переменными сначала выражают в уравнении переменную y через переменную x.
Наверняка вы уже умеете строить разнообразные графики уравнений с двумя переменными: ax + b = c – прямая, yx = k – гипербола, (x – a) 2 + (y – b) 2 = R 2 – окружность, радиус которой равен R, а центр находится в точке O(a; b).
Пример 1.
Построить график уравнения x 2 – 9y 2 = 0.
Решение.
Разложим на множители левую часть уравнения.
(x – 3y)(x+ 3y) = 0, то есть y = x/3 или y = -x/3.
Ответ: рисунок 1.
Особое место занимает задание фигур на плоскости уравнениями, содержащими знак абсолютной величины, на которых мы подробно остановимся. Рассмотрим этапы построения графиков уравнений вида |y| = f(x) и |y| = |f(x)|.
Первое уравнение равносильно системе
{f(x) ≥ 0,
{y = f(x) или y = -f(x).
То есть его график состоит из графиков двух функций: y = f(x) и y = -f(x), где f(x) ≥ 0.
Для построения графика второго уравнения строят графики двух функций: y = f(x) и y = -f(x).
Пример 2.
Построить график уравнения |y| = 2 + x.
Решение.
Заданное уравнение равносильно системе
{x + 2 ≥ 0,
{y = x + 2 или y = -x – 2.
Строим множество точек.
Ответ: рисунок 2.
Пример 3.
Построить график уравнения |y – x| = 1.
Решение.
Если y ≥ x, то y = x + 1, если y ≤ x, то y = x – 1.
Ответ: рисунок 3.
При построении графиков уравнений, содержащих переменную под знаком модуля, удобно и рационально использовать метод областей , основанный на разбиении координатной плоскости на части, в которых каждое подмодульное выражение сохраняет свой знак.
Пример 4.
Построить график уравнения x + |x| + y + |y| = 2.
В данном примере знак каждого подмодульного выражения зависит от координатной четверти.
1) В первой координатной четверти x ≥ 0 и y ≥ 0. После раскрытия модуля заданное уравнение будет иметь вид:
2x + 2y = 2, а после упрощения x + y = 1.
2) Во второй четверти, где x
3) В третьей четверти x
4) В четвертой четверти, при x ≥ 0, а y
График данного уравнения будем строить по четвертям.
Ответ: рисунок 4.
Пример 5.
Изобразить множество точек, у которых координаты удовлетворяют равенству |x – 1| + |y – 1| = 1.
Решение.
Нули подмодульных выражений x = 1 и y = 1 разбивают координатную плоскость на четыре области. Раскроем модули по областям. Оформим это в виде таблицы.
| Область | Знак подмодульного выражения | Полученное уравнение после раскрытия модуля |
| I | x ≥ 1 и y ≥ 1 | x + y = 3 |
| II | x | -x + y = 1 |
| III | x | x + y = 1 |
| IV | x ≥ 1 и y | x – y = 1 |
Ответ: рисунок 5.
На координатной плоскости фигуры могут задаваться и неравенствами .
Графиком неравенства с двумя переменными называется множество всех точек координатной плоскости, координаты которых являются решениями этого неравенства.
Рассмотрим алгоритм построения модели решений неравенства с двумя переменными :
- Записать уравнение, соответствующее неравенству.
- Построить график уравнения из пункта 1.
- Выбрать произвольную точку в одной из полуплоскостей. Проверить, удовлетворяют ли координаты выбранной точки данному неравенству.
- Изобразить графически множество всех решений неравенства.
Рассмотрим, прежде всего, неравенство ax + bx + c > 0. Уравнение ax + bx + c = 0 задает прямую, разбивающую плоскость на две полуплоскости. В каждой из них функция f(x) = ax + bx + c сохраняет знак. Для определения этого знака достаточно взять любую точку, принадлежащую полуплоскости, и вычислить значение функции в этой точке. Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.
Рассмотрим примеры графического решения наиболее часто встречающихся неравенств с двумя переменными.
1) ax + bx + c ≥ 0. Рисунок 6 .
2) |x| ≤ a, a > 0. Рисунок 7 .
3) x 2 + y 2 ≤ a, a > 0. Рисунок 8 .
4) y ≥ x 2 . Рисунок 9.
5) xy ≤ 1. Рисунок 10.
Если у вас появились вопросы или вы хотите попрактиковаться изображать на плоскости модели множества всех решений неравенств с двумя переменными с помощью математического моделирования, вы можете провести бесплатное 25-минутное занятие с онлайн репетитором после того, как зарегистрируетесь . Для дальнейшей работы с преподавателем у вас будет возможность выбрать подходящий для вас тарифный план.
Остались вопросы? Не знаете, как изобразить фигуру на координатной плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Линейное уравнение с двумя переменными — любое уравнение, которое имеет следующий вид: a*x + b*y =с . Здесь x и y есть две переменные, a,b,c — некоторые числа.
Здесь x и y есть две переменные, a,b,c — некоторые числа.
Решением линейного уравнения a*x + b*y = с, называется любая пара чисел (x,y) которая удовлетворяет этому уравнению, то есть обращает уравнение с переменными x и y в верное числовое равенство. Линейное уравнение имеет бесконечное множество решений.
Если каждую пару чисел, которые являются решением линейного уравнения с двумя переменными, изобразить на координатной плоскости в виде точек, то все эти точки образуют график линейного уравнения с двумя переменными. Координатами точками будут служить наши значения x и у. При этом значение х будет являться абсциссой, а значение у — ординатой.
График линейного уравнения с двумя переменными
Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения. Несложно догадаться, что график будет представлять собой прямую линию. Поэтому такие уравнения и называются линейными.
Алгоритм построения
Алгоритм построения графика линейного уравнения с двумя переменным.
1. Начертить координатные оси, подписать их и отметить единичный масштаб.
2. В линейном уравнении положить х = 0, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
3. В линейном уравнении в качестве у взять число 0, и решить полученное уравнение относительно х. Отметить полученную точку на графике
4. При необходимости взять произвольное значение х, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
5. Соединить полученные точки, продолжить график за них. Подписать получившуюся прямую.
Пример: Построить график уравнения 3*x — 2*y =6;
Положим х=0, тогда — 2*y =6; y= -3;
Положим y=0, тогда 3*x = 6; x=2;
Отмечаем полученные точки на графике, проводим через них прямую и подписываем её. Посмотрите на рисунок ниже, график должен получиться именно таким.
Прямоугольная система координат это пара перпендикулярных координатных линий, называемых осями координат, которые размещены так, что они пересекаются в их начале.
Обозначение координатных осей буквами х и у является общепринятым, однако буквы могут быть любые. Если используются буквы х и у, то плоскость называется xy-плоскость . В различных приложениях могут применяться отличные от букв x и y буквы, и как показано с нижерасположенных рисунках, есть uv-плоскости и ts-плоскости .
Упорядоченная пара
Под упорядоченной парой действительных чисел мы имеем в виду два действительных чисел в определённом порядке. Каждая точка P в координатной плоскости может быть связана с уникальной упорядоченной парой действительных чисел путём проведения двух прямых через точку P: одну перпендикулярно оси Х, а другую — перпендикулярно оси у.
Например, если мы возьмём (a,b)=(4,3), тогда на координатной полоскости
Построить точку Р(a,b) означает определить точку с координатами (a,b) на координатной плоскости. Например, различные точки построены на рисунке внизу.
В прямоугольной системе координат оси координат делят плоскость на четыре области, называемые квадрантами. Они нумеруются против часовой стрелки римскими цифрами, как показано на рисунке
Определение графика
Графиком уравнения с двумя переменными х и у, называется множество точек на ху-плоскости, координаты которых являются членами множества решений этого уравнения
Пример: нарисовать график y = x 2
Из-за того, что 1/x не определено, когда x=0, мы можем построить только точки, для которых x ≠0
Пример: Найдите все пересечения с осями
(a) 3x + 2y = 6
(b) x = y 2 -2y
(c) y = 1/x
Пусть y = 0, тогда 3x = 6 or x = 2
является искомой точкой пересечения оси x.
Установив, что х=0, найдем что точкой пересечения оси у является точка у=3.
Таким эе образом вы можете решить уравнение (b), а решения для (c) приведено ниже
x-пересечение
Пусть y = 0
1/x = 0 => x не может быть определено, то есть нет пересечения с осью у
Пусть x = 0
y = 1/0 => y также не определено, => нет пересечения с осью y
На рисунке внизу точки (x,y), (-x,y),(x,-y) и (-x,-y) обозначают углы прямоугольника.
График симметричен относительно оси х, если для каждой точки (x,y) графика, точка (x,-y) есть также точкой на графике.
График симметричен относительно оси y, если для каждой точки графика (x,y) точка (-x,y) также принадлежит графику.
График симметричен относительно центра координат, если для каждой точки (x,y) графика, точка (-x,-y) также принадлежит этому графику.
Определение:
График функции на координатной плоскости определяется как график уравнения y = f(x)
Постройте график f(x) = x + 2
Пример 2. Постройте график f(x) = |x|
График совпадает с линией y = x для x> 0 и с линией y = -x
для x
graph of f(x) = -x
Соединяя эти два графика, мы получаем
график f(x) = |x|
Пример 3. Постройте график
t(x) = (x 2 — 4)/(x — 2) =
= ((x — 2)(x + 2)/(x — 2)) =
= (x + 2) x ≠ 2
Следовательно, эта функция может быть записана в виде
y = x + 2 x ≠ 2
График h(x)= x 2 — 4 Or x — 2
график y = x + 2 x ≠ 2
Пример 4. Постройте график
Графики функций с перемещением
Предположим, что график функции f(x) известен
Тогда мы можем найти графики
y = f(x) + c — график функции f(x), перемещённый
ВВЕРХ на c значений
y = f(x) — c — график функции f(x), перемещённый
ВНИЗ на c значений
y = f(x + c) — график функции f(x), перемещённый
ВЛЕВО на c значений
y = f(x — c) — график функции f(x), перемещённый
Вправо на c значений
Пример 5. Постройте
график y = f(x) = |x — 3| + 2
Переместим график y = |x| на 3 значения ВПРАВО, чтобы получить график
Переместим график y = |x — 3| на 2 значения ВВЕРХ, чтобы получить график y = |x — 3| + 2
Постройте график
y = x 2 — 4x + 5
Преобразуем заданное уравнение следующим образом, прибавив к обеим частям 4:
y + 4 = (x 2 — 4x + 5) + 4 y = (x 2 — 4x + 4) + 5 — 4
y = (x — 2) 2 + 1
Здесь мы видим, что этот график может быть получен перемещением графика y = x 2 вправо на 2 значения, потому что x — 2, и вверх на 1 значение, потому что +1.
y = x 2 — 4x + 5
Отражения
(-x, y) есть отражением (x, y) относительно оси y
(x, -y) есть отражением (x, y) относительно оси x
Графики y = f(x) и y = f(-x) являются отражением друг друга относительно оси y
Графики y = f(x) и y = -f(x) являются отражением друг друга относительно оси x
График может быть получен отражением и перемещением:
Нарисуйте график
Найдём его отражение относительно оси y, и получим график
Переместим этот график вправо на 2 значения и получим график
Вот искомый график
Если f(x) умножена на положительною постояную c, то
график f(x) сжимается по вертикали, если 0
график f(x) растягивается по вертикали, если c > 1
Кривая не является графиком y = f(x) для любой функции f
График линейного уравнения с двумя переменными: алгоритм построения
Линейное уравнение с двумя переменными — любое уравнение, которое имеет следующий вид: a*x + b*y =с. Здесь x и y есть две переменные, a,b,c – некоторые числа.
Решением линейного уравнения a*x + b*y = с , называется любая пара чисел (x,y) которая удовлетворяет этому уравнению, то есть обращает уравнение с переменными x и y в верное числовое равенство. Линейное уравнение имеет бесконечное множество решений.
Если каждую пару чисел, которые являются решением линейного уравнения с двумя переменными, изобразить на координатной плоскости в виде точек, то все эти точки образуют график линейного уравнения с двумя переменными. Координатами точками будут служить наши значения x и у. При этом значение х будет являться абсциссой, а значение у – ординатой.
График линейного уравнения с двумя переменными
Графиком линейного уравнения с двумя переменными называется множество всевозможных точек координатной плоскости, координаты которых будут являться решениями этого линейного уравнения. Несложно догадаться, что график будет представлять собой прямую линию. Поэтому такие уравнения и называются линейными.
Поэтому такие уравнения и называются линейными.
Алгоритм построения
Алгоритм построения графика линейного уравнения с двумя переменным.
1. Начертить координатные оси, подписать их и отметить единичный масштаб.
2. В линейном уравнении положить х = 0, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
3. В линейном уравнении в качестве у взять число 0, и решить полученное уравнение относительно х. Отметить полученную точку на графике
4. При необходимости взять произвольное значение х, и решить полученное уравнение относительно у. Отметить полученную точку на графике.
5. Соединить полученные точки, продолжить график за них. Подписать получившуюся прямую.
Пример: Построить график уравнения 3*x – 2*y =6;
Положим х=0, тогда – 2*y =6; y= -3;
Положим y=0, тогда 3*x = 6; x=2;
Отмечаем полученные точки на графике, проводим через них прямую и подписываем её. Посмотрите на рисунок ниже, график должен получиться именно таким.
Нужна помощь в учебе?
Предыдущая тема: Линейное уравнение с двумя переменными: решение и свойства
Следующая тема:   Системы линейных уравнений с двумя переменными
Креативный урок алгебры в 9-м классе по теме «Графики уравнений, содержащих символ модуля»
Тема урока: Графики уравнений, содержащих символ модуля.
Предмет: алгебра.
Тип урока: комбинированный.
Рис. 1. Блок-схема урока
Продолжительность занятия: 90 минут.
Главная дидактическая цель урока: выявление области приложения темы «График уравнения» в алгебре и в её связи с геометрией, формирование знаний по данной теме при решении стандартных и нестандартных алгебраических задач. Развитие у учащихся навыков исследовательской работы.
Развитие у учащихся навыков исследовательской работы.
Цели урока:
- Формирование умений распознавать стандартные задачи в различных формулировках.
- Формирование способности к интеграции знаний из различных тем курса математики.
- Содействовать развитию логического мышления учащихся, умение выделять главное, обобщать.
- Формирование исследовательской, креативной работы учащихся.
- Воспитание графической культуры учащихся.
- Совершенствование коммуникативной культуры учащихся.
Оборудование: доска, мультимедийное оборудование, раздаточный дидактический материал для учащихся.
План урока
1. Блок мотивации. Изучая темы «Графики функций» и «Векторы», мы обнаруживаем тесную связь геометрии и алгебры, и, естественно, возникает вопрос – нельзя ли геометрические фигуры такие как квадрат, прямоугольник, ромб, треугольник задавать алгебраическими уравнениями и иследовать свойства этих фигур алгебраическими методами. Выявлению этой связи между геометрией и алгеброй и будет посвящён урок. Мы введём новое понятие «График уравнения» и рассмотрим графики уравнений в алгебраических и графических задачах. (3 мин.)
2. Блок творческого разогрева. Повторение определения функции и графика функции. Обсуждение необходимости введения понятия «График уравнения».
Устная работа (20 мин.)
Актуализация знаний учащихся: повторение, анализ, обобщение.
Работа учащихся в следующих режимах: диалог, обсуждение, самостоятельная деятельность.
Материалы для проведения устной работы оформлены на доске.
Повторение определения функции и графика функции.
На доске представлены следующие чертежи (Рис. 2).
Каждый ученик получает раздаточный материал с этими чертежами.
Обсуждение:
1) На каких чертежах представлены графики функций? Почему?
2) Графики каких функций представлены на этих чертежах?
3) На каких чертежах графики не задают функции? Почему?
Обсуждается необходимость введения понятия графика уравнения.
Определение: Графиком уравнения называют множество точек координатной плоскости, координаты которых удовлетворяют заданному уравнению.
Рис. 2. 3. Теоретический блок 1. Изображение множества точек, координаты которых удовлетворяют заданным условиям. Ведущие идеи: симметрия, сдвиг графика уравнения (Рис. 3).Рис. 3.
Обсуждается наилучший способ построения графика этого уравнения.
Варианты:
1. Решить задачу “в лоб”: раскрыть модули в четырёх случаях:
3. Замечаем, что переменные
входят в уравнение симметрично.
Так как, то график уравнения должен быть симметричным как относительно оси , так и относительно оси
Рис. 4
Рис. 5
4. Блок экспериментов.
Эксперимент. Преобразовать уравнение которое описывает квадрат так, чтобы уравнение задавало ромб.
Гипотеза: уравнение должно иметь вид:
После обсуждения учащиеся получают задание на два варианта:
Построить графики уравнений:
Рис. 6 Рис. 7
Рис. 8.
Гипотеза: график уравнения получается из графика уравнения в результате сдвига на две единицы вправо вдоль оси и на две единицы в отрицательном направлении вдоль оси График уравнения будет представлять собой квадрат, центр симметрии которого находится в точке Осями симметрии квадрата будут прямыеРис. 9.
9.
Выполняется непосредственная проверка гипотезы. Раскрываются модули в четырёх случаях:
6. Блок экспериментов 2.
Эксперимент 1. Построить график уравнения:
Рассматриваем четыре случая:
График уравнения представляет собой квадрат центром симметрии которого является точка сторона Рис. 10.
которого а площадь .
Рис. 11.Рис. 12
7. Теоретический блок 3. Методика применения полученных знаний и навыков при решении уравнений некоторых типов с модулем и параметром.
Задание: Решить уравнение
При решении уравнений и неравенств с одним неизвестным, содержащих параметр, удобно проводить исследование на координатно-параметрической плоскости (Значение параметра будем откладывать по вертикальной оси, а значение неизвестного по горизонтальной оси).
Построим на плоскости график данного уравнения. Для этого построим прямые и , которые разобьют плоскость на 4 части.Рис. 13
8. Блок постановки творческих задач.
Обсуждение и комментарии к домашнему заданию (7 мин.).
Домашнее задание к следующему уроку будет содержать:
1) Обязательная часть (индивидуальная работа) (Рис. 14).Рис. 14.
При решении задания 4 допускается совместное творчество.
2) Творческая часть (допускается совместное творчество) (Рис. 15).
Рис. 15.
15.
Учащиеся должны построить графики этих уравнений и убедиться в том, что одно уравнение описывает параллелограмм, а второе – треугольник. Учащимся предлагается поэкспериментировать с этими уравнениями, меняя коэффициенты при неизвестных, и понаблюдать как это влияет на геометрию получаемых геометрических фигур. Результаты этой самостоятельной работы учащиеся смогут продемонстрировать на следующем уроке.
Блок резюме.
1. Учащиеся формулируют главные выводы урока:
— Дано определение графика уравнения в сравнении с определением графика функции.
— Научились строить графики уравнений, содержащих символ модуля.
— Установили связь геометрии с алгеброй: различные геометрические фигуры могут быть заданы алгебраическими уравнениями. В частности, были построены квадрат, ромб и прямоугольник.
— Познакомились графическим методом решения уравнений с модулем и параметром, с использованием навыков полученных при построении графиков уравнений.
2. Оценивание работы учащихся: самооценка, взаимооценка, оценка работы учащихся учителем.
3. Выяснение мнения учащихся об уроке.
Ссылки на источники
- А. Г. Мордкович, Н. П. Николаев Алгебра 9. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2013.
- И. Ф. Шарыгин. Факультативный курс по математике 10. – М. «Просвещение», 1989.
- В. Г. Болтянский, Ю. В. Сидоров, М. И Шабунин. Лекции и задачи по элементарной математике. Издательство “Наука”, М. 1974.
Графики уравнений, содержащих знак модуля
Цель:
- закрепить методы построения графика линейной функции,
- закрепить умение учащихся задавать уравнением функцию, заданную при помощи графика,
- познакомить учащихся с тем, каким образом влияет знак модуля на отображение графика линейной функции
Оборудование: презентация (приложение 1)
Ход урока №1
При решении многих математических задач
необходимо быстро и точно строить графики любых
функций, изучаемых в школьном курсе алгебры. Т.к. на уроке предстоит много построений,
начинаем, вспоминая, как строить график линейной
функции y = kx + b на основе анализа
углового коэффициента и коэффициента смещения
(слайд 2)
Т.к. на уроке предстоит много построений,
начинаем, вспоминая, как строить график линейной
функции y = kx + b на основе анализа
углового коэффициента и коэффициента смещения
(слайд 2)
Сопоставляем уравнения и графики (слайд 3):
Построим в тетрадях в одной системе координат графики функций (y = —x; y = —x -4; y = -1/3 x – 2; y = 2x + 5; y = x + 1), проверяя себя при помощи слайда 4
Вспомним определение модуля числа x (слайд 5)
Рассматриваем, как можно построить график функции y = |x| на основании определения модуля, отбрасывая части прямых, не лежащих в полуплоскостях x < 0 и x> 0 (слайд 6)
Аналогично рассматриваем способ построения графика функции y = |x + 1| (слайд 7)
Сравнивая графики и уравнения функций (слайд 8-9),
делаем вывод о том, как можно построить график функции y = |x + a| — b смещением графика функции y = |x| (слайд 10-11)
Строим в тетрадях графики функций y = |x-3| + 3, y = |x – 3| — 2, y = |x+2| — 5, y = |x + 3| + 2 и проверяем себя при помощи слайда 12
Далее учащиеся должны на основе рисунка, представленного на слайде 13, задать функцию уравнением:
При построении графиков очень важно научить ребят анализировать область определения и множество значений функции и “переносить” указанные множества на координатную плоскость.
Заполняем таблицу (слайд 12):
D(y) E (y) y = |x| y = |x – 3| y = |x – 3| +2 y = — |x| y = |x + 2| -5 y = — |x +2| -5
И рассматриваем, как множества значений можно определить на основе графиков (слайд 15)
Учащимся предлагается определить D (y) и E(y) по рисунку (слайд 16):
Ученики самостоятельно придумывают уравнение функции по заданным D(y) и E(y) (слайд 17):
Анализируя графики и уравнения (слайд
18), ученики делают вывод о том, как влияет знак
минуса перед модульными скобками на график. И
самостоятельно задают уравнение по графикам,
представленным на слайде 19.
И
самостоятельно задают уравнение по графикам,
представленным на слайде 19.
Ход урока № 2
Устно проговариваем уравнения функций по графикам (слайд 20):
Аналогично схеме предыдущего урока (слайд 21-27) ученики знакомятся с тем, каким образом влияет коэффициент перед аргументом функции на график. В результате они должны научиться описывать уравнением следующие графики:
Для закрепления полученных знаний, в тетрадях в одной системе координат ребята строят следующие графики:
y = |0,5x| при -3 < x< 3;
y = 3 при -1 < x< 1;
y = -|x + 3| + 6 при -4 < x < -2;
y = -|x — 3| + 6 при 2 < x < 4;
y = |x + 3| + 4 при -4 < x < -2;
y = |x — 3| + 4 при 2 < x ? 4;
y = -|0,5x – 1,5| + 7 при -5 < x < -1;
y = -|0,5x + 1,5| + 7 при 1 < x < 5.
Проверяют себя по слайду 29:
Домашнее задание: придумать картину, состоящую из отрезков прямых, и описать ее при помощи уравнений функций.
Ход урока № 3
Построим графики функций y = |3x| — 3 и y = |3x – 3|. Как в каждом случае связаны y(x) и y(-x)?
Наличие условия y(x) = y(-x) означает симметрию относительно …?
Приведите примеры уравнений функции, графики которых будут симметричны относительно оси ординат
Если в модульные скобки заключается переменная
y, то мы получаем условие |y| = |-y|. Какую
симметрию задает это условие?
Какую
симметрию задает это условие?
На слайде 34 последовательно рассматриваем цепочку построения графиков:
y = 3x – 3, |y| = 3x – 3, |y| = |3x| — 3, |y| = |3x – 3| путем преобразований симметрии.
Выводим и запоминаем три правила:
Распределите, к какому типу из трех (y = f(|x|, |y| = f(x), y = |f(x)|), можно отнести каждое уравнение:
|y| = 2 – x, y = |3x — 4|, |x| + |y| = 2, |y| = 3x – 4, y = |3|x| — 4|, y = |3x| — 4, |y| = |3|x| — 4|, |y| = |3x – 4|.
Проверяем себя (слайд 35)
Строим последовательную цепочку графиков (тонкими линиями в тетрадях):
1) y = 3x – 4, y = |3x – 4|, y = |3|x| - 4|, |y| = |3|x| — 4|
2) y = 3x – 4, y = 3|x| — 4, y = |3|x| — 4|
Рассматриваем способ построения графика соответствия |x| + |y| = 2.
Самостоятельно строим график |x| — |y| = 2 и проверяем себя по слайду 39.
Домашнее задание: придумать пять уравнений соответствий с модулем, в которых встречаются все случаи, рассмотренные на уроке, и построить графики.
Построение графиков уравнений, содержащих модули
Тип урока: Урок формирования новых знаний.
Цели урока:
- Формировать умение строить графики уравнений содержащих модули.
- Развитие логического мышления, познавательного интереса.
- Развитие общеучебных навыков и умений – организационных, интеллектуальных и коммуникативных.
Оборудование: мультимедиа проектор, доска.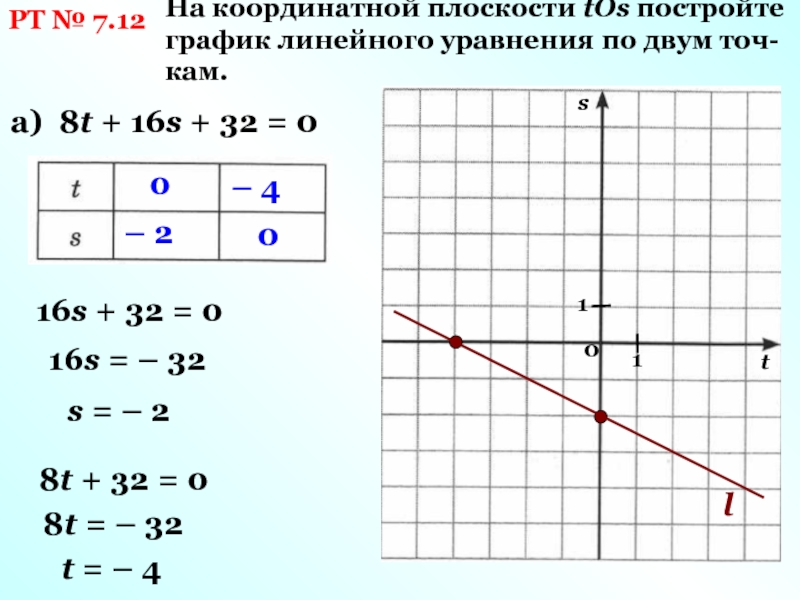
-
Вычислите. (слайд 1)
-
Решите уравнение. (слайд 2)
III.
Объяснение нового материала.1. Построить график уравнения (слайд 3)
Решение. (слайд 4)
По определению модуля имеем:
Построим график уравнения: (слайд 5)
- х=2у, если у≥0
- х=0, если у<0
- Получили график уравнения
2. Построить график уравнения .(слайд 6)
Решение. (слайд 7)
По определению модуля имеем:
Если у=0, то х – любое.
Выполним построение. (слайд 8)
- х = 1, если у>0;
- x = — 1, если у<0;
3. Построить график уравнения (слайд 9)
Решение. (слайд 10)
По определению модуля имеем:
- При х≥0, у≥0, уравнение х+у=4;
- При х≥0, у<0, уравнение х-у=4;
- При х<0, у≥0, уравнение –х+у=4;
- При х<0, у<0, уравнение –х-у=4.
(слайд 11)
Построить график уравнения (слайд 12)
Решение. (слайд 13)
По определению модуля имеем:
- При х≥0, у≥0, уравнение х-у=4;
- При х≥0, у<0, уравнение х+у=4;
- При х<0, у≥0, уравнение –х-у=4;
- При х<0, у<0, уравнение –х+у=4.
 2) ‘, [-2 2])
2) ‘, [-2 2])
И последний:Построить график функции y=tan(x/2) для интервала — π ≤ x ≤ π и -10 ≤ y ≤10.
ezplot('tan(x/2) ', [-pi pi]) axis([-pi pi -10 10])
В данном случае мы указали границы оси с помощью axis от -π до π.Если остались вопросы по поводу построения графиков функций в MATLAB, то обязательно пишите в комментариях, ответим.
Поделиться ссылкой:
ПохожееУрок алгебры на тему: «Графики линейных уравнений»
Технологическая карта урока математики в 7 классе
«Линейная функция и её график»
Предмет: математика
Класс: 7
Автор учебника: Ю.Н. Макарычев
Раздел программы: Линейная функция
Количество уроков по теме: 11
Место урока в системе уроков по данной теме: 5
Тема урока: «Линейная функция и её график»
Тип урока: комбинированный урок
Дидактическая цель урока:
способствовать формированию УУД в процессе изучения линейной функции, закрепление и применение новой информации, проверка уровня достижения планируемых результатов.
Планируемые результаты:
Предметные:
Знать понятие линейной функции, условия пересечения и параллельности графиков линейных функций.
Уметь записывать формулу линейной функции, строить график, характеризовать отличительные черты, задавать линейную функцию различными способами, распознавать линейную функцию по формуле.
Уметь структурировать свои знания.

Уметь формировать интерес к теме, давать определение понятиям, устанавливать причинно-следственные связи, выделять главное.
Метапредметные:
Познавательные умения:
Уметь аналитически мыслить, искать необходимую информацию, устанавливать причинно-следственные связи.
Уметь работать с книгой, отбирать необходимый материал из текста, делать выводы, структурировать информацию в виде схемы, вести самостоятельный поиск, выделять главное, сравнивать, обобщать, анализировать, проводить аналогию, устанавливать причинно-следственные связи.
Уметь осознано и произвольно строить речевые высказывания в устной и письменной форме, давать определение понятиям.
Уметь переносить новые знания в новые условия.
Уметь выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий, осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
Коммуникативные умения:
Уметь участвовать в коллективном обсуждении вопроса.
Уметь планировать учебное сотрудничество с учителем и сверстниками.
Уметь учитывать разные мнения, стремиться к координации различных позиций в сотрудничестве, формулировать собственное мнение, аргументировать и координировать её с позициями партнеров.
Уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; владеть монологической и диалогической формами речи.
Уметь работать в паре, уважительно относиться к точке зрения других, нести ответственность за успехи коллектива и свои лично.

Уметь слушать, учитывать мнение партнера, вести диалог, оказывать в сотрудничестве необходимую взаимопомощь, формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности, устанавливать и сравнивать разные точки зрения, прежде чем принимать решения и делать выбор.
Регулятивные умения:
Уметь концентрировать внимание, организовать рабочее место.
Уметь ставить учебную задачу на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно.
Уметь преодолевать трудности и препятствия на пути достижения цели.
Уметь отвечать на вопросы по плану, анализировать свои достижения, самостоятельно контролировать свое время и управлять им.
Уметь выполнять задания в соответствии с заданными правилами, контролировать и оценивать процесс и результаты своей деятельности, выделять и осознавать того, что уже усвоено и что ещё нужно усвоить, осознавать качество и уровень усвоения; оценивать результат работы, уметь самостоятельно контролировать своё время и управлять им.
Уметь оценивать результаты своей и чужой деятельности, контролировать оценку процесса и результат деятельности.
Личностные:
Уметь устанавливать связи между целью учебной деятельности и её мотивом.
Уметь осознавать проблемы, вести диалог на основе равноправных отношений и взаимного уважения, конструктивно разрешать конфликты.
Уметь точно и грамотно излагать свои мысли в устной и письменной математической речи.
Уметь развивать интеллектуальные способности, логическое мышление в процессе решения задач, сравнивать, выявлять закономерности, обобщать.

Уметь работать самостоятельно.
Методы:
Формы организации познавательной деятельности: фронтальная, парная, индивидуальная.
Средства обучения:
ИКТ: компьютер, проектор, экран, презентация.
Традиционные: учебник, доска
Структура урока:
Организационный момент
Целеполагание и мотивация
Актуализация знаний и умений
Изучение нового материала
Закрепление учебной информации
Применение новой информации (в знакомой и новой ситуации)
Проверка уровня усвоения учебного материала
Информация о домашнем задании
Подведение итогов
Таблица 1
Ход урока
Деятельностьучителя
Деятельность ученика
Планируемый результат
Организационный момент
Приветствие обучающихся, проверка готовности к уроку учащихся, оборудования, классного помещения, выявление отсутствующих.
Включаются в деловой ритм урока.
Регулятивные:
Уметь концентр внимание, организовать рабочее место.
Целеполагание и мотивация
Излагается перечень умений, которыми должен овладеть каждый на уроке.
Определяют, чему могут научиться на уроке.
Коммуникативные:
уметь участвовать в коллективном обсуждении вопроса.

Познавательные:
уметь видеть цель урока
Регулятивные:
уметь ставить учебную задачу на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно.
Личностные:
уметь устанавливать связи между целью учебной деятельности и её мотивом.
Коммуникативные:
уметь
планировать учебное сотрудничество с учителем и сверстниками.
Актуализация знаний и умений
Предлагает текст с пропусками слов:
Прямой пропорциональностью называется функция, которую можно задать формулой вида_________, где х _______ переменная, к ____________ число.
График прямой пропорциональности представляет собой_____, проходящую через ______.
Чтобы построить график функции у=кх достаточно найти координаты ___________ точки графика этой функции, отличной от____.
При к> 0 график прямой пропорциональности расположен в __________ координатных четвертях.
При к< 0 график прямой пропорциональности расположен в __________ координатных четвертях.
Работа в парах: вставляют пропущенные слова в тексте.
Предметные:
Уметь структурировать свои знания.
Личностные:
Уметь осознавать проблемы, вести диалог на основе равноправных отношений и взаимного уважения, конструктивно разрешать конфликты.
Коммуникативные:
уметь учитывать разные мнения, стремиться к координации различных позиций в сотрудничестве, формулировать собственное мнение, аргументировать и координировать её с позициями партнеров.

Познавательные
Уметь восстанавливать понятия, работать с текстом.
Изучение нового материала
Разъясняет базовые знания:
Что такое линейная функция?
Общий вид формулы линейной функции и их график.
Частные виды линейных функций.
Взаимное расположение графиков линейных функций.
Предлагает задания для творческой работыв парах: задать формулой графики линейных функций так, чтобы они описали квадрат.
Предлагает задание для самостоятельной работы в парах: найти отличительные черты графиков прямой пропорциональности и линейной функции.
Фиксируют в тетради основные понятия, строят графики.
Работа в парах: выполняют задание, отвечают на вопросы.
Познавательные: уметь аналитически мыслить, искать необходимую информацию, устанавливать причинно-следственные связи.
Личностные:
уметь точно и грамотно излагать свои мысли в устной и письменной математической речи.
Регулятивные:
уметь преодолевать трудности и препятствия на пути достижения цели.
Предметные:
знать понятие линейной функции, условия пересечения и параллельности графиков линейных функций.
Коммуникативные:
уметь слушать учителя и других учащихся,
уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; владеть монологической и диалогической формами речи.
Закрепление учебной информации
1. Какую функцию называем линейной?
2.
 Общий вид формулы, с помощью которой, задается линейная функция.
Общий вид формулы, с помощью которой, задается линейная функция.3. Частные случаи линейной функции.
4. Что обозначают коэффициенты к и в?
5. Условия параллельности прямых.
Предлагает закодировать учебную информацию в виде схемы: линейная функция и её частные случаи, запомнить главные формулы в схеме.
Предлагает задание на распознание линейной функции и определение ее коэффициентов. На столах у вас имеется математическое лото, где дается аналитическое и графическое задание функций. Задача соединить эти данные.
Работают с учебником, читают, анализируют, выделяют главное, дают ответы на вопросы друг другу.
Кодируют информацию в виде схемы.
Заполняют математическое лото.
Познавательные:
уметь работать с книгой, отбирать необходимый материал из текста, делать выводы, структурировать информацию в виде схемы.
Уметь вести самостоятельный поиск, отбор информации, ее преобразование, выделять главное, сравнивать, обобщать, анализировать, проводить аналогию, устанавливать причинно-следственные связи.
Уметь искать и выделять необходимую информацию; применять методы информационного поиска.
Уметь структурировать знания, осознано и произвольно строить речевые высказывания в устной и письменной форме, давать определение понятиям.
Предметные:
Уметь формировать интерес к теме, давать определение понятиям, устанавливать причинно-следственные связи, выделять главное.
Коммуникативные:
уметь работать в паре, уважительно относиться к точке зрения других, нести ответственность за успехи коллектива и свои лично.
уметь слушать, учитывать мнение партнера, вести диалог, оказывать в сотрудничестве необходимую взаимопомощь, формулировать собственное мнение и позицию, аргументировать и координировать её с позициями партнёров в сотрудничестве при выработке общего решения в совместной деятельности, устанавливать и сравнивать разные точки зрения, прежде чем принимать решения и делать выбор.

Регулятивные:
уметь отвечать на вопросы по плану, анализировать свои достижения, самостоятельно контролировать свое время и управлять им.
Применение новой информации (в знакомой и новой ситуации)
Предлагает выполнить следующие задания:
1.Определите являются ли прямые параллельными?
У = 5х+7 и у = — 5х+7
У = 3,6х+8 и у = 3,6х+18
У = — 6х-32 и у = — 6х
2.Представить формулу 4х + 6у = 0 линейной функции в стандартном виде.
3. № 317, 327.
Выполняют предложенные задания.
Предметные:
Уметь записывать формулу линейной функции, строить график, характеризовать отличительные черты, задавать линейную функцию различными способами, распознавать линейную функцию по формуле.
Познавательные:
уметь переносить новые знания в новые условия,
выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий, осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.
Личностные:
уметь развивать интеллектуальные способности, логическое мышление в процессе решения задач,
сравнивать, выявлять закономерности, обобщать.
Проверка уровня усвоения учебного материала
Предлагает выполнить самостоятельную работу (приложение).
Выполняют самостоятельную работу.
Личностные:
Уметь работать самостоятельно.
Регулятивные:
уметь выполнять задания в соответствии с заданными правилами, контролировать и оценивать процесс и результаты своей деятельности, выделять и осознавать того, что уже усвоено и что ещё нужно усвоить, осознавать качество и уровень усвоения; оценивать результат работы, уметь самостоятельно контролировать своё время и управлять им.

Подведение итогов
Подводятся итоги урока.
Что каждый из вас сегодня узнал, понял, открыл?
Что понравилось особенно, что не понравилось?
Учитель оценивает ответы учащихся учитывает правильность, уровень полноты ответа, качество выполненных заданий, самостоятельность, оригинальность.
Дают оценку своей работы и работы пары.
Регулятивная:
уметь оценивать результаты своей и чужой деятельности,
контролировать оценку процесса и результат деятельности.
Графические линейные уравнения
График линейного уравнения с двумя переменными представляет собой линию (поэтому его называют линейный ).
Если вы знаете, что уравнение линейно, вы можете построить его график, найдя любые два решения.
( Икс 1 , y 1 ) и ( Икс 2 , y 2 ) ,
нанесение этих двух точек на карту и построение линии, соединяющей их.
Пример 1:
Изобразите уравнение Икс + 2 y знак равно 7 .
Вы можете найти два решения, соответствующие Икс -перехватывает и y -перехватывает графика, установив сначала Икс знак равно 0 а потом y знак равно 0 .
Когда Икс знак равно 0 , мы получили:
0 + 2 y знак равно 7 y знак равно 3.
 5
5Когда y знак равно 0 , мы получили:
Икс + 2 ( 0 ) знак равно 7 Икс знак равно 7
Итак, две точки ( 0 , 3.5 ) и ( 7 , 0 ) .
Постройте эти две точки и проведите линию, соединяющую их.
Если уравнение находится в форма пересечения склонов или же точечно-наклонная форма , вы также можете использовать склон чтобы помочь вам построить график.
Пример 2:
Постройте линию y знак равно 3 Икс + 1 .
Из уравнения мы знаем, что y -перехват 1 , точка ( 0 , 1 ) и наклон 3 .Постройте точку ( 0 , 1 ) и оттуда идти вверх 3 единиц и вправо 1 единицы и нанесите на график вторую точку. Проведите линию, содержащую обе точки.
Горизонтальные и вертикальные линии иметь очень простые уравнения.
Пример 3:
Горизонтальная линия: y знак равно 3
Вертикальная линия: Икс знак равно — 2
Постройте математическое выражение — WebMath
Быстро! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Find allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DividingFractions, MultiplyingFractions, SubplicationFractions are, SubplicationFractions , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Any functionGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основМетрическая система, преобразование чисел, сложение чисел, вычисление с числами, вычисление с переменными Числа, деление чисел, умножение чисел, сравнение числовой строки, числовые строки, размещение значений чисел, произнесение чисел, округление чисел, вычитание частичных / параболических чисел, графическое построение чисел , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители с GCF Полиномы, умножение многочленов, возведение в степень Практика, математические задачиПропорции, что это такое Квадратные уравнения, квадратичные формулы Квадратное уравнение ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, РазделениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Методы Правые треугольники, Ветер, рисунок
Графические линейные уравнения с двумя переменными — Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Распознавайте взаимосвязь между решениями уравнения и его графиком.

- Постройте линейное уравнение, нанеся точки.
- График вертикальных и горизонтальных линий.
Прежде чем начать, пройдите тест на готовность.
- Оценить, когда.
Если вы пропустили эту проблему, просмотрите (рисунок). - Решить в общем.
Если вы пропустили эту проблему, просмотрите (рисунок).
Распознать взаимосвязь между решениями уравнения и его графика
В предыдущем разделе мы нашли несколько решений уравнения.Они перечислены на (Рисунок). Итак, упорядоченные пары, и являются некоторыми решениями уравнения. Мы можем построить эти решения в прямоугольной системе координат, как показано на (Рисунок).
Обратите внимание, как точки идеально совпадают? Соединяем точки линией, чтобы получился график уравнения. См. (Рисунок). Обратите внимание на стрелки на концах каждой стороны линии. Эти стрелки указывают на продолжение линии.
Каждая точка на линии является решением уравнения. Кроме того, каждое решение этого уравнения представляет собой точку на этой прямой.Пункты , а не на линии, не являются решением.
Обратите внимание, что точка с координатами находится на линии, показанной на (Рисунок). Если вы подставите и в уравнение, вы обнаружите, что это решение уравнения.
Итак, дело в решении уравнения. (Фраза «точка с координатами» часто сокращается до «точка».)
Значит, это не решение уравнения. Следовательно, дело не в контуре.См. (Рисунок). Это пример поговорки: «Картинка стоит тысячи слов». Линия показывает вам всех решений уравнения. Каждая точка на линии — это решение уравнения. И каждое решение этого уравнения находится на этой линии. Эта линия называется графиком уравнения.
График линейного уравнения
График линейного уравнения представляет собой линию.
- Каждая точка на линии является решением уравнения.

- Каждое решение этого уравнения — точка на этой прямой.
Используйте график, чтобы решить, будет ли каждая упорядоченная пара:
- решение уравнения.
- на линии.
ⓐ
ⓐ да, да ⓑ да, да
Используйте график, чтобы определить, составляет ли каждая заказанная пара:
- решение уравнения
- по линии
ⓐ
ⓐ нет, нет ⓑ да, да
Построение линейного уравнения по точкам
Есть несколько методов, которые можно использовать для построения графика линейного уравнения.Метод, который мы использовали для построения графиков, называется построением точек или методом построения точек.
Как построить уравнение по точкам
Постройте уравнение, нанеся точки.
Постройте уравнение, нанеся точки:.
Постройте уравнение, нанеся точки:.
Действия, которые необходимо предпринять при построении линейного уравнения с помощью точек, приведены ниже.
Постройте линейное уравнение путем нанесения точек.
- Найдите три точки, координаты которых являются решениями уравнения.Разложите их в виде таблицы.
- Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если нет, внимательно проверьте свою работу.
- Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Это правда, что для определения линии нужны только две точки, но использование трех точек — хорошая привычка. Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения.Это будет неправильная линия.
Если вы используете три точки, а одна неверна, точки не выровняются. Это говорит о том, что что-то не так, и вам нужно проверить свою работу.
 Посмотрите на разницу между частью (a) и частью (b) на (Рисунок).
Посмотрите на разницу между частью (a) и частью (b) на (Рисунок).Приведем еще один пример. На этот раз мы покажем последние два шага в одной сетке.
Изобразите уравнение.
Решение
Найдите три точки, которые являются решениями уравнения. Здесь, опять же, легче выбрать значения для.Вы понимаете почему?
Перечислим точки на (Рисунок).
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Постройте уравнение, нанеся точки:.
Постройте уравнение, нанеся точки:.
Когда уравнение включает дробь в качестве коэффициента, мы все равно можем подставлять любые числа вместо. Но математика будет проще, если мы сделаем «правильный» выбор значений.Таким образом, мы избежим дробных ответов, которые сложно построить точным графиком.
Изобразите уравнение.
Решение
Найдите три точки, которые являются решениями уравнения. Поскольку в этом уравнении дробь является коэффициентом, мы будем тщательно выбирать значения. Мы будем использовать ноль в качестве одного варианта и кратное 2 для других вариантов. Почему значения, кратные 2, являются хорошим выбором?
Точки показаны на (Рисунок).
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Изобразите уравнение.
Изобразите уравнение.
До сих пор все уравнения, которые мы построили на графике, были выражены в терминах. Теперь изобразим уравнение с одной и той же стороной и на одной стороне. Посмотрим, что получится в уравнении. Если в чем ценность?
Эта точка имеет дробную часть для координаты x , и, хотя мы можем построить график этой точки, трудно быть точным, указав дроби. Помните, что в этом примере мы тщательно выбирали значения для, чтобы вообще не отображать дроби.Если мы решим уравнение для, будет легче найти три решения уравнения.

Решения для, и показаны на (Рисунок). График представлен на (Рисунок).
Можете ли вы определить точку, которую мы нашли, пропустив на линии?
Изобразите уравнение.
Изобразите уравнение.
Изобразите уравнение.
Если вы можете выбрать любые три точки для построения линии, как вы узнаете, совпадает ли ваш график с тем, который показан в ответах в книге? Если точки пересечения графиков осей x и y совпадают, графики совпадают!
Уравнение на (Рисунок) было записано в стандартной форме, с обеими и на одной и той же стороне.Мы решили это уравнение всего за один шаг. Но для других уравнений в стандартной форме это не так просто решить, поэтому мы оставим их в стандартной форме. Мы все еще можем найти первую точку для построения, позволяя и решая для. Мы можем построить вторую точку, позволив, а затем решив для. Затем мы построим третью точку, используя другое значение для или.
Изобразите уравнение.
Решение
Мы перечисляем упорядоченные пары на (Рисунок). Нанесите точки, убедитесь, что они совпадают, и проведите линию.См. (Рисунок).
Изобразите уравнение.
Изобразите уравнение.
График вертикальные и горизонтальные линии
Можно ли построить уравнение только с одной переменной? Просто и нет, или просто без? Как мы составим таблицу значений, чтобы получить точки для построения?
Рассмотрим уравнение. Это уравнение имеет только одну переменную,. Уравнение говорит, что всегда равно , поэтому его значение не зависит от. Независимо от того, что есть, ценность всегда есть.
Итак, чтобы составить таблицу значений, впишите все значения. Затем выберите любые значения для. Поскольку не зависит от, вы можете выбрать любые числа, которые вам нравятся. Но чтобы уместить точки на нашем координатном графике, мы будем использовать 1, 2 и 3 для координат y .
 См. (Рисунок).
См. (Рисунок).Постройте точки из (Рисунок) и соедините их прямой линией. Обратите внимание на (Рисунок), что мы построили вертикальную линию .
Вертикальная линия
Вертикальная линия — это график уравнения вида.
Линия проходит через ось x в точке.
Изобразите уравнение.
Изобразите уравнение.
Изобразите уравнение.
Что делать, если в уравнении есть, но нет? Давайте изобразим уравнение в виде графика. На этот раз значение y — является константой, поэтому в этом уравнении не зависит от. Заполните 4 для всех (рисунок), а затем выберите любые значения для. Мы будем использовать 0, 2 и 4 для координат x .
График представляет собой горизонтальную линию, проходящую через ось y в точке 4. См. (Рисунок).
Горизонтальная линия
Горизонтальная линия — это график уравнения вида.
Линия проходит по оси y в точке.
Постройте уравнение
Изобразите уравнение.
Изобразите уравнение.
Уравнения для вертикальных и горизонтальных линий очень похожи на уравнения типа В чем разница между уравнениями и?
Уравнение включает и.Значение зависит от значения. Координата y изменяется в зависимости от значения. Уравнение имеет только одну переменную. Значение постоянно. Координата y всегда равна 4. Она не зависит от значения. См. (Рисунок).
Обратите внимание: на (Рисунок) уравнение дает наклонную линию, а дает горизонтальную линию.
График и в той же прямоугольной системе координат.
Решение
Обратите внимание, что в первом уравнении есть переменная, а во втором — нет.См. (Рисунок).
 Два графика показаны на (Рисунок).
Два графика показаны на (Рисунок).График и в той же прямоугольной системе координат.
График и в той же прямоугольной системе координат.
Ключевые понятия
- Построение линейного уравнения по точкам
- Найдите три точки, координаты которых являются решениями уравнения. Разложите их в виде таблицы.
- Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают.Если нет, внимательно проверьте свою работу!
- Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Повседневная математика
Стоимость дома на колесах. Робинсоны арендовали дом на колесах на неделю, чтобы поехать в отпуск. Аренда дома на колесах обходится им в 594 фунта плюс 0,32 фунта за милю, поэтому линейное уравнение дает стоимость проезда на несколько миль. Рассчитайте стоимость аренды за 400, 800 и 1200 миль, а затем нарисуйте линию.
? 722,? 850,? 978
Еженедельный заработок. В художественной галерее, где он работает, Сальвадору платят 200 фунтов в неделю плюс 15% от продаж, которые он совершает, поэтому уравнение дает сумму, которую он зарабатывает на продаже произведений искусства в долларах. Подсчитайте сумму, которую Сальвадор зарабатывает от продажи 900, 1600 и 2000 фунтов стерлингов, а затем изобразите эту линию.
Письменные упражнения
Объясните, как выбрать три значения x , чтобы составить таблицу для построения графика линии.
В чем разница между уравнениями вертикальной и горизонтальной линии?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
11.3: Построение графиков линейных уравнений (часть 1)
Распознавание связи между решениями уравнения и его графиком
В книге «Использование прямоугольной системы координат» мы нашли несколько решений уравнения 3x + 2y = 6.Они перечислены в таблице ниже. Итак, упорядоченные пары (0, 3), (2, 0), \ (\ left (1, \ dfrac {3} {2} \ right) \), (4, — 3) являются некоторыми решениями уравнение 3x + 2y = 6. Мы можем построить эти решения в прямоугольной системе координат, как показано на графике справа.
Обратите внимание, как точки идеально совпадают? Мы соединяем точки прямой линией, чтобы получить график уравнения 3x + 2y = 6. Обратите внимание на стрелки на концах каждой стороны линии. Эти стрелки указывают на продолжение линии.
Каждая точка на линии является решением уравнения. Кроме того, каждое решение этого уравнения представляет собой точку на этой прямой. Точки не в строке — это , а не решений!
Обратите внимание, что точка с координатами (- 2, 6) находится на линии, показанной на рисунке \ (\ PageIndex {1} \). Если вы подставите x = — 2 и y = 6 в уравнение, вы обнаружите, что это решение уравнения.
Рисунок \ (\ PageIndex {1} \)
Итак, (4, 1) не является решением уравнения 3x + 2y = 6.Следовательно, точка (4, 1) не находится на прямой. Это пример поговорки: «Картинка стоит тысячи слов». Линия показывает вам все решения уравнения. Каждая точка на линии — это решение уравнения. И каждое решение этого уравнения находится на этой линии. Эта линия называется графиком уравнения 3x + 2y = 6.
Определение: График линейного уравнения
График линейного уравнения Ax + By = C представляет собой прямую линию.
- Каждая точка на линии является решением уравнения.
- Каждое решение этого уравнения — точка на этой прямой.

Пример \ (\ PageIndex {1} \):
График y = 2x — 3 показан ниже.
Для каждой упорядоченной пары решите: а) Является ли упорядоченная пара решением уравнения? (б) Находится ли точка на линии?
(а) (0, 3) (б) (3, — 3) (в) (2, — 3) (г) (- 1, — 5)
Решение
Подставьте значения x и y в уравнение, чтобы проверить, является ли упорядоченная пара решением уравнения.
(а) $$ \ begin {split} (а) & \; (\ textcolor {blue} {0}, \ textcolor {red} {- 3}) \ qquad \ qquad \ quad \; (б) \; (\ textcolor {blue} {3}, \ textcolor {red} {3}) \ qquad \ qquad \ qquad \ quad (c) \; (\ textcolor {blue} {2}, \ textcolor {red} {- 3}) \ qquad \ qquad \ qquad \ quad (d) \; (\ textcolor {blue} {- 1}, \ textcolor {red} {- 5}) \\ y & = 2x — 3 \ qquad \ qquad \ quad y = 2x — 3 \ qquad \ qquad \ qquad \; у = 2х — 3 \ qquad \ qquad \ qquad \; \; \; y = 2x — 3 \\ \ textcolor {красный} {- 3} & \ stackrel {?} {=} 2 (\ textcolor {blue} {0}) — 3 \ qquad \ qquad \; \ textcolor {красный} {3} \ stackrel {?} {=} 2 (\ textcolor {blue} {3}) — 3 \ qquad \ qquad \; \ textcolor {красный} {- 3} \ stackrel {?} {=} 2 (\ textcolor {blue} {2}) — 3 \ qquad \ qquad \; \; \; \ textcolor {красный} {- 5} \ stackrel {?} {=} 2 (\ textcolor {blue} {- 1}) — 3 \\ -3 & = -3 \; \ checkmark \ qquad \ qquad \ quad \; \; 3 = 3 \; \ checkmark \ qquad \ qquad \ qquad -3 \ neq 1 \ qquad \ qquad \ qquad \ qquad -5 = -5 \; \ checkmark \\ (0, -3) \; & равно \; а \; решение \ ldotp \ quad (3, 3) \; является\; а \; решение \ ldotp \ qquad (2, -3) \; является\; нет\; а \; решение \ ldotp \ qquad (-1, -5) \; является\; а \; решение \ ldotp \ end {split} \]
(b) Постройте точки A: (0, — 3) B: (3, 3) C: (2, — 3) и D: (- 1, — 5).Точки (0, — 3), (3, 3) и (- 1, — 5) находятся на прямой y = 2x — 3, а точка (2, — 3) не на прямой.
Точки, которые являются решениями для y = 2x — 3, находятся на линии, но точка, которая не является решением, не находится на линии.

Упражнение \ (\ PageIndex {1} \):
Показан график y = 3x — 1. Для каждой упорядоченной пары решите: а) является ли упорядоченная пара решением уравнения? (б) точка на линии?
- (0, — 1)
- (2, 2)
- (3, — 1)
- (- 1, — 4)
- Ответ 1.
а. да б. нет
- Ответ 2.
а. нет, б. нет
- Ответ 3.
а. нет, б. нет
- Ответ 4.
а. да б. да
Построение линейного уравнения по точкам
Есть несколько методов, которые можно использовать для построения графика линейного уравнения. Метод, который мы использовали в начале этого раздела для построения графика, называется построением точек или методом точечного построения.
Давайте изобразим уравнение y = 2x + 1, нанеся точки. Начнем с поиска трех точек, которые являются решениями уравнения. Мы можем выбрать любое значение для x или y, а затем найти другую переменную.
Так как y изолирован в левой части уравнения, легче выбрать значения для x. В этом примере мы будем использовать 0, 1 и -2 для x. Мы подставляем каждое значение x в уравнение и решаем относительно y.
Мы можем организовать решения в таблице.См. Таблицу \ (\ PageIndex {1} \).
Таблица \ (\ PageIndex {1} \) y = 2x + 1 x y (х, у) 0 1 (0, 1) 1 3 (1, 3) -2 -3 (-2, -3) Теперь мы наносим точки на прямоугольную систему координат.
 Убедитесь, что точки совпадают. Если бы они не выстроились в очередь, это означало бы, что мы сделали ошибку и должны перепроверить всю нашу работу. См. Рисунок \ (\ PageIndex {2} \).
Убедитесь, что точки совпадают. Если бы они не выстроились в очередь, это означало бы, что мы сделали ошибку и должны перепроверить всю нашу работу. См. Рисунок \ (\ PageIndex {2} \).Рисунок \ (\ PageIndex {2} \)
Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии. Линия — это график y = 2x + 1.
Рисунок \ (\ PageIndex {3} \)
КАК ПОСТРОИТЬ ЛИНЕЙНОЕ УРАВНЕНИЕ ПО ТОЧКАМ ПЕРЕДАЧИ
Шаг 1.Найдите три точки, координаты которых являются решениями уравнения. Разложите их в виде таблицы.
Шаг 2. Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если нет, внимательно проверьте свою работу.
Шаг 3. Проведите линию через точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Это правда, что для определения линии нужны только две точки, но использование трех точек — хорошая привычка. Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения.Это будет неправильная линия. Если вы используете три точки, а одна неверна, точки не будут совпадать. Это говорит о том, что что-то не так, и вам нужно проверить свою работу. См. Рисунок \ (\ PageIndex {4} \).
Рисунок \ (\ PageIndex {4} \) — Посмотрите на разницу между (a) и (b). Все три точки на (а) выстроены в линию, так что мы можем провести через них одну линию. Три точки в (b) не совпадают. Мы не можем провести одну прямую линию через все три точки.
Пример \ (\ PageIndex {2} \):
Изобразите уравнение y = −3x.
Решение
Найдите три точки, которые являются решениями уравнения. Проще выбрать значения для x и решить для y. Вы понимаете почему?
Укажите точки в таблице.
y = −3x x y (х, у) 0 0 (0, 0) 1 -3 (1, -3) -2 6 (-2, 6) Постройте точки, убедитесь, что они совпадают, и проведите линию, как показано.

Упражнение \ (\ PageIndex {2} \):
Изобразите уравнение, нанеся точки: y = −4x.
- Ответ
-
Упражнение \ (\ PageIndex {3} \):
Изобразите уравнение, нанеся точки: y = x.
- Ответ
Когда уравнение включает дробь в качестве коэффициента при x, мы можем заменить x любыми числами. Но математика будет проще, если мы сделаем «правильный» выбор значений x.Таким образом, мы избежим дробных ответов, которые сложно построить точным графиком.
Пример \ (\ PageIndex {3} \):
Изобразите уравнение y = \ (\ dfrac {1} {2} \) x + 3.
Решение
Найдите три точки, которые являются решениями уравнения. Поскольку в этом уравнении дробь \ (\ dfrac {1} {2} \) является коэффициентом при x, мы будем тщательно выбирать значения x. Мы будем использовать ноль в качестве одного варианта и кратное 2 для других вариантов.
Баллы указаны в таблице.
y = \ (\ dfrac {1} {2} \) x + 3 x y (х, у) 0 3 (0, 3) 2 4 (2, 4) 4 5 (4, 5) Постройте точки, убедитесь, что они совпадают, и проведите линию, как показано.
Упражнение \ (\ PageIndex {4} \):
Изобразите уравнение: y = \ (\ dfrac {1} {3} \) x — 1
- Ответ
Упражнение \ (\ PageIndex {5} \):
Изобразите уравнение: y = \ (\ dfrac {1} {4} \) x + 2.

- Ответ
До сих пор во всех уравнениях, которые мы построили, y было выражено через x. Теперь изобразим уравнение с x и y на одной стороне.
Пример \ (\ PageIndex {4} \):
Изобразите уравнение x + y = 5.
Решение
Найдите три точки, которые являются решениями уравнения. Помните, что вы можете начать с любого значения x или y.
Перечислим точки в таблице.
х + у = 5 x y (х, у) 0 5 (0, 5) 1 4 (1, 4) 4 1 (4, 1) Затем нанесите точки, убедитесь, что они совпадают, и проведите линию.
Упражнение \ (\ PageIndex {6} \):
Изобразите уравнение: x + y = −2.
- Ответ
Упражнение \ (\ PageIndex {7} \):
Изобразите уравнение: x — y = 6.
- Ответ
В предыдущем примере три найденные точки было легко нанести на график. Но так бывает не всегда. Давайте посмотрим, что происходит в уравнении 2x + y = 3.Если y равно 0, каково значение x?
\ [\ begin {split} 2x + y & = 3 \\ 2x + \ textcolor {красный} {0} & = 3 \\ 2x & = 3 \\ x & = \ dfrac {3} {2} \ end {split} \]
Решением является точка \ (\ left (\ dfrac {3} {2}, 0 \ right) \). У этой точки есть дробь для координаты x. Хотя мы могли бы изобразить эту точку, трудно дать точную диаграмму дробей.
 Помните, что в примере y = \ (\ dfrac {1} {2} \) x + 3 мы тщательно выбирали значения для x, чтобы вообще не отображать дроби. Если мы решим уравнение 2x + y = 3 относительно y, будет легче найти три решения уравнения.
Помните, что в примере y = \ (\ dfrac {1} {2} \) x + 3 мы тщательно выбирали значения для x, чтобы вообще не отображать дроби. Если мы решим уравнение 2x + y = 3 относительно y, будет легче найти три решения уравнения.\ [\ begin {split} 2x + y & = 3 \\ y & = -2x + 3 \ end {split} \]
Теперь мы можем выбрать значения для x, которые будут давать координаты целыми числами. Показаны решения для x = 0, x = 1 и x = −1.
y = −2x + 3 x y (х, у) 0 3 (0, 3) 1 1 (1, 1) -1 5 (-1, 5) Пример \ (\ PageIndex {5} \):
Изобразите уравнение 3x + y = −1.
Решение
Найдите три точки, которые являются решениями уравнения.
Сначала решите уравнение относительно y.
\ [\ begin {split} 3x + y & = −1 \\ y & = −3x — 1 \ end {split} \]
Пусть x будет 0, 1 и −1, чтобы найти три точки. Заказанные пары показаны в таблице. Нанесите точки, убедитесь, что они совпадают, и проведите линию.
y = −3x — 1 x y (х, у) 0 -1 (0, -1) 1 -4 (1, -4) -1 2 (-1, 2) Если вы можете выбрать любые три точки для построения линии, как вы узнаете, совпадает ли ваш график с тем, который показан в ответах в книге? Если точки пересечения графиков осей x и y совпадают, графики совпадают.

Упражнение \ (\ PageIndex {8} \):
Изобразите каждое уравнение: 2x + y = 2.
- Ответ
Упражнение \ (\ PageIndex {9} \):
Изобразите каждое уравнение: 4x + y = −3.
- Ответ
Стандартная форма Уравнение линии с примерами, графиками и формулой
Обзор различных форм линейного уравнения
Есть много разных способов выразить уравнение линии.Есть форма пересечения откоса, форма точечного откоса, а также тема этой страницы. Каждый из них выражает уравнение линии, и у каждого есть свои плюсы и минусы. Например, форма точечного наклона позволяет легко найти уравнение линии, когда вы знаете только наклон и одну точку на линии. Стандартная форма также имеет несколько различных применений, но об этом позже.
Определение стандартной формы уравнения
Уравнение стандартной формы линии имеет следующую формулу:$ \ text {Формула}: \\ Ax + By = C \\ A \ ne 0 \\ B \ ne 0 $
Общая формула для пересечений по осям x и y
Для уравнения прямой в стандартной форме $$ Ax + By = C $$ где $$ A \ ne 0 $$ и $$ B \ ne 0 $$, вы можете использовать приведенные ниже формулы, чтобы найти точки пересечения по осям x и y.

$ \ text {X Intercept:} \\ \ frac C A = \ frac 6 3 = 2 $
$ \ text {Y Intercept:} \\ \ frac C B = \ frac 6 2 = 3 $
Примерные и не примерные уравнения
Примеры стандартной формы Без примеров $$ 3x + 5y = 3 $$ $$ 2y = 4x + 2 $$ $$ 2x — y = 6 $$ $$ x = 6 — y $$ $$ -2x + y = 7 $$ $$ y = 2x + 7 $$ Когда полезна стандартная форма?
Когда другие формы более полезны?
Видеоурок по уравнению линии в стандартной формеПример 1
Найдите точки пересечения и изобразите следующее уравнение: 3x + 2y = 6
Как найти точку пересечения по оси x:
Установить y = 0 3x + 2 (0) = 6 Решить относительно x Как найти точку пересечения оси Y:
Установить x = 0 3 (0) + 2у = 6 Решить для y Как построить график из стандартной формы
Пример 2
Постройте точки пересечения по осям x и y и проведите линию на миллиметровой бумаге!
Задача 1
Определите, какие уравнения внизу справа имеют стандартную форму.
Покажи ответ
- Уравнение 1: 2x + 5 = 2y
- Уравнение 2: 2x + 3y = 4
- Уравнение 3: y = 2x + 3
- Уравнение 4: 4x — $$ \ frac 1 2 $$ y = 11
Уравнение 2 и уравнение 4 — единственные в стандартной форме.
Уравнение 3 имеет форму пересечения наклона.
Задача 2
Определите, какие уравнения внизу справа имеют стандартную форму.
Покажи ответ- Уравнение 1: 11 = ¼x + ½y
- Уравнение 2: 2x + 5 + 2y = 3
- Уравнение 3: y — 2 = 3 (x — 4)
- Уравнение 4: $$ \ frac 1 2 $$ y — 4x = 0
Уравнение 1 и уравнение 4 — единственные в стандартной форме.
Уравнение 3 имеет форму точечного наклона.

Задача 3
Найдите точки пересечения и затем изобразите следующее уравнение 2x + 3y = 18.
Сначала найдите точки пересечения, установив y, а затем x равные нулю.Это довольно просто, поскольку линия уже имеет стандартную форму.
Покажи ответЗадача 4
Найдите точки пересечения и затем изобразите следующее уравнение 3x + 5y = 15.
Покажи ответЗадача 5
Найдите точки пересечения и затем изобразите следующее уравнение 3y — 2x = -12.
Покажи ответГрафические линейные уравнения | Ресурсы Wyzant
Теперь, когда у нас есть решенных уравнений с одной переменной, теперь мы будем работать над решением уравнений в двух переменных и графических уравнений на координатной плоскости.Графики очень важно для визуального представления взаимосвязи между двумя переменными в уравнении.
Для начала познакомимся с координатной плоскостью (или декартовым графом).

Координатная плоскость
Координатная плоскость была создана французским математиком Рене Декартом по заказу геометрически представить алгебраические уравнения.Часто поэтому координата плоскость называется декартовой плоскостью или графиком. При работе с уравнениями в более чем одна переменная, использование декартового графика может быть важным инструментом для составления уравнений легче визуализировать и понять.
Горизонтальная числовая линия — это , ось x , а вертикальная числовая линия — это ось Y . Точка пересечения обеих линий называется исходной точкой .
Каждая точка на графике изображена упорядоченной парой , где x всегда первое значение и y всегда является вторым значением в упорядоченной паре (x, y) . Это потому, что x — это независимая переменная , что означает, что это изменяемая переменная. Это делает y зависимой переменной , что означает что это зависит от того, как изменяется x.Мы рассмотрим это, когда начнем для построения графика уравнений в терминах x и y. Теперь, несмотря на то, что в пару порядков они связывают только с одной точкой на графике.
Построим точки A (0,0), B (1,2), C (-4,2), D (-3, -4), и E (4, -2) .
Обратите внимание, что A (0,0) — это начало координат, потому что его значения x и y равны 0.Для B (1,2) значение x будет равно 1, а значение y будет равно 2. Чтобы построить точку, мы должны пойти в положительном направлении по оси x, пока мы не дойдем до 1, затем мы поднимемся вверх по оси x. положительная ось Y, пока мы не достигнем 2.
 Здесь находится точка. Мы получаем свои баллы
просто сопоставив значение x и значение y, чтобы получить их местоположение, и мы можем сделать
это для любой пары координат.
Здесь находится точка. Мы получаем свои баллы
просто сопоставив значение x и значение y, чтобы получить их местоположение, и мы можем сделать
это для любой пары координат.Горизонтальные и вертикальные линии
На координатной плоскости мы знаем, что каждая точка должна иметь значения x и y.Когда мы решали уравнения с одной переменной, было легко увидеть, что у нас есть значение x. Чего мы не осознавали, так это того, что у нас также было значение y. Фактически, у нас было бесконечно много значений y. Точно так же, если бы мы решили уравнение с одной переменной в терминах y, у нас было бы бесконечно много значений x. Эти уравнения не образуют точки, а скорее горизонтальная или вертикальная линия.
Когда x равно числу, y может принимать любое значение, и это не изменит равенства.Мы могли бы представить уравнение как имеющее значение y с 0 в качестве коэффициента, поэтому нет независимо от того, какое значение принимает y, оно всегда будет умножаться на 0. Это сформирует вертикальную линия.
Точно так же, когда y равно числу, x может принимать любое значение, и это не повлияет на равенство. Мы могли бы представить уравнение, имеющее значение 0x , поэтому x может быть любым числом, и это не повлияет на уравнение.Этот график будет горизонтальным линия.
Это имеет смысл, потому что ось x — это y = 0 , а ось y — x = 0 .
Решения уравнений с двумя переменными
Мы видели выражения и уравнения одной переменной, в основном x.
 Вот выражение
Вот выражениеКогда мы подставляем разные значения x, мы также получаем другой результат.Поскольку этот вывод варьируется в зависимости от x, мы также можем использовать переменную для представления вывод x.
При работе с уравнениями с двумя переменными решения состоят из значений x и y. которые делают уравнение истинным при включении в уравнение. Эти решения будут оказываются упорядоченными парами, и мы увидим, что уравнения с двумя переменными могут иметь более одного решения, а часто и бесконечно много решений.
Учитывая уравнение
Определите, являются ли координаты (1,5), (2,6) и (-1,1) решениями к уравнению.
Начнем с (1,5) и подставим его в уравнение для x и y.
Это верно! Это означает, что данный момент является решением.
Попробуем (2,6)
Это неверно, потому что 6 не равно 7, следовательно, это , а не решение.
Наконец, подключим (-1,1) .
Это еще одно верное утверждение, поэтому (1,1) является решением уравнения.
Построим оба найденных нами решения для y = 2x + 3 на координатной плоскости
.Это не единственные решения этого уравнения.
 Один метод, который мы могли бы использовать, чтобы найти
другие решения нашего уравнения составляют таблицу значений x и y. Мы можем это сделать
вставляя разные значения x и находя соответствующие им значения y.
Один метод, который мы могли бы использовать, чтобы найти
другие решения нашего уравнения составляют таблицу значений x и y. Мы можем это сделать
вставляя разные значения x и находя соответствующие им значения y.Теперь, когда у нас есть несколько координатных точек, давайте нанесем их на график.
Мы видим, что точки образуют прямую линию, поэтому мы можем провести через них линию. Любая точка на этой прямой является решением уравнения y = 2x + 3 . Это безопасно сказать, что линия, которую мы нарисовали на графике, является решением нашего уравнения.
Для любого уравнения с двумя переменными мы можем попытаться построить график функции, подключив в случайных значениях x, чтобы получить соответствующие значения y. Таким образом, у нас много очков что мы можем построить график. Некоторые уравнения проще изобразить, поскольку они имеют заметную узоры. Следует иметь в виду, что большинство уравнений, с которыми мы работаем, будут в терминах x и y, потому что координатная плоскость образована осями x и y.
Давайте посмотрим на линейные уравнения.
Линейные уравнения
Линейные уравнения — это уравнения двух переменных, которые образуют линию на графике. А линейное уравнение определяется, где каждый член является либо константой, либо произведением константа и единственная переменная. Есть много разных способов, которыми линейные уравнения можно представить алгебраически и изобразить графически.
Вот различные формы линейных уравнений
Стандартная форма
В таком виде можно записать линейное уравнение в виде двух переменных, где A, B и C — константы.
 Эта форма полезна, потому что мы можем легко получить
x и y перехватывает , вставляя 0 для одной из переменных.Перехват
является пересечением прямой и оси x или y. Мы увидим, что эти
перехватчики помогут в построении линейных уравнений.
Эта форма полезна, потому что мы можем легко получить
x и y перехватывает , вставляя 0 для одной из переменных.Перехват
является пересечением прямой и оси x или y. Мы увидим, что эти
перехватчики помогут в построении линейных уравнений.Напишите следующее уравнение в стандартной форме и нанесите линию на график.
Сначала умножаем обе части на 3, чтобы избавиться от дроби.
Затем мы вычитаем 2x с обеих сторон, чтобы получить x и y на одной стороне
Давайте переставим его так, чтобы наше значение x было первым.
Это стандартная форма нашего исходного уравнения. Поскольку наше исходное уравнение можно записать в стандартной форме, мы знаем, что это линейное уравнение (если уравнение нельзя записать в стандартной форме, это не линейно).
Теперь давайте построим график уравнения, найдя наши точки пересечения. Во-первых, давайте найти точку пересечения y, подставив 0 вместо x.
Мы подставили 0 для x и получили -4 для y. Наша координата будет (0, -4) , что мы называем нашу точку перехвата y . Это называется нашим перехватом y, потому что это точка, где график уравнения пересекает ось y.
Давайте найдем точку пересечения x, подставив 0 вместо y.
Когда мы подключили y = 0, мы получили x = 6, поэтому наша координата (6,0) .Этот это точка пересечения x , потому что это точка, где график пересекает точку x ось. Поскольку у нас есть точки пересечения x и y, и мы знаем, что уравнение линейно (мы поместите его в стандартную форму), мы можем изобразить уравнение.
Эта линия является набором решений нашего уравнения. Следует отметить, что если мы знаем уравнение является линейным, требуется всего две точки, чтобы построить линию на графике.Только чтобы быть уверенным, всегда полезно построить более двух точек, чтобы проверить, коллинеарны (если образуют линию). Если мы не знаем, что это линейно, это полезно. нанести несколько точек, чтобы четко видеть кривую графика. Если бы нам дали этот граф без алгебраического представления, было бы трудно придумать стандартная форма уравнения, поэтому мы можем использовать следующие общие формы линейные уравнения, чтобы найти их.
Форма уклона-пересечения
Эта форма чаще всего используется для представления линейных уравнений. Эта форма лучший способ найти угол наклона и точку пересечения оси y линейного уравнения, где м — наклон, а b — точка пересечения по оси y.
Построим это уравнение, используя форму пересечения наклона.
Сравнивая с нашим общим уравнением угла наклона, мы видим, что м = 2/3 и b = -4 . Изобразив это на графике, мы можем получить нашу линию.
Поскольку у нас есть точка пересечения по оси Y и наклон, мы можем построить точку точки пересечения по оси Y и найти другая точка на линии, использующая уклон.Поскольку м = 2/3 , мы можем подняться на положительную величину. 2 и положительное 3 справа, чтобы получить следующую точку на линии. Мы можем повторить это процесс, чтобы получить строку нашего уравнения.
Форма точечного откоса
Наконец, у нас есть форма точечного уклона. Мы можем использовать представление, если у нас есть точки на линии (это не обязательно должно быть пересечение) и наклона, или, если у нас есть любые две точки на линии.
Найдите уравнение прямой, проходящей через точку (3, -2) с уклоном м = 2/3 . Давайте подставим значения в наше уравнение.
Мы подключаем (3, -2) к (x1, y1) и позволяем m = 2/3
У нас есть уравнение! Теперь попробуем с учетом двух баллов.
Найдите уравнение прямой через точки (-3, -6) и (3, -2) . Если мы знаем, что уравнение линейно, мы можем просто нарисовать точки и провести линию через их, но в данном случае мы хотим найти уравнение линии. Давайте подключим их в форму общего точечного наклона и посмотрим, что мы получим.
Поскольку мы не знаем наклона, но у нас есть две точки, мы можем подключить две точки в формулу наклона.
Преобразование форм линейных уравнений
Несмотря на то, что у нас есть три различных формы линейных уравнений, все они такой же. Причина, по которой у нас есть эти разные формы, заключается в том, что каждая из них полезна для различных геометрических представлений и способов работы с информацией у нас есть.Различные формы линейных уравнений могут быть преобразованы из одной формы в Другая.
(1) При преобразовании из стандартной формы ( Ax + By = C ) в угол наклона форме ( y = mx + b ), имеем
(2) При преобразовании из Стандартной формы ( Ax + By = C ) в Точечный уклон form [ (y-y1) = m (x-x1) ], имеем
Нахождение уравнения прямой
Если нам дан график линии и мы хотим найти его уравнение (или алгебраическое представление), мы можем найти его несколькими способами.
(1) Учитывая две точки на прямой, мы можем подставить их в формулу наклона, чтобы найти наклон, а затем использовать точку-наклон форма.
(2) Учитывая любую точку на линии и точку пересечения оси y, мы можем подключить их к формула наклона, чтобы найти наклон, а затем использовать либо точку-наклон, либо пересечение наклона форма.
(3) Для любой точки на линии и уклона используйте форму «точка-уклон».
(4) Учитывая точку пересечения оси y и наклон, используйте форму точки пересечения угла наклона.
Построение графика линейного уравнения
Учитывая любой тип уравнения (оно не обязательно должно быть линейным), мы можем вставить случайное x и получить значение y. Мы могли бы построить точки таким образом, но это утомительно. процесс и не совсем необходимо.Вот другие способы построения графика линейного уравнения.
(1) Дано уравнение в любой форме, подставьте любое значение x в уравнение и найти значение y. Нанесите точку на график и сделайте это снова хотя бы для одного больше точки. После того, как у нас будет две точки, проведите линию через точки для всех решений. к линейному уравнению. Если точки неколлинеарны (не совпадают), то либо уравнение не линейное, либо произошла арифметическая ошибка при нахождении их.
(2) Учитывая стандартную форму линейного уравнения ( Ax + By = C ), положим значение x равняется 0, чтобы найти точку пересечения y, а затем значение y равняется 0 для точки пересечения x. Нанесите точки на график и проведите через них линию.
(3) Учитывая форму пересечения наклона ( y = mx + b ), постройте точку пересечения оси y (0, b) и используйте уклон м , чтобы найти остальные точки на графике.
(4) Учитывая форму «точка-наклон» [ (y — y1) = m (x — x1) ], постройте точку (x1, y1) и используйте наклон m, чтобы найти остальные точки на график.
Системы линейных уравнений
Когда мы строим график более чем одного линейного уравнения одновременно, считается, что мы имеем система линейных уравнений. Решение этих систем даст нам точку, в которой линии перекресток, что весьма актуально в различных реальных приложениях и часто выполняется по экономике и математике высшего уровня.
4.2 Графики линейных уравнений с двумя переменными — элементарная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Решить проблемы со словом монеты
- Решение проблем со словами о билетах и штампах
- Решение проблем со смесью слов
- Используйте модель смеси для решения инвестиционных задач с использованием простых процентов
Будьте готовы 4,4
Прежде чем начать, пройдите тест на готовность.
Вычислить 3x + 23x + 2, когда x = −1x = −1.
Если вы пропустили эту проблему, просмотрите Пример 1.57.Будьте готовы 4.5
Решите 3x + 2y = 123x + 2y = 12 для yy в целом.
Если вы пропустили эту проблему, просмотрите Пример 2.63.Распознать взаимосвязь между решениями уравнения и его графика
В предыдущем разделе мы нашли несколько решений уравнения 3x + 2y = 63x + 2y = 6. Они перечислены в таблице 4.10. Итак, упорядоченные пары (0,3) (0,3), (2,0) (2,0) и (1,32) (1,32) являются некоторыми решениями уравнения 3x + 2y = 63x + 2у = 6.Мы можем построить эти решения в прямоугольной системе координат, как показано на рисунке 4.5.
3x + 2y = 63x + 2y = 6 xx г.г (х, у) (х, у) 0 3 (0,3) (0,3) 2 0 (2,0) (2,0) 1 3232 (1,32) (1,32) Таблица 4.10
Рисунок 4.5
Обратите внимание, как точки идеально совпадают? Соединяем точки линией, чтобы получить график уравнения 3x + 2y = 63x + 2y = 6. См. Рисунок 4.6. Обратите внимание на стрелки на концах каждой стороны линии. Эти стрелки указывают на продолжение линии.
Рисунок 4.6
Каждая точка на линии является решением уравнения. Кроме того, каждое решение этого уравнения представляет собой точку на этой прямой. Пункты , а не на линии, не являются решением.
Обратите внимание, что точка с координатами (−2,6) (- 2,6) находится на линии, показанной на рисунке 4.7. Если вы подставите x = −2x = −2 и y = 6y = 6 в уравнение, вы обнаружите, что это решение уравнения.
Рисунок 4.7
Итак, точка (−2,6) (- 2,6) является решением уравнения 3x + 2y = 63x + 2y = 6. (Фраза «точка с координатами (−2,6) (- 2,6)» часто сокращается до «точка (−2,6) (- 2,6)».)
Итак, (4,1) (4,1) не является решением уравнения 3x + 2y = 63x + 2y = 6.Следовательно, точка (4,1) (4,1) не находится на прямой. См. Рисунок 4.6. Это пример поговорки: «Картинка стоит тысячи слов». Линия показывает вам всех решений уравнения. Каждая точка на линии — это решение уравнения. И каждое решение этого уравнения находится на этой линии. Эта линия называется графиком уравнения 3x + 2y = 63x + 2y = 6.
График линейного уравнения
График линейного уравнения Ax + By = CAx + By = C представляет собой линию.
- Каждая точка на линии является решением уравнения.
- Каждое решение этого уравнения — точка на этой прямой.
Пример 4.10
Показан график y = 2x − 3y = 2x − 3.
Для каждой заказанной пары определите:
ⓐ Является ли упорядоченная пара решением уравнения?
Ⓑ Находится ли точка на линии?A (0, −3) (0, −3) B (3,3) (3,3) C (2, −3) (2, −3) D (−1, −5) (- 1, −5)
Решение
Подставьте значения x и y в уравнение, чтобы проверить, является ли упорядоченная пара решением уравнения.
- ⓐ
- ⓑ Постройте точки A (0,3) (0,3), B (3,3) (3,3), C (2, −3) (2, −3) и D (−1, — 5) (- 1, −5).
Точки (0,3) (0,3), (3,3) (3,3) и (−1, −5) (- 1, −5) находятся на прямой y = 2x − 3y. = 2x − 3, а точка (2, −3) (2, −3) не находится на прямой.
Точки, которые являются решениями y = 2x − 3y = 2x − 3, находятся на линии, но точка, которая не является решением, не находится на линии.
Попробуй 4.19
Используйте график y = 3x − 1y = 3x − 1, чтобы решить, будет ли каждая упорядоченная пара:
- решение уравнения.
- на линии.
ⓐ (0, −1) (0, −1) ⓑ (2,5) (2,5)
Попробовать 4.20
Используйте график y = 3x − 1y = 3x − 1, чтобы определить, составляет ли каждая упорядоченная пара:
- решение уравнения
- по линии
ⓐ (3, −1) (3, −1) ⓑ (−1, −4) (- 1, −4)
Построение линейного уравнения по точкам
Есть несколько методов, которые можно использовать для построения графика линейного уравнения. Метод, который мы использовали для построения графика 3x + 2y = 63x + 2y = 6, называется построением точек или методом построения точек.
Пример 4.11
Как построить график уравнения по точкам
Изобразите уравнение y = 2x + 1y = 2x + 1, нанеся точки.
Попробуйте 4.21
Изобразите уравнение, нанеся точки: y = 2x − 3y = 2x − 3.
Попробуйте 4.22
Изобразите уравнение, нанеся точки: y = −2x + 4y = −2x + 4.
Действия, которые необходимо предпринять при построении линейного уравнения с помощью точек, приведены ниже.
How To
Постройте линейное уравнение путем нанесения точек.
- Шаг 1. Найдите три точки, координаты которых являются решениями уравнения. Разложите их в виде таблицы.
- Шаг 2. Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если нет, внимательно проверьте свою работу.
- Шаг 3. Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Это правда, что для определения линии нужны только две точки, но использование трех точек — хорошая привычка.Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения. Это будет неправильная линия.
Если вы используете три точки, а одна неверна, точки не выровняются. Это говорит о том, что что-то не так, и вам нужно проверить свою работу. Посмотрите на разницу между частью (a) и частью (b) на рисунке 4.8.
Рисунок 4.8
Приведем еще один пример. На этот раз мы покажем последние два шага в одной сетке.
Пример 4.12
Изобразите уравнение y = −3xy = −3x.
Решение
Найдите три точки, которые являются решениями уравнения. Здесь, опять же, проще выбрать значения для xx. Вы понимаете почему?
Перечислим пункты в Таблице 4.11.
y = −3xy = −3x xx г.г (х, у) (х, у) 0 0 (0,0) (0,0) 1 −3−3 (1, −3) (1, −3) −2−2 6 (−2,6) (- 2,6) Таблица 4.11
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Попробуйте 4.23
Изобразите уравнение, нанеся точки: y = −4xy = −4x.
Попробуйте 4.24
Изобразите уравнение, нанеся точки: y = xy = x.
Когда уравнение включает дробь в качестве коэффициента xx, мы все равно можем заменить xx любыми числами. Но математика будет проще, если мы сделаем «хороший» выбор значений xx. Таким образом, мы избежим дробных ответов, которые сложно построить точным графиком.
Пример 4.13
Изобразите уравнение y = 12x + 3y = 12x + 3.
Решение
Найдите три точки, которые являются решениями уравнения. Поскольку в этом уравнении дробь 1212 является коэффициентом при x, x, мы будем тщательно выбирать значения xx. Мы будем использовать ноль в качестве одного варианта и кратное 2 для других вариантов. Почему кратное 2 — хороший выбор для значений xx?
Точки показаны в таблице 4.12.
y = 12x + 3y = 12x + 3 xx г.г (х, у) (х, у) 0 3 (0,3) (0,3) 2 4 (2,4) (2,4) 4 5 (4,5) (4,5) Таблица 4.12
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Попробуйте 4.25
Изобразите уравнение y = 13x − 1y = 13x − 1.
Попробуйте 4.26
Изобразите уравнение y = 14x + 2y = 14x + 2.
До сих пор во всех уравнениях, которые мы построили, yy было выражено через xx. Теперь изобразим уравнение с xx и yy на одной стороне. Давайте посмотрим, что происходит в уравнении 2x + y = 32x + y = 3. Если y = 0y = 0, каково значение xx?
Эта точка имеет дробную часть для координаты x , и, хотя мы можем построить график этой точки, трудно быть точными, указав дроби.Помните, что в примере y = 12x + 3y = 12x + 3 мы тщательно выбирали значения для xx, чтобы вообще не отображать дроби. Если мы решим уравнение 2x + y = 32x + y = 3 относительно yy, будет легче найти три решения уравнения.
2x + y = 3y = −2x + 32x + y = 3y = −2x + 3Решения для x = 0x = 0, x = 1x = 1 и x = −1x = −1 показаны в таблице 4.13. График представлен на Рисунке 4.9.
2x + y = 32x + y = 3 xx г.г (х, у) (х, у) 0 3 (0,3) (0,3) 1 1 (1,1) (1,1) -1-1 5 (−1,5) (- 1,5) Таблица 4.13
Рисунок 4.9
Можете ли вы найти точку (32,0) (32,0), которую мы нашли, положив y = 0y = 0 на линии?
Пример 4.14
Изобразите уравнение 3x + y = −13x + y = −1.
Решение
Найдите три точки, которые являются решениями уравнения. 3x + y = −13x + y = −1 Сначала решите уравнение для yy. y = −3x − 1y = −3x − 1 Таблица 4.14
Пусть xx равно 0, 1 и −1−1, чтобы найти 3 точки. Заказанные пары показаны в Таблице 4.15. Нанесите точки, убедитесь, что они совпадают, и проведите линию. См. Рисунок 4.10.
3x + y = −13x + y = −1 xx г.г (х, у) (х, у) 0 -1-1 (0, -1) (0, -1) 1 −4−4 (1, −4) (1, −4) -1-1 2 (−1,2) (- 1,2) Таблица 4.15
Рисунок 4.10
Попробуйте 4.27
Изобразите уравнение 2x + y = 22x + y = 2.
Попробуйте 4.28
Изобразите уравнение 4x + y = −34x + y = −3.
Если вы можете выбрать любые три точки для построения линии, как вы узнаете, совпадает ли ваш график с тем, который показан в ответах в книге? Если точки пересечения графиков осей x и y совпадают, графики совпадают!
Уравнение в примере 4.14 было записано в стандартной форме с xx и yy на одной стороне.Мы решили это уравнение для yy всего за один шаг. Но для других уравнений в стандартной форме решить для yy не так-то просто, поэтому мы оставим их в стандартной форме. Мы все еще можем найти первую точку для построения графика, положив x = 0x = 0 и решив для yy. Мы можем построить вторую точку, положив y = 0y = 0, а затем решив относительно xx. Затем мы построим третью точку, используя другое значение для xx или yy.
Пример 4.15
Изобразите уравнение 2x − 3y = 62x − 3y = 6.
Решение
Найдите три точки, которые являются решениями уравнения. 2x − 3y = 62x − 3y = 6 Сначала пусть x = 0x = 0. 2 (0) −3y = 62 (0) −3y = 6 Решить для гг. −3y = 6y = −2−3y = 6y = −2 Пусть теперь y = 0y = 0. 2x − 3 (0) = 62x − 3 (0) = 6 Решите для xx. 2x = 6x = 32x = 6x = 3 Нам нужна третья точка. Помните, что мы можем выбрать любое значение для xx или yy. Пусть x = 6x = 6. 2 (6) −3y = 62 (6) −3y = 6 Решить для гг. 12−3y = 6−3y = −6y = 212−3y = 6−3y = −6y = 2 Таблица 4.16
Мы перечисляем заказанные пары в Таблице 4.17. Нанесите точки, убедитесь, что они совпадают, и проведите линию. См. Рисунок 4.11.
2x − 3y = 62x − 3y = 6 xx г.г (х, у) (х, у) 0 −2−2 (0, -2) (0, -2) 3 0 (3,0) (3,0) 6 2 (6,2) (6,2) Таблица 4.17
Рисунок 4.11
Попробуйте 4.29
Изобразите уравнение 4x + 2y = 84x + 2y = 8.
Попробовать 4.30
Изобразите уравнение 2x − 4y = 82x − 4y = 8.
График вертикальные и горизонтальные линии
Можно ли построить уравнение только с одной переменной? Просто xx и без yy, или просто yy без xx? Как мы составим таблицу значений, чтобы получить точки для построения?
Рассмотрим уравнение x = −3x = −3. Это уравнение имеет только одну переменную xx.Уравнение говорит, что xx — это , всегда равно −3−3, поэтому его значение не зависит от yy. Независимо от того, что такое yy, значение xx всегда равно −3−3.
Итак, чтобы составить таблицу значений, запишите −3−3 для всех значений xx. Затем выберите любые значения для yy. Поскольку xx не зависит от yy, вы можете выбирать любые числа, которые вам нравятся. Но чтобы уместить точки на нашем координатном графике, мы будем использовать 1, 2 и 3 для координат y . См. Таблицу 4.18.
x = −3x = −3 xx г.г (х, у) (х, у) −3−3 1 (−3,1) (- 3,1) −3−3 2 (−3,2) (- 3,2) −3−3 3 (−3,3) (- 3,3) Таблица 4.18
Постройте точки из Таблицы 4.18 и соедините их прямой линией. Обратите внимание на рис. 4.12, что мы построили вертикальную линию .
Рисунок 4.12
Вертикальная линия
Вертикальная линия — это график уравнения вида x = ax = a.
Линия проходит через ось x в точке (a, 0) (a, 0).
Пример 4.16
Изобразите уравнение x = 2x = 2.
Решение
Уравнение имеет только одну переменную, xx, и xx всегда равно 2.Мы создаем Таблицу 4.19, где xx всегда равно 2, а затем вводим любые значения для yy. График представляет собой вертикальную линию, проходящую через ось x в точке 2. См. Рисунок 4.13.
x = 2x = 2 xx г.г (х, у) (х, у) 2 1 (2,1) (2,1) 2 2 (2,2) (2,2) 2 3 (2,3) (2,3) Таблица 4.19
Рисунок 4.13
Попробуйте 4.31
Изобразите уравнение x = 5x = 5.
Попробовать 4.32
Изобразите уравнение x = −2x = −2.
Что делать, если в уравнении есть yy, но нет xx? Построим график уравнения y = 4y = 4. На этот раз значение y — постоянное, поэтому в этом уравнении yy не зависит от xx. Введите 4 для всех yy в таблице 4.20, а затем выберите любые значения для xx. Мы будем использовать 0, 2 и 4 для координат x .
y = 4y = 4 xx г.г (х, у) (х, у) 0 4 (0,4) (0,4) 2 4 (2,4) (2,4) 4 4 (4,4) (4,4) Таблица 4.20
График представляет собой горизонтальную линию, проходящую через ось y в точке 4.См. Рисунок 4.14.
Рисунок 4.14
Горизонтальная линия
Горизонтальная линия — это график уравнения вида y = by = b.
Линия проходит по оси y в точке (0, b) (0, b).
Пример 4.17
Изобразите уравнение y = −1.y = −1.
Решение
Уравнение y = −1y = −1 имеет только одну переменную yy. Значение yy постоянно. Все упорядоченные пары в таблице 4.21 имеют одинаковую координату y .График представляет собой горизонтальную линию, проходящую через ось y в точке -1-1, как показано на рисунке 4.15.
y = −1y = −1 xx г.г (х, у) (х, у) 0 -1-1 (0, -1) (0, -1) 3 -1-1 (3, -1) (3, -1) −3−3 -1-1 (−3, −1) (- 3, −1) Таблица 4.21
Рисунок 4.15
Попробовать 4.33
Изобразите уравнение y = −4y = −4.
Попробовать 4.34
Изобразите уравнение y = 3y = 3.
Уравнения для вертикальных и горизонтальных линий очень похожи на уравнения типа y = 4x.y = 4x. В чем разница между уравнениями y = 4xy = 4x и y = 4y = 4?
Уравнение y = 4xy = 4x имеет как xx, так и yy. Значение yy зависит от значения xx. Координата y изменяется в соответствии со значением xx.Уравнение y = 4y = 4 имеет только одну переменную. Значение yy постоянно. Координата y всегда равна 4. Она не зависит от значения xx. См. Таблицу 4.22.
y = 4xy = 4x y = 4y = 4 xx г.г (х, у) (х, у) хх г.г (х, у) (х, у) 0 0 (0,0) (0,0) 0 4 (0,4) (0,4) 1 4 (1,4) (1,4) 1 4 (1,4) (1,4) 2 8 (2,8) (2,8) 2 4 (2,4) (2,4) Таблица 4.22
Рисунок 4.16
Обратите внимание: на рисунке 4.16 уравнение y = 4xy = 4x дает наклонную линию, а y = 4y = 4 дает горизонтальную линию.
Пример 4.18
График y = −3xy = −3x и y = −3y = −3 в той же прямоугольной системе координат.
Решение
Обратите внимание, что в первом уравнении есть переменная xx, а во втором — нет. См. Таблицу 4.23. Два графика показаны на рисунке 4.17.
y = −3xy = −3x y = −3y = −3 xx г.г (х, у) (х, у) хх г.г (х, у) (х, у) 0 0 (0,0) (0,0) 0 −3−3 (0, −3) (0, −3) 1 −3−3 (1, −3) (1, −3) 1 −3−3 (1, −3) (1, −3) 2 −6−6 (2, −6) (2, −6) 2 −3−3 (2, −3) (2, −3) Таблица 4.23
Рисунок 4.17
Попробовать 4.35
График y = −4xy = −4x и y = −4y = −4 в той же прямоугольной системе координат.
Попробовать 4.36
График y = 3y = 3 и y = 3xy = 3x в той же прямоугольной системе координат.
Раздел 4.2. Упражнения
Практика ведет к совершенству
Распознавать взаимосвязь между решениями уравнения и его графика
В следующих упражнениях для каждой упорядоченной пары определите:
ⓐ Является ли упорядоченная пара решением уравнения? Ⓑ Находится ли точка на линии?
55.у = х + 2у = х + 2
- ⓐ (0,2) (0,2)
- ⓑ (1,2) (1,2)
- ⓒ (−1,1) (- 1,1)
- ⓓ (−3, −1 ) (- 3, −1)
у = х-4у = х-4
- ⓐ (0, −4) (0, −4)
- ⓑ (3, −1) (3, −1)
- ⓒ (2,2) (2,2)
- ⓓ (1, — 5) (1, −5)
y = 12x − 3y = 12x − 3
- ⓐ (0, −3) (0, −3)
- ⓑ (2, −2) (2, −2)
- ⓒ (−2, −4) (- 2, −4)
- ⓓ (4,1) (4,1)
y = 13x + 2y = 13x + 2
- ⓐ (0,2) (0,2)
- ⓑ (3,3) (3,3)
- ⓒ (−3,2) (- 3,2)
- ⓓ (−6,0) (−6,0)
Построение линейного уравнения по точкам
В следующих упражнениях построите график путем нанесения точек.
Вертикальные и горизонтальные линии графика
В следующих упражнениях нанесите на график каждое уравнение.
В следующих упражнениях нарисуйте каждую пару уравнений в одной прямоугольной системе координат.
117.y = −12xy = −12x и y = −12y = −12
118.y = −13xy = −13x и y = −13y = −13
Смешанная практика
В следующих упражнениях нанесите на график каждое уравнение.
Повседневная математика
135.Стоимость дома на колесах. Робинсоны арендовали дом на колесах на неделю, чтобы поехать в отпуск. Аренда дома на колесах обошлась им в 594 доллара плюс 0,32 доллара за милю, поэтому линейное уравнение y = 594 + 0,32xy = 594 + 0,32x дает стоимость yy проезда xx миль. Рассчитайте стоимость аренды за 400, 800 и 1200 миль, а затем нарисуйте линию.
136.Еженедельный заработок. В художественной галерее, где он работает, Сальвадору платят 200 долларов в неделю плюс 15% от продаж, которые он делает, поэтому уравнение y = 200 + 0.15xy = 200 + 0,15x дает сумму yy, которую он зарабатывает за продажу xx долларов произведений искусства. Подсчитайте сумму, которую Сальвадор зарабатывает на продаже 900, 1600 и 2000 долларов, а затем нарисуйте эту линию.
Письменные упражнения
137.Объясните, как выбрать три значения x -, чтобы составить таблицу с графиком линии y = 15x − 2y = 15x − 2.
138.В чем разница между уравнениями вертикальной и горизонтальной линии?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
.
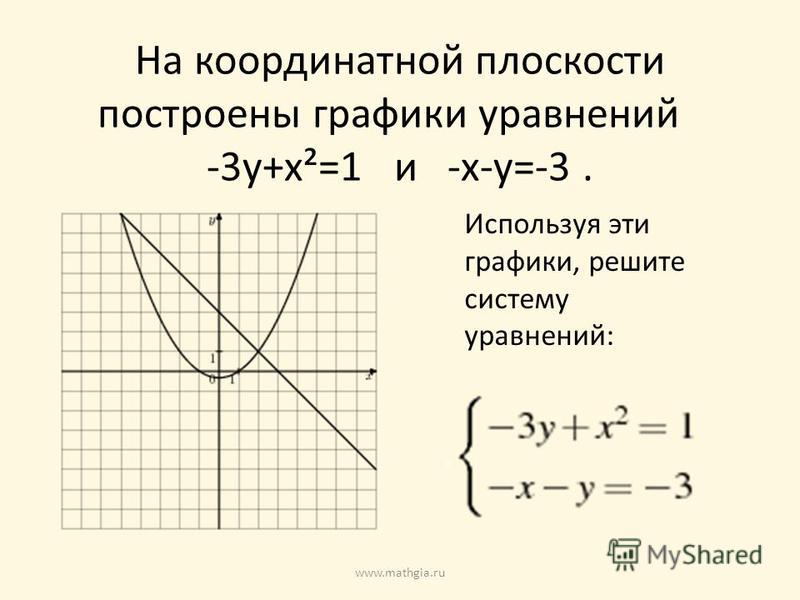 2) ‘, [-2 2])
2) ‘, [-2 2]) 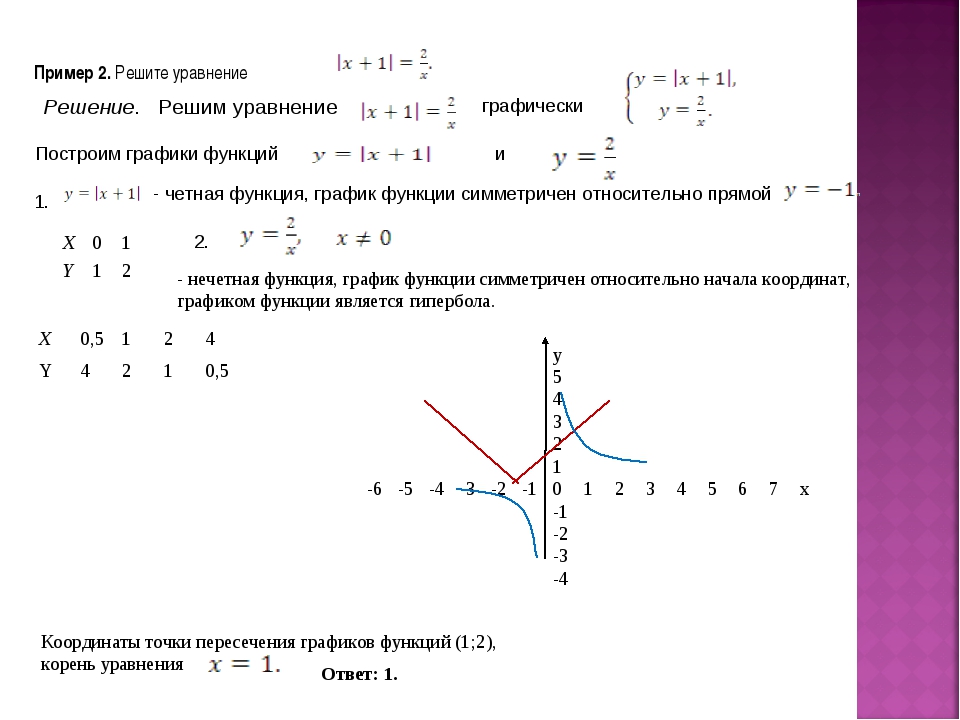

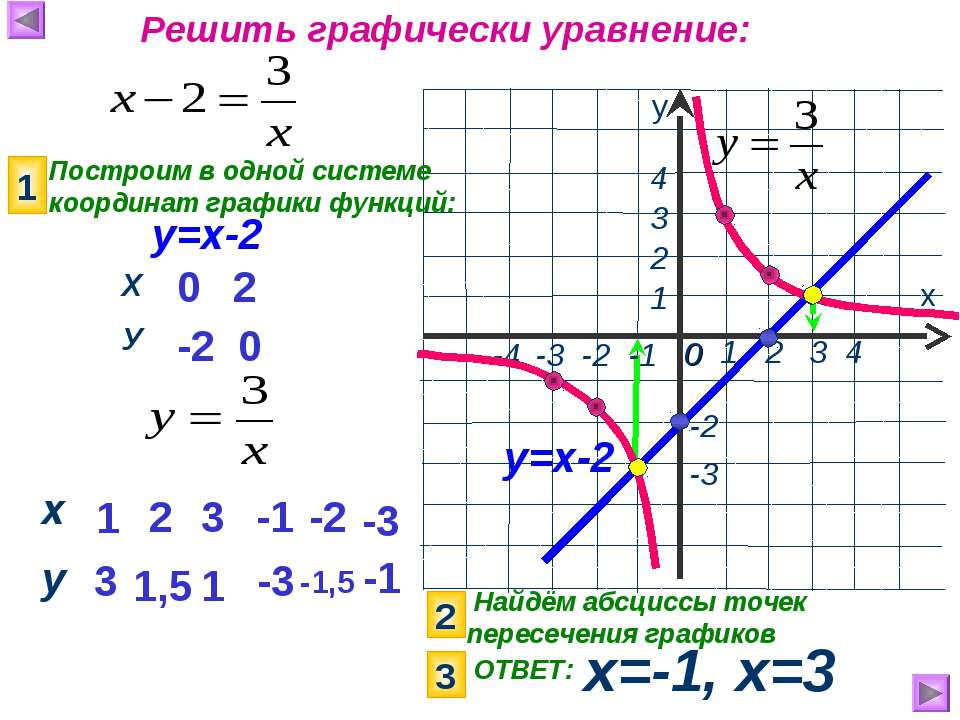

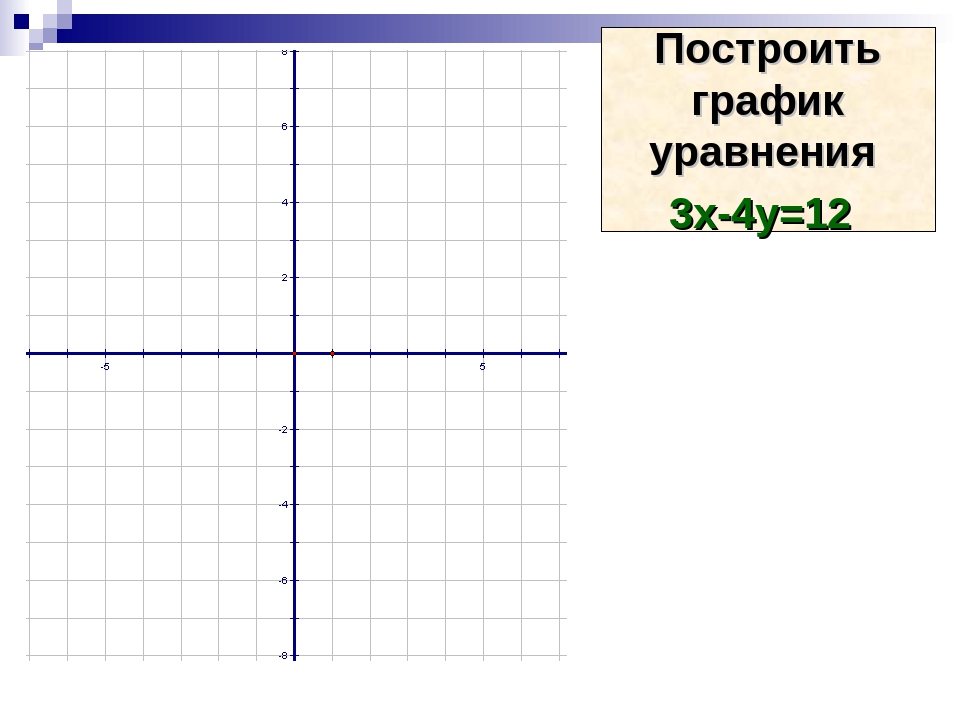
 Общий вид формулы, с помощью которой, задается линейная функция.
Общий вид формулы, с помощью которой, задается линейная функция.
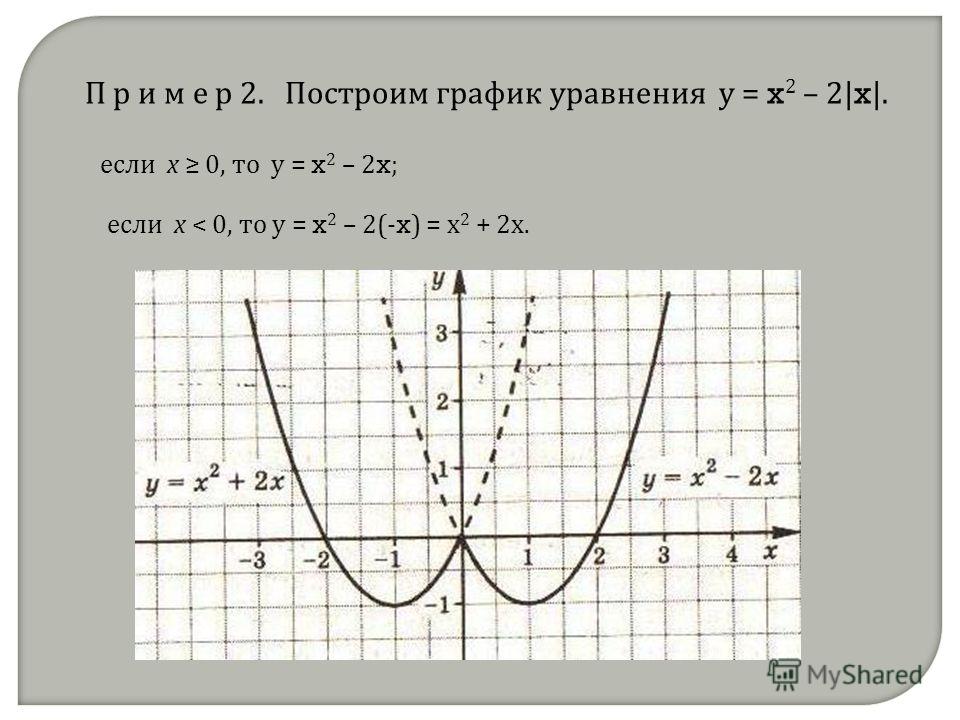
 5
5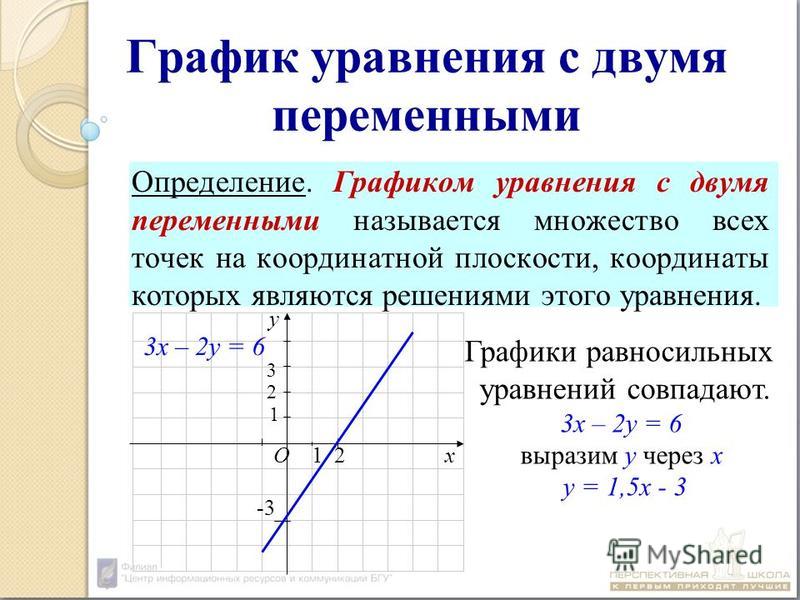

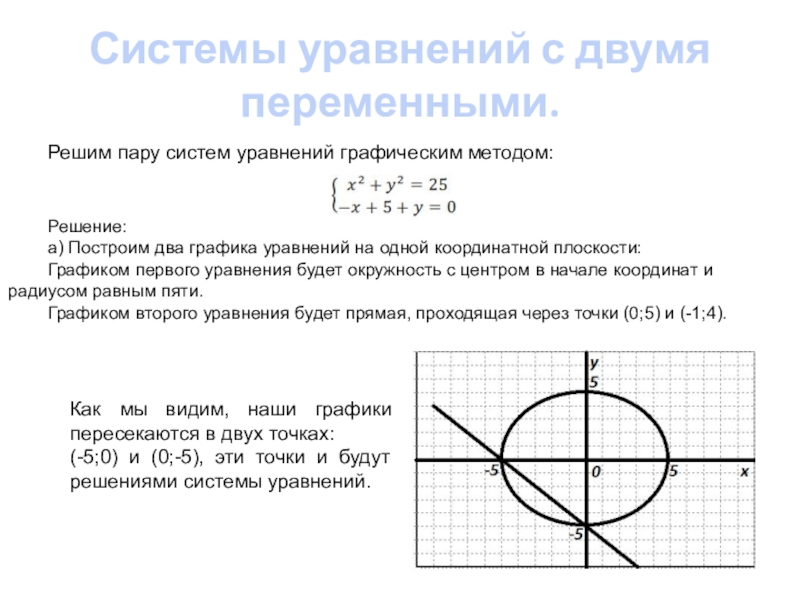 Посмотрите на разницу между частью (a) и частью (b) на (Рисунок).
Посмотрите на разницу между частью (a) и частью (b) на (Рисунок).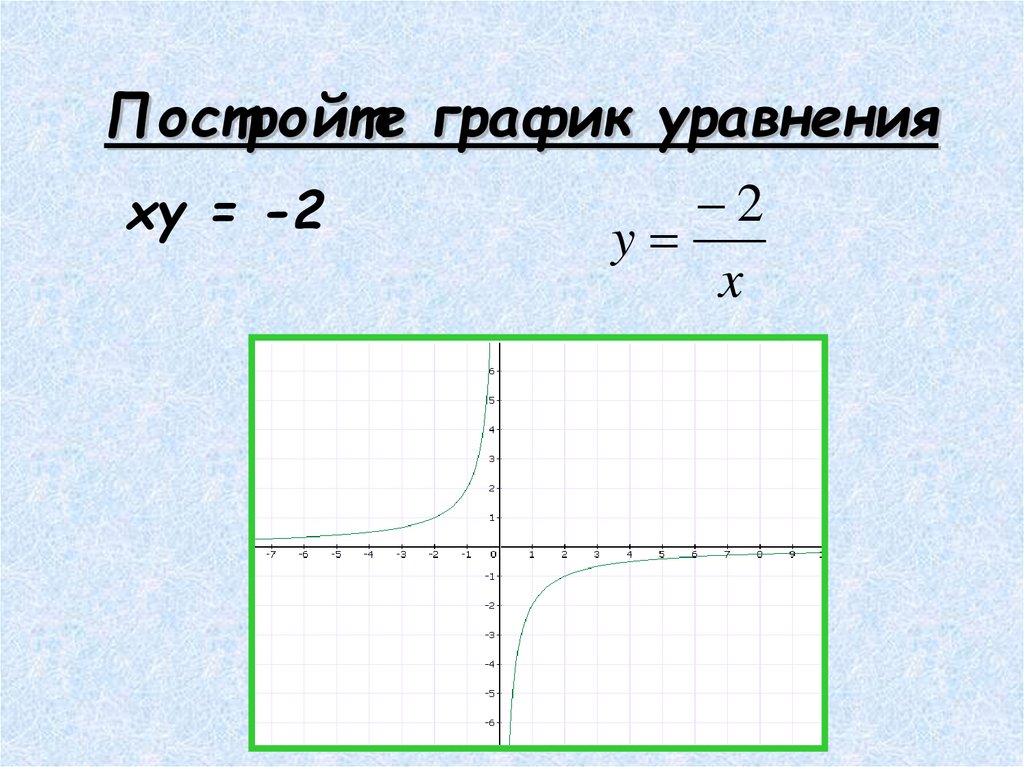
 См. (Рисунок).
См. (Рисунок).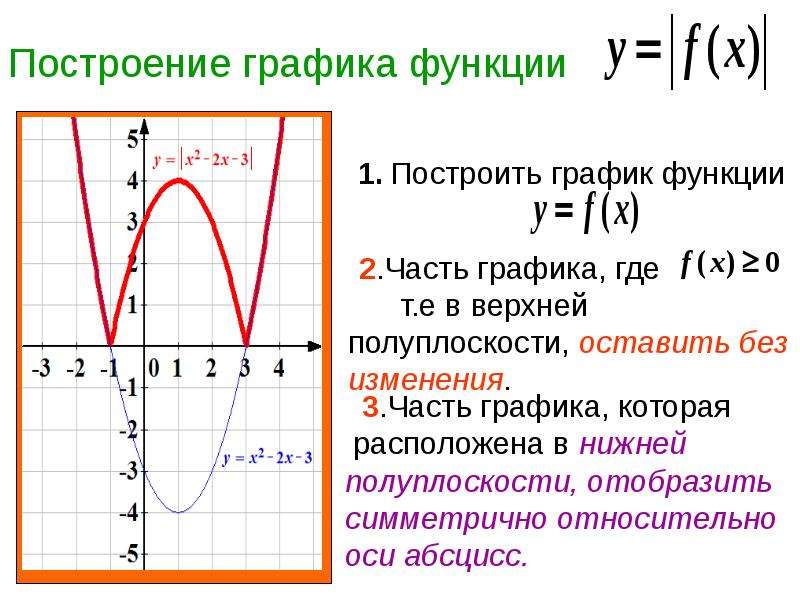 Два графика показаны на (Рисунок).
Два графика показаны на (Рисунок).


 Убедитесь, что точки совпадают. Если бы они не выстроились в очередь, это означало бы, что мы сделали ошибку и должны перепроверить всю нашу работу. См. Рисунок \ (\ PageIndex {2} \).
Убедитесь, что точки совпадают. Если бы они не выстроились в очередь, это означало бы, что мы сделали ошибку и должны перепроверить всю нашу работу. См. Рисунок \ (\ PageIndex {2} \).
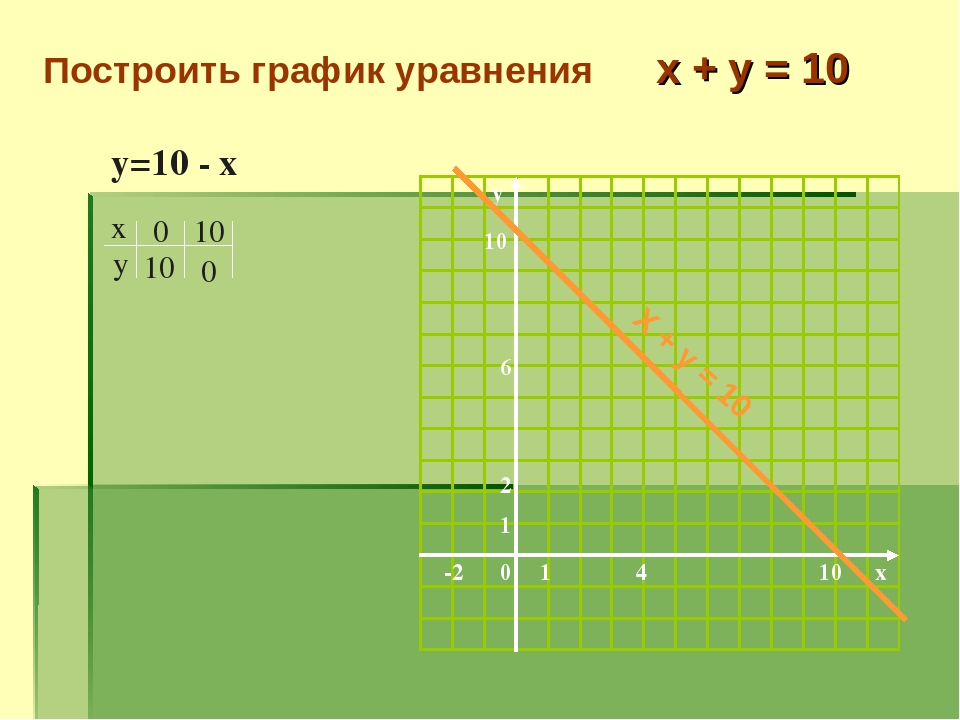
 Помните, что в примере y = \ (\ dfrac {1} {2} \) x + 3 мы тщательно выбирали значения для x, чтобы вообще не отображать дроби. Если мы решим уравнение 2x + y = 3 относительно y, будет легче найти три решения уравнения.
Помните, что в примере y = \ (\ dfrac {1} {2} \) x + 3 мы тщательно выбирали значения для x, чтобы вообще не отображать дроби. Если мы решим уравнение 2x + y = 3 относительно y, будет легче найти три решения уравнения.
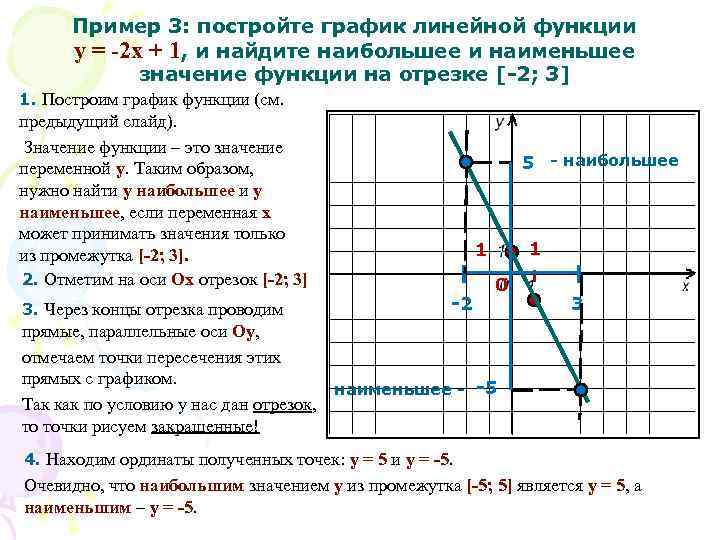



 Здесь находится точка. Мы получаем свои баллы
просто сопоставив значение x и значение y, чтобы получить их местоположение, и мы можем сделать
это для любой пары координат.
Здесь находится точка. Мы получаем свои баллы
просто сопоставив значение x и значение y, чтобы получить их местоположение, и мы можем сделать
это для любой пары координат. Вот выражение
Вот выражение Один метод, который мы могли бы использовать, чтобы найти
другие решения нашего уравнения составляют таблицу значений x и y. Мы можем это сделать
вставляя разные значения x и находя соответствующие им значения y.
Один метод, который мы могли бы использовать, чтобы найти
другие решения нашего уравнения составляют таблицу значений x и y. Мы можем это сделать
вставляя разные значения x и находя соответствующие им значения y. Эта форма полезна, потому что мы можем легко получить
x и y перехватывает , вставляя 0 для одной из переменных.Перехват
является пересечением прямой и оси x или y. Мы увидим, что эти
перехватчики помогут в построении линейных уравнений.
Эта форма полезна, потому что мы можем легко получить
x и y перехватывает , вставляя 0 для одной из переменных.Перехват
является пересечением прямой и оси x или y. Мы увидим, что эти
перехватчики помогут в построении линейных уравнений.
Ваш комментарий будет первым