Построение графика по точкам онлайн: Построение графика по точкам — Калькулятор Онлайн

1.2. Функции и их графики

1. Графики функций широко используются в различных разделах школьного курса математики в качестве наглядных опорных моделей, позволяющих сделать материал более доступным для восприятия. Развитие графических представлений, начатое на данном этапе изучения алгебры, продолжается далее при изучении конкретных функций.

При знакомстве с понятием «график функции» рекомендуем включить построение графика зависимости площади квадрата от его стороны, выражаемой формулой S = a². Напомним, что в учебнике парабола рассматривается позже при изучении темы «Одночлены», и там же (на 2-х уроках) происходит знакомство с кубической параболой. Предлагаем здесь на примере построения квадратичной параболы продемонстрировать применение графического калькулятора, а позже отводимые 2 урока посвятить формированию умения строить графики изучаемых функций в тетради и изучению их свойств.

Заметим, что в графическом калькуляторе не предусмотрена возможность переименования осей координат, поэтому при записи функций приходится использовать стандартные обозначения

x и у. То есть запись рассматриваемой зависимости будет иметь вид: y = x² , где x — длина стороны квадрата, а у — его площадь.

Составим следующую таблицу значений данной функции:

Для этого надо перейти из главного меню в режим таблиц (TABLE), удалить лишнее с помощью клавиши [F2] (DEL), ввести новую формулу, а затем, в режиме SET ([F5]) задать границы и шаг вычисления значений у:

Вернувшись к предыдущему экрану (нажав [EXIT]), даем графическому калькулятору указание заполнить таблицу, нажав клавишу [F6] (TABL).

Еще раз отметим, что таблицу, построенную на экране калькулятора, приходится смотреть по частям.

Теперь можно отметить найденные значения x и у в прямоугольной системе координат. Но для начала надо определить, какую именно часть координатной плоскости мы хотим увидеть на экране. Для этого в калькуляторе предусмотрен специальный режим View Window (т.

е. «окно вывода»). Вход в режим — последовательное нажатие клавиш [SHIFT] и [F3] (сверху над клавишей — желтая надпись V-Window). На экране появится таблица:

Возможно, таблица уже будет заполнена какими-нибудь значениями, оставшимися от предыдущих работ с графиками. Приведенные же на рисунке значения параметров определяют так называемое «стандартное» окно вывода для данной модели калькулятора. Для восстановления этих значений в приведенной таблице достаточно нажать клавишу [F1] (текущее значение INIT от «initial» — начальный). При стандартном окне вывода центр координат находится в центре экрана, масштаб по осям x и у одинаков, а размер точек экрана (напомним, размер экрана 127 x 63 точки) равен 0,1. Как видно из таблицы, стандартное окно включает в себя лишь очень небольшую часть координатной плоскости (12 меток по горизонтали и 6 меток по вертикали).

Попробуем отобразить найденные значения функции в стандартном окне. Для этого, нажав [EXIT], надо вернуться к рассматриваемой функции, повторить расчет таблицы (нажав [EXE] или [F6] (TABL)) и еще раз нажать клавишу [ЕХЕ] или [F6].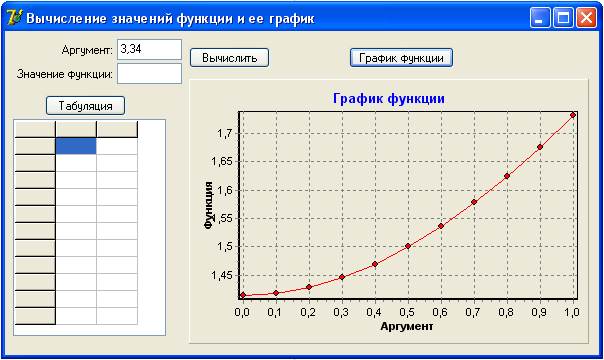 На экране появится:

Не все точки поместились в стандартном окне. Ведь среди вычисленных значений у максимальное равнялось 4, а размер окна ограничен у≤3,1. Сдвинем окно вывода, нажав два раза клавишу [REPLAY] вверх. Автоматически изменятся и параметры окна вывода, в чем можно убедиться, войдя в режим V-Window:

Возможно задать параметры окна вывода и непосредственно в режиме V-Window. С помощью клавиши [REPLAY] надо выделить цветом строку Xmin, набрать нужное значение и нажать [ЕХЕ]. Это значение и останется в строке. Затем — выбрать следующую строку (max, имеется в виду Xmax) и ввести туда другое число аналогичным способом. Точно также вводятся значения для Ymin и Ymax. Остальные значения калькулятор выберет сам автоматически. Размер точки и масштаб по осям координат при этом могут измениться. Масштаб по осям

x и у может стать различным. Например:

Это тот же самый график, но масштаб по осям в нем различен. Это видно по «черточкам», отмечающим единицы по осям координат.

Для дальнейшего рассмотрения примера вернемся к прежнему окну вывода, полученному сдвигом стандартного окна с сохранением его размера.

Всего в таблице было 9 пар чисел — значений x и у. Соответственно, на координатной плоскости было отмечено 9 точек (точка на пересечении осей координат не видна).

В отличие от обычной школьной практики, калькулятор позволяет увеличить количество отмечаемых точек. Предложим учащимся уменьшить шаг вычисления таблицы, сделав его 0,1 вместо 0,5. Тогда таблица будет состоять уже из 41 пары чисел, а график примет следующий вид:

Можно продолжать уменьшать шаг вычисления. Сделав его, например, равным 0,03, получим, что количество вычисляемых пар чисел достигнет 134, и точки на плоскости координат «сольются» в одну кривую.

Однако это еще не график функции. Это только ряд ее значений, отмеченных на плоскости координат.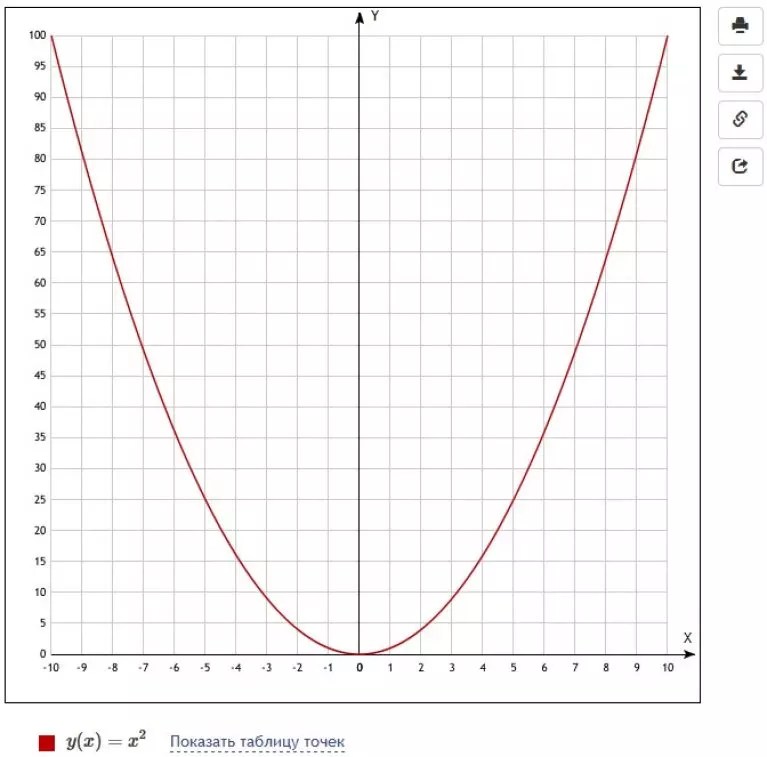 Чтобы убедиться в этом, надо предложить учащимся увеличить масштаб, как бы «приблизив» график. Сделать это на калькуляторе можно несколькими способами, но мы ограничимся самым наглядным из них.

Изменение масштаба можно производить в то время, когда на экран выведен график. Последовательное нажатие клавиш [SHIFT] и [F2] (сверху над клавишей желтым шрифтом написано ее вызываемое таким образом значение — Zoom, от английского слова «приближать», «увеличивать») приведет к изменению меню функциональных клавиш. Среди них появится новое значение у [F1] (ВОХ — основное значение этого английского слова — «коробка», но в данном случае это «прямоугольник»). Нажатие этой клавиши приведет к появлению на экране курсора в виде «крестика». Его можно перемещать по экрану с помощью клавиши [REPLAY]. Одновременно в нижней части экрана выводятся координаты курсора (X и Y) на плоскости координат.

После перемещения курсора в выбранную точку плоскости координат ее нужно отметить, нажав клавишу [ЕХЕ]. Теперь, при перемещении курсора по экрану, за ним будет «тянуться» прямоугольник, которым и надо выделить исследуемую часть графика. Повторное нажатие клавиши [ЕХЕ] приведет к тому, что выделенная часть графика будет «растянута» на весь экран (параметры окна вывода при этом, естественно, изменятся):

Вместе с тем, в калькуляторе предусмотрен специальный режим построения графиков функций, с которым теперь рекомендуется ознакомить учащихся.

Выйдя в главное меню (нажав клавишу [MENU]), следует выбрать клетку, отмеченную надписью GRAPH, и нажать [ЕХЕ] для перехода в режим построения графиков (далее — графический режим).

Появившаяся на экране таблица будет почти такой же, как и в табличном режиме, только вместо TABL у клавиши [F6] будет значение DRAW (от английского «рисовать»):

Близость интерфейсов данных режимов неслучайна, работа в них осуществляется по одним и тем же правилам. Ввод формулы, определение «окна вывода» (V-Window), изменение масштаба (Zoom) полностью аналогичны.

Обратим внимание на то, что при переходе из табличного в графический режим сохраняется и список ранее введенных функций. Здесь требуется проявить внимание и проверить, выделены ли цветом знаки равенства в записи функций (в некоторых моделях калькуляторов при смене режима работы выделения снимаются). Калькулятор рассматривает только те функции, в которых знаки равенства выделены, а остальные просто хранит в памяти до дальнейших указаний. Восстановление (равно как и снятие) выделения осуществляется нажатием клавиши [F1] (SEL от английского «select» — выбирать).

Отметим также, что не рассматривавшийся ранее режим STYL (клавиша [F4]) позволяет задать вид линии, которой рисуется график.

Рекомендуется также ознакомить учащихся с еще одним режимом анализа графиков — Trace (от английского «траектория», «слежение»). Переход в режим осуществляется тогда, когда на экран выведен график функции. Надо последовательно нажать клавиши [SHIFT] и [F1] (подписана сверху желтым шрифтом Trace).

Как и в режиме Zoom на экране появится курсор, но теперь он будет находиться на графике функции. С помощью клавиши [REPLAY] (вправо и влево) курсор можно перемещать по графику, а в это время в нижней строке экрана будут выводиться значения X и Y.

При стандартном окне вывода (или равном ему по размерам, как в данном случае) сдвиг курсора на одну позицию вправо или влево с помощью клавиши [REPLAY] эквивалентен изменению значения x на 0,1.

Разбор данного примера рекомендуется провести достаточно подробно. Это совершенно оправданно, так как, помимо освоения теоретического материала, учащиеся получат навыки построения графиков на калькуляторе. Овладев этим инструментом, они смогут успешно использовать его на всех последующих уроках, где будут рассматриваться те или иные функции и их графики.

2. Приведем примеры упражнений по теме «График функции», при выполнении которых рекомендуется использовать калькулятор.

Пример № 277

Функция задана формулой y = x(x — 3), где -2 ≤ x ≤ 2. Заполните таблицу (в учебнике приводится таблица с шагом 0,5) и постройте график функции.

После построения графика в тетради предложим учащимся сравнить его с построенным на калькуляторе. Для этого можно использовать проекционные возможности калькулятора.

Пример № 361 (из раздела «Дополнительные упражнения»).

Постройте в тетради график функции, заданной формулой, и сравните его с построенным на калькуляторе:

При построении графиков использовались окна вывода, отличные от стандартного. Однако на рисунках был сохранен одинаковый масштаб по обеим осям координат. Для этого, учитывая размеры экрана, интервал для x (т.е. Xmax — Xmin) брался в два раза больший, чем для у (Ymax — Ymin).

3. Усвоению понятия линейной функции способствуют упражнения, в которых в качестве примеров линейных функций рассматриваются графики реальных зависимостей.

Пример № 307

В бак налили воды, температура которой 10°С, и нагрели ее до 100°С, причем через каждую минуту температура повышалась на 1,5°С. Задайте формулой зависимость температуры воды у (в градусах Цельсия) от времени нагревания x (в минутах). Постройте график этой зависимости. Узнайте по графику:

• а) какую температуру имела вода через 5 мин., через 10 мин. после начала нагревания;
• б) через какое время вода нагрелась до 85°С.

Решение

Имеем формулу y = 1,5x + 10. Область определения функции y = 1,5x + 10 состоит из чисел от 0 до 60, а область ее значений — от 10 до 100. Это следует учесть при построении графика в тетради: можно выбрать масштаб по оси x — в 1 см 10 единиц, по оси у — в 1 см 20 единиц. Построим график по двум точкам (0; 10) и (60; 100) и по графику найдем точки (5; 17,5), (10; 25) и (50; 85).

Предложим учащимся построить график функции y = 1,5x + 10 на калькуляторе в заданной области вывода и «пошагать» по графику, отвечая на вопросы: через какое примерно время вода нагрелась до 30°С, до 50°С; какую примерно температуру имела вода через 35 мин. после начала нагревания? А еще через 10 мин.?

При предложенном на картинке окне вывода масштаб по x будет в два раза крупнее, чем по у (график «сплюснут» сверху), а сдвиг курсора в режиме Trace на одну позицию вправо или влево равен 1.

4. На примере работы с графиками прямой пропорциональности познакомим учащихся с новыми возможностями калькулятора. Для этого рассмотрим упражнение:

Пример № 330

Покажите схематически, как расположен график функции, заданной формулой: а) у = 1,7х; б) у = -3,1х; в) у = 0,9х; г) у = -2,3х. После работы в тетрадях и соответствующего вывода относительно коэффициента k предложим учащимся продолжить работу с заданными функциями.

• Построим на калькуляторе графики данных функций в одной координатной плоскости. Используем стандартное окно вывода:

В режиме Trace ([SHIFT] и [F1]), при одновременном построении графиков нескольких функций, курсор будет перемещаться по графику одной и той же функции при нажатии клавиши [REPLAY] вправо или влево. При нажатии клавиши [REPLAY] вверх или вниз курсор переместится на график следующей функции из списка построенных. Что это за функция, будет указано в верхней левой части экрана:

• По графику определим, какое значение принимает каждая из функций при x = -0,8.

Переместим курсор по графику любой из функций в точку, где x = -0,8. Нажимая клавишу [REPLAY] вверх или вниз, переместим курсор на все оставшиеся графики по очереди. Значение x при этом меняться не будет, а у будет соответствовать значению выбранной функции.

• По графику определим, при каком значении x каждая функция принимает значение, равное 1,5.

К сожалению, в режиме Trace сделать это можно только приблизительно. Курсор перемещается по графику (при стандартном окне вывода) с шагом 0,1. Точное значение у = 1,5 так найти не удастся. Для у = 1,7х: у = 1,5 при x, чуть меньшем 0,9.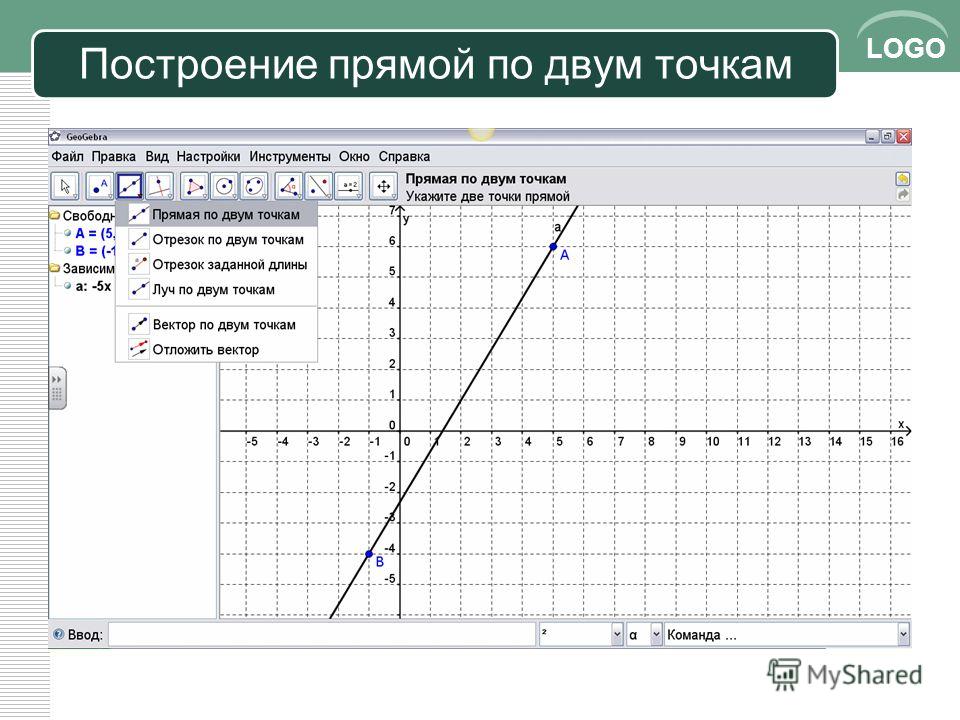

Для у = –3,1х: у = 1,5 при x, чуть большем -0,5.

Для у = 0,9х: у = 1,5 при x, чуть меньшем 1,7.

Для у = –2,3х: y = 1,5 при x между -0,6 и -0,7.

5. Взаимное расположение графиков линейных функций, заданных формулами вида y = kx + b, зависит от коэффициента при x: если коэффициенты при x различны, то графики пересекаются, если коэффициенты при x одинаковы, то графики параллельны. Советуем рисунки, приведенные в учебнике, продемонстрировать с помощью калькулятора.

Так, после рассуждений, приведенных на с. 61 в учебнике для функций y = 0,9x – 1 и y = 0,8x + 1, рекомендуем воспроизвести рисунок (рис. 31 из учебника) на экране калькулятора и «продолжить» его вправо, показав точку пересечения (20; 17).

Сначала построим графики с использованием стандартного окна вывода:

Из-за малого различия коэффициентов при x графики кажутся почти параллельными. Изменим масштаб, чтобы убедиться в обратном:

Обратим внимание на то, что, хотя границы для x и y заданы одинаково, из-за различия размеров экрана по вертикали и горизонтали реально масштаб по x в два раза крупнее, чем по y. Это наглядно видно по «черточкам» на осях.

Найти точку пересечения графиков можно в режиме Trace, а можно и точно в специальном режиме G-Solv (вход в режим — последовательное нажатие клавиш [SHIFT] и [F5]).

Режим G-Solv (от английских слов «graphic» — графический и «solve» — решать) специально предназначен для исследования графиков. В нем команд больше, чем функциональных клавиш, поэтому клавиша [F6] (в качестве значения обозначена пиктограмма ) предназначена для просмотра всего списка команд. Ее нажатие приводит к тому, что список команд меняется. Повторное нажатие восстанавливает первоначальный список команд.

Перечислим эти команды:

• ROOT (английское слово «root» означает «корень») служит для нахождения корней функции, то есть точек, в которых она пересекает ось x.
• MAX и MIN — определение максимальных и минимальных значений функции. Для линейной функции применение команд приведет к надписи «Not Found» — «не найдено»(понятие бесконечности калькуляторам неизвестно).
• Y-ICPT (от «intercept» — «пересекать») — определение точек пересечения графика с осью y.
• ISCT (от «intersect» — «перекрещиваться») — нахождение точек пересечения двух функций.
• Y-CAL, X-CAL — вычисление значения y по значению x и, наоборот, x по у.
• ∫dx — вычисление интеграла функции.

Все эти команды (кроме ISCT) могут быть выполнены только в отношении одного графика функции. Если функций несколько, исследовать их надо по очереди, используя команду SEL. Команда ISCT работает только при одновременном выводе на экран графиков двух функций.

Используем последнюю функцию для нахождения точки пересечения построенных графиков. Нажмем [F5] (ISCT). На экране появится курсор, помещенный в точку пересечения графиков. В нижней строке будут выведены его координаты:

На рис. 34 из учебника показаны графики функций y = kx + b при фиксированном b (на рисунке b = 3) и меняющемся k. Пример можно реализовать и исследовать на калькуляторе (окно вывода получено сдвигом стандартного окна):

В демонстрационном режиме, на усмотрение учителя, на данном примере можно ознакомить учащихся с еще одной возможностью калькуляторов — построением динамических графиков.

Вход в режим осуществляется через главное меню выбором пиктограммы DYNA:

Появившийся на экране список функций имеет такой же вид, что и при работе в табличном или графическом режимах. Только в верхней строке появится надпись «динамические функции». В списке функций могут сохраниться функции, оставшиеся от работ в других режимах. Во избежание путаницы их лучше удалить командой DEL (клавиша [F2]). В данном режиме в записи функций, помимо переменной x, необходимо использовать буквенные параметры. Напомним, что ввод букв на калькуляторе осуществляется последовательным нажатием клавиши [ALPHA] и клавиши, над которой написана красным нужная буква. Введем:

Значение параметров окна вывода сохраним из предыдущего примера:

Вернувшись к списку функций (нажав [EXIT]), надо войти в подменю описания параметров, нажав [F4] (значение VAR — от английского слова «variable» — переменная). Появится новое меню:

Теперь надо выбрать режим вывода динамического графика, нажав [F3] (SPEED — скорость, англ.) и войдя в соответствующее подменю. Появится таблица описания скоростных режимов. Рекомендуется выбрать [F1].

В этом режиме смена графиков будет осуществляться только после нажатия клавиши [EXE], в остальных случаях — автоматически, с большей или меньшей скоростью.

Возврат к предыдущему подменю — клавиша [EXIT].

Теперь надо войти в режим задания границ и шага изменения параметра k. Для этого надо нажать [F2] (SET — установка). Появится таблица, в которой с помощью клавиши [REPLAY] надо по очереди выделить каждую строку со значением параметра, заменить его на желаемое значение и нажать [EXE]. Будем менять k от -2 до 2 с шагом 0,5.

Выход из режима — клавиша [EXIT].

Параметры заданы; для начала построения графиков надо нажать клавишу [F6] (DYNA).

После завершения цикла построение графиков не прервется, а продолжится в обратном порядке (от k = 2 до k = -2) и т.д. Выход из режима — клавиша [EXIT].

Аналогичные действия можно предпринять и при разборе рис. 33 из учебника. Здесь у функции y = kx + b меняется параметр b при фиксированном k (k = 0,5). Сделать это снова можно в двух режимах: обычном графическом

(использовалось стандартное окно вывода)

и динамическом.

Плоттер

точек — (соединение линий/точек)

Поиск инструмента

Найдите инструмент в dCode по ключевым словам:

Просмотрите полный список инструментов dCode

Плоттер точек

Инструмент/плоттер для рисования до 4 точек (точечная диаграмма или кривая) на одном графике или 2D-плоскости (и соединения точек, если нужно) по своим координатам.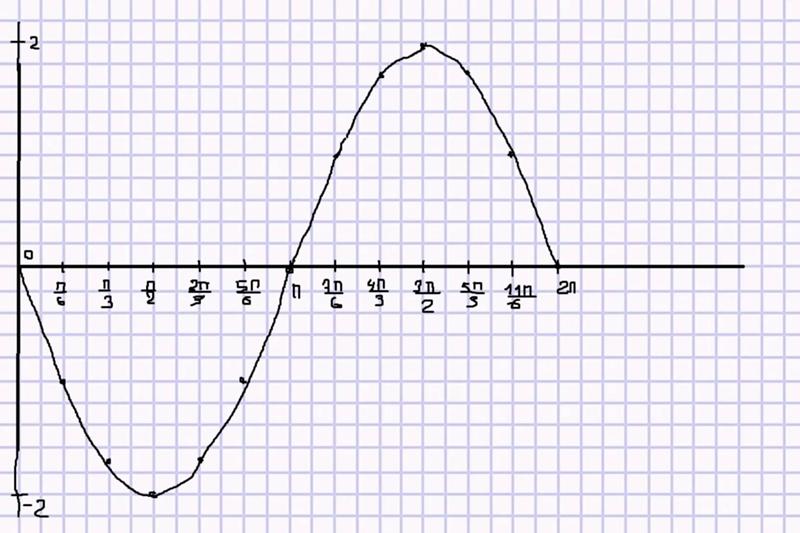

Результаты

Плоттер точек — dCode

Теги: Функции, Теория графов

Поделиться

dCode и другие

dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Точки графика с таблицей значений (x,y)

Загрузка…
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

Название горизонтальной оси X
Имя вертикальной оси Y
Легенда
Размер точки

Режим отображения

Только точки Начертить линию между точками

См. также: Функция поиска уравнений — Y-пересечение

2-й участок (на том же графике)

Загрузка…
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

Легенда

3-й участок (на том же графике)

Загрузка. ..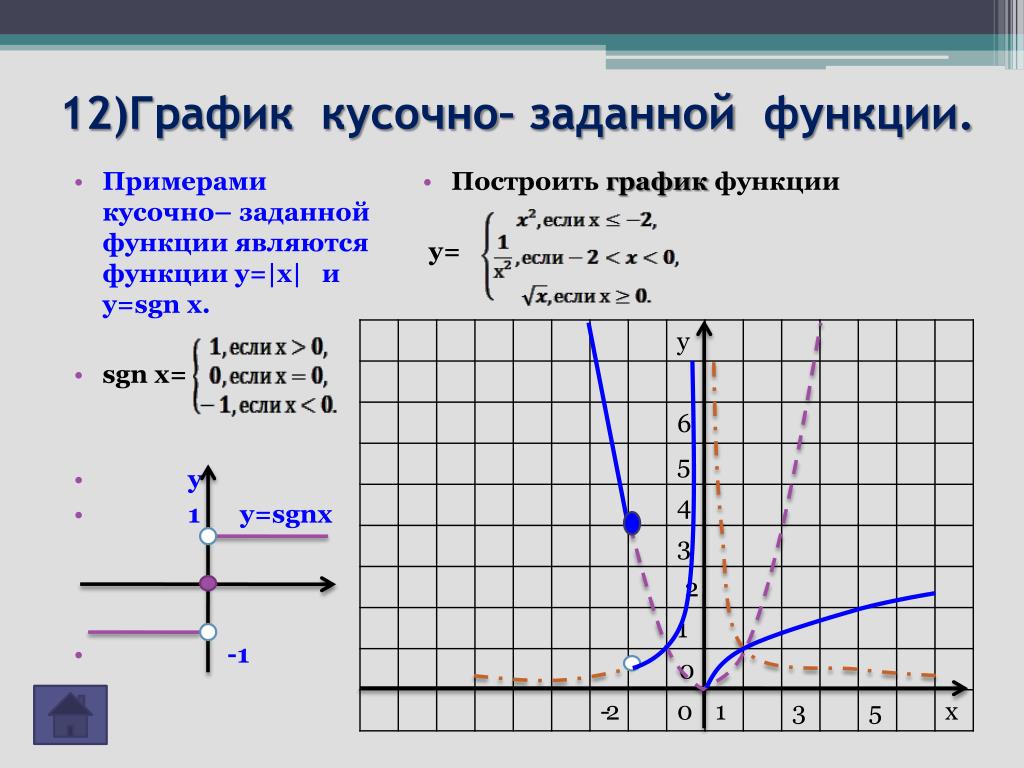
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

Легенда

4-й участок (на том же графике)

Загрузка…
(если это сообщение не исчезнет, ​​попробуйте обновить эту страницу)

Легенда

Ответы на вопросы (FAQ)

Что такое плоттер кривых? (Определение)

Картплоттер — это инструмент, используемый для визуализации кривой. Плоттер использует массив значений, чтобы определить, как следует рисовать кривую, чтобы она проходила через каждую точку.

Как нанести точки (x,y)?

Используйте график с двумерной системой координат, т. е. с горизонтальной осью $ x $ и вертикальной осью $ y $ (в идеале ортонормированная система отсчета).

Найдите положение каждой координаты точек на каждой оси, расположив значение абсциссы на оси $ x $ и значение ординаты на оси $ y $.

Положение точки находится на пересечении вертикальной линии, проходящей через абсциссу, и горизонтальной линии, проходящей через ординату.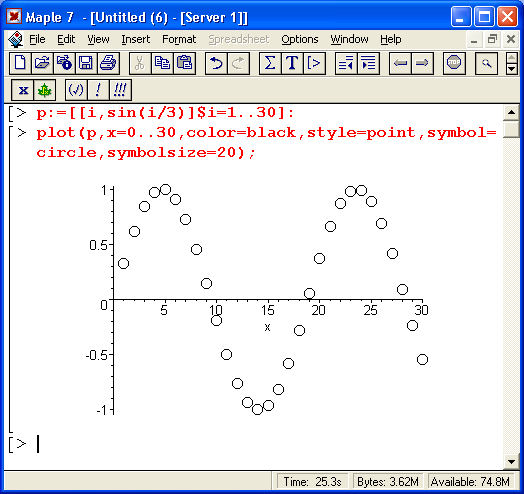

Пример: Поместите точку с координатами $ (x,y) = (1,2) $, точка находится в горизонтальном положении $ x = 1 $ и вертикальном положении $ y = 2 $

Для представления значений функции (аффинной, полиномиальной, экспоненциальной и т. д.) используйте изображение на специальной странице функций в dCode.

Как найти функцию, соответствующую точкам?

dCode предлагает средство поиска уравнений.

Кроме того, существуют методы интерполяции, позволяющие составить уравнение, проходящее через точки. См. интерполяцию Лагранжа или интерполяцию Невилла.

Как соединить точки?

Проведите линию между каждой найденной точкой и следующей так, чтобы получилась кривая, состоящая из частей.

Полученный путь может представлять рисунок, если порядок точек сохранен.

Как нарисовать 2 графика на одном графике?

Используйте вторую таблицу данных для указания координат. Укажите другую легенду, чтобы различать две кривые.

Зачем использовать точечный плоттер?

Линейные плоттеры полезны для визуализации того, как одна переменная зависит от другой, для понимания того, как взаимодействуют различные переменные, и могут использоваться для прогнозирования реакции одной переменной на изменения другой переменной.

Исходный код

dCode сохраняет право собственности на исходный код «Points Plotter». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Points Plotter», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, взломщик, транслятор) или «Points Plotter». Функции плоттера (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, сценарий или доступ к API для «Points Plotter» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.

Cite dCode

Копирование и вставка страницы «Points Plotter» или любых ее результатов разрешено (даже в коммерческих целях) при условии, что вы цитируете dCode!
Бесплатный экспорт результатов в виде файла .csv или .txt осуществляется нажатием значка export . , https://www.dcode.fr/points-плоттер

Резюме

• Точки графика с таблицей значений (x,y)
• Что такое график? (Определение)
• Как нанести точки (x,y)?
• Как найти функцию, соответствующую точкам?
• Как соединить точки?
• Как нарисовать 2 графика на одном графике?
• Зачем использовать точечный плоттер?

Аналогичные страницы

• Пересечение по оси Y
• Функция поиска уравнения
• Степень полинома
• Функция ошибки
• Область производной функции
• Логарифм
• Среднее значение функции
• СПИСОК ИНСТРУМЕНТОВ DCODE

Поддержка

• Paypal
901 36 Patreon
• Подробнее

 

Форум/Помощь

Ключевые слова

сюжет ,график,точка,координата,абсцисса,ордината

Ссылки

▲

Построение линейных диаграмм — Tableau

Применяется к: Tableau Desktop

Линейные диаграммы соединяют отдельные точки данных в представлении. Они обеспечивают простой способ визуализации последовательности значений и полезны, когда вы хотите увидеть тенденции во времени или спрогнозировать будущие значения. Дополнительные сведения о типе метки линии см. в разделе Метка линии.

Примечание . В представлениях, использующих тип линейной метки, вы можете использовать свойство «Путь» на карточке «Метки», чтобы изменить тип линейной метки (линейная, ступенчатая или скачкообразная) или закодировать данные путем соединения меток с использованием определенного порядка рисования. Подробнее см. в разделе Свойства пути в разделе Управление внешним видом меток в представлении

. Чтобы создать представление, отображающее сумму продаж и сумму прибыли за все годы, а затем использует прогнозирование для определения тренда, выполните следующие действия:

1. Подключиться к источнику данных Sample — Superstore.

2. Перетащите измерение даты заказа в Колонны.

   Tableau агрегирует дату по годам и создает заголовки столбцов.

3. Перетащите меру Продажи в ряды.

   Tableau агрегирует продажи как SUM и отображает простую линейную диаграмму.

4. Перетащите показатель «Прибыль» в «Строки» и поместите его справа от показателя «Продажи».

   Tableau создает отдельные оси вдоль левого поля для продаж и прибыли.

   Обратите внимание, что шкала двух осей различна: ось «Продажи» масштабируется от 0 до 700 000 долларов, а ось «Прибыль» — от 0 до 100 000 долларов. Это может затруднить понимание того, что объемы продаж намного превышают значения прибыли.

   При отображении нескольких показателей на линейной диаграмме можно выровнять или объединить оси, чтобы пользователям было проще сравнивать значения.

   Дополнительные сведения о выравнивании осей см. в разделе Сравнение двух показателей с использованием двух осей.

   Дополнительные сведения о применении одной оси для нескольких мер см. в разделе Объединение осей для нескольких мер в одну ось.

   С помощью любого из этих параметров вы можете создать комбинированную диаграмму, чтобы изменить тип метки для одного из ваших показателей.

   Дополнительные сведения см. в разделе Создание комбинированной диаграммы (назначение различных типов меток мерам).

5. Перетащите поле SUM(Profit) из строки на ось продаж, чтобы создать смешанную ось. Две бледно-зеленые параллельные полосы указывают на то, что Прибыль и Продажи будут использовать смешанную ось, когда вы отпустите кнопку мыши.

   Представление обновляется и выглядит следующим образом:

   Представление довольно разреженное, потому что мы рассматриваем суммирование значений за год.

6. Щелкните стрелку раскрывающегося списка в поле «Год (дата заказа)» на полке «Столбцы» и выберите «Месяц» в нижней части контекстного меню, чтобы увидеть непрерывный диапазон значений за четырехлетний период.

   Результирующий вид намного более детализирован, чем исходный вид:

   Обратите внимание, что перед концом каждого года значения становятся намного выше. Подобная закономерность известна как сезонность . Если мы включим функцию прогнозирования в представлении, мы сможем увидеть, следует ли нам ожидать, что очевидная сезонная тенденция сохранится в будущем.

7. Чтобы добавить прогноз, на панели аналитики перетащите модель прогноза в представление, а затем перетащите ее в прогноз.