Построение графика линейной функции онлайн: IIS 7.0 Detailed Error — 404.11

Y 4 x 4 xy график. Построение графиков онлайн. Построение графика линейной функции

«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.

«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).

«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а

«Квадратичная функция и её график» — Решение.у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.

«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения.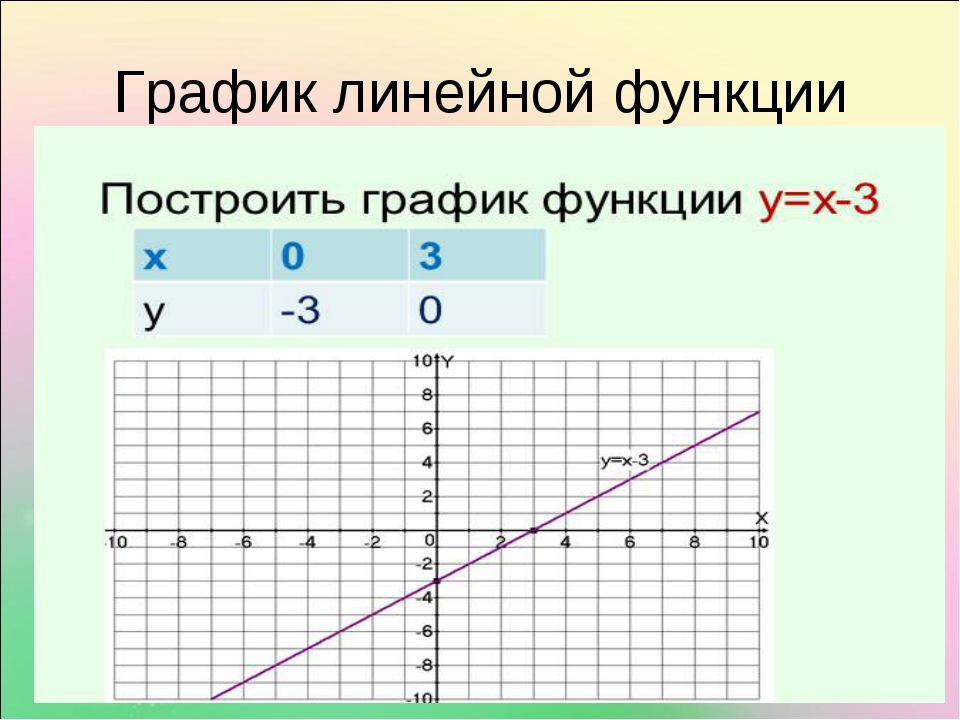

2) Построить ось симметрии x=-1. y.

Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.

Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.

1) Рассмотрим пример построения графика линейной функции: y=5x-2

Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку

В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2 . В другую ячейку формулу можно ввести аналогично (изменив D4 на D5 ) или использовать маркер автозаполнения.

В итоге мы получим табличку:

Теперь можно приступать к созданию графика.

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)

Появиться пустая область диаграмм.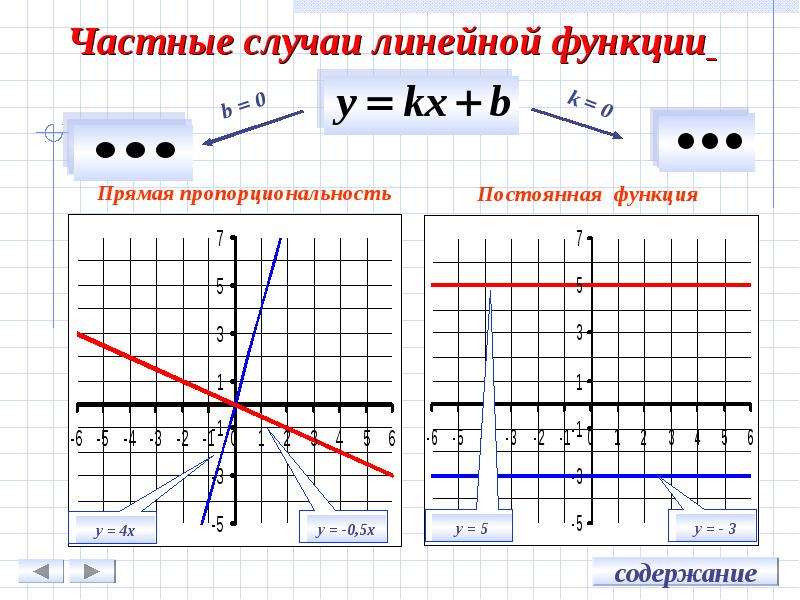 2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х .

Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.

Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.

Любые другие графики непрерывных функций строятся аналогично.

3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.

Рассмотрим это на примере функции у=1/х .

Функция определена на интервалах (- беск;0) и (0; +беск)

Создадим график функции на интервалах: [-4;0) и (0; 4].

Подготовим две таблички, где х изменяется с шагом

0,2 :

Находим значения функции от каждого аргумента х аналогично примерам выше.

На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно

Получаем график функции y=1/x

В дополнение привожу видео — где показан порядок действий, описанный выше.

В следующей статье расскажу как создать 3-мерные графики в Excel.

Спасибо за внимание!

Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х , а на оси ординат — значения функции у = f (х) .

Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.

Другими словами, график функции y = f (х) — это множество всех точек плоскости, координаты

х, у которых удовлетворяют соотношению y = f(x) .

На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х 2 — 2х .

Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».

С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x) , то для нахождения числа f(а) (т. е. значения функции в точке х = а ) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции

y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).

Например, для функции f(х) = х 2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.

График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х 2 — 2х принимает положительные значения при х и при х > 2 , отрицательные — при 0 наименьшее значение функция у = х 2 — 2х принимает при х = 1 .

Для построения графика функции f(x) нужно найти все точки плоскости, координаты х , у которых удовлетворяют уравнению y = f(x) . В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно — с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу

х придают конечное число значений — скажем, х 1 , х 2 , x 3 ,…, х k и составляют таблицу, в которую входят выбранные значения функции.

Таблица выглядит следующим образом:

Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x) . Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).

Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.

Пример 1 . Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:

Соответствующие пять точек показаны на рис. 48.

На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.

Для обоснования своего утверждения рассмотрим функцию

.

Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.

Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции,как правило, поступают следующим образом.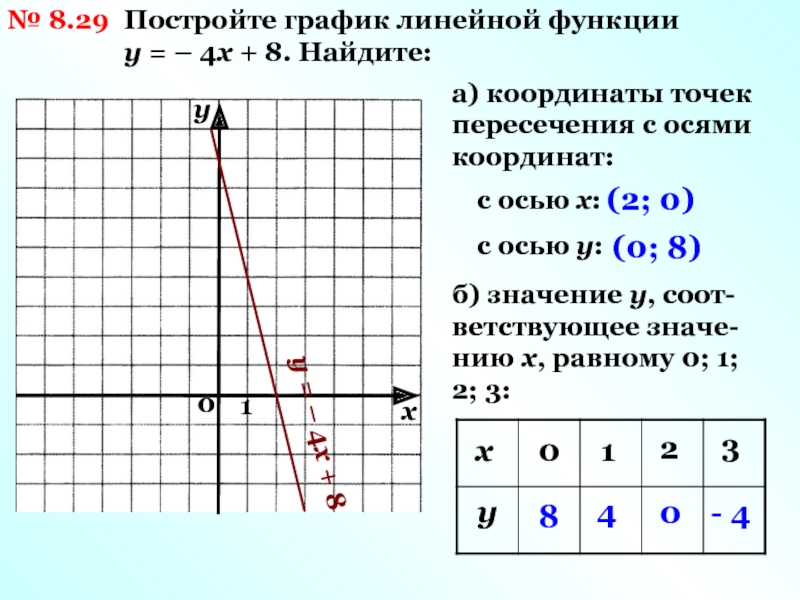

Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.

Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.

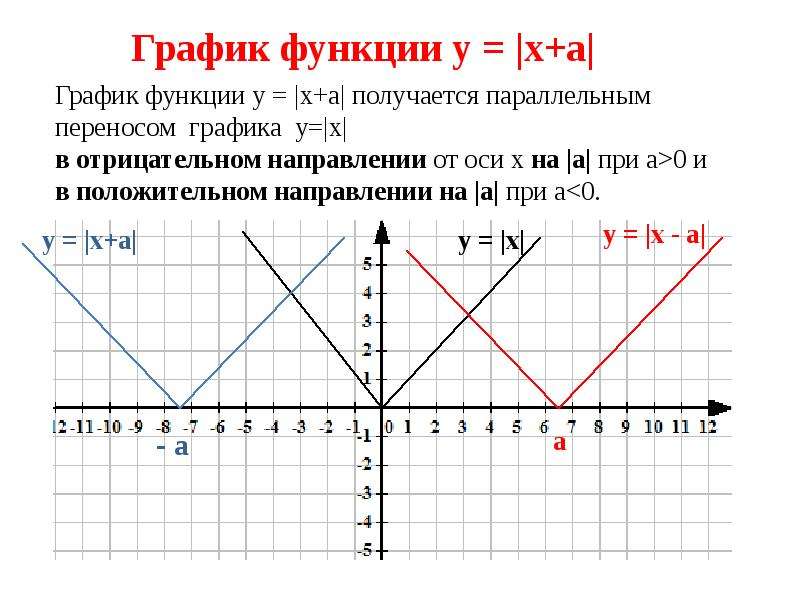
График функции у = |f(x)|.

Нередко приходится строить график функции y = |f(x) |, где f(х) — заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать

Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х) , у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции

y = f(x) , имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x) , которая лежит ниже оси х, следует симметрично отразить относительно оси х ).

Пример 2. Построить график функции у = |х|.

Берем график функции у = х (рис. 50, а) и часть этого графика при х (лежащую под осью х ) симметрично отражаем относительно оси х . В результате мы и получаем график функции у = |х| (рис. 50, б).

Пример 3 . Построить график функции y = |x 2 — 2x|.

Сначала построим график функции y = x 2 — 2x. График этой функции — парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции

у = |х 2 -2х| , исходя из графика функции у = х 2 — 2x

График функции y = f(x) + g(x)

Рассмотрим задачу построения графика функции y = f(x) + g(x).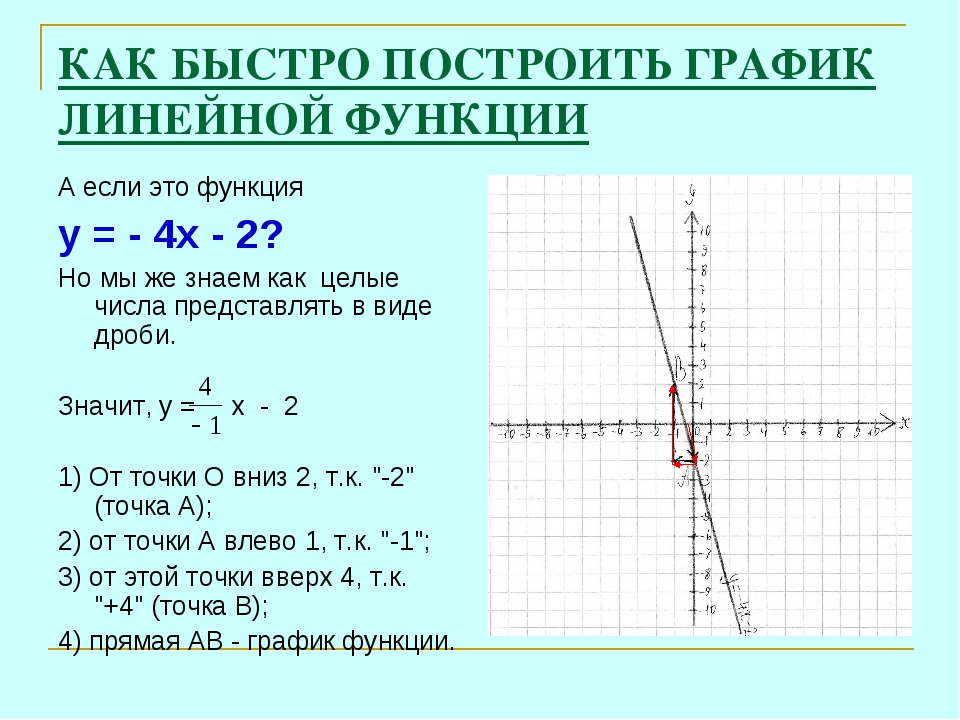 если заданы графики функций y = f(x) и y = g(x) .

Заметим, что областью определения функции y = |f(x) + g(х)| является множество всех тех значений х, для которых определены обе функции y = f{x) и у = g(х), т. е. эта область определения представляет собой пересечение областей определения, функций f{x) и g{x).

Пусть точки (х 0 , y 1 ) и (х 0 , у 2 ) соответственно принадлежат графикам функций y = f{x) и y = g(х) , т. е. y 1 = f(x 0), y 2 = g(х 0).

Тогда точка (x0;. y1 + y2) принадлежит графику функции у = f(х) + g(х) (ибо f(х 0) + g(x 0 ) = y1 +y2 ),. причем любая точка графика функции y = f(x) + g(x) может быть получена таким образом. Следовательно, график функции у = f(х) + g(x) можно получить из графиков функций y = f(x) . и y = g(х) заменой каждой точки (х n , у 1) графика функции y = f(x) точкой (х n , y 1 + y 2), где у 2 = g(x n ), т. 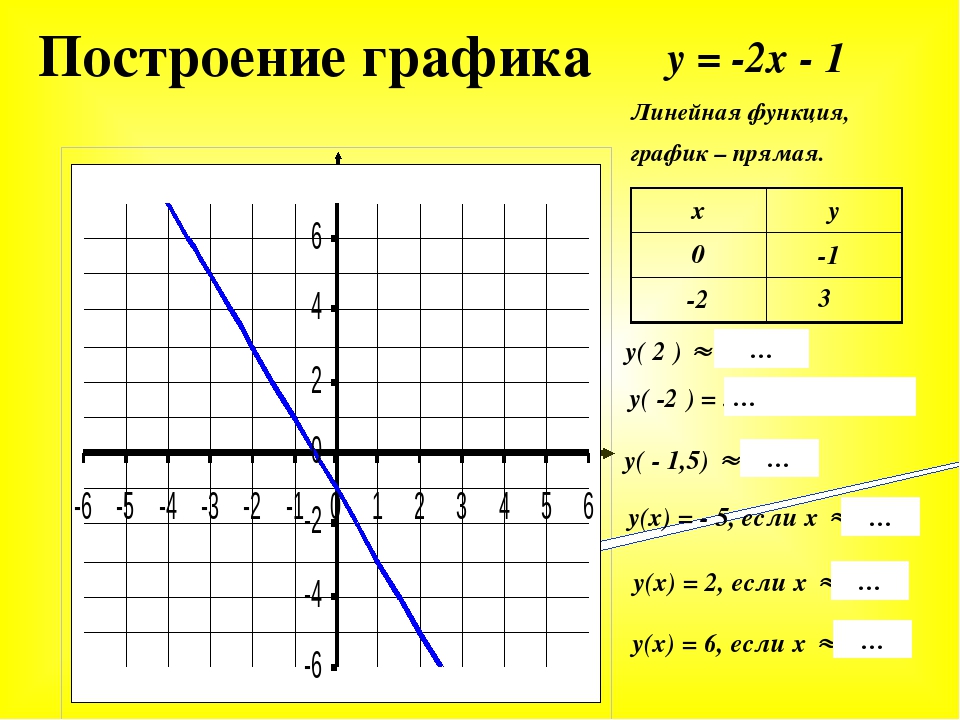е. сдвигом каждой точки (х n , у 1 ) графика функции y = f(x) вдоль оси у на величину y 1 = g(х n ). При этом рассматриваются только такие точки х n для которых определены обе функции y = f(x) и y = g(x) .

Такой метод построения графика функции y = f(x) + g(х ) называется сложением графиков функций y = f(x) и y = g(x)

Пример 4 . На рисунке методом сложения графиков построен график функции
y = x + sinx .

При построении графика функции y = x + sinx мы полагали, что f(x) = x, а g(x) = sinx. Для построения графика функции выберем точки с aбциссами -1,5π, -, -0,5, 0, 0,5,, 1,5, 2. Значения f(x) = x, g(x) = sinx, y = x + sinx вычислим в выбранных точках и результаты поместим в таблице.

В золотой век информационных технологий мало кто будет покупать миллиметровку и тратить часы для рисования функции или произвольного набора данных, да и зачем заниматься столь муторной работой, когда можно построить график функции онлайн. Кроме того, подсчитать миллионы значений выражения для правильного отображения практически нереально и сложно, да и несмотря на все усилия получится ломаная линия, а не кривая. Потому компьютер в данном случае – незаменимый помощник.

Что такое график функций

Функция – это правило, по которому каждому элементу одного множества ставится в соответствие некоторый элемент другого множества, например, выражение y = 2x + 1 устанавливает связь между множествами всех значений x и всех значений y, следовательно, это функция. Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.

На рисунке мы видим график функции y = x . Это прямая и у каждой ее точки есть свои координаты на оси X и на оси Y . Исходя из определения, если мы подставим координату X некоторой точки в данное уравнение, то получим координату этой точки на оси Y .

Сервисы для построения графиков функций онлайн

Рассмотрим несколько популярных и лучших по сервисов, позволяющих быстро начертить график функции.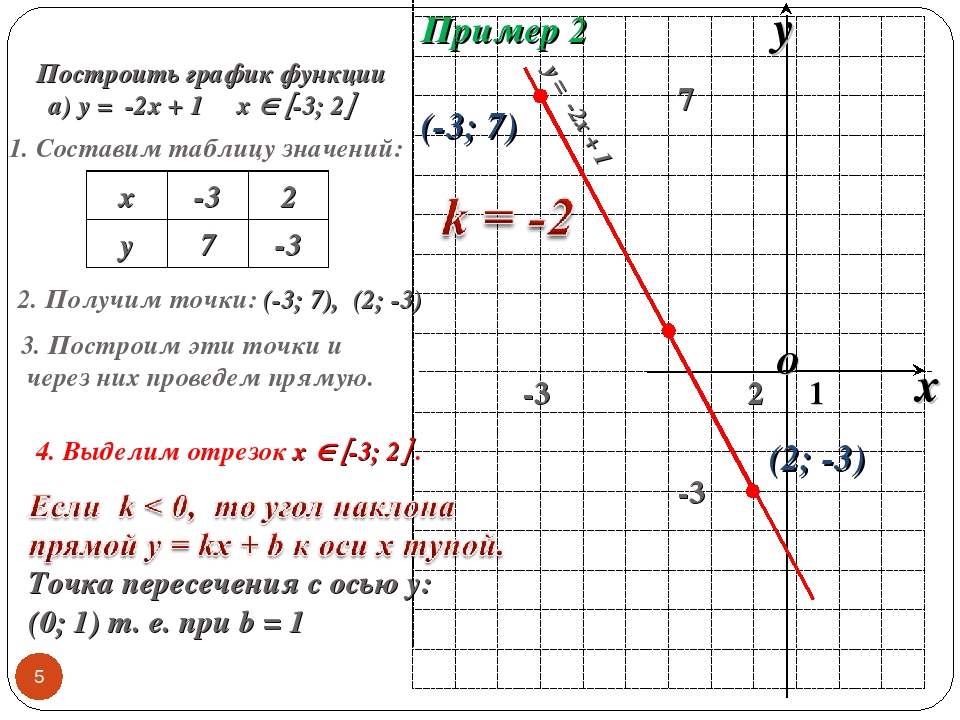

Открывает список самый обычный сервис, позволяющий построить график функции по уравнению онлайн. Umath содержит только необходимые инструменты, такие как масштабирование, передвижение по координатной плоскости и просмотр координаты точки на которую указывает мышь.

Инструкция:

1. Введите ваше уравнение в поле после знака «=».
2. Нажмите кнопку «Построить график» .

Как видите все предельно просто и доступно, синтаксис написания сложных математических функций: с модулем, тригонометрических, показательных — приведен прямо под графиком. Также при необходимости можно задать уравнение параметрическим методом или строить графики в полярной системе координат.

В Yotx есть все функции предыдущего сервиса, но при этом он содержит такие интересные нововведения как создание интервала отображения функции, возможность строить график по табличным данным, а также выводить таблицу с целыми решениями.

Инструкция:

1. Выберите необходимый способ задания графика.
2. Введите уравнение.
3. Задайте интервал.
4. Нажмите кнопку «Построить» .

Для тех, кому лень разбираться, как записать те или иные функции, на этой позиции представлен сервис с возможностью выбирать из списка нужную одним кликом мыши.

Инструкция:

1. Найдите в списке необходимую вам функцию.
2. Щелкните на нее левой кнопкой мыши
3. При необходимости введите коэффициенты в поле «Функция:» .
4. Нажмите кнопку «Построить» .

В плане визуализации есть возможность менять цвет графика, а также скрывать его или вовсе удалять.

Desmos безусловно – самый навороченный сервис для построения уравнений онлайн. Передвигая курсор с зажатой левой клавишей мыши по графику можно подробно посмотреть все решения уравнения с точностью до 0,001. Встроенная клавиатура позволяет быстро писать степени и дроби. Самым важным плюсом является возможность записывать уравнение в любом состоянии, не приводя к виду: y = f(x).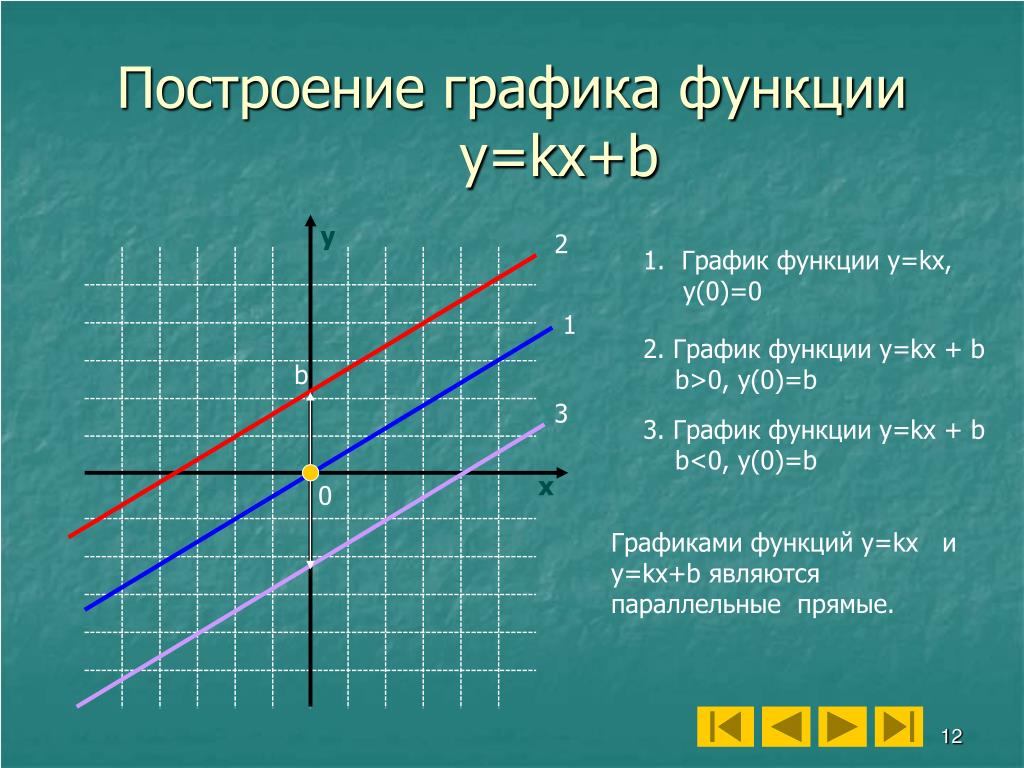

Инструкция:

1. В левом столбце кликните правой кнопкой мыши по свободной строке.
2. В нижнем левом углу нажмите на значок клавиатуры.
3. На появившейся панели наберите нужное уравнение (для написания названий функций перейдите в раздел «A B C»).
4. График строится в реальном времени.

Визуализация просто идеальная, адаптивная, видно, что над приложением работали дизайнеры. Из плюсов можно отметить огромное обилие возможностей, для освоения которых можно посмотреть примеры в меню в верхнем левом углу.

Сайтов для построения графиков функций великое множество, однако каждый волен выбирать для себя исходя из требуемого функционала и личных предпочтений. Список лучших был сформирован так, чтобы удовлетворить требования любого математика от мала до велика. Успехов вам в постижении «царицы наук»!

Графики линейной функции, содержащей модуль

1. Графики линейной функции, содержащей модуль.

2. I. Графики функций вида y = |kx+b|

Для построения графика функции y=|kx+b|
надо сохранить ту часть графика функции
y=kx+b, точки которой находятся на оси Ох
или выше этой оси, и симметрично отразить
относительно оси Ох ту часть графика
функции y=kx+b, которая расположена
ниже оси Ох.

3. Построение графика

y
1
у х 3
2
1. Построим
график функции
1
у х 3
2
х
0
4
у
-3
-1
2. Выполним
необходимые
преобразования
графика линейной
функции
0
x

4. II. Графики функций вида y= k|x|+b

Для построения графика функции
y= k|x|+b надо сохранить ту часть
графика функции y=kx+b, точки которой
находятся на оси Оу или справа от неё, и
симметрично отразить эту часть
относительно оси Оу.

5. Построение графика функции

у 3 x 2
y
1. Построить
график функции
у 3х 2
х
0
2
у
-2
4
x
0
2. Выполним
необходимые
преобразования
графика линейной
функции

6. Устная работа

y
3
2
Укажите
график для
функции,
заданной
формулой
1
x
0
1
у 3х 6

7. Устная работа

y
Укажите формулу,
соответствующую
данному графику
функции
x
0
1
1
№1. у х 3
3
1
№ 2. у х 3
3
№3. у
1
х 3
3

8. Устная работа

y
На рисунке
представлены
графики
функций
2
1
у 3х 5 и у х 1
3
3
Найдите корень
уравнения
2
1
3х 5 х 1
3
3
x
1
2
1
у х 1
3
3
у 3х 5

9. Устная работа

y
3
2
Укажите
график для
функции,
заданной
формулой
1
x
0
1
у 3х 6

10. Устная работа

y
Укажите формулу,
соответствующую
данному графику
функции
x
0
1
1
№1. у х 3
3
1
№ 2. у х 3
3
№3. у
1
х 3
3

11. Устная работа

y
На рисунке
представлены
графики
функций
2
1
у 3х 5 и у х 1
3
3
Найдите корень
уравнения
2
1
3х 5 х 1
3
3
x
1
2
1
у х 1
3
3
у 3х 5

12.

Построение графика функции 1
у
х 2
1
2
1
1. у х 2
2. у х 2
2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
1
у х 2
2
Первый вариант выполняет построения №1, второй вариант — №2.

13. Проверка работы I варианта

1
у х 2
2
х
0
4
у
-2
0
у
1
х 2
2
1
у х 2
2
y
x
0
1

14. Проверка работы II варианта

1
у х 2
2
х
0
4
у
-2
0
1
у х 2
2
1
у х 2
2
y
x
0 1
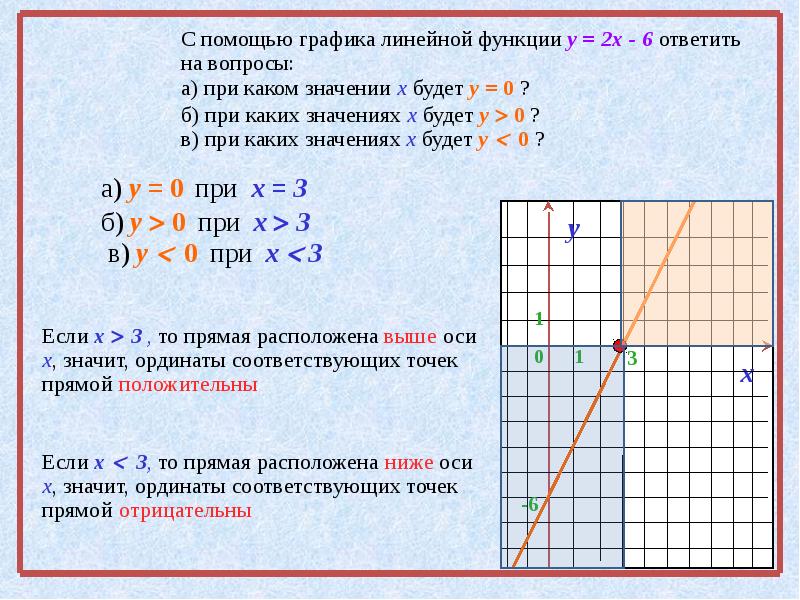
Исследуйте число решений
у 2 х 2 4х 24
2
b
уравнения
y
у 2х 4 2
y b
у 2х 4 2
Горизонтальная
прямая, проходящая
через точку с
ординатой b.
Ответ: если b
b=0, то уравнение имеет два корня; если 0
уравнение имеет четыре корня; если b=2, то
уравнение
имеет
три корня;
если
то
уравнение
Если
Если
Если
0
b>2
b
уравнение
то
то
уравнение
уравнение
имеет
корней
имеет
дваb>2,
корня
четыре
не
имеет.
корня.
Если
Если
b=2,
b=0,
то
то
уравнение
уравнение
имеет
имеет
три
два
корня.
корня.
имеет два корня.
x

16. При каком значении b уравнение имеет единственное решение

При каком значении b уравнение 3х 6 2 х b
имеет единственное решение
1. у 3х 6
y
2. у 2 х b
Ответ: при
b>-3
исходное
уравнение
имеет
единственно
е решение.
x
-3

18. Домашнее задание

у 2х 4
y
1
0
1
x

Линейная функция 7 класс онлайн-подготовка на Ростелеком Лицей

Линейная функция и ее график

Линейная функция – это функция вида y = kx+b, где х – независимая переменная, k и b – некоторые числа.

Нетрудно заметить, что прямая пропорциональность – частный случай линейной функции. При b = 0 линейная функция принимает вид y = kx, а это и есть прямая пропорциональность.

Рассмотрим две функции: y=4x+3 и y=4x и построим их графики.

х	-2	-1	0	1	2
у=4х	-8	-4	0	4	8
у=4х+3	-5	-1	3	7	11

 

 

Мы видим, что график функции y = 4x+3 представляет собой прямую, параллельную графику функции у = 4х. Прямая смещена на 3 единицы вверх.

Таким образом, график функции у = kx+b, где k ≠ 0 – это прямая, параллельная прямой у = kx.

Для построения прямой нам достаточно знать координаты двух точек. Пусть это будут точки пересечения графика с осями координат.

То есть таблица для построения графика функции y=4x+3 будет иметь вид:

Так же, как и в случае с прямой пропорциональностью, при k>0 функция возрастает, а при k<0 – функция убывает.

Число b, как мы отметили выше, обозначает, на сколько график функции смещен вверх или вниз относительно начала координат.

Если угловые коэффициенты прямых, являющихся графиками линейных функций, одинаковые, то прямые параллельны.

Если k = 0, то линейная функция приобретает вид y = b. Это прямая, параллельная оси х и проходящая через точку (0, b).

Например, построим график прямой у=5.

 

 

Область определения линейной функции такая же, как и у прямой пропорциональности – вся числовая прямая D(y) = (- ∞;∞). Область значений Е(у) = (- ∞;∞).

График дробно-линейной функции: алгоритм построенние, анализ, примеры

Построение графика функции $y = \frac{x+1}{x-1}$ последовательными преобразованиями гиперболы $y = \frac{1}{x}$

Начнём исследование с построения графика для $y = \frac{x+1}{x-1}$.

Выделим целую часть в дроби: $y = \frac{x+1}{x-1} = \frac{(x-1)+2}{x-1} = 1+ \frac{2}{x-1}$

Согласно §47-48 данного справочника, эта функция последовательно получается из гиперболы

$$ y = \frac{1}{x} \xrightarrow{2f(x)} y = \frac{2}{x} \xrightarrow{2f(x-1)} y = \frac{2}{x-1} \xrightarrow{2f(x-1)+1} y = \frac{2}{x-1} +1 $$

Шаг 1. 2f(x) – функция $y = \frac{1}{x}$ растягивается в 2 раза по оси OY, получаем $y = \frac{2}{x}$

Шаг 2. 2f(x-1) – функция $y = \frac{2}{x}$ сдвигается вправо на 1 по оси OX, получаем $y = \frac{2}{x-1}$

Шаг 3. 2f(x-1)+1 — функция $ y = \frac{2}{x-1}$ сдвигается вверх на 1 по оси OY, получаем $y = \frac{2}{x-1}+1$.

Анализ асимптот

Итоговым графиком $y = \frac{x+1}{x-1}$ является гипербола.

Ветки гиперболы ограничены двумя прямыми, которые называют асимптотами.

Ветки на бесконечности стремятся к этим прямым, но никогда их не достигают.

Рассмотрим смещение асимптот при построении.

Для исходного графика $y = \frac{1}{x}$ асимптотами являются оси координат, x=0,y=0

Для графика $y = \frac{2}{x}$ оси координат остаются асимптотами.

Для графика $y = \frac{2}{x-1}$ происходит сдвиг вправо, асимптоты x=1,y=0

Для графика $y = \frac{2}{x-1}+1$ происходит сдвиг вверх, конечные асимптоты x = 1, y = 1

Асимптоты служат хорошим ориентиром для построения графика гиперболы.

В данном случае, достаточно построить гиперболу $y = \frac{2}{x}$ и переместить её параллельным переносом, заданным переносом точки пересечения асимптот из (0;0) в (1;1).

Алгоритм построения графика дробно-линейной функции

На входе

$$ y = \frac{ax+b}{cx+d}, c \neq 0, ad-bc \neq 0 $$

Шаг 1. Выделить целую часть из дроби и представить её в виде $y = \frac{A}{x+B}+C$

Шаг 2. Построить график $y = \frac{A}{x}$.

Шаг 3. Построить горизонтальную асимптоту x = -B.

Шаг 4. Построить вертикальную асимптоту y = C.

Шаг 5. Переместить исходный график $y = \frac{A}{x}$ параллельным переносом точки пересечения асимптот из (0;0) в (-B;C).

Если необходимо, отметить дополнительные точки, соединить кривой.

Гипербола $y = \frac{A}{x+B}+C$ построена.

Примеры

Пример 1. Постройте график функции $y = \frac{x+1}{x-3}$

Выделяем целую часть: $y = \frac{x+1}{x-3} = \frac{(x-3)+4}{x-3} = \frac{4}{x-3} +1$

Исходная гипербола $y = \frac{4}{x}$.

Асимптоты: x = 3, y = 1.

Получаем:

Пример 2. Постройте график функции $y = \frac{x}{x+2}$

Выделяем целую часть: $y = \frac{x}{x+2} = \frac{(x+2)-2}{x+2} = \frac{2}{x+2} +1$

Исходная гипербола $y = -\frac{2}{x}$.

Асимптоты: x = -2, y = 1. 2-7x+12} = \frac{2x(x-4)}{(x-3)(x-4)} = {\left\{ \begin{array}{c} \frac{2x}{x-3} \\ x \neq 4 \end{array} \right.} $$

$x \neq 4$ — исключенная точка.

Выделим целую часть:

$$ y = \frac{2x}{x-3} = \frac{2x-6+6}{x-3} = \frac{2(x-3)+3}{x-3} = \frac{3}{x-3} +2 $$

Исходная гипербола $y = \frac{3}{x}$.

Асимптоты: x = 3, y = 2.

Учитывая исключенную точку, получаем:

Как построить график функции в Excel

Чтобы правильно построить линейный график функций в Excel необходимо выбрать точечную диаграмму с прямыми отрезками и маркерами. Естественно это не единственный, но весьма быстрый и удобный способ.

Для разного рода данных нужно использовать разные типы графиков. Убедимся в этом, разобрав практический пример с построением математического графика функций в Excel.

Построение графиков функций в Excel

Начнем из анализа и создания графика функций в Excel. Мы убедимся в том, что линейный график в Excel существенно отличается от графика линейной функции, который преподают в школе.

Линейная функция x=y имеет следующие значения: x1=0, x2=1, x3=7. Заполните таблицу этими значениями как показано на рисунке:

Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«График»-«График с маркерами».

В результате у нас созданы 2 линии на графике, которые наложены одна сверх другой. Так же мы видим, что линии сломаны, а значит, они не соответствуют презентации школьному графику линейной функции. Излом линий, получается, по причине того, что на оси X у нас после значений: 0, 1 сразу идет значение 7 (упущены 2,3,4,5,6).

Вывод один: данный способ графического построения данных нам не подходит. А значит щелкните по нему левой кнопкой мышки (чтобы сделать его активным) и нажмите клавишу DELETE на клавиатуре, чтобы удалить его.



Как построить график линейной функции в Excel

Чтобы создать правильный график функций в Excel выберите подходящий график.

Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с прямыми отрезками и маркерами».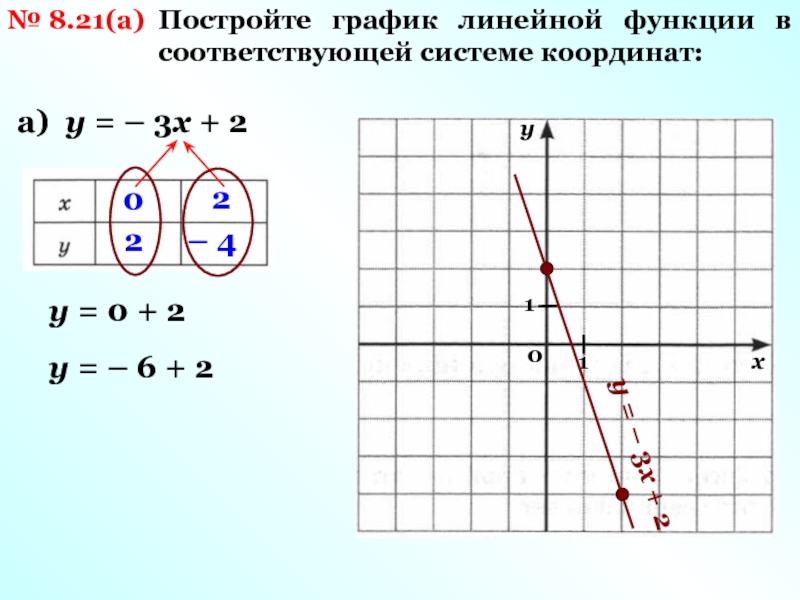

Как видно на рисунке данный график содержит одинаковое количество значений на осях X и Y. По умолчанию в шаблоне данного графика цена делений оси X равна 2. При необходимости ее можно изменить. Для этого:

• наведите курсор мышки на любое значение оси X чтобы появилась всплывающая подсказка «Горизонтальная ось (значений)» и сделайте двойной щёлочек левой кнопкой мышки;
• в появившемся окне «Формат оси» выберите пункт опции: «Параметры оси»-«цена основных делений»-«фиксированное» и установите значение 1 вместо 2.
• нажмите на кнопку «Закрыть».

Теперь у нас отображается одинаковое количество значений по всем осям.

Очень важно понимать разницу в предназначениях графиков Excel. В данном примере мы видим, что далеко не все графики подходят для презентации математических функций.

Примечание. В принципе первый способ можно было-бы оптимизировать под отображение линейной функции, если таблицу заполнить всеми значениями 0-7. Но это не всегда работающее решение, особенно в том случае если вместо значений будут формулы изменяющие данные. Одним словом если нужно забить гвоздь лучше взять молоток, чем микроскоп. Несмотря на то, что теоретически гвозди можно забивать и микроскопом.

Не существует универсальных графиков и диаграмм, которыми можно отобразить любой отчет. Для каждого типа отчета наиболее подходящее то или иное графическое представление данных. Выбор зависит от того что и как мы хотим презентовать. На следующих примерах вы убедитесь, что выбор имеет большое значение. Существует даже целая наука «Инфографика», которая учит лаконично презентовать информацию с максимальным использованием графики вместо текста, насколько это только возможно.

График линейной функции в 7 классе, определения, понятия, урок по алгебре

Дата публикации: 09 апреля 2017.

График линейной функции

График функции – это такое понятие в математике, которое дает наглядное геометрическое представление о функции.

Графиком линейной функции всегда является прямая. Как проще всего её построить?

Возьмем линейную функцию с двумя переменными, например, ax + by + с =0, где b ≠ 0.

Определим, чему равен y?
by = -ax — c

y = -$\frac{a}{b}x — \frac{c}{b}$.

Введём обозначения: k = -$\frac{a}{b}$ и m = — $\frac{c}{b}$.

Получаем запись нашего уравнения y = kx + m. Это уравнение называется линейным уравнением c двумя переменными, о таких уравнениях мы уже рассказывали.
Здесь х – независимая переменная; у – зависимая переменная.

Как мы уже говорили, графиком линейной функции y = kx + m является прямая.
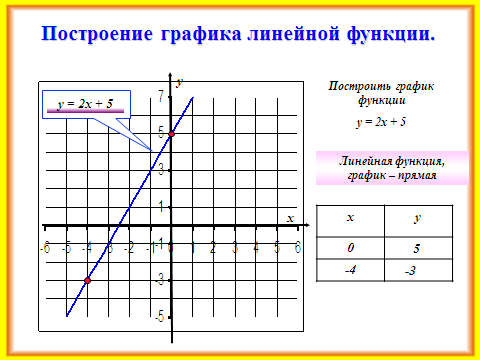
Построим график этой функции. Для примера, возьмём уравнение y = x + 2.

Составим небольшую таблицу.
Х      0      2
У      2      4

Отметим эти точки на координатной плоскости и получим вот такой график.

Давайте посмотрим, как на практике можно использовать график функции? Рассчитаем, на сколько дней хватит запаса яблок, если известно первоначальное количество яблок и количество яблок, которое магазин продает каждый день?

Задача.
На складе магазина находится 60 кг яблок. Каждый день магазин продает 12 кг этих фруктов. Сколько кг яблок останется на складе магазина через 2 дня, через 3 дня, через 5 дней?

Решение.
Построим математическую модель задачи: y= 60 — 12x.

Составим таблицу.
Х      2      3
У     36     24

По этим точкам построим график.
По графику можно предположить, какое количество яблок будет находится на складе магазина в любой день (от 1 до 5). Нужно помнить, что количество фруктов не может быть отрицательным.

Линейная функция — подготовка к ЕГЭ по Математике

Линейная функция — функция вида График линейной функции — прямая.

Для построения графика линейной функции достаточно двух точек — потому что через две несовпадающие точки всегда можно провести прямую, причем единственную.

Угловой коэффициент прямой

Величина k в формуле линейной функции называется угловым коэффициентом прямой

Если , линейная функция возрастает. Чем больше х, тем больше у, то есть график идет вправо и вверх.

Если , линейная функция убывает. Чем больше х, тем меньше у, то есть график идет вправо и вниз.

Угловой коэффициент k равен тангенсу угла наклона графика линейной функции к положительному направлению оси Х.

Пусть Чем больше k, тем круче вверх идет график функции.

А что же будет, если ? Мы получим горизонтальную прямую На рисунке показан график функции

Заметим, что прямая (также изображенная на рисунке) не является графиком функции в нашем обычном, школьном смысле слова. В самом деле — мы помним, что функция — это соответствие между двумя множествами, причем каждому элементу множества Х соответствует один и только один элемент множества Y.

Для прямой это не выполняется: значению соответствует бесконечно много значений у.

Если прямые параллельны.

При этом, чем больше b, тем выше расположен на координатной плоскости график функции.

Например, прямые и параллельны. Их угловые коэффициенты равны.

Если прямые перпендикулярны. Например, прямые и пересекаются под прямым углом. Произведение их угловых коэффициентов равно — 1.

Построение графика линейной функции 

График линейной функции построить легко — достаточно двух точек.

Оказывается, что привычный нам вид уравнения прямой — не единственно возможный.

Уравнение прямой можно записать также в виде

Построим, например, прямую, заданную уравнением

При получаем, что

При получаем, что

Значит, наша прямая проходит через точки и

Выразив у из уравнения , получим уравнение прямой вида

Если вы поступаете в вуз на специальность, связанную с математикой, — уже на первом курсе вы познакомитесь и с другими видами уравнения прямой.

Зачем изучать линейную функцию? 

Дело в том, что многие зависимости в природе и технике описываются формулой виде

Например, закон Ома для участка цепи: Напряжение U прямо пропорционально силе тока I.

Формула для равномерного прямолинейного движения: . Пройденное расстояние S прямо пропорционально времени.

Закон теплового расширения , который вам встретится в одной из задач под номером 10 варианта Профильного ЕГЭ по математике — тоже линейная функция. И таких примеров можно привести очень много.

Обратите внимание, что в формулу линейной функции аргумент х входит в первой степени. Мы просто умножаем х на угловой коэффициент k и прибавляем b.

Если в формулу функции входит аргумент в любой другой степени — например, в квадрате или в кубе, если мы делим на х, если в формуле присутствует или , или показательные или логарифмические выражения, зависящие от х, — график функции уже не будет прямой линией.

Бесплатный калькулятор для линейных функций

Что такое линейная функция?

Линейная функция — это функция, график которой представляет собой линию. Общий вид линейной функции таков, где m — наклон, а b — пересечение оси y. Вот пример:

Ваше упражнение: Это график вашей функции. Dein Browser использует HTML-Canvas-Tag nicht.Hol dir einen neuen. : P Корни в -1,333 пересечение оси Y в (0 | 4)

График линейной функции всегда представляет собой линию.

Слово, похожее на линейную функцию, — это линейная корреляция.

Каков наклон линейной функции?

Наклон линейной функции соответствует числу перед x. Он говорит, как могут единицы вы должны идти вверх / вниз, если вы идете на одну единицу вправо. Пример:

Ваше упражнение: Это график вашей функции. Dein Browser использует HTML-Canvas-Tag nicht. Hol dir einen neuen. : P Корни в 2,5 пересечение оси Y в (0 | -5)

Мы видим, что эта функция имеет наклон. Если мы переместимся на один квадрат вправо от любой точки на графике, мы должны пройти два квадрата вверх, чтобы снова оказаться на графике.

Другой пример, на этот раз с отрицательным наклоном:

Ваше упражнение: Это график вашей функции. Dein Browser использует HTML-Canvas-Tag nicht. Hol dir einen neuen. : P Корни в 1,333 пересечение оси Y в (0 | 4)

Эта линейная функция имеет наклон. Это означает, что всякий раз, когда мы идем на один квадрат вправо, нам нужно пройти на три квадрата вниз, чтобы снова оказаться на графике.

Что такое отрезок оси Y линейной функции?

Линия пересечения Y — это номер в конце функции.Как следует из названия, в нем указано, где функция пересекает ось Y. Если вы посмотрите на графики функций, вы увидите, что пересекает ось Y в точке, пересекает ось Y в точке.

Как рассчитать уравнение прямой из точки и наклона?

Вы должны вставить точку в уравнение, то есть одну координату для x, а другую для f (x). Вот пример: Предположим, мы знаем, что наша функция имеет наклон и проходит через (-2 | 5).

Как вычислить уравнение линейной функции из двух заданных точек?

Во-первых, мы должны вычислить наклон m, подставив координаты x и y точек в формулу.Это означает: вы вычисляете разность y-координат и делите ее на разность x-координат. Вот пример:
Как видим, сначала был рассчитан уклон. Чтобы найти уравнение функции, вы должны вставить точку и получить уравнение, которое дает точку пересечения оси Y.

Можно посмотреть еще примеры?

Конечно. Просто введите свои примеры выше, и они будут рассчитаны сразу, шаг за шагом. (Это идея Mathepower: Вы не просто смотрите на некоторые уже сделанные объяснения, но и получаете объяснение своих собственных расчетов!) Калькулятор линейных функций

— Онлайн-калькулятор линейных функций

Линейное уравнение определяется как уравнение, записанное с одной переменной, двумя переменными или так далее.Это уравнение будет линейной комбинацией переменной и константы.

Что такое калькулятор линейных функций?

«Калькулятор линейных функций» — это онлайн-инструмент, который помогает найти график для заданной линейной функции. Онлайн-калькулятор линейной функции поможет вам найти график для заданной линейной функции за несколько секунд.

Как пользоваться калькулятором линейных функций?

Пожалуйста, следуйте инструкциям ниже по использованию калькулятора:

• Шаг 1: Введите линейную функцию в данное поле ввода.
• Шаг 2: Нажмите кнопку «Вычислить» , чтобы найти график для заданной линейной функции.
• Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поле и ввести новую функцию.

Как построить график линейной функции?

Линейная функция — это функция вида f (x) = ax + b, a ≠ 0. Здесь x — переменная, a и b — константы.

Чтобы найти график для заданной линейной функции, выполните следующие действия:

• Шаг 1: Напишите уравнение y = f (x).
• Шаг 2: Подставьте любое значение для x в заданную линейную функцию и постройте график.

Давайте вкратце рассмотрим пример.

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. Cuemath находит решения простым и легким способом.

Забронируйте бесплатную пробную версию Class

Решенный пример:

Вычислить график для y = f (x) = 3x + 5

Раствор:

Дано: y = f (x) = 3x + 5

Для x = -2, y = -1

Для x = -1, y = 2

Для x = 0, y = 5

Для x = 1, y = 8

Для x = 2, y = 11

Нанесите эти точки на график.

Точно так же вы можете попробовать калькулятор для вычисления графика для следующих линейных функций:

• y = 2x + 5
• г = 5х — 4

Пошаговый калькулятор построения графиков линейных уравнений

Графики линейных уравнений всегда представляют собой прямую линию. И вам просто нужны две точки, чтобы нарисовать прямую линию (попробуйте!), Что является ключом к рисованию графиков.

Попробуйте воспользоваться нашим пошаговым калькулятором построения графиков линейных уравнений ниже! Вы также можете найти линейное уравнение данного графика, используя наше пошаговое руководство, прокручивая вниз.

Если у вас есть две точки или одна точка и уклон, вам нужно сначала найти форму пересечения уклона вашей линии. Используйте этот калькулятор, чтобы сделать это в первую очередь!

---

Построение линейного уравнения

Существует четыре простых шага для построения графика линейного уравнения:

1. Форма пересечения наклона: Первым шагом к построению графика линейного уравнения является получение нашего уравнения в форме пересечения наклона, y = mx + b
   , где m и b представляют собой числа. Введите несколько цифр для m и b.
2. Постройте точку пересечения оси y: Теперь помните, что нам нужны две точки, чтобы нарисовать линию. Проще всего получить точку пересечения по оси Y, где x = 0. Все, что нам нужно сделать, это добавить 0 для x в нашем уравнении: ⟹ y = (0) + y =
   Итак, первая точка, которую мы можем построить, это:
3. Постройте еще одну точку: Нам нужна еще одна точка , и мы можем найти его, подставив любое другое число вместо x. Мы собираемся выбрать x = 1, поэтому все, что нам нужно сделать, это подключить 1 для x в нашем уравнении: ⟹ y = (1) + y =
   Итак, вторая точка, которую мы можем построить, это:
4. Соедините линии: Все, что осталось сделать, это соединить точки 👏🏿👏🏾👏🏼!

Далее

---

Из графика в линейное уравнение

Есть пять простых шагов, чтобы получить линейное уравнение из графика:

1. Найдите две точки: Нам нужны две точки, чтобы вычислить наше уравнение.Итак, мы должны искать две точки, которые имеют целые числа как координаты x и y.
   Допустим, это наш график: мы собираемся выбрать две синие точки: (0,7) и (−1,4).
2. Получите наклон: Затем нам нужно использовать наши две точки, чтобы получить наклон линии. Давайте вспомним, как получить наклон …

   Формула наклона

   Допустим, у нас есть две точки: точка 1 с координатами (x1, y1) и точка 2 с координатами (x2, y2). Наклон задается изменением y на изменение x: m = slope = x1 −x2 y1 −y2
   Итак, с нашими двумя точками, наш наклон равен: x1 −x2 y1 — y2 = 0 — (- 1) 7−4 = 13 = 3
3. Форма пересечения наклона: Теперь мы можем подставить наш наклон в форму пересечения наклона, которая равна y = mx + b
   , где m это наклон.Подставляя наклон 3, мы получаем y = 3x + b
4. y-intercept: Наконец, нам нужно получить наше значение для b. Мы можем сделать это, подключив одну из исходных точек. Выберем первую точку: (0,7). Подключив, мы получим это: y = 3x + b⟹7 = 3 (0) + b
   . Если мы решим это уравнение, мы получим: 777 = 3 (0) + b = 0 + b = b
5. Окончательное уравнение: Теперь мы можем подставить наше значение b, чтобы получить уравнение: y = 3x + 7

---

Графики с линейными уравнениями: обзор и примеры

Построение графиков линейных уравнений — важный навык алгебры.Подобно тому, как рисование картины может помочь художнику выразить свои эмоции, создание графика может помочь математику объяснить и визуализировать отношения.

В этой статье мы рассмотрим , отображающий линейное уравнение с двумя переменными . Мы рассмотрим, как построить график линейных уравнений с использованием двух точек, точек пересечения, а также угла наклона и точки пересечения по оси Y. Кроме того, мы будем использовать преобразования для построения графиков линейных уравнений. Мы также обсуждаем построение горизонтальных и вертикальных линий и лучшие онлайн-калькуляторы для построения графиков.Этот пост полон примеров построения графиков линейных уравнений!

Давайте приступим.

Почему мы строим линейные уравнения в виде графиков?

Построение графиков линейных уравнений позволяет наглядно объяснить взаимосвязь между двумя переменными. Используя график, мы можем легко увидеть, что происходит с одной переменной при увеличении другой. Когда мы перемещаемся вправо по графику, значение переменной x увеличивается. Если линия перемещается вверх, переменная y также увеличивается, но если линия перемещается вниз, переменная y уменьшается.Если линия остается прежней, это означает, что переменная y не изменяется.

Например, предположим, что мы строим линейные уравнения y = 3x-1 и y = \ frac {1} {2} x-1.

у = 3х-1 у = \ гидроразрыва {1} {2} х-1

На изображениях выше легче визуализировать взаимосвязь между переменными для каждого графика. Мы видим два положительных угла наклона и ту же точку пересечения оси y, -1. Мы можем сравнивать графики, отмечая, что график линейного уравнения y = 3x-1 круче, чем y = \ frac {1} {2} x = 1.

Если мы построим их вместе, мы также легко сможем определить точки пересечения (что часто называют «решением» обеих линий).

Пересечение y = 3x-1 и y = \ frac {1} {2} x-1

В этом случае линии пересекаются в точке (0, -1), которая также является их пересечением по оси Y.

Подводя итог, можно сказать, что построение графиков может помочь математикам отображать отношения между двумя переменными, сравнивать характеристики двух графиков и определять наборы решений для линейных уравнений.

Вернуться к началу

Какая форма лучше всего подходит для построения графиков линейных уравнений?

Использование формы с пересечением наклона может упростить построение графиков.В форме пересечения угла наклона мы легко идентифицируем точку пересечения по оси Y и наклон графика. Использование этой формы дает нам пошаговый процесс, который мы всегда можем использовать для создания нашего графика.

Напоминаем, что вот три распространенные формы линейных уравнений:

Значения m и b в форме точки пересечения с уклоном — это наклон и точка пересечения по оси Y соответственно.

Форма «точка-уклон» также использует m для наклона, но может использовать любую точку на линии. Использование формы углового пересечения дает нам преимущество всегда , начиная с точки пересечения по оси y.

Стандартная форма не дает нам никакой информации для нашего графика. В конечном итоге мы могли бы изобразить линию, заданную в стандартной форме, но, вероятно, сначала нам нужно будет преобразовать ее в форму с пересечением наклона.

Вернуться к началу

Используйте наклон и точку пересечения по оси Y для построения графика линейного уравнения (пример)

Существует пошаговый процесс построения графиков линейных уравнений в форме углового пересечения, y = mx + b.

Например, изобразим уравнение y = 4x-2.

Шаг 1. Определите точку пересечения по оси Y и нанесите ее на график.

Мы видим, что в нашем уравнении y = 4x-2, число -2 стоит вместо b. Мы начнем наш график с построения точки (0, -2). Помните, точка пересечения y — это точка пересечения графика с осью y, поэтому координата x всегда равна 0.

Шаг 2: Используя уклон, определите подъем и пробег

Наклон можно выразить как \ frac {rise} {run}. В нашем уравнении y = 4x-2, число 4 находится на месте m. Следовательно, наклон равен 4, что можно выразить как \ frac {4} {1}.Это означает, что прибавка равна 4, а пробег — 1. Другими словами, график будет расти на 4 единицы вверх на каждую 1 единицу, которая проходит вправо.

Шаг 3: Используйте подъем и бег, чтобы построить следующую точку.

Мы посчитаем 4 единицы и 1 единицу вправо, чтобы нанести следующую точку на нашем графике. Это делает нашу следующую точку в (1,2).

Вернуться к началу

Шаг 4: Соедините две точки.

Теперь мы проводим линию через точку пересечения оси y (0, -2) и новую точку, которую мы построили, (1,2).Это график линейного уравнения y = 4x-2.

Вернуться к началу

Используйте две точки для построения графика линейного уравнения (пример)

Если нам даны две точки линейного уравнения, мы можем просто изобразить точки, а затем соединить точки.

Изобразим линию, проходящую через точки (-1,3) и (2, -1).

Сначала для нашего примера мы построим точки.

Теперь мы соединим их линией. Это график линейного уравнения, проходящего через две точки (-1,3) и (2, -1).

Вернуться к началу

Используйте точки пересечения для построения графика линейного уравнения (пример)

Мы можем использовать точки пересечения для построения графиков линейных уравнений точно так же, как мы использовали бы две точки. Помните, что пересечения по осям x и y также являются точками на графике.

Предположим, нам нужно построить линейное уравнение с отрезком оси y, равным 3, и отрезком оси x, равным 2. Это говорит нам о двух точках на графике. Мы знаем точку (0,3) на графике, потому что точка пересечения по оси Y равна 3. Мы также знаем, что точка (2,0) находится на графике, потому что точка пересечения по оси x равна 2.

Построим две известные нам точки.

Как и раньше, мы соединим две точки, чтобы построить график линейного уравнения.

Вот как построить график линейного уравнения, используя точки пересечения.

Вернуться к началу

Использование преобразований для построения графика линейного уравнения (пример)

При построении линейных уравнений нам может потребоваться преобразование для получения нового графика. Начнем с созданного нами графика y = 4x-2.Помните, что этот график имеет наклон 4 и точку пересечения оси Y -2.

Давайте теперь рассмотрим уравнение y = 4x + 1. Мы видим, что это уравнение имеет такой же наклон. Вместо того, чтобы начинать процесс построения графика заново, мы можем рассмотреть, как этот график изменился.

Мы видим, что точка пересечения оси Y изменилась с -2 на 1. Разница между -2 и 1 равна 3. Мы можем определить это с помощью вычитания: 1 — (- 2) = 3. Мы знаем, что график был преобразован в 3.

Чтобы прояснить это, давайте рассмотрим уравнения.Исходный график имеет y = 4x-2. Если мы добавим 3 к этому графику, мы получим y = 4x-2 + 3, что даст нам новое уравнение y = 4x + 1. Мы можем использовать эту информацию для создания нового графика. Все, что нам нужно сделать, это увеличить наши очки на 3 единицы.

Вместо построения графика (0, -2) мы построим график (0, -2 + 3), который равен (0,1). Помните, что перемещение графика вверх изменяет только координату y.

Аналогично, вместо построения графика (1,2), мы построим график (1,2 + 3, который равен (1,5).

Построим точки (0,1) и (1,5) и соединим их.

Теперь мы использовали преобразования, чтобы построить график линейного уравнения y = 4x + 1.

Вернуться к началу

Как построить горизонтальные и вертикальные линии

Построить горизонтальную линию

Построение горизонтальных и вертикальных линий немного отличается, потому что эти уравнения выглядят не так, как мы ожидали.

Начнем с горизонтальной линии. Создадим график из горизонтальной линии y = 2. Горизонтальные линии всегда имеют форму y = a, где a представляет собой действительное число.Это может быть трудно увидеть, но на самом деле это уравнение имеет форму точки наклона. У него просто нулевой наклон. Мы можем думать об этом так: y = 0x + 2.

Все горизонтальные линии имеют нулевой наклон. Сначала мы построим точку (0,2). Когда линия начинается с y =, мы начнем с нанесения точки на оси y. Мы знаем, что (0,2) находится на графике, потому что координата y равна 2.

Теперь мы создаем горизонтальную линию через точку (0,2). При всех значениях в этой строке координата y равна 2.Это график горизонтальной линии y = 2.

Построить вертикальную линию

Теперь мы можем построить вертикальную линию. Создадим график вертикальной линии x = 3. Вертикальные линии всегда имеют форму x = a, где a представляет собой действительное число. Вертикальные линии никогда не имеют формы точечного уклона, формы пересечения откоса или стандартной формы. Это связано с тем, что вертикальная линия имеет неопределенный наклон, поэтому она не может соответствовать ни одной из этих форм.

Сначала мы построим точку (3,0).Когда линия начинается с x =, мы начнем с нанесения точки на оси x. Мы знаем, что (3,0) находится на графике, потому что координата x равна 3.

Теперь мы создаем вертикальную линию через точку (3,0). При всех значениях в этой строке координата x равна 3. Это график вертикальной линии x = 3.

Это процесс, используемый для построения горизонтальных и вертикальных линий.

Вернуться к началу

Топ-3 онлайн-калькулятора для построения графиков линейных уравнений

Чтобы получить больше онлайн-тренировок по построению графиков, попробуйте использовать следующие ресурсы:

Desmos.com

В Desmos у вас есть много возможностей для настройки вашего графика! Этот инструмент очень удобен в использовании. Вы можете манипулировать уравнениями, чтобы понять, как различные части влияют на график. Вы можете построить несколько линий одновременно. Desmos даже позволяет включать фотографии в график, например:

Geogebra.org

В Geogebra вы также можете строить графики множества различных типов уравнений. Изучая Geogebra, вы также найдете отличные инструменты для создания геометрических фигур.

Meta-calculator.com

Использование мета-калькулятора больше похоже на использование традиционного калькулятора. Это может помочь вам чувствовать себя более комфортно при использовании портативного графического калькулятора в классе.

Вернуться к началу

Резюме: построение графиков с помощью линейных уравнений

В этом посте мы узнали много нового о построении графиков линейных уравнений.

• Мы можем построить линейные уравнения в виде графиков, чтобы показать взаимосвязи, сравнить графики и найти решения.
• Форма точечного уклона — лучшая форма для построения графиков линейных уравнений.
• Мы можем создать график, используя наклон и точку пересечения по оси Y, две точки или две точки пересечения.
• В Интернете доступно множество отличных ресурсов по графическим калькуляторам, например, Desmos, Geogebra и Meta-Calculator.

Щелкните здесь, чтобы ознакомиться с более полезными руководствами по обзору Albert Algebra 1.

Вернуться к началу

Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) — Mathplanet

Линейное уравнение — это уравнение с двумя переменными, график которого представляет собой линию.График линейного уравнения — это набор точек на координатной плоскости, которые все являются решениями уравнения. Если все переменные представляют собой действительные числа, можно изобразить уравнение, нанеся на график достаточно точек, чтобы распознать шаблон, а затем соединить точки, чтобы включить все точки.

Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.

---

Пример

Постройте функцию y = x + 2

Начните с выбора пары значений для x, например -2, -1, 0, 1 и 2 и вычислите соответствующие значения y.

х	Y = x + 2	Заказанная пара
-2	-2 + 2 = 0	(-2, 0)
-1	-1 + 2 = 1	(-1, 1)
0	0 + 2 = 2	(0, 2)
1	1 + 2 = 3	(1, 3)
2	2 + 2 = 4	(2, 4)

Теперь вы можете просто построить пять упорядоченных пар в координатной плоскости

На данный момент это пример дискретной функции.Дискретная функция состоит из изолированных точек.

Проведя линию через все точки и продолжая линию в обоих направлениях, мы получаем противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.

Если вы хотите использовать только две точки для определения вашей линии, вы можете использовать две точки, где график пересекает оси. Точка, в которой график пересекает ось x, называется точкой пересечения с осью x, а точка, в которой график пересекает ось y, называется точкой пересечения по оси y.Пересечение по оси x находится путем нахождения значения x, когда y = 0, (x, 0), а точка пересечения с y находится путем нахождения значения y, когда x = 0, (0, y).

Стандартная форма линейного уравнения —

$$ Ax + By = C, \: \: A, B \ neq 0 $$

Прежде чем вы сможете построить линейное уравнение в его стандартной форме, вы сначала должны решить уравнение относительно y.

$$ 2y-4x = 8 $$

$$ 2y-4x \, {\ color {green} {+ \, 4x}} = 8 \, {\ color {green} {+ \, 4x}} $$

$$ 2y = 4x + 8 $$

$$ \ frac {2y} {{\ color {green} 2}} = \ frac {4x} {{\ color {green} 2}} + \ frac {8} {{\ color {green} 2}} $

$$ y = 2x + 4 $$

Отсюда вы можете построить уравнение, как в примере выше.

График y = a представляет собой горизонтальную линию, где прямая проходит через точку (0, a)

В то время как график x = a представляет собой вертикальную линию, проходящую через точку (a, 0)

---

Видеоурок

Постройте график линейного уравнения y = 3x — 2

Написание и построение графиков линейных функций

Выражение линейной функции с помощью уравнения

Линейная функция представлена ​​уравнением:

y = mx + b , где:

y = координата y

m = наклон кривой

x = координата x

b = точка пересечения y, или точка пересечения оси y на графике

Давайте посмотрим, как мы можем использовать уравнение для график линейной функции.Как бы мы изобразили y = 2 x + 3? Уравнение говорит нам, что наклон линии (m) = 2, и она пересекает ось y (b) в точке 3. Чтобы построить график функции, нам нужно иметь несколько упорядоченных пар. Лучший способ получить эти точки — создать таблицу значений , которая показывает нам точки, которые находятся на линии. При создании таблицы значений всегда полезно использовать некоторые положительные и отрицательные значения для x , чтобы вы могли понять, как ведет себя линия.Предположим, что мы хотим построить график значений, когда x равно -2, -1, 0, 1 и 2. Таблица значений будет выглядеть так:

Теперь, когда у нас есть упорядоченные пары или значение для x и y , мы можем изобразить уравнение y = 2x + 3, нанеся эти пары на график.

Из графика видно, что линия пересекает ось y в точке 3 или в точке (0, 3) и что наклон линии вверх и вправо, что указывает на положительный наклон.Это согласуется с нашим уравнением: y = 2 x +3, поскольку наклон прямой в этом уравнении равен +2. Мы также можем отметить, что все упорядоченные пары, которые мы вычислили в нашей таблице значений , также находятся на графике, в частности, (-2, -1), (-1, 1), (0, 3), ( 1, 5) и (2, 7).

Написание линейной функции из графика

Давайте попробуем начать с графика и написать уравнение, которое с ним связано. Чтобы записать линейную функцию в виде y = m x + b, нам нужно будет определить наклон линии:

• уклон (м)
• y -перехват (б)

Из графика видно, что наклон линии отрицательный, потому что линия идет вниз и вправо.Похоже, что точка пересечения оси y (b) графика равна 2, что представлено точкой (0,2). Теперь нам нужно определить наклон линии. Для этого мы должны использовать как минимум две точки от линии. Выберем (-2, 4) и (0, 2). Мы можем использовать любые две точки, поскольку наклон — прямая линия. Для расчета уклона используем следующую формулу:

Используя наши две точки и подставив их в формулу, получаем:

m = (4-2) / (-2-0)

m = 2 / -2

m = -1

Теперь мы знаем, что наклон (m) = -1, а точка пересечения по оси y (b) равна 2.Когда мы сложим все это вместе, уравнение для линии на графике будет:

y = m x + b

y = -1 x + 2

Написание линейной функции из информации в словесной задаче

Иногда мы можем выразить словесную задачу как линейную функцию. Предположим, Мэтт отправляется в школьную поездку, которая стоит 300 долларов за аренду автобуса плюс 20 долларов за каждого ученика, который путешествует на автобусе. Чтобы Мэтт выразил эту взаимосвязь в виде линейной функции, ему необходимо определить, какая из переменных является зависимой, а какая независимой.В этой ситуации стоимость поездки зависит от того, сколько студентов поедет в нее, поэтому стоимость поездки должна быть зависимой переменной, y , а количество студентов — независимой переменной, x . Мы можем записать уравнение для этой связи как:

y = 20 x + 300

Если мы предположим, что в поездку отправятся 50 студентов, то поездка будет стоить 1300 долларов: (20 долларов x 50) + 300. Взаимосвязь между количеством студентов и стоимостью поездки является линейной, поскольку стоимость будет увеличиваться по мере того, как в поездку отправляется больше студентов.Когда это соотношение изображено на графике, это будет прямая линия.

Краткое содержание урока

Линейная функция , которая показывает взаимосвязь между двумя переменными и всегда приводит к прямой линии при построении графика, может быть выражена в виде графика, используя наклон и метод пересечения y , как уравнение, когда график предоставляется или из информации, заданной в словесной задаче.

В линейной функции одна из переменных независимая , что означает, что она не зависит от другой переменной и представлена ​​как y .Другая переменная, представленная как x , — это зависимая , что означает, что ее значение зависит от независимой переменной.

Уравнение линейной функции выражается следующим образом: y = m x + b, где m — наклон линии или ее крутизна, b представляет точку пересечения y или точку пересечения графика y -ось и x и y представляют точки на графике.

При построении линейной функции мы должны вычислить как минимум две точки, чтобы можно было провести линию между ними.Чтобы создать эти точки, мы можем использовать таблицу значений , где мы указываем значения для x , а затем используем уравнение нашей линейной функции для решения относительно y .

Уравнение прямой по двум точкам

Эти онлайн-калькуляторы находят уравнение прямой по двум точкам.
Первый калькулятор находит линейное уравнение в форме пересечения наклона, то есть. Он также выводит параметры наклона и пересечения и отображает линию на графике.
Второй калькулятор находит линейное уравнение в параметрической форме, то есть.Он также выводит вектор направления и отображает линию и вектор направления на графике.

Вы можете найти теорию под калькуляторами.

Уравнение наклона и пересечения линии из 2 точек

Первая точка

xy

Вторая точка

xy

Вычислить

Линейное уравнение

Наклон

Пересечение

Точность вычисления

Цифры после десятичной точки: 2

content_copy Ссылка сохранить Сохранить расширение Виджет

Уравнение параметрической линии из 2 точек

Первая точка

xy

Вторая точка

xy

Вычислить

Уравнение для x

Уравнение для y

Вектор направления

Точность вычисления

Цифры после десятичной точки: 2

content_copy Ссылка сохранить Сохранить расширение Виджет

Уравнение линии наклона-пересечения

Найдем угловую форму линейного уравнения по двум известным точкам и.