Применяя вышеизложенные свойства многочленов, рассмотрим возможные схемы графиков многочленов третьей степени . Пусть старший коэффициент многочлена a — положительное число. 1 случай. Многочлен имеет две точки экстремума, в этом случае его производная имеет два различных корня, т.е. дискриминант этого квадратного трехчлена . Эта ситуация отражается в частных случаях, когда многочлен имеет три различных действительных корня x1 , x2 , x3 , а также когда многочлен имеет два различных корня, один из которых имеет кратность два. В этом случае график имеет вид:
2 случай. У многочлена нет экстремумов, т.е. .
Аналогично строятся графики кубических парабол при отрицательном старшем коэффициенте. Получаем сводную таблицу различных видов графиков многочленов третьей степени: . Пример 5.2.
Пример 5.3.
страницы:1 2 3 |
Построение графиков функций, содержащих модуль
Тип урока: изучение и закрепление новых
знаний.
Цели урока:
Образовательная: освоить метод линейного сплайна для построения графиков, содержащих модуль; научить применять его в простых ситуациях;
Развивающая: развивать логическое и творческое мышление; формирование навыков самостоятельной деятельности, выработка внимания.
Воспитательная: привитие интереса к изучаемому предмету.Ход урока
Непрерывная кусочно-линейная функция называется линейным сплайном. Её график есть ломаная с двумя бесконечными крайними звеньями. Подобный график вы видите на рис.1
Эта функция задается тремя формулами
Но нетрудно заметить, что эту же функцию можно задать одной формулой, используя модули: у= ¦х¦ -¦х-1¦
Оказывается, что и любую кусочно–линейную функцию можно задать формулой вида
График любой такой функции – ломаная с
бесконечными крайними звеньями. Чтобы построить
такую ломаную. Достаточно знать все её вершины и
по одной точке на левом и правом бесконечных
звеньях. Эти соображения позволяют легко строить
графики функций такого вида без раскрытия
модулей, не переходя к их кусочному заданию.
Чтобы построить
такую ломаную. Достаточно знать все её вершины и
по одной точке на левом и правом бесконечных
звеньях. Эти соображения позволяют легко строить
графики функций такого вида без раскрытия
модулей, не переходя к их кусочному заданию.
Достаточно составить таблицу
Х Х0 Х1 Х2 … Хn X n+1 Y Y0 Y1 Y2 … Yn Y n+1
Где х0 и х n+1 – произвольные
значения х, такие, что x0 < x1 и x n+1
> xn,а x1….
Пример 1. Построить график функции у=3х+1 -¦х+1¦+2¦х¦
Точки смены формул: х+1=0, х=-1 и х=0.
Составим таблицу:
| х | -2 | -1 | 0 | 1 |
| у | -2 | 0 | 0 | 4 |
график изображен на рисунке 2.
Пример 2. задайте функцию у=х+¦х-2¦-¦х¦в виде кусочно-линейной и постройте график двумя способами.
I способ.
Подготовим таблицу для построения графика с учетом линейного сплайна:
х -1 0 2 3 у 1 2 0 1
Получим график (см.рис 3)
II способ.
Значение х, при которых выражения, стоящее под знаком модуля, меняют знак, х=2 их=0. значит они точки смены формул. Найдем эти формулы.
Если х<0, то у= х-х+2+х, у=х+2.
если 0x, то у=х-х+2-х, у= -х+2.
Если х>2, то у=х+х-2-х, у=х-2.
Очевидно, что график остается неизменным.
Закрепление изученного
Для закрепления изученного материала проводится самостоятельная работа
Учитель должен заранее подготовить чистые
листочки форматом в половину листа (примерно 6
штук на каждого ученика). Непосредственно перед
уроком, на перемене учитель записывает на доске
два варианта работы. Причем каждый вариант он
пишет особым цветным мелом. Степень трудности
вариантов различна. Оценка “4” примерно
соответствует тексту, написанному синим цветом,
оценка “5” — красному. Для того, чтобы работа
проходила быстро и организованно, учителю нужно
помнить наизусть
Непосредственно перед
уроком, на перемене учитель записывает на доске
два варианта работы. Причем каждый вариант он
пишет особым цветным мелом. Степень трудности
вариантов различна. Оценка “4” примерно
соответствует тексту, написанному синим цветом,
оценка “5” — красному. Для того, чтобы работа
проходила быстро и организованно, учителю нужно
помнить наизусть
ответы всех заданий, тогда его проверка будет
мгновенной. Кроме того, необходимо подготовить
специальный лист для учета каждого выполненного
задания ручки трёх цветов. На листе слева
помещается колонка с фамилиями учащихся, а
справа колонки, соответствующие количеству
заданий в работе. Какой бы вариант ни выбрал
ученик, соответствующую клеточку закрашивают
выбранным цветом. Ученики на своих листочках
выполняют первый пример выбранного варианта. Как
только пример решен. Ученик с листочком подходит
к учителю, который мгновенно видит, правильное
решение или нет.
Задания для самостоятельной работы.
| на “4” | на “5” |
| Постройте графики функции: | Постройте графики функций: |
| а) у = ¦х+1¦+ ¦х¦-¦х-2¦ | а) у = ¦х+2¦- ¦2х -4¦+¦х-3¦- ¦х+1¦ |
| б) у = ¦х+2¦+¦х¦- 2¦х-2¦ | б) у = 1- ¦2-х¦+¦3+х¦- ¦х¦ +¦х-1¦ |
| в) у = 2- ¦2х +5¦ | в) у = ¦х-5¦+¦х¦- 2¦1- х¦-¦х+3¦ |
| ответы смотри в Приложении 1, приложении 2 | |
а) рис. 4 4 |
|
| б) рис. 5 | б) рис.8 |
| в) рис. 6 | в) рис.9 |
3. Некоторые простые функции — построение графиков
3. Некоторые простые функции — построение графиков 3. Некоторые простые функции — построение графиков
Мы будем использовать х и х для этих примеров.
A. Линейные (прямолинейные) уравнения
Это один из самых важных типов уравнений в науке.
и мы часто пытаемся свести сложные уравнения к линейным
чтобы упростить их.
Общее уравнение для линейной функции:
Значение c является константой и представляет собой точку пересечения на y оси, с каких пор x = 0, y ( x ) = c .
Значением м является уклон или уклон линия. Положительное значение м означает увеличение уклона с увеличением x значение -ve означает, что оно уменьшается. Нулевое значение м указывает на горизонтальную линию, бесконечную значение м указывает на вертикальную линию.
Примеры
а) у ( х ) = 3 х + 5
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 5 | 10 |
| у | -4 | -1 | 2 | 5 | 8 | 11 | 14 | 20 | 35 |
б) y ( x ) = 2 x — 3 (отрицательная точка пересечения)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 5 |
| у | -9 | -7 | -5 | -3 | -1 | 1 | 3 | 7 |
в) y ( x ) = -4 x + 5 (отрицательный наклон)
| x | -3 | 9 0082 -2-1 | 0 | 1 | 2 | 3 | 4 | 5 | 10 | |
| у | 17 | 13 | 9 | 5 | 1 | -3 | -7 | -11 | -15 | -35 |
г) y = 0 х + 6 (нулевой градиент)
| х | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| у | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
e) y = 4 x (нулевая точка пересечения)
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| у | -12 | -8 | -4 | 0 | 4 | 8 | 12 |
f) p ( n ) = 3 n — 1
| n | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| р | -10 | -7 | -4 | -1 | 2 | 5 | 8 |
ж) φ(λ) = + 1
| λ | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| φ | -1 | -½ | 0 | ½ | 1 | 1½ | 2 | 2½ | 3 |
B. Квадратные уравнения
Квадратные уравнения
Это функции x 2 и
общего вида:
где a , b и c являются константами
Общая форма квадратичного уравнения — парабола . Ценности a и b определяют «резкость» параболы.
Знак а определяет ориентацию (вверх или вниз)
парабола. Значение c по-прежнему является перехватом на и ось.
Примеры
Числовой пример
у ( х ) = 2 х 2 + 4 х — 6
| х | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| у | 10 | 0 | -6 | -8 | -6 | 0 | 10 | 24 |
Обратите внимание, что в квадрате существуют два значения x для
каждое значение y (кроме точки поворота, см. далее).
Для такой функции мы часто хотим знать важные
особенности кривой: где она пересекает ось х ?
и у ось? Где находится минимум (или максимум)?
Каков наклон кривой при любом значении x ? Хорошо
показать, как решать эти вопросы позже.
далее).
Для такой функции мы часто хотим знать важные
особенности кривой: где она пересекает ось х ?
и у ось? Где находится минимум (или максимум)?
Каков наклон кривой при любом значении x ? Хорошо
показать, как решать эти вопросы позже.
C. Высшие многочлены
Функции с x 3 , x 4 , x 5 , и т.д. ., также существуют, и есть
вообще сложнее.
Примеры
i) кубические уравнения
y ( x ) = ax 3 + bx 2 + сх + д
ii) уравнения четвертой степени
y ( x ) = ax 4 + bx 3 + сх 2 + дх + е
D. Рациональные функции
например . у ( х ) =
у ( х ) =
Примечание: когда x = 1, функция становится неопределенной (т.е. y = бесконечность)
E. Тригонометрические функции (см. далее)
напр. у ( х ) = грех х
F. Экспоненциальные и логарифмические функции (см. далее)
напр. y ( x ) = e x , k ( T ) = A exp{- E 90 009 / RT ) Аррениус
уравнение
напр. y ( x ) = ln x , y ( x )) = ln (1- х 2 ).
Следующая лекция
Обзор функций построения морских графиков — документация seaborn 0.12.2
Большинство ваших взаимодействий с Сиборном будет происходить через набор функций построения графиков. В следующих главах учебника будут рассмотрены специфические функции, предлагаемые каждой функцией. В этой главе на высоком уровне будут представлены различные виды функций, с которыми вы столкнетесь.
В этой главе на высоком уровне будут представлены различные виды функций, с которыми вы столкнетесь.
Похожие функции для похожих задач
Пространство имен seaborn плоское; все функции доступны на верхнем уровне. Но сам код имеет иерархическую структуру с модулями функций, которые достигают схожих целей визуализации с помощью разных средств. Большинство документов структурировано вокруг этих модулей: вы встретите такие названия, как «реляционный», «дистрибутивный» и «категориальный».
Например, модуль распределения определяет функции, специализирующиеся на представлении распределения точек данных. Сюда входят знакомые методы, такие как гистограмма:
пингвинов = sns.load_dataset("пингвины")
sns.histplot (данные = пингвины, x = "flipper_length_mm", оттенок = "вид", несколько = "стек")
Наряду с аналогичными, но, возможно, менее знакомыми параметрами, такими как оценка плотности ядра:
sns.kdeplot(data=penguins, x="flipper_length_mm", hue="species", multiple="stack")
Функции внутри модуля имеют много общего кода и предлагают аналогичные функции, которые могут отсутствовать в других компонентах библиотеки (например, multiple="stack" в приведенных выше примерах). Они предназначены для облегчения переключения между различными визуальными представлениями при изучении набора данных, поскольку различные представления часто имеют взаимодополняющие сильные и слабые стороны.
Они предназначены для облегчения переключения между различными визуальными представлениями при изучении набора данных, поскольку различные представления часто имеют взаимодополняющие сильные и слабые стороны.
Функции на уровне фигур и на уровне осей
В дополнение к различным модулям существует сквозная классификация морских функций как «уровень осей» или «уровень фигур». Приведенные выше примеры являются функциями уровня осей. Они наносят данные на один объект matplotlib.pyplot.Axes , который является возвращаемым значением функции.
Напротив, функции уровня фигуры взаимодействуют с matplotlib через морской объект, обычно FacetGrid , который управляет фигурой. Каждый модуль имеет одну функцию уровня фигуры, которая предлагает единый интерфейс для различных функций уровня осей. Организация выглядит примерно так:
Например, displot() — это функция уровня фигуры для модуля распределения. По умолчанию он рисует гистограмму, используя тот же код, что и 9. 0794 histplot() за кадром:
0794 histplot() за кадром:
sns.displot(data=penguins, x="flipper_length_mm", hue="species", multiple="stack")
Чтобы вместо этого нарисовать график плотности ядра, используя тот же код, что и для kdeplot() , выберите его, используя параметр типа :
sns.displot(data=penguins, x="flipper_length_mm", hue="species", multiple="stack", kind="kde")
Вы заметите, что графики на уровне фигур в основном похожи на графики на уровне осей, но есть несколько отличий. Примечательно, что легенда находится вне сюжета. Они также имеют немного другую форму (подробнее об этом чуть позже).
Самая полезная функция, предлагаемая функциями уровня фигур, заключается в том, что они могут легко создавать фигуры с несколькими подграфиками. Например, вместо того, чтобы складывать три распределения для каждого вида пингвинов на одних и тех же осях, мы можем «гранить» их, нанеся каждое распределение по столбцам рисунка:
sns.displot(data=penguins, x="flipper_length_mm", hue="species", col="species")
Функции уровня фигуры оборачивают свои аналоги уровня осей и передают аргументы ключевого слова, характерные для типа (например, размер интервала для гистограммы), нижележащей функции. Это означает, что они не менее гибкие, но есть и обратная сторона: параметры, специфичные для вида, не отображаются в сигнатуре функции или строках документации. Некоторые из их функций могут быть менее заметными, и вам может потребоваться просмотреть две разные страницы документации, прежде чем понять, как достичь конкретной цели.
Функции уровня осей создают автономные графики
Функции уровня осей написаны так, чтобы действовать как вставные замены для функций matplotlib. Хотя они автоматически добавляют метки и легенды к осям, они не изменяют ничего, кроме осей, в которых они нарисованы. Это означает, что они могут быть составлены в произвольно сложные фигуры matplotlib с предсказуемыми результатами.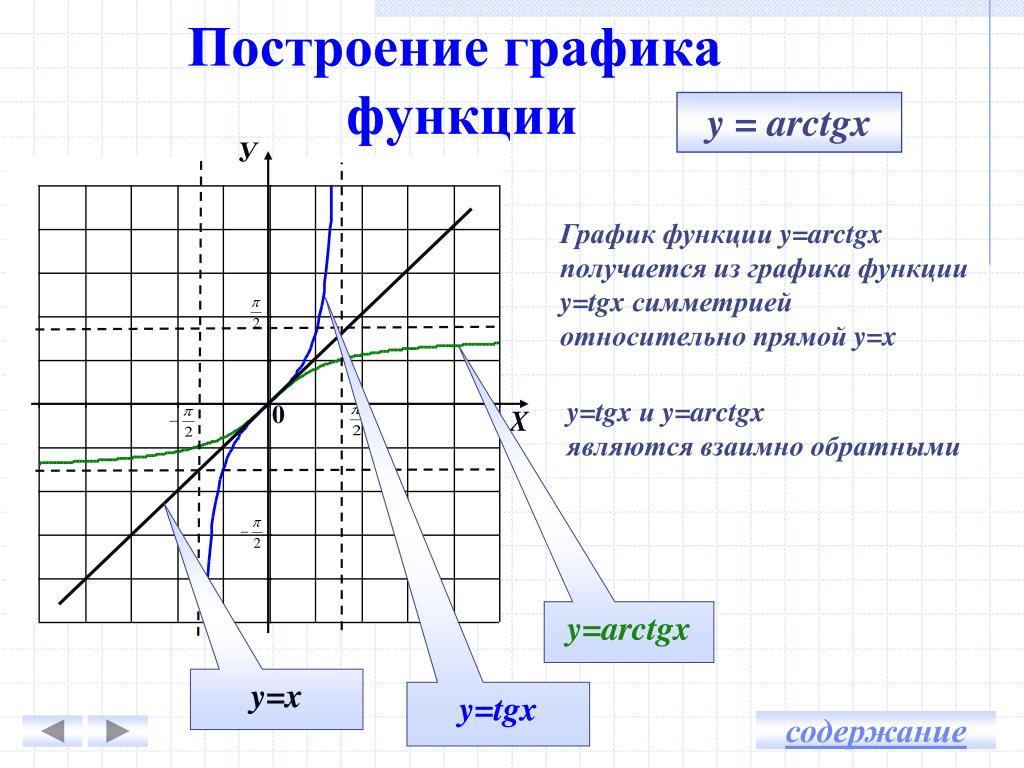
Функции уровня осей вызывают внутренний вызов matplotlib.pyplot.gca() , который подключается к интерфейсу конечного автомата matplotlib, чтобы они рисовали свои графики на «активных в данный момент» осях. Но они также принимают ax= аргумент, который интегрируется с объектно-ориентированным интерфейсом и позволяет указать, куда именно должен идти каждый график:
f, axs = plt.subplots(1, 2, figsize=(8, 4), gridspec_kw=dict(width_ratios=[4, 3])) sns.scatterplot(data=пингвины, x="flipper_length_mm", y="bill_length_mm", hue="species", ax=axs[0]) sns.histplot (данные = пингвины, x = "вид", оттенок = "вид", сжатие = 0,8, альфа = 0,8, легенда = ложь, топор = оси [1]) f.tight_layout()
Функции уровня фигуры владеют своей цифрой
Напротив, функции уровня фигуры не могут (легко) быть составлены с другими графиками. По замыслу они «владеют» своей собственной фигурой, включая ее инициализацию, поэтому нет понятия использования функции уровня фигуры для рисования графика на существующих осях. Это ограничение позволяет функциям уровня рисунка реализовывать такие функции, как размещение легенды за пределами графика.
Это ограничение позволяет функциям уровня рисунка реализовывать такие функции, как размещение легенды за пределами графика.
Тем не менее, можно выйти за рамки того, что предлагают функции уровня фигуры, обратившись к осям matplotlib на объекте, который они возвращают, и таким образом добавив другие элементы на график:0006
советов = sns.load_dataset("советы")
g = sns.relplot(data=tips, x="total_bill", y="tip")
g.ax.axline (xy1 = (10, 2), наклон = .2, цвет = "b", тире = (5, 2))
Настройка графиков из функции уровня фигуры
Функции уровня фигуры возвращают экземпляр FacetGrid , который имеет несколько методов для настройки атрибутов графика таким образом, чтобы он был «умным» в отношении организации подграфика. Например, вы можете изменить метки на внешних осях, используя одну строку кода:
г = sns.relplot(data=пингвины, x="flipper_length_mm", y="bill_length_mm", col="sex")
g.set_axis_labels("Длина плавника (мм)", "Длина купюры (мм)")
Хотя это удобно, это добавляет немного дополнительной сложности, так как вам нужно помнить, что этот метод не является частью API-интерфейса matplotlib и существует только при использовании функции уровня фигуры.
Задание размеров фигур
Чтобы увеличить или уменьшить размер графика matplotlib, вы устанавливаете ширину и высоту всей фигуры либо в глобальном параметре rcParams, либо при настройке графика (например, с помощью figsize параметр matplotlib.pyplot.subplots() ), или вызвав метод для объекта фигуры (например, matplotlib.Figure.set_size_inches() ). При использовании функции уровня осей в seaborn применяются те же правила: размер графика определяется размером фигуры, частью которой он является, и расположением осей на этой фигуре.
При использовании функции уровня фигуры есть несколько ключевых отличий. Во-первых, сами функции имеют параметры для управления размером фигуры (хотя на самом деле это параметры базовых FacetGrid , который управляет фигурой). Во-вторых, эти параметры, высота и аспект , параметризируют размер немного иначе, чем параметры ширины , высоты в matplotlib (используя параметры моря, ширина = высота * аспект ). Самое главное, что параметры соответствуют размеру каждого подучастка , а не размеру общей фигуры.
Самое главное, что параметры соответствуют размеру каждого подучастка , а не размеру общей фигуры.
Чтобы проиллюстрировать разницу между этими подходами, вот вывод по умолчанию matplotlib.pyplot.subplots() с одним подзаголовком:
f, топор = plt.subplots()
Фигура с несколькими столбцами будет иметь одинаковый общий размер, но оси будут сжаты по горизонтали, чтобы поместиться в пространство:
f, ax = plt.subplots(1, 2, sharey=True)
Напротив, график, созданный функцией уровня фигуры, будет квадратным. Чтобы продемонстрировать это, давайте настроим пустой график, используя FacetGrid напрямую. Это происходит за кулисами в таких функциях, как relplot() , displot() или catplot() :
г = sns.FacetGrid(пингвины)
При добавлении дополнительных столбцов сама фигура станет шире, так что ее подграфики будут иметь одинаковый размер и форму:
г = sns.FacetGrid(пингвины, col="секс")
И вы можете настроить размер и форму каждого участка без учета общего количества строк и столбцов на рисунке:
г = sns.FacetGrid(пингвины, col="пол", высота=3,5, аспект=0,75)
В результате вы можете назначать переменные огранки, не задумываясь о том, как вам нужно настроить общий размер фигуры. Недостатком является то, что когда вы хотите изменить размер фигуры, вам нужно помнить, что все работает немного иначе, чем в matplotlib.
Относительные достоинства функций уровня фигур
Вот краткое изложение плюсов и минусов, которые мы обсуждали выше:
Преимущества | Недостатки |
|---|---|
Простая огранка по переменным данных | Многие параметры не входят в сигнатуру функции |
Легенда вне графика по умолчанию | Не может быть частью большей фигуры matplotlib |
Простая персонализация на уровне фигурки | API отличается от matplotlib |
Параметризация другого размера фигуры | Различные параметры размера фигуры |
В целом, функции уровня фигурки добавляют дополнительную сложность, которая может запутать новичков, но их отличительные особенности придают им дополнительную силу. В учебной документации в основном используются функции уровня фигур, потому что они дают более четкие графики, и мы обычно рекомендуем их использовать для большинства приложений. Единственная ситуация, когда они не являются хорошим выбором, — это когда вам нужно создать сложную автономную фигуру, которая состоит из нескольких разных сюжетов. На этом этапе рекомендуется настроить фигуру напрямую с помощью matplotlib и заполнить отдельные компоненты с помощью функций уровня осей.
В учебной документации в основном используются функции уровня фигур, потому что они дают более четкие графики, и мы обычно рекомендуем их использовать для большинства приложений. Единственная ситуация, когда они не являются хорошим выбором, — это когда вам нужно создать сложную автономную фигуру, которая состоит из нескольких разных сюжетов. На этом этапе рекомендуется настроить фигуру напрямую с помощью matplotlib и заполнить отдельные компоненты с помощью функций уровня осей.
Объединение нескольких представлений данных
Две важные функции построения графиков у морских животных не вполне вписываются в рассмотренную выше классификационную схему. Эти функции, joinplot() и pairplot() , используют несколько видов графиков из разных модулей для представления нескольких аспектов набора данных на одном рисунке. Оба графика являются функциями уровня фигуры и по умолчанию создают фигуры с несколькими подграфиками. Но они используют разные объекты для управления фигурой: JointGrid и PairGrid соответственно.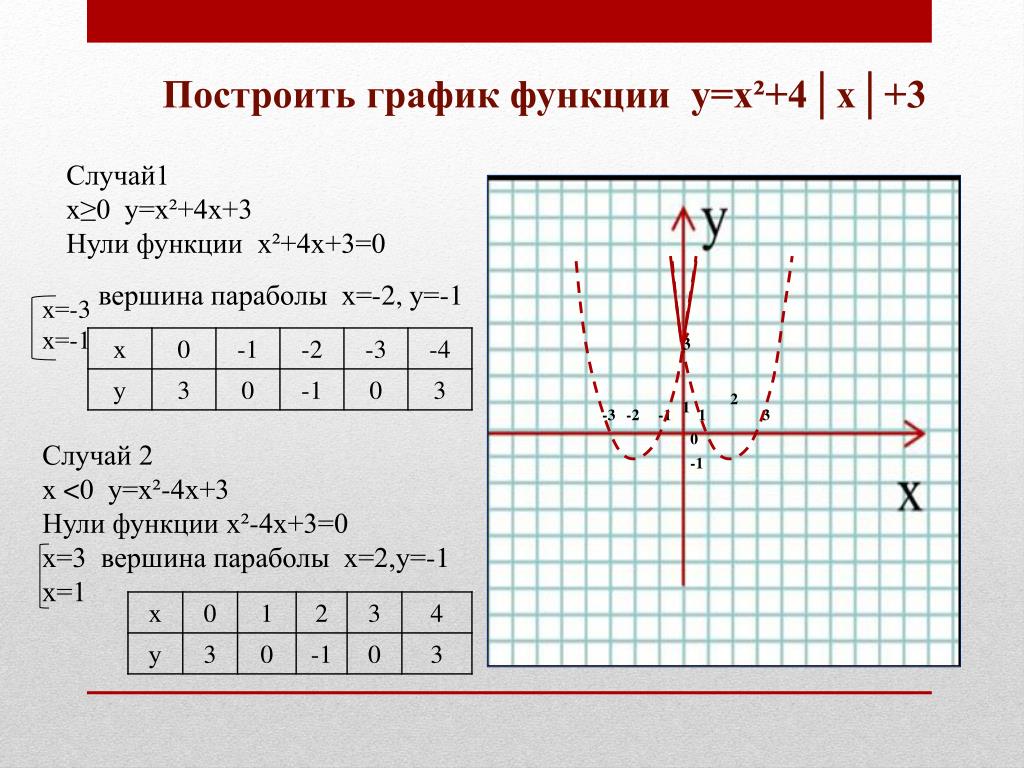


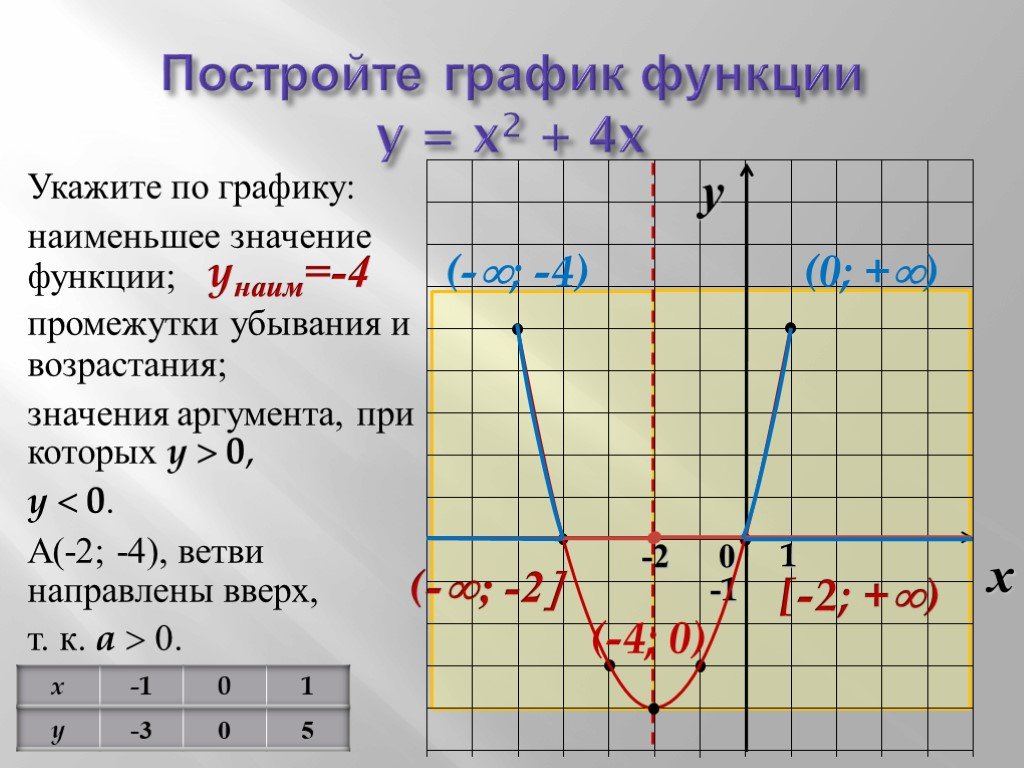 displot(data=penguins, x="flipper_length_mm", hue="species", col="species")
displot(data=penguins, x="flipper_length_mm", hue="species", col="species")
 FacetGrid(пингвины, col="секс")
FacetGrid(пингвины, col="секс")
Ваш комментарий будет первым