Построение годографа онлайн: Как построить годограф михайлова

Построение АФЧХ системы автоматического регулирования в среде Maple

Библиографическое описание:

Емельянова, Д. К. Построение АФЧХ системы автоматического регулирования в среде Maple / Д. К. Емельянова. — Текст : непосредственный // Молодой ученый. — 2016. — № 10 (114). — С. 197-201. — URL: https://moluch.ru/archive/114/30152/ (дата обращения: 29.03.2021).



Ключевые слова: регулирование, управление техническими системами, автоматическое управление, частотные характеристики.

Амплитудно-фазовые частотные характеристики широко используются при анализе устойчивости систем автоматического управления. Строить амплитудно-фазовые частотные характеристики сложных систем довольно трудоёмко, поэтому в данной статье мы рассмотрим построение их при помощи системы компьютерной алгебры Maple.

Построение АФЧХ рассмотрим на примере системы управления бесконтактным моментным двигателем с полезной нагрузкой.

Передаточную функцию системы можно задать или рассчитать. У нас система довольно сложная поэтому её передаточную функцию нам рассчитает Maple. Для этого сначала зададим передаточные функции регулятора, объекта управления и датчика угла, фиксирующего угловые отклонения.

Передаточную функцию объекта присвоим :

>

Передаточную функцию гироскопического датчика угла присвоим :

>

Передаточную функцию ПИД-регулятора зададим как сумму пропорционального, интегрального и дифференцирующего звеньев, присвоим :

>

Обобщенная структурная схема системы автоматического регулирование имеет вид:

Система замкнута отрицательной обратной связью, значит расчет передаточной функции системы должен производится по следующей формуле:

>

Полученный результат:

Но для построения амплитудно-частотных и фазо-частотных характеристик нам потребуется передаточная функция разомкнутой системы, поэтому рассчитаем и её:

>

Полученный результат:

Для построения АФЧХ потребуется выполнить небольшое преобразование, перейдя к комплексным числам.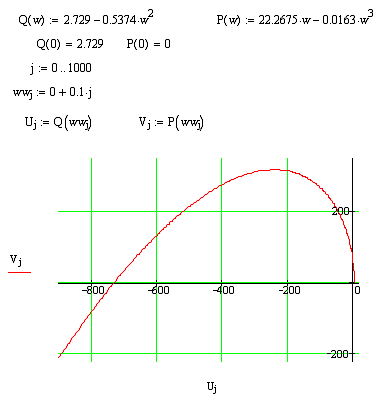 Необходимо в передаточной функции системы заменить оператор Лапласа на круговую частоту, умноженную на мнимую единицу. Известно, что круговая частота имеет следующую зависимость от частоты:

,

где — круговая частота, — частота.

Осуществим подстановку:

>

Команда subs(,) осуществляет подстановку первого элемента в скобках во второй.

Полученный результат:

Как известно АЧХ — это модуль комплексной функции. Модуль задается командой abs(). Команда evalc() поможет осуществить переход в комплексный вид.

>

Построение графиков осуществляется командой plot(,). Эта команда построит график функции, указанной первой в скобках. Через запятую в скобках необходима указать параметр, по которому строится график и диапазон его значений. АЧХ обычно строятся в логарифмическом масштабе, для этого можно использовать команду loglogplot, либо поставить галочку около опции «Логарифмический масштаб» в опциях графика.

>

Для построения ФЧХ нужно взять аргумент комплексной функции. Для выделения аргумента используется команда argument(). Команда evalc() поможет осуществить переход в комплексный вид.

>

Построим график ФЧХ командой plot:

>

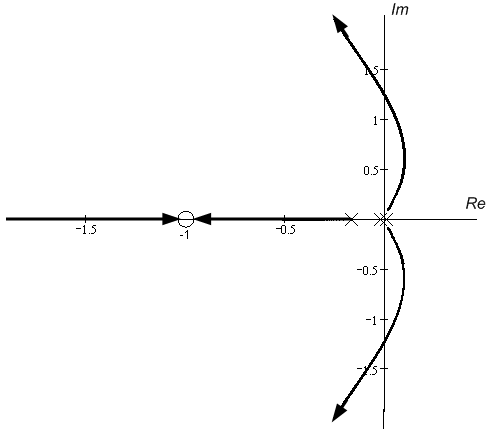
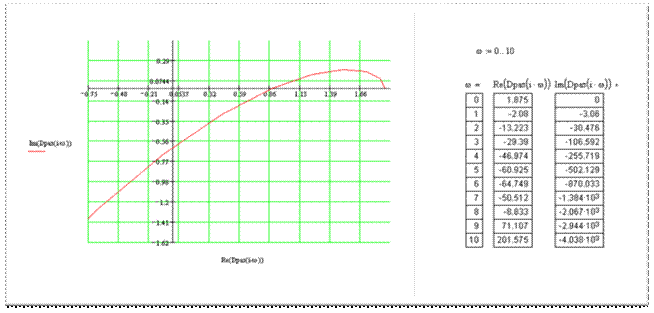
Для построения годографа Михайлова нам хватит команды plot. Только в этом случае необходимо указать, что надо взять мнимую и действительную части комплексной функции. Действительная часть выделяется командой Re(), имеющей в скобках функцию, над которой производится операция. Мнимая часть выделяется командой Im(), имеющей в скобках функцию, над которой производится операция.

>

Теперь, по построенным характеристикам можно легко судить об устойчивости исследуемой системы автоматического регулирования.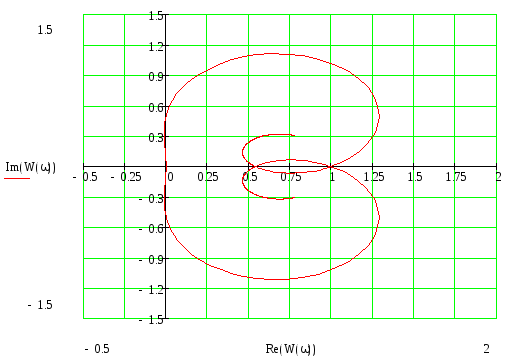

В данной статье мы рассмотрели легкий способ анализа сложных систем автоматического регулирования с помощью системы компьютерной алгебры Maple. Были показаны основные команды и функции, необходимые для успешного построения требуемых графиков и анализа функционирования системы.

Литература:

1. Петраков Ю. В. Драчев О. И. Теория автоматического управления технологическими системами — Машиностроение,2009г.. — 336 с.
2. Дьяконов В. П. Maple 10/11/12/13/14 в математических расчетах. — ДМК Пресс, 2011. — 800 с.

Основные термины (генерируются автоматически): команда, передаточная функция, комплексная функция, круговая частота, передаточная функция системы, полученный результат, автоматическое регулирование, автоматическое управление, действительная часть, комплексный вид.

Корневой годограф — в теории управления траектория, описываемая на комплексной плоскости полюсами передаточной функции динамической системы при изменении одного

                                     

1. Метод корневого годографа

Пусть передаточная функция замкнутой системы

W s = A s B s {\displaystyle Ws={\frac {As}{Bs}}},

причём порядок полинома числителя равен m {\displaystyle m}, порядок полинома знаменателя равен n, m ≤ n {\displaystyle n\!,m\leq n} для физически реализуемых систем.

Метод корневого годографа связывает динамические характеристики системы с поведением нулей и полюсов её передаточной функции, которые находятся из нулей и полюсов разомкнутой системы при изменении какого-либо параметра обычно коэффициента усиления разомкнутой системы. Замкнутая система связана с разомкнутой с помощью следующего соотношения:

W s = W Π 1 + W p {\displaystyle Ws={\frac {W_{\Pi }}{1+W_{p}}}}

Где W Π {\displaystyle W_{\Pi }} — передаточная функция прямой системы, W p {\displaystyle W_{p}} — передаточная функция разомкнутой системы. Эта формула справедлива только для отрицательной обратной связи, в противном случае знак после единицы будет отрицательным. {P}=\pm 2u+1\pi,u=0.1.2,\dots }

Метод корневого годографа позволяет подобрать коэффициент усиления системы управления, оценить колебательность движения, подобрать расположение нулей и полюсов корректирующих звеньев системы управления.

Построение корневых годографов — Студопедия

В большинстве случаев характеристическое уравнение исследуемой системы представимо в виде

(1)

где и полиномы комплексного переменного s, — некоторый параметр, который в дальнейшем будем называть варьируемым. (Таким параметром может служить, например, передаточный коэффициент k разомкнутой системы).

Траектории, которые описывают корни характеристического уравнения на плоскости S при изменении параметра системы от 0 до ∞ получили название корневых годографов. Построенные корневые годографы позволяют вычислить, как влияет на устойчивость и динамические характеристики системы изменение варьируемого параметра.

Имея характеристическое уравнение (1) с известными нулями входящих в него полиномов L(s) и D(s) можно приблизительно построить на плоскости S корневые годографы.

Для этого (1) переписываем в виде:

(2)

Учитывая, что s — комплексная переменная, (2) можно записать в виде двух уравнений: уравнения аргументов

π + 2πi, , (3)

и уравнения модулей

. (4)

Представим и в виде:

,

,

где и — коэффициент при s наивысшей степени,

, — нули полиномов и ,

m и n – порядки полиномов и .

Уравнение аргументов (3) можно переписать в следующем виде:

π + 2πi (5)

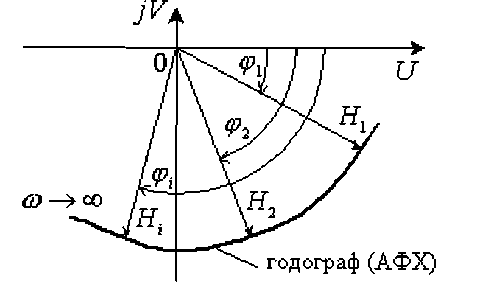
Из выражения (5) следует: точка s плоскости S принадлежит корневому годографу, если сумма аргументов векторов, проведенных из нулей функции в эту точку, за вычетом суммы аргументов векторов, проведенных из полюсов в эту же точку, равно π + 2πi.

(Сказанное показано на рис. 1)

Рис. 1.

На этом рисунке через обозначены аргументы векторов, проведенных из полюсов , аргумент вектора, проведенного из нуля .

На основании выражения (5) можно сформулировать следующие основные правила построения корневых годографов:

1. Вещественная ось плоскостей S является осью симметрии для корневых годографов и для асимптот корневых годографов.

2. При изменении от 0 до ∞ корневые годографы выйдя из полюсов функции , должны прийти в нули функции .

Если число полюсов n больше числа нулей m, то (n-m) ветвей корневого годографа уйдут в бесконечность. Если число нулей больше числа полюсов, то (n-m) ветвей корневого годографа придут из бесконечности.

3. Ветви корневых годографов, находящихся в бесконечности имеют асимптоты. Число асимптот равно . Асимптоты пересекаются в одной точке вещественной оси плоскости S, причем:

, (6)

и имеют углы наклона относительно положительного направления вещественной оси плоскости S:

π , i=0,1,2…|m-n|-1. (7)

4. Точки вещественной оси плоскости S справа от которых находится нечетное число нулей и полюсов функции обязательно принадлежат корневым годографам, а точки этой оси справа от которых находится четное число нулей и полюсов не могут принадлежать корневым годографам.

5. В некоторых точках вещественной оси плоскости S, принадлежащих корневым годографам, корневые годографы могут, встретившись, разойтись, один в верхнюю, а другой в нижнюю части плоскости S.

Сформулированные выше правила позволяют приближенно выполнить построение корневых годографов.

Рассмотрим некоторые примеры построения корневых годографов.

Построить корневые годографы для варьируемого параметра К для замкнутой системы, если передаточная функция разомкнутой системы:

Пример 1.

Решение: Характеристическое уравнение замкнутой системы . Представим его в виде . Отсюда видно, что количество нулей равно 0, а количество полюсов равно 4.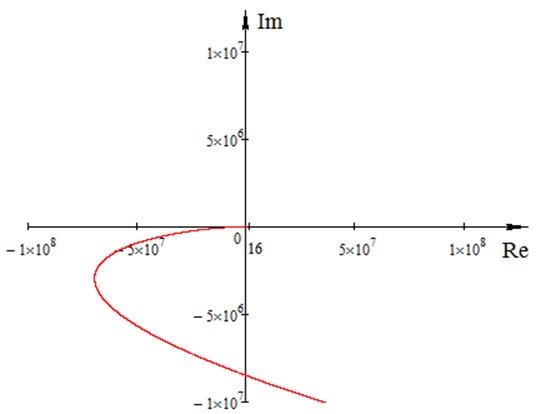 Их значения можно получить, найдя корни знаменателя. Получаем

Наносим полюса на комплексную плоскость. В соответствии с правилом 2 все корневые годографы должны уйти в бесконечность. Число асимптот равно 4-0=4. Определим точку, расположенную на вещественной оси, в которой пересекаются асимптоты –7,5

Определим углы, которые асимптоты составляют с положительным направлением вещественной оси (правило 3).

Наносим асимптоты на комплексную плоскость, как показано на рис.2. На этом же рисунке показаны корневые годографы, которые выходят из полюсов и уходят в бесконечность, неограниченно приближаясь к нарисованным асимптотам.

Рис.2

Пример 2.

Решение: Характеристическое уравнение замкнутой системы имеет вид

Отсюда .

Приравнивая к нулю числитель и знаменатель, получим нули и полюса корневых годографов

Наносим полюса и нули на комплексную плоскость, как показано на рис.2. В соответствии с правилом 1, два корневых годографа должны закончиться в бесконечности, кроме того в соответствии с правилом 4 ни одна из точек вещественной плоскости не принадлежит корневым годографам.

В соответствии с правилом 3, корневые годографы имеют 2 асимптоты, пересекающиеся с вещественной осью в точке

Углы между асимптотами и положительным направлением вещественной оси будут равны (правило 3)

С учетом сказанного корневые годографы будут иметь вид, показанный на рис.3. Корневые годографы выйдя из полюсов P₁ и P₂ закончатся в нулях N₁ и N₂. Корневые годографы выйдя из полюсов P₃ и P₄ уйдут в бесконечность неограниченно приближаясь к асимптотам, пересекающим вещественную ось в точке –55.

Рис.3

Пример 3.

Решение: Характеристическое уравнение замкнутой системы

Представим его в виде

Нули корневых годографов будут:

Полюса корневых годографов будут:

Наносим нули и полюса на комплексную плоскость, как показано на рис.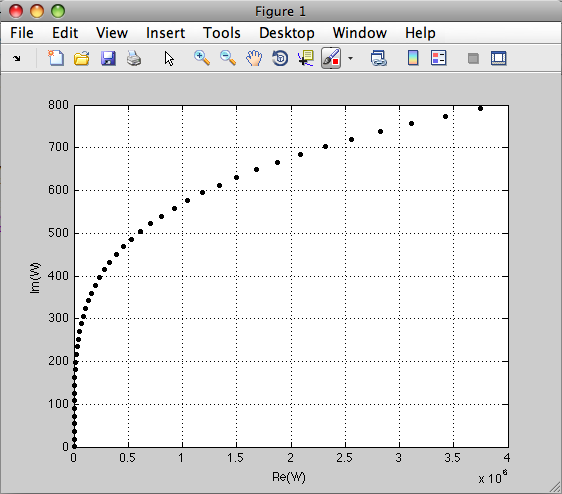 4. В соответствии с правилом 4, часть вещественной оси, лежащая левее нуля N₃ будет принадлежать корневым годографам, при этом этот отрезок оси является асимптотой для годографа, уходящего в бесконечность.

Корневые годографы, построенные в соответствии с изложенными выше правилами, изображены на том же рисунке. Два корневых годографа, выйдя из полюсов P₁ и P₂ придут в нули N₁ и N₂. Корневые годографы, выйдя из полюсов P₃ и P₄ сойдутся в одной точке на вещественной оси, равной примерно 84 и, затем один закончится нуле N₃, а другой уйдет в бесконечность.

Рис.4

Критерии устойчивости Михайлова

Содержание:

Критерии устойчивости Михайлова

По критерию Михайлова, предложенному А. В. в 1938 г., об устойчивости системы можно судить по кривой, построенной на основе характеристического полинома замкнутой системы. В системных уравнениях, замкнутых единичной обратной связью, характеристический полином является полиномом.

Существует общая форма нормализованного полинома. Как вы знаете, этот многочлен может вычислять корень характеристического уравнения замкнутой системы. Задача состоит в том, чтобы определить условие, когда все корни характеристического уравнения находятся слева от мнимой оси в частотной плоскости.

• В частотной плоскости каждый корень числа pi представлен либо точкой, либо вектором, проведенным от начала координат до этой точки. Изображение корня характеристического уравнения на комплексной плоскости в определении вектора по вектору. Векторное определение Текущая координата p, которая является комплексным числом, также геометрически представлена ​​в виде вектора.

Каждый фактор в выражении, который представляет собой разницу между двумя векторами, также является вектором, начальная точка которого находится в точке, определяющей маршрут, и конечная точка которой находится в точке, соответствующей текущим координатам.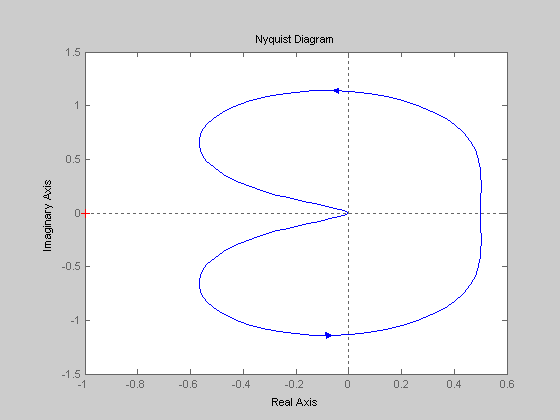 Выражение особенно полезно для текущего значения координаты p. Конец основного вектора в этом случае находится в точке на виртуальной оси, как показано на рисунке 4а, и движется вдоль этой оси при изменении ω.

Длина (модуль) и угол поворота каждого вектора изменяются. Общепринято, что вращение вектора против часовой стрелки является положительным. Когда вы изменяете, начало координат (то есть корень) поворачивается на угол + π с каждым базовым вектором в левой плоскости, а начало каждого вектора находится в правой полуплоскости.

Поскольку функция равна произведению базовых векторов, сама функция является вектором.

• Векторный модуль, называемый характеристикой, равен произведению базовых векторных модулей, а его аргумент является суммой этих векторных аргументов.

Изменение argD (jω) при изменении зависит от положения маршрута на частотной плоскости. Если все n корней характеристического уравнения замкнутой системы лежат в левой полуплоскости, соответствующей устойчивой системе, изменение ее изменит + nπ. То есть вектор вращается против часовой стрелки на угол nπ. Если хотя бы один корень характеристического уравнения отображается в правой полуплоскости, соответствующей нестабильной системе, вектор будет вращаться меньше, чем nπ, по мере его изменения.

На практике не нужно менять, просто меняйте. Характеристический многочлен имеет корень в правой полуплоскости, если фаза или полное приращение аргумента при изменении ω от 0 до ∞ равно порядку многочлена. В результате система регулирования стабильна. Если общее приращение аргумента мало, система нестабильна. Если указаны все коэффициенты и установлено конкретное значение частоты, это значение отображается в комплексной плоскости в виде точки с координатами или в виде вектора, соединяющего эту точку с началом координат. Когда значение частоты ω непрерывно изменяется от нуля до бесконечности, величина и направление вектора изменяются, и последняя кривая (годограф), называемая кривой Михайлова, записывается последней.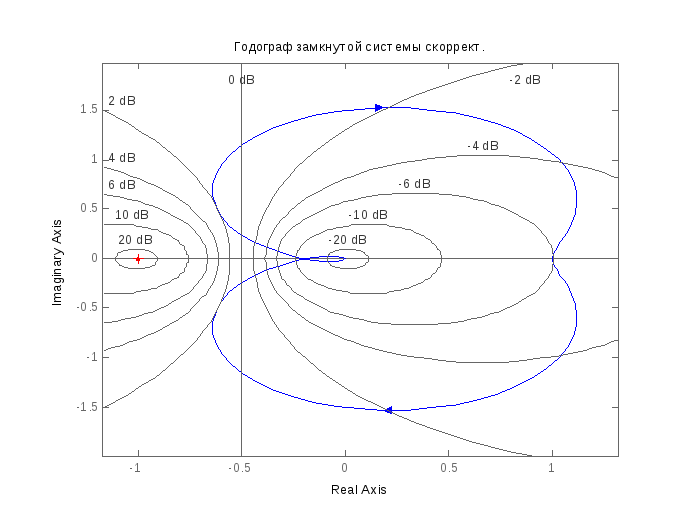

Видно, что кривая Михайлова устойчивой системы всегда имеет гладкую спиральную форму, конечная точка которой бесконечна в квадранте комплексной плоскости, а ее число равно порядку характеристического уравнения. Годограф Михайлова: Стабильная система от -1 до 5 порядка.

Система на границе устойчивости. Критерии устойчивости неустойчивой системы Михайлова можно сформулировать следующим образом: годограф Михайлова начинается с положительной вещественной оси, изменяется ω от положительной оси, степень характеристического уравнения замкнутой системы Система автоматического управления стабильна при прохождении через n квадрантов против часовой стрелки. Системы, которые не удовлетворяют этому условию, нестабильны. Число квадрантов, превышающих кривую Михайлова, вообще не может пройти.

Таким образом, нестабильность системы всегда связана с тем, что кривая Михайлова нарушает серию квадрантных проходов, что приводит к меньшему углу поворота вектора.

Фактически начальное представление характеристического многочлена замкнутой системы с заменой p используется для построения годографа Михайлова. На практике кривая Михайлова создается на основе точек, заданных с разными значениями частоты ω и рассчитываемых по формуле.

Результаты расчета сведены в таблицу, и соответственно создана кривая.

В этом случае вы получите характеристический комплекс, действительная часть которого содержит четную степень, а мнимая часть содержит нечетную степень. Из уравнения определяют частоту на пересечении действительной оси годографа Михайлова. Частота пересечения годографа мнимой оси определяется из уравнения.

Отрицательные корневые значения отбрасываются и вносятся изменения. Найденное значение присваивается выражению выражения. Определите пересечение годографа и координатных осей и создайте годограф. Когда система окажется стабильной. В этом случае отображается приблизительный вид годографа.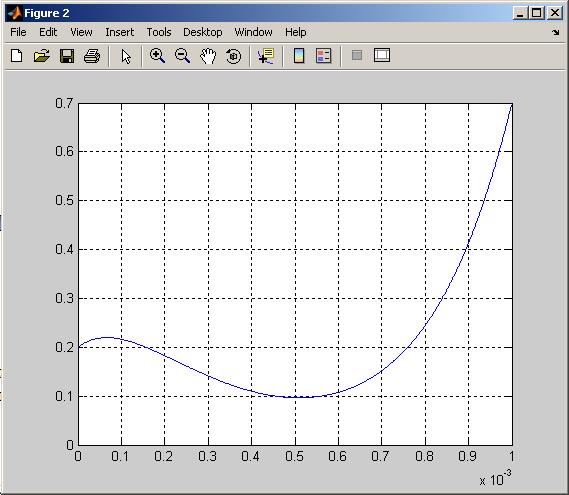 Михайлов годограф третьей стабильной системы.

Смотрите также:

Решение задач по теории автоматического управления

Программа для моделирования электронных схем

В Delta Design 3.0 система аналогового моделирования SimOne полностью интегрирована в среду проектирования

• Появилась возможность создания проекта аналогового моделирования SimOne
• Реализована новая панель «Модели»
• Перенесены библиотеки моделей из SimOne из отдельной версии
• Обеспечена возможность создания фильтров
• Реализовано задание сигналов через графическую оболочку.
• Обеспечена поддержка блоков при формировании SPICE-нетлиста
• Реализован инструмент «Щуп»

SimOne – современная высокоэффективная система схемотехнического моделирования, использующая наряду c классическими алгоритмами  оригинальные, основанные на современных численных методах.

SimOne многократно превосходит по скорости моделирования обычные SPICE-симуляторы при той же точности расчетов.

SimOne позволяет проводить полнофункциональное SPICE-моделирование радиоэлектронных схем, предлагая пользователю такие новые возможности как расчет периодических режимов схемы и анализ устойчивости.

Расчет периодических режимов позволяет определять поведение схемы в установившемся режиме без предварительных длительных расчетов переходных процессов.

Анализ устойчивости схемы позволяет определять, устойчива схема в текущей рабочей точке или нет,  выделять компоненты схемы, влияющие на ее устойчивость, проводить исследование устойчивости при изменении температуры или параметров моделей элементов.

Библиотека моделей компонентов содержит как встроенные SPICE-модели компонентов (SPICE-примитивы), так и обширную (более 30 000 шт. ) базу готовых моделей реальных схемных компонентов. Реализована удобная работа с тестовыми SPICE-библиотеками и графическими макромоделями.

Графическое отображение результатов моделирования и постпроцессорной обработки позволяет пользователю:

• Строить графики интересующих переменных и функций от них,
• Использовать функции курсоров для оценки параметров кривых,
• Производить измерения  и их пересчет при последующих запусках моделирования характеристик построенных кривых,
• Получать  спектральные характеристики кривых на основе быстрого преобразования Фурье.

SimOne может экспортировать результаты моделирования, а также уравнения цепи в численном и символьном видах, в MATLAB, Maple и MS Excel.

1. Высокая скорость моделирования. В десятки раз быстрее классических SPICE- программ.

Высокая скорость моделирования в SimOne достигается за счет применения оригинальных программных технологий, современных численных алгоритмов и использования параллельных вычислений.

Кодовый матричный процессор представляет собой высокоэффективную программную реализацию основных матричных операций, необходимых для проведения расчетов и  применяется во всех видах моделирования схемы.

Помощник симуляции  запоминает характерные особенности моделируемой схемы во время запуска текущего вида анализа и использует эту информацию при последующих запусках. Таким образом, его применение становится особенно эффективным при проведении многовариантных видов анализа схем, например — температурного или параметрического.

2. Высокая точность.

Обусловлена применением современных численных методов высшего порядка точности, поддержкой вычислений с представлением чисел повышенной точности.

3. Многоядерность и параллельное моделирование

Параллельный запуск различных вариантов анализа схемы проводится с использованием многоядерной архитектуры процессора. Запуск любого вида расчета позволяет пользователю продолжать работу со схемой и проводить параллельное моделирование.

4. Анализ устойчивости схемы.

Эта опция является отличительной особенностью пакета: анализ устойчивости схем отсутствует у подавляющего большинства конкурирующих программ. Анализ устойчивости схемы позволяет определять, устойчива схема в текущей рабочей точке или нет,  проводить исследование устойчивости при изменении температуры или параметров моделей элементов, выделяя те компоненты и параметры схемы, которые определяют ее устойчивость.

5. Экспорт результатов моделирования.

Рассчитанные переменные, выражения и составленные уравнения схемы могут быть экспортированы в известные инженерные математические пакеты Matlab, и Maple, Excel.

Моделирование электронных схем

Загрузить бесплатную версию пакета моделирования электронных схем SimOne

В пакете SimOne доступны основные виды анализа схем, существующие в классических SPICE-программах, таких как PSpice, MicroCAP, OrCad. Кроме этого, предлагается новый вид — анализ устойчивости схемы.

При разработке модуля моделирования электронных схем особое внимание уделялось повышению скорости и точности вычислений, в сравнении с конкурентами.

Вычислительное ядро нового поколения

Для всех видов анализа электронных схем используется вычислительное ядро нового поколения Code Matrix Processor™.

Многоядерность и параллельное моделирование

Запуск любого вида расчета позволяет пользователю продолжать работу со схемой и проводить параллельное моделирование.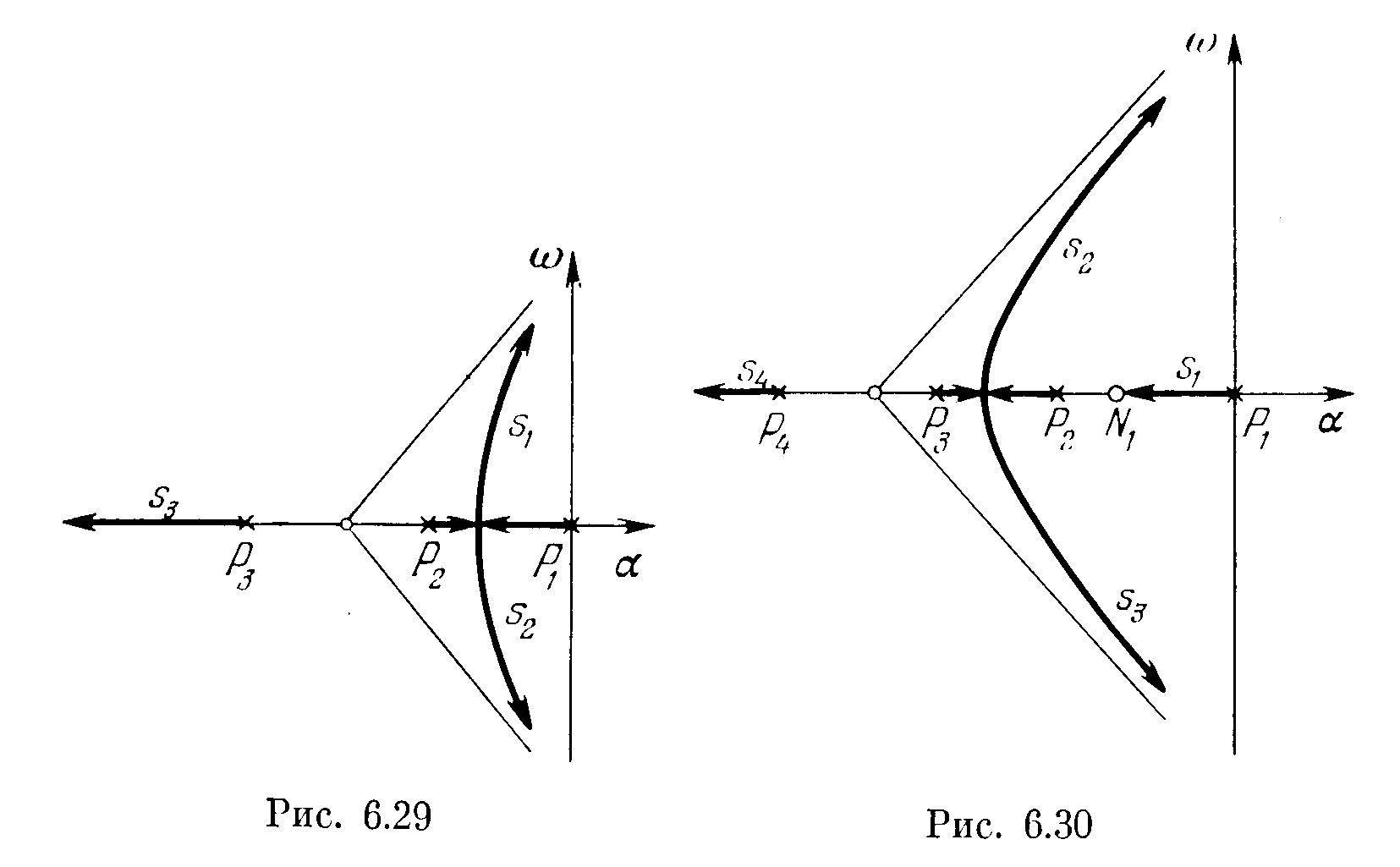

Новый вид анализа схем — расчет устойчивости — Stability Analysis

Позволяет оценивать надежность функционирования электронных схем на этапе проектирования.

Повышенная точность и скорость расчетов в режиме временного анализа (Transient analysis)

Оригинальный метод  интегрирования дифференциально-алгебраических уравнений.

Для интегрирования уравнений цепи пользователю предлагается оригинальный метод SimOne 4-го порядка точности. Этот метод имеет повышенную точность и устойчивость в сравнении с методами, применяемыми в обычном SPICE-моделировании и является лучшим методом для расчета больших схем.

Возможности

DC Sweep. Расчет статического режима схем по постоянному току.

AC Sweep. Частотный анализ. Расчет частотных характеристик линеаризованной цепи в рабочей точке.

Transient Analysis. Расчет переходных и установившихся временных процессов на длительных интервалах времени при воздействии сигналов произвольной формы.

Temperature Sweep. Моделирование поведения схемы при изменении рабочей температуры.

Parametric Sweep. Моделирование поведения схемы при изменении параметров сигналов, моделей схемных компонентов.

Stability Analysis. Анализ устойчивости схемы.

Серия видеороликов демонстрирует основные возможности SimOne

Справочное руководство по Delta Design SimOne доступно в разделе Документация

В SimOne доступны следующие виды анализа схем:

1. Расчет статического режима схем по постоянному току (DC Analysis)

Включает в себя расчет рабочей точки схемы, определение передаточных функций по постоянному току. Для решения нелинейных алгебраических уравнений предлагается набор методов: метод Ньютона–Рафсона, Damped Newton–Raphson, Gmin Stepping,Source Stepping.

2. Частотный анализ (AC Analysis)

Включает в себя расчет и построение частотных характеристик схемы, в том числе амплитудно-фазовой характеристики.

3. Анализ переходных процессов (Transient Analysis)

Используется оригинальный метод интегрирования дифференциально-алгебраических уравнений. Метод имеет повышенную точность и устойчивость в сравнении с методами, применяемыми в обычном SPICE-моделировании.

Вычисления в традиционных для SPICE-моделирования методах — методе Гира, трапеций, Эйлера производятся с помощью кодового матричного процессора, что позволяет  значительно сократить время расчета.

4. Анализ установившихся периодических режимов (PSS Analysis)

Расчет периодических режимов ведется с помощью пристрелочного метода Ньютона (Shooting Newton), при этом используется высокоэффективный подход — без явного формирования матрицы чувствительности (Matrix Free Approach). В качестве метода решения СЛАУ используется итерационный метод пространств Крылова — Gmres.

5. Температурный анализ (.TEMP)

Аналоговое моделирование поведения схемы при изменении рабочей температуры.

6. Параметрический анализ схемы (.PARAM)

Моделирование поведения схемы при изменении параметров сигналов, моделей схемных компонентов.

7. Анализ устойчивости схемы. (Stability Analysis)

Для анализа устойчивости схемы в окрестности рабочей точки пользователю предлагаются два независимых способа: на основе расчета собственных частот схемы и на основе критерия Михайлова. Результат анализа — вывод об устойчивости схемы, построение годографа Михайлова, вывод таблицы собственных частот схемы. Пользователь также имеет возможность построить график годографа Михайлова в заданном произвольном диапазоне и принять решение об устойчивости схемы самостоятельно.

(PDF) Новый взгляд на подход Фейнмана «годографом» к первому закону Кеплера

, их вывод с законом, разработанный Фейнманом, и сравнение обоих подходов с исходным выводом Ньютона

. Это сравнение имеет смысл, потому что все три вывода составляют

на языке синтетической евклидовой геометрии.

Предлагаемая ими геометрическая конструкция имеет много общих элементов с конструкциями до

(Максвелл, Фейнман,…), но они смотрят на проблему с другой точки зрения

, что ведет к двум важным выводам проблемы: конической природе

орбит и существованию «исключительной» кеплеровской постоянной движения

Я

. Стоит

подчеркнуть, что вывод является чисто алгебраическим и ни на каком этапе не следует прибегать к дифференциальному уравнению

(в отличие от подхода Фейнмана).

Стандартный вектор Лапласа – Рунге – Ленца (LRL)

A

, как известно, направлен от центра силы

к перигелию вдоль большой оси орбиты с модулем

e;

иначе

не имеет геометрической интерпретации

. Напротив, постоянный вектор

I

, который следует из этого подхода

, является изменением масштаба стандартного вектора LRL

A

на коэффициент

E1

,

EIA =

и допускает приятный и

прямая геометрическая интерпретация: как для эллиптических, так и для гиперболических орбит он идет от центра силы

, который является одним из фокусов орбиты, ко « второму » или « пустому » фокусу (он вырождается в вектор бесконечного модуля

вдоль конической оси для параболических орбит).

Начнем с того, что вспомним элементарное доказательство первого закона Кеплера, предложенное van

Haandel и Heckman в [9]. Рассмотрим орбиты Кеплера с

0¹

и

0 <

(мы уже знаем, что это эллипсы Кеплера, но предположим, что мы этого не знаем).

Как следствие сохранения энергии, движение в конфигурационном пространстве (или в плоскости движения

) ограничено внутренней частью окружности

с центром в начале координат и радиусом

E () —

.Вне этого круга кинетическая энергия будет отрицательной, и поэтому эта внешняя область

запрещена для классического движения. Этот круг

играет важную роль (но, как мы увидим позже

, эта роль не совсем как граница энергетически разрешенной области, хотя это

— это то, как ван Хаандель – Хекман представил конструкцию).

Пусть будет

вектор положения точки P на данной орбите, l

P

обозначает касательную линию к орбите

в точке P,

скорость частицы в точке P и

p

вектор импульса, который мы представим

присоединенным к началу координат O, i.Например, вектор

p

является результатом переноса вектора

mv

в начало координат O (напомним, мы предполагаем, что m = 1).

Геометрическое построение выполняется в два этапа.

1. Сначала продлите радиус-вектор

P rº

точки P (с потенциальным центром O в качестве начала координат) до тех пор, пока он

не пересечется с окружностью

в точке

. Это можно увидеть как результат масштабирования с коэффициентом

kE r1

) () —

, который отправляет вектор

P rº

в новый вектор с модулем, равным

kE rr kE1

) () () — = —

, поэтому этот векторный наконечник

лежит на окружности

.

2. Теперь рассмотрим изображение I

в отражении относительно линии l

P

.

Это построение может быть выполнено для любого ограниченного движения

0 <

в любом ограничивающем произвольном центральном потенциале; когда P движется по орбите, точка

перемещается на

, и можно ожидать, что точка I также будет перемещаться. Так обстоит дело с движениями в других центральных полях, но

Кеплеровское движение является исключительным в этом отношении, и мы получаем следующий результат.

Теорема 1. Когда P движется по орбите Кеплера

0 <

и точка

, определенная предыдущей конструкцией

, движется по окружности

, то точка I остается неподвижной.

Другими словами, I оказывается независимым от выбора точки P на орбите. Как мы увидим, как

, эта геометрическая «вневременная» конструкция, показанная на рисунке 2, будет отражать существование константы движения

, специфичной для потенциала Кеплера.

Eur. J. Phys. 37 (2016) 025004 J F Cariñena et al.

7

Построение траекторий движения инструмента с непрерывным ускорением с использованием кривых годографа Пифагора

Проблемы интерполяции широко изучались в компьютерном геометрическом проектировании (CAGD). Они состоят в построении кривых и поверхностей, которые точно проходят через заданный набор данных, таких как облака точек, касательные, кривизны, линии / плоскости и т. Д. В общем, эти кривые и поверхности представлены в параметризованной форме.Это представление не зависит от системы координат, оно хорошо адаптируется к геометрическим преобразованиям, а дифференциально-геометрические свойства кривых и поверхностей инвариантны при повторной параметризации. В этом контексте основной целью данной диссертации является представление схем интерполяции 2D и 3D данных с помощью алгебро-тригонометрических кривых пифагора-годографа (ATPH). Последние представляют собой параметрические кривые, определенные в смешанном алгебро-тригонометрическом пространстве, годограф которого удовлетворяет условию Пифагора.Это представление позволяет аналитически вычислить длину дуги кривой, а также рационально-тригонометрическую параметризацию кривых смещения. Эти свойства можно использовать для проектирования геометрических моделей во многих приложениях, включая производство, архитектурное проектирование, судостроение, компьютерную графику и многие другие. В частности, нас интересует геометрическое моделирование одонтологических объектов. С этой целью мы используем пространственные кривые ATPH для построения развивающихся пятен в трехмерных одонтологических объемах.Это может быть полезным инструментом для извлечения интересующей информации о зубных структурах. Мы даем обзор того, как некоторые подобные интерполяционные проблемы решались научным сообществом. Затем в главе 2 мы рассмотрим построение плоских сплайновых кривых C2 ATPH, которые интерполируют упорядоченную последовательность точек. Эта проблема имеет множество решений, их количество зависит от количества интерполирующих точек. Поэтому для их поиска мы используем два метода. Сначала мы вычисляем все решения гомотопическим методом.Однако эмпирически замечено, что только одно решение не имеет самопересечений. Следовательно, метод итераций Ньютона-Рафсона используется для прямого вычисления этого «хорошего» решения. Обратите внимание, что кривые сплайна C2 ATPH зависят от нескольких свободных параметров, которые позволяют получить разнообразие интерполянтов. Благодаря этим параметрам формы кривые ATPH доказывают свою эффективность. чтобы быть более гибкими и универсальными, чем их полиномиальные аналоги, хорошо известные кривые пятого порядка Пифагора-Годографа (PH) и полиномиальные кривые в целом. Эти параметры оптимально выбираются путем минимизации мер справедливости. Мы разрабатываем кривые ATPH, которые близко согласуются с хорошо известными тригонометрическими кривыми, изменяя параметры формы. Мы расширяем планарные кривые ATPH на случай пространственных кривых ATPH в главе 3. Эта характеристика дается в терминах кватернионов, поскольку это позволяет правильно проанализировать их свойства и упростить вычисления. Мы используем пространственные кривые ATPH для решения интерполяционной задачи Эрмита первого порядка.Полученные интерполянты ATPH зависят от трех свободных угловых значений. Как и в плоском случае, мы оптимально выбираем эти параметры путем минимизации интегральных мер формы. Этот процесс также используется для расчета интерполяционных кривых ATPH C1, которые близко аппроксимируют хорошо известные параметрические кривые 3D. Чтобы проиллюстрировать это представление, мы представляем процесс для некоторых спиралей. Затем в главе 4 мы используем эти сплайны C1 ATPH для управления развивающимися поверхностными пятнами, которые развертываются в объемах одонтологической компьютерной томографии (КТ), чтобы визуализировать информацию, представляющую интерес для медицинского работника.В частности, мы строим кусочно-конические поверхности вдоль гладких кривых ATPH для отображения информации, относящейся к анатомической структуре костей челюсти человека. Эта информация может быть полезна при клинической оценке, диагностике и / или плане лечения. Наконец, полученные результаты анализируются, и в главе 5 делаются выводы.

Произошла ошибка при настройке вашего пользовательского файла cookie

Произошла ошибка при настройке вашего пользовательского файла cookie

Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.

Настройка вашего браузера на прием файлов cookie

Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:

• В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить, хотите ли вы принимать файлы cookie.
• Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
• Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
• Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
• Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.

Почему этому сайту требуются файлы cookie?

Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.

Что сохраняется в файле cookie?

Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.

Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.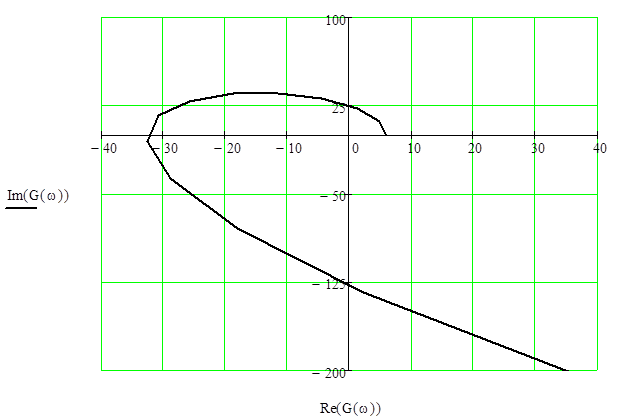

Алгебро-тригонометрические кривые годографа Пифагора для решения задач плоской и пространственной интерполяции и их использование для визуализации стоматологической информации в трехмерных томографических объемах — TEL

Abstract : Задачи интерполяции широко изучались в компьютерном геометрическом дизайне (CAGD). Они состоят в построении кривых и поверхностей, которые точно проходят через заданный набор данных, таких как облака точек, касательные, кривизны, линии / плоскости и т. Д.В общем, эти кривые и поверхности представлены в параметризованной форме. Это представление не зависит от системы координат, оно хорошо адаптируется к геометрическим преобразованиям, а дифференциально-геометрические свойства кривых и поверхностей инвариантны при повторной параметризации. В этом контексте основной целью данной диссертации является представление схем интерполяции 2D и 3D данных с помощью алгебро-тригонометрических кривых пифагора-годографа (ATPH). Последние представляют собой параметрические кривые, определенные в смешанном алгебро-тригонометрическом пространстве, годограф которого удовлетворяет условию Пифагора.Это представление позволяет аналитически вычислить длину дуги кривой, а также рационально-тригонометрическую параметризацию кривых смещения. Эти свойства можно использовать для проектирования геометрических моделей во многих приложениях, включая производство, архитектурное проектирование, судостроение, компьютерную графику и многие другие. В частности, нас интересует геометрическое моделирование одонтологических объектов. С этой целью мы используем пространственные кривые ATPH для построения развивающихся пятен в трехмерных одонтологических объемах.Это может быть полезным инструментом для извлечения интересующей информации о зубных структурах. Мы даем обзор того, как некоторые подобные интерполяционные проблемы решались научным сообществом. Затем в главе 2 мы рассмотрим построение плоских сплайновых кривых C2 ATPH, которые интерполируют упорядоченную последовательность точек. Эта проблема имеет множество решений, их количество зависит от количества интерполирующих точек. Поэтому для их поиска мы используем два метода. Сначала мы вычисляем все решения гомотопическим методом.Однако эмпирически замечено, что только одно решение не имеет самопересечений. Следовательно, метод итераций Ньютона-Рафсона используется для прямого вычисления этого «хорошего» решения. Обратите внимание, что кривые сплайна C2 ATPH зависят от нескольких свободных параметров, которые позволяют получить разнообразие интерполянтов. Благодаря этим параметрам формы кривые ATPH доказывают свою эффективность. чтобы быть более гибкими и универсальными, чем их полиномиальные аналоги, хорошо известные кривые пятого порядка Пифагора-Годографа (PH) и полиномиальные кривые в целом.Эти параметры оптимально выбираются путем минимизации мер справедливости. Мы разрабатываем кривые ATPH, которые близко согласуются с хорошо известными тригонометрическими кривыми, изменяя параметры формы. Мы расширяем планарные кривые ATPH на случай пространственных кривых ATPH в главе 3. Эта характеристика дается в терминах кватернионов, поскольку это позволяет правильно проанализировать их свойства и упростить вычисления. Мы используем пространственные кривые ATPH для решения интерполяционной задачи Эрмита первого порядка.Полученные интерполянты ATPH зависят от трех свободных угловых значений. Как и в плоском случае, мы оптимально выбираем эти параметры путем минимизации интегральных мер формы. Этот процесс также используется для расчета интерполяционных кривых ATPH C1, которые близко аппроксимируют хорошо известные параметрические кривые 3D. Чтобы проиллюстрировать это представление, мы представляем процесс для некоторых спиралей. Затем в главе 4 мы используем эти сплайны C1 ATPH для управления развивающимися поверхностными пятнами, которые развертываются в объемах одонтологической компьютерной томографии (КТ), чтобы визуализировать информацию, представляющую интерес для медицинского работника.В частности, мы строим кусочно-конические поверхности вдоль гладких кривых ATPH для отображения информации, относящейся к анатомической структуре костей челюсти человека. Эта информация может быть полезна при клинической оценке, диагностике и / или плане лечения. Наконец, полученные результаты анализируются и выводы делаются в главе 5.

Резюме : Проблемы интерполяции, связанные с большими исследованиями в рамках Conception Géométrique Assistée par Ordinateur.Это проблемы, согласованные с конструкцией курбов и поверхностей, которые проходят безупречно в соответствии с ансамблем донных построек. Dans ce cadre, l’objectif Principal de cette this est de presenter des méthodes d’interpolation de données 2D и 3D au moyen de Courbes Algébriques Trigonométriques à Hodographe Pythagorien (ATPH). Целевые компоненты используются для концепции геометрических моделей в стандартных приложениях. Особое внимание уделяется моделям одонтологических объектов.А этот плавник, мы используем les Courbes spatiales ATPH для создания конструкций поверхностей в одонтологических объемах. Начальный элемент, nous considérons la Construction de Courbes Plays ATPH avec continité C² qui interpolent un séquence ordonnée de points. Мы используем два метода для решения проблем и проблем. Nous étendons les Courbes самолетов ATPH в трехмерном пространстве. Эта caractérisation 3D используется для решения проблемы интерполяции Hermite de premier ordre.Nous использует эти шлицы. ATPH spatiales C¹ продолжает использовать направляющие для развертываемых граней, которые развернуты в одонтологических томах, а также в визуализаторе информации, созданной для профессионального использования. Cette information peut être utile dans l’évaluation Clinique, Diagnostic et / ou plan de traitement.

Построение класса кривых пятой степени с рациональными смещениями

Список литературы

[1] Фарин Дж. , Хошек Дж., Ким М. С. и др.Справочник по компьютерному геометрическому проектированию. Амстердам: Эльзевир, 2002. Google Scholar http://scholar.google.com/scholar_lookup?title=Farin G, Hoschek J, Kim M S и др. Справочник по компьютерному геометрическому проектированию. Амстердам: Эльзевир, 2002 и

[2] Фаруки Р. Т., Нефф К. А.Аналитические свойства кривых смещения плоскости. Comput Aided Geom Design, 1990, 7: 83-99. Google Scholar http://scholar.google.com/scholar_lookup?title=Farouki R T, Neff C. Аналитические свойства кривых смещения плоскости. Comput Aided Geom Design, 1990, 7: 83-99 &.

[3] Фам Б.Смещенные кривые и поверхности: краткий обзор. Comput Aided Design, 1992, 24: 223-229. Google Scholar http://scholar.google.com/scholar_lookup?title=Pham B. Смещение кривых и поверхностей: краткий обзор. Comput Aided Design, 1992, 24: 223-229 и

[4] Элбер Г.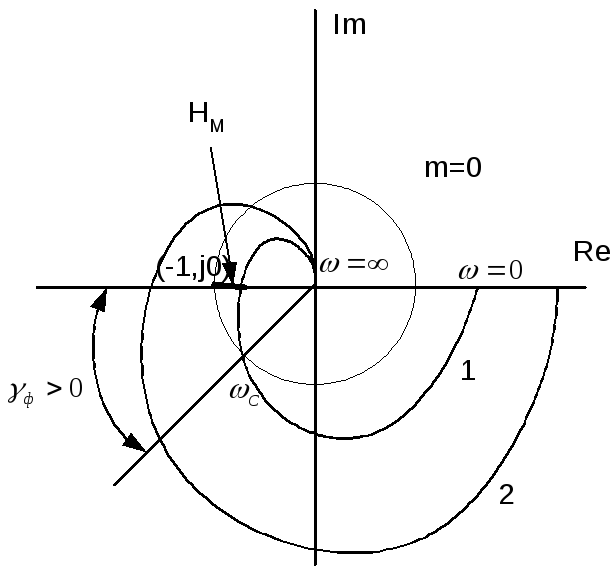 , Ли И. К., Ким М. С.Сравнение методов аппроксимации офсетной кривой. IEEE Comput Graph Appl, 1997, 17: 62-71. Google Scholar http://scholar.google.com/scholar_lookup?title=Элбер Дж., Ли И. К., Ким М. С. Сравнение методов аппроксимации кривой смещения. IEEE Comput Graph Appl, 1997, 17: 62-71 и

[5] Маэкава Т.Обзор смещенных кривых и поверхностей. Компьютерное проектирование, 1999, 31: 165-173. Google Scholar http://scholar.google.com/scholar_lookup?title=Maekawa T. Обзор кривых и поверхностей смещения. Comput Aided Design, 1999, 31: 165—173 и

[6] Фаруки Р. Т., Манджунатайя Дж., Никлас Д. и др.Интерполяторы с ЧПУ с переменной скоростью подачи для постоянной скорости съема материала по кривым Пифагора-годографа. Comput Aided Design, 1998, 30: 631-640. Google Scholar http://scholar.google.com/scholar_lookup?title=Farouki R T, Manjunathaiah J, Nichlas D, et al. Интерполяторы с ЧПУ с переменной скоростью подачи для постоянной скорости съема материала по кривым Пифагора-годографа. Comput Aided Design, 1998, 30: 631-640 и

[7] Фаруки Р. Т., Саккалис Т. Пифагорейские годографы. IBM J Res Dev, 1990, 34: 736-752. Google Scholar http: // ученый.google.com/scholar_lookup?title=Farouki RT, Sakkalis T. Годографы Пифагора. IBM J Res Dev, 1990, 34: 736-752 и

[8] Поттманн Х. Рациональные кривые и поверхности с рациональными смещениями. Comput Aided Geom Design, 1995, 12: 175-192. Google Scholar http: // ученый.google.com/scholar_lookup?title=Pottmann H. Рациональные кривые и поверхности с рациональными смещениями. Comput Aided Geom Design, 1995, 12: 175—192 и

[9] Фаруки Р. Т., Шир З. Рациональные пространственные кривые Пифагора-годографа. Comput Aided Geom Design, 2011, 28: 75-88. Google Scholar http: // ученый.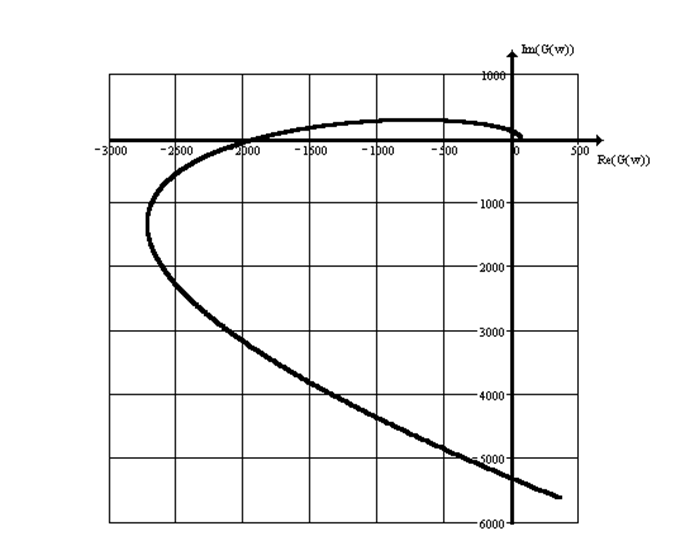 google.com/scholar_lookup?title=Farouki R T., Шир З. Рациональные пространственные кривые Пифагора-годографа. Comput Aided Geom Design, 2011, 28: 75-88 и

[10] Луна Х. П. Минковски Пифагоровы годографы. Comput Aided Geom Design, 1999, 16: 739-753. Google Scholar http: // ученый.google.com/scholar_lookup?title=Moon HP. Minkowski Пифагорейские годографы. Comput Aided Geom Design, 1999, 16: 739-753 и

[11] Саккалис Т., Фаруки Р. Т. Кривые годографа Пифагора в евклидовых пространствах размерности больше 3. J Comput Appl Math, 2012, 236: 4375-4382. Google Scholar http: // ученый.google.com/scholar_lookup?title=Sakkalis T, Farouki R.T. Кривые пифагора-годографа в евклидовых пространствах размерности больше 3. J Comput Appl Math, 2012, 236: 4375—4382 &

[12] Фаруки Р. Т., Нефф К. А. Интерполяция Эрмита с помощью пифагорейских квинтик годографов. Математические вычисления, 1995, 64: 1589-1609. Google Scholar http://scholar. google.com/scholar_lookup?title=Farouki R T, Neff C. A. Интерполяция Эрмита с помощью пифагорейских квинтик годографа. Математические вычисления, 1995, 64: 1589—1609 и

[13] Мун Х. П., Фаруки Р. Т., Чхве Х. И.Построение и анализ формы интерполянтов Эрмита PH пятой степени. Comput Aided Geom Design, 2001, 18: 93—115. Google Scholar http://scholar.google.com/scholar_lookup?title=Moon HP, Фаруки Р. Т., Чой Х. И. Построение и анализ формы интерполянтов Эрмита PH пятой степени.2 $ закругленные углы с кривыми Пифагора-годографа. Comput Aided Geom Design, 2014, 31: 127-139 и

[19] Фаруки Р. Т. Кривые Пифагора-Годографа: алгебра и геометрия неразделимы. Берлин: Springer, 2008. Google Scholar http: // ученый.google.com/scholar_lookup?title=Farouki R T. Кривые Пифагора-Годографа: алгебра и геометрия неразделимы. Берлин: Springer, 2008 г. и

[20] Фаруки Р. Т., Ютлер Б., Манни К. Кривые годографа Пифагора и связанные темы. Comput Aided Geom Design, 2008, 25: 4-5. Google Scholar http: // ученый.google.com/scholar_lookup?title=Farouki R T, Juttler B, Manni C. Кривые годографа Пифагора и связанные темы. Comput Aided Geom Design, 2008, 25: 4-5 и

[21] Косинка Я., Лавичка М. Пифагорейские кривые годографа: обзор последних достижений. Журнал Geom Graph, 2014, 18: 23-43. Google Scholar http: // ученый.google.com/scholar_lookup?title=Kosinka J, Lavička M. Кривые годографа Пифагора: обзор последних достижений. J Geom Graph, 2014, 18: 23-43 и

[22] Лу В. Офсетно-рациональные параметрические плоские кривые. Comput Aided Geom Design, 1995, 12: 601-616. Google Scholar http: // ученый.2 $ плоскости годографа. Comput Aided Geom Design, 1994, 11: 363-390 и

[24] Чой Х. И., Ли Д. С., Мун Х. П. Алгебра Клиффорда, спиновое представление и рациональная параметризация кривых и поверхностей. Adv Comput Math, 2002, 17: 5-48. Google Scholar http: // ученый.google.com/scholar_lookup?title=Choi HI, Lee DS, Moon HP. Алгебра Клиффорда, спиновое представление и рациональная параметризация кривых и поверхностей. Adv Comput Math, 2002, 17: 5-48 и

[25] Фаруки Р. Т., аль-Кандари М., Саккалис Т. Интерполяция Эрмита с помощью инвариантных относительно вращения пространственных кривых Пифагора-годографа.Adv Comput Math, 2002, 17: 369-383. Google Scholar http://scholar.google.com/scholar_lookup?title=Farouki R T, al-Kandari M, Sakkalis T. Интерполяция Эрмита с помощью инвариантных относительно вращения пространственных кривых Пифагора-годографа. Adv Comput Math, 2002, 17: 369-383 и

[26] Ван Г З, Фанг Л.О контрольных многоугольниках кривых Пифагора-годографа четвертой степени. Comput Aided Geom Design, 2009, 26: 1006-1015. Google Scholar http://scholar. google.com/scholar_lookup?title=Wang G Z, Fang L. C. Об контрольных многоугольниках четвертичных кривых Пифагора-годографа.Comput Aided Geom Design, 2009, 26: 1006-1015 и

[27] Юн Дж. Х., Чжэн В. Геометрический метод интерполяции Эрмита классом квинтик PH. J. Comput Aided Design Comput Graph, 2005, 17: 990-995. Google Scholar http: // ученый.Сплайн-кривые 2 $ PH пятого порядка. Comput Aided Geom Design, 2007, 24: 28—52 и

[29] Чой Х. И., Фаруки Р. Т., Квон С. Х. и др. Топологический критерий выбора пятых пифагорово-годографических интерполянтов Эрмита. Comput Aided Geom Design, 2008, 25: 411-433. Google Scholar http: // ученый.1 $ Интерполяция Эрмита с использованием шестнадцатеричных кривых PH. Sci Sin Math, 2014, 44: 799-804 и

[31] Ютлер Б. Интерполяция Эрмита кривыми годографа Пифагора седьмой степени. Математические вычисления, 2001, 70: 1089—1111. Google Scholar http: // ученый. google.com/scholar_lookup?title=Juttler B. Интерполяция Эрмита кривыми годографа Пифагора седьмой степени. Математические вычисления, 2001, 70: 1089—1111 и

[32] Чжэн З. Х, Ван Г. З., Ян П. Об контрольных полигонах пифагорейских септических кривых годографа. J Comput Appl Math, 2016, 296: 212—227. Google Scholar http://scholar.google.com/scholar_lookup?title=Zheng Z H, Wang G Z, Yang P. Об контрольных полигонах септических кривых годографа Пифагора. J Comput Appl Math, 2016, 296: 212—227 и

[33] Лу Х Дж, Чжэн Дж М, Цай Й Й и др.Геометрические характеристики класса кубических кривых с рациональными выносами. Comput Aided Design, 2015, 70: 36-45. Google Scholar http://scholar.google.com/scholar_lookup?title=Lu X J, Zheng J M, Cai Y Y и др. Геометрические характеристики класса кубических кривых с рациональными выносами.Comput Aided Design, 2015, 70: 36-45 и

[34] Фаруки Р. Т., Джаннелли К., Сестини А. Идентификация и «обратная инженерия» кривых Пифагора-годографа. Comput Aided Geom Design, 2015, 34: 21-36. Google Scholar http: // ученый. google.com/scholar_lookup?title=Farouki RT, Giannelli C, Sestini A. Идентификация и «обратная инженерия кривых Пифагора-годографа. Comput Aided Geom Design, 2015, 34: 21-36 и

% PDF-1.4 % % PDFsharp, версия 1.32.2608.0 (подробный режим) % Дата создания: 21.09.2016 05:33:10 % Время создания: 0,489 секунды % Размер файла: 238363 байта % Страниц: 11 % Объектов: 102 % ————————————————- ————————————————- 1 0 объект% PdfSharp.Pdf.PdfДокументИнформация > эндобдж % ————————————————- ————————————————- 2 0 obj% PdfSharp.Pdf.Advanced.PdfCatalog > эндобдж % ————————————————- ————————————————- 3 0 obj% PdfSharp.Pdf.PdfPages > эндобдж % ————————————————- ————————————————- 4 0 obj% PdfSharp.Pdf.PdfPage > / MediaBox [0 0 595 842] / Родитель 3 0 R /Ресурсы > /Шрифт > / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] / XObject > >> / Тип / Страница >> эндобдж % ————————————————- ————————————————- 5 0 объект% PdfSharp.Pdf.Advanced.PdfContent > транслировать q 1 0 0-1 0842 см -100 Тлз q BT / GS0 гс / F0 -12 Тс 223.7949 26.2559 Td (Геометрия) Tj 56.0156 0 Td (и) Tj 23,3555 0 Td (Вычисления) Tj 61,3652 0 Тд (1) Тдж 0 0 1 рг / F0 -18 Тс -341.6938 38.6279 Td (пифагорейский) Tj 108.0703 0 Td (Годограф) Tj 94.0693 0 Td (Кривые 🙂 Tj 67.0166 0 Td (Алгебра) Tj 67.043 0 Td (и) Tj 35.0332 0 Td (Геометрия) Tj 84.0234 0 Td (Inseparable) Tj ET 1,125 Вт 0 Дж 0 Дж [] 0 дн. 0 0 1 РГ / GS1 GS 22,837 66,143 м 572.163 66.143 л S BT 0 0 0 рг / F0 -10 Тс 219.6753 157.3799 Td (Алгебра) Tj 37,2461 0 Td (и) Tj 19,4629 0 Td (Геометрия) Tj 46.6797 0 Td (Inseparable) Tj -57.8076 71 Td (Bearbeitet) Tj 48. 3643 0 Td (фон) Tj -48.9087 12 Td (Rida) Tj 23,3447 0 Тд (Т) Тдж 8.8867 0 Td (Фаруки) Tj -99,2236 71 Тд (1.) Тдж 11.1182 0 Td (Auflage) Tj 36,6943 0 тд (2007г.) Тдж 27.8027 0 тд (буч.) Тдж 28.3496 0 Td (xvi,) Tj 17.7783 0 Td (728) Tj 19.4629 0 Td (S.) Tj 12,2266 0 Td (Твердый переплет) Tj -108.418 15 Td (ISBN) Tj 26.1182 0 тд (978) тдж 19,4629 0 Тд (3) Тдж 8,3398 0 тд (540) тдж 19.4629 0 тд (73397) тдж 30,5859 0 Тд (3) Тдж -116.7261 14 Td (Формат) Tj 34,4482 0 Td (\ (B) Tj 12,7783 0 Td (x) Tj 7.7783 0 Td (L \) 🙂 Tj 14,4482 0 Тд (15,5) Тдж 22,2412 0 Td (x) Tj 7,7783 0 Тд (23,5) Тдж 22,2412 0 Td (см) Tj -90.3247 14 Td (Gewicht 🙂 Tj 41,6797 0 тд (1268) тдж 25,0244 0 Тд (г) Тдж 0 0 1 рг / F0 -15 Тс -302,5745 222,6899 Td (Weitere) Tj 55.8472 0 Td (Fachgebiete) Tj 86.7261 0 Тд (>) Тдж 12.9272 0 Td (Mathematik) Tj 81,6943 0 Тд (>) Тдж 12.9272 0 Td (Numerik) Tj 60.0073 0 Td (und) Tj 29.1943 0 Td (Wissenschaftliches) Tj 131.7114 0 Td (Rechnen) Tj 64,2114 0 Тд (>) Тдж ET 0,938 Вт 25,497 578,119 м 569,503 578,119 л S BT 155,7507 594,3184 Td (Computeranwendungen) Tj 164.2822 0 Td (дюйм) Tj 15.8423 0 Td (der) Tj 25.8472 0 Td (Mathematik) Tj ET 155,751 595,367 м 439,249 595,367 л S BT 0 0 0 рг 251.2183 621.0698 Td (Zu) Tj 0 0 1 рг 21.6724 0 Td (Leseprobe) Tj ET 272,891 622,119 м 343,782 622,119 л S BT 0 0 0 рг 185.769 656.0698 Td (Schnell) Tj 50.8594 0 Td (und) Tj 29.1943 0 Td (portofrei) Tj 59.1943 0 Td (erhltlich) Tj 64.1968 0 Td (bei) Tj ET q 180,0004 0 0-65,5201 207,4998 732,5201 см / I0 Do Q BT / F1 -10 Тс 52.9907 756.3359 Td (Die) Tj 16.9385 0 Td (Онлайн-) Tj 30,5469 0 Td (Fachbuchhandlung) Tj 78.5938 0 Td (beck-) Tj 22.207 0 Td (shop.de) Tj 33,3301 0 Td (ist) Tj 11.9482 0 Td (spezialisiert) Tj 50.2588 0 Td (auf) Tj 15.2686 0 Td (Fachbcher,) Tj 51.6455 0 Td (insbesondere) Tj 54,707 0 Td (Recht,) Tj 28,3252 0 Td (Steuern) Tj 33.0469 0 Td (und) Tj 17.5 0 Td (Wirtschaft.) Tj -444,458 11.499 тд (Im) тдж 13.6084 0 Td (Sortiment) Tj 41.9434 0 Td (finden) Tj 28.0469 0 Td (Sie) Tj 15. 2783 0 Тд (алл) Чт 16.9336 0 Td (Medien) Tj 33.0469 0 Td (\ (Bcher,) Tj 37.207 0 Td (Zeitschriften,) Tj 56.0889 0 Td (CD,) Tj 22.7832 0 Td (электронные книги,) Tj 35 0 Td (и т. Д. \)) Tj 19.9854 0 Td (аллергия) Tj 20.2637 0 Td (Verlage.) Tj 36.6455 0 Td (Ergnzt) Tj 33.5938 0 Td (wird) Tj 20,8301 0 Тд (дас) Тдж 15.8301 0 Td (Программа) Tj -449,0356 11,499 Td (durch) Tj 25.2686 0 Td (Услуги) Tj 36.377 0 Td (wie) Tj 16.9385 0 Td (Neuerscheinungsdienst) Tj 95.2539 0 Td (или) Tj 20.2686 0 Td (Zusammenstellungen) Tj 88.0371 0 Td (von) Tj 17.5 0 Тд (Бчерн) Чт 36,377 0 Td (zu) Tj 11.9385 0 Td (Sonderpreisen.) Tj 62.207 0 Td (Der) Tj 17.4902 0 Td (Магазин) Tj 23.0615 0 Вт (впр.) Вт 21.9385 0 Тд (мех) Тдж -276,8848 11,499 Td (als) Tj 13.6084 0 Тд (8) Тдж 7.5 0 Td (Millionen) Tj 41.9434 0 Td (Продукты) Tj ET Q Q конечный поток эндобдж % ————————————————- ————————————————- 6 0 obj% PdfSharp.Pdf.Advanced.PdfExtGState > эндобдж % ————————————————- ————————————————- 7 0 obj% PdfSharp.Pdf.Advanced.PdfFontDescriptor > эндобдж % ————————————————- ————————————————- 8 0 obj% PdfSharp.Pdf.Advanced.PdfTrueTypeFont > эндобдж % ————————————————- ————————————————- 9 0 объект% PdfSharp.Pdf.Advanced.PdfExtGState > эндобдж % ————————————————- ————————————————- 10 0 объект% PdfSharp.Pdf.Annotations.PdfLinkAnnotation > / Граница [0 0 0] / BS> / М (Д: 20160921053310 + 02’00 ‘) / NM (951e6aea-460c-4850-b734-6ea326682974) / Rect [22.837 773.302 572.163 794] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ————————————————- ————————————————- 11 0 obj% PdfSharp.Pdf.Annotations.PdfLinkAnnotation > / Граница [0 0 0] / BS> / М (Д: 20160921053310 + 02’00 ‘) / NM (018ed82d-9ac9-4323-b65c-d5c9d950b506) / Rect [25. 497 261,751 569,503 279] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ————————————————- ————————————————- 12 0 obj% PdfSharp.Pdf.Annotations.PdfLinkAnnotation > / Граница [0 0 0] / BS> / М (Д: 20160921053310 + 02’00 ‘) / NM (2531ef6c-8735-4c7b-ae7d-78102818f224) / Rect [155.751 244.503 439.249 261.751] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ————————————————- ————————————————- 13 0 объект% PdfSharp.x] LѮ * `Dz? O0 $ | ܲ = `7; k = (, j_R ݢ J̃Emvc% 4pj%, 5iP`Q3Q1TX ÃvE} n} [Ys4] lg, KY) 6l9 | Tq {Z & O53Ԛu \ #

: fsVRd = Üy * kK + {KZȫFTIJ5ҬC-R | x Բ ord) 0 ޺ vCfCc0SF {.os (iuUv |, 6 $ r — * N> u8 {G כ G1 e2ͽ

Выделение глубоких, энергетически слабых волн в сейсмических записях DSS

Дядюра В.А., Соколовский О.И. (1984). Разделение мешающих регулярных волн. Москва, 68 стр. (по-русски).

Хорн Р. и Джонсон К. (1989). Матричный анализ. М .: Мир, 656 с.(по-русски).

Альберт Д.Г. и Декато С.Н. (2017) Измерения акустического и сейсмического окружающего шума в городской и сельской местности. Прикладная акустика, 119, 135–143. https://doi.org/10.1016/j.apacoust.2016.12.015.

Амундсен Л., Икелле Л. и Мартин Дж. (2000). Множественное затухание и P / S-разделение многокомпонентных данных OBC на неоднородном морском дне. Волновое движение, 32 (1), 67–78. https://doi.org/10.1016/S0165-2125(99)00047-5.

Борман, П., & Виландт, Э. (2013). Сейсмические сигналы и шум. В: П. Борман (ред.), Новое руководство по практике сейсмологической обсерватории 2 (NMSOP2) (стр. 1–62). Потсдам.

Грин, Д.Н., Бастоу, И.Д., Дэшвуд, Б., Ниппресс, С.Э.Дж. (2017). Характеристики широкополосного сейсмического шума в центре Лондона. Письма о сейсмологических исследованиях, 88 (1), 113–124. DOI: 10.1785 / 0220160128.

Харлан, У.С., Клаербут, Дж. Ф., и Рокка, Ф. (1984). Разделение сигнал / шум и оценка скорости. Геофизика, 49 (11), 1869—1880. https://doi.org/10.1190/1.1441600.

Хендрик, Н. (2006). Разделение полей многокомпонентных сейсмических волн с помощью спектральной матричной фильтрации. Расширенные тезисы ASEG, 1, 1–4. DOI: 10.1071 / ASEG2006ab065.

Поппелье, К., и Маллинсон, Д. (2015). Высокочастотный сейсмический шум, создаваемый разбивающимися на мелководье океанскими волнами, и связь с изменяющимся во времени состоянием моря. Письма о геофизических исследованиях, 42 (20), 8563–8569. https: // doi.org / 10.1002 / 2015GL066126.

Шварц, Б. (2019). Введение в сейсмическую дифракцию. Успехи геофизики, 60, 1—64. DOI: 10.1016 / bs.agph.2019.05.001.

Шварц, Б., & Гаевски, Д. (2017). Доступ к дифрагированному волновому полю путем когерентного вычитания. Международный геофизический журнал, 211 (1), 45–49. https://doi.org/10.1093/gji/ggx291.

Sollberger, D., Greenhalgh, S.A., Schmelzbach, C., Van Renterghem, C., Robertsson, J.О.А. (2018). 6-C поляризационный анализ с использованием точечных измерений поступательного и вращательного движения земли: теория и приложения. Международный геофизический журнал, 213 (1), 77–97. https://doi.org/10.1093/gji/ggx542.

Старостенко, В., Яник, Т., Стефенсон, Р., Грин, Д., Русаков, О., Чуба, В., Срода, П., Лисинчук, Д., Град, М., Гутерч, А. , Флух, Э., Тайбо, Х., Артемьева, И., Толкунов, А., Сидоренко, Г., Омельченко, В., Коломиец, К., Легостаева, О., Данновски, А., & Шульгин, А. (2016). Профиль WARR ДОБРЕ-2: земная кора через Крым между Приазовским массивом и северо-восточной частью бассейна Черного моря. В M. Sosson, R.A. Стивенсон и С.А. Адамия (ред.), Тектоническая эволюция восточной части Черного моря и Кавказа (стр. 199–220). Геол. Soc., Лондон, Spec. Опубл., 428. https://doi.org/10.1144/SP428.11.

Van Renterghem, C., Schmelzbach, C., Sollberger, D., & Robertsson, J.O.A. (2018). Разделение сейсмических волновых полей на основе пространственного градиента волнового поля.Международный геофизический журнал, 212 (3), 1588–1599.