Определение числа групп при построении гистограммы
Сегодня, говоря о статистике, я буду обсуждать гистограммы. Вообще говоря, гистограмма является наглядным отображением метода группировки, то есть распределения множества результатов измерений какой-либо величины по группам, в соответствии с существенным для данной группы признаком. Методы группировки широко применяются для обработки первичных данных.
Под первичными данными в статистике мы понимаем статистические ряды, которые называют рядами динамики, если речь идет об изменении явления во времени, либо рядами распределения, если речь идет о составе или структуре исследуемого явления.
Если речь идет о рядах, построенных на основе качественных признаков (например, предприятия по формам собственности), то такие ряды называются атрибутивными, если ряды построены по количественным признакам (например, предприятия по объему товарооборота), то они называются вариационными.
В зависимости от прерывности вариации признака различают дискретные и интервальные вариационные ряды.
Гистограмма представляет собой столбчатый график, построенный по полученным данным, которые разбиваются на несколько групп. Число данных, попавших в каждую группу (частота), выражается высотой столбика, соответствующего данной группе.
Гистограмму можно строить для любых рядов, при этом, если это атрибутивный либо дискретный вариационный ряд (например, число рабочих в каждом тарифном разряде), то число выделяемых групп равно числу вариантов значений признака. В случае же интервального вариационного ряда число групп будет зависеть от величины интервала, используемого для группировки данных.
Интервал — разница между максимальным и минимальным значениями признака в каждой группе. Понятно, что чем больше групп, тем меньше интервал и наоборот. Группы в таком случае иногда называют также классами интервалов.
Например, можно разбить полученные данные о численности рабочих на предприятиях на следующие группы:
до 25 человек,
25–50 человек,
50–100 человек,
свыше 100 человек.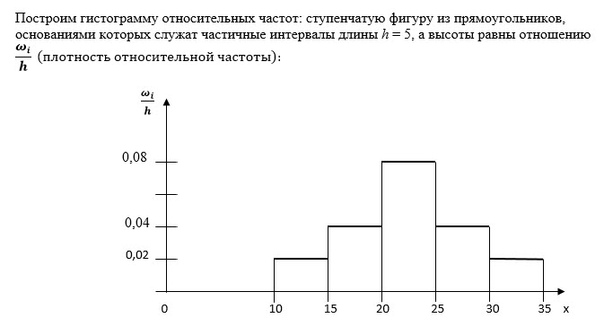
Тогда гистограмма будет содержать 4 столбика, высота которых будет соответствовать числу предприятий попавших в данную группу.
Заметим, кстати, что вышеприведенное распределение является примером использования неравных интервалов, выделенных, что называется, программой исследования, т. е. нами самими.
Вопрос выбора величины интервала (числа групп), используемого для группировки элементов интервального вариационного ряда, далеко не праздный. Помимо того, что гистограмма является отличным средством визуализации данных, она также является ни чем иным, как приближением функции распределения вероятности
Слишком большое число групп может дать слишком «скачущий» график, слишком малое – слишком «сглаженный». В идеале, очевидно, хотелось бы иметь число групп, дающее наименьшее отклонение от функции распределения вероятности, т.
е. позволяющее дать наиболее точную оценку настоящей функции распределения вероятности изучаемого явления.
В общем, математики этим занялись.
Первым, по всей видимости, был Стерджесc (Sturges, 1926). Он рассмотрел идеализированную частотную гистограмму из k классов, где i-ое значение было равно биномиальному коэффициенту . При достаточно больших k форма гистограммы приближалась к форме нормального распределения. Сумма всех значений была равна
.
Таким образом, для n результатов измерений величины, подчиняющейся нормальному распределению, число классов, используемых при построении гистограммы следует брать как и форма полученной гистограммы будет приближаться к форме нормального распределения для достаточно большого k. Это и есть формула Стерджесса. В этом виде она попала практически во все учебники по статистике.
Формула эта в настоящее время подвергается критике как раз за то, что она явным образом использует биномиальное распределение для аппроксимации нормального распределения, что не всегда применимо.
Считается, что эта формула позволяет строить удовлетворительные гистограммы при числе измерений менее 200.
Существует целый ряд альтернативных формул, некоторые из которых вычисляют длину интервала, после чего определяется число требуемых классов (см. здесь).
Рассмотрим пару таких формул:
Формула Скотта (Scott, 1979)
, где h — длина интервала, s — стандартное отклонение значений ряда измерений
Формула Фридмана Диакониса (Freedman and Diaconis, 1981)
, где h — длина интервала, (IQ) — разница между верхним и нижним квартилем.
Эти формулы довольно просты и обоснованы статистической теорией, и считаются предпочтительнее формулы Стерджесса.
Калькулятор ниже использует в качестве результатов измерений результаты генератора случайных чисел, встроенного в Javascript.
Поскольку функция распределения генератора практически постоянная, случайное число, полученное от генератора, можно дополнительно модифицировать, выбрав в поле «Функция .
..» что-нибудь интересное. Собственно, это позволит наблюдать более веселые графики, вместо практически прямой линии.
Помимо построения гистограммы с использованием числа классов, полученных по формуле Стерджесса, строятся гистограммы с числом классов по Скотту и Фридману/Диаконису, а также с числом классов, произвольно заданных пользователем.
Конечно, практического применения в этом калькуляторе никакого, но зато можно посмотреть на разницу в числе классов и внешний вид гистограммы.
Формула Стерджесса и другие способы определения числа групп при построении гистограммы
Число случайно генерируемых результатов наблюдений
Модифицирующая функцияНетЛогарифмКвадратКубКвадратный кореньФункция, модифицирующая результаты генератора случайных чисел
Точность вычисленияЗнаков после запятой: 2
Число классов по Стерджессу
Группировка с использованием формулы Стерджесса
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить close
Стандартное отклонение
Число классов по Скотту
Скотт
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить close
Первая квартиль
Третья квартиль
Число классов по Фридману/Диаконису
Фридман/Диаконис
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить close
Свое число классов
Группировка с использованием своего числа классов
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить close
онлайн гистограмма
Калькулятор строит гистограмму.
Количество групп можно определять по формуле Стерджесса, а можно и задавать вручную.
Работает калькулятор довольно просто — вам нужно ввести входные данные, сейчас перед вами уже есть данные вместе с графиком — это все нужно очистить, так как сделано для иллюстрации работы калькулятора.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.
C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.Считаем онлайн калькулятором число групп при построении гистограммы
Следующий калькулятор считает по формуле Стерджесса, а так же использует и другие способы определения количества групп для построения гистограммы.
И так, коротко о главном.
Гистограмма — это наглядное отображение способа группировки данных, множество результатов измерений той или иной величины распределяются по группам, в каждой группе есть свой критерий отбора в данную группу.
Такие методы группировки часто используют для обработки статистических рядов, то есть первичных данных.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.
C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
гистограмм — понимание свойств гистограмм, что они показывают, а также когда и как их использовать
гистограммы — понимание свойств гистограмм, что они показывают, а также когда и как их использовать | Статистика ЛаэрдЧто такое гистограмма?
Гистограмма — это график, который позволяет обнаружить и показать основное частотное распределение (форму) набора непрерывных данных. Это позволяет проверять данные на предмет их основного распределения (например,g.
, нормальное распределение), выбросы, асимметрия и т. д. Пример гистограммы и необработанных данных, из которых она была построена, показаны ниже:
| 36 | 25 | 38 | 46 | 55 | 68 | 72 | 55 | 36 | 38 |
| 67 | 45 | 22 | 48 | 91 | 46 | 52 | 61 | 58 | 55 |
Как построить гистограмму из непрерывной переменной?
Чтобы построить гистограмму из непрерывной переменной, вам сначала нужно разбить данные на интервалы, называемые интервалами .В приведенном выше примере возраст был разбит на интервалы, причем каждый интервал представляет 10-летний период, начинающийся с 20 лет. Каждая ячейка содержит количество вхождений оценок в наборе данных, содержащихся в этой ячейке. Для указанного выше набора данных частоты в каждом интервале сведены в таблицу вместе с оценками, которые способствовали увеличению частоты в каждом интервале (см.
Ниже):
| Бункер | Частота | Баллы, включенные в корзину |
| 20-30 | 2 | 25,22 |
| 30-40 | 4 | 36,38,36,38 |
| 40-50 | 4 | 46,45,48,46 |
| 50-60 | 5 | 55,55,52,58,55 |
| 60-70 | 3 | 68,67,61 |
| 70-80 | 1 | 72 |
| 80-90 | 0 | — |
| 90-100 | 1 | 91 |
Обратите внимание, что, в отличие от гистограммы, между столбцами нет «промежутков» (хотя некоторые столбцы могут «отсутствовать», не отражая частот).Это связано с тем, что гистограмма представляет собой непрерывный набор данных, и поэтому в данных нет пробелов (хотя вам придется решить, округлять ли вы оценки в большую или меньшую сторону на границах интервалов).
Выбор правильной ширины бункера
Нет правильного или неправильного ответа на вопрос, какой ширины должна быть корзина, но есть практические правила. Вы должны убедиться, что мусорные ведра не слишком маленькие или не слишком большие. Рассмотрим гистограмму, которую мы создали ранее (см. Выше): следующие гистограммы используют те же данные, но имеют либо гораздо меньшие, либо большие интервалы, как показано ниже:
Из гистограммы слева видно, что ширина бина слишком мала, потому что она показывает слишком много отдельных данных и не позволяет легко увидеть базовый шаблон (частотное распределение) данных.На другом конце шкалы находится диаграмма справа, где интервалы слишком велики, и мы снова не можем найти основную тенденцию в данных.
Гистограммы основаны на площади, а не высоте столбцов
На гистограмме это область полосы, которая указывает частоту появления для каждого интервала. Это означает, что высота полосы не обязательно указывает, сколько вхождений оценок было в каждой отдельной ячейке.
Это произведение высоты, умноженное на ширину бункера, указывает на частоту появления в этом бине.Одна из причин того, что высота полосок часто неправильно оценивается как показывающая частоту, а не площадь полосы, связана с тем, что многие гистограммы часто имеют равные интервалы (интервалы), и в этих обстоятельствах высота бина отражает частоту.
В чем разница между столбчатой диаграммой и гистограммой?
Основное отличие состоит в том, что гистограмма используется только для отображения частоты появления оценок в непрерывном наборе данных, который был разделен на классы, называемые ячейками.С другой стороны, гистограммы могут использоваться для множества других типов переменных, включая порядковые и номинальные наборы данных.
Главная О нас Связаться с нами Положения и условия Конфиденциальность и файлы cookie © Lund Research Ltd, 2018R hist () для создания гистограмм (с многочисленными примерами)
В этой статье вы научитесь использовать функцию hist () для создания гистограмм в программировании на языке R с помощью многочисленных примеров.
Гистограмма может быть создана с помощью функции hist () на языке программирования R.Эта функция принимает вектор значений, для которых строится гистограмма.
Давайте воспользуемся встроенным набором данных airquality , который содержит ежедневных измерений качества воздуха в Нью-Йорке с мая по сентябрь 1973 г. Документация
-R.
> ул (качество воздуха)
'data.frame': 153 набл. из 6 переменных:
$ Озон: внутренний 41 36 12 18 - нет данных 28 23 19 8 - нет ...
$ Solar.R: int 1 149 313 NA NA 299 99 19 194 ...
$ Wind: число 7,4 8 12,6 11,5 14,3 14,9 8,6 13,8 20,1 8.6 ...
$ Temp: внутр 67 72 74 62 56 66 65 59 61 69 ...
$ Месяц: int 5 5 5 5 5 5 5 5 5 5 ...
$ День: int 1 2 3 4 5 6 7 8 9 10 ... Мы будем использовать параметр температуры, который имеет 154 измерения в градусах Фаренгейта.
Пример 1: Простая гистограмма
Температура <- качество воздуха $ Temp
hist (Температура)
Мы видим выше, что есть 9 ячеек с одинаковыми разрывами.
В этом случае высота ячейки равна количеству наблюдений, попадающих в эту ячейку.
Мы можем передать дополнительные параметры, чтобы контролировать внешний вид нашего графика. Вы можете прочитать о них в разделе справки - hist .
Некоторые из наиболее часто используемых: main для обозначения заголовка, xlab и ylab для обозначения осей, xlim и ylim для определения диапазона осей, col для определения цвет и т. д.
Кроме того, с аргументом freq = FALSE мы можем получить распределение вероятностей вместо частоты.
Пример 2: Гистограмма с добавленными параметрами
# гистограмма с добавленными параметрами
hist (Температура,
main = "Максимальная дневная температура в аэропорту Ла-Гуардия",
xlab = "Температура в градусах Фаренгейта",
xlim = c (50,100),
col = "darkmagenta",
freq = FALSE
)
Обратите внимание, что по оси Y отложена плотность, а не частота. В этом случае общая площадь гистограммы равна 1.
Возвращаемое значение hist ()
Функция hist () возвращает список из 6 компонентов.
> h <- hist (Температура)
> ч
$ перерывы
[1] 55 60 65 70 75 80 85 90 95 100
$ counts
[1] 8 10 15 19 33 34 20 12 2
$ плотность
[1] 0,010457516 0,013071895 0,019607843 0,024836601 0,043137255
[6] 0,044444444 0,026143791 0,015686275 0,002614379
$ средние
[1] 57,5 62,5 67,5 72,5 77,5 82,5 87,5 92,5 97,5
$ xname
[1] «Температура»
$ эквидист
[1] ИСТИНА
attr (, "класс")
[1] "гистограмма"
Мы видим, что возвращается объект класса гистограмма , который имеет:
-
разрывы - места разрыва, -
отсчетов - количество наблюдений, попадающих в эту ячейку, -
density - плотность клеток, середины - середины ячеек, -
xname - имя аргумента x и -
equidist - логическое значение, указывающее, равномерно ли расположены разрывы или нет.
Мы можем использовать эти значения для дальнейшей обработки.
Например, в следующем примере мы используем возвращаемые значения для размещения счетчиков в верхней части каждой ячейки с помощью функции text () .
Пример 3. Использование возвращаемых значений гистограммы для меток с помощью text ()
h <- hist (Температура, ylim = c (0,40))
текст (h $ mids, h $ counts, labels = h $ counts, adj = c (0.5, -0.5))
Определение количества перерывов
С помощью аргумента breaks мы можем указать количество ячеек, которое мы хотим в гистограмме.Однако это число - всего лишь предположение.
R вычисляет наилучшее количество ячеек, учитывая это предложение. Ниже приведены две гистограммы для одних и тех же данных с разным количеством ячеек.
Пример 4: Гистограмма с разными изломами
hist (Температура, перерывы = 4, основная = «С перерывами = 4»)
hist (Температура, перерывы = 20, main = "С перерывами = 20")
На приведенном выше рисунке мы видим, что фактическое количество нанесенных ячеек больше, чем мы указали.
Мы также можем определить точки останова между ячейками как вектор. Это дает возможность строить гистограмму с неравными интервалами. В таком случае площадь ячейки пропорциональна количеству наблюдений, попадающих в эту ячейку.
Пример 5: Гистограмма с неравномерной шириной
hist (Температура,
main = "Максимальная дневная температура в аэропорту Ла-Гуардия",
xlab = "Температура в градусах Фаренгейта",
xlim = c (50,100),
col = "шоколад",
border = "коричневый",
разрывы = c (55,60,70,75,80,100)
)
NumPy, Matplotlib, Pandas и Seaborn - Настоящий Python
В этом руководстве вы будете оснащены для создания готовых к презентации графиков гистограмм Python с целым рядом вариантов и функций.
Если у вас есть вводные знания в Python и статистике, вы можете использовать эту статью в качестве универсального инструмента для построения и построения гистограмм в Python с использованием библиотек из его научного стека, включая NumPy, Matplotlib, Pandas и Seaborn.
Гистограмма - отличный инструмент для быстрой оценки вероятностного распределения, интуитивно понятного практически любой аудитории. Python предлагает несколько различных вариантов построения и построения гистограмм.Большинство людей знают гистограмму по ее графическому представлению, которое похоже на гистограмму:
Эта статья проведет вас через создание графиков, подобных приведенному выше, а также более сложных. Вот что вы расскажете:
- Построение гистограмм на чистом Python без использования сторонних библиотек
- Построение гистограмм с помощью NumPy для обобщения базовых данных
- Построение результирующей гистограммы с помощью Matplotlib, Pandas и Seaborn
Гистограммы в чистом Python
Когда вы готовитесь к построению гистограммы, проще всего думать не в терминах интервалов, а скорее сообщить, сколько раз появляется каждое значение (таблица частот).Словарь Python хорошо подходит для этой задачи:
>>> >>> # Сортировать не нужно, обязательно
>>> а = (0, 1, 1, 1, 2, 3, 7, 7, 23)
>>> def count_elements (seq) -> dict:
. .. "" "Подсчитать элементы из` seq`. "" "
... hist = {}
... для i в seq:
... hist [i] = hist.get (i, 0) + 1
... вернуть историю
>>> countted = count_elements (а)
>>> подсчитано
{0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1}
count_elements () возвращает словарь с уникальными элементами из последовательности в качестве ключей и их частотами (счетчиками) в качестве значений.Внутри цикла по seq , hist [i] = hist.get (i, 0) + 1 говорит: «для каждого элемента последовательности увеличьте его соответствующее значение в hist на 1.»
Фактически это именно то, что делает класс collections.Counter из стандартной библиотеки Python, который создает подклассы словаря Python и переопределяет его метод .update () :
Гистограмма в Excel - Easy Excel Tutorial
В этом примере показано, как создать гистограмму в Excel .
1. Сначала введите номера ячеек (верхние уровни) в диапазоне C4: C8.
2. На вкладке «Данные» в группе «Анализ» щелкните «Анализ данных».
Примечание: не можете найти кнопку анализа данных? Щелкните здесь, чтобы загрузить надстройку Analysis ToolPak.
3. Выберите «Гистограмма» и нажмите «ОК».
4. Выберите диапазон A2: A19.
5. Щелкните поле «Диапазон ячеек» и выберите диапазон C4: C8.
6. Щелкните кнопку параметра Диапазон вывода, щелкните поле Диапазон вывода и выберите ячейку F3.
7. Проверьте вывод диаграммы.
8. Щелкните OK.
9. Щелкните легенду справа и нажмите Удалить.
10. Надлежащим образом маркируйте мусорные ведра.
11. Чтобы удалить промежуток между полосами, щелкните полосу правой кнопкой мыши, выберите «Форматировать ряд данных» и измените ширину зазора на 0%.
12. Чтобы добавить границы, щелкните полосу правой кнопкой мыши, выберите «Форматировать ряд данных», щелкните значок «Заливка и линия», щелкните «Граница» и выберите цвет.
Результат:
Если у вас Excel 2016 или новее, просто используйте тип диаграммы «Гистограмма».
13. Выберите диапазон A1: A19.
14. На вкладке «Вставка» в группе «Диаграммы» щелкните символ гистограммы.
15. Щелкните Гистограмма.
Результат. Гистограмма с 3 ячейками.
Примечание. Excel использует обычное справочное правило Скотта для расчета количества ячеек и ширины ячеек.
16. Щелкните правой кнопкой мыши горизонтальную ось и выберите «Ось формата».
Появится панель «Ось формата».
17. Определите интервалы гистограммы. Мы будем использовать те же номера ящиков, что и раньше (см. Первое изображение на этой странице). Ширина бункера: 5. Количество ячеек: 6. Бункер перелива: 40. Бункер нижнего белья: 20.
Результат:
Напомним, мы создали следующую гистограмму с помощью Analysis ToolPak (шаги 1–12).
Вывод: метки ящиков выглядят по-разному, но гистограммы такие же.
В этом случае высота ячейки равна количеству наблюдений, попадающих в эту ячейку.
В этом случае общая площадь гистограммы равна 1.
.. "" "Подсчитать элементы из` seq`. "" "
... hist = {}
... для i в seq:
... hist [i] = hist.get (i, 0) + 1
... вернуть историю
>>> countted = count_elements (а)
>>> подсчитано
{0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1}
Ваш комментарий будет первым