Открытая Математика. Функции и Графики. Алгебраические операции над функциями
Построение графика суммы (произведения) двух функций производится сложением (умножением) ординат точек графиков с одинаковыми абсциссами. Приведем для примера графики функций y = x + sin x и y = x sin x, являющихся соответственно суммой и произведением графиков y = x и y = sin x.
Правило построения графика функции 1f(x), если график функции f(x) уже построен.
Если x = a – вертикальная асимптота графика функции f(x), то есть limx→a+0f(x)=∞ или limx→a-0f(x)=∞, то limx→a+01f(x)=0 или соответственно limx→a-01f(x)=0.
Таким образорм, в случае, когда x = a – двусторонняя вертикальная асимптота графика функции f(x), x = a будет нулем функции 1f(x).Если у графика функции f(x) есть горизонтальная асимптота y = 0 при x→∞, то limx→∞1f(x)=∞.

Если у графика функции f(x) есть горизонтальная асимптота y = b при x→∞, то график функции 1f(x) будет иметь горизонтальную асимптоту y=1b.
Если график функции f(x) пересекает ось абсцисс в точке (x0; 0), то есть x0 – нуль функции f(x): f(x0)=0, то x=x0 – вертикальная асимптота графика функции y=1f(x).
Если точка (x0; y0) – точка максимума (минимума) функции f(x) и y0≠0, то (x0; 1y0) – точка минимума (максимума) функции 1f(x).
Промежуткам возрастания (убывания) графика функции f(x) соответствуют промежутки убывания (возрастания) графика функции 1f(x).
Пусть известен график y = f (x) и нужно построить график функции y = |f (x)|. По определению,
|fx|={fxпри fx≥0,-fxпри fx<0.
Значит, часть графика, лежащую в верхней координатной полуплоскости, изменять не надо, а часть графика, лежащую в нижней координатной полуплоскости, нужно отобразить симметрично оси OX.
По определению,
|fx|={fxпри fx≥0,-fxпри fx<0.
Значит, часть графика, лежащую в верхней координатной полуплоскости, изменять не надо, а часть графика, лежащую в нижней координатной полуплоскости, нужно отобразить симметрично оси OX.
Пусть известен график y = f (x) и нужно построить график функции y = f (|x|). Заметим, что при x ≥ 0 f (|x|) = f (x), а функция y = f (|x|) четная. Поэтому, чтобы построить график функции y = f (|x|), нужно часть графика функции y = f (x), лежащую в левой координатной полуплоскости, отбросить, а часть графика, лежащую в правой координатной полуплоскости, отобразить симметрично относительно оси
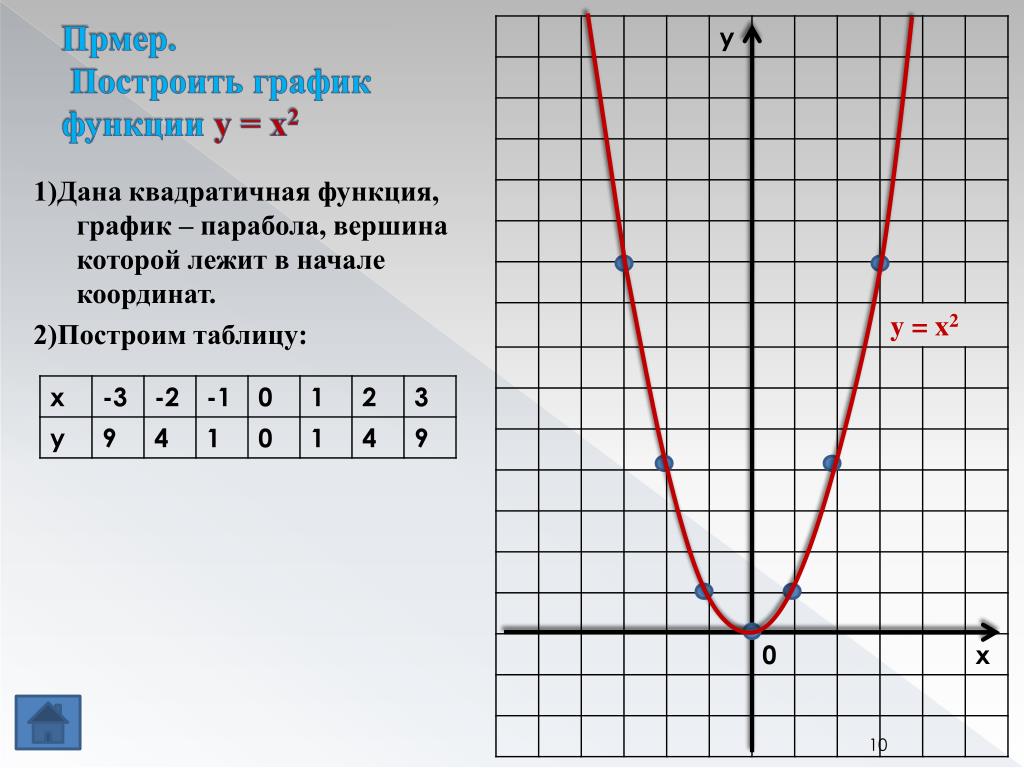 Множество точек, задаваемое уравнением |y| = f (x), рисуется следующим образом: строится график функции f (x), отбрасывается его часть, находящаяся ниже оси абсцисс, оставшаяся часть дополняется своим симметричным отражением относительно оси абсцисс.
Множество точек, задаваемое уравнением |y| = f (x), рисуется следующим образом: строится график функции f (x), отбрасывается его часть, находящаяся ниже оси абсцисс, оставшаяся часть дополняется своим симметричным отражением относительно оси абсцисс.Как строить функцию в Excel — Построение в Excel графиков математических и тригонометрических функций
Графика функций. Построение графиков функций в среде МS Excel
- Войнова Татьяна Олеговна, учитель математики
- Гусев Александр Николаевич, учитель информатики и ИКТ
Разделы: Математика
В настоящее время компьютеры используются во всех сферах деятельности человека. Внедрение информационных технологий в учебный процесс сегодня актуально. С целью повышения эффективности обучения учитель-предметник должен уметь использовать компьютерные технологии на своих уроках. Одним из популярных программных средств, используемых на уроках математики, является MS Excel.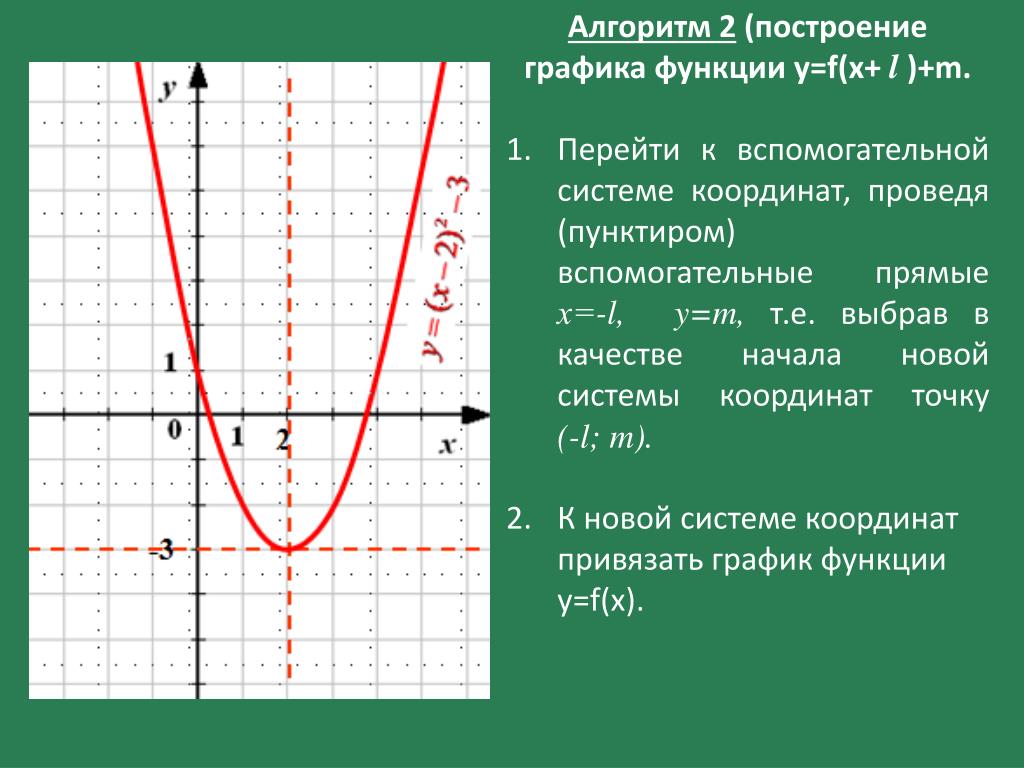
Известно, что одним из способов задания функции является графический. Графиком функции y=f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания обладает очень важным преимуществом: он самый наглядный из всех. Графики часто используются в физике и технике, так как иногда они являются единственно возможными.
Учащимся 8-го класса известны следующие виды функций:
-
- y=;
- y=|x|;
- y=kx2 (y=ax2+bx+c);
- y= ,
а также способы построения графиков функций y=f(x+l), y=f(x)+m, если известен график функции y=f(x) и элементарные методы исследования.
По каждому из указанных видов функций учащимся в качестве домашнего задания было предложено построить несколько графиков в одной и той системе координат для каждой группы, чтобы наглядно продемонстрировать их отличия. На уроке графики тех же функций дети построили в среде MS Excel и провели их исследование. В качестве групп функций были предложены следующие:
1-я группа- y=3x+5;
- y=x+5;
- y=3x+5;
- y=3x-1;
- y=-3x+5;
- y=-x+5;
2-я группа
3-я группа
- y=x2;
- y=x2-1;
- y=(x-1)2;
- y=x2-5x+4;
- y=-x2-1;
- y=-(x-1)2;
4-я группа
5-я группа
Работу учащихся опишем на примере построения графика функции y=:
- Определим промежуток построения графика функции.
 Пусть х1=-2, х2=2.
Пусть х1=-2, х2=2. - В ячейке А3 электронной таблицы введем начальное значение промежутка (-2).
- Разобьем промежуток на равные отрезки с учетом желаемой точности. Допустим, шаг разбиения равен 0,1. Для этого в ячейке А4 введем формулу =A3+0,1 и скопируем эту формулу в ячейки с А5 по А43.
Рис. 1. В ячейке А4 вводим формулу =A3+0,1
- Вычислим значение функции в начальной точке отрезка (в точке −2). Для этого в ячейку В3 введем формулу: =(A3+1)/(F3-1) (1).
Рис. 2. Вычислим значение функции в начальной точке отрезка
- Вычислим значения функции в каждой точке промежутка разбиения. Для этого скопируем формулу (1)в ячейки В4 — В43.
- Построим график функции. Для этого выделим числовой блок
Рис. 3. Построим график функции
ячейки А3 — В43, откроем вкладку «Вставка», выберем тип графика «Точечная» и вид «С гладкими кривыми». График функции y=построен.
Вывод:
Надеюсь, из кода всё понятно, но немного поясню.
Поскольку |y| может быть только больше нуля, нам нужно выделить значения функции, которые >= 0 и нарисовать в основной части графика только их. Для этого мы делаем булевую маску для всех значений f(x) (в моём коде это значение обозначено как y, но мой y это не y из вашей формулы).
ind = y >= 0
Более понятно можно записать так:
ind = (y >= 0)
В ind у нас теперь булева маска, содержащая True на тех позициях, где y >= 0 и False, где y < 0
Далее, мы отбираем по этой маске значения из наших массивов x и y:
x1 = x[ind]
y1 = y[ind]
А также мы отбираем остальные значения x и y, для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот:
x2 = x[~ind]
y2 = y[~ind]
После этого мы рисуем основной график, причём два раза — один раз используя f(x), а другой раз -f(x) (по формуле |y| = f(x) получается, что у нас есть два графика: y = f(x) и y = -f(x)).
И затем рисуем псевдо-график там, где функция f(x) могла бы продолжаться, но из-за условия равенства модулю |y| она в этом месте прерывается.
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
| ||||
Графики,содержащие знак модуля.Построение графиков,содержащих знак модуля. | Учебно-методический материал по алгебре (10 класс) по теме:
Исследовательская работа
«Построение графиков
функций, аналитическое выражение которых содержит знак абсолютной величины»
2008
Оглавление.
I. Введение——————————————————————————1
II. Основная часть.——————————————————————-1-13
Основная часть.——————————————————————-1-13
1. Историческая справка——————————————————- -3-4
2. Геометрическая интерпретация понятия |а|—————————- -4-5
3. График функции у=f |(х)|——————————————————5-8
4. График функции у = | f (х)| —————————————————8-10
5. График функции у=|f |(х)| | — —- ——————————————10-13
III. Заключение.————————————————————————-13
IV. Список литературы —————————————————————14
I. Введение.
Построение графиков функций одна их интереснейших тем в школьной математике. Один из крупнейших математиков нашего времени Израиль Моисеевич Гельфанд писал: «Процесс построения графиков является способом превращения формул и описаний в геометрические образы. Это – построение графиков – является средством увидеть формулы и функции и проследить, каким образом эти функции меняются. Например, если написано , то вы сразу видите параболу; если , вы видите параболу, опущенную на четыре единицы; если же , то вы видите предыдущую параболу, перевернутую вниз. Такое умение видеть сразу формулу, и ее геометрическую интерпретацию – является важным не только для изучения математики, но и для других предметов. Это умение, которое остается с вами на всю жизнь, подобно умению ездить на велосипеде, печатать на машинке или водить машину».
Это – построение графиков – является средством увидеть формулы и функции и проследить, каким образом эти функции меняются. Например, если написано , то вы сразу видите параболу; если , вы видите параболу, опущенную на четыре единицы; если же , то вы видите предыдущую параболу, перевернутую вниз. Такое умение видеть сразу формулу, и ее геометрическую интерпретацию – является важным не только для изучения математики, но и для других предметов. Это умение, которое остается с вами на всю жизнь, подобно умению ездить на велосипеде, печатать на машинке или водить машину».
Хотя уравнения с модулями мы начали изучать уже с 6-го – 7-го класса, где мы проходили самые азы уравнений с модулями, я выбрала именно эту тему, потому что считаю, что она требует более глубокого и досконального исследования. Я хочу получить более широкие знания о модуле числа, различных способах построения графиков, содержащих знак абсолютной величины.
Цель работы: изучить соответствующие теоретические материалы, выявить алгоритм построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины.
Объект исследования: линейные функции, аналитическое выражение которых содержит знак абсолютной величины.
Методы исследования: построение графиков функций.
II. Основная часть.
1. Историческая справка.
В первой половине ХVII века начинает складываться представление о функции как о зависимости одной переменной величины от другой. Так, французские математики Пьер Ферма (1601-1665) и Рене Декарт (1596-1650) представляли себе функцию как зависимость ординаты тоски кривой от ее абсциссы. А английский ученый Исаак Ньютон (1643-1727) понимал функцию как изменяющуюся в зависимости от времени координату движущейся точки.
Термин «функция» (от латинского function – исполнение , совершение) впервые ввел немецкий математик Готфрид Лейбниц(1646-1716). У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем швейцарский математик Иоганн Бернулли(1667-1748) и член Петербургской Академии наук знаменитый математик XVIII века Леонард Эйлер(1707-1783) рассматривали функцию как аналитическое выражение. У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.
У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово (омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п.
Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению.
Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна -a, если a меньше нуля:
Из определения следует, что для любого действительного числа a,
2. Геометрическая интерпретация понятия модуля |а|
Геометрическая интерпретация понятия модуля |а|
Каждому действительному числу можно поставить в соответствие точку числовой прямой, это точка будет геометрическим изображением данного действительного числа. Каждой точке числовой прямой соответствует её расстояние от начало отсчета, или длина отрезка, начало которого в точке начала отсчета, а конец – в данной точке. Длина отрезка всегда рассматривается как величина неотрицательная. Геометрической интерпретацией действительного числа служит вектор, выходящий из начала отсчета и имеющий конец в точке, изображающей данное число. Длина этого вектора будет геометрической интерпретацией модуля данного действительного числа.
-а 0 а
3. График функции у=f |(х)|
у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |
График этой функции симметричен относительно оси координат.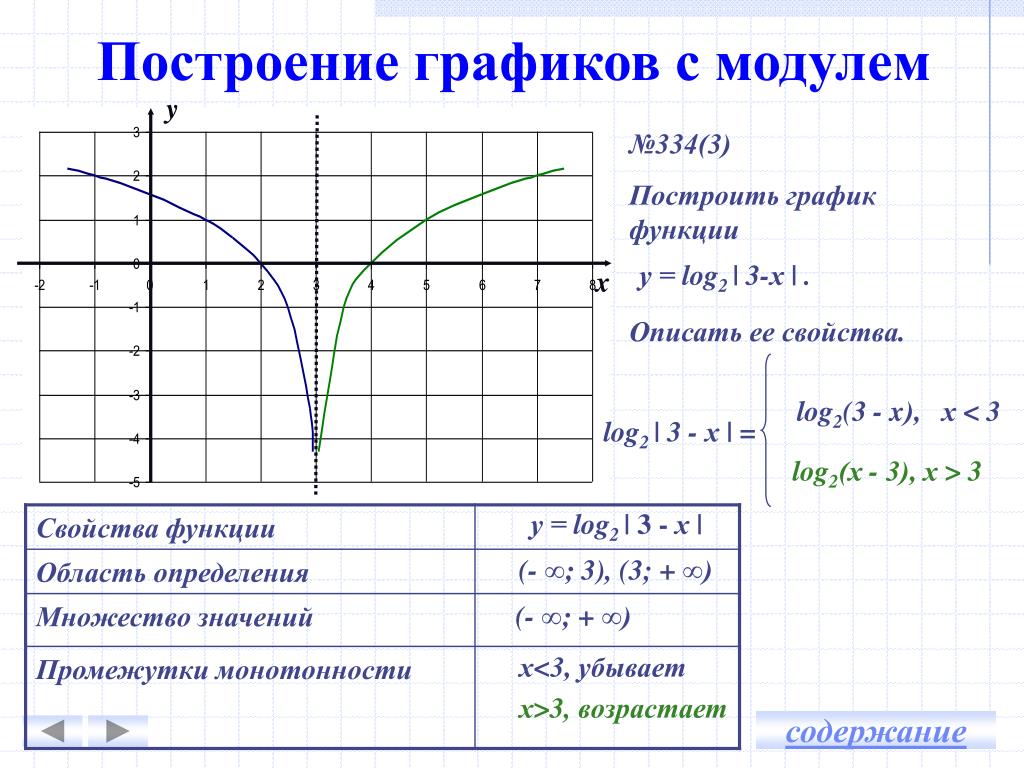
Следовательно, достаточно построить график функции у=f(х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.
Например, пусть графиком функции у=f(х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.
Рис.1
Рис.2.
1. Построить график функции у= |х|
- Если х≥0, то |х| =х и наша функция у=х, т.е. искомый график совпадает с биссектрисой первого координатного угла.
- Если х
Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)
Из сопоставления двух графиков: у=х и у= |х|, я сделала вывод, что второй получается из первого зеркальным отображением относительно ОХ той части первого графика, которая лежит под осью абсцисс. Это положение вытекает из определения абсолютной величины.
Это положение вытекает из определения абсолютной величины.
Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину? Для этого я рассмотрела несколько функций, и сделала для себя вывод.
2. Например: у=х2 — |х| -3
а) Строю у=х2 -х -3 для х>0.
Квадратичная функция, графиком является парабола, ветви которой направлены вверх, т.к. а = , а > 0
- х0 = —
у0 =-4
(2; -4) – координаты вершины параболы.
- х=0, у= -3
(0; — 3) координаты точки пересечения графика функции с осью ОУ.
- у =0, х2 -х -3 = 0
х2 -4х -12 = 0 Имеем, х1= — 2; х2 = 6.
(-2; 0) и (6; 0) – координаты точки пересечения графика функции с осью ОХ.
Если х
Значит, часть требуемого графика, соответствующая значениям х0.
б) Поэтому достраиваю для х
Вывод: Для построения графика функции у=f |(х)|
- Достаточно построить график функции у=f(х) для х>0;
- Строить для х
4. График функции у = | f (х)|
График функции у = | f (х)|
По определению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:
у=f(х), если f(х) ≥0; у = — f(х), если f(х)
Для любой функции у = f(х), если f(х) >0, то | f (х)| = f(х), значит в этой части график функции у = | f (х)| совпадает с графиком самой функции у=f(х). Если же f(х) f (х)| = — f(х),т.е. точка (х; | f (х)| ) симметрична точке (х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ «отрицательную» часть графика.
1. Построить график функции у= | х2 – х – 6 |.
а) Построить график функции у= х2 – х – 6 . Квадратичная функция, графиком является парабола, ветви направлены вверх, т.к. а = 1, а >1.
х0 = —
у0 = — (1/2; — 6,25) координаты вершины
х=0; у = -6 (0; -6) координаты точки пересечения с осью ОУ.
у= 0, х2 – х – 6=0
х1 = -2; х2 = 3. (-2;0) и (3;0) –координаты точек пересечения с осью ОХ
б) Часть графика, расположенного в нижней полуплоскости, отобразить симметрично оси ОХ. (Рис.5)
(Рис.5)
Вывод: Для построения графика функции у=|f(х) |
1.Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
(Рис.6, 7.)
5. График функции у=|f |(х)| |
Применяя, определение абсолютной величины и исследуя, графиков функции
у = | 2 · |х | — 3|
у = | х2 – 5 · |х| |
у = | |х3 | — 2 |, я нашла алгоритм построения графиков.
Для того чтобы построить график функции у=|f |(х)| | надо:
1. Построить график функции у=f(х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
1. у = | 2 · |х | — 3|
1) Строю у = 2х-3, для х>0. (1; -1) (; 0)
2) Строю прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ.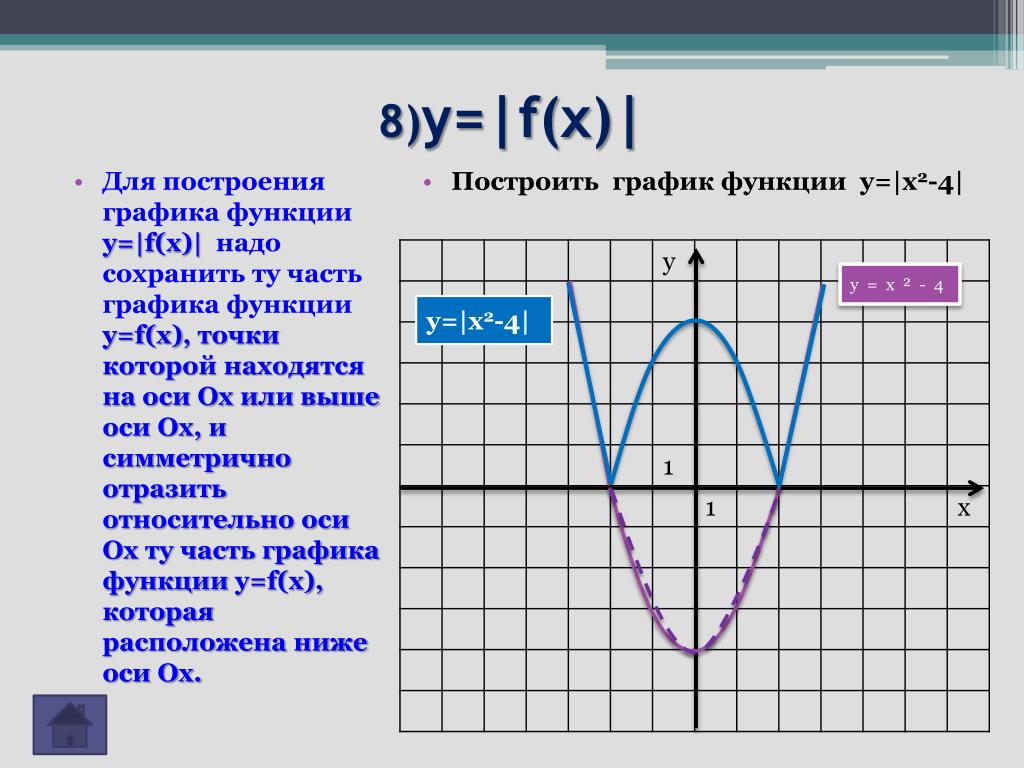 Рис.8
Рис.8
2. у = | х2 – 5 · |х| |
а) Строю график функции у = х2 – 5 х для х>0.
Квадратичная функция, графиком является парабола, ветви направлены, т.к. а=1, а>0
х0 = -;
у0 = 6,25 -12,5 = -6,25 (2,5; -6,25) – координаты вершины
х=0; у=0; (0; 0) – координаты точки пересечения с осью ОУ
у=0; х2 – 5 х =0 (0; 0) и ( 5; 0) – координаты точек пересечения с осью ОХ.
х1 =0; х2=5
(Рис.9)
б) Строю часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ.
3. у =| |х|3 | — 2 |
а) Строю у=х3 -2 для х > 0.
х1= 0; у1= -2
у2 = 0; х3 -2 =0
х2 =
б) Строю часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней полуплоскости, преобразовываю на верхнюю полуплоскость симметрично оси ОХ. (Рис.10)
(Рис.10)
III. Заключение.
При выполнении исследовательской работы я делала такие выводы:
— сформировала алгоритмы построения графиков функций, аналитическое выражение которых содержит знак абсолютной величины.
Алгоритм построения графика функции у=f |(х)|
1.Построить график функции у=f(х) для х>0;
2.Построить для х
Алгоритм построения графика функции у=|f(х) |
1.Построить график функции у=f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
Алгоритм построения графика функции у=|f |(х)| |
1. Построить график функции у=f(х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
— приобрела опыт построения графиков таких функций, как:
у=f |(х)|; у = | f (х)|; у=|f |(х)| |;
— научилась работать с дополнительной литературой и материалами, производить отбор
научных сведений;
— приобрела опыт выполнения графических работ на компьютере.
Список литературы:
- И. М.Гельфанд, Е.Г. Глаголева. Функции и графики. Издательство «Наука»
- Р.А. Калнин. Алгебра и элементарные функции. Издательство «Наука»
- М.К. Потапов, С.Н. Олехник. Конкурсные задачи по математики, Москва. «Наука»
- Ю. Н.Макарычев, Н.Г. Миндюк. Дополнительные главы к школьному учебнику.
Москва, «Просвещение».
у
0
х
0
у
х
х
у
х
у
Рис 3.
0
6
-6
-3
х
у
Рис.4
0
6
-6
-2
3
х
у
Рис.5
у
х
Рис.6
у
х
Рис.7
0
у
х
-3/2
3/2
-3
3
Рис.8
1
-1
-6
-6
0
5
5
Рис.9
-2
0
1
2
2
-2
у
х
Рис.10
Построение графиков/диаграмм — Задача
Построение графиков/диаграмм
Содержание
Мастер диаграмм
Настройка графиков/диаграмм
Построение графиков функций
Графическое решение системы уравнений
Операционно-стоимостной анализ процесса
Мастер диаграмм
На основе данных из ячеек Excel можно строить графики и диаграммы. Любое изменение данных приводит к изменению графика, диаграммы.
Любое изменение данных приводит к изменению графика, диаграммы.
Создание графиков и диаграмм в Excel максимально упрощено: вы выделяете диапазон ячеек с данными и нажимаете кнопку Мастер диаграмм на Панели инструментов либо пункт меню ВставкаДиаграмма – будет запущен мастер диаграмм. Мастер диаграмм последовательно проведет вас через весь процесс — выведет несколько диалоговых окон, в которых запросит у вас уточняющие данные, а затем автоматически построит график, диаграмму на текущем или новом листе.
Задача: Построить график функции Y=X2 для X=(1,2, … 20).
Выполните следующую последовательность действий:
Заполните диапазон ячеек A1:A20 значениями X=(1,2, … 20). Используйте заполнение по образцу.
Заполните диапазон ячеек В1:В20 формулами Y=X2 (=А1*А1 и т.
 д.). Используйте копирование и перетаскивание формул.
д.). Используйте копирование и перетаскивание формул.Выделите диапазон данных А1:В20 и нажмите кнопку Мастер диаграмм на Панели инструментов. Это приведет к запуску мастера – шаг 1 (рис. 1.13):
На шаге 1 мастера выберите тип графика и его вид, как на рис. 1.13. Здесь следует особо обратить внимание на текст подсказки, который показывает назначение графика выбранного вида. Нажмите кнопку Далее>.
На шаге 2 отображается диапазон ячеек (его можно изменить) и порядок применения данных – выберите «в столбцах» и нажмите Далее>.
На шаге 3 можно ввести название диаграммы, осей координат, настроить другие параметры. Нажмите Далее>.
На шаге 4 запрашивается место размещения диаграммы. Нажмите Готово>. Будет построен график Y=X2 и выведена Панель инструментов Диаграммы, с помощью которой можно манипулировать построенным графиком (рис.
 1.14).
1.14).
Рис. 1.13
Важным является правильный подбор типа диаграммы для отображаемых данных (шаг 1 мастера). Подумайте — что и как вы хотите отображать — изменение данных во времени, соотношение между наборами данных, соотношения или пропорции частей целого и пр. Если не удается подобрать с первого раза, попробуйте другие типы диаграмм на тех же данных, используя кнопку Тип диаграммы Панели инструментов Диаграммы (рис. 1.14).
Рис. 1.14
Поэксперементируйте с построенным графиком. В частности, запишите значения Х в ячейки А1:А20 в обратном порядке — 20, 19, …1. График будет изменен. Попробуйте также изменить тип диаграммы, например, на Круговая и осмыслить его.
Все элементы диаграммы можно выделять, удалять, перемещать, изменять; все элементы имеют всплывающие подсказки. Попробуйте выделить и растянуть диаграмму.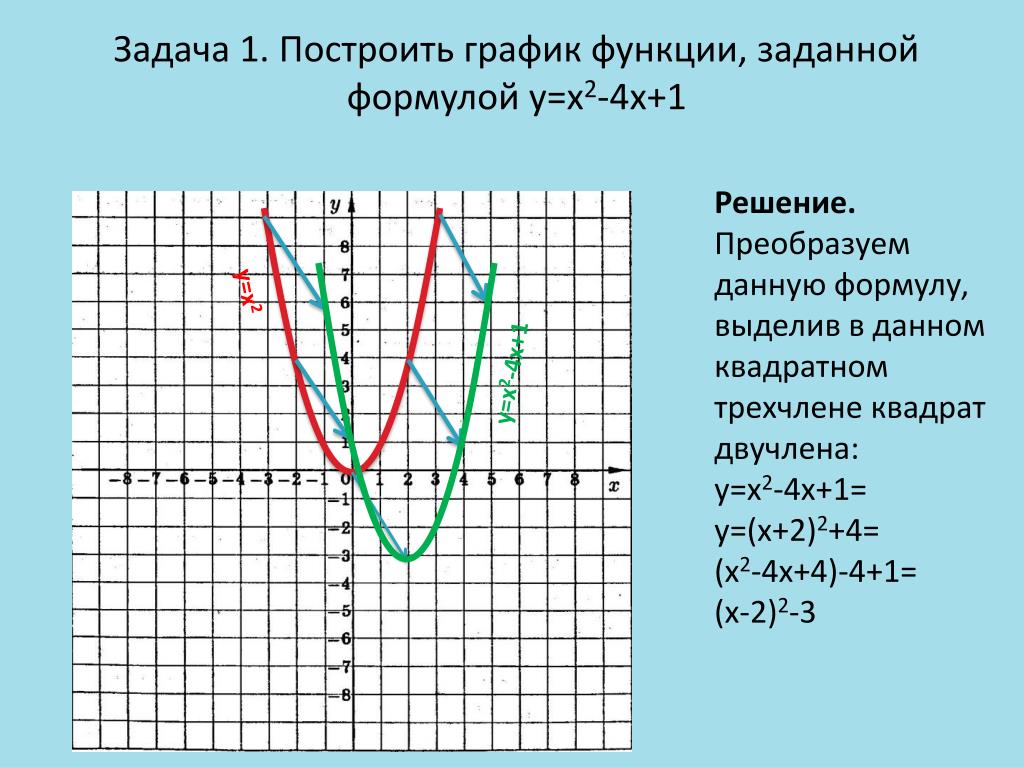 Подробнее в главе 2.
Подробнее в главе 2.
Настройка графиков/диаграмм
Для быстрого построения графиков важно удобное расположение данных в таблице. Но часто требуется строить графики на основании уже имеющихся табличных данных без их реорганизации. В таких случаях следует выполнять настройку графика на каждом шаге Мастера диаграмм.
Пусть имеются данные о продажах и прибылях по отделам, данные размещены по месяцам, как на рис. 1.15.
Рис. 1.15
Требуется построить график по колонке Продано, в котором выделены значения по отделам и итого. На рис. 1.16 приведен образец такого графика, но по колонке Маржа.
Рис. 1.16
Попытка построить график по колонке В без настроек не приведет к желаемому результату. Для реализации задуманного по колонке Продано следует выполнить следующие действия:
Выделите диапазон данных для графика — В1:В15.
 Вызовите Мастер диаграмм, выберите гистограмму объемного типа, перейдите на 2-й шаг Мастера в закладку Ряд – рис. 1.17. На 2-м шаге потребуется настроить ряды. На рис. 1.17 поле Ряд содержит список рядов, поле Имя — имя выбранного ряда, поле Значения – диапазон ячеек ряда.
Вызовите Мастер диаграмм, выберите гистограмму объемного типа, перейдите на 2-й шаг Мастера в закладку Ряд – рис. 1.17. На 2-м шаге потребуется настроить ряды. На рис. 1.17 поле Ряд содержит список рядов, поле Имя — имя выбранного ряда, поле Значения – диапазон ячеек ряда.Добавьте ряд с именем Оптовый: введите его в поле Имя. В поле Значения введите перечень адресов ячеек для ряда Оптовый =(Лист1!$B$3; Лист1!$B$8; Лист1!$B$13). Для быстрого набора перечня адресов поступите так: выделите содержимое поля Значения, встаньте на первую ячейку В3, затем, удерживая клавишу CTRL, встаньте на ячейку В8, затем на В13.
Добавьте ряд с именем Розничный: нажмите кнопку Добавить и для нового ряда повторите п.2. Здесь перечень адресов =(Лист1!$B$4; Лист1!$B$9; Лист1!$B$14).

Добавьте ряд с именем Итого: нажмите кнопку Добавить и для нового ряда повторите п.2. Здесь перечень адресов =(Лист1!$B$5; Лист1!$B$10; Лист1!$B$15).
В этом месте Вы должны получить список настроенных рядов, как на рис. 1.18. Осталось заполнить поле Подписи оси Х. В него запишите названия месяцев, т.е. перечень адресов =(Лист1!$A$1; Лист1!$A$6; Лист1!$A$11). Для быстрого набора воспользуйтесь приемом из п.2. Кнопкой Далее перейдите к следующему шагу.
В закладке Заголовки введите название диаграммы Продажи. В закладке Таблица данных установите флаг Таблица данных, который выводит таблицу с данными под графиком. Нажмите Далее и завершите построение диаграммы. Результат показан на рис. 1.19.
Наша задача выполнена. Руководитель, анализирующий данные о продажах и марже по графикам (рис.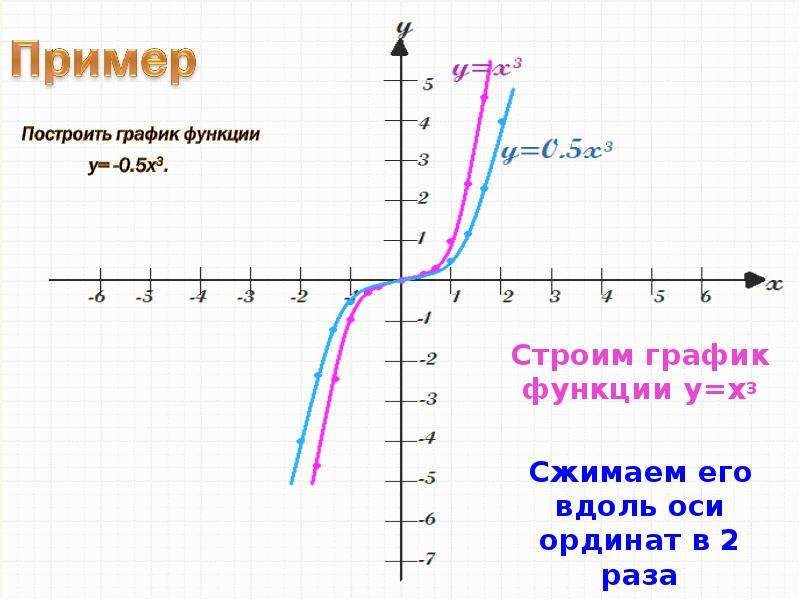 1.16 и рис. 1.19), наглядно увидит, что розничный отдел, отгружая меньше, дает больше прибыли.
1.16 и рис. 1.19), наглядно увидит, что розничный отдел, отгружая меньше, дает больше прибыли.
Рис. 1.17
Рис. 1.18
Рис. 1.19
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ
Excel предоставляет широкие возможности по графической визуализации различных функций, уравнений. Графики позволяют человеку адекватно оценить и воспринять проблему, получить приближенное графическое решение задачи.
Решение задачи построения графика в Excel состоит из двух основных шагов: а) формирования данных для графика в ячейках Excel; б) непосредственно построения и оформления графика.
В качестве первого примера построим графики функций y1=k(x2-1)/(x2+1) и y2=k(x2-10)/(x2+10) на интервале [–2; 2] с шагом 0.2 и k=-15; для функции y2 найдем максимальное, минимальное и среднее значения на интервале. На первом шаге необходимо получить таблицу со значениями аргументов и функций, как показано на рис. 2.1:
На первом шаге необходимо получить таблицу со значениями аргументов и функций, как показано на рис. 2.1:
Рис. 2.1
Как видно, в отдельную таблицу вынесены значения k, x0 и Шаг. Это даст возможность оперативного изменения основной таблицы для других начальных значений и просмотра происходящих изменений графика.
Значения основной таблицы получены по формулам:
ячейка В7 содержит абсолютную ссылку на ячейку В3, т.е. В7=B$3. Эта формула размножена (скопирована) на весь диапазон В7:В27;
ячейка С7 содержит относительную ссылку на ячейку С3, т.е. С7=C3. Ячейка С8 содержит формулу =C7+D$3 и эта формула размножена на весь диапазон С8:С27;
ячейка D7 содержит формулу =B$3*((C7*C7-1)/(C7*C7+1)). Эта формула размножена на весь диапазон D7:D27;
ячейка Е7 содержит формулу =B$3*((C7*C7-10)/(C7*C7+10)).
 Эта формула размножена на весь диапазон Е7:Е27;
Эта формула размножена на весь диапазон Е7:Е27;в ячейки Е28, Е29, Е30 записаны (кнопкой fx на Панели инструментов) статистические функции соответственно =МАКС(E7:E27), =МИН(E7:E27) и =СРЗНАЧ(E7:E27).
Воссоздайте в Excel таблицы, приведенные на рис. 2.1. Для ускорения ввода используйте автозаполнение, абсолютные и относительные ссылки на ячейки в формулах при копировании. Вопросы корректного копирования формул, заполнения и форматирования ячеек, использования функций были рассмотрены в предыдущих разделах.
По сформированным данным постройте график, как на рис. 2.2. Из предыдущих разделов известно, что для этого следует выделить диапазон ячеек D6:Е27 и запустить мастер диаграмм кнопкой Мастер диаграмм на Панели инструментов (или пункт меню ВставкаДиаграмма).
Рис. 2.2
По графику можно узнать значения функций в каждой точке.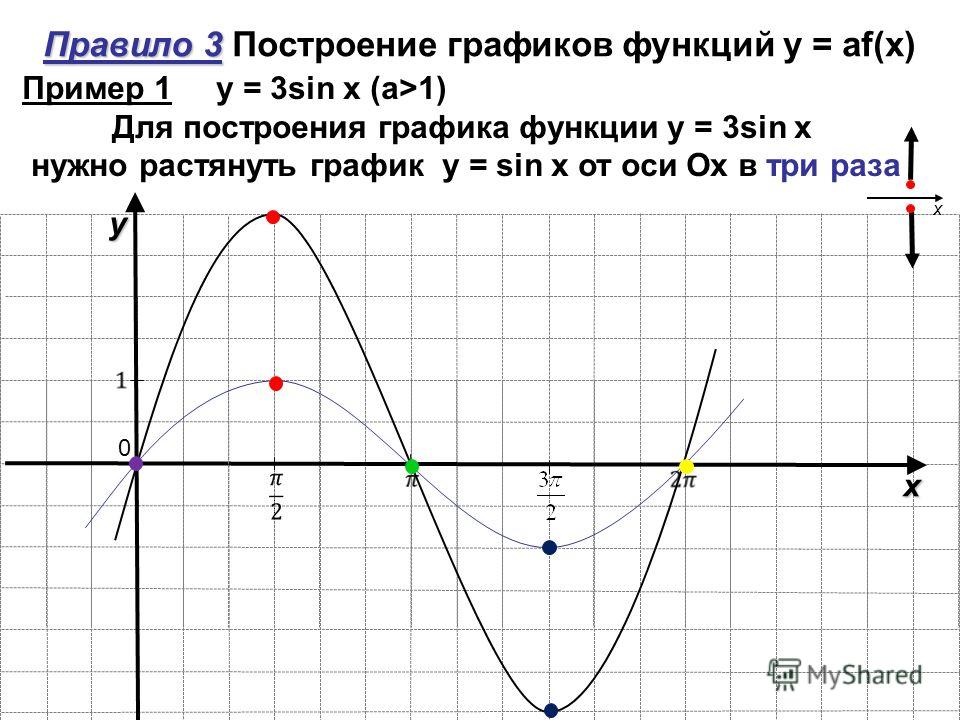 В частности, для установления максимального значения функции y2 наведите указатель мыши на наивысшую точку графика – будет выведена всплывающая подсказка для этой точки, как на рис. 2.2. Есть возможность «приписать» точкам на графике значения функции: щелкните правой кнопкой мыши по любой точке, во всплывающем меню выберите Формат рядов данных…, далее в закладке Подписи данных установите флаг значение и нажмите ОК.
В частности, для установления максимального значения функции y2 наведите указатель мыши на наивысшую точку графика – будет выведена всплывающая подсказка для этой точки, как на рис. 2.2. Есть возможность «приписать» точкам на графике значения функции: щелкните правой кнопкой мыши по любой точке, во всплывающем меню выберите Формат рядов данных…, далее в закладке Подписи данных установите флаг значение и нажмите ОК.
Изменяя начальные значения k, x0 и Шаг, просмотрите изменения в построенных графиках.
Построение кривых и поверхностей
Второй пример относится к курсу аналитической геометрии: построим эллипсоид — поверхность второго порядка, заданную уравнением x2/9 + y2/4 + z2 = 1. Пусть необходимо построить его верхнюю часть для Х [-3;3], Y [-2;2] c шагом 1 для Х и Y.
Данные для построения графика подготовлены на рис. 2/4) из группы Математические. Эта формула размножена на весь диапазон С8:G14.
2/4) из группы Математические. Эта формула размножена на весь диапазон С8:G14.
Воссоздайте в Excel таблицы, приведенные на рис. 2.3. По сформированным данным (диапазон B7:G14) постройте график, как на рис. 2.4. Тип графика должен быть Поверхность, вид – Проволочная (прозрачная) или Поверхность.
Рис. 2.4
Задания для самостоятельного выполнения:
Постройте график функции y=е2х на интервале х [0.5;2] с шагом 0.1.
Постройте график функции y=2х на интервале х [-2;2] с шагом 0.5.
Постройте график функции y=lnx на интервале х [0.5;10] с шагом 0.5.
Постройте график функции y=2cos3x*sinx на интервале х [0.1;1.8] с шагом 0.1.
Постройте параболу y=x2 на интервале х [-3;3] с шагом 0.
 25.
25.Постройте гиперболу y=1/2x на интервале х [0.1;10] с шагом 0.1.
Постройте верхнюю полуокружность x2 + y2 = 9 на интервале х [-3;3] с шагом 0.25.
Постройте верхнюю половину эллипса x2/9 + y2/4 = 1 на интервале х [-3.5;3.5] с шагом 0.25.
Постройте часть плоскости 2x + 4y –2z +2 = 0, лежащую в I квадранте: х [0;6] с шагом 0.5, y [0;6] с шагом 1.
Постройте верхнюю часть эллипсоида, заданного уравнением x2/9 + y2/4 + z2 = 1 для Х [-3;3], Y [-2;2] c шагом 0.5 для Х и Y.
Постройте верхнюю часть двухполостного гиперболоида, заданного уравнением x2/9 + y2/4 — z2 = -1, где х [-3;3], y [-2;2] c шагом 0.5 для x и y.
Постройте часть гиперболического параболоида, заданного уравнением x2/9 — y2/4 = 2z, где х [-3;3], y [-2;2] c шагом 0.
 5 для x и y.
5 для x и y.Постройте часть конуса, заданного уравнением x2/4 + y2/9 – z2/4 = 0, где х [-2;2] с шагом 0.5, y [-3;3] c шагом 1.
Графическое решение системы уравнений
Средствами Excel можно найти приближенное графическое решение системы уравнений с двумя неизвестными: точка пересечения графиков уравнений системы, если существует, будет решением системы, а точность решения определяется шагом дискретизации.
В качестве примера рассмотрим задачу нахождения точки равновесия между спросом и предложением, т.е. такой цены товара, когда спрос и предложение равны. Пусть спрос Y и предложение Z выражаются уравнениями
Y = 2/X + 2
Z = X2 + 1
Найти решение в интервале цен [0.1;2.5] с шагом 0.1. Данные для построения графиков приведены на рис. 2.5:
Рис. 2+1 и эта формула размножена на столбец С6:С30.
2+1 и эта формула размножена на столбец С6:С30.
Воссоздайте в Excel таблицы, приведенные на рис. 2.5. По сформированным данным (диапазон В5:С30) постройте график. Подведите указатель мыши к точке пересечения кривых на графике – всплывающая подсказка будет содержать искомое значение, как на рис. 2.6.
Рис. 2.6
Операционно-стоимостной анализ процесса
Данные, представленные графически, позволяют человеку наглядно увидеть проблемы и узкие места. Для иллюстрации рассмотрим следующий пример. Перед некоторой торговой организацией стоит задача сокращения расходов на выполнение заказов клиентов. Сбор заказов в организации выполняют торговые представители, документы на отгрузку выписываются в офисе организации. Товар отгружается со склада, который расположен в другом конце города.
Один из способов расчета и оптимизации расходов состоит в проведении операционно-стоимостного ABC-анализа (Activity Based Costs Calculation) процесса, принятого в системах моделирования и анализа бизнеса (ARIS, BPwin):
весь процесс разбивают на функции-операции;
каждой функции-операции приписывают ресурсы, оценивают стоимость единицы ресурса;
вычисляют стоимость однократного выполнения каждой функции-операции;
выявляют самые дорогие функции-операции и снижают их стоимость;
параллельно вычисляют коэффициенты участия каждой функции-операции в процессе, оценивают стоимость процесса в сумме всех заказов и пр.

Способы сокращения стоимости процессов могут быть следующими:
снижение трудоемкости операций за счет внедрения новых технологий;
высвобождение дорогих ресурсов (специалистов) от выполнения низкоквалифицированной работы;
исключение малозначимых функций и функций передачи и т.д.
На рис. 2.7 приведен список функций-операций процесса оформления и доставки заказа. По каждой строке вычислена стоимость с учетом затрат человеческих и материальных ресурсов. Колонка Стоимость (руб/мин) рассчитывается из месячной зарплаты, 20 рабочих дней в месяце, 8-часового рабочего дня. Колонка Расход (мин) есть среднее время выполнения операции ресурсом. Колонка Стоимость (руб/ед) есть стоимость используемого в операции материального ресурса, колонка Расход (ед) – его количество.
Воспроизведите таблицу из рис.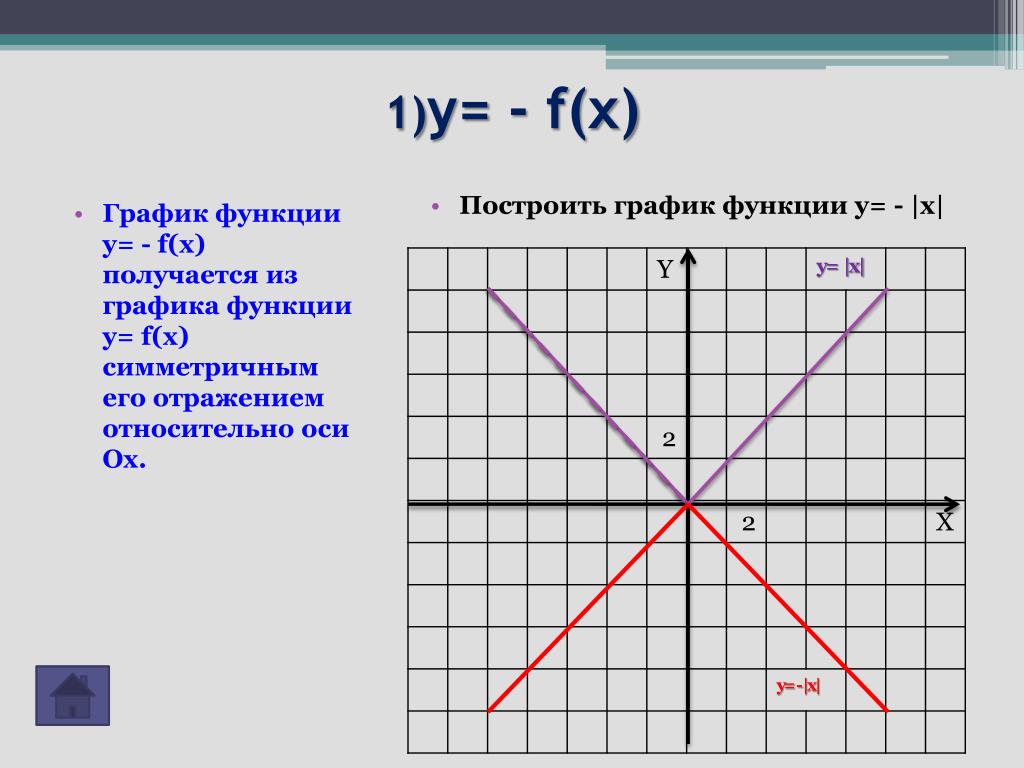 2.7. На основе колонки Стоимость функции постройте график – тип диаграммы выберите из группы Нестандартные, ЧБ гистограмма. На 2-ом шаге мастера диаграмм, в закладке Ряд введите Подписи оси Х из колонки Функции процесса таблицы. На 3-ем шаге мастера диаграмм, в закладке Таблица данных оставьте включенным флаг Таблица данных. В итоге должен получиться график, как на рис. 2.8.
2.7. На основе колонки Стоимость функции постройте график – тип диаграммы выберите из группы Нестандартные, ЧБ гистограмма. На 2-ом шаге мастера диаграмм, в закладке Ряд введите Подписи оси Х из колонки Функции процесса таблицы. На 3-ем шаге мастера диаграмм, в закладке Таблица данных оставьте включенным флаг Таблица данных. В итоге должен получиться график, как на рис. 2.8.
График наглядно демонстрирует наиболее дорогие функции-операции. Стоимость функции 2 можно сократить, передав ручной ввод заказов в обязанности оператора. Функцию 6 можно удалить, если использовать передачу документов в электронном виде, например по E-mail. Таким образом, проводят оптимизацию стоимости процессов, определяют удельный вес каждого процесса в структуре расходов компании и т.д.
Рис. 2.7
Рис. 2.8
Построение графиков функции и поверхностей ?в MS EXCEL
Презентация «Построение графиков функции и поверхностей в MS EXCEL»
Задание. 2.
2.
2.Выделим эту ячейку, установим указатель мыши на её маркере заполнения и протащим его так, чтобы заполнить диапазон B2:L12.
Просмотр содержимого документа
«Построение графиков функции и поверхностей ?в MS EXCEL»
Построение графиков функции в EXCEL
Задание. Построить график функции у = sin x на отрезке [– 2; 2] с шагом
h = 0,5.
у = sin x
№ 1 Построить график функции у = х 3 на отрезке
[– 3; 3] с шагом h = 0,5.
№ 2 Построить график функции y= x 3 +2x на отрезке [-2;2 ] с шагом h=0,5
№ 3 Построить график функции y=2х 3 +1 на отрезке [-1;2] с шагом h=0,25
№ 4 Построить график функции y=2х 3 – 1,5х + 3 на отрезке [-5;4] с шагом h=1,5
№ 5 Построить график функции y=2х 3 -10 на отрезке [-1;2] с шагом h=0,25
Решение уравнений графическим способом в EXCEL
Задание.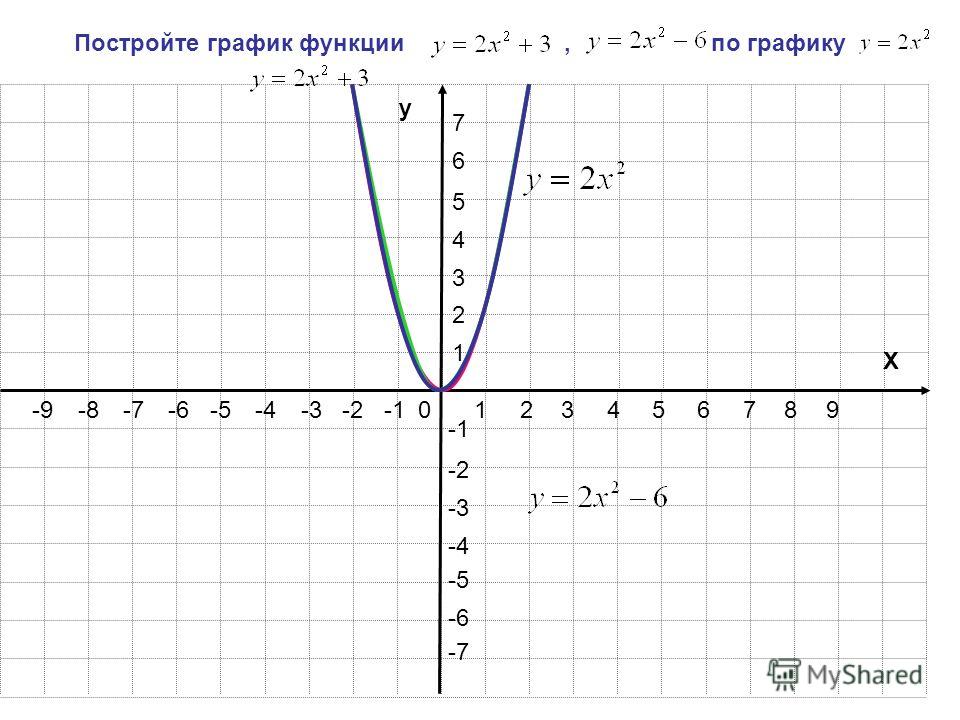 Решить уравнение Х 2 -5Х+6=0 графическим способом.
Решить уравнение Х 2 -5Х+6=0 графическим способом.
1 способ
У=Х 2 -5Х+6
Ответ: х1=2 и х2=3
2 способ
Х 2 -5Х+6=0
Х 2 -5Х= -6
У=Х 2 -5Х
У=-6
Х1
Х2
Решить уравнения графическим способом
х 2 -2х-3=0
х 2 + х – 6 = 0
– х 2 + 6х – 5 = 0
Решить систему уравнений
х 2 +у 2 =9
у-х=-3
х 2 +у 2 -1=0
у-х-1=0
х 2 +у 2 =4
у=0,5х 2 +2
Построение поверхностей в EXCEL
Рассмотрим пример построения поверхности z = x 2 + y 2 при x, y Є [-1,1]. 2 .
2 .
2. Выделим эту ячейку, установим указатель мыши на её маркере заполнения и протащим его так, чтобы заполнить диапазон B2:L12 .
Выделим диапазон ячеек A1:L12 и вызовем мастер диаграмм. Тип диаграммы – Поверхность и вид – Поверхность .
Задание: Построить поверхность
если
и шаг табуляции 1.
В ячейки A2:A18 ввести значения переменной X.
В ячейки B1:R1 ввести значения переменной Y.
В ячейку B2 ввести формулу
=КОРЕНЬ(64-$A2*B$1), скопировать ее в ячейки B3:B18, затем в С2:R18 5.
Выделить диапазон B2:R18 и в мастере диаграмм выбрать тип диаграммы поверхность
Задание. Построить гиперболический параболоид
и шаг табуляции 0,5.
если
Построить поверхность
z = -sin(x 2 + y 2 )+1 при x, y Є [-1,1].
преобразований функций | Колледж алгебры
Результаты обучения
- Графические функции с использованием вертикального и горизонтального сдвига.
- График работает с использованием отражений относительно оси x и оси y .
- Определите, является ли функция четной, нечетной или ни одной из ее графика.
- Графики работают с сжатием и растяжением.
- Комбинируйте преобразования.
Все мы знаем, что плоское зеркало позволяет нам видеть точное изображение себя и всего, что находится позади нас.Когда мы наклоняем зеркало, изображения, которые мы видим, могут сдвигаться по горизонтали или вертикали. Но что происходит, когда мы сгибаем гибкое зеркало? Подобно зеркалу карнавального дома, оно представляет нам искаженное изображение нас самих, растянутое или сжатое по горизонтали или вертикали. Аналогичным образом мы можем исказить или преобразовать математические функции, чтобы лучше адаптировать их к описанию объектов или процессов в реальном мире. В этом разделе мы рассмотрим несколько видов преобразований.
В этом разделе мы рассмотрим несколько видов преобразований.
Рисунок 1. (кредит: «Misko» / Flickr)
Смена
Один из видов преобразования включает в себя сдвиг всего графика функции вверх, вниз, вправо или влево. Самый простой сдвиг — это сдвиг по вертикали, , перемещение графика вверх или вниз, потому что это преобразование включает добавление положительной или отрицательной константы к функции. Другими словами, мы добавляем одну и ту же константу к выходному значению функции независимо от входа. Для функции [латекс] g \ left (x \ right) = f \ left (x \ right) + k [/ latex] функция [latex] f \ left (x \ right) [/ latex] сдвигается по вертикали [латекс] к [/ латекс] единиц.
Вертикальный сдвиг на [latex] k = 1 [/ latex] функции кубического корня [latex] f \ left (x \ right) = \ sqrt [3] {x} [/ latex].
Чтобы помочь вам представить себе концепцию вертикального сдвига, представьте, что [latex] y = f \ left (x \ right) [/ latex]. Следовательно, [латекс] f \ left (x \ right) + k [/ latex] эквивалентен [latex] y + k [/ latex]. Каждая единица [latex] y [/ latex] заменяется на [latex] y + k [/ latex], поэтому значение [latex] y \ text {-} [/ latex] увеличивается или уменьшается в зависимости от значения [ латекс] к [/ латекс]. Результат — сдвиг вверх или вниз.
Следовательно, [латекс] f \ left (x \ right) + k [/ latex] эквивалентен [latex] y + k [/ latex]. Каждая единица [latex] y [/ latex] заменяется на [latex] y + k [/ latex], поэтому значение [latex] y \ text {-} [/ latex] увеличивается или уменьшается в зависимости от значения [ латекс] к [/ латекс]. Результат — сдвиг вверх или вниз.
Общее примечание: вертикальный сдвиг
Дана функция [латекс] f \ left (x \ right) [/ latex], новая функция [latex] g \ left (x \ right) = f \ left (x \ right) + k [/ latex], где [latex] k [/ latex] — константа, представляет собой вертикальный сдвиг , функции [latex] f \ left (x \ right) [/ latex]. Все выходные значения изменяются на [латекс] k [/ латекс] единиц. Если [latex] k [/ latex] положительный, график сдвинется вверх. Если значение [latex] k [/ latex] отрицательное, график сдвинется вниз.
Пример: добавление константы к функции
Для регулирования температуры в зеленом здании вентиляционные отверстия возле крыши открываются и закрываются в течение дня.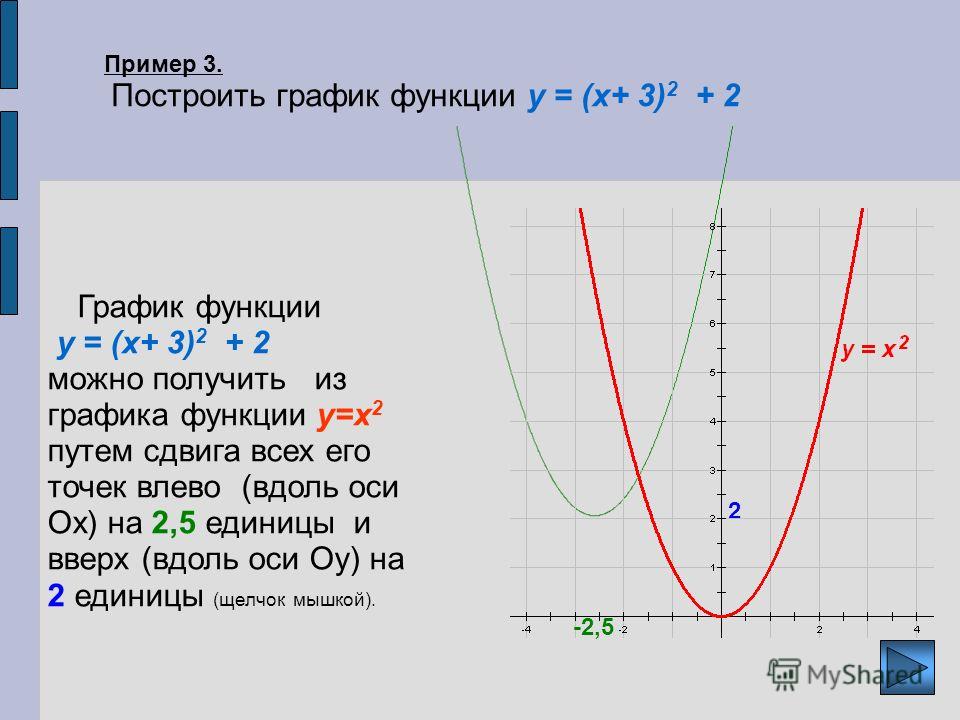 На рисунке 2 показана площадь открытых вентиляционных отверстий [латекс] V [/ латекс] (в квадратных футах) в течение дня в часах после полуночи, [латекс] t [/ латекс]. Летом управляющий помещения решает попытаться лучше регулировать температуру, увеличив количество открытых вентиляционных отверстий на 20 квадратных футов в течение дня и ночи. Нарисуйте график этой новой функции.
На рисунке 2 показана площадь открытых вентиляционных отверстий [латекс] V [/ латекс] (в квадратных футах) в течение дня в часах после полуночи, [латекс] t [/ латекс]. Летом управляющий помещения решает попытаться лучше регулировать температуру, увеличив количество открытых вентиляционных отверстий на 20 квадратных футов в течение дня и ночи. Нарисуйте график этой новой функции.
Мы можем нарисовать график этой новой функции, добавив 20 к каждому выходному значению исходной функции. Это приведет к смещению графика вверх по вертикали.
Обратите внимание, что для каждого входного значения выходное значение увеличилось на 20, поэтому, если мы вызовем новую функцию [latex] S \ left (t \ right) [/ latex], мы могли бы написать
[латекс] S \ left (t \ right) = V \ left (t \ right) +20 [/ латекс]
Это обозначение говорит нам, что для любого значения [latex] t, S \ left (t \ right) [/ latex] можно найти, оценив функцию [latex] V [/ latex] на том же входе и затем добавив 20 к результату. Это определяет [latex] S [/ latex] как преобразование функции [latex] V [/ latex], в данном случае вертикальное смещение на 20 единиц.Обратите внимание, что при вертикальном сдвиге входные значения остаются неизменными, а изменяются только выходные значения.
Это определяет [latex] S [/ latex] как преобразование функции [latex] V [/ latex], в данном случае вертикальное смещение на 20 единиц.Обратите внимание, что при вертикальном сдвиге входные значения остаются неизменными, а изменяются только выходные значения.
| [латекс] t [/ латекс] | 0 | 8 | 10 | 17 | 19 | 24 |
| [латекс] V \ влево (t \ вправо) [/ латекс] | 0 | 0 | 220 | 220 | 0 | 0 |
| [латекс] S \ левый (t \ правый) [/ латекс] | 20 | 20 | 240 | 240 | 20 | 20 |
Практическое руководство. Для табличной функции создайте новую строку для представления вертикального сдвига.

- Укажите строку или столбец вывода.
- Определите величину сдвига.
- Добавьте сдвиг к значению в каждой выходной ячейке. Добавьте положительное значение для увеличения или отрицательное значение для уменьшения.
Пример: сдвиг табличной функции по вертикали
Функция [латекс] f \ left (x \ right) [/ latex] приведена ниже. Создайте таблицу для функции [латекс] g \ left (x \ right) = f \ left (x \ right) -3 [/ latex].
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] f \ слева (x \ справа) [/ латекс] | 1 | 3 | 7 | 11 |
Формула [latex] g \ left (x \ right) = f \ left (x \ right) -3 [/ latex] говорит нам, что мы можем найти выходные значения [latex] g [/ latex], вычитая 3 из выходных значений [latex] f [/ latex].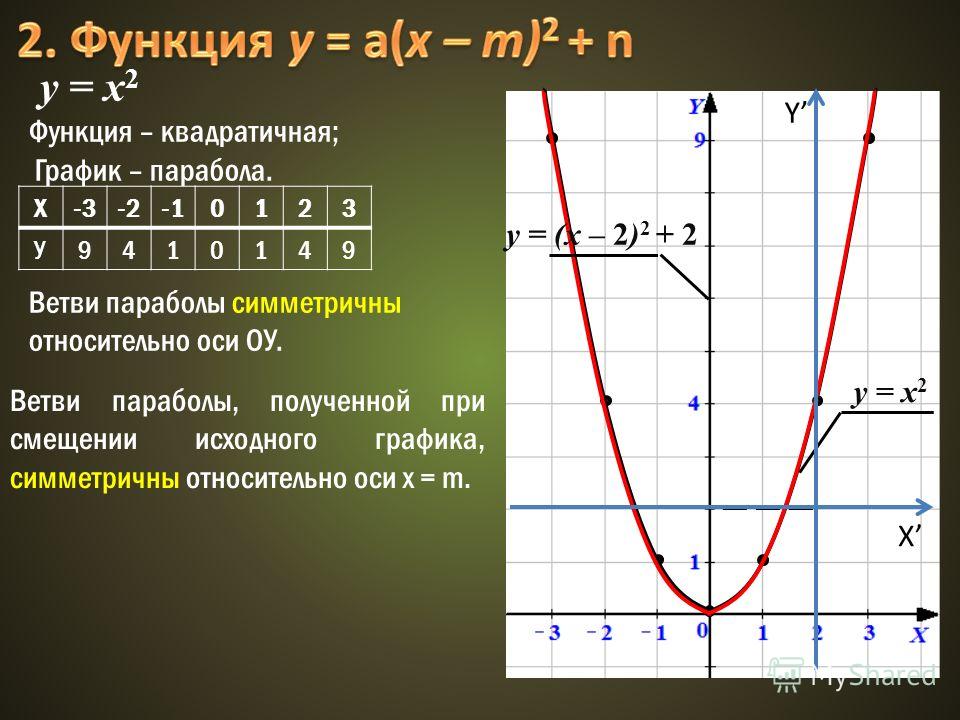 Например:
Например:
[латекс] \ begin {case} f \ left (2 \ right) = 1 \ hfill & \ text {Given} \ hfill \\ g \ left (x \ right) = f \ left (x \ right) -3 \ hfill & \ text {Заданное преобразование} \ hfill \\ g \ left (2 \ right) = f \ left (2 \ right) -3 \ hfill & \ hfill \\ = 1-3 \ hfill & \ hfill \\ = -2 \ hfill & \ hfill \ end {case} [/ latex]
Вычитая 3 из каждого значения [latex] f \ left (x \ right) [/ latex], мы можем заполнить таблицу значений для [latex] g \ left (x \ right) [/ latex].
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] f \ слева (x \ справа) [/ латекс] | 1 | 3 | 7 | 11 |
| [латекс] г \ левый (х \ правый) [/ латекс] | -2 | 0 | 4 | 8 |
Анализ решения
Как и в случае с предыдущим вертикальным сдвигом, обратите внимание, что входные значения остаются такими же, а изменяются только выходные значения. {2} + 30т + 10 [/ латекс]
{2} + 30т + 10 [/ латекс]
Определение горизонтальных сдвигов
Мы только что видели, что вертикальный сдвиг — это изменение вывода или вне функции. Теперь мы посмотрим, как изменения ввода внутри функции меняют ее график и значение. Сдвиг на вход приводит к перемещению графика функции влево или вправо, что известно как горизонтальный сдвиг .
Горизонтальный сдвиг функции [латекс] f \ влево (x \ вправо) = \ sqrt [3] {x} [/ latex].{2} [/ latex] — новая функция. Каждый вход уменьшается на 2 перед возведением функции в квадрат. В результате график сдвигается на 2 единицы вправо, потому что нам потребуется увеличить предыдущий ввод на 2 единицы, чтобы получить такое же значение вывода, как указано в [latex] f [/ latex].
Общее примечание: горизонтальный сдвиг
Дана функция [латекс] f [/ latex], новая функция [latex] g \ left (x \ right) = f \ left (xh \ right) [/ latex], где [latex] h [/ latex] является константой, представляет собой горизонтальный сдвиг функции [латекс] f [/ латекс]. Если значение [latex] h [/ latex] положительное, график сдвинется вправо. Если значение [latex] h [/ latex] отрицательное, график сдвинется влево.
Если значение [latex] h [/ latex] положительное, график сдвинется вправо. Если значение [latex] h [/ latex] отрицательное, график сдвинется влево.
Пример: добавление константы ко входу
Возвращаясь к нашему примеру с воздушным потоком в здании из Примера 2, предположим, что осенью менеджер по эксплуатации решит, что первоначальный план вентиляции начинается слишком поздно, и хочет начать всю программу вентиляции на 2 часа раньше. Нарисуйте график новой функции.
Показать решениеМы можем установить [latex] V \ left (t \ right) [/ latex] как исходную программу и [latex] F \ left (t \ right) [/ latex] как исправленную программу.
[латекс] \ begin {align} {c} V \ left (t \ right) & = \ text {исходный план вентиляции} \\ F \ left (t \ right) & = \ text {на 2 часа раньше} \ end {align} [/ latex]
На новом графике каждый раз поток воздуха такой же, как и исходная функция [латекс] V [/ латекс] через 2 часа. Например, в исходной функции [latex] V [/ latex] воздушный поток начинает изменяться в 8 часов утра, тогда как для функции [latex] F [/ latex] воздушный поток начинает меняться в 6 часов утра. Сопоставимые значения функции [латекс] V \ left (8 \ right) = F \ left (6 \ right) [/ latex].{\ text {2}} [/ latex] в 8 утра, поэтому [латекс] V \ left (10 \ right) = F \ left (8 \ right) [/ latex].
Сопоставимые значения функции [латекс] V \ left (8 \ right) = F \ left (6 \ right) [/ latex].{\ text {2}} [/ latex] в 8 утра, поэтому [латекс] V \ left (10 \ right) = F \ left (8 \ right) [/ latex].
В обоих случаях мы видим, что, поскольку [latex] F \ left (t \ right) [/ latex] начинается на 2 часа раньше, [latex] h = -2 [/ latex]. Это означает, что те же выходные значения достигаются, когда [латекс] F \ left (t \ right) = V \ left (t- \ left (-2 \ right) \ right) = V \ left (t + 2 \ right) [/латекс].
Анализ решения
Обратите внимание, что [latex] V \ left (t + 2 \ right) [/ latex] приводит к смещению графика на влево .
Горизонтальные изменения или «внутренние изменения» влияют на домен функции (вход), а не на диапазон и часто кажутся нелогичными. Новая функция [latex] F \ left (t \ right) [/ latex] использует те же выходы, что и [latex] V \ left (t \ right) [/ latex], но сопоставляет эти выходы с входами на 2 часа раньше, чем те [латекс] В \ левый (т \ правый) [/ латекс]. Другими словами, мы должны добавить 2 часа ко входу [latex] V [/ latex], чтобы найти соответствующий выход для [latex] F: F \ left (t \ right) = V \ left (t + 2 \ right )[/латекс].
Другими словами, мы должны добавить 2 часа ко входу [latex] V [/ latex], чтобы найти соответствующий выход для [latex] F: F \ left (t \ right) = V \ left (t + 2 \ right )[/латекс].
Практическое руководство. Для табличной функции создайте новую строку для представления горизонтального сдвига.
- Определите входную строку или столбец.
- Определите величину сдвига.
- Добавьте сдвиг к значению в каждой ячейке ввода.
Пример: сдвиг табличной функции по горизонтали
Функция [латекс] f \ left (x \ right) [/ latex] приведена ниже. Создайте таблицу для функции [латекс] g \ left (x \ right) = f \ left (x — 3 \ right) [/ latex].
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] f \ слева (x \ справа) [/ латекс] | 1 | 3 | 7 | 11 |
Формула [латекс] f \ left (x \ right) = f \ left (x — 3 \ right) [/ latex] говорит нам, что выходные значения [latex] g [/ latex] такие же, как выходные значение [latex] f [/ latex], когда входное значение на 3 меньше исходного значения. Например, мы знаем, что [латекс] f \ left (2 \ right) = 1 [/ latex]. Чтобы получить такой же результат от функции [latex] g [/ latex], нам понадобится входное значение, которое на 3 больше . Мы вводим значение, которое на 3 больше для [latex] g \ left (x \ right) [/ latex], потому что функция забирает 3 перед вычислением функции [latex] f [/ latex].
Например, мы знаем, что [латекс] f \ left (2 \ right) = 1 [/ latex]. Чтобы получить такой же результат от функции [latex] g [/ latex], нам понадобится входное значение, которое на 3 больше . Мы вводим значение, которое на 3 больше для [latex] g \ left (x \ right) [/ latex], потому что функция забирает 3 перед вычислением функции [latex] f [/ latex].
[латекс] \ begin {case} g \ left (5 \ right) = f \ left (5-3 \ right) \ hfill \\ = f \ left (2 \ right) \ hfill \\ = 1 \ hfill \ конец {case} [/ latex]
Продолжаем с другими значениями, чтобы создать эту таблицу.
| [латекс] x [/ латекс] | 5 | 7 | 9 | 11 |
| [латекс] x — 3 [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] f \ слева (x \ справа) [/ латекс] | 1 | 3 | 7 | 11 |
| [латекс] г \ левый (х \ правый) [/ латекс] | 1 | 3 | 7 | 11 |
В результате функция [latex] g \ left (x \ right) [/ latex] сдвинута вправо на 3. {2} [/ latex].{2} [/ latex], но значения [latex] x [/ latex] – сдвинуты вправо на 2 единицы. Раньше вершина находилась в точке (0,0), но теперь вершина находится в точке (2,0). График представляет собой базовую квадратичную функцию, сдвинутую на 2 единицы вправо, поэтому
{2} [/ latex].{2} [/ latex], но значения [latex] x [/ latex] – сдвинуты вправо на 2 единицы. Раньше вершина находилась в точке (0,0), но теперь вершина находится в точке (2,0). График представляет собой базовую квадратичную функцию, сдвинутую на 2 единицы вправо, поэтому
[латекс] g \ left (x \ right) = f \ left (x — 2 \ right) [/ латекс]
Обратите внимание, как мы должны ввести значение [latex] x = 2 [/ latex], чтобы получить выходное значение [latex] y = 0 [/ latex]; значения [latex] x [/ latex] должны быть на 2 единицы больше из-за сдвига вправо на 2 единицы.{2} \ hfill \ end {case} [/ latex]
Анализ решения
Чтобы определить, составляет ли сдвиг [латекс] +2 [/ латекс] или [латекс] -2 [/ латекс], рассмотрите единственную контрольную точку на графике. Для квадратичного удобно смотреть на вершину. В исходной функции [латекс] f \ left (0 \ right) = 0 [/ latex]. В нашей смещенной функции [latex] g \ left (2 \ right) = 0 [/ latex]. Чтобы получить выходное значение 0 из функции [latex] f [/ latex], нам нужно решить, будет ли работать знак плюс или минус, чтобы удовлетворить [latex] g \ left (2 \ right) = f \ left ( x — 2 \ right) = f \ left (0 \ right) = 0 [/ латекс]. Чтобы это сработало, нам нужно будет вычесть единиц 2 из наших входных значений.
Чтобы это сработало, нам нужно будет вычесть единиц 2 из наших входных значений.
Пример: интерпретация горизонтальных и вертикальных сдвигов
Функция [латекс] G \ left (m \ right) [/ latex] дает количество галлонов газа, необходимое для проезда [латексных] м [/ латексных] миль. Интерпретировать [латекс] G \ left (m \ right) +10 [/ latex] и [latex] G \ left (m + 10 \ right) [/ latex].
Показать решение[латекс] G \ left (m \ right) +10 [/ latex] можно интерпретировать как прибавление 10 к выходу, галлонов. Это газ, необходимый для проезда [латексных] м [/ латексных] миль, плюс еще 10 галлонов газа.График будет указывать на вертикальный сдвиг.
[латекс] G \ left (m + 10 \ right) [/ latex] можно интерпретировать как добавление 10 к входным милям. Итак, это количество галлонов газа, необходимое для проезда на 10 миль больше, чем [латексных] м [/ латексных] миль. График будет указывать на горизонтальный сдвиг.
Попробуйте
Учитывая функцию [latex] f \ left (x \ right) = \ sqrt {x} [/ latex], построить график исходной функции [latex] f \ left (x \ right) [/ latex] и преобразования [latex ] g \ left (x \ right) = f \ left (x + 2 \ right) [/ latex] на тех же осях. 2 + 3 [/ латекс]
2 + 3 [/ латекс]
Отражения
Еще одно преобразование, которое может быть применено к функции, — это отражение по оси [latex] x [/ latex] — или [latex] y [/ latex].Вертикальное отражение , отражает график по вертикали по оси [латекс] x [/ латекс], тогда как горизонтальное отражение , отражает график по горизонтали по оси [латекс] y [/ латекс]. Отражения показаны на рисунке 9.
Вертикальное и горизонтальное отражение функции.
Обратите внимание, что вертикальное отражение создает новый график, который является зеркальным отображением базового или исходного графика относительно оси [latex] x [/ latex]. Горизонтальное отражение создает новый график, который является зеркальным отображением базового или исходного графика относительно оси [latex] y [/ latex].
Общее примечание: размышления
Учитывая функцию [латекс] f \ left (x \ right) [/ latex], новая функция [latex] g \ left (x \ right) = — f \ left (x \ right) [/ latex] является вертикальное отражение функции [latex] f \ left (x \ right) [/ latex], иногда называемое отражением относительно (или над, или сквозь) [latex] x [/ latex] -оси.
Учитывая функцию [латекс] f \ left (x \ right) [/ latex], новая функция [latex] g \ left (x \ right) = f \ left (-x \ right) [/ latex] является горизонтальное отражение функции [latex] f \ left (x \ right) [/ latex], иногда называемое отражением относительно оси [latex] y [/ latex].
Как сделать: для данной функции отразите график как по вертикали, так и по горизонтали.
- Умножьте все выходные данные на –1 для вертикального отражения. Новый график является отражением исходного графика относительно оси [latex] x [/ latex].
- Умножьте все входные данные на –1 для горизонтального отражения. Новый график является отражением исходного графика относительно оси [latex] y [/ latex].
Пример: отражение графика по горизонтали и вертикали
Отразите график [латекса] s \ left (t \ right) = \ sqrt {t} [/ latex] (a) по вертикали и (b) по горизонтали.
Показать решение а. Отражение графика по вертикали означает, что каждое выходное значение будет отражаться по горизонтальной оси [latex] t [/ latex] –, как показано ниже.
Вертикальное отражение функции квадратного корня
Поскольку каждое выходное значение противоположно исходному выходному значению, мы можем записать
[латекс] V \ left (t \ right) = — s \ left (t \ right) \ text {или} V \ left (t \ right) = — \ sqrt {t} [/ latex]
Обратите внимание, что это внешнее изменение или вертикальный сдвиг, который влияет на выходные значения [latex] s \ left (t \ right) [/ latex], поэтому отрицательный знак принадлежит за пределами функции.
г. Отражение по горизонтали означает, что каждое входное значение будет отражаться по вертикальной оси, как показано ниже.
Горизонтальное отражение функции квадратного корня
Поскольку каждое входное значение противоположно исходному входному значению, мы можем написать
[латекс] H \ left (t \ right) = s \ left (-t \ right) \ text {или} H \ left (t \ right) = \ sqrt {-t} [/ latex]
Обратите внимание, что это внутреннее изменение или горизонтальное изменение, которое влияет на входные значения, поэтому отрицательный знак находится внутри функции.
Обратите внимание, что эти преобразования могут повлиять на домен и диапазон функций. В то время как исходная функция квадратного корня имеет домен [латекс] \ left [0, \ infty \ right) [/ latex] и диапазон [latex] \ left [0, \ infty \ right) [/ latex], вертикальное отражение дает [latex] V \ left (t \ right) [/ latex] определяет диапазон [latex] \ left (- \ infty, 0 \ right] [/ latex], а горизонтальное отражение дает [latex] H \ left (t \ right) [/ latex] функция домена [latex] \ left (- \ infty, 0 \ right] [/ latex].
Попробуйте
Отразите график [латекса] f \ left (x \ right) = | x — 1 | [/ latex] (a) по вертикали и (b) по горизонтали.
Показать решениеа)
б)
Пример: отражение табличной функции по горизонтали и вертикали
Задана функция [латекс] f \ left (x \ right) [/ latex]. Создайте таблицу для функций ниже.
- [латекс] g \ left (x \ right) = — f \ left (x \ right) [/ латекс]
- [латекс] h \ left (x \ right) = f \ left (-x \ right) [/ латекс]
- Для [latex] g \ left (x \ right) [/ latex] отрицательный знак за пределами функции указывает на вертикальное отражение, поэтому значения [latex] x [/ latex] остаются прежними, и каждое выходное значение будет быть противоположным исходному выходному значению.
[латекс] x [/ латекс] 2 4 6 8 [латекс] г \ левый (х \ правый) [/ латекс] –1 –3 –7 –11 - Для [latex] h \ left (x \ right) [/ latex] отрицательный знак внутри функции указывает на горизонтальное отражение, поэтому каждое входное значение будет противоположным исходному входному значению и [latex] h \ left Значения (x \ right) [/ latex] остаются такими же, как значения [latex] f \ left (x \ right) [/ latex].

[латекс] x [/ латекс] -2 −4 −6 −8 [латекс] h \ left (x \ right) [/ латекс] 1 3 7 11
Попробуйте
| [латекс] x [/ латекс] | -2 | 0 | 2 | 4 |
| [латекс] f \ слева (x \ справа) [/ латекс] | 5 | 10 | 15 | 20 |
Используя функцию [latex] f \ left (x \ right) [/ latex], приведенную в таблице выше, создайте таблицу для функций ниже.
а. [латекс] г \ влево (х \ вправо) = — е \ влево (х \ вправо) [/ латекс]
г. [латекс] h \ left (x \ right) = f \ left (-x \ right) [/ латекс]
[латекс] h \ left (x \ right) = f \ left (-x \ right) [/ латекс]
- [латекс] g \ left (x \ right) = — f \ left (x \ right) [/ latex]
[латекс] x [/ латекс] -2 0 2 4 [латекс] г \ левый (х \ правый) [/ латекс] [латекс] -5 [/ латекс] [латекс] -10 [/ латекс] [латекс] -15 [/ латекс] [латекс] -20 [/ латекс] - [латекс] h \ left (x \ right) = f \ left (-x \ right) [/ латекс]
[латекс] x [/ латекс] -2 0 2 4 [латекс] h \ left (x \ right) [/ латекс] 15 10 5 неизвестно
Определить, являются ли функции четными, нечетными или нет
Некоторые функции демонстрируют симметрию, поэтому на исходном графике появляются отражения. {3} [/ latex] или [latex] f \ left (x \ right) = \ frac {1} {x} [/ latex] были отражены на обеих осях , результатом будет исходный график.
{3} [/ latex] или [latex] f \ left (x \ right) = \ frac {1} {x} [/ latex] были отражены на обеих осях , результатом будет исходный график.
(a) Функция кубического инструментария (b) Горизонтальное отражение функции кубического инструментария (c) Горизонтальное и вертикальное отражение воспроизводят исходную кубическую функцию.
Мы говорим, что эти графики симметричны относительно начала координат. Функция с графиком, симметричным относительно начала координат, называется нечетной функцией .
Примечание: функция не может быть ни четной, ни нечетной, если она не обладает симметрией.{x} [/ latex] не является ни четным, ни нечетным. Кроме того, единственная функция, которая является как четной, так и нечетной, — это постоянная функция [latex] f \ left (x \ right) = 0 [/ latex].
Общее примечание: четные и нечетные функции
Функция называется четной функцией , если для каждого ввода [латекс] x [/ латекс]
[латекс] f \ left (x \ right) = f \ left (-x \ right) [/ латекс]
График четной функции симметричен относительно оси [latex] y \ text {-} [/ latex]. {3} + 2x [/ latex] четной, нечетной или ни одной?
{3} + 2x [/ latex] четной, нечетной или ни одной?
Не глядя на график, мы можем определить, является ли функция четной или нечетной, найдя формулы для отражений и определив, возвращают ли они нас к исходной функции.{3} + 2х [/ латекс]
Поскольку [latex] -f \ left (-x \ right) = f \ left (x \ right) [/ latex], это нечетная функция.
Анализ решения
Рассмотрим график [латекс] ф [/ латекс]. Обратите внимание, что график симметричен относительно начала координат. Для каждой точки [latex] \ left (x, y \ right) [/ latex] на графике соответствующая точка [latex] \ left (-x, -y \ right) [/ latex] также находится на графике. Например, (1, 3) находится на графике [latex] f [/ latex], а соответствующая точка [latex] \ left (-1, -3 \ right) [/ latex] также находится на графике.{2} +7 [/ latex] четное, нечетное или ни одно?
Сжатие и растяжение
Добавление константы к входам или выходам функции изменило положение графика по отношению к осям, но не повлияло на форму графика. Теперь мы исследуем эффекты умножения входов или выходов на некоторую величину.
Теперь мы исследуем эффекты умножения входов или выходов на некоторую величину.
Мы можем преобразовать внутреннюю часть (входные значения) функции или мы можем преобразовать внешнюю часть (выходные значения) функции. Каждое изменение имеет определенный эффект, который можно увидеть графически.
Вертикальное растяжение и сжатие
Когда мы умножаем функцию на положительную константу, мы получаем функцию, график которой растянут или сжимается по вертикали относительно графика исходной функции. Если константа больше 1, мы получаем вертикальное растяжение ; если константа находится между 0 и 1, мы получаем сжатие по вертикали . На приведенном ниже графике показана функция, умноженная на постоянные коэффициенты 2 и 0,5, и результирующие вертикальное растяжение и сжатие.
Вертикальное растяжение и сжатие
Общее примечание: вертикальное растяжение и сжатие
Дана функция [латекс] f \ left (x \ right) [/ latex], новая функция [latex] g \ left (x \ right) = af \ left (x \ right) [/ latex], где [ latex] a [/ latex] является константой, это вертикальное растяжение или вертикальное сжатие функции [латекс] f \ left (x \ right) [/ latex].
- Если [latex] a> 1 [/ latex], то график будет растянут.
- Если [latex] 0
- Если [latex] a <0 [/ latex], то будет комбинация вертикального растяжения или сжатия с вертикальным отражением.
Как: для данной функции построить график ее вертикального растяжения.
- Определите ценность [латекса] а [/ латекса].
- Умножьте все значения диапазона на [latex] a [/ latex].
- Если [latex] a> 1 [/ latex], график растягивается в [latex] a [/ latex] раз.
Если [latex] {0} <{a} <{1} [/ latex], график сжимается с коэффициентом [latex] a [/ latex].
Если [latex] a <0 [/ latex], график либо растягивается, либо сжимается, а также отражается относительно оси [latex] x [/ latex].
Пример: построение вертикального растяжения
Функция [latex] P \ left (t \ right) [/ latex] моделирует количество плодовых мушек в популяции с течением времени и изображена на графике ниже.
Ученый сравнивает эту популяцию с другой популяцией, [латекс] Q [/ латекс], рост которой происходит по той же схеме, но в два раза больше. Нарисуйте график этой популяции.
Показать решениеПоскольку генеральная совокупность всегда вдвое больше, выходные значения новой совокупности всегда вдвое превышают выходные значения исходной функции.
Если мы выберем четыре контрольных точки, (0, 1), (3, 3), (6, 2) и (7, 0), мы умножим все выходы на 2.
Ниже показано, где будут расположены новые точки для нового графика.
[латекс] \ begin {case} \ left (0, \ text {} 1 \ right) \ to \ left (0, \ text {} 2 \ right) \ hfill \\ \ left (3, \ text {} 3 \ right) \ to \ left (3, \ text {} 6 \ right) \ hfill \\ \ left (6, \ text {} 2 \ right) \ to \ left (6, \ text {} 4 \ right ) \ hfill \\ \ left (7, \ text {} 0 \ right) \ to \ left (7, \ text {} 0 \ right) \ hfill \ end {case} [/ latex]
Рисунок 16
Условно отношение записывается как
[латекс] Q \ left (t \ right) = 2P \ left (t \ right) [/ латекс]
Это означает, что для любого входа [latex] t [/ latex] значение функции [latex] Q [/ latex] в два раза больше значения функции [latex] P [/ latex]. Обратите внимание, что эффект на графике — это вертикальное растяжение графика, где каждая точка удваивает расстояние от горизонтальной оси. Входные значения [latex] t [/ latex] остаются прежними, а выходные значения в два раза больше, чем раньше.
Обратите внимание, что эффект на графике — это вертикальное растяжение графика, где каждая точка удваивает расстояние от горизонтальной оси. Входные значения [latex] t [/ latex] остаются прежними, а выходные значения в два раза больше, чем раньше.
Как сделать: учитывая табличную функцию и предполагая, что преобразование представляет собой вертикальное растяжение или сжатие, создайте таблицу для вертикального сжатия.
- Определите стоимость [латекса] а [/ латекса].
- Умножьте все выходные значения на [латекс] а [/ латекс].
Пример: поиск вертикального сжатия табличной функции
Функция [латекс] f [/ латекс] приведена в таблице ниже. Создайте таблицу для функции [латекс] g \ left (x \ right) = \ frac {1} {2} f \ left (x \ right) [/ latex].
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] f \ слева (x \ справа) [/ латекс] | 1 | 3 | 7 | 11 |
Формула [latex] g \ left (x \ right) = \ frac {1} {2} f \ left (x \ right) [/ latex] сообщает нам, что выходные значения [latex] g [/ latex] равны половине выходных значений [latex] f [/ latex] с теми же входами. Например, мы знаем, что [латекс] f \ left (4 \ right) = 3 [/ latex]. Тогда
Например, мы знаем, что [латекс] f \ left (4 \ right) = 3 [/ latex]. Тогда
[латекс] g \ left (4 \ right) = \ frac {1} {2} \ cdot {f} (4) = \ frac {1} {2} \ cdot \ left (3 \ right) = \ frac {3} {2} [/ латекс]
Мы делаем то же самое для других значений, чтобы создать эту таблицу.
| [латекс] x [/ латекс] | [латекс] 2 [/ латекс] | [латекс] 4 [/ латекс] | [латекс] 6 [/ латекс] | [латекс] 8 [/ латекс] |
| [латекс] г \ левый (х \ правый) [/ латекс] | [латекс] \ frac {1} {2} [/ латекс] | [латекс] \ frac {3} {2} [/ латекс] | [латекс] \ frac {7} {2} [/ латекс] | [латекс] \ frac {11} {2} [/ латекс] |
Анализ решения
В результате функция [latex] g \ left (x \ right) [/ latex] была сжата по вертикали с помощью [latex] \ frac {1} {2} [/ latex]. Каждое выходное значение делится пополам, поэтому высота графика составляет половину исходной высоты.
Каждое выходное значение делится пополам, поэтому высота графика составляет половину исходной высоты.
Попробуйте
Функция [латекс] f [/ латекс] приведена ниже. Создайте таблицу для функции [латекс] g \ left (x \ right) = \ frac {3} {4} f \ left (x \ right) [/ latex].
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] f \ слева (x \ справа) [/ латекс] | 12 | 16 | 20 | 0 |
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] г \ левый (х \ правый) [/ латекс] | 9 | 12 | 15 | 0 |
Пример: распознавание вертикального растяжения
График представляет собой преобразование функции инструментария [latex] f \ left (x \ right) = {x} ^ {3} [/ latex]. {3} [/ latex]
{3} [/ latex]
Попробуйте
Напишите формулу функции, которую мы получим, если растянем функцию инструментария идентификации в 3 раза, а затем сдвинем ее вниз на 2 единицы.
Горизонтальное растяжение и сжатие
Теперь мы рассмотрим изменения внутри функции. Когда мы умножаем входные данные функции на положительную константу, мы получаем функцию, график которой растянут или сжимается по горизонтали относительно графика исходной функции. Если константа находится между 0 и 1, мы получаем горизонтальное растяжение ; если константа больше 1, мы получаем горизонтальное сжатие функции.
Для функции [латекс] y = f \ left (x \ right) [/ latex], форма [latex] y = f \ left (bx \ right) [/ latex] приводит к горизонтальному растяжению или сжатию.{2} [/ латекс] в 2 раза.
Общее примечание: горизонтальное растяжение и сжатие
Дана функция [латекс] f \ left (x \ right) [/ latex], новая функция [latex] g \ left (x \ right) = f \ left (bx \ right) [/ latex], где [ latex] b [/ latex] является константой, это горизонтальное растяжение или горизонтальное сжатие функции [latex] f \ left (x \ right) [/ latex].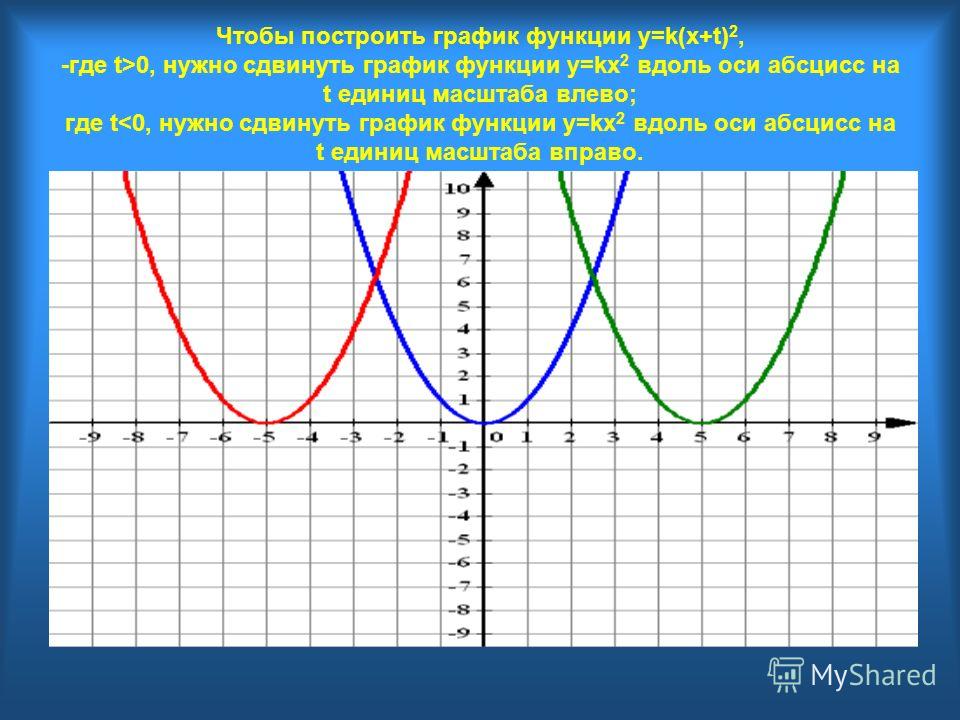
- Если [latex] b> 1 [/ latex], то график будет сжат с помощью [latex] \ frac {1} {b} [/ latex].
- Если [latex] 0
- Если [латекс] b <0 [/ латекс], то будет комбинация горизонтального растяжения или сжатия с горизонтальным отражением.
Как сделать: учитывая описание функции, нарисуйте горизонтальное сжатие или растяжение.
- Напишите формулу для представления функции.
- Установите [латекс] g \ left (x \ right) = f \ left (bx \ right) [/ latex], где [latex] b> 1 [/ latex] для сжатия или [латекс] 0 для растяжки.
Пример: построение графика горизонтального сжатия
Предположим, ученый сравнивает популяцию плодовых мух с популяцией, продолжительность жизни которой увеличивается вдвое быстрее, чем исходная популяция. Другими словами, эта новая популяция, [latex] R [/ latex], будет прогрессировать за 1 час на ту же величину, что и исходная популяция за 2 часа, а через 2 часа она будет прогрессировать так же, как и исходная популяция в 4 часа. Нарисуйте график этой популяции.
Нарисуйте график этой популяции.
Условно мы могли бы написать
[латекс] \ begin {align} & R \ left (1 \ right) = P \ left (2 \ right), \\ & R \ left (2 \ right) = P \ left (4 \ right), \ text { и в общем случае} \\ & R \ left (t \ right) = P \ left (2t \ right).\ end {align} [/ latex]
См. Ниже графическое сравнение исходной и сжатой совокупностей.
(a) Исходный график населения (b) Сжатый график населения
Анализ решения
Обратите внимание, что эффект на графике представляет собой сжатие по горизонтали, когда все входные значения составляют половину их исходного расстояния от вертикальной оси.
Пример: поиск горизонтального растяжения для табличной функции
Функция [латекс] f \ left (x \ right) [/ latex] приведена ниже.Создайте таблицу для функции [латекс] g \ left (x \ right) = f \ left (\ frac {1} {2} x \ right) [/ latex].
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] f \ слева (x \ справа) [/ латекс] | 1 | 3 | 7 | 11 |
Формула [латекс] g \ left (x \ right) = f \ left (\ frac {1} {2} x \ right) [/ latex] сообщает нам, что выходные значения для [latex] g [/ latex] такие же, как выходные значения для функции [latex] f [/ latex] на входе вдвое меньшего размера.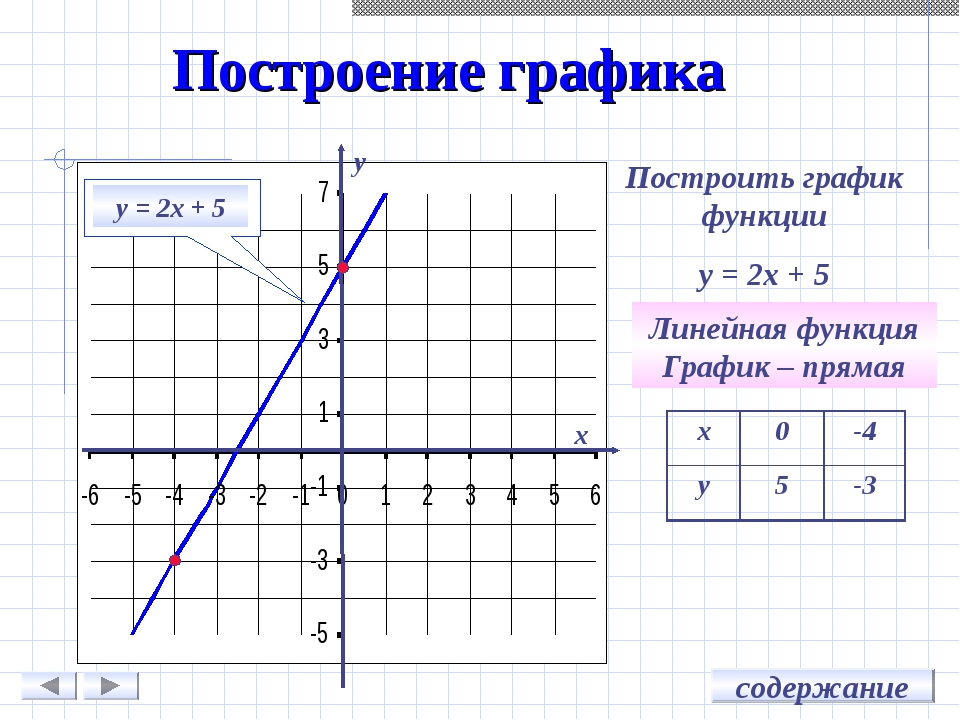 Обратите внимание, что у нас недостаточно информации, чтобы определить [латекс] g \ left (2 \ right) [/ latex], потому что [latex] g \ left (2 \ right) = f \ left (\ frac {1} {2} \ cdot 2 \ right) = f \ left (1 \ right) [/ latex], и у нас нет значения для [latex] f \ left (1 \ right) [/ latex] в нашей таблице. Наши входные значения для [latex] g [/ latex] должны быть вдвое больше, чтобы получить входные данные для [latex] f [/ latex], которые мы можем оценить. Например, мы можем определить [латекс] g \ left (4 \ right) \ text {.} [/ Latex]
Обратите внимание, что у нас недостаточно информации, чтобы определить [латекс] g \ left (2 \ right) [/ latex], потому что [latex] g \ left (2 \ right) = f \ left (\ frac {1} {2} \ cdot 2 \ right) = f \ left (1 \ right) [/ latex], и у нас нет значения для [latex] f \ left (1 \ right) [/ latex] в нашей таблице. Наши входные значения для [latex] g [/ latex] должны быть вдвое больше, чтобы получить входные данные для [latex] f [/ latex], которые мы можем оценить. Например, мы можем определить [латекс] g \ left (4 \ right) \ text {.} [/ Latex]
[латекс] g \ left (4 \ right) = f \ left (\ frac {1} {2} \ cdot 4 \ right) = f \ left (2 \ right) = 1 [/ latex]
Мы делаем то же самое для других значений, чтобы получить таблицу ниже.
| [латекс] x [/ латекс] | 4 | 8 | 12 | 16 |
| [латекс] г \ левый (х \ правый) [/ латекс] | 1 | 3 | 7 | 11 |
На этом рисунке показаны графики обоих этих наборов точек.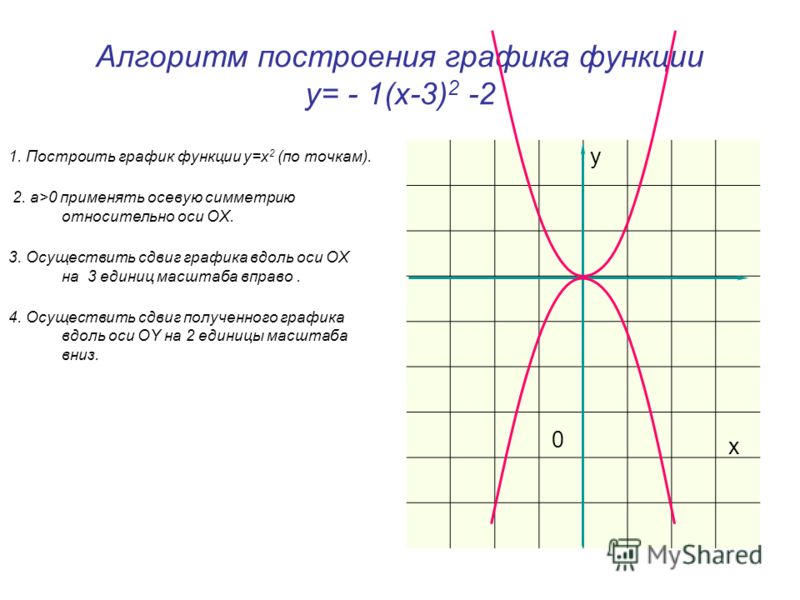
Анализ решения
Поскольку каждое входное значение было удвоено, в результате функция [latex] g \ left (x \ right) [/ latex] была растянута по горизонтали с коэффициентом 2.
Пример: распознавание горизонтального сжатия на графике
Свяжите функцию [латекс] g \ left (x \ right) [/ latex] с [латексом] f \ left (x \ right) [/ latex].
Показать решение График [латекса] g \ left (x \ right) [/ latex] выглядит как график [latex] f \ left (x \ right) [/ latex], сжатый по горизонтали. Поскольку [латекс] f \ left (x \ right) [/ latex] заканчивается на [latex] \ left (6,4 \ right) [/ latex] и [latex] g \ left (x \ right) [/ latex] заканчивается на [latex] \ left (2,4 \ right) [/ latex], мы видим, что значения [latex] x \ text {-} [/ latex] были сжаты с помощью [latex] \ frac {1} {3} [/ latex], потому что [latex] 6 \ left (\ frac {1} {3} \ right) = 2 [/ latex].Мы также можем заметить, что [латекс] g \ left (2 \ right) = f \ left (6 \ right) [/ latex] и [latex] g \ left (1 \ right) = f \ left (3 \ right) [/латекс]. В любом случае, мы можем описать это отношение как [латекс] g \ left (x \ right) = f \ left (3x \ right) [/ latex]. Это горизонтальное сжатие [латексом] \ frac {1} {3} [/ latex].
В любом случае, мы можем описать это отношение как [латекс] g \ left (x \ right) = f \ left (3x \ right) [/ latex]. Это горизонтальное сжатие [латексом] \ frac {1} {3} [/ latex].
Анализ решения
Обратите внимание, что коэффициент, необходимый для горизонтального растяжения или сжатия, является обратной величиной растяжения или сжатия. Итак, чтобы растянуть график по горизонтали с коэффициентом масштабирования 4, нам понадобится коэффициент [latex] \ frac {1} {4} [/ latex] в нашей функции: [latex] f \ left (\ frac {1} { 4} х \ справа) [/ латекс].Это означает, что входные значения должны быть в четыре раза больше, чтобы получить тот же результат, требуя, чтобы входные значения были больше, вызывая горизонтальное растяжение.
Попробуйте
Напишите формулу для функции извлечения квадратного корня из набора инструментов, растянутой по горизонтали в 3 раза.
Показать решение[латекс] g \ left (x \ right) = \ sqrt {\ frac {1} {3} x} [/ latex]
Последовательности преобразований
Теперь, когда у нас есть две трансформации, мы можем объединить их вместе.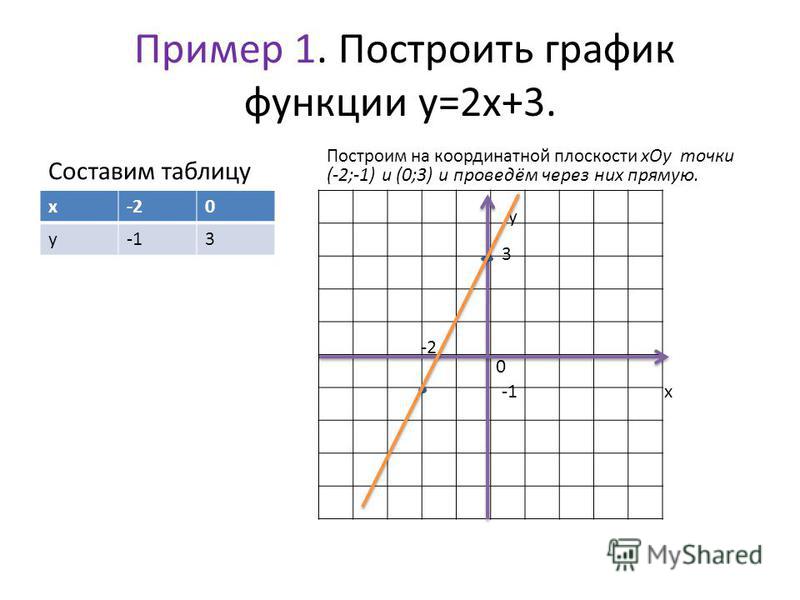 Вертикальные сдвиги — это внешние изменения, которые влияют на значения оси вывода ([latex] y \ text {-} [/ latex]) и сдвигают функцию вверх или вниз.Горизонтальные сдвиги — это внутренние изменения, которые влияют на значения оси ввода ([latex] x \ text {-} [/ latex]) и сдвигают функцию влево или вправо. Комбинация двух типов сдвигов приведет к смещению графика функции вверх или вниз на и вправо или влево.
Вертикальные сдвиги — это внешние изменения, которые влияют на значения оси вывода ([latex] y \ text {-} [/ latex]) и сдвигают функцию вверх или вниз.Горизонтальные сдвиги — это внутренние изменения, которые влияют на значения оси ввода ([latex] x \ text {-} [/ latex]) и сдвигают функцию влево или вправо. Комбинация двух типов сдвигов приведет к смещению графика функции вверх или вниз на и вправо или влево.
Как сделать: для функции и сдвига по вертикали и горизонтали нарисуйте график.
- Определите вертикальный и горизонтальный сдвиги по формуле.
- Вертикальный сдвиг является результатом добавления константы к выходу.Переместите график вверх для положительной константы и вниз для отрицательной константы.
- Горизонтальный сдвиг является результатом добавления константы ко входу. Переместите график влево для положительной константы и вправо для отрицательной константы.
- Примените сдвиги к графику в любом порядке.
Пример: построение графика комбинированных вертикальных и горизонтальных смещений
Дано [латекс] f \ left (x \ right) = | x | [/ latex], нарисуйте график [латекса] h \ left (x \ right) = f \ left (x + 1 \ right) -3 [/латекс].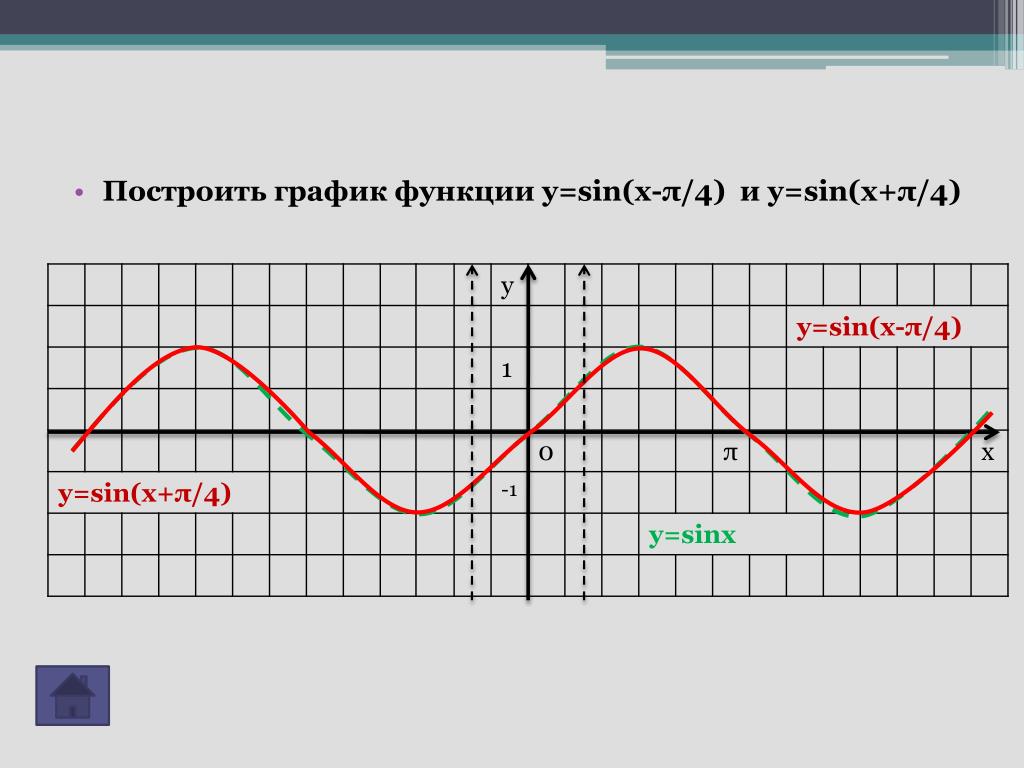
Функция [latex] f [/ latex] — это функция абсолютного значения нашего инструментария. Мы знаем, что этот график имеет V-образную форму с точкой в начале координат. График [latex] h [/ latex] трансформировал [latex] f [/ latex] двумя способами: [latex] f \ left (x + 1 \ right) [/ latex] — это изменение внутри функция, дающая горизонтальный сдвиг влево на 1, и вычитание на 3 в [латексе] f \ left (x + 1 \ right) -3 [/ latex] — это изменение за пределы функции, дающее вертикальный сдвиг вниз на 3. Преобразование графа проиллюстрировано ниже.
Давайте проследим одну точку графика [латекс] f \ left (x \ right) = | x | [/ latex].
- Точка [latex] \ left (0,0 \ right) [/ latex] преобразуется первой сдвигом влево на 1 единицу: [latex] \ left (0,0 \ right) \ to \ left (-1,0 \ справа) [/ латекс]
- Точка [латекс] \ left (-1,0 \ right) [/ latex] преобразуется следующей сдвигом вниз на 3 единицы: [latex] \ left (-1,0 \ right) \ to \ left (-1, -3 \ вправо) [/ латекс]
Ниже приведен график [латекс] ч [/ латекс].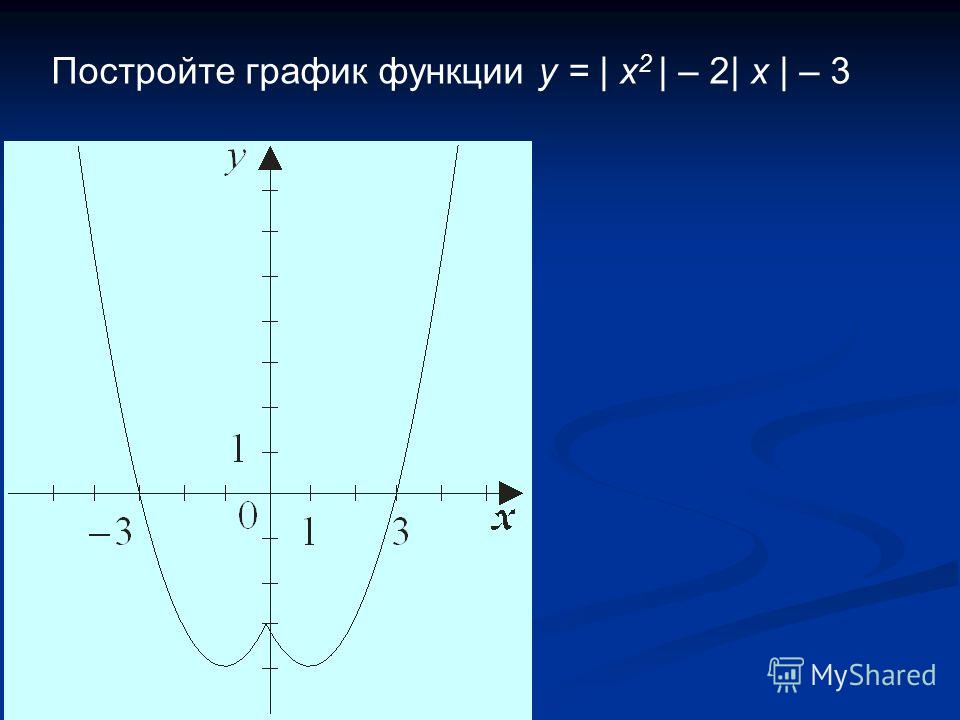
Попробуйте
Дано [латекс] f \ left (x \ right) = | x | [/ latex], нарисуйте график [латекса] h \ left (x \ right) = f \ left (x — 2 \ right) +4 [/латекс].
Проверьте свою работу с помощью онлайн-графического инструмента.
Показать решениеПример: определение комбинированных вертикальных и горизонтальных смещений
Напишите формулу для графика, показанного ниже, который является преобразованием функции извлечения квадратного корня из набора инструментов.
Показать решениеГрафик функции инструментария начинается с начала координат, поэтому этот график был сдвинут на 1 вправо и вверх 2. В обозначении функции мы могли бы записать это как
[латекс] h \ left (x \ right) = f \ left (x — 1 \ right) +2 [/ латекс]
Используя формулу для функции извлечения квадратного корня, мы можем написать
[латекс] h \ left (x \ right) = \ sqrt {x — 1} +2 [/ латекс]
Анализ решения
Обратите внимание, что это преобразование изменило домен и диапазон функции. {- t} +1 [/ latex], где [latex] k [/ latex] — это процент мастерства, который может быть достигнут после практических занятий [латекс] т [/ латекс].{-t} +1 [/ латекс]
{- t} +1 [/ latex], где [latex] k [/ latex] — это процент мастерства, который может быть достигнут после практических занятий [латекс] т [/ латекс].{-t} +1 [/ латекс]
Мы можем нарисовать график, применяя эти преобразования по одному к исходной функции. Давайте проследим по двум пунктам через каждое из трех преобразований. Выберем точки [латекс] (0, 1) [/ латекс] и [латекс] (1, 2) [/ латекс].
- Сначала мы применяем горизонтальное отражение: [latex] (0, 1) (–1, 2) [/ latex].
- Затем мы применяем вертикальное отражение: [latex] (0, −1) (1, –2) [/ latex].
- Наконец, мы применяем вертикальный сдвиг: [latex] (0, 0) (1, 1) [/ latex].
Это означает, что исходные точки [latex] (0,1) [/ latex] и [latex] (1,2) [/ latex] становятся [latex] (0,0) [/ latex] и [latex] ] (1,1) [/ latex] после применения преобразований.
На графиках ниже первый график является результатом горизонтального отражения. Второй результат вертикального отражения.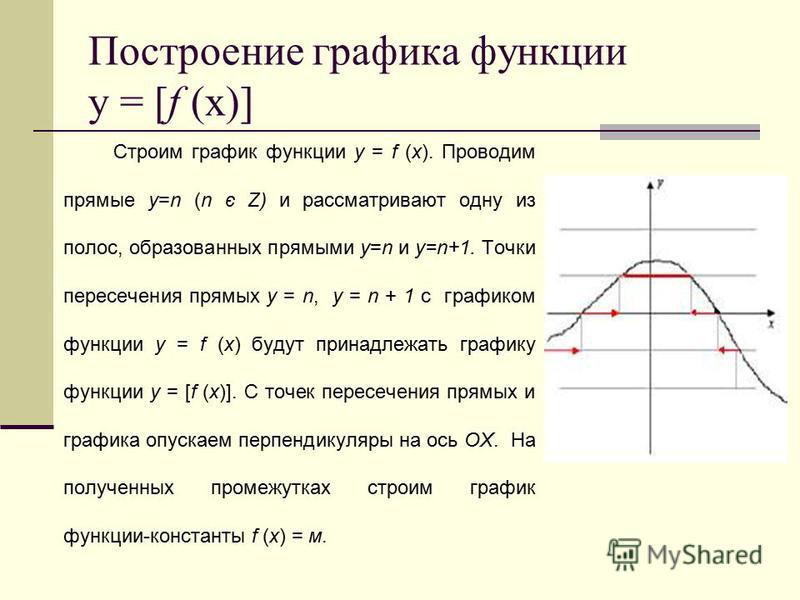 Третий результат вертикального смещения на 1 единицу.
Третий результат вертикального смещения на 1 единицу.
Анализ решения
В качестве модели для обучения эта функция будет ограничена доменом [latex] t \ ge 0 [/ latex] с соответствующим диапазоном [latex] \ left [0,1 \ right) [/ latex].{2} [/ латекс], граф [латекс] g \ left (x \ right) = — f \ left (x \ right) [/ latex] и [латекс] h \ left (x \ right) = f \ left (-x \ вправо) [/ латекс]. Обратите внимание на любое неожиданное поведение этих функций.
Показать решениеПримечание: [latex] g (x) = f (−x) [/ latex] выглядит так же, как [latex] f (x) [/ latex].
Комбинировать сдвиги и растяжки
При объединении преобразований очень важно учитывать порядок преобразований. Например, вертикальный сдвиг на 3, а затем вертикальное растяжение на 2 не создает такой же график, как вертикальное растяжение на 2, а затем вертикальный сдвиг на 3, потому что, когда мы сначала сдвигаем, как исходная функция, так и сдвиг растягиваются, в то время как только исходная функция растягивается, когда мы сначала растягиваем.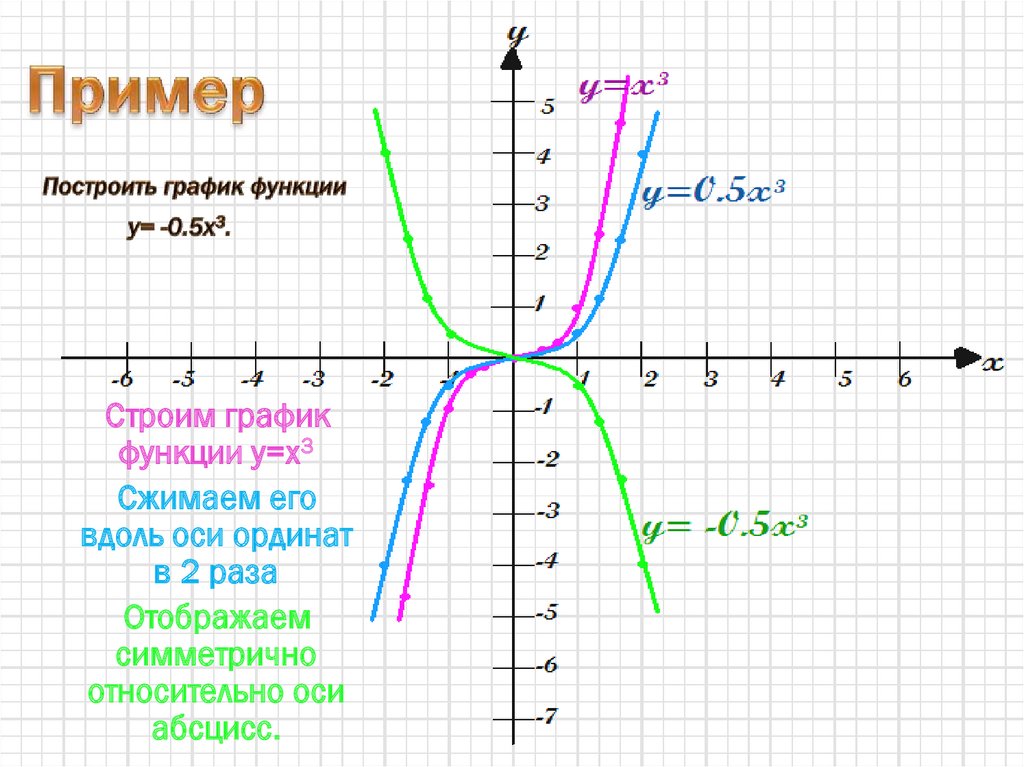
Когда мы видим такое выражение, как [latex] 2f \ left (x \ right) +3 [/ latex], с какого преобразования мы должны начать? Ответ здесь хорошо следует из порядка операций. Учитывая выходное значение [latex] f \ left (x \ right) [/ latex], мы сначала умножаем на 2, вызывая вертикальное растяжение, а затем прибавляем 3, вызывая вертикальный сдвиг. Другими словами, умножение перед сложением.
Горизонтальные преобразования немного сложнее. Когда мы пишем [latex] g \ left (x \ right) = f \ left (2x + 3 \ right) [/ latex], например, мы должны думать о том, как входные данные функции [latex] g [/ latex] относятся к входам функции [latex] f [/ latex].Предположим, мы знаем [латекс] f \ left (7 \ right) = 12 [/ latex]. Какой ввод в [latex] g [/ latex] будет производить этот вывод? Другими словами, какое значение [latex] x [/ latex] позволит [latex] g \ left (x \ right) = f \ left (2x + 3 \ right) = 12 [/ latex]? Нам понадобится [латекс] 2x + 3 = 7 [/ латекс]. Чтобы найти [latex] x [/ latex], мы сначала вычтем 3, что приведет к сдвигу по горизонтали, а затем разделим на 2, что приведет к сжатию по горизонтали.
С этим форматом очень сложно работать, потому что обычно намного проще растянуть график по горизонтали перед смещением.{2} [/ латекс]
Теперь мы можем более отчетливо наблюдать сдвиг по горизонтали влево на 2 единицы и сжатие по горизонтали. Факторинг таким образом позволяет нам сначала растянуть по горизонтали, а затем сместиться по горизонтали.
Общее примечание: объединение преобразований
При объединении вертикальных преобразований, записанных в форме [latex] af \ left (x \ right) + k [/ latex], сначала растяните по вертикали на [latex] a [/ latex], а затем сдвиньте по вертикали на [latex] k [/ латекс].
При объединении горизонтальных преобразований, записанных в форме [латекс] f \ left (bx + h \ right) [/ latex], сначала сдвиньте по горизонтали на [latex] h [/ latex], а затем растяните по горизонтали на [latex] \ frac { 1} {b} [/ латекс].
При объединении горизонтальных преобразований, записанных в форме [латекс] f \ left (b \ left (x + h \ right) \ right) [/ latex], сначала растяните по горизонтали на [латекс] \ frac {1} {b} [ / latex], а затем сдвинуть по горизонтали на [latex] h [/ latex].
Горизонтальные и вертикальные преобразования независимы. Не имеет значения, какие преобразования выполняются в первую очередь: по горизонтали или по вертикали.
Пример: поиск тройного преобразования табличной функции
Учитывая приведенную ниже таблицу для функции [latex] f \ left (x \ right) [/ latex], создайте таблицу значений для функции [latex] g \ left (x \ right) = 2f \ left (3x \ справа) +1 [/ латекс].
| [латекс] x [/ латекс] | 6 | 12 | 18 | 24 |
| [латекс] f \ слева (x \ справа) [/ латекс] | 10 | 14 | 15 | 17 |
Это преобразование состоит из трех этапов, и мы будем работать изнутри. Начиная с горизонтальных преобразований, [latex] f \ left (3x \ right) [/ latex] — это горизонтальное сжатие с помощью [latex] \ frac {1} {3} [/ latex], что означает, что мы умножаем каждый [латекс] x \ text {-} [/ latex] значение [latex] \ frac {1} {3} [/ latex].
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] f \ слева (3x \ справа) [/ латекс] | 10 | 14 | 15 | 17 |
Теперь рассмотрим вертикальные преобразования, мы начнем с вертикального растяжения, которое умножит выходные значения на 2. Мы применяем это к предыдущему преобразованию.
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] 2f \ left (3x \ right) [/ латекс] | 20 | 28 | 30 | 34 |
Наконец, мы можем применить вертикальный сдвиг, который добавит 1 ко всем выходным значениям.
| [латекс] x [/ латекс] | 2 | 4 | 6 | 8 |
| [латекс] g \ left (x \ right) = 2f \ left (3x \ right) +1 [/ латекс] | 21 | 29 | 31 | 35 |
Пример: поиск тройного преобразования графа
Используйте график [латекс] f \ left (x \ right) [/ latex], чтобы нарисовать график [латекса] k \ left (x \ right) = f \ left (\ frac {1} {2} x +1 \ вправо) -3 [/ латекс].
Показать решениеДля упрощения давайте начнем с выделения внутренней части функции.
[латекс] f \ left (\ frac {1} {2} x + 1 \ right) -3 = f \ left (\ frac {1} {2} \ left (x + 2 \ right) \ right) — 3 [/ латекс]
Факторизуя внутреннюю часть, мы можем сначала растянуть по горизонтали на 2, на что указывает [latex] \ frac {1} {2} [/ latex] внутри функции. Помните, что удвоенный размер 0 по-прежнему равен 0, поэтому точка [latex] (0,2) [/ latex] остается в [latex] (0,2) [/ latex], а точка [latex] (2,0 ) [/ latex] растянется до [latex] (4,0) [/ latex].
Затем мы сдвигаем по горизонтали влево на 2 единицы, как показано [latex] x + 2 [/ latex].
Наконец, мы сдвигаемся по вертикали на 3, чтобы завершить наш эскиз, на что указывает [latex] -3 [/ latex] снаружи функции.
Ключевые уравнения
Ключевые понятия
- Функцию можно сдвинуть по вертикали, добавив к выходу константу.
- Функцию можно сдвинуть по горизонтали, добавив к входу константу.
- Связывание сдвига с контекстом проблемы позволяет сравнивать и интерпретировать вертикальные и горизонтальные сдвиги.
- Вертикальный и горизонтальный сдвиги часто сочетаются.
- Вертикальное отражение отражает график относительно оси [latex] x \ text {-} [/ latex]. График можно отразить вертикально, умножив результат на –1.
- Горизонтальное отражение отражает график относительно оси [latex] y \ text {-} [/ latex].График можно отразить по горизонтали, умножив входные данные на –1.
- График можно отображать как по вертикали, так и по горизонтали. Порядок, в котором применяются отражения, не влияет на окончательный график.
- Функция, представленная в табличной форме, также может быть отражена путем умножения значений во входных и выходных строках или столбцах соответственно.
- Функцию, представленную в виде уравнения, можно отразить, применяя преобразования по одному.
- Четные функции симметричны относительно оси [latex] y \ text {-} [/ latex], тогда как нечетные функции симметричны относительно начала координат.
- Четные функции удовлетворяют условию [латекс] f \ left (x \ right) = f \ left (-x \ right) [/ latex].
- Нечетные функции удовлетворяют условию [латекс] f \ left (x \ right) = — f \ left (-x \ right) [/ latex].
- Функция может быть нечетной, четной или ни одной.
- Функцию можно сжать или растянуть по вертикали, умножив результат на константу.
- Функция может быть сжата или растянута по горизонтали путем умножения входных данных на константу.
- Порядок применения различных преобразований влияет на конечную функцию.И вертикальные, и горизонтальные преобразования должны применяться в указанном порядке. Однако вертикальное преобразование можно комбинировать с горизонтальным преобразованием в любом порядке.
Глоссарий
- четная функция
- функция, график которой не изменяется из-за горизонтального отражения, [латекс] f \ left (x \ right) = f \ left (-x \ right) [/ latex], и симметричен относительно [латекса] y \ text {- } [/ latex] ось
- горизонтальное сжатие
- преобразование, которое сжимает график функции по горизонтали путем умножения входных данных на константу [latex] b> 1 [/ latex]
- горизонтальное отражение
- преобразование, которое отражает график функции по оси y путем умножения входных данных на [latex] -1 [/ latex]
- сдвиг по горизонтали
- преобразование, которое сдвигает график функции влево или вправо путем добавления положительной или отрицательной константы ко входу
- горизонтальная растяжка
- преобразование, которое растягивает график функции по горизонтали путем умножения входных данных на константу [latex] 0
- нечетная функция
- функция, график которой не изменяется в результате комбинированного горизонтального и вертикального отражения, [латекс] f \ left (x \ right) = — f \ left (-x \ right) [/ latex], и симметричен относительно начала координат
- вертикальное сжатие
- преобразование функции, которое сжимает график функции по вертикали путем умножения выходных данных на константу [latex] 0
- вертикальное отражение
- преобразование, которое отражает график функции по оси x путем умножения выходных данных на [latex] -1 [/ latex]
- сдвиг по вертикали
- преобразование, которое сдвигает график функции вверх или вниз путем добавления положительной или отрицательной константы к выходным данным
- растяжка по вертикали
- преобразование, которое растягивает график функции по вертикали путем умножения результата на константу [latex] a> 1 [/ latex]
Логарифмические функции и их графики
4.2 — Логарифмические функции и их графикиФункция, обратная экспоненциальной функции
В разделе об экспоненциальных функциях мы утверждали, что экспоненциальные функции взаимно однозначны. Один к одному функции обладали тем особенным свойством, что они имели обратные это тоже функции. И, как многие из вас говорили в классе, и я так рад, что вы помните, функции «один-к-одному» могут применяться к обеим сторонам уравнения. Они также проходят горизонтальная линия тест.
Этот раздел посвящен обратной экспоненциальной функция.Обратной к экспоненциальной функции является логарифмическая функция. Помните, что обратное Функция получается переключением координат x и y. Это отражает график относительно прямой y = x. Как видно из графика справа, логарифмическая кривая является отражением экспоненциальной кривой.
В таблице ниже показано, как значения x и y точек экспоненциальной кривую можно переключить, чтобы найти координаты точек на логарифмической изгиб.
| Точка на экспоненциальной кривой | Соответствующая точка на логарифмической кривой |
|---|---|
| (-3, 1/8) | (1/8, -3) |
| (-2, 1/4) | (1/4, -2) |
| (-1, 1/2) | (1/2, -1) |
| (0, 1) | (1, 0) |
| (1, 2) | (2, 1) |
| (2, 4) | (4, 2) |
| (3, 8) | (8, 3) |
Сравнение экспоненциальных и логарифмических функций
Давайте посмотрим на некоторые свойства из двух функций.
Стандартная форма логарифмической функции: y = log a x
Обратите внимание: если «a» в приведенном выше выражении не является нижним индексом (ниже, чем «журнал»), тогда вам нужно обновить веб-браузер.
Рабочее определение логарифма
В экспоненциальной функции x был показателем.Назначение обратной функции — чтобы сообщить вам, какое значение x использовалось, когда вы уже знаете значение y. Итак, цель логарифм должен сказать вам показатель степени.
Таким образом, наше простое определение логарифма состоит в том, что это показатель степени.
Другой способ взглянуть на выражение «log a x» — это «до какой степени (экспоненты) нужно возвести получить х? «
Эквивалентные формы
Логарифмическая форма уравнения y = log a x эквивалентна экспоненциальной форме x = a y .
Чтобы переписать одну форму в другую, оставьте основу такой же и поменяйте сторону с двумя другими значения.
Свойства логарифмов
- журнал a 1 = 0, потому что 0 = 1
- Независимо от основания, если оно допустимо, логарифм 1 всегда равен 0. Это потому что логарифмические кривые всегда проходят через (1,0)
- log a a = 1, потому что a 1 = a
- Любое значение, возведенное в первую степень, означает, что такое же значение.
- журнал a a x = x
- Логарифмическое основание x и степень x являются обратными функциями. Всякий раз, когда обратный функции применяются друг к другу, они инвертируются, и вы остаетесь с в аргумент, в данном случае x.
- log a x = log a y означает, что x = y
- Если два бревна с одинаковым основанием равны, то аргументы должны быть равны.
- log a x = log b x означает, что a = b
- Если два логарифма с одним и тем же аргументом равны, то основания должны быть равны.
Обычная и натуральная бревна
На вашем калькуляторе есть две кнопки логарифма. Один помечен как «журнал» и другой отмечен «пер». Ни в одном из них нет записанной базы. Базу можно определить, однако, глядя на обратную функцию, которая написана над ключом и доступ осуществляется с помощью ключа 2 nd .
Десятичный логарифм (основание 10)
Когда вы видите записанный «журнал» без базы, предположите, что база равна 10.
То есть: журнал x = журнал 10 x.
Некоторые приложения, в которых используются десятичные логарифмы, относятся к pH (для измерения кислотности), децибелам. (интенсивность звука), шкала Рихтера (землетрясения).
Интересное (возможно) примечание о pH. «Глава 50: Канализация» деревни Кодекса Форсайта запрещает сброс отходов с pH ниже 5,5 или выше 10,5 (раздел 50.07).
Общие журналы служат и для другой цели. Каждое увеличение десятичного логарифма на единицу является результатом 10-кратного аргумента.То есть землетрясение силой 6,3 балла имеет 10 раз больше 5.3 землетрясение. Уровень децибел громкой рок-музыки или бензопилы (115 децибел = 11,5 бел) в 10 раз громче, чем цыплята внутри здания (105 децибел = 10,5 бел)
Натуральные логарифмы (основание е)
Помните тот номер e , который у нас был из предыдущего раздела? Вы знаете, тот, который был приблизительно 2,718281828 (но не повторяется и не прерывается). Это основа для естественного логарифм.
Когда вы видите написанное «ln», это означает, что основание — e .
То есть: ln x = log e x
Модели экспоненциального роста и спада — это одно приложение, в котором используются натуральные логарифмы. Этот включает непрерывное соединение, радиоактивный распад (период полураспада), рост населения. Обычно приложения, в которых процесс происходит постоянно. Теперь эти приложения были первыми упомянутые в экспоненциальном разделе, но вы сможете решить для других переменных вовлечены (после раздела 4) с использованием логарифмов.
В математике более высокого уровня натуральный логарифм является предпочтительным логарифмом. Есть несколько специальные свойства функции натурального логарифма и ее обратной функции, которые делают жизнь очень проще в исчислении.
Поскольку «ln x» и « e x » являются обратными функциями друг друга, каждый раз, когда «ln» и «e» появляются справа рядом друг с другом, между ними абсолютно ничего нет (то есть, когда они составлены друг с другом), затем они инвертируются, и вы остаетесь с Аргумент.
1.5 Экспоненциальные и логарифмические функции — Исчисление Том 1
Цели обучения
- Определите форму экспоненциальной функции.
- Объясните разницу между графиками и.
- Осознайте значение числа.
- Определите форму логарифмической функции.
- Объясните связь между экспоненциальными и логарифмическими функциями.
- Опишите, как вычислить логарифм с различным основанием.
- Определите гиперболические функции, их графики и основные тождества.
В этом разделе мы исследуем экспоненциальные и логарифмические функции. Мы используем свойства этих функций для решения уравнений, включающих экспоненциальные или логарифмические члены, и изучаем значение и важность числа. Мы также определяем гиперболические и обратные гиперболические функции, которые включают комбинации экспоненциальных и логарифмических функций. (Обратите внимание, что мы представляем альтернативные определения экспоненциальных и логарифмических функций в главе «Применение интеграций» и доказываем, что функции имеют одинаковые свойства в обоих определениях.)
Экспоненциальные функции возникают во многих приложениях. Один из распространенных примеров — рост населения.
Например, если популяция начинается с особей, а затем растет с ежегодной скоростью, ее популяция через 1 год составляет
.Население через 2 года —
человек. .В целом его население по прошествии лет
,, которая является экспоненциальной функцией. В более общем смысле, любая функция вида, где, является экспоненциальной функцией с основанием и экспонентой .Показательные функции имеют постоянные основания и переменные показатели. Обратите внимание, что функция формы для некоторой константы — это не экспоненциальная функция, а степенная функция.
Чтобы увидеть разницу между экспоненциальной функцией и степенной функцией, мы сравним функции и. На (Рисунок) мы видим, что оба и приближаются к бесконечности как. В конце концов, однако, становится больше чем и растет быстрее, чем. В обратном направлении, как, тогда как. Прямая — горизонтальная асимптота для.
На (рис.) Мы построили график обоих, чтобы показать, как графики различаются.
Оценка экспоненциальных функций
Напомним свойства показателя степени: если это положительное целое число, то мы определяем (с множителем). Если это отрицательное целое число, то для некоторого положительного целого числа и мы определяем. Кроме того, определяется как 1. Если — рациональное число, то, где и — целые числа и. Например, . Однако как определяется, если является иррациональным числом? Например, что мы подразумеваем под? Это слишком сложный вопрос, чтобы мы могли полностью ответить прямо сейчас; однако мы можем сделать приближение.На (Рисунок) мы перечисляем некоторые подходящие рациональные числа, а также представлены значения для каждого рационального числа. Мы утверждаем, что если мы выбираем рациональные числа, которые становятся все ближе и ближе к, значения становятся все ближе и ближе к некоторому числу. Мы определяем это число как.
| 1,4 | 1,41 | 1,414 | 1,4142 | 1,41421 | 1.414213 | |
| 2,639 | 2.65737 | 2,66475 | 2,665119 | 2,665138 | 2,665143 |
Рост бактерий
Решение
Количество бактерий через 6 часов определяется бактериями. Количество бактерий через 10 часов определяется бактериями. Количество бактерий через 24 часа определяется бактериями.
Учитывая экспоненциальную функцию, вычислить и.
Решение
.
Особый тип экспоненциальной функции часто появляется в реальных приложениях. Чтобы описать это, рассмотрим следующий пример экспоненциального роста, который возникает из-за начисления сложных процентов на сберегательный счет. Предположим, человек вкладывает доллары на сберегательный счет с годовой процентной ставкой, начисляемой ежегодно. Сумма денег через 1 год
.Сумма денег через 2 года
.В более общем плане сумма по прошествии лет составляет
.Если деньги накапливаются 2 раза в год, сумма денег через полгода составляет
.Сумма денег через 1 год
.По прошествии лет количество денег на счету
.В более общем плане, если деньги накапливаются раз в год, сумма денег на счете через несколько лет определяется функцией
.Что происходит как? Чтобы ответить на этот вопрос, допустим и пишем
,и изучите поведение as, используя таблицу значений ((рисунок)).
| 10 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 | |
| 2,5937 | 2,7048 | 2,71692 | 2,71815 | 2,718268 | 2,718280 |
Глядя на эту таблицу, кажется, что число приближается к числу от 2,7 до 2,8 как. На самом деле, действительно приближается к некоторому числу как.Мы звоним по этому номеру. С точностью до шести знаков после запятой,
.Буква была впервые использована для обозначения этого числа швейцарским математиком Леонардом Эйлером в 1720-х годах. Хотя Эйлер не открыл число, он показал много важных связей между логарифмическими функциями. Мы по-прежнему используем эти обозначения в честь работы Эйлера, потому что она встречается во многих областях математики и потому, что мы можем использовать ее во многих практических приложениях.
Возвращаясь к нашему примеру со сберегательным счетом, мы можем заключить, что если человек кладет доллары на счет с годовой процентной ставкой, непрерывно начисляемой, то тогда.Эта функция может быть вам знакома. Так как функции, связанные с базой, часто возникают в приложениях, мы называем функцию естественной экспоненциальной функцией . Эта функция интересна не только из-за определения числа, но также, как обсуждается далее, ее график имеет важное свойство.
Так как мы знаем, увеличивается. На (Рисунок) мы показываем график вместе с касательной линии к графику at. Мы дадим точное определение касательной в следующей главе; но неформально мы говорим, что касательная линия к графику at — это линия, которая проходит через точку и имеет тот же «наклон», что и в этой точке.Функция является единственной экспоненциальной функцией с касательной, имеющей наклон 1. Как мы увидим позже в тексте, наличие этого свойства делает естественную экспоненциальную функцию простейшей экспоненциальной функцией для использования во многих случаях.
Рисунок 3. График имеет касательную с наклоном 1 при.Используя наше понимание экспоненциальных функций, мы можем обсудить их обратные, то есть логарифмические функции. Они пригодятся, когда нам нужно рассмотреть любое явление, которое варьируется в широком диапазоне значений, например pH в химии или децибелы в уровнях звука.
Показательная функция взаимно однозначна, с доменом и диапазоном. Следовательно, у него есть обратная функция, называемая логарифмической функцией с основанием . Для любого логарифмическая функция с основанием, обозначенная, имеет домен и диапазон и удовлетворяет
если и только если .Например,
Кроме того, поскольку и являются обратными функциями,
.Наиболее часто используемая логарифмическая функция — это функция. Поскольку в основе этой функции лежит натуральное число, она называется натуральным логарифмом .Здесь мы используем обозначения или для обозначения. Например,
.Поскольку функции и противоположны друг другу,
,и их графики симметричны относительно линии ((Рисунок)).
Рис. 4. Функции и инвертируются друг с другом, поэтому их графики симметричны относительно линии.На этом сайте вы можете увидеть пример десятичной логарифмической шкалы.
В общем, для любой базы функция симметрична относительно линии с функцией. Используя этот факт и графики экспоненциальных функций, мы построим графики функций для нескольких значений ((Рисунок)).
Рисунок 5: Графики показаны для.Прежде чем решать некоторые уравнения, включающие экспоненциальные и логарифмические функции, давайте рассмотрим основные свойства логарифмов.
Правило: свойства логарифмов
Если, и — любое действительное число, то
Решение уравнений с экспоненциальными функциями
Решите каждое из следующих уравнений относительно.
Решить.
Решение
Решение уравнений с логарифмическими функциями
Решите каждое из следующих уравнений относительно.
Решить.
Решение
Оценивая логарифмическую функцию с помощью калькулятора, вы могли заметить, что единственными вариантами являются или log, называемый десятичным логарифмом , или ln, который является натуральным логарифмом. Однако экспоненциальные функции и логарифмические функции могут быть выражены с помощью любого желаемого основания. Если вам нужно использовать калькулятор для вычисления выражения с другой базой, вы можете сначала применить формулы замены базы.Используя это изменение основания, мы обычно записываем данную экспоненциальную или логарифмическую функцию в терминах естественных экспоненциальных и натуральных логарифмических функций.
Проба
Для первой формулы замены базы мы начнем с использования степенного свойства логарифмических функций. Мы знаем это по любой базе. Следовательно,
.Кроме того, мы знаем, что и являются обратными функциями. Следовательно,
.Объединяя эти два последних равенства, мы заключаем, что.
Чтобы доказать второе свойство, покажем, что
.Пусть, а. Мы это покажем. По определению логарифмических функций мы знаем, что и. Из предыдущих уравнений мы видим, что
.Следовательно,. Поскольку экспоненциальные функции взаимно однозначны, мы можем заключить, что.
□
Пеленальные столики
Используйте вычислительную утилиту, чтобы выполнить расчет по формуле изменения базы, представленной ранее.
Решение
Используйте второе уравнение с и:
.
Используйте формулу замены базы и вычислительную утилиту для оценки.
Вступление к главе: Шкала Рихтера для землетрясений
Рисунок 6: (кредит: модификация работы Робба Ханнавакера, NPS)В 1935 году Чарльз Рихтер разработал шкалу (теперь известную как шкала Рихтера ) для измерения силы землетрясения. Шкала представляет собой логарифмическую шкалу с основанием 10, и ее можно описать следующим образом: Рассмотрим одно землетрясение с магнитудой по шкале Рихтера и второе землетрясение с магнитудой по шкале Рихтера. Предположим, это означает, что землетрясение магнитуды сильнее, но насколько оно сильнее, чем другое землетрясение? Одним из способов измерения интенсивности землетрясения является использование сейсмографа для измерения амплитуды сейсмических волн.Если — амплитуда, измеренная для первого землетрясения, и — это амплитуда, измеренная для второго землетрясения, то амплитуды и магнитуды двух землетрясений удовлетворяют следующему уравнению:
.Рассмотрим землетрясение силой 8 баллов по шкале Рихтера и землетрясение силой 7 баллов по шкале Рихтера. Затем
.Следовательно,
,, что подразумевает или. Поскольку это в 10 раз больше, мы говорим, что первое землетрясение в 10 раз сильнее второго землетрясения.С другой стороны, если одно землетрясение силой 8 баллов по шкале Рихтера, а другое — 6 баллов, то относительная интенсивность двух землетрясений удовлетворяет уравнению
.Следовательно,. То есть первое землетрясение в 100 раз сильнее второго.
Как мы можем использовать логарифмические функции для сравнения относительной силы землетрясения магнитудой 9 баллов в Японии в 2011 году и землетрясения магнитудой 7,3 на Гаити в 2010 году?
Решение
Чтобы сравнить землетрясения в Японии и на Гаити, мы можем использовать уравнение, представленное ранее:
.
Таким образом, и мы заключаем, что землетрясение в Японии было примерно в 50 раз сильнее землетрясения на Гаити.
Сравните относительную силу землетрясения магнитудой 8,4 балла и землетрясения магнитудой 7,4 балла.
Землетрясение магнитудой 8,4 примерно в 10 раз сильнее землетрясения магнитудой 7,4.
Гиперболические функции определены в терминах определенных комбинаций и. Эти функции естественным образом возникают в различных инженерных и физических приложениях, включая изучение волн на воде и колебаний упругих мембран.Другое распространенное использование гиперболической функции — это представление висящей цепи или троса, также известного как цепная связь ((рисунок)). Если мы введем систему координат так, чтобы нижняя точка цепи лежала вдоль оси -оси, мы можем описать высоту цепи в терминах гиперболической функции. Сначала мы определяем гиперболические функции.
Рис. 7. Форму нити шелка в паутине можно описать с помощью гиперболической функции. Такая же форма применяется к цепи или тросу, подвешенному на двух опорах только под собственным весом.(Источник: «Mtpaley», Wikimedia Commons)Определение
Гиперболический косинус
Гиперболический синус
Гиперболический тангенс
Гиперболический косеканс
Гиперболический секанс
Гиперболический котангенс
Имя cosh рифмуется со словом «гоша», тогда как имя sinh произносится как «cinch». Tanh , sech , csch и coth произносятся как tanch, seech, coseech и cotanch соответственно.
Используя определение и принципы физики, можно показать, что высота подвесной цепи, такой как показанная на (Рисунок), может быть описана функцией для определенных констант и.
Но почему эти функции называются гиперболическими функциями ? Чтобы ответить на этот вопрос, подумайте о количестве. Используя определение и, мы видим, что
.Это тождество является аналогом тригонометрического тождества. Здесь для заданного значения точка лежит на единичной гиперболе ((Рисунок)).
Рисунок 8 — Гипербола единиц.Обратные гиперболические функции
Из графиков гиперболических функций мы видим, что все они взаимно однозначны, кроме и. Если мы ограничим области определения этих двух функций интервалом, тогда все гиперболические функции взаимно однозначны, и мы сможем определить обратные гиперболические функции. Поскольку сами гиперболические функции включают экспоненциальные функции, обратные гиперболические функции включают логарифмические функции.
Определение
Обратные гиперболические функции
Давайте посмотрим, как вывести первое уравнение.Остальные следуют аналогичным образом. Предполагать . Тогда, и, по определению функции гиперболического синуса,. Следовательно,
.Умножая это уравнение на, получаем
.Это можно решить как квадратное уравнение с решением
.Так как единственное решение — это решение с положительным знаком. Применяя натуральный логарифм к обеим частям уравнения, мы заключаем, что
.Вычисление обратных гиперболических функций
Оцените каждое из следующих выражений.
Решение
Оценить.
Решение
.
Для следующих упражнений оцените указанные экспоненциальные функции, как указано, с точностью до двух значащих цифр после запятой.
Решение
а. 125 г. 2.24 с. 9,74
Решение
а. 0,01 б. 10000 с. 46,42
Для следующих упражнений сопоставьте экспоненциальное уравнение с правильным графиком.
Для следующих упражнений нарисуйте график экспоненциальной функции. Определите область, диапазон и горизонтальную асимптоту.
11.
Решение
Домен: все действительные числа, Диапазон:, Горизонтальная асимптота на
12.
13.
Решение
Домен: все действительные числа, Диапазон:, Горизонтальная асимптота на
14.
15.
Решение
Домен: все действительные числа, Диапазон:, Горизонтальная асимптота на
16.
17.
Решение
Домен: все действительные числа, Диапазон:, Горизонтальная асимптота на
Для следующих упражнений запишите уравнение в эквивалентной экспоненциальной форме.
18.
19.
Решение
20.
21.
Решение
22.
23
Решение
24.
25.
Решение
Для следующих упражнений запишите уравнение в эквивалентной логарифмической форме.
26.
27.
Решение
28.
29.
Решение
30.
31.
Решение
32.
33.
Решение
34.
35.
Решение
Для следующих упражнений используйте данные графики логарифмических функций, чтобы определить их область определения, диапазон и вертикальную асимптоту.
36.
38.
40.
В следующих упражнениях используйте свойства логарифмов, чтобы записать выражения в виде суммы, разности и / или произведения логарифмов.
42.
43.
Решение
44.
45.
Решение
46.
47.
Решение
Для следующих упражнений точно решите экспоненциальное уравнение.
48.
49.
Решение
50.
51.
Решение
52.
53.
Решение
54.
55.
Решение
Для следующих упражнений решите точно логарифмическое уравнение, если возможно.
56.
57.
Решение
58.
59
Решение
60.
61.
Решение
62.
63.
Решение
В следующих упражнениях используйте формулу замены основания и основание 10 или основание для вычисления заданных выражений. Ответьте в точной и приблизительной форме с округлением до четырех знаков после запятой.
64.
65.
Решение
66
67.
Решение
68.
69.
Решение
70. Перепишите следующие выражения в экспонентах и упростите.
а.
г.
г.
г.
71. [T] Число бактерий в культуре через несколько дней можно смоделировать с помощью функции. Определите количество присутствующих бактерий через 15 дней.
Решение
72. [T] Спрос (в миллионах баррелей) на нефть в богатой нефтью стране задается функцией, где — цена (в долларах) барреля нефти. Найдите требуемое количество нефти (с округлением до миллиона баррелей) при цене от 15 до 20 долларов.
73. [T] Накопленная сумма инвестиций в размере 100 000 долларов США, проценты по которым непрерывно складываются в течение многих лет, определяется как. Найдите сумму, накопленную за 5 лет.
Решение
Приблизительно 131 653 доллара будет накоплено за 5 лет.
74. [T] Инвестиции накапливаются ежемесячно, ежеквартально или ежегодно и задаются функцией, где — стоимость инвестиции в определенный момент времени, является первоначальным вложенным принципом, является годовой процентной ставкой и количество раз в год начисляются проценты.При годовой процентной ставке 3,5% и начальном принципе в 100 000 долларов найдите сумму, накопленную за 5 лет для начисляемых процентов: a. ежедневно, б., ежемесячно, в. ежеквартально и d. ежегодно.
Решение
я. а. pH = 8 б. База ii. а. pH = 3 б. Кислота iii. а. pH = 4 б. Кислота
76. [T] Йод-131 — радиоактивное вещество, которое распадается в соответствии с функцией, где — начальное количество пробы вещества в днях.Определите, за сколько времени (с точностью до ближайшего дня) разложится 95% количества.
78. [T] Сумма, накопленная после того, как 1000 долларов инвестируется в течение многих лет с процентной ставкой 4%, моделируется функцией.
- Найдите сумму, накопленную за 5 лет и 10 лет.
- Определите, сколько времени потребуется, чтобы первоначальные инвестиции утроились.
79. [T] Известно, что бактериальная колония, выращенная в лаборатории, удваивается за 12 часов.Предположим, что изначально присутствует 1000 бактерий.
- Используйте экспоненциальную функцию, чтобы определить значение, которое представляет собой скорость роста бактерий. Округлить до четырех знаков после запятой.
- Определите приблизительно, сколько времени нужно для роста 200 000 бактерий.
Решение
а. б. часы
80. [T] Популяция кроликов в заповеднике удваивается каждые 6 месяцев. Предположим, изначально было 120 кроликов.
- Используйте экспоненциальную функцию, чтобы определить константу скорости роста.Округлить до четырех знаков после запятой.
- Используйте функцию в части а. чтобы приблизительно определить, сколько времени нужно, чтобы поголовье кроликов достигло 3500.
81. [T] Землетрясение 1906 года в Сан-Франциско имело магнитуду 8,3 балла по шкале Рихтера. В то же время в Японии землетрясение магнитудой 4,9 нанесло лишь незначительный ущерб. Насколько приблизительно больше энергии было выделено землетрясением в Сан-Франциско, чем землетрясением в Японии?
Решение
Землетрясение в Сан-Франциско имело или в несколько раз больше энергии, чем землетрясение в Японии.
От Y = X до создания полной искусственной нейронной сети
В какой-то момент вы могли спросить себя: Каково происхождение параметров искусственных нейронных сетей? Для чего нужен вес? Что делать, если не используется предвзятость?
В этом руководстве мы решили ответить на эти вопросы, перейдя от самой простой искусственной нейронной сети (ИНС) к чему-то гораздо более сложному. Начнем с построения модели машинного обучения без параметров — Y = X .
Затем мы будем постепенно добавлять некоторые параметры в модель, пока не построим единственный нейрон. Этот нейрон заставлен принимать один или несколько входных сигналов. Затем математическое представление нейрона отображается в графическое представление. Соединив несколько нейронов, можно создать полную ИНС. После прочтения этого урока я надеюсь, что цель весов и смещения ясна.
Начиная с простейшей модели Y = X
Строительные блоки машинного обучения на самом деле довольно просты.Даже абсолютные новички могут построить базовую модель машинного обучения. Говоря о машинном обучении с учителем, его цель — найти (то есть изучить) функцию, которая сопоставляет набор входных данных и набор выходных данных. После завершения самого обучения функция должна возвращать правильные выходные данные для каждого заданного входа. Обсудим одну из простейших задач согласно данным, приведенным в следующей таблице.
Имеется 4 образцов. Каждый образец имеет один вход и один выход.После просмотра данных нам нужно будет подготовить функцию, которая будет возвращать правильный вывод для каждого заданного ввода с наименьшей возможной ошибкой. Посмотрев на данные, мы, очевидно, замечаем, что выход Y идентичен входному X . Если X равно 2, то Y также равно 2. Если X равно 4, Y также равно 4.
Итак, нам нужна функция, которая принимает один вход X и возвращает единственный выход. Этот выход идентичен входу.Без сомнения, функция F (X) = X . Для простоты мы можем заменить F (X) на Y . Итак, функция будет Y = X .
Расчет ошибок
После нахождения подходящей модели машинного обучения (т. Е. Функции) нам необходимо протестировать ее, чтобы определить, правильно ли она предсказывает выходные данные или есть ли ошибка. Мы можем использовать простую функцию ошибок, которая вычисляет абсолютную разницу между правильным выходом и прогнозируемым выходом в соответствии со следующим уравнением.Он просматривает выборки данных, вычисляет абсолютную разницу между правильными и предсказанными выходными данными для каждой выборки и, наконец, суммирует все абсолютные разности и возвращает ее в переменную error . Символ N, используемый в операторе суммирования, представляет количество выборок.
Детали расчетов приведены в следующей таблице. Согласно этой таблице, функция правильно спрогнозировала все выходные данные, и, таким образом, общая ошибка составляет 0 .ОТЛИЧНО. Но не забывайте, что мы работаем над одной из самых простых задач для абсолютных новичков. Прежде чем изменить проблему, чтобы усложнить ее, мне нужно задать вопрос. В каждой модели машинного обучения есть 2 основных этапа: обучение (т.е. обучение) и тестирование. Мы рассмотрели базовый этап тестирования. Но где шаг обучения? Обучались ли мы в предыдущей модели? Ответ: НЕТ .
Обучение означает, что в модели есть некоторые параметры, которые изучаются из данных на этапе обучения.Функция предыдущей модели ( Y = X ) не имеет параметров для изучения. Функция просто выравнивает входные X и выходные Y без промежуточных параметров, чтобы сбалансировать взаимосвязь. В этом случае шаг обучения отсутствует, поскольку модель не является параметрической. Непараметрический означает, что у модели нет параметров, которые можно было бы изучить на основе данных. Популярным примером непараметрических моделей машинного обучения являются K-ближайшие соседи (KNN).
Вес как константа
Уточнив, что нет параметра для изучения, мы можем внести простую модификацию в используемые данные.Новые данные приведены в следующей таблице. Уловили модификации? На самом деле это довольно просто. Каждый выход Y больше не равен входу X — теперь он удваивает вход, который составляет 2X . Мы все еще можем использовать предыдущую функцию ( Y = X ) для прогнозирования выходных данных и вычисления общей ошибки.
Подробные сведения о расчетах ошибок приведены в следующей таблице. Общая ошибка в этом случае не равна 0 , как в предыдущем примере, а ее значение составляет 14 .Наличие ошибки в данных означает, что функция модели не может правильно выполнить сопоставление между входом и выходом.
Чтобы уменьшить ошибку, мы должны внести некоторые изменения в эту функцию. Вопрос в том, каковы источники модификаций в этой функции ( Y = X ), которые могут уменьшить ошибку предсказания? У функции всего 2 переменных: X и Y . Один представляет вход, а другой — выход. Мы не можем изменить ни одно из них.В заключение, функция непараметрическая, поэтому нет возможности изменить ее, чтобы уменьшить ошибку.
Но еще не все потеряно! Если функция в настоящее время не имеет параметра, почему бы не добавить один или несколько параметров? Не стесняйтесь проектировать свою модель машинного обучения таким образом, чтобы уменьшить количество ошибок. Если вы обнаружите, что добавление чего-либо к функции решает проблему, начните добавлять это сразу.
В новых данных выход Y вдвое больше входного X .Но функция не изменилась, чтобы отразить это, и мы по-прежнему используем Y = X . Мы можем изменить функцию, сделав вывод Y равным 2X , а не X . Следующая функция будет Y = 2X . После использования этой функции общая ошибка прогноза рассчитывается в соответствии со следующей таблицей. Общая ошибка снова равна 0. КРАСИВЫЙ.
Станет ли наша модель параметрической после добавления 2 к функции? НЕТ. Модель по-прежнему непараметрическая.Параметрическая модель изучает значения некоторых параметров на основе данных. Здесь значение рассчитывается независимо от данных, поэтому модель по-прежнему непараметрическая. В предыдущей модели 2 умножено на X , но значение 2 не зависит от данных. В результате модель остается непараметрической.
Давайте изменим предыдущие данные согласно следующей таблице.
Поскольку этап обучения отсутствует, мы можем перейти к этапу тестирования, на котором вычисляется ошибка прогнозирования после вычисления прогнозируемых выходных данных на основе последней функции ( Y = 2X ).Суммарная ошибка рассчитывается согласно следующей таблице. Общая ошибка больше не 0 , а теперь 14 . Почему так случилось?
Модель, используемая для решения этой проблемы, была создана, когда выход Y вдвое больше входного ( 2X ). Теперь результат Y больше не равен 2X , а равен 3X . Итак, ожидается, что мы обнаружим увеличение ошибки. Чтобы устранить эту ошибку, мы должны изменить функцию модели, используя 3 вместо 2 .Новая функция будет Y = 3X .
Новая функция Y = 3X сделает полную ошибку для новых данных 0 . Но при работе с предыдущими данными, в которых Y просто двойное X , возникнет ошибка. Итак, работая с исходными данными, мы должны использовать 3 для умножения на X , чтобы получить общую ошибку 0 . Работая с предыдущими данными, нам пришлось изменить его на 2 .
Похоже, что мы должны сами менять модель каждый раз, когда меняются данные. Это утомительно. Но выход есть. Мы можем избежать использования констант в функции и заменить их переменными. Это алгебра — область использования переменных, а не констант.
Вес как переменная
Вместо того, чтобы использовать 2 в Y = 2X или 3 в Y = 3X , мы можем использовать переменную w в Y = wX .Значение переменной w рассчитывается на основе данных. Поскольку модель теперь включает переменную, значение которой рассчитывается на основе данных, модель теперь является параметрической. Поскольку модель является параметрической, теперь будет этап обучения, на котором вычисляется значение этой переменной (параметра). Этот параметр — вес нейрона в ИНС. Давайте посмотрим, как модель узнает значение 2 параметра w при использовании предыдущих данных, в которых Y равно 2X .Данные снова приведены ниже.
Процесс работает путем инициализации параметра w начальным значением, которое обычно выбирается случайным образом. Для каждого значения параметра рассчитывается общая ошибка. Основываясь на некоторых значениях параметра, мы можем решить, в каком направлении уменьшается ошибка, что помогает выбрать лучшее (оптимальное) значение параметра.
Оптимизация параметров
Предполагая, что мы выбрали начальное значение 1.5 для w , тогда наша текущая функция Y = 1,5X . Мы можем вычислить общую ошибку на основе этой функции в соответствии со следующей таблицей. Ошибка 8. Поскольку ошибка все еще существует, мы можем изменить значение параметра w .
Но мы не знаем, в каком направлении следует изменить значение параметра w . Я имею ввиду, что лучше? Стоит ли увеличивать или уменьшать значение такого параметра? Поскольку в настоящее время мы не знаем, мы можем выбрать любое значение, большее или меньшее, чем текущее значение 1.5 .
Если предположить, что новое значение параметра w теперь равно 0,5 , тогда новая функция будет Y = 0,5X . Мы можем вычислить общую ошибку на основе этой функции. Когда w = 0,5 , ошибка составляет 21 . По сравнению с общей ошибкой, когда мы использовали предыдущее значение параметра w = 1,5 , которое было 8 , ошибка увеличилась. Это признак того, что мы можем двигаться в неправильном направлении.Мы можем изменить значение параметра w на другое значение больше 1,5 и посмотреть, не стало ли лучше.
Если новое значение w = 2,5 , новая функция будет Y = 2,5X . На основе этой функции теперь рассчитывается общая ошибка в соответствии со следующей таблицей. Теперь ошибка составляет 7 , что лучше, чем в предыдущих двух случаях, когда параметр w был равен 1,5 и 0,5 . Итак, когда мы увеличили значение w , чем 1.5 , ошибка уменьшилась. Мы можем продолжить увеличивать значение w .
Предполагая, что новое значение для w равно 3 , новая функция будет иметь вид Y = 3X . Общая ошибка рассчитывается на основе этой функции согласно новой таблице. Ошибка теперь 14 . Ошибка теперь больше, чем раньше.
Чтобы лучше понять ситуацию, мы можем суммировать ранее выбранные значения параметра w и соответствующие им ошибки в следующей таблице.Область значений параметра w , которые могут уменьшить ошибку, ограничена между 1,5 и 2,5 . Мы можем выбрать одно из двух значений. Процесс продолжит тестирование других значений до тех пор, пока, наконец, не придет к выводу, что значение 2 является наилучшим значением, позволяющим достичь наименьшей возможной ошибки, то есть 0 . Наконец, функция будет иметь вид Y = wX , когда w = 2 .
Это для данных, в которых Y равно 2X .Когда Y равно 3X , процесс повторяется до тех пор, пока мы не обнаружим, что наилучшее значение для параметра w равно 3 . К этому моменту цель использования веса в ИНС теперь ясна.
Теперь мы можем обсудить цель смещения. Для достижения нашей цели нам необходимо изменить данные. Новые данные приведены в следующей таблице.
Смещение как константа
Эти данные идентичны тем, которые использовались, когда Y = 2X , но мы добавили значение 1 к каждому значению Y .Мы можем протестировать предыдущую функцию Y = wX , где w = 2 , и вычислить общую ошибку в соответствии со следующей таблицей. Имеется общая ошибка 4 .
Согласно нашему предыдущему обсуждению, ошибка 4 означает, что значение w не лучшее, и мы должны изменять его, пока не достигнем ошибки 0 . Но в некоторых случаях использование только весов не приводит к ошибке 0 . Этот пример — свидетельство.
Используя только вес w , можем ли мы достичь ошибки 0? Ответ — нет. Используя только вес в этом примере, мы можем приблизиться к правильному результату, но все равно будет ошибка. Обсудим этот вопрос поподробнее.
Для первого примера, какое наилучшее значение для w в уравнении Y = wX , которое возвращает ошибку, равную 0 ? Это просто. У нас есть уравнение с 3 переменными, но мы знаем значения 2 переменных: Y и X .Это не учитывает единственную переменную w , которую можно легко вычислить, используя w = Y / X . Для первого образца Y равно 5 и X равно 2 , и, таким образом, w = Y / X = 5/2 = 2,5 . Таким образом, оптимальное значение для w , которое правильно предсказывает вывод первой выборки, составляет 2,5 . То же самое можно повторить и для второго образца.
Для второго образца Y = 7 и X = 3 . Таким образом, w = Y / X = 7/3 = 2.33 . Итак, оптимальное значение для w , которое правильно предсказывает вывод второй выборки, составляет 2,33 . Это значение отличается от оптимального значения w , которое работает с первым образцом. Согласно двум значениям w для первого и второго отсчетов, мы не можем найти единственное значение для w , которое правильно предсказывает их выходные данные. Использование w = 2,5 оставит ошибку во втором примере, а использование w = 2,33 оставит ошибку для первого образца.
В заключение, используя только вес, мы не можем достичь ошибки 0 . Чтобы исправить эту ситуацию, мы должны использовать предвзятость.
Ошибка 0 может быть достигнута добавлением значения 1 к результату умножения между w и X . Итак, новая функция — Y = wX + 1 , где w = 2 . Согласно следующей таблице, общая ошибка теперь равна 0. ОТЛИЧНО.
Смещение как переменная
Мы все еще используем постоянное значение 1 , которое нужно добавить к wX .Согласно нашему предыдущему обсуждению, использование постоянного значения в функции делает это значение зависимым от конкретной проблемы, а не общим.
В результате вместо константы 1 мы можем использовать переменную, скажем, b . Таким образом, новая функция — Y = wX + b . Переменная (параметр) b представляет смещение в ИНС. При решении задачи у нас теперь есть 2 параметра: w и b , чтобы определить их наилучшие значения.Это немного усложняет задачу. Вместо того, чтобы находить лучшее значение только для веса w , нас просят оптимизировать 2 параметра: w (вес) и b (смещение). На это уходит гораздо больше времени, чем раньше.
Чтобы найти оптимальные значения для 2 параметров, рекомендуется начать с оптимизации только одного параметра до достижения минимально возможной ошибки. Убедившись, что ошибка больше не уменьшается путем изменения этого параметра, мы можем начать оптимизацию следующего параметра.
Применяя эту стратегию к предыдущему примеру при оптимизации параметра w , мы заметим, что небольшое отклонение от w = 2 увеличивает ошибку. Это показатель того, что значение 2 является лучшим значением для параметра w , и мы можем начать оптимизацию следующего параметра b .
От математической формы к графической форме нейрона
На этом этапе мы вывели функцию Y = wX + b с двумя параметрами.Первый — это w , представляющий вес, а второй — b , представляющий смещение. Эта функция является математическим представлением нейрона в ИНС, которая принимает один вход. Входные данные — X с весом, равным w . Нейрон также имеет смещение b .
Умножив вес ( w ) на вход ( X ) и суммируя результат по смещению ( b ), на выходе получим Y , который является выходом нейрона, который рассматривается как вход к другим нейронам, связанным с ним.Нейрон также можно представить в виде графика, который суммирует всю эту информацию, как показано на рисунке ниже.
На рисунке вы можете найти соответствия между параметрами математической функции и нейронного графика. Есть одно уведомление. Смещение рассматривается как вес для ввода значения +1. Это позволяет легко управлять смещением как обычным вводом.
Нейрон с несколькими входами
К этому моменту цель веса и смещения теперь ясна, и мы также можем представить нейрон как в математической, так и в графической формах.Но нейрон по-прежнему принимает один вход. Как мы позволим ему поддерживать несколько входов? Это тоже довольно просто. Просто добавьте необходимые входные данные в уравнение и присвойте каждому из них вес. Если есть 3 входа, то математическая форма будет следующей:
Что касается графической формы, просто создайте новое соединение для каждого входа, затем поместите вход и вес на соединение. Это показано на следующем рисунке. Соединив несколько нейронов этой формы, мы можем создать полную искусственную нейронную сеть.Помните, что отправной точкой было всего Y = X .
Сумма продуктов
В математической форме мы замечаем, что повторяются разные термины. Эти члены умножают каждый вход на его соответствующий вес. Мы можем суммировать все эти продукты в операторе суммирования. Этот оператор будет отвечать за возврат суммы продуктов между каждым вводом и соответствующего веса.
Новая математическая форма нейрона приведена ниже.Обратите внимание, что суммирование начинается с 0, а не с 1. Это означает, что будет вес ( w ) и вход ( X ) с индексами 0. Такой вес с индексом 0 будет относиться к смещению b . Его входу всегда будет присвоен +1.
Вы также можете добавить смещение как отдельный член, добавляемый после завершения суммирования (как показано ниже). В этом случае суммирование начинается с 1.
Заключение
В этом руководстве очень подробно объясняется, как создать полную искусственную нейронную сеть, начиная с очень простой функции, Y = X .На протяжении всего урока мы изучали назначение весов и смещения. Кроме того, в учебнике отображается математическая форма и графическая форма нейрона.
Стоит отметить, что это руководство основано на моей книге Практические приложения компьютерного зрения, использующие глубокое обучение с CNN. Итак, вы можете прочитать больше в этой книге, которая доступна через самые популярные каналы распространения, включая Google Книги, Amazon, Amazon Kindle, Springer, Apress, O’Reilly и другие.Вы можете найти книгу в Springer по этой ссылке:
Практические приложения компьютерного зрения с использованием глубокого обучения с CNN
Развертывайте приложения глубокого обучения в производственной среде на нескольких платформах. Вы будете работать над компьютерным зрением …
Биография: Ахмед Гад получил степень бакалавра наук. диплом с отличием в области информационных технологий на факультете компьютеров и информации (FCI) Университета Менуфия, Египет, июль 2015 г.Поскольку он занял первое место на своем факультете, ему рекомендовали работать ассистентом преподавателя в одном из египетских институтов в 2015 году, а затем в 2016 году работать ассистентом преподавателя и исследователем на его факультете. Его текущие исследовательские интересы включают глубокое обучение, машинное обучение, искусственный интеллект, цифровую обработку сигналов и компьютерное зрение.
Оригинал. Размещено с разрешения.
Связанный:
8 Функции преподавания и обучения | Как студенты учатся: история, математика и естественные науки в классе
ПРИМЕЧАНИЯ1. | Изучение функций, как мы определяем его здесь, в значительной степени пересекается с темой «алгебры», традиционно преподаваемой в Соединенных Штатах в девятом классе, хотя национальные стандарты и стандарты многих штатов теперь рекомендуют изучать аспекты алгебры в более ранних классах (поскольку делается в большинстве других стран). Хотя функции являются важной частью алгебры, другие аспекты алгебры, такие как решение уравнений, в этой главе не рассматриваются. |
2. | Thomas, 1972, стр. 17. |
3. | Гольденберг, 1995; Leinhardt et al., 1990; Romberg et al., 1993. |
4. | Натан и Кёдингер, 2000. |
5. | Кёдингер и Натан, 2004. |
6. | Кёдингер и Натан, 2004. |
7. | Koedinger et al., 1997. |
8. | Кальчман, 2001. |
9. | Schoenfeld et al., 1993. |
10. | Schoenfeld et al., 1987. |
11. | Schoenfeld et al., 1998, стр. 81. |
12. | Chi et al., 1981. |
13. | Chi et al., 1981; Schoenfeld et al., 1993. |
14. | Кальчман, 2001. |
Chi, M.T.H., Feltovich, P.J., and Glaser, R. (1981). Категоризация и представление физических задач специалистами и новичками. Когнитивная наука , 5 , 121-152.
Гольденберг, Э. (1995). Множественные представления: средство понимания.У Д. Перкинса, Дж. Шварца, М. Уэста и М. Виске (редакторы), Программное обеспечение идет в школу: обучение пониманию с помощью новых технологий (стр. 155-171). Нью-Йорк: Издательство Оксфордского университета.
Кальчман М. (2001). Использование неопиажеской структуры для изучения и обучения математическим функциям . Докторская диссертация, Торонто, Онтарио, Университет Торонто.
Кёдингер, К.Р., и Натан, М.Дж. (2004). Реальная история проблем истории: влияние представлений на количественные рассуждения. Журнал обучающих наук , 13 (2).
Koedinger, K.R., Anderson, J.R., Hadley, W.H., and Mark, M.A. (1997). Интеллектуальное обучение идет в школу в большом городе. Международный журнал искусственного интеллекта в образовании , 8 , 30-43.
Лейнхардт, Г., Заславский, О., Стейн, М. (1990). Функции, графики и графики: задачи, обучение и обучение. Обзор исследований в области образования , 60 (1), 1-64.
Натан, М.Дж., и Кёдингер, К.Р. (2000). Убеждения учителей и исследователей о раннем развитии алгебры. Журнал исследований в области математического образования , 31 (2), 168-190.
Romberg, T., Fennema, E., and Carpenter, T.P. (1993). Интегрирующие исследования графического представления функций . Махва, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.
031Tangents.lbz
031Tangents.фунт-силаДве проблемы
В начале сегодняшнего обсуждения мы собираемся рассмотреть две довольно общие проблемы. По мере того, как мы работаем над решением этих проблем, мы начнем замечать некоторые сходства между ними.
- Большинство кривых имеют уникальную касательную в каждой точке кривой. Касательная линия — это линия, имеющая свойство просто касаться кривой в одной точке, не пересекая кривую. Есть ли общая процедура, которую мы можем использовать для вычисления касательной к произвольной точке кривой?
- Многие математические модели содержат величины, которые изменяются во времени и имеют постоянно меняющуюся скорость изменения.Для такой величины можем ли мы вычислить мгновенную скорость изменения , которая измеряет, насколько быстро величина изменяется в данный момент времени?
Касательная задача
Линия, касающаяся кривой в некоторой точке, просто касается кривой, не пересекая ее. До изобретения математического анализа геометры знали, что большинство кривых имеют уникальные касательные в каждой точке кривой. Во многих случаях они даже разработали хитроумные методы геометрического построения для построения касательных линий для самых разных кривых.
Ни один из этих методов строительства не имеет ничего общего с концепцией ограничения. В каждом случае конструкция производилась с использованием простых инструментов, таких как линейка и циркуль. Вот пример, чтобы дать вам представление об этих методах.
Геометрическая техника построения параболы заключается в рисовании линии, называемой директрисой, и точки, не лежащей на линии, называемой фокусом. Набор всех точек в пространстве, которые лежат на равном расстоянии от фокуса, и директриса очерчивает кривую, называемую параболой.Например, парабола с фокусом (0,4) и директрисой, равной прямой y = -4 , имеет уравнение y = x 2 /16.
Рассмотрим зеленую линию, которая соединяет фокус (0,4) с точкой, где вертикальная синяя линия касается направляющей в точке (r, -4) . Если вы проведете линию, проходящую через середину зеленой линии и точку, где встречаются две синие линии, вы построили касательную линию к параболе.
Проблема с этими методами построения касательных в том, что они требовали значительной смекалки, а также были очень специфичны для кривых.Техника, которую использовали для построения касательной к параболе, сильно отличалась от техники, используемой для построения касательной к эллипсу, и вообще не работала бы для чего-то вроде графика функции y = x 3 / 16 .
Использование предела для построения касательной
Предположим, мы хотим вычислить уравнение прямой, касательной к графику y = x 3 /16 в точке (2,1 / 2) . Чтобы вычислить это уравнение, нам нужно знать наклон касательной в этой точке.
Это усложняет то, что для вычисления наклона нам нужны две точки на рассматриваемой прямой. Здесь нам остается работать только с одним. Один из способов оценить наклон — это отметить, что если вы слегка наклоните касательную линию, она коснется кривой в двух точках, а не только в одной — если мы сможем выяснить, где находятся эти две точки, мы можем вычислить наклон этой секущей линия и используйте ее для оценки наклона касательной.
По мере того, как вы приближаете точку (a, a, 3 /16) к точке (2, 1/2) , секущая линия становится все больше и больше похожей на касательную.В пределе наклон секущей становится равным
Линия, проходящая через (2,1 / 2) с наклоном 3/4, имеет уравнение
или
Мгновенная скорость изменения
Исчисление — это исследование величин, которые изменяются непрерывно. Центральный вопрос в расчетах — как определить мгновенную скорость изменения некоторой величины. Если это количество описывается отношением
y = f (x)
скорость изменения y по отношению к x в течение некоторого интервала в x определена как
Математики используют более компактную нотацию, называемую дельта-нотацией, для описания изменений.В дельта-нотации скорость изменения составляет
.Более конкретно, мы определяем эту скорость изменения, выбирая два близких значения x , x 1 и x 2 , и вычисляя дельты x и y из этих двух.
Чтобы вычислить мгновенную скорость изменения, мы вычисляем скорость изменения для очень малого и принимаем предел, равный 0.
Чуть более удобный способ сделать это — зафиксировать одно из двух значений x и принять предел, поскольку первый x перемещается произвольно близко ко второму x .
В качестве альтернативы вы можете выразить x 1 как x 2 + h для некоторого небольшого числа h и принять предел как h переходит в 0.
Наконец, поскольку у нас остался только один x, мы опускаем нижний индекс и рассматриваем
мы называем эту величину мгновенной скоростью изменения f (x) при x или, альтернативно, производной от f (x) при x .
Пример
Математическая модель размера популяции бактерий, растущих в культуре, говорит, что после x часов размер популяции составляет
Каков мгновенный темп роста населения при x = 3 часов?
Предел здесь не может быть решен с помощью алгебраических уловок, поэтому мы должны оценить его численно.
| ч | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 3,6568542494 | ||||||||
| 0,1 | 2,311444133449163 | ||||||||
| 0,05 | 2,1 | 441356901 2,1441356901 9 21441356901||||||||
| 511 | 07 | 07 | 07 | 7 | 2,079657760523101 | ||||
| 0,000001 | 2,079443703673078 |
Скорость изменения при x = 3 составляет приблизительно
Производная
Предел
называется производной от f (x) при x .Мы видели, что этот предел (или очень похожие ограничения) проявляются, когда мы пытаемся вычислить наклон касательных линий или оценить мгновенные скорости изменения. В следующих нескольких лекциях мы изучим этот предел и разработаем методы его более быстрого и легкого вычисления.
Домашнее задание
Раздел 2.7: 1, 2, 5, 7, 8, 15, 16, 22, 27, 28
Общественный колледж МесаКонцепции алгебры колледжа — MAT 150 онлайн Задача: Найдите точку на графике кривой y = x 2 + 1, ближайшую к фиксированной точке (4,1). Предпосылки: Эта проблема относится к классу задач, обычно называемых проблемами минимизации, минимальными / максимальными проблемами или проблемами экстремумов. Курсы математического анализа традиционно решают этот тип проблем, задав любой из следующих вопросов:
В каждой задаче мы пытаемся найти наименьшее или наибольшее значение. Хотя исчисление можно использовать для нахождения точных решений этих проблем, мы будем использовать алгебру и наши графические калькуляторы для аппроксимации решения.Часть нашего решения, относящаяся к алгебре, на самом деле такая же, как если бы мы использовали исчисление. Переформулировка задачи: Найдите точку (x, y) на графике кривой y = x 2 + 1, ближайшую к фиксированной точке (4,1). Сначала давайте нарисуем график, чтобы получить более четкое представление о том, что происходит. Мы пытаемся найти точку A (x, y) на графике параболы y = x 2 + 1, которая является ближайшей к Переформулировка задачи: Найдите точку A (x, y) на графике параболы, y = x 2 + 1, что минимизирует расстояние d между кривой и точка B (4,1). Задача разбивается на три части:1. Поскольку мы хотим минимизировать d, нам нужна функция, описывающая расстояние между (x, y) и (4,1).
Часть 2:Используя графический калькулятор, мы рисуем график d и ищем точку, в которой встречается минимальное значение d. Используя функцию трассировки, мы можем увидеть, что минимальное значение d находится (приблизительно) в точке (x, d ) = (1,12817, 3,4123 ) То есть d — это минимум , когда x приблизительно равен 1,12817.
Часть 3:Помните, что мы предполагаем, что найдет точку (x, y) на графике параболы, y = x 2 + 1, что минимизирует d . Пока мы знаем x и знаем d, но мы еще не нашли y. Итак, чтобы ответить на исходный вопрос, ближайшая точка параболы y = x 2 + 1 к точке (4,1) приблизительно равна (1. |

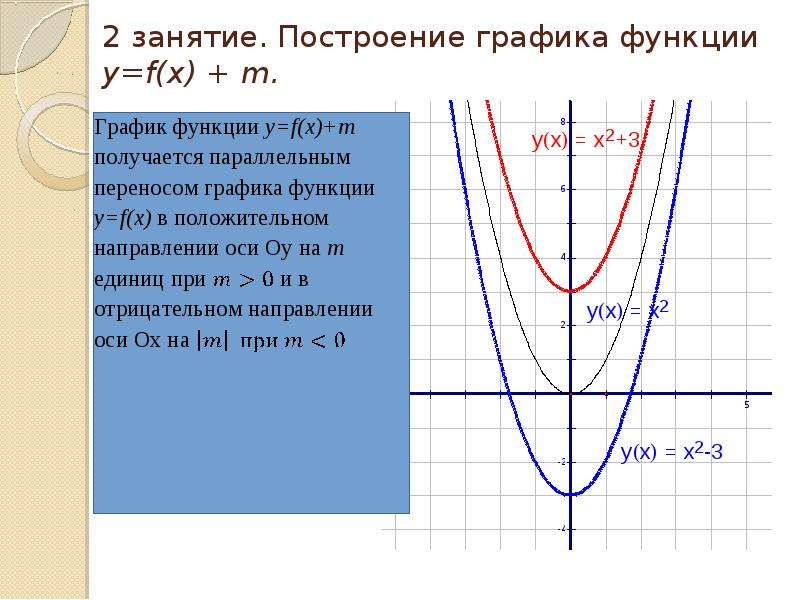 Пусть х1=-2, х2=2.
Пусть х1=-2, х2=2.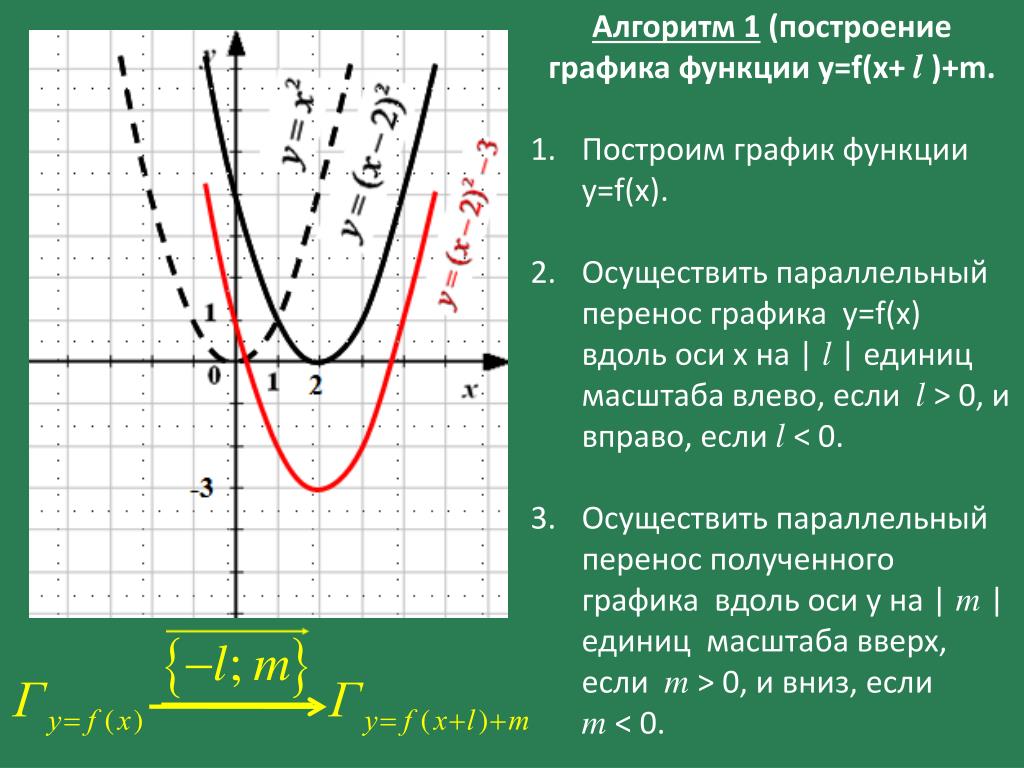 Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y. А недостаток — в том, что сервис не полностью переведен на русский язык.
А недостаток — в том, что сервис не полностью переведен на русский язык. ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
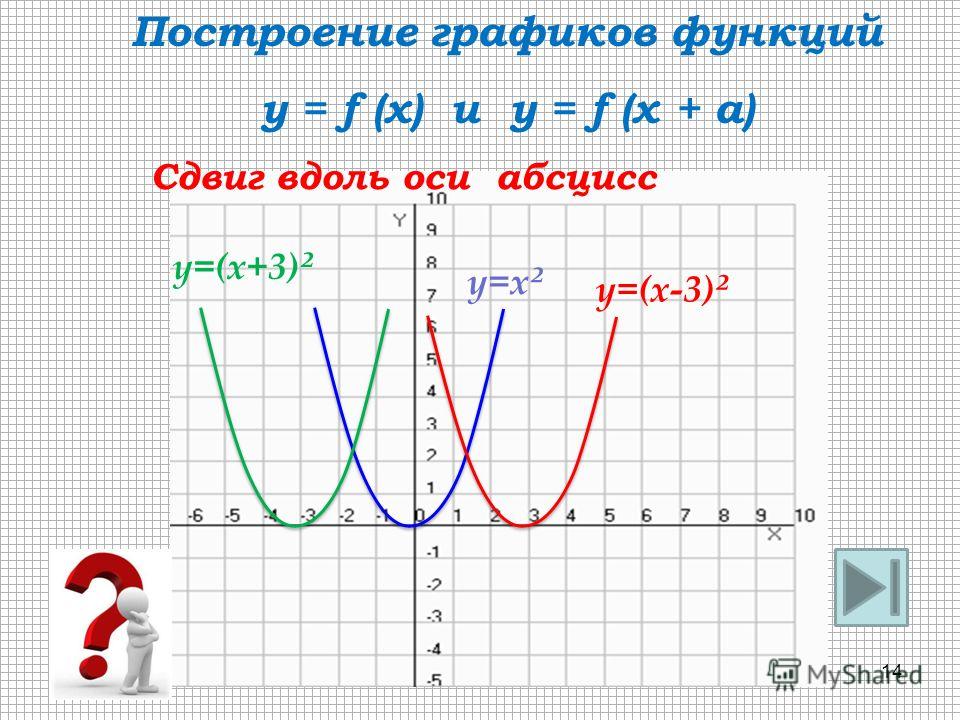 5, b = -1.
5, b = -1.
 Здесь пример для y = 0,5 x (a = 1/2
Здесь пример для y = 0,5 x (a = 1/2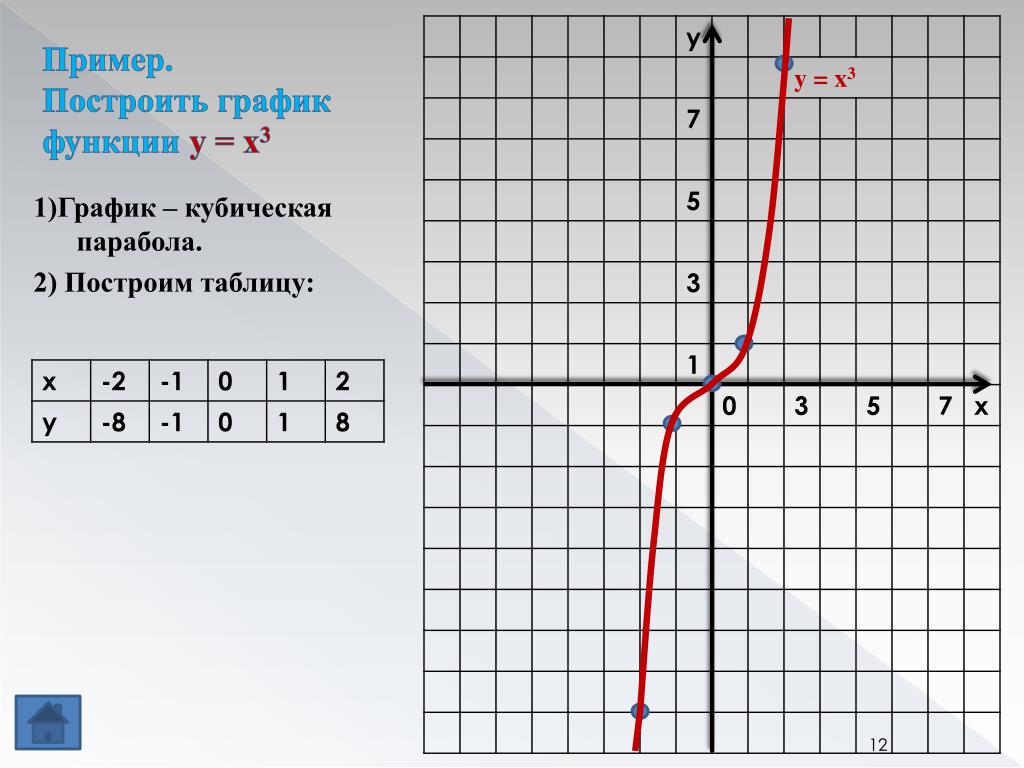 Случаи с коэффициентами изучаются в разделе «Движение графиков функций».
Случаи с коэффициентами изучаются в разделе «Движение графиков функций». Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.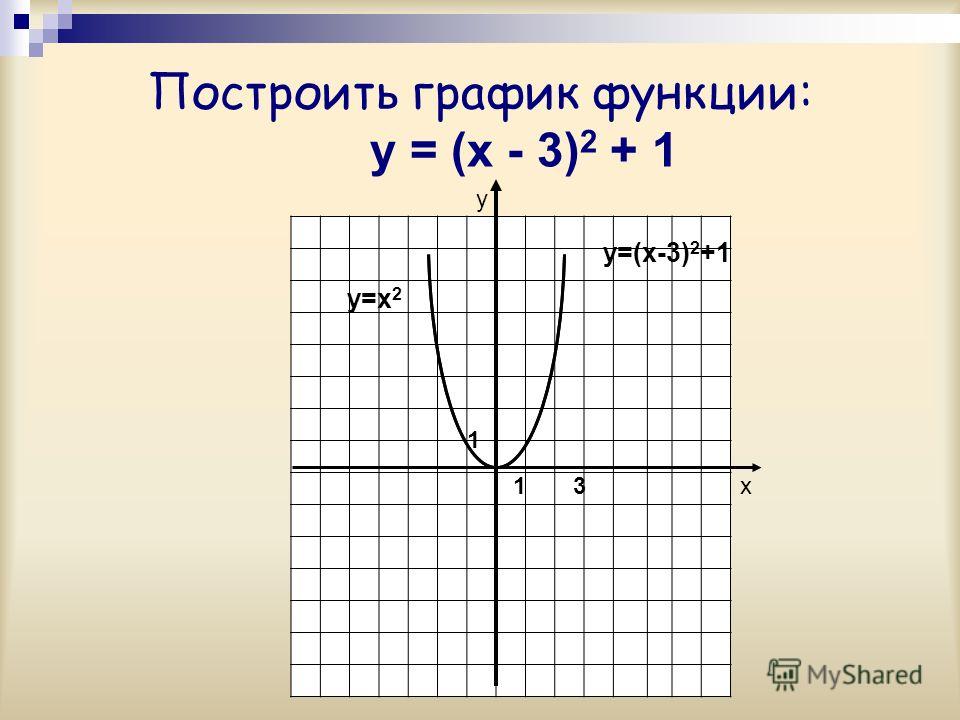
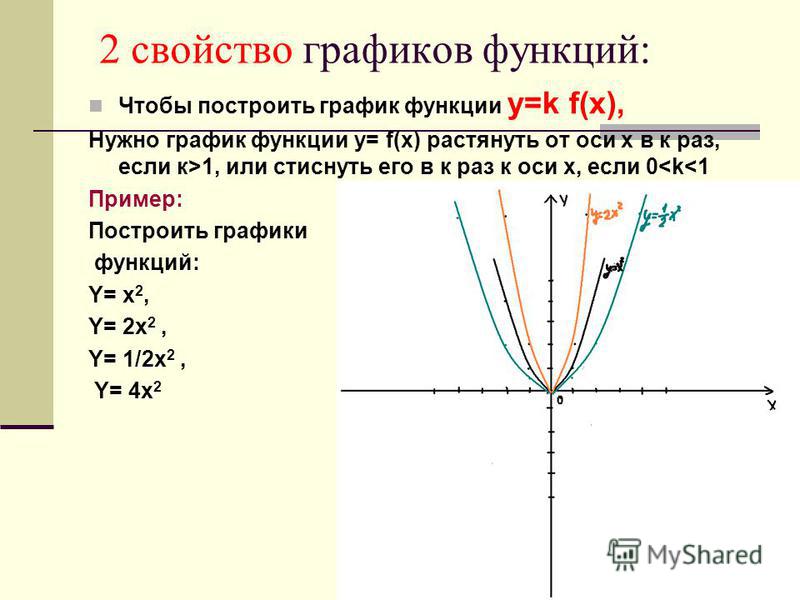
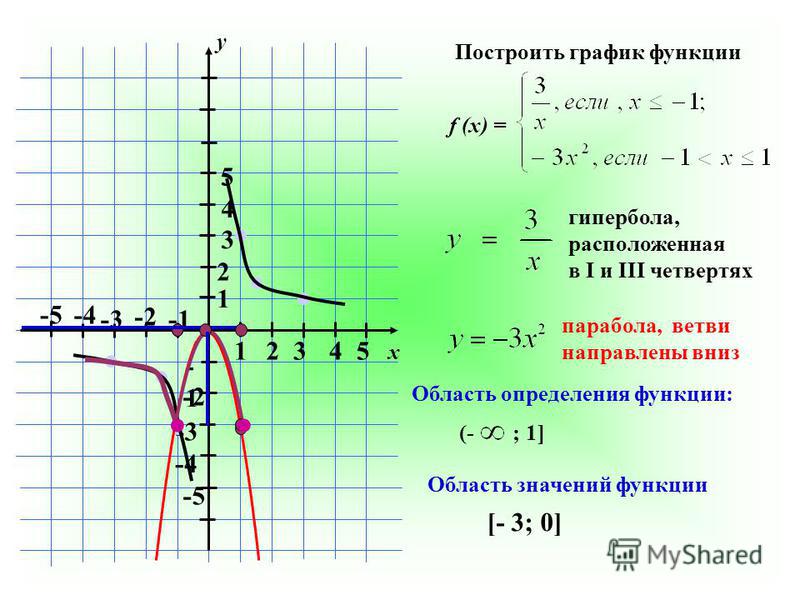 Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.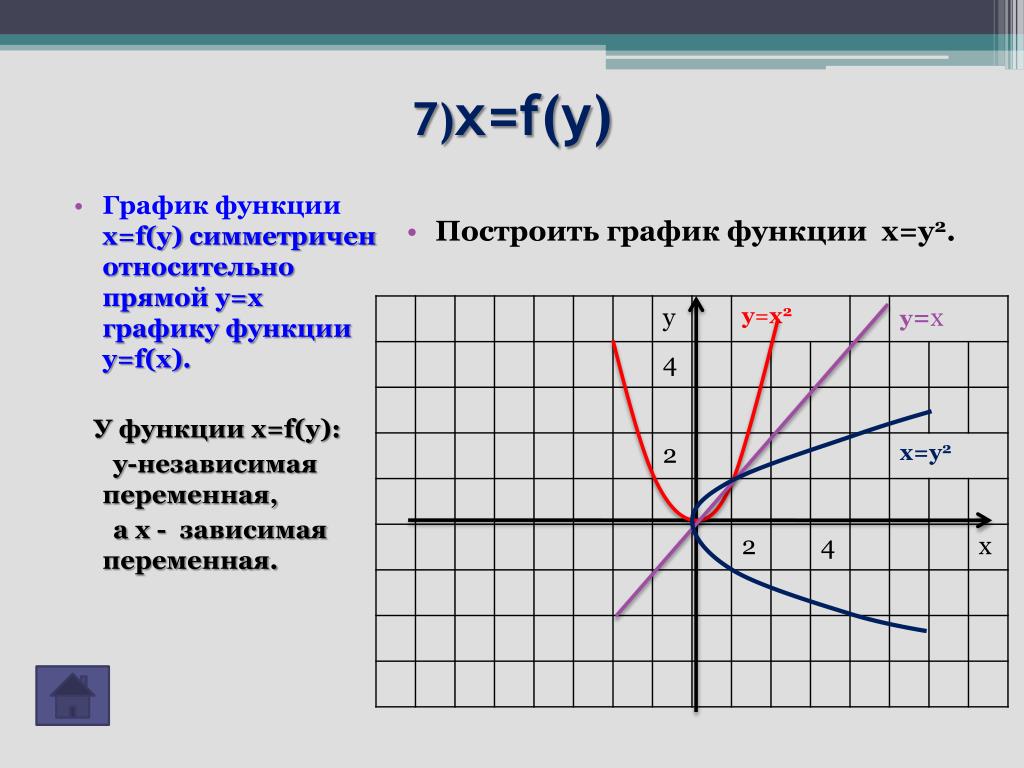 6) .
6) .
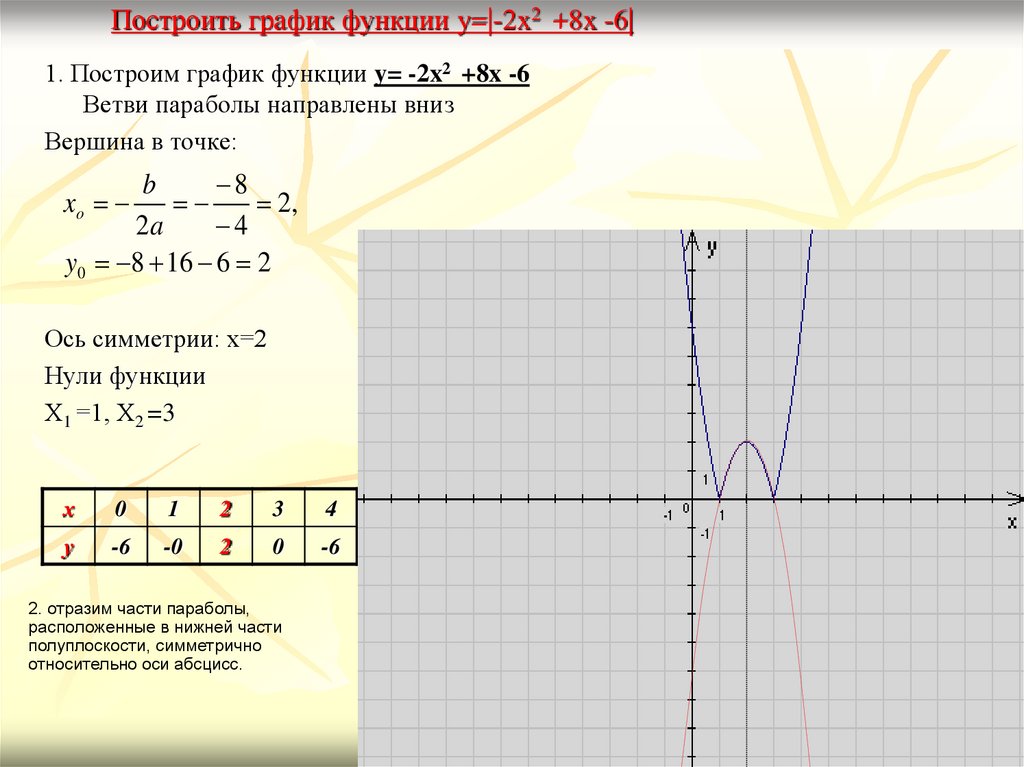 Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.
Соответственно, графиком функции будет называться множество точек, координаты которых удовлетворяют заданному выражению.


 д.). Используйте копирование и перетаскивание формул.
д.). Используйте копирование и перетаскивание формул. 1.14).
1.14). Вызовите Мастер диаграмм, выберите гистограмму объемного типа, перейдите на 2-й шаг Мастера в закладку Ряд – рис. 1.17. На 2-м шаге потребуется настроить ряды. На рис. 1.17 поле Ряд содержит список рядов, поле Имя — имя выбранного ряда, поле Значения – диапазон ячеек ряда.
Вызовите Мастер диаграмм, выберите гистограмму объемного типа, перейдите на 2-й шаг Мастера в закладку Ряд – рис. 1.17. На 2-м шаге потребуется настроить ряды. На рис. 1.17 поле Ряд содержит список рядов, поле Имя — имя выбранного ряда, поле Значения – диапазон ячеек ряда.
 Эта формула размножена на весь диапазон Е7:Е27;
Эта формула размножена на весь диапазон Е7:Е27; 25.
25. 5 для x и y.
5 для x и y.

Ваш комментарий будет первым