Построение функции двух переменных онлайн: Построение графика функции онлайн

Экстремум функции нескольких переменных онлайн

Примеры решенийНайти производную Определитель матрицы Ранг матрицы Умножение матрицМетод Гаусса Точки разрыва функции Найти интегралДиф уравнения онлайнМетод множителей Лагранжа

Назначение сервиса. Онлайн-калькулятор используется для нахождения в онлайн режиме наибольшего и наименьшего значения функции двух переменных (см. пример). Решение оформляется в формате Word.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Правила ввода функций:

Для функции трех переменных можно использовать матрицу Гессе. Функция z = f(x,y) имеет максимум в точке M₀(x₀;y₀), если f(x₀ ;y₀) > f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M₀(x₀;y₀), если f(x₀;y₀) 0;y₀) и отличных от неё. Максимум и минимум функции называются экстремумами функции.
Исследование функции двух переменных на экстремум проводят по следующей схеме.
1. Находят частные производные dz/dx и dz/dy.
2. Решают систему уравнений:
и таким образом находят критические точки функции.
3. Находят частные производные второго порядка:
4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x₀;y₀).
5. Делаю вывод о наличии экстремумов:
а) если AC – B² > 0 и

A < 0 , то в точке M имеется максимум;
б) если AC – B² > 0 и A > 0 , то в точке M имеется минимум;
в) если AC – B² < 0, то экстремума нет;
г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым;

Пример №1. Найти экстремумы функции f(x,y)=x³+xy²+x²+y² и определить по критерию Сильвестра их тип.
Решение.
1. Найдем первые частные производные.


2. Решим систему уравнений.
3x²+2x+y²=0
2xy+2y=0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = -1
y²+1=0
Данная система уравнений не имеет решения.

б) Из первого уравнения выражаем y и подставляем во второе уравнение:


или


или
Откуда x₁ = -2/3; x₂ = 0; x₃ = -2/3; x₄ = 0
Данные значения x подставляем в выражение для y. Получаем: y₁ = 0; y₂ = 0; y₃ = 0; y₄ = 0
Количество критических точек равно 2: M₁(-2/3;0), M₂(0;0)
3. Найдем частные производные второго порядка.



4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀).
Вычисляем значения для точки M₁(-2/3;0)



AC — B² = -4/3 Вычисляем значения для точки M₂(0;0)



AC — B² = 4 > 0 и A > 0 , то в точке M₂(0;0) имеется минимум z(0;0) = 0
Вывод: В точке M₂(0;0) имеется минимум z(0;0) = 0

Пример №2. Исследовать функцию на экстремум классическим методом: Z=8x2+2xy-5x+6.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

2.7. Графики функций двух переменных

MatLab предлагает различные способы визуализации функций двух переменных: построение трехмерных графиков и линий уровня, параметрически заданных линий и поверхностей.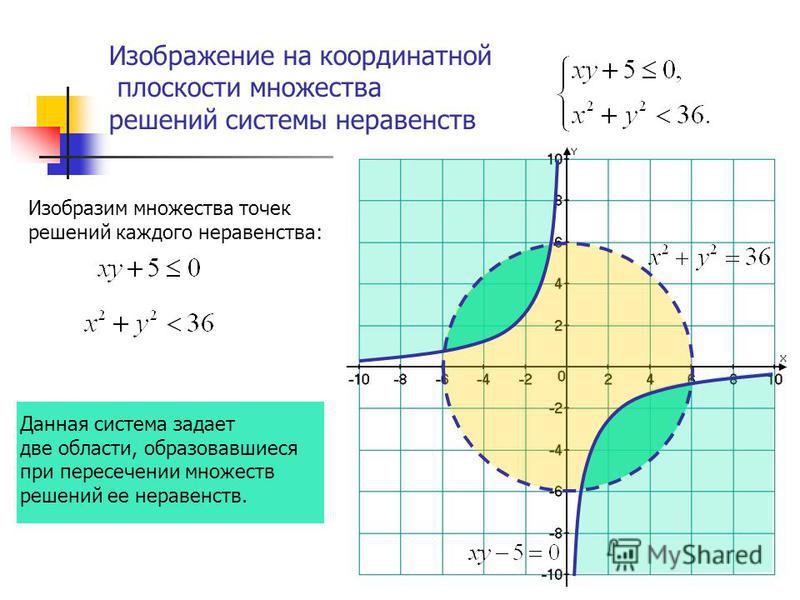 2 – команду вывода результата не подавлять.

3. Построить график функции командой

>> mesh (X, Y, Z)

4. Для более точного построения следует выбрать меньший шаг сетки. Выберите шаг сетки 0,05 и снова постройте график функции

z (x, y).

Изучение цветовых эффектов производите на примере графика, полученного при выполнении самостоятельной работы. Используя новую команду, копируйте заново этапы построения сетки и вычисления функции и изменяйте команду вывода графика.

1. Команда surf строит каркасную поверхность графика функции и заливает каждую клетку поверхности определенным цветом, причем в пределах каждой клетки цвет постоянный:

>> surf (X, Y, Z)

2. Команда shading убирает каркасные линии:

>> shading (X, Y, Z)

3. Команда

shading integr плавно заливает поверхность цветом, зависящим от значений функции.

4. Вернуться к первоначальному виду графика, определенному командой mesh, можно при помощи shading faceted.

5. Сделать каркасную поверхность прозрачной можно командой hidden of.

6. Убрать невидимую часть поверхности можно командой hidden on.

7. В MatLab можно вывести рядом с графиком столбик, устанавливающий соответствие между цветом и значением функции (colorbar).

Задание 9. Постройте при помощи surf график поверхности, заданной в задании 8, и дополните его информацией о цвете:

>> surf (X,Y,Z)

>> colorbar

8. Чтобы сделать вывод о значении функции в той или иной точке плоскости

xy, следует использовать команду meshc или surfc. Эти команды размещают на плоскости xy линии уровня функции (линии постоянства функции).

9. MatLab позволяет строить поверхности, состоящие из линий уровня. Для задания из самостоятельной работы вместо команды построения графика введите следующие команды:

>> levels = (0:0.01:0.5)

>> contour3 (X, Y, Z, levels)

>> colorbar

Установка цветовой палитры

Простым, но эффективным способом цветового оформления графика является установка цветовой палитры при помощи функции

colormap.

Пример (примените к графику из самостоятельной работы):

>> surfc (X, Y, Z)

>> colorbar

>> colormap (autumn)

>> title (‘График функции z (x, y)’)

>> xlabel (‘x’)

>> ylabel (‘y’)

>> zlable (‘z’)

Таблица 2. 2

Исчисление II. Функции нескольких переменных

Онлайн-заметки Пола
Главная / Исчисление II / Трехмерное пространство / Функции нескольких переменных

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.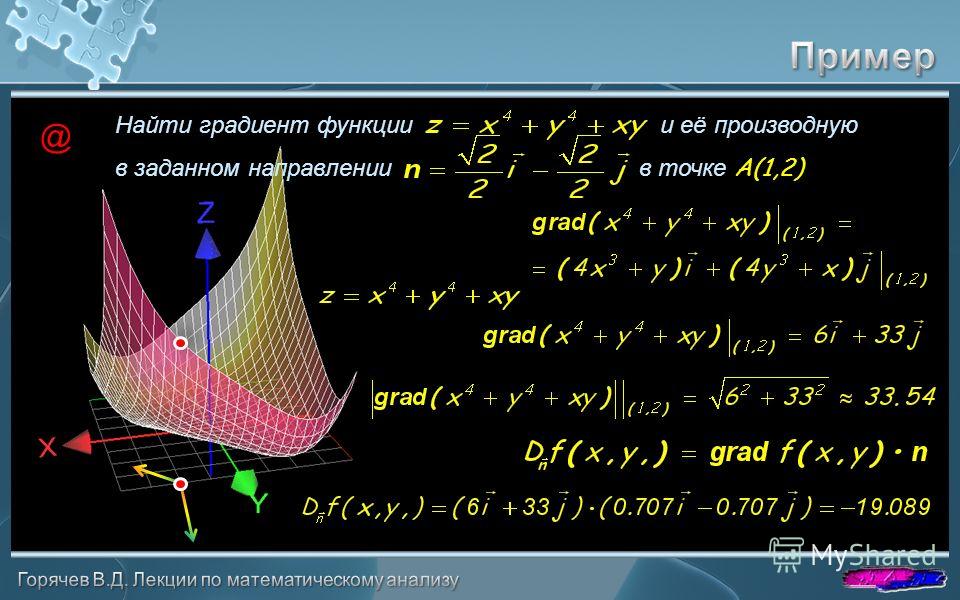

Раздел 12.5: Функции нескольких переменных 92}-4\).

Это эллиптический параболоид и пример квадратичной поверхности. Мы видели несколько из них в предыдущем разделе. Квадратичные поверхности мы будем довольно часто встречать позже в Calculus III.

Еще один распространенный граф, который мы будем часто встречать в этом курсе, — это граф плоскости. У нас есть соглашение о графическом отображении плоскостей, которое немного облегчит их графическое представление и, надеюсь, визуализацию.

Напомним, что уравнение плоскости задается

\[ax + by + cz = d\]

или если мы решим это для \(z\), мы можем записать это в терминах обозначения функций. Это дает,

\[f\left( {x,y} \right) = Ax + By + D\]

Чтобы нарисовать плоскость, мы обычно находим точки пересечения с тремя осями, а затем рисуем треугольник, соединяющий эти три точки. Этот треугольник будет частью плоскости, и он даст нам довольно приличное представление о том, как должна выглядеть сама плоскость. Например, давайте изобразим плоскость, заданную

\[f\влево( {x,y} \right) = 12 — 3x — 4y\]

Для построения графика, возможно, было бы проще записать это как

. \[z = 12 — 3x — 4y\hspace{0.25in} \Rightarrow \hspace{0.25in}\,\,\,\,\,3x + 4y + z = 12\]

Теперь каждая из точек пересечения с тремя главными осями координат определяется тем фактом, что две координаты равны нулю. Например, пересечение с осью \(z\) определяется как \(x = y = 0\). Итак, три точки пересечения равны 9.0004

\[\ begin{align*}& x — {\mbox{axis:}}\left({4,0,0} \right)\\ & y — {\mbox{axis:}}\left({0 ,3,0} \right)\\ & z — {\mbox{ось:}}\left({0,0,12} \right)\hspace{0,25 дюйма}\end{align*}\]

Вот график самолета.

Теперь, чтобы расширить это, графики функций вида \(w = f\left( {x,y,z} \right)\) будут четырехмерными поверхностями. Конечно, мы не можем их изобразить в виде графика, но указать на это не помешает.

Далее мы хотим поговорить об областях определения функций более чем одной переменной. Напомним, что домены функций одной переменной \(y = f\left( x \right)\) состояли из всех значений \(x\), которые мы могли подставить в функцию и получить обратно действительное число. Теперь, если задуматься, это означает, что область определения функции одной переменной представляет собой интервал (или интервалы) значений от числовой прямой или одномерного пространства.

Область определения функций двух переменных, \(z = f\left( {x,y} \right)\), являются областями из двумерного пространства и состоят из всех пар координат, \(\left( {x ,y} \right)\), чтобы мы могли подключиться к функции и получить действительное число. 92}} \справа)\)

Показать все решения Скрыть все решения

a \(f\left( {x,y} \right) = \sqrt {x + y} \) Показать решение

В этом случае мы знаем, что не можем извлечь квадратный корень из отрицательного числа, поэтому это означает, что мы должны потребовать,

\[х + у \ge 0\]

Вот набросок графика этого региона.

b \(f\left( {x,y} \right) = \sqrt x + \sqrt y \) Показать решение 92} > 16\]

Итак, областью определения этой функции является множество точек, лежащих полностью вне сферы радиуса 4 с центром в начале координат.

Следующая тема, которую мы должны рассмотреть, это кривых уровня или кривых контура . Кривые уровня функции \(z = f\left( {x,y} \right)\) — это двумерные кривые, которые мы получаем, полагая \(z = k\), где \(k\) — любое число. Итак, уравнения кривых уровня имеют вид \(f\left( {x,y} \right) = k\). Обратите внимание, что иногда уравнение будет иметь вид \(f\left( {x,y,z} \right) = 0\), и в этих случаях уравнения кривых уровня будут \(f\left( {x, у,к} \справа) = 0\).

Вероятно, вы уже видели кривые уровня (или контурные кривые, называйте их как хотите) раньше. Если вы когда-либо видели карту высот участка земли, то это не что иное, как контурные кривые для функции, которая дает высоту земли в этой области. 2}} \). Нарисуйте несколько из них. 92}} \]

Вспомним из раздела Quadric Surfaces, что это верхняя часть «конуса» (или поверхности в форме песочных часов).

Обратите внимание, что для данной проблемы это не требовалось. Это было сделано для практики определения поверхности, и это может пригодиться в будущем.

Теперь о настоящей проблеме. Кривые уровня (или контурные кривые) для этой поверхности задаются уравнением и находятся при подстановке \(z = k\). В нашем примере это 9.2}\]

где \(k\) — любое число. Итак, в этом случае кривые уровня представляют собой окружности радиуса \(k\) с центром в начале координат.

Мы можем изобразить их одним из двух способов. Мы можем отобразить их либо на самой поверхности, либо отобразить их в двухмерной системе координат. Вот каждый график для некоторых значений \(k\).

Обратите внимание, что мы можем думать о контурах с точки зрения пересечения поверхности, которая задается \(z = f\left( {x,y} \right)\) и плоскости \(z = k\). Контур будет представлять собой пересечение поверхности и плоскости.

Для функций вида \(f\left( {x,y,z} \right)\) мы иногда будем рассматривать поверхностей уровня . Уравнения поверхностей уровня задаются формулой \(f\left({x,y,z} \right) = k\), где \(k\) — любое число.

Последняя тема в этом разделе посвящена трассировкам . В чем-то они похожи на контуры. Как отмечалось выше, мы можем думать о контурах как о пересечении поверхности, заданной \(z = f\left({x,y} \right)\), и плоскости \(z = k\). Следы поверхностей — это кривые, которые представляют собой пересечение поверхности и плоскости, задаваемой \(x = a\) или \(y = b\). 92}\]

, и это будет отображено на плоскости, заданной \(x = 1\).

Ниже приведены два графика. График слева представляет собой график, показывающий пересечение поверхности и плоскости, заданной \(x = 1\). Справа график поверхности и трасса, которую мы ищем в этой части.

Для \(y = 2\) мы сделаем почти то же самое, что и в первой части. 2}\]

и вот эскизы для этого дела.

Системы линейных уравнений: две переменные

Результаты обучения

• Решайте системы уравнений с помощью графиков, подстановок и сложений.
• Найдите несовместимые системы уравнений, содержащие две переменные.
• Выразите решение системы зависимых уравнений, содержащей две переменные, используя стандартные обозначения.

Производитель скейтбордов представляет новую линейку досок. Производитель отслеживает свои затраты, которые представляют собой сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он зарабатывает на продаже своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов нужно произвести и продать, чтобы можно было получить прибыль? В этом разделе мы рассмотрим линейные уравнения с двумя переменными, чтобы ответить на эти и подобные вопросы.

(кредит: Томас Сёренес)

Введение в системные решения

Чтобы исследовать ситуации, подобные ситуации с производителем скейтбордов, мы должны понимать, что имеем дело с более чем одной переменной и, вероятно, с более чем одним уравнением. Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.

В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными.

[латекс]\begin{align}2x+y&=15\\[1mm] 3x-y&=5\end{align}[/latex]

Решение системы линейных уравнений с двумя переменными: любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. В этом примере упорядоченная пара [латекс](4,7)[/латекс] является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы нахождения такого решения, если оно существует.

[латекс]\begin{align}2\left(4\right)+\left(7\right)&=15 &&\text{True} \\[1mm] 3\left(4\right)-\ left(7\right)&=5 &&\text{True} \end{align}[/latex]

Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейных уравнений по количеству решений. непротиворечивая система уравнений имеет по крайней мере одно решение. Непротиворечивая система считается независимой системой , если она имеет единственное решение, как в примере, который мы только что рассмотрели. Две линии имеют разные наклоны и пересекаются в одной точке плоскости. Непротиворечивая система считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые и -перехваты.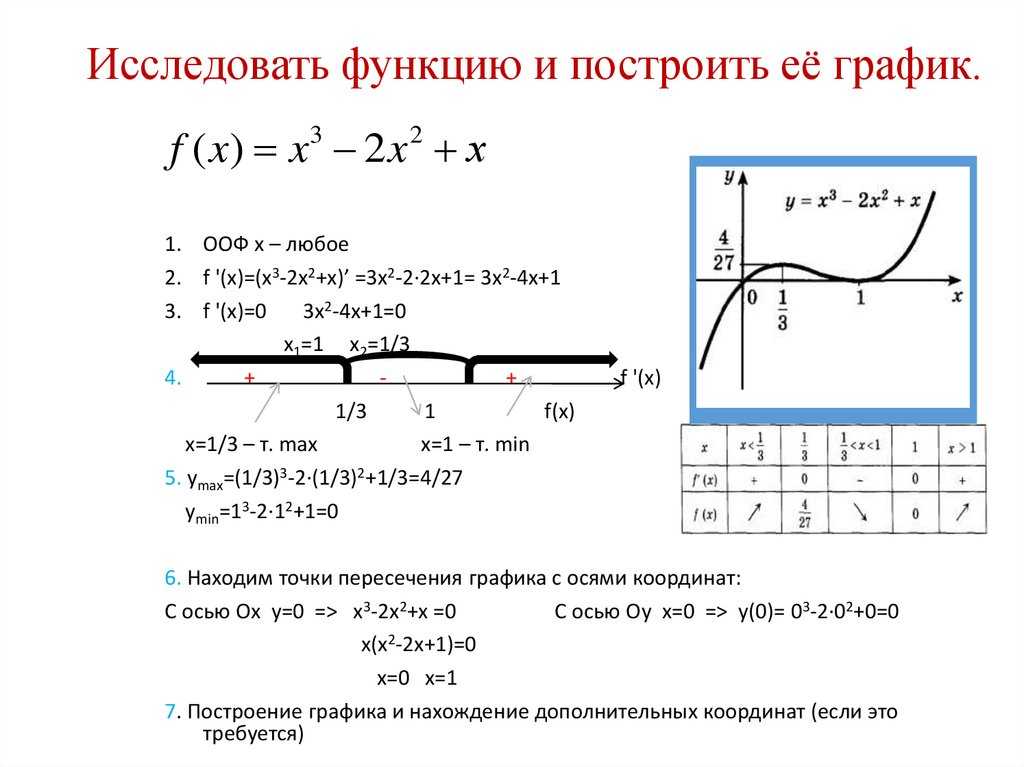 Другими словами, прямые совпадают, поэтому уравнения представляют одну и ту же прямую. Каждая точка на прямой представляет собой пару координат, удовлетворяющую системе. Таким образом, существует бесконечное множество решений.

Другим типом системы линейных уравнений является противоречивая система , в которой уравнения представляют две параллельные линии. Линии имеют одинаковый наклон и разные г- перехватов. Нет общих точек для обеих прямых; следовательно, система не имеет решений.

Общее примечание: Типы линейных систем

Существует три типа систем линейных уравнений с двумя переменными и три типа решений.

• Независимая система имеет ровно одну пару решений [латекс]\влево(х,у\вправо)[/латекс]. Точка пересечения двух прямых является единственным решением.
• Несовместимая система не имеет решения. Обратите внимание, что две линии параллельны и никогда не пересекаются.
• Зависимая от система имеет бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.

Ниже приведено сравнение графических представлений каждого типа системы.

Как: Имея систему линейных уравнений и упорядоченную пару, определить, является ли упорядоченная пара решением.

1. Подставьте упорядоченную пару в каждое уравнение в системе.
2. Определить, верны ли утверждения в результате замены в обоих уравнениях; если да, то упорядоченная пара является решением.

Пример: Определение того, является ли упорядоченная пара решением системы уравнений

Определить, является ли упорядоченная пара [латекс]\влево(5,1\вправо)[/латекс] решением данной системы уравнений.

[латекс]\begin{align}x+3y&=8\\ 2x-9&=y \end{align}[/latex]

Показать решение

Попробуйте

Определите, является ли упорядоченная пара [латекс]\левый(8,5\правый)[/латекс] решением следующей системы.

[латекс]\begin{align}5x-4y&=20\\ 2x+1&=3y\end{align}[/latex]

Показать решение

Решение систем уравнений с помощью графика

Существует несколько методов решения систем линейных уравнений. Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, построив график системы уравнений на одном и том же наборе осей.

Пример: решение системы уравнений с двумя переменными с помощью графика

Решите следующую систему уравнений с помощью графика. Определите тип системы.

[латекс]\begin{align}2x+y&=-8\\ x-y&=-1\end{align}[/latex]

Показать решение

Попробуйте

Решите следующую систему уравнений с помощью графика.

[латекс]\begin{gathered}2x — 5y=-25 \\ -4x+5y=35 \end{gathered}[/latex]

Показать решение

Вопросы и ответы

Можно ли использовать графику, если система непоследовательна или зависима?

Да, в обоих случаях мы по-прежнему можем построить график системы, чтобы определить тип системы и решения. Если две прямые параллельны, то система не имеет решений и несовместна. Если две линии идентичны, система имеет бесконечные решения и является зависимой системой.

Попробуйте

Постройте график трех различных систем с помощью графического онлайн-инструмента. Классифицируйте каждое решение как последовательное или непоследовательное. Если система непротиворечива, определите, зависима она или независима. Возможно, вам будет проще построить каждую систему по отдельности, а затем очистить свои записи, прежде чем строить следующую.
1)
[латекс]5x-3y = -19[/латекс]
[латекс]x=2y-1[/латекс]

2)
[латекс]4x+y=11[/латекс]
[латекс ]-2y=-25+8x[/латекс]

3)
[латекс]у = -3х+6[/латекс]
[латекс]-\frac{1}{3}у+2=х[/ латекс]

Показать решение

Решение систем уравнений путем подстановки

Решение линейной системы с двумя переменными с помощью графика хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод. Рассмотрим еще два метода решения система линейных уравнений более точная, чем графическая. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение для решения второй переменной. Напомним, что мы можем решать только для одной переменной за раз, поэтому метод подстановки ценен и практичен.

Как: Имея систему из двух уравнений с двумя переменными, решите ее методом подстановки.

1. Решите одно из двух уравнений для одной из переменных относительно другой.
2. Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.
3. Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
4. Проверьте решение обоих уравнений.

Пример. Решение системы уравнений с двумя переменными подстановкой

Решите следующую систему уравнений путем замены.

[латекс]\begin{align}-x+y&=-5 \\ 2x-5y&=1 \end{align}[/latex]

Показать решение

Попробуйте

Решите следующую систему уравнений методом замены.

[латекс]\begin{align}x&=y+3 \\ 4&=3x — 2y \end{align}[/latex]

Показать решение

Вопросы и ответы

Можно ли использовать метод подстановки для решения любой линейной системы с двумя переменными?

Да, но метод работает лучше всего, если одно из уравнений содержит коэффициент 1 или –1, чтобы нам не приходилось иметь дело с дробями.

Следующее видео длится около 10 минут и содержит мини-урок по использованию метода подстановки для решения системы линейных уравнений. Мы представляем три разных примера, а также используем инструмент построения графиков, чтобы обобщить решение для каждого примера.

Решение систем уравнений с двумя переменными методом сложения

Третий метод решения систем линейных уравнений — это метод сложения, этот метод также называется методом исключения . В этом методе мы добавляем два слагаемых с одной и той же переменной, но с противоположными коэффициентами, так что сумма равна нулю. Конечно, не во всех системах два члена одной переменной имеют противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения путем умножения, чтобы исключить одну переменную путем сложения.

Как: Имея систему уравнений, решить ее методом сложения.

1. Напишите оба уравнения с x – и y – переменными слева от знака равенства и константами справа.
2. Напишите одно уравнение над другим, выстраивая соответствующие переменные. Если одна из переменных в верхнем уравнении имеет противоположный коэффициент той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную. Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
3. Решите полученное уравнение для оставшейся переменной.
4. Подставьте это значение в одно из исходных уравнений и найдите вторую переменную.
5. Проверьте решение, подставив значения в другое уравнение.

Пример: Решение системы методом сложения

Решите данную систему уравнений методом сложения.

[латекс]\begin{align}x+2y&=-1 \\ -x+y&=3 \end{align}[/latex]

Показать решение

Попробуйте IT

 

Пример: Использование метода сложения при необходимости умножения одного уравнения

Решите данную систему уравнений методом сложения .

[латекс]\begin{align}3x+5y&=-11 \\ x — 2y&=11 \end{align}[/latex]

Показать решение

Попробуйте

Решите систему уравнений сложением.

[латекс]\begin{align}2x — 7y&=2\\ 3x+y&=-20\end{align}[/latex]

Показать решение

Пример: Использование метода сложения, когда требуется умножение обоих уравнений

Решите данную систему уравнений с двумя переменными методом сложения.

[латекс]\begin{align}2x+3y&=-16 \\ 5x — 10y&=30\end{align}[/latex]

Показать решение

Пример: Использование метода сложения в системах уравнений, содержащих дроби

Решите данную систему уравнений с двумя переменными методом сложения.

[латекс]\begin{align}\frac{x}{3}+\frac{y}{6}&=3 \\[1 мм] \frac{x}{2}-\frac{y}{ 4}&=1 \end{выравнивание}[/latex]

Показать решение

Попробуйте

Решите систему уравнений сложением.

[латекс]\begin{align}2x+3y&=8\\ 3x+5y&=10\end{align}[/latex]

Показать решение

в следующем видео мы представляем больше примеров того, как использовать метод сложения (исключения) для решения системы двух линейных уравнений.

Классификация решений систем

Теперь, когда у нас есть несколько методов решения систем уравнений, мы можем использовать эти методы для выявления несовместимых систем. Напомним, что несовместимая система состоит из параллельных линий, которые имеют одинаковый наклон, но разные [latex]y[/latex] -перехваты. Они никогда не пересекутся. При поиске решения для несогласованной системы мы придем к ложному утверждению, например [латекс]12=0[/латекс].

Пример: Решение несовместимой системы уравнений

Решите следующую систему уравнений.

[латекс]\begin{gathered}&x=9 — 2y \\ &x+2y=13 \end{gathered}[/latex]

Показать решение

Попробуйте

Решите следующую систему уравнений с двумя переменными.

[латекс]\begin{gathered}2y — 2x=2\\ 2y — 2x=6\end{gathered}[/latex]

Показать решение

Выражение решения системы зависимых уравнений с двумя переменными

Напомним, что зависимая система уравнений с двумя переменными — это система, в которой два уравнения представляют одну и ту же прямую. Зависимые системы имеют бесконечное число решений, потому что все точки на одной прямой находятся также и на другой прямой. После использования подстановки или сложения результирующее уравнение будет тождеством, например [латекс]0=0[/латекс].

Пример: поиск решения зависимой системы линейных уравнений

Найдите решение системы уравнений методом сложения .

[латекс]\begin{gathered}x+3y=2\\ 3x+9y=6\end{gathered}[/latex]

Показать решение

Запись общего решения

В предыдущем примере мы представили анализ решения следующей системы уравнений:

[латекс]\begin{gathered}x+3y=2\\ 3x+9y=6\ конец {собрано}[/латекс]

После недолгих вычислений мы обнаружили, что эти два уравнения совершенно одинаковы. Затем мы записали общее решение как [латекс]\влево(х, -\фракция{1}{3}х+\фракция{2}{3}\право)[/латекс]. Почему мы должны писать решение таким образом? В некотором смысле это представление говорит нам о многом. Он говорит нам, что x может быть чем угодно, x это x . Это также говорит нам, что y будет зависеть от x , точно так же, как когда мы пишем функциональное правило. В этом случае, в зависимости от того, что вы положили на x , y будет определено через x как [латекс]-\frac{1}{3}x+\frac{2}{3}[/latex].

Другими словами, существует бесконечно много ( x , y ) пар, удовлетворяющих этой системе уравнений, и все они попадают на прямую [latex]f(x)-\frac{1}{3 }x+\frac{2}{3}[/latex].

 

Попробуйте

Решите следующую систему уравнений с двумя переменными.

[латекс]\begin{собранный}y — 2x=5 \\ -3y+6x=-15 \end{собранный}[/latex]

Показать решение

Использование систем уравнений для исследования прибыли

Используя то, что мы узнали о системах уравнений, мы можем вернуться к проблеме производства скейтбордов в начале раздела. Функция дохода производителя скейтбордов — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением [латекс]R=xp[/латекс], где [латекс]х=[/латекс] количество и [латекс]р=[/латекс] цена. Функция дохода показана оранжевым цветом на графике ниже.

Функция затрат — это функция, используемая для расчета затрат на ведение бизнеса. Он включает постоянные затраты, такие как арендная плата и заработная плата, и переменные затраты, такие как коммунальные услуги. Функция стоимости показана синим цветом на графике ниже. Ось x представляет количество в сотнях единиц. Ось y представляет либо затраты, либо доход в сотнях долларов.

Точка, в которой пересекаются две линии, называется точкой безубыточности . Из графика видно, что при производстве 700 единиц стоимость составляет 3300 долларов, а выручка также составляет 3300 долларов. Другими словами, компания безубыточна, даже если она произведет и продаст 700 единиц. Они не зарабатывают и не теряют деньги.

Заштрихованная область справа от точки безубыточности представляет объемы, при которых компания получает прибыль. Заштрихованная область слева представляет объемы, по которым компания несет убытки. Функция прибыли представляет собой функцию дохода минус функция затрат, записанную как [латекс]Р\влево(х\вправо)=R\влево(х\вправо)-С\влево(х\вправо)[/латекс]. Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.

Пример: нахождение точки безубыточности и функции прибыли с помощью подстановки

Учитывая функцию затрат [латекс]C\влево(х\вправо)=0,85x+35{,}000[/латекс] и функцию дохода [латекс]R\влево(х\вправо)=1,55x[/ латекс], найти точку безубыточности и функцию прибыли.

Показать решение

Написание системы линейных уравнений с учетом ситуации

Редко можно получить уравнения, которые точно моделируют поведение, с которым вы сталкиваетесь в бизнесе, скорее, вы, вероятно, столкнетесь с ситуацией, для которой вам известна ключевая информация, как в примере выше. Ниже мы суммируем три ключевых фактора, которые помогут вам преобразовать ситуацию в систему.

Как сделать: Дана ситуация, представляющая систему линейных уравнений, напишите систему уравнений и найдите решение.

1. Определите вход и выход каждой линейной модели.
2. Определите наклон и y — точку пересечения каждой линейной модели.
3. Найдите решение, установив две линейные функции равными другой и найдя x , или найдите точку пересечения на графике.

Теперь давайте попрактикуемся в применении этих ключевых факторов. В следующем примере мы определяем, сколько различных типов билетов продано, учитывая информацию об общем доходе и количестве билетов, проданных на мероприятие.

Пример: Написание и решение системы уравнений с двумя переменными

Стоимость билета в цирк составляет 25 долларов США для детей и 50 долларов США для взрослых. В определенный день посещаемость цирка составляет 2000 человек, а общий доход от продажи билетов составляет 70 000 долларов. Сколько детей и сколько взрослых купили билеты?

Показать решение

Попробуйте

Билеты в цирк стоят 4 доллара для детей и 12 долларов для взрослых. Если было куплено 1650 талонов на питание на общую сумму 14 200 долларов, сколько детей и сколько взрослых купили талоны на питание?

Показать решение

Иногда решение может принимать система уравнений. В нашем следующем примере мы помогаем ответить на вопрос: «Какая компания по аренде грузовиков даст наибольшую ценность?»

Пример: построение системы линейных моделей для выбора компании по аренде грузовиков

Джамал выбирает между двумя компаниями по аренде грузовиков. Первый, Keep on Trucking, Inc., взимает авансовый платеж в размере 20 долларов, а затем 59 центов за милю. Второй, Move It Your Way, взимает авансовый платеж в размере 16 долларов, а затем 63 цента за милю. ^[1] Когда компания Keep on Trucking, Inc. станет лучшим выбором для Джамала?

Показать решение

Приложения для систем кажутся почти бесконечными, но мы покажем еще одно. В следующем примере мы определяем количество 80% раствора метана, которое нужно добавить к 50% раствору, чтобы получить окончательный раствор 60%.

Пример. Решение задачи о химической смеси

У химика есть 70 мл 50% раствора метана. Какое количество 80%-ного раствора она должна добавить, чтобы конечный раствор состоял из 60%-ного метана?

Показать решение

Try IT

Ключевые понятия

• Система линейных уравнений состоит из двух или более уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
• Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо.
• Системы уравнений классифицируются как независимые с одним решением, зависимые с бесконечным числом решений и несовместные без решения.
• Одним из методов решения системы линейных уравнений с двумя переменными является построение графика. В этом методе мы наносим уравнения на один и тот же набор осей.
• Другой метод решения системы линейных уравнений — подстановка. В этом методе мы находим одну переменную в одном уравнении и подставляем результат во второе уравнение.
• Третий метод решения системы линейных уравнений — сложение, в котором мы можем исключить переменную, добавляя противоположные коэффициенты соответствующих переменных.
• Часто бывает необходимо умножить одно или оба уравнения на константу, чтобы облегчить исключение переменной при сложении двух уравнений.
• Любой метод решения системы уравнений приводит к ложному утверждению для несовместимых систем, поскольку они состоят из параллельных линий, которые никогда не пересекаются.
• Решение системы зависимых уравнений всегда будет верным, поскольку оба уравнения описывают одну и ту же прямую.
• Системы уравнений можно использовать для решения реальных задач, включающих более одной переменной, например связанных с доходом, затратами и прибылью.

Глоссарий

метод сложения алгебраический метод, используемый для решения систем линейных уравнений, в котором уравнения складываются таким образом, что исключается одна переменная, что позволяет решить полученное уравнение для оставшейся переменной; Затем подстановка используется для определения первой переменной

точки безубыточности точки, в которой функция затрат пересекает функцию дохода; где прибыль равна нулю

непротиворечивая система система, для которой существует единственное решение всех уравнений в системе и которая является независимой системой, или если существует бесконечное число решений, и она является зависимой системой

функция стоимости функция, используемая для расчета затраты на ведение бизнеса; обычно состоит из двух частей: постоянных затрат и переменных затрат

зависимая система система линейных уравнений, в которой два уравнения представляют одну и ту же прямую; существует бесконечное число решений зависимой системы

несовместная система система линейных уравнений, не имеющая общего решения, так как они представляют собой параллельные прямые, не имеющие общих точек или прямых

независимая система система линейных уравнений, имеющая ровно одно решение, пара [латекс]\слева (x,y\right)[/latex]

функция прибыли функция прибыли записывается как [latex]P\left(x\right)=R\left(x\right)-C\left(x\ справа)[/latex], доход минус стоимость

функция дохода функция, используемая для расчета дохода, просто записывается как [latex]R=xp[/latex], где [latex]x=[/latex] количество и [latex]p=[/latex] цена

замена метод алгебраический метод, используемый для решения систем линейных уравнений, в котором одно из двух уравнений решается для одной переменной, а затем подставляется во второе уравнение для решения второй переменной

система линейных уравнений набор из двух или несколько уравнений с двумя или более переменными, которые необходимо рассматривать одновременно.