Web in Math: Как строить графики функций в Wolfram
Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5
В двух предыдущих примерах мы задавали область значений аргумента х. А что будет, если мы не будем задавать область значений х?
Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:
Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.
Как и в одномерном случае, Wolfram | Alpha автоматически определяет подходящий диапазон значений аргументов, где функция имеет наиболее характерный вид. В случае, если Wolfram | Alpha не может найти подходящий диапазон, то это скорее всего потому, что система не смогла определить такой диапазон, где функция имеет наиболее интересное поведение. В этом случае, мы можем задать диапазон вручную, как это было сделано выше. Посмотрите следующие примеры:
Wolfram | Alpha строит отдельный график для каждой функции в списке. Вот еще несколько примеров:
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям).
 Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.
Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.
Источник by Sam Blake
Больше информации по использованию Wolfram|Alpha вы найдете в блоге
Matplotlib. Урок2. Работа с инструментом pyplot
Практически все задачи, связанные с построением графиков, можно решить, используя возможности, которые предоставляет модуль pyplot. В рамках данного урока мы рассмотрим базовые возможности модуля для построения графиков.
Для того, чтобы запустить любой из примеров, продемонстрированных в первом уроке (“Matplolib. Урок 1. Быстрый старт), вам предварительно нужно было импортировать pyplot из библиотеки Matplolib. В настоящее время среди пользователей этого инструмента принято импорт производить следующим образом:
Урок 1. Быстрый старт), вам предварительно нужно было импортировать pyplot из библиотеки Matplolib. В настоящее время среди пользователей этого инструмента принято импорт производить следующим образом:
import matplotlib.pyplot as plt
Создатели Matplolib постарались сделать его похожим в использовании на MATLAB, так что если вы знакомы с последним, то разобраться с библиотекой будет проще.
Основы работы с pyplotПостроение графиковОсновным элементом изображения, которое строит pyplot является Фигура (Figure), на нее накладываются один или более графиков, осей, надписей и т.п. Для построения графика используется команда plot(). В самом минимальном варианте можно ее использовать без параметров:
import matplotlib.pyplot as plt %matplotlib inline plt.plot()
В результате будет выведено пустое поле:
Далее команду импорта и magic-команду для Jupyter (первая и вторая строки приведенной выше программы) мы использовать не будем.
Если в качестве параметра функции plot() передать список, то значения из этого списка будут отложены по оси ординат (ось y), а по оси абсцисс (ось x) будут отложены индексы элементов массива:
plt.plot([1, 7, 3, 5, 11, 1])
Для того, чтобы задать значения по осям x и y необходимо в plot() передать два списка:
plt.plot([1, 5, 10, 15, 20], [1, 7, 3, 5, 11])Текстовые надписи на графике
Наиболее часто используемые текстовые надписи на графике это:
- наименование осей;
- наименование самого графика;
- текстовое примечание на поле с графиком;
- легенда.
Рассмотрим кратко данные элементы, более подробный рассказ о них будет в одном из ближайших уроков.
Наименование осейДля задания подписи оси x используется функция xlabel(), оси y – ylabel(). Разберемся с аргументами данных функций. Здесь и далее аргументы будем описывать следующим образом:
Разберемся с аргументами данных функций. Здесь и далее аргументы будем описывать следующим образом:
- Имя_аргумента: тип(ы)
Для функций xlabel()/ylabel() основными являются следующие аргументы:
- xlabel (или ylabel):str
- Текст подписи.
- labelpad : численное значение либо None; значение по умолчанию: None
- Расстояние между областью графика, включающую оси, и меткой.
Функции xlabel()/ylabel() принимают в качестве аргументов параметры конструктора класса matplotlib.text.Text, некоторые из них нам могут пригодиться:
- fontsize или size: число либо значение из списка: {‘xx-small’, ‘x-small’, ‘small’, ‘medium’, ‘large’, ‘x-large’, ‘xx-large’}.
- Размер шрифта.
- fontstyle: значение из списка: {‘normal’, ‘italic’, ‘oblique’}.
- fontweight: число в диапазоне от 0 до 1000 либо значение из списка: {‘ultralight’, ‘light’, ‘normal’, ‘regular’, ‘book’, ‘medium’, ‘roman’, ‘semibold’, ‘demibold’, ‘demi’, ‘bold’, ‘heavy’, ‘extra bold’, ‘black’}.

- Толщина шрифта.
- color: одни из доступных способов определения цвета см. Цвет линии.
Пример использования:
plt.xlabel('Day', fontsize=15, color='blue')Аргументов у этих функций довольно много и они позволяют достаточно тонко настроить внешний вид надписей. В рамках этого урока мы только начинаем знакомиться с инструментом
Для задания заголовка графика используется функция title():
plt.title('Chart price', fontsize=17)Из параметров отметим следующие:
- label: str
- Текст заголовка.
- loc: значение из набора {‘center‘, ‘left‘, ‘right‘}
- Выравнивание заголовка.
Для функции title() также доступны параметры конструктора класса matplotlib. text.Text, часть из них представлена в описании аргументов функций xlabel() / ylabel().
text.Text, часть из них представлена в описании аргументов функций xlabel() / ylabel().
За размещение текста на поле графика отвечает функция text(), которой вначале передаются координаты позиции надписи, после этого – текст самой надписи.
plt.text(1, 1, 'type: Steel')Легенда
Легенда будет размещена на графике, если вызвать функцию legend(), в рамках данного урока мы не будем рассматривать аргументы этой функции.
Разместим на уже знакомом нам графике необходимый набор подписей.
x = [1, 5, 10, 15, 20]
y = [1, 7, 3, 5, 11]
plt.plot(x, y, label='steel price')
plt.title('Chart price', fontsize=15)
plt.xlabel('Day', fontsize=12, color='blue')
plt.ylabel('Price', fontsize=12, color='blue')
plt.legend()
plt.grid(True)
plt.text(15, 4, 'grow up!')К перечисленным опциям мы добавили сетку, которая включается с помощью функции grid(True).
В этом параграфе мы рассмотрим основные параметры и способы их задания для изменения внешнего вида линейного графика. Matplotlib предоставляет огромное количество инструментов для построения различных видов графиков. Так как наиболее часто встречающийся вид графика – это линейный, ему и уделим внимание. Необходимо помнить, что настройка графиков других видов, будет осуществляться сходным образом.
Параметры, которые отвечают за отображение графика можно задать непосредственно в самой функции plot():
plt.plot(x, y, color='red')
Либо воспользоваться функцией setp(), через которую можно модифицировать нужные параметры:
plt.setp( color='red', linewidth=1)Стиль линии графика
Стиль линии графика задается через параметр linestyle, который может принимать значения из приведенной ниже таблицы.
| Значение параметра | Описание |
| ‘-‘ или ‘solid’ | Непрерывная линия |
| ‘–‘ или ‘dashed’ | Штриховая линия |
| ‘-.’ или ‘dashdot’ | Штрихпунктирная линия |
| ‘:’ или ‘dotted’ | Пунктирная линия |
| ‘None’ или ‘ ‘ или ” | Не отображать линию |
Стиль линии можно передать сразу после указания списков с координатами без указания, что это параметр linewidth.
x = [1, 5, 10, 15, 20] y = [1, 7, 3, 5, 11] plt.plot(x, y, '--')
Либо можно воспользоваться функцией setp():
x = [1, 5, 10, 15, 20] y = [1, 7, 3, 5, 11] line = plt.plot(x, y) plt.setp(line, linestyle='--')
Результат будет тот же, что на рисунке выше.
Для того, чтобы вывести несколько графиков на одном поле необходимо передать соответствующие наборы значений в функцию plot().
x = [1, 5, 10, 15, 20] y1 = [1, 7, 3, 5, 11] y2 = [i*1.2 + 1 for i in y1] y3 = [i*1.2 + 1 for i in y2] y4 = [i*1.2 + 1 for i in y3] plt.plot(x, y1, '-', x, y2, '--', x, y3, '-.', x, y4, ':')
Тот же результат можно получить, вызвав plot() для построения каждого графика по отдельности. Если вы хотите представить каждый график отдельно на своем поле, то используйте для этого subplot() (см. Размещение графиков на разных полях)
plt.plot(x, y1, '-') plt.plot(x, y2, '--') plt.plot(x, y3, '-.') plt.plot(x, y4, ':')Цвет линии
Задание цвета линии графика производится через параметр color (или c, если использовать сокращенный вариант). Значение может быть представлено в одном из следующих форматов:
- RGB или RGBA кортеж значений с плавающей точкой в диапазоне [0, 1] (пример: (0.
 1, 0.2, 0.3)
1, 0.2, 0.3) - RGB или RGBA значение в hex формате (пример: ‘#0a0a0a’)
- строковое представление числа с плавающей точкой в диапазоне [0, 1] (определяет цвет в шкале серого) (пример: ‘0.7’)
- символ из набора {‘b’, ‘g’, ‘r’, ‘c’, ‘m’, ‘y’, ‘k’, ‘w’}
- имя цвета из палитры X11/CSS4
- цвет из палитры xkcd(https://xkcd.com/color/rgb/), должен начинаться с префикса ‘xkcd:’
- цвет из набора Tableau Color (палитра T10), должен начинаться с префикса ‘tab:’
Если цвет задается с помощью символа из набора {‘b’, ‘g’, ‘r’, ‘c’, ‘m’, ‘y’, ‘k’, ‘w’}, то он может быть совмещен со стилем линии в рамках параметра fmt функции plot().
Например штриховая красная линия будет задаваться так: ‘–r’, а штрих пунктирная зеленая так ‘-.g’
x = [1, 5, 10, 15, 20] y = [1, 7, 3, 5, 11] plt.plot(x, y, '--r')Тип графика
До этого момента мы работали только с линейными графиками, функция plot() позволяет задать тип графика: линейный либо точечный, при этом для точечного графика можно указать соответствующий маркер. Приведем пару примеров:
Приведем пару примеров:
plt.plot(x, y, 'ro')
plt.plot(x, y, 'bx')
Размер маркера можно менять, об этом более подробно будет рассмотрено в уроке, посвященном точечным графикам.
Размещение графиков на разных поляхСуществуют три основных подхода к размещению нескольких графиков на разных полях:
- использование функции subplot() для указания места размещения поля с графиком;
- использование функции subplots() для предварительного задания сетки, в которую будут укладываться поля;
- использование GridSpec, для более гибкого задания геометрии размещения полей с графиками в сетке.
В этом уроке будут рассмотрены первые два подхода.
Работа с функцией subplot()Самый простой способ представить графики в отдельных полях – это использовать функцию supplot() для задания их мест размещения. До этого момента мы не работали с Фигурой (Figure) напрямую, значения ее параметров, задаваемые по умолчанию, нас устраивали. Для решения текущей задачи придется один из параметров – размер подложки, задать вручную. За это отвечает аргумент figsize функции figure(), которому присваивается кортеж из двух float элементов, определяющих высоту и ширину подложки.
До этого момента мы не работали с Фигурой (Figure) напрямую, значения ее параметров, задаваемые по умолчанию, нас устраивали. Для решения текущей задачи придется один из параметров – размер подложки, задать вручную. За это отвечает аргумент figsize функции figure(), которому присваивается кортеж из двух float элементов, определяющих высоту и ширину подложки.
После задания размера, указывается местоположение, куда будет установлено поле с графиком с помощью функции subplot(). Чаще всего используют следующие варианты вызова subplot:
subplot(nrows, ncols, index)
- nrows: int
- Количество строк.
- ncols: int
- Количество столбцов.
- index: int
- Местоположение элемента.
subplot(pos)
- pos:int
- Позиция, в виде трехзначного числа, содержащего информацию о количестве строк, столбцов и индексе, например 212, означает подготовить разметку с двумя строками и одним столбцов, элемент вывести в первую позицию второй строки.
 Этот вариант можно использовать, если количество строк и столбцов сетки не более 10, в ином случае лучше обратиться к первому варианту.
Этот вариант можно использовать, если количество строк и столбцов сетки не более 10, в ином случае лучше обратиться к первому варианту.
- Позиция, в виде трехзначного числа, содержащего информацию о количестве строк, столбцов и индексе, например 212, означает подготовить разметку с двумя строками и одним столбцов, элемент вывести в первую позицию второй строки.
Рассмотрим на примере работу с данными функциями:
# Исходный набор данных x = [1, 5, 10, 15, 20] y1 = [1, 7, 3, 5, 11] y2 = [i*1.2 + 1 for i in y1] y3 = [i*1.2 + 1 for i in y2] y4 = [i*1.2 + 1 for i in y3] # Настройка размеров подложки plt.figure(figsize=(12, 7)) # Вывод графиков plt.subplot(2, 2, 1) plt.plot(x, y1, '-') plt.subplot(2, 2, 2) plt.plot(x, y2, '--') plt.subplot(2, 2, 3) plt.plot(x, y3, '-.') plt.subplot(2, 2, 4) plt.plot(x, y4, ':')
Второй вариант использования subplot():
# Вывод графиков plt.subplot(221) plt.plot(x, y1, '-') plt.subplot(222) plt.plot(x, y2, '--') plt.subplot(223) plt.plot(x, y3, '-.') plt.subplot(224) plt.plot(x, y4, ':')Работа с функцией subplots()
Одно из неудобств использования последовательного вызова функций subplot() заключается в том, что каждый раз приходится указывать количество строк и столбцов сетки. Для того, чтобы этого избежать, можно воспользоваться функцией subplots(), из всех ее параметров, нас пока интересуют только первые два, через них передается количество строк и столбцов сетки. Функция subplots() возвращает два объекта, первый – это Figure, подложка, на которой будут размещены поля с графиками, второй – объект или массив объектов Axes, через которые можно получить полных доступ к настройке внешнего вида отображаемых элементов.
Для того, чтобы этого избежать, можно воспользоваться функцией subplots(), из всех ее параметров, нас пока интересуют только первые два, через них передается количество строк и столбцов сетки. Функция subplots() возвращает два объекта, первый – это Figure, подложка, на которой будут размещены поля с графиками, второй – объект или массив объектов Axes, через которые можно получить полных доступ к настройке внешнего вида отображаемых элементов.
Решим задачу вывода четырех графиков с помощью функции subplots():
fig, axs = plt.subplots(2, 2, figsize=(12, 7)) axs[0, 0].plot(x, y1, '-') axs[0, 1].plot(x, y2, '--') axs[1, 0].plot(x, y3, '-.') axs[1, 1].plot(x, y4, ':')
Результат будет аналогичный тому, что приведен в разделе “Работа с функцией subplot()”.
P.S.Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Методы графического сложения, вычитания.
Чтобы построить график функции y = f(x) + g(x) , надо построить на одном чертеже графики y = f(x) и y = g(x) , потом при каждом x сложить ординаты двух графиков.
Если необходимо построить график разности двух функций y = f(x) — g(x) ,
то этот случай сводится к построению суммы: y = f(x) + ( — g(x)) .
Причем, график функции y = — g(x) получается из графика функции y = g(x) симметричным отражением относительно оси OX .
В случае, когда вторая функция — константа, то графическое сложение означает сдвиг графика первой функции по вертикали на эту константу, причем, если константа положительная, то сдвиг осуществляется вверх, а если отрицательная, то вниз.
Чтобы построить график функции y=f(x)·g(x) , надо построить на одном чертеже графики y=f(x) и y=g(x) , потом при каждом x перемножить ординаты двух графиков.
Графическое деление выполняется аналогично произведению.
В частном случае при построении графика функции y=A·f(x) , где A — константа надо график функции y=f(x) растянуть в |A| раз по вертикали, при условии |A|≥1 , или сжать в раз по вертикали, если |A|<1 , и затем полученный график отобразить симметрично относительно оси OX, если A<0 .
В данном параграфе рассмотрены следующие примеры:
| Умножение двух функций: | Делениее двух функций: |
| Умножение функции на константу A > 0: | Умножение функции на константу A < 0: |
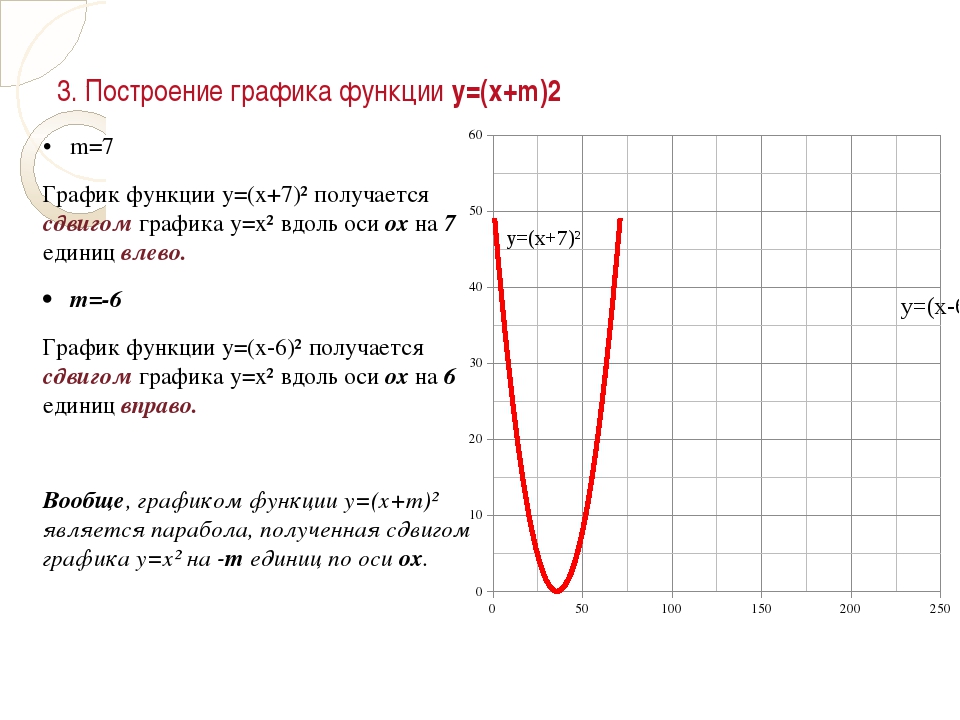
Построение графика функции по точкам.
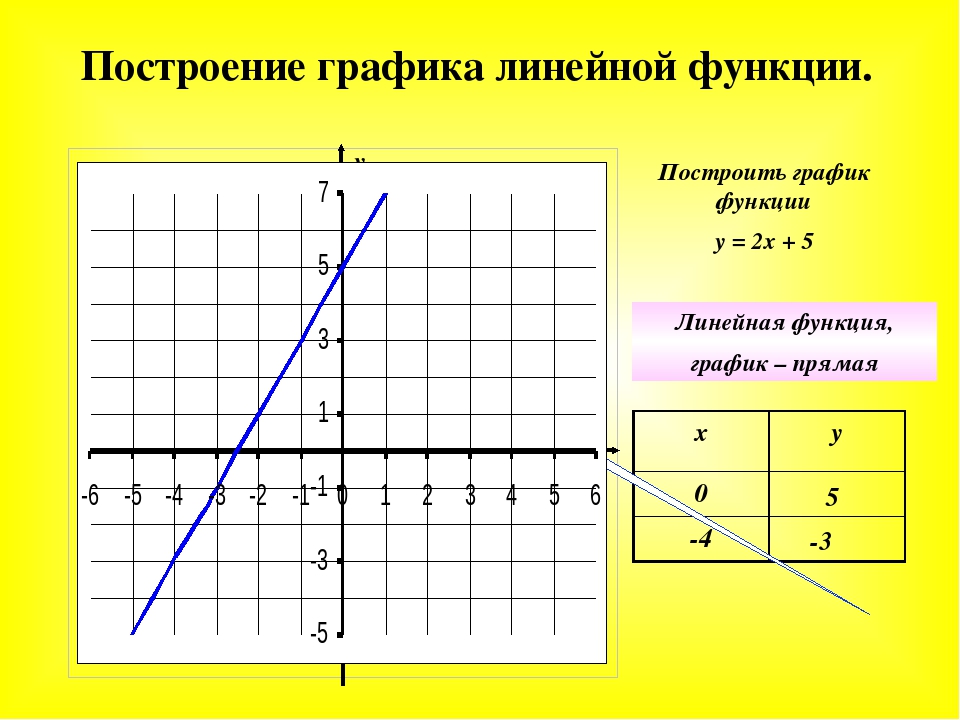 Построение нескольких графиков в одной системе координат
Построение нескольких графиков в одной системе координатМетодические указания по проведению лабораторных работ по дисциплине 1422 в среде Mathcad.
В рамках данных лабораторных работ вам предстоит построить ряд графиков, на основе данных, формируемых моделирующей программой.
Перед выполнением лабораторных работ с моделирующей программой рекомендуется потренироваться строить графики на следующих примерах.
1. Построим по точкам график функции y(x)=x2 в диапазоне от 0 до 5 с шагом 0.1 для этого в рабочем поле Mathcad а) укажем диапазон изменений переменной х. Набираем следующую комбинацию клавиш:
х : 0 , 0 . 1 ; 5
На экране появится следующая картина:
x:=0,0.1..50
Обратите внимание:
• Mathcad регистрочувствителен!
• следите, за тем, где точки, а где запятые,
•
0.1- это второе значение переменной х, а не значение шага!!!
(хоть они и совпадают) . б) Зададим функцию у(х) Набираем:
б) Зададим функцию у(х) Набираем:
y ( x ) : x Shift+6 2 Enter
в) поместив курсор ниже введенных выражений, так , чтобы вокруг него было достаточно места, наберем комбинацию
Она создаст нам заготовку под график, в которой для нас важны пока только черные поля для ввода переменных в центре нижней и левой границ графика.
В нижнем поле набираем
В левом поле
После нажатия Enter на экране будет нарисован график, подобный показанному на рис.1.1
Рисунок 1.1
Дважды щелкнув по графику можно изменить стиль его оформления (цвет, тип и толщину линий, подписи и типы осей, заголовок и др.) C этими настройками предлагается ознакомиться самостоятельно.
Внимание! Для адекватного отображения кириллицы необходимо щелкнуть мышью по любой переменной внутри Mathcad-документа и выбрать любой из шрифтов, имя которого заканчивается на «cyr» или «CYR»
2. Построение графиков по массивам точек. Предположим,
нам задан следующий массив точек:
Построение графиков по массивам точек. Предположим,
нам задан следующий массив точек:
|
0 |
1 |
2 |
3 |
5 |
8 |
13 |
|
1 |
1,7 |
2,82 |
3,4 |
4,46 |
5,64 |
7,21 |
а) Обозначим его через А и внесем в Mathcad следующим образом:
A : Ctrl+M
В появившемся диалоговом окне
зададим число строк 2, число столбцов 7.
б) Для индексации элементов массива (а точнее для обращения к отдельным, автоматически проиндексированным элементам массива) введем дискретную переменную I i : 0 ; 6 Enter
Обратите внимание, что
• в Mathcad индексация элементов массива всегда начинается с 0,
• по умолчанию (если он явно не задан) шаг изменения дискретной переменной равен единице в) щелкаем мышью на свободном месте документа и набираем
для создания заготовки графика в уже знакомых нам нижнем и левом полях соответственно набираем:
A [ 0 , i Enter
A [ 1 , i Enter
на экране увидим картину, подобную показанной на рис. 1.2
Рисунок 1.2
3. Построение нескольких графиков в одной системе координат. Зададимся целью добавить в нашей первой СК график
y1(x)=x3/4
для этого а) ВЫШЕ!!! первой СК набираем:
y 1 ( x ) : x Shift+6 3 / 4
б) Щелкаем мышью в левой части графика, там, где мы вводили
y(x). клавишами управления курсором добиваемся, чтобы синий уголок текстового
курсора охватывал весь текст у(х), и более того, был бы правым нижним
углом
клавишами управления курсором добиваемся, чтобы синий уголок текстового
курсора охватывал весь текст у(х), и более того, был бы правым нижним
углом
в) набираем запятую, у нас появится поле ввода для еще одной линии на графике. г) вводим в это поле
y 1 ( x ) Enter
И в СК появляется еще одна линия.
Аналогичным образом вторая линия добавляется и при построении графика по значениям таблицы.
A [ *** , i Enter
Нужно лишь вместо *** следует указывать номер строки и очень внимательно следить, чтобы синяя рамочка выделяла ВСЕ поле, отвечающее за отдельную линию графика.
2 ЛАБОРАТОРНАЯ РАБОТА №2
ИССЛЕДОВАНИЕ ВЛИЯНИЯ LC-ПАРАМЕТРОВ КАНАЛА СВЯЗИ НА ФОРМУ СИГНАЛА.
Данная
лабораторная работа состоит из двух частей: в первой части Вам предстоит
анализировать изменение синусоидального сигнала, во второй части искажение
импульса с заданным по варианту профилем.
2.1. Анализ изменения синусоидального сигнала
Откройте новый документ Mathcad, задайте частоту f (согласно варианту)
|
f : 1 0 Shift+6 и функцию изменения входного сигнала |
6 |
Enter |
U 1 ( t , f ) : s i n ( f * t )
Задайте диапазон изменения времени:
t : 0 , 1 0 Shift+6 — 8 ; 1 0 Shift+6
Постройте график.
Реальная (не идеальная) линия связи может быть представлена следующей электрической схемой:
Нетрудно показать, что передаточная функция одного звена будет задаваться формулой:
где р- оператор Лапласа
R – активное сопротивление звена
L — индуктивность звена
C — емкость звена
Передаточная функция всей цепи будет равна произведению передаточных функций элементарных звеньев. Для простоты предполагаем, что R,L,C- параметры всех звеньев идентичны. Сигнал на выходе цепи (в операторной форме) будет выглядеть как:
Иллюстрированный самоучитель по Mathematica 3/4 › Графика и звук › Перестроение и комбинирование графиков [страница — 186] | Самоучители по математическим пакетам
Перестроение и комбинирование графиков
При построении графиков часто требуется изменение их вида и тех или иных параметров и опций. Этого можно достичь повторением вычислений, но при этом скорость работы с системой заметно снижается. Для ее повышения удобно использовать специальные функции перестроения и вывода графиков, учитывающие, что узловые точки уже рассчитаны и большая часть опций уже задана. В этом случае удобно использовать следующую функцию-директиву:
- Show [plot] – построение графика;
- Show [plot, option › value] – построение графика с заданной опцией;
- Show [plot1, plot2,…] – построение нескольких графиков с наложением их друг на друга.
Директива Show полезна также и в том случае, когда желательно, не трогая исходные графики, просмотреть их при иных параметрах. Соответствующие опции, меняющие параметры графиков, можно включить в состав директивы Show. Другое полезное применение директивы – объединение на одном графике нескольких графиков различных функций или объединение экспериментальных точек и графика теоретической зависимости. Для этого также удобна функция Display-Together, которая будет описана при описании пакета расширения Graphics в уроке 14. В отличие от функции Show, она позволяет объединять графики без предварительного построения каждого из них.
Рисунок 8.9 показывает создание двух графических объектов g1 и g2 с отложенным выводом, а затем построение графиков функций и применение директивы Show для создания объединенного графика. В этом случае директива Show вначале строит исходные графики отдельно, а затем создает объединенный график. В приведенных ниже примерах оставлен только объединенный график, другие удалены командой меню Edit › Clear.
Рис. 8.9. Построение двух графических объектов и их объединение
Разумеется, при использовании директивы Show надо побеспокоиться о выравнивании масштабов графиков, налагаемых друг на друга. Полезно особо обратить внимание на возможность присваивания графиков функций переменным (в нашем примере – g1 и g2) в качестве значений. Такие переменные становятся графическими объектами, используемыми директивой Show для вывода на экран дисплея.
Директива Show часто применяется, когда надо построить на одном графике кривую некоторой функции и представляющие ее узловые точки (например, при построении кривых регрессии в облаке точек исходных данных).
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
| ||||
Построение графиков функций двух переменных
Военное дело Построение графиков функций двух переменных
просмотров — 410
В Mathcad возможно построение графиков функций двух переменных в прямоугольной (декартовой), сферической и цилиндрической системах координат. Рассмотрим, как в них задаются координаты точки.
В декартовой системе координат положение точки в пространстве задается тремя координатами (рис. 4.7): (x, y z). Для построения графика должна быть задана функция, описывающая закон изменения аппликаты .
В сферической системе координат (рис. 4.8) положение точки задается радиусом , углами и . Для построения графика должна быть задана функция, описывающая закон изменения .
В цилиндрической системе координат (рис. 4.9) положение точки задается углом , радиусом и координатой . При построении графика в цилиндрической системе координат должна быть задана зависимость .
Для построения поверхности в выбранной системе координат крайне важно:
1. Определить функцию двух переменных.
2. Выбрать вид графика, нажав одну из кнопок панели инструментов Graph: — в виде поверхности, образованной линиями сетки, — в виде линий уровня, — в виде прямоугольных параллелепипедов с одинаковыми основаниями, — в виде отдельных точек, принадлежащих его поверхности. Тип графика впоследствии может быть изменен на вкладке General диалогового окна 3-D Plot Format, ĸᴏᴛᴏᴩᴏᴇ вызывается командой Format/Graph/3D Plot или командой Format из контекстного меню, появляющегося при щелчке правой кнопкой мыши в области графика (или двойной щелчок мышью на области графика).
| 3. В ячейке под системой координат ввести имя функции, описывающей поверхность. По умолчанию график функции будет построен в декартовой системе координат. Для задания сферической или цилиндрической системы координат крайне важно в диалоговом окне задания формата графика 3-D Plot Format задать на вкладке Quick Plot Data ( поле Coordinate System) желаемую систему координат (рис. 4.10): Cartesian (декартова), Spherical (сферичекая), Cylindrical (цилиндрическая). | Рисунок 4.10- Вкладка Quick Plot Data диалогового окна 3-D Plot Format |
К примеру (рис. 4.11), функция в декартовой системе координат описывает плоскость, параллельную плоскости xy, в цилиндрической – цилиндр радиусом 10, в сферической – сферу радиусом 10.
Рисунок 4.11 – Построение графика в цилиндрической, сферической и декартовой системах координат.
На рис. 4.12 приведен график функции в виде поверхности, линий уровня, отдельных точек, принадлежащих графику, прямоугольных параллелепипедов и др. Mathcad предоставляет большие возможности в области форматирования графиков (см. методические указания к лабораторным работам).
Рисунок 4.12 – Возможности форматирования графиков
Для построения графика функции двух переменных можно использовать предварительно созданную матрицу, каждый элемент которой равен аппликате поверхности. Для этого вместо имени функции следует ввести имя матрицы (рис.4.13).
Рисунок 4.13- Использование значений элементов массива в качестве аппликат при построении трехмерного графика
На вкладке Quick Plot Data диалогового окна 3-D Plot Format (рис. 4.10) бывают введены начальное (start) и конечное (end) значения аргументов функции двух переменных и шаг их изменения (задается косвенно в поле # of Grids – число линий сетки). На рис. 4.14 график состоит из 8 фрагментов сферы, для каждого из которых соответствующим образом заданы начальное и конечное значение углов (Range 1) и (Range 2) (см. рис. 4.8).
Рисунок 4.14 – Использование диалогового окна 3-D Plot Format для ввода начальных и конечных значений аргументов, выбора системы координат.
Для построения графика функции двух переменных, заданной параметрически, в ячейке под областью графика следует ввести в круглых скобках через запятую имена функций, задающих законы изменения их декартовых координат.
Размер области любого графика может быть изменен. Для этого его крайне важно выделить, переместить указатель мыши на черный маркер, расположенный на правой, нижней стороне рамки или в правом нижнем углу области графика, нажать левую кнопку мыши и, не отпуская, перемещать в нужном направлении.
Создание макета мозаичной диаграммы — MATLAB tiledlayout
Когда вы создаете макет мозаичной диаграммы, некоторые из свойств TileSpacing и Padding предоставляют другой результат или имеют новые имена.
Новые варианты TileSpacing : «свободно» , «компактно» , «плотно» и «нет» . Новые варианты Padding : «свободная» , «компактная» и «плотная» . В следующих таблицах описано, как предыдущие параметры соотносятся с новыми параметрами.
TileSpacing Изменения
Предыдущий TileSpacing Option | R2021a TileSpacing Option | Как обновить свой код |
|---|---|---|
| | Рассмотрите возможность замены экземпляров Вариант |
| | Никаких изменений не требуется. |
| Не применимо | | |
| | Параметр Чтобы сохранить интервал между рамками графика, измените экземпляры |
Заполнение Изменения
Предыдущий Заполнение Опция | R2021a Заполнение Опция | Как обновить код |
|---|---|---|
| | Рассмотрите возможность замены экземпляров Вариант |
| | Никаких изменений не требуется. |
| | Рассмотрите возможность замены экземпляров Параметр |
Quick-R: объединение графиков
R позволяет легко объединить несколько графиков в один общий график, используя функцию
par () или layout () .
С помощью функции par () вы можете включить опцию mfrow = c ( nrows , ncols ) для создания матрицы из nrows x ncols графиков, которые заполняются построчно. mfcol = c ( nrows , ncols ) заполняет матрицу по столбцам.
# 4 фигуры, расположенные в 2 строки и 2 столбца
прикрепить (mtcars)
par (mfrow = c (2,2))
plot (wt, mpg, main = "Scatterplot of wt vs. mpg")
plot ( wt, disp, main = "Диаграмма рассеяния wt vs disp")
hist (wt, main = "Гистограмма wt")
boxplot (wt, main = "Boxplot of wt")
нажмите для просмотра
# 3 фигуры, расположенные в 3 ряда и 1 столбец
прикрепить (mtcars)
par (mfrow = c (3,1))
hist (wt)
hist (миль на галлон)
hist (disp)
нажмите для просмотра
Функция layout () имеет вид layout ( mat ) , где
mat — матричный объект, определяющий расположение N фигур для построения.
# Одна цифра в строке 1 и две цифры в строке 2
attach (mtcars)
layout (matrix (c (1,1,2,3), 2, 2, byrow = TRUE))
hist (wt)
гист (миль на галлон)
гист (дисп)
нажмите для просмотра
При желании вы можете включить параметры widths = и heights = в функцию layout () для более точного управления размером каждой фигуры. Эти параметры имеют вид
widths = вектор значений ширины столбцов
heights = вектор значений высот строк.
Относительная ширина указывается числовыми значениями. Абсолютная ширина (в сантиметрах) указывается с помощью функции lcm () .
# Одна цифра в строке 1 и две цифры в строке 2
# строка 1 составляет 1/3 высоты строки 2
# столбец 2 равен 1/4 ширины столбца 1
прикрепить (mtcars)
макет (матрица (c (1,1,2,3), 2, 2, byrow = TRUE),
widths = c (3,1), heights = c (1,2))
hist (wt)
hist (миль на галлон)
hist (disp)
нажмите для просмотра
Подробности см. В справке (макет) .
Создание расстановки фигур с точным управлением
В следующем примере к диаграмме рассеяния добавляются две ящичные диаграммы для создания расширенного графика.
# Добавить коробчатые диаграммы к диаграмме рассеивания
par (fig = c (0,0.8,0,0.8), new = TRUE)
plot (mtcars $ wt, mtcars $ mpg, xlab = "Car Weight",
ylab = " Миль на галлон ")
номиналов (fig = c (0,0.8,0.55,1), новое = TRUE)
boxplot (mtcars $ wt, horizontal = TRUE, axes = FALSE)
par (fig = c (0.65,1 , 0,0.8), new = TRUE)
boxplot (mtcars $ mpg, axes = FALSE)
mtext ("Enhanced Scatterplot", side = 3, external = TRUE, line = -3)
нажмите для просмотра
Чтобы понять этот график, представьте, что вся область графика идет от точки (0,0) в нижнем левом углу до (1,1) в правом верхнем углу.Формат параметра fig = представляет собой числовой вектор вида c (x1, x2, y1, y2). Первый fig = устанавливает диаграмму рассеяния от 0 до 0,8 по оси x и от 0 до 0,8 по оси y. Верхняя прямоугольная диаграмма изменяется от 0 до 0,8 по оси x и от 0,55 до 1 по оси y. Я выбрал 0,55, а не 0,8, чтобы верхняя цифра была приближена к диаграмме рассеяния. Правый прямоугольный график изменяется от 0,65 до 1 по оси x и от 0 до 0,8 по оси y. Опять же, я выбрал значение, чтобы приблизить правую коробчатую диаграмму к диаграмме рассеяния.Вы должны поэкспериментировать, чтобы понять это правильно.
fig = запускает новый график, поэтому для добавления к существующему используйте new = TRUE .
Вы можете использовать это, чтобы объединить несколько графиков в любом порядке в один график.
к практике
Попробуйте бесплатную первую главу этого интерактивного курса визуализации данных, в которой рассматривается комбинирование графиков.
Как построить две вещи на одной оси Y в Excel | Small Business
Правильно отформатированные диаграммы и графики могут помочь вам понять закономерности и тенденции, скрытые в необработанных данных электронной таблицы Excel.Например, если вы сравниваете динамику акций двух компаний за последний год, вы можете создать диаграмму, которая показывает цены акций каждой компании на одной диаграмме с одинаковыми осями X и Y. Microsoft Excel 2013 позволяет добавлять наборы данных в диаграмму по одному. Однако, если ваши данные расположены в правильном порядке, вы можете построить оба набора данных одновременно.
Добавление наборов данных по одному
Запустите Excel и загрузите электронную таблицу, содержащую данные, которые вы хотите построить.
Выберите первый набор данных осей X и Y для диаграммы.
Щелкните вкладку «Вставить», а затем выберите тип и подтип диаграммы, который вы хотите создать. Например, если вы строите график курсов акций с течением времени, вы можете использовать линейный график или диаграмму рассеяния. Этот набор данных обозначен как «Серия 1».
Щелкните правой кнопкой мыши пустое место на диаграмме, нажмите «Выбрать данные», а затем нажмите «Добавить».
Выберите значения оси Y для второго набора данных и нажмите «Enter».«Этот набор данных помечен как« Серия 2. »
График Два набора данных одновременно
Запустите Excel и начните новый пустой рабочий лист.
Введите данные по оси X в крайний левый столбец рабочего листа . Например, введите месяцы с 1 по 12 в столбце «A.»
Введите значение оси Y для первого набора данных в соседнем столбце. Например, введите цены акций для первой компании в столбце «B». . «
Введите значения оси Y для второго набора данных в столбец рядом с первым набором.Например, введите цены акций второй компании в столбце «C.»
Выберите все данные, которые вы хотите построить, щелкните вкладку «Вставить», а затем выберите тип и подтип диаграммы, которые вы хотите построить. На диаграмме должен отображаться отдельный график для первого и второго рядов данных на общей оси Y.
Ссылки
Писатель Биография
Аллен Бетеа пишет статьи по программированию, веб-дизайну, операционным системам и компьютерному оборудованию с 2002 года. Он имеет степень бакалавра наук UNC-Chapel Hill и степень AAS в области офисных технологий, машиностроения / черчения. и интернет-технологии.Аллен имеет обширный опыт работы с настольным и системным программным обеспечением для операционных систем Windows и Linux.
Построение графиков в Excel — наложение графиков
Наложение графиков
Содержание
- Наложение графиков
- Переформатирование нового графика
Введение
Если вы хотите объединить данные из двух графиков, а не создавать новый график с нуля, вы можете наложить на два, используя простую копию и вставить операцию.Перед наложением двух графиков примите во внимание следующее:
- Имеют ли два графика одну и ту же независимую переменную (ось X)? В противном случае не пытайтесь их объединить.
- Есть ли у двух графиков одна и та же зависимая переменная (ось Y)? В противном случае не пытайтесь их объединить.
- Как соотносятся данные на двух графиках? Обычно ты будет создавать вторую независимую переменную при наложении графики.Например, это могут быть два уровня общей переменной. В приведенном ниже примере два графика представляют два разных типа алюминиевый сплав.
- Имеют ли два графика одинаковые шкалы переменных и одинаковый диапазон? ценностей? Например, если первый график имеет значения зависимых переменных время от 0,1 до 2,5 секунд, а второй график — от 250 до 3500 секунд, масштаб наложенного графика, чтобы показать второго значения, будет очень трудно увидеть значения первое.
Наложение графиков
Ниже представлен график прочности на разрыв одного типа алюминия:
График был выбран щелчком внутри внешнего поля график. Обратите внимание, что когда выбран график, черные ящики (или «ручки») показать по периметру. Выбрав график, вы также можете увидеть независимые (деформация) и зависимые (стресс) данные выделены слева фиолетовым и синим цветом соответственно.Поскольку в графе есть только один независимый переменная, в легенде нет необходимости. Информация о том, что Независимые и зависимые переменные относятся к этому в названии.
В этом примере первый и второй график и их данные на той же странице рабочего листа:
Обратите внимание, что независимые и зависимые переменные идентичны, хотя диапазоны шкал немного отличаются.Второй график имеет Значения напряжения в диапазоне примерно до 70000 фунтов на квадратный дюйм по сравнению с 13500 psi на первом графике. На втором графике значения деформации только до приблизительно 0,20 дюйма / дюйм по сравнению с 0,38 дюйма / дюйм в первом варианте.
Чтобы наложить два графика, вы должны сначала создать копию одного графиков для использования в качестве основы для нового графика. Вам нужна копия на случай что-то происходит в процессе наложения. Для копирования графика:
- Выберите первую диаграмму (в данном случае 1100 Aluminium), щелкнув где-нибудь внутри внешней коробки (ручки задней коробки появятся вокруг периметр).
- Выберите в меню Правка> Копировать .
- Щелкните новую ячейку таблицы, которая приблизительно соответствует левый верхний угол того места, куда вы хотите поместить новый график.
- Выберите в меню « Правка»> «Вставить ».
Эта новая копия будет использоваться в качестве основы для наложенного графика. В настоящее время выберите второй график, чтобы начать процесс наложения:
- Выберите второй график (например,г., 2024 Алюминий) так выглядят ручки.
- Выберите в меню Правка> Копировать .
- Щелкните копию первого графика (например, 1100 Aluminium), чтобы ручки Это критический шаг, поскольку он указывает цель, в которой второй график нужно скопировать.
- Выберите в меню « Правка»> «Вставить ».
На новом наложенном графике теперь должны отображаться оба набора данных:
Обратите внимание, что название взято из второго графика (Алюминий 2024 г.).Также заметил, что при корректировке шкалы зависимой переменной (Напряжение) чтобы учесть больший диапазон второго графика, независимая переменная масштаб обрезал больший диапазон первого графика.
Вернуться к началу
Переформатирование нового графика
Вы можете настроить диапазон шкал, выбрав новый график и двойной щелчок на оси значение:
Выберите вкладку Масштаб и установите необходимый диапазон шкалы и единицы измерения.
В настоящее время в обеих сериях данных используются один и тот же цвет и символ. Это можно изменить, дважды щелкнув на одной из точек данных. на графике:
Теперь вы можете выбрать вкладку Patterns и выбрать новый стиль Style , Foreground и Background для маркеров ряда данных.
Поскольку у вас есть две независимые переменные на новом графике, вы тоже хочу показать легенду.Вы можете сделать это, выбрав график и выбирая Chart> Chart Options … , выбирая Legends вкладку и установите флажок Показать легенду .
Если текст в легенде не отражает должным образом второй независимый уровни переменных, вам нужно будет изменить это, выбрав график и переход к Диаграмма> Исходные данные …
- Выберите вкладку Series .
- Теперь выберите Series , имя которого нужно изменить.
- Введите новое имя в поле Имя :. Это может быть в виде показано выше, или просто введя имя (без кавычек) в поле.
Название на графике можно изменить, щелкнув один раз на заголовок и , выделив текст , который вы хотите изменить. В окончательный график в нашем примере выглядит так:
Вернуться к началу
Настроить-объединить-упорядочить-график СводкаДиалоговое окно Merge Graph Windows позволяет вам выбрать, какие графики вы хотите объединить, выбирая из любого графика в проекте.В нем также есть элементы управления, позволяющие указать, как вы хотите расположить отдельные графики на новой странице. Панель инструментов Object Edit позволяет быстро выравнивать и изменять размер нескольких слоев. Диалоговое окно Layer Management позволяет добавлять, упорядочивать и связывать слои на одной странице графика. Мини-панель инструментов (начиная с Origin 2020) позволяет легко и интерактивно редактировать элементы графика. Чему вы научитесьИз этого туториала Вы узнаете, как:
Выравнивание слоев с помощью панели инструментов редактирования объекта
Отображение противоположных осей с нелинейной формулойГрафический слой Origin 2D — это набор осей X, Y, причем противоположные оси могут быть включены как для X, так и для Y.Кроме того, противоположные оси могут также отображать метки с использованием любой заданной пользователем нелинейной формулы относительно первичной оси.
Использование управления слоями для связывания и расположения слоевИнструмент управления слоями можно использовать для позиционирования, изменения размера, обмена и связывания слоев:
Объединить несколько графиковВ этом разделе мы объединяем два графика из разных подпапок одного проекта, рассматривая четыре слоя в одном графике как единое целое.
|
Построение нескольких переменных
При исследовательском анализе данных часто бывает необходимо построить аналогичные графики сразу нескольких переменных. Например, рандомизированное испытание может рассматривать несколько исходов или опрос может содержать большое количество вопросов. Некоторые пакеты, например Minitab, позволяют легко помещать несколько переменных на один график с опцией «несколько Y».Вот способ добиться того же, используя R и ggplot2 .
Поворот дольше: преобразование переменных в строки
ggplot2 не обеспечивает удобных средств для одновременного построения нескольких переменных, поскольку обычно это признак того, что ваши данные не «аккуратны». Например, в ситуациях, когда вы хотите построить два столбца на графике в виде точек с разными цветами, эти два столбца часто действительно представляют одну и ту же переменную, и существует скрытый фактор группирования, который отличает точки данных, которые вы хотите раскрасить по-разному.Обычный ответ в этом сценарии состоит в том, что вы должны реструктурировать свои данные перед их построением. В качестве бонуса, вероятно, будет проще анализировать ваши данные в этой форме.
Аналогичным образом, если вы хотите разбить график на панели (или фасеты, в ggplot2 -speak), вы должны построить одну переменную ответа с переменной группировки, чтобы указать, на какой панели должны быть отображены данные. Лучшее Структура ваших данных зависит от того, что вы пытаетесь с ними делать, и в этой ситуации, даже если ваши данные находятся в правильной форме для анализа, она может быть неправильной для некоторых графиков, которые вы хотите построить.
К счастью, преобразовать данные в правильную форму несложно с помощью пакета tidyr и функции pivot_longer () . В этом примере я собираюсь посмотреть на макет данных опроса с шестью вопросами, хранящимися в переменных с Q1 до Q6 . Исходный фрейм данных выглядит так:
# # # Тибл: 300 x 7
# # группа Q1 Q2 Q3 Q4 Q5 Q6
# #
# # 1 В 4 1 4 1 2 3
# # 2 B 5 2 5 4 3 3
# # 3 В 5 4 4 2 2 3
# # 4 B 5 1 5 2 4 3
# # 5 A 5 2 5 1 1 2
# # 6 A 5 3 5 3 2 2
# # 7 A 4 3 5 1 4 1
# # 8 В 4 3 5 1 2 1
# # 9 В 4 4 4 1 3 2
# # 10 B 4 4 5 2 5 4
# # #... с еще 290 строками Вы можете преобразовать это в более длинный фрейм данных, где номер вопроса хранится в одном столбце, а ответ — в отдельном столбце:
long_data <- Survey_data%>%
pivot_longer (Q1: Q6, names_to = "question", values_to = "response")
print (long_data) # # # Тибл: 1,800 x 3
# # ответ на групповой вопрос
# #
# # 1 B Q1 4
# # 2 B 2 квартал 1
# # 3 B Q3 4
# # 4 B 4 квартал 1
# # 5 B Q5 2
# # 6 B Q6 3
# # 7 B Q1 5
# # 8 B 2 квартал
# # 9 B Q3 5
# # 10 B 4 квартал
# # #... с еще 1790 строками Вам даже не нужно хранить данные «длинной формы» как отдельную переменную. Если вы не собираетесь использовать данные в этой форме для чего-либо еще, проще передать данные прямо в ggplot2 . Здесь я использую функцию facet_wrap () для отображения каждого вопроса на отдельной панели, чтобы мы могли видеть распределение всех вопросов сразу:
survey_data%>%
pivot_longer (Q1: Q6, names_to = "question", values_to = "response")%>%
ggplot (aes (x = ответ)) +
geom_bar () +
facet_wrap (vars (вопрос), ncol = 3) +
labs (x = "Ответ (по шкале от 1 до 5)", y = "Количество респондентов") Вы можете использовать вопрос в качестве фактора в любом другом месте, где вы использовали бы категориальную переменную с ggplot.Например, вы можете создать коробчатые диаграммы:
Survey_data%>%
pivot_longer (Q1: Q6, names_to = "question", values_to = "response")%>%
ggplot (aes (y = ответ, x = вопрос)) +
geom_boxplot () +
labs (x = "Вопрос", y = "Ответ (по шкале от 1 до 5)") Это также хорошая демонстрация того, что ящичные диаграммы редко являются лучшим способом представления данных шкалы Лайкерта.
Любые другие переменные сохраняются после вызова pivot_longer () , поэтому вы можете e.г. сравните ответы на вопросы опроса на основе демографической переменной:
Survey_data%>%
pivot_longer (Q1: Q6, names_to = "question", values_to = "response")%>%
ggplot (aes (x = ответ, цвет = группа)) +
facet_wrap (vars (вопрос), ncol = 3) +
geom_point (stat = "count") +
geom_line (stat = "count") +
labs (x = «Ответ (по шкале от 1 до 5)», y = «Количество респондентов») По умолчанию R сортирует уровни факторов в алфавитном порядке.Это не всегда то, что вам нужно в данной ситуации — часто порядок переменных в вашем фрейме данных имеет какое-то значение. Функция fct_inorder () позволяет вам изменить порядок уровней фактора в порядке их первого появления в файле. Если вы используете это со столбцом, созданным pivot_longer () , коэффициент будет упорядочен по порядку столбцов в исходном фрейме данных.
Нарисуйте 2 графика на одном графике (пример R)
В этой статье показано, как нарисовать несколько графиков в одном окне графика на языке программирования R.
Учебник R структурирован следующим образом:
Перейдем к примеру кода!
Шаг 1: Постройте участок в R
Во-первых, мы собираемся нарисовать базовую диаграмму рассеяния в R. Давайте создадим несколько случайных данных:
set.seed (2525) # Установите посевной материал для воспроизводимости x1 <- rnorm (1000) # Нормально распределенный x1 y1 <- x1 + rnorm (1000) # Коррелированный y1 |
set.seed (2525) # Установить семя для воспроизводимости x1 <- rnorm (1000) # Нормально распределенный x1 y1 <- x1 + rnorm (1000) # Коррелированный y1
С помощью следующего программного кода мы можем нарисовать диаграмму рассеяния в R:
plot (x1, y1, col = "# 1b98e0", pch = 8) # График рассеяния x1 и y1 |
plot (x1, y1, col = "# 1b98e0", pch = 8) # Plot диаграмма рассеяния x1 & y1
Рисунок 1: Диаграмма рассеяния в R.
На следующем этапе мы построим второй график в том же окне графика. Так что продолжайте читать…
Шаг 2: Наложение второго графика
Рассмотрим следующий пример данных:
x2 <- runif (200, -1, 2) # Равномерно распределенный x2 y2 <- - x2 + runif (200) # Коррелированный y2 |
x2 <- runif (200, -1, 2) # Равномерно распределенный x2 y2 <- - x2 + runif (200) # Коррелированный y2
Мы можем объединить данные нашего нового примера с нашим графиком, который мы создали на шаге 1, следующим образом:
точек (x2, y2, col = "# 353436", pch = 15) # Наложение графика рассеяния x2 и y2 |
точек (x2, y2, col = "# 353436", pch = 15) # Наложение диаграммы рассеяния x2 и y2
Рисунок 2: Добавление второго графика к графику.
Примечание: Синтаксис R на шаге 2 такой же, как и на шаге 1, за исключением функции R, которую мы использовали: На шаге 1 мы использовали функцию plot () ; и на шаге 2 мы использовали функцию точек () .
Шаг 3: начертите линию наложения на график
Мы также можем смешать нашу исходную графику с линией (или несколькими линиями). Создадим еще данные:
x3 <- c (0, 2.5, -1, 0) # Некоторые точки на оси x y3 <- c (0, 4, 2, -3) # Некоторые точки на оси y |
x3 <- c (0, 2.5, -1, 0) # Некоторые точки на оси x y3 <- c (0, 4, 2, -3) # Некоторые точки на оси Y
Теперь мы можем использовать функцию lines () , чтобы добавить линию к нашему ранее созданному графику:
строк (x3, y3, col = "yellow", lwd = 3) # Наложение строки |
строк (x3, y3, col = "yellow", lwd = 3) # Наложение строки
Рисунок 3: Добавить линию к графику в R.
Примечание: В этом примере мы использовали диаграммы рассеяния и сплошные линии. Однако мы могли бы применить те же принципы к другим графикам и графикам (например, гистограмма, прямоугольная диаграмма, график плотности, гистограмма, QQplot и так далее…).
Видео и другие ресурсы
Я записал видео, в котором более подробно описывается пример этого урока. Нажмите ниже, чтобы посмотреть видео:
Пожалуйста, примите файлы cookie YouTube для воспроизведения этого видео. Согласившись, вы получите доступ к контенту YouTube, услуги, предоставляемой третьей стороной.
Политика конфиденциальности YouTube
Если вы примете это уведомление, ваш выбор будет сохранен, и страница обновится.
Принять контент YouTube
Хотите узнать о графиках в R еще больше? Тогда я могу порекомендовать взглянуть на следующую памятную памятку по графике, которую я создал на своем веб-сайте:
Кроме того, вы можете ознакомиться с некоторыми соответствующими руководствами, которые я опубликовал на своем веб-сайте:
Вкратце: В этом руководстве вы научились строить два графика и линию на одном графике.Помните о функциях точек и линий, поскольку они являются основой для рисования нескольких графиков на одной панели графика.

 1, 0.2, 0.3)
1, 0.2, 0.3) Этот вариант можно использовать, если количество строк и столбцов сетки не более 10, в ином случае лучше обратиться к первому варианту.
Этот вариант можно использовать, если количество строк и столбцов сетки не более 10, в ином случае лучше обратиться к первому варианту.
Ваш комментарий будет первым