Подробнее про Параметрическое представление
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) - другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксеканс asech(x), гиперболический арккосеканс acsch(x) - функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) - знак числа:
sign(x) - для теории вероятности:
функция ошибок erf(x) (интеграл вероятности), функция Лапласа laplace(x) - Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
- Тригонометрические интегралы: Si(x), Ci(x), Shi(x), Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.
 5, не 7,5
5, не 7,5
Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности
‘) window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: rtb_id, blockId: ‘R-A-1616620-2’ }) })
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
Сообщество Экспонента
- вопрос
- 06.04.2023
Цифровая обработка сигналов
Добрый день, уважаемые участники форума! Подскажите, пожалуйста, как можно забрать те данные, по которым был построен график спектра сигнала? Они мне нужны для дальнейшей нормировки в excel.
Добрый день, уважаемые участники форума! Подскажите, пожалуйста, как можно забрать те данные, по которым был построен график спектра сигнала? Они мне нужны для дальнейшей нормировки в excel.
- вопрос
- 04.04.2023
Цифровая обработка сигналов
End
End
1 Ответ
- вопрос
- 02.04.2023
Другое
Добрый день/вечер! подскажите, пожалуйста, как настроить матлаб чтобы можно было работать с ним удаленно. то есть он развернут на одной ПЭВМ, а мне нужно подключится с другой ПЭВМ, но не к виндоус чер…
Добрый день/вечер! подскажите, пожалуйста, как настроить матлаб чтобы можно было работать с ним удаленно. то есть он развернут на одной ПЭВМ, а мне нужно подключится с другой ПЭВМ, но не к виндоус чер…
- Публикация
- 29.03.2023
Глубокое и машинное обучение(ИИ)
Но давайте будем честными, для не технических менеджеров продуктов, дизайнеров и предпринимателей, внутреннее устройство ChatGPT может показаться как волшебный черный ящик. Не волнуйтесь! В этой статье я постараюсь объяснить технологию и модель, лежащие в осно. ..
..
Это перевод статьи: https://bootcamp.uxdesign.cc/how-chatgpt-really-works-explained-for-non-technical-people-71efb078a5c9
Автор: Guodong (Troy) Zhao
Выход ChatGPT, созданного OpenAI в конце прошлого года, был явлением феноменальным — даже моя бабушка спрашивает об этом. Его возможности генерировать язык, похожий на человеческий, вдохновляют людей экспериментировать с его потенциалом в различных продуктах. Его крайне успешный запуск даже поставил давление на гигантов технологической отрасли, таких как Google, чтобы спешить выпустить свою собственную версию ChatGPT.
- ИИ
- ChatGPT
- OpenAI
- Искусственный интеллект
- NLP
- GPT
29.03.2023
- вопрос
- 27.03.2023
Цифровая обработка сигналов, Системы связи, Математика и статистика, Автоматизация испытаний, Встраиваемые системы, Радиолокация, Другое, Изображения и видео
Прошу помочь в реализации программы написанной в AppDesigner. оптический волновод , входные параметры, законы геометрической оптики , построение мод (волн) учитывая вышеперечисленные параметры,…
оптический волновод , входные параметры, законы геометрической оптики , построение мод (волн) учитывая вышеперечисленные параметры,…
Прошу помочь в реализации программы написанной в AppDesigner. оптический волновод , входные параметры, законы геометрической оптики , построение мод (волн) учитывая вышеперечисленные параметры,…
- оптика
- Оптические системы
- Волоконная оптика
27.03.2023
- вопрос
- 23.03.2023
Глубокое и машинное обучение(ИИ), Математика и статистика
Задача восстановления тока ТТ в режиме насыщения. Имеется 3 строки данных: эталонный ток i1; измеренный i2 и расчетный намагничивающий ток iµ. На вход ТТ подается i1. На выходе получае…
Задача восстановления тока ТТ в режиме насыщения. Имеется 3 строки данных: эталонный ток i1; измеренный i2 и расчетный намагничивающий ток iµ. На вход ТТ подается i1. На выходе получае…
4 Ответа
- нормализация
- масштабирование
23. 03.2023
03.2023
- вопрос
- 22.03.2023
Цифровая обработка сигналов, Автоматизация испытаний, Другое
Добрый вечер.Не получается реализовать low-pass фильтр в Simulink, но обо всём по порядку. Я пытаюсь сделать модель синхронного детектирования газов, в реальности установка такая: треугольный сигнал 2…
Добрый вечер.Не получается реализовать low-pass фильтр в Simulink, но обо всём по порядку. Я пытаюсь сделать модель синхронного детектирования газов, в реальности установка такая: треугольный сигнал 2…
1 Ответ
- MATLAB
- Simulink
22.03.2023
- вопрос
- 22.03.2023
Другое
Добрый день, не могли бы Вы подсказать, как я могу получить необходимое расширение в матлаб.
Добрый день, не могли бы Вы подсказать, как я могу получить необходимое расширение в матлаб.
- вопрос
- 21.03.2023
Робототехника и беспилотники, Системы управления, Электропривод и силовая электроника, Другое
Добрый день! Помогите, пожалуйста, необходимо создать какую-нибудь модель связанную с автомобилем. Возможно систему топлива, либо связанную с электротехникой, либо что-то другое.
Возможно систему топлива, либо связанную с электротехникой, либо что-то другое.
Добрый день! Помогите, пожалуйста, необходимо создать какую-нибудь модель связанную с автомобилем. Возможно систему топлива, либо связанную с электротехникой, либо что-то другое.
13 Ответов
- автомобильные системы
- автомобиль
21.03.2023
- вопрос
- 14.03.2023
Изображения и видео
Здравствуйте, подскажите пожалуйста в чем может быть ошибка «Undefined function ‘wnr’ for input arguments of type ‘double'». %Restoring an image with a Wiener filter len = 21; theta = 11; % Clas…
Здравствуйте, подскажите пожалуйста в чем может быть ошибка «Undefined function ‘wnr’ for input arguments of type ‘double'». %Restoring an image with a Wiener filter len = 21; theta = 11; % Clas…
5 Ответов
Параметрическая кривая
Параметрическая криваяПараметрическая кривая
Параметрическая кривая — это кривая в 2D и 3D, где вы используете параметр для определения координат кривой. Например, координаты (s·cos(s), s·sin(s)) для параметра s от 0 до 10 π определяют спираль в 2D. Чтобы создать параметрическую кривую, на панели инструментов «Геометрия» в меню «Дополнительные примитивы (3D или 2D)» выберите «Параметрическая кривая» (). Вы также можете щелкнуть правой кнопкой мыши узел Geometry, чтобы добавить этот узел из контекстного меню. Затем введите свойства параметрической кривой, используя следующие разделы:
Например, координаты (s·cos(s), s·sin(s)) для параметра s от 0 до 10 π определяют спираль в 2D. Чтобы создать параметрическую кривую, на панели инструментов «Геометрия» в меню «Дополнительные примитивы (3D или 2D)» выберите «Параметрическая кривая» (). Вы также можете щелкнуть правой кнопкой мыши узел Geometry, чтобы добавить этот узел из контекстного меню. Затем введите свойства параметрической кривой, используя следующие разделы:
Параметр
Укажите имя параметра в поле Имя (имя по умолчанию: s). Также определите интервал значений параметров в полях Минимум (по умолчанию: 0) и Максимум (по умолчанию: 1).
Выражения
Введите выражения, определяющие функции параметра для каждой пространственной координаты в полях x, y (r и z в осевой 2D-симметрии, xw и yw в рабочих плоскостях) и (только в 3D) z. Чтобы создать описанную ранее спираль с параметром s, введите s*cos(s) в поле x и s*sin(s) в поле y.
Самопересекающиеся кривые не поддерживаются, за исключением замкнутых кривых (т. |
По умолчанию выражения x, y (r и z в осевой симметрии 2D, xw и yw в рабочих плоскостях) и (в 3D) z определяют координаты точек на кривой в стандартной системе координат. Однако это можно изменить с помощью настроек в разделах «Положение», «Ось» (только 3D) и «Угол вращения». Это полезно, если вы создали параметрическую кривую правильной формы, но хотите переместить ее в другое положение или ориентацию. Эти настройки можно рассматривать как определение локальной системы координат, в которой определяется параметрическая кривая.
Кривые с самопересечениями могут выглядеть правильно при отображении, но неправильно обрабатываются другими геометрическими операциями и операциями построения сетки. Это также применимо, если две разные части кривой соприкасаются, даже если они не пересекаются. Однако допускаются простые замкнутые кривые.
Позиция
Введите положение начала локальной системы координат, используя поля x, y (r и z в осевой симметрии 2D, xw и yw в рабочих плоскостях) и (только 3D) поля z.
Ось
В 3D введите ось, вокруг которой вы хотите повернуть локальную систему координат. Ось может быть выбрана параллельно одной из осей координат или введена в декартовых или сферических координатах. Ось Z локальной системы координат параллельна этой оси.
Угол поворота
Введите угол, на который вы хотите повернуть локальную систему координат (по умолчанию: 0 градусов). В 2D локальная система координат вращается вокруг своего начала. В 3D локальная система координат вращается вокруг своей оси Z, которая параллельна оси, определенной в предыдущем разделе.
Система координат
Система координат, в которой интерпретируются указанные выше положение, ось и углы поворота. В списке Рабочая плоскость выберите плоскость xy (по умолчанию для стандартной глобальной декартовой системы координат) или выберите любую рабочую плоскость, определенную над этим узлом в геометрической последовательности. Если вы выберете рабочую плоскость, рабочая плоскость и ее система координат появятся в графическом окне с использованием дополнительной триады координат с направлениями xw, yw и zw (которые затем используются для указания положения кривой).
Расширенные настройки
Программное обеспечение представляет параметрическую кривую в виде B-сплайна, который рассчитывается для аппроксимации математической кривой, определяемой координатами x, y в 2D, r и z в 2D осевой симметрии, xw и yw в рабочих плоскостях и x, y и z в трехмерных выражениях. Количество узловых точек на сплайне автоматически увеличивается до тех пор, пока аппроксимация кривой не будет удовлетворять допуску, указанному в поле Относительный допуск, или пока не будет достигнуто количество узлов, указанное в поле Максимальное количество узлов. Допуск измеряется относительно пространственной диагонали ограничивающей рамки параметрической кривой.
Если параметризация кривой неравномерна или включает сингулярности, установите флажок Перепараметрировать с использованием длины дуги, чтобы перепараметрировать кривую, возможно, обеспечивая лучшую параметризацию без сингулярностей.
Выбор результирующих сущностей
Установите флажок Результирующий выбор объектов, чтобы создать предопределенные выборки (для всех применимых уровней — объектов, доменов, границ, ребер и точек) в последующих узлах последовательности геометрии. Чтобы также сделать все или один из типов результирующих объектов (областей, границ, ребер и точек), из которых состоит параметрическая кривая, доступными для выбора во всех применимых списках выбора (например, в настройках физики и материалов), выберите параметр из списка Показать в физике (Показать в экземплярах, если в геометрической детали; Показать в 3D в геометрии плоскости под рабочей плоскостью в 3D-компоненте): Все уровни, Выбор границы (только 2D), Выбор кромки (только 3D), или Выбор точки. По умолчанию используется выбор кромки в 3D и выбор границы в 2D. Эти выборки не отображаются как отдельные узлы выбора в дереве модели. Выберите «Выкл.», чтобы не делать выбор доступным за пределами геометрической последовательности. В списке Цвет выберите цвет для выделения результирующего выбора объектов. См. Цвета выделения.
Чтобы также сделать все или один из типов результирующих объектов (областей, границ, ребер и точек), из которых состоит параметрическая кривая, доступными для выбора во всех применимых списках выбора (например, в настройках физики и материалов), выберите параметр из списка Показать в физике (Показать в экземплярах, если в геометрической детали; Показать в 3D в геометрии плоскости под рабочей плоскостью в 3D-компоненте): Все уровни, Выбор границы (только 2D), Выбор кромки (только 3D), или Выбор точки. По умолчанию используется выбор кромки в 3D и выбор границы в 2D. Эти выборки не отображаются как отдельные узлы выбора в дереве модели. Выберите «Выкл.», чтобы не делать выбор доступным за пределами геометрической последовательности. В списке Цвет выберите цвет для выделения результирующего выбора объектов. См. Цвета выделения.
Совокупный выбор
Если вы хотите, чтобы результирующие объекты участвовали в кумулятивном выборе, выберите кумулятивный выбор из списка Участвовать в (по умолчанию Нет, не дает никакого вклада) или нажмите кнопку Создать, чтобы создать новый кумулятивный выбор (см. Накопительный выбор ).
Накопительный выбор ).
Справка Graphmatica — Рисование параметрических графиков
Справка Graphmatica — Рисование параметрических графиковВВЕДЕНИЕ В ПАРАМЕТРИЧЕСКИЕ ГРАФЫ
Параметрический график, как и полярный график, использует другой метод вычисления точек на плоскости для получения кривых, которые может быть трудно вычислить с использованием обычных прямоугольных координат. Они уникальны тем, что декартовы координаты x и y рассчитываются на основе третьей переменной («параметр» x и y ), которую традиционно называют t (не путать с t используется Graphmatica для представления тета). t разрешено увеличиваться от начала указанного вами домена до конца. Для каждого значения вычисляются функции x(t) и y(t), чтобы получить координату (x,y), которая отображается на графике. Затем Graphmatica соединяет эти точки, чтобы сформировать гладкую кривую — если что-то, что вы рисуете, начинает выглядеть неровным, вам, вероятно, нужно отрегулировать точность.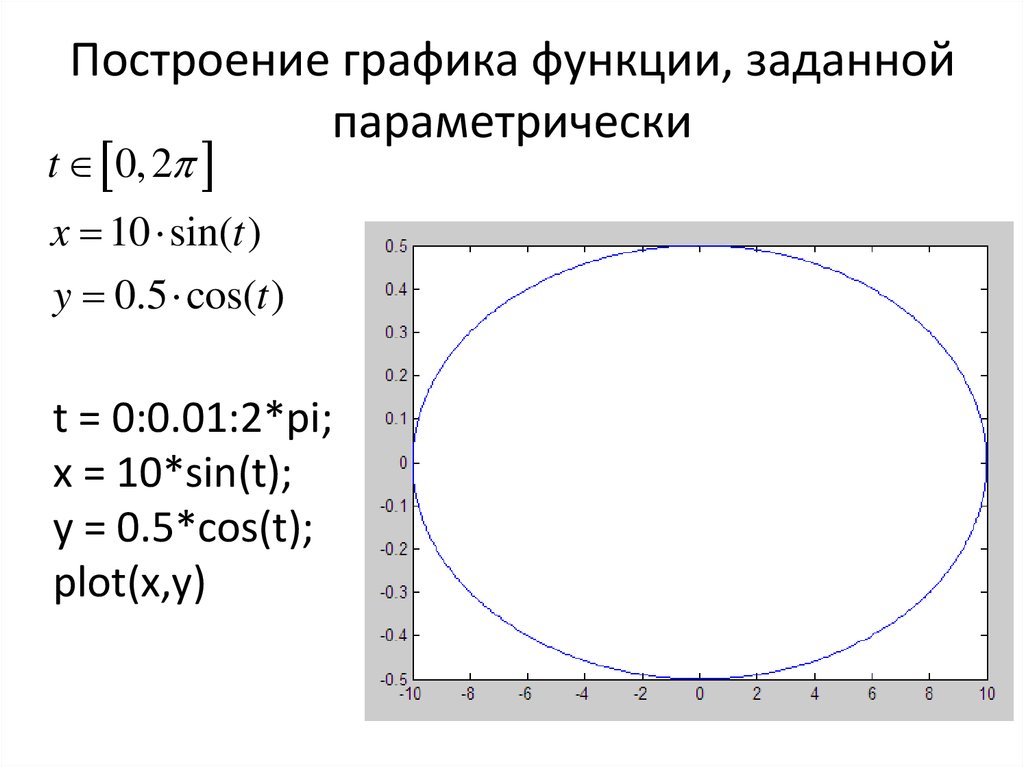
 5, не 7,5
5, не 7,5 е. когда начальная и конечная точки совпадают).
е. когда начальная и конечная точки совпадают).
Ваш комментарий будет первым