Парабола: формулы, примеры решения задач
Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы имеет вид:
,
где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.
На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.
В математическом анализе принята другая запись уравнения параболы:
y = ax²,
то есть ось параболы выбрана за ось координат. Можно заметить, что ax² — это квадратный трёхчлен ax² + bx
График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.Фокус параболы имеет координаты
Директриса параболы определяется уравнением .
Расстояние r от любой точки параболы до фокуса определяется формулой .
Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.
Пример 1. Определить координаты фокуса параболы
Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае — в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:
Находим координаты фокуса параболы:
Пример 2. Составить уравнение директрисы параболы
Решение.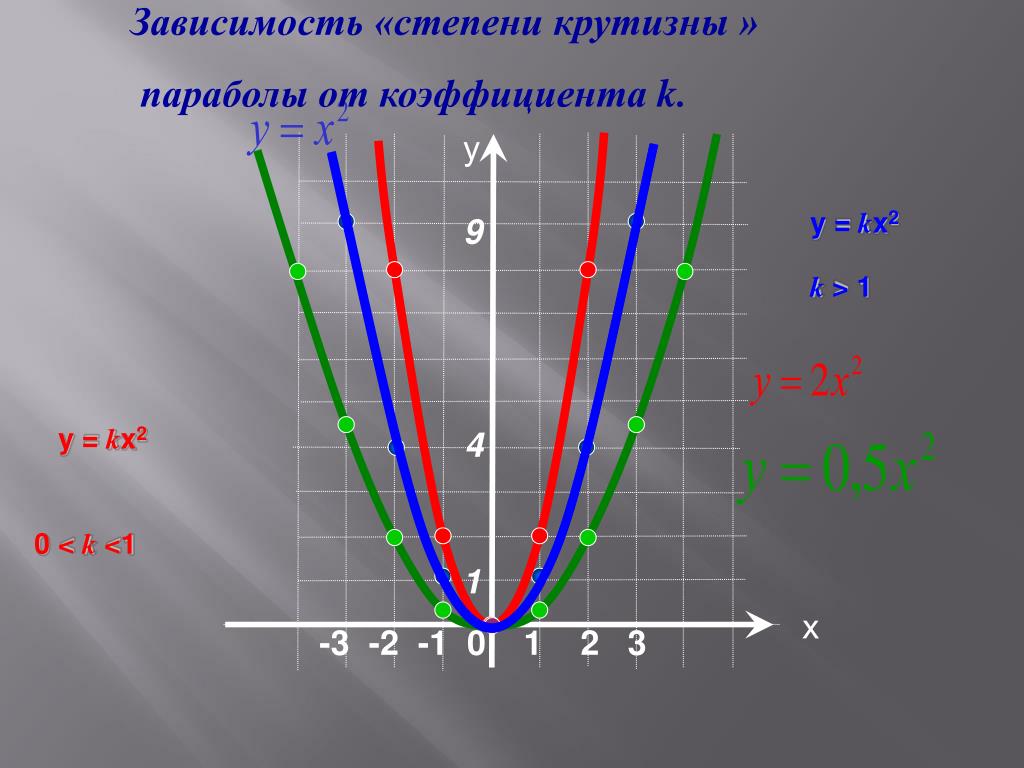
Находим p:
Получаем уравнение директрисы параболы:
Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.
Решение. Параметр p — это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:
Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.
Парабола обладает следующим оптическим свойством: все лучи, исходящие
из источника света, находящегося в фокусе параболы, после отражения оказываются направленными
параллельно её оси.
Это свойство параболы используется при изготовлении прожекторов,
автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения
(фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей,
двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.
Поделиться с друзьями
Другие материалы по теме Кривые второго порядка
Решение высшей математики онлайн
‹— Назад В школьном курсе математики достаточно подробно изучалась парабола, которая, по определению, являлась графиком квадратного трехчлена. Здесь мы дадим другое (геометрическое) определение параболы. Определение 12.7 Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
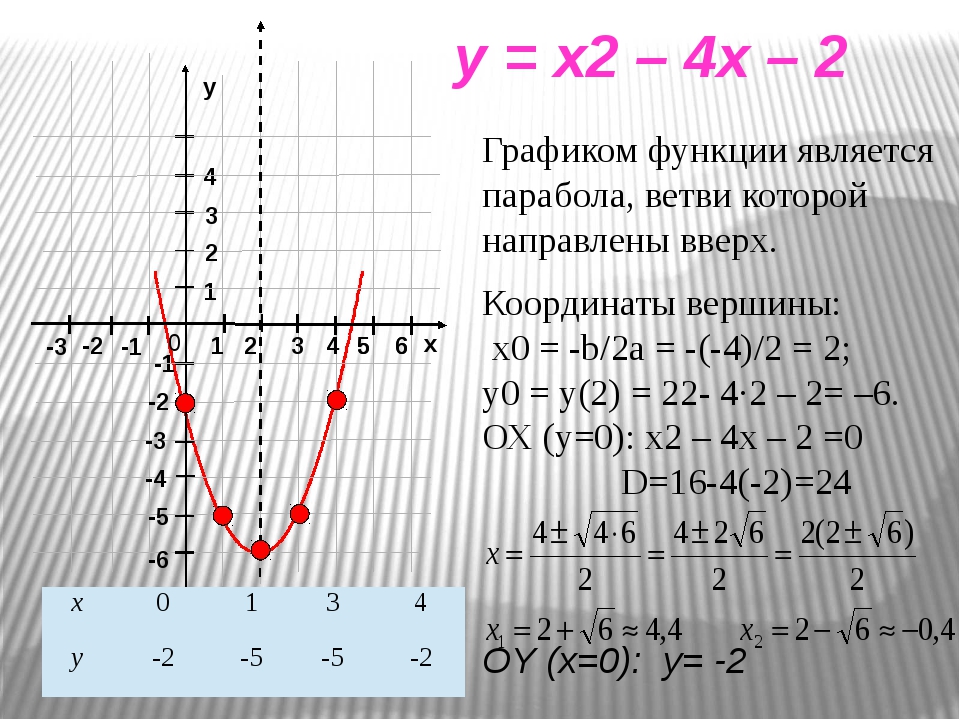Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса опустим перпендикуляр на директрису . Начало координат расположим на середине отрезка , ось направим вдоль отрезка так, чтобы ее направление совпадало с направлением вектора . Ось проведем перпендикулярно оси (рис. 12.15).Рис.12.15.| (12.10) |
Доказательство. В выбранной системе координат фокусом параболы служит точка , а директриса имеет уравнение (рис. 12.15).
Пусть — текущая точка параболы.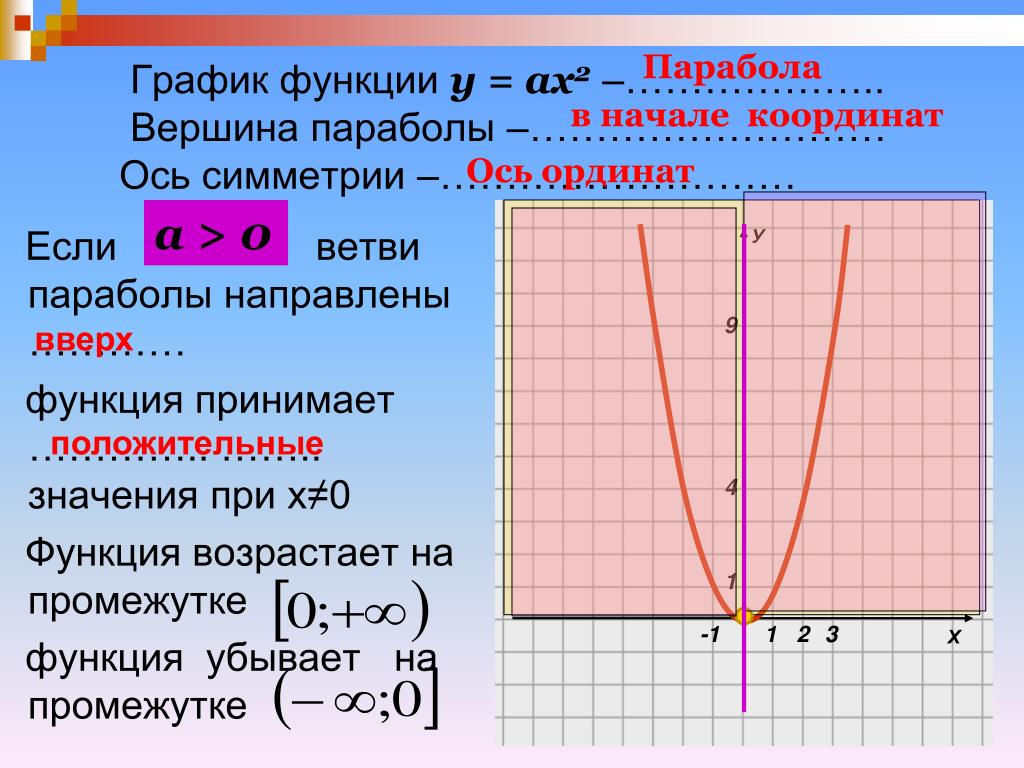
Тогда по формуле (10.4) для плоского случая находим
Точка пересечения оси симметрии с параболой называется вершиной параболы.
Если переобозначить переменные , , то уравнение (12.10) можно записать в виде
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований (рис.
12.16).Рис.12.16.Парабола Пример 12.6 Постройте параболу . Найдите ее фокус и директрису.Решение. Уравнение является каноническим уравнением параболы, , . Осью параболы служит ось , вершина находится в начале координат, ветви параболы направлены вдоль оси . Для построения найдем несколько точек параболы. Для этого придаем значения переменному и находим значения . Возьмем точки , , . Учитывая симметрию относительно оси , рисуем кривую (рис. 12.17)
Фокус лежит на оси на расстоянии от вершины, то есть имеет координаты . Директриса имеет уравнение , то есть .
Парабола так же, как и эллипс, обладает свойством, связанным с отражением света (рис. 12.18). Свойство сформулируем опять без доказательства.
Рис.12.18.Отражение светового луча от параболыЭто свойство означает, что луч света, вышедший из фокуса , отразившись от параболы, дальше пойдет параллельно оси этой параболы.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Эдгар По — Тень.
Парабола читать онлайнЭдгар Аллан По
Тень. Парабола
Если я пойду и долиною тени…
Псалом Давида[1]Вы, читающие, находитесь еще в числе живых; но я, пишущий, к этому времени давно уйду в край теней. Ибо воистину странное свершится и странное откроется, прежде чем люди увидят написанное здесь. А увидев, иные не поверят, иные усумнятся, и все же немногие найдут пищу для долгих размышлений в письменах, врезанных здесь железным стилосом.
Тот год был годом ужаса и чувств, более сильных, нежели ужас, для коих на земле нет наименования. Ибо много было явлено чудес и знамений, и повсюду, над морем и над сушею, распростерлись черные крыла Чумы[2]. И все же тем, кто постиг движения светил, не было неведомо, что небеса предвещают зло; и мне, греку Ойносу[3], в числе прочих, было ясно, что настало завершение того семьсот девяносто четвертого года, когда с восхождением Овна планета Юпитер сочетается с багряным кольцом ужасного Сатурна. Особенное состояние небес, если я не ошибаюсь, сказалось не только на вещественной сфере земли, но и на душах, мыслях и воображении человечества.
Над бутылями красного хиосского вина, окруженные стенами роскошного зала, в смутном городе Птолемаиде[4], сидели мы ночью, всемером. И в наш покой вел только один вход: через высокую медную дверь; и она, вычеканенная искуснейшим мастером Коринносом, была заперта изнутри. Черные завесы угрюмой комнаты отгораживали от нас Луну, зловещие звезды и безлюдные улицы — но предвещанье и память Зла они не могли отгородить. Вокруг нас находилось многое — и материальное и духовное, — что я не могу точно описать: тяжесть в атмосфере… ощущение удушья…. тревога и, прежде всего, то ужасное состояние, которое испытывают нервные люди, когда чувства бодрствуют и живут, а силы разума почиют сном. Мертвый груз давил на нас. Он опускался на наши тела, на убранство зала, на кубки, из которых мы пили; и все склонялось и никло — все, кроме языков пламени в семи железных светильниках, освещавших наше пиршество. Вздымаясь высокими, стройными полосами света, они горели, бледные и недвижные; и в зеркале, образованном их сиянием на поверхности круглого эбенового стола, за которым мы сидели, каждый видел бледность своего лица и непокойный блеск в опущенных глазах сотрапезников.
И, зыблясь меж завес покоя, она в конце концов застыла на меди дверей. Но тень была неясна, бесформенна и неопределенна, не тень человека и не тень бога — ни бога Греции, ни бога Халдеи, ни какого-либо египетского бога. И тень застыла на меди дверей, под дверным сводом, и не двинулась, не проронила ни слова, но стала недвижно на месте, и дверь, на которой застыла тень, была, если правильно помню, прямо против ног юного Зоила, облаченного в саван. Но мы семеро, увидев тень выходящего из черных завес, не посмели взглянуть на нее в упор, но опустили глаза и долго смотрели в глубину эбенового зеркала. И наконец я, Ойнос, промолвив несколько тихих слов, вопросил тень об ее обиталище и прозвании. И тень отвечала: «Я — Тень, и обиталище мое вблизи от птолемаидских катакомб, рядом со смутными равнинами Элизиума, сопредельными мерзостному Харонову проливу[6]». И тогда мы семеро в ужасе вскочили с мест и стояли, дрожа и трепеща, ибо звуки ее голоса были не звуками голоса какого-либо одного существа, но звуками голосов бесчисленных существ, и, переливаясь из слога в слог, сумрачно поразили наш слух отлично памятные и знакомые нам голоса многих тысяч ушедших друзей.
Библия, Псалом Давида, XXII, 4
В рассказе получили отражение впечатления писателя от эпидемии холеры в Балтиморе летом 1835 г.
…греку Ойносу… — Условное имя, по-гречески «Ойнос» означает «вино».
Птолемаида — древнее название города Акка в Палестине.
Зоил — древнегреческий философ (IV в. до н.э.) , получил известность как ниспровергатель авторитетов.
…Харонову проливу. — Харон (греч. миф.) — перевозчик душ умерших через воды подземного царства.
новые лекции онлайн-курса Николая Андреева
Образовательный центр «Сириус» продолжает на YouTube-канале новый цикл видеолекций по математике. Автор и ведущий – заведующий лаборатории популяризации и пропаганды математики в Математическом институте имени В.А. Стеклова РАН, создатель научно-популярного сайта «Математические этюды» Николай Андреев.
Курс состоит из 12 онлайн-встреч. Первые три занятия вышли на прошлой неделе и доступны в записи, сегодня публикуем три новых.
На них поговорим о том, что общего у чипсов и математики, в чем кроется тайна числа Пи и как в два счета вычислить площадь самой сложной геометрической фигуры.
Лекция 4. Площади фигур
На этом занятии Николай Андреев подробно разберет площади различных фигур. Математик наглядно продемонстрирует, что найти точную площадь многоугольника можно, если перевести его в прямоугольник. После этой лекции вы научитесь легко и быстро высчитывать площадь практически любой геометрической фигуры, от треугольника до трапеции.
Лекция 5. Конические сечения
Что такое шары Дандалена, и каким образом чипсы связаны с математикой? На эти вопросы вы найдете ответ вместе с Николаем Андреевым на лекции про конические сечения – линии пересечения плоскости с круговым конусом.
Вы рассмотрите главные типы конических сечений – эллипс, параболу и гиперболу и узнаете, какие их оптические свойства применяются в медицине, в работе спутниковых тарелок и при построении телескопов.
Лекция 6. Окружность и круг
Занятие Николая Андреева посвящено окружности и кругу. Вместе с математиком вы поговорите про формулу длины окружности и число Пи, которое ученые изучают с древних времен, но до сих пор знают про него немного. Еще вы порассуждаете про формулу площади круга и узнаете, каким образом можно использовать конус в быту и на железной дороге.
Квадратичная функция и ее график
На уроках математики в школе Вы уже познакомились с простейшими свойствами и графиком функции y = x2.
Давайте расширим знания по квадратичной функции.
Задание 1.
Построить график функции y = x2. Масштаб: 1 = 2 см. Отметьте на оси Oy точку F(0; 1/4). Циркулем или полоской бумаги измерьте расстояние от точки F до какой-нибудь точки M параболы. Затем приколите полоску в точке M и поверните ее вокруг этой точки так, чтобы она стала вертикальной. Конец полоски опустится немного ниже оси абсцисс (рис. 1). Отметьте на полоске, насколько она выйдет за ось абсцисс. Возьмите теперь другую точку на параболе и повторите измерение еще раз. Насколько теперь опустился край полоски за ось абсцисс?
Результат: какую бы точку на параболе y = x2 вы не взяли, расстояние от этой точки до точки F(0; 1/4) будет больше расстояния от той же точки до оси абсцисс всегда на одно и то же число – на 1/4.
Можно сказать иначе: расстояние от любой точки параболы до точки (0; 1/4) равно расстоянию от той же точки параболы до прямой y = -1/4.
Эта замечательная точка F(0; 1/4) называется фокусом параболы y = x2, а прямая y = -1/4 – директрисой этой параболы. Директриса и фокус есть у каждой параболы.
Интересные свойства параболы:
1. Любая точка параболы равноудалена от некоторой точки, называемой фокусом параболы, и некоторой прямой, называемой ее директрисой.
2. Если вращать параболу вокруг оси симметрии (например, параболу y = x2 вокруг оси Oy), то получится очень интересная поверхность, которая называется параболоидом вращения.
Поверхность жидкости во вращающемся сосуде имеет форму параболоида вращения. Вы можете увидеть эту поверхность, если сильно помешаете ложечкой в неполном стакане чая, а потом вынете ложечку.
3. Если в пустоте бросить камень под некоторым углом к горизонту, то он полетит по параболе (рис. 2).
4. Если пересечь поверхность конуса плоскостью, параллельной какой-либо одной его образующей, то в сечении получится парабола (рис.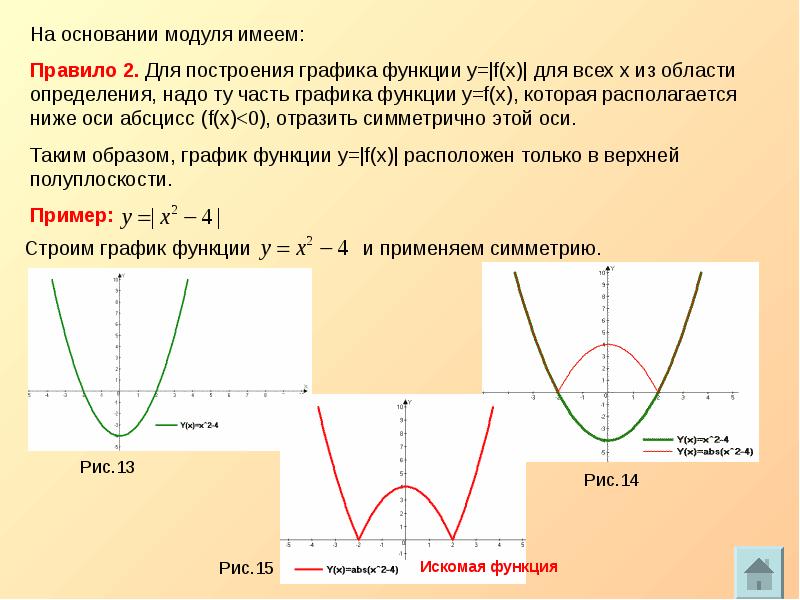
3).
5. В парках развлечений иногда устраивают забавный аттракцион «Параболоид чудес». Каждому, из стоящих внутри вращающегося параболоида, кажется, что он стоит на полу, а остальные люди каким-то чудом держаться на стенках.
6. В зеркальных телескопах также применяют параболические зеркала: свет далекой звезды, идущий параллельным пучком, упав на зеркало телескопа, собирается в фокус.
7. У прожекторов зеркало обычно делается в форме параболоида. Если поместить источник света в фокусе параболоида, то лучи, отразившись от параболического зеркала, образуют параллельный пучок.
Построение графика квадратичной функции
На уроках математики вы изучали получение из графика функции y = x2 графиков функций вида:
1) y = ax2 – растяжение графика y = x2 вдоль оси Oy в |a| раз (при |a| < 0 – это сжатие в 1/|a| раз, рис. 4).
2) y = x2 + n – сдвиг графика на n единиц вдоль оси Oy, причем, если n > 0, то сдвиг вверх, а если n < 0, то вниз, (или же можно переносить ось абсцисс).
3) y = (x + m)2 – сдвиг графика на m единиц вдоль оси Ox: если m < 0, то вправо, а если m > 0, то влево, (рис. 5).
4) y = -x2 – симметричное отображение относительно оси Ox графика y = x2.
Подробнее остановимся на построении графика функции y = a(x – m)2 + n.
Квадратичную функцию вида y = ax2 + bx + c всегда можно привести к виду
y = a(x – m)2 + n, где m = -b/(2a), n = -(b2 – 4ac)/(4a).
Докажем это.
Действительно,
y = ax2 + bx + c = a(x2 + (b/a) x + c/a) =
= a(x2 + 2x · (b/a) + b2/(4a2) – b2/(4a2) + c/a) =
= a((x + b/2a) 2 – (b2 – 4ac)/(4a2)) = a(x + b/2a) 2 – (b2 – 4ac)/(4a).
Введем новые обозначения.
Пусть m = -b/(2a), а n = -(b2 – 4ac)/(4a),
тогда получим y = a(x – m)2 + n или y – n = a(x – m)2.
Сделаем еще замены: пусть y – n = Y, x – m = X (*).
Тогда получим функцию Y = aX2, графиком которой является парабола.
Вершина параболы находится в начале координат. X = 0; Y = 0.
Подставив координаты вершины в (*), получаем координаты вершины графика y = a(x – m)2 + n: x = m, y = n.
Таким образом, для того, чтобы построить график квадратичной функции, представленной в виде
y = a(x – m)2 + n
путем преобразований, можно действовать следующим образом:
a) построить график функции y = x2;
б) путем параллельного переноса вдоль оси Ox на m единиц и вдоль оси Oy на n единиц – вершину параболы из начала координат перевести в точку с координатами (m; n) (рис. 6).
Запись преобразований:
y = x2 → y = (x – m)2 → y = a(x – m)2 → y = a(x – m)2 + n.
Пример.
С помощью преобразований построить в декартовой системе координат график функции y = 2(x – 3)2– 2.
Решение.
Цепочка преобразований:
y = x2(1) → y = (x – 3)2(2) → y = 2(x – 3)2(3) → y = 2(x – 3)2 – 2 (4).
Построение графика изображено на рис. 7.
Вы можете практиковаться в построении графиков квадратичной функции самостоятельно. Например, постройте в одной системе координат с помощью преобразований график функции y = 2(x + 3)2 + 2. Если у вас возникнут вопросы или же вы захотите получить консультацию учителя, то у вас есть возможность провести бесплатное 25-минутное занятие с онлайн репетитором после регистрации. Для дальнейшей работы с преподавателем вы сможете выбрать подходящий вам тарифный план.
Остались вопросы? Не знаете, как построить график квадратичной функции?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.
tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Читать онлайн «Парабола замысла» автора Кончаловский Андрей Сергеевич — RuLit
Андрей Михалков-Кончаловский.
Парабола замысла.
М.,”Искусство”. 1977г
Книга посвящена профессии режиссера, его работе над фильмом – от замысла до встречи со зрителем. Привлекая богатый материал своих постановок – “Романс о влюбленных”, “Первый учитель”, “Дворянское гнездо”, “Дядя Ваня”,- автор рассматривает широкий круг дискуссионных вопросов современной теории и практики. Книга дает интересный материал для размышлений как профессионалам кинематографистам, так и любителям киноискусства.
Вступление.
4
Сценарий. 8
“Кинематографичность” и кинематографичность. 8
“Романс о влюбленных”. Первое потрясение. 10
Сценарный ход. 15
Начало параболы.. 16
С точки зрения зрителя. 18
Мир. 21
“Как в жизни” и “как в искусстве”. 21
Кстати, о Шекспире. 24
За “синей птицей”. 26
“Кирпичики” мира. 30
Сотворение мира. Подготовка. 33
Изображение. 33
Художник. Искажение мира. 35
Немного о костюме. 38
Несколько слов об еще одной существенной частности. 40
Поиски актеров. 41
Пробы.. 42
Герои. 43
Сочинение биографий. 46
Актеры на эпизоды.. 48
Второй план. 50
Композитор. 52
Режиссерский сценарий. 53
ОТСТУПЛЕНИЕ О ПРАВДЕ ЭКРАНА. 57
Похвала документалистике.
57
Метод съемки. 58
Импровизация. 61
Барьер подсознания. 63
О профессионализме и профессионалах. 66
Жанр. 70
За рамкой кадра. 72
Субъективная камера. 74
СОТВОРЕНИЕ МИРА. СЪЕМКА.. 76
Образ целого. 76
Ростки правды.. 77
Будь проклято это кино. 78
Момент условности. 81
Торт на третье. 85
Издержки риска. 87
Пробуждение на бетонном полу. 89
Ангел пролетел. 93
Сотворение мира. Монтаж.. 95
Силовые поля. 95
Высшее из искусств. 96
Ритм.. 99
Текучесть формы.. 101
Зритель. 106
Пятое рождение. 106
Дилемма. 107
Странности любви. 108
Пирамида восприятия. 110
Почему?. 110
Зритель и критик.
111
Куда ж нам плыть?. 113
Вместо заключения. 115
Мысль написать эту книгу возникла у меня во время беседы с космонавтом Феоктистовым, организованной “Литературной газетой”. Тогда по ходу диалога невольно пришла мысль сравнить две траектории — фильма и космического корабля. Тут есть общее даже в производственной терминологии: “запуск фильма” — “запуск ракеты”. Правда, на стороне техники пока что явные преимущества. Траектория космического корабля контролируется точными, способными делать миллионы операций в секунду вычислительными машинами. Любое внезапное отклонение от намеченного курса — помехи, ошибки, непредвиденные случайности — ЭВМ может тут же учесть, внести соответствующие коррективы, вернуть корабль на заданную траекторию. Но ведь и путь, который проходит фильм от момента запуска (даже еще раньше — от рождения сценарного замысла), испытывает влияние тысячи разных отклоняющих воздействий: объективных, не зависящих от нас; субъективных, проистекающих уже по нашей воле, ибо по ходу работы приходят новые решения, открываются новые возможности.
А помимо всего прочего режиссеру невольно порой приходится производить тысячу дипломатических ухищрений: обещать редакторам и руководству студии очередной шедевр, что-то утаивать от автора сценария, доказывать актерам, что жаждешь делать то, чего делать совсем не намерен.
Вся режиссура в кино — сплошной компромисс. Да, и в театре, я думаю, тоже. Все время приходится искать решения из всех возможных наиболее приемлемые — иногда даже самые вынужденные, скоропалительные, от отчаяния и безысходности, занят в театре актер, — приходится снимать другого. Забыли бороду в гримерной — возникает спасительная “находка”: пусть актер играет спиной. Нужна солнечная погода, а во все время экспедиции — на небе ни одного просвета. Задумана массовка на триста человек, а ассистентам с великим трудом удалось собрать пятьдесят. Сняли замечательный кадр, а пленка оказалась бракованной, заново переснять его уже невозможно. И все эти компромиссы не дают режиссеру задремать на ходу — постоянно приходится что-то придумывать, что-то изобретать, чтобы хоть как-то сохранить первоначальный замысел.
То есть то, ради чего делается фильм.
Процесс создания фильма, на мой взгляд, точнее всего было бы уподобить траектории летящего снаряда. Чтобы накрыть цель, артиллерист заведомо берет прицел с превышением: он знает, что снаряд не полетит по прямой — ветер, гравитация, сопротивление воздуха окажут свое воздействие, выгнут первоначальную прямую в дугу параболы.
Титта Руффо ★ Парабола моей жизни читать книгу онлайн бесплатно
ТИТТА РУФФО И ЕГО ВОСПОМИНАНИЯ
Перевод с итальянского и вступительная статья А. БУШЕН
Книга воспоминаний Титта Руффо, названная им «Парабола моей жизни»,— правдивое описание нелегкого жизненного и творческого пути одного из величайших вокалистов-баритонов первой половины XX века. Мемуары эти, занимательные и поучительные, привлекательны своей искренностью, прямотой и бесхитростной откровенностью.
Жизнь знаменитого артиста с самого начала и до конца складывалась не гладко.. На его долю выпали жизненные и творческие конфликты, требовавшие от него активного участия и немедленного разрешения. Такой уж он был человек и такая была у него судьба.
У многих прославленных итальянских певцов и голос и актерские способности в какой-то степени «прорезывались» с детства. Будущие артисты мальчиками пели в церковных хорах, а иногда выступали и на сценах. Так или иначе приобщаясь к музыке, они в той или иной форме тренировали слух и память. Ничего подобного нет в детстве Титта Руффо. Суровым и безрадостным было его детство. Да и было ли оно у прославившегося на весь мир певца? С восьми лет малыш уже работал, раздувая мехи в кузнице, и начал он работать по собственной инициативе, из какого-то удивительного для ребенка горячего желания во что бы то ни стало помочь нуждавшейся семье. Вот уже с какого времени наметились отличительные черты характера этого незаурядного человека — неукротимая работоспособность, желание жить собственным тРУДОм.
На первый взгляд кажется, что ничто в ребенке не свидетельствовало о его творческих способностях. Но так кажется только на первый взгляд. Правда, никаких воспоминаний об изобретательных играх или хотя бы выдумках, живо отображающих детское мировосприятие, у него не сохранилось. На работе он, несомненно, уставал. Иначе и быть не могло. Во всяком случае даже в воскресный день ему не хочется побегать и порезвиться. Он предпочитает оставаться дома, сидеть с мамой у окна и подчас засыпать у нее на коленях. Но вот что характерно: хотя ему не рассказывают сказок, не читают интересных историй и даже грамоте его не учат, у этого ребенка какая-то необыкновенно повышенная душевная чувствительность, не по возрасту обостренная наблюдательность, особое, почти художественное восприятие внешнего облика людей, легко воспламеняющееся богатое воображение. И все эти особенности характера и душевной организации сыграют впоследствии свою роль в формировании выдающегося дарования певца-актера. Слуховые впечатления раннего детства Титта Руффо также не способствовали развитию у ребенка музыкальных навыков. Резкие звуки ударов молота по наковальне, лязг железа, разные звоны, шумы и стуки кузнечной мастерской — вот чем с самых первых дней жизни питается нежное детское ухо. О благозвучных музыкальных впечатлениях Титта Руффо не упоминает. Возможно, что их и не было. Он не знает даже, что у него отличный слух музыканта и безотказная память. Но когда при переезде в Рим он слышит песенку «О Кароли», которую напевает хозяин гостиницы, мелодия, как он сам пишет, входит в его сознание и он запоминает ее на всю жизнь.
Растет будущий певец в весьма неблагополучной семейной обстановке. Мало того, что семья живет чуть ли не впроголодь и между отцом и матерью нет доброго согласия, отец Руффо, человек мятежный, не лишенный таланта, но уязвленный в своих художественных стремлениях, озлобленный засасывающей нуждой, вложил все свои мечты и надежды в старшего сына, красивого белокурого Этторе. Мальчика и балуют, и учат, и стараются получше одеть. А от младшего, внешне ничем не примечательного Руффо, отец не ждет ничего хорошего. Он заставляет его почти бесплатно работать в своей мастерской, не учит ничему, кроме ремесла, жесток с ним, несправедливо придирчив и, наконец, повздорив с сыном, гонит тринадцатилетнего мальчугана вон из дома. И мальчик бесстрашно пускается в неизвестность, не имея в кармане ни одного сольдо, и начинает самостоятельную жизнь с того, что ночует в Альбано на кладбище, устроившись в заброшенной гробнице. Конечно же, маленькому путешественнику могло взгрустнуться, ему было и холодно и неуютно — все это естественно. Но достаточно слова прохожего, назвавшего конусообразный памятник могилой Горациев и Куриациев*, чтобы детская фантазия заработала вовсю. Будущий артист в сонном забытьи видит себя в некоем театральном аспекте, взрослым человеком в костюме римского воина с золотым шлемом на голове, в пурпурной мантии, с мечом в руке…
Читать дальше{2} + b x + c $$$.Поскольку парабола проходит через точку $$$ \ left (1, 4 \ right) $$$, то $$$ 4 = a + b + c $$$.
Поскольку парабола проходит через точку $$$ \ left (2, 9 \ right) $$$, то $$$ 9 = 4 a + 2 b + c $$$.
Поскольку парабола проходит через точку $$$ \ left (-1, 6 \ right) $$$, то $$$ 6 = a — b + c $$$.
Таким образом, мы получили следующую систему: \ begin {cases} a + b + c = 4 \\ 4 a + 2 b + c = 9 \\ a — b + c = 6 \ end {ases}
Решая ее (шаги см. В калькуляторе системы линейных уравнений), мы получаем $$$ a = 2 $$$, $$$ b = -1 $$$, $$$ c = 3 $$$.{2} + \ frac {23} {8} $$$.
Без формы перехвата.
Вершина: $$$ \ left (\ frac {1} {4}, \ frac {23} {8} \ right) $$$.
Фокус: $$$ \ left (\ frac {1} {4}, 3 \ right) $$$.
Эксцентриситет: $$$ 1 $$$.
Директриса: $$$ y = \ frac {11} {4} $$$.
Latus rectum: $$$ y = 3 $$$.
Длина прямой кишки: $$$ \ frac {1} {2} $$$.
Ось симметрии: $$$ x = \ frac {1} {4} $$$.
Основной параметр: $$$ \ frac {1} {4} $$$.
Нет x-перехватчиков.
y-перехват: $$$ \ left (0, 3 \ right) $$$.
График: , чтобы построить график параболы, посетите калькулятор построения графика параболы (выберите вариант «Неявный»).
Калькулятор параболы — бесплатный онлайн калькулятор параболы
Калькулятор графиков параболы вычисляет график для данного уравнения параболы. Парабола определяется как геометрическое место всех точек, которые находятся на равном расстоянии от фиксированной линии и фиксированной точки.Парабола получается путем разрезания конуса параллельно его краю.
Что такое калькулятор параболы?
Parabola Graph Calculator — это онлайн-инструмент, который помогает вычислить график для данного уравнения параболы. Этот онлайн-калькулятор параболического графика поможет вам рассчитать график за несколько секунд. Чтобы использовать этот калькулятор графа параболы, введите уравнение параболы в данное поле ввода.
Как пользоваться калькулятором параболы?
Выполните следующие действия, чтобы рассчитать график с помощью онлайн-калькулятора параболических графиков:
- Шаг 1: Откройте онлайн-калькулятор параболы Cuemath.
- Шаг 2: Введите уравнение параболы в данное поле ввода калькулятора графика параболы.
- Шаг 3: Нажмите кнопку «Вычислить» , чтобы вычислить график для данного уравнения параболы.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поле и ввести новое уравнение параболы.
Как работает калькулятор графиков параболы?
Парабола получается путем разрезания конуса параллельно его краю.Он имеет П-образную форму как вытянутую геометрическую плоскость. Общий вид параболы имеет вид y 2 = 4ax
Общее уравнение параболы:
y = a (x — h) 2 + k (обычный)
x = a (y — k) 2 + h (сбоку)
Где (h, k) — вершина параболы, а a — перпендикулярное расстояние от фокуса до точки на кривой.
Давайте разберемся в этом с помощью следующего примера.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. Cuemath находит решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенный пример на графике параболыПостройте график параболы по уравнению y 2 — 4y + 4x — 4 = 0 и проверьте его с помощью калькулятора графика парабол?
Решение:Данное уравнение можно переписать в виде (y — 2) 2 = −4 (x — 2)
Представляет собой параболу с вершиной V (2, 2), раскрывающуюся влево, потому что a = –1 (отрицательное значение).
Фокус будет находиться на расстоянии 1 единицы слева от (2, 2), то есть на (1, 2)
Директриса будет располагаться на 1 единицу правее (2, 2), т.е. это будет x = 3
Точно так же вы можете использовать калькулятор параболического графика и вычислить:
- y 2 = 15x
- (у + 8) 2 = −8 (х + 5)
- лет 2 -10 лет + 6x + 9 = 0
☛
Статьи по теме:Алгебра — Параболы
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-2: Параболы
В этом разделе мы хотим посмотреть на график квадратичной функции.2} + bx + c \]
Графики квадратичных функций называются параболами . Вот несколько примеров парабол.
Все параболы имеют неопределенную U-образную форму, и у них будет самая высокая или самая низкая точка, которая называется вершиной . Параболы могут открываться вверх или вниз и могут иметь или не иметь \ (x \) — точки пересечения, и они всегда будут иметь одну точку пересечения \ (y \).
Также обратите внимание, что парабола, которая открывается вниз, всегда открывается вниз, а парабола, которая открывается вверх, всегда открывается.Другими словами, парабола не сразу развернется и не начнет открываться, если она уже начала открываться вниз. Точно так же, если он уже начал открываться, он не развернется и не начнет внезапно открываться.
Пунктирная линия с каждой из этих парабол называется осью симметрии . Каждая парабола имеет ось симметрии, и, как показано на графике, график по обе стороны от оси симметрии является зеркальным отображением другой стороны.Это означает, что если мы знаем точку на одной стороне параболы, мы также будем знать точку на другой стороне, основываясь на оси симметрии. Мы увидим, как найти эту точку, когда рассмотрим несколько примеров.
Нам, вероятно, следует сделать быстрый обзор перехватов, прежде чем двигаться дальше. Пересечения — это точки, в которых график будет пересекать ось \ (x \) или \ (y \). Мы также видели график в разделе, где мы вводили точки пересечения, где точка пересечения просто касалась оси, но не пересекала ее.
Поиск перехвата — довольно простой процесс. Чтобы найти \ (y \) — точку пересечения функции \ (y = f \ left (x \ right) \), все, что нам нужно сделать, это установить \ (x = 0 \) и оценить, чтобы найти \ (y \ ) координаты. Другими словами, \ (y \) — точка пересечения — это точка \ (\ left ({0, f \ left (0 \ right)} \ right) \). Мы находим перехват \ (x \) — почти таким же образом. Мы устанавливаем \ (y = 0 \) и решаем полученное уравнение для координат \ (x \). Итак, нам нужно будет решить уравнение
\ [е \ влево (х \ вправо) = 0 \]А теперь вернемся к параболам.Есть базовый процесс, который мы всегда можем использовать, чтобы получить довольно хороший набросок параболы. Вот.
Создание эскизов парабол
- Найдите вершину. Мы скоро обсудим, как это найти. Это довольно просто, но есть несколько способов его найти, поэтому мы обсудим их отдельно.
- Найдите \ (y \) — точку пересечения, \ (\ left ({0, f \ left (0 \ right)} \ right) \).
- Решите \ (f \ left (x \ right) = 0 \), чтобы найти координаты \ (x \) точек пересечения \ (x \), если они существуют.Как мы увидим в наших примерах, у нас может быть 0, 1 или 2 \ (x \) — перехватов.
- Убедитесь, что у вас есть хотя бы одна точка с каждой стороны вершины. Это необходимо для того, чтобы получить точный набросок. Если парабола имеет два пересечения \ (x \), то эти точки у нас уже будут. Если он имеет точку пересечения 0 или 1 \ (x \), мы можем либо просто вставить другое значение \ (x \), либо использовать точку пересечения \ (y \) и ось симметрии, чтобы получить вторую точку.
- Нарисуйте график.На данный момент мы набрали достаточно очков, чтобы получить довольно хорошее представление о том, как будет выглядеть парабола.
Теперь мы рассмотрим две формы параболы. Эта первая форма значительно упростит построение парабол. К сожалению, большинство парабол не в такой форме. Вторая форма является более распространенной и потребует немного (и лишь немного) дополнительной работы, чтобы нарисовать график параболы.
Давайте посмотрим на первую форму параболы.2} + k \]
Есть две части информации о параболе, которые мы можем мгновенно получить из этой функции. Во-первых, если \ (a \) положительно, тогда парабола откроется, а если \ (a \) отрицательна, тогда парабола откроется. Во-вторых, вершиной параболы является точка \ (\ left ({h, k} \ right) \). Будьте очень осторожны со знаками при получении здесь вершины.
Итак, когда нам посчастливится иметь такую форму параболы, мы получаем вершину бесплатно.2} — 8 \) Показать решение
Сначала нам нужно найти вершину. Однако нам нужно быть осторожными со знаками. Сравнивая наше уравнение с приведенной выше формой, мы видим, что у нас должны быть \ (h = — 3 \) и \ (k = — 8 \), поскольку это единственный способ получить правильные знаки в нашей функции. Следовательно, вершина этой параболы равна
\ [\ left ({- 3, — 8} \ right) \]Теперь давайте найдем точку пересечения \ (y \). Это не что иное, как быстрая оценка функции.2} — 8 = 2 \ left (9 \ right) — 8 = 10 \ hspace {0,25 дюйма} y — {\ mbox {intercept:}} \ left ({{\ mbox {0,10}}} \ right) \]
Далее нам нужно найти \ (x \) — точки пересечения. Это означает, что нам нужно будет решить уравнение. Однако, прежде чем мы это сделаем, мы можем сказать, будут ли они у нас или нет, еще до того, как мы начнем решать уравнение.
В этом случае у нас есть \ (a = 2 \), что положительно, и поэтому мы знаем, что парабола раскрывается. Также вершина — это точка ниже оси \ (x \).2} & = 4 \\ x + 3 & = \ pm \ sqrt 4 = \ pm 2 \\ x & = — 3 \ pm 2 \ hspace {0,25in} \ Rightarrow \ hspace {0,25in} x = — 1, \, \, x = — 5 \ end {align *} \]
Два интерцептора x равны
\ [\ left ({- 5,0} \ right) \ hspace {0,25 дюйма} {\ mbox {и}} \ hspace {0,25 дюйма} \ left ({- 1,0} \ right) \]Итак, на данный момент у нас есть точки по обе стороны от вершины, так что мы официально закончили поиск точек.Тем не менее, давайте немного поговорим о том, как найти вторую точку, используя точку пересечения \ (y \) — и ось симметрии, так как это нам нужно будет сделать в конце концов.
Во-первых, обратите внимание, что точка пересечения \ (y \) — имеет координату \ (x \), равную 0, в то время как вершина имеет координату \ (x \), равную -3. Это означает, что точка пересечения \ (y \) находится на расстоянии 3 вправо от оси симметрии, поскольку она будет двигаться прямо вверх от вершины.
Теперь левая часть графика будет зеркальным отображением правой части графика.Итак, поскольку есть точка в \ (y = 10 \), которая находится на расстоянии 3 вправо от оси симметрии, также должна быть точка в \ (y = 10 \), которая находится на расстоянии 3 до слева от оси симметрии.
Итак, поскольку координата \ (x \) вершины равна -3, а эта новая точка находится на расстоянии 3 влево, ее координата \ (x \) должна быть -6. 2} — 1 \) Показать решение
Хорошо, мы не будем вдаваться в подробности.2} — 1 = — 4 — 1 = — 5 \]
Перехватчик \ (y \) — это \ (\ left ({0, — 5} \ right) \).
Теперь мы знаем, что вершина начинается ниже оси \ (x \), а парабола открывается вниз. Это означает, что не может быть \ (x \) — пересечений, поскольку ось \ (x \) находится над вершиной, а парабола всегда будет открываться вниз. Это означает, что в целом нет причин проходить процесс решения, чтобы найти то, чего не будет.
Но давайте все равно сделаем это.2} & = — 1 \\ x — 2 & = \ pm \, i \\ x & = 2 \ pm \, i \ end {align *} \]
Итак, мы получили комплексные решения. Сложные решения всегда будут указывать на отсутствие \ (x \) — перехватов.
Теперь нам нужны точки по обе стороны от вершины, поэтому мы будем использовать точку пересечения \ (y \) и ось симметрии, чтобы получить вторую точку. Пересечение \ (y \) — это расстояние в два слева от оси симметрии и находится в \ (y = — 5 \), поэтому должна быть вторая точка только с тем же значением \ (y \). расстояние 2 вправо от оси симметрии.2} + 4 \) Показать решение
Это на самом деле довольно просто построить график. Сначала мы заметим, что он откроется вверх.
Итак, вершина, вероятно, является точкой, в которой большинство студентов сталкиваются здесь с проблемами. Поскольку у нас есть x 2 , это означает, что у нас должно быть \ (h = 0 \), и поэтому вершина равна \ (\ left ({0,4} \ right) \).
Обратите внимание, что это означает, что с этой параболой не будет никаких \ (x \) — пересечений, поскольку вершина находится выше оси \ (x \), а парабола открывается вверх.2} + 4 = 4 \ hspace {0,25 дюйма} y — {\ mbox {intercept:}} \ left ({0,4} \ right) \]
Перехватчик \ (y \) точно такой же, как вершина. Такое случается время от времени, поэтому не стоит слишком беспокоиться об этом. Хотя это будет означать, что на этот раз мы не сможем использовать \ (y \) — точку пересечения, чтобы найти вторую точку с другой стороны вершины. Фактически, у нас даже нет точки, кроме вершины!
Итак, нам нужно найти точки по обе стороны от вершины.2} + 4 = 8 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} \ left ({2,8} \ right) \ end {align *} \]
Обратите внимание, что мы могли бы получить здесь вторую точку, используя ось симметрии, если бы захотели.
Вот набросок графика.
Итак, мы видели несколько примеров этой формы параболы. Однако, как отмечалось ранее, большинство парабол не даны в такой форме. Итак, нам нужно взглянуть на то, как построить параболу в общем виде.2} + bx + c \]
В этой форме знак \ (a \) будет определять, будет ли парабола открываться вверх или вниз, как это было в предыдущем наборе примеров. 2} + 4x + 4 \) Показать решение
В этой заключительной части мы имеем \ (a = 1 \), \ (b = 4 \) и \ (c = 4 \).2} + 4 \ left ({- 2} \ right) + 4 = 0 \ end {align *} \]
Итак, вершина \ (\ left ({- 2,0} \ right) \). Обратите внимание, что поскольку координата \ (y \) этой точки равна нулю, она также является точкой пересечения с \ (x \). Фактически, это будет единственный \ (x \) — перехватчик для этого графа. Это имеет смысл, если мы примем во внимание тот факт, что вершина в данном случае является самой низкой точкой на графике, и поэтому график просто не может касаться оси \ (x \) где-либо еще.
Тот факт, что эта парабола имеет только один \ (x \) — точку пересечения, можно проверить, решив, как мы делали до этого момента в других примерах.2} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = — 2 \ end {align *} \]
Конечно, есть только один \ (x \) — перехватчик. Обратите внимание, что это будет означать, что нам придется использовать ось симметрии, чтобы получить вторую точку пересечения \ (y \) — в этом случае.
Кстати, перехватчик \ (y \) в данном случае равен \ (\ left ({0,4} \ right) \). Это означает, что вторая точка — это \ (\ left ({- 4,4} \ right) \).
Вот набросок графика.2} — 6x + \ frac {3} {2}} \ right) \]
Обратите внимание, что это часто приводит к дроблению проблемы, с которой нам нужно иметь дело. Также обратите внимание, что если нам посчастливилось получить коэффициент 1 при члене x 2 , нам не нужно будет выполнять этот шаг.
Вот здесь процесс действительно начинает отличаться от того, что мы видели до этого момента. Мы по-прежнему берем половину коэффициента при \ (x \) и возводим его в квадрат.2} — 6x + 9 — 9 + \ frac {3} {2}} \ right) \]
Мы складываем и вычитаем это количество внутри скобок, как показано. Обратите внимание, что все, что мы здесь делаем, это добавляем ноль, так как 9-9 = 0! Указанный здесь порядок важен. 2} — \ frac {{15}} {2}} \ right) \]
В качестве последнего шага мы снова умножаем 2.2} + 24 \ end {align *} \]
Math 1010 онлайн — Параболы
Math 1010 on-line — ПараболыКафедра математики — Колледж наук — Университет Юты
Параболы
График.
Рисунок 1. Парабола
В график уравнения с участием и является набором всех точки в декартова координатная плоскость координаты которого удовлетворяют уравнению. В график функции — это график уравнения Например, на рисунке 1 показан график уравнения
Этот конкретный график является примером параболы . Обратите внимание, что это симметричен относительно оси, которая называется осью или линией симметрии .Самая низкая точка параболы (которая в данном случае является началом координат) называется его вершиной .Мы будем использовать этот график и уравнение, чтобы проиллюстрировать некоторые идеи, которые имеют гораздо более широкое применение. Давайте подумаем о том, чтобы сделать некоторые изменения:
Изменение масштаба
Предположим, мы умножаем значение на константу. Назовем это . Таким образом, мы получаем новое уравнение
Если это то же уравнение, что и раньше. Рассмотрим другие возможности, однако:
Рисунок 2.Несколько парабол
На рис.2 показаны графики этих уравнений для
Графики можно аналогичным образом отражать, растягивать или сжимать в горизонтальное направление путем умножения на константу. Тем не мение, в данном простом примере этот эффект эквивалентен вертикальное масштабирование с куда .
Переводы
Рассмотрим теперь эффект вычитания константы из:
Это эквивалентно
и поэтому он имеет эффект поднятие графика по единицам.Конечно, если есть отрицательный, график понижен (по ед.).Вычитание константы из имеет тот же эффект в горизонтальное направление. Рассмотрим уравнение
а также сравните его с исходным уравнением. Как в , никогда не бывает отрицательным. Он принимает минимальное значение () при. Таким образом, график представляет собой график смещенных единиц в право. Если отрицательно, график сдвигается на единицы левый.
Рис. 3. Переведенные параболы
Горизонтальные и вертикальные смещения можно комбинировать, и любые подобные комбинация называется переводом .Общий вид применяемый перевод предоставлен
который часто пишется как Перевод не меняет форма или ориентация графика. Меняет только свой место нахождения. На рисунке 3 показаны переводы графика с участиемЗавершенная квадратная форма
Завершенная квадратная форма квадратичной функции равна
Его граф представляет собой параболу, которой составляет вершину . Если открывается, если открывается вниз.(Если график — это горизонтальная линия, которую вы можете представить как вырожденную парабола.) Вертикальная линия — это ось , линия или . симметрия параболы.Понятно, как общий квадратичный многочлен
можно преобразовать в стандартную форму. Просто завершите квадрат, как проиллюстрировано в следующем примере:График этого конкретного уравнения представлен на рисунке 4. Получившаяся парабола имеет вершину (. полученный из стандартной параболы путем ее тщательного отражения. ось, растягивая ее по вертикали и переводя на 1 единицу в слева и 8 единиц вверх.Обратите внимание, что все эти свойства могут быть немедленно прочитать уравнение
Рисунок 4. Другая парабола
Масштабирование и перевод графиков
Проиллюстрированные здесь принципы применимы к любому уравнению, поэтому давайте переформулируйте их:
Как обычно, рекомендую не запоминать эти факты. Скорее подумайте о том, что происходит, с точки зрения взаимодействия между график и уравнение, и выяснить эффект того, что вы делать или что вам нужно делать, а не полагаться на воспоминания загадочные факты.
Как найти вершину параболы
Роберт О
Наш предыдущий урок был посвящен уравнению параболы. Парабола, имеющая вершину в начале координат, имеет вид:
Из этого общего уравнения мы можем легко определить, открывается ли парабола вверх, вниз, влево или вправо.В приведенном выше виде легко определить вершину параболы. Вершина всегда находится в начальной точке (0, 0). Общее уравнение принимает следующий вид:
Что происходит, когда вершина не находится в начале координат?В некоторых случаях вершина параболы никогда не находится в точке (0, 0).Уравнение такой параболы, следовательно, принимает другую показанную форму:
Параболы с вершиной, удаленной от начала координат, также могут открываться вверх, вниз, влево или вправо.
Как найти ключевые точки и линии вертикальной параболы?Любое уравнение вертикальной параболы, вершина которой находится вдали от точки (0, 0), принимает вид:
В таком случае:
Focus, F = (h, k + p)
Directrix (y = kp)
Vertex = (-h, -k)
Как найти ключевые точки и линии горизонтальной параболы?Любое уравнение горизонтальной параболы, вершина которой находится вдали от точки (0, 0), принимает вид:
В таком случае:
Focus, F = (h + p, k)
Directrix (y = hp)
Vertex = (-h, -k)
На графике ниже показан пример параболической кривой.
Решенные задачиПример 1:
Что такое точка фокусировки, вершина и уравнение директрисы параболы, уравнение которой:
Решение
Начнем с переписывания уравнение в общем виде уравнения параболы, вершина которой удалена от начала координат.
Затем заполните квадрат для выражения слева.
Следующие алгебраические тождества помогут вам очень быстро завершить квадрат:
Затем факторизуйте оба выражения.
Уравнение имеет вид
, где h = -3, k = +3Это вертикальная парабола, которая открывается вниз, поскольку x-коэффициент отрицателен.
Далее найдите значение p.
Теперь мы можем найти все точки и уравнения, которые нам нужны.
Фокус находится на
Вершина находится на (3, -3)
Directrix — это линия, уравнение которой равно
Пример 2:
Нарисуйте график параболы, задаваемый по формуле:
Решение
В этом случае у нас уже есть стандартное уравнение параболы.Что нам нужно сделать, так это получить все параметры, которые нам нужны для рисования кривой.
Первое наблюдение состоит в том, что мы имеем дело с горизонтальной параболой, поскольку y имеет наибольшую степень. Второе наблюдение заключается в том, что эта парабола открывается влево, поскольку коэффициент y отрицателен.
Далее мы находим все ключевые точки и уравнение директрисы и линии симметрии.
Вершина (-h, -k) задается координатами (-3, 1)
Ось симметрии, y = k = 1
Фокус задается координатами (h + p, k).-16 = 4р.п = -4. Следовательно, фокус F находится в (-7, 1)
Линия директрисы,
Чтобы точно нарисовать параболу, нам понадобятся еще две точки, конечные точки. Форма выражения для вычисления двух наборов координат:
Используя эти выражения, конечными точками будут (-7, -7) и (-7,9).Теперь у нас есть все необходимое для точного наброска рассматриваемой параболы. Обратите внимание на ключевые точки, нанесенные на график ниже:
ПримечанияВы можете легко найти вершину любой параболы, выразив ее уравнение в стандартной форме.Не забудьте использовать метод завершения квадрата, чтобы выразить любое параболическое уравнение в стандартной форме. Используя уравнение параболы в стандартной форме, вы можете определить ориентацию ее линии симметрии. Наблюдением вы также можете определить, открывается ли он влево, вправо, вверх или вниз.
Для любой параболы, вершина которой не находится в начале координат, вершиной является (-h, -k). Или поменяйте местами знаки h и k в стандартном уравнении.
Об авторе
Этот урок подготовил Роберт О.Он имеет степень бакалавра инженерных наук в области электротехники и электроники. Он карьерный учитель, возглавлял кафедру языков и занимал различные руководящие должности. Он пишет для Full Potential Learning Academy.
Онлайн-калькулятор параболических графиков
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| . | √ | ⬅ | ➡ | ||||||
| F | _ | ÷ | | | ( | * | / | ⌫ | ||
| A | ↻ | x | y | = | + | — | G | 907||
Ваш комментарий будет первым