Квадратичная функция, как построить параболу
Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Построение квадратичной функции
Квадратичная функция задается формулой y = ax2 + bx + c
 В уравнении существует следующее распределение:
В уравнении существует следующее распределение:
|
График квадратичной функции — парабола, которая имеет следующий вид для y = x2:
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x2, нужно составить таблицу:
x | −2 | −1 | 0 | 1 | 2 |
y | 4 | 1 | 0 | 1 | 4 |
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x2 при любых значениях остальных коэффициентов.
График функции y = –x2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x | −2 | −1 | 0 | 1 | 2 |
y | −4 | −1 | 0 | −1 | −4 |
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a < 0, то ветви параболы напрaвлены вниз.
Как строить график квадратичной функции — учитывать значения х, в которых функция равна нулю. Иначе это можно назвать нулями функции. На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.
На графике нули функции f(x) — это точки пересечения у = f(x) с осью ОХ.
Так как ордината (у) любой точки на оси ОХ равна нулю, поэтому для поиска координат точек пересечения графика функции у = f(x) с осью ОХ, нужно решить уравнение f(x) = 0.
Для наглядности возьмем функцию y = ax2 + bx + c, для построения которой нужно решить квадратное уравнение ax2 + bx + c = 0. В процессе найдем дискриминант D = b2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D < 0, то уравнение не имеет решений и парабола не имеет точек пересечения с осью ОХ. Если a > 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Уравнение квадратичной функции имеет вид y = ax
2 + bx + c.Разберем общий алгоритм на примере y = 2x2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x2 + 3x — 5.
D = b2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
√D = 7
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x2 + 3x — 5 = 0
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
Уравнение квадратичной функции имеет вид y = a * (x — x₀)
2 + y₀Рассмотрим пример: y = 2 * (x — 1)2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x2,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая.
Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
Подбор аппроксимирующей кривой для экспериментальных данных в COMSOL Multiphysics
Мы часто обрабатываем в COMSOL Multiphysics экспериментальные данные. Обычно они характеризуют свойства материалов или другие входные параметры модели. Однако экспериментальные данные часто бывают зашумленными; они содержат погрешности эксперимента, которые мы не хотели бы вносить в модель. В этой статье мы расскажем, как подбирать гладкие кривые и поверхности под экспериментальные данные, используя базовые функциональные возможности COMSOL Multiphysics.
Обычно они характеризуют свойства материалов или другие входные параметры модели. Однако экспериментальные данные часто бывают зашумленными; они содержат погрешности эксперимента, которые мы не хотели бы вносить в модель. В этой статье мы расскажем, как подбирать гладкие кривые и поверхности под экспериментальные данные, используя базовые функциональные возможности COMSOL Multiphysics.
Подбор кривой как задача минимизации функции
Давайте посмотрим на график с экспериментальными точками, представленный ниже. Мы видим, что данные зашумлены, а выборка по оси x неравномерна. Эти экспериментальные данные могут характеризовать материал. Если характеристика материала зависит от переменной, расчитываемой в ходе решения, (например, теплопроводность, зависящая от температуры), то эти изначальные данные обычно не желательно напрямую использовать для конечно-элементного анализа. Такие зашумленные входные данные часто могут вызывать проблемы со сходимостью решателя по причинам, рассмотренным здесь.
Это похоже на задачу оптимизации, но мы не вводим ограничений на коэффициенты и предполагаем, что функция имеет единственный минимум. В точке этого минимума производные функции по коэффициентам будут равны нулю. Поэтому для подбора наилучшей функции мы должны найти такие значения коэффициентов, что
\frac{\partial R} {\partial c_0} = \frac{\partial R} {\partial c_1} = \frac{\partial R} {\partial c_2} =\frac{\partial R} {\partial c_3} = 0
Оказывается, эту задачу можно решить с помощью базовых функций COMSOL Multiphysics. Давайте посмотрим, как это сделать.
Решение задачи в COMSOL
Мы начинаем с создания нового файла с одномерным компонентом. Мы воспользуемся интерфейсом физики Global ODEs and DAEs (Глобальные обыкновенные дифференциальные уравнения и алгебраические дифференциальные уравнения), чтобы найти искомые коэффициенты, и будем использовать стационарный решатель. Для простоты выберем безразмерную единицу длины, как показано на снимке экрана ниже.
В настройках узла 1D component (Одномерный компонент) в поле Unit system (Система единиц) выберите None (Безразмерная).
Далее зададим геометрию. Геометрия задачи состоит из интервала (экспериментальные точки в нашем случае лежат в интервале от 0 до 1) и множества точек по оси x для каждой экспериментальной точки. Вы можете просто скопировать этот набор точек из электронной таблицы и вставить в поле
Добавьте точки, соответствующие экспериментальным данным, в интервал.
Считайте экспериментальные данные с помощью функции Interpolation (Интерполяция). Присвойте набору данных удобное имя (на снимке экрана внизу использовано просто D), активируйте опцию Use spatial coordinates as arguments (Использовать пространственные координаты в качестве аргументов) и убедитесь, что выбран вариант интерполяции между точками данных по умолчанию — Linear (Линейная).
Настройки импорта экспериментальных данных.
Задайте оператор интегрирования (Integration) на всех областях. Вы можете оставить наименование по умолчанию, intop1. Он будет использоваться для вычисления указанного выше интеграла.
Оператор интегрирования задан на всех областях.
Теперь задайте две переменных. Одна из них будет вашей функцией F, а другая — функцией R, которую требуется минимизировать. Так как в поле Geometric Entity Level (Уровень геометрических объектов) выбран вариант Entire Model (Вся модель), функция F будет задана на всей области как функция пространственной переменной x. С другой стороны, R везде задана скалярным значением и также доступна по всей модели. Как показано на снимке экрана ниже, мы можем ввести F как функцию c_0, c_1, c_2, c_3, а сами коэффициенты определим позднее.
Определение подбираемой функции и целевой функции минимизации.
Далее мы используем интерфейс Global Equations (Глобальные уравнения), чтобы определить четыре уравнения, которым удовлетворяют четыре наших коэффициента. Если вы помните, мы хотим, чтобы производная функции R по каждому коэффициенту обращалась в нуль. Используя дифференциальный оператор d(f(x),x), мы можем ввести это условие так:
Если вы помните, мы хотим, чтобы производная функции R по каждому коэффициенту обращалась в нуль. Используя дифференциальный оператор d(f(x),x), мы можем ввести это условие так:
Глобальные уравнения используются для нахождения коэффициентов подбираемой функции.
Наконец, мы должны наложить на нашу одномерную область подходящую сетку. Как вы помните, ранее мы разместили в каждой точке экспериментальных данных геометрическую точку. С помощью подфункции Distribution (Распределение) функции Edge Mesh (Сетка на ребрах) мы можем разместить ровно один элемент между каждой парой точек данных. Дополнительных элементов не требуется, так как мы предполагаем, что интерполяция между точками набора данных линейная, но и меньшим числом элементов мы не обойдемся, не пропустив некоторые экспериментальные точки данных.
На каждом интервале данных должен располагаться один элемент.
Теперь мы можем решить стационарную задачу для нахождения численных значений коэффициентов, а затем построить результаты.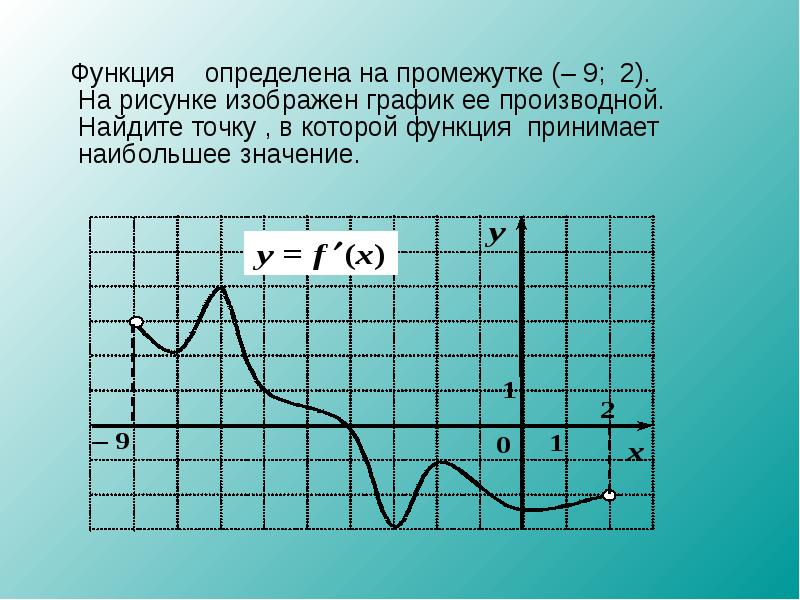 На графике ниже мы видим построенный набор начальных точек, линейную интерполяцию между ними и подобранную функцию, полученную при расчете. Мы минимизировали интеграл от квадрата разности между этими кривыми на данном интервале и получили гладкую и простую функцию, достаточно хорошо аппроксимирующую наши данные.
На графике ниже мы видим построенный набор начальных точек, линейную интерполяцию между ними и подобранную функцию, полученную при расчете. Мы минимизировали интеграл от квадрата разности между этими кривыми на данном интервале и получили гладкую и простую функцию, достаточно хорошо аппроксимирующую наши данные.
Экспериментальные данные с линейной интерполяцией (черный) и подобранная функция (красный).
Дальнейшие расширения
Проделанная нами работа на самом деле достаточно проста, и подобные кривые можно рассчитать в любом редакторе электронных таблиц и во многих других программных инструментах. Но этот же подход позволяет достичь гораздо большего. Мы не ограничены использованием данной подобранной функции. Вы можете выбрать любую функцию, но лучше выбирать функцию, являющуюся суммой набора ортогональных функций. Например, можно попробовать следующую функцию:
F(x) = c_0 + c_1sin ( \pi x /4 ) + c_2cos ( \pi x /4 ) + c_3sin ( \pi x /2 ) + c_4cos ( \pi x /2 )
Имейте в виду, что вычисляемые коэффициенты, входящие в подбираемую функцию, должны быть линейными. Следует избегать нелинейных коэффициентов аппроксимации, таких как F(x) = c_0 + c_1sin ( \pi x /c_3 ) + c_2cos ( \pi x /c_4), поскольку такая задача может оказаться слишком нелинейной, чтобы сходиться.
Следует избегать нелинейных коэффициентов аппроксимации, таких как F(x) = c_0 + c_1sin ( \pi x /c_3 ) + c_2cos ( \pi x /c_4), поскольку такая задача может оказаться слишком нелинейной, чтобы сходиться.
Но что делать, если у вас есть двухмерный или трехмерный набор данных? Вы можете применить к ним точно такой же подход. Разница в том, что теперь мы задаем двухмерную или трехмерную область. Области не обязательно должны быть декартовыми, вы можете переключиться на другую систему координат.
Давайте посмотрим на некоторый набор данных, измеренных на показанной ниже области.
Набор данных на двухмерной области. Мы хотим подобрать поверхность, наиболее соответствующую высотам этих точек.
Так как данные собраны на этой кольцеобразной области и, по видимости, изменяются в зависимости от радиальной и азимутальной координат (r, \theta), а не от декартовых координат, мы можем подобрать такую функцию:
F(x) = c_0 + c_1r cos ( \theta ) +c_2 r sin ( \theta )+ c_3(2r^2-1) + c_4 r^2 cos ( 2\theta ) +c_5 r^2 sin ( 2\theta )
Мы можем следовать такой же процедуре, как и раньше. Теперь мы будем интегрировать по двухмерной области, а не по кривой, и запишем выражение с использованием цилиндрической системы координат.
Теперь мы будем интегрировать по двухмерной области, а не по кривой, и запишем выражение с использованием цилиндрической системы координат.
Рассчитанная поверхность наилучшего приближения показана выше.
Заключение
Вы видите, что базовые функци пакета COMSOL Multiphysics предоставляют чрезвычайно гибкие возможности для поиска кривых наилучшего приближения в одномерном, двухмерном и трехмерном пространствах с помощью описанных методов.
В некоторых случаях может потребоваться не ограничиваться простым подбором кривых и вводить дополнительные ограничения. Тогда вы можете воспользоваться модулем Оптимизация, который также может подбирать эти кривые и решать множество других задач. Введение в подбор кривых с помощью модуля Оптимизация и в связанную задачу оценки параметров вы найдете здесь:
Настройка политик клиента в организации — Skype for Business Online
- Чтение занимает 3 мин
-
- Применяется к:
- Skype for Business
Оцените свои впечатления
Да Нет
Хотите оставить дополнительный отзыв?
Отзывы будут отправляться в корпорацию Майкрософт. Нажав кнопку «Отправить», вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.
Нажав кнопку «Отправить», вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.
Отправить
Спасибо!
В этой статье
Важно!
Поддержка Skype для бизнеса Online прекратится 31 июля 2021 г. Если до этой даты пользователи Skype для бизнеса Online не будут переведены в Microsoft Teams, для них будет автоматически запланирован переход с помощником. Если вы хотите самостоятельно обновить организацию до Teams, настоятельно рекомендуем начать планирование пути обновления уже сегодня. Необходимо помнить, что успешный переход требует и технической подготовки, и подготовки пользователей, поэтому для подготовки перехода на Microsoft Teams обязательно воспользуйтесь нашим руководством по обновлению.
Политики клиента помогают определить функции Skype для бизнеса online, доступные пользователям. Например, вы можете предоставить одним пользователям право передавать файлы и запретить это другим пользователям.
Параметры политики клиента можно настроить во время создания политики или с помощью cmdlet Set-CsClientPolicy изменить параметры существующей политики.
Задание политик клиента
Примечание
Для всех настроек политики клиента в Skype для бизнеса Online нужно использовать Windows PowerShell. Нельзя использовать Центр администрирования Skype для бизнеса.
Начните Windows PowerShell
Примечание
Соединитель Skype для бизнеса Online в настоящее время является частью последнего модуля Teams PowerShell. Если вы используете последний общедоступный выпуск Teams PowerShell, вам не нужно устанавливать соединитель Skype для бизнеса Online.
Установите модуль Teams PowerShell.

Откройте Windows PowerShell командную команду и запустите следующие команды:
# When using Teams PowerShell Module Import-Module MicrosoftTeams $credential = Get-Credential Connect-MicrosoftTeams -Credential $credentialДополнительные сведения о запуске Windows PowerShell см. в Подключение всех службах Microsoft 365 или Office 365 в одном окне Windows PowerShell или Настройка компьютера дляWindows PowerShell.
Отключение эмотиконов, уведомлений о присутствии и запрет на сохранение мгновенных сообщений
Чтобы создать политику для настроек, запустите следующую команду:
New-CsClientPolicy -Identity ClientPolicy -DisableEmoticons $true -DisablePresenceNote -$true -DisableSavingIM $trueДополнительные возможности см. в поле New-CsClientPolicy.
Чтобы предоставить новую политику всем пользователям в организации, запустите следующую команду:
Grant-CsClientPolicy -identity "amos. [email protected]" -PolicyName ClientPolicy
[email protected]" -PolicyName ClientPolicy
См. дополнительные новости о cmdlet Grant-CsClientPolicy.
Если вы уже создали политику, вы можете изменить существующую политику с помощью cmdlet Set-CsClientPolicy, а затем применить параметры к пользователям с помощью cmdlet Grant-CsClientPolicy.
Разрешение перехода по URL-адресам или гиперссылкам в мгновенных сообщениях
Чтобы создать политику для настроек, запустите следующую команду:
New-CsClientPolicy -Identity URLClientPolicy -EnableURL $trueДополнительные возможности см. в поле New-CsClientPolicy.
Чтобы предоставить новую политику всем пользователям в организации, запустите следующую команду:
Grant-CsClientPolicy -identity "[email protected]" -PolicyName URLClientPolicyСм. дополнительные новости о cmdlet Grant-CsClientPolicy.
Если вы уже создали политику, вы можете изменить существующую политику с помощью cmdlet Set-CsClientPolicy, а затем применить параметры к пользователям с помощью cmdlet Grant-CsClientPolicy.
Запрет отображения последних контактов
Чтобы создать политику для настроек, запустите следующую команду:
New-CsClientPolicy -Identity ContactsClientPolicy -ShowRecentContacts $falseДополнительные возможности см. в поле New-CsClientPolicy.
Чтобы предоставить новую политику Amos Marble, запустите следующую команду:
Grant-CsClientPolicy -identity "[email protected]" -PolicyName ContactsClientPolicyСм. дополнительные новости о cmdlet Grant-CsClientPolicy.
Если вы уже создали политику, вы можете изменить существующую политику с помощью cmdlet Set-CsClientPolicy, а затем применить параметры к пользователям с помощью cmdlet Grant-CsClientPolicy.
Хотите узнать больше о Windows PowerShell?
Windows PowerShell is all about managing users and what users are allowed or not allowed to do. С Windows PowerShell вы можете управлять Microsoft 365 или Office 365 и Skype для бизнеса Online, используя единый пункт администрирования, который упростит выполнение ваших повседневных задач.
 Чтобы начать работу с Windows PowerShell, ознакомьтесь с приведенными ниже разделами.
Чтобы начать работу с Windows PowerShell, ознакомьтесь с приведенными ниже разделами.Windows PowerShell имеет множество преимуществ в скорости, простоте и эффективности работы по сравнению с использованием только Центр администрирования Microsoft 365, например при внесении изменений для множества пользователей одновременно. Подробнее об этих преимуществах можно узнать в следующих разделах:
Создание настраиваемых политик внешнего доступа
Блокировка передачи файлов по точкам
Настройка политик conferencing в организации
Определение функции
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана (, т. е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-4: Определение функции
Теперь нам нужно перейти ко второй теме этой главы. Однако, прежде чем мы это сделаем, нам нужно сделать быстрое определение.
Определение отношения
Отношение — это набор упорядоченных пар.
Это кажется странным определением, но оно нам понадобится для определения функции (что является основной темой этого раздела). Однако, прежде чем мы фактически дадим определение функции, давайте посмотрим, сможем ли мы понять, что такое отношение. 2} — 4 \).Вот упорядоченные пары, которые мы использовали.
2} — 4 \).Вот упорядоченные пары, которые мы использовали.
Любые из следующих отношений являются отношениями, потому что они состоят из набора упорядоченных пар.
\ [\ begin {align *} & \ left \ {{\ left ({- 2,5} \ right) \, \, \, \, \ left ({- 1,0} \ right) \, \, \, \, \, \ left ({2, — 3} \ right)} \ right \} \\ & \ left \ {{\ left ({- 1,0} \ right) \, \, \, \, \ left ({0, — 3} \ right) \, \, \, \, \ left ({2, — 3} \ right) \, \, \, \, \ left ({3,0} \ right) \, \, \, \, \ left ({4,5} \ right)} \ right \} \\ & \ left \ {{\ left ({3,0} \ right) \, \, \, \ , \ left ({4,5} \ right)} \ right \} \\ & \ left \ {{\ left ({- 2,5} \ right) \, \, \, \, \ left ({- 1,0} \ right) \, \, \, \, \ left ({0, — 3} \ right) \, \, \, \, \ left ({1, — 4} \ right) \, \ , \, \, \ left ({2, — 3} \ right) \, \, \, \, \ left ({3,0} \ right) \, \, \, \, \ left ({4, 5} \ right)} \ right \} \ end {align *} \] Конечно, есть еще много отношений, которые мы могли бы сформировать из списка упорядоченных пар, приведенного выше, но мы просто хотели перечислить несколько возможных отношений, чтобы привести некоторые примеры. Также обратите внимание, что мы также можем получить другие упорядоченные пары из уравнения и добавить их в любое из приведенных выше отношений, если захотим.
Также обратите внимание, что мы также можем получить другие упорядоченные пары из уравнения и добавить их в любое из приведенных выше отношений, если захотим.
Теперь вы, вероятно, спрашиваете, почему мы заботимся об отношениях, и это хороший вопрос. Некоторые отношения очень специфичны и используются почти на всех уровнях математики. Следующее определение говорит нам, какие отношения являются этими особыми отношениями.
Определение функции
Функция — это отношение, для которого каждое значение из набора первых компонентов упорядоченных пар связано ровно с одним значением из набора вторых компонентов упорядоченной пары.
Ладно, это полный рот. Посмотрим, сможем ли мы понять, что это значит. Давайте посмотрим на следующий пример, который, надеюсь, поможет нам во всем этом разобраться.
Пример 1 Следующее отношение является функцией. \ [\ left \ {{\ left ({- 1,0} \ right) \, \, \, \, \ left ({0, — 3} \ right) \, \, \, \, \ left ( {2, — 3} \ right) \, \, \, \, \ left ({3,0} \ right) \, \, \, \, \ left ({4,5} \ right)} \ right \} \] Показать решение Из этих упорядоченных пар мы получаем следующие наборы первых компонентов ( i. Для набора вторых компонентов обратите внимание, что «-3» встречается в двух упорядоченных парах, но мы указали его только один раз. Чтобы понять, почему это отношение является функцией, просто выберите любое значение из набора первых компонентов. Теперь вернитесь к отношению и найдите каждую упорядоченную пару, в которой это число является первым компонентом, и перечислите все вторые компоненты из этих упорядоченных пар.Список вторых компонентов будет состоять ровно из одного значения. Например, давайте выберем 2 из набора первых компонентов. Из отношения мы видим, что существует ровно одна упорядоченная пара с 2 в качестве первого компонента, \ (\ left ({2, — 3} \ right) \). Следовательно, список вторых компонентов (, т.е. список значений из набора вторых компонентов), связанный с 2, представляет собой ровно одно число -3. Обратите внимание, что нас не волнует, что -3 является вторым компонентом второго упорядоченного номинала в отношении.Это вполне приемлемо. Мы просто не хотим, чтобы было больше одной упорядоченной пары с 2 в качестве первого компонента. Мы рассмотрели одно значение из набора первых компонентов для нашего быстрого примера, но результат будет таким же для всех остальных вариантов. Независимо от выбора первых компонентов с ним будет связан ровно один второй компонент. Следовательно, это отношение является функцией. Чтобы действительно почувствовать, что нам говорит определение функции, мы, вероятно, должны также проверить пример отношения, которое не является функцией. Не беспокойтесь о том, откуда взялась эта связь. Из набора первых компонентов выберем 6. Теперь, если мы перейдем к соотношению, мы увидим, что есть две упорядоченные пары с 6 в качестве первого компонента: \ (\ left ({6,10} \ right) \ ) и \ (\ left ({6, — 4} \ right) \). Список вторых компонентов, связанных с 6, будет: 10, -4. Список вторых компонентов, связанных с 6, имеет два значения, поэтому это отношение не является функцией. Обратите внимание на тот факт, что если мы выбрали -7 или 0 из набора первых компонентов, то в списке вторых компонентов, связанных с каждым из них, будет только одно число. Это не имеет значения. Тот факт, что мы нашли даже одно значение в наборе первых компонентов с более чем одним вторым компонентом, связанным с ним, достаточно, чтобы сказать, что это отношение не является функцией. В качестве последнего комментария к этому примеру отметим, что если мы удалим первую и / или четвертую упорядоченную пару из отношения, у нас будет функция! Итак, надеюсь, у вас есть хоть какое-то представление о том, что нам говорит определение функции. Теперь, когда мы заставили вас пройти собственно определение функции, давайте дадим еще одно «рабочее» определение функции, которое будет гораздо более полезным для того, что мы здесь делаем. Фактическое определение работает с отношением. Однако, как мы видели с четырьмя отношениями, которые мы указали до определения функции, и с отношением, которое мы использовали в примере 1, мы часто получаем отношения из некоторого уравнения. Важно отметить, что не все отношения основаны на уравнениях! Отношение из второго примера, например, было просто набором упорядоченных пар, которые мы записали для этого примера, и не было получено из какого-либо уравнения. Однако, как бы то ни было, все функции, которые мы собираемся использовать в этом курсе, основаны на уравнениях. Поэтому давайте напишем определение функции, которая признает этот факт. Прежде чем мы дадим «рабочее» определение функции, мы должны указать, что это НЕ фактическое определение функции, данное выше. Это просто хорошее «рабочее определение» функции, которое связывает вещи с видами функций, с которыми мы будем работать в этом курсе. Функция — это уравнение, для которого любой \ (x \), который можно вставить в уравнение, даст ровно один \ (y \) из уравнения. Вот оно. Это определение функций, которые мы собираемся использовать, и, вероятно, будет легче понять, что оно означает. Прежде чем мы рассмотрим это, обратите внимание, что мы использовали фразу «\ (x \), который может быть подключен» в определении. Далее, имея дело с функциями, мы всегда будем предполагать, что и \ (x \), и \ (y \) будут действительными числами.Другими словами, мы на время забудем о том, что знаем что-либо о комплексных числах, пока будем заниматься этим разделом. Хорошо, теперь давайте вернемся к определению функции и рассмотрим несколько примеров уравнений, которые являются функциями, и уравнений, которые не являются функциями. «Рабочее» определение функции гласит, что если мы возьмем все возможные значения \ (x \), подставим их в уравнение и решим для \ (y \), мы получим ровно одно значение для каждого значения \ ( Икс\).На этом этапе игры может быть довольно сложно на самом деле показать, что уравнение является функцией, поэтому в основном мы будем обсуждать его. С другой стороны, часто довольно легко показать, что уравнение не является функцией. Итак, нам нужно показать, что независимо от того, какое \ (x \) мы подставляем в уравнение и решаем для \ (y \), мы получим только одно значение \ (y \). Также обратите внимание, что значение \ (y \), вероятно, будет различным для каждого значения \ (x \), хотя это не обязательно. Давайте начнем с того, что подставим некоторые значения \ (x \) и посмотрим, что произойдет. Итак, для каждого из этих значений \ (x \) мы получили единственное значение \ (y \) из уравнения.Теперь этого недостаточно, чтобы утверждать, что это функция. Чтобы официально доказать, что это функция, нам нужно показать, что она будет работать независимо от того, какое значение \ (x \) мы подставляем в уравнение. Конечно, мы не можем подставить в уравнение все возможные значения \ (x \). Это просто невозможно физически. Однако давайте вернемся и посмотрим на те, которые мы подключили. Для каждого \ (x \) после подключения мы сначала умножили \ (x \) на 5, а затем прибавили к нему 1.2} + 1 = 9 + 1 = 10 \ end {align *} \] А теперь давайте немного подумаем о том, что мы делали с оценками. Итак, похоже, что это уравнение также является функцией. Обратите внимание, что получить одинаковое значение \ (y \) для разных \ (x \) — это нормально.2} & = 10 + 1 = 11 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \ sqrt {11} \ end {align *} \] Теперь помните, что мы решаем для \ (y \), и это означает, что в первом и последнем случаях выше мы фактически получим два разных значения \ (y \) из \ (x \), и поэтому это уравнение НЕ является функцией. Обратите внимание, что у нас могут быть значения \ (x \), которые приведут к единственному \ (y \), как мы видели выше, но это не имеет значения. Если даже одно значение \ (x \) дает более одного значения \ (y \), при решении уравнения не будет функцией. Итак, это уравнение не является функцией. Напомним, что из предыдущего раздела это уравнение круга. Круги никогда не бывают функциями. Надеюсь, эти примеры позволили вам лучше понять, что такое функция. Теперь нам нужно перейти к так называемой нотации функции . Обозначения функций будут широко использоваться в большинстве оставшихся глав этого курса, поэтому их важно понимать.2} — 5x + 3 \] Буква, которую мы используем, не имеет значения. Важна часть «\ (\ left (x \ right) \)». Буква в скобках должна соответствовать переменной, используемой справа от знака равенства. Очень важно отметить, что \ (f \ left (x \ right) \) на самом деле не более чем действительно причудливый способ записи \ (y \). Если вы запомните это, вы можете обнаружить, что работать с обозначениями функций становится немного проще. Кроме того, это НЕ умножение \ (f \) на \ (x \)! Это одна из наиболее распространенных ошибок, которые делают люди, когда впервые сталкиваются с функциями.2} — 5x + 3 \] и спросите, каково его значение для \ (x = 4 \). В терминах обозначений функций мы будем «спрашивать» об этом, используя обозначение \ (f \ left (4 \ right) \). Итак, когда в скобках есть что-то, кроме переменной, мы действительно спрашиваем, каково значение функции для этой конкретной величины. Теперь, когда мы говорим значение функции, мы действительно спрашиваем, каково значение уравнения для этого конкретного значения \ (x \). Вот \ (f \ left (4 \ right) \).2} — 5} \ right) \) Показать все решения Скрыть все решения
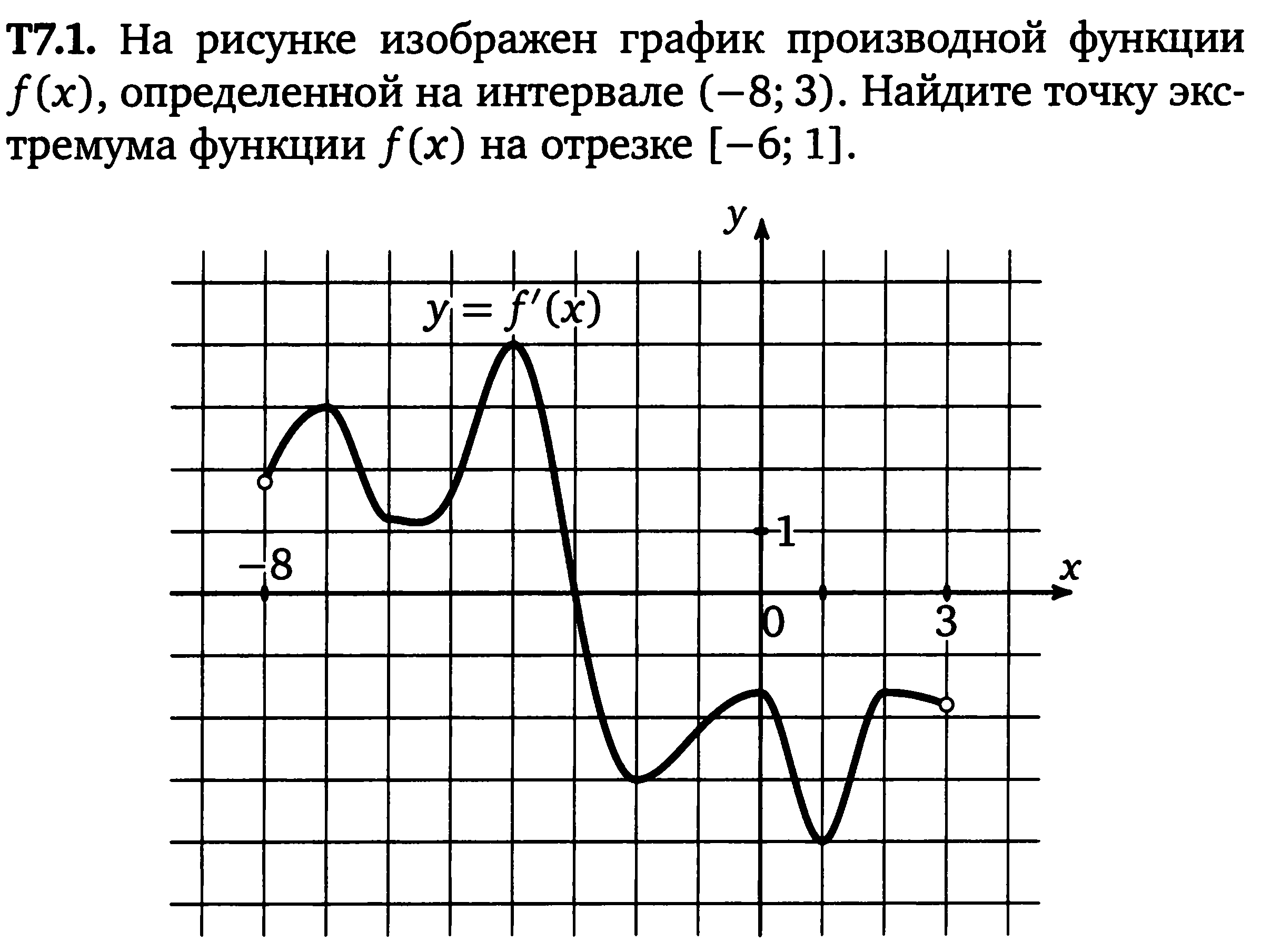
a \ (f \ left (3 \ right) \) и \ (g \ left (3 \ right) \) Показать решение Хорошо, у нас есть две оценки функций, которые нужно выполнить, и у нас также есть две функции, поэтому нам нужно будет решить, какую функцию использовать для оценок. Убедитесь, что здесь вы правильно разбираетесь с негативными знаками. Теперь второй. Мы достигли разницы. Напомним, когда мы впервые начали говорить об определении функций, мы заявили, что будем иметь дело только с действительными числами. Другими словами, мы подставляем только действительные числа и хотим, чтобы в качестве ответов возвращались только действительные числа.2} — 2 \ влево (0 \ вправо) + 8 = 8 \] Опять же, не забывайте, что это не умножение! По какой-то причине ученикам нравится думать об этом как об умножении и получать нулевой ответ. Будь осторожен. Остальные оценки теперь будут немного другими. Как показывает этот, нам не нужно просто указывать числа в скобках. Однако оценка работает точно так же. Мы вставляем \ (x \) справа от знака равенства в скобки.2} — 2t + 8 \] Обратите внимание, что в этом случае это почти то же самое, что и наша исходная функция, за исключением того, что на этот раз мы используем \ (t \) в качестве переменной. А теперь давайте немного посложнее, или, по крайней мере, они кажутся более сложными. Однако все не так плохо, как может показаться. Сначала мы оценим \ (f \ left ({t + 1} \ right) \). Этот работает точно так же, как и предыдущая часть.2} + 1} \ end {выровнять *} \] Оценка функций — это то, чем мы будем много заниматься в следующих разделах и главах, поэтому убедитесь, что вы можете это сделать. Пока мы говорим об оценке функций, мы должны теперь поговорить о кусочных функциях . На самом деле мы уже видели пример кусочной функции, даже если в то время мы не называли его функцией (или кусочной функцией).Вспомните математическое определение абсолютной величины. Это функция, и если мы используем обозначение функции, мы можем записать ее следующим образом: Это также пример кусочной функции. Кусочная функция — это не что иное, как функция, которая разбита на части, и какой фрагмент вы используете, зависит от значения \ (x \). оценивают каждое из следующих действий. Прежде чем приступить к оценкам, обратите внимание, что мы используем разные буквы для функции и переменной, чем те, которые мы использовали до этого момента.Это не повлияет на работу оценки. Не зацикливайтесь на том, чтобы видеть \ (f \) для функции и \ (x \) для переменной, что вы не сможете решить любую проблему, в которой нет этих букв. Теперь, чтобы выполнить каждую из этих оценок, первое, что нам нужно сделать, это определить, какому неравенству удовлетворяет число, и оно будет удовлетворять только одному неравенству. В этом случае число 1 удовлетворяет среднему неравенству, поэтому мы будем использовать среднее уравнение для оценки. Эта оценка часто вызывает проблемы у студентов, несмотря на то, что на самом деле это одна из самых простых оценок, которые мы когда-либо проводим. Мы знаем, что оцениваем функции / уравнения, подставляя номер переменной. В этом случае нет переменных. Это не проблема. Поскольку переменных нет, это просто означает, что мы на самом деле ничего не подключаем, и получаем следующее: Опять же, как и со второй частью, нам нужно быть немного осторожнее с этой.В этом случае число удовлетворяет среднему неравенству, так как это число со знаком равенства в нем. Не радуйтесь тому факту, что предыдущие две оценки имели одинаковое значение. Иногда это будет происходить. Для окончательной оценки в этом примере число удовлетворяет нижнему неравенству, поэтому мы будем использовать нижнее уравнение для оценки. Кусочные функции не так часто возникают в классе алгебры, однако они возникают в нескольких местах в более поздних классах, поэтому вам важно понимать их, если вы собираетесь перейти к большему количеству математических классов. В качестве последней темы нам нужно вернуться и коснуться того факта, что мы не всегда можем подключить каждый \ (x \) к каждой функции. Мы кратко говорили об этом, когда давали определение функции, и мы видели пример этого, когда оценивали функции. Во-первых, нам нужно избавиться от пары определений. Область уравнения — это набор всех \ (x \), которые мы можем вставить в уравнение и получить действительное число для \ (y \). Диапазон уравнения — это набор всех \ (y \), которые мы когда-либо можем получить из уравнения. Обратите внимание, что мы действительно имели в виду использовать уравнение в определениях выше вместо функций.Это действительно определения уравнений. Однако, поскольку функции также являются уравнениями, мы можем также использовать определения функций. Определение диапазона уравнения / функции для многих функций может быть довольно трудным, поэтому мы не будем вдаваться в подробности. Здесь нас гораздо больше интересует определение областей функций. Согласно определению, домен — это набор всех \ (x \), которые мы можем подключить к функции и получить действительное число. Итак, мы получим деление на ноль, если подставим \ (x = — 5 \) или \ (x = 2 \). Это означает, что нам нужно избегать этих двух чисел. Однако все остальные значения \ (x \) будут работать, поскольку они не дают деления на ноль. Тогда домен В этом случае у нас не будет задач деления на ноль, так как у нас нет дробей.У нас действительно есть квадратный корень в задаче, поэтому нам нужно позаботиться о том, чтобы извлечь квадратный корень из отрицательного числа. Эта часть будет работать немного иначе, чем предыдущая. Это довольно простое линейное неравенство, которое мы должны решить на данный момент.2} + 4}} \) Показать решение В этом случае у нас есть дробь, но обратите внимание, что знаменатель никогда не будет равен нулю для любого действительного числа, поскольку x 2 гарантированно будет положительным или нулевым, и добавление 4 к этому будет означать, что знаменатель всегда будет минимум 4. Другими словами, знаменатель никогда не будет равен нулю. Итак, все, что нам нужно сделать, это позаботиться о квадратном корне в числителе. Для этого нам потребуется Теперь мы можем фактически подставить любое значение \ (x \) в знаменатель, однако, поскольку у нас есть квадратный корень в числителе, мы должны убедиться, что все \ (x \) удовлетворяют неравенство выше, чтобы избежать проблем. В этой заключительной части нам нужно беспокоиться как о квадратном корне, так и о делении на ноль. Давайте сначала позаботимся о квадратном корне, поскольку это, вероятно, наложит наибольшее ограничение на значения \ (x \). Итак, чтобы квадратный корень оставался довольным (, то есть без квадратного корня из отрицательных чисел), нам потребуется это, Итак, по крайней мере, нам нужно потребовать, чтобы \ (x \ ge \ frac {1} {2} \), чтобы избежать проблем с квадратным корнем.2} — 16 = \ left ({x — 4} \ right) \ left ({x + 4} \ right) = 0 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = — 4, \, \, х = 4 \] Теперь обратите внимание, что \ (x = — 4 \) не удовлетворяет неравенству, которое нам нужно для квадратного корня, и поэтому значение \ (x \) уже исключено квадратным корнем. Тогда домен для этой функции — В этой статье Норман Вильдбергер объясняет, как определить квадратичную функцию, проходящую через три точки. {{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{0, — 3,0,5} \ right \} \]
{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{0, — 3,0,5} \ right \} \]
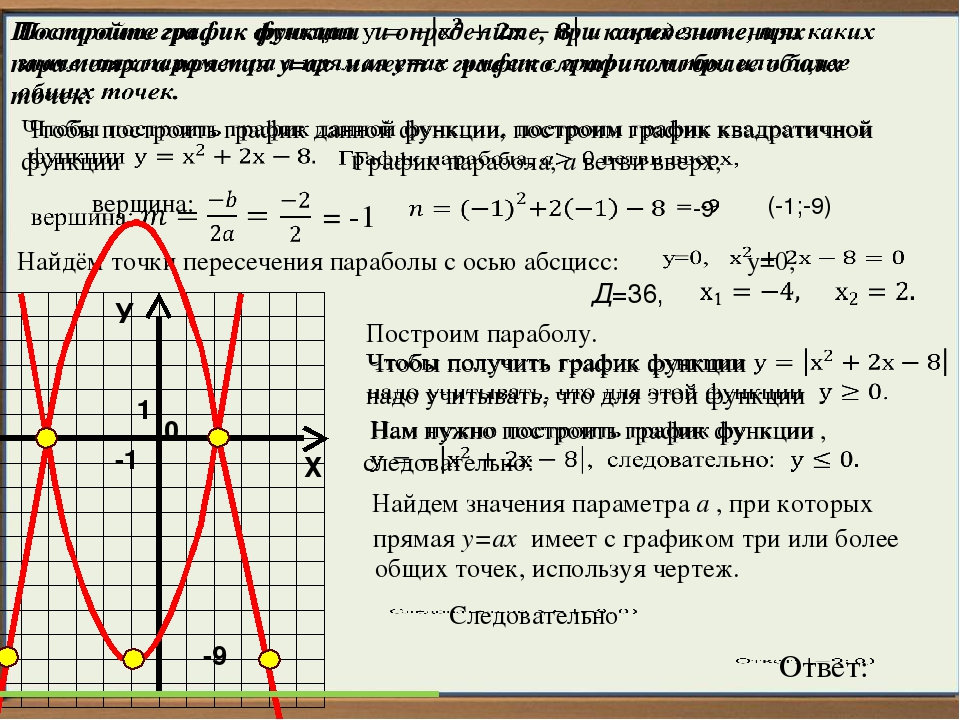 {{\ mbox {st}}}} {\ mbox {components:}} \ left \ {{6, — 7,0} \ right \} \ hspace {0.{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{10,3,4, — 4} \ right \} \]
{{\ mbox {st}}}} {\ mbox {components:}} \ left \ {{6, — 7,0} \ right \} \ hspace {0.{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{10,3,4, — 4} \ right \} \]
 Это также может быть верно для отношений, которые являются функциями. Их не обязательно выводить из уравнений.
Это также может быть верно для отношений, которые являются функциями. Их не обязательно выводить из уравнений. «Рабочее определение» функции
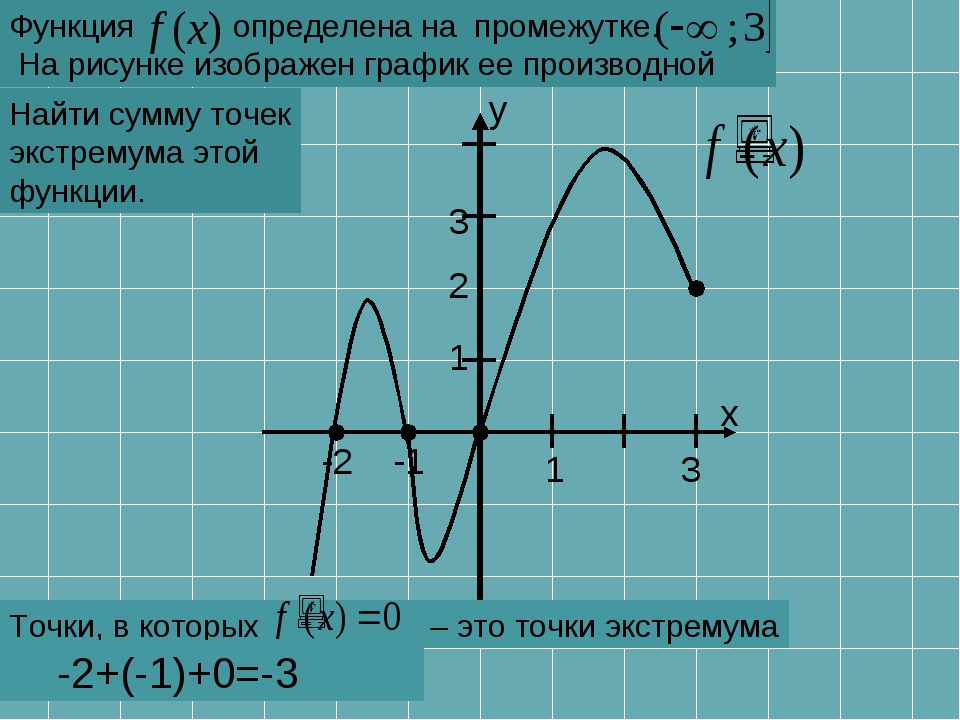 Это означает, что не все \ (x \) могут быть включены в уравнение, и это на самом деле правильно. Мы вернемся и обсудим это более подробно в конце этого раздела, однако на данном этапе просто помните, что мы не можем делить на ноль, и если мы хотим, чтобы действительные числа были исключены из уравнения, мы не можем извлечь квадратный корень из отрицательное число. Итак, с этими двумя примерами ясно, что мы не всегда сможем подставить каждое \ (x \) в какое-либо уравнение.
Это означает, что не все \ (x \) могут быть включены в уравнение, и это на самом деле правильно. Мы вернемся и обсудим это более подробно в конце этого раздела, однако на данном этапе просто помните, что мы не можем делить на ноль, и если мы хотим, чтобы действительные числа были исключены из уравнения, мы не можем извлечь квадратный корень из отрицательное число. Итак, с этими двумя примерами ясно, что мы не всегда сможем подставить каждое \ (x \) в какое-либо уравнение. 2} = 4 \) Показать все решения Скрыть все решения
Показать обсуждение
2} = 4 \) Показать все решения Скрыть все решения
Показать обсуждение
a \ (y = 5x + 1 \) Показать решение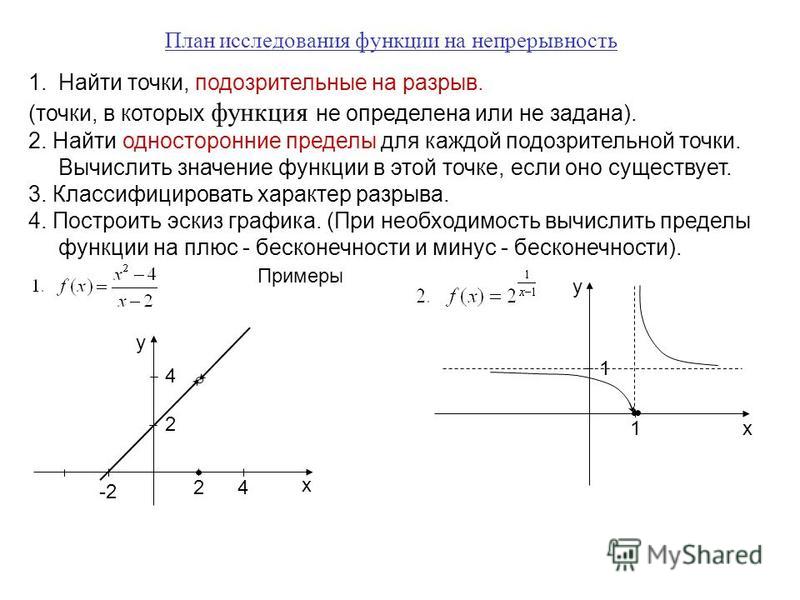
 Сначала мы возводили в квадрат значение \ (x \), которое мы подключили. Когда мы возводим в квадрат число, будет только одно возможное значение. Затем мы добавляем к этому 1, но опять же, это даст одно значение.
Сначала мы возводили в квадрат значение \ (x \), которое мы подключили. Когда мы возводим в квадрат число, будет только одно возможное значение. Затем мы добавляем к этому 1, но опять же, это даст одно значение. 2} = 4 \ hspace {0.2} = 4 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \, 2 \]
2} = 4 \ hspace {0.2} = 4 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \, 2 \]
 Главное здесь — обратить внимание на букву перед круглой скобкой. Для \ (f \ left (3 \ right) \) мы будем использовать функцию \ (f \ left (x \ right) \), а для \ (g \ left (3 \ right) \) мы будем использовать \ (g \ влево (х \ вправо) \).2} — 2 \ влево ({- 10} \ вправо) + 8 = 100 + 20 + 8 = 128 \]
Главное здесь — обратить внимание на букву перед круглой скобкой. Для \ (f \ left (3 \ right) \) мы будем использовать функцию \ (f \ left (x \ right) \), а для \ (g \ left (3 \ right) \) мы будем использовать \ (g \ влево (х \ вправо) \).2} — 2 \ влево ({- 10} \ вправо) + 8 = 100 + 20 + 8 = 128 \]
d \ (f \ left (t \ right) \) Показать решение
e \ (f \ left ({t + 1} \ right) \) и \ (f \ left ({x + 1} \ right) \) Показать решение Вы обнаружите, что несколько последующих разделов будет очень трудным для понимания и / или выполнения работы, если вы не имеете хорошего представления о том, как работает оценка функций.
Вы обнаружите, что несколько последующих разделов будет очень трудным для понимания и / или выполнения работы, если вы не имеете хорошего представления о том, как работает оценка функций. 2} + 4} & {{\ mbox {if}} t \ le — 4} \\ {10} & {{\ mbox {if}} — 4 15} \ end {array}} \ right. \]
2} + 4} & {{\ mbox {if}} t \ le — 4} \\ {10} & {{\ mbox {if}} — 4 15} \ end {array}} \ right. \]
Показать все решения Скрыть все решения
Показать обсуждение Когда мы определяем, какому неравенству удовлетворяет число, мы используем уравнение, связанное с этим неравенством.2} + 4 = 52 \]
Когда мы определяем, какому неравенству удовлетворяет число, мы используем уравнение, связанное с этим неравенством.2} + 4 = 52 \]
c \ (g \ left (1 \ right) \) Показать решение
d \ (g \ left ({15} \ right) \) Показать решение Затем, как и в предыдущей части, мы получаем
Затем, как и в предыдущей части, мы получаем
e \ (g \ left ({21} \ right) \) Показать решение Теперь нам нужно взглянуть на это немного подробнее.
Теперь нам нужно взглянуть на это немного подробнее. Домен и диапазон
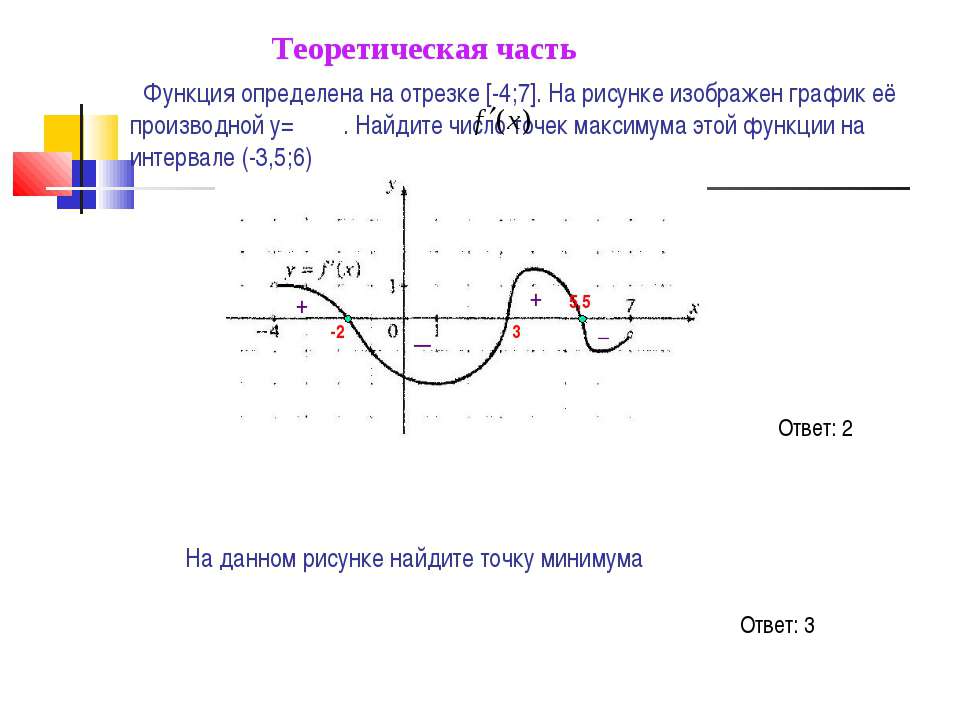 На данный момент это означает, что нам нужно избегать деления на ноль и извлечения квадратных корней из отрицательных чисел.2} + 3x — 10 = \ left ({x + 5} \ right) \ left ({x — 2} \ right) = 0 \ hspace {0,25in} x = — 5, \, \, x = 2 \ ]
На данный момент это означает, что нам нужно избегать деления на ноль и извлечения квадратных корней из отрицательных чисел.2} + 3x — 10 = \ left ({x + 5} \ right) \ left ({x — 2} \ right) = 0 \ hspace {0,25in} x = — 5, \, \, x = 2 \ ]
b \ (f \ left (x \ right) = \ sqrt {5 — 3x} \) Показать решение В этой части мы определили значение (я) \ (x \), которого следует избегать. В этом случае напрямую получить домен будет так же просто. Чтобы избежать квадратного корня из отрицательных чисел, все, что нам нужно сделать, это потребовать, чтобы
В этой части мы определили значение (я) \ (x \), которого следует избегать. В этом случае напрямую получить домен будет так же просто. Чтобы избежать квадратного корня из отрицательных чисел, все, что нам нужно сделать, это потребовать, чтобы 2} — 16}} \) Показать решение
2} — 16}} \) Показать решение С другой стороны, \ (x = 4 \) удовлетворяет неравенству. Это означает, что можно подставить \ (x = 4 \) в квадратный корень, однако, поскольку это даст деление на ноль, нам нужно будет избегать этого.
С другой стороны, \ (x = 4 \) удовлетворяет неравенству. Это означает, что можно подставить \ (x = 4 \) в квадратный корень, однако, поскольку это даст деление на ноль, нам нужно будет избегать этого. Квадратичная функция через три точки
 Это полезный навык сам по себе.
Это полезный навык сам по себе. Уникальный круг, проходящий через три неколлинеарных точки
Линия определяется двумя точками.Круг, с другой стороны, определяется тремя точками, если эти точки не лежат на одной прямой (все три точки не могут лежать на одной линии). Построение круга, проходящего через три точки, является стандартным упражнением в евклидовой геометрии: мы строим серединные перпендикуляры отрезков прямых, определяемых этими тремя точками, а затем эти три прямые пересекаются в центре описанной окружности треугольника (размер нормали {ABC} ), а именно центр единственного круга, который проходит через все три точки.2 + bx + c}), который проходит через точки (normalsize {[0,1], [1,5]}) и (normalsize {[2,3]}). Подставляя каждую из трех точек в уравнение, получаем
[Большой {1 = c}] [Большой {5 = a + b + c}] [Большой {3 = 4a + 2b + c}]
Это три уравнения с тремя неизвестными. Это более сложно, но в данном конкретном случае все проще, поскольку первое уравнение уже говорит нам, что (normalsize {c = 1}), поэтому два других уравнения становятся (normalsize {a + b = 4}) и (normalsize {2a + b = 1}).2 + 7x + 1}). Вот график:
Это более сложно, но в данном конкретном случае все проще, поскольку первое уравнение уже говорит нам, что (normalsize {c = 1}), поэтому два других уравнения становятся (normalsize {a + b = 4}) и (normalsize {2a + b = 1}).2 + 7x + 1}). Вот график: Решение трех линейных уравнений с тремя неизвестными
Поскольку два линейных уравнения представляют собой две прямые на плоскости, их общее решение соответствует геометрическому пересечению этих двух линий. Для трех линейных уравнений с тремя неизвестными ситуация фактически соответствует общей точке пересечения трех плоскостей в трехмерном пространстве!
К счастью, древние китайцы смогли разработать общую методику решения таких систем уравнений. Здесь мы просто пытаемся найти простой практический метод.2 + bx + c}), который проходит через точки (normalsize {[1,3], [2, -1]}) и (normalsize {[4,1]}). Это означает, что у нас есть три уравнения, по одному для каждой точки — поскольку мы знаем, что данные точки должны удовлетворять неизвестному уравнению. Три уравнения:
[Большой {3 = a + b + c} ярлык {b1p} тег {1}] [Большой {-1 = 4a + 2b + c} ярлык {b2p} тег {2}] [Большой {1 = 16a + 4b + c}. ярлык {b3p} тег 3]
Какая стратегия? Это просто: мы пытаемся исключить одну из переменных, оставляя нам два уравнения с двумя неизвестными. Мы знаем, как решить эту проблему.Чтобы получить два уравнения с двумя переменными, давайте исключим (normalsize {c}) из первых двух уравнений. Мы делаем это, вычитая одно из другого, скажем, вычитая первое из второго:
[Большой {-4 = 3a + b} ярлык {b4p} тег {4}]
Пожалуйста, убедитесь, что вы понимаете, как мы это получили. Теперь сделаем то же самое с двумя последними уравнениями: возьмем третье уравнение и вычтем второе:
[Большой {2 = 12a + 2b}]
Мы можем сделать это немного проще, разделив все коэффициенты на (размер нормали {2}), чтобы получить
[Большой {1 = 6a + b}. ярлык {b5p} тег {5}]
Теперь мы рассматриваем (normalsize {(ref {b5p})}) и (normalsize {(ref {b4p})}) как новые уравнения и используем их для нахождения (normalsize {a}) и (normalsize {b}).
Три уравнения:
[Большой {3 = a + b + c} ярлык {b1p} тег {1}] [Большой {-1 = 4a + 2b + c} ярлык {b2p} тег {2}] [Большой {1 = 16a + 4b + c}. ярлык {b3p} тег 3]
Какая стратегия? Это просто: мы пытаемся исключить одну из переменных, оставляя нам два уравнения с двумя неизвестными. Мы знаем, как решить эту проблему.Чтобы получить два уравнения с двумя переменными, давайте исключим (normalsize {c}) из первых двух уравнений. Мы делаем это, вычитая одно из другого, скажем, вычитая первое из второго:
[Большой {-4 = 3a + b} ярлык {b4p} тег {4}]
Пожалуйста, убедитесь, что вы понимаете, как мы это получили. Теперь сделаем то же самое с двумя последними уравнениями: возьмем третье уравнение и вычтем второе:
[Большой {2 = 12a + 2b}]
Мы можем сделать это немного проще, разделив все коэффициенты на (размер нормали {2}), чтобы получить
[Большой {1 = 6a + b}. ярлык {b5p} тег {5}]
Теперь мы рассматриваем (normalsize {(ref {b5p})}) и (normalsize {(ref {b4p})}) как новые уравнения и используем их для нахождения (normalsize {a}) и (normalsize {b}). 2-20л + 17право)). Обратите внимание, что это не функция.
2-20л + 17право)). Обратите внимание, что это не функция.
линейных функций
линейных функцийЛинейная функция популярна в экономике. Это привлекательно, потому что это просто и легко обрабатывать математически. У него много важных приложений.
Линейные функции — это функции, график которых представляет собой прямую линию.
Линейная функция имеет следующий вид
y = f (x) = a + bx
Линейная функция имеет одну независимую переменную и одну зависимую переменную. Независимая переменная — это x, а зависимая переменная — это y.
a — постоянный член или точка пересечения по оси y. Это ценность зависимого переменная при x = 0.
b — коэффициент независимой переменной. Он также известен как
наклон и дает скорость изменения зависимой переменной.
Чтобы построить график линейной функции:
1. Найдите 2 точки, которые удовлетворяют уравнению
2. Участок
3. Соедините точки прямой линией
Пример:
y = 25 + 5x
пусть x = 1
, тогда
y = 25 + 5 (1) = 30пусть x = 3
, тогда
y = 25 + 5 (3) = 40
Простой пример линейного уравнения
Компания имеет постоянные затраты на установку и оборудование в размере 7000 долларов США, а также переменные
стоимость 600 долларов за каждую единицу продукции.
Каковы общие затраты при различных уровнях выпуска?
пусть x = единицы продукции
пусть C = общая стоимость
C = постоянные затраты плюс переменные затраты = 7000 + 600 x
| выход | Итого |
15 шт. | C = 7000 + 15 (600) = 16000 |
| 30 шт. | C = 7000 + 30 (600) = 25000 |
Линейные уравнения можно складывать, умножать или делить.
Простой пример сложения линейных уравнений
C (x) — функция стоимости
C (x) = постоянные затраты + переменные затраты
R (x) — функция дохода
R (x) = продажная цена (количество проданных единиц)
прибыль равна выручке за вычетом затрат
P (x) — функция прибыли
P (x) = R (x) — C (x)
x = количество произведенных и проданных единиц
Данные:
Компания получает 45 долларов за каждую проданную единицу продукции.Имеет переменную стоимость
25 долларов США за единицу и фиксированная стоимость 1600 долларов США.
Какова его прибыль, если он продаст (а) 75 предметов, (б) 150 предметов и (в) 200 предметов?
R (x) = 45x C (x) = 1600 + 25x P (x) = 45x — (1600 + 25x) = 20x — 1600
| пусть x = 75 | P (75) = 20 (75) — 1600 = -100 А потеря |
| пусть x = 150 | P (150) = 20 (150) — 1600 = 1400 |
| пусть x = 200 | P (200) = 20 (200) — 1600 = 2400 |
[индекс]
Домен
и диапазон — Бесплатная справка по математике
При работе с функциями часто встречаются два термина: домен и диапазон .Что такое домен ? Что такое диапазон ? Почему они важны? Как мы можем определить домен и диапазон для данной функции?
Определение домена
Домен : набор всех возможных входных значений (обычно это переменная «x»), которые производят допустимый выход из конкретной функции. Это набор всех значений, для которых функция математически определена. Довольно часто домен представляет собой набор всех действительных чисел , поскольку многие математические функции могут принимать любой ввод.
Это набор всех значений, для которых функция математически определена. Довольно часто домен представляет собой набор всех действительных чисел , поскольку многие математические функции могут принимать любой ввод.
Например, многие упрощенные алгебраические функции имеют области, которые могут показаться … очевидными. Какова область определения функции \ (f (x) = 2x + 1 \)? Какие значения мы можем ввести для входа (x) этой функции? Ну ничего! Ответ — все реальные числа. Только когда мы дойдем до определенных типов алгебраических выражений, нам нужно будет ограничить область.
Мы также можем продемонстрировать домен визуально. Рассмотрим простое линейное уравнение, подобное приведенному ниже графику, построенному на основе функции \ (y = \ frac {x} {2} +10 \).Какие значения являются допустимыми входными данными? Это не вопрос с подвохом — можно вводить любое действительное число! Домен функции — это все действительные числа, потому что вы ничего не можете вставить для x, что не сработает. Визуально мы видим это как линию, которая продолжается вечно в направлениях x (влево и вправо).
Визуально мы видим это как линию, которая продолжается вечно в направлениях x (влево и вправо).
Для других линейных функций (линий) линия может быть очень и очень крутой, но если вы представите себе «уменьшение масштаба» достаточно далеко, в конечном итоге любое значение x будет отображаться на графике. С другой стороны, прямая горизонтальная линия была бы наиболее ярким примером неограниченной области всех действительных чисел.
Какие функции не имеют области , состоящей из всех действительных чисел? Что могло бы помешать нам, изучающим алгебру, вставить любое значение во входные данные функции? Что ж, если домен — это набор всех входных данных, для которых определена функция, то логически мы ищем пример функции, которая нарушает для определенных входных значений. Нам нужна функция, которая для определенных входов не дает действительного выхода , то есть функция не определена для этого входа.Вот пример:
$$ \ огромный y = \ frac {3} {x-1} $$
Эта функция определена для почти любого действительного x.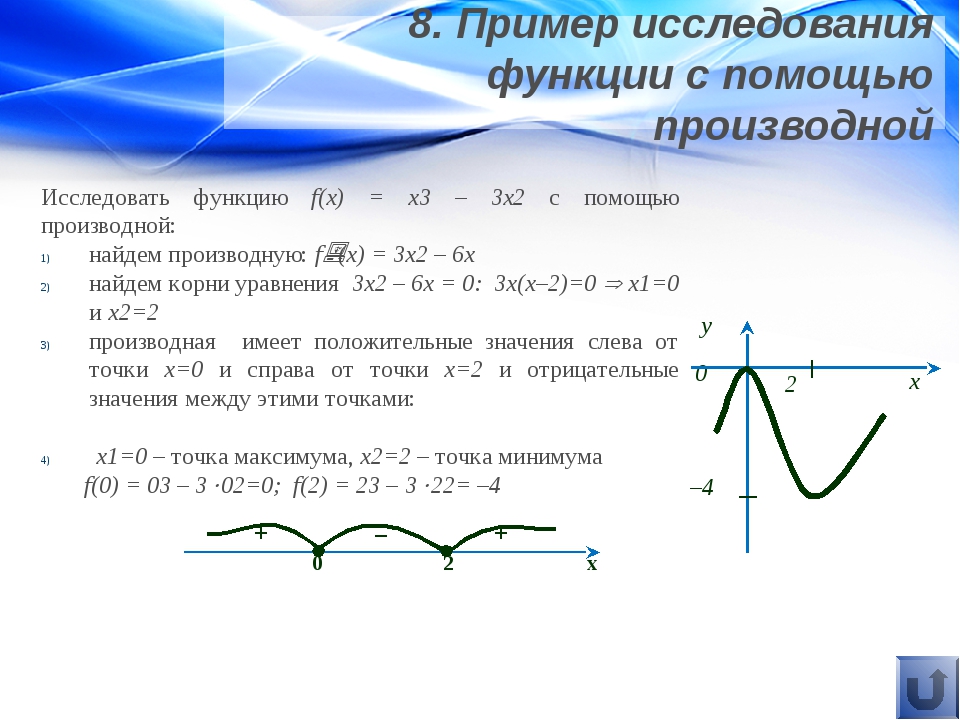 Но каково значение y, когда x = 1? Ну, это \ (\ frac {3} {0} \), то есть undefined . Деление на ноль не определено. Следовательно, 1 не входит в область действия этой функции. Мы не можем использовать 1 в качестве входных данных, потому что это нарушает функцию. Все остальные действительные числа являются допустимыми входными данными, поэтому доменом являются все действительные числа, кроме x = 1. Имеет смысл, правда?
Но каково значение y, когда x = 1? Ну, это \ (\ frac {3} {0} \), то есть undefined . Деление на ноль не определено. Следовательно, 1 не входит в область действия этой функции. Мы не можем использовать 1 в качестве входных данных, потому что это нарушает функцию. Все остальные действительные числа являются допустимыми входными данными, поэтому доменом являются все действительные числа, кроме x = 1. Имеет смысл, правда?
Деление на ноль — одно из самых распространенных мест, на которое обращают внимание при решении области определения функции.Найдите места, которые могут привести к делению на ноль, и запишите значения x, при которых знаменатель будет равен нулю. Это ваши ценности, которые нужно исключить из домена.
Если деление на ноль — обычное место для поиска ограничений в домене, то знак «квадратный корень», вероятно, является вторым по распространенности. Конечно, мы знаем, что это действительно называется радикальным символом, но, несомненно, вы называете это знаком квадратного корня. Почему это вызывает проблемы с доменом? Потому что, по крайней мере, в области действительных чисел, мы не можем найти квадратный корень из отрицательного значения.
Почему это вызывает проблемы с доменом? Потому что, по крайней мере, в области действительных чисел, мы не можем найти квадратный корень из отрицательного значения.
Что, если нас попросят найти домен \ (f (x) = \ sqrt {x-2} \). Какие значения исключены из домена? Значение меньше 2 приводит к отрицательному числу внутри квадратного корня, что является проблемой. Следовательно, в домене все действительные числа больше или равны 2.
У каких других функций есть домены, в которых не все являются действительными числами? Некоторые «обратные» функции, такие как обратные триггерные функции, также имеют ограниченную область применения. Поскольку синусоидальная функция может иметь только выходов от -1 до +1, ее обратная функция может принимать только входов от -1 до +1.Область обратного синуса от -1 до +1. Однако, , наиболее распространенный пример ограниченной области — это, вероятно, проблема деления на ноль. Когда вас просят найти домен функции, начните с простого: сначала найдите любые значения, которые заставляют вас делить на ноль. Помните также, что мы не можем извлечь квадратный корень из отрицательного числа, поэтому следите за ситуациями, когда подкоренное выражение («материал» внутри знака квадратного корня) может привести к отрицательному значению. В этом случае это будет недопустимый ввод, поэтому домен не будет включать такие значения.
Помните также, что мы не можем извлечь квадратный корень из отрицательного числа, поэтому следите за ситуациями, когда подкоренное выражение («материал» внутри знака квадратного корня) может привести к отрицательному значению. В этом случае это будет недопустимый ввод, поэтому домен не будет включать такие значения.
Определение диапазона
Диапазон : Диапазон — это набор всех возможных выходных значений (обычно это переменная y или иногда выражается как \ (f (x) \)), которые возникают в результате использования определенной функции.
Диапазон простой линейной функции почти всегда будет , все действительные числа . График типичной линии, такой как показанный ниже, будет продолжаться бесконечно в любом направлении y (вверх или вниз). Диапазон негоризонтальной линейной функции — это все действительные числа, независимо от того, насколько пологим может выглядеть наклон.
Есть одно заметное исключение: когда y равно константе (например, \ (y = 4 \) или \ (y = 19 \)).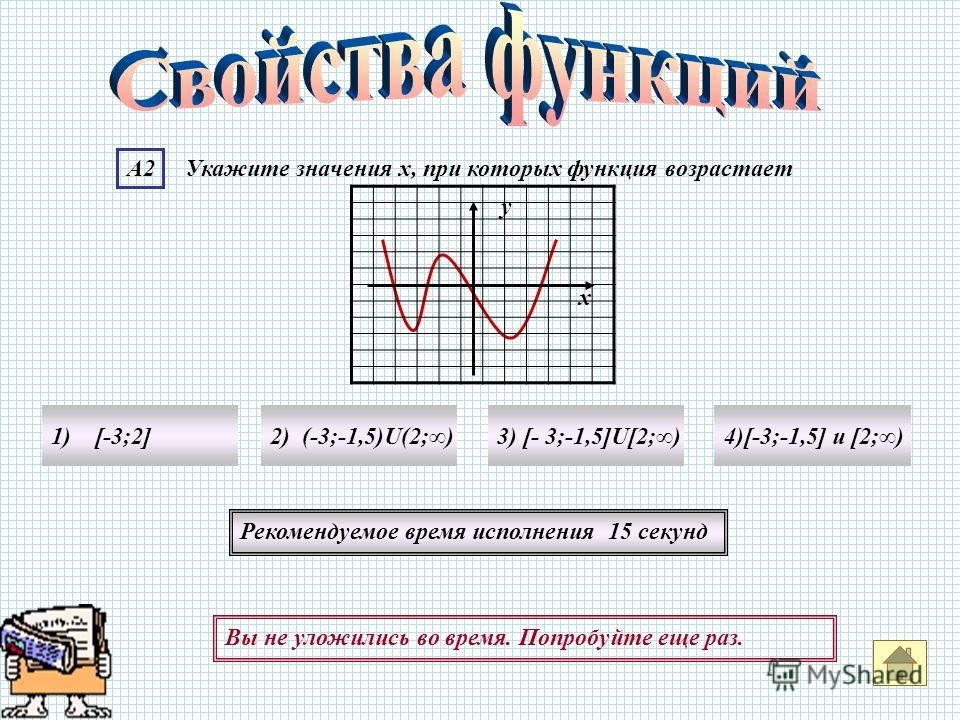 Когда у вас есть функция, в которой y равно константе, ваш график представляет собой действительно горизонтальную линию, как график ниже для \ (y = 3 \). В этом случае диапазон — это только одно-единственное значение. Никакие другие возможные значения не могут быть получены из этой функции!
Когда у вас есть функция, в которой y равно константе, ваш график представляет собой действительно горизонтальную линию, как график ниже для \ (y = 3 \). В этом случае диапазон — это только одно-единственное значение. Никакие другие возможные значения не могут быть получены из этой функции!
Многие другие функции имеют ограниченный диапазон. Хотя только несколько типов имеют ограниченные домены, вы часто будете видеть функции с необычными диапазонами.4 \) и т.д …) приведет, например, только к положительному результату. Функции специального назначения, такие как тригонометрические функции, также, безусловно, будут иметь ограниченные возможности.
Сводка : Область функции — это все возможные входных значений, для которых функция определена, а диапазон — все возможные выходных значений.
Если вы все еще не уверены, вы можете разместить свой вопрос на нашей доске сообщений или прочитать урок другого веб-сайта по домену и диапазону, чтобы получить другую точку зрения. Или вы можете использовать калькулятор ниже, чтобы определить домен и диапазон ЛЮБОГО уравнения:
Или вы можете использовать калькулятор ниже, чтобы определить домен и диапазон ЛЮБОГО уравнения:
Калькулятор домена и диапазона
8. Функции разделения
Авторы: Д. Ху и М. Борн
Большинство функций, с которыми вы знакомы, определены одинаково для всех значений x . Однако есть некоторые функции, которые в разных доменах определяются по-разному. Они известны как функции разделения , (или кусочно-определенные функции).
Поскольку функции разделения могут иметь совершенно разное поведение в разных доменах (то есть для разных значений x ), функция разделения довольно часто бывает прерывистой (и, как мы узнаем позже, ее нельзя дифференцировать) .
Пример 1 — Обычная функция для сравнения
f ( x ) = — x 2 + 4
График f ( x ) = — x 2 + 4, непрерывная функция.
Эта функция не является функцией разделения.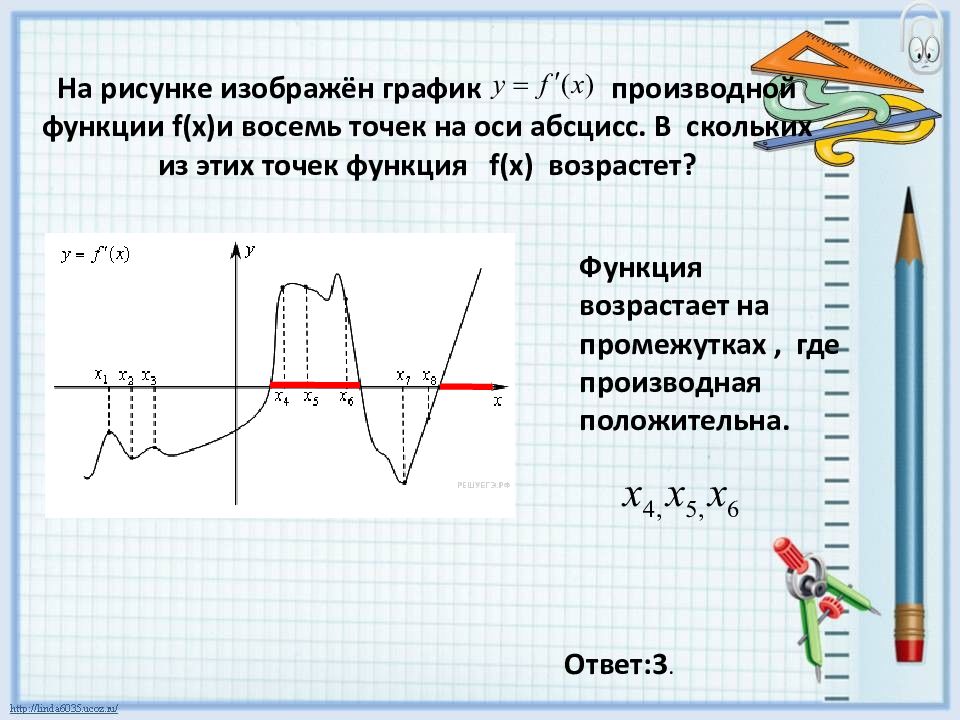 2 + 2, текст (для) x> = 1):}`
2 + 2, текст (для) x> = 1):}`
В области x <1 у нас есть прямая с наклоном 2 и y — пересечение `3`.Когда x приближается к «1», значение функции приближается к «5» (но не достигает его из-за знака «<« »).
Теперь перейдем к области `x ≥ 1`.
Когда x = 1, функция имеет значение
.f (1) = — (1) 2 + 2 = −1 +2 = 1.
По мере продвижения вправо функция принимает значения на основе f ( x ) = — x 2 + 2. Это парабола.
График функции разделения.
Эта функция имеет разрыв в точке `x = 1`, но на самом деле она определена для` x = 1` (и имеет значение `1`).
Позже мы узнаем о дифференциации. Эта функция дифференцируема для всех значений x , кроме x = 1.
Пример 3
График функции разделения:
`f (x) = {(- 2x-8, текст (для) x <-2), (3x + 2, текст (для) x> -2):}`
Ответ
В области `x <-2` функция определяется как:
`y = -2x — 8`
По мере того, как x приближается к «-2» с левой стороны, мы можем видеть, что значение функции приближается к «-4».
Теперь для регион `x> -2`. Функция на этой стороне определена как
`y = 3x + 2`
Когда x приближается к «-2» справа, мы видим, что значение функции также приближается к «-4».
Функция не определена в x = -2, поэтому она не является непрерывной. Мы изобразим это открытым кружком на графике.
12345-1-2-3-4-551015-5xy (-2, -4)`y = -2x-8`
`y = 3x + 2`
График функции разделения.2-8x + 10` (парабола).
Итак, чтобы определить значение функции при конкретном значении x , сначала необходимо решить, в какой «кусок» попадает это значение. Только тогда мы сможем узнать, какое выражение использовать.
Обратите внимание, что функция определена для всех x , но имеет разрывов в точках «-2» и «2».
Вот некоторые значения функции для этой функции разделения:
| x | -4 | -3 | -2 | –1 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|---|---|---|
| f ( x ) | 0.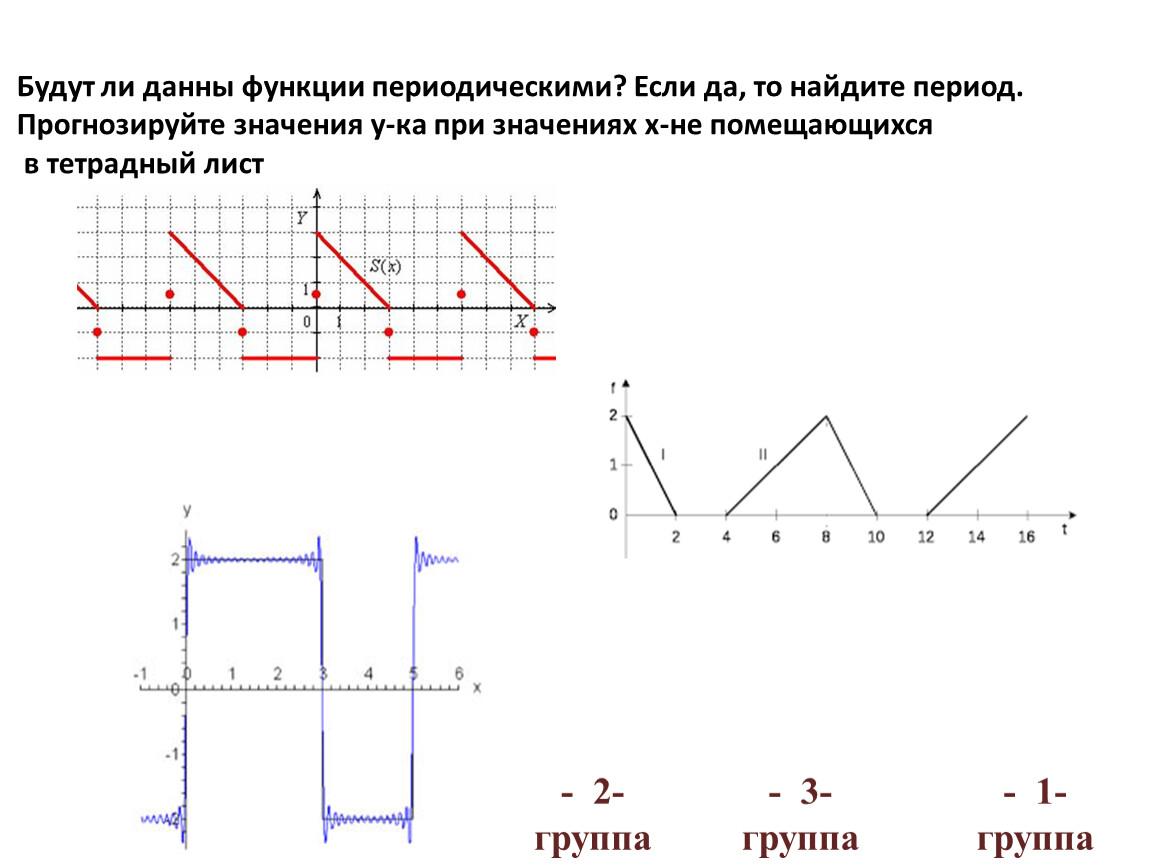 757 757 | -0,141 | 3 | 2,5 | 2 | 1,5 | -2 | -5 | -6 |
Пример 5 — Функция разделения (непрерывный)
`f (x) = {(x, текст (для) x <0), (1 / 5sin \ 5x, текст (для) x> = 0):}`
График кусочно-определенной функции.
Эта функция разделена на две части.
Для отрицательных значений x функция идентична f ( x ) = x (прямая линия).
Для неотрицательных значений x функция идентична `f (x) = 1/5 sin \ 5x`. Опять же, функция определена для всех значений x . Однако в этом случае функция непрерывна (и дифференцируема) всюду.
| x | -2 | –1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| f ( x ) | -2 | –1 | 0 | -0.192 | -0,109 |
Специальное обозначение
Некоторые функции разделения используются настолько широко, что им даны специальные обозначения.
Пример 6 — Функция абсолютного значения
f ( x ) = | x |
График функции абсолютного значения `f (x) = | x |`.
Это функция абсолютного значения . Это действительно функция разделения, состоящая из двух частей:
`f (x) = {(- x, текст (для) x <0), (x, текст (для) x> = 0):}`
Функция непрерывна везде, но дифференцируема только при ненулевых значениях x .
| x | -2 | –1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| f ( x ) | 2 | 1 | 0 | 1 | 2 |
Пример 7 — Пошаговая функция
Вы также столкнетесь с функциями разделения при анализе сигналов (см. Ряд Фурье и Преобразования Лапласа). Например, функция в электронике может быть определена как
`f (t) = {(- 1, текст (для), -3 <= t <0), (1, текст (для), 0 <= t <3):}`
График ступенчатой функции.
UserDef-FitFunc СводкаПомимо более 200 встроенных функций подгонки, вы также можете создавать свои собственные функции подгонки в Origin. Ряд инструментов Origin поддерживает настройку ваших собственных функций, в том числе:
Требуется минимальная версия Origin: Origin 2016 SR0 Что вы узнаетеИз этого туториала Вы узнаете, как:
Как создать функцию подгонки и использовать ее для подгонки кривой Данные, которые мы собираемся подогнать, — это файл ConcentrationCurve.dat по пути Функция подгонки, которую нужно создать и использовать, показана ниже: в котором — зависимая переменная — независимая переменная и все параметры подгонки. Метод 1. Использование приложения Simple Fit
Метод 2: Использование Органайзера функций подгонки и NLFit ToolШаг 1. Создание функции подгонки с помощью органайзера функций подгонки В этом разделе мы покажем, как создать определяемую пользователем функцию подгонки в построителе функций подгонки .
Шаг 2: Выполните подгонку кривой с помощью инструмента NLFit Tool
|
Как рассчитать, примеры, практические задачи, рисунки
Ошибка: Нажмите «Не робот» и повторите попытку.
Краткий обзор
Если $$ x $$ приближается к одной из точек перехода функции, вам необходимо проверить оба односторонних предела.
Примеры
Пример 1
Определите $$ \ displaystyle \ lim \ limits_ {x \ to4} f (x) $$, если $$ f $$ определен, как показано ниже.
$$ е (х) = \ влево \ {% \ begin {array} {ll} 2x + 3, & x
Шаг 1 Оцените односторонние пределы.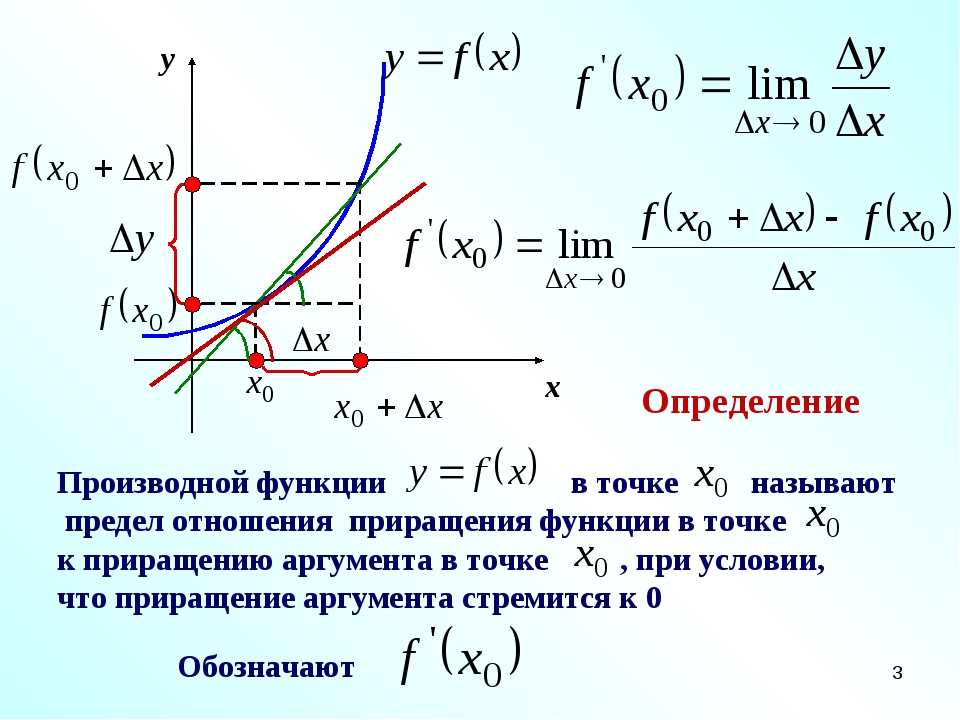 +} (5x-9) = 5 (4) -9 = 11
\ end {выровнять *}
$$
+} (5x-9) = 5 (4) -9 = 11
\ end {выровнять *}
$$
Если односторонние ограничения совпадают, ограничение существует.
Ответ: $$ \ displaystyle \ lim \ limits_ {x \ to4} f (x) = 11 $$, если $$ f $$ определен, как указано выше.
Пример 2
Вычислить $$ \ displaystyle \ lim \ limits_ {x \ to0} f (x) $$, когда $$ f $$ определен следующим образом. 2 + 4, & х
2 + 4, & х
Изучите односторонние пределы.+} \ sqrt x = \ sqrt 0 = 0 \ end {выровнять *} $$
Шаг 2Если односторонние ограничения различны, ограничение не существует.
Ответ: $$ \ displaystyle \ lim \ limits_ {x \ to0} f (x) $$ не существует, если $$ f $$ определен, как указано выше.
Пример 3
Предположим, что $$ f $$ определен, как показано ниже. +} \ left (\ frac 2 3 x + b \ right) = \ frac {2 (5)} 3 + b = \ frac {10} 3 + b
\ end {выровнять *}
$$
+} \ left (\ frac 2 3 x + b \ right) = \ frac {2 (5)} 3 + b = \ frac {10} 3 + b
\ end {выровнять *}
$$
Установите два предела равными друг другу и решите.
$$ \\ \ begin {align *} \ frac {10} 3 + b & = 7 \\ [6pt] b & = 7 — \ frac {10} 3 \\ [6pt] b & = \ frac {11} 3 \ end {выровнять *} \\ $$
Ответ: $$ b = \ frac {11} 3 $$
Практические задачи
Проблема 1
Вычислить $$ \ displaystyle \ lim_ {x \ to 2} f (x) $$, если $$ f $$ определен следующим образом. +} \ left (3x + 4 \ right) = 3 (2) +4 = 10 \ end {выровнять *} $$
Шаг 2 ОтвечатьОтвет: $$ \ displaystyle \ lim \ limits_ {x \ to2} f (x) = 10 $$, если $$ f $$ определен, как указано выше.
Проблема 2
Вычислить $$ \ displaystyle \ lim_ {x \ to 4} f (x) $$, если $$ f $$ определен следующим образом. +} \ frac 1 4 x = \ frac 4 4 = 1 \ end {выровнять *} $$
Шаг 2 ОтвечатьОтвет: $$ \ displaystyle \ lim_ {x \ to 4} f (x) = 1 $$, если $$ f $$ определен, как указано выше.
Проблема 3
Вычислить $$ \ displaystyle \ lim_ {x \ to 1} f (x) $$, если $$ f $$ определен следующим образом.+} \ frac 1 {x-1} = \ frac 1 0 \ qquad \ mbox {Деление на ноль!} \ end {выровнять *} $$
Шаг 2 ОтвечатьОтвет: $$ \ displaystyle \ lim_ {x \ to1} f (x) $$ не существует, если $$ f $$ определен, как указано выше.
Проблема 4
Вычислить $$ \ displaystyle \ lim_ {x \ to-5} f (x) $$, когда $$ f $$ определен, как показано ниже. +} \ left (2x + \ frac 8 3 \ right) = 2 (-5) + \ frac 8 3 = — \ frac {22} 3 \ end {выровнять *} $$
Шаг 2 ОтвечатьОтвет: $$ \ displaystyle \ lim_ {x \ to-5} f (x) $$ не существует, если $$ f $$ определен, как указано выше.
Проблема 5
Определите значение $$ b $$, чтобы $$ \ displaystyle \ lim_ {x \ to-6} f (x) $$ существовал, когда $$ f $$ определен, как показано ниже.+} \ left (\ frac 1 2 x + 9 \ right) = \ frac {-6} 2 + 9 = -3 + 9 = 6 \ end {выровнять *} $$
Шаг 2Установите два односторонних предела равными друг другу и решите.
Отвечать$$ \ begin {align *} 36 + b & = 6 \\ b & = -30 \ end {выровнять *} $$
Ответ: $$ b = -30 $$
Проблема 6
Определите значение $$ m $$, чтобы $$ \ displaystyle \ lim_ {x \ to3} f (x) $$ существовал, когда $$ f $$ определяется следующим образом. +} (mx-4) = 3m-4 \ end {выровнять *} $$
Шаг 2Приравняйте два предела и решите.
Отвечать$$ \\ \ begin {align *} 3м-4 & = 13 \\ [6pt] 3m & = 17 \\ [6pt] m & = \ frac {17} 3 \ end {выровнять *} \\ $$
Ответ: $$ m = \ frac {17} 3 $$
Проблема 7
Определите значение (я) $$ m $$ и $$ b $$, поэтому $$ \ displaystyle \ lim_ {x \ to 4} f (x) = 10 $$, когда $$ f $$ определен, как показано ниже. +} (5x + b) = 20 + b. \ end {выровнять *} $$
Шаг 2Поскольку оба предела должны равняться 10, составьте систему уравнений и решите.
Отвечать$$ \\ \ begin {align *} 4m + 2b & = 10 \\ 20 + b & = 10 \\ [12pt] % 4m + 2b & = 10 \\ b & = -10 && \ mbox {Решите относительно \ (b \) во втором уравнении.} \\ [12pt] % 4m + 2 (-10) & = 10 && \ mbox {Подставьте значение \ (b \) в другое уравнение.} \\ 4м — 20 & = 10 \\ 4 м & = 30 \\ [6 пт] m & = \ frac {30} 4 \\ [6pt] m & = \ frac {15} 2 \ end {выровнять *} \\ $$
Ответ: $$ m = \ frac {15} 2 $$ и $$ b = -10 $$.
Ошибка: Нажмите «Не робот» и повторите попытку.
 Чтобы начать работу с Windows PowerShell, ознакомьтесь с приведенными ниже разделами.
Чтобы начать работу с Windows PowerShell, ознакомьтесь с приведенными ниже разделами.


 Но есть альтернативный инструмент Fitting Function Organizer , который также можно использовать для создания определяемых пользователем функций подгонки (откройте его, выбрав Инструменты : Органайзер функций подгонки или нажав F9 ).
Но есть альтернативный инструмент Fitting Function Organizer , который также можно использовать для создания определяемых пользователем функций подгонки (откройте его, выбрав Инструменты : Органайзер функций подгонки или нажав F9 ). 303 .
303 . Файл .FDF для него будет храниться в папке пользовательских файлов .
Файл .FDF для него будет храниться в папке пользовательских файлов .

Ваш комментарий будет первым