Как найти k и b по графику линейной функции?
В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции, т.е. найти \(k\) и \(b\) по графику. Примеры таких заданий (решения будут внизу статьи):
В статье я расскажу про два простых способа найти \(k\) и \(b\), если известен график линейной функции.
Способ 1
Первый способ основывается на трех фактах:
-
Линейная функция пересекает ось \(y\) в точке \(b\).
Примеры:Но не советую определять так \(b\), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.
Примеры:
-
Если функция возрастает, то знак коэффициента \(k\) плюс, если убывает – минус, а если постоянна, то \(k=0\).
Примеры:
-
Чтоб конкретнее определить \(k\) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить \(k\) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.
Примеры:
Пример (ЕГЭ)
Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.
\(b=3\) – это сразу видно. Функция идет вниз, значит \(k<0\).
Достроим прямую до прямоугольного треугольника. Вершинами будут жирные точки, которые нам дали в задаче.
\(k=-\frac{AC}{BC}=-\frac{1}{3}\).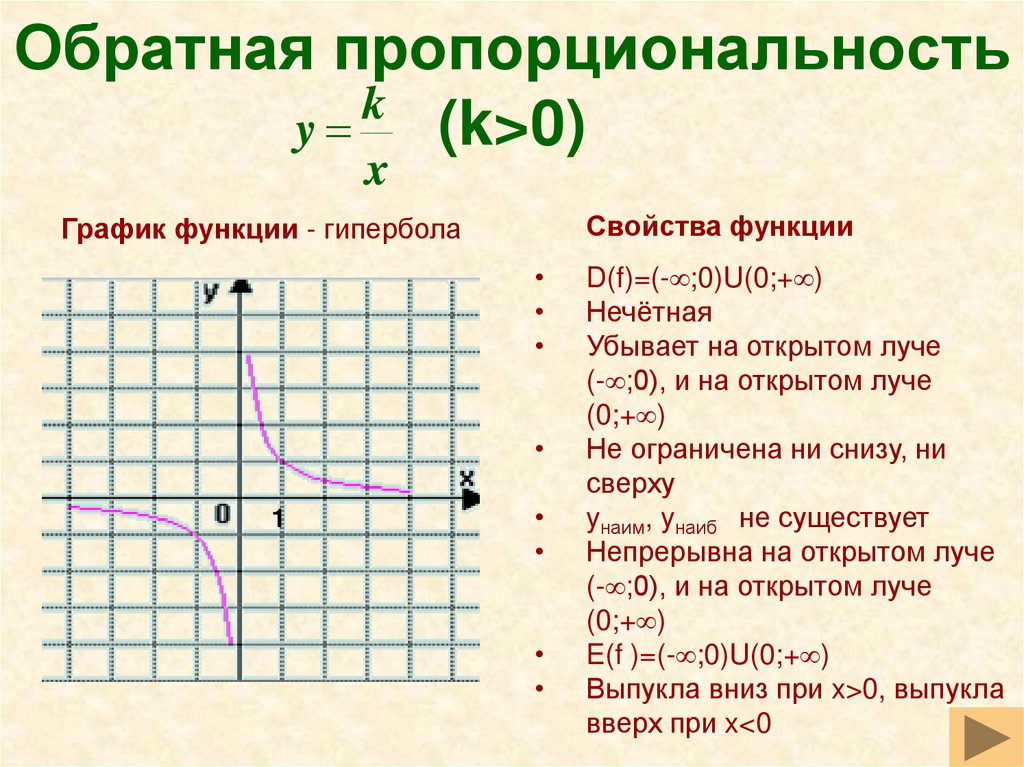
Получается \(g(x)=-\frac{1}{3}x+3\).
Способ 1 быстрее способа 2, но не во всех ситуациях помогает. Поэтому важно владеть и вторым способом тоже.
Способ 2
Вы обращали внимание, что в задачах ЕГЭ на прямых всегда жирно выделяют 2 точки? Так вот, чтобы найти формулу линейной функции, достаточно подставить координаты этих точек в формулу \(f(x)=kx+b\) и решить получившуюся систему уравнений.
Пример (ЕГЭ)
Обозначим жирные точки какими-нибудь буквами и найдем их координаты.
\(A(-2;2)\) и \(B(2;-5)\) подставим эти значения вместо \(x\) и \(f(x)\) в формулу \(f(x)=kx+b\):
Получим:
\(\begin{cases}2=-2k+b\\-5=2k+b\end{cases}\)
Теперь найдем \(k\) и \(b\), решив эту систему.
Для этого сложим уравнения друг с другом, чтобы исчезло \(k\):
\(2+(-5)=-2k+b+2k+b\)
\(-3=2b\)
\(b=-1,5\)
Теперь подставим найденное \(b\) во второе уравнение системы и найдем \(k\):
\(-5=2k-1,5\)
\(-5+1,5=2k\)
\(-3,5=2k\)
\(k=-1,75\)
Получается \(f(x)=-1,75x-1,5\).
Остается последний шаг – вычислим при каком иксе функция, то есть \(f(x)\), равна \(16\):
\(16=-1,75x-1,5\)
\(17,5=-1,75x\)
\(x=-10\).
Ответ:
\(-10\).Пример (ЕГЭ)
Чтоб решить задачу, нам понадобятся формулы каждой из двух функций. Давайте формулу нижней функции найдем с помощью способа 1, а формулу верхней с помощью способа 2. Начнем с нижней функции.
Функция \(f(x)\) возрастает, значит \(k>0\). \(k=+\frac{AC}{BC}=\frac{4}{4}=1,b=1\). \(f(x)=x+1\).
Теперь перейдем к функции \(g(x)\). Найдем координаты точек \(D\) и \(E\): \(D(-2;4)\), \(E(-4;1)\). Можно составить систему:
\(\begin{cases}4=-2k+b\\1=-4k+b\end{cases}\)
Вычтем второе уравнение из первого, чтоб убрать \(b\):
\(4-1=-2k+b-(-4k+b)\)
\(3=2k\)
\(k=1,5\)
Найдем \(b\):
\(4=-2\cdot 1,5+b\)
\(4=-3+b\)
\(b=7\)
\(g(x)=1,5x+7\).
\(x+1=1,5x+7\)
\(x-1,5x=7-1\)
\(-0,5x=6\)
\(x=6:(-0,5)\)
\(x=-12\).
Ответ: \(-12\).
Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».
Смотрите также:
Как определить a, b и c по графику параболы
Общая схема исследования графика функции
Skip to contentArtman Исследование функции
Схема исследования функции
- Найти область значений E(f) и область определения D(f) функции;
- Определить четность или нечетность функции, периодичность функции;
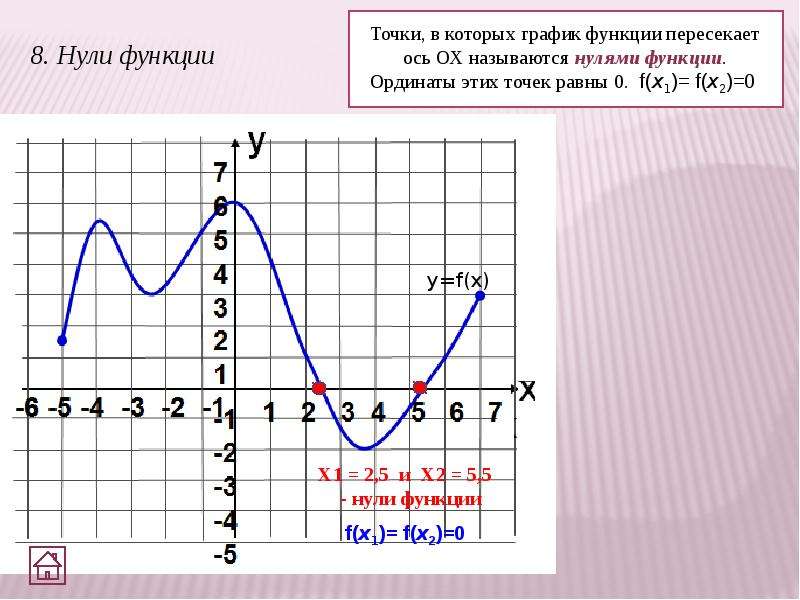
- Найти точки пересечения графика функции с осями координат;
- Нахождение вертикальной, горизонтальной и наклонной асимптоты;
- Определение критических точек, экстремумов функции, наибольшее и наименьшее значение, интервалы монотонности функции — возрастания и убывания функции;
- Определение интервалов вогнутости, выпуклости, точек разрыва и перегиба функции;
- Построить график исходной функции (построить график, касательную и её производную онлайн). 4}}} = 0$
x=2 точка разрыва функции
Функция выпукла вверх при x∈(−∞;2)
Функция выпукла вниз при x∈(2;+∞)
Точки перегиба нет.
7.Строим график функции
3498
Онлайн график можно построить здесь.
Пунктирной линией показана производная функции.Моделирование кусочно-определенной функции по ее графику — Криста Кинг Математика
Построение кусочно-функции по ее графику
Кусочно-определенная функция (также называемая кусочно-определенной функцией) — это функция, состоящая из различных «частей», каждая из которых имеет собственную «подфункцию» (собственное алгебраическое выражение) и собственную «подобласть». (своя часть области определения всей кусочной функции).
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Мы назовем «подфункцию» для каждой части функцией для этой части. Кусочная функция определяется путем задания алгебраического выражения функции для каждой части и ее области определения. Областью определения куска кусочной функции может быть как интервал, так и одна точка.
Определение кусочной функции записывается в таком виде:
???f(x)=\begin{cases}\text{Function}_1 & \quad x\text{-values}\\\text{Function}_2 & \quad x\text{-values} \ \\text{Функция}_3 & \quad x\text{-значения}\\\text{Функция}_4 & \quad x\text{-значения}\end{cases}???
Конечно, кусочная функция не обязательно должна состоять из четырех частей. В нем может быть от двух частей до бесконечного количества частей. Обычно их всего два или три.
Давайте посмотрим на пример определения кусочной функции и на то, как построить график функции. 92??? и область ???x<3???, которая является (частью) параболы, которая открывается вверх и имеет вершину в начале координат.
2)???, или ???(3,9)???, чтобы показать, что точка ???(3,9)??? не является точкой графика этой кусочной функции.Вы также можете написать уравнение кусочной функции, когда вам дан график.
Как разбить на части кусочную функцию
Пройти курс
Хотите узнать больше об Алгебре 2? У меня есть пошаговый курс для этого. 🙂
Узнать больше
Определение кусочной функции
Пример
Какое определение кусочной функции показано на графике?
Работать над графиком будем слева направо.
Горизонтальная линия слева имеет ???y???-значение ???-3??? и включает все значения ???x??? в интервале ???x<-2??? (все действительные числа ???x???, которые меньше ???-2???). Для этого произведения мы пишем ???-3??? для функции (постоянная функция, значение которой равно ???-3???) и ???x<-2??? для своего домена.Наклонная линия имеет наклон ???5/4??? и ???y???-перехват ???-1/2???. Чтобы увидеть, как получить наклон, обратите внимание, что точки ???(-2,-3)??? и ???(2,2)??? находятся на этой линии, поэтому
???y=\frac{5}{4}x-\frac{1}{2}???
Для этой части мы пишем
???f(x)=\frac{5}{4}x-\frac{1}{2}???
для функции и ???-2\le x\le 2??? для своего домена.
Горизонтальная линия справа имеет ???y???-значение ???2??? и включает все значения ???x??? в интервале ???x>2???. Для этой части мы пишем ???2??? для функции и ???x>2??? для своего домена.
Соединяя три части вместе, мы определяем эту кусочную функцию следующим образом:
???f(x) = \begin{cases} -3 & \quad x < -2 \\ \frac{5}{4} x-\frac12 & \quad -2 \leq x \leq 2\\ 2 & \quad x > 2 \end{case}???
Вам может быть интересно, как мы решаем, какая часть этой функции получает ???\le??? или ???\ge??? знак и какая часть получает ?????? знак.
Правда в том, что это не имеет значения, пока каждый ???x??? в область определения всей кусочной функции входит в область определения ровно одной ее части — и, конечно, что функция для этой части дает правильное значение ???f(x)???. Можно и так написать:???f(x)=\begin{cases}-3 & \quad x \leq -2 \\\frac{5}{4}x-\frac{1}{2} & \quad -2 < x <2\\2 & \quad x \geq 2\end{cases}???
Но это нельзя было записать как
???f(x)=\begin{cases}-3 & \quad x \leq -2 \\\frac{5}{4}x-\frac{1 {2} & \quad -2 \leq x \leq 2\\2 & \quad x \geq 2\end{case}???
потому что здесь ???-2??? входит в домены двух разных частей функции, как и ???2???.
92???, а его домен ???x<2???.Второй частью графика является точка ???(2,8)???, поэтому функция для этой части ???8??? и его домен ???x=2???.
Последняя часть графика является частью линии ???y=-x+8???. Чтобы увидеть это, мы сначала вычислим наклон по точкам ???(8,0)??? и ???(2,6)???, оба находятся на этой строке.
2 & \quad\text{if}\quad x < 2\\ 8 & \quad\text{if}\quad x =2 \\ -x+8 & \quad\text{if}\quad x>2 \end{case}???Получить доступ к полному курсу Алгебра 2
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 2, алгебра II, кусочные функции, кусочно-определенные функции, функции моделирования, моделирование кусочно-функций
0 лайковСправка онлайн — Справка Origin
Все книгиКниги, не связанные с программированием Руководство пользователя Учебные пособия Быстрая справка Справка OriginКниги по программированию X-Function Origin C LabTalk Programming Python Python (внешний) Automation Server LabVIEW VI Приложения Разработка приложений Code Builder Лицензия МОКА Орглаб
Матрица значений Z одновременно создается при создании трехмерного функционального графика.
Содержимое
- 1 сетка
- 2 Шкала
- 2.1 Откуда и куда
- 2.2 Авто
- 3 Z(х,у)
- 4 Определение
- 4.1 Показать сценарий LabTalk
- 5 График выходной функции
Сетка Сетка
При построении графика 3D-функции Origin сначала создает матрицу, на основе которой создается график. Укажите размеры матрицы в поле редактирования Columns and Rows. Это определит плотность сетки 3D-поверхности.
Весы
От и до
Укажите начало и конец диапазонов x и y.
Авто
Установите этот флажок, чтобы Origin автоматически определял диапазон XY. Это выбрано по умолчанию, когда Выбрано Добавить в Active Graph . Вы можете снять этот флажок, чтобы указать начало и конец диапазона X/Y в текстовых полях From и To .
Z(х,у)
Введите здесь формулу поверхности.
Общие математические и статистические функции распределения доступны, если щелкнуть треугольную кнопку справа от текстового поля Z(x,y). Подробную информацию об этих функциях см. в описании встроенных функций LabTalk.
Кроме того, вы можете ввести функцию прямо в текстовое поле, используя любые операторы, распознаваемые Origin. Для умножения необходимо включить оператор умножения (*). Вы также можете вызвать любой из источников, даже недоступный из всплывающего меню с треугольной кнопкой или из любых функций, которые вы определили. Вы также можете использовать именованный диапазон в своем выражении.
Если нажать кнопку «Показать в отдельном окне» под треугольной кнопкой, откроется новое диалоговое окно Z(x,y)= с более широким полем ввода и панелью предварительного просмотра. Панель предварительного просмотра показывает матрицу, рассчитанную из Z(x,y) вы определили. Нажмите кнопку треугольника, чтобы переключаться между режимом данных и режимом изображения, и выберите отображение значений XY или индексов.
Вы можете проверить результат и при необходимости отредактировать формулу в поле ввода.Определение
Определите имена и значения переменных. Эти переменные можно использовать в определении функции. Если переменная еще не определена, но используется в теле функции, она будет выделена красным цветом.
Показать сценарий LabTalk
Установите этот флажок, чтобы определить переменные с помощью сценариев LabTalk. Если вы уже определили некоторые переменные в таблице Definition , установите этот флажок, чтобы отобразить эквиваленты этих определений в сценариях LabTalk.
В дополнение к встроенным функциям или функциям, определяемым пользователем, здесь поддерживаются любые сценарии LabTalk. Вы можете использовать переменные диапазона, строковые переменные, циклы и X-функции, доступные в LabTalk. Сценарии, введенные здесь, будут выполняться перед определением формулы.
Существует быстрый способ загрузить условный элемент управления или сценарий цикла, когда вы выполняете сценарий в поле Перед формулой Script .
4}}} = 0$
2)???, или ???(3,9)???, чтобы показать, что точка ???(3,9)??? не является точкой графика этой кусочной функции.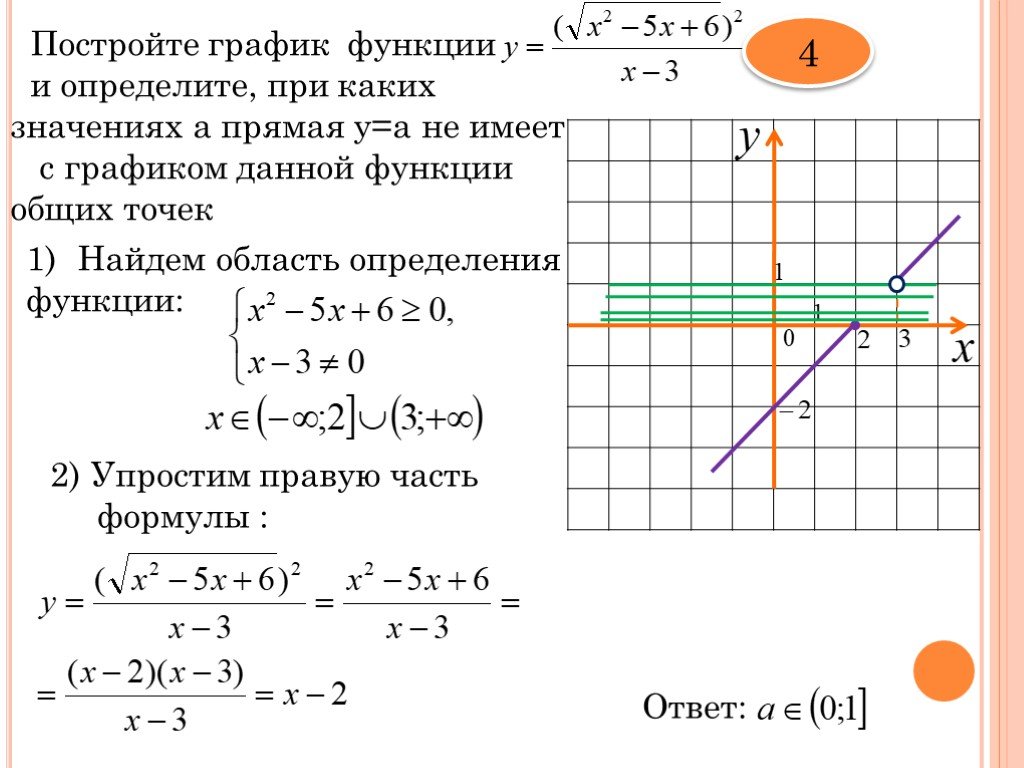
Правда в том, что это не имеет значения, пока каждый ???x??? в область определения всей кусочной функции входит в область определения ровно одной ее части — и, конечно, что функция для этой части дает правильное значение ???f(x)???. Можно и так написать: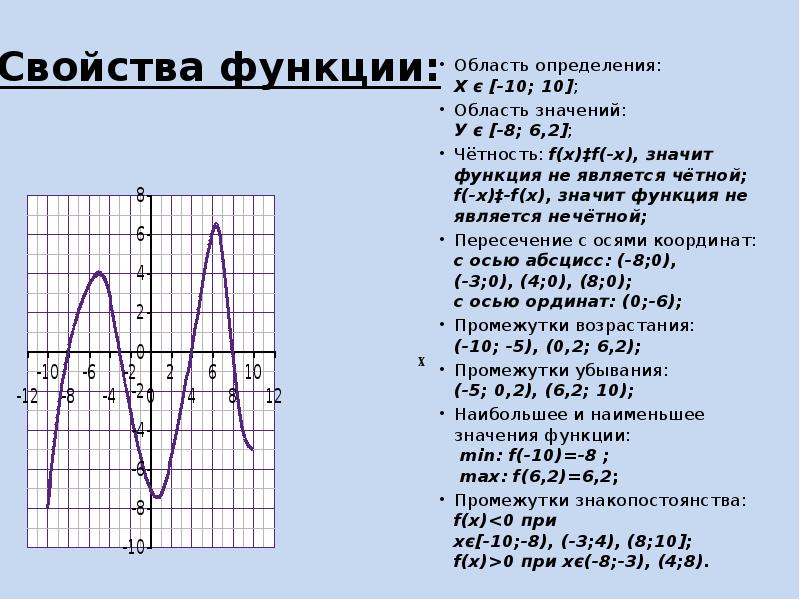
2 & \quad\text{if}\quad x < 2\\ 8 & \quad\text{if}\quad x =2 \\ -x+8 & \quad\text{if}\quad x>2 \end{case}???
Вы можете проверить результат и при необходимости отредактировать формулу в поле ввода.
Ваш комментарий будет первым