Построение геометрических фигур по точкам на координатной плоскости
Данная программа позволит Вам построить практически любой многоугольник. Все что Вам надо сделать, это ввести количество точек, которые Вы хотите соединить, затем ввести их координаты и программа построит Вашу геометрическую фигуру на координатной плоскости.
Сейчас Вам нужно выбрать количество точек, которое Вы хотите соединить. Помните, что фигура должна быть замкнута, тоесть ломаная должна начинаться и заканчиваться одной и той же точкой. Суммарное количество точек будет на 1 больше количества вершин многоугольника.
Также, при помощи нашей программы, можно просто строить фигуры, делать чертежи к задачам. Для этого надо указать, что Вы хотите убрать координатные оси и не хотите около каждой точки писать ее координаты. Для таких рисунков Вам понадобится размеченая плоскость, для узнавания точек, которые вы хотите соединить.
Ниже Вы можете посмотреть примеры использования программы!
Сколько точек Вы хотите соединить?
Примеры использования программы
1) Изображение схемотичного рисунка к задаче. Подобный рисунок был нужен, когда на нашем
форуме просили решить задачу —
тема на форуме.
Подобный рисунок был нужен, когда на нашем
форуме просили решить задачу —
тема на форуме.
Рисунок к данной задаче.
Для того, чтобы наисовать такую схему нужно отменить координатные оси и отменить писание координат точек.
2) Рисунок к задаче, построение фигуры по точкам. Наример построение высоты в треугольнике.
Рисунок к данной задаче.
Программа имеет много применений, только надо включить фантазию!
Если после использования данного онлайн калькулятора (Построение геометрических фигур по точкам) у Вас возникли какие-то вопросы по работе сервиса или вопросы образовательного характера, то Вы всегда можете задать их на нашем форуме.
Вы поняли, как решать? Нет?Помощь с решением
Координатная плоскость 6 класс онлайн-подготовка на Ростелеком Лицей
Координатная плоскость.
Общаясь друг с другом, люди часто говорят: «Оставьте свои координаты». В этом смысле «координатами» могут быть: номер телефона, домашний адрес, место работы, Е-mail. Это нужно для того, чтобы человека было легко найти.
В этом смысле «координатами» могут быть: номер телефона, домашний адрес, место работы, Е-mail. Это нужно для того, чтобы человека было легко найти.
Именно в этом и состоит суть координат или, как обычно говорят, системы координат: это правило, по которому определяется положение того или иного объекта.
Например, в кинотеатре, чтобы найти свое место в зале, сначала мы ищем свой ряд, затем своё место. В поезде, чтобы найти свое место, сначала мы ищем свой вагон, затем номер места.
Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами. Чтобы определить местонахождение объекта по карте, нужно знать его координаты.
Также систему координат можно проследить при игре в шахматы и морской бой.
В игру “Морской бой” играют на 100-клеточной доске или на бумаге в клеточку, рисуя таблицу 10 х 10. Каждая клетка на игровом поле определяется буквой и цифрой. Буквами помечены горизонтали игрового поля, а цифрами – вертикали.
Буквами помечены горизонтали игрового поля, а цифрами – вертикали.
Аналогичная система координат используется и в шахматах, только горизонтали на шахматной доске всегда обозначают латинскими буквами.
Такого рода “клеточные координаты” обычно используются на военных, морских, геологических картах. Применяются они и на туристических схемах городов для облегчения поиска нужной улицы или какой-либо достопримечательности.
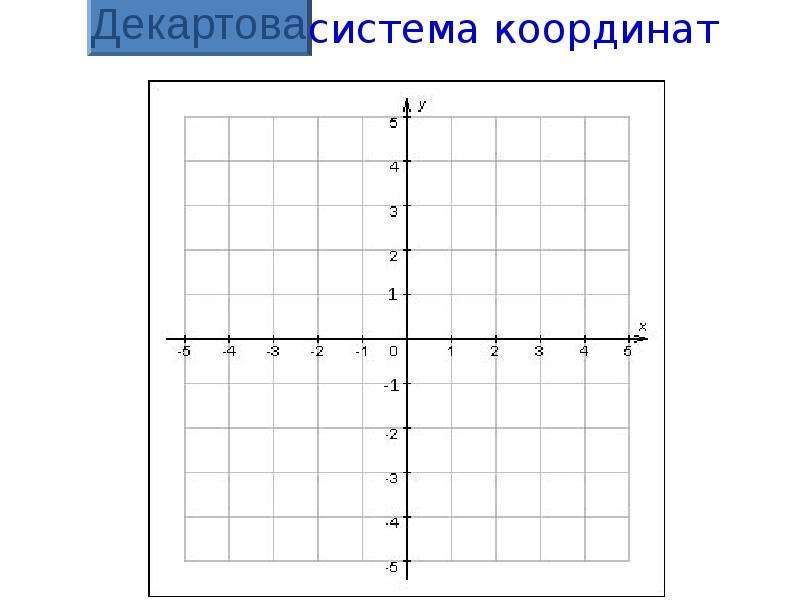
Общематематическое значение метода координат открыли французские математики XVII в. Пьер Ферма и Рене Декарт. В 1637 году Рене Декарт впервые опубликовал изложение метода координат, поэтому прямоугольную систему координат называют также — «Декартова система координат».
Термины «абсцисса» и «ордината» (образованные от латинских слов «отсекаемый» и «упорядоченный») были введены в 70-80 гг. XVII в. немецким математиком Вильгельмом Лейбницем.
Разберёмся, как задать координаты точки на плоскости.
Для этого на плоскости строят две перпендикулярные прямые (обычно одну из них располагают горизонтально, а другую – вертикально) и вводят на каждой из них обычные координаты. Эти координаты согласованны между собой. Точка пересечения прямых О называется началом координат. Эта буква выбрана не случайно, а по сходству написания с цифрой 0 или как первая буква латинского слова origo – начало. Сами координатные прямые называют осями координат.
Эти координаты согласованны между собой. Точка пересечения прямых О называется началом координат. Эта буква выбрана не случайно, а по сходству написания с цифрой 0 или как первая буква латинского слова origo – начало. Сами координатные прямые называют осями координат.
Горизонтальную ось называют осью абсцисс (или осью Х), вертикальную ось называют осью ординат (или осью Y). Плоскость, на которой задана система координат, называется координатной плоскостью, которая разделяется осями абсцисс и ординат на четверти.
Посмотрим, как определяется положение точки на координатной плоскости.
Пусть M — некоторая точка плоскости. Проведем через нее прямую MA, перпендикулярную координатной прямой X, и прямую MB, перпендикулярную координатной прямой Y.
Так как точка A имеет координату 4, а точка B координату 3, то положение точки M определяется парой чисел (4, 3). Эту пару чисел называют координатами точки M.
Число 4 называют абсциссой точки M, а число 3 — ординатой точки M.
Точку M сабсциссой 4 и ординатой 3 обозначают так: M (4, 3). На первом месте пишут абсциссу точки, а на втором ее ординату.
Если переставить координаты местами, то получится другая точка N (3, 4), которая тоже изображена на рисунке.
Каждой точке на координатной плоскости соответствует пара чисел: ее абсцисса и ордината; и наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Расстояние между точками по координатам
Данный онлайн калькулятор считает расстояние между двумя точками двумерной плоскости исходя из координат этих точек. Вы можете посчитать длину отрезка между двумя точками или длину линии между двумя точками на основе координат этих точек.
Значения координат могут быть положительными и отрицательными числами или так же равными 0. Так же можно использовать десятичные значения.
Положение точек не принципиально, главное введите правильно координаты каждой из точек.
Укажите координаты:
Результат:
Решение:
Отправить ссылку в:На двумерной плоскости координаты точки — это два числа, где первым числом указывается абсцисса (координата x), а вторым — ордината точки (координата y).
Каждая точка координатной плоскости имеет две координаты.
Формула для расчёта расстояния между двумя точками
На двумерной плоскости расстояние между двумя точками по их координатам расчитывается по следующей формуле:
AB = \sqrt{(B_x — A_x)^2 + (B_y — A_y)^2}
- AB — отрезок между точками A и B
- Ax — координата x в точке A
- Ay — координата y в точке A
- Bx — координата x в точке B
- By — координата y в точке B
Задания на координатной плоскости «Построение фигур по точкам» (6 класс)
Изобразите фигуру на координатной плоскости, приняв за единичный отрезок один сантиметр:
Голова: (-4; 9), (-4; 5), (-3; 5), (-3; 9), (-2; 7), (-2; 5), (-1; 3), (-2; 2), (-5; 2), (-6; 3), (-5; 5), (-5; 7), (-4; 9).
Мордочка: (-5; 3,5), (-4,5; 4), (-4; 3,5), (-5; 3,5). (-3; 3,5), (-2,5; 4), (-2; 3,5), (-3; 3,5). (-3,5; 3), (-3,5; 2,5). (-4,5; 3), (-4; 2,5), (-3; 2,5), (-2,5; 3).
Туловище: (-4; 2), (-5; 1), (-7; 1), (-7; 0), (-5; 0), (-5; -2), (-7; -2), (-7; -3), (-5; -4), (-7; -4), (-7; -4,5), (-4; -4,5), (-4; -3), (-3; -3), (-3; -4,5), (0; -4,5), (0; -4), (-2; -4), (0; -3), (0; -2), (-2; -2), (-2; 0), (0; 0), (0; 1), (-2; 1), (-3; 2).
(Зайчик)
Изобразите фигуру на координатной плоскости, приняв за единичный отрезок один сантиметр:
Голова: (-4; 9), (-4; 5), (-3; 5), (-3; 9), (-2; 7), (-2; 5), (-1; 3), (-2; 2), (-5; 2), (-6; 3), (-5; 5), (-5; 7), (-4; 9).
Мордочка: (-5; 3,5), (-4,5; 4), (-4; 3,5), (-5; 3,5). (-3; 3,5), (-2,5; 4), (-2; 3,5), (-3; 3,5). (-3,5; 3), (-3,5; 2,5). (-4,5; 3), (-4; 2,5), (-3; 2,5), (-2,5; 3).
Туловище: (-4; 2), (-5; 1), (-7; 1), (-7; 0), (-5; 0), (-5; -2), (-7; -2), (-7; -3), (-5; -4), (-7; -4), (-7; -4,5), (-4; -4,5), (-4; -3), (-3; -3), (-3; -4,5), (0; -4,5), (0; -4), (-2; -4), (0; -3), (0; -2), (-2; -2), (-2; 0), (0; 0), (0; 1), (-2; 1), (-3; 2).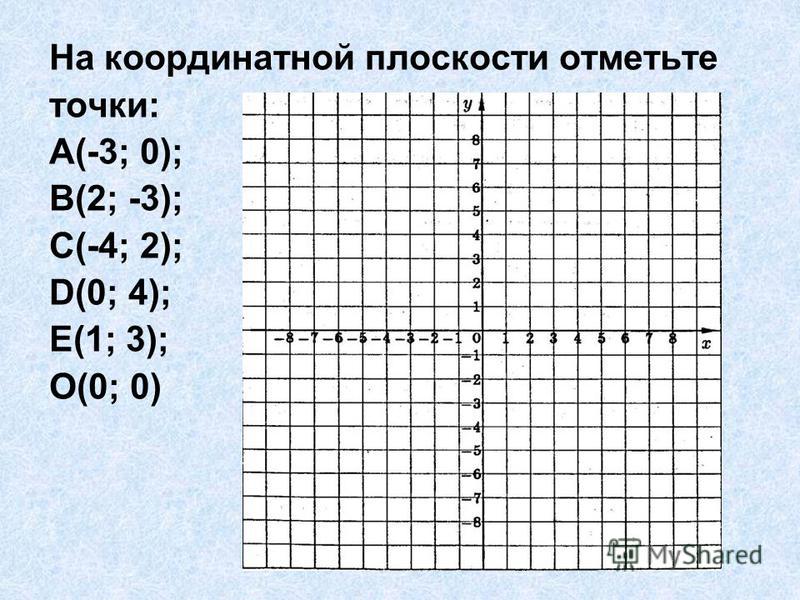
(Зайчик)
Изобразите фигуру на координатной плоскости, приняв за единичный отрезок один сантиметр:
Голова: (-4; 9), (-4; 5), (-3; 5), (-3; 9), (-2; 7), (-2; 5), (-1; 3), (-2; 2), (-5; 2), (-6; 3), (-5; 5), (-5; 7), (-4; 9).
Мордочка: (-5; 3,5), (-4,5; 4), (-4; 3,5), (-5; 3,5). (-3; 3,5), (-2,5; 4), (-2; 3,5), (-3; 3,5). (-3,5; 3), (-3,5; 2,5). (-4,5; 3), (-4; 2,5), (-3; 2,5), (-2,5; 3).
Туловище: (-4; 2), (-5; 1), (-7; 1), (-7; 0), (-5; 0), (-5; -2), (-7; -2), (-7; -3), (-5; -4), (-7; -4), (-7; -4,5), (-4; -4,5), (-4; -3), (-3; -3), (-3; -4,5), (0; -4,5), (0; -4), (-2; -4), (0; -3), (0; -2), (-2; -2), (-2; 0), (0; 0), (0; 1), (-2; 1), (-3; 2).
(Зайчик)
Изобразите фигуру на координатной плоскости, приняв за единичный отрезок один сантиметр:
Голова: (-4; 9), (-4; 5), (-3; 5), (-3; 9), (-2; 7), (-2; 5), (-1; 3), (-2; 2), (-5; 2), (-6; 3), (-5; 5), (-5; 7), (-4; 9).
Мордочка: (-5; 3,5), (-4,5; 4), (-4; 3,5), (-5; 3,5). (-3; 3,5), (-2,5; 4), (-2; 3,5), (-3; 3,5). (-3,5; 3), (-3,5; 2,5). (-4,5; 3), (-4; 2,5), (-3; 2,5), (-2,5; 3).
Туловище: (-4; 2), (-5; 1), (-7; 1), (-7; 0), (-5; 0), (-5; -2), (-7; -2), (-7; -3), (-5; -4), (-7; -4), (-7; -4,5), (-4; -4,5), (-4; -3), (-3; -3), (-3; -4,5), (0; -4,5), (0; -4), (-2; -4), (0; -3), (0; -2), (-2; -2), (-2; 0), (0; 0), (0; 1), (-2; 1), (-3; 2).
(Зайчик)
Изобразите фигуру на координатной плоскости, приняв за единичный отрезок один сантиметр:
Голова: (-4; 9), (-4; 5), (-3; 5), (-3; 9), (-2; 7), (-2; 5), (-1; 3), (-2; 2), (-5; 2), (-6; 3), (-5; 5), (-5; 7), (-4; 9).
Мордочка: (-5; 3,5), (-4,5; 4), (-4; 3,5), (-5; 3,5). (-3; 3,5), (-2,5; 4), (-2; 3,5), (-3; 3,5). (-3,5; 3), (-3,5; 2,5). (-4,5; 3), (-4; 2,5), (-3; 2,5), (-2,5; 3).
Туловище: (-4; 2), (-5; 1), (-7; 1), (-7; 0), (-5; 0), (-5; -2), (-7; -2), (-7; -3), (-5; -4), (-7; -4), (-7; -4,5), (-4; -4,5), (-4; -3), (-3; -3), (-3; -4,5), (0; -4,5), (0; -4), (-2; -4), (0; -3), (0; -2), (-2; -2), (-2; 0), (0; 0), (0; 1), (-2; 1), (-3; 2).
(Зайчик)
Изобразите фигуру на координатной плоскости, приняв за единичный отрезок один сантиметр:
Голова: (-4; 9), (-4; 5), (-3; 5), (-3; 9), (-2; 7), (-2; 5), (-1; 3), (-2; 2), (-5; 2), (-6; 3), (-5; 5), (-5; 7), (-4; 9).
Мордочка: (-5; 3,5), (-4,5; 4), (-4; 3,5), (-5; 3,5). (-3; 3,5), (-2,5; 4), (-2; 3,5), (-3; 3,5). (-3,5; 3), (-3,5; 2,5). (-4,5; 3), (-4; 2,5), (-3; 2,5), (-2,5; 3).
Туловище: (-4; 2), (-5; 1), (-7; 1), (-7; 0), (-5; 0), (-5; -2), (-7; -2), (-7; -3), (-5; -4), (-7; -4), (-7; -4,5), (-4; -4,5), (-4; -3), (-3; -3), (-3; -4,5), (0; -4,5), (0; -4), (-2; -4), (0; -3), (0; -2), (-2; -2), (-2; 0), (0; 0), (0; 1), (-2; 1), (-3; 2).
(Зайчик)
Изобразите фигуру на координатной плоскости, приняв за единичный отрезок один сантиметр:
Голова: (-4; 9), (-4; 5), (-3; 5), (-3; 9), (-2; 7), (-2; 5), (-1; 3), (-2; 2), (-5; 2), (-6; 3), (-5; 5), (-5; 7), (-4; 9).
Мордочка: (-5; 3,5), (-4,5; 4), (-4; 3,5), (-5; 3,5). (-3; 3,5), (-2,5; 4), (-2; 3,5), (-3; 3,5). (-3,5; 3), (-3,5; 2,5). (-4,5; 3), (-4; 2,5), (-3; 2,5), (-2,5; 3).
Туловище: (-4; 2), (-5; 1), (-7; 1), (-7; 0), (-5; 0), (-5; -2), (-7; -2), (-7; -3), (-5; -4), (-7; -4), (-7; -4,5), (-4; -4,5), (-4; -3), (-3; -3), (-3; -4,5), (0; -4,5), (0; -4), (-2; -4), (0; -3), (0; -2), (-2; -2), (-2; 0), (0; 0), (0; 1), (-2; 1), (-3; 2).
(Зайчик)
Изобразите фигуру на координатной плоскости, приняв за единичный отрезок один сантиметр:
Голова: (-4; 9), (-4; 5), (-3; 5), (-3; 9), (-2; 7), (-2; 5), (-1; 3), (-2; 2), (-5; 2), (-6; 3), (-5; 5), (-5; 7), (-4; 9).
Мордочка: (-5; 3,5), (-4,5; 4), (-4; 3,5), (-5; 3,5). (-3; 3,5), (-2,5; 4), (-2; 3,5), (-3; 3,5). (-3,5; 3), (-3,5; 2,5). (-4,5; 3), (-4; 2,5), (-3; 2,5), (-2,5; 3).
Туловище: (-4; 2), (-5; 1), (-7; 1), (-7; 0), (-5; 0), (-5; -2), (-7; -2), (-7; -3), (-5; -4), (-7; -4), (-7; -4,5), (-4; -4,5), (-4; -3), (-3; -3), (-3; -4,5), (0; -4,5), (0; -4), (-2; -4), (0; -3), (0; -2), (-2; -2), (-2; 0), (0; 0), (0; 1), (-2; 1), (-3; 2).
(Зайчик)
|
Дата проведения |
Мероприятие |
Преподаватель |
Категория участников, условия и ограничения |
|
02.02.2021 18.00 |
Обществознание. Экономические вопросы |
Дубынина Анна Валерьевна, кандидат экономических наук, доцент |
Продолжительность 40-45 минут
|
|
09.02.2021 18.00 |
Математика. Простейшие текстовые задачи. Чтение графиков и диаграмм |
Завьялов Олег Геннадьевич, кандидат физико-математических наук, доцент |
Продолжительность 40-45 минут
|
|
16. 18.00 |
Математика. Квадратная решетка, координатная плоскость |
Подповетная Юлия Валерьевна, доктор педагогических наук, профессор |
Продолжительность 40-45 минут
|
|
02.03.2021 18.00 |
Обществознание. |
Дубынина Анна Валерьевна, кандидат экономических наук, доцент |
Продолжительность 40-45 минут
|
|
16.03.2021 18.00 |
Математика. Простейшие уравнения |
Завьялов Олег Геннадьевич, кандидат физико-математических наук, доцент |
Продолжительность 40-45 минут
|
|
23. 18.00 |
Математика. Вычисления и преобразования |
Подповетная Юлия Валерьевна, доктор педагогических наук, профессор |
Продолжительность 40-45 минут
|
|
30.03.2021 |
Математика. Начала теории вероятностей |
Завьялов Олег Геннадьевич, кандидат физико-математических наук, доцент |
Продолжительность 40-45 минут
|
— заполнение онлайн, для печати, заполняемое, пустое
Комментарии и помощь по построителю координатной плоскости
На графике линия, представляющая наиболее положительное значение, окрашена в красный цвет (оранжевая линия — синяя). Но вы также можете увидеть это в приведенных ниже данных. Я также могу визуализировать распределение значений переменных и то, как они менялись с течением времени. Это было бы полезно, если бы вы пытались сравнить наборы данных, сделанные разными людьми.X -3-4 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 1-2-3-4-5-6-7-8 — 9-10-11-12-13-14-15-16-17-18-19-20-21-22-23-24-25-26-27-28-29-30-31-32 1 Всего — 2,050 -1,950 -1,690 -1,530 -1,240 -1,190 -1,040-900-775-640-480-320-270-200 -160 -140 -120 -120-80-60-50-40-30-20-10 0 2 3 4 5 6 X -1,850 -1,660 -1,530 -1,240 -1,190 -1,040-900-775-640-480-320-270-200 -160 -140 -120 -120-80-60-50-40-30 -20-10 0 2 3 4 5 6 6 7 7 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 1-1-2-3-4-5 — 6-7-8-9-10-11-12-13-14-15-16-17-18-19-20-21-22-23-24-25-26-27-28-29-30 — 31-32 0-1 3 4 5 6 6 7 8 Итого -2,550-2,360 -2,220 -1,950 -1,680 -1,380 -1,260 -1,090-800-720-600-480-400-360-280-240-200-160 -140-120-120-80-60-50-40-30-20-10 0 2 3 4 5 6 7 Результаты математики.com.xls
Это было бы полезно, если бы вы пытались сравнить наборы данных, сделанные разными людьми.X -3-4 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 1-2-3-4-5-6-7-8 — 9-10-11-12-13-14-15-16-17-18-19-20-21-22-23-24-25-26-27-28-29-30-31-32 1 Всего — 2,050 -1,950 -1,690 -1,530 -1,240 -1,190 -1,040-900-775-640-480-320-270-200 -160 -140 -120 -120-80-60-50-40-30-20-10 0 2 3 4 5 6 X -1,850 -1,660 -1,530 -1,240 -1,190 -1,040-900-775-640-480-320-270-200 -160 -140 -120 -120-80-60-50-40-30 -20-10 0 2 3 4 5 6 6 7 7 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 1-1-2-3-4-5 — 6-7-8-9-10-11-12-13-14-15-16-17-18-19-20-21-22-23-24-25-26-27-28-29-30 — 31-32 0-1 3 4 5 6 6 7 8 Итого -2,550-2,360 -2,220 -1,950 -1,680 -1,380 -1,260 -1,090-800-720-600-480-400-360-280-240-200-160 -140-120-120-80-60-50-40-30-20-10 0 2 3 4 5 6 7 Результаты математики.com.xls
Видеоинструкция и помощь по заполнению и заполнению координатной сетки
Инструкции и справка по онлайн-форме координатной плоскости
Привет, я Роб, добро пожаловать в математические шалости. В этом уроке мы собирались узнать кое-что, что является важной основой для множества математических задач, включая те, с которыми вы столкнетесь при изучении базовой алгебры. Мы собирались узнать о построении графиков, что в основном означает использование математических соотношений и превращение их в картинки. Привет, друзья, добро пожаловать! назад к Радости построения графиков Мы собираемся продолжить с того места, где мы остановились. У нас уже есть эта прекрасная красивая функция прямо здесь. Но для этого нужен друг. нужно соединить эти точки, потому что они все друзья И что делают друзья Они остаются на связи О, и посмотрите на это вы можете лучше понять это. Это способ помочь вам буквально УВИДЕТЬ, как работает математика. Когда математика — это просто набор чисел и символов на странице, это может быть довольно абстрактно и сложно связать с ним Но построение графиков похоже на окно в абстрактный мир математики, которое помогает нам увидеть его более ясно. это платформа или этап, на котором будет происходить построение графика.
В этом уроке мы собирались узнать кое-что, что является важной основой для множества математических задач, включая те, с которыми вы столкнетесь при изучении базовой алгебры. Мы собирались узнать о построении графиков, что в основном означает использование математических соотношений и превращение их в картинки. Привет, друзья, добро пожаловать! назад к Радости построения графиков Мы собираемся продолжить с того места, где мы остановились. У нас уже есть эта прекрасная красивая функция прямо здесь. Но для этого нужен друг. нужно соединить эти точки, потому что они все друзья И что делают друзья Они остаются на связи О, и посмотрите на это вы можете лучше понять это. Это способ помочь вам буквально УВИДЕТЬ, как работает математика. Когда математика — это просто набор чисел и символов на странице, это может быть довольно абстрактно и сложно связать с ним Но построение графиков похоже на окно в абстрактный мир математики, которое помогает нам увидеть его более ясно. это платформа или этап, на котором будет происходить построение графика. Но чтобы понять, как это работает, нам сначала нужно начать с его ближайшего родственника; Числовая линия Вы помните, как работает числовая линия справа Числовая линия начинается с нуля и представляет положительные числа, когда вы двигаетесь вправо, и отрицательные числа, когда вы перемещаетесь влево И обычно есть отметки, показывающие, где находится каждое целое число по пути. клонирование этой числовой линии и поворот копии против часовой стрелки на 90 градусов так, чтобы вторая числовая линия была перпендикулярна первой и пересекалась в своих нулевых точках. Теперь у нас есть числовая плоскость. числовая линия, но это второе измерение делает ее намного более полезной С помощью простой 1-мерной числовой линии мы могли бы показать, где были расположены различные числа вдоль этой линии, путем рисования или нанесения точек. Но независимо от того, сколько точек мы наносим, они всегда находятся на одной линии. с помощью двумерной числовой плоскости мы можем наносить точки в любом месте этой двумерной области, и это открывает целый новый мир возможностей.
Но чтобы понять, как это работает, нам сначала нужно начать с его ближайшего родственника; Числовая линия Вы помните, как работает числовая линия справа Числовая линия начинается с нуля и представляет положительные числа, когда вы двигаетесь вправо, и отрицательные числа, когда вы перемещаетесь влево И обычно есть отметки, показывающие, где находится каждое целое число по пути. клонирование этой числовой линии и поворот копии против часовой стрелки на 90 градусов так, чтобы вторая числовая линия была перпендикулярна первой и пересекалась в своих нулевых точках. Теперь у нас есть числовая плоскость. числовая линия, но это второе измерение делает ее намного более полезной С помощью простой 1-мерной числовой линии мы могли бы показать, где были расположены различные числа вдоль этой линии, путем рисования или нанесения точек. Но независимо от того, сколько точек мы наносим, они всегда находятся на одной линии. с помощью двумерной числовой плоскости мы можем наносить точки в любом месте этой двумерной области, и это открывает целый новый мир возможностей. С помощью одномерной числовой линии построение точек было легким. просто нужно было одно число, чтобы сообщить вам, где построить точку.Но с двумерной числовой плоскостью вам действительно нужны ДВА числа для построения каждой точки. Эти два числа называются координатами, потому что они имеют одинаковый ранг или порядок, и они работают вместе, чтобы указать местоположения точки на числовой плоскости На самом деле, именно поэтому числовую плоскость часто называют координатной плоскостью. Это этап для построения координат. Координаты используют специальный формат, чтобы помочь вам их распознать. Два числа помещены в круглые скобки с запятой между ними. как разделитель Итак, когда вы видите 2 запятую 5…
С помощью одномерной числовой линии построение точек было легким. просто нужно было одно число, чтобы сообщить вам, где построить точку.Но с двумерной числовой плоскостью вам действительно нужны ДВА числа для построения каждой точки. Эти два числа называются координатами, потому что они имеют одинаковый ранг или порядок, и они работают вместе, чтобы указать местоположения точки на числовой плоскости На самом деле, именно поэтому числовую плоскость часто называют координатной плоскостью. Это этап для построения координат. Координаты используют специальный формат, чтобы помочь вам их распознать. Два числа помещены в круглые скобки с запятой между ними. как разделитель Итак, когда вы видите 2 запятую 5…
Квадрант I в координатной плоскости | Анализ данных Стандарты по математике для 5-х классов
Квадрант I в координатной плоскости | Стандарты анализа данных по математике для 5-х классовМеню Javascript от Deluxe-Menu.com
| Подпишитесь на нашу рассылку |
объявление
Представьте данные с помощью упорядоченных пар в первом квадранте системы координат.
0506.5.2
Ссылки проверены 16.09.2014
- Billy Bug — Проведите Билли до координат, где прячется еда. координаты 0-10 | координаты 0-5 также
- Построение графиков в квадранте 1 в координатной плоскости — план урока из домена учителя в WNET
- Навыки построения графиков — в чем смысл? Найдите точку на сетке (выберите Easy для задач Quadrant 1)
- Grid Graph — определение и нанесение точек на сетку
- Введение в координатную плоскость и координаты — диалог между наставником и учеником, который будет использоваться для представления плоскости
- Сегмент линии: Координатная геометрия — Отрегулируйте сегмент линии ниже, перетащив оранжевую точку в точку A или B, и посмотрите, как ведет себя сегмент AB.Вы также можете перетащить исходную точку на (0,0).
- Линии в координатной геометрии — введение в определение линии
- Lost My Marbles Handout — текстовый документ с расширенными полями об использовании координатной сетки — [этот документ можно открыть с помощью MS Word]
- Создайте координатную плоскость — вы можете создать один квадрант или все четыре, а затем использовать плоскость с интерактивной доской или другим проекционным устройством.
- Сетки чтения — найдите Херкла на пересечении сетки [Эта ссылка с истекшим сроком действия доступна в Интернет-архиве Wayback Machine.Если страница не загружается быстро, нажмите Нетерпеливый? в правом нижнем углу страницы.]
- Простая игра с координатами — учащиеся исследуют первый квадрант декартовой системы координат, определяя координаты точек или запрашивая построение конкретной точки.
- Простая игра в лабиринт — учащиеся исследуют первый квадрант декартовой системы координат, направляя робота через минное поле, разложенное на плоскости.
- Worksheet Generator — Распечатайте ваши собственные пустые рабочие листы координатной плоскости, вы определяете количество сеток на листе и то, пронумерованы ли сетки или нет.
- Продвинутый [используются все 4 квадранта]
тип = а>
- Знакомство с координатной плоскостью — упражнение, состоящее из 62 задач [Эта ссылка с истекшим сроком действия доступна в Интернет-архиве Wayback Machine.
Если страница не загружается быстро, нажмите Нетерпеливый? в правом нижнем углу страницы.]
- Координатная плоскость — урок из четырех частей, который включает введение, подробное объяснение, примеры и практические упражнения для проверки понимания учащимися
- Координатная плоскость — для практики студентов создайте свои собственные рабочие листы координатной плоскости в онлайн-генераторе математических листов.
- Координатная плоскость — 4 квадранта — Эта рабочая тетрадь на одном листе имела координатную плоскость с девятью цветными точками. Используйте интерактивную доску и попросите учащихся перетащить точки, чтобы представить упорядоченную пару, которую вы укажете.
- Coordinate Plane Game — игра на время с использованием Flash-анимации, определение упорядоченной пары для данной точки на плоскости
- Игра с общими координатами — учащиеся изучают декартову систему координат, определяя координаты точек или запрашивая нанесение определенной точки.

- Навыки построения графиков — в чем смысл? Найдите точку на сетке (выберите Средний или Жесткий для всех четырех квадрантов)
- Горизонтальная линия (координатная геометрия) — перетащите точки A или B и обратите внимание на то, что линия является горизонтальной, если они обе имеют одинаковую координату y.
- Найдите пришельцев — ваша задача — ввести координаты пришельцев, когда они появятся в самолете.
- Math Open Reference: Coordinate Plane — Перетащите точку A. При перетаскивании обратите внимание на два числа, которые определяют его положение на плоскости. Перетащите начало координат, чтобы изменить положение осей.
- Maze Game — Это упражнение позволяет пользователю практиковать свои навыки построения точек, заставляя его перемещать робота через минное поле в заданное место.Перемещения осуществляются путем указания координат нового места.
Чтобы победить, путь не должен пересекать мину.
- Maze Game — Ученики используют свои знания о точках на графике, чтобы переместить робота к цели, избегая при этом мин.
- Quiz — введите упорядоченные пары для каждой из четырех точек на координатной плоскости [Эта ссылка с истекшим сроком действия доступна в Интернет-архиве Wayback Machine. Если страница не загружается быстро, нажмите Нетерпеливый? в правом нижнем углу страницы.]
- Spy Guys Interactive — Использование упорядоченных пар — [для 6 класса] интерактивный видеоурок
- Запас на полках — Вы продавец. Заполните полки, используя координатную плоскость. также
- Вертикальная линия (координатная геометрия) — перетащите точки A или B и обратите внимание на то, что линия является вертикальной, когда они обе имеют одинаковую координату x.
Internet4classrooms — результат совместных усилий
Сьюзан Брукс и Билл Байлз.
объявление
401169734 DE 1 настольный компьютер, а не планшет, а не iPad device-widthКоординатная сетка Классные бесплатные онлайн-математические игры для детей
КООРДИНАТНАЯ СЕТКА ИГРЫ
Играйте в эти игры с координатной сеткой, чтобы попрактиковаться и укрепить свои навыки работы с координатной сеткой в увлекательной игровой форме.
Безопасно приведите кита к финишу.Вам нужно будет планировать заранее, так как как только вы нажмете кнопку «Переместить», кит не остановится, пока не достигнет финишной черты или не столкнется с препятствием!
CCSS: 5.G.A.1, 6.NS.C.6c
Стреляйте водой по бомбе, расположенной в правильных координатах x, y, чтобы обезвредить ее до того, как она взорвется. Не стреляйте водой не в ту бомбу, иначе она взорвется!
Откройте для себя загадочную картину, нанеся заданные упорядоченные пары на координатную сетку.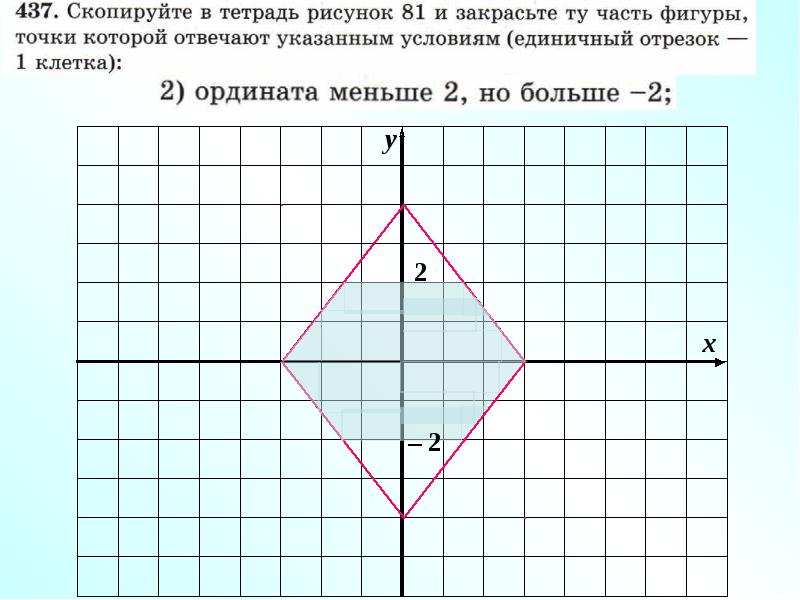 Выберите игру в квадранте I или во всех четырех квадрантах.В этой игре нет ограничений по времени, так что не торопитесь, создавая загадочную картинку.
Выберите игру в квадранте I или во всех четырех квадрантах.В этой игре нет ограничений по времени, так что не торопитесь, создавая загадочную картинку.
Продолжение Graphing Puzzle с 20 новыми картинками, которые нужно создать. Откройте для себя загадочную картину, нанеся заданные упорядоченные пары на координатную сетку. Выберите игру в квадранте I или во всех четырех квадрантах. В этой игре нет ограничений по времени, так что не торопитесь, создавая загадочную картинку.
Math встречает Missile Command в этой увлекательной математической игре с координатной сеткой. Защитите свои города, используя ракеты, чтобы уничтожить приближающиеся метеоры.Подключите координаты X, Y метеоров и нажмите FIRE для запуска.
CCSS: 5.G.A.1, 6.NS.C.6.c
Помогите пчелам доставить мед в нужное место в улье, используя их упорядоченную пару.
CCSS: 5.G.A.1, 6.NS.C.6.c
Очистите квадранты, удалив злоумышленников, определив упорядоченную пару, связанную с их местоположением.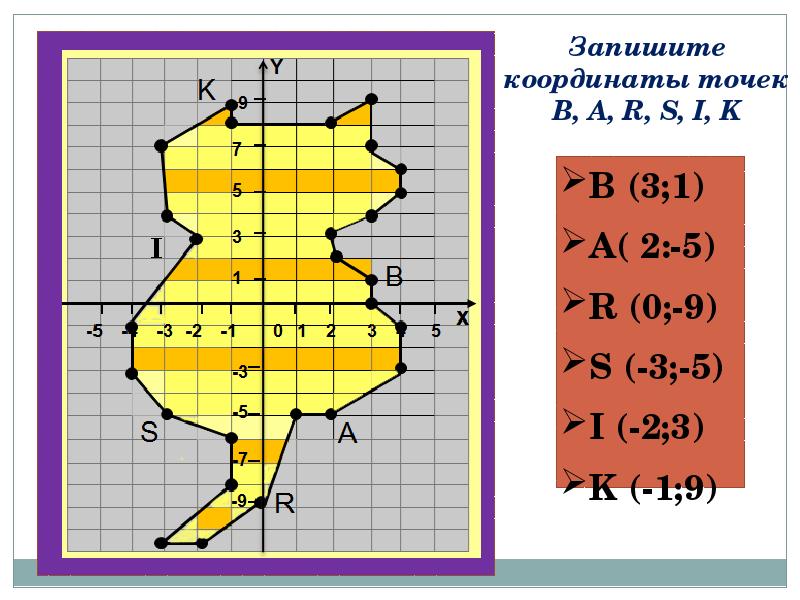 Выберите для игры в обычном или временном режиме в квадранте 1 или во всех 4 квадрантах.
Выберите для игры в обычном или временном режиме в квадранте 1 или во всех 4 квадрантах.
CCSS: 6.NS.C.6.b, 6.NS.C.6.c
Версия 2 игры с координатной сеткой Rocket Down с улучшенной графикой и игровым процессом. Выберите для игры следующие режимы: Untimed, Beginner, Advanced и Expert
CCSS: 5.G.A.1, 6.NS.C.6c
Fly MathPup, чтобы получить кости, используя пару координат, которую дает вам MathPup. Избегайте столкновений с астероидами и не позволяйте инопланетянам украсть все кости MathPup.
CCSS: 5.G.A.1, 5.G.A.2
Перемещайтесь по координатам x, y, чтобы вовремя добраться до финиша, собирая монеты и избегая препятствий.Прочтите внутриигровые инструкции или посмотрите видео с советами и инструкциями: Видео с координатами лодки
CCSS: 6.NS.C.6.b, 6.NS.C.6.c
Возьмите топливные баки, расположенные на координатной сетке, чтобы замедлить вашу ракету для безопасной посадки. Слишком тяжело приземлиться, и игра окончена, чувак!
Слишком тяжело приземлиться, и игра окончена, чувак!
CCSS: 5.G.A.1, 6.NS.C.6c
Управляйте лодкой так, чтобы флаг появился на координатной сетке, избегая препятствий.
Откройте для себя загадочную картинку Хэллоуина, нанеся заданные упорядоченные пары на координатную сетку.Выберите игру в квадранте I или во всех четырех квадрантах. В этой игре нет ограничений по времени, так что не торопитесь, создавая загадочную картинку.
Координатная плоскость— определение, факты и примеры
Координатная плоскость — это двумерная плоскость, образованная пересечением вертикальной линии, называемой осью y, и горизонтальной линии, называемой осью x. Это перпендикулярные линии, которые пересекаются друг с другом в нуле, и эта точка называется началом координат.
Что такое координатная плоскость?
Координатная плоскость — это двумерная поверхность, образованная двумя числовыми линиями.Он образуется, когда горизонтальная линия, называемая осью X, и вертикальная линия, называемая осью Y, пересекаются в точке, называемой началом координат. Числа на координатной сетке используются для определения точек. Координатная плоскость может использоваться для построения точек, линий и многого другого. Он действует как карта и дает точные указания от одной точки к другой.
Числа на координатной сетке используются для определения точек. Координатная плоскость может использоваться для построения точек, линий и многого другого. Он действует как карта и дает точные указания от одной точки к другой.
Определение координатной плоскости
Определение координатной плоскости следующее: Координатная плоскость , также известная как сетка прямоугольной координатной плоскости , представляет собой двумерную плоскость, образованную пересечением вертикальной линии, называемой осью Y, и горизонтальной линии, называемой ось X.
Координатная плоскость
График координат , иногда называемый координатной плоскостью , состоит из двух числовых линий, называемых осями, которые проходят перпендикулярно друг другу.
Координаты
Координаты — это набор из двух значений, которые определяют местоположение определенной точки на сетке координатной плоскости, более известной как координатная плоскость. Точка в координатной плоскости называется ее упорядоченной парой (x, y), записанной в скобках, соответствующей координате X и координате Y.Эти координаты могут быть положительными, нулевыми или отрицательными, в зависимости от положения точки в соответствующих квадрантах.
Точка в координатной плоскости называется ее упорядоченной парой (x, y), записанной в скобках, соответствующей координате X и координате Y.Эти координаты могут быть положительными, нулевыми или отрицательными, в зависимости от положения точки в соответствующих квадрантах.
Квадранты на координатной плоскости
Квадрант может быть определен как область / часть декартовой или координатной плоскости, полученная, когда две оси пересекаются друг с другом.
- Первый квадрант: x> 0, y> 0
- Второй квадрант: x <0, y> 0
- Третий квадрант: x <0, y <0
- Четвертый квадрант: x> 0, y <0
Определение точки на координатной плоскости
Теперь, когда мы уже знакомы с координатной плоскостью и ее частями, давайте обсудим, как определять точки на координатной плоскости.Чтобы найти точку на координатной плоскости, выполните следующие действия:
- Шаг 1: Найдите точку.

- Шаг 2: Найдите квадрант, глядя на знаки его координат X и Y.
- Шаг 3: Найдите координату X или абсциссу точки, считывая количество единиц, в которых точка находится справа / слева от начала координат по оси X.
- Шаг 4: Найдите координату Y или ординату точки, считывая количество единиц, в которых точка находится выше / ниже начала координат по оси Y.
Давайте посмотрим на примеры координатной плоскости. Посмотрите на рисунок, показанный ниже.
- Шаг 1: Обратите внимание на синюю точку на графике координат.
- Шаг 2: Он находится во втором квадранте.
- Шаг 3: Точка находится на расстоянии 3 единиц от начала координат по отрицательной оси X.
- Шаг 4: Точка находится на расстоянии 2 единиц от начала координат вдоль положительной оси Y.
Таким образом, точка на графике имеет координаты (-3, 2).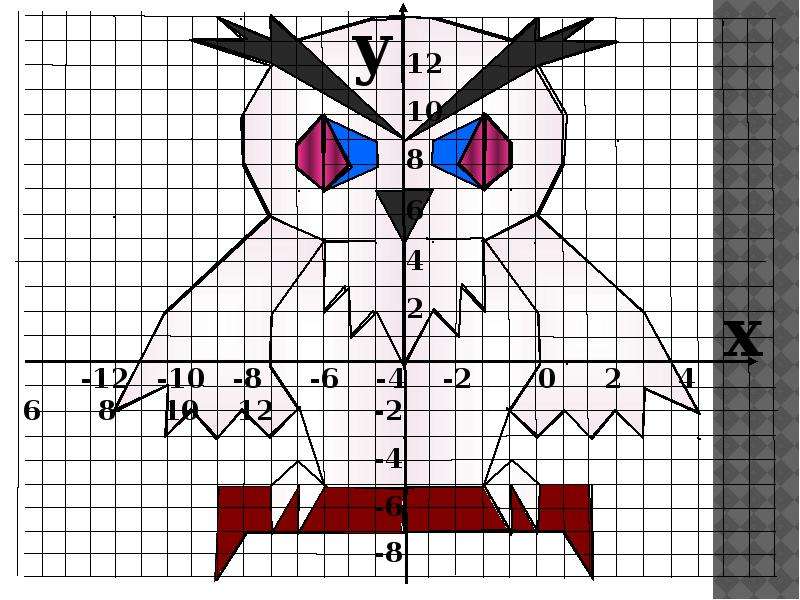
Построение точки на координатной плоскости
В этом разделе мы узнаем, как построить точку на координатной плоскости. Возьмем для примера точку P = (5, 6). Чтобы нанести точку на координатную плоскость, выполните следующие действия:
- Шаг 1. Постройте два перпендикуляра: ось X и ось Y.
- Шаг 2: Начните с начала координат. Переместите 5 единиц вправо по положительной оси X.
- Шаг 3: Переместите на 6 единиц вверх вдоль положительной оси Y.
- Шаг 4: Отметьте точку пересечения. Обозначьте это как (5, 6).
Обратите внимание, что P находится в первом квадранте. Кроме того, это называется положительной координатной плоскостью, поскольку значение обеих координат для любой точки в этом квадранте будет положительным.
Важные точки на координатной плоскости:
- Первый квадрант (+, +), известный как квадрант положительных координат, представлен римской цифрой I.

- Второй квадрант (-, +) представлен римской цифрой II.
- Третий квадрант (-, -) представлен римской цифрой III.
- Четвертый квадрант (+, -) представлен римской цифрой IV.
- Координаты любой точки заключаются в скобки.
Попробуйте решить этот сложный вопрос:
Найдите любые три точки, лежащие в положительной координатной плоскости, для которых абсцисса и ордината равны и неотрицательны.
Темы, связанные с координатной плоскостью
Часто задаваемые вопросы о координатной плоскости
Что такое координатная плоскость в геометрии?
Координатная плоскость — это двумерная плоскость, образованная пересечением оси x, горизонтальной линии и оси y, вертикальной линии.Эти перпендикулярные линии пересекаются друг с другом в точке, называемой началом координат.
Кто изобрел координатную плоскость?
Система координат была изобретена в 17 веке французским математиком Рене Декартом.
Какие части координатной плоскости?
Координатные плоскости включают оси (ось X и ось Y), начало координат (0,0) и четыре квадранта.
Что такое начало на координатной плоскости?
Точка пересечения двух осей координатной плоскости является началом координат координатной плоскости.Координаты начала координат (0, 0).
Что такое координата XY?
Координата XY — это двухмерная плоскость с осями координат, осью X и осью Y, перпендикулярными друг другу.
Как построить координатную плоскость?
Координатная плоскость может быть построена следующим образом:
- Шаг 1. Возьмите лист миллиметровой бумаги или сетки.
- Шаг 2: Проведите горизонтальную линию. Эта линия называется осью x и используется для определения значений x.
- Шаг 3: Проведите вертикальную линию. Эта линия называется осью y и используется для определения значений y. Чтобы показать, что ось на самом деле
Примечание: чтобы показать, что эти оси на самом деле идут вечно в обоих направлениях, используйте маленькие стрелки на каждом конце линии.
Когда бы вы использовали координатную плоскость?
Декартова плоскость координат x и y хорошо работает во многих ситуациях в реальной жизни, например, при планировании размещения различных предметов мебели в комнате, можно нарисовать двумерную сетку, представляющую комнату и, таким образом, подходящую можно использовать единицу измерения.
Как построить график на координатной плоскости?
Любую точку или объект можно изобразить в координатах, используя координаты. Координаты заданных точек могут быть нанесены на график в соответствующих квадрантах координатной плоскости и объединены для образования конкретной формы или объекта.
Сколько квадрантов находится в координатной плоскости?
В координатной плоскости четыре квадранта. Эти четыре квадранта представлены римскими цифрами I, II, III и IV в зависимости от знаков координат.
Как прочитать координатную плоскость?
Мы можем считать координатную плоскость следующим образом:
- Шаг 1: Найдите квадрант, в котором расположена данная точка, посмотрев на знаки ее координат x и y.

- Шаг 2: Считайте количество единиц, в которых точка находится справа / слева от начала координат по оси x, чтобы найти ее координату x.
- Шаг 3: Считайте количество единиц, в которых точка находится вверх / вниз от исходной точки вдоль оси y, чтобы найти ее координату y.
игр, заданий и рабочих листов онлайн
Вы здесь: Главная → Интернет-ресурсы → Геометрия → Координатная плоскостьЭто тщательно подобранный и аннотированный список онлайн-игр, рабочих листов и заданий для координатной плоскости. Подходит для 4-7 классов.
Координатная плоскость
Рабочие листы с координатной сеткой
Учащиеся наносят точки на карту, сообщают координаты точек, строят фигуры из точек, отражают фигуры по оси x или y или перемещают (переводят) их вверх, вниз, влево или вправо.Вы можете настроить рабочие листы, выбрав количество проблем, рабочую область, границу вокруг проблем и многое другое.
/ рабочие листы /  php
php
Билли Баг возвращается на основные игры
Переместите Билли Бага к месту кормления с заданными координатами.
www.primarygames.co.uk/pg2/bug2/bug2.html
Поймай муху
Подождите, пока муха приземлится на координатной сетке, затем введите ее координаты, и лягушка ее съест.
hotmath.ru / hotmath_help / games / ctf / ctf_hotmath.swf
В поисках игры Top Quark
Каждый игрок получает шесть кварков, которые они прячут на сетке. Игроки используют координаты, чтобы найти скрытые кварки своего противника.
education.jlab.org/topquarkgame/
Координатная игра
Вы увидите красный кружок на сетке. Введите координаты и нажмите «Проверить».
www.bgfl.org/bgfl/custom/resources_ftp/
Graphit
Графический инструмент, который отображает как функции, так и упорядоченные пары.
www.shodor. org/interactivate/activities/Graphit/
org/interactivate/activities/Graphit/
Graph Mole
Забавная игра о нанесении точек на координатную плоскость. Постройте точки до того, как крот съест овощи.
funbasedlearning.com/algebra/graphing/default.htm
Вот простой способ подготовить студентов к формальной геометрии. Ключ к геометрии Рабочие тетради знакомят учащихся с широким спектром геометрических открытий, поскольку они делают пошаговые построения. Используя только карандаш, циркуль и линейку, учащиеся начинают с рисования линий, деления углов пополам и воспроизведения сегментов. Позже они создают сложные конструкции, включающие более дюжины шагов, и им предлагается сформулировать свои собственные обобщения. Когда они закончат, учащиеся познакомятся со 134 геометрическими терминами и будут готовы к формальным доказательствам.
=> Узнать больше
Викторина по координатной сетке от ThatQuiz.org
Эта викторина состоит из 10 вопросов и просит либо нанести точку, либо указать координаты данной точки. Вы также можете изменить параметры викторины по своему вкусу.
Вы также можете изменить параметры викторины по своему вкусу.
www.thatquiz.org/tq-7/?-j8-l5-m2kc0-na-p0
Флаер функций
Создание графиков функций, но также позволяет манипулировать
константы и коэффициенты в любой функции, чтобы пользователь мог исследовать эффекты на графике, изменяя эти числа.Отличный инструмент!
www.shodor.org/interactivate/
Скорость изменения линейных функций
Эти великолепные интерактивные графики иллюстрируют концепции линейности и наклона. Пользователи могут перетащить ползунок, чтобы изменить скорость изменения (стоимость минуты использования телефона) и узнать, как изменения этой скорости влияют на линейный график, отображающий накопление (общую стоимость вызовов). Предоставленные обсуждения помогают учителю в том, как их использовать.
www.nctm.org/standards/content.aspx?id=26883
Desmos
Бесплатный онлайн-калькулятор для построения графиков, невероятно простой и интуитивно понятный в использовании, но при этом очень мощный. Вы можете использовать параметры с ползунками, определять свои собственные функции и константы, неравенства графиков, производные и многое другое. Вы можете сохранять, отправлять по электронной почте, распечатывать и встраивать свои графики.
Вы можете использовать параметры с ползунками, определять свои собственные функции и константы, неравенства графиков, производные и многое другое. Вы можете сохранять, отправлять по электронной почте, распечатывать и встраивать свои графики.
www.desmos.com
См. Также раздел программного обеспечения для построения графиков.
Книги
Доктор математики знакомит с геометрией: изучать геометрию легко! Просто спросите доктораМатематика!
Приложение к геометрии средней школы, Доктор математики знакомит с геометрией имеет светлый тон, четкую компоновку и юмористические карикатуры Джессики Уолк-Стэнли. Самое приятное то, что объяснения математических вопросов точны и ясны. Вы найдете ответы на десятки реальных вопросов от студентов, которым нужна была помощь в понимании основных понятий геометрии. В этой книге рассматриваются углы, треугольники, четырехугольники, площадь, периметр, число Пи, части круга, многогранники, площадь поверхности, объем, сети, конгруэнтные преобразования и симметрия. Цена ~ 12 долларов за новый, ~ 6 долларов за б / у.
Цена ~ 12 долларов за новый, ~ 6 долларов за б / у.
www.amazon.com
Гарольд Джейкобс Геометрия
Популярный выбор геометрии среди школьников на дому, хорошо написанный. Также прочтите мой обзор.
Геометрия: управляемый запрос
Отличный выбор для школьной геометрии. Я написал подробный обзор этой книги и приложения к ней Home Study Companion — Geometry , последнее написано Дэвидом Чендлером.
Как построить точки на координатной плоскости
Координатная плоскость — это двумерная плоскость с осью x (горизонтальной) и осью y (вертикальной).Эти оси пересекаются, образуя перпендикулярную линию, разделяющую координатную плоскость на четыре квадранта.
Как использовать координатную плоскость
Вы используете координатные плоскости для нанесения точек на графики. Каждый квадрант написан римскими цифрами и расположен в разных местах на плоскости. Например, первый квадрант (Квадрант I) находится справа от вертикальной оси и над горизонтальной осью:
Изображение предоставлено: Desmos
Когда вас попросят построить точки на графике, вам будут предложены упорядоченные пары, записанные в круглых скобках. Например, если точка имеет значение x, равное 1, и значение y, равное -2, она будет записана как (1, -2). Первое число представляет координату x, точку на горизонтальной оси, а второе число представляет координату y, точку на вертикальной оси.
Например, если точка имеет значение x, равное 1, и значение y, равное -2, она будет записана как (1, -2). Первое число представляет координату x, точку на горизонтальной оси, а второе число представляет координату y, точку на вертикальной оси.
Квадрант, в котором находится каждая точка, зависит от того, являются ли координаты точки отрицательными или положительными числами. Вот разбивка того, как классифицируется каждый квадрант:
Квадрант I: Положительные значения x и y
Квадрант II: Положительные значения y, отрицательные значения x
Квадрант III: Отрицательные значения x и y
Квадрант IV: Положительные значения x, отрицательные значения y
Давайте определим квадранты каждой заданной точки, в которых сначала указано значение x, а второе — значение y:
Пункт A: (3, 2)
Поскольку эта точка имеет положительное значение x, равное 3, и положительное значение y, равное 2, она принадлежит квадранту I.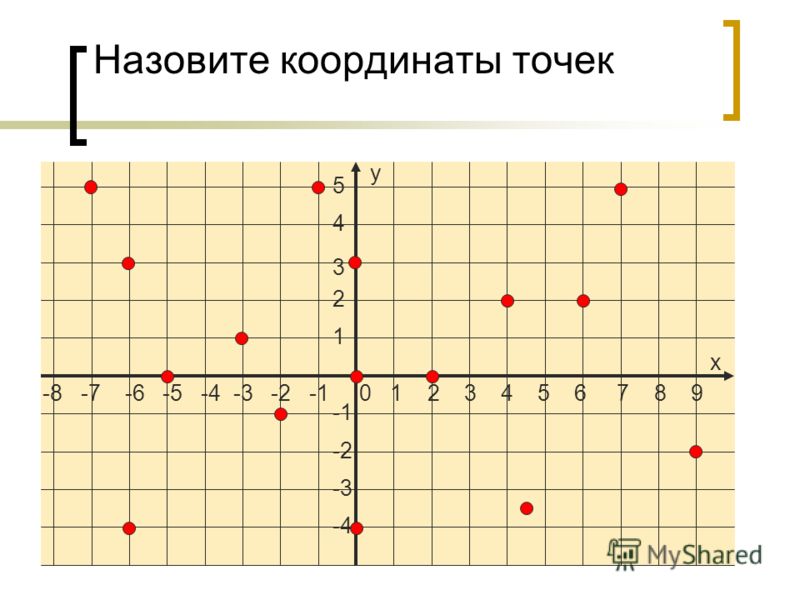
Пункт B: (-2, 2)
Значение y положительное, но значение x отрицательное, поэтому эта точка перейдет в Квадрант II.
Точка C: (-2, -1)
Оба значения x и y отрицательны, поэтому эта точка находится в квадранте III.
Пункт D: (3, -1)
Значение x положительно, а значение y отрицательно, поэтому эта точка находится в квадранте IV.
Изображение предоставлено: Desmos
Когда вы используете координатную плоскость?
Каждый раз, когда вы наносите точки на отрицательную или положительную ось x или y, вы используете координатную плоскость.Когда вы знаете, как наносить точки и определять соответствующие им квадранты, вы можете начать рисовать линейные уравнения, экспоненциальные значения и многое другое. Обучение использованию координатной плоскости — одно из самых полезных и фундаментальных понятий в математике.
Дополнительные домашние задания по математике
Координатная плоскость
Пустые координатные плоскости на этой странице включают варианты с метками на оси или на краю сетки, а также версии с метками квадрантов. Вы можете найти полные 4-х квадрантные координатные плоскости, а также просто пустые 1-квадрантные координатные плоскости в настройках макетов для решения нескольких домашних задач на одной странице.
Вы можете найти полные 4-х квадрантные координатные плоскости, а также просто пустые 1-квадрантные координатные плоскости в настройках макетов для решения нескольких домашних задач на одной странице.
Ярлыки квадрантов координатной плоскости
8 рабочих листов координатной плоскости 424
На этих печатаемых координатных плоскостях каждый квадрант помечен более светлым фоновым текстом в сетке. Запутались со всеми этими этикетками с римскими цифрами I, II, II, IV? Вы будете знать, где они.
Метки квадрантов координатной плоскостиПустые рабочие страницы координатной плоскости
28 Рабочих листов координатной плоскости 425
Распечатайте эти пустые страницы координат с блоками имени и даты, когда у вас есть уравнения для построения графиков для домашнего задания! Домашнее задание, которое вы сдадите на урок геометрии или алгебры, будет выглядеть академически грамотно.
Пустые рабочие страницы координатной плоскостиКоординатная плоскость без этикеток
8 Таблицы координатной плоскости 426
Печатные координатные плоскости в дюймах и метрических размерах в нескольких размерах, отлично подходят для диаграмм рассеяния, построения уравнений, геометрических задач или других подобных математических задач. Это полные четырехквадрантные координатные плоскости, пустые без нумерации осей. Возвращаетесь к 7 классу геометрии? Это страница миллиметровой бумаги для вас. Стандартные размеры сетки 1/4 дюйма, 1/5 дюйма, 1/8 дюйма и 1/10 дюйма.Метрические размеры с сеткой 1 сантиметр, 5 миллиметров, 2,5 миллиметра и 2 миллиметра.
Это полные четырехквадрантные координатные плоскости, пустые без нумерации осей. Возвращаетесь к 7 классу геометрии? Это страница миллиметровой бумаги для вас. Стандартные размеры сетки 1/4 дюйма, 1/5 дюйма, 1/8 дюйма и 1/10 дюйма.Метрические размеры с сеткой 1 сантиметр, 5 миллиметров, 2,5 миллиметра и 2 миллиметра.
Координатная плоскость с помеченной осью
8 рабочих листов координатной плоскости 427
Печатные координатные плоскости в дюймах и метрических размерах различных размеров, отлично подходят для построения уравнений, геометрических задач или других подобных математических задач. Это полные четырехквадрантные графы. Эти координатные плоскости имеют метки непосредственно вдоль оси x и оси y.
Координатная плоскость с помеченной осьюКоординатная плоскость с маркированными краями
8 Таблицы координатной плоскости 428
Печатные координатные плоскости в дюймах и метрических размерах различных размеров, отлично подходят для построения уравнений, геометрических задач или других подобных математических задач. Это полные четырехквадрантные графы. Эти координатные плоскости имеют метки оси x и оси y вдоль внешнего края страницы.
Это полные четырехквадрантные графы. Эти координатные плоскости имеют метки оси x и оси y вдоль внешнего края страницы.
Квадрант координатной плоскости 1
24 Таблицы координатной плоскости 429
Эта печатаемая координатная плоскость с показанным только квадрантом 1 отлично подходит для ознакомления с действиями по построению графиков в 3-м, 4-м или 5-м классе или в любое время до введения отрицательных чисел.
Квадрант плоскости координат 1Пустые страницы с координатной плоскостью для печати
Коллекция координатных плоскостей в формате PDF для печати на этой странице содержит ряд различных макетов, которые должны соответствовать потребностям большинства классов средней или старшей школы по алгебре. Координатные плоскости имеют размеры в обычных или метрических единицах, как и на чистой миллиметровой бумаге на сайте.
Существуют версии координатной плоскости с метками осей и без них, а также версии, в которых номера квадрантов отображаются светлым текстом на заднем плане каждого квадранта. Существуют также версии координатной плоскости с метками на краях, а не на каждой оси, что иногда может немного облегчить построение уравнений.
Существуют также версии координатной плоскости с метками на краях, а не на каждой оси, что иногда может немного облегчить построение уравнений.
Что такое квадранты координатной плоскости?
Поскольку координатная плоскость естественным образом разделена осью x и осью y, она создает четыре прямоугольные области, которые называются квадрантами. Каждый квадрант соответствует области, содержащей точки с одинаковым положительным или отрицательным знаком. Например, по соглашению верхний правый квадрант называется квадрантом 1 и содержит только точки, которые имеют как положительные значения x, так и положительные значения y.Распределение знаков координатных точек и соответствующих им квадрантов показано в таблице ниже …
| Квадрант | Знаки координат |
|---|---|
| I | (+, +) |
| II | (-, +) |
| III | (-, -) | IV | (+, -) |
Квадрант 1 Координатные плоскости
Квадрант 1 координатной плоскости имеет дело с положительными значениями оси x и оси y, и часто ученики в первую очередь начинают рисовать линейные функции.
 02.2021
02.2021 03.2021
03.2021 0506.5.2
0506.5.2 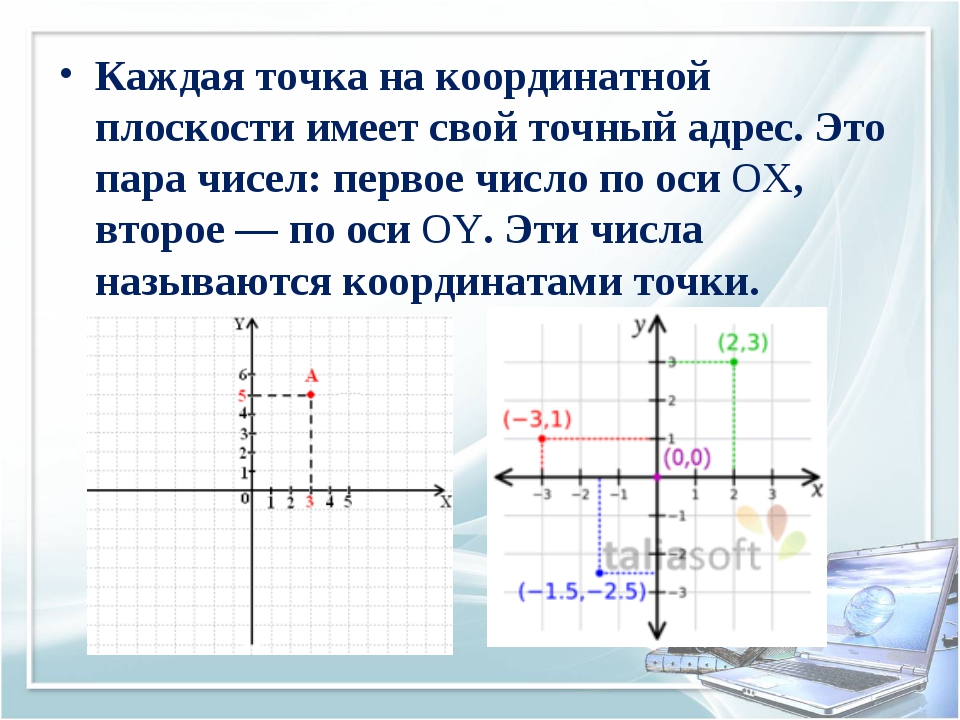
 Если страница не загружается быстро, нажмите Нетерпеливый? в правом нижнем углу страницы.]
Если страница не загружается быстро, нажмите Нетерпеливый? в правом нижнем углу страницы.]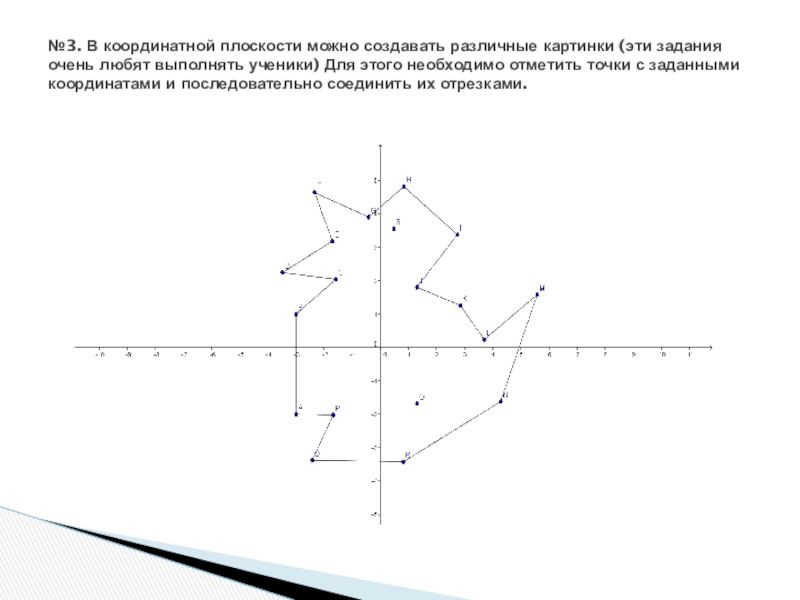
 Чтобы победить, путь не должен пересекать мину.
Чтобы победить, путь не должен пересекать мину. 

Ваш комментарий будет первым