Онлайн функция график: Построение графика функции онлайн

Как построить график функции y=f(x+m)+n, если известен график функции y=f(x) (28 слайдов)

Нажмите для просмотра

Читать онлайн!

Слайд 1

Как построить график функции y=f(x+m)+n, если известен график функции y=f(x)

Слайд 2

Какая из формул задаёт:
— прямую пропорциональность; -обратную пропорциональность; -линейную функцию, график которой проходит через начало координат.
2)
1)

Слайд 3

На одном из рисунков изображена парабола. Укажите этот рисунок.

Слайд 4

На одном из рисунков изображена гипербола. Укажите этот рисунок.

Слайд 5

Соединить линиями соответствующие названия графиков функции:
гипербола
прямая
парабола

Слайд 6

Соединить линиями соответствующие названия графиков функции:
гипербола
прямая
парабола

Слайд 7

Повторим изученное
У
Опишите свойства функции, используя график.
-1
Х
-2

Слайд 8

у
у= х²+ 3
Функция у = х² + 3; вершина (0; 3)

у= х²
Функция у = х²; вершина (0; 0)
х
Сдвиг графика функции у = х² вдоль оси ОУ на 3 единицы вверх.

Слайд 9

у
Функция у = х²; вершина (0; 0)
у= х²
Сдвиг графика функции у = х² вдоль оси ОУ на 5 единиц вниз.
х
у= х²­ 5
— 5
Функция у = х² — 5; вершина (0; -5)

Слайд 10

Построение графиков функций y = f (x) и y = f (x + a)
Сдвиг вдоль оси абсцисс
y=(x+3)²
y=x²
y=(x-3)²

Слайд 11

Построение графиков функций y = f (x) и y = f (x) +n
Сдвиг вдоль оси ординат
y=x²+3
y=x²
y=x²-3

Слайд 12

График функции График функции y = f(x + m) получается параллельным переносом графика функции y=f(x) вдоль оси х на |m| единиц масштаба влево, если m > 0 и вправо, если m

Слайд 13

График функции График функции y = f(x)+n получается параллельным переносом графика функции y=f(x) вдоль оси y на |n| единиц масштаба вверх, если n > 0 и вниз, если n

Слайд 14

Самостоятельная работа. №1. Постройте графики функций. Ответьте на вопросы.
Запишите названия графиков____________________________________________ Какие изменения вы заметили у графика второй функции относительно базового графика?_________________________

Слайд 15

№2 Постройте графики функций. Ответьте на вопросы.
Запишите названия графиков_______________________ Какие изменения вы заметили у графика второй функции относительно основного графика?_____________

Слайд 16

Выводы: основные преобразования графиков элементарных функций:
Сжатие и растяжение графика вдоль оси y у=k f(x). Преобразование симметрии относительно оси x у = — f(x) Сдвиг вдоль оси абсцисс y = f (x + a) Сдвиг вдоль оси ординат y = f (x) +n

Слайд 17

вправо
вниз
вправо
вверх

Слайд 18

На одном из рисунков изображен график функции Укажите номер этого рисунка.
На каком рисунке изображён график функции y= —

Слайд 19

Задайте формулой функцию по графику, изображенному на рисунке.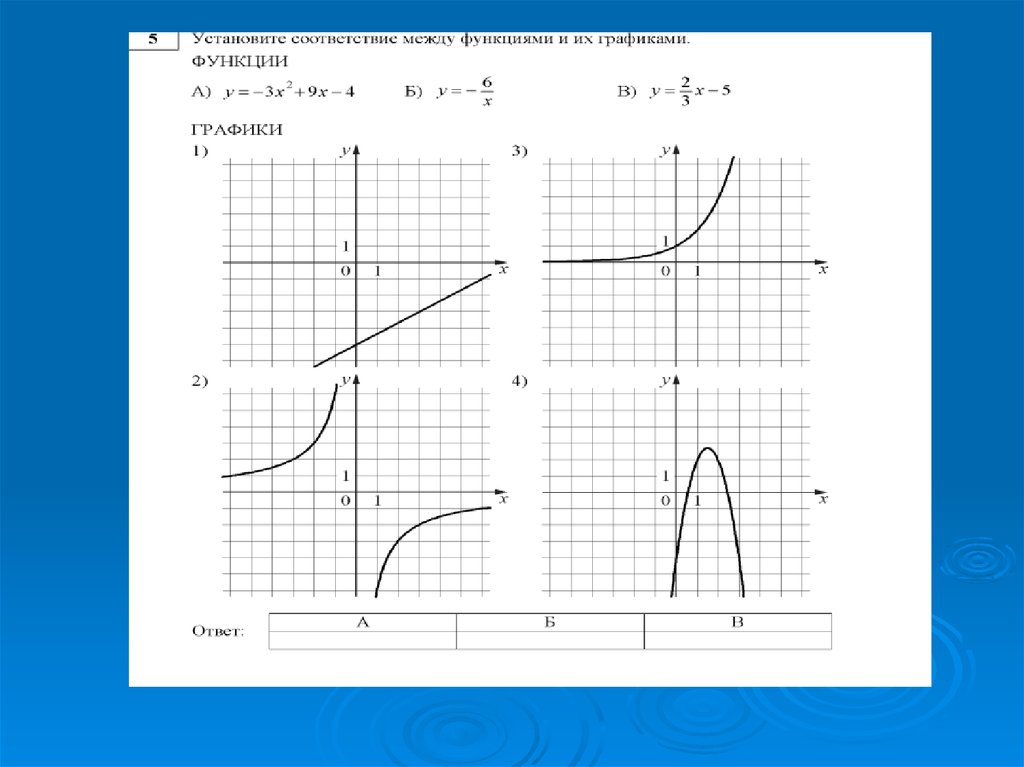

Слайд 20

Слайд 21

y
Алгоритм 1.
у=4
1. Построить график функции y=f(x)

4 ед.
2. Осуществить параллельный перенос графика y=f(x) вдоль оси х на |m| единиц масштаба влево, если m>0, и вправо, если mx
5 ед.
3. Осуществить параллельный перенос полученного на втором шаге графика вдоль оси у на |n| единиц масштаба вверх, если n>0, и вниз, если nХ=5

Слайд 22

y
Алгоритм 2.
у=4
1. Перейти к вспомогательной системе координат, проведя (пунктиром) вспомогательные прямые х=-m, y=n, т.е. выбрав в качестве начала новой системы координат точку (-m,n).
4 ед.
x
5 ед.
2. К новой системе координат привязать график функции y=f(x).
Х=5

Слайд 23

y
-4
x
-5

Слайд 24

y
-4
x

Слайд 25

y
x
-4

Слайд 26

Готовимся к экзамену!
Ответ: 2

Слайд 27

Готовимся к экзамену!

Ответ: 3

Слайд 28

^ Наверх

X

Благодарим за оценку!

Мы будем признательны, если Вы так же поделитесь этой презентацией со своими друзьями и подписчиками.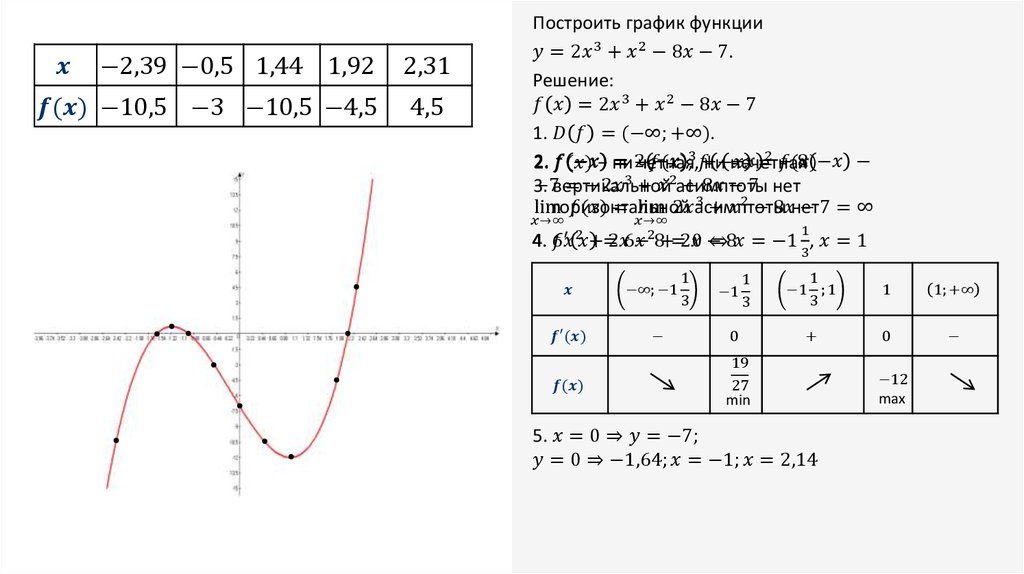

График функции — MathCracker.com

Алгебра Учебники

---

График функции — это набор упорядоченных пар \((x,y)\). Или график функции — это концептуализация, которую мы делаем набором пар \((x,y)\) в системе координат. Я говорю, что это концептуализация, потому что то, как мы представляем граф, в некоторой степени является оптической иллюзией.

Почему я так говорю? Ну посмотрите. Что вы думаете, когда я говорю «график». Проверьте цифру перед.

Итак, это график. Набор пар \((x, y)\), или, как мы их еще называем, точек. Ниже выделен конкретный момент, посмотрите

Уловка, или визуальная иллюзия, заключается в том, что точка теоретически не имеет размеров (ни ширины, ни длины). Итак, эта «кривая», которую мы рисуем для представления графика, это своего рода удобный способ представления графика, но мы обманываем нас, потому что это представление имеет кривую, имеющую толщину.

Итак, это не для вашего парада, это просто для того, чтобы прояснить, что то, что вы понимаете под графиком, это скорее

представление графа, который удобен и заслуживает доверия.

Графики, связанные с функциями

Один действительно простой способ определить график — использовать функцию \(f(x)\). Действительно, график, определяемый функцией \(f(x)\), представляет собой набор всех точек \((x, f(x))\) для \(x \in D\), где \(D\) — это область определения функции \(f\).

Представление такое же, как и на предыдущих графиках, только теперь мы делаем следующее:

В этом случае наиболее очевидное различие состоит в том, что второй компонент пары \((x,y)\) — это не просто какое-либо значение \(y\). Второй компонент — \(f(x)\), поэтому он однозначно определяется \(x\). 2\).

Понятие гладкости функции формально рассматривается в исчислении с понятием непрерывной функции. Но не вдаваясь в подробности, мы можем сказать, что на данный момент мы будем думать, что непрерывная функция — это функция, имеющая «гладкий» график, а прерывистая функция — это функция, которая не является гладкой или имеет «скачки». ".

ПРИМЕР 2

Функция \(f(x) = sin(x)\) непрерывна?

ОТВЕЧАТЬ:

Что ж, опять же, для проверки нам потребуется формальный анализ непрерывности. Но в свете приведенного выше неформального определения давайте проверим его график. Компьютер дает нам следующее:

Я бы сказал, что приведенный выше график выглядит очень гладким, без каких-либо скачков, поэтому, используя наше наивное определение, я бы сказал, что \(f(x) = \sin x\) непрерывно.

ПРИМЕР 3

Функция \( f\left( x \right)=\left\{ \begin{array}{cc}-1 &\,\,\,\,\text{for } x\le 1 \\ \\ x & \,\,\,\,\,\,\text{for }x>1 \\ \end{array} \right.\) непрерывна?

ОТВЕЧАТЬ:

Чтобы ответить на вопрос, нам нужно построить график. Компьютер дает нам следующее:

Обратите внимание, что есть скачок в точке \(x = 1\), поэтому я бы сказал, что на графике выше есть скачок, и, следовательно, эта функция является прерывистой.

---

Подробнее о графиках

Использование графиков для представления функции может сыграть решающую роль для понимания поведения функции.

Существует достаточно аналитических инструментов (вычислений), чтобы понять поведение функции \(f(x)\) без необходимости ее построения. Но очень практично видеть график, потому что это действительно быстрый способ получить представление о том, что делает функция. 2 = 1\), которое, как мы уже знаем, определяет отношение, а не функцию.

Если вам нужно построить график, попробуйте график функций чтобы получить хорошее представление о том, как ведет себя функция.

---

Учебники по алгебре Непрерывные графики Разрывные графы График График функции

509 Превышен предел пропускной способности

509 Превышен предел пропускной способности Сервер временно не может обслуживать ваши запрос из-за того, что владелец сайта достиг своего ограничение пропускной способности.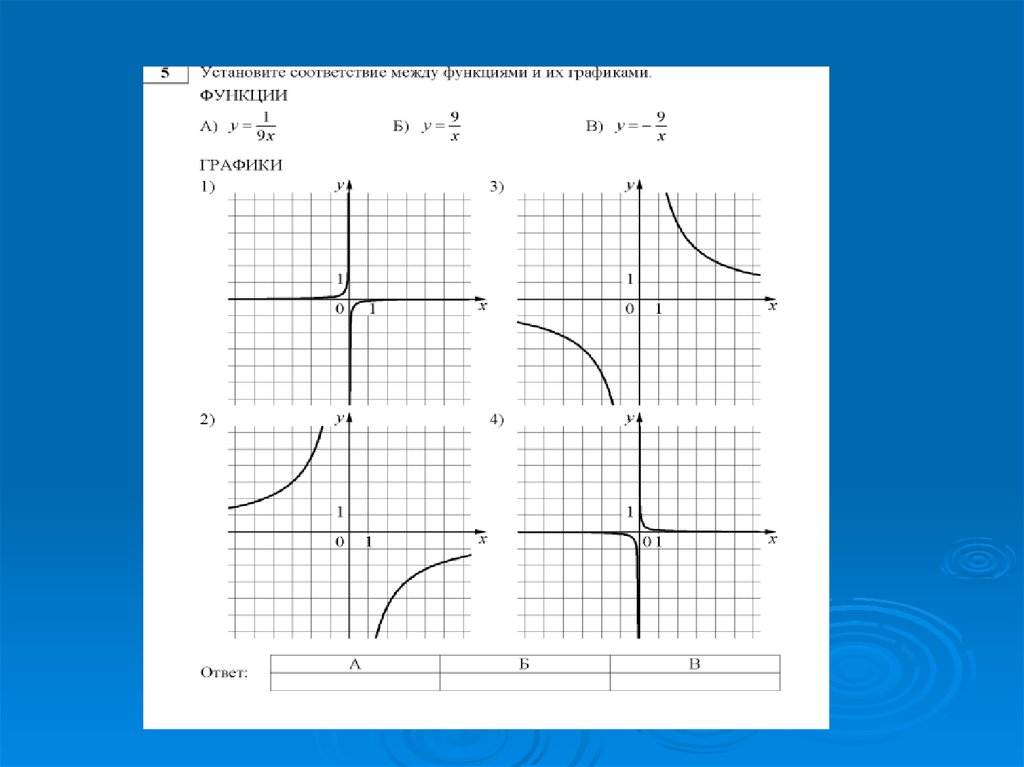 Пожалуйста, попробуйте позже.

Онлайн-инструмент для чтения значений изображений графиков и сохранения их в формате CSV/JSON

Используйте онлайн-инструмент для чтения графиков для извлечения значений из изображений графиков . Для 2D-графиков используйте 2D-ридер

1) Выберите изображение в формате png, jpg или gif и нажмите « Перейти ».
2) Измените размер синего прямоугольника, чтобы установить линейку для масштабирования оси. Установите значения для масштабирования по осям X и Y соответственно.
3) Дважды щелкните, чтобы вставить фиксированные точки кривой. Щелкните правой кнопкой мыши, чтобы удалить точки (на планшете долго трогать).
4) Нажмите « Создать кривую », чтобы получить образец кривой. Используйте элементы управления ниже, чтобы перерисовать вывод.
5) Прокрутите вниз, чтобы увидеть дополнительные параметры и просмотреть сгенерированные данные CSV.

Мы приветствуем обратную связь. В настоящее время собираю идеи для следующего обновления версии. Спасибо!

Выберите изображение

0,0

Настройки осей (обозначены синим прямоугольником)

y-высокий:

г-младший:

Логарифмическая ось Y (бета)

Масштабирование по оси X (для дат используйте формат: ГГГГММДД)

х-низкий:

х-высокий:

Логарифмическая ось X (бета)

Шаг по оси X Количество интервалов (не дат)

значение:

Выборка кривой (с использованием фиксированных точек)

точек интерполяция

Линейный

Сплайн