Функции и ее графики — презентация онлайн
Похожие презентации:
Функции и их графики. Определение графика функции
Функция. Графики функций
Функция. Графики функций
Готовимся к ГИА. Элементарные функции
Функции и графики
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Касательная к графику функции
Функция у=х2 и её график
Функция и её свойства
Функция у=кх², ее свойства и график
1. Функция
Графики функций2. Виды функций
ЛинейнаяПрямая пропорциональность
Обратная пропорциональность
Квадратичная
Кубическая
Квадратный корень
Модуль
Преобразование графиков
3. Линейная функция
у = kх + bу = 2х +1
график – прямая
у
х 0 1
у 1 3
0
х
4. Прямая пропорциональность
у = kх график – прямая, проходящаячерез (0;0)
у
у = 3х
х 0 1
у 0 3
0
х
5.
 Обратная пропорциональностьk
Обратная пропорциональностьkу= x
4
у= x
x=0
х 4 2 1 -4 -2 -1
у 1 2 4 -1 -2 -4
График — гипербола
у
0
х
6. Квадратичная функция
у = ах2у=
а=0
х2
график – парабола
у
х -2 -1 0 1 2
у 4 1 0 1 4
0
х
Преобразование симметрии
относительно оси x:
f(x) ―>- f(x)
y=x²
7
8. Кубическая функция
у = ах3 а = 0 график – кубическаяпарабола
у
3
у=х
х -2 -1 0 1 2
у -8 -1 0 1 8
0
х
9. Квадратный корень
у= хграфик – ветвь параболы
в первой четверти
у
х 0 4 9
у 0 2 3
0
х
10. Модуль
у= х{
х =
x, если х > 0
-x, если х < 0
у
х 0 3 -3
у 0 3 3
0
х
Построение графика
у
у = 2х + 5
7
Построить график
функции
5
у = 2х + 5
Линейная функция
График – прямая
3
1
-6 -5 -4 -3 -2 -1-1 0
-3
1 2
3 4
х
х
у
5 6
0
5
-4
-3
-5
содержание
7
у = -2х + 3
у
у = 1,5х -2
7
5
5
3
3
1
1
х
у
х
-6 -5 -4 -3 -2 -1-1 0 1 2 3 4 5 6 -6 -5 -4 -3 -2 -1-1 0 1 2 3 4 5 6
(0; 3)
-3
-3
-5
-5
(0; -2)
График функции у = kх + b проходит через точку …(0;
b)
k – угловой коэффициент
содержание
4
3
2
20:08
13
Построение графиков функций
y = f (x) и y = f (x + a)
Сдвиг вдоль оси абсцисс
y=(x+3)²
y=x²
y=(x-3)²
14
Построение графиков функций
y = f (x) и y = f (x) +n
Сдвиг вдоль оси ординат
y=x²
y=x²+3
y=x²-3
15
Преобразование графиков
Вершина параболы:
20:08
17
20:08
18
20:08
19
20.
 Установите соответствие между формулой и названием графикаА) Прямая;
Установите соответствие между формулой и названием графикаА) Прямая;Б) Ветвь параболы;
В) Гипербола;
Г) Парабола;
Д) Прямая,
проходящая через
начало координат
Запишите название каждой функции
21. Самопроверка
1) Квадратичнаяфункция
2) Прямая
пропорциональност
ь;
3) Обратная
пропорциональност
ь;
4) Линейная функция;
5) Квадратный корень
из х;
6) Линейная функция
23. Домашнее задание: Тест по теме «Функции и их графики»
English Русский Правила
Сложение графиков функций
СЛОЖЕНИЕ ГРАФИКОВ
Иногда функция, график которой должен быть построен, представляется как сумма двух или нескольких простейших функций. Графики простейших функций уже известны и без труда могут быть построены. В этом случае, рассмотрим способ сложения графиков.
Алгоритм. 1) Строим графики функций каждого слагаемого
2) Ординаты второго графика откладывают от соответствующих
ординат первого графика (можно пользоваться измерительным
циркулем).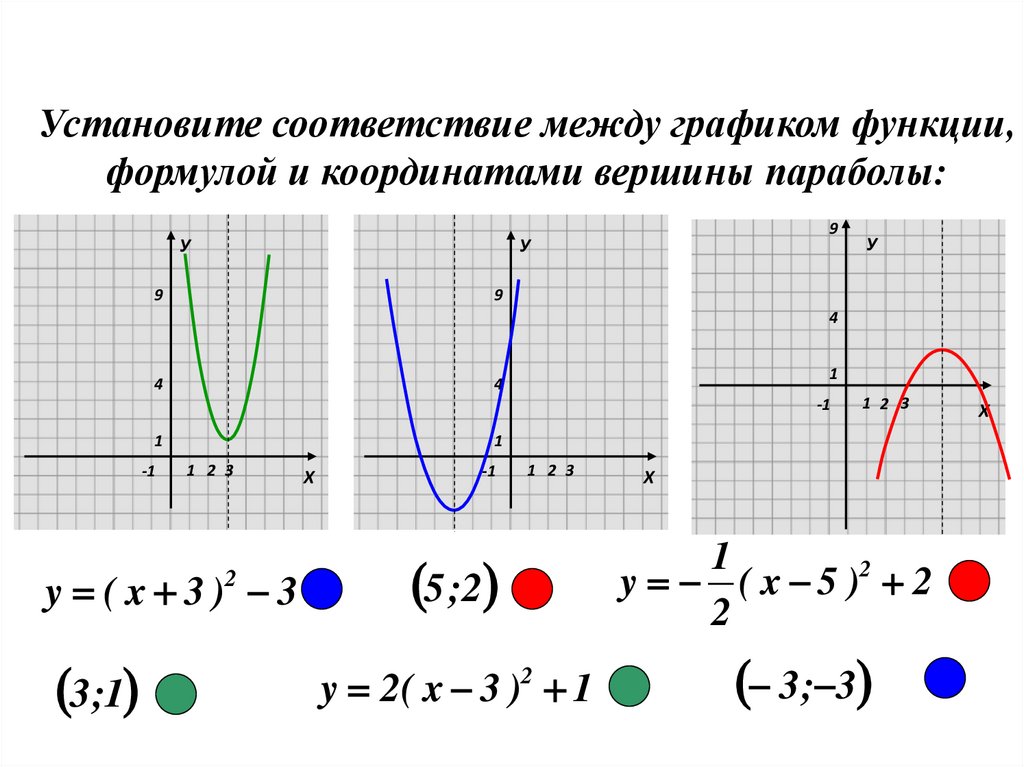
Пример 1. Построить график функции
Представим эту функцию в виде суммы двух функций: , где
. На одной системе координат строим графики этих функций.
Затем, каждую точку графика функции смещаем параллельно оси Оу на расстояние, равное ординате графика функции в соответствующей абсциссе. То есть, при ордината графика функции равна 2, а ордината графика функции равна 0, поэтому ставим точку . Далее, при ордината графика функции равна 0, а ордината графика функции равна 1, поэтому ставим точку . При ордината графика функции равна -2, а ордината графика функции равна 8, поэтому ставим точку . При ордината графика функции равна 4, а ордината графика функции равна -1, поэтому ставим точку . И так далее. Получаем график функции
Для того, чтобы график был как можно точнее, необходимо брать значимые точки, т.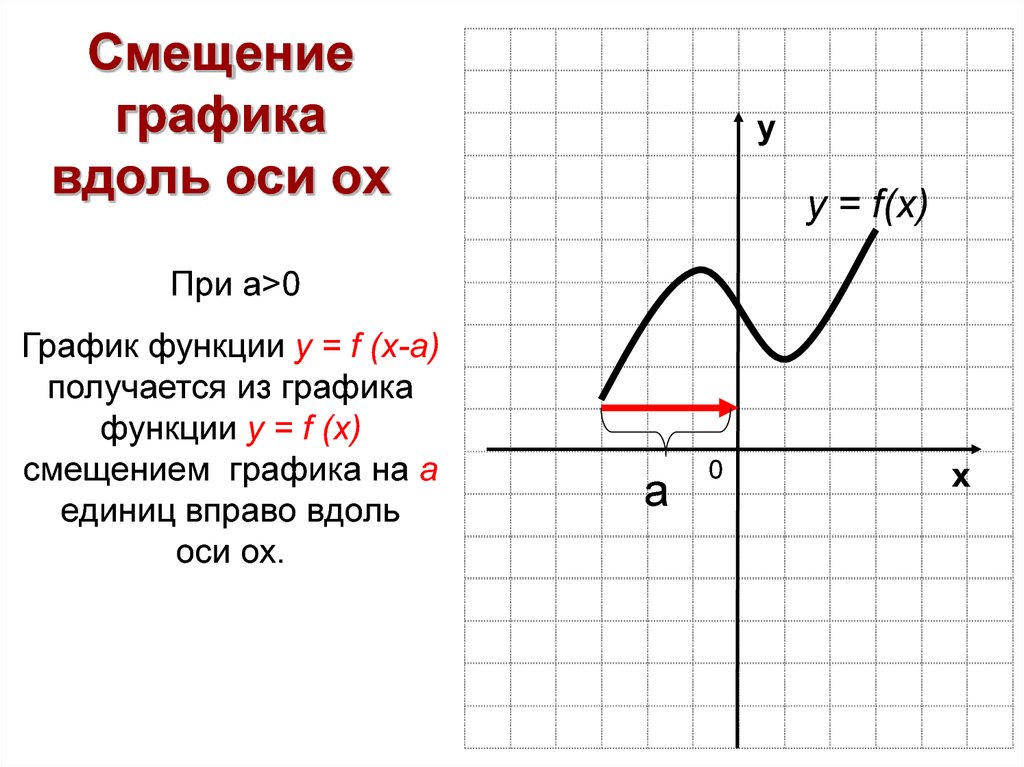 е. те, в которых происходит значимое событие для графика (пересечение с осями, точки перегиба, или точки, в которых график меняет своё направление).
е. те, в которых происходит значимое событие для графика (пересечение с осями, точки перегиба, или точки, в которых график меняет своё направление).
Определим свойства функции
Область определения:
Область значений:
Чётность функции:
Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
Точка пересечения с осью Оу:
Найдём точки экстремума:
.
.
Найдём экстремумы функции:
.
.
Функция возрастает при .
Функция убывает при .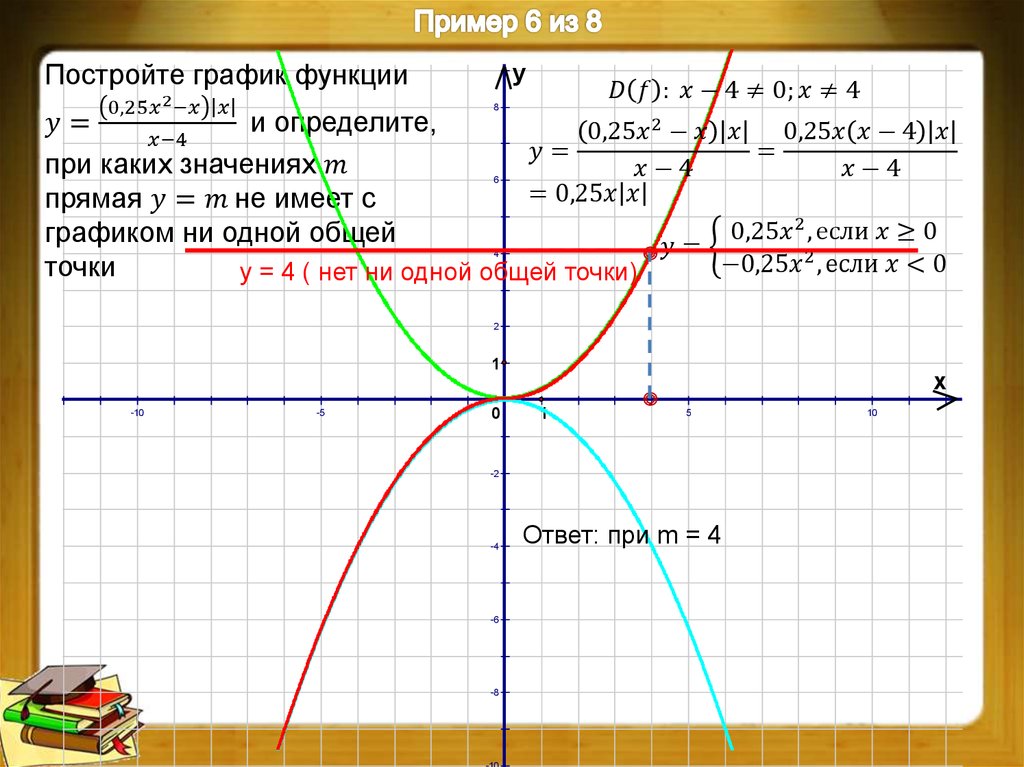
Пример 2. Построить график функции
Представим эту функцию в виде суммы двух функций: , где
. На одной системе координат строим графики этих функций.
Производим аналогичные действия:
И так далее…
Получаем график функции .
Определим свойства функции
Область определения:
Область значений:
Чётность функции:
Значит, функция не является ни чётной, ни нечётной и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
Точка пересечения с осью Оу:
Точки пересечения с осью Ох:
Значит, точки пересечения с осью Ох —
Найдём точки экстремума:
. .
.
Найдём экстремумы функции:
.
Функция убывает при .Функция возрастает при .
Пример 3. Построить график функции
Представим эту функцию в виде суммы двух функций: , где
. На одной системе координат строим графики этих функций. Затем производим сложение.
Определим свойства функции
Область определения:
Область значений:
Чётность функции: Значит, функция является чётной, и её график симметричен относительно оси Оу.
Точка пересечения с осью Оу:
Точки пересечения с осью Ох:
Значит, точки пересечения с осью Ох —
Найдём точки экстремума:
. .
.
Найдём экстремумы функции:
.
Функция возрастает при .
Функция убывает при .
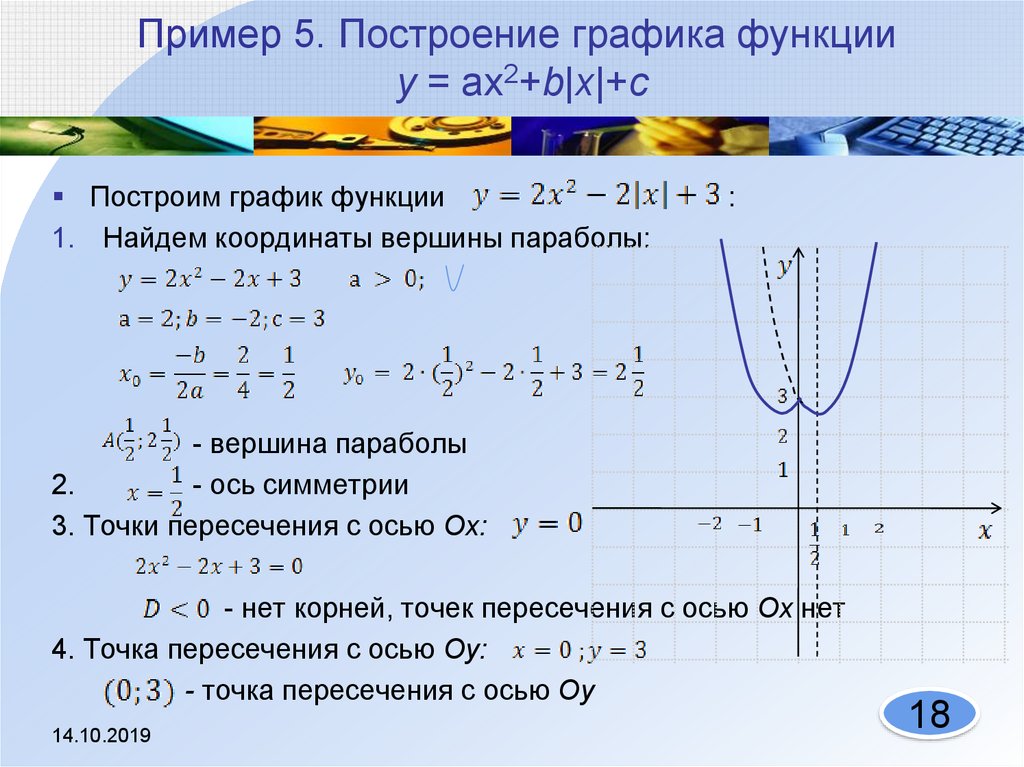
Пример 4. Построить график функции
Представим эту функцию в виде суммы двух функций: , где
. На одной системе координат строим графики этих функций. Затем производим сложение.
Аналогичные вычисления для отрицательного аргумента. Получаем график функции
Определим свойства функции
Область определения:
Область значений:
Чётность функции: Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.

Точка пересечения с осью Оу:
Точки пересечения с осью Ох:
. Значит, точки пересечения с осью Ох —
Найдём точки экстремума:
. .
Найдём экстремумы функции:
.
Функция возрастает при .
Функция убывает при .
Особый случай представляется при сочетании обратной пропорциональности с каким-нибудь другим графиком. Приведём такой пример.
Пример 5. Построить график функции
Представим эту функцию в виде суммы двух функций: , где
. На одной системе координат строим графики этих функций.
Что происходит? Так как график обратной пропорциональности не пересекает оси координат, то он и будет исходным.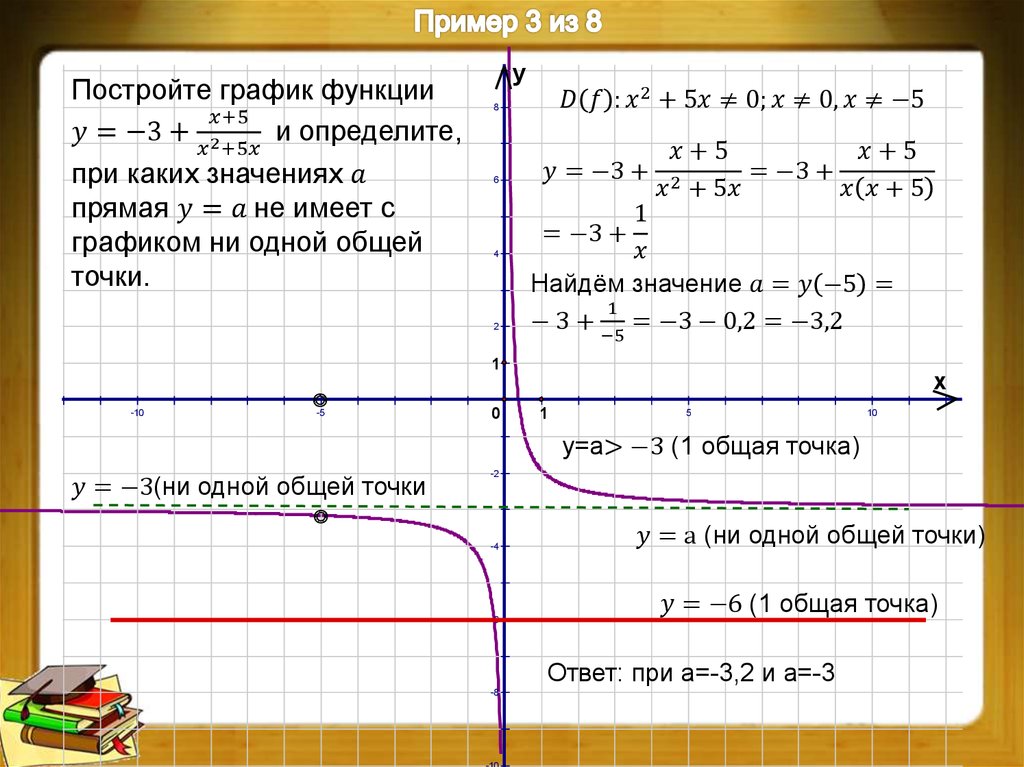 К его ординатам будем прибавлять ординаты графика функции .
К его ординатам будем прибавлять ординаты графика функции .
График функции-суммы при значениях х, бесконечно близких к 0, практически сливается с графиком функции , располагаясь чуть выше его. А при очень больших значениях график функции-суммы почти сливается с графиком , располагаясь чуть выше его при положительных х, и чуть ниже при отрицательных х.
Определим свойства функции
Область определения:
Область значений:
Чётность функции:
Значит, функция не является ни чётной, ни нечётной, и её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
Точек пересечения с осью Оу нет.
Точки пересечения с осью Ох:
Значит, точка пересечения с осью Ох
Найдём точки экстремума:
;
Найдём экстремумы функции:
.
Функция возрастает при .
Функция убывает при .
4
Онлайн-инструмент для чтения значений изображений графиков и сохранения их в формате CSV/JSON
Используйте онлайн-инструмент для чтения графиков для извлечения значений из изображений графиков . Для 2D-графиков используйте 2D-ридер
1) Выберите изображение в формате png, jpg или gif и нажмите « Перейти ».
2) Измените размер синего прямоугольника, чтобы установить линейку для масштабирования оси. Установите значения для масштабирования по осям X и Y
соответственно.
4) Нажмите « Создать кривую », чтобы получить образец кривой.
 Используйте элементы управления ниже, чтобы перерисовать вывод.
Используйте элементы управления ниже, чтобы перерисовать вывод. 5) Прокрутите вниз, чтобы просмотреть дополнительные параметры и просмотреть сгенерированные данные CSV.
[2023.01.12] Новая версия graphreaderV2 готова к тестированию. На данный момент есть еще несколько ошибок. Обратная связь приветствуется.
Выберите изображение
0,0
Настройки осей (обозначены синим прямоугольником)
y-высокий:
г-младшая:
Логарифмическая ось Y (бета)
Масштабирование по оси X (для дат используйте формат: ГГГГММДД)
х-низкий:
х-высокий:
Логарифмическая ось X (бета)Шаг по оси X Количество интервалов (не дат)
значение:
Выборка кривой (с использованием фиксированных точек)
Точка интерполяция
Линейный
Сплайн
Start and end-points will determine the x-range.»> Машина оценка
Стандарт
Плавные изгибы
Крутые кривые
Постобработка
Нет
Средний
Скользящее среднее
Линейная регрессия, порядок:
Скользящее среднее, длина:
Сплайновая аппроксимация, порядок:
Вывод данных
Точность, вывод десятичных знаков:
Разделитель CSV: ,;табуляция
Показать данные в новом окне (Blob)Вставленные фиксированные точки
Выборочная кривая
Кривая после обработки
Поле выходных данных
Как график функций на TI-84 плюс
: Джефф МакКалла и C. C. Edwards и
C. Edwards и
Обновлено: 10-19-2022 2
от книги: 10-19-2022
1 от книги: 10-19-2022 2
1 от книги: 10-19-2022
1. TI-84 Plus CE Графический калькулятор для чайников
Графический калькулятор TI-84 Plus CE для чайников
Обзорная книга Купить на Amazon
После того, как вы ввели функции в калькулятор TI-84 Plus и отформатировали график, вы почти готовы начать увлекательное построение графиков. Как только вы освоите построение графиков, вам не нужно будет выполнять все эти шаги.Отключение графиков статистики (при необходимости)
Верхняя строка в редакторе Y= сообщает вам о графическом статусе графиков статистики. Если Plot1 , Plot2 или Plot3 выделен, тогда этот график статистики будет построен вместе с графиком ваших функций.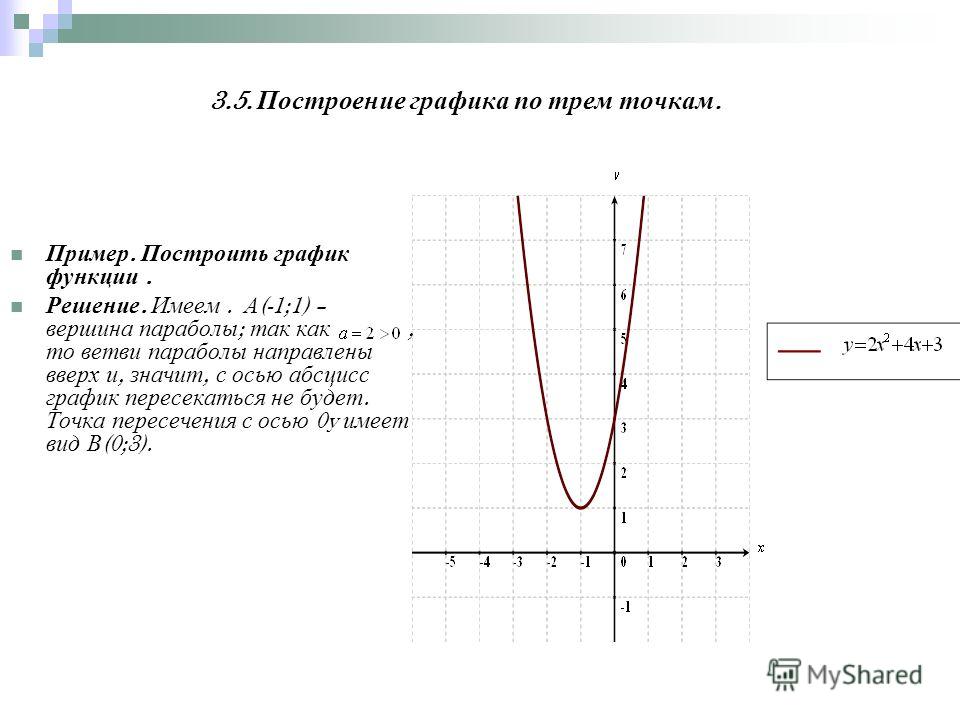 Если он не выделен, он не будет отображаться на графике. На первом экране выделено Plot1 , и оно будет отображаться вместе с функциями в редакторе Y=.
Если он не выделен, он не будет отображаться на графике. На первом экране выделено Plot1 , и оно будет отображаться вместе с функциями в редакторе Y=.Чтобы отключить выделенный график статистики в редакторе Y=, используйте клавиши
, чтобы поместить курсор на выделенный график статистики, а затем нажмите [ENTER]. Смотрите второй экран. Тот же самый процесс используется для повторного выделения графика статистики, чтобы позднее построить его график.
Когда вы строите графики функций, графики статистики могут доставлять неудобства, если они включены, когда вы на самом деле не хотите, чтобы они отображались на графике. Наиболее распространенным симптомом этой проблемы является сообщение об ошибке ОШИБКА: НЕДОПУСТИМОЕ ИЗМЕРЕНИЕ, которое само по себе почти не дает вам понимания того, что вызывает проблему. Поэтому, если вы не планируете строить график статистики вместе со своими функциями, убедитесь, что все графики статистики отключены!
Выбор и отмена функции на TI-84 Plus
Отменить выбор (отключить) Y 1 и Y 2 , сняв выделение с их знаков равенства. Это делается в редакторе Y= с помощью клавиш
Это делается в редакторе Y= с помощью клавиш, чтобы поместить курсор на знак равенства, а затем нажать [ENTER], чтобы переключить знак равенства между выделенным и невыделенным. Калькулятор отображает функцию только тогда, когда выделен ее знак равенства!
Вы видите разницу между двумя экранами?
Настройка окна графика TI-84 Plus
Когда вы рисуете функцию, вы обычно не можете видеть весь график. Вы ограничены просмотром графического окна, которое обычно показывает только небольшую часть функции. Есть четыре значения, определяющие видимую часть координатной плоскости: Xmin, Xmax, Ymin и Ymax. Нажмите [WINDOW] для отображения текущих переменных окна. Требуется практика, чтобы найти хорошее окно просмотра функции, которую вы строите. Вот шаги, необходимые для установки окна вашего графика:Нажмите [WINDOW] для доступа к оконному редактору.
После каждой переменной окна введите числовое значение, подходящее для отображаемых функций.
 Нажимайте e после ввода каждого числа.
Нажимайте e после ввода каждого числа.При вводе нового значения окна старое значение автоматически очищается.
Убедитесь, что (Xmin < Xmax) и (Ymin < Ymax), иначе вы получите сообщение об ошибке ERROR: WINDOW RANGE.
Редактирование переменных окна — это хорошее место для начала поиска хорошего окна просмотра. Кроме того, использование функций масштабирования может быть необходимо для улучшения графического окна. Ниже приводится объяснение переменных, которые необходимо установить для настройки окна графика:
Xmin и Xmax: Это, соответственно, наименьшее и наибольшее значения x на оси x .
Если вы не знаете, какие значения понадобятся вашему графику для Xmin и Xmax , нажмите [ZOOM][6], чтобы вызвать команду ZStandard . Эта команда автоматически отображает ваши функции в стандартном окне просмотра.Xscl: Это расстояние между делениями на оси x . (Поосторожнее с делениями; слишком большое их количество делает ось похожей на железнодорожный путь.
Если вы хотите полностью отключить галочки, установите Xscl=0 и Yscl=0 . Двадцать или меньше делений делают ось x красивой.)
Двадцать или меньше делений делают ось x красивой.)Ymin и Ymax: Это, соответственно, наименьшее и наибольшее значения y , которые будут размещены на оси y .
Если вы присвоили значения Xmin и Xmax , но не знаете, какие значения присвоить Ymin и Ymax , нажмите [ZOOM][0], чтобы вызвать команду ZoomFit . Эта команда использует Xmin и Xmax 9.0006, чтобы определить соответствующие настройки для Ymin и Ymax , а затем автоматически рисует график.Yscl: Это расстояние между делениями на оси y . (Как и в случае с осью x , слишком много делений делают ось похожей на железнодорожный путь. Пятнадцать или меньше делений — хорошее число для оси y .)
Xres: Этот параметр определяет разрешение графика.
 Можно установить любое из целых чисел от 1 до 8. Когда Xres устанавливается равным 1, калькулятор оценивает функцию для каждого из 133 пикселей по оси
Можно установить любое из целых чисел от 1 до 8. Когда Xres устанавливается равным 1, калькулятор оценивает функцию для каждого из 133 пикселей по оси Xres обычно устанавливается равным 1. Если вы строите график большого количества функций, калькулятору может потребоваться некоторое время для их построения при таком разрешении. Если вы измените Xres на более высокое число, ваша функция будет строиться быстрее, но вы можете получить не такой точный график.
TraceStep и
Эти две переменные связаны друг с другом, и TraceStep всегда в два раза больше, чем
, которое определяет, как ваш курсор перемещается на экране графика в режиме «свободной трассировки». TraceStep управляет скачком значения X при отслеживании функции на экране графика.

Нажмите [GRAPH], чтобы построить график функций.
Остановка или приостановка графика TI-84 Plus
После нажатия [GRAPH] обычно возникает небольшая задержка перед тем, как вы начнете видеть свою функцию на графике слева направо. Если калькулятору требуется много времени для построения графика ваших функций (возможно, у вас слишком маленькое значение для Xres ), нажмите [ВКЛ], чтобы завершить процесс построения графика.Просто нажмите [ENTER], чтобы приостановить построение графика, а затем снова нажмите [ENTER], чтобы возобновить построение графика. См. следующие два экрана. Обратите внимание на эллиптический индикатор занятости в правом верхнем углу экрана, указывающий на то, что ваш калькулятор активно работает.
Об этой статье
Эта статья взята из книги:
- TI-84 Plus CE Graphing Calculator For Dummies,
Об авторах книги:
Джеффалла Макспал Мэри, учитель математики в St.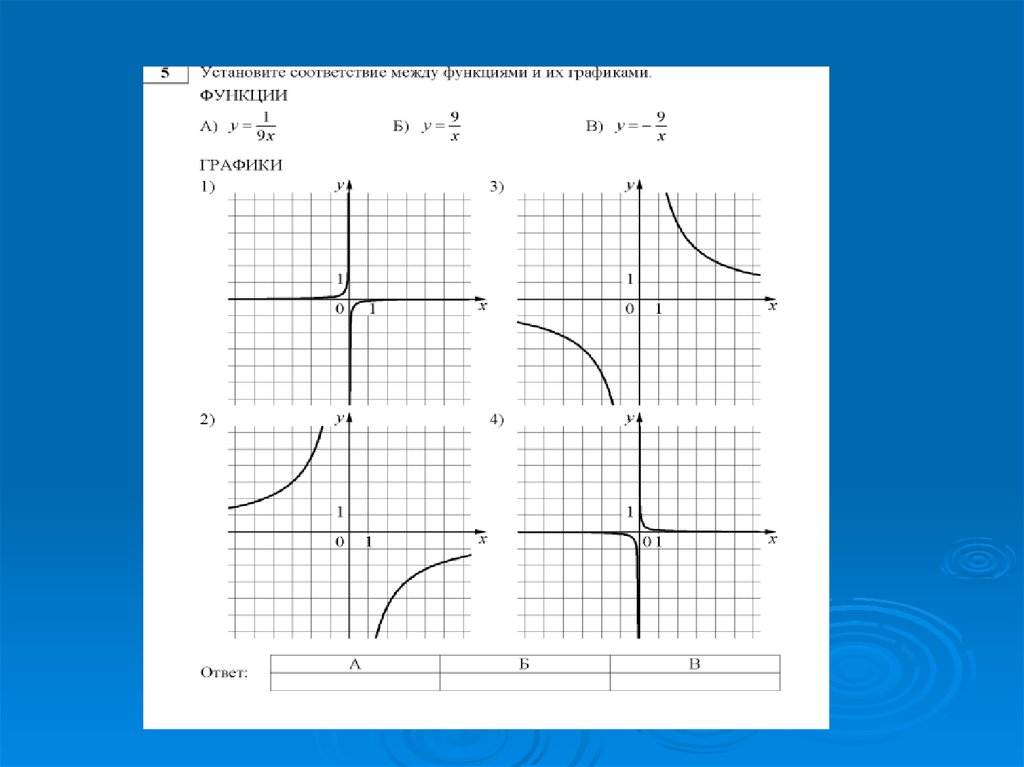

 Нажимайте e после ввода каждого числа.
Нажимайте e после ввода каждого числа.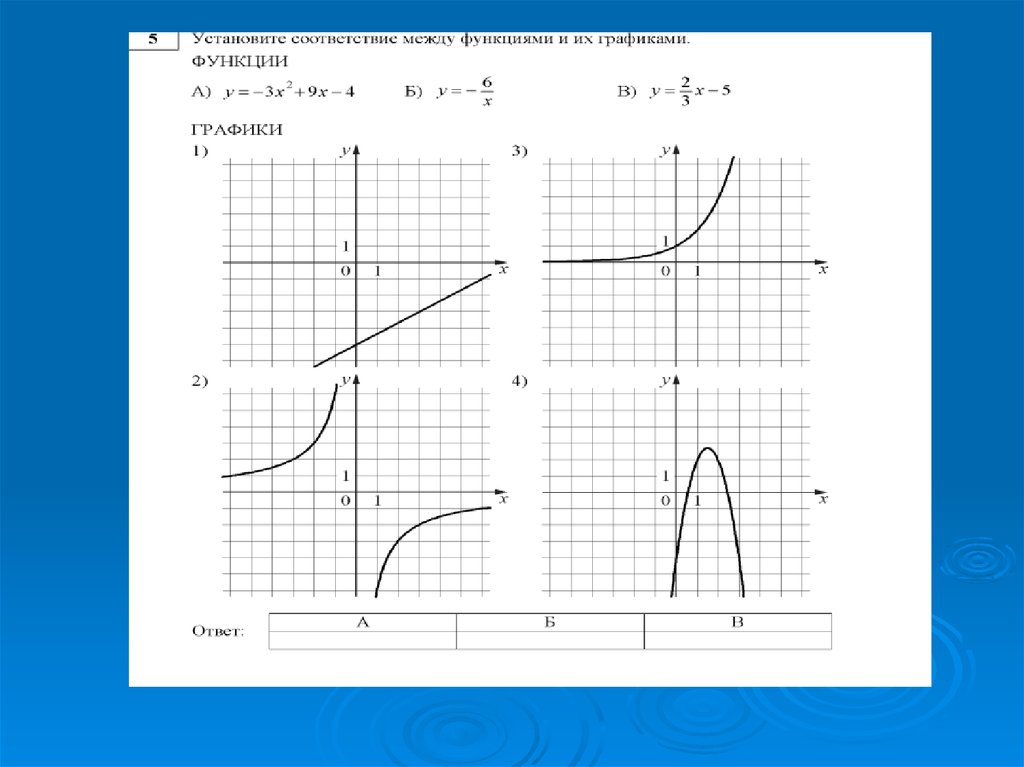 Двадцать или меньше делений делают ось x красивой.)
Двадцать или меньше делений делают ось x красивой.) Можно установить любое из целых чисел от 1 до 8. Когда Xres устанавливается равным 1, калькулятор оценивает функцию для каждого из 133 пикселей по оси
Можно установить любое из целых чисел от 1 до 8. Когда Xres устанавливается равным 1, калькулятор оценивает функцию для каждого из 133 пикселей по оси 
Ваш комментарий будет первым