Кусочная функция онлайн: Построение графиков кусочно-непрерывных функций | Онлайн калькулятор

2

Методическая разработка урока «Построение графиков кусочных функций»

Методическая разработка урока по математике и информатике , 9 класс.

Учителя Солуян Н.Н. и Пастух О.М.

Интегрированный урок по теме «Повторение. Построение графиков кусочных функций».

Цель урока: повторить, закрепить и обобщить умения обучающихся строить и читать графики кусочных функций, решать задания из ГИА.

Тип урока: урок обобщения и систематизации знаний.

Задачи:

Образовательные — обеспечить повторение, обобщение и систематизацию материала темы. Создать условия контроля (самоконтроля) усвоения знаний и умений.

Развивающие — способствовать формированию умения применять приемы: сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.

Воспитательные — содействовать воспитанию интереса к математике и информатике, активности, умения общаться, общей культуры.

Методы обучения: использование ИКТ, частично — поисковый. Работа по обобщающей схеме, создание презентаций, работа по решению экзаменационных заданий, системные обобщения, самопроверка, взаимопроверка.

Формы организации урока: фронтальная, индивидуальная, групповая.

Оборудование и материалы: интерактивная доска, мультимедийный проектор, компьютер, магнитная доска, указка.

ХОД УРОКА.

1. Организационный момент.

Построение графиков кусочных функций мы изучали еще в 7 классе, а в экзаменационных материалах содержатся задачи по данной теме. Поэтому сегодня на уроке мы будем повторять, обобщать, приводить в систему изученный материал, решать задания из ГИА.

Итак, проверим домашнее задание.

2. Проверка домашнего задания.

а)У доски: задание из ГИА: Для каждого графика укажи соответствующую ему формулу.

А					Б			1
								2
В					Г			3
								4
	А	Б	В	Г

б) заполни таблицу

№	Формула	Название графика	Схематические рисунки
1
2
3
4
5
6
7

Учитель: Вспомним, какие основные алгебраические функции мы изучали и что представляют графики этих функций?

/ Идет опрос класса по обобщающей схеме на интерактивной доске (слайд 2)/

Учитель: А теперь посмотрим, как справились с домашнем заданием.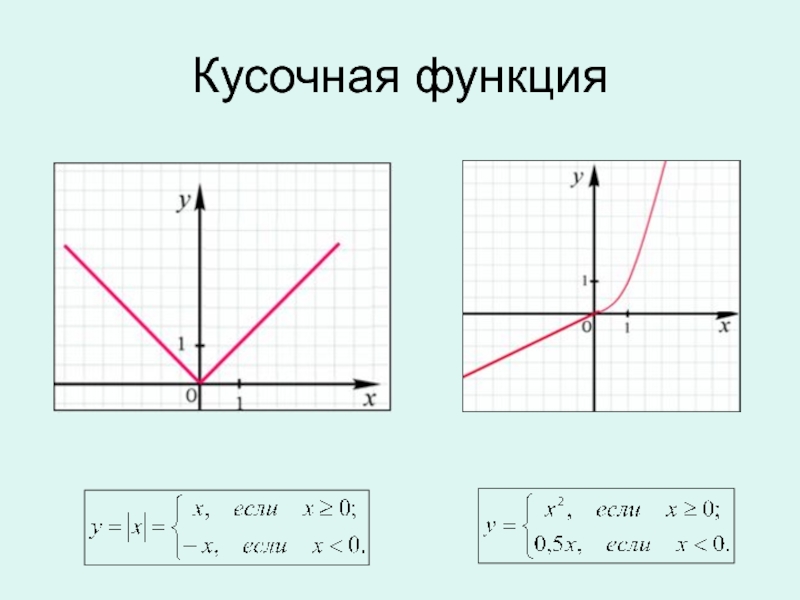

/ Проверка таблицы и устного задания/

3.Построение графиков.

Учитель: В чем особенность графиков кусочных функций? Повторим как строить графики кусочных функций.

/ Идет работа по слайдам./

Задание 1: построить график функции (слайд 3,4)

Задание 2: построить график функции. Задать пошаговые команды компьютеру. (слайд 5,6)

Обычно на экзамене дают и какое- либо дополнительное задание. Например, определите при каких значениях К прямая у = К имеет с графиком функции только одну общую точку. (слайд 7)

Учитель: А теперь решим задание из ГИА.И.В. Ященко, вариант 9, №22.

Мы видим, что выполнение таких заданий достаточно трудоемко и требует много времени. Поэтому, следующее задание из сборника Е.А. Бунимович, вариант 6, № 21подготовили заранее в виде презентации под руководством учителя информатики Костюрина В. и Гончарова А. (слайд 8-19)

Учитель информатики: Почему при решении задачи по математике вы в своей работе ставите цель моделирования?

А на следующей презентации выполненной Бондаренко Д.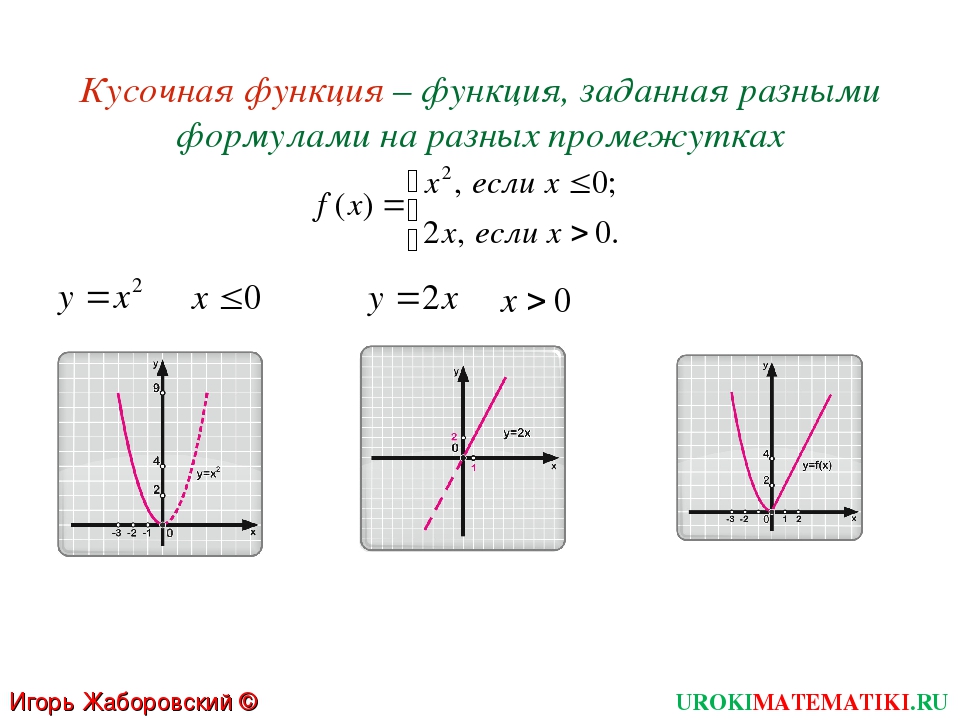 и Трофименко А.рассмотрим построение еще одной кусочной функции. (слайд 20 — 24)

1. Построить график функции

2.Укажите промежуток, на котором функция возрастает.

Учитель информатики: Какую модель получили в результате решения задачи?

4 Блок информатики.

Учитель информатики: На уроках информатики мы с вами прошли тему «Моделирование», строили различные модели. Сейчас вы увидели еще примеры моделей в математике. Давайте вспомним некоторые определения из данной темы. Я предлагаю вам решить устно следующий тест … (слайд 25-30). Молодцы ребята. Теперь вы знаете что, решение любой задачи в математике сводится к построению модели на формальном языке.

5. Обучающая работа в группах.

Учитель Сегодня на уроке мы повторили как по формуле построить график, а бывает обратная задача: по графику определить формулу задающею функцию.

Задание: График функции состоит из двух лучей, исходящих из точек А и В и части параболы. Задайте эту функцию формулой.

Программу данного задания из ГИА приготовил заранее Фадеев А. (слайд 31 — 37)

Рассмотрим луч, исходящий из т. А.

— Каким уравнением можно задать этот луч?

у=кх + в

Значит, нам надо определить к и в. Для этого по графику выберем по две точки с координатами выраженными целыми числами.

Решить систему методом сложения.

Значит, уравнение первой части графика у = 5х + 7, при х -1.

Для определения остальных частей графика разобьемся на группы:

1 вариант определяют часть АВ,

2 вариант- луч исходящий из т.В.

Проверим правильность выбранных ответов.

6. Итог урока.

Итак, сегодня мы с вами повторили, как строить графики кусочных функций.

Какой алгоритм мы будем при этом применять?

7. Домашнее задание.

Ященко, вариант 10. №22, Бунимович, вариант3, № 22, вариант 2, №22.

А сейчас, я бы хотела, чтобы вы оценили при помощи смайликов свое отношение к уроку.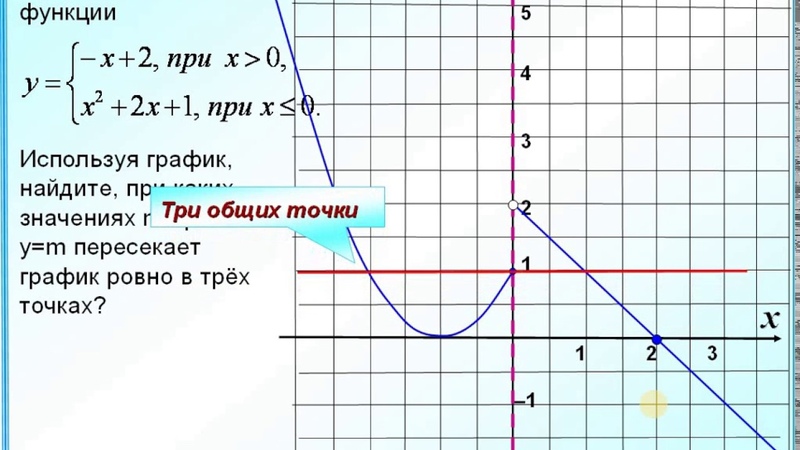 (слайд 38)

Вы просили кусочные функции, я даю вам кусочные функции! – mathcoachblog

НОВИНКА: По многочисленным просьбам этого поста я создал учебник по ограничениям предметной области и кусочным функциям. Наслаждаться!

Нельзя сказать, что mathcoachblog не прислушивается к потребностям своих подписчиков! Одна из приятных вещей в ведении блога — проверка путей, по которым люди попадают в блог. Какие поиски заставили их прибыть сюда? Из каких стран мои посетители? Какие поисковые фразы приводят их к блогу?

Каждый день в обязательном порядке появляется тема, которая появляется в поисковых запросах посетителей блога. Вот выборка терминов только за последнюю неделю:

• Калькулятор кусочно-графического онлайн
• График кусочной функции онлайн калькулятор
• Калькулятор кусочных функций онлайн
• Калькулятор графических кусочных функций онлайн
• Онлайн-график кусочных функций
• Графический онлайн-калькулятор кусочных функций
• Как сделать кусочную функцию на Desmos

Хорошо, ребята, я понял.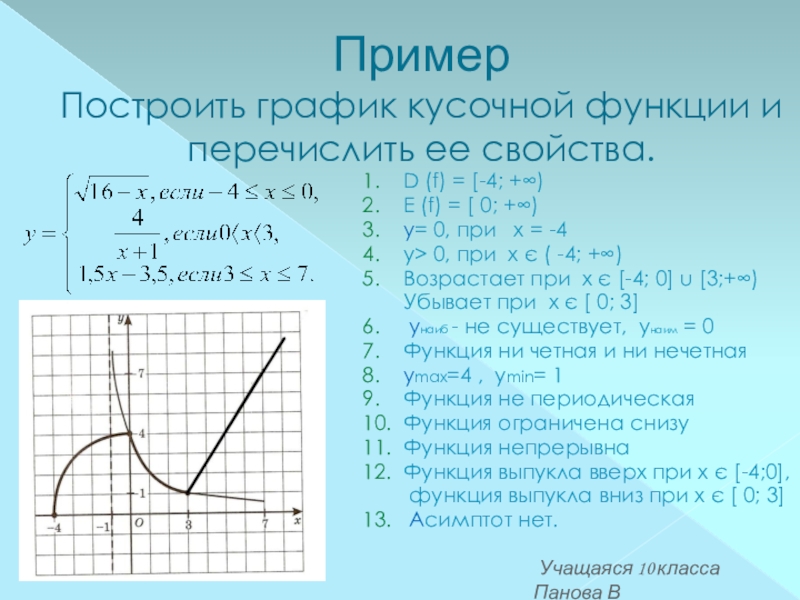 Мы хотим построить график кусочных функций. Итак, давайте зажжем эту свечу.

ГРАФИК КУСОЧНЫХ ФУНКЦИЙ НА DESMOS

База знаний Desmos содержит инструкции по построению графика кусочной функции и удобный видеоурок. Но я приведу здесь несколько примеров и несколько советов по обучению. Допустим, мы хотим построить график этой кусочной функции:

В калькуляторе Desmos двоеточия используются для отделения ограничений домена от их функций. И запятые используются, чтобы иметь несколько правил функций в одной команде. Таким образом, приведенная выше кусочная функция будет введена как:

Затем функция выглядит очень красиво:

Ползунки можно использовать для изучения непрерывности кусочной функции. Рассмотрим следующую задачу:

Для каких значений x кусочная функция ниже непрерывна?

В Desmos начните с определения ползунка для параметра «a». Для себя я решил ограничить домен от -10 до 10 и иметь количество шагов 0,5.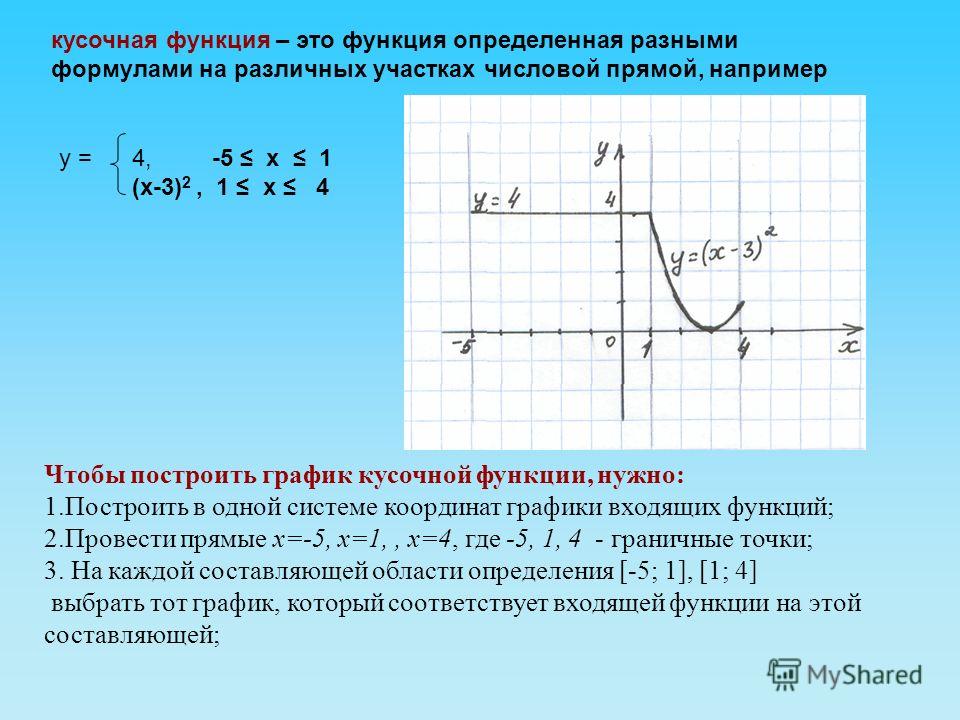 Затем и можно использовать в кусочной функции. Щелкните значок ниже, чтобы поиграть с документом онлайн. Функции обмена — еще один аспект Desmos, который значительно улучшился за последний год.

ТАК, ПОЧЕМУ ВЫ ИЗБЕГАЕТЕ «РАВНЫХ» В СВОИХ ФУНКЦИЯХ?

ОК, умник, да… да, я как бы избегал равных частей ограничений домена. Что-то аккуратное (странное, глупое) происходит, когда в ограничениях домена используется равенство. Давайте изобразим эту функцию в виде графика:

Щелкните эту ссылку, чтобы узнать, что произошло, когда я попытался ввести эту функцию в Desmos. Ребята из Desmos, как правило, следят за этими вещами, поэтому давайте посмотрим, есть ли у них предложения.

В будущем я хочу подробнее изучить новую функцию таблицы и сообщу об этом. Но у меня сложилось впечатление, что это дополнение, которое без проблем работает с существующим потрясающим калькулятором.

Кроме того, пока я в настроении поделиться, вот небольшой файл, который я создал для использования в единице абсолютного неравенства.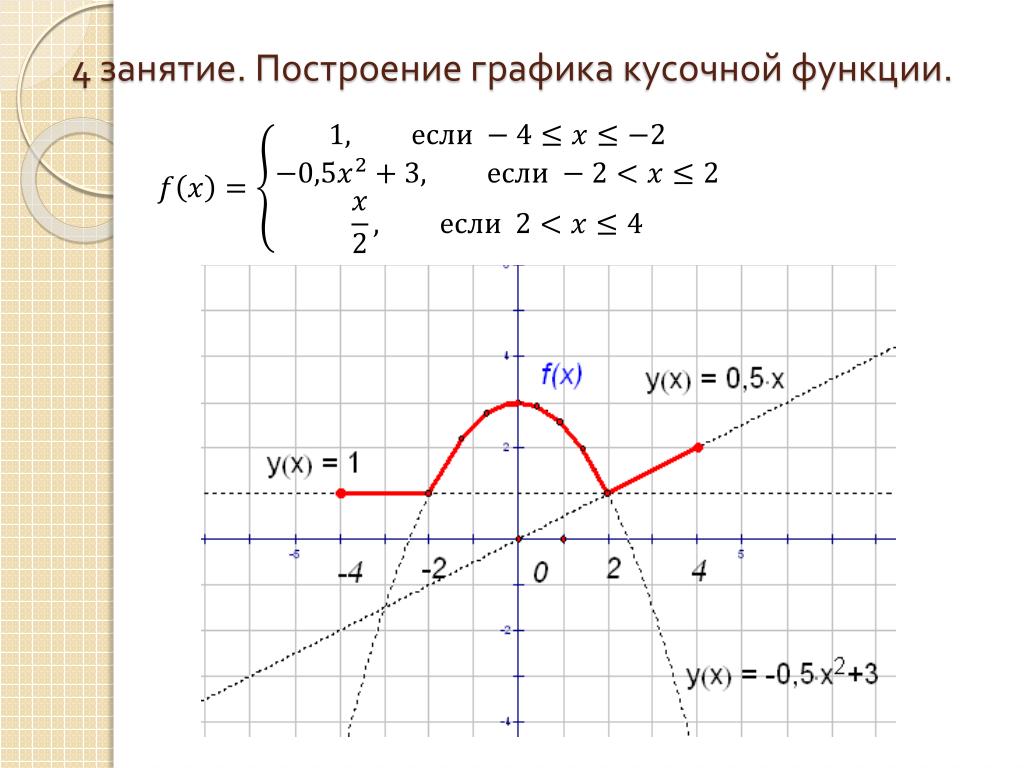 Нажмите ниже, чтобы проверить это. Буду рад вашему вкладу!

И, наконец, я начал этот пост с того, что поделился некоторыми поисковыми запросами, по которым люди находят мой блог. В большинстве случаев я могу объяснить эти термины и то, почему люди в конечном итоге оказываются здесь. Но это….ну….это, у меня ничего нет….. 92 + 2x + 3 при x >

= 0

Как задать условия?

Вот несколько примеров установки условий:

х≠0

х не ноль

х > пи

x больше, чем число Пи

-пи/2

x меньше или равно числу Пи, пополам, но не строго больше, чем число Пи пополам

истинный

означает «иначе»

На этой странице можно получить различные действия с кусочно-определенной функцией, а также для большинства услуг — получить подробное решение.