Как строить графики функций: Как построить график функции у = f(x) + m, если известен график функции у = f(x) — урок. Алгебра, 8 класс. — Магазин Apple iPhone в Перми

Содержание

Пакеты компьютерной алгебры (Пустовалова О.Г.)

Перейти к основному содержанию

Извините, не удалось найти запрашиваемый Вами файл

Подробнее об этой ошибке

Перейти на… Перейти на…Удаленный доступ к приложениям ЮФУУчебная карта дисциплины ПНВ весна 2023Как установить MATLABОсновы MatLab в примерах и задачахМатериалы к Лекциям 1 и 2. Основы MATLAB. ГрафикиМатериалы к лекции 3. Основные типы данныхМатериалы к лекции 4. Дескрипторная графика в MATLABМатериалы к лекции 5. Разреженные матрицыМатериалы к лекции 6. Основы программированияМатериалы к лекции 7. Функции. Интерполяция. АппроксимацияМатериалы к лекции 8. Решение нелинейных уравнений. Интегрирование. ДифференцированиеЛекция 9. Создание пользовательского графического интерфейса в MATLABТест к лекциямОсновы работы в среде MatLabВыложите решение к Занятию 1Выложите решение к Занятию 2Решение СЛАУНастройка свойств графического окнаВыложите решение к Занятию 3Матрицы и векторыАнимация.

Базовые типы данных. Работа с файламиВыложите решение к Занятию 4Лабораторная работа. Int, Double, CharВыложите решение к Занятию 5Занятие 6. Процедурно-ориентированное программирование в MATLABВыложите решение к Занятию 6Решение нелинейных систем и уравненийВыложите решение к Занятию 7Решение уравнений. Сдать до 19 апреляИнтерполяция. Сдать до 26 апреляGUI. Сдать до 16 мая

Пропустить Навигация

В начало
- Страницы сайта

Microsoft Excel позволяет визуально представлять данные с помощью графиков и диаграмм. Люди могут использовать эту программу для построения графиков функций, которые показывают решения заданной формулы. Понимание шагов, которые необходимо предпринять при построении графика функции в Excel, может помочь вам определить прибыль вашей организации или другие связанные переменные.

Чтобы построить график функций в Excel, сначала откройте программу на компьютере или устройстве. Найдите зеленый значок с надписью x над электронной таблицей либо в панели управления, либо путем поиска приложений по адресу Excel. Затем вы можете открыть существующий файл электронной таблицы или создать новый, нажав кнопку Новый опция.

В верхней части таблицы Excel введите заголовки, чтобы различать, какой столбец является входным, а какой — выходным. В ячейку A1 введите x для представления столбца входных данных. Затем введите y в ячейке B1 для выходных переменных. Вы также можете использовать более конкретные заголовки, например Количество продаж и Доход для обозначения столбцов.

Затем введите свои входные переменные в колонку под заголовком x. Это значения x, которые вы хотите использовать на горизонтальной оси вашего графика, и они могут быть отрицательными, положительными, дробными или любой комбинацией этих типов чисел. Если бы ваш график отображал числа от 10 до 100, вы бы включили в него 10 в ячейке A2, 20 в ячейке A3, 30 в ячейке A4 и так далее через 100 в A11.

После ввода нужного количества переменных выделите все переменные x в столбце A, выделив A2 и перетащив курсор вниз до последней ячейки, которую вы хотите построить. Необходимо определить значение значений столбца A, чтобы Excel знал, что каждое значение в A равно значению x. Для этого нажмите кнопку Формулы в верхней части страницы. На вкладке Определенные имена в группе, щелкнуть Определить имя и введите x в Имя поле. Нажмите OK применить свои изменения.

В ячейке B2 введите = с вашей формулой непосредственно после нее без пробела. Например, если организация хочет определить количество продаж, необходимое для определенного продукта, чтобы покрыть его стоимость, она может набрать =(A2*25)-2500. Здесь 25 представляет собой цену для своего товара, 2,500 представляет собой общие затраты на производство товара и * символ представляет собой знак умножения.

Скопируйте свою формулу из ячейки B2, выделив ячейку B2 и нажав на кнопку Копировать кнопка в Буфер обмена группа на вашем Главная вкладка. Затем щелкните и перетащите по ячейкам от B2 до последней переменной, которую вы хотите включить в свой график. Затем щелкните стрелку под Вставить значок в Буфер обмена группу и выберите Формулы. Когда вы это сделаете, Excel автоматически введет решения каждой функции в ваш столбец. В нашем предыдущем примере, если бы в A2 была переменная 150, тогда Excel вычислит, что (150*25)-2500, чтобы ввести 1 250 для ячейки B2.

После заполнения выходного столбца выделите все ячейки с данными, включая заголовки. Затем нажмите кнопку Вставить в верхней части электронной таблицы и нажмите кнопку Разброс в Диаграммы раздел. Далее выберите тип графика для вашей функции, и Excel может опубликовать его непосредственно в вашей электронной таблице.

Используйте инструменты графика для редактирования своего графика. После вставки графика в таблицу Excel используйте инструменты диаграммы в верхней части страницы, чтобы изменить стиль, расположение, оси и другие элементы графика.

Функция в Excel — это заданная формула, которую человек использует для применения набора вычислений к введенным данным. Это позволяет им выполнить математическую операцию. Ссылается на x, входные данные — это числа, которые кто-то вводит в функцию для определения переменной, которую он пытается обнаружить.

Например, если абонемент на кофе стоит 10 долларов в месяц, сотрудник может использовать x чтобы выяснить, сколько подписок им нужно за два месяца, чтобы заработать $500, используя формулу ($10x)*2=$500. Выход, или y, результат вашего уравнения. Компании часто используют эту функцию для построения графика прибыль минус затраты при различных уровнях продаж. Она также может помочь организациям найти общие затраты путем построения графика постоянных затрат при различных приращениях переменных затрат.

Функция состоит из знака равенства, имени функции и одного или нескольких аргументов. Примером функции является =SUMA1:A14. Функция — это действие, которое человек хочет предпринять. Например, SUM представляет собой сложение всех ячеек в аргументе. Аргументы — это то, что человек хочет вычислить, например A1:A14, что приведет к сложению всех значений в ячейках от A1 до A14.

При использовании Excel легко комбинировать функции на одном графике. После того, как первый набор построен на графике, и вы хотите добавить другой набор функций данных, под кнопкой Инструменты диаграммы, нажмите на Дизайн вкладку и затем выберите Выберите источник данных кнопка. Затем, чтобы добавить переменные к вашей диаграмме, нажмите кнопку Добавить кнопка под Серия. Откроется новое диалоговое окно, в котором можно ввести имя новой серии, значения x и y. После нажатия кнопки OK в диалоговом окне и кнопки Выберите источник данных экран, второй набор данных добавляется к графику.

Полное руководство по отображению функции на графике за 3 простых шага
Предварительный просмотр руководства: Как представить функцию на графике.
Графические функции помогают анализировать поведение различных функций на координатной плоскости. Это полное руководство исследует и ответит на следующее:
Как построить график функции
Как изобразить поведение функции на графике
Как определить x и y-перехваты функции
Как определить асимптоты функции
Визуализируя форму и движение функции на координатной плоскости, мы можем получить представление о ее свойствах и сделать предсказания относительно ее значений.
Однако, хотя построить график линии (линейные функции) или построить график параболы (квадратичные функции) относительно просто, с более высокими порядками и другими сложными функциями обычно работать сложнее. Таким образом, это руководство научит вас строить график любой функции за 3 простых шага, используя силу преобразований и другие основы построения графиков.
Как построить график функции: основные понятия
Функция представляет собой математический способ определения связи между двумя или более переменными. Мы можем представить эти отношения с помощью математических символов, как мы это делаем в алгебре, или визуально, изобразив функцию на декартовой плоскости.
Представляя функцию на графике, мы можем идентифицировать различные свойства, которые иначе могут быть неочевидны. Некоторые из важных свойств, которые мы можем наблюдать при построении графика функции:
Пробелы — ввод/с в функции, которая не выводит ничего значимого
Критические точки — точки пересечения, максимальные точки, точки перегиба являются одними из ключевых точек, которые полезны для задач оптимизации, проектирования и т. д.
Вертикальные и горизонтальные асимптоты. Поведение функций при стремлении входных данных к крайним значениям, таким как положительная или отрицательная бесконечность
Как построить график функции: 2 подхода функция на график.
Нанесите на график несколько точек (пар вход-выход) функции и нарисуйте прямую линию или плавную кривую, соединяющую точки. В этом методе, как правило, чем больше точек вы нанесете, тем точнее будет график.
Нарисуйте родительский график функции, а затем примените соответствующие преобразования к графику на декартовой плоскости. Щелкните здесь, чтобы узнать больше о родительских графах и родительских функциях.
Если вы строите график функции с использованием преобразований, вам необходимо иметь четкое представление о различных типах преобразований. Ниже приведен список основных преобразований, которые можно увидеть в функциях.
Как построить график функции: пример №1 (линейная функция)
Давайте разработаем пример, чтобы понять шаги, необходимые для визуализации функции на графике.
График: f(x) = 2x — 3
Чтобы выразить эту функцию на графике (и все функции в этом руководстве), мы будем использовать следующий трехэтапный метод:
Шаг 1 : Определите критические точки и/или любые асимптоты
Шаг 2: Определите точки функции
Шаг 3: Нарисуйте линию или кривую и удлините
Теперь давайте продолжим и применим эти три шага к этому первому примеру:
Шаг 1: Определите критические точки и/или любой асимптоты
В этом примере у нас есть линейная функция.
Критические точки — точки пересечения y и x.
Шаг 2. Определяем точки функции
Здесь мы можем выбрать несколько значений x, которые удобны и имеют смысл в контексте задачи. График линейной функции представляет собой прямую линию, поэтому для построения графика достаточно определить две различные точки. Поскольку у нас уже есть точки пересечения x и y, мы можем перейти к рисованию графика.
Шаг 3. Нарисуйте линию или кривую и удлините
С помощью линейки или линейки соедините точки линией. Расширьте линию по мере необходимости, чтобы охватить соответствующий домен и диапазон функции.
Как построить график функции: Линейная функция
Как построить график функции: пример № 2 (квадратичная функция)
Давайте попробуем другой пример, включающий квадратичную функцию 92 — 3*(3) — 8
f(3) = -12,5
Вершина : (3, -12,5)
Шаг 2: Определите точки функции
Выберите несколько значений x на обоих сторон от 3 и запишите соответствующие значения y в таблицу.
Пример #2: Таблица функций
Шаг 3. Нарисуйте линию или кривую и удлините
Нанесите точки и нарисуйте плавную U-образную кривую, проходящую через все точки.
Как построить график функции: Квадратичная функция
Как построить график функции: пример №3 (рациональная функция)
Давайте попробуем построить график рациональной функции.
График: f(x) = (x+3)/(x-2)
Когда дело доходит до более сложных функций, таких как рациональные функции, нам нужно больше знать о наличии асимптот, пробелов и других свойств. .
Шаг 1: Определите критические точки и/или любые асимптоты
Y-пересечение = (значение функции при x = 0)
X-пересечение = -3 (решение f(x) = 0)
Мы можем приравнять знаменатель рациональной функции для определения любых вертикальных асимптот.
X — 2 = 0
X = 2, является вертикальной асимптотой f(x)
Диапазон f(x) равен {y ∈ R | y ≠ 1}, таким образом, y = 1 будет горизонтальной асимптотой.
Шаг 2: Определить точки функции
Выберите несколько значений x по обе стороны от 2 и запишите соответствующие значения y в таблицу.
Пример #3: Таблица функций
Шаг 3. Нарисуйте линию или кривую и удлините
Укажите вертикальную и горизонтальную асимптоты пунктирными линиями. Отметьте точки и нарисуйте плавную кривую/и, соединяющую точки.
Как построить график функции: Рациональная функция
Как построить график функции: пример № 4 (логарифмическая функция)
График: f(x) = 3log2x-2
Шаг 1: Определение родительской функции
Это логарифмическая функция, следовательно, родительская функция, p(x), будет log(x).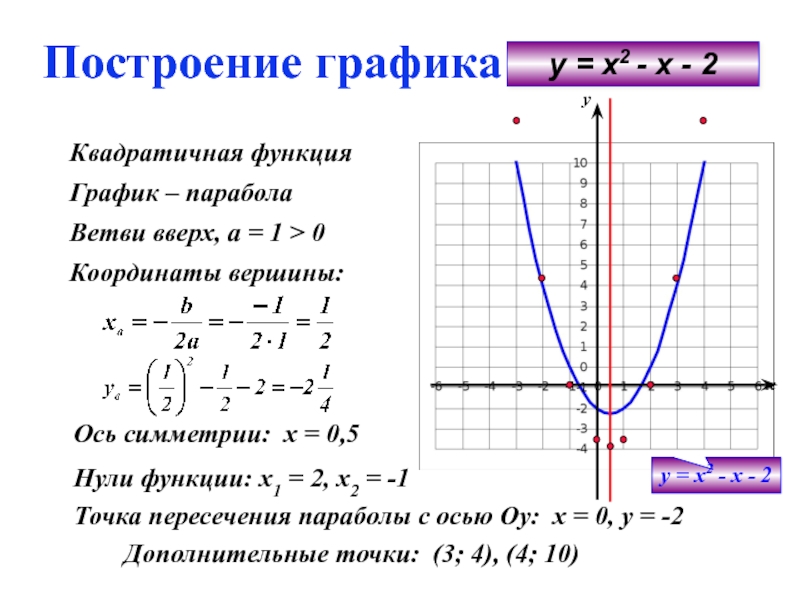 Родительский граф:
.
Логарифмическая родительская функция
Шаг 2: Определить преобразование f(x)
Приведенная в примере функция состоит из комбинации двух преобразований.
log(x) -> — Вертикальное расширение в 3 раза
3log(x) -> — Вертикальное смещение на -2 единицы
Шаг 3. Примените преобразование с к родительский граф
Пример №4: Трансформация №1 (расширение по вертикали в 3 раза)
Пример №4: Трансформация №2 (вертикальный сдвиг на -2 единицы)
Больше математических ресурсов, которые вам понравятся:
Когда были изобретены шахматы и где они возникли?
Подробнее →
Шахматы — это спорт. Вот почему
Подробнее →
Как настроить шахматную доску — объяснение
Подробнее →
Кто пишет буквы в математике? — решено
Подробнее →
Что такое последнее число?—Объяснение
Подробнее →
Как построить график функции и ее обратной функции (4 ключевых шага) — JDM Educational
и другие предметы. Тем не менее, это также помогает узнать, как построить график обратной функции.
Итак, как изобразить функцию и обратную ей функцию? Сначала определите тип функции, которую представляет f(x) (например, линейная). Затем создайте таблицу для f(x) с двумя столбцами: значения x и y. Затем постройте график f(x), нанеся точки и используя форму функции. Наконец, нарисуйте обратную функцию f ^-1 (x) путем переключения значений x и y из графика f(x).
Конечно, некоторые функции не имеют обратных функций (функция должна быть взаимно однозначной, пройдя тест горизонтальной линии, чтобы иметь обратную функцию). В этих случаях мы не сможем построить график обратной функции.
В этой статье мы поговорим о 4 ключевых шагах построения графика функции и ее обратной функции. Мы также рассмотрим несколько примеров для общих функций, чтобы сделать процесс понятным.
Начнем.
Как построить график функции и ее обратной функции
Есть 4 ключевых шага, если вы хотите построить график функции и ее обратной функции:
1. Определите тип функции – функция f(x) может быть линейной , экспоненциальная, триггерная функция или что-то еще. Этот шаг поможет вам нарисовать функцию позже. Когда у вас будет представление о том, как выглядит функция, вы узнаете, допустили ли вы ошибку при построении графика или в таблице значений на следующем шаге.
2. Создайте таблицу значений – таблица значений должна иметь два столбца: один для значений x (входы) и один для значений y (выходы). Выберите хороший образец значений x и подключите их к f(x), чтобы получить значения y. Эта таблица поможет вам набросать функцию после того, как у вас будет несколько точек.
3. Нарисуйте график функции – для построения графика f(x) мы начнем с построения точек из нашей таблицы на шаге 2. После того, как это будет сделано, мы можем набросать общую форму графика для соединения точек на основе на тип функции, который мы определили на шаге 1.
4. Нарисуем обратный – на график f ^-1 (x) начнем с переключения значений x и y для точек из нашей таблицы на шаге 2. Итак, точка (2, 5) на график f(x) даст нам точку (5, 2) на графике f ^-1 (x).
Помните, что мы также можем найти уравнение для обратной функции, взяв уравнение y = f(x), поменяв местами x и y, а затем найдя y. Затем мы можем просто построить график f ^-1 (x) из этого уравнения.
Когда мы изображаем функцию f(x) и обратную ей функцию, они будут выглядеть как зеркальные отражения на линии y = x. Это имеет смысл, поскольку определение инверсии говорит нам, что f(f ^-1 (x)) = f ^-1 (f(x)) = x.
Когда у квадратного уравнения нет решения…
Пожалуйста, включите JavaScript
Когда у квадратного уравнения нет решения?
Также имейте в виду, что область определения обратной функции f ^-1 (x) является диапазоном функции f(x). Точно так же диапазон обратного f ^-1 (x) — область определения функции f(x).
Давайте рассмотрим несколько примеров, чтобы показать, как работает этот процесс. Мы начнем с простой функции: линии.
Пример 1: график линейной функции и обратный график
Допустим, у нас есть линейная функция f(x) = 2x + 6. мх + б).
На втором этапе мы создаем таблицу значений для этой функции (показана ниже).
x f(x)
-2 2
-1 903 95 4
0 6
1 8
2 10
Таблица значений
для f(x) = 2x + 6.
На третьем шаге мы построим график функции, используя точки в нашей таблице и общую форму графика ( на фото ниже).
График линейной функции f(x) = 2x + 6,
Для нашего четвертого шага мы рисуем обратное, меняя координаты x и y для каждой точки в нашей таблице (на фото ниже).
График линейной функции f(x) = 2x + 6 (синий) и обратной ей, f ^-1 (x) = (x – 6) / 2 (красный).
Чтобы найти уравнение для обратной функции, мы меняем местами x и y, затем находим y:
f(x) = 2x + 6 [исходная функция]
y = 2x + 6 [используйте y вместо f(x)]
x = 2y + 6 [переключатель x и y]
x – 6 = 2y
(x – 6) / 2 = y
Итак, мы получаем f ^-1 (x ) = (х – 6) / 2, или f ^-1 (x) = (x / 2) – 3.
Мы можем проверить нашу работу, составив f(x) и f ^-1 (x), чтобы показать, что f(f ^-1 (х)) = х и f ^-1 (f(х)) = х.
Пример 2. График функции абсолютного значения и обратный график
Допустим, у нас есть абсолютная функция f(x) = |x|.
Для нашего первого шага мы идентифицируем это как кусочную функцию с двумя частями: f(x) = x для x >= 0 и f(x) = -x для x < 0 (обе части линейны).
На втором этапе мы создаем таблицу значений для этой функции (показана ниже).
9039 4 -1
x f(x)
-2 2
1
0 0
1 1
2 2
Таблица значений
для f(x) = |x|.
На третьем шаге мы рисуем функцию, используя точки в нашей таблице и общую форму графика (на фото ниже).
График функции абсолютного значения f(x) = |x|.
Глядя на этот график, мы видим, что он не прошел тест горизонтальной линии. Например, мы можем нарисовать линию y = 2, которая пересекает график в точках x = -2 и x = 2.
Это означает, что график не является взаимно однозначным, и поэтому он не имеет обратного.
Пример 3: График кубической функции и обратный график
Допустим, у нас есть кубическая функция f(x) = x ³ – 8.
Для нашего первого шага мы идентифицируем это как кубическую функцию (она имеет y = ax ³ + bx ² + cx + d, где b и c равны нулю).
На втором этапе мы создаем таблицу значений для этой функции (показана ниже).
x f(x)
-4 -72
-3 -35
-2 -16
-1 -9
0 -8
1 — 7
2 0
3 19
4 56
5 117
Таблица значений
для f(x) = x ³ – 8.
На третьем шаге мы рисуем функцию, используя точки в нашей таблице и общую форму графика (на фото ниже).
График кубической функции f(x) = x ³ – 8.
Для нашего четвертого шага мы нарисуем обратную зависимость, поменяв местами координаты x и y для каждой точки в нашей таблице (рисунок ниже).
График кубической функции f(x) = f(x) = x ³ – 8 (синий) и обратная ей, f ^-1 (x) = (x + 8) ^1/3 ( красный).
Чтобы найти уравнение для обратной функции, мы меняем x и y местами, затем находим y:
f(x) = x ³ – 8 [исходная функция]
y = x ³ – 8 [используйте y вместо f(x)] 900 20
х = у ³ – 8 [переключатель x и y]
x + 8 = y ³
(x + 8) ^1/3 = y 90 020
Итак, получаем ф ^-1 (x) = (x + 8) ^1/3 или f ^-1 (x) = ³ √(x + 8).
Мы можем проверить нашу работу, составив f(x) и f ^-1 (x), чтобы показать, что f((f ^-1 (x)) = x и f ^-1 (f(x)) = x.
Пример 4: График экспоненциальной функции и обратный график
Допустим, у нас есть экспоненциальная функция f(x) = 2 ^x.
Для нашего первого шага мы идентифицируем ее как экспоненциальную функцию (она имеет вид y = b ^x, где b — положительная константа).
На втором этапе мы создаем таблицу значений для этой функции (показана ниже).0385 x f(x) -2 1/4 -1 1 /2 0 1 1 2 2 4 3 8 Таблица значений х .
На третьем шаге мы построим график функции, используя точки в нашей таблице и общую форму графика (см. рисунок ниже).
График показательной функции f(x) = 2 ^x .
В качестве четвертого шага мы рисуем обратное, меняя координаты x и y для каждой точки в нашей таблице (см. рисунок ниже).
График экспоненциальной функции f(x) = f(x) = 2 ^x (синий) и обратной функции, f ^-1 (x) = log ₂ (x) (красный).
Чтобы найти уравнение для обратной функции, мы меняем местами x и y, затем находим y:
f(x) = 2 ^x [исходная функция]
y = 2 ^x [используйте y вместо f(x)]
x = 2 ^y [переключите x и y]
900 04 лог ₂ (х) = у
Итак, получаем f ^-1(x) = log ₂(x).
Мы можем проверить нашу работу, составив f(x) и f ^-1 (x), чтобы показать, что f((f ^-1 (x)) = x и f ^-1 (f(x) ) = x
Примечание: экспоненциальная функция a ^x имеет обратную log _и (х), и наоборот.
(Вы можете узнать, как найти формулу экспоненциальной функции здесь.)
Пример 5: График триггерной функции и обратный график (синус)
Допустим, у нас есть тригонометрическая функция f(x) = sin(x) .
Для нашего первого шага мы идентифицируем это как тригонометрическую функцию (это означает, что она повторяется).
На втором этапе мы создаем таблицу значений для этой функции (показана ниже).
903 94 1/2
x f(x)
0 0
π/6
(30)
π/4
(45) √(2 )/2
π/3
(60) √(3)/2
π/2
(90) 1
π
(180) 0
3π/2
(270) -1
2π
(360) 0
Таблица значений
для f(x) = 2 ^x .
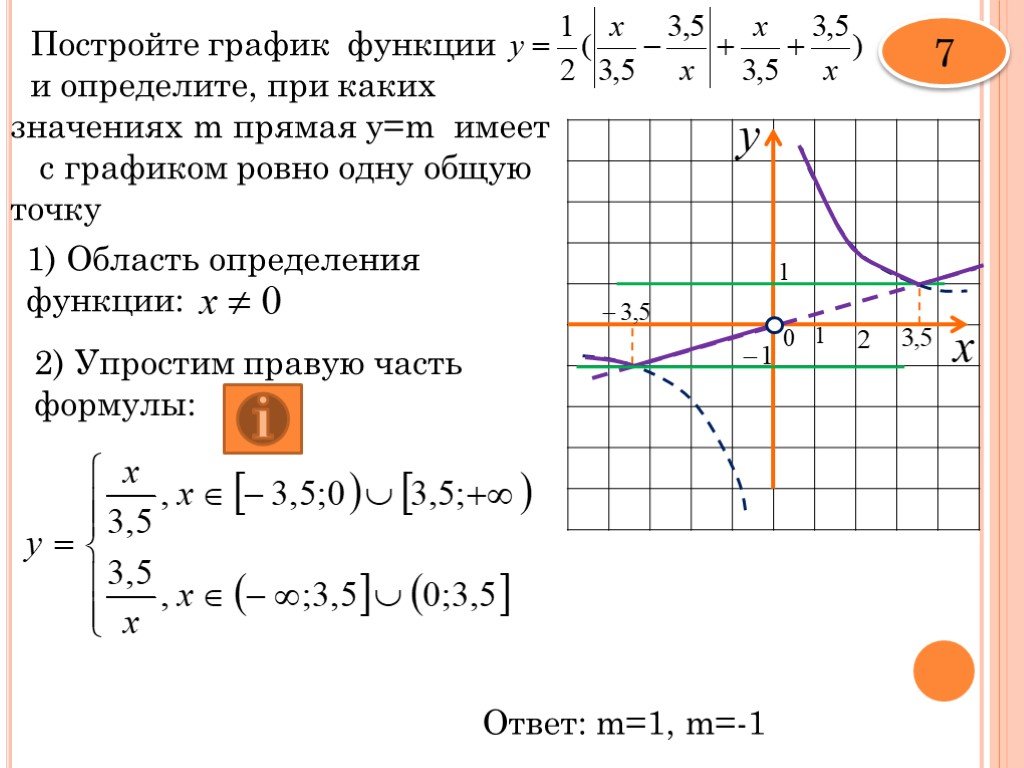
На третьем шаге мы рисуем функцию, используя точки в нашей таблице и общую форму графика (на фото ниже).
График тригонометрической функции f(x) = sin(x), показывающий только один период от x = 0 до x = 2π (360 градусов).
Обратите внимание, что эта функция не является взаимно однозначной в области действительных чисел. Если мы ограничим область определения одним периодом функции (0 <= x <= 2π), то сможем найти обратную.
В качестве четвертого шага мы рисуем обратное, меняя координаты x и y для каждой точки в нашей таблице (см. рисунок ниже).
График тригонометрической функции f(x) = sin(x) (синий) и обратной функции f ^-1 (x) = arcsin(x) (красный).
Обратная функция записывается как f ^-1 (x) = sin ^-1 (x) или f ^-1 (x) = arcsin(x).
Примечание: график для косинуса будет выглядеть аналогично, но со смещением на 90 градусов (π/2 радиана) влево. Инверсия косинуса будет похожа на инверсию синуса со сдвигом на 90 градусов (π/2 радиана) вниз.