Как Разделить Число на Произведение
Поможем понять и полюбить математику
Начать учиться
На математике в 4 классе мы уже знаем, как делить и умножать одно число на другое. А сейчас будет еще интереснее: научимся делить число на произведение двух при помощи специальных правил.
Основные определения
Давайте для начала вспомним, что такое деление, умножение и, как их правильно записывать.
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
- Запись: 2 * 3 = 6, где 2 — множимое, 3 — множитель, 6 — произведение.
- 2 * 3 = 3 + 3 = 6
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же.
- Например: 3 * 2 = 2 + 2 + 2 = 6.

Поэтому и множитель, и множимое называют сомножителями.
Деление — арифметическое действие обратное умножению.
- Запись: 20 : 5 = 4 или 20/5 = 4, где 20 — делимое, 5 — делитель, 4 — частное.
В этом случае произведение делителя 5 и частного 4, в качестве проверки, дает делимое 20.
Если в результате деления, частное является не целым числом, то его можно представить в виде дроби.
Свойства деления в виде формул:
Распределительные свойства |
(a + b) : c = a : c + b : c |
(a — b) : c = a : c — b : c |
(a * b) : c = (a : c) * b = (b : c) * a |
a : (b * c) = (a : b) : c = (a : c) : b |
Действия с единицей и нулём |
a : 1 = a |
| a : a = 1 |
0 : a = 0 (a ≠ 0) |
на нуль делить нельзя |
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Способы деления числа на произведение
Число можно разделить на произведение двумя способами. Сформулируем правило деления числа на произведение для каждого способа и попрактикуемся на примерах.
1 способ
Чтобы разделить число на произведение, нужно сначала выполнить умножение в скобках, а затем разделить число на полученный результат. |
Так, например, чтобы найти значение выражения: 666 : (3 * 2), нужно сначала перемножить то, что находится в скобках: 3 * 2 = 6.
Затем и разделить 666 на полученный результат: 666 : 6 = 111. Значит 666 : (3 * 2) = 666 : 6 = 111.
Если число, которое нужно разделить на произведение, делится на каждый сомножитель, из которого состоит данное произведение — можно воспользоваться вторым способом.
2 способ
Чтобы разделить число на произведение, нужно разделить это число на первый сомножитель, а полученный результат разделить на второй сомножитель. |
Например, чтобы найти значение выражения: 120 : (5 * 6), нужно сначала разделить 120 на 5: 120 : 5 = 24. Далее, полученное частное 24 разделить на 6: 24 : 6 = 4. А Теперь 120 : (5 * 6) = (120 : 5) : 6 = 24 : 6 = 4.
Так как от перестановки множителей произведение не меняется, то множители можно легко поменять местами: 120 : (6 * 5) и разделить 120 сначала на 6, а затем полученный результат разделить на 5: 120 : (6 * 5) = (120 : 6) : 5 = 20 : 5 = 4.
Проще говоря, не важно на какой множитель первым делить число — результат будет одинаковым. Проверим:
120 : (5 * 6) = (120 : 5) : 6 = 24 : 6 = 4
тоже самое, что и
120 : (6 * 5) = (120 : 6) : 5 = 20 : 5 = 4.
Из этого примера делаем вывод, что значение частного не изменится от порядка выполнения действий.
Эти правила иногда называют свойствами деления числа на произведение. Но, по сути, неважно, как это называть. Главное — как это работает. Далее попрактикуемся на примерах.
Примеры деления числа на произведение
Пример 1. Применить правило деления числа на произведение двух чисел:
24 : ( 3 * 4).
Как рассуждаем:
- Чтобы разделить число на произведение, вычислим сначала произведение в скобках: 3 * 4 = 12.
- Подставляем полученное число в выражение:
24 : ( 3 * 4) = 24 : 12 = 2.
Вот и ответ. А теперь решим это же выражение другим способом.
- Чтобы разделить число на произведение чисел, нужно сначала число 24 разделить на первый множитель 3.
 А после, разделить полученный на второй множитель 8:
А после, разделить полученный на второй множитель 8:
24 : ( 3 * 4) = 24 : 3 : 4 = 8 : 4 = 2.
А как можно еще решить это выражение?
- Чтобы число разделить на произведение, нужно сначала число 24 разделить на второй множитель 4. И полученный результат разделить на первый множитель 3:
24 : ( 3 * 4) = 24 : 4 : 3 = 6 : 3 = 2.
Вот, как это работает! Мы нашли значение выражения разными способами, при этом результаты получились одинаковыми.
Пример 2. Вычислить: тысячу разделить на произведение двадцати и пяти.
Ответ:
1000 : (20 * 5) = 1000 : 100 = 100
1000 : (20 * 5) = 1000 : 20 : 5 = 50 : 5 = 10
1000 : (20 * 5) = 1000 : 5 : 2 = 200 : 2 = 10
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
118.7K
Область допустимых значений функции
К следующей статье
Разложение многочлена способом группировки
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Деление в столбик ➗ примеры и правила, как научиться
Онлайн-урок по теме «деление в столбик»
Записаться
567.1K
Деление — это разбиение целого на равные части. Эта математическая операция пригодится не только на уроках математики, но и в повседневной жизни. В этой статье расскажем, как это делать самостоятельно. Для этого разберем примеры для 3 и 4 классов, где покажем деление двузначных и трехзначных чисел.
Эта математическая операция пригодится не только на уроках математики, но и в повседневной жизни. В этой статье расскажем, как это делать самостоятельно. Для этого разберем примеры для 3 и 4 классов, где покажем деление двузначных и трехзначных чисел.
Деление с остатком
Прежде чем перейти к делению в столбик на двузначные и трехзначные числа, давайте вспомним, что значит «разделить с остатком». Если кратко, это такое деление, в результате которого получается остаток меньше делителя:
Например, делим 19 на 5. Наибольшее число, которое делится на 5 до 19 — это 15. Проверяем: 5 × 3 = 15, 19 − 15 = 4. Ответ: 3 и остаток 4. Записываем так: 19 : 5 = 3 (4).
Еще пример: делим 29 на 6. Также определяем максимальное число, которое делится на 6 до 29. Подходит 24. Ответом будет 4 и остаток 5. А записываем: 29 : 6 = 4 (5).
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Как правильно делить в столбик
Делить столбиком проще, чем высчитывать в уме. Этот способ наглядный, помогает держать во внимании каждый шаг и запомнить алгоритм, который потом будет срабатывать автоматически.
Деление трехзначного числа на однозначное
Рассмотрим пример деления трехзначного числа на однозначное в столбик — 322 : 7. Для начала определимся с терминами:
- 322 — делимое или то, что необходимо поделить;
- частное — результат действия.
Шаг 1. Слева размещаем делимое 322, справа делитель 7, между ставим уголок, а частное посчитаем и запишем под делителем.
Шаг 2. Смотрим на делимое слева направо, находим первое неполное делимое — оно должно быть больше делителя или равно ему.
Для этого рассмотрим первую цифру делимого. Она меньше делимого: 3 < 7 — не подходит. Рассмотрим теперь две первые цифры делимого: 32 ﹥7. Подходит!
Теперь нужно определить, сколько раз наш делитель 7 содержится в числе 32. Выполним деление с остатком. В результате деления 32 на 7 получили неполное частное 4 и остаток 4.
Важно
Результат вычитания должен быть меньше делителя. Если это не так, значит, есть ошибка в расчетах. Нужно увеличить выбранное число и выполнить действие еще раз.
Шаг 3. Запишем следующую цифру делимого справа от остатка 4. Говорят «сносим двойку». Получим следующее делимое — 42.
Шаг 4. Сколько раз делитель 7 содержится в числе 42? Кажется, шесть раз. Проверяем: 7 × 6 = 42, 42 = 42 — все верно. Записываем 6 к четверке справа — это вторая цифра частного. Делаем вычитание в столбик 42 из 42, в остатке получаем 0. Значит, числа разделились нацело.
Значит, числа разделились нацело.
Мы закончили решать пример и в результате получили целое число 46.
Деление трехзначного числа на двузначное с примерами
Теперь разберем случаи деления трехзначных чисел на двузначные для 3 класса. Будьте внимательны: мы перешли к самому сложному.
Пример №1.
Разделим трехзначное число 324 на двузначное 81.
Шаг 1. В этом случае 324 будет делимым, его нужно поместить в уголок слева. 81 — это делитель, его вписываем справа.
Шаг 2. Чтобы понять, как делить в столбик на двузначное число, сначала нужно найти то, которое сможем разделить на 81. 3 и 32 не подходят — они меньше делителя. Поэтому придется искать частное к изначальному делимому методом подбора. Умножаем в столбик 81: сначала на 2, потом на 3 и на 4. 81*4=324. Подходит!
Подходит!
Шаг 3. Записываем 4 в столбик под делителем. Это и есть ответ.
Ответ: 324:81=4.
Пример №2.
Продолжим разбираться, как делить столбиком многозначные числа, на следующем примере. В этот раз разделим 368 на 92.
Шаг №1. Здесь трехзначное число 368 будет делимым, а двузначное 92 — делителем. Расставляем их в столбике по своим местам.
Шаг №2. Теперь мы должны понять, какое наибольшее число в составе делимого можно нацело поделить на 92. 3 и 36 не подходят, придется снова подбирать частное. Для этого возьмем десятки и поделим их: 36:9=4. Проверим, подходит ли это число — умножим 92 на 4 столбиком.
Шаг №4. Подошло! Вписываем 4 в окошко для частного в столбике.
Ответ: 368:92=4.
Как делить однозначные и многозначные числа в столбик с остатком
Как мы писали в начале, это такое же деление, только в результате получается неровное число. Теперь разберем те же примеры, только поделим в столбик.
Пример №1
Разделим двузначное число 19 на однозначное 5. В этом случае 19 будет делимым, а 5 — делителем.
Шаг 1. Рисуем уголок. Делимое 19 ставим слева, а делитель 5 — справа.
Шаг 2. Подбираем наибольшее число до 19, которое нацело делится на 5. Это 15. Проверяем, так ли это: 5*3=15. Теперь 3 можно записать в столбик под делителем, а 15 — под делимым.
Шаг 3. Вычитаем число, которое получили делением нацело, из делимого. 19-15=4. Это остаток.
Это остаток.
Ответ: 19:5=3
Пример №2.
Разделим двузначное число 29 на однозначное 6. Теперь 29 будет делимым, а 6 — делителем.
Шаг 1. Располагаем числа в столбике. Как обычно, 29 ставим на место делимого справа, а делитель 6 — слева от уголка.
Шаг 2. Теперь найдем число до 29, которое можно целиком разделить на 6. Проверим, подходит ли 24: 6*4=24. Записываем 24 под делимым 29, а 4 — в свободном отсеке снизу уголка. Это будет целая часть в результате деления.
Шаг 3. Вычитаем из делимого 29 число, которое мы получили в шаге 2. 29-24=5. Это остаток от деления.
Ответ: 29:9=4(5)
Примеры на деление в столбик для 3 класса
Давайте закрепим знания на практике. Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье. Это задание со звездочкой.
Ниже мы оставили примеры деления двузначных и трехзначных чисел для 3 класса. Решите их столбиком, а после проверьте полученные цифры — чур, не подглядывать! Обратите внимание: в сложном уровне есть деление многозначных чисел на двузначные, которые мы не разбирали в статье. Это задание со звездочкой.
Легкий уровень | Средний уровень | Сложный уровень |
27:3= 48:4= 56:8= 72:9= 95:5= | 270:15= 504:14= 315:5= 728:8= 855:9= | 1749:11= 1080:45= 3888:72= 5248:64= 4818:66= |
Ответы:
- легкий уровень: 9; 12; 7; 8; 19;
- средний уровень: 18; 36; 63; 91; 95;
- сложный уровень: 159; 24; 54; 82; 73.

Если вам интересно, как еще можно научить ребенка делить двузначные и трехзначные числа, приглашаем на вводный урок в Skysmart! На на онлайн-курсах по математике для детей можно закрепить тему «Деление в столбик» и разобраться в других разделах из школьной программы.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
218.2K
Как умножать в столбик
К следующей статье
Как найти площадь прямоугольника
Получите план обучения, который поможет понять и полюбить математику
ПремиумНа вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Определим уровень и подберём курс
Расскажем, как
проходят занятия
Как сделать длинное деление? Определение, этапы, метод, примеры
Определение длинного деления
В математике l длинное деление — это математический метод деления больших чисел на более мелкие группы или части. Это помогает разбить проблему на простые и легкие шаги . Длинные деления имеют делимые, делители, частные и остатки. В задаче на длинное деление делимое — это большое число, которое делится на другое число, называемое делителем 9.0006 . Частное есть результат деления, а избыточное количество, которое нельзя разделить, называется остатком .
Это помогает разбить проблему на простые и легкие шаги . Длинные деления имеют делимые, делители, частные и остатки. В задаче на длинное деление делимое — это большое число, которое делится на другое число, называемое делителем 9.0006 . Частное есть результат деления, а избыточное количество, которое нельзя разделить, называется остатком .
Связанные игры
Пример длинного деления
Вот пример, который поможет нам понять эту концепцию:
Поскольку 75 не кратно 4, оно не делится на 4 и оставит остаток в конце.
Связанные рабочие листы
Символ деления
Чтобы показать, что два числа делятся, мы можем добавить между ними знак деления «÷». Так, например, если нам нужно показать 36, разделенное на 6, мы можем записать это как 36 ÷ 6.
Мы также можем представить это в форме дроби как 366.
Шаги для выполнения длинного деления
Есть пять шагов, чтобы легко решить любую задачу на длинное деление.
Давайте рассмотрим приведенные ниже примеры, чтобы лучше понять концепцию.
Деление десятичных чисел с помощью длинного деления
Длинное деление также можно использовать для деления десятичных чисел на равные группы. Он следует тем же шагам, что и при делении в длину, а именно — разделить, умножить, вычесть, свести и повторить или найти остаток.
Вот пример длинного деления с десятичными дробями.
Интересные факты о длинном делении
- Если делимое равно 0, частное всегда будет равно нулю.
- Остаток всегда меньше делимого.
- Умножение частного на делитель и добавление остатка даст делимое.
(делитель x частное) + остаток = делимое
- Когда остаток равен 0, делимое является произведением делителя и частного.
Делитель x Частное = Делимое, когда остаток = 0
Заключение
Длинное деление — это инструмент, позволяющий разделить большие числа на несколько меньших групп или частей. Когда мы делим делимое на делитель, полученное частное представляет собой количество групп, которые можно составить, а остаток определяет, сколько элементов или чисел останется несгруппированным. Чтобы еще лучше понять эту концепцию, ознакомьтесь с широким спектром интересных упражнений, доступных на SplashLearn, и станьте мастером деления на деления!
Когда мы делим делимое на делитель, полученное частное представляет собой количество групп, которые можно составить, а остаток определяет, сколько элементов или чисел останется несгруппированным. Чтобы еще лучше понять эту концепцию, ознакомьтесь с широким спектром интересных упражнений, доступных на SplashLearn, и станьте мастером деления на деления!
Решенные примеры на длинное деление
Вопрос 1: Разделите 726 на 4
Ответ:
Следовательно, частное задачи равно 181, а остаток равен 4 900 Вопрос 15 900 2. 900 остаток при делении 248 на 8?
Ответ:
Следовательно, частное задачи равно 31, а остаток равен 0.
Вопрос 3: Мама Лейлы собрала все семейные фотографии и хотела поместить их все в альбом. Если каждая страница альбома может содержать 9фотографий, сколько страниц альбома ей понадобится, если фотографий 285?
Ответ:
Частное задачи равно 31, а остаток равен 6. Значит, ей нужно 31 + 1 (для оставшихся шести картинок) или 32 страницы.
Значит, ей нужно 31 + 1 (для оставшихся шести картинок) или 32 страницы.
Практические задачи на длинное деление
1
При делении 426 на 4 мы получаем остаток как
2
4
6
частное как 106 и остаток как 2,
2
Найдите дивиденд, если делитель равен 8, коэффициент 71, а остаток — 4.
562
560
576
572
Правильный ответ — 572
Dividend = (DivisiSISISTISTIST). Остаток = (8 x 71) + 4 = 572
3
Найдите цифру, которая может заменить A в следующей задаче на деление.
3
4
5
6
Правильный ответ: 6
A × 5 = 30. Таким образом, A должно быть 30 ÷ 5 или 6,
Часто задаваемые вопросы о длинном делении
Может ли делитель быть 0?
Нет, деление на 0 в математике вообще не определено.
Что такое метод длинного деления?
В математике длинное деление — это математический метод деления больших чисел на несколько меньших групп или частей. Число, которое мы делим на маленькие группы, называется делимым, число, на которое мы делим, называется делителем. Это помогает разбить проблему на простые и легкие шаги.
Как мы можем проверить частное и остаток от задачи деления?
Мы можем проверить частное и остаток от деления, используя формулу деления: (Делитель x Частное) + Остаток = Делимое
В чем разница между прямым делением и коротким делением?
Короткое деление удобно для деления больших чисел на однозначные числа, тогда как длинное деление удобно для деления больших чисел на числа с двумя и более цифрами.
Длинное деление — метод | Шаги
Длинное деление — это метод деления больших чисел, который разбивает задачу деления на несколько последовательных шагов. Как и в обычных задачах на деление, делимое делится на делитель, который дает результат, известный как частное, а иногда и остаток. Давайте узнаем , как разделить , используя метод деления в длину , а также примеры деления в длину с ответами, которые включают этапы деления в этой статье.
Как и в обычных задачах на деление, делимое делится на делитель, который дает результат, известный как частное, а иногда и остаток. Давайте узнаем , как разделить , используя метод деления в длину , а также примеры деления в длину с ответами, которые включают этапы деления в этой статье.
| 1. | Что такое метод длинного деления? |
| 2. | Части длинной дивизии |
| 3. | Как сделать длинное деление? |
| 4. | Часто задаваемые вопросы о Long Division |
Что такое метод длинного деления?
Полное деление — это метод деления больших чисел на шаги или части, разбивающий задачу деления на последовательность более простых шагов. Это наиболее распространенный метод, используемый для решения задач, основанных на делении. Обратите внимание на следующий метод длинного деления, чтобы увидеть, как шаг за шагом делить и проверять делитель, делимое, частное и остаток.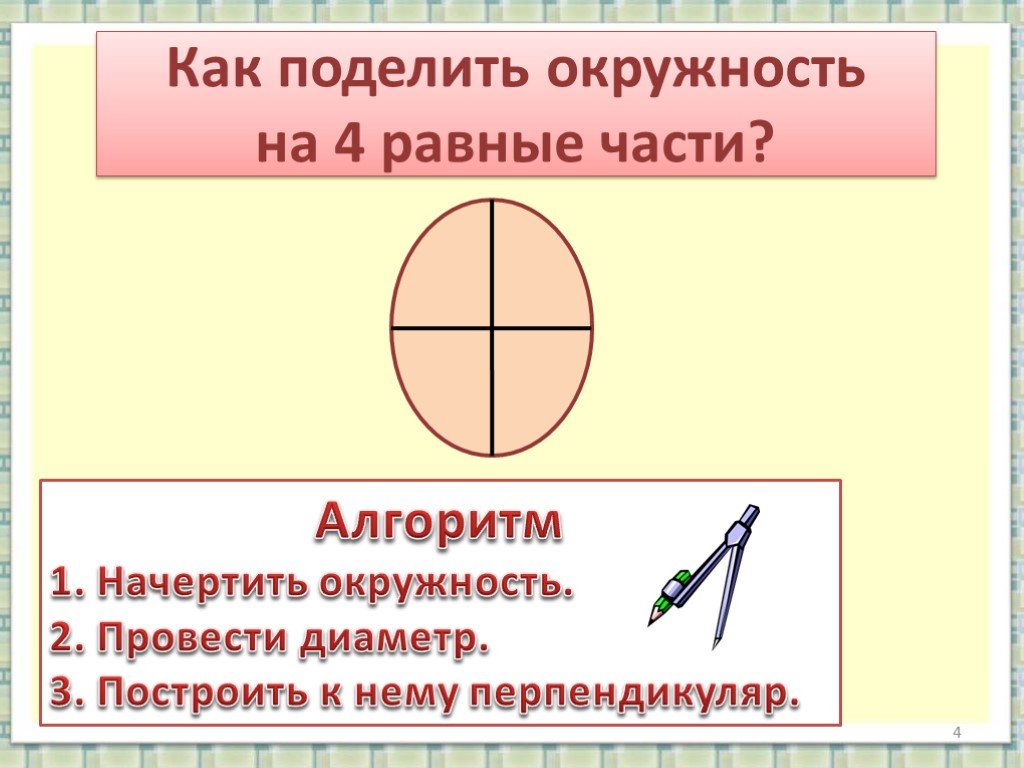
Приведенный выше пример также показал нам, как разделить 2 цифры на 1 цифру.
Части длинной дивизии
При выполнении деления в длинное число нам необходимо знать важные части деления в длинное число. Основные части длинного деления могут быть перечислены следующим образом:
- Дивиденд
- Делитель
- Частное
- Остаток
В следующей таблице описаны части длинного деления со ссылкой на приведенный выше пример.
| Дивиденд | Число, которое необходимо разделить. | 75 |
|---|---|---|
| Делитель | Число, на которое делится делимое. | 4 |
| Частное | Результат деления. | 18 |
| Остаток | Оставшаяся часть или число, оставшееся после деления, которое нельзя разделить дальше. | 3 |
Как сделать длинное деление?
Деление — одна из четырех основных математических операций, остальные три — сложение, вычитание и умножение. В арифметике длинное деление — это стандартный алгоритм деления больших чисел, разбивающий задачу деления на ряд более простых шагов. Давайте узнаем о шагах, которые выполняются в длинном делении.
В арифметике длинное деление — это стандартный алгоритм деления больших чисел, разбивающий задачу деления на ряд более простых шагов. Давайте узнаем о шагах, которые выполняются в длинном делении.
Ступени длинной части
Чтобы выполнить деление, нам нужно понять несколько шагов. Делимое отделяется от делимого правой скобкой 〈)〉 или вертикальной чертой 〈|〉, а делимое отделяется от частного винкулумом (чертой чертой). Теперь давайте проследим за длинными шагами деления, приведенными ниже, чтобы понять процесс.
- Шаг 1: Возьмите первую слева цифру делимого. Проверьте, больше ли эта цифра делителя или равна ему.
- Шаг 2: Затем разделите на делитель и запишите ответ сверху как частное.
- Шаг 3: Вычтите результат из цифры и запишите разницу ниже.
- Шаг 4: Запишите следующую цифру делимого (если она есть).
- Шаг 5: Повторите тот же процесс.

Давайте взглянем на приведенные ниже примеры для лучшего понимания концепции. При делении в длинное мы можем столкнуться с проблемами, когда остатка нет, а в некоторых вопросах есть остаток. Итак, сначала научимся делению, при котором мы получаем остаток.
Деление с остатком
Случай 1: Когда первая цифра делимого больше или равна делителю.
Пример: Разделить 435 ÷ 4
Решение: Ниже приведены шаги этого длинного деления:
- Шаг 1: Здесь первая цифра делимого равна 4, и оно равно 4. делитель. Итак, 4 ÷ 4 = 1. Итак, 1 записывается сверху как первая цифра частного.
- Шаг 2: Вычтите 4 — 4 = 0. Уменьшите вторую цифру делимого и поместите ее рядом с 0.
- Шаг 3: Теперь 3 < 4. Следовательно, мы пишем 0 как частное и записываем следующую цифру делимого и кладем ее рядом с 3.
- Шаг 4: Итак, у нас есть 35 в качестве нового делимого.
 Мы видим, что 35 > 4, но 35 не делится на 4, поэтому мы ищем число чуть меньше 35 в таблице 4. Мы знаем, что 4 × 8 = 32, что меньше 35, поэтому мы идем на это. .
Мы видим, что 35 > 4, но 35 не делится на 4, поэтому мы ищем число чуть меньше 35 в таблице 4. Мы знаем, что 4 × 8 = 32, что меньше 35, поэтому мы идем на это. . - Шаг 5: Запишите 8 в частном. Вычесть: 35 — 32 = 3.
- Шаг 6: Теперь 3 < 4. Таким образом, 3 — остаток, а 108 — частное.
Случай 2: Когда первая цифра делимого меньше делителя.
Пример: Разделить 735 ÷ 9
Решение: Разделим это, используя следующие шаги.
- Шаг 1: Так как первая цифра делимого меньше делителя, в частном поставьте ноль и запишите следующую цифру делимого. Теперь рассмотрим первые 2 цифры, чтобы продолжить деление.
- Шаг 2: 73 не делится на 9, но мы знаем, что 9 × 8 = 72, так что действуем.
- Шаг 3: Запишите 8 в частном и вычтите 73 — 72 = 1.
- Шаг 4: Сбросьте 5.
 Число, которое будет рассматриваться сейчас, равно 15.
Число, которое будет рассматриваться сейчас, равно 15. - Шаг 5: Поскольку 15 не делится на 9, но мы знаем, что 9 × 1 = 9, берем 9.
- Шаг 6: Вычтите: 15 — 9 = 6. Запишите 1 в частном.
- Шаг 7: Теперь 6 < 9. Таким образом, остаток = 6 и частное = 81.
Случай 3: Это случай деления в большую сторону без остатка.
Деление без остатка
Пример: Разделить 900 ÷ 5
Решение: Давайте посмотрим, как делить шаг за шагом.
- Шаг 1: Считаем первую цифру делимого и делим ее на 5. Здесь будет 9÷ 5.
- Шаг 2: Теперь 9 не делится на 5, а 5 × 1 = 5, поэтому запишите 1 как первую цифру в частном.
- Шаг 3: Напишите 5 под 9 и вычтите 9 — 5 = 4.
- Шаг 4: Поскольку 4 < 5, мы уменьшим 0 из делимого до 40.

- Шаг 5: 40 делится на 5, а мы знаем, что 5 × 8 = 40, поэтому запишем 8 в частном.
- Шаг 6: Запишите 40 под 40 и вычтите 40 — 40 = 0,
- Шаг 7: Снизьте следующий 0 из делимого. Поскольку 5 × 0 = 0, мы пишем 0 как оставшееся частное.
- Шаг 9: Следовательно, частное = 180 и после деления не остается остатка, то есть остаток = 0.
Задачи на деление в длинное число также включают задачи, связанные с делением в длинное на двузначное число, полиномами в длинное деление и делением в длинное с десятичными дробями. Давайте получим представление об этом в следующих разделах.
Длинное деление на двузначное число
Длинное деление на двузначное число означает деление числа на двузначное число. Для длинного деления на двузначное число мы рассматриваем обе цифры делителя и проверяем делимость первых двух цифр делимого.
Например, если нам нужно разделить 7248 на 24, мы можем сделать это с помощью длинных шагов деления. Давайте посмотрим, как разделить шаг за шагом.
- Шаг 1: Поскольку это длинное деление на двузначное число, мы проверим делимость первых двух цифр делимого. Первые 2 цифры делимого 72 и они больше делителя, поэтому приступим к делению.
- Шаг 2: Используя таблицу умножения 24, мы знаем, что 24 × 3 = 72. Поэтому мы пишем 3 в частном и 72 под делимым, чтобы вычесть их. Вычесть 72 — 72 = 0,
- Шаг 3: Сократите следующее число из делимого, т. е. 4. Теперь нужно рассмотреть число 4.
- Шаг 4: Поскольку 4 меньше 24, мы положим 0 в качестве следующего частного, поскольку 24 × 0 = 0, и напишем 0 под 4, чтобы вычесть 4 — 0 = 4
- Шаг 5: Выведите следующее число из делимого, т. е. 8, и поместите его рядом с этим 4. Число, которое следует рассмотреть, равно 48.

- Шаг 6: Используя таблицу умножения 24, мы знаем, что 24 × 2 = 48. Поэтому мы пишем 2 в частном и 48 под делимым, чтобы вычесть их. Вычтите 48 — 48 = 0. Таким образом, остаток = 0 и частное = 302. Это означает, что 7248 ÷ 24 = 302.
Длинное деление многочленов
Если нет общих множителей между числителем и знаменателем или если вы не можете найти множители, вы можете использовать процесс деления в длину, чтобы упростить выражение. Для получения дополнительной информации о полиномах деления в длину посетите страницу Полиномы деления.
Деление в длинное с десятичными дробями
Деление в длинное с десятичными дробями можно легко выполнить так же, как и обычное деление. Нам просто нужно помнить о десятичных дробях и копировать их по мере поступления. Для получения дополнительной информации о делении в длинное с десятичными дробями посетите страницу Деление десятичных дробей.
Как делить десятичные дроби на целые числа?
Когда нам нужно разделить десятичные дроби на целые числа, мы следуем той же процедуре деления в большую сторону и помещаем десятичную дробь в частное всякий раз, когда она появляется. Давайте разберемся в этом с помощью примера.
Давайте разберемся в этом с помощью примера.
Пример: Разделить 36,9 ÷ 3
Решение: Давайте посмотрим, как делить шаг за шагом.
- Шаг 1: Здесь первая цифра делимого 3 и равна делителю. Итак, 3 ÷ 3 = 1. Итак, 1 записывается сверху как первая цифра частного, а произведение 3 записывается под делимым 3.
- Шаг 2: Вычесть 3 — 3 = 0. Сократите вторую цифру делимого и поместите ее рядом с 0, то есть 6
- Шаг 3: Используя таблицу умножения 3, мы знаем, что 3 × 2 = 6. Поэтому мы пишем 2 в частном и 6 под делимым, чтобы вычесть их. Вычесть 6 — 6 = 0,
- Шаг 4 : Теперь идет десятичная точка в делимом. Итак, поместите десятичную дробь в частное после 12 и продолжите нормальное деление.
- Шаг 5: Выведите следующее число из делимого, т. е. 9. Теперь нужно рассмотреть число 9.
- Шаг 6: Используя таблицу умножения 3, мы знаем, что 3 × 3 = 9.
 Поэтому мы пишем 3 в частном и 9 под делимым, чтобы вычесть их. Вычтите 9 — 9 = 0. Таким образом, остаток = 0 и частное = 12,3. Это означает, что 36,9 ÷ 3 = 12,3 .
Поэтому мы пишем 3 в частном и 9 под делимым, чтобы вычесть их. Вычтите 9 — 9 = 0. Таким образом, остаток = 0 и частное = 12,3. Это означает, что 36,9 ÷ 3 = 12,3 .
Советы и рекомендации по длинному делению:
Ниже приведены несколько важных советов и приемов, которые помогут вам при работе с длинным делением:
- Остаток всегда меньше делителя.
- При делении делитель не может быть равен 0.
- Деление — это повторное вычитание, поэтому мы можем проверить наше частное и повторными вычитаниями.
- Мы можем проверить частное и остаток от деления, используя формулу деления: Делимое = (Делитель × Частное) + Остаток.
- Если остаток равен 0, то мы можем проверить наше частное, умножив его на делитель. Если произведение равно делимому, то частное верно.
☛ Связанные статьи
- Формула длинного деления
- Длинное деление многочленов
- Длинное деление с остатками Рабочие листы
- Полное деление без остатка Рабочие листы
- Длинное деление с двузначными делителями Рабочие листы
- Калькулятор длинного деления
Cuemath — одна из ведущих мировых обучающих платформ по математике, которая предлагает онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Часто задаваемые вопросы о длинном дивизионе
Что такое длинное деление в математике?
Длинное деление — это процесс деления больших чисел удобным способом. Число, которое делится на более мелкие группы, называется делимым, число, на которое мы делим его, называется делителем, значение, полученное после выполнения деления, называется частным, а число, оставшееся после деления, называется остатком.
Как сделать длинное деление?
Следующие шаги объясняют процесс длинного деления. Эта процедура объясняется примерами выше на этой странице.
- Запишите делимое и делитель на соответствующих позициях.
- Возьмите первую слева цифру делимого.
- Если эта цифра больше или равна делителю, то разделите ее на делитель и сверху запишите ответ как частное.

- Запишите произведение под делимым и вычтите результат из делимого, чтобы получить разницу. Если эта разность меньше делителя, а в делимом не осталось чисел, то это считается остатком и производится деление. Однако, если в делимом больше цифр, которые нужно перенести вниз, мы продолжаем тот же процесс, пока в делимом не останется больше цифр.
Каковы этапы длинного деления?
Ниже приведены 5 основных шагов деления в большую сторону. Например, давайте посмотрим, как мы делим 52 на 2.
- Шаг 1: Рассмотрим первую цифру делимого, которая в этом примере равна 5. Здесь 5 > 2. Мы знаем, что 5 не делится на 2.
- Шаг 2: Мы знаем, что 2 × 2 = 4, поэтому запишем 2 как частное.
- Шаг 3: 5 — 4 = 1 и 1 < 2 (Записав произведение 4 под делимым, мы их вычтем).
- Шаг 4: 1 < 2, поэтому мы уменьшаем 2 из делимого и теперь получаем 12 в качестве нового делимого.

- Шаг 5: Повторяйте процесс до тех пор, пока не получите остаток меньше делителя. 12 делится на 2, так как 2 × 6 = 12, поэтому мы пишем 6 в частном, а 12 — 12 = 0 (остаток).
Следовательно, частное равно 26, а остаток равен 0.
Как выполнить длинное деление с двумя цифрами?
При длинном делении на 2 цифры считаем обе цифры делителя и проверяем на делимость первых двух цифр делимого. Если первые 2 цифры делимого меньше делителя, то учитывают первые три цифры делимого. Продолжайте деление так же, как мы делим обычные числа. Эта процедура объясняется приведенными выше примерами на этой странице под заголовком «Длинное деление на двузначное число».
Что такое длинное деление многочленов?
В алгебре длинное деление многочленов — это алгоритм деления многочлена на другой многочлен той же или более низкой степени. Например, (4x 2 — 5x — 21) является многочленом, который можно разделить на (x — 3) по определенным правилам, что даст в результате 4x + 7 в качестве частного.

 А после, разделить полученный на второй множитель 8:
А после, разделить полученный на второй множитель 8:

 Мы видим, что 35 > 4, но 35 не делится на 4, поэтому мы ищем число чуть меньше 35 в таблице 4. Мы знаем, что 4 × 8 = 32, что меньше 35, поэтому мы идем на это. .
Мы видим, что 35 > 4, но 35 не делится на 4, поэтому мы ищем число чуть меньше 35 в таблице 4. Мы знаем, что 4 × 8 = 32, что меньше 35, поэтому мы идем на это. .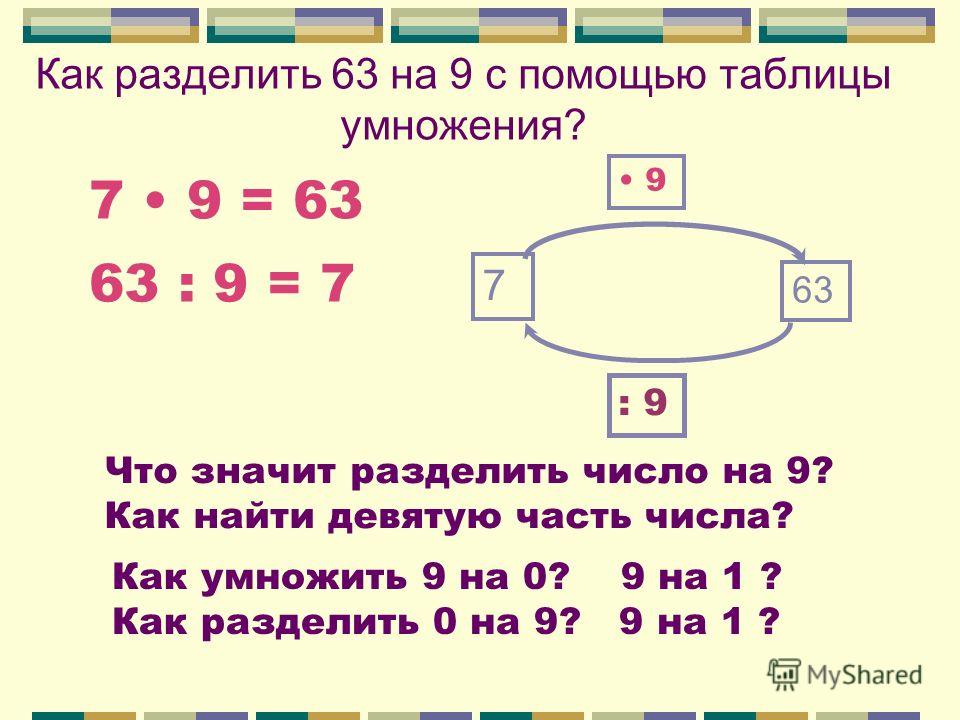 Число, которое будет рассматриваться сейчас, равно 15.
Число, которое будет рассматриваться сейчас, равно 15.

 Поэтому мы пишем 3 в частном и 9 под делимым, чтобы вычесть их. Вычтите 9 — 9 = 0. Таким образом, остаток = 0 и частное = 12,3. Это означает, что 36,9 ÷ 3 = 12,3
Поэтому мы пишем 3 в частном и 9 под делимым, чтобы вычесть их. Вычтите 9 — 9 = 0. Таким образом, остаток = 0 и частное = 12,3. Это означает, что 36,9 ÷ 3 = 12,3 

Ваш комментарий будет первым