Как построить график функции по уравнению – Функции. Основные виды, графики, способы задания

Алгебра. Урок 5. Графики функций

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме «Графики функций».

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

 

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) — горизонтальная ось.

Ось ординат (ось y ) — вертикальная ось.

 

Функция — это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.

 

Линейная функция – функция вида y=ax+b где a и b — любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b:

 

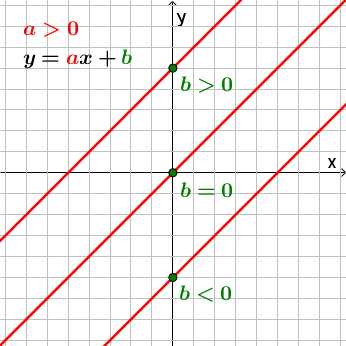
Если a>0, прямая будет проходить через I и III координатные четверти.

b — точка пересечения прямой с осью y.

 

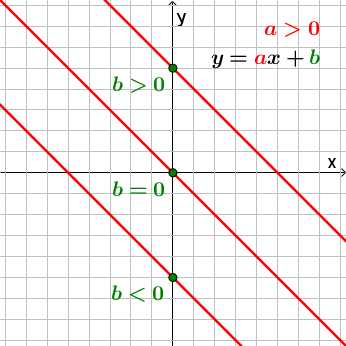
Если a<0, прямая будет проходить через II и IV координатные четверти.

b — точка пересечения прямой с осью y.

 

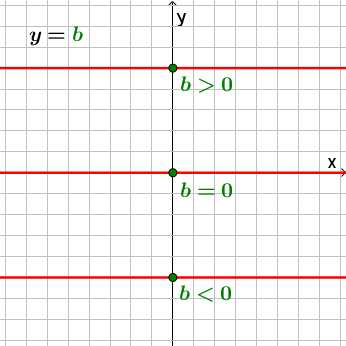
Если a=0, функция принимает вид y=b.

 

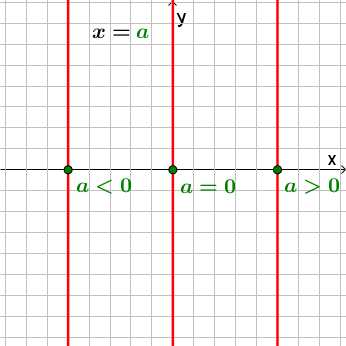
Отдельно выделим график уравнения x=a.

Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

 

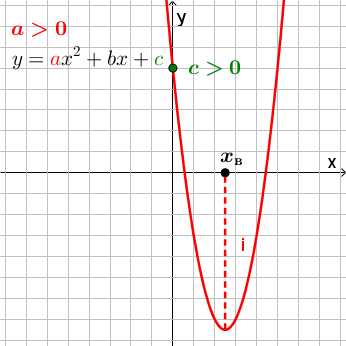
Графиком функции y=ax2+bx+c является парабола.

Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a,b,c:

1. Коэффициент a указывает на то, куда направлены ветки параболы.

• Если a>0 , ветки параболы направлены вверх.
• Если a<0 , ветки параболы направлены вниз.

1. Коэффициент c указывает, в какой точке парабола пересекает ось y.
2. Коэффициент b помогает найти xв — координату вершины параболы.

xв=−b2a

1. Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .

• Если D>0 — две точки пересечения.
• Если D=0 — одна точка пересечения.
• Если D<0 — нет точек пересечения.

 

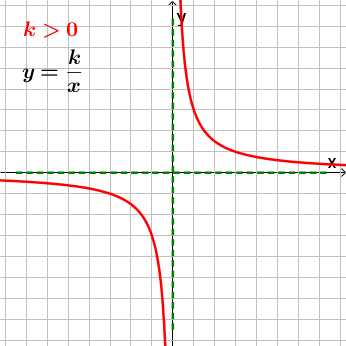
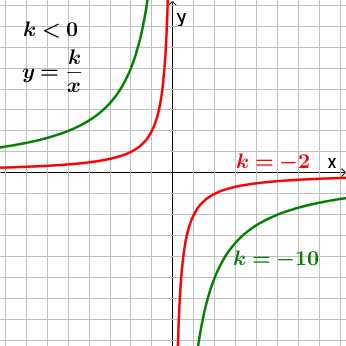
Графиком функции y=kx является гипербола.

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k>0, то ветви гиперолы проходят через I и III четверти.

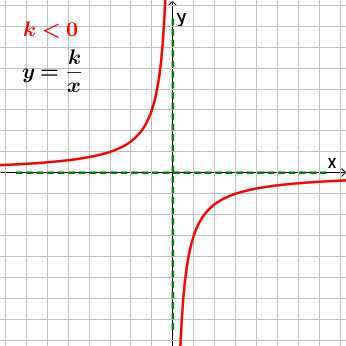
Если k  <  0, ветви гиперболы проходят через II и IV четверти.

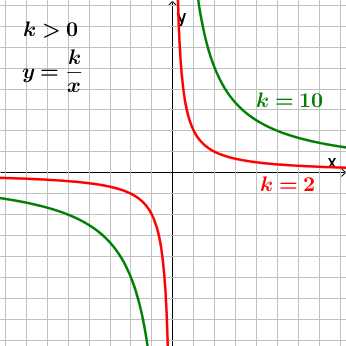
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y.

 

 

Функция y  =  x имеет следующий график:

 

Функция y = f(x)возрастает на интервале, если большему значению аргумента (большему значению x) соответствует большее значение функции (большее значение y).

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y = f(x)убывает на интервале, если большему значению аргумента (большему значению x) соответствует меньшее значение функции (большее значение y).

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

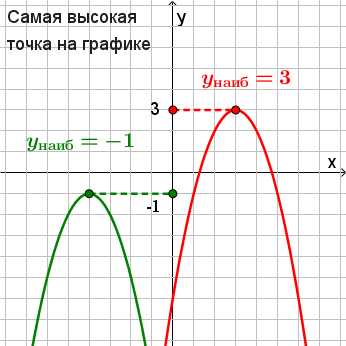
Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наибольшим значением функции.

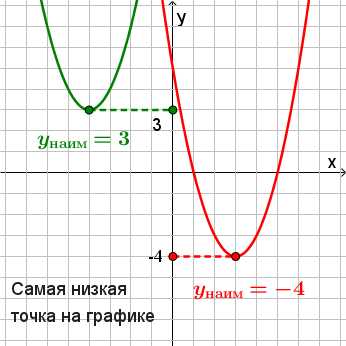
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наименьшим значением функции.

 

 

Скачать домашнее задание к уроку 5.

 

epmat.ru

Как построить график функции

В этой статье разобран самый простой метод получения графика функции.

Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.

Итак, алгоритм по шагам:

1. Представьте, как выглядит ваш график.

Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти

здесь. Этот пункт желательный, но не обязательный.

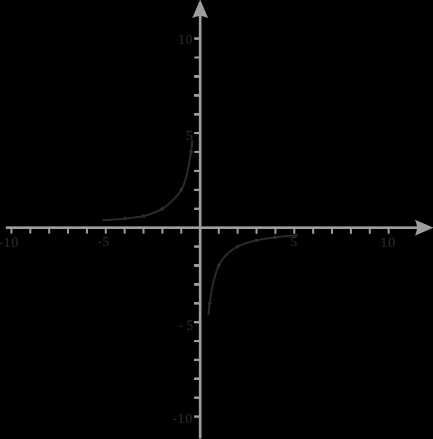
Пример: Построить график функции \(y=-\)\(\frac{2}{x}\)

Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти. Её график выглядит как-то так:

2. Составьте таблицу точек, принадлежащих графику:

Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».

Пример: \(y=-\)\(\frac{2}{x}\)

при \(x=-1\)		\(y=-\)\(\frac{2}{-1}\)\(=2\)
при \(x=0\)		\(y\) — не существует (делить на ноль нельзя)
при \(x=1\)		\(y=-\)\(\frac{2}{1}\)\(=-2\)
при \(x=2\)		\(y=-\)\(\frac{2}{2}\)\(=-1\)
при \(x=3\)		\(y=-\)\(\frac{2}{3}\)
при \(x=4\)		\(y=-\)\(\frac{2}{4}\)\(=-\)\(\frac{1}{2}\)

Результат вычислений удобно представлять в виде таблицы, примерно такой:

\(x\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)
\(y\)	\(2\)	\(-\)	\(-2\)	\(-1\)	\(-\)\(\frac{2}{3}\)	\(-\)\(\frac{1}{2}\)

Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.

4. Постройте координатную плоскость и отметьте на ней точки из таблицы.

Пример:

5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.

Пример:  Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с   \(x=-2\), \(x=-4\), \(x=\)\(\frac{1}{2}\) и \(x=-\)\(\frac{1}{2}\)

при \(x=-2\)		\(y=-\)\(\frac{2}{-2}\)\(=1\)
при \(x=-4\)		\(y=-\)\(\frac{2}{-4}\)\(=\)\(\frac{1}{2}\)
при \(x=\)\(\frac{1}{2}\)		\(y=-\)\(\frac{2}{\frac{1}{2}}\)\(=-2:\)\(\frac{1}{2}\)\(=-2 \cdot 2=-4\)
при \(x=-\)\(\frac{1}{2}\)		\(y=-\)\(\frac{2}{-\frac{1}{2}}\)\(=-2:(-\)\(\frac{1}{2}\)\()\)\(=-2 \cdot (-2)=4\)

\(x\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(-2\)	\(-4\)	\(\frac{1}{2}\)	\(-\)\(\frac{1}{2}\)
\(y\)	\(2\)	\(-\)	\(-2\)	\(-1\)	\(-\)\(\frac{2}{3}\)	\(-\)\(\frac{1}{2}\)	\(1\)	\(\frac{1}{2}\)	\(-4\)	\(4\)

6. Постройте график

Теперь аккуратно и плавно соединяем точки.

Готово!

Скачать статью

cos-cos.ru

Квадратичная функция и ее график

В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.

Функция вида , где  называется квадратичной функцией.

В уравнении квадратичной функции:

a — старший коэффициент

b — второй коэффициент

с  — свободный член.

Графиком квадратичной функции является квадратичная парабола, которая для функции  имеет вид:

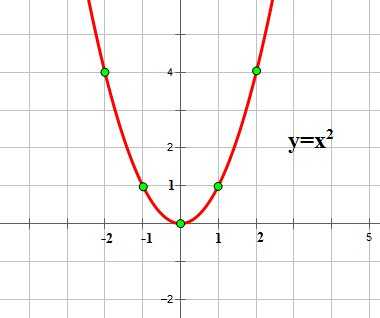
Обратите внимание на точки, обозначенные зелеными кружками — это, так называемые «базовые точки». Чтобы найти координаты этих точек для функции , составим таблицу:

Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции  при любых значениях остальных коэффициентов.

График  функции  имеет вид:

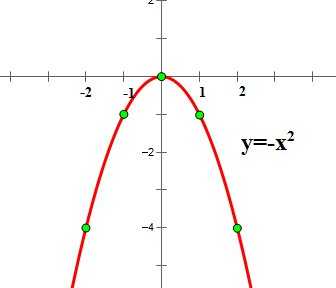
Для нахождения координат базовых точек составим таблицу:

 

Обратите внимание, что график функции  симметричен графику функции относительно оси ОХ.

Итак, мы заметили:

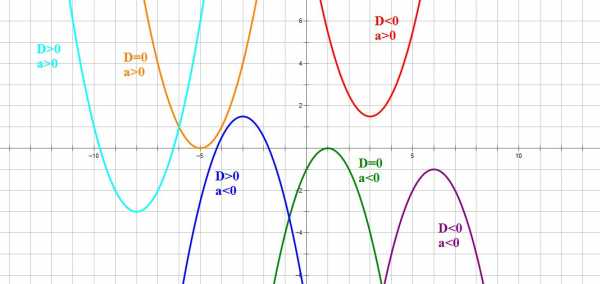
Если старший коэффициент a>0, то ветви параболы напрaвлены вверх.

Если старший коэффициент a<0, то ветви параболы напрaвлены вниз.

Второй параметр для построения графика  функции — значения х, в которых функция равна нулю, или нули функции. На графике нули функции  — это точки пересечения графика функции с осью ОХ.

Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты  точек  пересечения графика функции с осью ОХ, нужно решить уравнение .

В случае квадратичной функции  нужно решить квадратное уравнение .

Теперь внимание!

В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.

И здесь возможны три случая:

1. Если ,то уравнение  не имеет решений, и, следовательно, квадратичная парабола  не имеет точек пересечения с осью ОХ. Если ,то график функции выглядит как-то так:

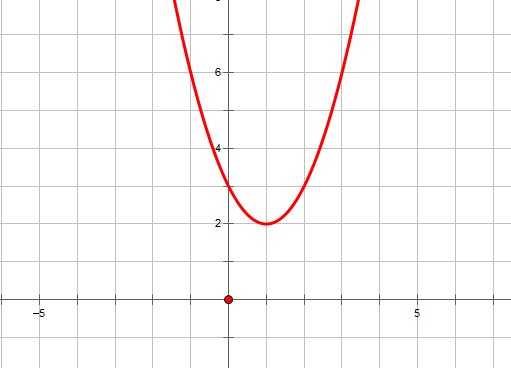
2. Если ,то уравнение  имеет одно решение, и, следовательно, квадратичная парабола   имеет одну точку пересечения с осью ОХ. Если ,то график функции выглядит примерно так:

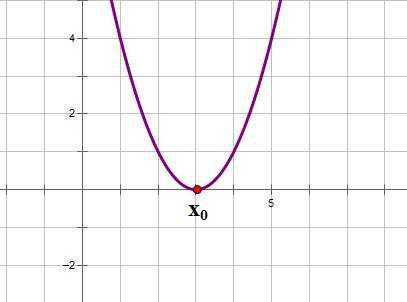
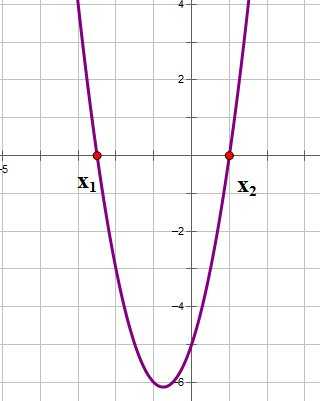
3.  Если ,то уравнение  имеет два решения, и, следовательно, квадратичная парабола   имеет две точки пересечения с осью ОХ:

,  

Если ,то график функции выглядит примерно так:

Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.

Следующий важный параметр графика квадратичной функции — координаты вершины параболы:

 

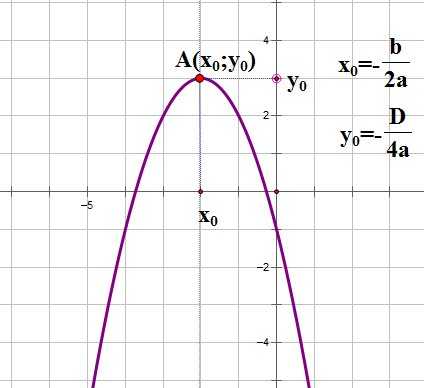
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.

И еще один параметр, полезный при построении графика функции — точка пересечения параболы  с осью OY.

Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы  с осью OY, нужно в уравнение параболы вместо х подставить ноль: .

То есть точка пересечения параболы с осью OY имеет координаты (0;c).

Итак, основные параметры графика квадратичной функции показаны  на рисунке:

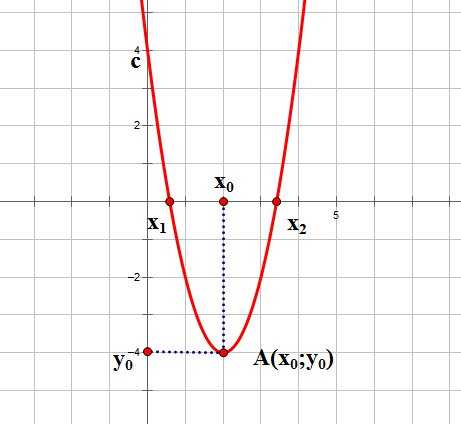
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.

1. Функция задана формулой .

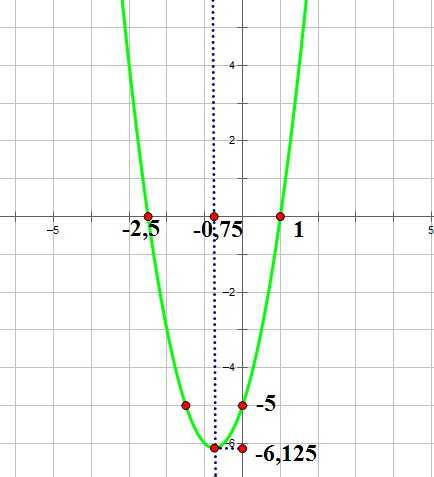
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции 

1. Направление ветвей параболы.

Так как ,ветви параболы направлены вверх.

2. Найдем дискриминант квадратного трехчлена 

 

Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.

Для того, чтобы найти их координаты, решим уравнение: 

,  

3.   Координаты  вершины параболы:

4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.

Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:

Этот способ можно несколько упростить.

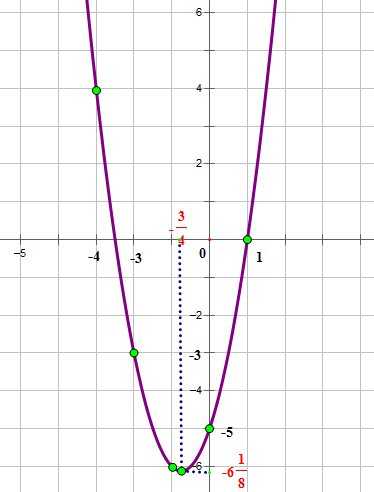
1. Найдем координаты вершины параболы.

2. Найдем координаты точек, стоящих справа и слева от вершины.

Воспользуемся результатами построения графика функции

Кррдинаты вершины параболы

Ближайшие к вершине точки, расположенные  слева от вершины имеют абсциссы соответственно -1;-2;-3

Ближайшие к вершине точки, расположенные справа имеют абсциссы  соответственно 0;1;2

Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их  в таблицу:

Нанесем эти точки на координатную плоскость и соединим плавной линией:

2.  Уравнение квадратичной функции имеет вид  — в этом уравнении — координаты вершины параболы

или в уравнении квадратичной функции  , и второй коэффициент — четное число.

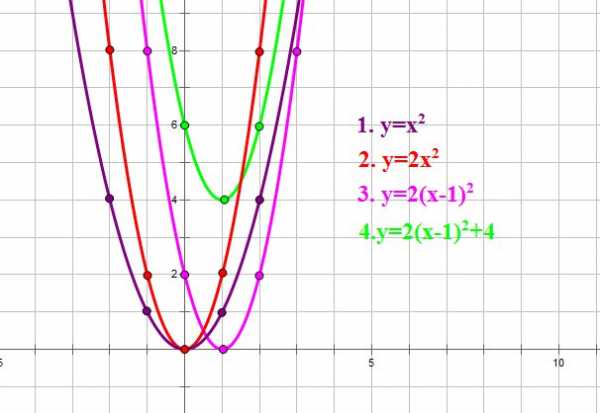
Построим для примера график функции .

Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно

• сначала построить график функции ,
• затем одинаты всех точек графика умножить на 2,
• затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
• а затем вдоль оси OY на 4 единицы вверх:

Теперь рассмотрим построение  графика функции . В уравнении этой функции , и второй коэффициент — четное число.

Выделим в уравнении функции полный квадрат: 

Следовательно,  координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):

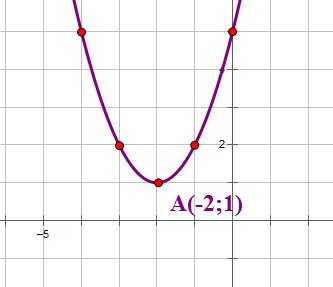
3.  Уравнение квадратичной функции имеет вид y=(x+a)(x+b)

Построим для примера график функции y=(x-2)(x+1)

1. Вид уравнения функции позволяет легко найти нули функции — точки пересечения графика функции с осью ОХ:

(х-2)(х+1)=0, отсюда 

2. Координаты вершины параболы:

3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.

Нанесем эти точки на  координатную плоскость и построим график:

 

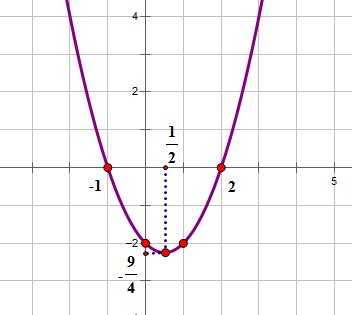
График квадратичной функции.

Перед вами график квадратичной функции вида .

Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
— ширины графика функции от значения коэффициента ,
— сдвига графика функции вдоль оси от значения  ,

— сдвига графика функции вдоль оси от значения  
— направления ветвей параболы от знака коэффициента
— координат вершины параболы от значений и :

Скачать таблицу квадратичная функция

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Строим графики функций, содержащие модуль. Часть 1

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

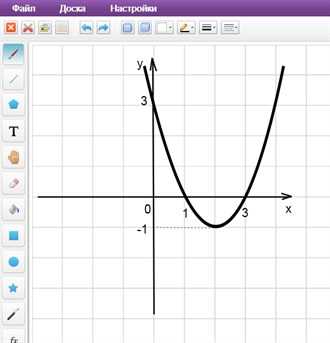
Пример 1. Изобразить график функции y = |x² – 4x + 3|

1) Строим график функции y = x² – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

0x : y = 0.

x² – 4x + 3 = 0.

x₁ = 3, x₂ = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

0y: x = 0.

y = 0² – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

x_в = -(-4/2) = 2, y_в = 2² – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

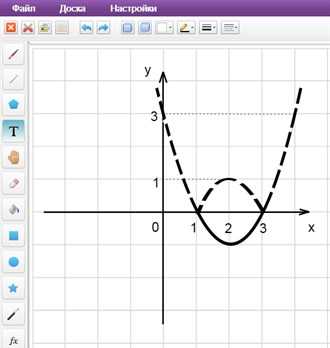
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2, изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x² – 4 · |x| + 3

Так как x² = |x|², то исходную функцию можно переписать в следующем виде: y = |x|² – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x² – 4 · x + 3 (см. также рис. 1).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

4) Окончательный график изображен на рисунке (рис. 3).

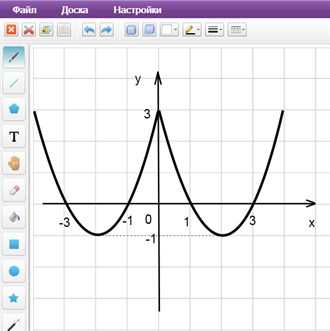
Пример 3. Изобразить график функции y = log₂|x|

Применяем схему, данную выше.

1) Строим график функции y = log₂x (рис. 4).

Далее повторяем пункты 2)-3) предыдущего примера и получаем окончательный график (рис. 5).

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже  являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому , их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

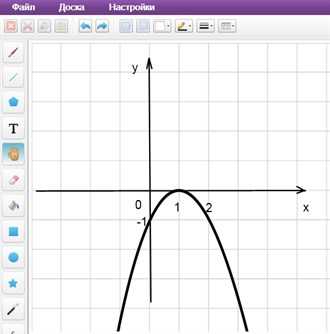
Пример 4. Изобразить график функции y = |-x² + 2|x| – 1|.

1) Заметим, что x²= |x|². Значит, вместо исходной функции y = -x² + 2|x| – 1

можно использовать функцию y = -|x|² + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x|² + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x² + 2x – 1 (рис. 6).

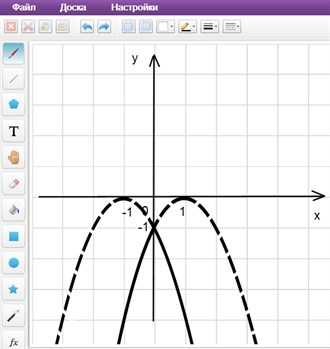
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7).

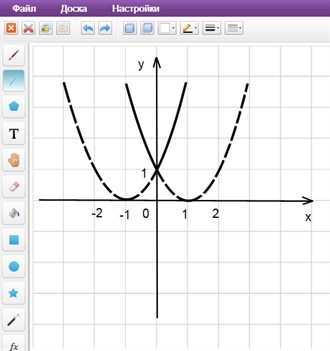
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8).

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a)  Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9).

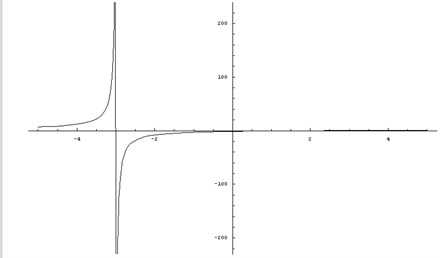
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

Далее повторяем пункты b)-c) из предыдущего примера и получаем следующий график функции (рис. 10).

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11).

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru