Как начертить график функции: Как построить график функции у = f(x) + m, если известен график функции у = f(x) — урок. Алгебра, 8 класс.

Как построить график линейной функции? | 7 класс

Содержание

Вспомним, что такое график функции:

Графиком функции называется множество точек плоскости, абсциссы которых равны значениям аргумента $x$, а ординаты – соответствующим значениям функции $y$.

Как мы уже выяснили, график линейной функции представляет из себя прямую линию. 

Для его построения нет необходимости находить координаты более двух точек. То есть, чтобы построить график линейной функции, достаточно подставить в заданную формулу всего два значения $x$

Значит, нужно:

1. Подставить в функцию 2 любых значения $x$ и получить соответствующие значения $y$.
2. Мы получили координаты 2 точек. Отметим их на координатной плоскости.
3. Проведём через эти 2 точки прямую линию.

Построим график функции $y=2x+1$

Для удобства состоим таблицу значений $x$ и $y$.

Переменная	Значение 1	Значение 2
$x$
$y$

Какие $x$ взять? Удобно брать небольшие числа, например $0$ и $1$

Переменная	Значение 1	Значение 2
$x$	$\color{#3D68EB}0$	$\color{#ED7858}1$
$y$

Теперь нужно посчитать $y$. Подставляем по очереди 2 значения $x$ в нашу функцию:

$x=\color{#3D68EB}0$
$y=2x+1$
$y=2 \cdot 0 + 1 = \color{#253f8d}1$

$x=\color{#ED7858}1$


$y=2x+1$
$y=2 \cdot 1 + 1 = \color{#eb3d3d}3$

Вписываем полученные значения в таблицу и отмечаем точки:

Переменная	Значение 1	Значение 2
$x$	$\color{#3D68EB}0$	$\color{#ED7858}1$
$y$	$\color{#253f8d}1$	$\color{#eb3d3d}3$

Проводим через эти точки прямую линию. График готов.

{
    "questions": [{
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 2,
                    "b": 1
                }
            }
        },
        "content": "Постройте график функции $y=2x+1$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 2,
                    "b": 2
                }
            }
        },
        "content": "Постройте график функции $y=2x+2$[[graph]]"
    }, {
        "widgets": {
            "graph": {
                "type": "graph",
                "func": "line",
                "settings": { "cells": 12 },
                "answer": {
                    "k": 1,
                    "b": 1
                }
            }
        },
        "content": "Постройте график функции $y=x+1$[[graph]]"
    }]
}

Доведите навык до совершенства с помощью тренажёра построения графиков линейной функции.

5

Оценить урок

Поделиться уроком →

Что можно улучшить?

Изложение материала

Непонятное объяснение

Урок неполный, не хватает информации

Урок перегружен, слишком много информации

Тесты плохого качества

Тестов недостаточно

Тестов слишком много

Тесты слишком легкие

Тесты слишком сложные

Изображения

Изображения плохого качества

Изображений недостаточно

Изображений слишком много

Другое




Войдите, чтобы оценивать уроки

Что нужно исправить?




Спасибо, что помогаете нам стать лучше!

Следующий урок

Коэффициенты k и b

Комментарии

График линейной функции | ЮКлэва

Чтобы понять то, что здесь будет написано, тебе нужно хорошо знать, что такое линейная функция.

Начнем с небольшой проверки:

• Как выглядит линейная функция в общем виде (формула)?
• Почему она называется линейной?
• Как влияет коэффициент при \( \displaystyle x\) на график линейной функции?

Если хоть один вопрос вызвал затруднения, прочти тему «Линейная функция».

Приступим к покорению линий и графиков!

График линейной функции – коротко о главном

График линейной функции – прямая линия. Прямую можно провести через две точки.

Чтобы построить график линейной функции вида y=kx+b, нужно:

• вычислить координаты любых двух точек (взять любые два значения аргумента x и вычислить соответствующие два значения y,
• для каждой пары ( x;y ) найти точку в системе координат, и провести прямую через эти две точки.

Рассмотрим пример для функции \( y=2x+1\):

Проще всего найти функцию, если аргумент: \( x=0:y\left( 0 \right)=2\cdot 0+1=1\).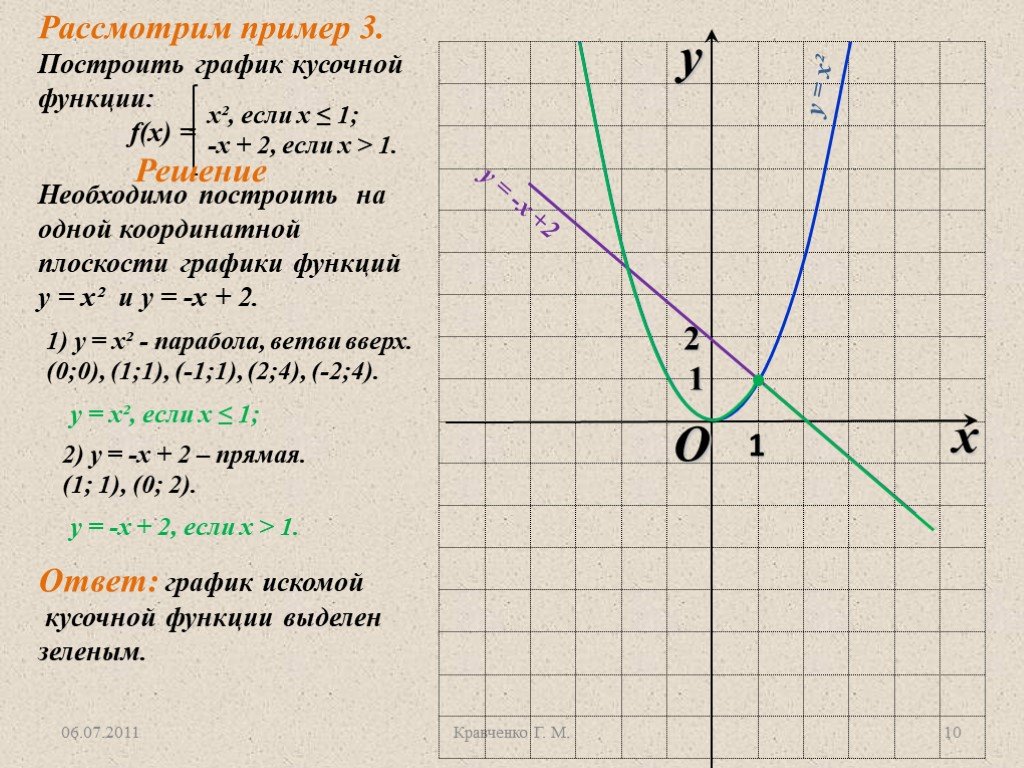

Итак, первая точка имеет координаты \( \left( 0;1 \right)\).

Теперь возьмем любое другое число в качестве \( x\), например, \( x=1:y\left( 1 \right)=2\cdot 1+1=3\).

Вторая точка имеет координаты \( \left( 1;3 \right)\).

Угловой коэффициент \( \displaystyle k\) – это тангенс угла наклона прямой.

Для его нахождения выберем две точки \( \displaystyle A\) и \( \displaystyle B\) на графике и построим прямоугольный треугольник с гипотенузой \( \displaystyle AB\)

\( \displaystyle k=tg\alpha =\frac{BC}{AC}=\frac{2}{1}=2\)

Построение графика линейной функции

Итак, ты уже умеешь обращаться с линейной функцией, анализировать ее график и строить его по точкам. Кстати, сколько нужно точек, чтобы построить график линейной функции?

Скажу сразу, эта тема настолько простая, что много нового ты здесь не выучишь. Но ты научишься не теряться во всяких нестандартных ситуациях.

Итак, дамы и господа, линейная функция:

\( \displaystyle y=kx+b\)

Построение графика линейной функции: ты берешь два каких-либо икса, (например, \( \displaystyle 0\) и \( \displaystyle 1\)), подставляешь их в формулу, находишь соответствующие игреки.

Затем отмечаешь эти две точки на координатной плоскости, прикладываешь линейку, и график готов. Просто и быстро, и ничего выдумывать не надо.

Но бывает, что функция задана по-другому, например, неявно. Сейчас разберем, как быстро справляться с такими ситуациями.

Пример неявно заданной линейной функции

Постройте график уравнения \( \displaystyle 2y+3x=6\).

Ну а что тут сложного? Чтобы произвести построение графика линейной функции выражаем y и строим по точкам.

Это да, но можно сделать проще и интересней!

Выясним, в какой точке эта прямая будет пересекать ось \( \displaystyle Ox\).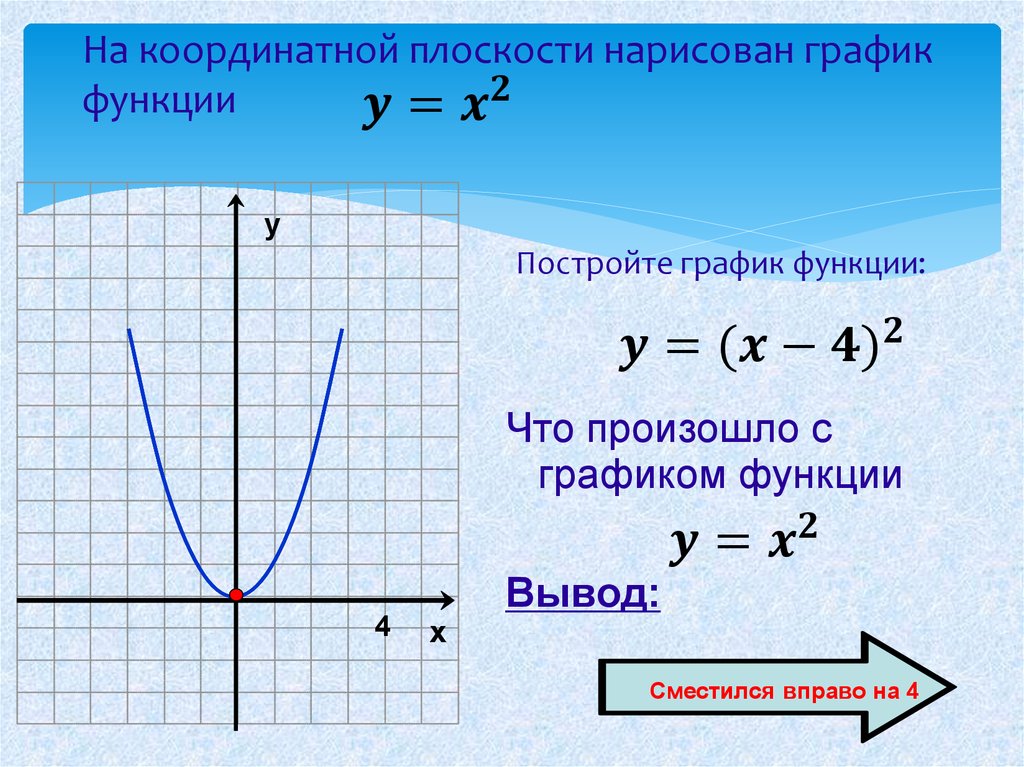

Что характерно для этой точке? Правильно, \( \displaystyle y=0\). Так и пишем:

\( \displaystyle 2\cdot 0+3x=6\text{ }\Rightarrow \text{ }x=2\)

А теперь проделаем то же самое с другой осью: в какой точке график пересекает ось \( \displaystyle Oy\)?

\( \displaystyle x=0\text{ }\Rightarrow \text{ }2y+3\cdot 0=6\text{ }\Rightarrow \text{ }y=3\)

Бум! Вот и они – две точки графика. Осталось только приложить линейку:

Согласись, это было быстро и просто!

А теперь сам:

\( \displaystyle 4x-5y=3\)

Ладно, а как еще можно задать функцию?

Ну, например словесно:

Прямая проходит через точку \( \displaystyle A\left( 2;3 \right)\), а ее угловой коэффициент равен \( \displaystyle 0,75\).

Ну что же, вспоминаем: что такое угловой коэффициент?

Что такое угловой коэффициент

Это, с одной стороны, коэффициент при \( \displaystyle x\), а с другой – это тангенс угла между прямой и осью \( \displaystyle Ox\).

Вот это мы и используем когда делаем построение графика линейной функции: ставим точку \( \displaystyle A\), и рисуем прямоугольный треугольник так, что один его катет параллелен оси \( \displaystyle Ox\), а другой – перпендикулярен.

При этом второй катет должен быть ровно в \( \displaystyle 0,75\) раз больше первого.

Очень удобно в этом случае, чтобы первый катет был равен \( \displaystyle 4\), тогда второй будет равен \( \displaystyle 3\):

4 примера построения графика линейных функций

Пример №1

Прямая, уравнение которой имеет вид \( y=-2x+b\) (\( b\) неизвестно), проходит через точку \( M\left( 1;2 \right)\). Постройте ее.

Справился?

Должно получиться вот так:

Пример №2

Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).

Строить график прямой \( y=-1,5x+1\) нельзя.

О, это что-то новенькое. Про параллельность прямых мы еще не учили.

Но как обычно, все просто. Нарисуем несколько параллельных прямых на координатной плоскости:

Что у них общего? Вообще, какие параметры важны для графиков? Конечно же, коэффициенты \( k\) и \( b\).

И сразу становится ясно: раз \( k\) отвечает за наклон, а наклон у них одинаковый (это же параллельные прямые, а ось \( Ox\) – секущая), значит, у них одинаковый коэффициент \( k\)!

Вернемся к задаче. Напомню условие:

Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( 3;1 \right)\) и параллельной прямой \( y=-1,5x+1\).

Итак, угловой коэффициент нашей прямой \( y=-1,5x+1\) равен угловому коэффициенту прямой , то есть \( -1,5\). Теперь задача становится точь в точь как мы решали до этого:

Пример №3

Произведи построение графика линейной функции и найди уравнение прямой, проходящей через точку \( A\left( -1;2 \right)\) и параллельной прямой \( y=2x+8\).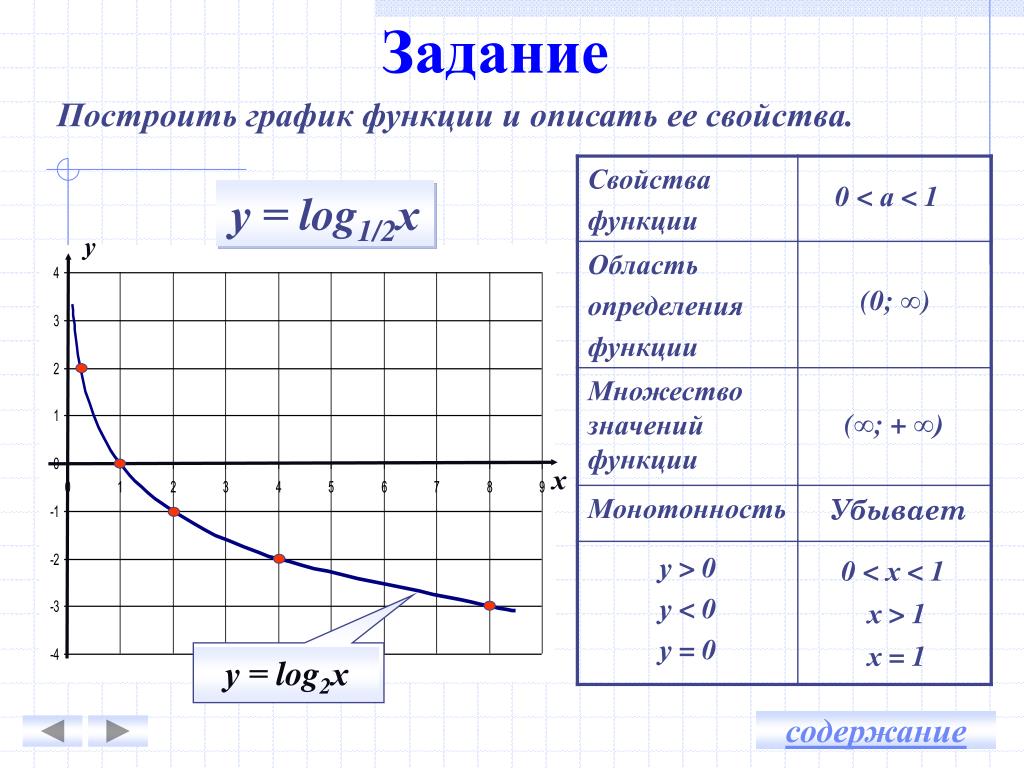 {2}}-1}{x+1}=\frac{\left( x-1 \right)\left( x+1 \right)}{x+1}=x-1\)

Вот и все!

А, нет, не все… еще ведь ОДЗ: на ноль делить нельзя, бла бла бла…

Ладно, ничего сложного здесь нет: \( x+1\ne 0\text{ }\Rightarrow \text{ }x\ne -1\).

Это и есть все отличие от обычной прямой: просто надо будет выколоть из графика одну точку: \( y=x-5\).

Бонус: Вебинары из нашего курса подготовки к ЕГЭ по математике

Элементарные функции и их графики (ЕГЭ 18. Задача с параметром)

Задачи с параметром из ЕГЭ зачастую предполагают исследование функций или хотя бы знание их свойств.

Чтобы научиться исследовать функции, для начала лучше всего научиться строить их графики. 

На этом уроке мы рассмотрим основные элементарные функции, научимся строить их графики и узнаем, как на них влияют разные параметры (коэффициенты в функциях).  

Мы рассмотрим: 

• степенную функцию (линейную, квадратичную, обратную зависимость, корни), 
• тригонометрические и обратные тригонометрические, 
• показательную и 
• логарифмическую функции.

Преобразования графиков функций (ЕГЭ 18. Задачи с параметром)

Научились строить график какой-то функции? А что, если я теперь поменяю один из коэффициентов? Или «заключу» часть функции в модуль? 

Можно ли не строить для этого новый график, а просто передвинуть/растянуть старый?

 Можно! И на этом уроке мы научимся производить такие трансформации. 

Благодаря таким трансформациям мы станем понимать, как выглядят графики функций при всех значениях параметра и научимся решать задачи из ЕГЭ на эту тему.

Как набросать любой график на глаз

Уравнения в математике полезны, но они также неэффективны — для каждого значения x вам нужно выполнить отдельный расчет, чтобы выяснить, что такое y. Графики берут это уравнение и превращают его в визуальное представление, на которое вы можете смотреть и сразу же видеть, что происходит при различных значениях x, как изменяется функция и многое другое!

Однако, когда вы впервые изучаете графики, все сводится к запоминанию основных уравнений и того, как будут выглядеть их графики, начиная с линейных уравнений в форме пересечения наклона. Однако по мере того, как вы переходите к более сложным уравнениям, таким как квадратные уравнения и тригонометрия, вас часто просят запомнить формы таких уравнений —

— где вы должны запомнить точную настройку уравнения и то, что означает каждый член на графике, будь то вершина, наклон, точки пересечения, масштабирование, горизонтальные или вертикальные сдвиги и многое другое!

Но зачем запоминать все эти а, в, к и з, если это будет полезно только в нескольких конкретных случаях?!

Вместо этого в следующий раз, когда вам понадобится узнать, как должен выглядеть график функции, попробуйте выполнить эти шаги, чтобы быстро набросать любой график!

Для демонстрации воспользуемся уравнением:

Это похоже на полиномиальные уравнения, которые вы, возможно, видели в классе, но они кубические, поэтому у нас нет очевидных форм уравнений, которые можно было бы использовать для построения графика.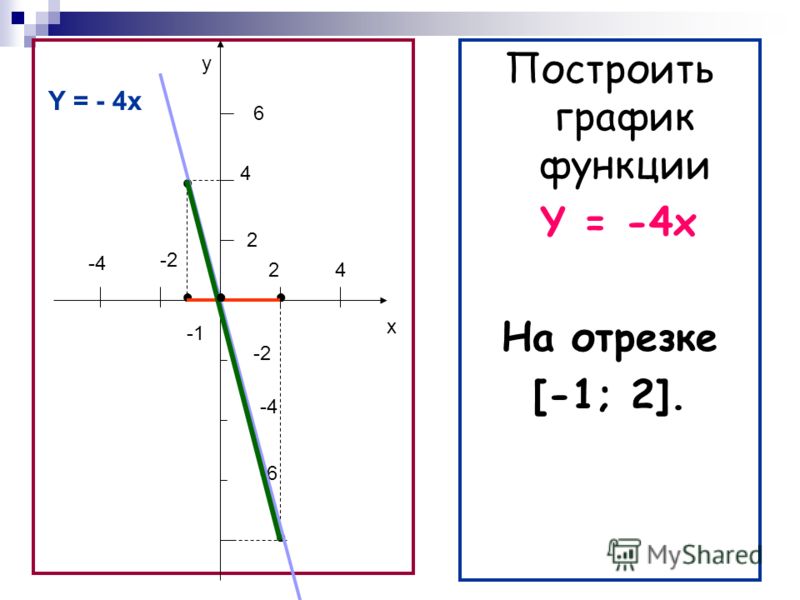 Итак, как построить график этой функции?

1. График x = 0

Первое, что мы хотим сделать, это получить несколько точек на нашем графике, поэтому мы хотим выбрать те, которые будет легко вычислить. Практически для любого уравнения подставить x = 0 и решить для y можно быстро и легко сделать на глаз, и почти всегда можно обойтись без калькулятора. Для нашего примера уравнения:

Итак, первая точка, которую мы поместим на наш график, это (0, -4).

а. Если вы можете легко найти его, постройте график y = 0

Далее, в некоторых случаях y = 0 тоже довольно легко решить. Если вы можете быстро решить y = 0 , это еще один хороший момент, который нужно решить сразу. В данном случае:

Итак, теперь у нас есть точка (-2, 0) для добавления к нашему графику!

б. Бонус: нанесите несколько простых для расчета точек, таких как x = 1 и x = -1

. В зависимости от графика может быть легко подставить небольшие целые числа, такие как 1 или -1.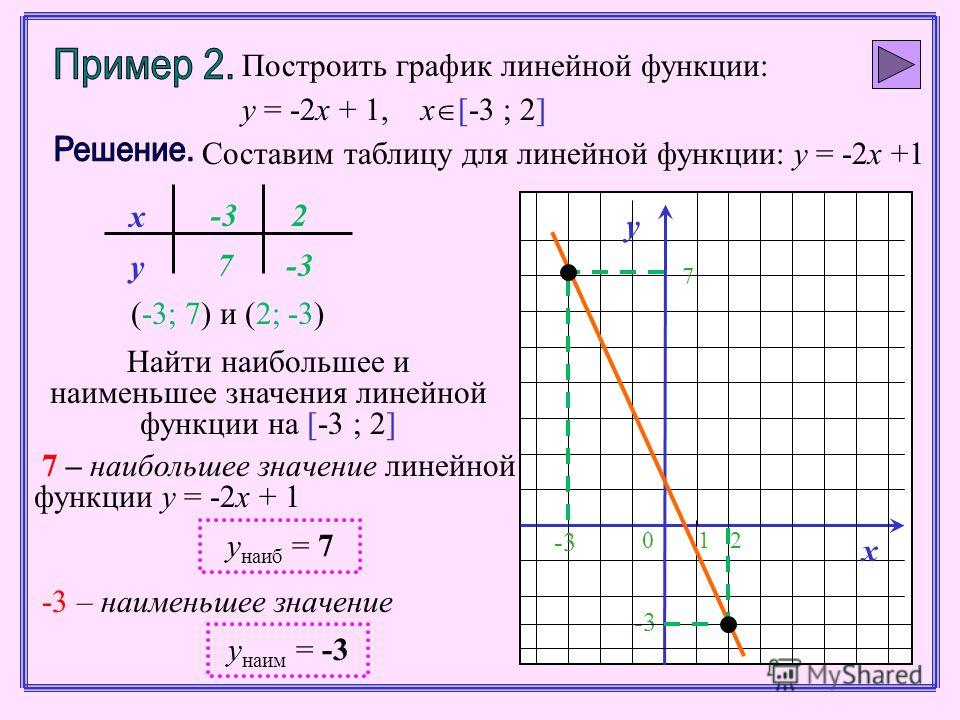 Чем больше точек вы можете добавить к своему графику, тем лучше вы сможете увидеть, какую форму он в конечном итоге примет. Однако придерживайтесь точек, которые легко рассчитать. Цель этого метода — быстро найти всего несколько точек — если вы собираетесь вычислять каждую точку на графике, вы не экономите время!

Для этого уравнения мы получим:

и

Итак, теперь у нас есть четыре точки: (0,-4), (-2,0), (1,-18) и ( -1, -2). Давайте нанесем эти точки и посмотрим, как они выглядят!

Мы можем начать видеть, как график обретает форму, но нам понадобится больше информации, прежде чем мы закончим.

2. Выяснить, что происходит, когда x действительно велико (в положительном и отрицательном направлении)

Любая линия, которую мы рисуем, должна заканчиваться стрелками на обоих концах, чтобы мы знали, что происходит по мере продвижения. далее по оси x как в положительном, так и в отрицательном направлении. Это то, что называется «конечным поведением». Чтобы выяснить, что это такое, мы подставим два числа в исходное уравнение — большое положительное число и большое отрицательное число. Теперь мы на самом деле не собираемся выбирать число и использовать наш калькулятор, чтобы выяснить, что произойдет, мы просто посмотрим, как части уравнения повлияют на конечный результат.

Например, подставив большое положительное число в нашу кубическую функцию, мы получим:

Добавление 1 к большому положительному числу почти не изменит его — затем, когда мы возведем его в куб, оно станет действительно большим положительным числом.

Однако действительно большое положительное число станет отрицательным при умножении на -2, а вычитание 2 не будет иметь большого значения, поэтому конечным результатом будет действительно большое отрицательное число.

Если мы попробуем то же самое для другой стороны графика, подставив вместо x большое отрицательное число, мы получим:

Большое отрицательное число в кубе — это действительно большое отрицательное число, но на этот раз, когда оно умножается на -2, оно становится действительно большим положительным числом.

o, для нашего графика мы нашли, что при больших положительных x, y большие и отрицательные, а при больших отрицательных x, y большие и положительные. Давайте добавим это к нашему графику со стрелками.


3. Опционально: ищите любые «значимые» значения x

Некоторые уравнения имеют необычные особенности или особые точки, которые вы можете заметить, взглянув на уравнение – обратите особое внимание на любые точки, в которых большая часть уравнения может стать нулем. Это может помочь вам найти корни, асимптоты или другие места, где форма графика изменяется необычным образом.

Например, в уравнении, которое мы рассматривали,

Этот термин интересен тем, что если x = -1, вся часть уравнения станет равной нулю. Конечно, мы уже нашли эту точку ранее, но это говорит нам о том, что x = -1 — это «особая» точка в уравнении — возможно, здесь форма графика как-то сдвинется.

4. Соедини точки и закончи!

На данный момент мы сделали все, что могли — у нас есть несколько точек на графике, мы знаем, как он будет выглядеть на концах, и мы определили любые необычные точки или особенности.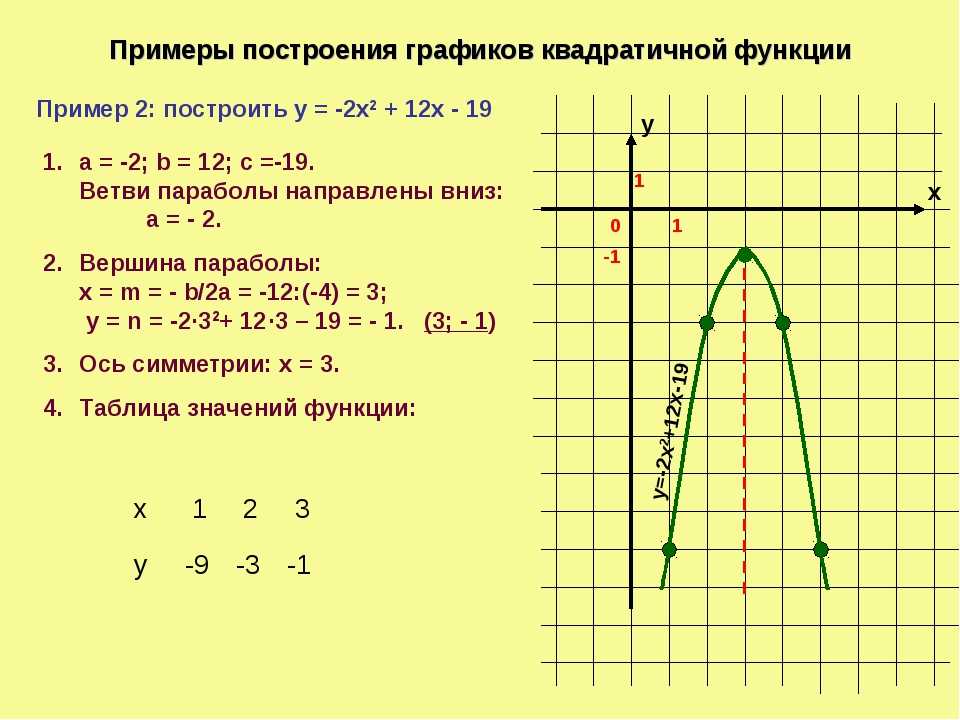 Мы можем не знать точно, что это такое, но мы готовы что-то нарисовать.

Возможно, мы до сих пор не знаем точно, какова форма графика, но здесь вы можете использовать основы для каждого основного уравнения. Мы знаем, что наша линия будет гладкой и максимально простой, но при этом будет попадать во все точки. Если мы в целом знаем, какого рода это уравнение (полиномиальное, радикальное, экспоненциальное), у нас есть хотя бы некоторое предположение, какова будет его общая форма.

В нашем примере у нас достаточно точек, чтобы набросать одну сторону нашего уравнения, но отрицательная сторона немного неясна, поэтому давайте подумаем, что мы можем сказать о другом типе многочлена, квадратном уравнении.

Для нашей кубической функции мы знаем, что квадратичные функции всегда симметричны относительно своей вершины, но это не совсем работает, потому что мы знаем, что в одном направлении мы получим положительное значение, а в другом — отрицательное.

Итак, давайте предположим что-то подобное — может быть, наша «особая» точка при x = -1 — это , как вершина, но в этой точке форма графика такая же, но движется в противоположном направлении.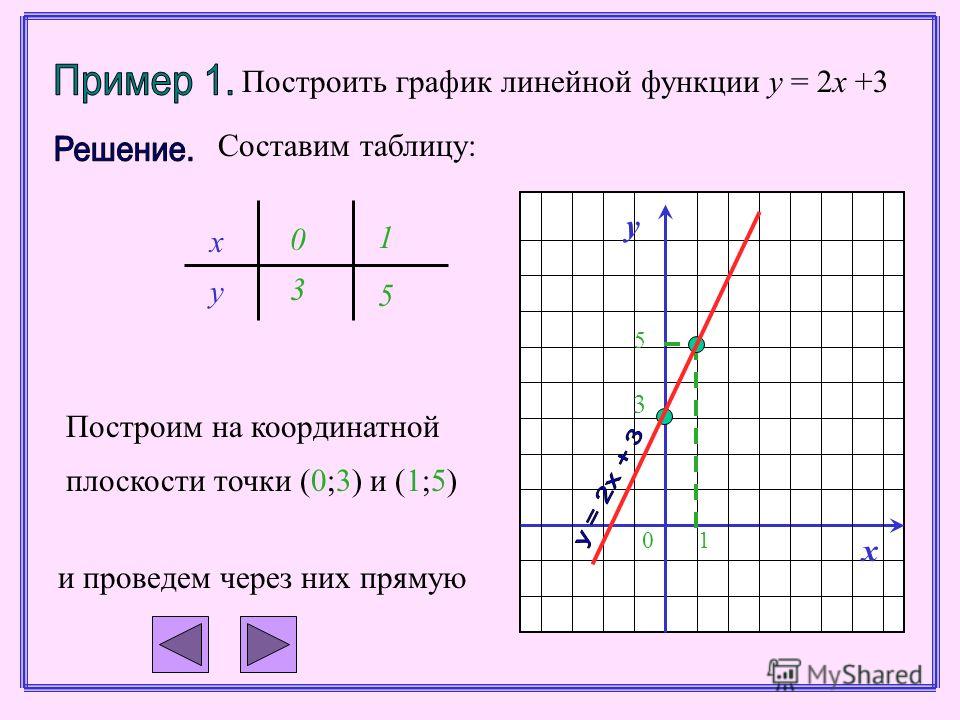 (Для справки я нарисовал пунктирную линию на x = — 1, но, конечно, это не будет частью настоящего окончательного графика.)

Поехали! Это не идеальный график, но за несколько быстрых шагов мы, по крайней мере, в общих чертах знаем, как этот график будет выглядеть. Если вам интересно, вот как это уравнение выглядит, когда оно построено на компьютере.

Этот метод работает для огромного количества функций — многочленов, радикалов, экспонент, логарифмов, тригонометрических функций и многого другого! Просто будьте осторожны, когда вы доберетесь до функций с несколькими y или членами: в этих случаях графики будут необычными, сложными формами, поэтому нарисуйте много точек (x, y), прежде чем пытаться соединить все точки!

Как нарисовать график функции с ограничениями

Как нарисовать график функции с ограничениями :


Здесь мы увидим, как нарисовать график функции с ограничениями.

Вопрос 1 :


Нарисуйте график функции f, удовлетворяющей заданным значениям:

f(0) не определено

lim _{x -> 0 2} f(x)  =  3 4

2)  =  6

lim _{x -> 2} f(x)  =  3

Решение:

Из заданного вопроса

• Мы поняли, что функция не определена, когда x = 0.
• Когда значение x приближается к 0 слева и справа, предельное значение будет приближаться до 4.
• Когда x = 2, значение y будет равно 6.
• Когда значение x приближается к 2 слева и справа, предельное значение приближается к 3.

Значение x приближается слева и справа, предел будет приближаться к значению 4.

Когда x приближается к 2 слева и справа, предел приближается к 3. Рисунок, приведенный выше, иллюстрирует условие.

Когда x = 2, f(x), то есть значение y, будет равно 6.

Таким образом, рисунок, приведенный выше, является требуемым графом приведенных утверждений.

Вопрос 2:


Нарисуйте график функции f, удовлетворяющей заданным значениям:0131  f(x) = 0

lim  _{x -> 2}  f(x)  не существует


Решение:

Из заданного значения

быть 0.

Когда x = 2, значение y будет равно 0.

Когда x стремится к 2, функция не существует. Чтобы показать это, мы должны показать график с различными значениями y.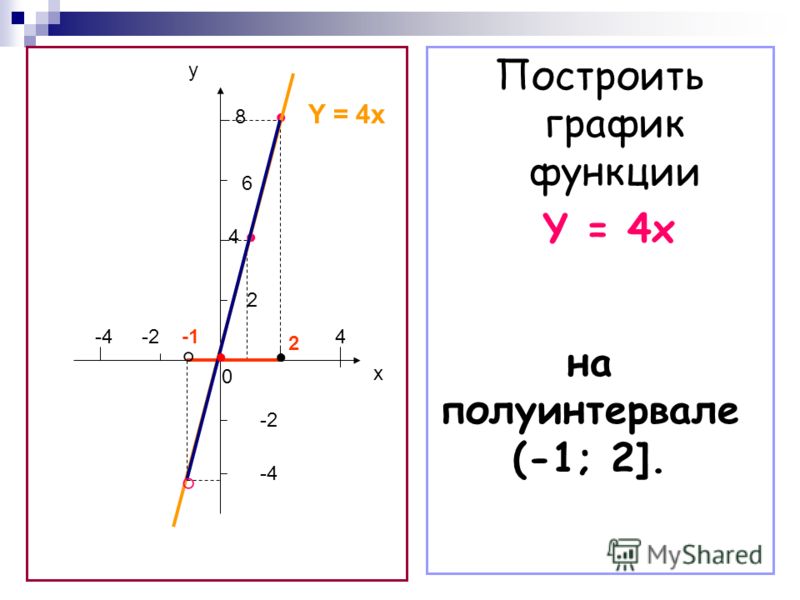

Вопрос 3 :

Напишите краткое описание значения обозначения lim _{x -> 8} f(x)  =  25

Решение:

Когда x приближается с левой и правой стороны, значение предела будет приближаться к 25.

lim х -> 8 — f(x) = 25

lim х -> 8 + f(x) = 25

Вопрос 4:

Если f(2) = 4, можете ли вы сделать вывод о пределе f(x) при приближении x к 2?

Решение:

Данное утверждение представляет собой, когда x = 2, значение y будет равно 4.

Случай 1:

Когда x приближается с левой и правой стороны, мы получим примерно одинаковые значения, или

Случай 2:

Когда x приближается слева и справа, мы получим разные значения.

Следовательно, мы не можем ничего сказать о пределе f(x) при приближении x к 2?

Вопрос 5 :

Если предел f(x) при приближении x к 2 равен 4, можете ли вы сделать какой-нибудь вывод о f(2)? Объясните рассуждения.

Решение:

Дано:

lim _{x -> 2} f(x) = 4

Отсюда мы можем понять, что

lim х -> 2 — f(x) = 4

lim х -> 2 + f(x) = 4

когда x приближается к 2 слева и справа, предел приближается к 4.  

Следовательно, мы ничего не можем сказать о f(2).

Вопрос 6 :

Оценить: 

lim x->3 (x ² -9)/(x — 3), если он существует, найдя f(3 ⁺ ) и f(3 ^— )

Решение :

   =  im _x->3 (x ²  -9)/(x — 3)

 (  =  im _{x->3 3)/(x — 3)}

   =  im _x->3 (x + 3)


im x->3+  f(x)  =  3 + 3   =  6

im x->3-  f(x)  =  3 + 3   =  6

Вопрос 7:

Проверьте существование LIM _{x -> 1} F (x)

Решение:

Если предел x -> 1, затем

Lim _{x- > 1} — f(x)  =  lim _{x-> 1} + f(x)

f(x)  =  (x — 1)/(x — 1) f(x) = 1 lim x -> 1 + f(x) = 1

f(x) = -(x — 1)/(x — 1) f(x) = -1 lim x-> 1 — f(x) = -1

Так как lim _{x -> 1} — f(x) ≠  lim  _{x -> 1} + f(x), предела не существует.