Maxima — Руководства
Впервые было опубликовано в «Linux Format» №11 (85), ноябрь 2006 г.
«А рисовать вы тоже умеете?» — «Рисовать? Кого-нибудь привлечем»
Как мы уже говорили в прошлый раз, количество различных
функций в Maxima разработчики постарались свести к минимуму, а
широту размаха каждой конкретной функции, соответственно, к
максимуму. Соблюдается эта тенденция и в функциях построения
графиков: основных таких функций всего две, с очевидными, как
всегда, названиями — plot2d и plot3d (одно из значений слова plot — график, а
аббревиатуры 2d и 3d переводятся
как двумерный и трехмерный). Если говорить
точнее, возможности графической отрисовки не встроены в Maxima,
а реализованы посредством внешних программ, в чем и
прослеживается пресловутый Unix-way: «одна задача — одна
программа». По умолчанию, построением графиков
занимается gnuplot
openmath. Gnuplot необходимо установить
(вручную либо автоматически — как зависимость Maxima) из
пакета gnuplot-nox, либо
просто gnuplot, а для работы openmath нужен командный интерпретатор wish, входящий обычно
в пакет tk; и, начиная с версии 5.10.0, еще и
xMaxima.Теперь кратко — о возможностях. Начнем
с plot2d. Кратчайший вариант ее вызова
такой: plot2d(выражение, [символ, начало, конец]),
где выражение задает функцию, график которой нужно построить,
символ — неизвестное (он, понятное дело, должен быть
единственным неопределенным символом, входящим в выражение), а
начало и конец задают отрезок оси Х для построения
графика; участок по оси Y в таком варианте записи
выбирается автоматически, исходя из минимума и максимума функции
на заданном промежутке.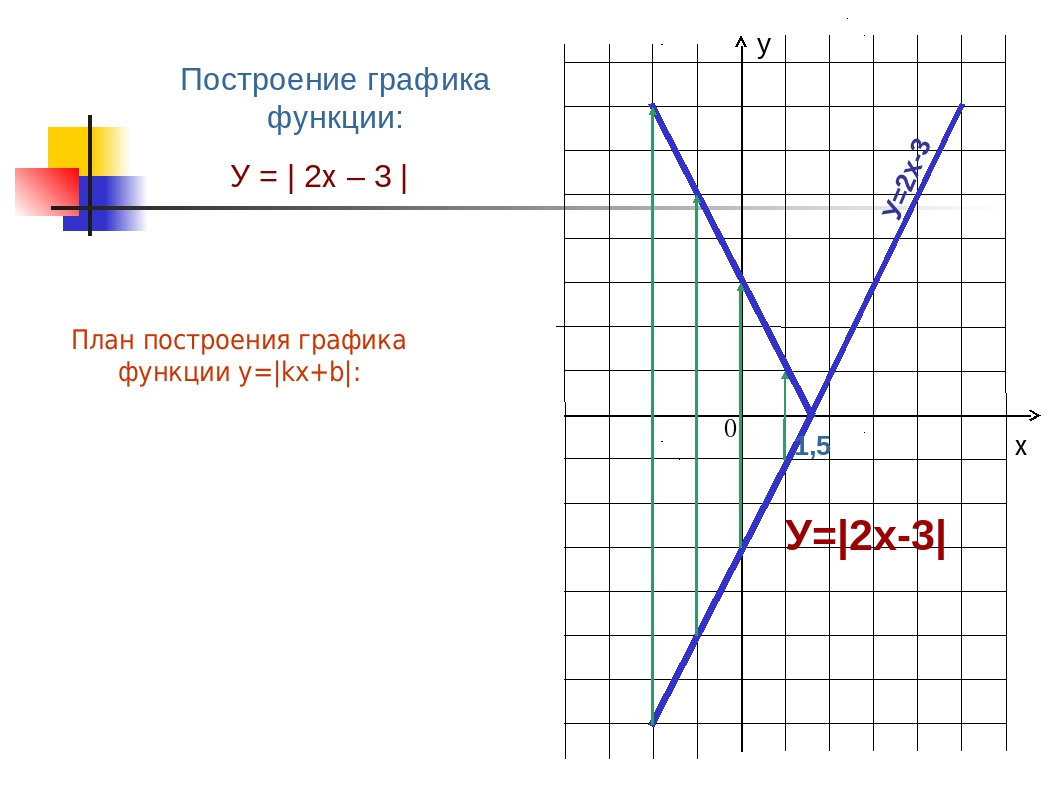
integrate, а в виде списка. Это
связано с тем, что plot2d может принимать еще и
дополнительные аргументы — в таком случае они перечисляются
следом за таким списком, что исключает всякую путаницу.После вызова функции plot2d в таком варианте
откроется окно gnuplot, в котором будет отображен
затребованный график. Никакой интерактивной работы с полученным
изображением gnuplot не предусматривает, кроме
автоматического его масштабирования при изменении размеров
окна. Насмотревшись вдоволь, можно закрыть окно с графиком
клавишей Q, либо, в случае работы с Maxima в
редакторе TeXmacs или wxMaxima, просто переключиться обратно в
интерфейс, оставив окно
gnuplot открытым, и
продолжить работу:В некоторых случаях автоматический подбор отображаемого
участка вертикальной оси может нас не устроить. Например, он
работает не очень хорошо, если функция имеет на заданном
промежутке точку разрыва, хотя бы один из односторонних пределов
в которой равен бесконечности: тогда промежуток по
оси Y будет выбран слишком большим. Да и в других
случаях может понадобиться изменить умолчательное поведение. Для
этого предусмотрен такой вариант вызова
функции: plot2d(выражение, [символ, начало, конец],
[y, начало, конец]). Здесь буква y используется в качестве обозначения вертикальной оси, а
остальные два параметра имеют тот же смысл, что и выше.
gnuplot достаточно прост и даже аскетичен, но здесь можно очень и очень
многое менять с помощью дополнительных опций. Некоторые из
которых будут освещены чуть ниже, а остальные можно изучить по
документации к
Некоторые из
которых будут освещены чуть ниже, а остальные можно изучить по
документации к gnuplot.Чтобы построить на одной и той же картинке одновременно два
графика (или больше), просто передайте
функции plot2d вместо отдельного выражения их
список:
Здесь [x, 0.01, 5] вместо [x, 0, 5] я написал «по привычке» — Maxima 5.9.x выдавала ошибку, если
заданная функция была не определена на одном из концов
интервала. В 5.10.0 мне эту ошибку воспроизвести не удалось; так
что есть основания полагать, что поведение в таких случаях
поправили.
Может plot2d строить и графики параметрически
заданных функций. Для этого используется список с ключевым
словом parametric: plot2d([parametric, x-выражение, y-выражение,
[переменная, начало, конец],
[nticks, количество]]). Здесь x-выражение и y-выражение задают зависимость координат от
параметра, то есть, по сути, это две функции
вида x(t), y(t), где
t — переменная параметризации. Эта же переменная должна
фигурировать в следующем аргументе-списке, а
параметры начало, конец, как и в двух
других рассмотренных случаях, задают отрезок, в пределах
которого этот параметр будет изменяться. Последний
аргумент-список, с ключевым словом nticks, задает
количество кусочков, на которые будет разбит интервал изменения
параметра при построении графика. Этот аргумент опционален, но
на практике он нужен почти всегда: умолчательное
значение
nticks равно 10; согласитесь,
редко бывает нужно в качестве графика получить ломаную из 10
отрезков. Вот пример построения графика параметрической
функции:Кроме parametric, функция plot2d понимает еще одно ключевое
слово: discrete. Предназначено оно, как нетрудно
догадаться, для отображения на плоскости дискретных множеств;
точнее говоря, конечных наборов точек. По записи аргументов
такой вариант распадается еще на
два:
Предназначено оно, как нетрудно
догадаться, для отображения на плоскости дискретных множеств;
точнее говоря, конечных наборов точек. По записи аргументов
такой вариант распадается еще на
два: plot2d([discrete, x-список, y-список]) и plot2d([discrete, [x, y]-список]). В первом
варианте координаты задаются как два отдельных
списка
[x1, x2, …, xn], [y1, y2, ,…, yn], а во
втором — как список пар координат отдельных
точек [[x1, y1], [x2, y2], …, [xn, yn]].Если мы, к примеру, имеем набор статистических значений, зависящих от номера, мы можем отобразить его, задав в качестве x-координат сами эти номера, то есть натуральные числа:
По умолчанию множество отображается в виде ломаной с
вершинами в заданных точках; такое поведение можно изменить и
получить вывод, к примеру, в виде отдельных точек. Это
достигается использованием специальных опций, применимых как
к plot2d, так и к plot3d, поэтому
давайте перейдем к рассмотрению последней.
Придаем объем
Функция plot3d имеет два варианта вызова: один
для явного задания функции и один для параметрического. В обоих
случаях функция принимает три аргумента. Для явно заданной
функции:
plot3d(выражение, [переменная1, начало, конец],
[переменная2, начало, конец]); аргументы
аналогичны plot2d, с той разницей, что здесь
независимых переменных две.Построение нескольких поверхностей на одном графике не
поддерживается — потому, вероятно, что на таком рисунке
проблематично было бы что-либо разглядеть. Посему для
параметрически заданной функции ключевое слово parametric не
требуется: вызов с первым аргументом-списком уже не с чем
перепутать. График параметрически заданной функции строится
так:
График параметрически заданной функции строится
так: plot3d([выражение1, выражение2, выражение3],
[переменная1, начало, конец], [переменная2, начало, конец]),
где выражения отвечают, по порядку, x(u, v), y(
С помощью параметрической формы можно строить и пространственные кривые. Для этого просто нужно задать второй, фиктивный, параметр, чтобы Maxima не ругалась на неправильный синтаксис вызова функции:
И отсюда мы плавно переходим к опциям функций построения
графиков, посредством использованной выше
опции grid. Каждая опция имеет некоторое
умолчательное значение, а изменить его можно, добавив к
аргументам список
вида [имя-опции, значение]. Строго говоря,
рассмотренные выше y и nticks также
являются опциями; в предпоследнем примере мы задали
опции nticks значение 120, а в примере
перед ним в качестве значения опции y использовалась пара чисел 0, 5. В документации к
Maxima символ
x, выступавший в примерах выше в
качестве обязательного параметра, также приводится как опция; на
самом деле опцией он является только в
случае parametric и действует тогда так же, как и
опция y, только по другой
оси. Опция grid, использованная выше, применима к
трехмерным графикам вместо опции nticks,
используемой для двумерных. Она, также как и y,
задается в виде двух целых значений, которые для поверхностей
задают размер ячеек сетки, в виде которой отображается
поверхность; первое число — вдоль оси X, второе —
вдоль оси Y; либо, в случае параметрического задания,
по первому и по второму параметру соответственно. Для кривых из
этих параметров действует только один, но писать нужно опять же
оба, дабы не нарушать синтаксис; и здесь этот параметр имеет в
точности тот же смысл, что
Для кривых из
этих параметров действует только один, но писать нужно опять же
оба, дабы не нарушать синтаксис; и здесь этот параметр имеет в
точности тот же смысл, что nticksС претензией на красоту
Первая опция, которую мы рассмотрим, задает формат вывода
результата; так она и
называется: plot_format. Формат может принимать
одно из четырех значений, первое из которых действует по
умолчанию: gnuplot, mgnuplot, openmath и ps. В умолчательном варианте
(значение gnuplot) данные для отображения
передаются напрямую программе gnuplot, которая сама
по себе имеет достаточно гибкое управление, и параметры ей можно
передавать прямо из Maxima с помощью дополнительных опций
функций plot2d/3d. Параметров этих
настолько много, что gnuplot могла бы стать темой
отдельной статьи; так что обращайтесь за ними к документации
по gnuplot. В противовес своим богатым
возможностям, gnuplot имеет перед следующими двумя
интерфейсами (если откровенно — скорее, лишь перед одним из них)
только один недостаток: она генерирует статичное изображение,
тогда как mgnuplot и openmath позволяют в реальном
времени масштабировать и передвигать картинку,
а plot3d — еще и вращать линию или поверхность в
разные стороны в пространстве.
Следующий вариант — mgnuplot — является
дополнительным интерфейсом к gnuplot, написанным на
Tcl/Tk, но динамика у него настолько «задумчивая», а остальные
возможности настолько бедны, что я не вижу смысла
останавливаться на нем подробнее.
И перехожу сразу к openmath. Он тоже не очень-то
поддается управлению, зато предоставляет хорошую
интерактивность, особенно ценную в трехмерном варианте: после
того, как объект сгенерирован, его можно масштабировать и очень
динамично вращать, разглядывая со всех сторон. Особенно это
помогает для сложных поверхностей, когда, глядя на статичную
«сетку»
Особенно это
помогает для сложных поверхностей, когда, глядя на статичную
«сетку» gnuplot, непросто понять форму
поверхности. Справедливости ради нужно отметить,
что gnuplot позволяет задавать точку обзора
трехмерного объекта в качестве одного из многочисленных
параметров, то есть хотя картинка и статична, но с какой стороны
на нее смотреть, мы можем указать произвольно.
Ну и последнее значение опции plot_format подталкивает Maxima к непосредственной генерации
PostScript-документа с изображением. Но и здесь надо сказать:
генерировать PostScript-вывод умеет и все тот
же gnuplot.
Большинство остальных опций относятся только к формату
вывода gnuplot. А мы рассмотрим еще одну
универсальную, пригодную для всех форматов и преобразующую не
результирующее изображение, а сам процесс построения графика;
точнее, систему координат. Называется эта
опция transform_xy, по умолчанию она
равна false. Передавать ей нужно выражение,
сгенерированное функцией make_transform([x, y, z],
f1(x, y, z), f2(x, y, z), f3(x, y, z)). Кроме того,
существует одно встроенное преобразование, известное
как polar_xy и
соответствующее make_transform([r, th, z], r*cos(th),
r*sin(th), z), то есть переходу к полярной цилиндрической
системе координат. В качестве примера
использования transform_xy приведу преобразование к
полярным сферическим координатам, раз уж во встроенном виде его
нет:
Обратите внимание: в первом аргументе-списке к make_transform последним должен идти зависимый символ, то есть тот, который будет выступать функцией от двух других.
Если вам нужно постоянно работать со сферическими
координатами, можете задать,
скажем, spherical_xy:make_transform([t, f, r],
r*sin(f)*sin(t), r*cos(f)*sin(t), r*cos(t)), и затем при
построении графиков писать [transform_xy,
spherical_xy].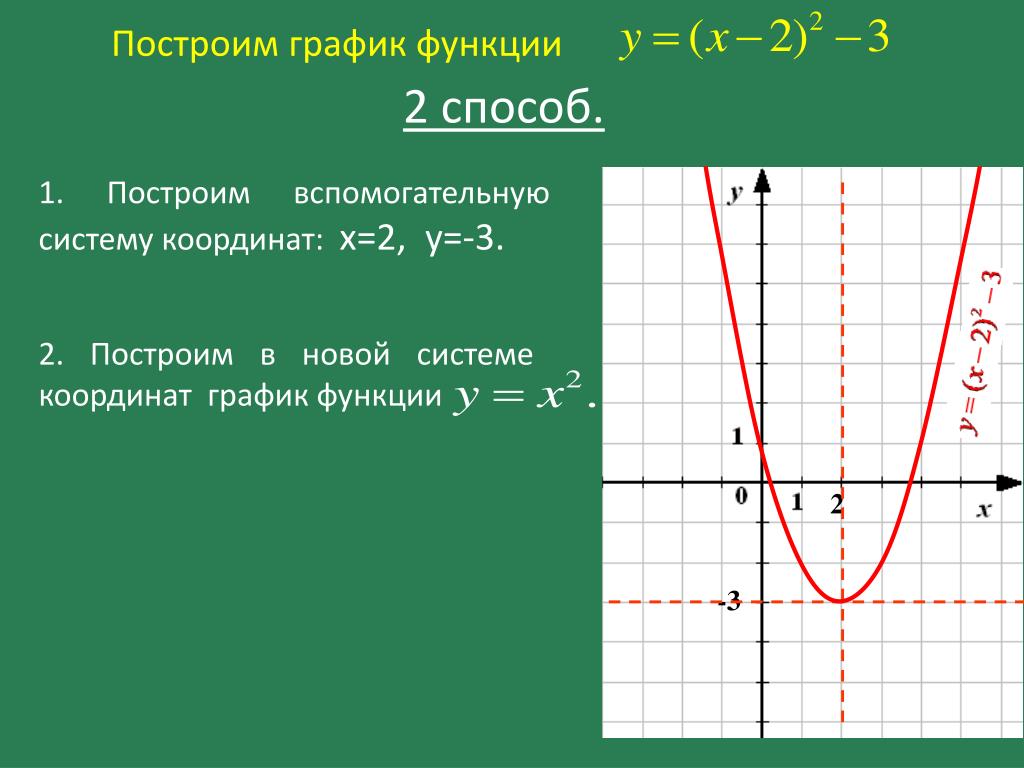 Ветвитесь и повторяйтесь До сих пор мы двигались
только по прямой, а теперь поговорим о средствах «изменения
траектории»: условном операторе и циклах.
Ветвитесь и повторяйтесь До сих пор мы двигались
только по прямой, а теперь поговорим о средствах «изменения
траектории»: условном операторе и циклах.
Начнем с условия. В Maxima, в отличие от большинства
«традиционных» процедурных и объектных языков программирования,
где существует так называемый условный оператор, привычная
связка if—then—else является не синтаксической конструкцией, а самым настоящим
оператором. По своему действию он больше всего похож на
тернарный оператор языка C, только с более «человеческим»
синтаксисом: if условие then выражение1 else выражение2. При
выполнении «условия» из двух «выражений» вычисляется только
первое и возвращается как результат оператора; в противном
случае выполняется только второе и оно же является значением
всего выражения if—then—else.
Часть конструкции else выражение2, как и в большинстве
языков программирования, опциональна. Если ее нет, а условие
все-таки не выполнилось, результат оператора if будет равен false.
При этом, конечно же, никто вам не мешает использовать этот
оператор как обычную условную конструкцию, а возвращаемое
значение просто игнорировать. С другой стороны,
оператор if можно применять, например, для задания
рекурсивных последовательностей:
Немного о самих условиях, которые могут проверяться
оператором if. Условия >, <, >=, <= записываются и расшифровываются традиционно, так же как и логические
операторы and, or, not. А
вот о равенствах-неравенствах нужно сказать пару слов. Равенство
в Maxima есть двух видов: синтаксическое и
логическое. Знаком
Знаком = обозначается как раз первое, а
второе вычисляется с помощью функции equal(). Чтобы
не быть многословными, отличие синтаксического равенства от
логического продемонстрируем на примере; здесь дополнительно
используется предикат по имени is, которые
проверяет на истинность свой аргумент.
Ну и неравенств, соответственно, тоже существует два, с тем
же смыслом. Синтаксическое неравенство обозначается достаточно
непривычно — через #; видимо, этот символ
разработчики сочли наиболее визуально схожим со знаком ≠. Ну а
логическое неравенство обозначено
через notequal().
Конечно, кроме упомянутых сравнений в условном операторе
можно использовать любые предикаты, то есть функции,
возвращающие логические
значения true/false. Функций таких
достаточно много, но все они достаточно просты, поэтому не буду
тратить время на их описание: его можно почерпнуть в том же
объеме из документации.
Напоследок перейдем к циклам. Цикл в Maxima будто бы тоже один. Но он имеет столько различных вариантов, что назвать это все одним оператором цикла язык не поворачивается. Вот как выглядят основные разновидности:
for переменная:начало step шаг thru конец do выражениеfor переменная:начало step шаг while условие do выражениеfor переменная:начало step шаг unless условие do выражение
Первый прокручивает цикл, изменяя переменную с
заданным шагом от начала до конца; второй — от начала и пока
выполняется условие; третий — наоборот,
пока условие не выполняется. К примеру, мы можем
получить список из первых десяти членов последовательности из
позапрошлого примера:
Как видите, в качестве оператора цикл в простейшем его виде,
в отличие от условия, использовать смысла нет, так как его
возвращаемое значение всегда равно done. В этом
примере один из элементов циклического оператора не указан; шаг,
как видите, может быть опущен и по умолчанию равен
единице. Самое интересное в этом операторе то, что опустить
позволяется любую его часть, кроме
В этом
примере один из элементов циклического оператора не указан; шаг,
как видите, может быть опущен и по умолчанию равен
единице. Самое интересное в этом операторе то, что опустить
позволяется любую его часть, кроме do; и в том
числе в любых комбинациях. К примеру, опустив
кроме step еще и for, мы получаем из
этого же оператора традиционные циклы while и unless (второй и третий варианты). А проделав то
же самое с первым вариантом записи, получим цикл без счетчика
вида thru число do выражение, который
просто повторится заданное число раз. Можно, наоборот, опустить
условие окончания и получить цикл с индексной переменной, но
бесконечный. А оставив только do, получим самый
простой вариант бесконечного цикла. Из таких бесконечных циклов
можно выйти с помощью оператора return(выражение) (точнее, конечно, конструкции из двух операторов
вида if условие then return(выражение)), который
прервет выполнение цикла и вместо done вернет заданное
выражение. Естественно, оператор return() можно
применять во всех видах циклов, а не только в бесконечных.
Но и это еще не все. Кроме всех уже рассмотренных вариаций,
цикл может принимать еще две ипостаси. Во-первых,
вместо step может использоваться
конструкция next выражение, смысл которой лучше
тоже продемонстрировать на примере
После next может стоять любое вычислимое
выражение относительно индекса цикла, и применяться эта
конструкция может во всех трех вариантах цикла
(thru/while/unless).
А «во-вторых» — это еще один отдельный вариант
цикла: for переменная in список do выражение; либо
расширенная
форма: for переменная in список условие do выражение. Здесь
цикл будет прокручен с
Здесь
цикл будет прокручен с переменной, изменяющейся по
всем элементам списка; плюс можно задать еще и
дополнительное условие на прерывание цикла. Вот
теперь мы с циклами действительно закончили. Как видите, все
достаточно разнообразно. Я, признаться, ничего, что здесь не
реализовано, и придумать не смог.
Но рассказ о циклах и условном операторе остается неполным,
пока я не рассказал о группировке выражений — ведь в обычном
варианте после then или do можно
написать всего одно из них. А группировка, или, как ее принято
называть, составной оператор, в Maxima — это опять-таки самый
настоящий оператор, который тоже, как и положено оператору,
возвращает некоторое значение. Обозначается он скобками, самыми
что ни на есть круглыми и обыкновенными; а разделяются
сгруппированные операторы/выражения внутри этих скобок не менее
обыкновенными запятыми. Возвращаемым значением составного
оператора является последнее вычисленное выражение.
С условным оператором, столь разнообразными циклами и составным оператором мы уже можем, комбинируя их между собой и с любыми другими функциями и выражениями Maxima, писать полноценные программы с использованием богатого символьного математического аппарата. Естественно, теперь нам захочется сохранять эти программы в виде внешних файлов, чтобы не набирать их каждый раз вручную, а подгружать одной короткой командой. Об этом, а также о математических аналогах объявления переменных — в завершающей статье цикла.
Мы также поговорим о математических аналогах объявления переменных и рассмотрим практические примеры с применением уже достаточно богатого известного нам инструментария.
как построить – сложное простыми словами — ЕГЭ/ОГЭ
График модуля, как построить – очень просто. Особенно, если знать несколько закономерностей. О них расскажу в статье. С помощью них вы поймете как построить график модуля легко и играючи. Без поиска пробных точек.
Особенно, если знать несколько закономерностей. О них расскажу в статье. С помощью них вы поймете как построить график модуля легко и играючи. Без поиска пробных точек.
На самом деле построение графиков функций с модулями – это удовольствие. Раньше они вызывали у вас в лучшем случае пренебрежение? Забудьте – после прочтения статьи вы будете первым по скорости построения графика.
Построение различных видов графиков, содержащих модуль:
- Воландеморт среди модулей
- Как калькулятор может помочь при построении графика?
- Как построить график модуля и одновременно решить уравнение
- Война среди модулей
Господа, перед тем, как мы приступим к светской беседе с модулем. (В которой отдадим дань уважения каждому его виду). Я бы хотел обратить ваше внимание, что модуль никогда не бывает отрицательным. Отсюда и все особенности его графика.
Подмечайте фишки каждой функции, но главное – держите в голове его «неотрицательность».
Главный миф о сложности графиков модуля – полный модуль по правой частиЗабудьте сказки про сложность модуля – ведь теперь вы скоро узнаете о методе «Зеркало».
Модуль всей правой части y = |f(x)| отражает график относительно оси X. Все, что было под осью Ox зеркально отражается наверх.
Почему так? Обратите внимание, что значение функции (то есть y) является результатом вычисления модуля. Оно не может быть отрицательным. Согласны? Значит, его заменяют на противоположное ему по знаку. А в построении функций эти зеркальные превращения и есть смена знака у функции.
Уже чувствуете себя как Алиса в Зазеркалье? Ничего страшного – объясню на примере:
Пример: y = |X – 3|
Видите, график функции y = |X – 3| состоит из двух ветвей. Первая y = X – 3, а вторая y = – (X – 3) = 3 – X.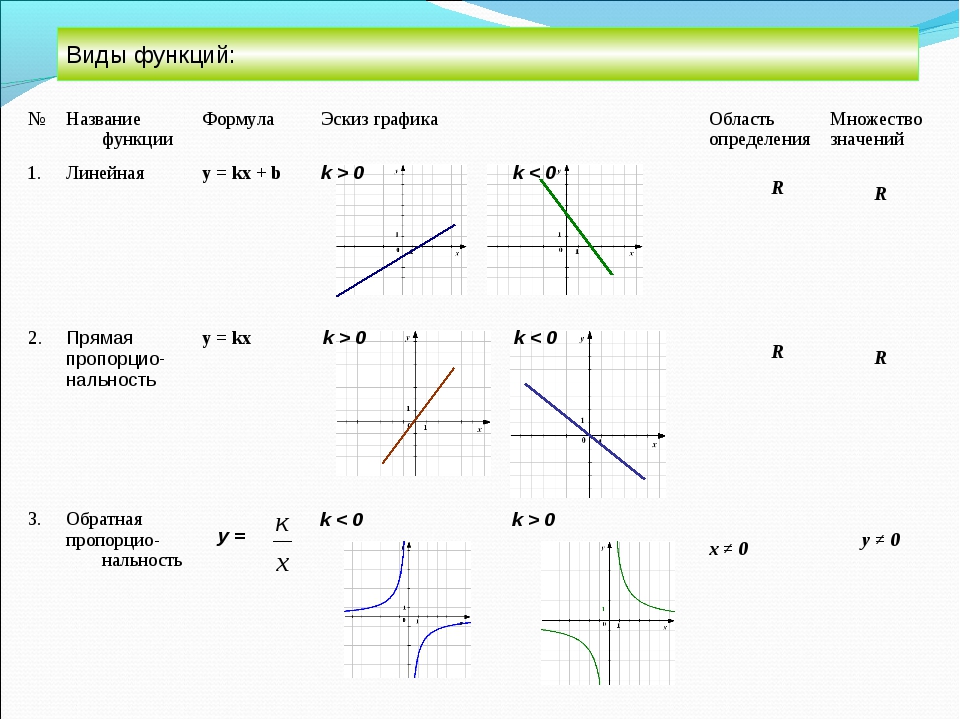 Все по определению модуля – не придраться. Зеркально отраженная функция и есть противоположная по знаку той, которую отражали.
Все по определению модуля – не придраться. Зеркально отраженная функция и есть противоположная по знаку той, которую отражали.
Можете так себя проверять – сначала просто отзеркальте конец, который улетает в отрицательную бесконечность (под ось Ох). А потом посмотрите, действительно ли он совпадает с минусовой версией подмодульного выражения. Уверяю, если вы были аккуратны – совпадет.
*Читайте понятное определение модуля в статье «Простая инструкция: как решать любые уравнения с модулем». После ее прочтения вы научитесь расправляться со всеми видами уравнений с модулем с помощью всего 1 инструкции!
А теперь перейдем к функции, которая заставляет поежиться от недовольства слишком многих. Если б они знали, что ее настолько просто начертитить…то стали бы решать уравнения с ней только графически.
Воландеморт среди модульных функций — Полный модуль по правой частиМодуль всей левой части |y| = f(x) отражает график относительно оси X. Все, что было над осью Oх зеркально отражается вниз.
Смотрим, что является результатом вычисления подмодульного выражения? Ага, все, что стоит справа. Значит, в данном случае Рубиконом является ось Oy – отзеркаливаем относительно нее.
Пример: |y| = X – 3
Мы разобрали две базы графиков с модулями. Дальше уже идут вариации с дополнительными математическими па: поднимите график, опустите, сузьте – расширьте. Давайте и их разберем!
Как калькулятор может помочь при построении графика? — График содержащий модуль
Это пример сложной функции, такие функции строятся по этапам. Сложной – не потому что она поддается только сильнейшим умам. Просто в ней собрано несколько последовательных действий: модуль и сложение с «потусторонним членом».
С такими функциями работает способ «калькулятор».
Представьте, что вам нужно вычислить выражение: (217 – 327)/72. С чего вы начнете? Вероятно, с возведения в степень, продолжите подсчетом числителя и только потом перейдете к делению. Будете идти от малого к большому.
Тот же метод работает и со сложной функцией. Начните с ядра и продолжайте справляться со всеми остальными прибамбасами вокруг него.
Пример: y = |x–3| + 5 ( ядром является график прямой y=x-3)
1. Y = X – 3 {строим график прямой}
2. Y = |X –3| {отражаем график относительно оси X}
3. Y = |X – 3| + 5 {поднимаем график 2. на +5}.
Вспомните суперспособности графиков – положительное число поднимает график, а отрицательное опускает (вверх/вниз относительно оси Ox). Причем, нет ничего страшного в том, что модульная галка окажется под прямой Ox (в отрицательной области) – это необходимые последующие действия с графиком.
Иногда в качестве «потустороннего члена» выступает переменная. Тут уж хитрить с отражениями и подниманиями – не получится. Придется раскрывать алгебраически модуль для каждого интервала – и уже по вычисленному выражению чертить ветви графика.
О том, как легко раскрыть модуль – написано в статье – Решение уравнений с модулем.
А мы двигаемся навстречу забора из модуля. По правде, такой вид функций очень полезно уметь чертить. Этот скилл способен сэкономить вам время. Ведь частенько по графику намного точнее и проще найти корни уравнения такого вида.
Как построить график модуля и одновременно решить уравнение — Модуль внутри модуляПример: y = ||X–2|–3|
{Порядок действий как при работе со сложной функцией – пользуемся методом «Калькулятор»}
1. Y = X – 2
Y = X – 2
2. Y = |X – 2|
3. Y = |X – 2|–3
4. Y = ||X – 2|–3|
Согласитесь, что раскрывать уравнения такого типа довольно муторно. Да и велик риск просчитаться. Начертить график и по нему оценить корни (иногда точно их посчитать) супер просто.
Поэтому графический метод решения уравнений нужно эксплуатировать на все 100% именно в этом случае.
Теперь нас ждет один из самых непредсказуемых графиков из всего рода модулей. Никогда не знаешь, что именно он приподнесет. Но и с этой неприятной неожиданностью научимся работать)
Война среди модулей — Несколько модулей
Что делать если в бой вступает сразу несколько модулей? – К сожалению, бороться с ними приходится с помощью арифметики и алгебры. Приходится аккуратно раскрывать на разных областях. Так же, как при решении модульных уравнений – алгебраически.
*Подробнее о том, как раскрывать модуль читайте в статье «Простая инструкция: как решать любые уравнения с модулем». В ней на пальцах объяснено, как раскрыть забор из модулей и НЕ запутаться.
Y = |X–2|+|X+2|
I ) X ∈ (–∞;–2] {1 модуль с «–» , 2 модуль с «–»}
Y1 = – (X – 2) – (X + 2)
Y1 = – X + 2 – X – 2
Y1 = –2X
II ) X ∈ (–2;2] {1 модуль с «–» , 2 модуль с «+»}
Y2 = – (X – 2) + (X + 2)
Y2 = – X + 2 + X + 2
Y2 = 4
III) X ∈ (2; +∞) {1 модуль с «+» , 2 модуль с «+»}
Y3 = (X – 2) + (X + 2)
Y3 = 2X
Вот такая галочка получилась из трех кусочков различных функций.
Вы уже заметили, что все модульные функции являются кусочно заданными? Их особенностью является то, что они существуют только на определенных интервалах.
Главное в модулях – понять закономерности. Дальше все пойдет как по маслу. Надеюсь, мне удалось хоть немного прояснить график модуля, как его построить и не надорваться в счете.
Остались вопросы? – обращайтесь! Я с удовольствием проведу первую консультацию бесплатно. Запишитесь на первое бесплатное занятие: напишите мне на почту или в сообщениях ВКонтакте)
До встречи, Ваш Михаил
Графики тригонометрических функций кратных углов. График функции y=sin x График функции y sin x 2
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у = sin x . Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Урок и презентация на тему: «Функция y=sin(x). Определения и свойства»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X).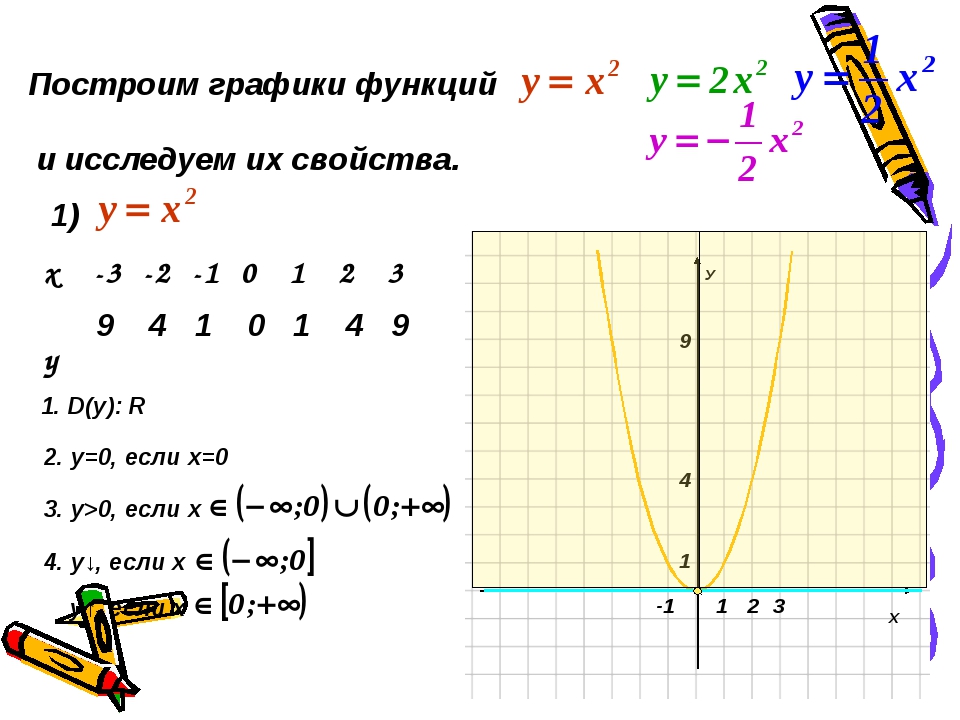 Будем строить наш график последовательно, применяя наши свойства. Начнем
строить график на отрезке .
Будем строить наш график последовательно, применяя наши свойства. Начнем
строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
«Йошкар-Олинский техникум сервисных технологий»
Построение и исследование графика тригонометрической функции y=sinx в табличном процессоре MS Excel
/методическая разработка/
Йошкар – Ола
Тема . Построение и исследование графика тригонометрической функции y = sinx в табличном процессоре MS Excel
Тип урока – интегрированный (получение новых знаний)
Цели:
Дидактическая цель — исследовать поведение графиков тригонометрической функции y = sinx в зависимости от коэффициентов с помощью компьютера
Обучающие:
1. Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
2. Показать внедрение компьютерных технологий в обучение математике, интеграцию двух предметов: алгебры и информатики.
3. Формировать навыки использования компьютерных технологий на уроках математики
4. Закрепить навыки исследования функций и построения их графиков
Развивающие:
1. Развивать познавательный интерес учащихся к учебным дисциплинам и умение применять свои знания в практических ситуациях
2. Развивать умения анализировать, сравнивать, выделять главное
Развивать умения анализировать, сравнивать, выделять главное
3. Способствовать повышению общего уровня развития студентов
Воспитывающие :
1. Воспитывать самостоятельность, аккуратность, трудолюбие
2. Воспитывать культуру диалога
Формы работы на уроке – комбинированная
Дидактическое оснащение и оборудование:
1. Компьютеры
2. Мультимедийный проектор
4. Раздаточный материал
5. Слайды презентации
Ход урока
I . Организация начала урока
· Приветствие студентов и гостей
· Настрой на урок
II . Целеполагание и актуализация темы
Для исследования функции и построения ее графика требуется много времени, приходится выполнять много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.
Сегодня мы научимся строить графики тригонометрических функций в среде табличного процессора MS Excel 2007.
Тема нашего занятия «Построение и исследование графика тригонометрической функцииy = sinx в табличном процессоре»
Из курса алгебры нам известна схема исследования функции и построения ее графика. Давайте вспомним как это сделать.
Слайд 2
Схема исследования функции
1. Область определения функции (D(f))
2. Область значения функции Е(f)
3. Определение четности
4. Периодичность
5. Нули функции (y=0)
6. Промежутки знакопостоянства (у>0, y
7. Промежутки монотонности
8. Экстремумы функции
III . Первичное усвоение нового учебного материала
Откройте программу MS Excel 2007.
Построим график функции y=sinx
Построение графиков в табличном процессоре MS Excel 2007
График данной функции будем строить на отрезке x Є [-2π; 2π]
Значения аргумента будем брать с шагом, чтобы график получился более точным.
Т. к. редактор работает с числами, переведем радианы в числа, зная что П ≈ 3,14 . (таблица перевода в раздаточном материале).
1. Находим значение функции в точке х=-2П. Для остальных значение аргумента соответствующие значения функции редактор вычисляет автоматически.
2. Теперь у нас имеется таблица со значениями аргумента и функции. С помощью этих данных мы должны построить график этой функции с помощью мастера диаграмм.
3. Для построения графика надо выделить нужный диапазон данных, строки со значениями аргумента и функции
4..jpg»>
Выводы записываем в тетрадь (Слайд 5)
Вывод. График функции вида у=sinx+k получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОУ на k единиц
Если k >0, то график смещается вверх на k единиц
Если k
Построение и исследование функции вида у= k *sinx, k — const
Задание 2. На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.
(Чтобы заново не задавать значение аргумента давайте скопируем имеющиеся значения. Теперь вам надо задать формулу, и по полученной таблице построить график.)
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
https://pandia.ru/text/78/510/images/image005_66.gif»>x , на интервале (-2π; 2π) и проследите как изменяется вид графика.
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 8)
https://pandia.ru/text/78/510/images/image008_35.jpg»>
Выводы записываем в тетрадь (Слайд 11)
Вывод. График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
Если k >1, то график смещается вправо вдоль оси ОХ
Если 0
IV . Первичное закрепление полученных знаний
Дифференцированные карточки с заданием на построение и исследование функции при помощи графика
Y=6 *sin(x) | Y= 1-2 sin х | Y= — sin (3х+ ) | |
1. Область определения | |||
2. Область значения | |||
3. Четность | |||
4. Периодичность | |||
5. Промежутки знакопостоянства | |||
6. Промежутки монотонности | |||
Функция возрастает | |||
Функция убывает | |||
7. | |||
Минимум | |||
Максимум |
V . Организация домашнего задания
Построить график функции y=-2*sinх+1 , исследовать и проверить правильность построения в среде электронной таблицы Microsoft Excel. (Слайд 12)
VI . Рефлексия
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам? |
Графическое изображение основных функций и их … Пошаговое решение математических задач
4.4 — ИЗОБРАЖЕНИЕ БАЗОВЫХ ФУНКЦИЙ И ИХ ВАРИАЦИИ
Многие из графиков, обсуждаемых в главе 3, являются графиками функций. При проверке вертикальной линии любая прямая линия, которая не является вертикальной, является графиком функции, как и график любой вертикальной параболы.2 + 5 = (g {omicron} h) (x)
В оставшейся части этого раздела мы обсудим графики нескольких основных функций, которые не являются ни линейными, ни квадратичными. Графики этих функций состоят из частей различных прямых линий или прямых линий и кривых.
ФУНКЦИИ АБСОЛЮТНОГО ЗНАЧЕНИЯ Одной из распространенных функций, которая не является линейной и неквадратичной, является функция абсолютного значения, определяемая следующим образом: f (x) = | x | или у = | х |. Поскольку | x | можно найти для любого действительного числа x, домен равен (-inf, inf.Кроме того, | x |> = 0 для любого действительного числа x, поэтому диапазон равен (0, inf. Когда | x |> = 0, тогда y = | x | = x, поэтому y = x отображается на графике для неотрицательных значений x. С другой стороны, если x <0, то y = | x | = -x и y = -x нанесен на график для отрицательных значений x. График представляет собой объединение двух лучей. Окончательный график показан на рисунке 4.6. При проверке вертикальной линии график является графиком функции. Обратите внимание, что график f (x) = | x | симметричен относительно оси y.
Пример 2
ИЗОБРАЖЕНИЕ ФУНКЦИИ АБСОЛЮТНОГО ЗНАЧЕНИЯ
График f (x) = | x-2 |.
Обратите внимание, что это составная функция g {omicron} h, где g (x) = | x | и h (x) = x — 2. Область определения f — (-inf, inf, а диапазон — (0, inf. Этот граф имеет ту же форму, что и y = | x |, но «вершина» .point переводится на 2 единицы вправо, от (0,0) до (2,0). См. рисунок 4.7. Ось симметрии — это вертикальная линия от x = 2 до (2,0)
Пример 3
ИЗОБРАЖЕНИЕ ФУНКЦИИ АБСОЛЮТНОГО ЗНАЧЕНИЯ
График f (x) = | 3x +4 | +1.
Значение f (x) = y всегда больше или равно 1, поскольку | 3x + 4 |> = 0.Таким образом, y-значение «vertax» равно 1, а диапазон равен [1, inf]. Область определения: (-inf, inf. Значение x «вершины» можно найти, подставив 1 вместо y в уравнении.
y = | 3x +4 | +1
1 = | 3x +4 | +1 Пусть y = 1.
0 = | 3x +4 | Вычтем 1.
x = -4 / 3Solve 3x + 4 = 0
Построение нескольких других упорядоченных пар приводит к графику на рисунке 4.8. На графике показана «вершина», переведенная в (-4 / 3,1).Ось симметрии x = -4 / 3. Коэффициент при x, 3, определяет наклон двух лучей, образующих график. У одного наклон 3, у другого -3. Поскольку абсолютное значение наклонов больше 1, лучи круче, чем лучи, образующие график y = | x |.
ЧАСТИ ОПРЕДЕЛЕННЫХ ФУНКЦИЙ Графики функций абсолютного значения в примерах 2 и 3 состоят из частей двух различных прямых линий. Такие функции, называемые функциями , определенными кусочно , часто определяются разными уравнениями для разных частей области.
Пример 4 ИЗОБРАЖЕНИЕ ФУНКЦИИ ОПРЕДЕЛЕННОЙ ЧАСТИ
Построить график функции
Мы должны построить график каждой части домена отдельно. Если x <= 2, эта часть графика имеет конечную точку в x = 2. Найдите значение y, заменив 2 на xin y = x + 1, чтобы получить y = 3. Еще одна точка необходима для построения графика этой части графика. Выберите значение x меньше 2. Выбор x = -1 дает y = -1 + 1 = 0. Нарисуйте график через (2,3) и (-1,0) в виде луча с концом в (2,3).Аналогично изобразите луч для x> 2. Этот луч будет иметь открытую конечную точку, когда x = 2 и y = -2 (2) + 7 = 3. Выбор x = 4givesy = -2 (4) + 7 = -1. Луч, проходящий через (2,3) и (4, -1), завершает граф. В этом примере два луча
встречаются в точке (2,3), хотя это не всегда так. График показан на рисунке 4.9
Пример 5 ИЗОБРАЖЕНИЕ ФУНКЦИОНАЛЬНОЙ ОПРЕДЕЛЕННОЙ ЧАСТИ
График
Изобразите луч y = x + 2, выбрав x так, чтобы x <= 0, с твердой конечной точкой в точке (0,2).Луч имеет наклон 1 и точку пересечения с y 2. Тогда график y = 1/2 для x> 0. Этот график будет половиной параболы с открытой конечной точкой в точке (0,0). См. Рисунок 4.10. Обратите внимание, что в этом примере две части не совпадают.
НАИБОЛЬШИЕ ЦЕЛОЧНЫЕ ФУНКЦИИ Другой тип функции с графиком, состоящим из отрезков прямой, — это функция наибольшего целого числа, записанная y = [x], и определенная следующим образом:
[x] — наибольшее целое число, меньшее или равное x.
Например, [8] = 8, [- 5] = — 5, [{Pi}] = 3, [12, 1/9] = 12, [-2.001] = -3 и так далее.
Пример 6 ИЗОБРАЖЕНИЕ НАИЛУЧШЕЙ ЦЕЛОЙ ФУНКЦИИ
График y = [x]
Для любого значения x в интервале 0,1, [x] = 0. Кроме того, для x в 1,2, [x] = 1. Этот процесс продолжается; x в 2,3, значение [x] равно 2. Значения y постоянны между целыми числами, но они скачут при целых значениях x. Это делает график, показанный на рисунке 4.11, серией отрезков линии. В каждом случае левая конечная точка сегмента включается, а правая конечная точка исключается.Область определения функции: (- inf, inf, а диапазон — это набор целых чисел, {…, — 2, -1,0,1,2, …}.
Каждый из графиков в примерах 6, 7 и 8 состоит из серии горизонтальных отрезков линии. (См. Рисунки 4.11, 4.12 и 4.13.) Функции, формирующие эти графики, называются пошаговыми функциями.
ПРОСТОЙ
Специальные функции, называемые пошаговыми функциями, используются, когда ожидается, что значение диапазона останется постоянным для данного интервала значений домена.Например, плата за парковку часто рассчитывается путем взимания определенной фиксированной платы за первый час и другой платы за каждый дополнительный час (или долю часа).
Предположим, что ежедневная парковка в центре города взимает базовую плату в размере 5 долларов за первый час и 1 доллар за каждый дополнительный час или его часть. Максимальная плата за день составляет 15 долларов США. Парковка на 7 часов будет стоить 5 долларов + 1 доллар (6) = 11 долларов.
РЕШИТЬ КАЖДУЮ ПРОБЛЕМУ
A. Сколько будет стоить парковка у Downtown Daily Parking для 3 человек.5 часов?
Б. Мелисса и ее дети планируют провести весь день в поездке по городу. Сколько ей будет стоить парковка на ежедневной парковке в центре города на 12 часов?
ОТВЕТА A. Это будет стоить 8 долларов. Б. это будет стоить 15 долларов, максимальная суточная оплата.
Пример 7 ИЗОБРАЖЕНИЕ ШАГОВОЙ ФУНКЦИИ
График y = [1 / 2x + 1
Попробуйте некоторые значения x в уравнении, чтобы увидеть, как ведут себя значения y. Здесь приведены некоторые образцы заказанных пар.
Эти упорядоченные пары предполагают, что если x находится в интервале 0,2, то y = 1.Для x в 2,4, y = 2
2 и так далее. График представлен на рисунке 4.12. Опять же, домен (-inf, inf. Диапазон: {…- 1,0,1,2, …}.
Функция наибольшего целого числа может использоваться для описания многих распространенных практик ценообразования, встречающихся в повседневной жизни, как показано в следующем примере.
Пример 8 ПРИМЕНЕНИЕ НАИЛУЧШЕЙ ЦЕЛОЙ ФУНКЦИИ
Компания экспресс-почты взимает 10 долларов за посылку весом 1 фунт или меньше. Каждый дополнительный фунт или его часть стоит на 3 доллара больше.Найдите стоимость отправки посылки весом 2 фунта; 2,5 фунта; 5,8 фунтов. Изобразите упорядоченные пары (фунты, стоимость). Это график функции?
Стоимость упаковки весом 2 фунта составляет 10 долларов за первый фунт и 3 доллара за второй фунт, что в сумме составляет 13 долларов. Для пакета на 2,5 фунта стоимость будет такая же, как и для 3 фунтов: 10 + 2 (3) = 16 или 16 долларов. Пакет за 5,8 фунта будет стоить столько же, сколько пакет за 6 фунтов: 10 + 5 (3) = 25 или 25 долларов. График этой ступенчатой функции показан на рисунке 4.13. Обратите внимание, что в этом случае включены nght конечных точек вместо левых конечных точек.
ОБРАТНЫЕ ФУНКЦИИ
Сложение и вычитание — обратные операции: начиная с числа x, прибавляя 5 и вычитая 5, в результате возвращается x. Точно так же некоторые функции противоположны друг другу. Например, функции
f (x) = 8x и g (x) = 1 / 8x
инвертируют друг друга. Это означает, что если выбрано значение x, такое как x = 12, так что
ф (х) = 8 * 12 = 96
вычисление g (96) дает
г (96) = 1/8 * 96 = 12
Таким образом, g [f (12)] = 12.
Кроме того, f [g (12)] = 12. Для этих функций f и g можно показать, что f [g (x)] = x и g [f (x)] = x для любого значения x.
В этом разделе будет показано, как начать с такой функции, как f (x) = 8x, и получить обратную функцию g (x) = (1/8) x. Не все функции имеют обратные функции. Единственные функции, у которых есть обратные функции, — это взаимно однозначные функции.
ФУНКЦИИ ОДИН К ОДНОМ Для функции y = 5x-8 любые два разных значения x дают два разных значения y.2 = 16. Такая функция, как y = 5x -8, где разные элементы из домена всегда приводят к разным элементам из диапазона, называется функцией «один-к-одному».
ФУНКЦИЯ ОДИН К ОДНОМУ Функция f является взаимно однозначной функцией, если для элементов aandb из do main функции f из
a! = B следует f (a)! = F (b)
Пример 1 ОПРЕДЕЛЕНИЕ СООТВЕТСТВИЯ ФУНКЦИИ ОДИН К ОДНОМУ
Определите, является ли каждая из следующих функций взаимно однозначной.
(a) f (x) = -4x + 12
Предположим, что a! = B.2) = root (25-9) = 4
Здесь, хотя 3! = — 3, f (3)! = F (-3). По определению, это не взаимно однозначная функция.
Как показано в Примере 1 (b), способ показать, что функция не является взаимно однозначной, состоит в том, чтобы создать пару неравных чисел, которые приводят к одному и тому же значению функции. Существует также полезный графический тест, который показывает, является ли функция взаимно однозначной. Этот тест горизонтальной линии для однозначных функций можно резюмировать следующим образом.
ТЕСТ ГОРИЗОНТАЛЬНОЙ ЛИНИИ Если каждая горизонтальная линия пересекает график функции не более чем в одной точке, то функция взаимно однозначна.
ПРИМЕЧАНИЕ В примере 1 (b) график функции представляет собой полукруг. Существует бесконечно
горизонтальных линий, которые разрезают график полукруга на две точки, поэтому проверка горизонтальной линии показывает, что функция не является взаимно однозначной.
Пример 2 ИСПОЛЬЗОВАНИЕ ТЕСТА ГОРИЗОНТАЛЬНОЙ ЛИНИИ
Используйте тест горизонтальной линии, чтобы определить, являются ли графики на рисунках 4.14 и 4.15 графиками взаимно однозначных функций.
(а)
Каждая точка, в которой горизонтальная линия пересекает график, имеет то же значение y, но другое значение x.Поскольку более одного (здесь трех) различных значений x приводят к одному и тому же значению y, функция не является взаимно однозначной.
(б)
Каждая горизонтальная линия будет пересекать график на Рисунке 4.15 ровно в одной точке. Эта функция взаимно однозначная.
ОБРАТНЫЕ ФУНКЦИИ Как упоминалось ранее, определенные пары взаимно однозначных функций «отменяют» друг друга. Например, если
f (x) = 8x + 5 и g (x) = (x-5) / 8
f (10) = 8 * 10 + 5 = 85 и g (85) = (85-5) / 8 = 10
Начиная с 10, мы «применили» функцию f, а затем «применили» функцию g к результату, который вернул число 10.См. Рисунок 4.16. Аналогичным образом для этих же функций проверьте, что
f (3) = 29 и g (29) = 3,
f (-5) = — 35 и g (-35) = — 5
г (2) = — 3/8 и f (-3/8) = 2
В частности, для этих функций
f [g (x)] = 2 и 8 [f (2)] = 2
Фактически для любого значения x
f [g (x)] = x и g [f (x)] = x
или (f {omicron} g) (x) = x и (g {omicron} f ) (х) = х
Из-за этого свойства g называется инверсией f. -1 — это набор действительных чисел.-1 — зеркальное отображение по отношению к этой линии.
ПРОСТОЙ
Обратные функции используются государственными учреждениями и другими предприятиями для отправки и получения закодированной информации. Используемые ими функции обычно очень сложные. Простой пример включает функцию f (x) = 2x + 5. Если каждой букве алфавита присвоено числовое значение в соответствии с ее положением (a = 1, …, z = 26, слово АЛГЕБРА будет закодировано как 7 29 1
177.-1 (x) = корень (3, x + 1)
Инженерная математика — графики функций
На предыдущем уроке вы узнали о функциях и различных способах представления функции. Один из способов представления функции — использование графиков. В этом уроке вы изучите графики функций и поймете, как определить область и диапазон функции по ее графику. Вы узнаете о тестировании вертикальной линии и о том, как найти ноль функции .
График функции — это упорядоченная пара.
x = длина по оси x. y = f (x) = длина по оси y.
Давайте нарисуем график функции и посмотрим, как он работает.
График функции (x, f (x))Приведенная выше диаграмма ясно показывает, что график имеет
для некоторого входа x.Поиск домена и диапазона с использованием графика функции
Вы можете легко найти домен и диапазон функции, используя график функции. Постройте график функции, используя алгебраическое уравнение функции.
См. График ниже
Определение области и диапазона по графикуНа графике некоторые точки закрыты или заполнены, а некоторые из них не заполнены или открыты.
- Точки (-3, 1), (-2, -2) и (1, -2) находятся в области определения функции
- Однако (3, 3) не определен и не находится в области определения функции.
Следовательно,
Область функции
находится в интервале [-3, 3) . Мы взяли крайнее левое и крайнее правое значения x в качестве домена. Но не забывайте проверять, открыт интервал или закрыт.Диапазон функций
На приведенной выше диаграмме самая высокая и самая низкая точки определены как (-2, 2) и (1, -2) соответственно.Тогда диапазон функции, использующей график, составляет закрытый интервал [2, -2] , потому что обе точки определены.
Тест вертикальной линии для графика
Вы можете определить, принадлежит ли график функции или нет, используя тест вертикальной линии.
Тест вертикальной линииНа приведенной выше диаграмме красная линия пересекает график A в одном месте. График A принадлежит функции. Линия пересекает график B в двух местах. Это не график функции.
Иногда график не определяется для некоторых функций, и в результате линия вообще не пересекает график.Но это не означает, что это не график функции, просто потому, что он не определен, как в случае графика C.
Обнуление функции
Ранее вы узнали о перехватах уравнения. График функции имеет точку пересечения по оси x, равную (a, 0). Нуль функции — это значение x, для которого
. Ноль функцииНа графике, показанном выше, ноль графика — это точка (2, 0), где график пересекает ось x. На некоторых графиках больше одного нуля, потому что они пересекают ось x более одного раза.
Статьи по теме:
Как построить график любого изображения. Пересечение искусства и математики | Кэт Льюис
Если вам когда-нибудь будет скучно, я бы порекомендовал необычный вид развлечения. Он находится на академическом, математически загруженном веб-сайте, известном как Wolfram Alpha.
Введите «Банановая кривая» в строку поиска.
Для тех, у кого более требовательное художественное чутье, вы можете попробовать «кривую, похожую на Северуса Снейпа». Или всегда есть «первая» и «вторая» кривые Альберта Эйнштейна.«И если вы не склонны тратить дополнительные семь секунд работы, чтобы удовлетворить свое любопытство, вот изображение« кривой, похожей на Симбу »:
(http://m.wolframalpha.com/input/?i) = simba + curve & x = 0 & y = 0)Математика теперь не кажется такой нехудожественной, не так ли? Но как именно осуществить эти визуальные подвиги с помощью только графического программного обеспечения и человеческого мозга?
По своей сути координатный граф — это визуальное представление взаимосвязи между числами или переменными. Но это работает и наоборот: формулы представляют собой математическое представление изображений, которые они создают при построении графиков.Эта перспектива внезапно предлагает совершенно новый набор возможностей, поскольку изображения теперь можно создавать только с помощью чисел, символов и графического программного обеспечения.
Это может показаться знакомым для дизайнера или цифрового художника. Разве программное обеспечение для создания векторных иллюстраций, такое как Adobe Illustrator, не полагается на математику? Да, и во многом это похожая идея. Пользователь вводит изображение, будь то простая линия, типографика или сложный набросок, и программа сохраняет это изображение в виде математических уравнений и геометрических фигур.¹ Опора на математику делает векторные иллюстрации бесконечно масштабируемыми.
Это подводит нас к простому примеру создания изображения с графиком: кривой Бэтмена. Это изображение было популярно в Интернете в старые добрые времена, еще в 2011 году. Но, несмотря на устаревший характер мемов, оно служит вневременным примером того, как сочетание математических функций может создать эстетически узнаваемый и даже привлекательный образ. Первоначальным создателем графика был учитель средней школы Дж.Мэтью Регистр, который стремился вдохновить своих учеников на математику.
(http://santacruzmathguy.tumblr.com/image/8270375482)При разбиении уравнения каждый член в круглых скобках представляет отдельный набор линий на графике Бэтмена. Например, самый первый член (группа переменных в первых скобках) — это внешние крылья летучей мыши, основанные на общей формуле овала. В отличие от графиков, которые вы изучаете по алгебре в старшей школе, которые могут длиться вечно, эти линии обрабатываются с помощью математических понятий, таких как мнимые числа.Это уравнение Бэтмена невозможно изобразить на обычном графическом калькуляторе. Он был разработан для более надежного графического программного обеспечения под названием Mathematica, хотя TI-89 все еще может рисовать некоторые довольно надежные изображения (см. Соответствующие ссылки ниже).
Теоретически этот метод построения графиков можно использовать для создания любого значительно упрощенного изображения на координатной сетке. Однако это требует много времени и субъективно — г-н Регистр приводит пяти-шестичасовые временные рамки для создания своего первоначального уравнения.
Но есть и другой способ, который делает возможными сложные иллюстративные кривые Wolfram Alpha, такие как «симба-подобная» кривая выше.Он основан на так называемом преобразовании Фурье. Этот инструмент используется для записи любой функции в виде суммы функций синуса и косинуса. Изначально меня познакомил с графами Wolfram Alpha и основами математики, лежащими в их основе, моим профессором физики AP, другим учителем, который, как и г-н Регистр, глубоко заботился об образовательном опыте и фундаментальном понимании своих учеников.
Преобразование Фурье является расширением ряда Фурье, концепции исчисления, которая объясняет, как любую периодическую (также известную как повторяющуюся) функцию можно записать как сумму синусов и косинусов.Фактически, многие функции требуют бесконечного количества синусов и косинусов. Оказывается, синусы и косинусы могут быть полезны не только для раздражения студентов, изучающих тригонометрию; изучение рядов Фурье и способов управления ими — это целая область математики, известная как гармонический анализ. Преобразование Фурье было открыто Жаном Батистом Жозефом Фурье, который в 1822 году после серии статей опубликовал книгу по математике тепла. Он был первым человеком, математически представившим распространение тепла; он также был изобретателем обозначений для определенных интегралов.²
Ряды Фурье приближают функцию, и каждый «шаг» в процессе — каждая дополнительная функция синуса или косинуса — приближает приближение к той функции, которая воспроизводится. Добавьте еще один синус или косинус, чтобы добиться более реалистичного «изображения». Вот почему серия может быть бесконечной; приближение становится все лучше и лучше, но по-настоящему не становится точным. Весь процесс выглядит примерно так:
(https://giphy.com/search/fourier)Преобразование Фурье — это математический инструмент, связанный с рядами Фурье.Преобразование разбивает функцию на набор синусоид или периодических функций. Это удобно, потому что эти периодические функции затем могут быть записаны в виде синусов и косинусов с использованием ряда Фурье. Да, вы правильно прочитали: любую математическую функцию можно создать, сложив варианты sin (x) и cos (x) .
Преобразование Фурье изобилует практическими приложениями в науке и технике, особенно потому, что в реальном мире меньше проблем с непрерывностью и конвергенцией, чем в теоретической математике.И как только вы можете использовать преобразование Фурье для преобразования любой функции в синусы и косинусы, ну, предел бесконечности (шутка, предел sin (x) , когда x стремится к бесконечности, не существует).
Если продолжить странное повсеместное распространение синусов и косинусов, график — это не единственное, что можно преобразовать в синусоиды с помощью преобразования Фурье. Математический инструмент также используется при обработке изображений на основе пикселей. Чтобы понять, как это возможно, нужно вернуться к основам того, что такое периодическая функция.Общая форма читается как A sin (bx) + c , где каждый коэффициент (A, b и c) описывает разные характеристики графика. В этом формате A — это амплитуда, b — период, а c — фазовый сдвиг. Используя аналогичную информацию, пиксели изображения можно «закодировать» в синусоидальную функцию. Например, «интенсивность» пикселя соответствует амплитуде (A) синусоидальной функции, а «местоположение» пикселя — фазовому сдвигу (c) .³
Таким образом, преобразование Фурье создает уникальное представление все изображение.Для каждого изображения существует только одно преобразование Фурье, и наоборот, только одно изображение для каждого преобразования Фурье. По сути, каждое когда-либо созданное цифровое изображение соответствует цепочке синусоид; этот математический инструмент столь же богат и разнообразен, как цифровая фотография и искусство.
Если вы посмотрите назад на любую из кривых изображения Wolfram Alpha, вы увидите, что уравнения представляли собой головокружительно длинные строки — как вы уже догадались — синусов и косинусов. Преобразование Фурье делает возможными все эти графические изображения.И что интересно, это небольшое подмножество математики преследует то же самое, что и многие области искусства и дизайна: поиск лучшего представления визуального явления. Специфика сильно различается, но уловки с перспективой и веса линий — это инструменты во многом такие же, как исчисление и косинусы.
Помимо графиков новизны в Wolfram Alpha, было несколько попыток использовать преобразование Фурье в более художественных целях. Одним из наиболее интересных, которые я обнаружил, было (очевидно, устаревшее или никогда не выпускавшееся) приложение для рисования под названием «DrawAnything.«Приложение пыталось научить своих пользователей рисовать любое загруженное изображение с помощью преобразования Фурье. Каждый «шаг» в созданном в приложении учебном пособии по рисованию будет шагом в приближении преобразования Фурье. Идея удачная — объедините математику и рисование, переходите от простого к сложному так же, как рисовали бы что-нибудь. Однако ясно, что он был разработан кем-то, кто больше интересовался рядами Фурье, чем рисованием, потому что простейшая фаза ряда Фурье не похожа на то, как обычно строится рисунок.
Синусы и косинусы вряд ли волшебным образом превратят любого художника в математика, точно так же, как красивый график вряд ли волшебным образом превратит любого математика в художника. Но синусоиды намного красивее, чем можно было ожидать. По сути, каждая картина, фотография или сцена, которые вас вдохновили, находятся на расстоянии одного преобразования Фурье от уравнения на экране. Они говорят, что картинка стоит тысячи слов; Я не уверен, кто такие , , хотя готов поспорить, что им платят за рисование.Но если картинка стоит тысячи слов, то, ну, значит, и функция. В конце концов, они совпадают — строка за строкой, пиксель за пикселем.
OpenAlgebra.com: отношения, графики и функции
В этом разделе мы изучим функции более глубоко и начнем с определения отношения как любого набора упорядоченных пар.Пример отношения может выглядеть как {(2,3), (2,5), (0,1)}. Здесь мы имеем отношение, состоящее из трех упорядоченных пар или точек в декартовой системе координат.Мы знакомы с упорядоченными парами и обычно видим их как ( x , y ). Обычно значение x (первый компонент) будет независимой переменной или входом, а значение y (второй компонент) является зависимой переменной или выходом.
Пример {(2,3), (2,5), (0,1)} — это НЕ как функция, потому что значение x 2 присвоено более одного значения y , а именно 3 и 5. Для каждого значения x может быть только одно значение y .Затем мы определяем домен как набор значений x , а диапазон — как набор значений y , для которых определено отношение.
Пример:
Совет : если при просмотре списка упорядоченных пар есть повторяющиеся значения x , то отношение не является функцией. Обычно это означает, что есть вход с несколькими выходами. (Это не относится к значениям y )
Определите, являются ли отношения функциями. Если да, укажите домен и диапазон.
Обратите внимание: если мы сможем провести вертикальную линию, дважды пересекающую график, мы сможем идентифицировать одно значение x с двумя соответствующими значениями y . Следовательно, это не может быть функцией.
В качестве альтернативы, если какая-либо вертикальная линия пересекает график только один раз, она представляет функцию.
Используйте тест вертикальной линии, чтобы определить, представляет ли график функцию.
Будьте готовы указать домен и диапазон с учетом графика. Не забудьте думать о графике как о бесконечном наборе упорядоченных пар ( x , y ). По графику определите значения x и y .Сначала оттенок в домене и диапазоне, затем преобразуйте в обозначение интервала.
На этом этапе должно быть ясно, что показанный круг не является функцией. Тем не менее, мы все еще можем определить область и диапазон отношения, которое оно представляет.
Видео на YouTube:
—
Построение графиков на Python | Set 1
Эта серия статей познакомит вас с построением графиков на Python с помощью Matplotlib, который, возможно, является самой популярной библиотекой для построения графиков и визуализации данных для Python.
Установка
Самый простой способ установить matplotlib — использовать pip. Введите в терминале следующую команду:
pip install matplotlib
ИЛИ вы можете загрузить его отсюда и установить вручную.
Начало работы (нанесение линии)
00 |
Вывод:
. Код кажется очевидным. Были выполнены следующие шаги:
- Определите ось x и соответствующие значения оси y в виде списков.
- Изобразите их на холсте с помощью функции .plot () .
- Дайте имя оси x и оси y с помощью функций .xlabel () и .ylabel () .
- Дайте название своему сюжету с помощью функции .title () .
- Наконец, для просмотра вашего графика мы используем функцию .show () .
Построение двух или более линий на одном участке
|
Выход:
- Здесь мы строим две линии на одном графике. Мы различаем их, давая им имя ( метка ), которое передается в качестве аргумента.plot () функция.
- Небольшое прямоугольное поле с информацией о типе линии и ее цвете называется легендой. Мы можем добавить легенду к нашему графику, используя функцию .legend () .
C Настройка участков
Здесь мы обсудим некоторые элементарные настройки, применимые практически к любому участку.
|
00 Как видите, мы выполнили несколько настроек, например
- , установив ширину линии, стиль линии и цвет линии.
- установка маркера, цвет лица маркера, размер маркера.
- переопределение диапазона осей x и y. Если переопределение не выполнено, модуль pyplot использует функцию автоматического масштабирования для установки диапазона и масштаба оси.
Столбиковая диаграмма
|
Выход:
Здесь мы используем plt.bar () для построения гистограммы.Передаются координаты x левой стороны стержней вместе с высотой стержней.вы также можете дать какое-то имя координатам оси x, указав tick_labels
Histogram
44 44 'Моя гистограмма' ) |
Вывод:
Здесь мы используем функцию plt.hist () для построения гистограммы.частот передаются как список возрастов .Диапазон может быть установлен путем определения кортежа, содержащего минимальное и максимальное значение.Следующим шагом является определение диапазона значений « bin », то есть разделение всего диапазона значений на серию интервалов, а затем подсчет количества значений, попадающих в каждый интервал.Здесь мы определили интервалов: = 10. Итак, всего 100/10 = 10 интервалов.
Диаграмма рассеяния
|
Выход:
Здесь 915 , мы используем функцию plt.scatter () для построения диаграммы рассеяния. Как линия, мы также определяем x и соответствующие значения оси y. маркер аргумент используется для установки символа для использования в качестве маркера.Его размер можно определить с помощью параметра s . Круговая диаграмма
import matplotlib.pyplot as plt
действия = '' 917 917 ' 917 спящий ' , ' работа ' , ' играй ' ]
фрагменты = [ 3 7 917 917 917 917 917 917 917 24 , 6 ]
цвета = [ 'r' , 'y' ', 'b' ]
plt.пирог (срезы, метки = действия, цвета = цвета,
startangle = 90 , тень = 24 True 24 ( 0 , 0 , 0,1 , 0 ),
радиус = 1.2 , autopct = '% 1.1f %%' )
plt.legend ()
12900
Вывод вышеуказанной программы выглядит следующим образом:
- Здесь мы строим круговую диаграмму, используя метод plt.pie () .
- Прежде всего, мы определяем меток , используя список под названием activity .
- Затем можно определить часть каждой метки с помощью другого списка, называемого срезов .
- Цвет каждой метки определяется с помощью списка цветов .
- shadow = True покажет тень под каждой меткой на круговой диаграмме.
- startangle поворачивает начало круговой диаграммы на заданные градусы против часовой стрелки от оси x.
- explode используется для задания доли радиуса, на которую мы смещаем каждый клин.
- autopct используется для форматирования значения каждой метки. Здесь мы установили отображение процентного значения только с точностью до 1 знака после запятой.
Графические кривые данного уравнения
import matplotlib.pyplot as plt
import numpy as np
917 917 917 917 917 917 917 917 .arange ( 0 , 2 * (нп.pi), 0,1 )
y = np.sin (x)
plt.plot (x, y)
3 917 .show ()
Результат вышеупомянутой программы выглядит следующим образом:
Здесь мы используем NumPy , который является универсальным пакетом обработки массивов на Python.
- Чтобы установить значения оси x, мы используем np.Метод arange () , в котором первые два аргумента предназначены для диапазона, а третий - для пошагового приращения. Результатом является массив с большим количеством символов.
- Чтобы получить соответствующие значения оси Y, мы просто используем предопределенный метод np.sin () для массива numpy.
- Наконец, мы строим точки, передавая массивы x и y функции plt.plot () .
Итак, в этой части мы обсудили различные типы графиков, которые мы можем создать в matplotlib. Есть и другие участки, которые не были освещены, но самые важные из них обсуждаются здесь -
Эта статья предоставлена Nikhil Kumar .Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью на сайте deposit.geeksforgeeks.org или отправить свою статью по электронной почте: grant@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам. Пожалуйста, напишите комментарий, если вы обнаружите что-то неправильное, или если вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.
Внимание компьютерщик! Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS .
Пошаговое руководство по построению квадратичной функции
автор Каталин Давид
Чтобы нарисовать график функции в декартовой координате
системе нам понадобятся две перпендикулярные линии xOy (где O -
точка пересечения x и y), называемая «координатными осями»
и единица измерения.
Точка в этой системе имеет две координаты.
M (x, y): M - название точки, x - абсцисса, измеряется по Ox, y - ордината и измеряется по Oy.
Две координаты представляют собой расстояния от точки до двух осей.
Если рассматривать функцию f: A -> B (A - область
определения, B - область значений), то точка, найденная на графике
функция имеет вид P (x, f (x)).
Пример
f: A -> B, f (x) = 3x - 1
Если x = 2 => f (2) = 3 × 2 - 1 = 5 => P (2, 5) & in; Gf (где Gf - график функции).2- \ frac {\ Delta} {4a} $
, где Δ = b 2 - 4ac
Если a> 0, минимальное значение f (x) будет $ - \ frac {\ Delta} {4a} $, которое получается, если $ x = - \ frac {b} {2a} $.
Граф будет представлять собой выпуклую параболу , вершина которой (точка поворота параболы) равна $ V (- \ frac {b} {2a}; - \ frac {\ Delta} {4a}) $.
Если a <0, максимальное значение f (x) будет $ - \ frac {\ Delta} {4a} $.
которое получается, если $ x = - \ frac {b} {2a} $.Графом будет вогнутая парабола , вершина которой равна $ V (- \ frac {b} {2a}; - \ frac {\ Delta} {4a}) $.
Парабола симметрична относительно прямой, пересекающей $ x = - \ frac {b} {2a} $,
которая называется «осью симметрии» .
Вот почему, когда мы присваиваем значения x , мы
выберите значения, симметричные относительно $ - \ frac {b} {2a} $.
При рисовании графика очень важны точки пересечения с осями координат.
|,Точка, найденная на оси Ox , имеет форму P (x, 0) , потому что расстояние от нее до Ox равно 0. Если точка найдена как на Ox , так и на графике функции, он также имеет вид P (x, f (x)) ⇒ f (x) = 0 .
Таким образом, чтобы найти координаты точек пересечения с осью Ox , необходимо решить уравнение f (x) = 0 . Получаем уравнение a 2 + bx + c = 0 .
Решения уравнения зависят от знака Δ = b 2 - 4ac .
У нас бывают следующие ситуации:
1) Δ <0
уравнение не имеет решений в R (набор действительных чисел) график не пересекает Ox . Форма графика будет:
или же
2) Δ = 0
уравнение имеет два равных решения $ x_1 = x_2 = - \ frac {b} {2a} $
График касается оси Ox в вершине параболы.Форма графика:
или
3) Δ> 0
уравнение будет иметь два разных решения.
$ x_1 = \ frac {-b- \ sqrt {\ Delta}} {2a} $ и
$ x_2 = \ frac {-b + \ sqrt {\ Delta}} {2a} $
График функции будет пересекать ось Ox в точках M (x 1 и Ox . График будет иметь следующий вид:
или же
||. Точка на оси Oy имеет вид R (0, y) , поскольку расстояние от нее до Oy равно 0 .Если точка найдена как на Oy , так и на графике функции, она также имеет вид R (x, f (x)) ⇒ x = 0 ⇒ R (0, f (0)) .
В случае квадратичной функции
f (0) = a × 0 2 + b × 0 + c ⇒ R (0, c).
Необходимые шаги для построения графика квадратичной функции
f: R → R
f (x) = ax 2 + bx + c
1. Рисуем таблицу переменных, в которую записываем некоторые важные значения для x .
2. Находим координаты вершины $ V (- \ frac {b} {2a}; - \ frac {\ Delta} {4a}) $.
3. Также пишем 0 в таблице и симметричный 0 относительно $ - \ frac {b} {2a} $.
или
4. Определим точку пересечения с осью Ox , решив уравнение f (x) = 0 , и запишем в таблице x 1 и x 2 .
Δ> 0 ⇒
Δ <0 ⇒ точек пересечения нет.В этом случае мы выберем два удобных значения, симметричных относительно $ - \ frac {b} {2a} $
Δ = 0 ⇒ граф касается Ox прямо в своей вершине. Мы снова выберем два удобных значения, симметричных относительно $ - \ frac {b} {2a} $.
Чтобы лучше определить форму графика, мы также можем выбрать другие пары значений для x , но они также должны быть симметричными относительно $ - \ frac {b} {2a} $.
5. Записываем все эти значения в систему координат и рисуем график, соединяя точки.
Пример 1
f: R → R
f (x) = x 2 - 2x - 3
a = 1, b = -2, c = -3
Δ = b 2 - 4 × a × c = (-2) 2 - 4 × 1 × (-3) = 16
$ - \ frac {b} {2a} = \ frac {2} {2} = 1 $
⇒ V (1; -4)
1. $ - \ frac {\ Delta} {4a} = - \ frac {16} {4} = - 4 $
2. f (0) = -3
Симметричность 0 относительно 1 равна 2.
f (2) = -3
3. f (x) = 0 ⇒ x 2 - 2x - 3 = 0
Δ = 16> 0
$ x_1 = \ frac {-b- \ sqrt {\ Delta}} {2a} = \ frac {2 -4} {2} = - 1 $ $ x_1 = \ frac {2 + 4} {2} = 3 $
Мы нашли точки:
A (-1; 0)
B (0; -3)
V (1; -4)
C (2; -3)
D (3; 0)
График будет:
Пример 2
f: R → R
f (x) = -x 2 - 2x + 8
a = -1, b = -2, c = 8
Δ = b 2 - 4 × a × c = (-2) 2 - 4 × (-1) × 8 = 36
$ - \ frac {b} {2a} = \ frac {2} {- 2} = - 1 $
⇒ V (-1; 9)
1.$ - \ frac {\ Delta} {4a} = - \ frac {-36} {- 4} = 9 $
2. f (0) = 8
f (-2) = 8 (симметрия 0 относительно -1 равна -2)
3. f (x) = 0 ⇒ -x 2 - 2x + 8 = 0
Δ = 36
x 1 = 2 и x 2 = -4
A (-4; 0)
B (-2; 8)
V (-1; 9)
C (0; 8)
D (2; 0)
Пример 3
f: R → R
f (x) = x 2 - 4x + 4
a = 1, b = -4, c = 4
Δ = b 2 - 4 × a × c = ( -4) 2 - 4 × 1 × 4 = 0
$ - \ frac {b} {2a} = \ frac {4} {2} = 2 $
⇒ V (2; 0)
1.$ - \ frac {\ Delta} {4a} = 0 $
2. f (0) = 4
f (4) = 4 (симметричность 0 относительно 2 равна 4)
3. f (x) = 0 ⇒ x 2 - 4x + 4 = 0
Δ = 0
x 1 = x 2 = $ - \ frac {b} {2a} $ = 2
A (-2; 9)
B (0; 4)
V (2; 0)
C (4; 4)
D (5; 9)
Пример 4
f: R → R
f (x) = -x 2 + 4x - 5
a = -1, b = 4, c = -5
Δ = b 2 - 4 × a × c = 4 2 - 4 × (-1) × (-5) = 16-20 = -4
$ - \ frac {b} {2a} = \ frac {-4} {- 2} = 2 $
⇒ V (2; -1)
1.$ - \ frac {\ Delta} {4a} = - \ frac {-4} {- 4} = - 1 $
2. f (0) = -5
f (4) = -5 (симметричность 0 относительно 2 равна 4)
3. f (x) = 0 ⇒ -x 2 + 4x - 5 = 0,
Δ <0
Уравнение не имеет решения.
Мы должны выбрать значения, симметричные относительно 2
A (-1; -10)
B (0; 5)
В (2; -1)
C (4; -5)
D (5; -10)
Если область определения не R (набор действительных чисел), а интервал, мы стираем часть графика, соответствующую значениям x , которые не найдены в интервале.Необходимо записать конечные точки в таблицу.
Пример 5
f: [0; + ∞) → R
f (x) = x 2 - 2x - 3
a = 1, b = -2, c = -3
Δ = b 2 - 4 × a × c = (-2 ) 2 - 4 × 1 × (-3) = 16
$ - \ frac {b} {2a} = 1 $
⇒ V (1; -4)
1. $ - \ frac {\ Delta} {4a} = - 4 $
2. f (0) = -3
f (2) = -3 (симметричный 0 относительно 1 равен 2)
3. f (x) = 0 ⇒ x 2 - 2x - 3 = 0,
Δ = 16
x 1 = -1 ∉ [0; ∞)
х 2 = 3
А (0; -3)
В (1; -4)
В (2; -3)
С (3; 0)
Как создать параболу - анимированная
. Экстремумы функции
Экстремумы функции 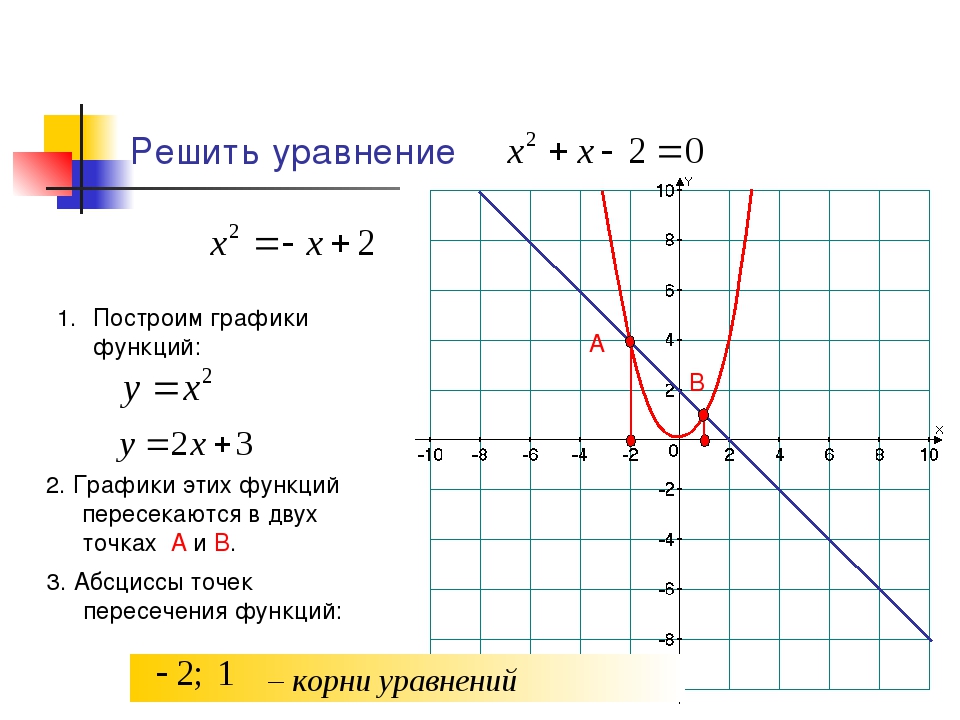
 Это значения, которые соответствуют первым компонентам
упорядоченный
пары, с которыми он связан. Если вам нужен обзор домена,
смело переходите к Tutorial
30: Введение в функции.
Это значения, которые соответствуют первым компонентам
упорядоченный
пары, с которыми он связан. Если вам нужен обзор домена,
смело переходите к Tutorial
30: Введение в функции.  Найти на
минимум четыре упорядоченных парных решения.
Найти на
минимум четыре упорядоченных парных решения. Также
использовать
график для определения области и диапазона функции.
Также
использовать
график для определения области и диапазона функции.
Ваш комментарий будет первым