Нажмите "Enter", чтобы перейти к содержанию

Как чертить график функции: Построение графиков функций онлайн

Содержание

Как построить график функции y = f(x + l) + m. Алгебра, 8 класс: уроки, тесты, задания.

1. Вспомогательная система координат

Сложность: лёгкое

1
2. Параллельный перенос графика функции

Сложность: лёгкое

2
3. Направление сдвига графика функции

Сложность: лёгкое

2
4. Формула функции

Сложность: среднее

2
5.
 Уравнение параболы

Сложность: среднее

2
6. Значение функции

Сложность: среднее

2
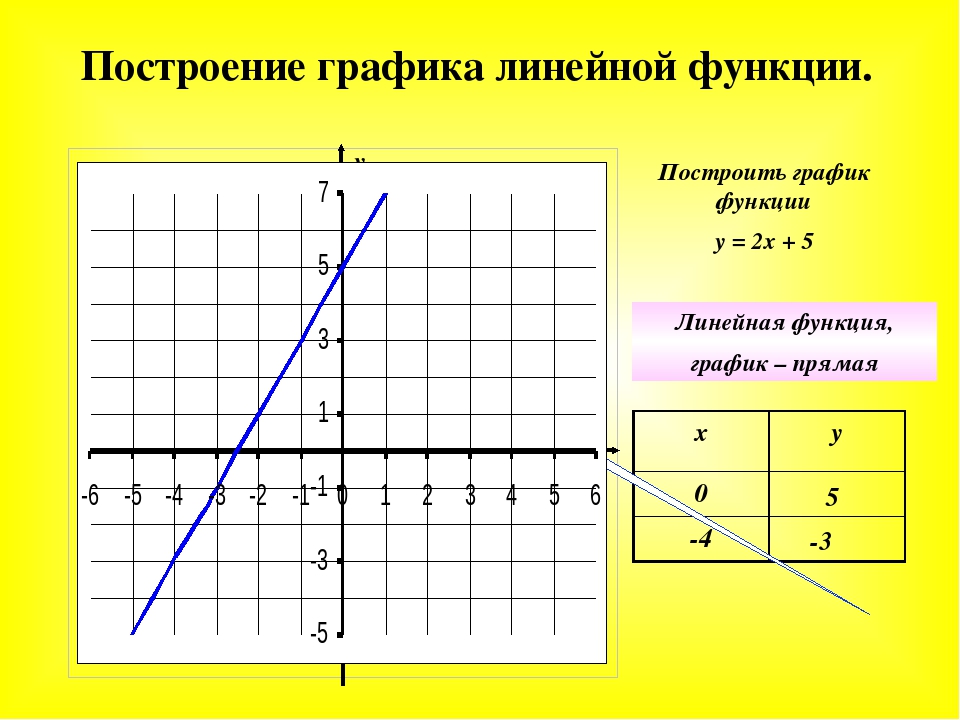
7. Построение графика квадратичной функции вида y = (x + a)² + b

Сложность: среднее

3
8. Метод выделения полного квадрата

Сложность: сложное

3
9.
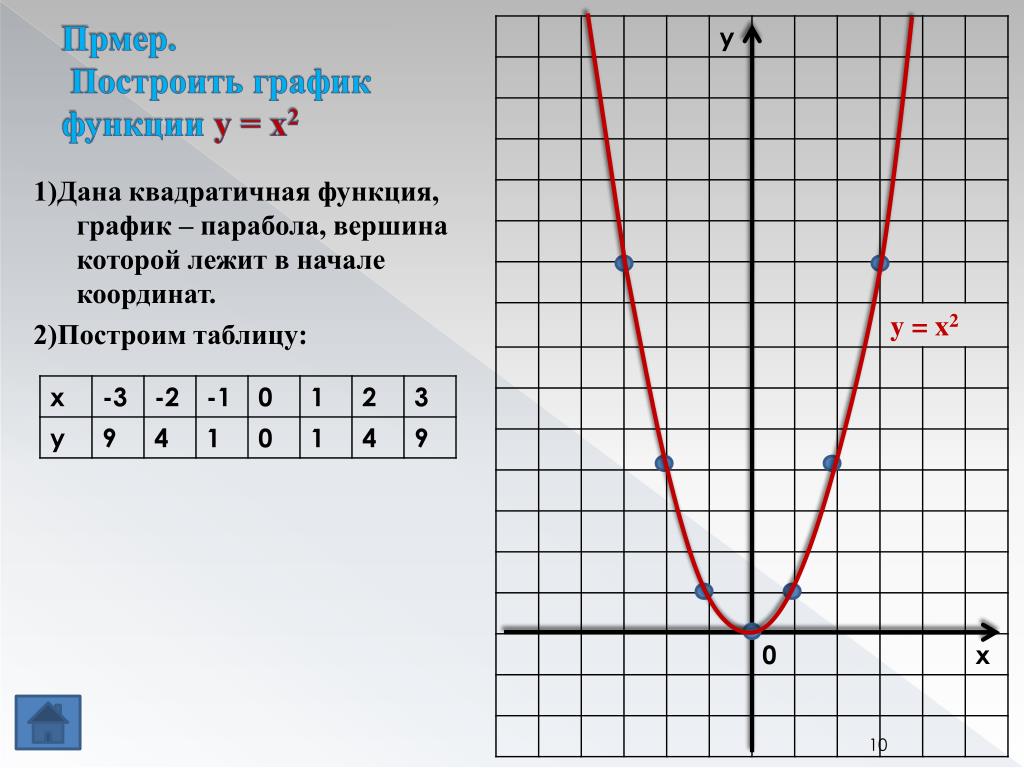
Функции

Сложность: сложное

3
10. Графическое решение системы уравнений

Сложность: сложное

3

Как построить график функции в Wolfram|Alpha

Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20

Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5

В двух предыдущих примерах мы задавали область значений аргумента х.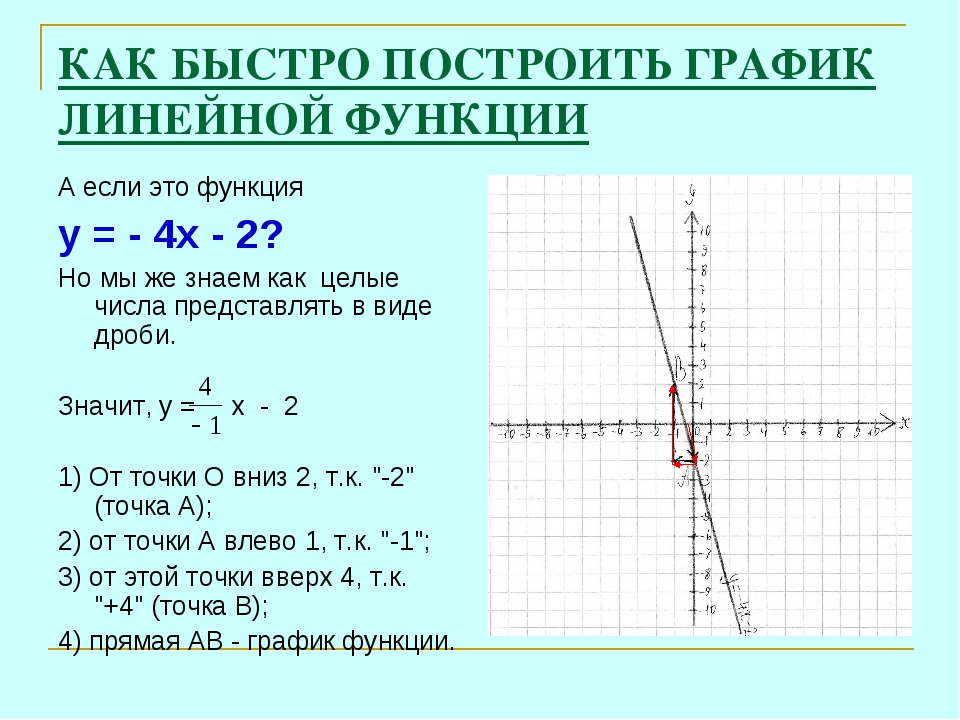 А что будет, если не задавать область значений х?

Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:

Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс 

plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.

Сравните:

Кроме того, изображение построенного графика будет крупнее, если вы используете префикс plot.

Одновременно в Wolfram | Alpha можно строить графики нескольких функций.

Если навести мышь на левый нижний угол изображения, то становятся доступными две ссылки: Save as image и Copyable planetext. Рассмотрим такой график:

Первая ссылка Save as image, которая открывается в левом нижнем углу изображения, позволяет сохранить построенный график, как картинку на компьютере пользователя — при нажатии на Save as image автоматически начнется загрузка изображения:

Вторая ссылка Copyable planetext позволяет увидеть код, аналогичный тому, который используется системой Matematica для построения графиков:

Теперь рассмотрим, как в Wolfram | Alpha построить графики функций двух переменных. 2 cos(x) для x от -6 до 6 и y от -2 до 2

Как и в одномерном случае, Wolfram | Alpha автоматически определяет подходящий диапазон значений аргументов, где функция имеет наиболее характерный вид. В случае, если Wolfram | Alpha не может найти подходящий диапазон, то это скорее всего потому, что система не смогла определить такой диапазон, где функция имеет наиболее интересное поведение. В этом случае, мы можем задать диапазон вручную, как это было сделано выше. Посмотрите следующие примеры:

А что, если вы захотите построить одновременно несколько графиков функций двух переменных?

Wolfram | Alpha строит отдельный график для каждой функции в списке. Вот еще несколько примеров:

Новой функцией Wolfram | Alpha является возможность строить графики действительной и мнимой частей комплексно-значных функций двух переменных:
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям). 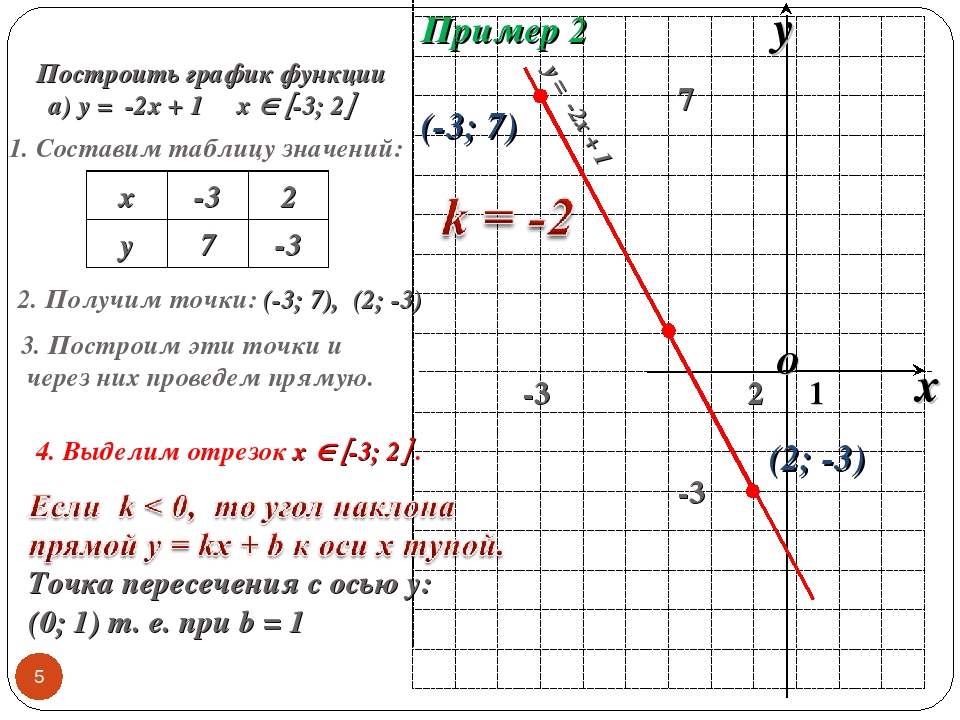Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.

Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.

Источник by Sam Blake

Опубликовано в блоге Web in Math

Как построить график функции в Python с помощью библиотеки plotnine



Я был давним пользователем R, недавно перешедшим на Python, и я пытался перенести свои знания о построении графиков с ggplot2, поскольку это так интуитивно понятно. Plotnine , предположительно, является самой ggplot2-эской библиотекой построения графиков, и я успешно воссоздал с ее помощью большинство графиков, за исключением критически важных plot регулярных функций. 2 + 2.5 > graph <- ggplot(data.frame(x=c(-5,5)), aes(x=x)) + + stat_function(fun = basic_plot) > graph python r plot ggplot2 plotnine
Поделиться Источник Coolio2654     19 января 2018 в 21:20

2 ответа

  • Как построить график функции cos для конкретного значения Pi в Matlab?

    Для конкретной функции, x(n) = A Cos(ωn+θ) , для ω = π/6 и θ = π/3 Я не могу построить график. Для общей косинусной функции я могу построить ее с помощью: x = -pi:0.01:pi; plot(x,cos(x)) Но как построить график для конкретных значений pi Омеги и теты?

  • Как построить линейный график с черепахой Python?

    этот вопрос, возможно, задавался и раньше, однако он не работает для меня. Есть ли какой-нибудь способ построить линейный график с помощью python turtle? Я понятия не имею, с чего начать, за исключением from turtle import Turtle Спасибо за любую помощь.


5

Вам не нужен numpy, он просто отлично работает по «standard»-му пути! 🙂

from plotnine import *
import pandas as pd

(ggplot(pd.DataFrame(data={"x": [-5, 5]}), aes(x="x"))
    + stat_function(fun=lambda x: x**2+2.5))

Поделиться erocoar     19 января 2018 в 23:13


1

Одно из главных отличий, которое вызвало у меня проблемы, было то же самое, что и в вопросе. Конкретно:

в R году aes(x = x) или aes(x)

в плотнине aes(х = ‘x’)

Поделиться bill fite     30 мая 2018 в 08:18

Похожие вопросы:


Как построить график/plot 2D лапласиана Гауссовой (LoG) функции в MATLAB или python?

Привет. Я пытаюсь построить график 3-D, подобный приведенному ниже, который иллюстрирует лапласиан 2-D функции Гаусса (LoG). Как я могу сделать это через MATLAB или python? Фрагменты кода были бы…


Построить график вызовов в python, включая модули и функции?

У меня есть куча сценариев для выполнения задачи. И мне действительно нужно знать график вызовов проекта, потому что он очень запутан. Я не могу выполнить код, потому что для этого ему нужны…


Как построить график с помощью ggplot2

У меня есть задача, и мне нужно построить график с помощью ggplot2. У меня есть вектор рейтинга (Samsung S4 ratings от своих пользователей) Я генерирую эти данные с помощью этого: TestRate<-…


Как построить график функции cos для конкретного значения Pi в Matlab?

Для конкретной функции, x(n) = A Cos(ωn+θ) , для ω = π/6 и θ = π/3 Я не могу построить график. Для общей косинусной функции я могу построить ее с помощью: x = -pi:0.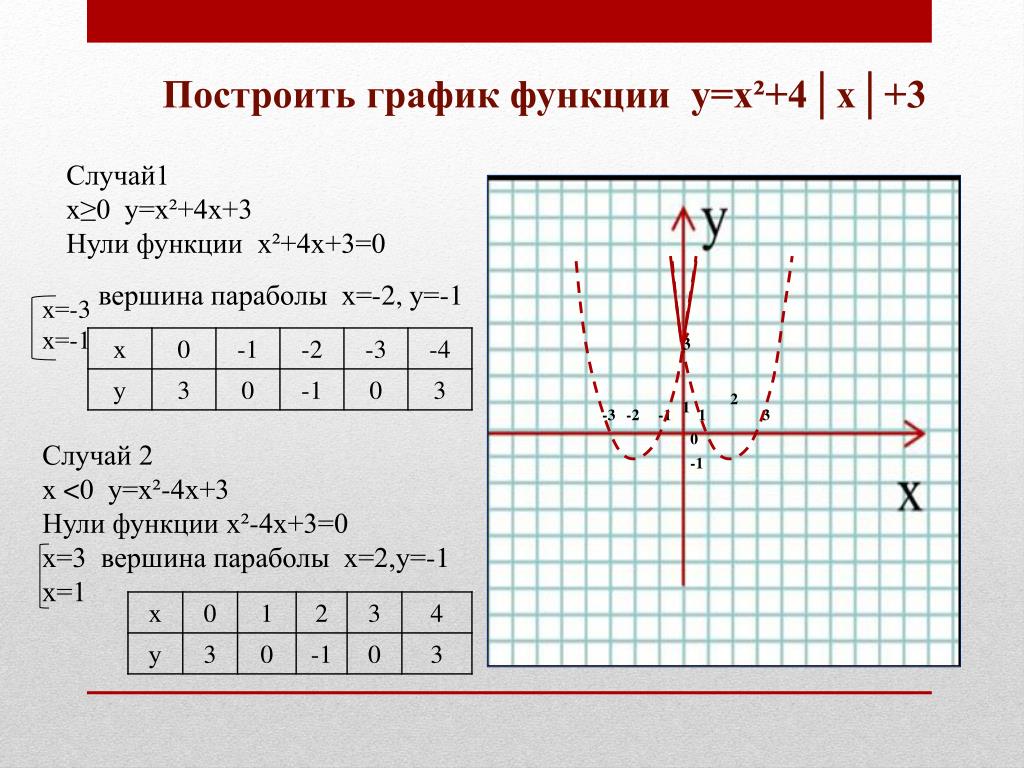 01:pi; plot(x,cos(x)) Но как…


Как построить линейный график с черепахой Python?

этот вопрос, возможно, задавался и раньше, однако он не работает для меня. Есть ли какой-нибудь способ построить линейный график с помощью python turtle? Я понятия не имею, с чего начать, за…


Python Plotnine — создание штабелированной гистограммы

Я пытался нарисовать сложенную гистограмму с помощью плотнина. Этот график представляет собой инвентаризацию на конец месяца в пределах того же Category. SubCategory-это то, что должно быть сложено….


Высокого разрешения сохранение изображений с plotnine

Я пытаюсь использовать plotnine для сохранения изображения с высоким разрешением png. С тестовым набором данных это выглядит следующим образом: from plotnine import * import pandas as pd import…


Как построить график времени с помощью pyplot?

У меня есть csv с двумя столбцами, один с названиями дней недели и один со временем входа сотрудника в систему. Как мне построить этот график с помощью matplotlib или pyplot ? не могу понять, как…


Plotnine: Как удалить ggplot: (xxx) тип раздражающего вывода текста при построении графика

Запуск Блокнота jupyter (python) Построение графиков с использованием библиотеки Python Plotnine Я рисую график и ниже выходного графика раздражает ggplot2: (number) output Обычно вы ставите ; в…


Построить минимальные и максимальные интервалы с помощью Plotnine?

В настоящее время я могу построить минимальный и максимальный интервал с помощью matplotlib, однако я хочу сделать то же самое с библиотекой plotnine, возможно ли это? Я пытаюсь, но безуспешно…

Как построить график кусочной функции

☰

Кусочные функции — это функции, заданные разными формулами на разных числовых промежутках. Например,

Такая запись обозначает, что значение функции вычисляется по формуле √x, когда x больше или равен нулю. Когда же x меньше нуля, то значение функции определяется по формуле –x2. Например, если x = 4, то f(x) = 2, т. к. в данном случае используется формула извлечения корня. Если же x = –4, то f(x) = –16, т. к. в этом случае используется формула –x2 (сначала возводим в квадрат, потом учитываем минус).

Чтобы построить график такой кусочной функции, сначала строятся графики двух разных функций не зависимо от значения x (т. е. на всей числовой прямой аргумента). После этого от полученных графиков берутся только те части, которые принадлежат соответствующим диапазонам x. Эти части графиков объединяются в один. Понятно, что в простых случаях чертить можно сразу части графиков, опустив предварительную прорисовку их «полных» вариантов.

Для приведенного выше примера для формулы y = √x получим такой график:

Здесь x в принципе не может принимать отрицательных значений (т. е. подкоренное выражение в данном случае не может быть отрицательным). Поэтому в график кусочной функции уйдет весь график уравнения y = √x.

Построим график функции f(x) = –x2. Получим перевернутую параболу:

В данном случае в кусочную функции мы возьмем только ту часть параболы, для которой x принадлежит промежутку (–∞; 0). В результате получится такой график кусочной функции:

Рассмотрим другой пример:

Графиком функции f(x) = (0.6x – 0.5)2 – 1.7 будет видоизмененная парабола. Графиком f(x) = 0.5x + 1 является прямая:

В кусочной функции x может принимать значения в ограниченных промежутках: от 1 до 5 и от –5 до 0. Ее график будет состоять из двух отдельных частей. Одну часть берем на промежутке [1; 5] от параболы, другую — на промежутке [–5; 0] от прямой:

Строим графики функций, содержащие модуль. Часть 1

Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.

1. Построение графика функции y = |f(x)|

Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.

Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.

1) Построить аккуратно и внимательно график функции y = f(x).

2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.

3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 1. Изобразить график функции y = |x2 – 4x + 3|

1) Строим график функции y = x2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.

0x : y = 0.

x2 – 4x + 3 = 0.

x1 = 3, x2 = 1.

Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).

0y: x = 0.

y = 02 – 4 · 0 + 3 = 3.

Следовательно, парабола пересекает ось 0y в точке (0, 3).

Координаты вершины параболы:

xв = -(-4/2) = 2, yв = 22 – 4 · 2 + 3 = -1.

Следовательно, точка (2, -1) является вершиной данной параболы.

Рисуем параболу, используя полученные данные (рис. 1)

2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.

3) Получаем график исходной функции (рис. 2, изображен пунктиром).

2. Построение графика функции y = f(|x|)

Заметим, что функции вида y = f(|x|) являются четными:

y(-x) = f(|-x|) = f(|x|) = y(x).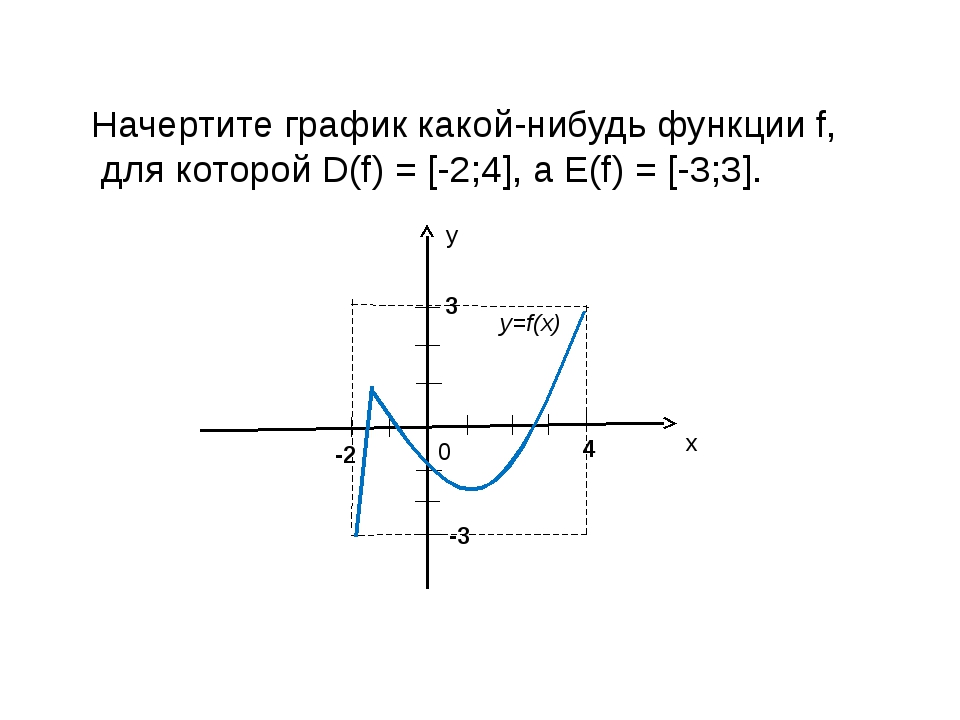 Значит, графики таких функций симметричны относительно оси 0y.

Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.

1) Построить график функции y = f(x).

2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 2. Изобразить график функции y = x2 – 4 · |x| + 3

Так как x2 = |x|2, то исходную функцию можно переписать в следующем виде: y = |x|2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.

1) Строим аккуратно и внимательно график функции y = x2 – 4 · x + 3 (см. также рис. 1).

2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.

3) Отображаем правую часть графика симметрично оси 0y.

4) Окончательный график изображен на рисунке (рис. 3).

Пример 3. Изобразить график функции y = log2|x|

Применяем схему, данную выше.

1) Строим график функции y = log2x (рис. 4).

Далее повторяем пункты 2)-3) предыдущего примера и получаем окончательный график (рис. 5).

3. Построение графика функции y = |f(|x|)|

Заметим, что функции вида y = |f(|x|)| тоже  являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому , их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.

Чтобы построить график функции y = |f(|x|)|, необходимо:

1) Построить аккуратно график функции y = f(|x|).

2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.

3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.

4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).

Пример 4. Изобразить график функции y = |-x2 + 2|x| – 1|.

1) Заметим, что x2= |x|2. Значит, вместо исходной функции y = -x2 + 2|x| – 1

можно использовать функцию y = -|x|2 + 2|x| – 1, так как их графики совпадают.

Строим график y = -|x|2 + 2|x| – 1. Для этого применяем алгоритм 2.

a) Строим график функции y = -x2 + 2x – 1 (рис. 6).

b) Оставляем ту часть графика, которая расположена в правой полуплоскости.

c) Отображаем полученную часть графика симметрично оси 0y.

d) Полученный график изображен на рисунке пунктиром (рис. 7).

2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.

3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.

4) Полученный график изображен на рисунке пунктиром (рис. 8).

Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|

1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.

a)  Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9).

Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.

Далее повторяем пункты b)-c) из предыдущего примера и получаем следующий график функции (рис. 10).

2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.

3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.

4) Окончательный график изображен на рисунке (рис. 11).

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Как построить в Word график функции?

Как построить в Word график функции?

Ответ мастера:

График функции является разновидностью диаграммы в приложениях Microsoft Office, которая отображает зависимость какого-то одного показателя от другого, например, стоимость заказа от цены товара. Также график может отображать динамическое изменение разных значений, например, изменение температуры воздуха за неделю.

Чтобы строить графики в Word, нужно использовать дополнение для пакета Microsoft Office. Оно называется «Построитель графиков». Такое приложение позволяет рисовать графики заданных функций в виде полилиний. Загрузить такое дополнение можно по ссылке http://www. softportal.com/getsoft-1561-postroitel-grafikov-2.html. Далее установите приложение на ваш ПК. Теперь запустите Word и можете выполнять построение таблицы с данными для вашего графика функции.

Включите возможность запуска макросов для хорошего использования дополнений. Чтобы это сделать, в меню «Сервис» выберите «Макрос», потом «Безопасность». В новом окне выберите низкий или средний уровень безопасности. Также установите поддержку Visual Basic for Applications.

Теперь нажмите на «Вид» и выберите в «Панели инструментов» команду Graph Builder. Этим вы активируете кнопку построителя. Или можно кликнуть правой кнопкой мыши на любую панель инструментов и поставить галочку напротив Graph Builder. Теперь нажмите на кнопку «Запуск графопостроителя» и в новом окне, которое открылось, выполните установки для построения графика в Word.

Установите галочки около тех элементов, которые вам нужны. Если нужно, включите подписи осей, отображение сетки, стрелки или деления. Возле надписи F(x)= нажмите левой кнопкой мыши на стрелку, и выберите необходимую функцию. Возле нужной системы координат, декартовой или полярной, установите переключатель. Выберите высокую или среднюю точность построения. Теперь установите размер сетки, для чего напишите нужные значения в соответствующих полях. Далее установите требуемую единицу измерения графика, например, точки или миллиметры. В пункте «Таблица значений» сделайте ссылку на те значения, которые нужно использовать для построения графика. Выберите нужный язык и нажмите «Рисовать».

Графики тригонометрических функций. Синусоида | Подготовка к ЕГЭ по математике

Категория: Справочные материалыФункции и графики

Смешное видео по теме 

График функции y=sinx

Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции .

Переносим  все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.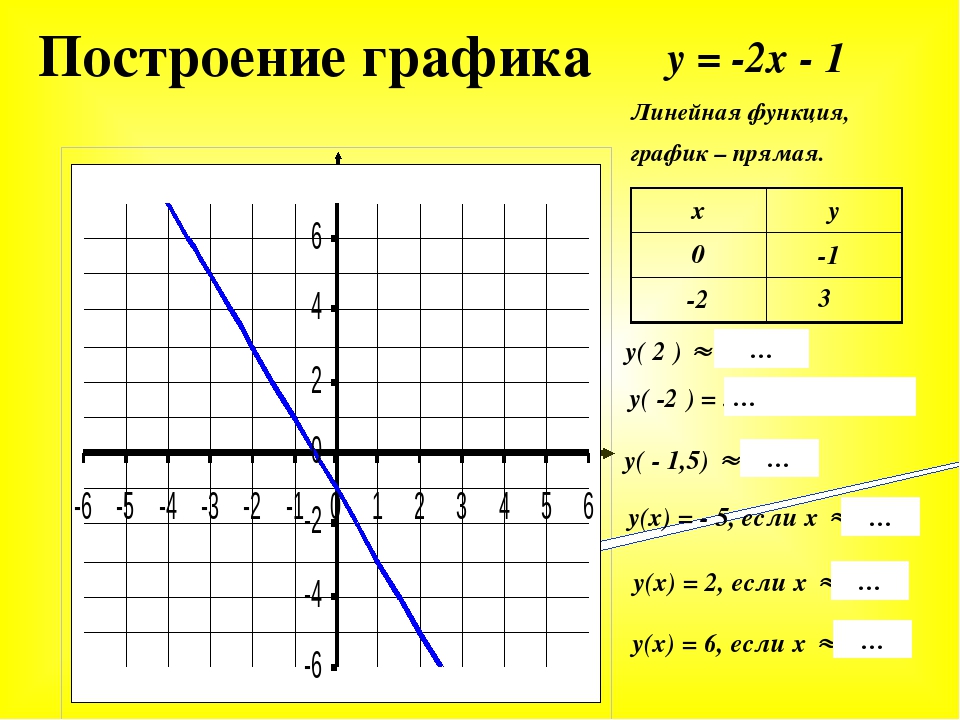

По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.

.

Переносим  все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.

По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.

 

Нанесенные на координатную плоскость точки подсказывают нам плавную кривую.  Это и есть график функции на

Поскольку на тригонометрическом круге значения синуса повторяются через каждый круг (несколько кругов), то не составит труда построить график функции и на всей числовой прямой.

Указанный выше фрагмент графика синуса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции :

График функции называется синусоидой. График симметричен относительно начала координат.

График функции y=cosx

Точно также, как мы строили график при помощи тригонометрического круга, мы могли бы построить и .

Поступим несколько иначе.

Согласно формулам приведения .

Из чего мы делаем вывод, что график функции будет получен смещением графика функции на   единиц влево.

То  есть график функции  – это все таже синусоида, но теперь уже, симметричная относительно оси ординат.

 

Преобразования синусоиды

Приглашаю посмотреть  небольшой видеоролик о том, как  меняется поведение синусоиды в зависимости от  умножения аргумента или функции на некоторое число или от прибавления к аргументу или функции некоторого числа.

GraphPad Prism 9 Curve Fitting Guide

Prism предлагает график для функционального анализа, но на самом деле он не анализирует какие-либо данные. Скорее, он генерирует кривые на основе выбранного вами уравнения и вводимых вами параметров.

Как построить график функции

1. Начните с любой таблицы или графика данных, щелкните «Анализировать», откройте папку «Создать кривую» и выберите «Построить график функции».

2. На первой вкладке (Функция) выберите уравнение, начальное и конечное значения X и количество кривых, которые вы хотите построить.

3. На второй вкладке (Параметры) выберите, хотите ли вы также построить первую производную, вторую производную или интеграл функции. «Кривая» на самом деле представляет собой набор координат X и Y, которые определяют серию точек, которые соединяются, образуя кривую. Вы можете выбрать количество отрезков линии, которые будут определять кривую. Нет особых причин изменять значение по умолчанию (150), если только вы не хотите построить только часть кривой на некоторых графиках, и в этом случае вам следует увеличить это значение.

4. На третьей вкладке (Значения параметров) введите значения параметров (или щелкните значок крючка для анализа крючка или информационных констант).

Советы по построению функции

Построение семейства кривых

Если вы решили построить более одной кривой (выбор на первой вкладке), остальная часть диалогового окна работает немного иначе.

Вам нужно, чтобы один параметр в уравнении изменялся от кривой к кривой. Не определяйте это в уравнении. Вместо этого определите значения на третьей вкладке.

Вы также захотите пометить столбцы вычисляемой таблицы. Есть два способа сделать это. Укажите внизу второй вкладки (Параметры), хотите ли вы пометить каждую кривую вручную (введите метки в верхней части третьей вкладки) или вы хотите, чтобы каждый столбец был помечен с использованием значения одного из параметров. Последнее обычно имеет больше смысла и проще.

Если вам нужно сделать что-то более сложное, помните, что вы можете написать уравнение, чтобы некоторые строки применялись только к определенным наборам данных.Поместите перед строкой, которая относится только к столбцу A и т. Д.

В верхней части третьей вкладки перечислены все кривые, которые вы создадите. Выберите одну или несколько из этих кривых (или нажмите «выбрать все»), а затем введите значения параметров ниже. Часто вам нужно сначала щелкнуть «выбрать все» и ввести большинство параметров. Затем щелкайте по одной кривой за раз и введите значение параметра, который варьируется между кривыми.

Отображение каждой кривой на отдельном графике

По умолчанию Prism создает график, содержащий все кривые на одном графике.Если вы хотите, чтобы каждая кривая отображалась на своем графике, перейдите к таблице результатов, нажмите «Создать» и выберите «График существующих данных». В появившемся диалоговом окне выберите создание одного графика для каждого набора данных (в данном контексте набор данных представляет собой кривую).

Если вы планируете увеличить масштаб и построить только часть кривой

Кривая по умолчанию определяется как 150 линейных сегментов. Это создает плавную кривую. Но если вы затем измените диапазон значений X, показанный на графике, будет видна только часть этих линейных сегментов, а кривая может показаться грубой.Чтобы решить эту проблему, вернитесь в диалоговое окно параметров на вкладку «Параметры» и увеличьте количество сегментов линии до гораздо большего значения.

Объединение двух кривых на одном графике

Приведенный ниже график объединяет две построенные функции на одном графике. В первый раз, когда я построил график функции, я выбрал гауссово распределение с X в диапазоне от -3 до 3. Я установил среднее значение 0,0, стандартное отклонение 1,0 и амплитуду 100,0 (произвольно, поскольку я скрыл эту ось). . Затем я повторил этот анализ, но на этот раз установил диапазон X от 1.3 до 3,0. Я поместил обе кривые на один график (Изменить … Добавить наборы данных — помните, что кривая, сгенерированная этим анализом, является «набором данных» для Prism). Для более короткой кривой я решил создать заливку области.

Графики функций квадратного корня

Родительская функция функций формы ж Икс знак равно Икс — а + б является ж Икс знак равно Икс .

Обратите внимание, что домен из ж Икс знак равно Икс является Икс ≥ 0 и классифицировать является y ≥ 0 .

График ж Икс знак равно Икс — а + б можно получить, переведя график ж Икс знак равно Икс к а единиц вправо, а затем б единиц вверх.

Пример:

Нарисуйте график y знак равно Икс — 1 + 2 из родительского графа y знак равно Икс .

Решение:

Шаг 1. Нарисуйте график y знак равно Икс .

Шаг 2. Переместите график y знак равно Икс к 1 единицы справа, чтобы получить график y знак равно Икс — 1 .

Шаг 3. Переместите график y знак равно Икс — 1 к 2 единиц до получения графика y знак равно Икс — 1 + 2 .

Область определения функции y знак равно Икс — 1 + 2 является Икс ≥ 1 .

Диапазон функции y знак равно Икс — 1 + 2 является y ≥ 2 .

Как нарисовать любой график на глаз

Уравнения в математике полезны, но они также неэффективны — для каждого значения x вам нужно выполнить отдельный расчет, чтобы выяснить, что такое y. Графики берут это уравнение и превращают его в визуальное представление, во что-то, на что вы можете посмотреть и сразу увидеть, что происходит при разных значениях x, как изменяется функция и многое другое!

Однако, когда вы впервые изучаете графики, все дело в запоминании основных уравнений и того, как будут выглядеть их графики, начиная с линейных уравнений в форме углового пересечения.Однако по мере того, как вы переходите к более сложным уравнениям, таким как квадратичная и тригонометрия, вас часто просят запомнить формы таких уравнений, как эти —

— где вы должны запомнить точную настройку уравнения и то, что означает каждый термин на графике, будь то вершина, наклон, пересечения, масштабирование, горизонтальный или вертикальный сдвиг или многое другое!

Но зачем запоминать все эти a, c, k и h, если это будет полезно только в некоторых конкретных случаях ?!

Вместо этого, в следующий раз, когда вам нужно будет узнать, как должен выглядеть график функции, попробуйте эти шаги, чтобы быстро нарисовать любой график!

Для демонстрации воспользуемся уравнением:

Он похож на полиномиальные уравнения, которые вы, возможно, видели в классе, но он кубический, поэтому у нас нет очевидных форм уравнений, которые можно было бы использовать для построения графика.Итак, как построить график этой функции?

Первое, что мы хотим сделать, это поднять несколько точек на нашем графике, поэтому мы хотим выбрать те, которые будет легко вычислить. Практически для любого уравнения подстановка x = 0 и решение относительно y выполняется быстро и легко на глаз, и почти всегда можно выполнить без калькулятора. Для нашего примера уравнения:

Итак, первая точка, которую мы поставим на нашем графике, — это (0, -4).

а. Если вы можете легко найти его, постройте y = 0

Далее, в некоторых случаях y = 0 тоже довольно легко решить.Если вы можете быстро решить для y = 0 , это еще один хороший момент, который нужно решить прямо сейчас. В данном случае:

Итак, теперь у нас есть точка (-2, 0), которую нужно добавить к нашему графику!

г. Бонус — нанесите несколько легко вычисляемых точек, например x = 1 & x = -1

В зависимости от графика может быть легко подставить небольшие целые числа, такие как 1 или -1. Чем больше точек вы можете добавить к своему графику, тем лучше вы сможете увидеть, какую форму он в конечном итоге примет. Однако придерживайтесь тех пунктов, которые легко вычислить.Цель этого метода — быстро найти всего несколько точек — если вы собираетесь вычислять каждую точку на графике, вы не экономите себе время!

Для этого уравнения мы получим:

и

Итак, теперь у нас есть четыре точки: (0, -4), (-2,0), (1, -18) и (-1, -2). Давайте нарисуем эти точки и посмотрим, как они выглядят!

Мы можем увидеть, как график обретает форму, но нам понадобится дополнительная информация, прежде чем мы закончим.

Какая бы линия мы ни рисовали, она должна заканчиваться стрелками на обоих концах, чтобы мы знали, что происходит, когда мы идем дальше по оси x как в положительном, так и в отрицательном направлении.Это то, что называется «конечным поведением». Чтобы выяснить, что это такое, мы собираемся подставить два числа в наше исходное уравнение — большое положительное число и большое отрицательное число. На самом деле мы не собираемся выбирать число и использовать наш калькулятор, чтобы выяснить, что происходит, мы просто собираемся посмотреть, как части уравнения повлияют на конечный результат.

Например, подставив большое положительное число в нашу кубическую функцию, получим:

Добавление 1 к большому положительному числу почти не изменит его — тогда, когда мы кубим его в куб, оно станет действительно большим положительным числом.

Однако действительно большое положительное число станет отрицательным при умножении на -2, и вычитание 2 не имеет большого значения, поэтому конечным результатом будет действительно большое отрицательное число.

Если мы попробуем то же самое для другой стороны графика, подставив большое отрицательное число для x, мы получим:

Большое отрицательное число в кубе — это действительно большое отрицательное число, но на этот раз, когда оно умножится на -2, оно станет действительно большим положительным числом.

o, для нашего графика мы обнаружили, что при больших положительных значениях x, y большое и отрицательное, а при больших отрицательных x, y большое и положительное. Давайте добавим это к нашему графику со стрелками.

У некоторых уравнений есть необычные особенности или особенности, которые вы можете заметить, взглянув на уравнение — обратите внимание, в частности, на любые точки, где большая часть уравнения может стать нулем. Это может помочь вам найти корни, асимптоты или другие места, где форма графика изменяется необычным образом.

Например, с уравнением, которое мы рассматривали,

Этот член интересен, потому что если x = -1, вся часть уравнения станет нулевой. Конечно, мы уже нашли эту точку ранее, но это говорит нам, что x = -1 — это «особая» точка в уравнении — возможно, что форма графика здесь каким-то образом изменится.

На этом этапе мы сделали все, что могли — у нас есть несколько точек на графике, мы знаем, как он будет выглядеть на концах, и выявили любые необычные точки или особенности.Возможно, мы не знаем точно, что это такое, но мы готовы что-то нарисовать.

Возможно, мы все еще не знаем точно, как выглядит график, но здесь вы можете использовать основы для каждого основного уравнения. Мы знаем, что наша линия будет гладкой и максимально простой, но при этом все равно попадет во все наши точки. Если мы в целом знаем, что это за уравнение (полиномиальное, радикальное, экспоненциальное), у нас есть хотя бы некоторые предположения, какова будет его общая форма.

В нашем примере у нас достаточно точек, чтобы набросать одну сторону нашего уравнения, но отрицательная сторона немного неясна, поэтому давайте подумаем, что мы можем сказать о другом типе многочлена, квадратном уравнении.

Что касается нашей кубической функции, мы знаем, что квадратичные функции всегда симметричны относительно своей вершины, но это не совсем работает, потому что мы знаем, что в одном направлении мы закончим положительно, а в другом нам нужно пойти отрицательным.

Итак, давайте угадаем что-то подобное — может быть, наша «особая» точка в x = -1 — это , как вершина, но в этой точке форма графика такая же, но движется в противоположном направлении. (Для справки я поставил пунктирную линию в точке x = — 1, но, конечно, это не будет частью настоящего окончательного графика.)

Поехали! Это не идеальный график, но, сделав несколько быстрых шагов, мы, по крайней мере, в общих чертах узнаем, как этот график будет выглядеть. Если вам интересно, вот как выглядит это уравнение, построенное на компьютере.

Этот метод работает с огромным набором функций — многочленами, радикалами, экспонентами, логарифмами, тригонометрическими функциями и многим другим! Просто будьте осторожны, когда дойдете до функций с несколькими y или членами: в этих случаях графики будут необычными, сложными формами, поэтому нарисуйте много точек (x, y), прежде чем пытаться соединить все точки!

Вы хотите пообщаться с репетитором математики в Нью-Йорке, Бостоне или онлайн?

Хотите прочитать больше сообщений в блоге по математике? Читайте ниже!

Как построить график функций на TI-83/84

Как построить график функций на TI-83/84

Авторские права 20012020 Стэн Браун

Резюме: На TI-83/84 довольно легко построить какой-то график. для данной функции.Эта страница поможет вам с хитростями, которые могут не быть очевидным. Вы сможете найти асимптоты, пересечения, пересечения, корни и т. д.

См. Также: Как оценивать функции с помощью TI-83/84
Как построить график кусочных функций на TI-83/84

Методы, описанные в этой заметке, будут работать с любой функцией, но в целях иллюстрации можно использовать

Построение графика вашей функции

Шаг 1: Удалите ненужные участки.

Вам нужно искать любые ранее установленные участки, которые могут мешает вашему новому. Нажмите [ Y = ] (верхняя левая кнопка). Посмотрите на верхнюю часть экран. Если какой-либо из Plot1 Plot2 Plot3 выделен, курсор на него и нажмите [ ENTER ], чтобы отключить его. (Информация не теряется; вы всегда можно вернуться и активировать любой сюжет.) Чтобы убедиться, что у вас есть отключили сюжет, переместите курсор в сторону от него и убедитесь, что он не выделено.
(Иногда вы можете захотеть график более чем одной функции на те же топоры.В этом случае обязательно отключите все функции. вы не хотите строить графики.) Теперь проверьте строки, начинающиеся с Y1 = , Y2 = и так далее. Если есть = знак выделен, либо удалить все уравнение или деактивировать, но оставить в памяти. Чтобы удалить уравнение, установите курсор к нему и нажмите кнопку [ CLEAR ]. Чтобы отключить его без удаляя это, курсор на знак = и нажмите [ ENTER ].

Мой экран выглядел так после того, как я отключил все старые сюжеты и функции.

Шаг 2: Введите функцию.

Если ваша функция еще не в форме y =, используйте алгебру, чтобы преобразовать его, прежде чем продолжить.

Два предупреждения:
  • Для x используйте клавишу [ x, T, θ, n ], а не Клавиша [] (раз).
  • TI-83/84 следует стандартному порядку операций. Если есть операции сверху или снизу дроби, вы должны использовать скобки для x + 2 разделить на x — 3, вы не можете просто ввести x + 2 / x − 3.
 Курсор на одну из линий Y = , нажмите [ CLEAR ], если необходимо, и войдите в функцию.

Проверьте свою работу и исправьте ошибки.

Например, если вы видите звезду * вместо X , вы случайно использовал временную клавишу вместо [ x, T, θ, n ].		 Используйте клавишу [ ◄ ] и перепечатайте все ошибки.

Чтобы удалить лишние символы, нажмите [ DEL ].

Если вам нужно вставить символы, найдите желтый INS выше клавишу [ DEL ]. Нажмите [ 2nd DEL make INS ] и введите дополнительные символы. Как только вы нажмете кнопку курсора, TI-83/84 возвращается в режим перепечатки.

Шаг 3: Отобразите график.

Zoom Standard обычно хороший отправная точка. Он выбирает стандартные параметры от −10 до +10 для x и y . Нажмите [ ZOOM ] [ 6 ].

Общие проблемы

Если вы нигде не видите свой график функции, ваше окно вероятно, ограничен областью плоскости xy график просто не проходит. В зависимости от функции один из этих техники будет работать:

  • ZoomFit — хорошая первая попытка. Нажмите [ ZOOM ] [ 0 ]. (Спасибо Мэрилин Уэбб за это предложение.)

  • Можете попробовать уменьшить масштаб (как собираетесь выше, чтобы увидеть больше плоскости xy ), нажав [ ZOOM ] [ 3 ] [ ENTER ].

  • Наконец, вы можете напрямую настроить окно, чтобы выбрать конкретный область, край.

По поводу других проблем см. TI-83/84 Устранение неисправностей.

Настройка вашего графика

Вы можете внести множество изменений, чтобы улучшить вид графика функции.

Масштабирование

Окно — это ваше поле зрения в плоскость xy , а там есть два основных способа его отрегулировать. В этом разделе рассказывается о масштабирование, простое и подходящее для большинства ситуаций. В в следующем разделе рассказывается о ручной настройке параметры окна для полной гибкости.

Вот краткое изложение техник масштабирования, которые вы, вероятно, использование:

  • Вы уже встречались со стандартным зумом, который [ ZOOM ] [ 6 ].Это хорошая отправная точка для большинство графиков.

  • Вы также встретили зум-фит, который [ ZOOM ] [ 0 ]. Он сдвигает поле обзора вверх или вниз, чтобы отобразить график функции, и он также может растягиваться или сжать график по вертикали.

  • Чтобы уменьшить масштаб , чтобы получить большее поле зрения с меньшей детализацией, нажмите [ ZOOM ] [ 3 ] [ ENTER ]. Вы снова увидите график, с мигающим курсором зума .Вы можете нажать [ ENTER ] еще раз, чтобы уменьшить масштаб еще раз.

  • К увеличить , фокусируясь на части графика с подробнее, нажмите [ ZOOM ] [ 2 ], но не пока нажмите [ ENTER ]. График снова отображается с мигающим курсор масштабирования в центре экрана. Используйте клавиши со стрелками чтобы переместить курсор масштабирования в ту часть графика, на которой вы хотите сфокусироваться, а затем нажмите [ ENTER ]. После того, как график отобразится снова, вы курсор масштабирования все еще мигает, и вы можете снова переместить его и нажать [ ENTER ] для получения более подробной информации.

  • Окно просмотра прямоугольное, а не квадратное. Когда ваши оси x и y имеют одинаковые числовые настройки график фактически растянут на 50% по горизонтали. Если вам нужен сюжет, где Оси x и y имеют одинаковый масштаб, нажмите [ ZOOM ] [ 5 ] для квадратного увеличения .

Есть еще другие варианты масштабирования. Какая-то долгая зима Вечером вы можете прочитать о них в инструкции.

Регулировка окна

Вы можете настроить параметры окна, чтобы увидеть больше график, чтобы сосредоточиться только на одной части или получить больше или меньше тиков Метки. Если да, нажмите [ WINDOW ].

  • Xmin и Xmax слева и справа края окна.
  • Xscl контролирует расстояние между отметками метки на оси x . Например, Xscl = 2 ставит деления делаются каждые 2 единицы по оси x .Больший Xscl деления деления дальше друг от друга, а меньший Xscl помещает их ближе друг к другу.
  • Ymin и Ymax являются нижний и верхний края окна.
  • Yscl интервалы между деления на оси y .
  • Xres — это число 18 включительно. С 1, по умолчанию калькулятор найдет значение y в x -значениях соответствует каждому пикселю по оси x .С 2 расчет происходит каждые 2 пикселя и так далее. Более высокие значения рисуют графики быстрее, но мелкие детали могут быть потеряны. Мой совет, просто уходи это на 1.

Цветные ТИ-84 имеют два дополнительных окна параметры:

  • Δx — это расстояние x между центрами соседние пиксели. Калькулятор определяет это автоматически из Xmin и Xmax , так что вам не нужно возиться с ним. Однако, если вы его измените, калькулятор определит Xmax от Xmin и Δx .
  • TraceStep — размер шага при нажатии ◄ или ► при перемещении по графику. По умолчанию это вдвое больше значение Δ , но вы можете изменить его, если хотите к.

На увеличьте часть графика для более детального просмотра , увеличить Xmin или Ymin или оба, или уменьшите Xmax или Ymax . Затем нажмите [ ГРАФИК ].

Если вы хотите видеть больше плоскости x y , сжатой до меньший масштаб, уменьшите Xmin и / или Ymin , или увеличьте Xmax или Ymax .Затем нажмите [ ГРАФИК ].

Графические окна, показанные в вашем учебнике, могут иметь небольшие числа напечатаны по четырем краям. Чтобы ваше графическое окно выглядело как в учебнике, нажмите [ WINDOW ] и используйте цифры слева и справа края для Xmin и Xmax , число на нижний край для Ymin и номер на верхнем крае для Ymax .

Регулировка сетки

Сетка — это точки (точки или линии, в цвете TI-84s) по всему окну до отметки на осях, вроде миллиметровой бумаги.Сетка помогает вы видите координаты точек на графике.

Если у вас есть черно-белый TI-83/84, и вы видите много бегущих горизонтальных линий по графику, это означает, что ваш Xscl тоже путь маленькие, а отметки идут вместе линиями. Точно так же Yscl — это количество единиц y между отметки. Связка вертикальных линий означает ваш Yscl очень маленький. Нажмите [ WINDOW ] и исправьте любое из этих проблемы.

Чтобы включить или выключить сетку: Найдите желтый FORMAT над [ ZOOM ]. ключ. Нажмите [ 2-й ZOOM составляет FORMAT ].

Курсор на нужную сетку или GridOff и нажмите [ ENTER ], чтобы заблокировать это внутри.

Затем нажмите [ GRAPH ], чтобы вернуться к вашему графику.

Color TI-84 могут отображать сетку в виде точек или линий.На экране [ 2nd ZOOM make FORMAT ] вы можете выбрать GridOff , GridDot или GridLine и вы также можете назначить цвет сетке.

Изучение графика

Домен и асимптоты

Во-первых, просто посмотрите на форму графика. Вертикальная асимптота должна торчать как больной большой палец, например x = 3 с этой функцией. (Подтвердите вертикальные асимптоты проверка определения функции.Положив x = 3 в определение функции делает знаменатель равным нулю, что говорит вам что у вас есть асимптота.)

Color TI-84 обладают способностью обнаруживать асимптоты: нажмите [ 2nd ZOOM make FORMAT ] и измените Detect Asymptotes на На . Это часто создает более реалистичную картину график, как в этом случае, но это также может затруднить просмотр асимптота.Вот обе версии:

Домен определенно исключает любые значения x , где есть вертикальные асимптоты. Но дополнительные значения также могут быть исключены, даже если они не так очевидны на графике. Например, график f ( x ) = ( x +1) / ( x +1) выглядит как простая парабола, но домен не включает x = -1.

Горизонтальные асимптоты обычно очевидны.Но иногда кажущаяся асимптота на самом деле не такова, просто выглядит нравится, потому что ваше поле зрения слишком маленькое или слишком большое. Всегда выполняйте некоторую алгебраическую работу, чтобы подтвердить асимптоты. Эта функция, кажется, имеет y = 1 в качестве горизонтальной асимптоты. поскольку x становится очень маленьким или очень большим, и фактически из функции определение вы можете видеть, что это правда.

Значения функций

При отображении графика нажмите [ TRACE ], а затем интересующее вас значение x .TI-83/84 будет перемещать курсор в эту точку на графике, и отобразит соответствующий y значение внизу.

Значение x должно быть в пределах текущего просмотра. окно. Если вы получили сообщение ERR: INVALID , нажмите [ 1 ] для Выйти из . потом настройте окно просмотра и попробуйте еще раз.

Перехваты

Вы можете проследить по графику, чтобы найти любую точку пересечения. Перехваты графика — это место пересечения или касания оси:

x точка пересечения, где график пересекает или касается оси x , потому что y = 0
y перехват, где график пересекает или касается оси y , потому что x = 0

Чаще всего его x перехватывает вас интересует, потому что x пересечения графика y = f ( x ) являются решениями в уравнение f ( x ) = 0, также известное как нули функция.

Чтобы найти перехватов x : Вы можете просто нажать [ TRACE ] и курсор влево и вправо, увеличивая масштаб, чтобы получить более точное приближение. Но гораздо проще заставить TI-83/84 найти перехватчик за вас.

Найдите точку пересечения x на глаз. Например, этот график кажется иметь точку пересечения x где-то между x = −3 и х = -1. Найдите желтый CALC над [ TRACE ] ключ.Нажмите [ 2nd TRACE make CALC ] [ 2 ]. (Вы выбираете 2: ноль , потому что точки пересечения x являются нулями функции.)
Введите левую и правую границы. [ (-) ] 3 [ ENTER ] [ (-) ] 1 [ ENTER ]

Не нужно гадать; просто нажмите [ ENTER ] опять таки.

Два предупреждения с пересечениями x :

  • Поскольку TI-83/84 выполняет приближения, вы всегда должны проверять TI-83/84 ответьте в определении функции, чтобы убедиться, что выходит y ровно 0.
  • Когда вы найдете перехваты x , убедитесь, что вы нашли их все. Этот конкретная функция имеет только одну во всей своей области, но с другими функции вам, возможно, придется искать дополнительные перехваты x за пределами область просмотра.

Найти перехватчик y еще проще: нажмите [ TRACE ] 0 и прочтите точку пересечения y .

Эта точка пересечения y выглядит примерно как −2/3, и при подключении x = 0 в определении функции вы видите, что перехват равно −2/3.

Несколько функций

На одном экране можно отобразить несколько функций. Просто нажмите [ Y = ] и введите вторую функцию рядом с Y2 = . Нажмите [ GRAPH ], чтобы увидеть два графика. вместе.

Чтобы выбрать функцию для отслеживания, нажмите [ ▲ ] или [ ▼ ]. Левый верхний угол показывает, какую функцию вы отслеживаете.

Перекресток

Когда вы строите график нескольких функций на одном и том же наборе осей, вы TI-83/84 может сказать вам, где пересекаются графики.Это эквивалентно решению системы уравнений графическим способом.

Подход нефа состоит в том, чтобы проследить по одному графику, пока он пересекает другой, но опять же, вы можете добиться большего. Хорошо проиллюстрировать найти пересечения y = (6/5) x — 8 с уже построенной функцией weve.

Постройте график обеих функций на одном наборе осей. Уменьшить, если необходимо найти все решения.

Пресс [ 2-й TRACE составляет CALC ] [ 5 ].

Вам будет предложено Первая кривая? При необходимости, нажмите [ ▲ ] или [ ▼ ], чтобы выбрать один из интересующие вас кривые. Нажмите [ ENTER ].

Вам будет предложено Вторая кривая? При необходимости, нажмите [ ▲ ] или [ ▼ ], чтобы выбрать другая интересующая вас кривая. Нажмите [ ENTER ].
Глазное яблоко приблизительное решение. Например, на этом графике кажется, есть решение около x = 2. При появлении запроса Guess? , введите свое предположение. В этом случае, поскольку ваше предположение равно 2, вам следует нажать 2 [ ENTER ].
Повторите эти действия для любых других решений.

Как всегда, очевидные решения следует подтверждать подставляя в оба уравнения. В TI-83/84 используется метод последовательного приближений, которые могут создать уродливую десятичную дробь, когда на самом деле есть точное решение в виде дроби или радикала.

.

Published in Разное

Ваш комментарий будет первым

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *