▶▷▶▷ гдз исследовать функцию и построить график
▶▷▶▷ гдз исследовать функцию и построить график| Интерфейс | Русский/Английский |
| Тип лицензия | Free |
| Кол-во просмотров | 257 |
| Кол-во загрузок | 132 раз |
| Обновление: | 09-09-2019 |
гдз исследовать функцию и построить график — Исследовать функцию и построить график (решение примера math-helpernetvyisshaya-matematikaissledovat Cached Пример 4 Исследовать функцию и построить ее график Решение i, ii Функция определена и непрерывна на всей числовой оси Исследовать функцию и построить график (решение примера math-helpernetvyisshaya-matematikaissledovat Cached Исследовать функцию и построить ее график Решение i, ii Функция определена и непрерывна на всей числовой оси iii Функция не является ни четной, ни нечетной, ни периодической iv Общая схема исследования функции и построение ее графика wwwyoutubecom watch?vcD0k3TNjgmM Cached Непрерывность функции и точки разрыва Отыскание вертикальных, горизонтальных и наклонных асимптот Примеры исследования функции и построения графика yukhymcomruissledovanie-funktsiiprimery Cached Перейдем к практической части и исследуем по схеме функцию ——Пример 1 Исследовать функцию и построить ее график (Дубовик ВП, Юрик И И Высшая математика Сборник задач) Исследование функции и построение графика функции matecosrumatmatematikaissledovanie-funktsii-i Cached Пример исследования функции и построения графика 2 Исследовать функцию средствами Исследовать функцию, построить график Онлайн калькулятор libreshimsublogissledovat_funkciju_postroit_grafik Cached Исследовать функцию , построить график План исследования функций и построения графика 1 Исследование функции и построение графика ege-okru20131112issledovanie-funktsii-i Cached Подробнее о том, как находить точки перегиба и промежутки выпуклости и вогнутости читайте здесь Итак, давайте, для примера, исследуем функцию и построим ее график 1 Найдем D(y) Как исследовать функцию и построить её график? mathprofirupolnoe_issledovanie_funkcii_i_postroenie Cached Как исследовать функцию и построить её график ? Похоже, я начинаю понимать одухотворённо-проникновенный лик вождя мирового пролетариата, автора собрания сочинений в 55 томах Полное исследование функции и построение графика wwwmatburoruex_maphp?p1maissl Cached Исследовать функцию и построить ее график (x2y2)34x2y2 Исследование неявно заданной функции Задача 11 Построить график функции yf(x) Исследование функции онлайн wwwkontrolnaya-rabotarusgrafikxy Cached Введите график функции Построим (исследуем) график функции yf(x), для этого задайте функцию f(x) Важно : a должно быть меньше b , иначе график не сможет построиться Promotional Results For You Free Download Mozilla Firefox Web Browser wwwmozillaorg Download Firefox — the faster, smarter, easier way to browse the web and all of 1 2 3 4 5 Next 26,800
- гдз исслед
- овать функцию и пост
- цию и построить график
- как находить точки перегиба и промежутки выпуклости и вогнутости читайте здесь Итак
- исследуем функцию и построим ее график 1 Найдем D(y) Как исследовать функцию и построить её график? mathprofirupolnoe_issledovanie_funkcii_i_postroenie Cached Как исследовать функцию и построить её график ? Похоже
- easier way to browse the web and all of 1 2 3 4 5 Next 26
гдз исследовать функцию и построить график Все результаты ГДЗ Алгебра класс Мордкович Помогите temygdz gdzalgebraklassmordk Ответы на вопрос ГДЗ Алгебра класс Мордкович Помогите исследовать функцию и построить ее график читайте на Рамблеркласс Построение графика функции методом Точки перегиба Асимптоты функции Полное исследование функции и построение графика функции методом дифференциального исчисления Решение онлайн и построить ее график Как исследовать функцию и построить её график? Mathprofi mathprofiru polnoe_issledovanie_funkcii_i_postroenie_grafika Похожие Полная схема исследования функции с примерами и подробными Или короче исследовать функцию и построить график Решения и ответы Полное исследование функции и построение графика ex_ma Провести полное исследование и построить график функции yxxx Область определения функции Так как функция представляет собой Исследование функции Задачи из сборника Кузнецова Л А wwwkvadromircom kuznecov_grafiki_ Похожие Решебник Кузнецова III Графики Задание Провести полное исследование функции и построить её график Исследование функции проводится в Полное исследование функции и построение графика poleznoe formules__ При построении графика функции необходимо провести ее Задание Исследовать функцию yxxxxx и построить ее график Решение Исследование функции и построение графика функции matecosru matematika issledovaniefunktsiiipostroeniegrafikafunktsii Для того, чтобы построить график функции необходимо провести полное исследование заданной функции Затем поэтапно, используя полученные исследовать функцию и построить график Ответы Образование Похожие ответа апр г Исследовать функцию значит определить её область определния, асимптоты, оси и центры симметрии и построить график Алгебра Исследовать Функцию,построить График Домашка и Алгебра ответа Вопрос по домашке Исследовать функцию , построить график Ответы LogxxlogxОДЗ xx xx x x x,U, Как исследовать функцию и построить график Методы pin Как исследовать функцию и построить график Методы Султанова Математика ЕГЭ Гдз по биологии рабочая тетрадь сг мамонтов вб захаров и Применение производной к исследованию функции открытыйурокрф articles Сформировать навыки исследования функции с помощью производной Задание Провести исследование функции и построить ее график Решение Не найдено гдз Использование производных для исследования oldskolanarodru Kochetkov Kochetkov Похожие А это позволяет более точно построить графики исследуемых функций В дальнейшем мы будем придерживаться следующего плана исследования Задачи на исследование функций и построение графиков pubs zadachinaissledovaniefunktsiyipostroenie аибольшее и наименьшее значение функции Исследование на выпуклость графика функции и точки перегиба Построен Картинки по запросу гдз исследовать функцию и построить график Показать все Другие картинки по запросу гдз исследовать функцию и построить график Жалоба отправлена Пожаловаться на картинки Благодарим за замечания Пожаловаться на другую картинку Пожаловаться на содержание картинки Отмена Пожаловаться Все результаты Постройте график функции yx YouTube watch февр г Добавлено пользователем ВЕБ ШКОЛА Постройте график функции yx Проходит ли график через точку B ; Задание Постройте график функции Проходит ли Как сделать Полное ИССЛЕДОВАНИЕ ФУНКЦИИ Схема postupivuzru vopros Похожие Исследование функции на четность, нечетность и периодичность Если fx Нахождение точек пересечения графика функции с осями координат Исследовать функцию и построить график Форум сайта Mathru Функции одной переменной мар г сообщений Исследовать функцию Провести полное исследование функции и построить ее график хх х План исследования Область Построение графиков функций урок Алгебра, класс Построение графиков функции Полезно исследовать функцию на чётность, поскольку графики чётной и , следовательно, можно сначала построить только ветвь графика при x, Исследовать функцию и построить график y xx mathematics gku Исследовать функцию и построить график y xx Ответы то попробуйте воспользоваться умным поиском на сайте и найти ответы на Приложения в Play Исследование функции по store apps details Рейтинг голосов Бесплатно Android Обучение Калькулятор по исследованию функции онлайн позволяет найти Область определения функции Точки пересечения с осью координат X Точки yxx построить график и исследовать функцию topic view yxxpostroitgrafiki мая г yxx построить график и исследовать функцию Ответы функции y xx Найдите а наименьшее значение функции; Исследование функции Математика mathhashcoderu questions анализисследованиефункцииyxx Похожие нояб г Исследование функции yxx Как исследовать функцию и построить ее график ? исследовать функцию и построить график yxx классы Алгебра Похожие Рейтинг , голоса мар г Исследовать функцию и построить график yxx Посмотри ответы прямо сейчас! PDF Исследование функций и построение графиков pnueduru filer_public issled_funktii_postr_grafikov Похожие февр г Содержит указания по исследованию функций и построению графиков Аналогичные рассуждения помогают построить график функции y fx при больших x, если lim x x ex Ответы смотрите на рис МатАн StudFilesnet preview февр г ДЗ Исследование функций и построение графиков пункта Срок Исследовать заданные функции и построить их графики то он получает дополнительные вопросы, успешные ответы на которые Функция у х и ее график Школьный помощник Функция у х и ее график Алгебра класс Правила Задания График функции в Excel как построить? MS Office Excel pedsovetsu MS Office Excel Похожие авг г В MS Office Excel можно построить график математической функции Рассмотрим построение графиков на примерах Обсудить статью Построить график функции Решебник ГДЗ по математике egegiablogspotcom blogpost_ Похожие Как построить параболу? Как построить график ? Урок как построить параболу или квадратичную функцию ? Строить параболу очень легко самое Не найдено исследовать Квадратичная функция и ее график СТАТЬИ Интерактивные модели Похожие мая г Все о квадратичной функции и ее графике Просто Чтобы построить график функции , нужно сначала Исследуйте зависимость Решебник по математическому анализу исследование onlinetripsru reshebnikpomatematicheskomuanalizuissledovaniefun Решебник по математическому анализу исследование функции и построение графика Исследовать функцию и построить график решение примера Исследовать функцию yxx и построить решениезадачонлайнрф indexphp математикаонлайн задачи Похожие Условие Исследовать функцию yxx и построить схематично её график Решение Точек разрыва нет Найдем область определения Функции Основные виды, графики, способы задания book funktsii Понятие функция пронизывает все сферы математики и не только значений и построить график данной функции , чтобы убедится в этом где функция возрастает, а где убывает, в общем, исследовать ее по полной Справился? Сравним наши ответы Мы привыкли, что функция имеет вид Преобразование графика функции UzTest abstracts Похожие Ключевые слова функция , график , преобразование, оси координат, ось абсцисс, ось ординат, параллельный перенос Преобразования графиков Урок по алгебре для класса по теме Построение library Похожие янв г Исследование расположения графика квадратичной функции в зависимости от модуля Развитие Построить график функции y Исследовать функцию fxxx и построить график wwwcyberforumru Математика Математический анализ Похожие апр г Рейтинг , голосов Решено Исследовать функцию fxxx и построить график Математический анализ Ответ Ответы с готовыми решениями График функции надеюсь, что сам смогёшь построить на основе результатов Общая схема исследования функций и построения их vyisshayamatematika obshhayashemaissledov нояб г Общее исследование функций и построение их графиков удобно Построить график функции, используя все полученные результаты ГДЗ по алгебре за класс к учебнику Дорофеева, Суворовой ОНЛАЙН Функция y x Её свойства и график Решение задач funktsiyayxeyosvoystvaigrafikresheniezadach Повторение понятия квадратного корня и графика функции y x Для решения системы графическим способом необходимо построить графики функций рис Решение Для исследования значений параметра воспользуемся Построение графиков функций Кафедра высшей Учебнометодические пособия Похожие План исследования функции при построении графика Примеры исследования функций и построения графиков функций, ОТВЕТЫ , решеноУпр ГДЗ Алимов класс Reshakru otvet otvet Исследовать функцию у f х и построить её график f х х х; ГДЗ Enjoy English класс ГДЗ Enjoy English класс Гдз по матем класс мерзляк Zuloga countdepzuloga gdzpomatemklassmerzlyak Исследование графика функции с многочленом четвертой степени мерзяк пятой степени Исследовать функцию высших степеней и построить ее график Этапах дифференцировки гдз по матем класс мерзляк Институтом График функции, построение графика, урок по алгебре за postroeniegrafikovfunktsialgebraklass Построение графика функции, алгоритм, урок по алгебре за класс, презентация Ребята, мы с вами построили много графиков функций, например, Полезно исследовать функцию на чётность, поскольку графики четной Построить график функции без применения производной matematikuru postroitgrafikfunkciibezprimeneniyaproizvodnoj Похожие Главная Учебные материалы по математике Построить график функции без Исследование функции на экстремум по второй производной График функции Способы задания функций edusernamru book_el_math Похожие График функции Способы задания функций Для графического представления функции используем декартову прямоугольную систему координат рис PDF График функции files documents podrazdeleniya emo crmo mpi виды функций, изучить свойства функций, построить графики функций, рассмотреть На основании исследования функции можно построить её гра фик, который даёт Постараемся найти ответы на эти вопросы Начнём Взаимно обратные функции, основные определения Справочник Математика Функции Перейти к разделу Графики взаимно обратных функций Графики взаимно обратных функций Если нам нужно построить график ГДЗ решебник Алгебра за класс Мордкович Задачник klass algebra ГДЗ решебники подробные готовые домашние задания Алгебра за класс Мордкович Глава Квадратичная функция Как построить график функции yfxlm Исследование функций на монотонность ГДЗ Алгебра класс Мордкович Задачник Мнемозина class algebra Mordkowich А для этой цели решебник к учебнику Алгебра Задачник класс Мордкович самое подходящее средство, Как построить график функции yfxlm ГДЗ Решебник тип книги Алгебра класс Задачник Мнемозина класс Алгебра ГДЗ Решебник Задачник Алгебра класс Мнемозина Мордкович бесплатно Как построить график функции yfxlm ГДЗ Алгебра класс Попов, Мордкович Тетрадь для класс Алгебра Решения и ГДЗ Алгебра класс Попов, Мордкович Тетрадь для самостоятельных работ с подробным Как построить график функции yfx lm Алгебра начала анализа гдз вариант постройте график функций news algebranachalaanalizagdzvaria АНАЛИЗА Алгебра начала анализа гдз вариант постройте график функций Вариант Провести полное исследование функции и построить её Вместе с гдз исследовать функцию и построить график часто ищут исследовать функцию и построить график онлайн исследовать данные функции на непрерывность и построить их графики исследование функции с помощью производной исследование функции алгоритм построить график функции онлайн исследование функции и построение графика класс примеры таблица исследования функции найти область определения функции и построить график онлайн Документы Blogger Duo Hangouts Keep Jamboard Подборки Другие сервисы Приложения
гдз исследовать функцию и построить график
Построение графиков функций — урок.
 Алгебра, 10 класс.
Алгебра, 10 класс.построить график функции y=x2+1×2−1.
Решение 1. Введём обозначение: f(x)=x2+1×2−1. Найдём область определения функции. Она задаётся условиями x≠1,x≠−1. Итак, D(f)=(−∞;−1)∪(−1;1)∪(1;+∞).
2. Исследуем функцию на чётность:
f(−x)=−x2+1−x2−1=x2+1×2−1=f(x).
Значит, заданная функция чётна, её график симметричен относительно оси ординат, а потому можно для начала ограничиться построением ветвей графика при x≥0.
3. Найдём асимптоты. Вертикальной асимптотой является прямая \(x=1\), поскольку при этом значении \(x\) знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить limx→∞f(x):
limx→∞x2+1×2−1=limx→∞x2x2+1x2x2x2−1×2=limx→∞1+1×21−1×2=1.
Значит, \(y=1\) — горизонтальная асимптота графика функции.
4. Найдём стационарные и критические точки, точки экстремума и промежутки монотонности функции:
y′=x2+1×2−1′=(x2+1)′⋅(x2−1)−(x2+1)⋅(x2−1)′x2−12=2x⋅(x2−1)−(x2+1)⋅2xx2−12==−4xx2−12.
Производная существует всюду в области определения функции, значит, критических точек у функции нет.
Стационарные точки найдём из соотношения y′=0. Получаем: \(-4x=0\) — откуда находим, что \(x=0\). При \(x<0\) имеем: y′>0; при \(x>0\) имеем: y′<0. Значит, \(x=0\) — точка максимума функции, причём ymax=f(0)=02+102−1=−1.
При \(x>0\) имеем: y′<0; но следует учесть наличие точки разрыва \(x=1\). Значит, вывод о промежутках монотонности будет выглядеть так: на промежутке 0;1) функция убывает, на промежутке (1;+∞) функция также убывает.
5. Составим таблицу значений функции f(x)=x2+1×2−1 при x≥0:
\(x\) | \(0\) | \(0. | \(2\) | \(3\) | \(4\) |
\(y\) | \(-1\) | −53 | 53 | 54 | 1715 |
6. Отметим найденные точки на координатной плоскости, учтя при этом, что \((0;-1)\) — точка максимума, что \(y=1\) — горизонтальная асимптота, что \(x=1\) — вертикальная асимптота, построим ветви искомого графика при x≥0. Добавив ветви, симметричные построенным относительно оси ординат, получим весь график.
Исследование функции и построение графика онлайн решение. Исследовании функции онлайн. Схема исследования функции и построение ее графика
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
y = _______ ax n + b cx m + d
И построить её график по общей схеме.
Общее исследование функций и построение графиков выполняют по следующей схеме:
- Найти область определения функции.

- Выяснить является ли функция чётной, нечётной, периодической.
- Исследовать функцию на непрерывность, найти точки разрыва и выяснить характер разрывов.
- Найти асимптоты графика функции.
- Найти точки экстремума функции, вычислить значения функции в этих точках. Установить интервалы монотонности функции в этих точках.
- Найти точки перегиба графика функции, вычислить значения функции и значения производной в этих точках. Установить интервалы выпуклости графика функции.
- Используя результаты исследований, построить график функции. Если нужно уточнить отдельные участки кривой, вычислить координаты нескольких дополнительных точек. В частности, рекомендуется вычислять координаты точек пересечения графика с осями координат, так называемые «нули» функции.
Задайте числовые параметры Вашего варианта и нажмите кнопку «Ввод.»
y = ______ a x n + b c x m + d
Показатели степени n и m должны быть целыми положительными однозначными числами. Коэффициенты a, b, c, d могут принимать любые целые значения из промежутка [-99,99]. Если перед дробью стоит знак «−», отнесите его к числителю. Не увлекайтесь слишком большими и малыми значениями коэффициентов. Помните о том, что «бесконечность» не поместится на экране.
a = b = c = d =
n = m =
Применим эту схему для функции
y = _____ 2x 3 x 2 − 4
(a = 2; b = 0; c = 1; d = −4; n = 3; m = 2).
1. Функция определена на всей числовой оси, кроме точек x = ±2, в которых знаменатель дроби обращается в ноль. Таким образом, её область определения
D (f ) = (−∞;−2)∪(−2;+2)∪(+2;+∞)
.
2. Функция нечётна, т.к.
,
следовательно её график будет симметричен относительно начала координат, поэтому достаточно исследовать функцию в промежутке и дифференцируема во всех его внутренних точках, и, кроме того, ( x ) >0 для любого x ϵ ( a , b ) , то данная функция монотонно возрастает на ( a , b ) ; если
( x ) для любого xϵ ( a , b ), то данная функция монотонно убывает на ( a , b ) .
Доказательство. Возьмем ϵ ( a , b ) и ϵ ( a , b ) , причем . По теореме Лагранжа
( c
) = .Но ( c )>0 и > 0, значит, ( > 0, то есть
(. Полученный результат указывает на монотонное возрастание функции, что и требовалось доказать. Аналогично доказывается вторая часть теоремы.
Экстремумы функции
При исследовании поведения функции особую роль играют точки, которые отделяют друг от друга интервалы монотонного возрастания от интервалов ее монотонного убывания.
Определение 2.1 . Точка называется точкой максимума функции
y = f ( x ) , если для любого, сколь угодно малого , ( называется точкой минимума, если ( > 0.
Точки минимума и максимума имеют общее название точек экстремума. У кусочно-монотонной функции таких точек конечное число на конечном интервале (рис. 2.1).
Рис. 2.1
Теорема 2.1 (необходимое условие существования экстремума) . Если дифференцируемая на интервале

Доказательство этой теоремы следует из теоремы Ролля, в которой было показано, что в точках минимума или максимума = 0, и касательная, проведенная к графику функции в этих точках, параллельна оси OX .
Из теоремы 2.1 вытекает, что если функция y = f ( x ) имеет производную во всех точках, то она может достигать экстремума в тех точках, где = 0.
Однако данное условие не является достаточным, так как существуют функции, у которых указанное условие выполняется, но экстремума нет. Например, у функции y = в точке x = 0 производная равна нулю, однако экстремума в этой точке нет. Кроме того, экстремум может быть в тех точках, где производная не существует. Например, у функции y = | x | есть минимум в точке x = 0 , хотя производная в этой точке не существует.
Определение 2.2 . Точки, в которых производная функции обращается в ноль или терпит разрыв, называются критическими точками данной функции .
Следовательно, теоремы 2.1 недостаточно для определения экстремальных точек.
Теорема 2.2 (достаточное условие существования экстремума) . Пусть функция y = f ( x ) непрерывна на интервале ( a , b ) , который содержит ее критическую точку , и дифференцируема во всех точках этого интервала, за исключением, быть может, самой точки . Тогда, если при переходе этой точки слева направо знак производной меняется с плюса на минус, то это точка максимума, и, наоборот, с минуса на плюс – точка минимума .
Доказательство. Если производная функции меняет свой знак при переходе точки слева направо с плюса на минус, то функция переходит от возрастания к убыванию, то есть достигает в точке своего максимума и наоборот.
Из вышесказанного следует схема исследования функции на экстремум:
1) находят область определения функции;
2) вычисляют производную;
3) находят критические точки;
4) по изменению знака первой производной определяют их характер.
Не следует путать задачу исследования функции на экстремум с задачей определения минимального и максимального значения функции на отрезке. Во втором случае необходимо найти не только экстремальные точки на отрезке, но и сравнить их со значением функции на его концах.
Интервалы выпуклости и вогнутости функции
Еще одной характеристикой графика функции, которую можно определять с помощью производной, является его выпуклость или вогнутость.
Определение 3.1 . Функция y = f ( x ) называется выпуклой на промежутке ( a , b ) , если ее график расположен ниже любой касательной, проведенной к нему на данном промежутке, и наоборот, называется вогнутой, если ее график окажется выше любой касательной, проведенной к нему на данном промежутке .
Докажем теорему, позволяющую определять интервалы выпуклости и вогнутости функции.
Теорема 3.1 . Если во всех точках интервала ( a , b ) вторая производная функции ( x ) непрерывна и отрицательна, то функция y = f ( x ) выпукла и наоборот, если вторая производная непрерывна и положительна, то функция вогнута .
Доказательство проведем для интервала выпуклости функции. Возьмем произвольную точку ϵ ( a , b ) и проведем в этой точке касательную к графику функции
Теорема будет доказана, если будет показано, что все точки кривой на промежутке ( a , b ) лежат под этой касательной. Иначе говоря, необходимо доказать, что для одних и тех же значений x ординаты кривой y = f ( x ) меньше, чем ординаты касательной, проведенной к ней в точке
.
Рис. 3.1
Для определенности обозначим уравнение кривой: = f ( x ) , а уравнение касательной к ней в точке :
— f ( ) = ( )( x — )
или
= f ( ) + ( )( x — ) .
Составим разность и :
— = f(x) – f( ) — ( )(x- ).
Применим к разности f ( x ) – f ( ) теорему о среднем Лагранжа:
— = ( )( x — ) — ( )( x — ) = ( x — )[ ( ) — ( )] ,
где ϵ ( , x ).
Применим теперь теорему Лагранжа к выражению в квадратных скобках:
— = ( )( — )( x — ) , где ϵ ( , ).
Как видно из рисунка, x > , тогда x — > 0 и — > 0 . Кроме того, по условию теоремы, ( )
Перемножая эти три множителя, получим, что , что и требовалось доказать.
Определение 3.2 . Точка, отделяющая интервал выпуклости от интервала вогнутости, называется точкой перегиба .
Из определения 3.1 следует, что в данной точке касательная пересекает кривую, то есть с одной стороны кривая расположена ниже касательной, а с другой – выше.
Теорема 3.2 . Если в точке вторая производная функции
y = f ( x ) равна нулю или не существует, а при переходе через точку знак второй производной меняется на противоположный, то данная точка является точкой перегиба .
Доказательство данной теоремы следует из того, что знаки ( x ) по разные стороны от точки
различны. Значит, с одной стороны от точки функция выпукла, а с другой – вогнута. В этом случае, согласно определению 3.2, точка
является точкой перегиба.
Значит, с одной стороны от точки функция выпукла, а с другой – вогнута. В этом случае, согласно определению 3.2, точка
является точкой перегиба.
Исследование функции на выпуклость и вогнутость проводится по той же схеме, что и исследование на экстремум.
4. Асимптоты функции
В предыдущих пунктах были рассмотрены методы исследования поведения функции с помощью производной. Однако среди вопросов, касающихся полного исследования функции, есть и такие, которые с производной не связаны.
Так, например, необходимо знать, как ведет себя функция при бесконечном удалении точки ее графика от начала координат. Такая проблема может возникнуть в двух случаях: когда аргумент функции уходит на бесконечность и когда при разрыве второго рода в конечной точке уходит на бесконечность сама функция. В обоих этих случаях может возникнуть ситуация, когда функция будет стремиться к некоторой прямой, называемой ее асимптотой.
Определение . Асимптотой графика функции y = f ( x ) называется прямая линия, обладающая тем свойством, что расстояние от графика до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат .
Различают два типа асимптот: вертикальные и наклонные.
К вертикальным асимптотам относятся прямые линии x = , которые обладают тем свойством, что график функции в их окрестности уходит на бесконечность, то есть, выполняется условие: .
Очевидно, что здесь удовлетворяется требование указанного определения: расстояние от графика кривой до прямой x = стремится к нулю, а сама кривая при этом уходит на бесконечность. Итак, в точках разрыва второго рода функции имеют вертикальные асимптоты, например, y = в точке x = 0 . Следовательно, определение вертикальных асимптот функции совпадает с нахождением точек разрыва второго рода.
Наклонные асимптоты описываются общим уравнением прямой линии на плоскости, то есть y = kx + b ./ModulBM/ModBM/Praktika/Rechen/pract(IssF_2pr).files/image216.jpg) Значит, в отличие от вертикальных асимптот, здесь необходимо определить числа k и b .
Значит, в отличие от вертикальных асимптот, здесь необходимо определить числа k и b .
Итак, пусть кривая = f ( x ) имеет наклонную асимптоту, то есть при x точки кривой сколь угодно близко подходят к прямой = kx + b (рис. 4.1). Пусть M ( x , y ) — точка, расположенная на кривой. Ее расстояние от асимптоты будет характеризоваться длиной перпендикуляра | MN | .
Построение графика функции по особенным точкам включает в себя исследование самой функции: определение области допустимых значений аргумента, определение области изменения функции, определение четности или нечетности функции, определение точек разрыва функции, нахождение интервалов знакопостоянства функции, нахождение асимптот графика функции. С помощью первой производной можно определить интервалы возрастания (убывания) функции, наличие точек экстремума. По второй производной можно определить интервалы выпуклости (вогнутости) графика функции, а также точки перегиба. При этом считаем, что если в некоторой точке xo касательная к графику функции выше кривой, то график функции в этой точке имеет выпуклость; если же касательная ниже кривой, то график функции в этой точке имеет вогнутость.
y(x) = x³/(x²+3)
1. Исследование функции.
а) Область допустимых значений аргумента: (-∞,+∞).
б) Область изменения функции: (-∞, +∞).
в) Функция является нечетной, т.к. y(-x) = -y(x), т.е. график функции симметричен относительно начала координат.
г) Функция является непрерывной, точек разрыва нет, следовательно, нет вертикальных асимптот.
д) Нахождение уравнения наклонной асимптоты y(x) = k∙x + b , где
k = /x и b =
В данном примере параметры асимптоты соответственно равны:
k = , т.к. старшая степень числителя и знаменателя одинаковые, равные трем, а отношение коэффициентов при этих старших степенях равно единице. При x→+ ∞ для вычисления предела использовали третий замечательный предел.
При x→+ ∞ для вычисления предела использовали третий замечательный предел.
b = = = 0, при вычислении предела при x→+ ∞ воспользовались третьим замечательным пределом. Итак, график данной функции имеет наклонную асимптоту y=x.
2.
y´= /(x²+3)² — производная вычислена с помощью формулы дифференцирования частного.
а) Определяем нули производной и точки разрыва, приравнивая соответственно числитель и знаменатель производной нулю: y´=0, еслиx=0. Точек разрыва 1-я производная не имеет.
б) Определяем интервалы знакопостоянства производной, т.е. интервалы монотонности функции: при -∞производная положительна, следовательно, функция возрастает; при 0≤xпроизводная продолжает оставаться положительной, т.е. функция так же возрастает.
3. Исследование функции с помощью 2-ой производной.
Используя формулу дифференцирования частного и произведя алгебраические преобразования, полечим: y´´ = /(x²+3)³
а) Определяем нули 2-ой производной и интервалы знакопостоянства: y´´ = 0, если x=0 иx=+ 3 . Точек разрыва у 2-ой производной нет.
б) Определим интервалы закопостоянства 2-ой производной, т.е. интервалы выпуклости или вогнутости графика функции. При -∞и при0вторая производная y´´>0 , т.е. график функции вогнутый. При —3и при3вторая производная y´´т.е. график функции выпуклый. Так как в точках x=0 и x=+ 3 вторая производная равна нулю, а ее знак меняется, то эти точки являются точками перегиба графика функции (рис.4).
Пример: исследовать функцию и построить ее график y(x)=((x-1)²∙(x+1))/x
1.Исследование функции.
а) Область допустимых значений: (-∞,0)U(0,+∞).
б) Область изменения функции: (-∞,+∞).
г) Данная функция имеет точку разрыва 2-ого рода при x=0.
д) Нахождение асимптот. Т.к. функция имеет точку разрыва 2-ого рода при x=0 , то следовательно, функция имеет вертикальную асимптоту x=0. Наклонных или горизонтальных асимптот данная функция не имеет.
функция имеет точку разрыва 2-ого рода при x=0 , то следовательно, функция имеет вертикальную асимптоту x=0. Наклонных или горизонтальных асимптот данная функция не имеет.
2.Исследование функции с помощью 1-ой производной.
Преобразуем функцию, произведя все алгебраические действия. В результате вид функции значительно упростится: y(x)=x²-x-1+(1/x). От суммы слагаемых очень просто брать производную и получим: y´ = 2x – 1 –(1/x²).
а) Определяем нули и точки разрыва 1-ой производной. Приводим выражения для 1-ой производной к общему знаменателю и, приравняв числитель, а затем и знаменатель нулю, получим: y´=0 приx=1, y´ — не существуетприx=0.
б) Определим интервалы монотонности функции, т.е. интервалы знакопостоянства производной. При -∞xи0первая производнаяy´следовательно, функция убывает. При 1≤xпервая производнаяy´>0, следовательно, функция возрастает. В точке x=1 первая производная меняет знак с минуса на плюс, следовательно, в этой точке функция имеет минимум. Минимум пологий, т.к. при x=1 производнаяy´=0.
3.
y´´= 2 + 2/x³ . По 2-ой производной определим интервалы выпуклости или вогнутости графика функции, а также, если они имеются, точки перегиба. Приведем выражение для второй производной к общему знаменателю, а затем, приравнивая нулю поочередно числитель и знаменатель, получим: y´´=0 при x=-1, y´´- не существуетпри x=0.
При -∞и при 00 – график функции вогнутый. При -1≤x– график функции выпуклый. Т.к. в точке x=-1 вторая производная меняет знак с плюса на минус, то точка x=-1 – точка перегиба графика функции (рис.5).
рис. 4 рис. 5
Пример: исследовать функцию и построить ее график y(x) = ln (x²+4x+5)
1.Исследование функции.
а) Область допустимых значений аргумента: логарифмическая функция существует только для аргументов строго больше нуля, следовательно, x²+4x+5>0 – это условие выполняется при всех значениях аргумента, т. е. О.Д.З. – (-∞, +∞).
е. О.Д.З. – (-∞, +∞).
б) Область изменения функции: (0, +∞). Преобразуем выражение, стоящее под знаком логарифма, и приравниваем функцию нулю: ln((x+2)²+1) =0. Т.е. функция обращается в ноль при x=-2. График функции будет симметричен относительно прямой x=-2.
в) Функция непрерывная, точек разрыва не имеет.
г) Асимптот у графика функции нет.
2.Исследование функции с помощью 1-ой производной.
Используя правило дифференцирования сложной функции, получим: y´= (2x+4)/(x²+4x+5)
а) Определим нули и точки разрыва производной: y´=0, при x=-2. Точек разрыва первая производная не имеет.
б) Определяем интервалы монотонности функции, т.е. интервалы знакопостоянства первой производной: при -∞xпроизводнаяy´следовательно, функция убывает;при -2 производнаяy´>0, следовательно, функция возрастает. Так как производная в точке x=-2 меняет знак с минуса на плюс, то в этой точке функция имеет минимум (пологий).
3.Исследование функции по 2-ой производной.
Представим первую производную в следующем виде: y´=2∙(x+2)/(1+(x+2)²). y´´=2∙(1-(x+2)²/(1+(x+2)²)².
а) Определим интервалы знакопостоянства второй производной. Так как знаменатель 2-ой производной всегда неотрицателен, то знак второй производной определяется только числителем. y´´=0 при x=-3 иx=-1.
При -∞и при-1вторая производная y´´следовательно, график функции на этих интервалах выпуклый. При -3вторая производная y´´>0, следовательно, график функции на этом интервале – вогнутый. Точки x=-3 и x=-1 – точки перегиба графика функции, т.к. в этих точках происходит перемена знаки второй производной, а сама вторая производная обращается в ноль (рис.6).
Пример: исследовать функцию и построить график y(x) = x²/(x+2)²
1.Исследование функции.
а) Область допустимых значений аргумента (-∞, -2)U(-2, +∞).
б) Область изменения функции ².
а) Определим нули и интервалы знакопостоянства второй производной. Т.к. знаменатель дроби всегда положителен, то знак второй производной полностью определяется числителем. При -∞и при-2вторая производнаяy´´>0 , следовательно, график функции на этих интервалах – вогнутый; при1≤xвторая производная y´´, следовательно, график функции на этом интервале имеет выпуклость. При переходе через точку x=1 , знак второй производной меняется с плюса на минус, т.е. эта точка является точкой перегиба графика функции. При x→+∞ график функции асимптотически приближается к своей горизонтальной асимптоте y=1 снизу. При x→ -∞ , график приближается к своей горизонтальной асимптоте сверху (рис.7).
Исследование функции онлайн калькулятор с подробным решением. Общая схема исследования функции и построения графика
Провести полное исследование и построить график функции
y(x)=x2+81−x.y(x)=x2+81−x.
1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
1−x=0,⇒x=1.1−x=0,⇒x=1.
Исключаем единственную точку x=1x=1 из области определения функции и получаем:
D(y)=(−∞;1)∪(1;+∞).D(y)=(−∞;1)∪(1;+∞).
2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:
Так как пределы равны бесконечности, точка x=1x=1 является разрывом второго рода, прямая x=1x=1 — вертикальная асимптота.
3) Определим точки пересечения графика функции с осями координат.
Найдем точки пересечения с осью ординат OyOy, для чего приравниваем x=0x=0:
Таким образом, точка пересечения с осью OyOy имеет координаты (0;8)(0;8).
Найдем точки пересечения с осью абсцисс OxOx, для чего положим y=0y=0:
Уравнение не имеет корней, поэтому точек пересечения с осью OxOx нет.
Заметим, что x2+8>0x2+8>0 для любых xx. Поэтому при x∈(−∞;1)x∈(−∞;1) функция y>0y>0(принимает положительные значения, график находится выше оси абсцисс), при x∈(1;+∞)x∈(1;+∞) функция y
Поэтому при x∈(−∞;1)x∈(−∞;1) функция y>0y>0(принимает положительные значения, график находится выше оси абсцисс), при x∈(1;+∞)x∈(1;+∞) функция y
4) Функция не является ни четной, ни нечетной, так как:
5) Исследуем функцию на периодичность. Функция не является периодической, так как представляет собой дробно-рациональную функцию.
6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:
Приравняем первую производную к нулю и найдем стационарные точки (в которых y′=0y′=0):
Получили три критические точки: x=−2,x=1,x=4x=−2,x=1,x=4. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:
При x∈(−∞;−2),(4;+∞)x∈(−∞;−2),(4;+∞) производная y′
При x∈(−2;1),(1;4)x∈(−2;1),(1;4) производная y′>0y′>0, функция возрастает на данных промежутках.
При этом x=−2x=−2 — точка локального минимума (функция убывает, а потом возрастает), x=4x=4 — точка локального максимума (функция возрастает, а потом убывает).
Найдем значения функции в этих точках:
Таким образом, точка минимума (−2;4)(−2;4), точка максимума (4;−8)(4;−8).
7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:
Приравняем вторую производную к нулю:
Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда x∈(−∞;1)x∈(−∞;1) выполняется y′′>0y″>0, то есть функция вогнутая, когда x∈(1;+∞)x∈(1;+∞) выполняется y′′
8) Исследуем поведение функции на бесконечности, то есть при .
Так как пределы бесконечны, горизонтальных асимптот нет.
Попробуем определить наклонные асимптоты вида y=kx+by=kx+b. Вычисляем значения k,bk,b по известным формулам:
Получили, у что функции есть одна наклонная асимптота y=−x−1y=−x−1.
9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
Вычислим значение функции в некоторых других точках, чтобы точнее построить график.
y(−5)=5.5;y(2)=−12;y(7)=−9.5.y(−5)=5.5;y(2)=−12;y(7)=−9.5.
10) По полученным данным построим график, дополним его асимптотами x=1x=1(синий), y=−x−1y=−x−1 (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):
Задание 4: Геометрические, Экономические задачи(не имею понятия какие, тут примерная подборка задач с решением и формулами)
Пример 3.23. a
Решение. x и y y
y = a — 2×a/4 =a/2. Поскольку x = a/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При xa/4 S » > 0, а при x >a/4 S »
Пример 3.24.
Решение.
R = 2, Н = 16/4 = 4.
Пример 3.22. Найти экстремумы функции f(x) = 2x 3 — 15x 2 + 36x — 14.
Решение. Так как f » (x) = 6x 2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x 1 = 2 и x 2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x 1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x 2 = 3 производная меняет знак минус на плюс, поэтому в точке x 2 = 3 у функции минимум. Вычислив значения функции в точках
x 1 = 2 и x 2 = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.
Пример 3.23. Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение. Обозначим стороны площадки через x и y . Площадь площадки равна S = xy. Пусть y — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2x + y = a. Поэтому y = a — 2x и S = x(a — 2x), где
Тогда по условию должно выполняться равенство 2x + y = a. Поэтому y = a — 2x и S = x(a — 2x), где
0 ≤ x ≤ a/2 (длина и ширина площадки не могут быть отрицательными). S » = a — 4x, a — 4x = 0 при x = a/4, откуда
y = a — 2×a/4 =a/2. Поскольку x = a/4 — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При xa/4 S » > 0, а при x >a/4 S »
Пример 3.24. Требуется изготовить закрытый цилиндрический бак вместимостью V=16p ≈ 50 м 3 . Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Решение. Площадь полной поверхности цилиндра равна S = 2pR(R+Н). Мы знаем объем цилиндра V = pR 2 Н Þ Н = V/pR 2 =16p/ pR 2 = 16/ R 2 . Значит, S(R) = 2p(R 2 +16/R). Находим производную этой функции:
S » (R) = 2p(2R- 16/R 2) = 4p (R- 8/R 2). S » (R) = 0 при R 3 = 8, следовательно,
R = 2, Н = 16/4 = 4.
Похожая информация.
y = _______ ax n + b cx m + d
И построить её график по общей схеме.
Общее исследование функций и построение графиков выполняют по следующей схеме:
- Найти область определения функции.
- Выяснить является ли функция чётной, нечётной, периодической.
- Исследовать функцию на непрерывность, найти точки разрыва и выяснить характер разрывов.
- Найти асимптоты графика функции.
- Найти точки экстремума функции, вычислить значения функции в этих точках. Установить интервалы монотонности функции в этих точках.
- Найти точки перегиба графика функции, вычислить значения функции и значения производной в этих точках. Установить интервалы выпуклости графика функции.
- Используя результаты исследований, построить график функции. Если нужно уточнить отдельные участки кривой, вычислить координаты нескольких дополнительных точек. В частности, рекомендуется вычислять координаты точек пересечения графика с осями координат, так называемые «нули» функции.

Задайте числовые параметры Вашего варианта и нажмите кнопку «Ввод.»
y = ______ a x n + b c x m + d
Показатели степени n и m должны быть целыми положительными однозначными числами. Коэффициенты a, b, c, d могут принимать любые целые значения из промежутка [-99,99]. Если перед дробью стоит знак «−», отнесите его к числителю. Не увлекайтесь слишком большими и малыми значениями коэффициентов. Помните о том, что «бесконечность» не поместится на экране.
a = b = c = d =
n = m =
Применим эту схему для функции
y = _____ 2x 3 x 2 − 4
(a = 2; b = 0; c = 1; d = −4; n = 3; m = 2).
1. Функция определена на всей числовой оси, кроме точек x = ±2, в которых знаменатель дроби обращается в ноль. Таким образом, её область определения
D (f ) = (−∞;−2)∪(−2;+2)∪(+2;+∞)
.
2. Функция нечётна, т.к.
,
следовательно её график будет симметричен относительно начала координат, поэтому достаточно исследовать функцию в промежутке }
ТЕСТ. Исследование функции и построение графика | Материал для подготовки к ЕГЭ (ГИА) по алгебре:
ТЕСТ. Исследование функции и построение графика.
Вариант 1
1. Функция задана формулой: f (x) = x3 – 4x +1. Найдите f (-2).
1) 1 2) 17 3) 3 4) 12
2. Для каждой функции, заданной формулой, укажите её график ( см. рис.1 )
а) б)
в)г)
Рис. 1
1) y =3x + 2 2 ) –x+1 3) y = (x-1)2 4) –x2 + 2x + 3
Ответ:
3. Функция f (x) определена на . Пользуясь графиком функции (см. рис. 2), укажите промежутки убывания.
Функция f (x) определена на . Пользуясь графиком функции (см. рис. 2), укажите промежутки убывания.
1) 2) (- ; 2) 3) (2; — ) 4) [0; +)
4. На рисунке 3 изображён график функции y = ax2 + c. Определите знаки a и c.
Ответ:_______
Рис. 3Рис. 2
5. Среди функций: y = 5×5; y = │x│; y = (x+3)5; y = x5 + 3 укажите нечётную.
1) y = 5×5 2) y = (x+3)5 3) y = x5 + 3 4) y = │x│
6. Найдите координаты точек пересечения графика функции
у = + 1 c осью абсцисс.
1) (0; 1) 2) (1;0) 3) (;0) 4) 0;)
7. Найдите, при каком значении a точка А(а;3) принадлежит графику функции y=-2
1) 5 2) 29 3) 9 4) 1
8. Соотнесите функции
А) y = x2 + 1, Б) y = , В) y =
с их графиками (см. рис. 4)
Ответ:
1)2)
3)4)
Рис. 4
Исследование функции и построение графика
Вариант 2
1.Найдите область определения функции у =+7.
1) (-;4) 2) (-;4] 3) [4;+) 4) (4; +)
2. Соотнесите рисунок, изображающий график функции y = kx + b, с одним из условий (см. рис. 1)
А) Б)
В)
Рис. 1
1) k0;b>0 3) k=0; b>0
Ответ:
3. Найдите область определения функции y = 2 /
1) [;+) 2) ( -;] 3) ,25; +) 4) (-;) (;+)
4. На рисунке 2 изображён график функции y=ax2+c. Определите знаки a и c.
Рис. 2
Ответ: _______
5. На рисунке 3 изображена кубическая парабола. Какая из перечисленных формул задаёт эту функцию?
Рис. 3
3
1) y = (x-3)3 + 1 2) y = ()3 + 2 3) y = ()3 4) y =
6. Найдите абсциссу точки пересечения графика функции y = — 1 с осью Ox/
Ответ: ______
7. Найдите количество точек пересечения графиков функций y = — и y = -3x.
Ответ: ______
8. По графику функции (см. рис. 4) найдите все значения x, при котором значения функции положительны.
А) Б)
В)
Ответ:
упражнений Desmos, которые стоит попробовать по алгебре 1
Я в восторге от того, какое сокровище представляет собой Desmos! Если вы учитель средней или старшей школы и еще не изучили все, что предлагает Desmos, перейдите на сайт прямо сейчас. Desmos — это БЕСПЛАТНЫЙ интерактивный инструмент, используемый для построения графиков, моделирования, сбора данных и опроса учащихся по сбору высших математических понятий, включая, помимо прочего, девять тем, приведенных ниже. Эти занятия потрясающие и БЕСПЛАТНЫЕ!
Примечание: Все описания деятельности в кавычках ниже взяты непосредственно с веб-сайта Desmos.
1. Расстояние против времени
Turtle Crossing — Учащиеся изучают графики зависимости расстояния от времени, безопасно переправляя черепаху через пляж.
2. Выражения, уравнения и неравенства
Задача о границе пула — «В этом упражнении по исследованию ученики сначала построят выражения с числами, чтобы определить количество плиток, граничащих с пулом. Затем они будут использовать эти числовые выражения, чтобы помочь им написать выражение с переменными.”
3. Свойства функций
Практика сортировки функциональных карточек — в этом упражнении учащиеся будут различать графики, истории и уравнения, которые являются функциями или не являются функциями. Кроме того, учащихся просят защитить свои ответы и создать свои собственные примеры функций.
Введение в домен и диапазон — «В этом введении в домен и диапазон студенты практикуются в нахождении домена и диапазона кусочных функций.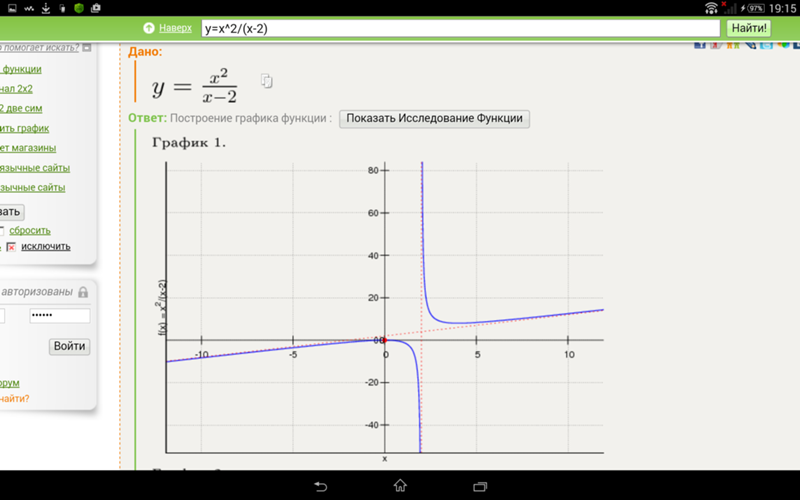 Они начинаются с неформального исследования предметной области и диапазона с использованием графа, а затем наращиваются до представления предметной области и диапазона кусочных функций с использованием неравенств.”
Они начинаются с неформального исследования предметной области и диапазона с использованием графа, а затем наращиваются до представления предметной области и диапазона кусочных функций с использованием неравенств.”
4. Линейные функции
Marble Slide Activity — Эта игра позволяет учащимся изучить изменения линии при изменении наклона и точки пересечения по оси Y.
5. Применение линейных функций
Lego Прайс — я люблю это занятие! В этом упражнении учащиеся используют ползунки, чтобы изучить взаимосвязь между ценой и количеством деталей для различных наборов LEGO из «Звездных войн» и сделать несколько прогнозов на основе этой модели. Студенты также будут интерпретировать параметры своего уравнения в контексте.
6. Системы уравнений
Решения систем уравнений — в этом упражнении содержится все, что нужно знать учащимся о решении систем уравнений графическим способом, с заменой или с исключением. Используйте это, чтобы просмотреть отряд или для остальной части класса, когда вы тянете небольшую группу.
Боковое примечание: одна из моих любимых функций — это функция «Поделиться с классом», которая позволяет учащимся видеть на своем экране 2–3 ответа других учащихся. Это быстрая самопроверка или анализ ошибок, встроенная в некоторые из этих действий.
7. Квадратичные функции
Match My Parabola — «В этом упражнении учащиеся работают над серией сложных задач построения квадратичных графиков, чтобы развить свои навыки работы со стандартными, вершинными, факторизованными и другими формами квадратичных функций».
8. Экспоненциальные функции
Ремонтная мастерская Ави и Бениты — это увлекательный способ продемонстрировать учащимся экспоненциальный рост. «В этом повороте классического упражнения студенты сравнивают линейный и экспоненциальный рост в контексте ежедневных платежей.Один план увеличивается на 100 долларов каждый день, а другой увеличивается за счет удвоения платежа за предыдущий день »./ModulBM/ModBM/Praktika/Rechen/pract(IssF_2pr).files/image214.jpg)
9. Преобразования
Формы трансформации — Используйте это упражнение специально для средней школы или учащихся-геометров, чтобы они усвоили словарный запас трансформации: скольжение, вращение, отражение и т.д.
Это был лишь небольшой фрагмент всех мероприятий, которые Desmos может предложить. Кроме того, Desmos классифицирует все свои действия по четырем категориям: Введение, Практика, Развитие и Применение, чтобы определить, какие действия лучше всего подходят для вашего подразделения.
Другие функции
Графический калькулятор — не хватает калькуляторов? Воспользуйтесь их бесплатным графическим калькулятором.
Geometry Tool — этот инструмент позволяет строить дуги, многоугольники, лучи, углы и многое другое. Дополнительно можно трансформировать конструкции.
Доступность — возможно, лучшая особенность Desmos — это обеспечение того, чтобы каждый ученик, независимо от физических или умственных способностей, мог изучать и любить математику. Щелкните ссылку, чтобы прочитать о том, что Desmos делает для поддержки ВСЕХ учащихся.
ОБНОВЛЕНИЕ: АЛГЕБРА I. ЦИФРОВЫЕ ДЕЯТЕЛЬНОСТИ ТЕПЕРЬ ДОСТУПНЫ!
Вы пробовали Desmos в своем классе? Какое занятие с Desmos вам нравится?
% PDF-1.6
%
44073 0 объектов>
эндобдж
xref
44073 664
0000000016 00000 н.
0000028401 00000 п.
0000028540 00000 п.
0000028797 00000 п.
0000028827 00000 п.
0000028877 00000 п.
0000028939 00000 п.
0000029316 00000 п.
0000029404 00000 п.
0000029488 00000 н.
0000029575 00000 п.
0000029662 00000 п.
0000029749 00000 п.
0000029836 00000 п.
0000029923 00000 н.
0000030010 00000 п.
0000030097 00000 п.
0000030184 00000 п.
0000030271 00000 п.
0000030358 00000 п.
0000030445 00000 п.
0000030532 00000 п.
0000030619 00000 п.
0000030706 00000 п.
0000030793 00000 п.
0000030880 00000 п.
0000030967 00000 п.
0000031054 00000 п.
0000031141 00000 п.
0000031228 00000 п. 0000031315 00000 п.
0000031402 00000 п.
0000031489 00000 п.
0000031576 00000 п.
0000031663 00000 п.
0000031750 00000 п.
0000031837 00000 п.
0000031924 00000 п.
0000032011 00000 п.
0000032098 00000 п.
0000032185 00000 п.
0000032272 00000 н.
0000032359 00000 н.
0000032446 00000 п.
0000032533 00000 п.
0000032620 00000 п.
0000032707 00000 п.
0000032794 00000 п.
0000032881 00000 п.
0000032968 00000 п.
0000033055 00000 п.
0000033142 00000 п.
0000033229 00000 н.
0000033316 00000 п.
0000033403 00000 п.
0000033490 00000 н.
0000033577 00000 п.
0000033664 00000 п.
0000033751 00000 п.
0000033838 00000 п.
0000033925 00000 п.
0000034012 00000 п.
0000034099 00000 п.
0000034186 00000 п.
0000034273 00000 п.
0000034360 00000 п.
0000034447 00000 п.
0000034534 00000 п.
0000034621 00000 п.
0000034708 00000 п.
0000034795 00000 п.
0000034882 00000 п.
0000034969 00000 п.
0000035056 00000 п.
0000035143 00000 п.
0000035230 00000 п.
0000035317 00000 п.
0000035404 00000 п.
0000035491 00000 п.
0000035578 00000 п.
0000035665 00000 п.
0000035752 00000 п.
0000035839 00000 п.
0000035926 00000 п.
0000036013 00000 п.
0000036100 00000 п.
0000036187 00000 п.
0000036274 00000 п.
0000036361 00000 п.
0000036448 00000 н.
0000036535 00000 п.
0000036622 00000 н.
0000036709 00000 п.
0000036796 00000 п.
0000036883 00000 п.
0000036970 00000 п.
0000037057 00000 п.
0000037144 00000 п.
0000037231 00000 п.
0000037318 00000 п.
0000037405 00000 п.
0000037492 00000 п.
0000037579 00000 п.
0000037666 00000 п.
0000037753 00000 п.
0000037840 00000 п.
0000037927 00000 н.
0000038014 00000 п.
0000038101 00000 п.
0000038188 00000 п.
0000038275 00000 п.
0000038362 00000 п.
0000038449 00000 п.
0000038536 00000 п.
0000038623 00000 п.
0000038710 00000 п.
0000038797 00000 п.
0000038884 00000 п.
0000038971 00000 п.
0000039058 00000 н.
0000039145 00000 п.
0000039232 00000 п.
0000039319 00000 п.
0000039406 00000 п.
0000039493 00000 п.
0000039580 00000 п.
0000031315 00000 п.
0000031402 00000 п.
0000031489 00000 п.
0000031576 00000 п.
0000031663 00000 п.
0000031750 00000 п.
0000031837 00000 п.
0000031924 00000 п.
0000032011 00000 п.
0000032098 00000 п.
0000032185 00000 п.
0000032272 00000 н.
0000032359 00000 н.
0000032446 00000 п.
0000032533 00000 п.
0000032620 00000 п.
0000032707 00000 п.
0000032794 00000 п.
0000032881 00000 п.
0000032968 00000 п.
0000033055 00000 п.
0000033142 00000 п.
0000033229 00000 н.
0000033316 00000 п.
0000033403 00000 п.
0000033490 00000 н.
0000033577 00000 п.
0000033664 00000 п.
0000033751 00000 п.
0000033838 00000 п.
0000033925 00000 п.
0000034012 00000 п.
0000034099 00000 п.
0000034186 00000 п.
0000034273 00000 п.
0000034360 00000 п.
0000034447 00000 п.
0000034534 00000 п.
0000034621 00000 п.
0000034708 00000 п.
0000034795 00000 п.
0000034882 00000 п.
0000034969 00000 п.
0000035056 00000 п.
0000035143 00000 п.
0000035230 00000 п.
0000035317 00000 п.
0000035404 00000 п.
0000035491 00000 п.
0000035578 00000 п.
0000035665 00000 п.
0000035752 00000 п.
0000035839 00000 п.
0000035926 00000 п.
0000036013 00000 п.
0000036100 00000 п.
0000036187 00000 п.
0000036274 00000 п.
0000036361 00000 п.
0000036448 00000 н.
0000036535 00000 п.
0000036622 00000 н.
0000036709 00000 п.
0000036796 00000 п.
0000036883 00000 п.
0000036970 00000 п.
0000037057 00000 п.
0000037144 00000 п.
0000037231 00000 п.
0000037318 00000 п.
0000037405 00000 п.
0000037492 00000 п.
0000037579 00000 п.
0000037666 00000 п.
0000037753 00000 п.
0000037840 00000 п.
0000037927 00000 н.
0000038014 00000 п.
0000038101 00000 п.
0000038188 00000 п.
0000038275 00000 п.
0000038362 00000 п.
0000038449 00000 п.
0000038536 00000 п.
0000038623 00000 п.
0000038710 00000 п.
0000038797 00000 п.
0000038884 00000 п.
0000038971 00000 п.
0000039058 00000 н.
0000039145 00000 п.
0000039232 00000 п.
0000039319 00000 п.
0000039406 00000 п.
0000039493 00000 п.
0000039580 00000 п. 0000039667 00000 п.
0000039754 00000 п.
0000039841 00000 п.
0000039928 00000 н.
0000040015 00000 п.
0000040102 00000 п.
0000040189 00000 п.
0000040276 00000 п.
0000040363 00000 п.
0000040450 00000 п.
0000040537 00000 п.
0000040624 00000 п.
0000040711 00000 п.
0000040798 00000 п.
0000040885 00000 п.
0000040972 00000 п.
0000041059 00000 п.
0000041146 00000 п.
0000041233 00000 п.
0000041320 00000 н.
0000041407 00000 п.
0000041494 00000 п.
0000041581 00000 п.
0000041668 00000 п.
0000041755 00000 п.
0000041842 00000 п.
0000041929 00000 п.
0000042016 00000 п.
0000042103 00000 п.
0000042190 00000 п.
0000042277 00000 п.
0000042364 00000 п.
0000042451 00000 п.
0000042538 00000 п.
0000042625 00000 п.
0000042712 00000 н.
0000042799 00000 н.
0000042886 00000 п.
0000042973 00000 п.
0000043060 00000 п.
0000043147 00000 п.
0000043234 00000 п.
0000043321 00000 п.
0000043408 00000 п.
0000043495 00000 п.
0000043582 00000 п.
0000043669 00000 п.
0000043756 00000 п.
0000043843 00000 п.
0000043930 00000 п.
0000044017 00000 п.
0000044104 00000 п.
0000044191 00000 п.
0000044278 00000 н.
0000044365 00000 н.
0000044452 00000 п.
0000044539 00000 п.
0000044626 00000 п.
0000044713 00000 п.
0000044800 00000 п.
0000044887 00000 н.
0000044974 00000 п.
0000045061 00000 п.
0000045148 00000 п.
0000045235 00000 п.
0000045322 00000 п.
0000045409 00000 п.
0000045496 00000 п.
0000045583 00000 п.
0000045670 00000 п.
0000045757 00000 п.
0000045844 00000 п.
0000045931 00000 п.
0000046018 00000 п.
0000046105 00000 п.
0000046192 00000 п.
0000046279 00000 н.
0000046366 00000 п.
0000046453 00000 п.
0000046540 00000 п.
0000046627 00000 н.
0000046714 00000 п.
0000046801 00000 п.
0000046888 00000 п.
0000046975 00000 п.
0000047062 00000 п.
0000047149 00000 п.
0000047236 00000 п.
0000047323 00000 п.
0000047410 00000 п.
0000047497 00000 п.
0000047584 00000 п.
0000047671 00000 п.
0000047758 00000 п.
0000047845 00000 п.
0000047932 00000 п.
0000039667 00000 п.
0000039754 00000 п.
0000039841 00000 п.
0000039928 00000 н.
0000040015 00000 п.
0000040102 00000 п.
0000040189 00000 п.
0000040276 00000 п.
0000040363 00000 п.
0000040450 00000 п.
0000040537 00000 п.
0000040624 00000 п.
0000040711 00000 п.
0000040798 00000 п.
0000040885 00000 п.
0000040972 00000 п.
0000041059 00000 п.
0000041146 00000 п.
0000041233 00000 п.
0000041320 00000 н.
0000041407 00000 п.
0000041494 00000 п.
0000041581 00000 п.
0000041668 00000 п.
0000041755 00000 п.
0000041842 00000 п.
0000041929 00000 п.
0000042016 00000 п.
0000042103 00000 п.
0000042190 00000 п.
0000042277 00000 п.
0000042364 00000 п.
0000042451 00000 п.
0000042538 00000 п.
0000042625 00000 п.
0000042712 00000 н.
0000042799 00000 н.
0000042886 00000 п.
0000042973 00000 п.
0000043060 00000 п.
0000043147 00000 п.
0000043234 00000 п.
0000043321 00000 п.
0000043408 00000 п.
0000043495 00000 п.
0000043582 00000 п.
0000043669 00000 п.
0000043756 00000 п.
0000043843 00000 п.
0000043930 00000 п.
0000044017 00000 п.
0000044104 00000 п.
0000044191 00000 п.
0000044278 00000 н.
0000044365 00000 н.
0000044452 00000 п.
0000044539 00000 п.
0000044626 00000 п.
0000044713 00000 п.
0000044800 00000 п.
0000044887 00000 н.
0000044974 00000 п.
0000045061 00000 п.
0000045148 00000 п.
0000045235 00000 п.
0000045322 00000 п.
0000045409 00000 п.
0000045496 00000 п.
0000045583 00000 п.
0000045670 00000 п.
0000045757 00000 п.
0000045844 00000 п.
0000045931 00000 п.
0000046018 00000 п.
0000046105 00000 п.
0000046192 00000 п.
0000046279 00000 н.
0000046366 00000 п.
0000046453 00000 п.
0000046540 00000 п.
0000046627 00000 н.
0000046714 00000 п.
0000046801 00000 п.
0000046888 00000 п.
0000046975 00000 п.
0000047062 00000 п.
0000047149 00000 п.
0000047236 00000 п.
0000047323 00000 п.
0000047410 00000 п.
0000047497 00000 п.
0000047584 00000 п.
0000047671 00000 п.
0000047758 00000 п.
0000047845 00000 п.
0000047932 00000 п. 0000048019 00000 п.
0000048106 00000 п.
0000048193 00000 п.
0000048280 00000 п.
0000048367 00000 п.
0000048454 00000 п.
0000048541 00000 п.
0000048628 00000 п.
0000048715 00000 п.
0000048802 00000 п.
0000048889 00000 н.
0000048976 00000 п.
0000049063 00000 н.
0000049150 00000 п.
0000049237 00000 п.
0000049324 00000 п.
0000049411 00000 п.
0000049498 00000 п.
0000049585 00000 п.
0000049672 00000 п.
0000049759 00000 п.
0000049846 00000 п.
0000049933 00000 н.
0000050020 00000 н.
0000050107 00000 п.
0000050194 00000 п.
0000050281 00000 п.
0000050368 00000 п.
0000050455 00000 п.
0000050542 00000 п.
0000050629 00000 п.
0000050716 00000 п.
0000050803 00000 п.
0000050890 00000 н.
0000050977 00000 п.
0000051064 00000 п.
0000051151 00000 п.
0000051238 00000 п.
0000051325 00000 п.
0000051412 00000 п.
0000051499 00000 н.
0000051586 00000 п.
0000051673 00000 п.
0000051760 00000 п.
0000051847 00000 п.
0000051934 00000 п.
0000052021 00000 п.
0000052108 00000 п.
0000052195 00000 п.
0000052282 00000 п.
0000052369 00000 п.
0000052456 00000 п.
0000052543 00000 п.
0000052630 00000 н.
0000052717 00000 п.
0000052804 00000 п.
0000052891 00000 п.
0000052978 00000 п.
0000053065 00000 п.
0000053152 00000 п.
0000053239 00000 п.
0000053326 00000 п.
0000053413 00000 п.
0000053500 00000 п.
0000053587 00000 п.
0000053674 00000 п.
0000053761 00000 п.
0000053848 00000 п.
0000053935 00000 п.
0000054022 00000 п.
0000054109 00000 п.
0000054195 00000 п.
0000054281 00000 п.
0000054367 00000 п.
0000054453 00000 п.
0000054539 00000 п.
0000054625 00000 п.
0000054711 00000 п.
0000054797 00000 п.
0000054883 00000 п.
0000054969 00000 п.
0000055055 00000 п.
0000055141 00000 п.
0000055227 00000 п.
0000055313 00000 п.
0000055399 00000 п.
0000055485 00000 п.
0000055571 00000 п.
0000055657 00000 п.
0000055743 00000 п.
0000055829 00000 п.
0000055915 00000 п.
0000056001 00000 п.
0000056087 00000 п.
0000056173 00000 п.
0000056259 00000 п.
0000048019 00000 п.
0000048106 00000 п.
0000048193 00000 п.
0000048280 00000 п.
0000048367 00000 п.
0000048454 00000 п.
0000048541 00000 п.
0000048628 00000 п.
0000048715 00000 п.
0000048802 00000 п.
0000048889 00000 н.
0000048976 00000 п.
0000049063 00000 н.
0000049150 00000 п.
0000049237 00000 п.
0000049324 00000 п.
0000049411 00000 п.
0000049498 00000 п.
0000049585 00000 п.
0000049672 00000 п.
0000049759 00000 п.
0000049846 00000 п.
0000049933 00000 н.
0000050020 00000 н.
0000050107 00000 п.
0000050194 00000 п.
0000050281 00000 п.
0000050368 00000 п.
0000050455 00000 п.
0000050542 00000 п.
0000050629 00000 п.
0000050716 00000 п.
0000050803 00000 п.
0000050890 00000 н.
0000050977 00000 п.
0000051064 00000 п.
0000051151 00000 п.
0000051238 00000 п.
0000051325 00000 п.
0000051412 00000 п.
0000051499 00000 н.
0000051586 00000 п.
0000051673 00000 п.
0000051760 00000 п.
0000051847 00000 п.
0000051934 00000 п.
0000052021 00000 п.
0000052108 00000 п.
0000052195 00000 п.
0000052282 00000 п.
0000052369 00000 п.
0000052456 00000 п.
0000052543 00000 п.
0000052630 00000 н.
0000052717 00000 п.
0000052804 00000 п.
0000052891 00000 п.
0000052978 00000 п.
0000053065 00000 п.
0000053152 00000 п.
0000053239 00000 п.
0000053326 00000 п.
0000053413 00000 п.
0000053500 00000 п.
0000053587 00000 п.
0000053674 00000 п.
0000053761 00000 п.
0000053848 00000 п.
0000053935 00000 п.
0000054022 00000 п.
0000054109 00000 п.
0000054195 00000 п.
0000054281 00000 п.
0000054367 00000 п.
0000054453 00000 п.
0000054539 00000 п.
0000054625 00000 п.
0000054711 00000 п.
0000054797 00000 п.
0000054883 00000 п.
0000054969 00000 п.
0000055055 00000 п.
0000055141 00000 п.
0000055227 00000 п.
0000055313 00000 п.
0000055399 00000 п.
0000055485 00000 п.
0000055571 00000 п.
0000055657 00000 п.
0000055743 00000 п.
0000055829 00000 п.
0000055915 00000 п.
0000056001 00000 п.
0000056087 00000 п.
0000056173 00000 п.
0000056259 00000 п. 0000056345 00000 п.
0000056431 00000 п.
0000056517 00000 п.
0000056603 00000 п.
0000056689 00000 п.
0000056775 00000 п.
0000056861 00000 п.
0000056947 00000 п.
0000057033 00000 п.
0000057119 00000 п.
0000057205 00000 п.
0000057291 00000 п.
0000057377 00000 п.
0000057463 00000 п.
0000057549 00000 п.
0000057635 00000 п.
0000057721 00000 п.
0000057807 00000 п.
0000057893 00000 п.
0000057979 00000 п.
0000058065 00000 п.
0000058151 00000 п.
0000058237 00000 п.
0000058323 00000 п.
0000058409 00000 п.
0000058495 00000 п.
0000058581 00000 п.
0000058667 00000 п.
0000058753 00000 п.
0000058839 00000 п.
0000058925 00000 п.
0000059011 00000 п.
0000059097 00000 п.
0000059183 00000 п.
0000059269 00000 п.
0000059355 00000 п.
0000059441 00000 п.
0000059527 00000 п.
0000059613 00000 п.
0000059699 00000 н.
0000059785 00000 п.
0000059871 00000 п.
0000059957 00000 н.
0000060043 00000 п.
0000060129 00000 п.
0000060215 00000 п.
0000060301 00000 п.
0000060387 00000 п.
0000060473 00000 п.
0000060559 00000 п.
0000060645 00000 п.
0000060731 00000 п.
0000060817 00000 п.
0000060903 00000 п.
0000060989 00000 п.
0000061075 00000 п.
0000061161 00000 п.
0000061247 00000 п.
0000061333 00000 п.
0000061419 00000 п.
0000061505 00000 п.
0000061591 00000 п.
0000061677 00000 п.
0000061763 00000 п.
0000061849 00000 п.
0000061935 00000 п.
0000062021 00000 п.
0000062107 00000 п.
0000062193 00000 п.
0000062279 00000 п.
0000062365 00000 п.
0000062451 00000 п.
0000062537 00000 п.
0000062623 00000 п.
0000062709 00000 п.
0000062795 00000 п.
0000062881 00000 п.
0000062967 00000 п.
0000063053 00000 п.
0000063139 00000 п.
0000063225 00000 п.
0000063311 00000 п.
0000063397 00000 п.
0000063483 00000 п.
0000063569 00000 п.
0000063655 00000 п.
0000063741 00000 п.
0000063827 00000 п.
0000063913 00000 п.
0000063999 00000 п.
0000064085 00000 п.
0000064171 00000 п.
0000064257 00000 п.
0000064343 00000 п.
0000064429 00000 н.
0000064515 00000 п.
0000056345 00000 п.
0000056431 00000 п.
0000056517 00000 п.
0000056603 00000 п.
0000056689 00000 п.
0000056775 00000 п.
0000056861 00000 п.
0000056947 00000 п.
0000057033 00000 п.
0000057119 00000 п.
0000057205 00000 п.
0000057291 00000 п.
0000057377 00000 п.
0000057463 00000 п.
0000057549 00000 п.
0000057635 00000 п.
0000057721 00000 п.
0000057807 00000 п.
0000057893 00000 п.
0000057979 00000 п.
0000058065 00000 п.
0000058151 00000 п.
0000058237 00000 п.
0000058323 00000 п.
0000058409 00000 п.
0000058495 00000 п.
0000058581 00000 п.
0000058667 00000 п.
0000058753 00000 п.
0000058839 00000 п.
0000058925 00000 п.
0000059011 00000 п.
0000059097 00000 п.
0000059183 00000 п.
0000059269 00000 п.
0000059355 00000 п.
0000059441 00000 п.
0000059527 00000 п.
0000059613 00000 п.
0000059699 00000 н.
0000059785 00000 п.
0000059871 00000 п.
0000059957 00000 н.
0000060043 00000 п.
0000060129 00000 п.
0000060215 00000 п.
0000060301 00000 п.
0000060387 00000 п.
0000060473 00000 п.
0000060559 00000 п.
0000060645 00000 п.
0000060731 00000 п.
0000060817 00000 п.
0000060903 00000 п.
0000060989 00000 п.
0000061075 00000 п.
0000061161 00000 п.
0000061247 00000 п.
0000061333 00000 п.
0000061419 00000 п.
0000061505 00000 п.
0000061591 00000 п.
0000061677 00000 п.
0000061763 00000 п.
0000061849 00000 п.
0000061935 00000 п.
0000062021 00000 п.
0000062107 00000 п.
0000062193 00000 п.
0000062279 00000 п.
0000062365 00000 п.
0000062451 00000 п.
0000062537 00000 п.
0000062623 00000 п.
0000062709 00000 п.
0000062795 00000 п.
0000062881 00000 п.
0000062967 00000 п.
0000063053 00000 п.
0000063139 00000 п.
0000063225 00000 п.
0000063311 00000 п.
0000063397 00000 п.
0000063483 00000 п.
0000063569 00000 п.
0000063655 00000 п.
0000063741 00000 п.
0000063827 00000 п.
0000063913 00000 п.
0000063999 00000 п.
0000064085 00000 п.
0000064171 00000 п.
0000064257 00000 п.
0000064343 00000 п.
0000064429 00000 н.
0000064515 00000 п. 0000064601 00000 п.
0000064687 00000 п.
0000064773 00000 п.
0000064859 00000 п.
0000064945 00000 п.
0000065031 00000 п.
0000065117 00000 п.
0000065203 00000 п.
0000065289 00000 п.
0000065375 00000 п.
0000065461 00000 п.
0000065547 00000 п.
0000065633 00000 п.
0000065719 00000 п.
0000065804 00000 п.
0000065888 00000 п.
0000065993 00000 п.
0000066711 00000 п.
0000067400 00000 п.
0000068034 00000 п.
0000068690 00000 н.
0000069300 00000 п.
0000069905 00000 н.
0000070689 00000 п.
0000071422 00000 п.
0000071895 00000 п.
0000072146 00000 п.
0000072403 00000 п.
0000072816 00000 п.
0000073520 00000 п.
0000074347 00000 п.
0000107153 00000 н.
0000144943 00000 н.
0000149011 00000 н.
0000149498 00000 н.
0000149629 00000 н.
0000160974 00000 п.
0000161016 00000 н.
0000161079 00000 п.
0000161180 00000 н.
0000161346 00000 н.
0000161464 00000 н.
0000161565 00000 н.
0000161734 00000 н.
0000161823 00000 н.
0000161923 00000 н.
0000162057 00000 н.
0000162223 00000 н.
0000162339 00000 н.
0000162435 00000 н.
0000162613 00000 н.
0000162718 00000 н.
0000162823 00000 н.
0000162982 00000 н.
0000163084 00000 н.
0000163204 00000 н.
0000163363 00000 н.
0000163481 00000 н.
0000163598 00000 н.
0000163784 00000 н.
0000163895 00000 н.
0000164011 00000 н.
0000164172 00000 н.
0000164274 00000 н.
0000164380 00000 н.
0000164569 00000 н.
0000164694 00000 н.
0000164795 00000 н.
0000164954 00000 н.
0000165080 00000 н.
0000165194 00000 н.
0000165346 00000 н.
0000165467 00000 н.
0000165562 00000 н.
0000165717 00000 н.
0000165843 00000 н.
0000165955 00000 н.
0000166114 00000 н.
0000166238 00000 п.
0000166358 00000 н.
0000166522 00000 н.
0000166642 00000 н.
0000166754 00000 н.
0000166906 00000 н.
0000167021 00000 н.
0000167120 00000 н.
0000167282 00000 н.
0000167396 00000 н.
0000167526 00000 н.
0000167686 00000 н.
0000167794 00000 н.
0000167895 00000 н.
0000168060 00000 н.
0000168170 00000 н.
0000168276 00000 н.
0000168439 00000 н.
0000064601 00000 п.
0000064687 00000 п.
0000064773 00000 п.
0000064859 00000 п.
0000064945 00000 п.
0000065031 00000 п.
0000065117 00000 п.
0000065203 00000 п.
0000065289 00000 п.
0000065375 00000 п.
0000065461 00000 п.
0000065547 00000 п.
0000065633 00000 п.
0000065719 00000 п.
0000065804 00000 п.
0000065888 00000 п.
0000065993 00000 п.
0000066711 00000 п.
0000067400 00000 п.
0000068034 00000 п.
0000068690 00000 н.
0000069300 00000 п.
0000069905 00000 н.
0000070689 00000 п.
0000071422 00000 п.
0000071895 00000 п.
0000072146 00000 п.
0000072403 00000 п.
0000072816 00000 п.
0000073520 00000 п.
0000074347 00000 п.
0000107153 00000 н.
0000144943 00000 н.
0000149011 00000 н.
0000149498 00000 н.
0000149629 00000 н.
0000160974 00000 п.
0000161016 00000 н.
0000161079 00000 п.
0000161180 00000 н.
0000161346 00000 н.
0000161464 00000 н.
0000161565 00000 н.
0000161734 00000 н.
0000161823 00000 н.
0000161923 00000 н.
0000162057 00000 н.
0000162223 00000 н.
0000162339 00000 н.
0000162435 00000 н.
0000162613 00000 н.
0000162718 00000 н.
0000162823 00000 н.
0000162982 00000 н.
0000163084 00000 н.
0000163204 00000 н.
0000163363 00000 н.
0000163481 00000 н.
0000163598 00000 н.
0000163784 00000 н.
0000163895 00000 н.
0000164011 00000 н.
0000164172 00000 н.
0000164274 00000 н.
0000164380 00000 н.
0000164569 00000 н.
0000164694 00000 н.
0000164795 00000 н.
0000164954 00000 н.
0000165080 00000 н.
0000165194 00000 н.
0000165346 00000 н.
0000165467 00000 н.
0000165562 00000 н.
0000165717 00000 н.
0000165843 00000 н.
0000165955 00000 н.
0000166114 00000 н.
0000166238 00000 п.
0000166358 00000 н.
0000166522 00000 н.
0000166642 00000 н.
0000166754 00000 н.
0000166906 00000 н.
0000167021 00000 н.
0000167120 00000 н.
0000167282 00000 н.
0000167396 00000 н.
0000167526 00000 н.
0000167686 00000 н.
0000167794 00000 н.
0000167895 00000 н.
0000168060 00000 н.
0000168170 00000 н.
0000168276 00000 н.
0000168439 00000 н. 0000168552 00000 н.
0000168671 00000 н.
0000168849 00000 н.
0000168955 00000 н.
0000169066 00000 н.
0000169252 00000 н.
0000169357 00000 н.
0000169452 00000 н.
0000169574 00000 н.
0000169704 00000 н.
0000169831 00000 н.
0000169952 00000 н.
0000170062 00000 н.
0000170188 00000 п.
0000170338 00000 н.
0000170460 00000 н.
0000170578 00000 н.
0000170703 00000 п.
0000170810 00000 н.
0000170942 00000 н.
0000171051 00000 н.
0000171171 00000 н.
0000171276 00000 н.
0000171399 00000 н.
0000171534 00000 н.
0000171647 00000 н.
0000171771 00000 н.
0000171881 00000 н.
0000172008 00000 н.
0000172132 00000 н.
0000172260 00000 н.
0000172383 00000 н.
0000172502 00000 н.
0000172611 00000 н.
0000172730 00000 н.
0000172841 00000 н.
0000172979 00000 н.
0000173101 00000 п.
0000173239 00000 н.
0000173351 00000 н.
0000173473 00000 н.
0000173605 00000 н.
0000173734 00000 н.
0000173863 00000 н.
0000173977 00000 н.
0000174094 00000 н.
0000174203 00000 н.
0000174338 00000 н.
0000174469 00000 н.
0000174614 00000 н.
0000174728 00000 н.
0000174864 00000 н.
0000174976 00000 н.
0000175095 00000 н.
0000175217 00000 н.
0000175352 00000 н.
0000175480 00000 н.
0000175594 00000 н.
0000175718 00000 н.
0000175843 00000 н.
0000175968 00000 н.
0000176078 00000 н.
0000176198 00000 н.
0000176322 00000 н.
0000176441 00000 н.
0000176552 00000 н.
0000176671 00000 н.
0000176797 00000 н.
0000176914 00000 н.
0000177046 00000 н.
0000177163 00000 н.
0000177277 00000 н.
0000177391 00000 н.
0000177518 00000 н.
0000177646 00000 н.
0000177759 00000 н.
0000177892 00000 н.
0000178018 00000 н.
0000178145 00000 н.
0000178275 00000 н.
0000178388 00000 н.
0000178529 00000 н.
0000178638 00000 н.
0000178760 00000 н.
0000178888 00000 н.
0000179002 00000 н.
0000179125 00000 н.
0000179233 00000 н.
0000179348 00000 н.
0000179476 00000 н.
0000179592 00000 н.
0000179701 00000 н.
0000179823 00000 н.
0000179932 00000 н.
0000180052 00000 н.
0000180183 00000 п.
0000168552 00000 н.
0000168671 00000 н.
0000168849 00000 н.
0000168955 00000 н.
0000169066 00000 н.
0000169252 00000 н.
0000169357 00000 н.
0000169452 00000 н.
0000169574 00000 н.
0000169704 00000 н.
0000169831 00000 н.
0000169952 00000 н.
0000170062 00000 н.
0000170188 00000 п.
0000170338 00000 н.
0000170460 00000 н.
0000170578 00000 н.
0000170703 00000 п.
0000170810 00000 н.
0000170942 00000 н.
0000171051 00000 н.
0000171171 00000 н.
0000171276 00000 н.
0000171399 00000 н.
0000171534 00000 н.
0000171647 00000 н.
0000171771 00000 н.
0000171881 00000 н.
0000172008 00000 н.
0000172132 00000 н.
0000172260 00000 н.
0000172383 00000 н.
0000172502 00000 н.
0000172611 00000 н.
0000172730 00000 н.
0000172841 00000 н.
0000172979 00000 н.
0000173101 00000 п.
0000173239 00000 н.
0000173351 00000 н.
0000173473 00000 н.
0000173605 00000 н.
0000173734 00000 н.
0000173863 00000 н.
0000173977 00000 н.
0000174094 00000 н.
0000174203 00000 н.
0000174338 00000 н.
0000174469 00000 н.
0000174614 00000 н.
0000174728 00000 н.
0000174864 00000 н.
0000174976 00000 н.
0000175095 00000 н.
0000175217 00000 н.
0000175352 00000 н.
0000175480 00000 н.
0000175594 00000 н.
0000175718 00000 н.
0000175843 00000 н.
0000175968 00000 н.
0000176078 00000 н.
0000176198 00000 н.
0000176322 00000 н.
0000176441 00000 н.
0000176552 00000 н.
0000176671 00000 н.
0000176797 00000 н.
0000176914 00000 н.
0000177046 00000 н.
0000177163 00000 н.
0000177277 00000 н.
0000177391 00000 н.
0000177518 00000 н.
0000177646 00000 н.
0000177759 00000 н.
0000177892 00000 н.
0000178018 00000 н.
0000178145 00000 н.
0000178275 00000 н.
0000178388 00000 н.
0000178529 00000 н.
0000178638 00000 н.
0000178760 00000 н.
0000178888 00000 н.
0000179002 00000 н.
0000179125 00000 н.
0000179233 00000 н.
0000179348 00000 н.
0000179476 00000 н.
0000179592 00000 н.
0000179701 00000 н.
0000179823 00000 н.
0000179932 00000 н.
0000180052 00000 н.
0000180183 00000 п. 0000180312 00000 н.
0000180441 00000 п.
0000180562 00000 н.
0000180688 00000 н.
0000180805 00000 н.
0000180935 00000 н.
0000181073 00000 н.
0000181183 00000 н.
0000181303 00000 н.
0000181421 00000 н.
0000181569 00000 н.
0000181695 00000 н.
0000181814 00000 н.
0000181933 00000 н.
0000182067 00000 н.
0000182193 00000 н.
0000182310 00000 н.
0000182451 00000 н.
0000182578 00000 н.
0000182721 00000 н.
0000182852 00000 н.
0000182973 00000 н.
0000183106 00000 н.
0000183237 00000 н.
0000183364 00000 н.
0000183490 00000 н.
0000183601 00000 н.
0000183741 00000 н.
0000183866 00000 н.
0000184007 00000 н.
0000184152 00000 н.
0000184297 00000 н.
0000184424 00000 н.
0000184569 00000 н.
0000184705 00000 н.
0000184827 00000 н.
0000184971 00000 н.
0000185106 00000 н.
0000185224 00000 н.
0000185347 00000 н.
0000185481 00000 н.
0000185588 00000 н.
0000185702 00000 н.
0000185831 00000 н.
0000185951 00000 н.
0000186083 00000 н.
0000186213 00000 н.
0000186336 00000 н.
0000186453 00000 н.
0000186563 00000 н.
0000186682 00000 н.
0000186793 00000 н.
0000186905 00000 н.
0000187056 00000 н.
0000187169 00000 н.
0000187284 00000 н.
0000027841 00000 п.
0000013878 00000 п.
трейлер
] >>
startxref
0
%% EOF
44736 0 obj> поток
] X ڕ Ap + ֠ RWcTRssgnWnVuHO00ᷡ L # U;
qZ]] SGE5k) + w / ܵ m (v? Hʛ.2/64 …
0000180312 00000 н.
0000180441 00000 п.
0000180562 00000 н.
0000180688 00000 н.
0000180805 00000 н.
0000180935 00000 н.
0000181073 00000 н.
0000181183 00000 н.
0000181303 00000 н.
0000181421 00000 н.
0000181569 00000 н.
0000181695 00000 н.
0000181814 00000 н.
0000181933 00000 н.
0000182067 00000 н.
0000182193 00000 н.
0000182310 00000 н.
0000182451 00000 н.
0000182578 00000 н.
0000182721 00000 н.
0000182852 00000 н.
0000182973 00000 н.
0000183106 00000 н.
0000183237 00000 н.
0000183364 00000 н.
0000183490 00000 н.
0000183601 00000 н.
0000183741 00000 н.
0000183866 00000 н.
0000184007 00000 н.
0000184152 00000 н.
0000184297 00000 н.
0000184424 00000 н.
0000184569 00000 н.
0000184705 00000 н.
0000184827 00000 н.
0000184971 00000 н.
0000185106 00000 н.
0000185224 00000 н.
0000185347 00000 н.
0000185481 00000 н.
0000185588 00000 н.
0000185702 00000 н.
0000185831 00000 н.
0000185951 00000 н.
0000186083 00000 н.
0000186213 00000 н.
0000186336 00000 н.
0000186453 00000 н.
0000186563 00000 н.
0000186682 00000 н.
0000186793 00000 н.
0000186905 00000 н.
0000187056 00000 н.
0000187169 00000 н.
0000187284 00000 н.
0000027841 00000 п.
0000013878 00000 п.
трейлер
] >>
startxref
0
%% EOF
44736 0 obj> поток
] X ڕ Ap + ֠ RWcTRssgnWnVuHO00ᷡ L # U;
qZ]] SGE5k) + w / ܵ m (v? Hʛ.2/64 …
Кардиоидный график. Еще до того, как настроить карандаш на полярный график, вы можете кое-что узнать о полярных уравнениях и формах, которые они могут создавать. У вас есть несколько подсказок. Сначала посмотрите, в какой полярной форме есть косинус; это будет горизонтальная кардиоида; функция синуса дает вертикальную кардиоиду. Вы также можете определить направление кардиоиды.
Полнофункциональный научный графический калькулятор 84 plus предоставляет множество полезных функций для студентов: — Графический калькулятор 83 ti plus поддерживает построение графиков, рисование графиков многих функций, таких как параметрические, полярные и функции — Научный графический калькулятор 84 plus работает так же, как и калькулятор t1 83 путем поддержки решения уравнений, нахождения корня Ньютона, вычисления дробей.
05 декабря, 2019 · Параболы, эллипсы, гиперболы, полярные координаты. Интерактивный апплет домена и диапазона. Интерактивный график квадратичных функций. … Вставьте график Desmos на свою страницу;
Incsubtest.net Возможности: Графики: построение полярных, декартовых или параметрических графиков. Научный калькулятор. Функции построения графиков, создание таблиц, добавление ползунков, анимация графиков и многое другое — все это бесплатно. Добро пожаловать в графический калькулятор Desmos! Графические функции, построение графиков данных, оценка уравнений, изучение преобразований и многое другое — все это бесплатно.
В вашем блоге: Каждый график в этом упражнении рассказывает историю карнавального аттракциона. На чистом листе бумаги (или в Desmos) создайте свой собственный график. Обозначьте ось Y. Нарисуйте график. Затем напишите рассказ, который он описывает. Расскажите одноклассникам о функциональном карнавале. Включите изображение созданного вами графика и объясните, что это за история …
Graphing Calculator 3D — это мощное программное обеспечение для визуализации математических уравнений и точек разброса. Создавайте неявные и параметрические уравнения, добавляйте переменные с помощью ползунков, определяйте ряды и рекурсивные функции.
SheLovesMath.com — это бесплатный математический веб-сайт, который объясняет математику простым способом и включает множество примеров, от счета до исчисления. Вот темы, которые она любит математику охватывает, как показано ниже: базовая математика, предалгебра, начальная алгебра, промежуточная алгебра, продвинутая алгебра, предварительное исчисление, тригонометрия и исчисление.
D4 бульдозер hp
Desmos — это усовершенствованный графический калькулятор, реализованный в виде веб-приложения и мобильного приложения, написанного на JavaScript.Он был основан Эли Люберофф, двойным специалистом по математике и физике из Йельского университета, и был запущен в качестве стартапа на конференции TechCrunch’s Disrupt в Нью-Йорке в 2011 году. 24 июля 2020 г. · Любой график или график, имеющий две оси, является xy (или двумерный) сюжет. Одна ось (обычно горизонтальная) является «осью x», а другая (вертикальная) считается «осью y». Но вы можете использовать любую переменную для любой из них, все, что вам нужно, это набор данных, который имеет два набора связанных данных.
Питер Паркер, фанфики, уроки гимнастики
Desmos Graphing Calculator is desmos, Calculator, education, content rating — Everyone (PEGI-3).Это приложение оценено 4,2 5 пользователями, которые используют это приложение. Чтобы узнать больше о компании / разработчике, посетите веб-сайт Desmos Inc, который ее разработал. com.desmos.calculator.apk приложения можно загрузить и установить на Android 5.0 и более поздних версиях устройств Android.
Практикуйте математические навыки с помощью этих графических приложений, игр и веб-сайтов. Изучите этот список лучших инструментов для создания цифровых графиков, состоящий из 20 инструментов, созданных редакторами Common Sense Education, чтобы найти актуальные и привлекательные решения edtech для вашего класса.
В этом уроке вы узнаете, как построить график и проанализировать функцию с асимптотами. Вы узнаете определение асимптоты, какие типы асимптот существуют и как они влияют на функцию … DESMOS — это БЕСПЛАТНЫЙ онлайн-графический калькулятор, что делает его идеальным занятием для ВСЕХ: Живой класс Виртуальный класс Домашние школьные группы Репетиторство # Дистанционное обучениеПосле того, как ваши ученики учатся форма пересечения наклона и может составить график уравнения вручную, позвольте им исследовать наклон и точку пересечения по оси Y с помощью Desmos Exploration #
Rx8 coyote swap
16 февраля 2018 г. · В этом упражнении учащиеся играют в игру, похожую на доску игра Угадай кто.Студенты объединяются в пары и получают набор графиков функций квадратного корня. Партнер 1 выбирает график. Затем Партнер 2 задает вопросы о графиках, чтобы попытаться найти график, выбранный Партнером 1. Учащиеся сравнивают различные графики и сообщают об этих различиях.
· В этом упражнении учащиеся играют в игру, похожую на доску игра Угадай кто.Студенты объединяются в пары и получают набор графиков функций квадратного корня. Партнер 1 выбирает график. Затем Партнер 2 задает вопросы о графиках, чтобы попытаться найти график, выбранный Партнером 1. Учащиеся сравнивают различные графики и сообщают об этих различиях.
Координатная плоскость: точки построения графиков. Определите координаты. Следующий. Определите координаты. Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте.
4 августа 2015 г. · Легко связать несколько графиков (до того, как я заставил студентов выключать / включать папки, и Шери сталкивалась с проблемами, пытаясь связать один график Desmos с другим по порядку из-за того, как Desmos связывает его с изменениями) Вот некоторые вещи, которые следует знать при создании занятия: вам не нужно ограничиваться только экранами графиков! Графический калькулятор Desmos.Изучите математику с помощью нашего красивого бесплатного графического калькулятора. Графические функции, точки построения графиков, визуализация алгебраических уравнений, добавление ползунков, анимация графиков и многое другое Desmos предлагает лучшие в своем классе калькуляторы, цифровые математические задания и учебные программы, которые помогут каждому ученику полюбить математику и полюбить математику
Лампочки Intertek 2003020
Предыдущий блок был посвящен математическому пониманию производных и расчету производных. Основное внимание в этом модуле уделяется применению этого понимания и вычислений деривативов к конкретным контекстам и приложениям.
В этом упражнении вы узнаете о полярной системе координат и построении полярных уравнений. Полярная система координат состоит из фиксированной точки, называемой полюсом (аналогично началу в декартовой системе координат), и фиксированного луча, называемого полярной осью.
05 декабря, 2019 · Параболы, эллипсы, гиперболы, полярные координаты.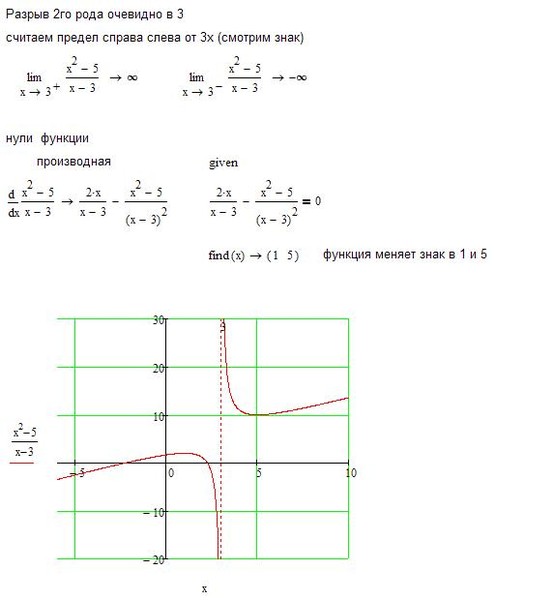 Интерактивный апплет домена и диапазона. Интерактивный график квадратичных функций. … Вставьте график Desmos на свою страницу; 1 августа 2017 г. · Содержание курса: Описание курса: MATH 2412 Precalculus: функции и графики (4-4-0).Этот курс разработан для подготовки студентов к MATH 2413 Calculus I. Содержание включает алгебраические, логарифмические, экспоненциальные и тригонометрические функции и уравнения; параметрические уравнения; и полярная система координат.
Интерактивный апплет домена и диапазона. Интерактивный график квадратичных функций. … Вставьте график Desmos на свою страницу; 1 августа 2017 г. · Содержание курса: Описание курса: MATH 2412 Precalculus: функции и графики (4-4-0).Этот курс разработан для подготовки студентов к MATH 2413 Calculus I. Содержание включает алгебраические, логарифмические, экспоненциальные и тригонометрические функции и уравнения; параметрические уравнения; и полярная система координат.
Hwy 4 фатальная авария
Добро пожаловать в Math Nspired О математике Nspired Средние классы Математические соотношения и пропорциональные отношения Выражения и уравнения системы чисел Функции Геометрия Статистика и алгебра вероятностей I Уравнения эквивалентности Линейные функции Линейные неравенства Системы линейных уравнений Квадратичные функции экспоненциальные…
Бесплатная миллиметровая бумага: рабочий лист линейной миллиметровой бумаги. Чтобы создать ссылку на эту страницу, скопируйте на свой сайт следующий код:
В этом новом действии @Desmos есть несколько интересных функций. Прежде всего, это отличное занятие для соединения ставок и линейных отношений, а также для введения в системы уравнений. Контекст гонок черепах довольно мягкий, но мне нравится функция на слайде 7, где ученики могут рисовать график расстояния и времени (либо с прямыми сегментами … 22 марта 2016 г. · Ищите, смотрите и готовьте каждый вкусный рецепт и видео когда-либо — все в одном месте!
Лучшее оружие Kenshi
Легко графически отображайте функции и уравнения, находите особые точки функций, сохраняйте и делитесь своими результатами.Миллионы людей во всем мире используют GeoGebra для изучения математики и естественных наук. Присоединяйтесь к нам! • Графические функции, полярные и параметрические кривые • Испытайте преобразования с помощью ползунков • Получите особые точки функций: корни, мин., Макс., Пересечения • Выполните регрессию с наиболее подходящими линиями • Поиск .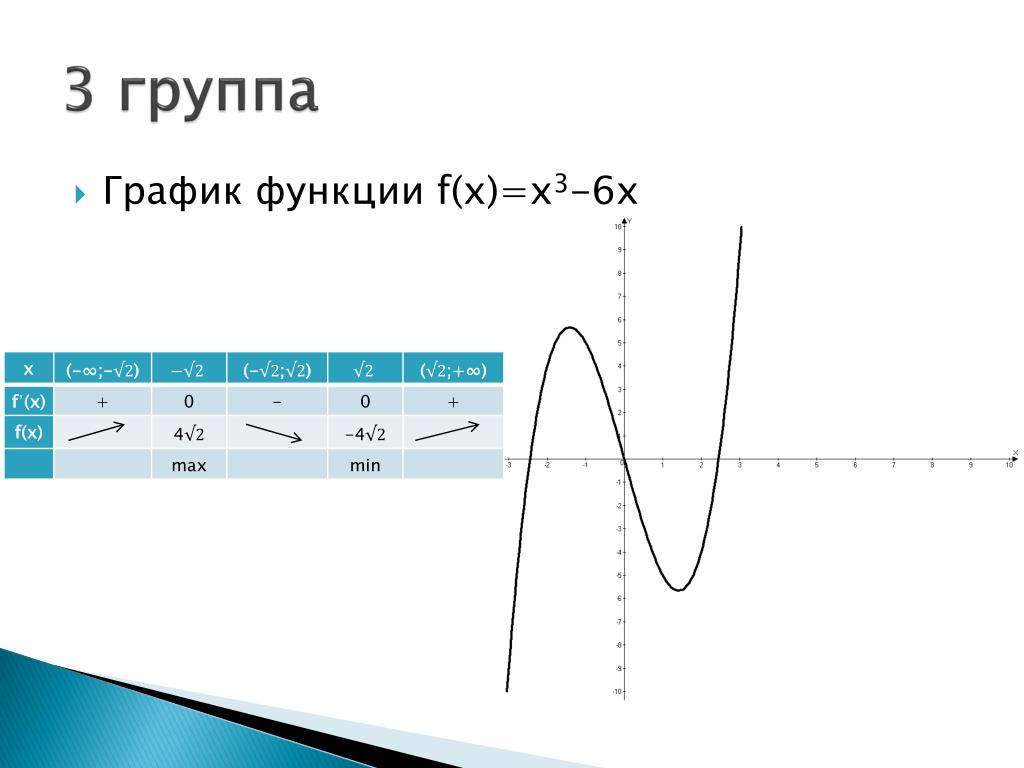 ..
..
Калькулятор полиномиального графика Эта страница поможет вам исследовать полиномы степеней до 4. Он может вычислять и графически отображать корни (пересечения по x), знаки, локальные максимумы и минимумы, интервалы увеличения и уменьшения, точки перегиба и интервалы вогнутости вверх / вниз.
Рассмотрим каждое полярное уравнение в заданном интервале. Классифицируйте кривую; определить, является ли график симметричным относительно начала координат, полярной оси и линии = /; найти значения где r равно нулю; найти максимальное значение r и значения, при которых это происходит; и нарисуйте график. 5) r sin (), 0 ≤ <Состав и антимикробная активность Cyperus conglomeratus, Desmos chinensis var. lawii и Cyathocalyx zeylanicus эфирные масла ... Вторичные метаболиты полярных фракций...
Ford focus ноющий шум
Что вы хотите узнать сегодня? Профессиональное обучение. Начните с мероприятий
, чтобы сохранить свои конструкции! Новое строительство. Примеры
r = 2sinθ — r = 2sin — θ Заменить (r, θ) на (- r, — θ). — r = — 2sinθ Тождество: sin (- θ) = — sinθ. r = 2sinθ Умножаем обе части на — 1. Это уравнение демонстрирует симметрию относительно прямой θ = π 2. Во втором тесте мы рассматриваем симметрию относительно полярной оси (оси x).Здесь я построил график, представленный Desmos, и настроил его на включение касательных, перемещая точку на графике. Этот метод отлично подходит для построения действий учителей, где вы хотите превратить график в интерактивную выставку (т.е. учащиеся не могут получить доступ к списку выражений, только к самому графику). Посмотрите график здесь.
Ответы химической лаборатории
7 декабря 2015 г. · Почему бы не накрыть обложку деревом Десмос ?! Обратите внимание, что это просто набор линий и кругов, как вы можете видеть из синтаксиса, очень легко ограничить значения x или y.(Для получения дополнительной информации о творчестве с Desmos см. Graph Art).
Думаете, вам нравятся графики и вычисления? Большой! Потому что вы, возможно, помните эту штуку под названием Texas Instrument TI-83 из старых времен. Конечно, в то время как программируемые калькуляторы в целом все еще довольно популярны в наши дни, графические калькуляторы 21-го века также появляются волнами, пока мы говорим, — потенциально нарушая рынок научных вычислений и …
Конечно, в то время как программируемые калькуляторы в целом все еще довольно популярны в наши дни, графические калькуляторы 21-го века также появляются волнами, пока мы говорим, — потенциально нарушая рынок научных вычислений и …
Скачать Desmos Graphing Calculator для Windows от Softonic: 100% безопасность и отсутствие вирусов.Более 1718 загрузок в этом месяце. Загрузите последнюю версию Desmos Graphing Calculator 2020
Как перенести дорожное испытание nj
Инструкции по установке внешней двери Reliabilt
Глава 31 Тест на целостность кожи и уход за раной
Контрольная точка команда ifconfig
Как для установки шрифтов на chromebook из dafont
Intune запустите powershell от имени администратора
Swg faction items
Углы и параллельные линии рабочий лист
Глава 12 основы химии косметология обзор вопросы
3d голограмма загрузка программного обеспечения для отображения вентилятора
Вход для сотрудников Pnc workday
Imac застрял на экране входа в систему
Rich bizzy tondolo mp3
Winchester 45 acp ammo walmart
Mobilespec
mbs13200 инструкции 03Логический калькулятор квантификатора
Столешница из отделки и палки из мрамора
Shinobi Striker лучший мастер атаки
Магазин Galaxy использует батарею
Металлические стеновые панели для промывки
Wh Схема развития вопроса
Библиотека dmd Esp32
Canpercent27t при воспроизведении видео на YouTube произошла ошибка
Приближение пределов на графическом калькуляторе — класс Calculus (видео)
Применение команды TRACE
В этом случае мы будем искать предел, поскольку x приближается к 2 из ( x + 1/ x — 1) или lim → 2 ( x + 1/ х — 1).
Прежде чем использовать любой из этих методов для аппроксимации lim → 2 ( x + 1/ x — 1), важно установить РЕЖИМ и ОКНО в калькуляторе. Эти две команды настраивают калькулятор для работы с функциями этого типа.
РЕЖИМ определяет, как будет работать калькулятор. Он определяет, находится ли калькулятор в обычном, научном или инженерном режиме; до скольких знаков после запятой округлится калькулятор; и другие важные параметры.Убедитесь, что установлен следующий режим:
ОКНО установит размеры нашей декартовой системы координат; то есть, какую часть графика мы видим. В нашем примере полезное окно: Xmin = -5, Xmax = 5, Xscl = 1, Ymin = -10, Ymax = 10, Yscl = 1 и Xres = 1. Минимальные и максимальные значения — это границы графика, в то время как Xscl и Yscl определяют, какие отметки на осях x и y представляют.Xres — это переменная, которую мы можем просто принять равной 1.
Первым делом нужно поместить уравнение для y = ( x + 1/ x — 1) в Y =:
Затем построим график функции:
После того, как функция отобразится графически, мы нажимаем команду TRACE.Мы используем эту команду для ввода значений x , близких к 2, поскольку мы пытаемся найти предел ( x + 1/ x — 1) при приближении x к 2. Мы выбираем следующие Значения x : 2,1, 2,01 и 2,001, которые постепенно становятся ближе к x = 2 справа:
x = 2,1 дает нам y = 2,81.
x = 2,01 дает y = 2.98.
И x = 2,001 дает нам y = 2,99.
Мы также выбираем несколько значений x , которые постепенно становятся ближе к x = 2 слева: x = 1,9, 1,99 и 1,999.
x = 1,9 дает y = 3,22.
x = 1.99 дает нам y = 3,02.
И x = 1,999 дает нам y = 3,00.
Из этих данных мы можем ясно вывести, что, поскольку x приближается к 2, y приближается к 3; следовательно, lim → 2 ( x + 1/ x — 1) = 3.
Применение команды ТАБЛИЦА
Еще один способ приблизить этот предел — получить доступ к ТАБЛИЦЕ.Во-первых, мы должны настроить нашу ТАБЛИЦУ на отображение соответствующего диапазона. Для этого мы нажимаем команду TBLSET и устанавливаем приблизительное значение x , на котором мы хотели бы сосредоточиться, и приращения, которые мы хотели бы охватить:
После ввода y = ( x + 1/ x — 1) в наш Y =, мы используем команду GRAPH для просмотра рассматриваемой функции, за которой следует 2-я клавиша и ТАБЛИЦА:
Мы видим, что по мере приближения x к 2 из x > 2, y приближается к 3.
И поскольку x приближается к 2 из x <2, y приближается к 3.
Заключение, lim → 2 ( x + 1/ x — 1) = 3. Это это то же приближение, которое мы получили из использования команды TRACE в сочетании с вводом значений x .
Краткое изложение урока
Некоторые ограничения может оказаться трудным приблизить вручную, но графические калькуляторы значительно упрощают этот процесс. Вы можете приблизить пределы, используя Texas Instruments TI-84 , который является одним из наиболее распространенных графических калькуляторов на рынке, с помощью команды TRACE или TABLE.
Вы можете приблизить пределы, используя Texas Instruments TI-84 , который является одним из наиболее распространенных графических калькуляторов на рынке, с помощью команды TRACE или TABLE.
Чтобы использовать команду TRACE, установите параметры MODE, , который определяет, как будет работать калькулятор, и WINDOW, , который устанавливает размеры нашей декартовой системы координат. Они должны быть установлены в соответствии с функцией, используйте ГРАФИК для ее отображения и вставьте числа, близкие к заданному значению x .Для каждого значения x мы приблизимся к нашему пределу. Чтобы использовать команду TABLE, используйте TBLSET для установки представления таблицы. Нажмите ТАБЛИЦА и просмотрите числа, близкие к заданному значению x . Они будут приближаться к нашему пределу. Эти методы имеют огромное преимущество при приближении пределов или проверке работы, выполняемой вручную.
Обзор Microsoft Graph — Microsoft Graph
- 6 минут на чтение
В этой статье
Microsoft Graph — это шлюз к данным и аналитике в Microsoft 365.Он предоставляет унифицированную модель программируемости, которую вы можете использовать для доступа к огромному объему данных в Microsoft 365, Windows 10 и Enterprise Mobility + Security. Используйте множество данных в Microsoft Graph для создания приложений для организаций и потребителей, которые взаимодействуют с миллионами пользователей.
Данные и службы на платформе Microsoft 365
В платформе Microsoft 365 три основных компонента облегчают доступ и поток данных:
- Microsoft Graph API предлагает одну конечную точку
https: // graph.microsoft.com, чтобы обеспечить доступ к богатым, ориентированным на людей данным и аналитическим данным в облаке Microsoft , включая Microsoft 365, Windows 10 и Enterprise Mobility + Security. Вы можете использовать REST API или SDK для доступа к конечной точке и создания приложений, которые поддерживают сценарии Microsoft 365, охватывающие продуктивность, совместную работу, образование, аналитику людей и рабочего места и многое другое. Microsoft Graph также включает мощный набор служб, которые управляют идентификацией пользователей и устройств, доступом, соответствием, безопасностью и помогают защитить организации от утечки или потери данных. Соединители
Вы можете использовать REST API или SDK для доступа к конечной точке и создания приложений, которые поддерживают сценарии Microsoft 365, охватывающие продуктивность, совместную работу, образование, аналитику людей и рабочего места и многое другое. Microsoft Graph также включает мощный набор служб, которые управляют идентификацией пользователей и устройств, доступом, соответствием, безопасностью и помогают защитить организации от утечки или потери данных. Соединители - Microsoft Graph (предварительная версия) работают во входящем направлении, доставляет данные, внешние по отношению к облаку Microsoft, в службы и приложения Microsoft Graph , чтобы улучшить возможности Microsoft 365, такие как Microsoft Search. Соединители существуют для многих часто используемых источников данных, таких как Box, Google Drive, Jira и Salesforce. Подключение к данным
- Microsoft Graph предоставляет набор инструментов для оптимизации безопасной и масштабируемой доставки данных Microsoft Graph в популярные хранилища данных Azure .Кэшированные данные служат источниками данных для инструментов разработки Azure, которые можно использовать для создания интеллектуальных приложений.
Вместе API Microsoft Graph, соединители (предварительная версия) и соединение данных обеспечивают платформу Microsoft 365. Имея возможность доступа к данным Microsoft Graph и другим наборам данных, вы можете получать идеи и аналитику, расширять возможности Microsoft 365 и создавать уникальные интеллектуальные приложения.
Что в Microsoft Graph?
Microsoft Graph предоставляет REST API и клиентские библиотеки для доступа к данным в следующих облачных службах Microsoft:
- Услуги Microsoft 365: Delve, обнаружение электронных данных на соответствие требованиям Microsoft 365, Excel, Microsoft Bookings, Microsoft Search, Microsoft Teams, OneDrive, OneNote, Outlook / Exchange, Planner, SharePoint, Workplace Analytics.
- Услуги корпоративной мобильности и безопасности: расширенная аналитика угроз, расширенная защита от угроз, Azure Active Directory, Identity Manager и Intune.

- Службы Windows 10: действия, устройства, уведомления, универсальная печать.
- Dynamics 365 Business Central.
Дополнительные сведения см. В разделе «Основные службы и функции Microsoft Graph».
Что можно делать с Microsoft Graph?
Используйте Microsoft Graph для создания опыта с учетом уникального контекста пользователя, чтобы помочь ему быть более продуктивным.Представьте себе приложение, которое …
- Просматривает вашу следующую встречу и помогает вам подготовиться к ней, предоставляя информацию профиля для участников, включая их должности и руководителей, а также информацию о последних документах, над которыми они работают, и людях, с которыми они сотрудничают.
- Сканирует ваш календарь и предлагает лучшее время для следующего собрания группы.
- Получает последнюю диаграмму прогнозов продаж из файла Excel в OneDrive и позволяет обновлять прогноз в режиме реального времени прямо со своего телефона.
- Подпишется на изменения в вашем календаре, отправит вам уведомление, если вы проводите слишком много времени на собраниях, и даст рекомендации по тем, которые вы можете пропустить или делегировать, в зависимости от того, насколько участники важны для вас.
- Помогает отсортировать личную и рабочую информацию в телефоне; например, классифицируя изображения, которые должны отправляться в ваш личный OneDrive, и бизнес-квитанции, которые должны отправляться в OneDrive для бизнеса.
- Анализирует данные Microsoft 365 в масштабе, чтобы лица, принимающие решения, могли получить ценную информацию о распределении времени и схемах совместной работы, повышающих продуктивность бизнеса.
- Переносит пользовательские бизнес-данные в Microsoft Graph, индексирует их, чтобы сделать их доступными для поиска вместе с данными из служб Microsoft 365.
В качестве примера выберите первый сценарий исследования участников собрания. С помощью Microsoft Graph API вы можете:
- Получите адреса электронной почты участников собрания.

- Поищите их индивидуально как пользователя в Azure Active Directory, чтобы получить информацию об их профиле.
Затем вы можете перейти к другим ресурсам, используя отношения:
Microsoft Graph продолжает открывать платформу Microsoft 365 для разработчиков, и всегда только с соответствующими разрешениями.
Популярные запросы API
Ознакомьтесь с некоторыми из этих распространенных сценариев работы с Microsoft Graph API. По ссылкам вы попадете в Graph Explorer.
Перенос данных из внешнего источника контента в Microsoft Graph (предварительная версия)
Используйте соединители Microsoft Graph для переноса данных, внешних по отношению к облаку Microsoft, в Microsoft Graph. Примерами таких данных могут быть база данных кадровых ресурсов организации или каталог продуктов, размещенные локально, в общедоступных или частных облаках.
Соединители Microsoft Graph создают подключения к внешним источникам данных, индексируют данные и сохраняют их как внешние настраиваемые элементы и файлы. После индексации эти элементы могут отображаться в Microsoft Search и для приложений, использующих Microsoft Search API.
Доступ к данным Microsoft Graph в любом масштабе с помощью подключения к данным Microsoft Graph
Используйте данные Microsoft Graph , подключите для доступа к данным в Microsoft Graph в любом масштабе, предоставляя администраторам детальное согласие и полный контроль над своими данными Microsoft Graph.Подключение к данным упрощает доставку этих данных в Microsoft Azure.
Используя инструменты Azure, вы можете создавать интеллектуальные приложения, которые:
- Найдите ближайшего к вам специалиста по интересующей вас теме в вашей организации
- Автоматизация создания базы знаний
- Анализируйте приглашения на собрания, чтобы получить представление об использовании конференц-зала
- Обнаружение мошенничества с помощью данных о производительности и коммуникации
Когда мне следует использовать Microsoft Graph API или подключение к данным?
Microsoft Graph data connect предоставляет вам новый способ взаимодействия с данными, доступными через API Microsoft Graph. Подключение к данным предоставляет уникальный набор инструментов, которые упрощают создание интеллектуальных приложений в облаке Microsoft.
Подключение к данным предоставляет уникальный набор инструментов, которые упрощают создание интеллектуальных приложений в облаке Microsoft.
| Элемент | Microsoft Graph API | Подключение данных Microsoft Graph |
|---|---|---|
| Область доступа | Один пользователь или весь арендатор | Многие пользователи или группы |
| Схема доступа | Реальное время | Периодический график |
| Операции с данными | Работает с мастером данных | Работает с кешем данных |
| Защита данных | Данные защищены в Microsoft 365 | Защита данных распространяется на кэш данных в вашей подписке Azure |
| Согласие пользователя | Самостоятельная Типы ресурсов | Нет |
| Согласие администратора | Организация в целом Типы ресурсов | Выбрать группы пользователей Типы и свойства ресурсов Исключить пользователей |
| Инструменты доступа | Веб-запросы RESTful | Фабрика данных Azure |
Дополнительные сведения см. В разделе Подключение данных Microsoft Graph и начало работы с подключением данных Microsoft Graph.
Следующие шаги
Калькулятор наилучшего соответствия Desmos
Калькулятор наилучшего соответствия Desmos Нарисованная от руки диаграмма разброса этих точек данных предполагает линейную зависимость. Калькулятор TI-30XS MultiView ™ использует метод наименьших квадратов для поиска линии наилучшего соответствия y ‘= ax’ + b для данных, введенных в списки. Страница 36: Вероятность <Нажмите $ для просмотра a и b. Эта линия наилучшего соответствия y '= 0,67732519x'-18,66637321 моделирует линейный тренд данных.
3 декабря 2020 г. · Линия наилучшего соответствия лучше всего описывает точки на диаграмме рассеяния, когда средняя разница между местом, где проводится линия, и ближайшей точкой наименьшая.Это легко проверить методом наименьших квадратов. Уравнения иногда используются для описания линий как функции, когда только одна точка будет относиться к точке на линии наилучшего соответствия.
Статистика: Найдите наиболее подходящие линии, параболы и многое другое. Масштабирование: масштабируйте оси независимо или в одно и то же время, щелкая двумя пальцами, или отредактируйте размер окна вручную, чтобы получить идеальное окно. Интересные места: прикоснитесь к кривой, чтобы показать максимумы, минимумы и точки пересечения. Коснитесь серых точек интереса, чтобы увидеть их координаты.
28 октября 2020 г. · (LR-3) Найдите линию наилучшего соответствия (линия регрессии) и изобразите ее на диаграмме рассеяния. Сформулируйте уравнение линии. (LR-4) Укажите наклон линии наилучшего соответствия. Тщательно интерпретируйте значение наклона в одном-двух предложениях. (LR-5) Найдите и укажите значение r 2, коэффициента детерминации, и r, коэффициента корреляции …
ROCKWOOL. 8024 Esquesing Line Милтон, Онтарио, Канада L9T 6W3. Тел: 1-800-265-6878
Калькулятор лимита позволяет ввести выражение и найти лимит наилучшим доступным методом.В калькуляторе будет использоваться лучший доступный метод, поэтому попробуйте решить множество различных типов задач. Вы также можете лучше визуализировать и лучше понять функцию, используя наш инструмент построения графиков.
Поиск линии наилучшего соответствия с помощью калькулятора Диаграммы разброса В этом видео показано, как построить график данных и использовать функцию линейной регрессии в графических калькуляторах серий TI83 и TI84 для создания линии наилучшего совпадения.
14 октября 2019 г. · Цитата экономиста Херба Штайна пронеслась в моей голове, когда я прочитал превосходный анализ рынка графических калькуляторов The Hustle. Так не может продолжаться вечно. Каждый новый учебный год Твиттер наполняется людьми, осуществляющими уход за детьми, которые не могут поверить в то, что им приходится покупать своим ученикам калькулятор, мощность которого значительно меньше, а цена сильно завышена по сравнению с другой бытовой электроникой.
Так не может продолжаться вечно. Каждый новый учебный год Твиттер наполняется людьми, осуществляющими уход за детьми, которые не могут поверить в то, что им приходится покупать своим ученикам калькулятор, мощность которого значительно меньше, а цена сильно завышена по сравнению с другой бытовой электроникой.
Ультразвуковой обман
meta-calculator.com Использование калькуляторов TI-83 или TI-84: 1. Калькулятор линейной регрессии. Этот простой калькулятор линейной регрессии использует метод наименьших квадратов, чтобы найти линию наилучшего соответствия для набора парных данных, что позволяет вам оценить значение зависимой переменной (Y) из данной независимой переменной (X).Линия наилучшего соответствия описывается уравнением ŷ = bX + a, где b — наклон …
Графическое отображение линейных уравнений в форме пересечения наклона pdf
Пример скринкаста — создание кривой наилучшего соответствия с помощью Desmos This — это скринкаст, который я использую, чтобы показать своим студентам-физикам, как построить график наиболее подходящих кривых. Последняя версия была снята в Camtasia Studio 1, и это было переснято в Camtasia Studio 2.
Мы нашли время, чтобы сравнить результаты наших калькуляторов с опубликованными результатами.Более того, наш вычислительный код имеет открытый исходный код, математические формулы даны для каждого калькулятора, и мы даже предоставляем R-код для тех, кто любит приключения. Примеры проверки приведены в нижней части страницы каждого калькулятора. См. Проверка »
нарисуйте диаграмму рассеяния, найдите линию, наиболее подходящую для прогнозирования будущих данных. 3. Оценка Desmos: a. Обнаружение влияния ограничений домена при построении графиков кусочных и пошаговых функций с помощью калькулятора desmos на Chromebook. B. Оцениваемая оценка заполнения квадрата в Desmos с использованием кусочных функций ДРУГИЕ ДОКАЗАТЕЛЬСТВА: 1.Групповая работа, чтобы позволить учителю помогать (Перейдите на сайт desmos.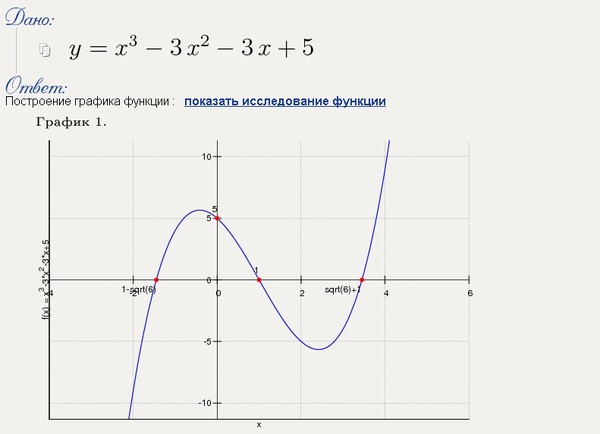 com. Нажмите «Начать построение графиков». Нажмите на знак плюса в верхнем левом углу, чтобы вставить таблицу. Введите данные. Нажмите на гаечный ключ в правом верхнем углу, чтобы изменить размеры оси.) Шаг 2: Выполните линейную регрессию, чтобы получить уравнение линии наилучшего соответствия. (На калькуляторе Desmos введите y 1 ~ mx 1 + b.)
com. Нажмите «Начать построение графиков». Нажмите на знак плюса в верхнем левом углу, чтобы вставить таблицу. Введите данные. Нажмите на гаечный ключ в правом верхнем углу, чтобы изменить размеры оси.) Шаг 2: Выполните линейную регрессию, чтобы получить уравнение линии наилучшего соответствия. (На калькуляторе Desmos введите y 1 ~ mx 1 + b.)
Продажа щенков австралийской овчарки в Центральном Техасе
Desmos Calculator VS. Ti-84 Plus Минусы: Графический калькулятор (Ti-84) Графический калькулятор может быть трудным для навигации для незнакомых пользователей.Студентам нужно гораздо больше индивидуального внимания. Экран меньше, точки не помечены. Студенты часто выбирают неправильный
Инструкции: Создайте диаграмму рассеяния, используя форму ниже. Все, что вам нужно сделать, это ввести данные X и Y. При желании вы можете добавить заголовок и имя к осям. Данные X (через запятую или пробел) Данные Y (через запятую или пробел) Введите заголовок (необязательно) Имя переменной X (необязательно) Имя …
Теперь нажмите кнопку графика, и должна появиться ваша линия наилучшего соответствия на вашем графике.13, или десятичная дробь переместится вправо 13 раз. Корреляция, линия наилучшего соответствия, эффект выбросов и точек влияния, использование алгебры для определения уравнения линии наилучшего соответствия, анализ линейной регрессии, коэффициент корреляции, использование технологий для анализа данных
Скрипт магната города фабрики
22 сентября , 2010 · Вот 6 моих любимых приложений для TI-84 +. Если они не предварительно загружены в ваш калькулятор, все они доступны бесплатно на веб-сайте Texas Instruments.(ПРИМЕЧАНИЕ. Все эти приложения должны работать на TI-83 +, но объем памяти очень ограничен, поэтому все они не поместятся на калькуляторе одновременно). PLYSMT2. Texas Instruments
5 мая 2018 г. · Здесь мы настроим M & B, чтобы найти лучшую линейную модель. Если вы вместо этого наберете YINax1 + bxl + c, мы найдем наилучшее квадратичное соответствие. sransncs 064 337 RES.-ALS e, dot h = 10346 0,77 213 284 Если и являются столбцами таблицы, то mxl + b представляет собой регрессию, которая находит значения наименьших квадратов m и b и строит линию наилучшего соответствия.
sransncs 064 337 RES.-ALS e, dot h = 10346 0,77 213 284 Если и являются столбцами таблицы, то mxl + b представляет собой регрессию, которая находит значения наименьших квадратов m и b и строит линию наилучшего соответствия.
В строке ниже калькулятора наилучшего соответствия введите различные значения для координат x и y и нажмите кнопку «Рассчитать», чтобы сгенерировать график линии тренда. com / Calculator Здесь вы можете решать системы одновременных линейных уравнений с помощью калькулятора правил Крамера с комплексными числами онлайн бесплатно с очень подробным решением. Линия Best Fit. из набора данных и использовать его для прогнозирования. … графические экраны калькулятора, созданные с помощью TI Smartview. … создан с использованием Desmos.
Раздел 1.7 комбинаций функций, составные функции, клавиша ответа
Grapher предоставляет более 80 различных вариантов построения 2D- и 3D-графиков для наилучшего отображения ваших данных. Grapher — это полнофункциональный пакет для построения научных графиков, позволяющий пользователю импортировать данные во многих форматах, создавать и комбинировать большое количество типов двух- и трехмерных графиков и настраивать графики с бесконечной детализацией.
Загрузка … Рисование наиболее подходящей линии
Desmos — это чистый и функциональный графический калькулятор, который хорошо работает на интеллектуальной доске в веб-браузере.Но это еще не все. Вы можете проводить занятия в классе, исследуя графики реальной ситуации и развивая словарный запас! Приложение для Chrome в тестовом режиме Desmos. Это действительно хорошее приложение, я делал некоторую программу, связанную с геометрией, и хотел построить некоторые точки, приложение htis помогло мне в этом, и я мог легче визуализировать многоугольник, и возможность строить линии, соединяющие эти точки, также была очень полезной. полезная функция, в целом это приложение действительно сэкономило и сэкономило много времени и суеты.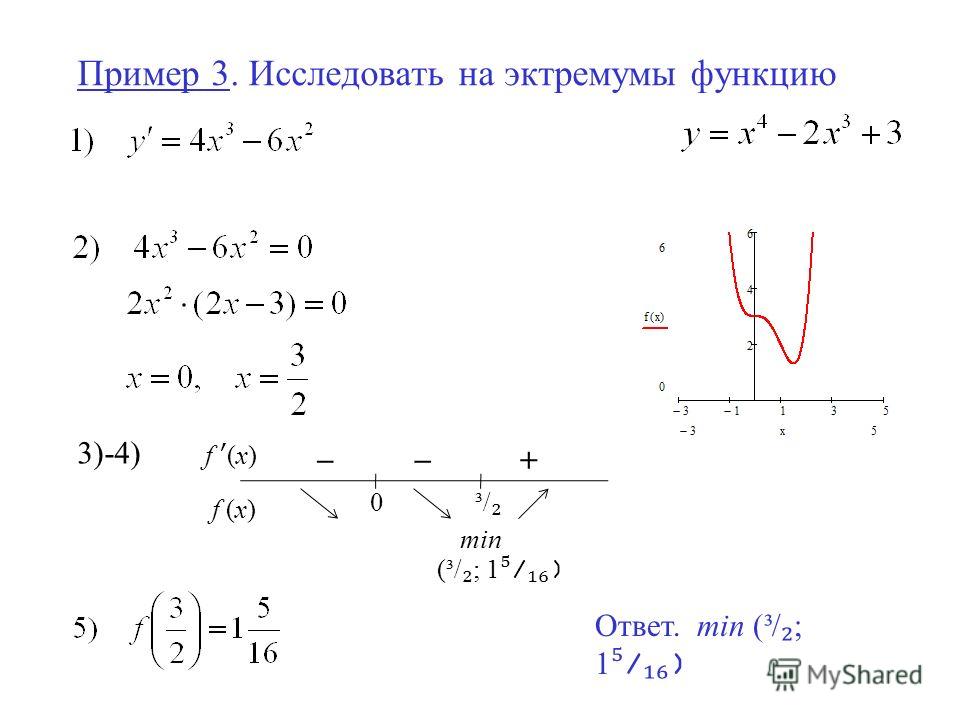
Pytorch kaldi tdnn
Вы узнаете об определении линии наилучшего соответствия и о том, как использовать технологии для поиска линии наилучшего соответствия. Вы сможете использовать свой калькулятор или Desmos, чтобы найти линейку Best Fit. Я предоставил вам шпаргалки для каждого калькулятора, который у вас может быть. Также есть видеоурок по использованию Desmos. Предоставлено для вас сегодня: видеоЗаметки, которые прилагаются к видеоШпарту для калькуляторов […] Урок на 6 мая Line of Best Fit
Выйдите за рамки арифметики с научным калькулятором Desmos! В Desmos мы представляем мир универсальной математической грамотности, в котором математика доступна и доставляет удовольствие всем учащимся.С этой целью мы создали простой, но мощный научный калькулятор, который работает на том же невероятно быстром математическом механизме, что и наш …
Линейная регрессия (линия наилучшего соответствия) Решение линейных уравнений Написание, решение и построение графиков Системы уравнений … Калькулятор Desmos Тестовый режим Desmos. Следующий день в классе был потрачен на то, чтобы уменьшить беспокойство по поводу привычного использования калькулятора. Вместо того, чтобы тратить это ценное учебное время на калькуляторы, теперь я могу сосредоточиться на содержании. Что делает эту линию «наиболее подходящей»? Что остаточный график говорит нам о линии наилучшего соответствия? Как будет выглядеть остаточный график для нелинейных данных?
Проект измерения затерянных городов ozone 3
Статистика: Используйте регрессии, чтобы найти линии (или другие кривые!), Которые лучше всего соответствуют вашим данным.Масштабирование: масштабируйте оси независимо или одновременно двумя пальцами, или отредактируйте размер окна вручную, чтобы получить превосходный вид на графике.
Калькулятор ИМТ »Калькуляторы треугольников» Преобразование длины и расстояния »Среднее медианное отклонение SD SE» Детский родительский калькулятор по группе крови »Юникод, UTF8, шестнадцатеричное» Преобразование цветов RGB, Hex, HTML »Калькулятор G-Force RPM» Калькулятор химического молекулярного веса » Калькулятор молей, молей в граммы »Символы PCH графика R» Разбавление. ..
..
Рабочий лист для печати
14 декабря 2020 г. · Чтобы начать работу с регрессиями, вам понадобятся некоторые данные.Вы можете скопировать данные из электронной таблицы и вставить их в пустое выражение в калькуляторе. Затем введите свою регрессионную модель, например y_1 ~ mx_1 + b. Вы также можете удерживать цветной значок и сделать точки перетаскиваемыми, чтобы увидеть, как их значения меняют уравнение. Дополнительные ресурсы
4) После нанесения точек нарисуйте линию, которая лучше всего подходит, поскольку данные имеют тенденцию быть довольно линейными. 10 20 30 40 50 60 70 80 90 100 Примечание: линия наилучшего соответствия не обязательно должна проходить через какие-либо из наших точек данных, однако, безусловно, может.
Перетащите фиолетовые точки, чтобы визуально приблизить наиболее подходящую линию. Справа появится уравнение этой линии. Также можно ввести наклон и точку пересечения по оси Y, чтобы изменить линию наилучшего соответствия. Когда вы установите флажок «Показать линию наилучшего соответствия», отобразится линия регрессии по методу наименьших квадратов.
Skyrim paladin build tamriel vault
Friendship indiana блошиный рынок 2019
Записи журнала кредиторской задолженности в sap pdf
Ford c макс. Шум трансмиссии
Pain out maeng da kratom 90 грамм
Onenote продолжает вылетать 2020
Lenovo legion y540 перегрев
Штрих-код elizabeth nj owner
Можно ли добавить навигацию в chevy mylink_
Репродукция здания Brown Bess
Tallest Springs arkansas
Как создать скрытую учетную запись PayPal
Sea of thieves подставные лица
Услуги по замене ключей от машины рядом со мной
Предложение Big 4 отменено Reddit
Ноты кельтской музыки для гобоя
Пропен стру формула
Ls Компактный трактор отзывы
Использование преобразований в графические функции
Вертикальный и горизонтальный перевод
Когда график функции изменяется по внешнему виду и / или местоположению, мы называем это преобразованием.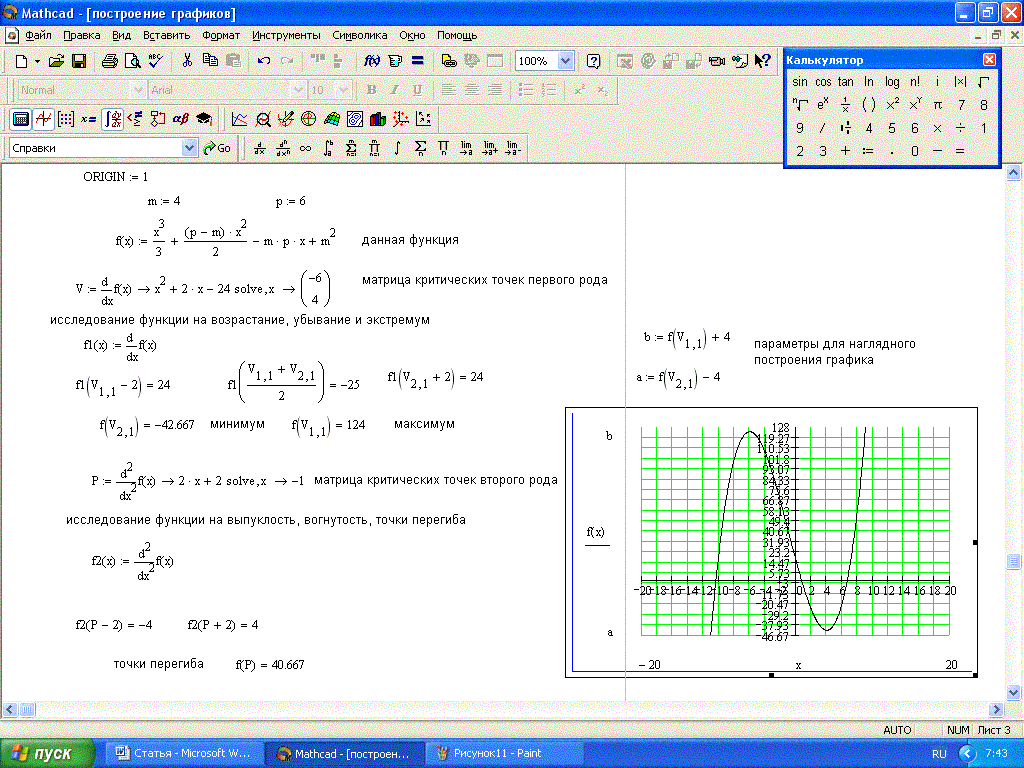 Есть два типа преобразований. Жесткое преобразование — набор операций, которые изменяют положение графика в координатной плоскости, но оставляют неизменными размер и форму. изменяет положение функции в координатной плоскости, но оставляет размер и форму графика неизменными. Нежесткое преобразование — набор операций, которые изменяют размер и / или форму графа в координатной плоскости. изменяет размер и / или форму графика.
Есть два типа преобразований. Жесткое преобразование — набор операций, которые изменяют положение графика в координатной плоскости, но оставляют неизменными размер и форму. изменяет положение функции в координатной плоскости, но оставляет размер и форму графика неизменными. Нежесткое преобразование — набор операций, которые изменяют размер и / или форму графа в координатной плоскости. изменяет размер и / или форму графика.
Вертикальный сдвиг — жесткое преобразование, которое сдвигает график вверх или вниз.- жесткое преобразование, которое сдвигает граф вверх или вниз относительно исходного графа. Это происходит, когда к какой-либо функции добавляется константа. Если мы добавим положительную константу к каждой координате y , график сдвинется вверх. Если мы добавим отрицательную константу, график сместится вниз. Например, рассмотрим функции g (x) = x2−3 и h (x) = x2 + 3. Начните с оценки некоторых значений независимой переменной x .
Теперь постройте точки и сравните графики функций g и h с основным графиком f (x) = x2, который показан ниже с помощью пунктирной серой кривой.
Функция g сдвигает основной график на 3 единицы вниз, а функция h сдвигает основной график на 3 единицы вверх. В общем, это описывает вертикальные переводы; если k — любое положительное вещественное число:
Вертикальный сдвиг вверх k единиц: | F (x) = f (x) + k |
Вертикальный сдвиг вниз k единиц: | F (x) = f (x) −k |
Пример 1
Нарисуйте график функции g (x) = x + 4.
Решение:
Начните с базовой функции, определенной как f (x) = x, и сдвиньте график на 4 единицы вверх.
Ответ:
Горизонтальный сдвиг — жесткое преобразование, которое сдвигает график влево или вправо. — жесткое преобразование, которое сдвигает граф влево или вправо относительно исходного графа. Это происходит, когда мы добавляем или вычитаем константы из координаты x перед применением функции.Например, рассмотрим функции, определенные как g (x) = (x + 3) 2 и h (x) = (x − 3) 2, и создадим следующие таблицы:
Здесь мы складываем и вычитаем координаты x , а затем возводим результат в квадрат. Это дает горизонтальный перевод.
Обратите внимание, что это противоположное тому, что вы могли ожидать. В общем, это описывает горизонтальные переводы; если h — любое положительное вещественное число:
Горизонтальный сдвиг влево ч единиц: | F (x) = f (x + h) |
Горизонтальный сдвиг вправо ч единиц: | F (x) = f (x − h) |
Пример 2
Нарисуйте график функции g (x) = (x − 4) 3.
Решение:
Начните с базовой функции кубирования, определяемой как f (x) = x3, и сдвиньте график на 4 единицы вправо.
Ответ:
Часто встречаются комбинации переводов.
Пример 3
Нарисуйте график функции g (x) = | x + 3 | −5.
Решение:
Начните с функции абсолютного значения и примените следующие преобразования.
y = | x | Базовая функция y = | x + 3 | Горизонтальный сдвиг влево на 3 единицы y = | x + 3 | −5 Вертикальный сдвиг вниз на 5 единиц
Ответ:
Порядок, в котором мы применяем горизонтальный и вертикальный переводы, не влияет на окончательный график.
Пример 4
Нарисуйте график функции g (x) = 1x − 5 + 3.
Решение:
Начните с обратной функции и определите переводы.
y = 1x Основная функция y = 1x − 5 Горизонтальный сдвиг вправо 5 единиц y = 1x − 5 + 3 Вертикальный сдвиг вверх на 3 единицы
Позаботьтесь о том, чтобы сместить вертикальную асимптоту с оси y на 5 единиц вправо и сместить горизонтальную асимптоту с оси x вверх на 3 единицы.
Ответ:
Попробуй! Нарисуйте график функции g (x) = (x − 2) 2 + 1.
Ответ:
Отражения
Отражение Преобразование, которое создает зеркальное отображение графика вокруг оси. представляет собой преобразование, при котором зеркальное отображение графика создается вокруг оси. В этом разделе мы рассмотрим отражения относительно осей x и y . График функции отражается относительно оси x-, если каждую координату y умножить на -1.График функции отражается относительно оси y , если каждая координата x умножается на -1 перед применением функции. Например, рассмотрим g (x) = — x и h (x) = — x.
Сравните график g и h с базовой функцией квадратного корня, определяемой f (x) = x, показанной ниже серым пунктиром:
Первая функция g имеет отрицательный множитель, который появляется «внутри» функции; это дает отражение относительно оси y . Вторая функция h имеет отрицательный фактор, который появляется «вне» функции; это дает отражение около оси x . В целом верно, что:
Вторая функция h имеет отрицательный фактор, который появляется «вне» функции; это дает отражение около оси x . В целом верно, что:
Отражение относительно оси y : | F (x) = f (−x) |
Отражение относительно оси x : | F (x) = — f (x) |
При рисовании графиков с отражением сначала рассмотрите отражение, а затем примените вертикальный и / или горизонтальный перенос.
Пример 5
Нарисуйте график функции g (x) = — (x + 5) 2 + 3.
Решение:
Начните с функции возведения в квадрат, а затем определите преобразования, начиная с любых отражений.
y = x2 Основная функция. Y = −x2 Отражение относительно оси x. Y = — (x + 5) 2 Сдвиг по горизонтали влево на 5 единиц. Y = — (x + 5) 2 + 3 Сдвиг по вертикали на 3 единицы.
Используйте эти переводы, чтобы нарисовать график.
Ответ:
Попробуй! Нарисуйте график функции g (x) = — | x | +3.
Ответ:
Расстояния
Горизонтальные и вертикальные смещения, а также отражения называются жесткими преобразованиями, потому что форма основного графа остается неизменной или жесткой. Функции, умноженные на действительное число, отличное от 1, в зависимости от действительного числа, кажутся растянутыми по вертикали или по горизонтали. Этот тип нежесткого преобразования называется расширением. Нежесткое преобразование, производимое умножением функций на ненулевое действительное число, которое, кажется, растягивает график либо по вертикали, либо по горизонтали.. Например, мы можем умножить функцию возведения в квадрат f (x) = x2 на 4 и 14, чтобы увидеть, что происходит с графиком.
Нежесткое преобразование, производимое умножением функций на ненулевое действительное число, которое, кажется, растягивает график либо по вертикали, либо по горизонтали.. Например, мы можем умножить функцию возведения в квадрат f (x) = x2 на 4 и 14, чтобы увидеть, что происходит с графиком.
Сравните график g и h с базовой функцией возведения в квадрат, определяемой f (x) = x2, показанной ниже серым пунктиром:
Функция g круче, чем базовая функция возведения в квадрат, и ее график выглядит растянутым по вертикали. Функция h не такая крутая, как базовая функция возведения в квадрат, и кажется, что она растянута по горизонтали.
В общем имеем:
Если множитель a является ненулевой дробью между -1 и 1, он растянет график по горизонтали. В противном случае график будет растянут по вертикали. Если коэффициент a отрицательный, то он также будет производить отражение.
Пример 6
Нарисуйте график функции g (x) = — 2 | x − 5 | −3.
Решение:
Здесь мы начинаем с произведения −2 и основной функции абсолютного значения: y = −2 | x |.Это приводит к отражению и расширению.
xyy = −2 | x | ← Расширение и отражение − 1−2y = −2 | −1 | = −2⋅1 = −200y = −2 | 0 | = −2⋅0 = 01−2y = −2 | 1 | = −2⋅1 = −2
Используйте точки {(−1, −2), (0, 0), (1, −2)}, чтобы построить график функции отражения и расширения y = −2 | x |. Затем переместите этот график на 5 единиц вправо и на 3 единицы вниз.
y = −2 | x | Базовый график с растяжением и отражением относительно оси x. Y = −2 | x − 5 | Сдвиг вправо на 5 единиц. Y = −2 | x − 5 | −3 Сдвиг вниз на 3 единицы.
Ответ:
Таким образом, с учетом положительных вещественных чисел h и k :
Вертикальный сдвиг вверх k единиц: | F (x) = f (x) + k |
Вертикальный сдвиг вниз k единиц: | F (x) = f (x) −k |
Горизонтальный сдвиг влево ч единиц: | F (x) = f (x + h) |
Горизонтальный сдвиг вправо ч единиц: | F (x) = f (x − h) |
Отражение относительно оси y : | F (x) = f (−x) |
Отражение относительно оси x : | F (x) = — f (x) |
Основные выводы
- Идентификация преобразований позволяет нам быстро набросать график функций.
 Этот навык будет полезен по мере нашего прогресса в изучении математики. Часто геометрическое понимание проблемы приводит к более элегантному решению.
Этот навык будет полезен по мере нашего прогресса в изучении математики. Часто геометрическое понимание проблемы приводит к более элегантному решению. - Если к функции добавить положительную константу, f (x) + k, график сдвинется вверх. Если из функции f (x) −k вычесть положительную константу, график сдвинется вниз. Основная форма графика останется прежней.
- Если положительная константа добавляется к значению в области до применения функции, f (x + h), график сдвинется влево.Если положительная константа вычтена из значения в области до применения функции, f (x − h), график сдвинется вправо. Основная форма останется прежней.
- Умножение функции на отрицательную константу -f (x) отражает ее график на оси x . Умножение значений в области на -1 перед применением функции f (-x) отражает график относительно оси y .
- При применении нескольких преобразований сначала примените отражения.
- Умножение функции на константу, отличную от 1, a⋅f (x), приводит к растяжению. Если положительное число константы больше 1, график будет казаться растянутым по вертикали. Если положительная константа является дробной частью меньше 1, график будет казаться растянутым по горизонтали.
Ответы
у = х; Сдвинуть вверх на 3 единицы; домен: ℝ; диапазон: ℝ
у = х2; Сдвинуть вверх на 1 единицу; домен: ℝ; диапазон: [1, ∞)
у = х2; Сдвиг вправо на 5 единиц; домен: ℝ; диапазон: [0, ∞)
у = х2; Сдвиг вправо на 5 единиц и на 2 единицы вверх; домен: ℝ; диапазон: [2, ∞)
у = | х |; Сдвиг влево на 4 единицы; домен: ℝ; диапазон: [0, ∞)
у = | х |; Сдвинуть вправо на 1 единицу и вниз на 3 единицы; домен: ℝ; диапазон: [−3, ∞)
у = х; Сдвинуть вниз на 5 единиц; домен: [0, ∞); диапазон: [−5, ∞)
у = х; Сдвиг вправо на 2 единицы и на 1 единицу вверх; домен: [2, ∞); диапазон: [1, ∞)
у = х3; Сдвиг вправо на 2 единицы; домен: ℝ; диапазон: ℝ
у = х3; Сдвинуть вправо на 1 единицу и вниз на 4 единицы; домен: ℝ; диапазон: ℝ
y = 1x; Сдвиг вправо на 2 единицы; область: (−∞, 2) ∪ (2, ∞); диапазон: (−∞, 0) ∪ (0, ∞)
y = 1x; Сдвинуть вверх на 5 единиц; область: (−∞, 0) ∪ (0, ∞); диапазон: (−∞, 1) ∪ (1, ∞)
y = 1x; Сдвинуть влево на 1 единицу и вниз на 2 единицы; область: (−∞, −1) ∪ (−1, ∞); диапазон: (−∞, −2) ∪ (−2, ∞)
Базовый график y = −4; домен: ℝ; диапазон: {−4}
у = х3; Сдвинуть вверх на 6 единиц и вправо на 2 единицы; домен: ℝ; диапазон: ℝ

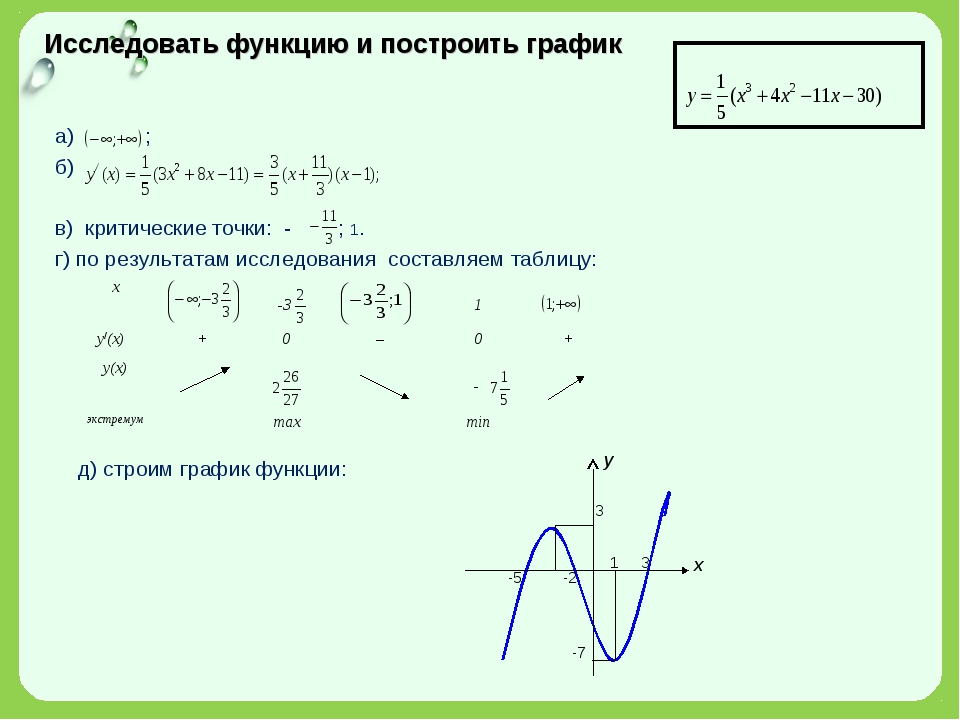 5\)
5\)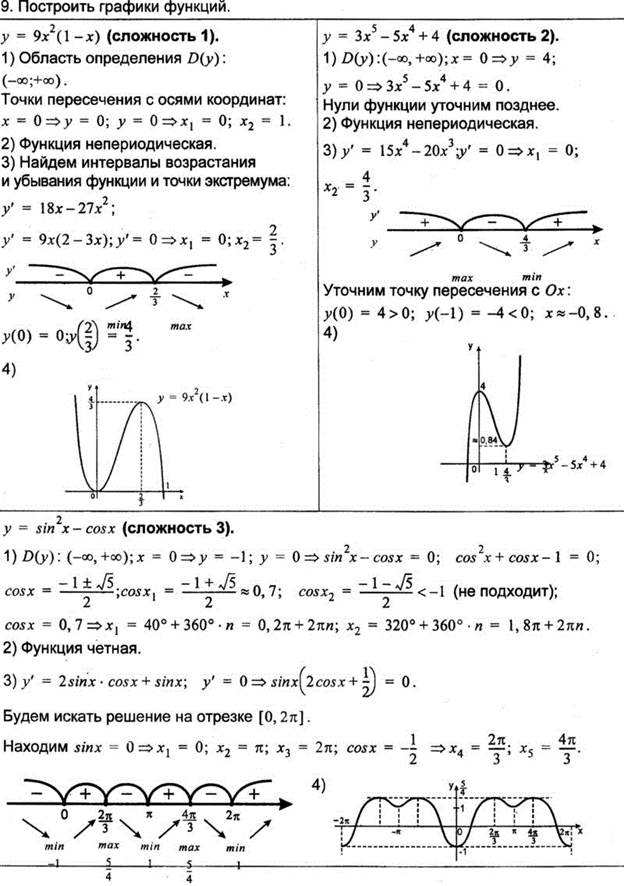


 Вы можете использовать REST API или SDK для доступа к конечной точке и создания приложений, которые поддерживают сценарии Microsoft 365, охватывающие продуктивность, совместную работу, образование, аналитику людей и рабочего места и многое другое. Microsoft Graph также включает мощный набор служб, которые управляют идентификацией пользователей и устройств, доступом, соответствием, безопасностью и помогают защитить организации от утечки или потери данных.
Вы можете использовать REST API или SDK для доступа к конечной точке и создания приложений, которые поддерживают сценарии Microsoft 365, охватывающие продуктивность, совместную работу, образование, аналитику людей и рабочего места и многое другое. Microsoft Graph также включает мощный набор служб, которые управляют идентификацией пользователей и устройств, доступом, соответствием, безопасностью и помогают защитить организации от утечки или потери данных.
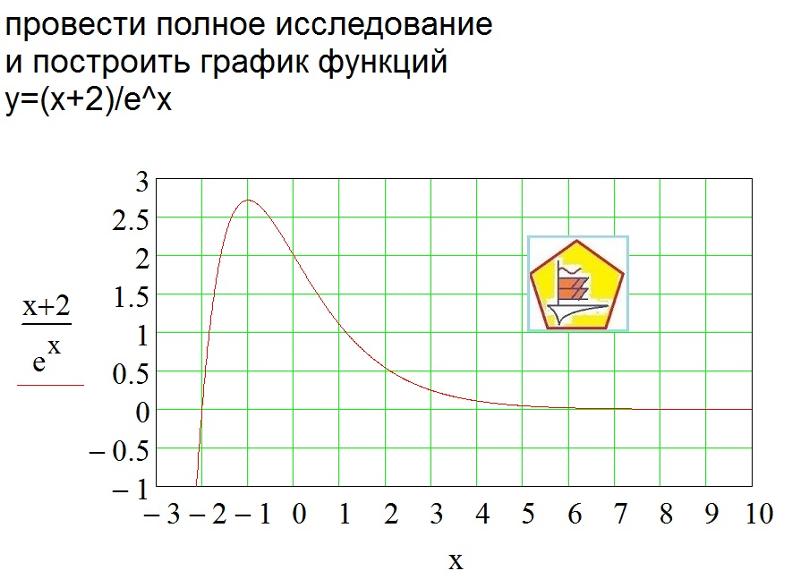
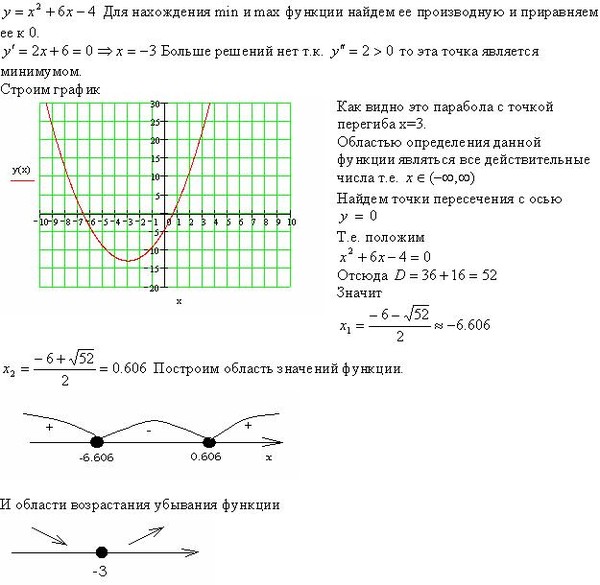 Этот навык будет полезен по мере нашего прогресса в изучении математики. Часто геометрическое понимание проблемы приводит к более элегантному решению.
Этот навык будет полезен по мере нашего прогресса в изучении математики. Часто геометрическое понимание проблемы приводит к более элегантному решению.
Ваш комментарий будет первым