Графики математика: Ошибка: 404 Материал не найден — Магазин Apple iPhone в Перми

Содержание

Наглядная математика. Графики функций.7-11 классы | Zeltix.ru

Наглядная школа

Предметы Математика
Классы 7, 8, 9, 10, 11

Наличие: Есть в наличии

Модель: 4640008173687

Интерактивное учебное пособие разработано с учётом ФГОС и примерной программы по математике основного и среднего общего образования. Материал интерактивного учебного пособия «Наглядная математика. Графики функций» содержит темы учебных курсов по алгебре 7-11 классов.

Пособие можно использовать с любыми учебниками, входящими в Федеральный перечень. В темы включены тестовые контрольные задания, интерактивные упражнения на усвоение теоретического материала и на отработку практических навыков.
В пособии использованы следующие медиаобъекты: аудиолекции, интерактивные модели различных явлений, процессов, интерактивные задания, в том числе с возможностью изменять числовые и графические параметры. Графики функций можно распечатать, создавая рабочую картотеку для индивидуальных работ.
Отличительной особенностью интерактивного учебного пособия «Графики функций» является создание собственной тематической последовательности курса с возможностью включить дополнительные медиаобъекты в структуру самого пособия.
Пособия помогут педагогу организовать работу на уроке с учётом особенностей и возможностей класса.

Содержание:

Линейная функция
Квадратичная функция
Преобразование графика квадратичной функции
Степенная функция
Функция y = sin x
Функция y = cos x
Функции y = tg x, y = ctg x
Обратные тригонометрические функции
Показательная и логарифмическая функции
Графическое и аналитическое задание функций
Преобразование графиков функций
Преобразование графиков тригонометрических функций

Характеристики
Видеокарта с памятью 64 MБ
Дополнительная информация 300 МБ свободного места на жестком диске,Устройство для чтения компакт-дисков,Рекомендуется подключение к интернету для активации программы
ОЗУ 1 Гб
Операционная система Microsoft® Windows® XP и выше Mac OS X : Leopard/Snow Leopard Linux: Ubuntu/Fedora/Suse
Процессор 1 ГГц
Разрешение экрана не менее 1024 Х 768
Рекомендуемые товары
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ — Уральский архитектурно-художественный университет
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ И ТЕХНИЧЕСКОЙ ГРАФИКИ
Зав. кафедрой ТИТОВ Сергей Cергеевич,
профессор, доктор физ.-мат. наук
Тел. (343) 221-29-47, вн. тел. 4281, e-mail [email protected]

Кафедра прикладной математики и технической графики начала функционировать в вузе с момента его создания. Уже тогда было ясно, что традиционная, так называемая высшая, математика не в состоянии удовлетворить потребности современной архитектуры и молодого тогда ещё дизайна. Требовались новые подходы, учёт специфики вуза, ориентация на выпускающие кафедры, на участие в комплексном проектировании, привлечение современного математического инструментария. Для встраивания кафедры математики в общий строй смежных кафедр потребовалось высококвалифицированное и грамотное математическое и компьютерное моделирование.
В 1978 году руководство Свердловского архитектурного института делает нетривиальный ход и приглашает на заведование кафедрой кандидата архитектуры, старшего научного сотрудника, архитектора-практика Николая Максимовича Зубова. Под его руководством сотрудники кафедры занимались анализом архитектурных ситуаций с использованием математических методов, разработкой критериев оптимальности архитектурных композиций по разнообразным параметрам, оценкой их информационной насыщенности. В это время было создано много методических материалов, активно велась научно-исследовательская работа со студентами. Кафедра стала называться кафедрой технических средств архитектурного проектирования и высшей математики. Именно с этого периода математическая кафедра стала всё более превращаться в некую разновидность художественной мастерской, в студию, в мансарду авангардистов (которых не всегда понимают остальные).

В 1986 году кафедра была переименована в кафедру «Прикладной математики и технической графики» (ПМиТГ). Этот период характерен бурным внедрением компьютеров новых поколений и обучением всех сотрудников института началам компьютерных знаний и технологий. С этого времени руководство поручило заведование кафедрой кандидату физико-математических наук Сергею Сергеевичу Титову.

Основным научно-методическим направлением кафедры является разработка новых методов преподавания математики и компьютерных дисциплин применительно к образованию архитекторов и дизайнеров.
Спектр дисциплин, преподаваемых членами кафедры, очень широк. Это и блок традиционных дисциплин, включающий черчение, начертательную геометрию, технический рисунок, математику, и такие курсы как информационные технологии в проектировании, компьютерная графика, компьютерное обеспечение дизайн-проектирования и др. При этом дисциплины традиционного блока читаются с использованием оригинальных, разработанных на кафедре методик.
Программы курсов строятся с учетом специфики нашего вуза. Так, например, изучая редактор AutoCAD, студенты-архитекторы сдают такие контрольные мероприятия как план этажа, малоэтажное здание, интерьер, а студенты специализации «Дизайн одежды» чертят выкройки, ювелиры в редакторе 3D Studio MAX создают настенные украшения, вазы, перстни и т.п. Переходным моментом от второго к третьему курсу служит компьютерная практика, где полученные на данном этапе знания используются не только в учебном, но и в прикладном аспекте: студенты выполняют задания по вводу графической и текстовой информации о реальных объектах.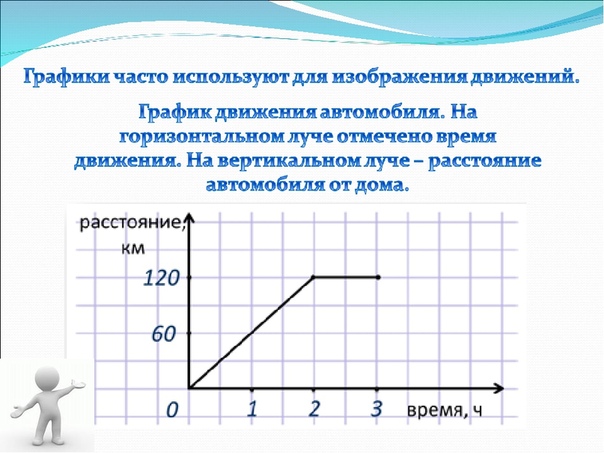
При изучении графического пакета возможен как структурный метод изложения, когда последовательно раскрывается структура пакета и возможности его команд и инструментов, так и подход, основанный на технологии создания графической продукции, или ассоциативный подход.
Проводится поиск новых программных средств, необходимых будущим архитекторам и дизайнерам. Сложность заключается в том, что за пределами имеющихся “модных” компьютерных пакетов остается большая область задач, требующих для своего решения математического моделирования в предпроектном компьютерном анализе архитектурных ситуаций.

Кафедра поддерживает постоянные связи с выпускающими кафедрами и, разрабатывая задания по дисциплинам, ориентируется на курсовое и дипломное проектирование. Так, например, контрольные задания специализации «Графический дизайн» были составной частью курсовых проектов – макетирование страницы, верстка календаря, оформление агитационных плакатов, конверта для пластинки или компакт-диска и др. На специальности «Дизайн одежды» выполняется работа по конфекционированию изделий.
Кафедра прикладной математики и технической графики на протяжении многих лет занималась созданием математических моделей планировочных ситуаций, возникающих при проектировании населенных мест, жилых, общественных и промышленных зданий, и программной реализацией этих моделей, разработан целый комплекс таких моделей, охватывающий широкий спектр планировочных ситуаций, включающий в себя оптимизационные, геометрические, оценочные и комбинаторные алгоритмы, а также алгоритмы численного анализа. Результаты работы отражены в многочисленных публикациях членов кафедры, представлены на ряде Всесоюзных и региональных конференций и семинаров.

Бóльшая часть преподавателей и сотрудников кафедры имеют ученые степени и звания, активно привлекается к работе молодёжь.
Web in Math: Как строить графики функций в Wolfram
Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20
Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5
В двух предыдущих примерах мы задавали область значений аргумента х.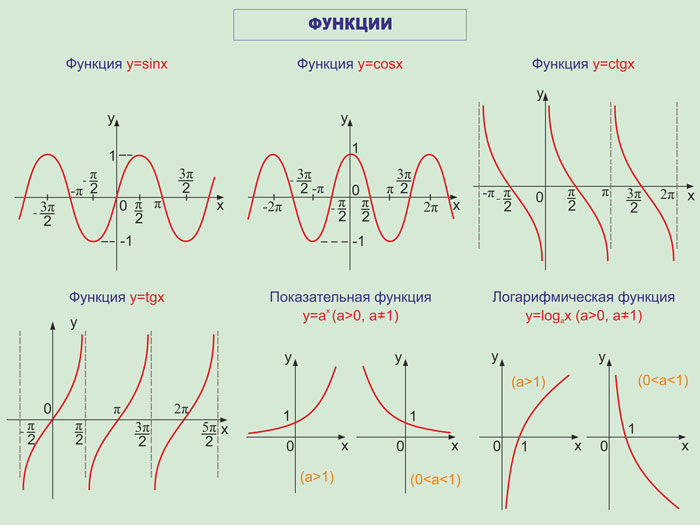 А что будет, если мы не будем задавать область значений х?

Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:
Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.
Сравните:
Кроме того, изображение построенного графика будет крупнее, если вы используете префикс plot.
Одновременно в Wolfram | Alpha можно строить графики нескольких функций.
Если навести мышь на левый нижний угол изображения, то становятся доступными две ссылки: Save as image и Copyable planetext. Рассмотрим такой график:
Первая ссылка Save as image, которая открывается в левом нижнем углу изображения, позволяет сохранить построенный график, как картинку на компьютере пользователя — при нажатии на Save as image автоматически начнется загрузка изображения:

Вторая ссылка Copyable planetext позволяет увидеть код, аналогичный тому, который используется системой Matematica для построения графиков:
Теперь рассмотрим, как в Wolfram | Alpha построить графики функций двух переменных. 2 cos(x) для x от -6 до 6 и y от -2 до 2
Как и в одномерном случае, Wolfram | Alpha автоматически определяет подходящий диапазон значений аргументов, где функция имеет наиболее характерный вид. В случае, если Wolfram | Alpha не может найти подходящий диапазон, то это скорее всего потому, что система не смогла определить такой диапазон, где функция имеет наиболее интересное поведение. В этом случае, мы можем задать диапазон вручную, как это было сделано выше. Посмотрите следующие примеры:

А что, если вы захотите построить одновременно несколько графиков функций двух переменных?
Wolfram | Alpha строит отдельный график для каждой функции в списке. Вот еще несколько примеров:
Новой функцией Wolfram | Alpha является возможность строить графики действительной и мнимой частей комплексно-значных функций двух переменных:
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям). Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.
Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.

Источник by Sam Blake
Больше информации по использованию Wolfram|Alpha вы найдете в блоге
Квадратичная и кубическая функции и их графики 7 класс онлайн-подготовка на Ростелеком Лицей
84. Функции у = х² и у = х³ и их графики
Начнем с функции у = х². Самый простой пример зависимости, которую может выражать эта функция – это зависимость площади квадрата от его стороны.
Построим график этой функции по точкам.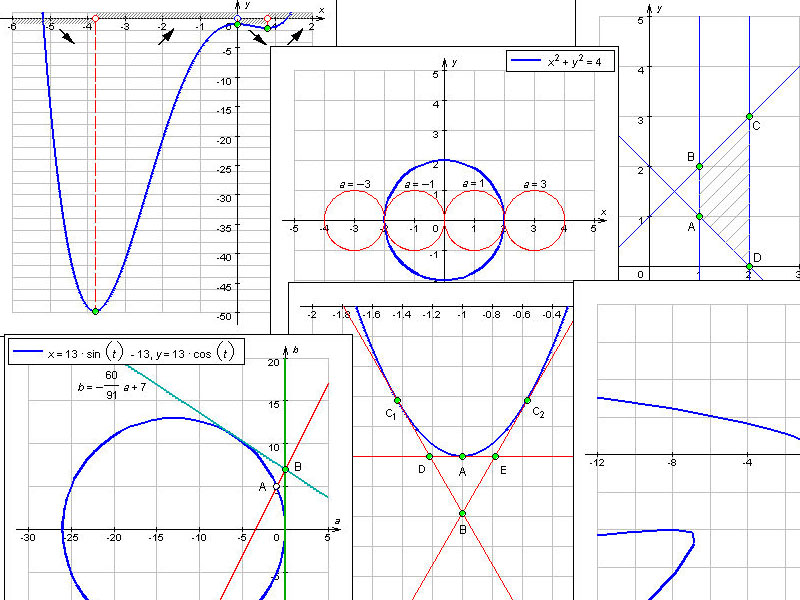

х

-3

-2

-1

0

1

2

3

у

9

4

1

0

1

4

9

Отметим точки на координатной плоскости и соединим их плавной кривой.

Получился график, который называется квадратичная парабола. Исследуем его.
Область определения D(y) = (- ∞;∞).

Область значений Е(у) = [0;∞).

Точки пересечения с осями координат х = 0, у =0²=0. Единственная точка пересечения с осями – (0;0).

Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞).

График функции у=х² симметричен относительно оси у.

Рассмотрим функцию y=x³ Приведите пример зависимости, которую может выражать эта функция. Простой пример такой зависимости – зависимость объема куба от длины ребра.
Построим график функции по точкам.

х

-3

-2

-1

0

1

2

3

у

-27

-8

-1

0

1

8

27

График этой функции тоже называется параболой. Это кубическая парабола.
Исследуем его
Область определения. D(y) = (- ∞;∞).

Область значений Е(у) = (- ∞;∞).

Точка пересечения с осями координат, как и в случае с графиком у=х², одна – (0;0).

График функции возрастает на всей области определения.

При х0 y>0.

График функции симметричен относительно начала координат.

Функции и их графики — математика, уроки
Цель, стоящая перед обучающимися: показать знания, умения и навыки, полученные при изучении предыдущего материала.
Цель, строящая перед педагогом: определить уровень усвоения материала, активизировать деятельность детей, подготовить учащихся к решению заданий из ГИА
Методы: словесный, практический, наглядный, интерактивный метод контроля (письменный: работа по карточкам), устный.
Критерии достижения цели:
— мотивирование на отдаленную перспективу; стимулирование оценкой к дальнейшему достижению поставленной цели
Совместная деятельность: фронтальная работа с классом;
Методы стимулирования учебной активности:
оценочный, убеждение, создание комфортных взаимоотношений, взаимодоверия.
Критерии оценивания ответов:
— оценивание по уровню подготовленности, качества выполненного задания и полноты ответа; активности.
2
Дома вы должны были повторить материал по данной теме, давайте посмотрим ,как вы справились с этим заданием
Фронтальная работа с классом по вопросам
1Так что же такое функция?
2 Что называют областью определения функции?
3 Что называется областью значения функции?
4 Что называется графиком функции?
5 Давайте вспомним все функции, которые мы изучали, формулы их задающие , и их графики.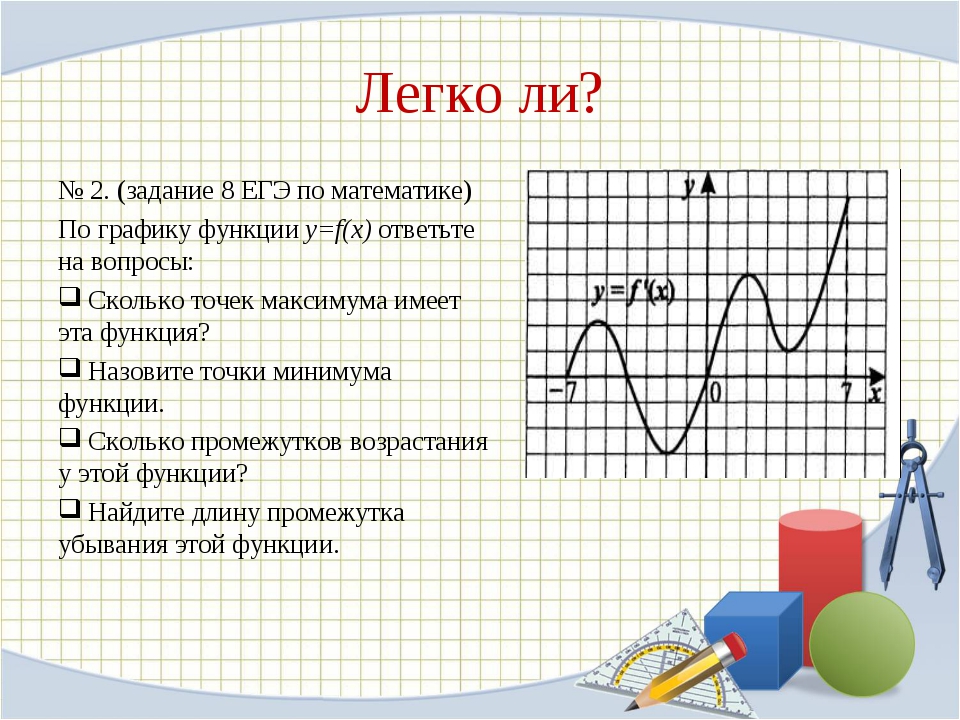
(После того, как дети назовут все функции и формулы показать
Слайд 3
6 Что вы мне можете рассказать об этих функциях, какими свойствами они обладают?
Слайд 4
7 Давайте вспомним преобразование графиков (Работа с презентацией преобразование графиков)
Как из графика функции у =ах² можно получить график функции: У=ах²+п у=а(х –m)²
у=а(х-m)²+п
8 Какой график соответствует функции у = ?
Слайд 5
9 Какой график соответствует функции у=-2(х-2)²+2
Слайд 6
10 Какой график соответствует функции у=|x-2|+2? Слайд 7
11 Какой из формул задается график данных функций? Слайды 8-11
Слайды 12-14
Математика для компьютерной графики
Математика для компьютерной графики
Грег Терк, август 1997 г.
«Какую математику мне нужно изучить, чтобы изучать компьютерную графику?» Это пожалуй, самый частый общий вопрос, который студенты задают мне о компьютере графика. Ответ зависит от того, насколько глубоко вы хотите углубиться в эту область. Если вы хотите начать использовать готовые графические программы, тогда ответ в том, что вам, вероятно, совсем не нужно знать математику. Если хочешь чтобы пройти вводный курс компьютерной графики, тогда вам следует прочитать первые два раздела ниже для моих рекомендаций (алгебра, тригонометрия и линейная алгебра).Если вы хотите когда-нибудь стать исследователем графики то я считаю, что вы должны рассматривать свое математическое образование как непрерывный процесс на протяжении всей вашей карьеры.
Если вы не особо любите математику, есть ли еще шанс работает в поле? Да, некоторые области компьютерной графики не очень озабочен математическими идеями. Не стоит отказываться от графики просто потому, что вы не математический волшебник. Однако вполне вероятно, что вы иметь больше свободы в выборе тем исследования, если у вас есть желание узнать о новых математических идеях.
Нет однозначного ответа на вопрос, какая математика важна в компьютере. графика. Для разных областей в данной области требуются разные математические техники, и ваши собственные интересы, вероятно, приведут вас к некоторым темам и может никогда не трогать других. Ниже приведены описания ряда областей в математика, которую я считаю полезной в компьютерной графике. Не чувствую что вам нужно быть экспертом в каждой из этих областей, чтобы стать графическим Исследователь! Я намеренно включил много областей ниже, чтобы дать достаточно широкий взгляд на математические идеи, используемые в графике.Однако многие исследователи никогда не будет нуждаться в рассмотрении некоторых тем, о которых я упоминаю ниже.
Наконец, хотя это должно быть ясно из прочтения, высказанные мнения в этом документе полностью мои собственные. Вполне вероятно, что вы получите другой список тем или, по крайней мере, разные акценты от других людей кто работает в компьютерной графике. Теперь перейдем к списку тем.
Алгебра и тригонометрия
Алгебра и тригонометрия в старших классах, вероятно, самые важные области, которые нужно знать, чтобы начать изучать компьютерную графику.Просто примерно каждый день мне нужно определить одно или несколько неизвестных из простого набора уравнений. Почти так же часто мне нужно выполнять простую тригонометрию, например определение длины края какой-то геометрической фигуры на основе других длины и углы. Алгебра и тригонометрия — это предметы, которые будут решать такие повседневные задачи в компьютерной графике.
А как насчет геометрии, которую мы изучаем в средней школе? Это может быть сюрприз, но наша школьная геометрия не очень часто нужна большинству задания по компьютерной графике.Причина в том, что геометрия, как она есть во многих школах преподается на самом деле курс построения математических доказательства. Хотя доказательная конструкция определенно является ценным интеллектуалом инструмент, фактические теоремы и доказательства из вашего урока геометрии не часто используется в компьютерной графике. Если вы пойдете в аспирантуру по математике связанной области (включая компьютерную графику), то вы вполне можете оказаться доказательства теорем, но это не обязательно, чтобы начать графика.
Если вы хорошо разбираетесь в алгебре и тригонометрии, то вы вполне готов начать читать вводную книгу по компьютерной графике. Большинство таких книг содержат хотя бы сокращенное введение к следующему Важная область математики для компьютерной графики, а именно линейная алгебра.
Рекомендация книги:
Компьютерная графика: принципы и практика
Джеймс Фоули, Андрис ван Дам, Стивен Файнер, Джон Хьюз
Эддисон-Уэсли
[огромная книга, но все же моя любимая]
Линейная алгебра
Идеи линейной алгебры используются во всей компьютерной графике.По факту, любая область, которая связана с числовыми представлениями геометрии часто собирает вместе числа, такие как позиции x, y, z, в математические объекты, называемые векторами. Векторы и связанные с ними математические объект, называемый матрицей, все время используется в графике. Язык векторов и матриц — это элегантный способ описания (среди прочего) способ, которым объект может быть повернут, сдвинут (сдвинут) или увеличен или меньше (в масштабе). Линейная алгебра обычно предлагается либо в продвинутый класс средней школы или в колледже.Всем, кто желает работать в компьютерная графика должна в конечном итоге получить прочное основание в этом предмете. Однако, как я упоминал ранее, многие учебники по графике дают разумную введение в эту тему — достаточно часто, чтобы пройти первый курс в графике.
Рекомендация книги:
Линейная алгебра и ее приложения
Гилберт Стрэнг
Academic Press
Исчисление
Знание математического анализа — важная часть продвинутой компьютерной графики.Если вы планируете заниматься графикой, я настоятельно рекомендую получить базовый заземление в исчислении. Это верно не только потому, что это коллекция инструментов, которые часто используются в полевых условиях, но также потому, что многие исследователи описывать свои проблемы и решения на языке математического анализа. В Кроме того, ряд важных математических областей требует исчисления как предпосылка. Это единственная область математики в дополнение к базовым алгебра, которая может открыть для вас больше всего дверей в компьютерной графике в терминах вашего будущего математического понимания.
Исчисление — последняя из тем, о которых я упомяну, и которая часто встречается введен в средней школе. Следующие темы почти всегда можно найти в курсы колледжа.
Дифференциальная геометрия
Эта область математики изучает уравнения, управляющие геометрией гладкие кривые и поверхности. Если вы пытаетесь выяснить, в каком направлении перпендикулярна (указывает прямо от) гладкой поверхности ( «нормальный вектор»), то вы используете дифференциальную геометрию. Изготовление автомобиля движение с определенной скоростью по криволинейной траектории также является дифференциальным геометрия.В графике есть обычная техника для создания плавного поверхность кажется шероховатой, известной как «рельефное отображение», и этот метод использует дифференциальная геометрия. Если вы планируете работать с кривыми и поверхностями для создание формы (называемое «моделированием» в графическом поле), тогда вам следует изучить хотя бы основы дифференциальной геометрии. Многопараметрическое исчисление является предпосылкой для этой области.
Рекомендация книги:
Элементарно-дифференциальная геометрия
Барретт О’Нил
Academic Press
Численные методы
Почти каждый раз, когда мы представляем числа и манипулируем ими на используемом нами компьютере приблизительные, а не точные значения, и из-за этого всегда есть возможность появления ошибок.Более того, часто бывает много различные подходы к решению данной численной задачи и некоторые методы будет быстрее, точнее или потребует меньше памяти, чем другие. Учеба из этих проблем имеет ряд названий, включая «численные методы» и «научные вычисления». Это очень обширная область, и некоторые другие области математики, которые я упомяну, могут считаться подобластями под этим зонтиком. Эти подобласти включают теорию выборки, матрицу уравнения, численное решение дифференциальных уравнений и оптимизация.
Рекомендация книги:
Числовые рецепты на языке C: Искусство научных вычислений
Уильям Пресс, Сол Теукольски, Уильям Веттерлинг и Брайан Фланнери
Издательство Кембриджского университета
[это очень ценный справочник, но обычно не используется в качестве учебника]
Теория выборки и обработка сигналов
Снова и снова в компьютерной графике мы представляем какой-то объект, например изображение. или поверхность как набор чисел, которые хранятся в обычном двумерный массив.Каждый раз, когда мы это делаем, мы создаем «выборку» представление объекта. Хорошее понимание теории выборки важно, если мы хотим использовать и контролировать качество таких представления. Распространенная проблема сэмплирования применительно к графике: неровные края, которые могут появиться на силуэте объекта, когда он нарисованный на экране компьютера. Появление таких неровных краев (одна форма явления, известного как «наложение спектров») очень отвлекает, и это может быть сведены к минимуму за счет использования хорошо изученных методов теории выборки.На В основе теории выборки лежат такие концепции, как свертка, фурье преобразование, а также пространственные и частотные представления функций. Эти идеи также важны в области обработки изображений и аудио.
Рекомендация книги:
Преобразование Фурье и его приложения
Рональд Н. Брейсуэлл
McGraw Hill
Матричные уравнения
В компьютерной графике возникает множество проблем. требующие численного решения матричных уравнений.Некоторые проблемы требующие матричные методы включают: поиск лучшей позиции и ориентация для соответствия одного объекта другому (один пример «наименьшего квадратов), создавая поверхность, которая покрывает заданный набор точки с минимальными перегибами (шлицы тонкой пластины) и моделирование такие материалы, как вода или ткань. Приходят матричные постановки задач достаточно часто в графике, что я ставлю эту область очень высоко в моем списке темы, которые нужно знать.
Рекомендация книги:
Матричные вычисления
Джин Голуб и Чарльз Ван Лоан
Издательство Университета Джона Хопкинса
Физика
Очевидно, что физика — это отдельная область изучения, а не подкатегория математики.Тем не менее, физика и математика тесно связаны друг с другом в нескольких областях компьютерной графики. Примеры графических задач, связанных с физикой, включают в себя то, как свет взаимодействует с поверхностями объектов, как свет отражается в сложная среда, движения людей и животных, а также движение вода и ветер. Знание физики важно для моделирования всех эти явления. Это тесно связано с решением дифференциальных уравнений, о котором я расскажу дальше.
Численные решения дифференциальных уравнений
Я считаю, что методы решения дифференциальных уравнений чрезвычайно важна для компьютерной графики. Как мы только что обсуждали, большая часть компьютерная графика предназначена для моделирования физических систем из реальных Мир. Как в воде образуются волны и как животное ходит по земле два примера физического моделирования. Моделирование физических систем очень часто приводит к численному решению дифференциальных уравнений. Примечание что это на самом деле очень отличается от символических решений дифференциальной уравнения. Символические решения — это точные ответы, и обычно их можно найти только для очень простых систем уравнений.Иногда курс колледжа «Дифференциальные уравнения» исследуют только символические решения, и это не сильно поможет при большинстве проблем с компьютерной графикой.
В физическом моделировании мир разбивается на маленькие части, которые представлены в виде больших векторов. Тогда отношения между частями мир фиксируется записями в матрицах. Решение матрицы возникающие уравнения обычно не выполняются точно, а вместо этого выполняются выполнив длинную серию вычислений, которая дает приблизительную решение в виде списка чисел. Вот какие численные решения дифференциальные уравнения о. Отметим, что решение матрицы уравнения является неотъемлемой частью численных решений дифференциальных уравнения.
Оптимизация
Довольно часто в компьютерной графике мы ищем описание объект или набор объектов, удовлетворяющий какой-либо желаемой цели. Примеры включают поиск положений источников света, которые дают определенный «чувствовать», как освещена комната, выясняя, как анимированный персонаж может двигать конечностями, чтобы выполнить определенное действие, а также позиционировать формы и текст на странице, чтобы результат не выглядел загроможденным.Каждый из них примеры можно сформулировать как проблему оптимизации. Десять лет назад было мало в литературе по графике, в которой использовались методы оптимизации, но в последнее время в этой области все больше и больше используется оптимизация. я думаю что оптимизация будет и дальше играть все более важную роль в компьютерная графика.
Вероятность и статистика
В компьютерной графике есть несколько областей, в которых используются вероятность и / или статистика. Конечно, когда исследователи проводят исследования используя человека, им требуются статистические методы для выполнения анализ данных.Области, связанные с графикой, которые часто используют человеческие субъекты включают виртуальную реальность и взаимодействие человека с компьютером (HCI). Кроме того, многие компьютерные описания реального мира включают использование различные вероятности того, что данное действие произойдет. Вероятность того, что ветвь дерева будет ветвиться во время роста или что синтетическое животное решит ходить в определенном направлении — два примера этого. Наконец, некоторые методы решения сложных уравнений используют случайные числа для оцените их решения.Важным примером этого является класс методы, известные как методы Монте-Карло, которые часто используются для определения того, как свет распространяется в окружающей среде. Это всего лишь несколько способов, которыми вероятность и статистика используются в компьютерной графике.
Вычислительная геометрия
Вычислительная геометрия — это изучение эффективных способов представления и манипулировать геометрией внутри компьютера. Типичные проблемы включают тестирование сталкиваются ли два объекта, решая, как разбить многоугольник на треугольников и поиск ближайшей точки в группе к заданному местоположению.Эта область представляет собой смесь алгоритмов, структур данных и математики. Исследователи в области графики, которые работают над созданием фигур (моделированием), много рисуют. на этой территории.
Рекомендации по книгам:
Вычислительная геометрия на языке C
Джозеф О’Рурк
Издательство Кембриджского университета
[текст для студентов]
Вычислительная геометрия: Введение
Франко Препарата и Майкл Шамос
Springer-Verlag
[классический текст, несколько датированный]
Заключительные слова: Прикладная и чистая математика
Одна общая тема для многих математических тем, связанных с графика в том, что они с прикладной стороны, а не с теоретической сторона математики.Это не должно вызывать удивления. Многие из проблемы компьютерной графики тесно связаны с проблемами, которые физики и инженеры изучали, и математический аппарат физика и инженеров — это в подавляющем большинстве инструменты, которые используют исследователи графики. Большинство тем, составляющих теоретическую («чистую») математику, редко применяется в компьютерной графике. Это не следует воспринимать как абсолютное правда, однако. Стоит обратить внимание на примеры из других областей: молекулярная биология теперь использует теорию узлов для изучения ДНК. динамика и субатомная физика используют абстрактную теорию групп.Кто может сказать, когда тема «чистой» математики будет использована в компьютере графика?
Есть несколько областей математики, которые кажутся необходимыми. важны, но никогда не играют большой роли в компьютерной графике. Пожалуй, самая интересная из этих областей — топология. Обычный Описание топологии одним предложением — это исследование того, почему пончик и кофейная чашка такие же. Ответ заключается в том, что это обе поверхности с одним отверстие. Здесь речь идет об идеях из топологии.Разве поверхности не большие часть компьютерной графики? Да, но оказывается, что большинство идей в топологию, полезную для графики, можно изучить на первом курсе в дифференциальная геометрия. Дифференциальная геометрия изучает * формы * поверхности, тогда как топология изучает такие вещи, как то, какие части поверхности рядом с какими другими частями. Я видел очень мало топологий, для использования в графике, и я считаю, что это связано с тем, что большая часть топологии связаны с довольно абстрактными множествами, и что большая часть топологии далека от из концепций трехмерного евклидова пространства, которое так важно для большая часть графики.Бывают случаи, когда формализм топологии ( символическая запись) — удобный способ выразить идеи в графике, но Реальные инструменты абстрактной топологии так редко играют роль в графике. Изучите этот прекрасный предмет ради самого себя, но не ждите немедленного расплата за графику!
Меня несколько раз спрашивали, может ли абстрактная алгебра (теория групп, кольца и т. д.) или теория чисел играют важную роль в компьютерной графике. Немного что я видел. Эти предметы, как и топология, полны красивые идеи.К сожалению, эти идеи редко попадают в компьютерная графика.
Математика для компьютерной графики
Математика для компьютерной графики
Грег Терк, август 2019 г.
Двадцать два года назад я написал эссе о том, для чего важна математика. компьютерная графика. Этот документ теперь довольно устарел, и я решил, что пришло время вернуться к этому вопросу. Я пишу это эссе частично для студенты колледжа, которые хотят знать, какие курсы могут иметь отношение к изучению компьютерная графика.По этой причине отмечу отделы, которые скорее всего предложат курсы по заданной теме. Надеюсь, это очевидно, что вы делаете не нужно быть студентом колледжа, чтобы прочитать это эссе!
Компьютерная графика использует множество различных областей математики для создания инструментов, которые помогают выполнять различные вычислительные задачи. Пока ты хочешь заниматься компьютерная графика, вам также следует запланировать дальнейшее изучение математических техники. В компьютерной графике очень мало уголков, которые не делают использование некоторых форм математики.
Самый важный момент, который я хочу передать в этом эссе, заключается в следующем. Математические темы, которые часто наиболее полезны для графики: так называемые численные методы. Это инструменты, которые принимают абстрактные математические понятия (дифференцирование, интегрирование, обращение матриц и т. д.) и превратить их в конкретные алгоритмы, которые мы можем использовать для поиска числовых результаты к рассматриваемой проблеме. Когда вы впервые узнаете на уроке математики, как дифференцировать и интегрировать, вы начинаете делать это символически.(Для Например, производная синусоидальной функции — косинус.) В графике нам нужно уметь переводить символический ответ на данную проблему в числовой техника, которая может быть реализована на компьютере. По этой причине наиболее часто курсы прикладной математики (не чистой математики), которые относится к графике.
Численные методы, которые полезны для графики, часто одинаковы. инструменты, которые используют разные инженеры. Это означает, что иногда самые полезные курсы графики могут отсутствовать на математическом факультете.Вместо этого они могут быть найдены в других отделах, таких как электротехника или механика инженерное дело.
В этом эссе я собираюсь коснуться четырех основных областей компьютерной графики. Эти области:
Моделирование — создание описания трехмерных форм объектов
Анимация — перемещение объектов
Синтез изображений, также называемый рендерингом — создание изображений из трехмерных фигур
Манипуляции с изображениями и видео
Я собираюсь посетить математику, полезную для графики, в таком порядке, чтобы (приблизительно) соответствует порядку четырех тем, перечисленных выше.Примечание что моделирование и анимация часто используют схожую математику. То же самое верно для другой пары — синтез изображения и манипуляции с изображением / видео часто используют аналогичные математические инструменты. Однако прежде чем перейти к какой-либо из этих тем, я собираюсь начните с математики, необходимой для первого курса графики.
Основы математики: линейная алгебра и тригонометрия
Наиболее важными темами для начала работы с графикой являются линейная алгебра и Тригонометрия. Обычно мы описываем расположение объекта 3D-графики. в соответствии с его координатами x, y и z.Затем мы можем применить следующие операции с 3D-объектом: перемещение (перемещение), масштабирование (изменение размера) и поворот. Перевод и масштабирование выполняются с помощью сложения и умножения, соответственно. Вращение выполняется с использованием синуса и косинуса, поэтому необходимо тригонометрия. Координаты x, y и z объекта могут быть удобно представлен в виде трехмерного вектора, а операции перемещения, масштабирования и поворота могут можно описать как умножение на матрицу (размером 3×3 или 4×4). Это один причин, по которым знания в области линейной алгебры важны для начала графика.Также полезны несколько других концепций линейной алгебры, включая инверсию матрицы, скалярное произведение и перекрестное произведение.
Многопараметрическое исчисление
Многие из наиболее сложных тем в компьютерной графике используют инструменты Многопараметрическое исчисление. Эти темы обычно сохраняются на секунду или треть. курс по математике. Многие из представлений, которые используются в компьютере графика являются функциями нескольких переменных и поэтому требуют инструментов для рассуждения о производных и интегралах таких функций.Если вы хотите учиться компьютерная графика помимо первого курса в этом районе, я настоятельно рекомендую пройти полную последовательность уроков по математике, которые предлагает ваша школа.
Дифференциальная геометрия
Дифференциальная геометрия — это измерение свойств кривых и поверхностей, и эти методы очень важны для моделирования в графике. Общий задачи, связанные с графикой, которые подпадают под эту область, включают определение касательные, измерение кривизны, оценка длины и площади, а также поиск кратчайшие пути.Часто методы дифференциальной геометрии сочетаются с методы оптимизации (подробнее об этом ниже). К счастью, многие математические факультеты предложить бакалавриат по дифференциальной геометрии.
Вычислительная геометрия
Вычислительная геометрия — это изучение алгоритмов, которые эффективно и надежно решать геометрические задачи. Некоторые общие проблемы в этой области включают поиск выпуклые оболочки, поиск ближайших соседей к заданной точке запроса, определение пересечение двух поверхностей и триангуляция многоугольника.Инструменты вычислительная геометрия часто используется как в моделировании, так и в анимации (например, для обнаружения столкновений). Строго говоря, вычислительная геометрия — это раздел теории информатики, а не математики. У вас больше шансов лучше найти курс вычислительной геометрии на факультете информатики чем на математическом факультете.
Числовая линейная алгебра
Единственная тема прикладной математики, которая, пожалуй, самая важная во всем мире. Широкий спектр графических задач — это числовая линейная алгебра.Обычно изучение численных методов линейной алгебры обычно не рассматривается в первый курс линейной алгебры. Проблемы линейной алгебры, возникающие из компьютерная графика часто требует настройки и решения больших линейных систем уравнения, с очень большими матрицами и тысячами или десятками тысяч неизвестные. Вы узнаете простые методы решения матричных уравнений в Первый курс линейной алгебры не подходит для таких задач. Вместо этого вам нужно научиться описывать линейные системы в виде разреженной матрицы (многое другое эффективную память) и узнайте об итерационных методах решения таких системы.Некоторые из этих используемых методов включают методы Якоби, Гаусса-Зейделя и метод сопряженных градиентов. Иногда вы можете столкнуться с другими связанными численные задачи, такие как поиск собственных векторов и собственных значений.
Оптимизация
Многие проблемы как в моделировании, так и в анимации описывают данную задачу как Проблема оптимизации. Допустим, мы хотим создать гладкий объект, который проходит через заданный набор точек. Во-первых, рассматриваемый объект представлен численно, например, набор треугольников, описывающий форму поверхность.Затем мы представляем желаемое качество объекта численно, например, гладкость поверхности. Теперь проблема в том, чтобы найти положения вершин треугольников, которые максимизируют меру гладкости, при прохождении заданного набора точек. Такая минимизация задача описывается как большая линейная система уравнений, а итеративная для решения такой системы используются численные методы.
Уравнения в частных производных
Анимация таких материалов, как вода, резина и снег, требует численных методов. для уравнений с частными производными (PDE).Уравнения, возникающие из эти проблемы включают уравнения диффузии, уравнения переноса, уравнения Лапласа. уравнения и уравнения Пуассона. Их часто можно решить, повернув проблему в большую линейную систему уравнений, или формулируя задачу как одну из ограниченная оптимизация. Вы вряд ли узнаете много нового об этих методы в классе исчисления. Методы решения таких проблем: чаще учился на инженерных курсах и курсах численных методов. А хорошо известный метод решения некоторых из этих проблем известен как Finite Элементный метод (МКЭ).Хотя это далеко не единственный метод решения некоторые из этих проблем, это один из наиболее важных методов, и часто курсы посвящены этому подходу. Мало того, что эти числовые техники, важные для компьютерной анимации, они также часто возникают в 3D проблемы моделирования.
Обыкновенные дифференциальные уравнения
Анимацию персонажей (людей, животных, роботов) часто выполняют представление персонажа в виде набора жестких объектов, которые соединены суставами.Например, руку человека можно описать как предплечье. сегмент, сегмент нижнего плеча и локтевой сустав, соединяющий эти два сегменты. Движение персонажа, описанного таким образом, регулируется численное интегрирование обыкновенных дифференциальных уравнений (ОДУ). Увы, а типичный курс ODE, скорее всего, не даст вам помочь в этом, потому что такие курсы изобилуют символическими решениями, а не численные решения. Курс численных методов гораздо более вероятен. обсудить соответствующие численные методы (прямой Эйлера, метод средней точки, неявная интеграция, Рунге-Кутта и др.)
Обработка сигналов
Многие области синтеза изображений и обработки изображений затрагивают сигнал. обработка. Действительно, эти методы иногда также актуальны для моделирования. а также анимация. Обычно мы представляем изображение в виде 2D-сетки пикселей, где каждому пикселю присвоен цвет. Этот обычный массив значений цвета может быть мыслится как цифровое представление 2D-функции, и это «Сигнал». Мы можем выполнять операции с нашим изображением (сигналом), такие как контраст модификация, размытие, деформация, повышение резкости и т. д.Форма поверхности или движение анимированного персонажа также можно рассматривать как сигнал, сделать эти методы актуальными и для моделирования, и для анимации. Часто лучший способ анализировать и обрабатывать сигналы — преобразовывать их в другой представление с помощью таких инструментов, как преобразование Фурье. Обработка сигналов активно используется при изучении электроники и аудио, поэтому курсы по этой теме часто преподают на электротехническом факультете.
Методы интеграции Монте-Карло
В то время как проблемы с анимацией обычно приводят к дифференциальным уравнениям, те синтеза изображений обычно представляют собой интегральные уравнения.Количество света, которое достигает светочувствительного элемента в камере, или наш глаз — это сумма всех свет идет со всех сторон, и этот свет мог исходить из несколько разных источников света и отражались от множества разных материалы. Такую сумму световых путей можно записать в виде интегрального уравнения. Хотя вы можете узнать об основных квадратурных методах вычисления интегралов в вводный класс исчисления, оказывается, что такие методы не работают для проблем с легким транспортом.Вместо этого случайная выборка множества разных источников света Пути — гораздо лучший путь. Эти методы называются Монте Carlo Methods, и эти методы рандомизации были названы в честь курорта с тем же названием, где игорные заведения — большой бизнес. К сожалению, курсы по Монте-Карло техники довольно редки.
Рост машинного обучения
Если вы изучаете информатику, вы, несомненно, знаете, что область машинного обучения в последнее время стало огромным. (Пишу это в 2019 году.) В в частности, методы глубоких нейронных сетей стали свидетелями взрыва Мероприятия. Вероятно, неудивительно, что глубокое обучение имело большое влияние в компьютерной графике. Нейронные сети используются во многих графических материалах. задачи, в том числе: куда снимать лучи для лучшего расчета освещения, шумоподавление изображений, управление движением виртуальных персонажей, классификация 3D модели, а также для редактирования изображений. Если вы хотите изучать графику, важно чтобы изучить инструменты машинного обучения, и особенно узнать о нейронных сети.Обратите внимание, что машинное обучение тесно связано с математическим темы вероятности и статистики.
В глуши
Некоторые темы математики не так часто используются в графике, как те, которые я упомянули выше. В старой версии этого эссе я сказал, что топология и абстрактная алгебра не использовались для графики. Теперь мне нужно исправить сам.
Топология
Как оказалось, один из моих докторантов, Юджин Чжан, защитил диссертацию. работа в компьютерной графике, в первую очередь из области топологии.Он изучили, как создавать и редактировать векторные и тензорные поля на основе критических точки полей. Анализ связи между этими критическими точками это очень проблема топологии. Его работа — не единственный такой случай, и есть несколько других техник в графике, которые в значительной степени опираются на идеи из топологии.
Абстрактная алгебра
Абстрактная алгебра — это изучение таких объектов, как группы, кольца и поля. Хотя многие из этих математических конструкций не особенно полезны для компьютерной графики, исследователь по имени Кен Турковски указал мне, что Теория групп действительно играет важную роль в графике.Когда мы описываем ориентации 3D-объекта, и когда мы хотим изменить его ориентацию, мы используют теорию групп. Пространство всех трехмерных ориентаций известно как группа SO (3), и оказывается, что это довольно нелогичный математический объект. Исследователи графики использовали несколько различных способов описания элементов. в этой группе и операции над этими элементами, включая матрицы 3×3, кватернионы и экспоненциальные отображения. Описание плавных изменений ориентации часто заставляет исследователей графики изучать SO (3).
Теория чисел
Темой теории чисел является изучение целых чисел, а исследователи в в этой области исследуются такие вопросы, как распределение простых чисел. Как известно, Великая теорема Ферма (теперь решенная!) — это проблема теории чисел. Математик Дж. Х. Харди написал книгу под названием «Математик. Извинение », в котором он описывает красоту чистой математики. Один из Темой его книги является то, что его собственная область знаний, теория чисел, является темой это нужно ценить само по себе.Он продолжает говорить это число теория действительно не имеет практического применения реальные проблемы. Насколько я знаю, теория чисел не особо пригодится в компьютерной графике. Если вы решите изучать теорию чисел, вам следует: сделайте это для красоты темы, а не для какого-либо возможного применения в графика.
% PDF-1.4 % 3 0 obj > эндобдж 4 0 obj > эндобдж 7 0 объект (I Предварительные сведения) эндобдж 8 0 объект > эндобдж 11 0 объект (Обзор математики) эндобдж 12 0 объект > эндобдж 15 0 объект (Предварительные сведения: числа и множества) эндобдж 16 0 объект > эндобдж 19 0 объект (Векторные пространства) эндобдж 20 0 объект > эндобдж 23 0 объект (Определение векторных пространств) эндобдж 24 0 объект > эндобдж 27 0 объект (Диапазон, линейная независимость и основания) эндобдж 28 0 объект > эндобдж 31 0 объект (Наш фокус: Rn) эндобдж 32 0 объект > эндобдж 35 0 объект (Линейность) эндобдж 36 0 объект > эндобдж 39 0 объект (Матрицы) эндобдж 40 0 объект > эндобдж 43 0 объект (Скаляры, векторы и матрицы) эндобдж 44 0 объект > эндобдж 47 0 объект (Проблема модели: A =) эндобдж 48 0 объект > эндобдж 51 0 объект (Нелинейность: дифференциальное исчисление) эндобдж 52 0 объект > эндобдж 55 0 объект (Дифференциация) эндобдж 56 0 объект > эндобдж 59 0 объект (Оптимизация) эндобдж 60 0 объект > эндобдж 63 0 объект (Проблемы) эндобдж 64 0 объект > эндобдж 67 0 объект (Числовой анализ и анализ ошибок) эндобдж 68 0 объект > эндобдж 71 0 объект (Сохранение чисел с дробными частями) эндобдж 72 0 объект > эндобдж 75 0 объект (Представления с фиксированной точкой) эндобдж 76 0 объект > эндобдж 79 0 объект (Представления с плавающей запятой) эндобдж 80 0 объект > эндобдж 83 0 объект (Больше экзотических вариантов) эндобдж 84 0 объект > эндобдж 87 0 объект (Ошибка понимания) эндобдж 88 0 объект > эндобдж 91 0 объект (Ошибка классификации) эндобдж 92 0 объект > эндобдж 95 0 объект (Кондиционирование, стабильность и точность) эндобдж 96 0 объект > эндобдж 99 0 объект (Практические аспекты) эндобдж 100 0 объект > эндобдж 103 0 объект (Пример в крупном масштабе: суммирование) эндобдж 104 0 объект > эндобдж 107 0 объект (Проблемы) эндобдж 108 0 объект > эндобдж 111 0 объект (II линейная алгебра) эндобдж 112 0 объект > эндобдж 115 0 объект (Линейные системы и LU-декомпозиция) эндобдж 116 0 объект > эндобдж 119 0 объект (Разрешимость линейных систем) эндобдж 120 0 объект > эндобдж 123 0 объект (Стратегии специальных решений) эндобдж 124 0 объект > эндобдж 127 0 объект (Операции со строками кодирования) эндобдж 128 0 объект > эндобдж 131 0 объект (Перестановка) эндобдж 132 0 объект > эндобдж 135 0 объект (Масштабирование строки) эндобдж 136 0 объект > эндобдж 139 0 объект (Устранение) эндобдж 140 0 объект > эндобдж 143 0 объект (Исключение Гаусса) эндобдж 144 0 объект > эндобдж 147 0 объект (Форвардная замена) эндобдж 148 0 объект > эндобдж 151 0 объект (Назад Замена) эндобдж 152 0 объект > эндобдж 155 0 объект (Анализ исключения Гаусса) эндобдж 156 0 объект > эндобдж 159 0 объект (Факторизация LU) эндобдж 160 0 объект > эндобдж 163 0 объект (Построение факторизации) эндобдж 164 0 объект > эндобдж 167 0 объект (Реализация LU) эндобдж 168 0 объект > эндобдж 171 0 объект (Проблемы) эндобдж 172 0 объект > эндобдж 175 0 объект (Проектирование и анализ линейных систем) эндобдж 176 0 объект > эндобдж 179 0 объект (Решение квадратных систем) эндобдж 180 0 объект > эндобдж 183 0 объект (Регрессия) эндобдж 184 0 объект > эндобдж 187 0 объект (Наименьших квадратов) эндобдж 188 0 объект > эндобдж 191 0 объект (Дополнительные примеры) эндобдж 192 0 объект > эндобдж 195 0 объект (Специальные свойства линейных систем) эндобдж 196 0 объект > эндобдж 199 0 объект (Положительно определенные матрицы и факторизация Холецкого) эндобдж 200 0 объект > эндобдж 203 0 объект (Редкость) эндобдж 204 0 объект > эндобдж 207 0 объект (Анализ чувствительности) эндобдж 208 0 объект > эндобдж 211 0 объект (Матричные и векторные нормы) эндобдж 212 0 объект > эндобдж 215 0 объект (Номера условий) эндобдж 216 0 объект > эндобдж 219 0 объект (Проблемы) эндобдж 220 0 объект > эндобдж 223 0 объект (Пробелы в столбцах и QR) эндобдж 224 0 объект > эндобдж 227 0 объект (Структура нормальных уравнений) эндобдж 228 0 объект > эндобдж 231 0 объект (Ортогональность) эндобдж 232 0 объект > эндобдж 235 0 объект (Стратегия для неортогональных матриц) эндобдж 236 0 объект > эндобдж 239 0 объект (Ортогонализация по Граму-Шмидту) эндобдж 240 0 объект > эндобдж 243 0 объект (Прогнозы) эндобдж 244 0 объект > эндобдж 247 0 объект (Ортогонализация по Граму-Шмидту) эндобдж 248 0 объект > эндобдж 251 0 объект (Преобразования домохозяев) эндобдж 252 0 объект > эндобдж 255 0 объект (Сниженная факторизация QR) эндобдж 256 0 объект > эндобдж 259 0 объект (Проблемы) эндобдж 260 0 объект > эндобдж 263 0 объект (Собственные векторы) эндобдж 264 0 объект > эндобдж 267 0 объект (Мотивация) эндобдж 268 0 объект > эндобдж 271 0 объект (Статистика) эндобдж 272 0 объект > эндобдж 275 0 объект (Дифференциальные уравнения) эндобдж 276 0 объект > эндобдж 279 0 объект (Спектральное вложение) эндобдж 280 0 объект > эндобдж 283 0 объект (Свойства собственных векторов) эндобдж 284 0 объект > эндобдж 287 0 объект (Симметричные и положительно определенные матрицы) эндобдж 288 0 объект > эндобдж 291 0 объект (Специальные свойства Этот раздел можно пропустить, если у читателей недостаточно знаний, но он включен для полноты.) эндобдж 292 0 объект > эндобдж 295 0 объект (Вычисление собственных значений) эндобдж 296 0 объект > эндобдж 299 0 объект (Итерация мощности) эндобдж 300 0 объект > эндобдж 303 0 объект (Обратная итерация) эндобдж 304 0 объект > эндобдж 307 0 объект (Перемещение) эндобдж 308 0 объект > эндобдж 311 0 объект (Поиск нескольких собственных значений) эндобдж 312 0 объект > эндобдж 315 0 объект (Чувствительность и кондиционирование) эндобдж 316 0 объект > эндобдж 319 0 объект (Проблемы) эндобдж 320 0 объект > эндобдж 323 0 объект (Разложение по сингулярным значениям) эндобдж 324 0 объект > эндобдж 327 0 объект (Получение СВД) эндобдж 328 0 объект > эндобдж 331 0 объект (Расчет СВД) эндобдж 332 0 объект > эндобдж 335 0 объект (Приложения СВД) эндобдж 336 0 объект > эндобдж 339 0 объект (Решение линейных систем и псевдообратной системы) эндобдж 340 0 объект > эндобдж 343 0 объект (Разложение на внешние произведения и приближения низкого ранга) эндобдж 344 0 объект > эндобдж 347 0 объект (Матричные нормы) эндобдж 348 0 объект > эндобдж 351 0 объект (Проблема Procrustes и мировоззрение) эндобдж 352 0 объект > эндобдж 355 0 объект (Анализ основных компонентов \ (PCA \)) эндобдж 356 0 объект > эндобдж 359 0 объект (Проблемы) эндобдж 360 0 объект > эндобдж 363 0 объект (III Нелинейные методы) эндобдж 364 0 объект > эндобдж 367 0 объект (Нелинейные системы) эндобдж 368 0 объект > эндобдж 371 0 объект (Задачи с одной переменной) эндобдж 372 0 объект > эндобдж 375 0 объект (Характеризация проблем) эндобдж 376 0 объект > эндобдж 379 0 объект (Непрерывность и деление пополам) эндобдж 380 0 объект > эндобдж 383 0 объект (Анализ поиска корней) эндобдж 384 0 объект > эндобдж 387 0 объект (Итерация с фиксированной точкой) эндобдж 388 0 объект > эндобдж 391 0 объект (Метод Ньютона) эндобдж 392 0 объект > эндобдж 395 0 объект (Метод секанса) эндобдж 396 0 объект > эндобдж 399 0 объект (Гибридные методы) эндобдж 400 0 объект > эндобдж 403 0 объект (Случай с одной переменной: резюме) эндобдж 404 0 объект > эндобдж 407 0 объект (Проблемы с несколькими переменными) эндобдж 408 0 объект > эндобдж 411 0 объект (Метод Ньютона) эндобдж 412 0 объект > эндобдж 415 0 объект (Делая Ньютон быстрее: Квазиньютон и Бройен) эндобдж 416 0 объект > эндобдж 419 0 объект (Кондиционирование) эндобдж 420 0 объект > эндобдж 423 0 объект (Проблемы) эндобдж 424 0 объект > эндобдж 427 0 объект (Безусловная оптимизация) эндобдж 428 0 объект > эндобдж 431 0 объект (Неограниченная оптимизация: мотивация) эндобдж 432 0 объект > эндобдж 435 0 объект (Оптимальность) эндобдж 436 0 объект > эндобдж 439 0 объект (Дифференциальная оптимальность) эндобдж 440 0 объект > эндобдж 443 0 объект (Оптимальность через свойства функции) эндобдж 444 0 объект > эндобдж 447 0 объект (Одномерные стратегии) эндобдж 448 0 объект > эндобдж 451 0 объект (Метод Ньютона) эндобдж 452 0 объект > эндобдж 455 0 объект (Поиск золотого сечения) эндобдж 456 0 объект > эндобдж 459 0 объект (Многовариантные стратегии) эндобдж 460 0 объект > эндобдж 463 0 объект (Градиентный спуск) эндобдж 464 0 объект > эндобдж 467 0 объект (Метод Ньютона) эндобдж 468 0 объект > эндобдж 471 0 объект (Оптимизация без производных: BFGS) эндобдж 472 0 объект > эндобдж 475 0 объект (Проблемы) эндобдж 476 0 объект > эндобдж 479 0 объект (Ограниченная оптимизация) эндобдж 480 0 объект > эндобдж 483 0 объект (Мотивация) эндобдж 484 0 объект > эндобдж 487 0 объект (Теория ограниченной оптимизации) эндобдж 488 0 объект > эндобдж 491 0 объект (Алгоритмы оптимизации) эндобдж 492 0 объект > эндобдж 495 0 объект (Последовательное квадратичное программирование \ (SQP \)) эндобдж 496 0 объект > эндобдж 499 0 объект (Барьерные методы) эндобдж 500 0 объект > эндобдж 503 0 объект (Выпуклое программирование) эндобдж 504 0 объект > эндобдж 507 0 объект (Проблемы) эндобдж 508 0 объект > эндобдж 511 0 объект (Итерационные линейные решатели) эндобдж 512 0 объект > эндобдж 515 0 объект (Градиентный спуск) эндобдж 516 0 объект > эндобдж 519 0 объект (Получение итерационной схемы) эндобдж 520 0 объект > эндобдж 523 0 объект (Конвергенция) эндобдж 524 0 объект > эндобдж 527 0 объект (Сопряженные градиенты) эндобдж 528 0 объект > эндобдж 531 0 объект (Мотивация) эндобдж 532 0 объект > эндобдж 535 0 объект (Субоптимальность градиентного спуска) эндобдж 536 0 объект > эндобдж 539 0 объект (Создание A-сопряженных направлений) эндобдж 540 0 объект > эндобдж 543 0 объект (Формулировка алгоритма сопряженных градиентов) эндобдж 544 0 объект > эндобдж 547 0 объект (Условия сходимости и остановки) эндобдж 548 0 объект > эндобдж 551 0 объект (Предварительная подготовка) эндобдж 552 0 объект > эндобдж 555 0 объект (CG с предварительной подготовкой) эндобдж 556 0 объект > эндобдж 559 0 объект (Общие предварительные кондиционеры) эндобдж 560 0 объект > эндобдж 563 0 объект (Другие итерационные схемы) эндобдж 564 0 объект > эндобдж 567 0 объект (Проблемы) эндобдж 568 0 объект > эндобдж 571 0 объект (IV Функции, производные и интегралы) эндобдж 572 0 объект > эндобдж 575 0 объект (Интерполяция) эндобдж 576 0 объект > эндобдж 579 0 объект (Интерполяция в одной переменной) эндобдж 580 0 объект > эндобдж 583 0 объект (Полиномиальная интерполяция) эндобдж 584 0 объект > эндобдж 587 0 объект (Альтернативные базы) эндобдж 588 0 объект > эндобдж 591 0 объект (Кусочная интерполяция) эндобдж 592 0 объект > эндобдж 595 0 объект (Гауссовские процессы и кригинг) эндобдж 596 0 объект > эндобдж 599 0 объект (Многопараметрическая интерполяция) эндобдж 600 0 объект > эндобдж 603 0 объект (Теория интерполяции) эндобдж 604 0 объект > эндобдж 607 0 объект (Линейная алгебра функций) эндобдж 608 0 объект > эндобдж 611 0 объект (Аппроксимация кусочно-полиномами) эндобдж 612 0 объект > эндобдж 615 0 объект (Проблемы) эндобдж 616 0 объект > эндобдж 619 0 объект (Численное интегрирование и дифференцирование) эндобдж 620 0 объект > эндобдж 623 0 объект (Мотивация) эндобдж 624 0 объект > эндобдж 627 0 объект (Квадратура) эндобдж 628 0 объект > эндобдж 631 0 объект (Интерполяционная квадратура) эндобдж 632 0 объект > эндобдж 635 0 объект (Квадратурные правила) эндобдж 636 0 объект > эндобдж 639 0 объект (Квадратура Ньютона-Котеса) эндобдж 640 0 объект > эндобдж 643 0 объект (Квадратура Гаусса) эндобдж 644 0 объект > эндобдж 647 0 объект (Адаптивная квадратура) эндобдж 648 0 объект > эндобдж 651 0 объект (Несколько переменных) эндобдж 652 0 объект > эндобдж 655 0 объект (Кондиционирование) эндобдж 656 0 объект > эндобдж 659 0 объект (Дифференциация) эндобдж 660 0 объект > эндобдж 663 0 объект (Дифференциация базовых функций) эндобдж 664 0 объект > эндобдж 667 0 объект (Конечные различия) эндобдж 668 0 объект > эндобдж 671 0 объект (Выбор размера шага) эндобдж 672 0 объект > эндобдж 675 0 объект (Интегрированные количества) эндобдж 676 0 объект > эндобдж 679 0 объект (Проблемы) эндобдж 680 0 объект > эндобдж 683 0 объект (Обыкновенные дифференциальные уравнения) эндобдж 684 0 объект > эндобдж 687 0 объект (Мотивация) эндобдж 688 0 объект > эндобдж 691 0 объект (Теория ODE) эндобдж 692 0 объект > эндобдж 695 0 объект (Основные понятия) эндобдж 696 0 объект > эндобдж 699 0 объект (Существование и Уникальность) эндобдж 700 0 объект > эндобдж 703 0 объект (Модельные уравнения) эндобдж 704 0 объект > эндобдж 707 0 объект (Схемы изменения времени) эндобдж 708 0 объект > эндобдж 711 0 объект (Вперед Эйлер) эндобдж 712 0 объект > эндобдж 715 0 объект (Обратный Эйлер) эндобдж 716 0 объект > эндобдж 719 0 объект (Трапециевидный метод) эндобдж 720 0 объект > эндобдж 723 0 объект (Методы Рунге-Кутты) эндобдж 724 0 объект > эндобдж 727 0 объект (Экспоненциальные интеграторы) эндобдж 728 0 объект > эндобдж 731 0 объект (Многозначные методы) эндобдж 732 0 объект > эндобдж 735 0 объект (Схемы Ньюмарка) эндобдж 736 0 объект > эндобдж 739 0 объект (Сетка в шахматном порядке) эндобдж 740 0 объект > эндобдж 743 0 объект (Делать) эндобдж 744 0 объект > эндобдж 747 0 объект (Проблемы) эндобдж 748 0 объект > эндобдж 751 0 объект (Уравнения в частных производных) эндобдж 752 0 объект > эндобдж 755 0 объект (Мотивация) эндобдж 756 0 объект > эндобдж 759 0 объект (Основные определения) эндобдж 760 0 объект > эндобдж 763 0 объект (Модельные уравнения) эндобдж 764 0 объект > эндобдж 767 0 объект (Эллиптические УЧП) эндобдж 768 0 объект > эндобдж 771 0 объект (Параболические PDE) эндобдж 772 0 объект > эндобдж 775 0 объект (Гиперболические PDE) эндобдж 776 0 объект > эндобдж 779 0 объект (Деривативы как операторы) эндобдж 780 0 объект > эндобдж 783 0 объект (Численное решение УЧП) эндобдж 784 0 объект > эндобдж 787 0 объект (Решение эллиптических уравнений) эндобдж 788 0 объект > эндобдж 791 0 объект (Решение параболических и гиперболических уравнений) эндобдж 792 0 объект > эндобдж 795 0 объект (Метод конечных элементов) эндобдж 796 0 объект > эндобдж 799 0 объект (Примеры на практике) эндобдж 800 0 объект > эндобдж 803 0 объект (Обработка изображений в градиентной области) эндобдж 804 0 объект > эндобдж 807 0 объект (Фильтрация с сохранением границ) эндобдж 808 0 объект > эндобдж 811 0 объект (Жидкости на основе сетки) эндобдж 812 0 объект > эндобдж 815 0 объект (Делать) эндобдж 816 0 объект > эндобдж 819 0 объект (Проблемы) эндобдж 820 0 объект > эндобдж 823 0 объект> поток x څ Q = O0 + nL% blǗ8 # ZRXi] j) EpA: 0 ݗ {w ހ jz UV5 / =
3L;% lc1 * d9 ~ Ҭ @ Ei $ D4G «Cx vJzs: Ȕ6T 帡 L B $ E8% ^ l (9LZKӶMQLBSIde5 CtpІ.ksrQZiz | gO
Математика векторной графики
Это каркасное изображение головы человека является примером файла масштабируемой векторной графики (SVG). Каркасы используются в качестве основы для CGI (компьютерных изображений) в видео. Каркас в основном состоит из треугольников.
Векторное искусство широко используется в кино и игровой индустрии. Он состоит из комбинации основных математических фигур, называемых примитивами , , которые описаны ниже.
(См. Некоторую предысторию этой темы здесь: Vector Art.)
Полигоны
Многоугольник — это многогранная фигура. Самый простой двумерный многоугольник — это треугольник. Вот первые 5 правильных многоугольников (треугольник, квадрат, пятиугольник, шестиугольник, семиугольник).
Конечно, мы могли бы использовать и неправильные многоугольники:
Вышеупомянутая поверхность каркаса в основном состоит из треугольников, но вы также можете найти и неправильные многоугольники.
Круг
Круг также часто используется в векторной графике. Окружность с радиусом r имеет уравнение:
x ² + y ² = r ²
См. «Круг» для получения дополнительной информации.2 = 1`
Для получения дополнительной информации см. Эллипс.
Кривые Безье
Кривые Безье соединяют 2 или более точек плавной кривой. У нас может быть:
а. Линейные кривые Безье
Это просто прямая линия, проходящая через 2 точки.
Ранее мы узнали, что прямые могут быть записаны в виде
`y = mx + b`
(Подробнее о прямых линиях)
Например, мы можем соединить точки `A (1, 4)` и `B (-3, 12)` прямой линией `y = -2x + 6`.
Чтобы получить уравнение этой линии, я использовал формулу
y — y ₁ = м ( x — x ₁)
г. 2 + cx + d`
Решение этих четырех одновременных уравнений для a , b , c , d (с использованием системы компьютерной алгебры) дает мне следующую кубическую кривую, проходящую через 4 точки:
`у = 0.2 + 15.77x-9`
Вот итоговая кривая, проходящая через 4 заданные точки:
Интерактивные графики кривых Безье
В следующем интерактиве вы можете изучить примеры, приведенные для 4 типов кривых Безье, упомянутых выше.
В каждом случае перетащите точек и посмотрите эффект на кривой. (Уравнения отображаются серым цветом при перетаскивании, потому что после изменения кривой уравнение больше не применяется.)
Используя такие кривые, мы создаем векторную графику.
Авторские права © www.intmath.com
Рисование кривых Безье в графической программе
Когда вы используете графическую программу для рисования кривых Безье, она выполняет всю необходимую математику за вас в фоновом режиме.
В примере слева я создал 3 векторные стрелки, которые в данном случае являются кривыми, проходящими через 2 точки. На третьем графике вы можете увидеть, как он выглядит в процессе создания, аналогично четвертой интерактивной кривой выше. Я могу перетащить ручки в любую форму кривой, какую захочу.
Позже я могу отредактировать форму стрелки или размер вектора, и это не будет потери качества. Это очень сложно сделать с растровым изображением — вам нужно будет начать заново и нарисовать все целиком.
7 способов исследовать математику коронавируса с помощью New York Times
Ежедневные новости о коронавирусе наполнены математикой: темпами и данными, диаграммами и графиками, прогнозами и вероятностями. Математическая и статистическая грамотность имеют фундаментальное значение для понимания нашего нынешнего кризиса.Вот семь способов, которыми студенты и учителя могут использовать ресурсы New York Times, чтобы заниматься математикой пандемии Covid-19.
Поиграйте с параметрами.
В чем смысл социального дистанцирования? Когда можно будет безопасно вернуться к нормальной жизни? Используя этот интерактивный журнал Times (прокрутите вниз раздел «Мнение», чтобы найти полную модель), учащиеся могут поиграть с различными параметрами пандемии и изучить последствия государственной политики.
Используя ползунки для изменения, например, уровня вмешательства (например,g., умеренный или агрессивный) или продолжительность вмешательства (например, 14 дней или 60 дней), студенты могут видеть, как меняются результаты. И, играя с моделью, они смогут ответить на такие вопросы, как: «Какое влияние оказывает сокращение периода нашего социального дистанцирования?» или «Что произойдет, если мы откладываем начало нашего вмешательства?»
Студенты также могут использовать этот инструмент, чтобы глубже погрузиться в более сложные задания, например, определить, когда уже слишком поздно начинать легкое вмешательство, изучить, как заразность влияет как на высоту, так и на форму графика, или проанализировать, насколько это более эффективно для вмешательств быть агрессивным или долгим.
Изучите скорость изменения.
В этой статье представлены несколько интересных графиков, отражающих темпы изменения коронавирусных инфекций. «Темпы роста с течением времени» (см. Выше) показывают новые случаи заражения за день в выбранных местах, что позволяет учащимся сравнивать и сравнивать распространение вируса в определенных городах. Студенты также могут решить фундаментальный вопрос исчисления, связав, как график скорости изменения количества соотносится с графиком количества.То есть, что график новых заражений за день говорит нам о графике общего числа заражений?
«Темпы роста по количеству случаев» — это упражнение по повышению грамотности в области данных, поскольку оно отображает новые инфекции в зависимости от количества инфекций на душу населения в зависимости от времени. Что нам говорит этот график? Как мы можем ожидать, что частота новых инфекций изменится по мере увеличения числа инфекций на 1000 человек? Когда дело доходит до «сглаживания кривой», что будет признаком успеха на этом графике?
Каждый раз, когда мы смотрим на данные, касающиеся скорости заражения и передачи, мы должны убедиться, что понимаем истинный характер этих данных.Этот урок об «опасных числах» — это место для начала.
Изучите транспортные сети.
«Как вирус вышел» подробно описывает распространение коронавируса по регионам и миру, и тем самым привносит идеи элементарной теории сетей в анализ распространения вируса. Учащиеся могут рассмотреть роль связности в передаче вируса: сколько трафика существует между различными узлами различных региональных и глобальных сетей, и как этот трафик сочетается с характеристиками вируса, такими как его базовое репродуктивное число и инкубационный период, создать пандемию?
Студенты могут также анализировать эти данные о мобильности из США наряду с показателями заболеваемости Covid-19, заболеванием, вызываемым вирусом, и искать корреляции.Будет ли путь распространения вируса отличаться в местах, где люди много перемещаются, по сравнению с местами, где люди остаются на своих местах?
Сравнить данные.
В связи с отсутствием подробной государственной базы данных о зарегистрированных случаях коронавируса The New York Times создала собственное хранилище данных о коронавирусе. Самый простой способ получить доступ к этим данным — через постоянно обновляемую статью The Times «Коронавирус в США: последняя карта и количество случаев». Там вы можете изучить карту, на которой отмечены случаи заболевания, а также сравнить количество случаев и смертей, зарегистрированных на уровне штата и округа.Вы также можете посетить страницу New York Times на GitHub, чтобы собрать данные по каждому штату и округу в Соединенных Штатах. Где самые высокие показатели заражения? Где самые низкие? Где распространение болезни начинает ускоряться? И каковы основные причины этих чисел?
Учащиеся могут использовать эти данные для отслеживания распространения вируса в своих штатах и округах. Они могут сравнивать и противопоставлять условия в регионах США, делать собственные представления данных и прогнозировать возможное распространение вируса в своем сообществе на основе того, что происходит в других местах.
Определите, какие меры имеют наибольшее значение.
Количество людей, проходящих тестирование на коронавирус, — еще одна возможность проявить статистическую грамотность. Первый график в этой статье дает возможность обсудить разницу между измерением общего количества проведенных тестов и тестов на душу населения. Соединенные Штаты, похоже, впереди по общему количеству тестов, но отстают по количеству тестов на душу населения: что важнее, когда дело доходит до сдерживания распространения коронавируса? Если тестируется слишком мало людей, как это влияет на нашу интерпретацию данных зарегистрированных случаев? В статье также показаны показатели тестирования на душу населения для отдельных штатов, которые учащиеся могут использовать в рамках более широкого анализа данных о Covid-19: как показатели тестирования в вашем штате сравниваются с показателями в других штатах вашего региона? С нацией?
Посмотрите в прошлое.
Пандемия Covid-19 — не первый эпидемиологический кризис, с которым столкнулся мир. В этой статье New York Times публикуются данные и фотографии пандемий гриппа в 1918 и 1968 годах, а также вспышек других инфекционных заболеваний. Студенты могут изучать эпидемии прошлого, а также сравнивать и противопоставлять текущий путь распространения коронавируса. Например, студенты могут посмотреть, как страны пытаются «сгладить кривую» Covid-19, и сравнить эти усилия с аналогичными усилиями во время гриппа в 1918 году (через National Geographic).
Проанализировать экономический эффект.
Укомплектование персоналом | Математика для программистов
Мягкое введение в некоторые из наиболее полезных математических концепций, которые должны быть в вашем наборе инструментов разработчика.
Кристофер Хаупт, New Relic
Заглянуть внутрь
Чтобы получить работу в области науки о данных, машинного обучения, компьютерной графики и криптографии, вам необходимо привнести в команду сильные математические навыки. Математика для программистов обучает математике, необходимой вам для этой жаркой карьеры, концентрируясь на том, что вам нужно знать как разработчику. Эта книга, наполненная большим количеством полезной графики и более 200 упражнений и мини-проектов, открывает дверь к интересной и прибыльной карьере в некоторых из самых популярных на сегодняшний день областях программирования.
о технике
Избегайте математического жаргона: эта единственная в своем роде книга использует Python для обучения математике, необходимой для создания игр, моделирования, трехмерной графики и алгоритмов машинного обучения.Узнайте, как оживают алгебра и исчисление, когда вы видите их в коде!
о книге
В Математика для программистов вы познакомитесь с важными математическими концепциями с помощью практического программирования. Эта книга, наполненная графикой и более чем 200 упражнениями и мини-проектами, открывает путь к интересной и прибыльной карьере в некоторых из самых популярных на сегодняшний день областях. Изучая основы линейной алгебры, исчисления и машинного обучения, вы овладеете ключевыми библиотеками Python, которые используются для превращения их в реальные программные приложения.
что внутри
Векторная геометрия для компьютерной графики
Матрицы и линейные преобразования
Основные понятия из исчисления
Моделирование и оптимизация
Обработка изображений и звука
Алгоритмы машинного обучения для регрессии и классификации
о ридере
Для программистов с базовыми навыками алгебры.
об авторе
Пол Орланд — программист, разработчик программного обеспечения и энтузиаст математики. Он является соучредителем Tachyus, стартапа, создающего программное обеспечение для прогнозной аналитики для энергетической отрасли. Вы можете найти его на сайте www.paulor.land.
БЕСПЛАТНАЯ доставка внутри страны при заказе трех и более печатных книг
Строгий, но доступный обзор математики, лежащей в основе ряда современных областей программирования.
Дэн Шейх, BCG Digital Ventures
Интересный, практичный, рекомендую для всех уровней.
Винсент Чжу, rethinkxsocial.com
Он предоставляет мост для программистов, которым необходимо освежить свои математические навыки, и делает хорошую работу по тому, чтобы сделать математику менее загадочной и более доступной.
Роберт Уолш, Excalibur Solutions
лучших вакансий для математиков | Математика Карьера
Некоторые люди считают диплом по математике специальной степенью, которая может подготовить вас только к работе по исследованию или преподаванию математики.Однако ничто не могло быть дальше от истины. Обладатели математической степени способны освоить ряд уникальных профессий, используя приобретенные навыки, такие как критическое и аналитическое мышление, рациональное принятие решений, а также способность решать сложные проблемы на рабочем месте.
Имея степень математика, можно подготовить человека к ряду профессий. Это включает в себя работу в области самой математики и уникальную карьеру, в которой используются особые навыки, которые развиваются в математике.
Что можно делать со степенью математика?
Математика включает в себя ряд дисциплин, многие из которых имеют практическое применение за пределами чистой математики. Любой, кто специализируется или просто изучает эти навыки в колледже, может продолжить карьеру, которая использует математику на регулярной основе.
В конечном счете, обладатели математической степени не должны чувствовать себя привязанными к карьере только в этой области — хотя это допустимый вариант. Степень математики или время, проведенное в математических классах, могут подготовить человека к работе по широкому кругу профессий, где его знания могут быть применены на практике.
Академия и исследования
Продвинутая математика может найти свое применение в исследованиях и академических кругах в ряде других областей. Алгоритмы становятся все более распространенными в таких областях, как информатика и робототехника, где продвинутая математика необходима для вывода наших знаний на новый уровень. Между тем методы статистического анализа используются во всех видах исследований, от медицинских исследований до обследований общественного транспорта. Практически во всех возможных областях математика имеет важное значение для будущего академических исследований.
Бухгалтерский учет
Математика и бухгалтерский учет — это естественное сочетание. Математические методы необходимы для выполнения основных задач бухгалтерского учета, таких как суммирование расходов или расчет процентов по ссуде. Однако более продвинутая математика также может помочь в разработке бухгалтерских технологий, позволяя бухгалтерам глубже изучать финансовые тенденции и анализировать доступные им необработанные данные.
Космология и воздухоплавание
Когда дело доходит до исследования Вселенной, математика находится в авангарде всех наших усилий.Космологи используют передовую математику для создания моделей межзвездных событий. Это позволяет нам изучать такие вещи, как образование галактик или происхождение Вселенной, которые мы не можем наблюдать напрямую.
Тем временем авиационные инженеры используют математику для создания новых и более эффективных воздушных и космических аппаратов, способных доставлять людей и зонды дальше в космос.
Наука о данных
В век информации данные являются важной частью самых разных областей.Благодаря популярности мобильных телефонов, персональных компьютеров и ноутбуков, а также повсеместному распространению Интернета, собирается и записывается больше данных в большем количестве мест, чем когда-либо прежде. Все, от правительства и военных до рекламодателей и представителей индустрии развлечений, хотят иметь возможность анализировать эти данные для принятия решений и выполнения операций. Люди со степенью в области науки о данных узнают, как разбираться в огромных объемах данных, накапливаемых ежедневно, и как их анализировать. Спектр конкретных вакансий и работодателей в этой области огромен и продолжает расти, поскольку мы находим все более уникальные способы сбора и интерпретации данных.
Образование
Естественно, наличие таланта к общению и страсть к математике может иметь неоценимое значение для обучения будущих поколений. Математика является важным и часто необходимым предметом на всех уровнях образования, от детского сада до аспирантуры, и учащимся любого возраста и происхождения нужны инструкторы, которые помогут им продвинуться и добиться успеха. Математика имеет решающее значение для любого студента, стремящегося к карьере STEM и во многих областях искусства. Всегда есть потребность в преподавателях, которые знакомы с принципами математики и могут объяснять концепции учащимся в увлекательной и увлекательной форме.
Инженерное дело
Во многих отношениях инженерия является основой современного общества. Инженеры несут ответственность за многие вещи, которые мы считаем само собой разумеющимся в нашей повседневной жизни, такие как наши дороги, электрические системы, автомобили и здания. Каждое из этих технологических чудес было смоделировано и протестировано с использованием математики еще до начала строительства, поэтому инженерам необходим высокий уровень знакомства с математикой.
Финансы и банковское дело
Финансовые рынки включают в себя огромное количество транзакций, обрабатываемых через Интернет практически мгновенно.Точные алгоритмы необходимы для обеспечения единообразия всей этой финансовой информации на разных платформах без вмешательства человека. Алгоритмы также могут помочь финансовым специалистам или специалистам в области анализа данных анализировать большие объемы информации, прогнозировать тенденции в финансовом секторе и выявлять рискованные инвестиции.
Здравоохранение
Математика повсюду в отрасли здравоохранения. На самом базовом уровне медицинские работники должны использовать математику каждый день, чтобы оценить жизненно важные признаки пациента или определить правильную дозу конкретного лекарства.Однако в более сложных ситуациях математика и анализ данных помогают врачам анализировать потребности пациентов и оптимизировать способы оказания помощи.
Метеорология
Метеорологи выполняют сложную задачу по предсказанию погодных условий во всем мире. Математические концепции и теория позволяют метеорологам изучать сложные погодные системы, находить закономерности и анализировать погодные явления с точки зрения их отдельных компонентов. Затем метеорологи могут использовать свои математические модели для прогнозирования погодных условий, помогая людям заранее строить планы и даже спасая жизни.
Путешествие
По данным FAA, ежедневно в воздух выполняется более 43 000 рейсов. Математика играет важную роль в построении траектории полета этих самолетов, обеспечивая безопасность в небе для путешественников.
Математика также важна для прогнозирования будущих тенденций в сфере путешествий. Авиакомпании используют эту информацию для расчета цен на билеты на будущие рейсы с учетом таких факторов, как расстояние, расходы на топливо и привычки отдельных пассажиров.
Разнообразные карьеры для математиков
Лица с математическим образованием или другой высшей математической подготовкой могут найти широкое разнообразие профессий, где они смогут применить свои навыки. Ниже вы найдете информацию о некоторых из множества разнообразных карьер, доступных для математических специальностей, например, о любом необходимом дополнительном образовании, математических навыках, которые использовал бы человек в этой карьере, и стандартных зарплатах.
Актуарий
Актуарии пытаются проанализировать различные финансовые риски, которые компания может взять на себя в мире, полном неопределенности.Чтобы хорошо выполнять свою работу, актуарии используют математику для количественной оценки потенциальных преимуществ и недостатков того или иного бизнес-действия. Сводя эти решения к чистым цифрам, актуарии помогают компаниям сделать правильный выбор.
Актуарий требует использования передовых методов статистики и финансового анализа. Кроме того, CareerCast оценил эту работу как вторую лучшую работу — первым был математик.
Требуется образование
актуариям потребуется как минимум степень бакалавра математики или математической области бизнеса, такой как финансы.
Требуются математические навыки
Актуарии должны хорошо разбираться в статистике — области математики, которая занимается измерением риска и вознаграждения в условиях неопределенности.
Заработная плата
актуариев могут рассчитывать на заработок от 81 000 до 136 000 долларов, в зависимости от опыта, местоположения и типа работодателя.
Авиадиспетчер
Авиадиспетчеры несут ответственность за управление мировым небом.Они составляют и выполняют планы полетов самолетов, и их работа необходима для обеспечения безопасного полета тысяч самолетов каждый день. Диспетчеры воздушного движения должны будут иметь возможность выполнять быстрые вычисления, связанные с курсом и скоростью самолета, чтобы гарантировать, что самолеты могут вовремя добраться до места назначения, избегать сложных погодных условий и не мешать другим самолетам.
Требуется образование
Для авиадиспетчеров не требуется строгой степени, хотя степень бакалавра в любой области может помочь удовлетворить требования к работе.Однако авиадиспетчерам необходимо пройти обучение в Академии FAA в Оклахоме, прежде чем они смогут получить сертификат.
Требуются математические навыки
Диспетчеры УВД должны уметь интерпретировать данные в реальном времени о скорости и курсе самолета, чтобы быстро отслеживать и строить планы полета тысяч самолетов каждый день. В то время как большая часть тяжелой работы выполняется компьютером, авиадиспетчеры нуждаются в твердом понимании лежащей в основе математики, а также в динамической способности применять данные для управления загруженными аэропортами и обеспечения безопасности полетов по расписанию.
Заработная плата
В 2018 году средняя зарплата авиадиспетчера составляла 124 540 долларов.
Архитектор
Архитекторы проектируют здания, которые выглядят эстетично и выдерживают собственный вес, поэтому хороший архитектор должен обладать глазом и артистизмом, и математикой. Вам, как архитектору, нужно будет рассчитать вес и несущую способность различных частей здания. Вам также нужно будет использовать точные измерения и углы, чтобы давать четкие инструкции людям, которые в конечном итоге строят на основе ваших планов.
Требуется образование
Хотя степень математики обеспечивает прочную и актуальную основу для карьеры архитектора, будущие архитекторы также должны планировать получение степени бакалавра или магистра архитектуры. Эти программы сосредоточены на эстетических элементах архитектуры, а также учат человека применять соответствующие инженерные и математические навыки.
Требуются математические навыки
Архитекторы должны быть хорошо знакомы с базовой геометрией и тригонометрией, поскольку их работа требует от них построения точных углов и формирования устойчивых форм.Эти математические знания также должны сочетаться с инженерными навыками, связанными с конструкцией здания. Архитекторам также могут потребоваться навыки статистики, чтобы оценить потенциальные затраты клиента на завершение проекта.
Заработная плата
Архитекторы могут рассчитывать на заработок от 58 000 до 107 000 долларов, в зависимости от опыта, местоположения и работодателя.
Астронавт
Астронавты находятся на переднем крае освоения космоса. Известно, что астронавты — это люди, которые действительно могут отправиться в космос на ракетах, шаттлах и экспериментальных космических кораблях.Однако многие люди могут не осознавать, что астронавты также несут ответственность за выполнение множества исследований, пока они находятся в космосе.
Требуется образование
Согласно НАСА, астронавты должны иметь как минимум степень бакалавра в области STEM. Им также потребуется либо три года соответствующего профессионального опыта, либо 1000 часов налета на реактивном самолете в качестве командира воздушного судна.
Требуются математические навыки
Астронавты должны уметь выполнять сложную алгебру, тригонометрию, исчисление и обыкновенные дифференциальные уравнения.Эти математические навыки могут иметь отношение к исследованиям, которые они должны проводить на орбите, или они могут быть необходимы для тонких вычислений в полете, которые астронавты должны выполнять для поддержания орбиты или выполнения маневра входа в атмосферу Земли.
Заработная плата
Заработная плата астронавтов определяется в соответствии с общим графиком оплаты труда федерального правительства. В зависимости от академических достижений, опыта и обязанностей космонавта он может рассчитывать на заработок от 65 140 до 100 701 долларов в год.Астронавты, работающие в частных компаниях по исследованию космоса, могут зарабатывать больше или меньше этой суммы.
Атмосферный ученый / метеоролог
Ученые-атмосферники и метеорологи несут ответственность за измерение и изучение погодных условий на Земле. Их работа вносит свой вклад во множество различных областей и может быть использована всеми, от вашего местного новостного канала до НАСА. Метеорологам потребуется использовать передовую математику для количественной оценки сложных систем, влияющих на погоду.
Требуется образование
Метеорологи могут получить степень бакалавра математики, чтобы получить степень магистра в области атмосферных наук или метеорологии.Метеоролог может начать свою карьеру только со степенью бакалавра, однако более высокая степень часто может открыть больше возможностей для работы.
Требуются математические навыки
Метеорологам потребуется глубокое понимание алгебры, исчисления и тригонометрии для моделирования и прогнозирования погодных систем. Им также потребуются навыки в области статистики, чтобы управлять большими объемами атмосферных данных, с которыми они работают ежедневно.
Заработная плата
Метеорологи и исследователи атмосферы могут рассчитывать зарабатывать от 33 000 до 101 000 долларов в год.Эта сумма будет варьироваться в зависимости от опыта, академической успеваемости и других факторов, влияющих на оплату труда.
Биостатист
Биостатисты несут ответственность за оценку больших объемов биологических данных. Их работа может использоваться в исследованиях в медицине, помогая врачам понять, какие состояния необходимо лечить, и какие методы лечения наиболее эффективны для широких слоев населения.
Требуется образование
Биостатисты часто имеют как минимум степень бакалавра в области математики или связанной с математикой области.Однако для более продвинутых биостатистических работ часто требуется аспирантура.
Требуются математические навыки
Статистика составляет основу работы биостатиста. Если вы хотите стать биостатистом, вы должны хорошо разбираться в методах и методах статистики.
Заработная плата
Биостатисты могут рассчитывать на заработок от 56 000 до 113 000 долларов в год, в зависимости от степени, которую они имеют, опыта работы и вида исследований, которые они проводят.
Картограф
Картографы несут ответственность за создание карт. Обычно они работают с различными организациями, такими как атласы, газеты или даже технологические компании. U.S. News & World Report оценивает картографию как инженерную работу №1. Как картограф, вы должны уметь точно моделировать географию реального мира на картах. Высокая точность и хорошее понимание геометрии — важные навыки для любого картографа.
Требуется образование
Картографы должны иметь как минимум степень бакалавра математики, а также опыт и / или дополнительное образование в области картографии, геологии или гражданского строительства.Приложения для картографии могут быть самыми разнообразными, но все они будут широко использовать математические и географические знания.
Требуются математические навыки
Картографы должны быть очень довольны продвинутыми навыками в геометрии, например, как перенести трехмерную область на двухмерную карту.
Заработная плата
Согласно U.S. News & World Report , картографы могут рассчитывать зарабатывать от 50 000 до 81 000 долларов в год.Средняя зарплата картографов составляет 63 990 долларов.
Компьютерный аниматор
Поскольку компьютеры повсеместно используются в современном мире, существует постоянная потребность в людях, которые могут создавать многие компьютерные системы и контент, которые потребители используют ежедневно. Одно из неожиданных применений математических навыков в области вычислений — работа компьютерным аниматором. Компьютерные аниматоры должны обладать навыками как в художественной части анимации, так и в математике, необходимой для управления компьютерной программой при создании сложной анимации.Как говорит главный ученый Pixar Тони ДеРоуз: «Компьютерная анимация часто связана с моделированием объектов в большем масштабе и с большей детализацией, чем даже физики обычно имеют дело в своих вычислениях».
Требуется образование
Многие компьютерные аниматоры имеют дипломы в области компьютерной анимации. Однако степени по математике и графическому дизайну могут также дать человеку некоторые навыки, необходимые для того, чтобы стать компьютерным аниматором.
Требуются математические навыки
Компьютерные аниматоры должны хорошо разбираться в сложной геометрии, прикладной математике и линейной алгебре.Эти математические навыки можно использовать для преобразования компьютерного кода в яркие и подробные изображения.
Заработная плата
В 2018 году компьютерные аниматоры получали среднюю зарплату 72 520 долларов в год.
Криптоаналитик или криптограф
Криптоаналитики и криптографы — одни из ведущих профессионалов в относительно новой области кибербезопасности. Поскольку потребители и компании все чаще используют Интернет для обмена конфиденциальной информацией, криптографам крайне важно найти новые способы обеспечения безопасности данных.В то же время криптоаналитики работают над расшифровкой опасной информации, которую распространяют преступные организации и террористы. Обе эти задачи основаны на использовании сложных математических алгоритмов для создания и взлома систем безопасности для мировых данных.
Требуется образование
Криптографы и криптоаналитики должны иметь как минимум степень бакалавра в области математики, информатики или другой смежной области. Более высокая степень может открыть новые возможности для более сложной работы в криптографии.
Требуются математические навыки
Ожидается, что криптографы и криптоаналитики будут иметь сильную математическую подготовку и быть уверенными в сложных математических понятиях, таких как абстрактная алгебра, статистика и теория чисел.
Заработная плата
Поскольку криптографы и криптоаналитики выполняют такую важную работу и обладают таким высоким уровнем квалификации, они получают очень высокие зарплаты. Заработная плата криптографа может начинаться от 108000 долларов и достигать 201 500 долларов в год.
Экономист
Экономисты исследуют некоторые важные вопросы, связанные с финансами, поведением потребителей и бизнесом. Чтобы изучить эти вопросы с объективной точки зрения, они часто используют математику для моделирования сложных экономических систем, анализа данных о поведении потребителей и прогнозирования будущего нашей экономики. Экономисты могут работать в компании, составляя экономические прогнозы и помогая компании принимать финансовые решения; государственные, федеральные и местные органы власти, помогающие формировать политику и предоставлять правительственным чиновникам экономический анализ; или университеты, занимающиеся исследованиями в области экономики и обучающими следующему поколению экономистов.
Требуется образование
Многие экономисты имеют степень бакалавра математики, а также политологию или экономику. Однако дальнейшее образование в этой области может подготовить человека к более продвинутой должности в области экономики.
Требуются математические навыки
Экономистам необходимо иметь сильное математическое образование по сравнению с другими специальностями, связанными с бизнесом. Некоторые математические навыки, необходимые для работы, включают статистику, дифференциальные уравнения, исчисление и теорию игр.
Заработная плата
Экономисты могут рассчитывать на прибыль от 44 000 до 132 000 долларов в год. Эта цифра может значительно колебаться в зависимости от области, в которой работает экономист, и уровня полученного образования.
Гейм-дизайнер
Гейм-дизайнеры создают и разрабатывают различные типы игр, включая видеоигры, компьютерные игры, мобильные игры и приложения, а также настольные игры. Существуют независимые игровые дизайнеры, но обычно они нанимают компании развлечений или разработки программного обеспечения.Гейм-дизайнеры могут проектировать персонажей или пейзажи, создавать различные уровни или головоломки в игре или сосредоточиться на написании кода для игры. Игровые дизайнеры с большим опытом могут даже курировать других дизайнеров, управлять проектами или тестировать ранние версии игр.
Требуется образование
Это еще одна область, в которой те, у кого есть математическая степень, будут иметь прочную основу, но, вероятно, им потребуется дополнительная степень или дальнейшее образование для построения карьеры. Помимо изучения математики, большинству гейм-дизайнеров необходимо иметь степень бакалавра в области цифровых медиа, графического дизайна, компьютерной инженерии или информатики.Если гейм-дизайнер имеет степень в области цифровых медиа или графического дизайна, ее необходимо дополнить курсовыми работами, связанными с математикой, информатикой или инженерией.
Требуются математические навыки
Геймдизайнеры должны быть знакомы с теорией игр, информатикой или инженерией. Им также необходимо уметь применять свои теоретические математические знания на практике при разработке компьютерных или видеоигр.
Заработная плата
По данным U.S. Bureau of Labor Statistics (BLS), средняя годовая заработная плата разработчиков программного обеспечения (группа, включающая дизайнеров игр) в 2018 году составила 105 590 долларов в год. Однако средняя годовая заработная плата мультимедийных художников и аниматоров в 2018 году составляла 72 520 долларов. Фактическая оплата будет зависеть от полученной степени и уровня опыта.
Аналитик медицинских данных
Аналитики медицинских данных организуют, управляют, анализируют и интерпретируют большие объемы данных, чтобы предоставлять понимание и информацию поставщикам медицинских услуг и администраторам.Их работа позволяет другим специалистам в области здравоохранения улучшать качество своей помощи, оптимизировать свои операции и сокращать расходы. По сути, аналитики медицинских данных просматривают данные из множества различных источников и интерпретируют их, чтобы другие могли принимать информированные, основанные на данных решения о предоставлении медицинских услуг. Обычно они делятся своими выводами с помощью визуализаций, таких как графики или диаграммы, и отчетов. Аналитики медицинских данных работают со всеми видами организаций здравоохранения, включая местные медицинские центры, фармацевтические компании, больницы, а также правительства штатов и федеральное правительство.
Требуется образование
Аналитикам медицинских данных требуется степень бакалавра в области математики, статистики, биостатистики, науки о данных, управления медицинской информацией или в смежных областях. В зависимости от организации может потребоваться или порекомендоваться дополнительная сертификация или образование.
Требуются математические навыки
Несмотря на то, что математический опыт важен, аналитикам медицинских данных необходимо хорошо разбираться в статистике и хорошо разбираться в ней.Также могут быть полезны дополнительные навыки, связанные с информатикой.
Заработная плата
Аналитики данных здравоохранения могут рассчитывать на заработок от 46 000 до 96 000 долларов в год. Средняя годовая зарплата аналитика медицинских данных составляет 67 377 долларов.
Количественный спортивный трейдер
Специалисты по количественной торговле спортом анализируют спортивный рынок, разрабатывают стратегии ставок и используют их анализ для заключения пари в реальном времени. Они часто нанимаются более крупными организациями и работают с отдельными клиентами, как правило, из компаний в сфере информации, технологий, финансовых услуг и компьютерного программного обеспечения.Спортивные трейдеры должны внимательно следить за выбранным видом спорта, командой и игроками, чтобы составлять коэффициенты, корректировать цены и контролировать ставки.
Требуется образование
Хотя степень может быть необязательна для поиска работы в этой области, большинство трейдеров, занимающихся количественной торговлей спортом, имеют степень бакалавра в области математики, статистики или смежной области STEM.
Требуются математические навыки
Спортивные трейдеры должны хорошо разбираться в продвинутой математике, уделяя особое внимание статистике.Также может потребоваться опыт программирования или знания в области информатики.
Заработная плата
Спортивные трейдеры могут рассчитывать на заработок от 15 500 до 147 500 долларов в год, хотя среднегодовой показатель по стране составляет 59 124 долларов. Факторы, влияющие на компенсацию, включают прибыль, полученную от ставок, опыт и место работы.
Конструктор американских горок
Дизайнеры и инженеры американских горок придумывают дизайн американских горок для производителей и поставщиков.Они должны спланировать каждую часть подстаканника, начиная от курса и заканчивая винтами, с помощью которых можно скрепить отдельные части. Дизайнеры американских горок также должны учитывать, как различные факторы повлияют на горки, и обеспечить их безопасность.
Требуется образование
Дизайнеры американских горок могут начать со степенью математика, а также, вероятно, потребуется степень бакалавра инженерных наук, таких как гражданское, электрическое, электронное, механическое или строительное проектирование. Также может потребоваться дополнительная лицензия, например, Профессиональная инженерная лицензия.Поскольку эта область может быть конкурентоспособной, начинающие дизайнеры американских горок могут захотеть рассмотреть возможность получения либо двойной степени бакалавра, либо степени магистра, либо даже того и другого, хотя это может не быть требованием.
Требуются математические навыки
В большинстве инженерных отраслей большое внимание уделяется математике, в том числе исчислению и статистике. Курсы дизайна, физики и компьютерной инженерии также могут помочь подготовить студентов к карьере дизайнера американских горок.
Заработная плата
Разные инженеры получают разную зарплату.По данным BLS, средняя заработная плата инженеров-строителей в 2018 году составляла 86 640 долларов в год; для инженеров-электриков и электронщиков — 99 070 долларов; а для инженеров-механиков — 87 370 долларов. Заработок может сильно различаться в зависимости от опыта, профессиональной лицензии и работодателя.
Инженер-программист
Инженеры-программисты кодируют, проектируют, разрабатывают, поддерживают, тестируют и оценивают компьютерное программное обеспечение, мобильные приложения и операционные системы. Они либо работают в организации в качестве внутренних сотрудников, либо заключают контракты с внешними организациями, такими как стартапы и компании, занимающиеся разработкой программного обеспечения или технологий.BLS ожидает, что потребность в инженерах-программистах вырастет на 24% с 2016 по 2026 год, и по мере роста спроса и дальнейшего развития технологий могут появиться дополнительные возможности для изучения программной инженерии.
Требуется образование
Инженеры-программисты обычно нуждаются в степени бакалавра в области компьютерных наук, математики, разработки программного обеспечения или в смежных областях. В зависимости от организации также может потребоваться степень магистра в области STEM или смежных областях.
Требуются математические навыки
Для карьеры в области разработки программного обеспечения может потребоваться широкий спектр математических навыков или, по крайней мере, они могут быть полезны.Инженеры-программисты должны быть знакомы с исчислением, конкретной математикой, геометрией, теорией графов, линейной алгеброй, теорией множеств и статистикой.
Заработная плата
Инженеры-программисты могут рассчитывать на заработок от 71 000 до 145 000 долларов в год. В настоящее время средняя заработная плата инженеров-программистов составляет 103 035 долларов в год.
Вам не суждено стать математиком или учителем математики, если вы решите получить степень математика. Бесценные навыки и концепции, полученные в результате изучения математики, подготовят вас к работе в различных областях.Ваши знания могут быть использованы в бесчисленных работах, и вы сможете применить свои математические знания практически в любой профессии, которую выберете.
Рекомендуемая литература
Какие степени бакалавра имеют самый высокий потенциал заработка?
Подготовка к поступлению в аспирантуру: ресурсы и советы
Что делать после окончания колледжа
Источники
AlgebraLab.org, «Карьера авиадиспетчеров»
Американское математическое общество, «Математика и космология»
Хрон.com, «Как использовать математику в карьере в сфере здравоохранения»
Chron.com, «Math Health Careers»
CNN, «Секреты ценообразования авиакомпаний»
EDN, «Математика метеорологии»
FAA.gov, «Воздушное движение в цифрах»
FAA.gov, «Авиационная карьера»
Glassdoor.com, «Заработная плата актуария»
Glassdoor.com, «Заработная плата аналитика данных в области здравоохранения»
Google, «Как работает поиск»
НАСА, «Требования к астронавтам»
Национальная медицинская библиотека, «Статистика медицинских исследований»
PayScale.com, «Заработная плата биостатиста»
PayScale.com, «Заработная плата экономиста»
PayScale.com, «Заработная плата метеоролога»
Бюро статистики труда США, «Архитектура и инженерия»
Бюро статистики труда США, «Мультимедийные художники и аниматоры»
U.

Характеристики
Видеокарта	с памятью 64 MБ
Дополнительная информация	300 МБ свободного места на жестком диске,Устройство для чтения компакт-дисков,Рекомендуется подключение к интернету для активации программы
ОЗУ	1 Гб
Операционная система	Microsoft® Windows® XP и выше Mac OS X : Leopard/Snow Leopard Linux: Ubuntu/Fedora/Suse
Процессор	1 ГГц
Разрешение экрана	не менее 1024 Х 768