Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Алгебра | Координатная плоскость |
Элементарные преобразования графика функции y = f (x ) перечислены в следующей таблице.
| Преобразование | Описание | Рисунок |
y = f (x + c), | В случае c > 0 график функции | |
В случае c < 0 график функции | ||
y = f (x) + c, | В случае c > 0 график функции | |
В случае c < 0 график функции | ||
| y = – f (x) | График функции y = f (x) симметрично отражается относительно оси Ox. | |
| y = f ( – x) | График функции y = f (x) симметрично отражается относительно оси Oy. | |
| В случае k > 1 происходит | |
В случае 0 < k < 1 происходит растяжение графика функции | ||
В случае – 1 < k < 0 происходит растяжение графика функции | ||
В случае k < – 1 происходит | ||
| В случае k > 1 происходит | |
В случае 0 < k < 1 происходит | ||
В случае – 1 < k < 0 происходит | ||
В случае k < – 1 происходит | ||
| y = | f (x)| | Часть графика функции y = f (x), расположенная в области | |
| y = f (| x|) | Ось Oy является осью симметрии Часть графика функции y = f (x), расположенная в области |
| Преобразование y = f (x + c), где c – число | |
В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | | |
В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | | |
| Преобразование y = f (x) + c, где c – число | |
В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | | |
В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | | |
| Преобразование y = – f (x) | |
График функции y = f (x) симметрично отражается относительно оси Ox. | |
| Преобразование y = f ( – x) | |
График функции y = f (x) симметрично отражается относительно оси Oy. | |
| Преобразование y = f (kx), где k – число | |
В случае k > 1 происходит сжатие графика функции | |
В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. | |
В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. | |
В случае k < – 1 происходит сжатие графика функции | |
| Преобразование y = k f (x), где k – число | |
В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. | |
В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. | |
В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. | |
В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. | |
| Преобразование y = | f (x)| | |
Часть графика функции | |
| Преобразование y = f (| x|) | |
Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции | |
| Преобразование y = f (x + c), где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок: |
| Преобразование y = f (x) + c, где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок: |
| Преобразование y = – f (x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок: |
| Преобразование y = f ( – x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок: |
| Преобразование y = f (kx), где k – число |
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок: |
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. Рисунок: |
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
| Преобразование y = k f (x), где k – число |
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок: |
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. Рисунок: |
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
| Преобразование y = | f (x)| |
Описание: Часть графика функции y = f (x), расположенная в области , остаётся на месте. Рисунок: |
| Преобразование y = f (| x|) |
Описание: Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции y = f (x), расположенная в области остаётся на месте. Часть графика функции y = f (| x|), расположенная в области x < 0, получается из части графика, расположенной в области при помощи симметричного отражения относительно оси Oy. Рисунок: |
Примеры элементарных преобразований графика функции y = x2 приведены в следующей таблице.
| Функция | График |
| y = x2 = f (x) | |
y = x2 + 4x + 4 = (x + 2)2 = = f (x + 2) | |
y = x2 – 4x + 4 = (x – 2)2 = = f (x – 2) | |
| y = x2 + 2 = f (x)+ 2 | |
| y = x2 – 2 = f (x) – 2 | |
| y = – x2 = – f (x) | |
| y = 2x2 = 2 f (x) |
Функция: y = x2 = f (x) График: |
Функция: y = x2 + 4x + 4 = График: |
Функция: y = x2 – 4x + 4 = График: |
Функция: y = x2 + 2 = График: |
Функция: y = x2 – 2 = График: |
Функция: y = – x2 = График: |
Функция: y = 2x2 = График: |
Примеры элементарных преобразований графика функции y = x2 – 6 x + 5 приведены в следующей таблице.
| Функция | График |
| y = x2 – 6x + 5 = = f (x) | |
| y = x2 + 6x + 5 = = f (– x) | |
| y = 4x2 – 12x + 5 = = f (2x) | |
| y = | x2 – 6x + 5| = = | f (x)| | |
| y = x2 – 6 | x| + 5 = = f (| x|) |
Функция: y = x2 – 6x + 5 = График: |
Функция: y = x2 + 6x + 5 = График: |
Функция: y = 4x2 – 12x + 5 = График: |
Функция: y = | x2 – 6x + 5| = График: |
Функция: y = x2 – 6 | x| + 5 = График: |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Онлайн калькуляторы и программы для построения графиков функций
Онлайн калькуляторы и программы для построения графиков функций
В статье рассматриваются назначение и особенности
онлайн калькуляторов и программ для построения графиков функций, таких как
линейная, квадратичная, тригонометрическая. Определены основные геометрические
преобразования графиков данных функций и приведены примеры и алгоритмы их
построения с помощью онлайн калькуляторов и программ.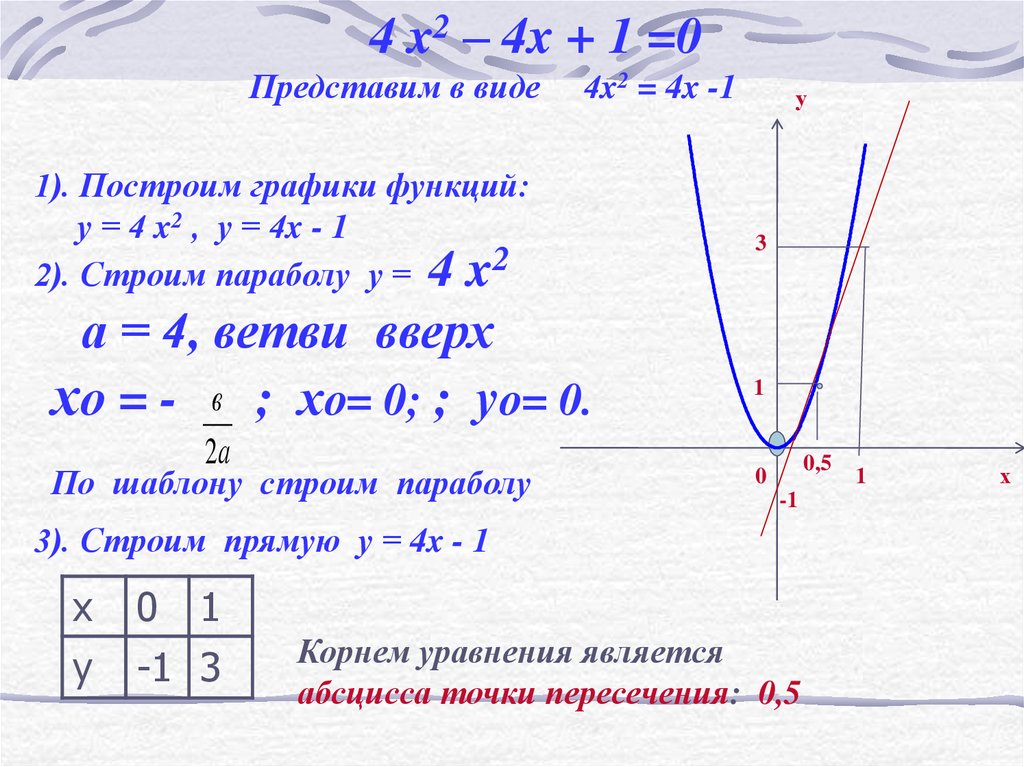
Понятие функции является одним из основных понятий в школьном курсе математики. Изучение функций одной переменной начинается с 7 класса. В рамках школьной программы учащиеся не только знакомятся с понятием функции одной переменной, но и строят графики функций. Существует ряд геометрический преобразований графиков функций, к которым относятся сдвиг, параллельный перенос, сжатие, растяжение. В школьном курсе математики данным преобразованиям уделяется внимание в связи с этим необходимо предлагать разные средства для их изучения. Одним из таких средств являются онлайн калькуляторы и математические программы. Рассмотрим ряд таких средств для проведения геометрических преобразований графиков функций, выделив их преимущества и недостатки.
Онлайн калькулятор, располагающийся по
адресу http://www.webmath.ru/ [3]
имеет следующие особенности: в нем дан список функций и констант для правильного ввода; для построения
графиков функции можно указать интервалы по осям координат; возможно построение
нескольких графиков на одной координатной плоскости; есть возможность изменять
масштаб; имеется удобная сетка, показаны промежуточные значения; есть
возможность посмотреть решения типовых задач; можно строить графики функций,
заданных параметрически; не дает информации об исследовании функции.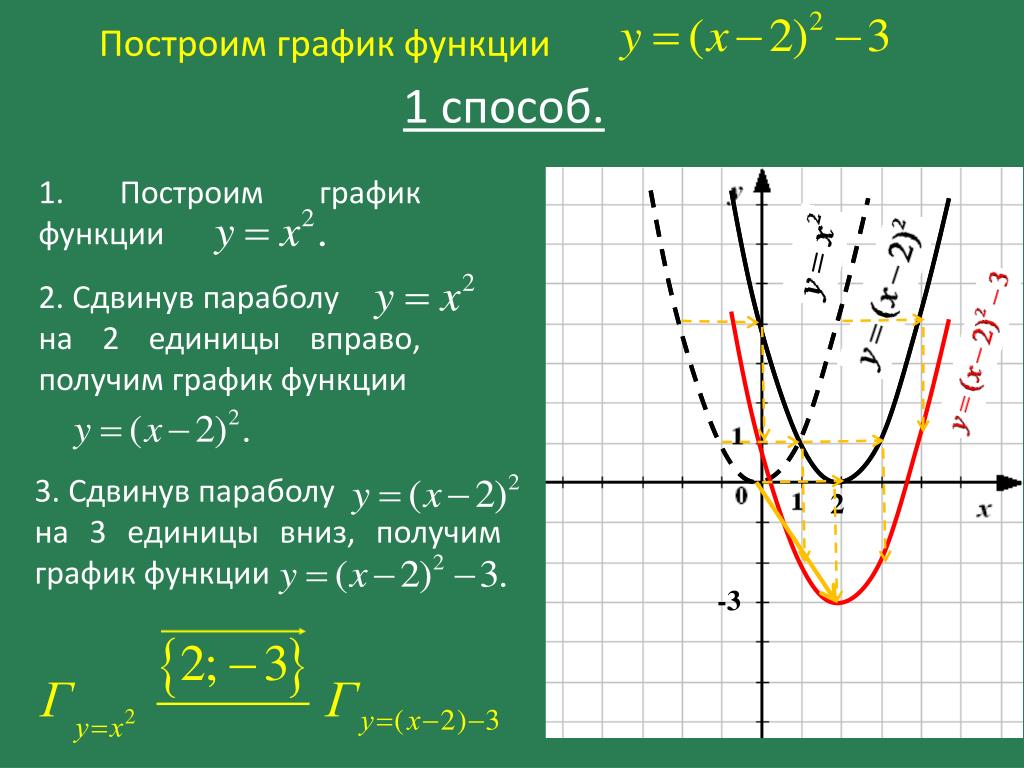
Онлайн калькулятор по адресу http://graph.reshish.ru/ [6] имеет следующие особенности: можно изменять масштаб графика, а так же передвигаться по координатной плоскости для детального изучения поведения графика функции. Представлена удобная сетка для отслеживания точек пересечения, указаны все промежуточные значения, есть возможность построения нескольких графиков функций на одной координатной плоскости.
Простой и удобный интерфейс в онлайн калькуляторе, который находится по адресу http://www.yotx.ru/. [5] В нем приведена справка ввода функций. Он позволяет строить график функции не только заданной аналитически, но и по точкам, в полярной системе координат и заданной параметрически. Добавлены и другие функции, например, можно выбрать цвет графика и интервал, на котором он будет построен. Так же на сайте можно открыть учебник.
При вводе функции на
сайте онлайн калькулятора http://grafikus.ru/ [1] необходимо использовать только простую функцию,
при вводе сложной были выявлены ошибки.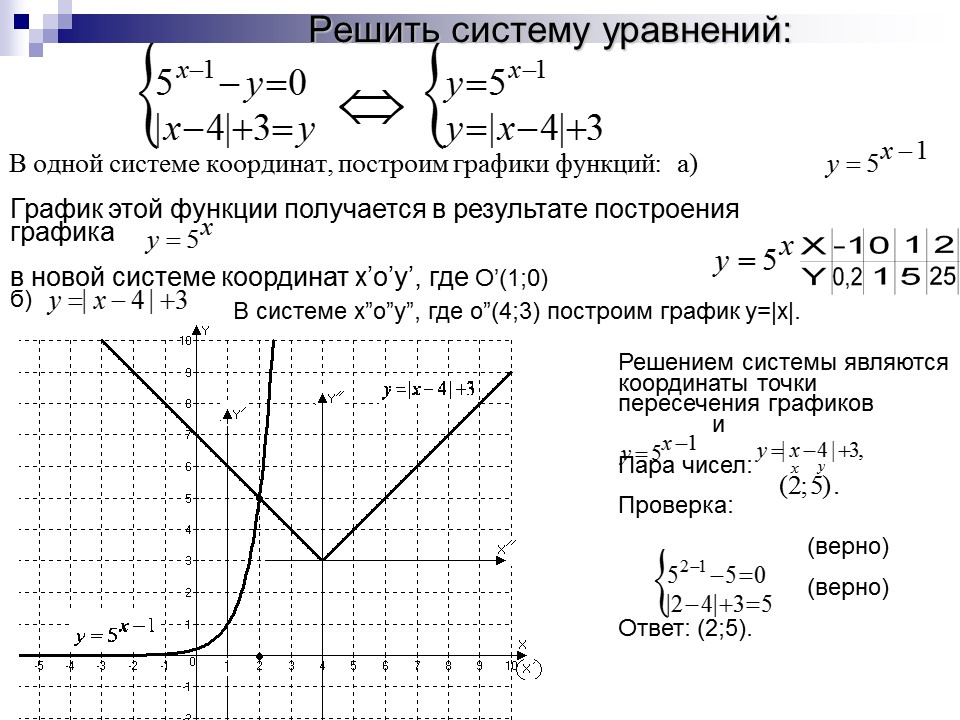
На главной странице другого онлайн калькулятора http://easyto.me/services/graphic/ [2] расположена подробная инструкция, как ввести функцию с таблицей ввода основных видов функций. Перед построением графика функции необходимо выбрать цвет и толщину линий. Координатная плоскость стандартная, позволяет изменять масштаб, двигать курсив по осям координат. Есть возможность построения нескольких графиков на одной плоскости, в таком случае приведена таблица с историей всех ранее построенных графиков.
На сайте онлайн калькулятора http://function-graph.ru/
[7] график строится быстро, после его построения можно менять цвет линий,
интервал осей координат. Есть возможность скачать график в формате рисунка.
Дано подробное описание, как работать с этим онлайн-сервисом, приведена таблица
поддерживаемых функций.
Теперь рассмотрим несколько математических пакетов, работающих в оффлайн-режиме.
Graph. Программа предназначена для построения графиков функций. Поддерживает все известные функции, позволяет выбирать цвет и толщину линий, интервалы. После построения графика можно выделять некоторые его части, сохранять его в виде рисунка, а также копировать в документы с координатной плоскостью. Поддерживает возможность импорта данных из других документов. Выводит координаты необходимых точек, позволяет оставлять комментарии на графиках.
1C Математический конструктор. Программа предлагает решение ряда математических задач: как
алгебраических, так и геометрических. Обратим внимание только на ту часть,
которая позволяет строить графики функций и работать с ними. При построении
графика функции с помощью геометрических преобразований пользователь сам увидит
все этапы его построения на графике и формулы в общем виде рядом с этими
графиками, что является познавательным и интересным.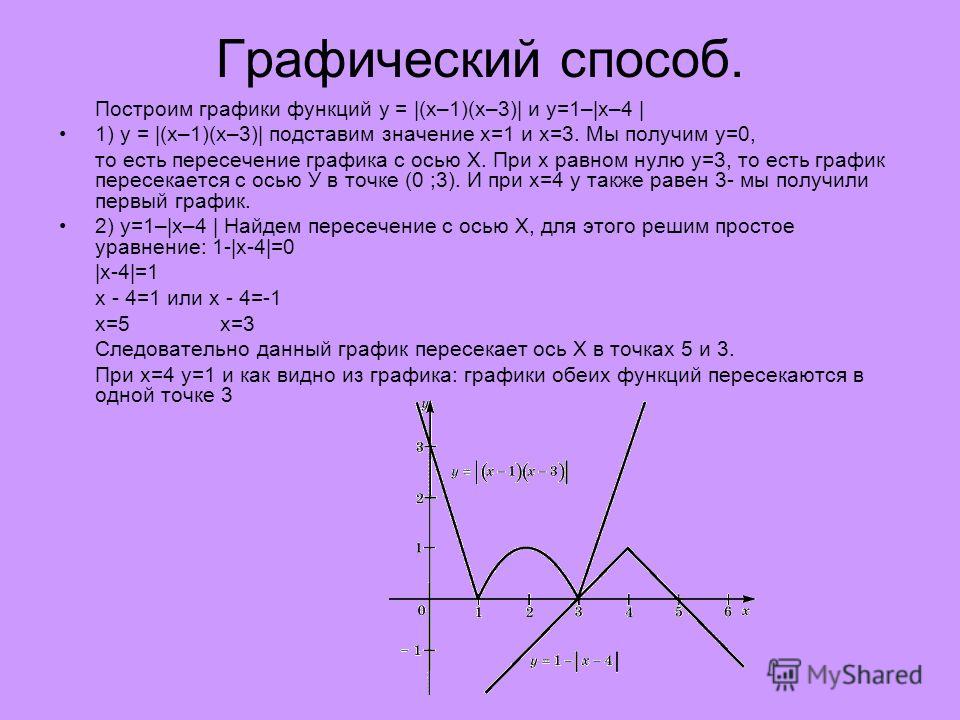
Grapher. Приложение позволяет строить графики различных функций и математических выражений. Есть возможность ввода параметрических графиков функций, а также строить графики функций в полярной системе координат. Программа позволяет строить несколько графиков функций подряд, при этом можно выбрать разные цвета линий. В программе имеется каталог с уже готовыми графиками функций, при этом ведется история ваших построенных графиков. При возникших сложностях можно обратиться с помощью к каталогу с описанием типов графиков и их примерами.
Рассмотрим геометрические преобразования графиков функций, таких как линейная, квадратичная, тригонометрические, и как с помощью этих программ их производить.
Выделяют всего три основных вида геометрических преобразований графиков функций:
1) Растяжение или сжатие.
1.1) Растяжение или сжатие вдоль оси OY.
Общий вид: , k – const, k>0. Алгоритм построения: → при k>0 растягиваем график в k раз вдоль оси ординат, при 0< k<1 сжимаем график в раз вдоль оси ординат.
Например: построим график функции .
Алгоритм построения: → .
Используем для выполнения задания онлайн калькулятор «webmath». Так, как на этом сайте есть возможность строить несколько графиков одновременно, то мы увидим два графика: и (рис.1). Второй график получился путем растяжения исходного вдоль оси OY. Аналогичный алгоритм построения графика функции .
Рис.1. Графики функций , . в онлайн калькуляторе «webmath»
1.2) Растяжение или сжатие вдоль оси OX.
Общий вид , k – const, k>0. Алгоритм построения: → при k>0 сжимаем график в k раз вдоль оси абцисс, при 0< k<1 растягиваем график в раз вдоль оси абцисс.
Пример: построим график функции с помощью онлайн калькулятора «graph.reshish.ru».
Алгоритм построения: →.
Онлайн калькулятор «graph.reshish.ru» также позволяет построить два графика на одной координатной плоскости и (рис.2). Второй график получился путем растяжения исходного вдоль оси OX. Аналогичный алгоритм построения графика функции .
Рис. 2. Графики функций , в онлайн калькуляторе «graph.reshish.ru»
2) Симметричное отображение.
2.1) Симметричное отображение относительно оси OX.
Общий вид . Алгоритм построения: → отображаем график симметрично относительно оси абцисс.
Пример: необходимо построить график функции в онлайн калькуляторе «yotx.ru».
Алгоритм построения: →
В онлайн калькуляторе «yotx.ru» невозможно построить два графика одновременно, поэтому построим сначала график функции (рис.3), а затем выполним преобразование, а именно, построим график функции (рис. 4).
Рис. 3. График функции в онлайн калькуляторе «yotx.ru»
Рис. 4. График функции в онлайн калькуляторе «yotx.ru»
2.2) Симметричное отображение относительно оси OY.
Общий вид . Алгоритм построения: → отображаем график симметрично относительно оси ординат.
Пример: необходимо построить график функции в онлайн калькуляторе «easyto.me/services/graphic».
Алгоритм построения: →
В онлайн калькуляторе «easyto. me/services/graphic» очень легко
построить два графика на одной координатной плоскости, причем при вводе функций
всплывают подсказки.
me/services/graphic» очень легко
построить два графика на одной координатной плоскости, причем при вводе функций
всплывают подсказки.
Рис. 5. Графики функций , в онлайн калькуляторе «easyto.me/services/graphic»
3) Параллельный перенос (сдвиг) вдоль осей координат.
3.1) Параллельный перенос по оси OY.
Общий вид , A-const. Алгоритм построения: → При А>0 поднимаем график на А единиц вверх по оси ординат, при А<0 опускаем график вниз по оси ординат.
Пример: построим график функции при помощи онлайн калькулятора «function-graph.ru».
Алгоритм построения: →
В этом онлайн калькуляторе все графики обновляются самостоятельно. Добавляем построение еще одного графика и вводим две функции. Два графика строятся на одной координатной плоскости (рис. 6).
Рис. 6 Графики функций ,
в онлайн калькуляторе «function-graph.ru»
6 Графики функций ,
в онлайн калькуляторе «function-graph.ru»
3.2) Параллельный перенос по оси OX.
Общий вид , a-const. Алгоритм построения: → При a >0 сдвигаем график на a единиц вправо по оси абцисс, при a <0 сдвигаем график влево по оси абцисс.
Пример: построим график функции c помощью программы Graph.
Алгоритм построения: →
Для построения графиков необходимо на панели задач выбрать Функции →Добавить и ввести необходимую функцию Для наглядности выбираем разный цвет для разных графиков.
В этой программе позволено строить несколько графиков функций на одной координатной плоскости (рис.7).
Рис. 7. Графики функций , в программе Graph
Построим
несколько графиков функций в программе 1С Математический конструктор. Например, , , .
Например, , , .
Выбираем необходимый вид графика на панели команд, вводим заданные константы, благодаря которым происходит сдвиг или симметричное отображение графиков. Формулы в общем виде можно увидеть слева от графиков на рисунке 8.
Рис. 8. Графики функций , , в программе 1С Математический конструктор
Построим график сложной функции с помощью программы Grapher.
Для начала дадим определение сложной функции:
Сложная функция — функция от функции. Если величина y является функцией от u, то есть , а u, в свою очередь, функцией от x, то есть , то является сложной функцией. [4]
Пусть задана функция . Для построения графика в программе необходимо выбрать на панели задач Графики →Добавить и вводим функцию, выбираем цвет и толщину линии. Результат на рисунке 9.
Рис.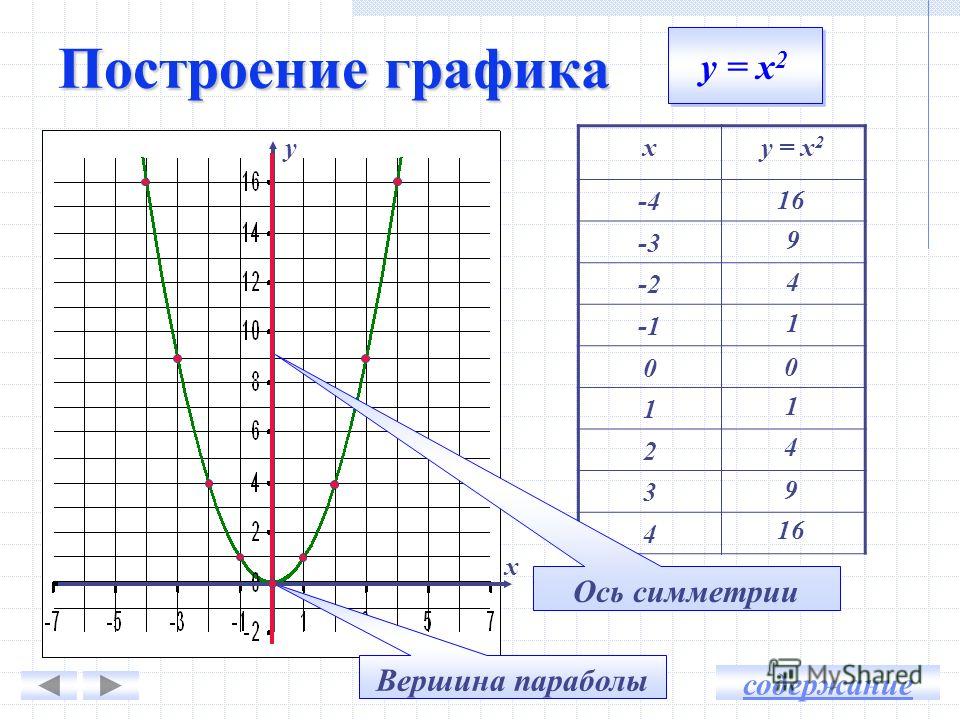 9. График функции в программе Grapher
9. График функции в программе Grapher
Таким образом, был рассмотрен ряд онлайн калькуляторов и программ, с помощью которых можно не только построить графики простых и сложных функций, но и производить различные геометрические преобразования этих графиков. Был проведен анализ этих программ на наличие достоинств и недостатков, а так же выведены алгоритмы построения графиков функций, рассмотрены основные геометрические преобразования, приведены примеры функций, графики которых и были построены в тестируемых программах и онлайн калькуляторах.
В заключении можно отметить, что большинство анализируемых в статье онлайн калькуляторов и программ являются многофункциональными и позволяют не только строить графики сложных функций, но и выполнять геометрические преобразования над ними.
Список используемой литературы
1. Графики
онлайн. Построить график функции [Электронный ресурс] // математический онлайн
калькулятор URL: http://grafikus.ru/ (дата обращения: 07.12.2015)
Графики
онлайн. Построить график функции [Электронный ресурс] // математический онлайн
калькулятор URL: http://grafikus.ru/ (дата обращения: 07.12.2015)
2. Лучший построитель графиков функций [Электронный ресурс] // математический онлайн калькулятор URL: http://easyto.me/services/graphic/ (дата обращения: 07.12.2015)
3. Образовательные онлайн сервисы. Построение графиков функций онлайн [Электронный ресурс] // математический онлайн калькулятор URL: http://www.webmath.ru/web/prog31_1.php (дата обращения: 06.12.2015)
4. Общий толковый словарь русского языка http://tolkslovar.ru/ [Электронный ресурс] // математический онлайн калькулятор URL: (дата обращения: 10.12.2015)
5. Построение графиков функций онлайн [Электронный ресурс] // математический онлайн калькулятор URL: http://www.yotx.ru/ (дата обращения: 06.12.2015)
6.
Построить график функции онлайн [Электронный ресурс] //
математический онлайн калькулятор URL: http://graph.reshish. ru/ (дата обращения:
07.12.2015)
ru/ (дата обращения:
07.12.2015)
7. Построить график функции онлайн [Электронный ресурс] // математический онлайн калькулятор URL: http://function-graph.ru/ (дата обращения: 07.12.2015)
2} = |x|$, поэтому
$$f(x) = x + |x| = \left\{\begin{array}{lr} 2x &: \text{if } x \ge 0 \\ 0 &: \text{if } x < 0 \end{array}\right.$$
В качестве графического онлайн-калькулятора я бы предложил Wolfram Alpha.
$\endgroup$
6
$\begingroup$
Вы можете попробовать Calcpad, это бесплатно как для онлайн, так и для ПК:
http://calcpad.net/Calculator 93 * (x < 0)
Условия в скобках возвращают 1 для «верно» и 0 для «ложно», что позволяет создать выражение, подобное приведенному выше. Он будет правильно вычислять:
f(-2) = 8
f(0) = 0,5
f(2) = -2
Однако он не будет правильно отображаться как одна функция. Вы должны использовать команду «multiple» plot. Он имеет следующий синтаксис:
Вы должны использовать команду «multiple» plot. Он имеет следующий синтаксис:
$Plot{x1 | у1 и х2 | у2 и х3 | y3 @ x = a : b}
Для вашего примера введите следующее… 93*(x < 0) @ x = -1 : 1}
… и вы получите этот график:
График 2
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Домен и диапазон функции
Домен функции функция — это полный набор возможных значений независимой переменной.
После завершения этого урока перейдите к нашему интерактивному калькулятору, который поможет вам найти домен и диапазон функции.
Область определения этой функции `x ≥ −4`, поскольку x не может быть меньше `-4`. Чтобы понять почему, попробуйте ввести в свой калькулятор некоторые числа меньше `-4` (например, `-5` или `-10`) и больше `-4` (например, `-2` или `8`). Единственные, которые «работают» и дают нам ответ, это те, которые больше или равны `-4`. Это сделает число под квадратным корнем положительным.
В общем, мы определяем домен каждой функции, ища те значения независимой переменной (обычно x ), которые нам разрешено использовать. (Обычно мы должны избегать 0 внизу дроби или отрицательных значений под знаком квадратного корня).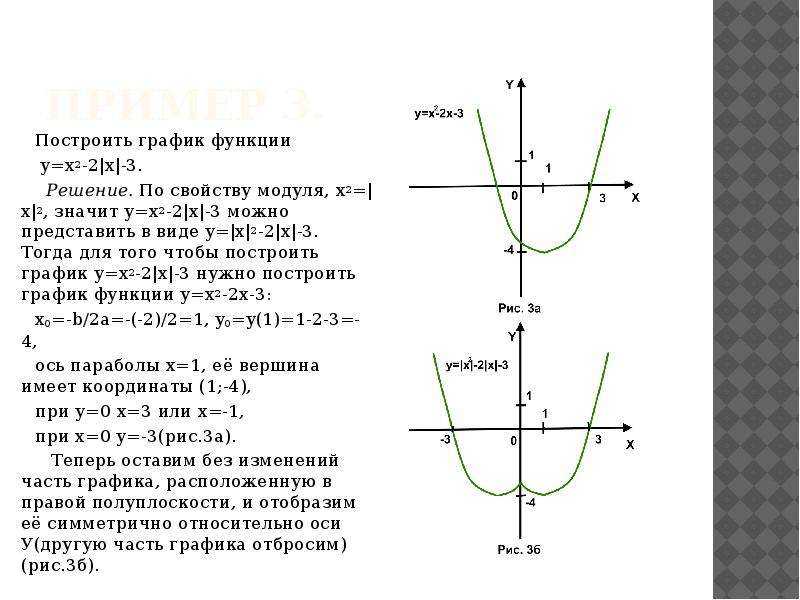
Серия функция – это полный набор всех возможных результирующих значения зависимой переменной ( y, обычно ), после того как мы подставили домен.
Мы замечаем, что кривая находится либо на горизонтальной оси, либо выше нее. Независимо от того, какое значение x мы попробуем, мы всегда получим нулевое или положительное значение y . Мы говорим, что диапазон в этом случае равен y ≥ 0.
Кривая всегда продолжается вертикально, за пределами того, что показано на графике, поэтому диапазон представляет собой все неотрицательные значения `y`.
12345-1-2-3-4-5-6-71-1xyДиапазон: `-1
Домен из y = sin x — это «все значения x », поскольку ограничений на значения для x нет. (Поместите любое число в функцию «sin» вашего калькулятора. Любое число должно работать, и вы получите окончательный ответ в диапазоне от −1 до 1. )
)
Из эксперимента с калькулятором и наблюдения за кривой мы можем увидеть диапазон равен y между -1 и 1. Мы могли бы записать это как -1 ≤ y ≤ 1.
Откуда взялся этот график? Мы узнаем о графиках sin и cos позже в разделе Графики sin x и cos x
Примечание 1: Поскольку мы предполагаем, что для значений x должны использоваться только действительные числа, приводят к делению на ноль или к мнимые числа (возникающие при нахождении квадратного корня из отрицательного числа) не включаются. В главе «Комплексные числа» рассказывается больше о мнимых числах, но мы не включаем такие числа в эту главу.
Примечание 2: При выполнении примеров с квадратным корнем многие люди спрашивают: «Разве мы не получаем 2 ответа, один положительный и один отрицательный, когда находим квадратный корень?» Квадратный корень имеет не более одного значения, а не двух. См. это обсуждение: Квадратный корень 16 — сколько ответов?
См. это обсуждение: Квадратный корень 16 — сколько ответов?
Примечание 3: Мы говорим о домене и диапазоне функций , которые имеют не более одно y -значение для каждого x -значения, а не отношения (которые могут иметь более один.).
Поиск домена и диапазона без использования графика
Всегда намного проще определить домен и диапазон, читая его с графика (но мы должны убедиться, что мы увеличиваем и уменьшаем масштаб графика, чтобы убедиться, что мы видим все нам нужно посмотреть). Тем не менее, у нас не всегда есть доступ к программному обеспечению для построения графиков, а набросок графика обычно требует в первую очередь знания о разрывах и так далее.
Как упоминалось ранее, необходимо проверить следующее:
- Нет отрицательных значений под знаком квадратного корня 92-9`, который, как мы узнаем, можно записать как `(x+3)(x-3)`. Таким образом, наши значения для «x» не могут включать «-3» (из первой скобки) или «3» (из второй).

В любом случае нам не нужно беспокоиться о `-3`, потому что мы решили на первом шаге, что `x >= -2`.
Таким образом, домен для этого случая равен `x >= -2, x != 3`, который мы можем записать как `[-2,3)uu(3,oo)`.
Чтобы определить диапазон, мы рассматриваем верх и низ дроби отдельно.
Числитель: 92-9)` приближается к `0`, так что `f(x)` перейдет к `-oo` по мере приближения к `x=3`.
Для `x>3`, когда `x` чуть больше, чем `3`, значение основания чуть больше `0`, поэтому `f(x)` будет очень большим положительным числом.
Для очень больших `x` верхняя часть велика, но нижняя часть будет намного больше, поэтому в целом значение функции будет очень маленьким.
Таким образом, мы можем заключить, что диапазон равен `(-oo,0]uu(oo,0)`.
Взгляните на график (который мы все равно рисуем, чтобы убедиться, что мы на правильном пути): 92-9)`.
Сводка
В общем, мы определяем домен по ищем те значения независимой переменной (обычно x ), которые мы разрешили использовать .
 (Мы должны избегать 0 внизу дроби или отрицательных значений под знаком квадратного корня).
(Мы должны избегать 0 внизу дроби или отрицательных значений под знаком квадратного корня).Диапазон находится путем нахождения результирующих значений y после подстановки возможных значений x .
Упражнение 1 92+ 2`.
Ответ
Домен: Функция
ф ( х ) = х 2 + 2
определяется для всех реальных значений x (поскольку нет ограничений на значение x ).
Следовательно, домен `f(x)` равен
«все реальные значения x «.
Диапазон: Начиная с x 2 никогда не бывает отрицательным, x 2 + 2 никогда не меньше `2`
Следовательно, диапазон `f(x)` равен
«все действительные числа `f(x) ≥ 2`».
Мы видим, что x может принимать любое значение на графике, но результирующие значения y = f ( x ) больше или равны 2.
123-1-2-312345678910- 1xf(x)
Диапазон: `y>=2`
Домен: Все `x`
Примечание
- Важно маркировать оси при построении графиков. Это помогает понять, что представляет собой график.
- Мы видели, как рисовать такие графики в Графике функции.
Нужна миллиметровка?
Значок миллиметровкиСкачать миллиметровку
(b) `f(t)=1/(t+2)`
Ответ
Домен: Функция
`f(t)=1/(t+2)`
не определен для т = -2, так как это значение приведет к делению на ноль. (Внизу дроби будет 0.)
Следовательно, домен из f ( t ) равен
«все действительные числа кроме -2»
Диапазон: Независимо от того, насколько большим или маленьким станет t , f ( t ) никогда не будет равно нулю.

[ Почему? Если мы попытаемся решить уравнение относительно 0, произойдет следующее:
`0=1/(t+2)`
Умножаем обе части на ( t + 2) и получаем
`0 = 1`
Это невозможно.]
Итак, диапазон из f ( t ) равен
«все действительные числа, кроме нуля».
На графике видно, что функция не определена для `t = -2` и что функция (значения y ) принимает все значения, кроме `0`.
1234-1-2-3-4-5-6-712345-1-2-3-4-5tf(t)Домен: Все `t ≠ -2`
Диапазон: Все `f(t) ≠ 0`
(c) `g(s)=sqrt(3-s)`
Ответ
Функция
`g(s)=sqrt(3-s)`
не определен на самом деле числа больше 3, что приведет к мнимым значениям за г ( с ).
Следовательно, домен для g ( s ) равен «все действительные числа, с ≤ 3″.
 2+ 4` для
`х > 2`
2+ 4` для
`х > 2`Ответ
Функция `f(x)` имеет домен из «все действительные числа, `x > 2`», как определено в вопросе. (Здесь нет результирующих квадратных корней из отрицательных чисел или деления на ноль.)
Чтобы найти диапазон :
- Когда `x = 2`, `f(2) = 8`
- Когда x увеличивается с `2`, `f(x)` становится больше `8` (Попробуйте подставить некоторые числа, чтобы понять почему.)
Следовательно, диапазон — «все действительные числа, `f(x) > 8`» x = 2`, и диапазон не включает f(2) = 8`.
123456510152025xf(x)(2, 8)Домен: Все `x>2`
Диапазон:
Все `f(x) > 8`Функция является частью параболы. [Подробнее о параболе.]
Упражнение 2
Дополнительные примеры областей и диапазонов
Если вы пропустили это ранее, вы можете увидеть больше примеров домена и диапазона в разделе Обратные тригонометрические функции.
См.
 также Калькулятор доменов и диапазонов.
также Калькулятор доменов и диапазонов.Мы запускаем мяч в воздух и находим высота h , в метрах, как функция времени t , в секундах, равно
ч = 20 т − 4,9 т 2
Найти домен и диапазон для функции ч ( т ).
Ответ
Как правило, отрицательные значения времени не имеют значение. Кроме того, нам нужно предположить, что снаряд ударяется о землю, а затем останавливается — он не уходит под землю.
Итак, нам нужно рассчитать, когда он упадет на землю. Это будет при ч = 0. Итак, решаем:
20 т − 4,9 т 2 = 0
Факторинг дает:
(20 − 4,9 т ) т = 0
Это верно, когда
`т = 0\»с»`,
или
`t=20/4.
 9 = 4,082 текста(ов)`
9 = 4,082 текста(ов)`Следовательно, домен функции h равен
«все настоящие значения t такие, что `0 ≤ t ≤ 4,082`»
Из выражения функции видно, что это парабола с вершиной вверх. (Это имеет смысл, если вы думаете о подбрасывании мяча вверх. Он поднимается на определенную высоту, а затем снова падает.)
Каково максимальное значение h ? Воспользуемся формулой максимума (или минимума) квадратичной функции.
Максимальное значение t , которое дает
`t = -b/(2a) = -20/(2 xx (-4,9)) = 2,041 с `
Максимальное значение
20(2,041) − 4,9(2,041) 2 = 20,408 м
Наблюдая за функцией ч , мы видим, что по мере увеличения t ч сначала увеличивается до максимума 20,408 м, то ч снова убывает до нуля, как и ожидалось.






 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.

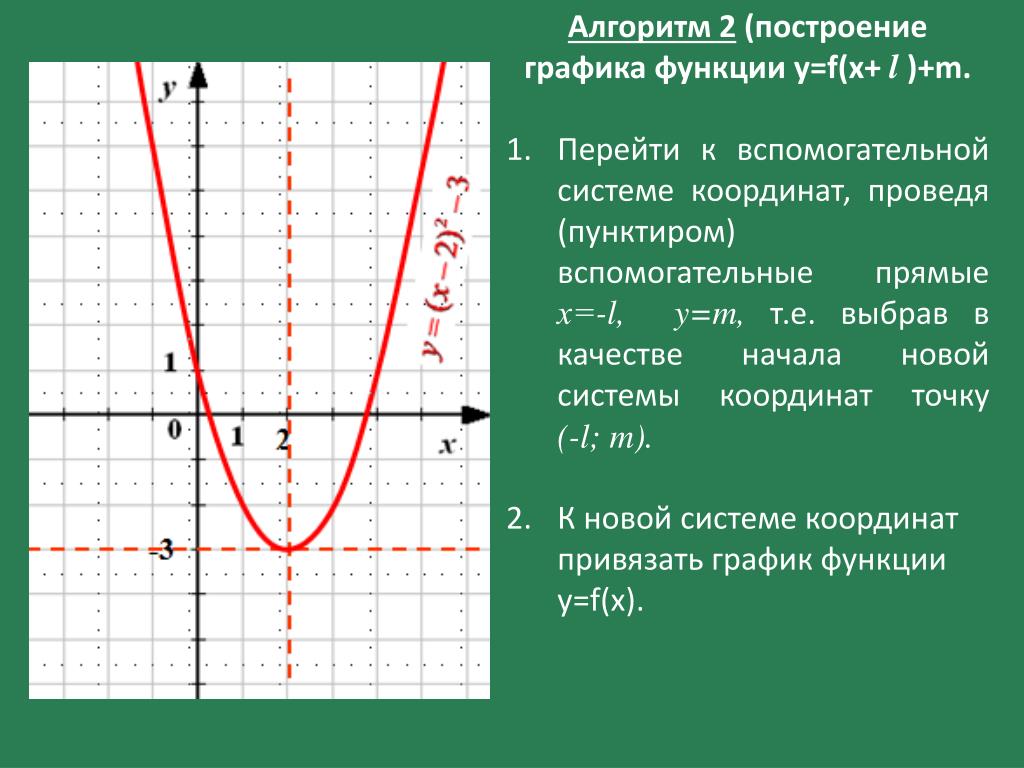 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.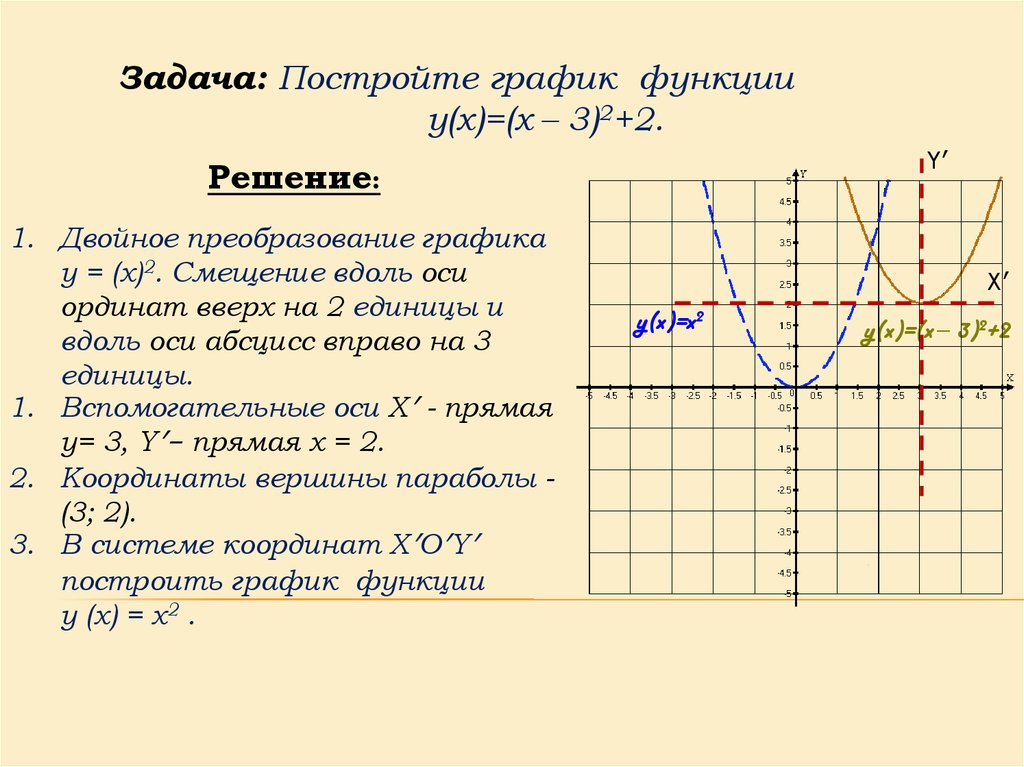
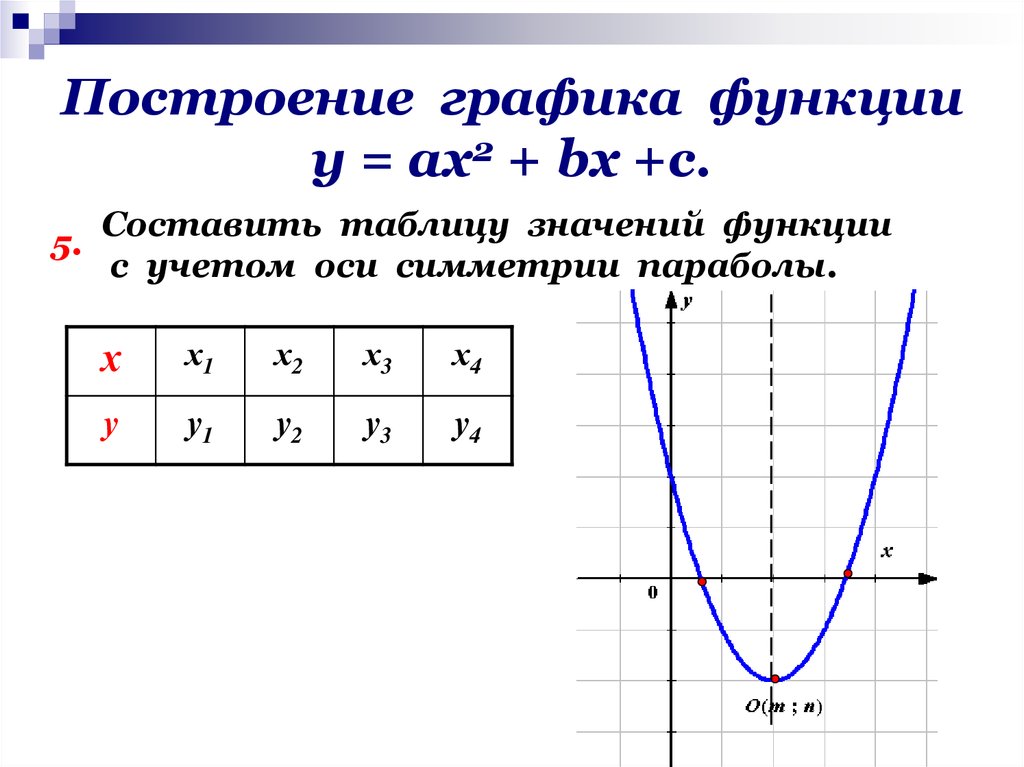 (Мы должны избегать 0 внизу дроби или отрицательных значений под знаком квадратного корня).
(Мы должны избегать 0 внизу дроби или отрицательных значений под знаком квадратного корня).

 2+ 4` для
`х > 2`
2+ 4` для
`х > 2` также Калькулятор доменов и диапазонов.
также Калькулятор доменов и диапазонов. 9 = 4,082 текста(ов)`
9 = 4,082 текста(ов)`
Ваш комментарий будет первым